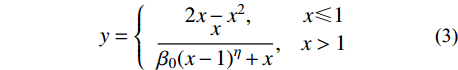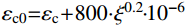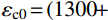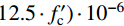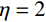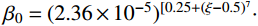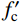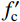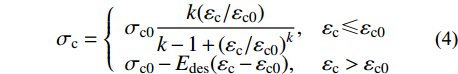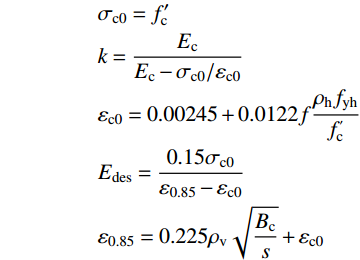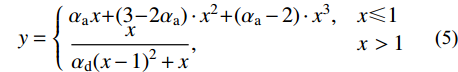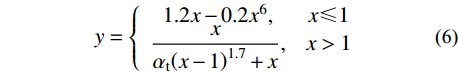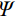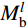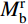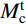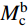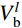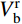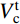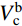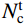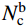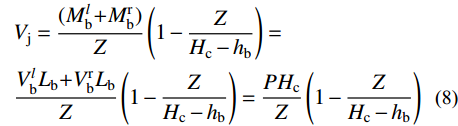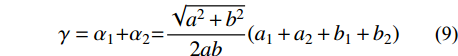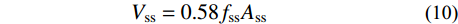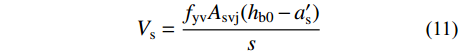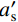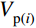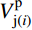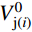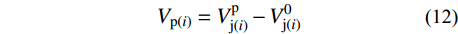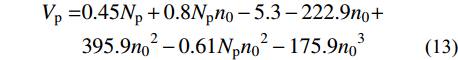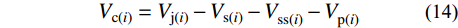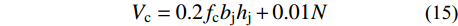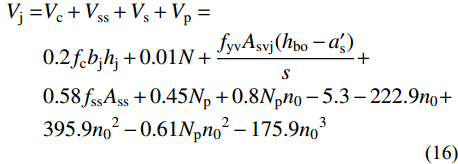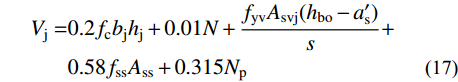SHEAR PERFORMANCE ANALYSIS ON COMPOSITE JOINTS CONNECTING PRESTRESSED STEEL REINFORCED CONCRETE BEAMS AND STEEL-TUBE REINFORCED CONCRETE COLUMNS
-
摘要: 基于ABAQUS平台,建立了预应力型钢混凝土梁-钢管混凝土叠合柱框架中节点精细化数值有限元模型,计算得到了柱顶水平荷载-位移滞回和单调加载曲线。在对比计算单调加载和实测滞回曲线基础上,研究了节点在柱顶水平荷载下的破坏全过程,细致考察了框架中节点的混凝土、型钢骨架、钢筋骨架以及预应力筋的应力状态,探讨了此类框架节点的破坏机理;基于参数分析结果,研究了轴压比、预应力度、核心区钢管配钢率和配箍率对节点柱顶水平荷载-位移曲线和核心区剪力-剪切变形的影响,提出了节点核心区受剪承载力计算公式。研究结果表明,当节点试件水平荷载达到峰值点时,核心区钢管、箍筋及预应力筋均达到屈服,核心区混凝土被压碎,此时可作为节点核心区抗剪承载力计算的标志;提出的节点核心区的抗剪承载力计算公式,可供工程设计参考。Abstract: Based on ABAQUS platform, a refined numerical finite element model of joints in prestressed steel reinforced concrete beam-concrete filled steel tubular composite column frame was established, and the lateral hysteretic and monotonic load-displacement curves at the column top were calculated. On the basis of the comparison of the calculated monotonic and the measured hysteresis curves, the failure process of the joints under lateral loading at the column top was studied, and the stress for concrete, steel skeleton, steel bars and prestressing tendons were carefully investigated, in which the failure mechanism was discussed. Otherwise, the influences of axial compression ratio, prestressing level, steel tube ratio and stirrup ratio in the panel zone on the lateral load-displacement curve at column top and shear-shear deformation in the panel zone were studied according to the results of parameter analysis. Finally, the formulas for calculating the shear capacity in the panel zone of the joint were proposed. The results showed that the steel-tube, stirrups and prestressed tendons reached the yield and the concrete crushed in the panel zone when the lateral load reached the peak value, which could be deemed as the sign for calculating the shear capacity. The presented formula for calculating the shear capacity could be used for a reference in engineering design.
-
预应力型钢混凝土结构能充分满足现代建筑对大跨度及抗震的需求,得到了广泛的研究与应用[1-2]。但预应力型钢混凝土梁内预应力筋和纵筋在通过框架节点时,可能会贯穿柱内型钢、削弱节点承载力,同时施工工艺也较为复杂。为此,本课题组基于相关研究提出采用钢管混凝土叠合柱替代普通型钢混凝土柱,构成了一种新型的预应力型钢混凝土框架结构[3-6]。采用钢管混凝土叠合柱后,预应力型钢混凝土结构的框架柱施工得以简化,框架梁内的预应力筋和纵筋可方便从钢管两侧穿越节点,保证了节点内钢管的连续性。
鉴于钢管混凝土叠合柱优良的受力性能[7-12],近年来较多学者对采用钢管混凝土叠合柱的框架节点开展了较多的研究。廖飞宇等[13]建立了可用于钢管混凝土叠合柱-钢梁节点全过程受力分析的有限元模型,明晰了节点的工作机理;钱炜武等[14-15]建立了带楼板的钢管混凝土叠合柱-钢梁节点数值模型,指出节点核心区剪力由管内混凝土、钢管壁、管外混凝土、箍筋和钢梁腹板共同承担;聂建国等[16]开展试验和有限元分析,指出采用外加强环连接的钢筋混凝土梁-钢管混凝土叠合柱节点具有良好的抗震性能,能保证节点发生梁端弯曲破坏;赵剑等[17]建立了钢管混凝土叠合柱-钢筋混凝土梁节点的有限元模型,较好地模拟了节点的滞回性能。此外,邓志恒等[18]研究结果表明钢管混凝土叠合柱-预应力混凝土梁框架节点的钢管在核心区能够有效地约束核心区混凝土,节点核心区斜裂缝发展较为缓慢。
目前,对于施加预应力的型钢混凝土梁-钢管混凝土叠合柱框架节点的设计方法鲜见报道。为此,本文拟结合试验结果,采用有限元程序ABAQUS建立预应力型钢混凝土梁-钢管混凝土叠合柱组合框架节点有限元分析模型,进一步研究节点的破坏过程和受力机理,建立预应力型钢混凝土梁-钢管混凝土叠合柱节点核心区受剪承载力计算公式,为此类框架节点的设计提供一定的参考依据。
1 数值模型的建立
1.1 材料本构关系
1.1.1 混凝土
混凝土采用ABAQUS提供的塑性损伤模型(Concrete Damaged Plastic Model),并通过腾智明和邹离湘[19]提出的“焦点法”来定义混凝土在单轴反复拉压下的加、卸载准则。依据“焦点法”加、卸载准则,单轴受力情况下混凝土受压和受拉损伤指标dc和dt分别按式(1)和式(2)计算。
dc=1−σc+ncσc0Ec(ncσc0/Ec+εc),dc⩾ (1) {d_{\rm{t}}} = 1 - \frac{{\sigma {}_{\rm{t}} + {n_{\rm{t}}}{\sigma _{{\rm{t0}}}}}}{{{E_{\rm{t}}}({n_{\rm{t}}}{\sigma _{{\rm{t0}}}}/{E_{\rm{c}}} + {\varepsilon _{\rm{t}}})}},\;\;\;{\rm{ }}{d_{\rm{t}}} \geqslant 0\;\; (2) 式中:σc和σt分别为混凝土受压和受拉应力;σc0和σt0分别为混凝土峰值受压和受拉应力;nc和nt分别为混凝土受压和受拉损伤指标系数;Ec为混凝土弹性模量。
由于钢管和箍筋对混凝土的约束程度存在较大差异,因而对梁柱截面内各部位的混凝土采用不同的单轴受压本构关系。
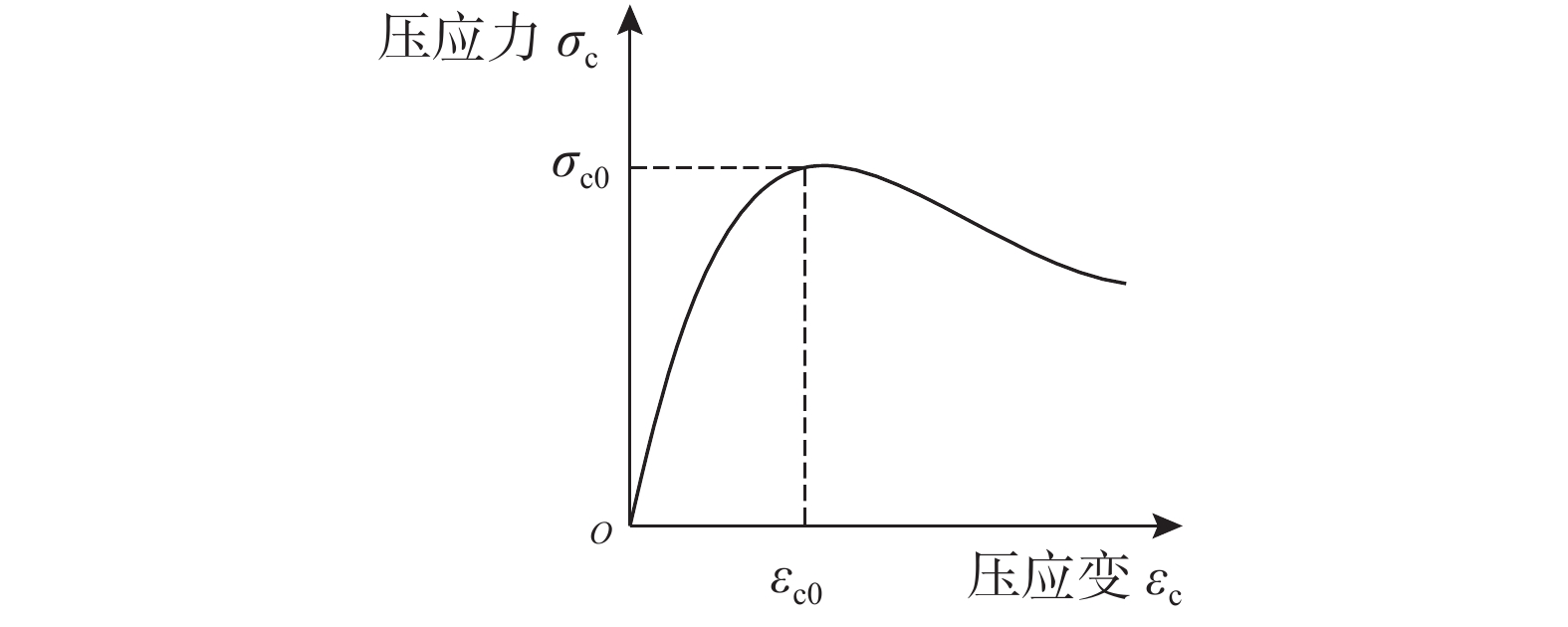
对于钢管内混凝土,采用韩林海[20]提出的适用于ABAQUS分析的钢管约束混凝土受压应力-应变(σc-εc)本构关系,如图1所示。其函数表达式详见式(3)。
y = \left\{ {\begin{array}{*{20}{c}} {2x - {x^2}},&{x \leqslant 1} \\ {\dfrac{x}{{{\beta _0}{{(x - 1)}^\eta } + x}}},&{x > 1} \end{array}} \right. (3) 式中:
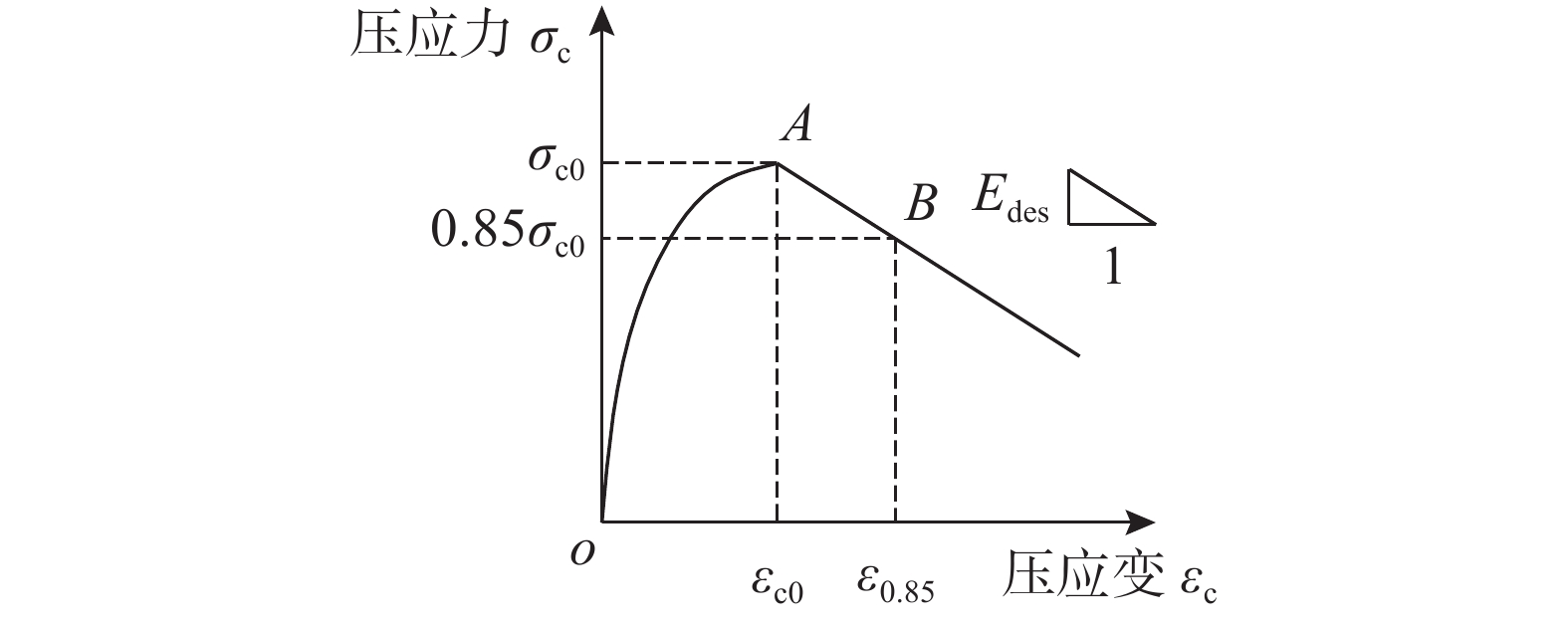
{\sigma _{{\rm{c0}}}} \!\!=\!\! f_{\rm{c}}^{\prime } ;{\varepsilon _{{\rm{c}}0}}\!\! =\!\! {\varepsilon _{\rm{c}}} \!+\! 800 \!\cdot\! {\xi ^{0.2}} \!\!\cdot \!\!{10^{ - 6}} ;{\varepsilon _{{\rm{c0}}}}\! =\! (1300 \!+ 12.5 \cdot f_{\rm{c}}') \cdot {10^{ - 6}} ;\eta = 2 ;{\beta _0} = (2.36 \times {10^{ - 5}})^{[0.25 + {(\xi - 0.5)^7} }\cdot {(f_{\rm{c}}')^{0.5}} \cdot 0.5 \geqslant 0.12 。x=εc/εc0,y=σc/σc0;σc0和εc0分别为峰值应力及相应的应变;{f_{\rm {c}}^{\prime }} 为混凝土圆柱体抗压强度,取{f_{\rm {c}}^{\prime }} =0.8fcu,fcu为混凝土立方体抗压强度;ξ为钢管约束效应系数。梁、柱箍筋约束下的受压混凝土模型采用An和Han[21]提出的箍筋约束受压应力-应变(σc-εc)关系,如图2所示,函数表达式见式(4)。
{\sigma _{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {{\sigma _{{\rm{c}}0}}\dfrac{{k({\varepsilon _{\rm{c}}}/{\varepsilon _{{\rm{c}}0}})}}{{k - 1 + {{({\varepsilon _{\rm{c}}}/{\varepsilon _{{\rm{c0}}}})}^k}}}},&{{\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{{\rm{c}}0}}} \\ {{\sigma _{{\rm{c}}0}} - {E_{{\rm{des}}}}({\varepsilon _{\rm{c}}} - {\varepsilon _{{\rm{c}}0}})},&{{\varepsilon _{\rm{c}}} > {\varepsilon _{{\rm{c}}0}}} \end{array}} \right. (4) 式中:ρh为体积配箍率;fyh为箍筋屈服强度;s为箍筋间距;Bc为箍筋约束下混凝土的截面宽度。
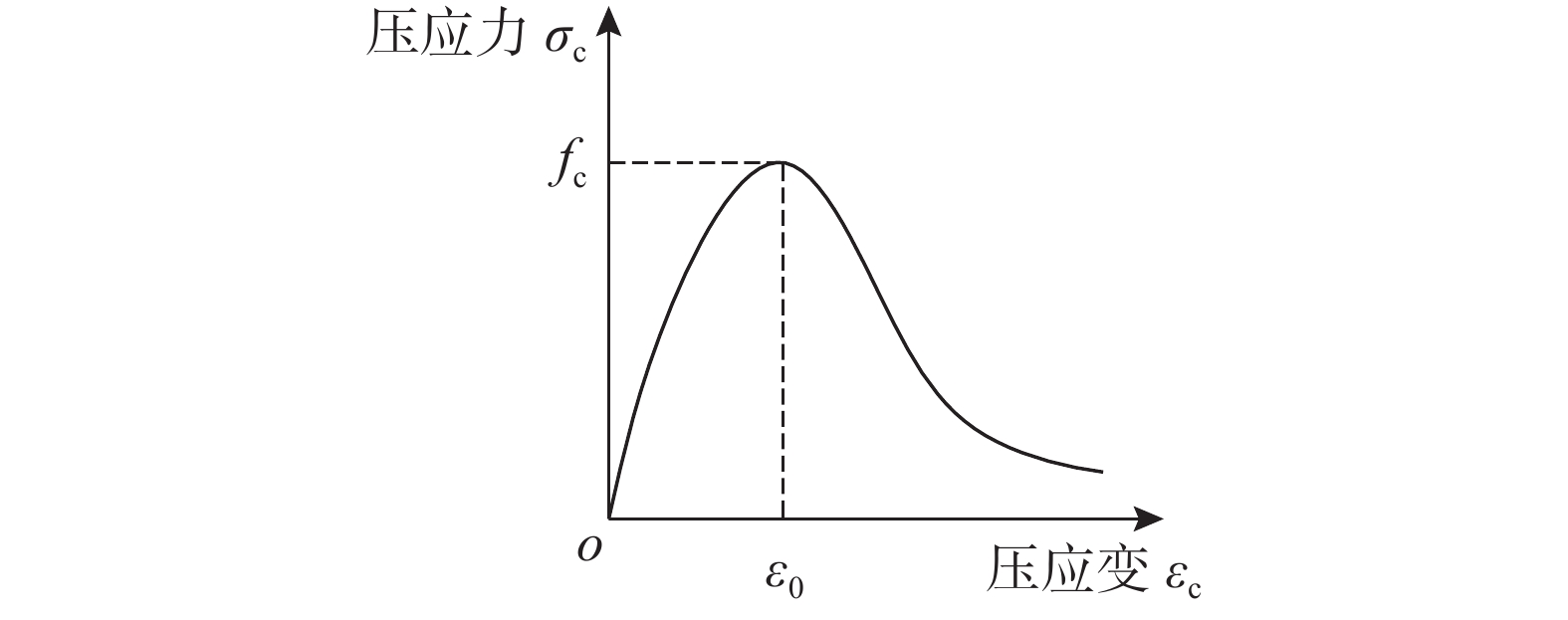
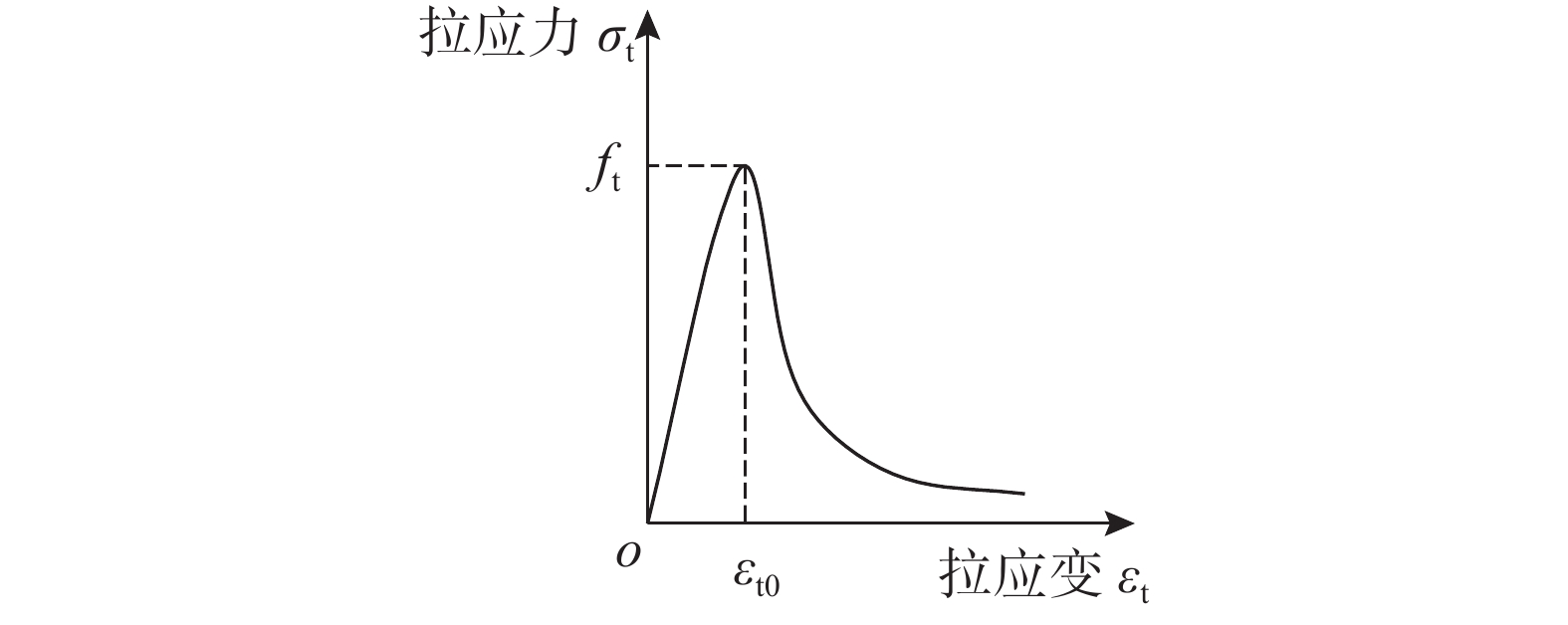
\begin{split}&{\sigma _{{\rm{c}}0}} = f_{\rm{c}}^{\prime}\\ &k = \frac{{{E_{\rm{c}}}}}{{{E_{\rm{c}}} - {\sigma _{{\rm{c}}0}}/{\varepsilon _{{\rm{c}}0}}}}\\ &{\varepsilon _{{\rm{c}}0}} = 0.00245 + 0.0122f\frac{{{\rho _{\rm{h}}}{f_{{\rm{yh}}}}}}{{f_{\rm{c}}^{\rm{'}}}}\\ &{E_{{\rm{des}}}} = \frac{{0.15{\sigma _{{\rm{c}}0}}}}{{{\varepsilon _{0.85}} - {\varepsilon _{{\rm{c}}0}}}}\\ &{\varepsilon _{0.85}} = 0.225{\rho _{\rm{v}}}\sqrt {\frac{{{B_{\rm{c}}}}}{s}} + {\varepsilon _{{\rm{c}}0}} \end{split} 梁柱截面混凝土保护层受压以及所有混凝土受拉应力-应变关系均采用《混凝土结构设计规范》(GB 50010−2010)建议的受压和受拉本构模型[22]。混凝土单轴受压应力-应变(σc-εc)关系如图3所示,其关系式见式(5)。混凝土单轴受拉时应力-应变(σt-εt)关系见图4,表达式见式(6)。
y = \left\{ \!\!{\begin{array}{*{20}{l}} {{\alpha _{\rm{a}}}x \!+\! (3\! - \!2{\alpha _{\rm{a}}}) \cdot {x^2}\! +\! ({\alpha _{\rm{a}}} - 2) \cdot {x^3}},&{x \leqslant 1} \\ {\dfrac{x}{{{\alpha _{\rm{d}}}{{\left( {x - 1} \right)}^2} + x}}},&{x\, > {\rm{1}}} \end{array}} \right. (5) 式中:x=εc/ε0,y=σc/fc,fc为混凝土单轴抗压强度,可取fc=0.76fcu;ε0为与fc相应的混凝土压应变;αa、αd分别为单轴受压应力-应变曲线上升段、下降段的参数值。
y = \left\{ {\begin{array}{*{20}{c}} {1.2x - 0.2{x^6}},\quad&{x \leqslant {\rm{1}}} \\ {\dfrac{x}{{{\alpha _{\rm{t}}}{{\left( {x - 1} \right)}^{1.7}} + x}}},&{x > {\rm{1}}} \end{array}} \right. (6) 式中:x=εt/εt0,y=σt/ft,ft为混凝土的单轴抗拉强度,ft=0.395(fcu)0.55;εt0为与ft相应的混凝土峰值拉应变;αt为单轴受拉下降段参数值。
混凝土受压和受拉损伤指标系数nc和nt的建议取值如下:对于钢管约束下的混凝土,nc=2,nt=1;对于箍筋约束下的混凝土,nc=1.2,nt=1;对于保护层混凝土,nc=1,nt=1。
混凝土的膨胀角
\varPsi 取36°,流动势偏量值ζ取0.1,初始的双轴抗压屈服强度与单轴抗压屈服强度之比σb0/σc0取1.16,拉伸子午面上和压缩子午面上的第二应力不变量之比Kc取0.6667,粘性系数μ 取0.0015。刚度恢复系数ωt和ωc分别取为0和0.7。1.1.2 钢管、工字钢、纵筋及箍筋
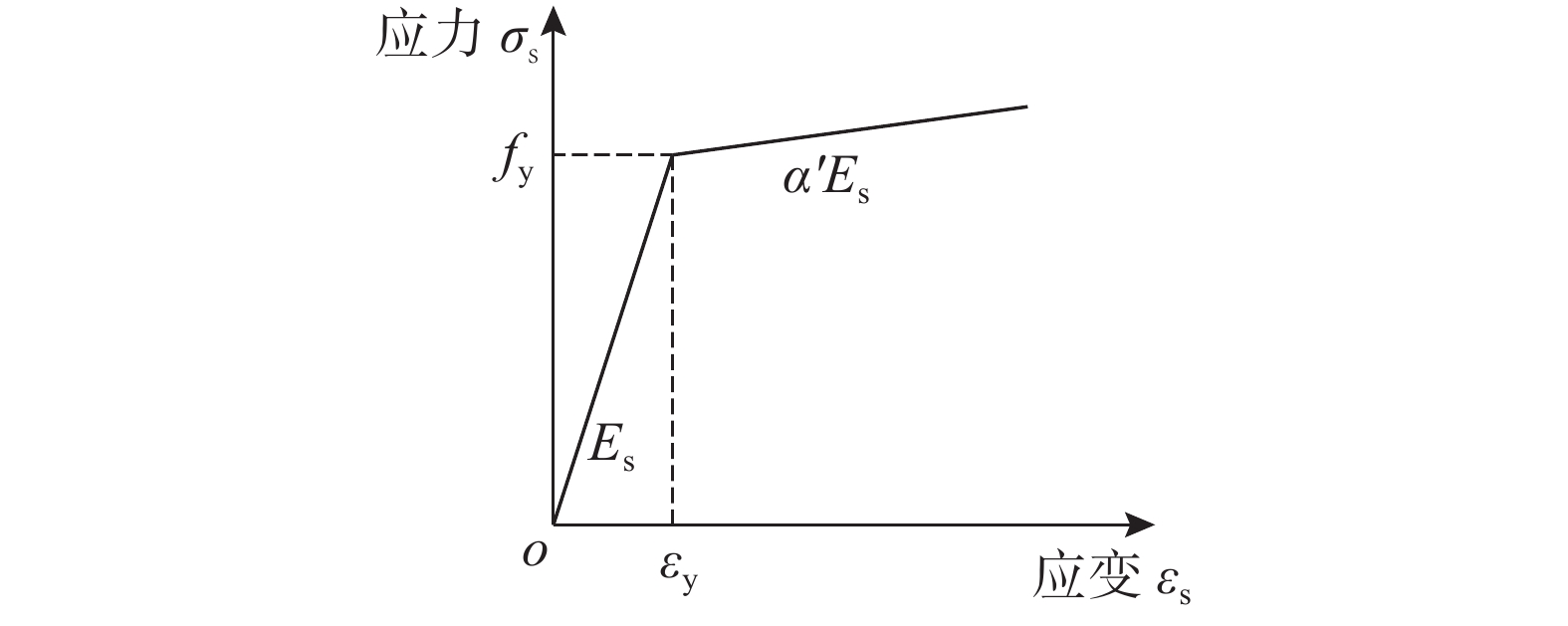
梁柱内钢管、工字钢、纵筋和箍筋等钢材的本构关系均采用随动强化模型,并定义Back-Stresses来模拟钢材在往复荷载下的Bauschinger效应,对应的应力-应变关系如图5所示,图5中Es为钢材初始弹性模量;fy和εy分别为钢材屈服强度和屈服应变;钢材强化段刚度(α'Es)取为0.01Es。
1.1.3 预应力筋
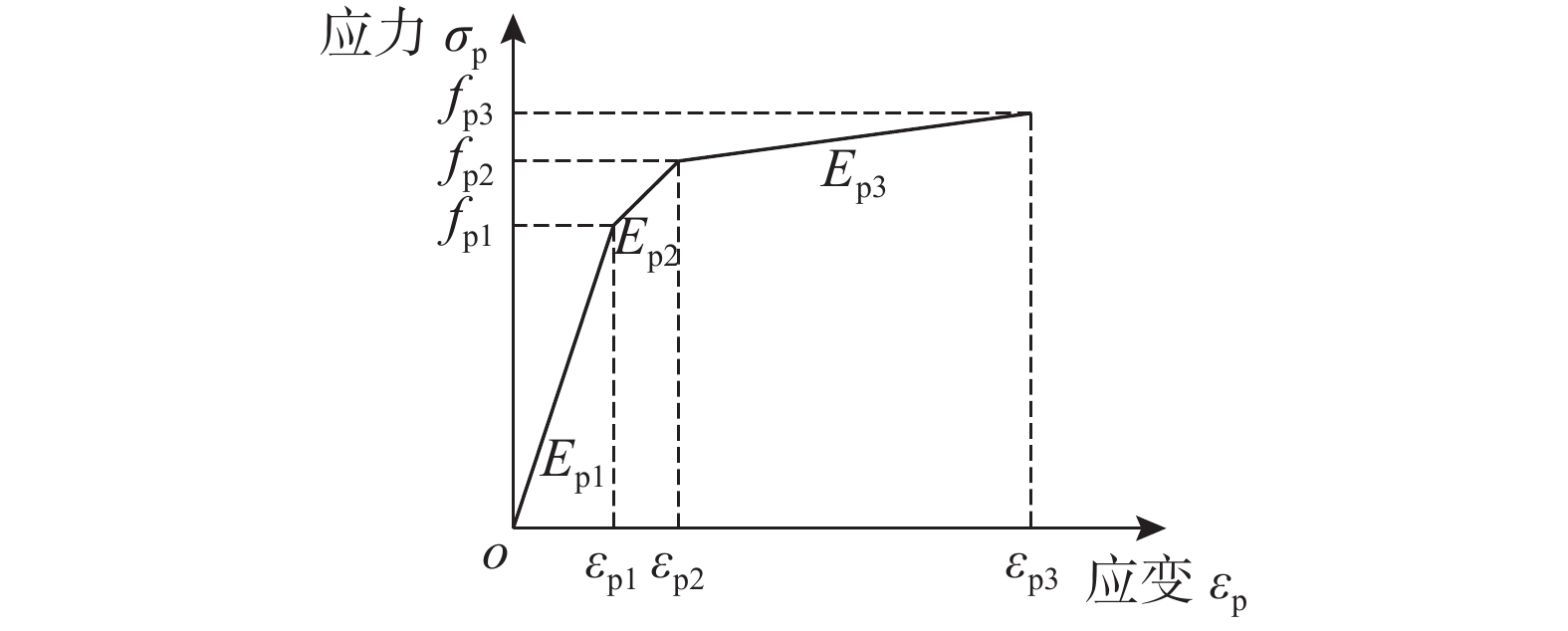
预应力筋的本构关系采用三折线模型[23]。如图6所示。图6中Ep1为比例阶段的弹性刚度;Ep2为非比例阶段的弹性刚度;Ep3为条件屈服后的屈服刚度;fp1、εp1分别为预应力筋在比例极限点处的应力和应变;fp2、εp2分别为预应力筋在屈服点处的应力和应变;fp3、εp3分别为预应力筋在极限点处的应力和应变。相关参数取值见表1。
表 1 预应力筋的参数Table 1. Parameters of prestressing tendons比例极限应变εp1(%) 屈服应变εp2(%) 极限应变εp3(%) 比例极限应力fp1 屈服应力fp2 0.65 0.93 5.2 0.78 fp3 0.87 fp3 1.2 单元类型与接触
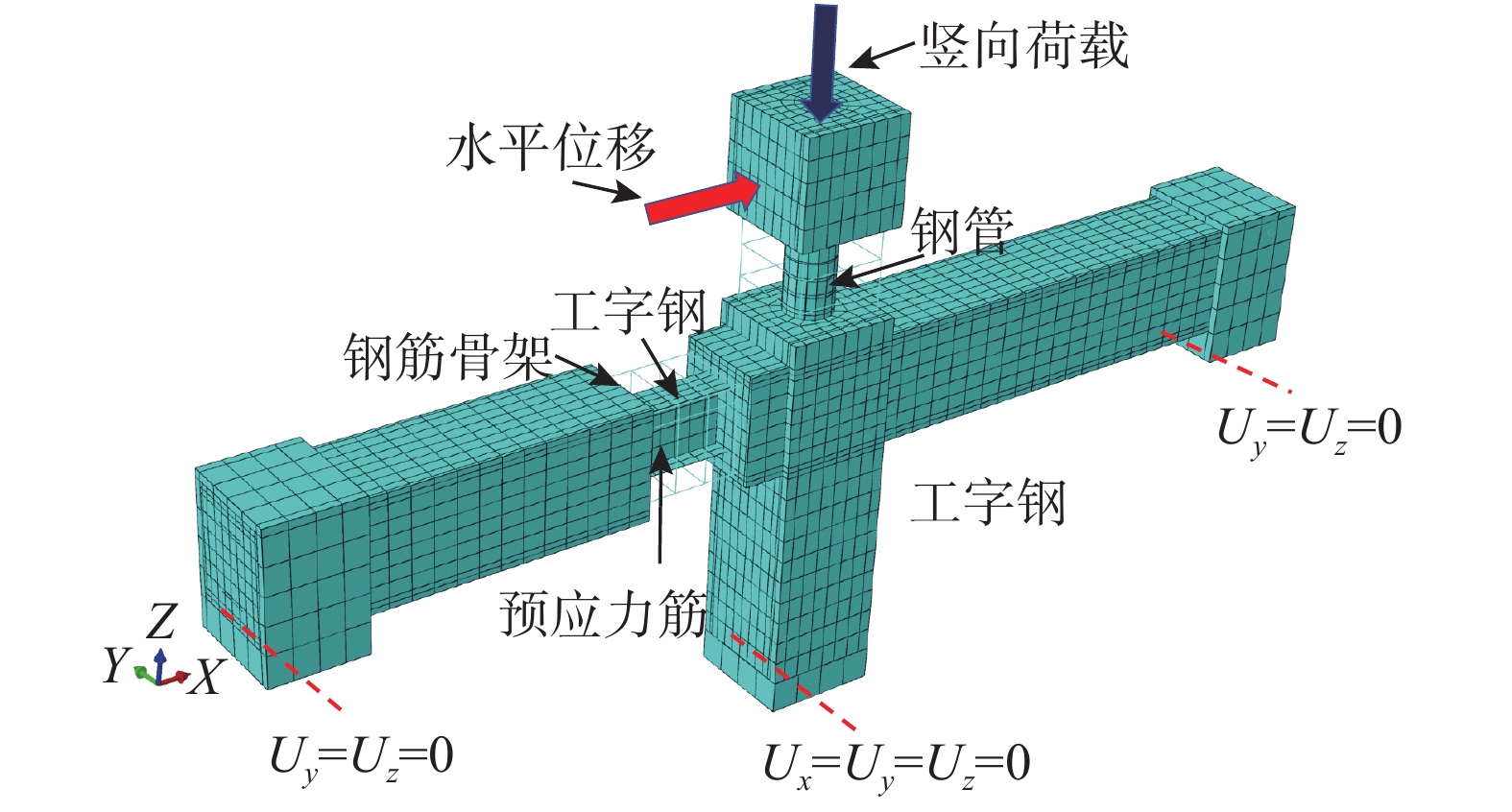
有限元模型如图7所示。混凝土采用8节点缩减积分三维实体单元C3D8R;钢管和工字钢采用4节点缩减积分壳单元S4R;纵筋、箍筋和预应力筋均采用2节点三维桁架单元T3D2。
模型建立过程中仅考虑了钢管与其内外混凝土之间的接触。在法线方向使用“硬接触”,默认钢管与混凝土在垂直方向的压力可以传递但不能相互穿透;在切线方向,混凝土与钢管之间的摩擦服从库伦摩擦准则[24-25]。此外,模型中未考虑纵筋、箍筋以及H型钢与混凝土的粘结滑移,通过Embed技术将其埋入混凝土中,预应力采用降温法施加。
2 试验验证
2.1 试验概况
在前期工作中[26],完成了3个预应力型钢混凝土梁-钢管混凝土叠合柱框架中节点试件SJ-1、SJ-2和SJ-3在水平低周往复荷载作用下的滞回性能试验,节点试件尺寸如图8所示。节点试件混凝土强度等级均为C40;钢筋强度等级均为HRB400;预应力筋采用1670级
2.2 计算结果
采用前述ABAQUS建立的预应力型钢混凝土梁-钢管混凝土叠合柱节点数值模型,分别计算了三个节点试件在水平荷载下的荷载-位移(P-Δ)滞回曲线和单调加载曲线,并与试验结果进行对比。
2.2.1 滞回计算
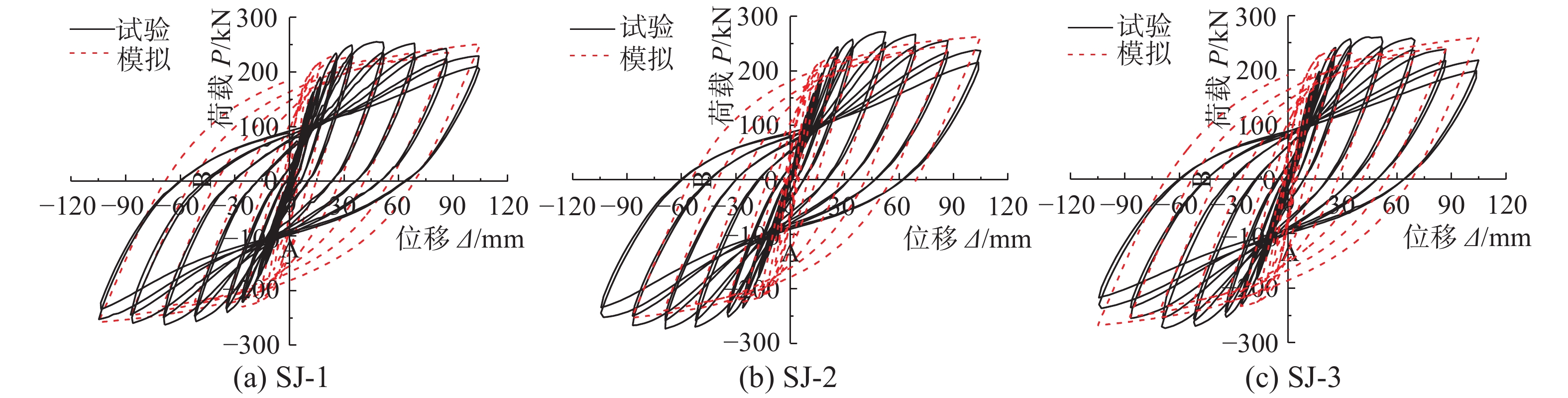
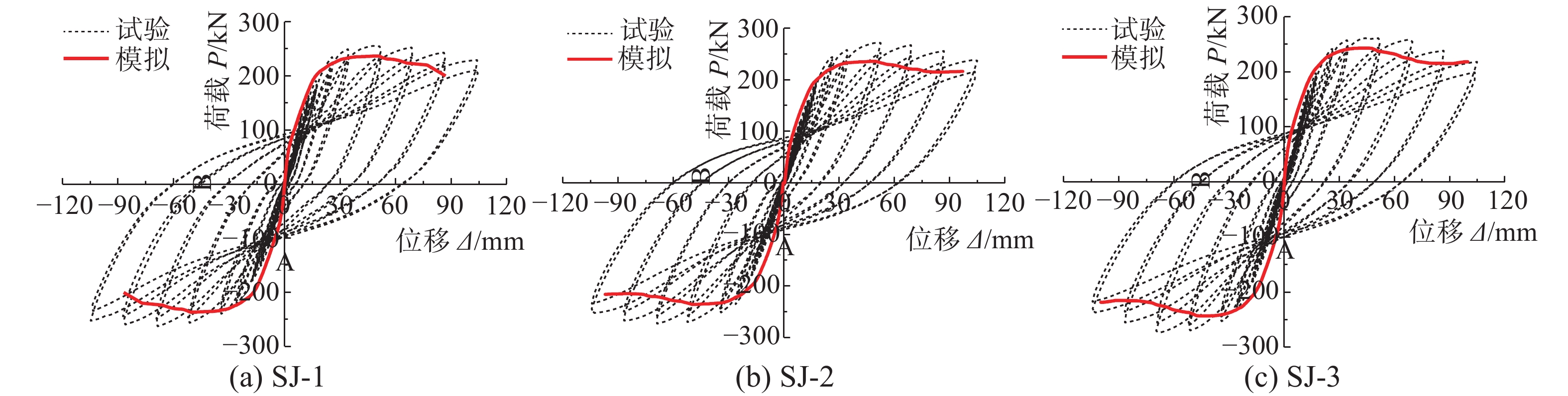
图10给出了计算与试验滞回曲线的对比。可以看出:1)计算滞回曲线卸载刚度与试验结果较为接近,而反向再加载刚度偏大,反向加载曲线均通过了屈服点,但卸载后并未直接指向反向卸载点,计算结果相对于试验曲线过于饱满;2)计算滞回曲线的外包线未出现明显的下降段;3)计算峰值荷载与试验值较为接近,分别相差9.0%、8.8%和7.3%。造成前述计算滞回曲线反向再加载刚度偏大、过于饱满、且未出现明显下降段的原因可能是混凝土开裂后裂缝重新闭合的过程,无法通过混凝土塑性损伤模型中的刚度恢复系数ωt和ωc准确考虑造成的缘故。
2.2.2 单调加载计算
图11为计算单调加载下柱顶水平荷载-位移曲线与实测滞回曲线的对比,计算时采用位移加载,以加载至水平荷载下降至峰值荷载的85%左右或接近加载位移停止。从图11中可以看出:1) 3个节点试件的计算峰值荷载与试验值较为接近,分别相差约7.45%、14.76%、8.26%;2)计算单调加载曲线在达到峰值荷载后具有下降段,且下降趋势与试验结果较为一致,能较好地反映组合框架节点在水平荷载作用的力学性能。此外,部分单调加载曲线出现了荷载降低、再些微上升的现象,其原因可能是混凝土压碎后,程序仍默认其具有一定的承载力,而钢筋屈服后强度仍继续增加。
3 受力全过程分析
由于计算所得单调加载下柱顶水平荷载-位移曲线能较好地反映框架节点试件在峰值荷载后的强度退化性能,据此本文将基于单调加载下的有限元计算结果对预应力型钢混凝土梁-钢管混凝土叠合柱组合框架节点试件在柱顶水平荷载下的受力全过程开展细致的分析。
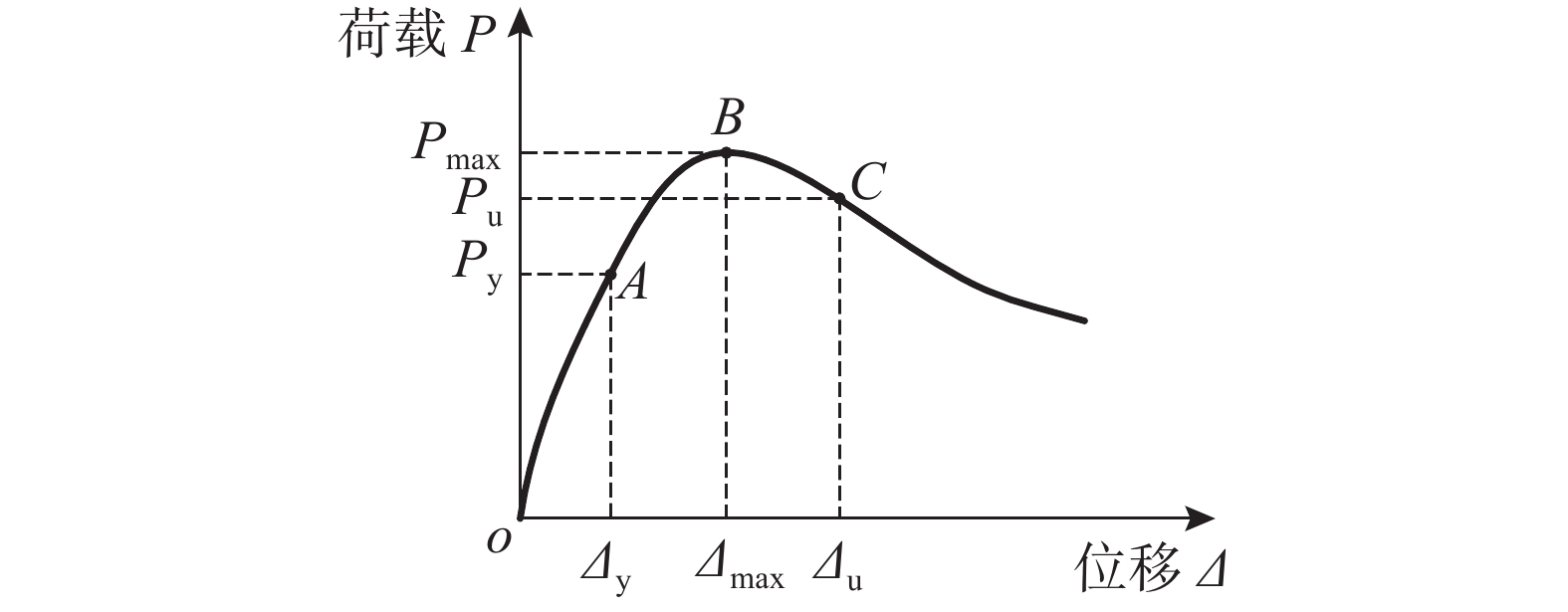
图12为典型的单调加载水平荷载-位移曲线,图12中A为屈服点,B为峰值荷载点,C为破坏点。Py和Δy为屈服荷载及相应的位移;Pmax和Δmax为峰值荷载及相应的位移;Pu和Δu分别为节点破坏时的极限荷载及相应的位移,这里取Pu=0.85Pmax。
本文将以试件SJ-2为例,通过考察单调加载柱顶水平荷载-位移曲线上的屈服点、峰值点、破坏点对应的混凝土、型钢骨架、钢筋和预应力筋的应力,对框架节点的受力全过程进行细致分析,探究其工作机理。
3.1 混凝土
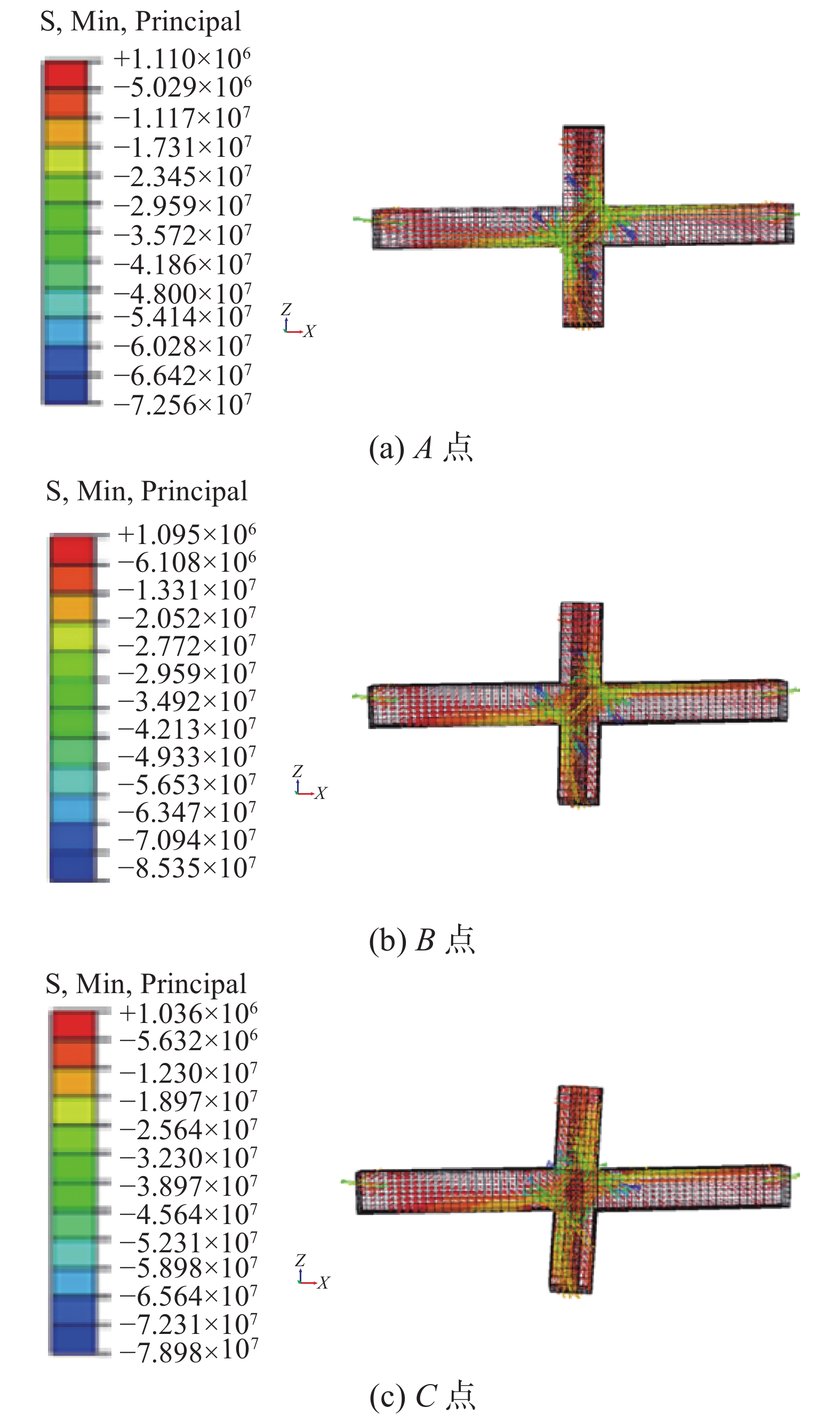
图13给出了框架节点核心区混凝土在不同时刻下的主压应力分布。可以看出:A点时,核心区混凝土已初步形成斜压杆,与柱相连的左梁下端和右梁上端处的主压应力均相对较大;达到B点时,混凝土斜压杆的压应力增大,此时梁端和核心区混凝土均已被压碎;到C点时,由于混凝土超过峰值应变,核心区的主压应力值相较于峰值点有一定程度的降低。
3.2 型钢骨架
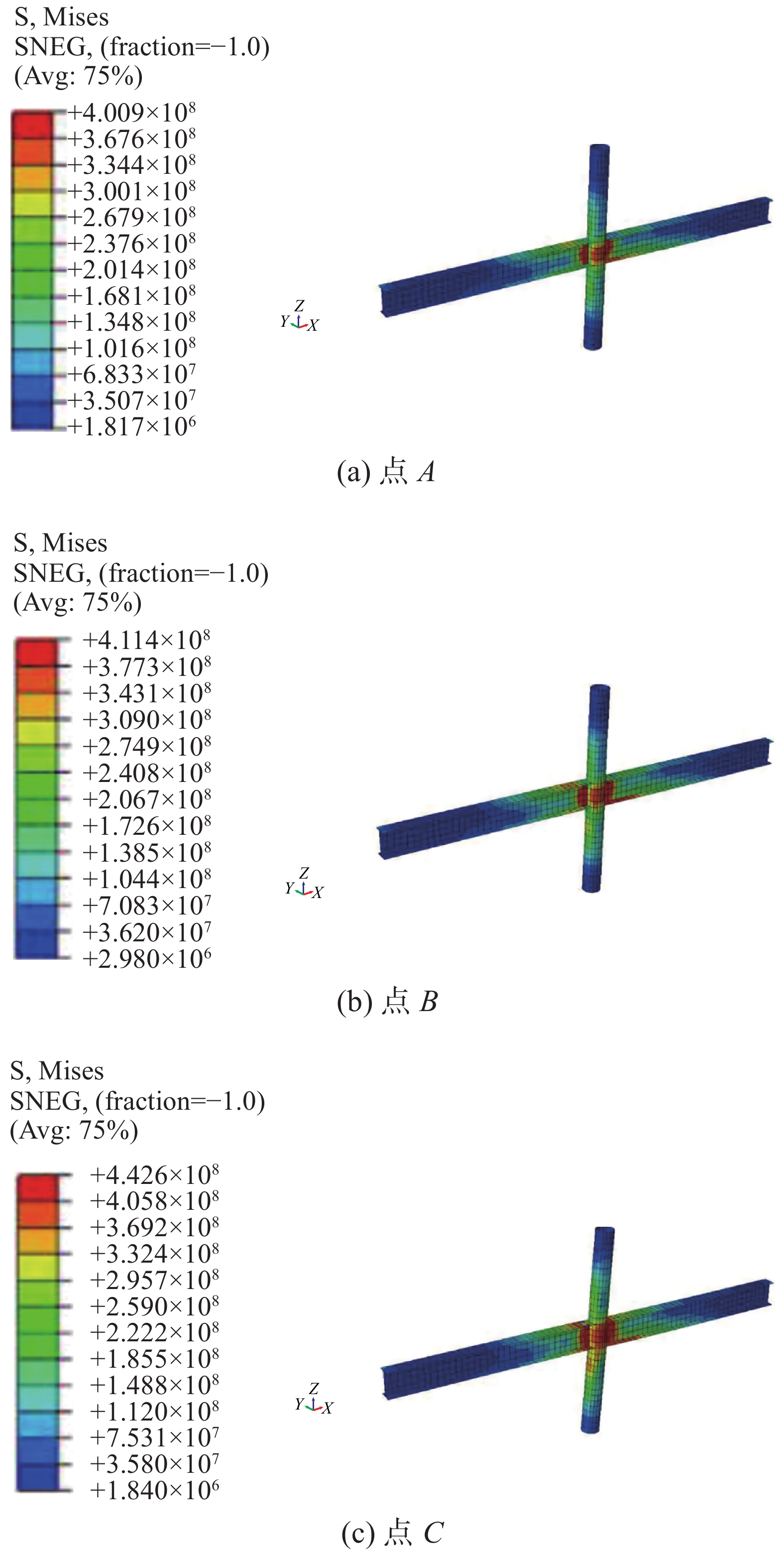
图14给出了节点试件内部型钢骨架(钢管和钢梁)在各特征点处的Mises应力分布。在A点时,核心区钢管已几乎完全屈服,钢梁端部上、下翼缘也出现了一定程度的屈服,同时还可发现与钢管相连的部分钢梁腹板也已接近屈服;在B点时,核心区范围内钢管和钢梁腹板已完全屈服,节点核心区承载力达到最大值,表明达到峰值荷载时,核心区范围内钢梁腹板可承担一定的水平剪力;达到C点时,核心区范围内的工字钢腹板和翼缘的屈服范围进一步所扩大,同时,Mises应力略有增加。
3.3 钢筋骨架与预应力筋
图15给出了梁柱内钢筋骨架及预应力筋的Mises应力在加载过程中的变化情况。A点时,核心区箍筋和预应力筋均已经达到屈服,但梁、柱端的纵筋和箍筋未屈服;B点时,梁端及柱端纵筋应力继续增加,预应力筋屈服范围增大;C点时,梁端的纵筋和箍筋均达到屈服,由于核心区和梁端部混凝土被压碎,而预应力筋的最大应力略有降低。
综上分析可知,当节点试件水平荷载达到峰值点时,核心区钢管、箍筋及预应力筋均达到了屈服,核心区混凝土也被压碎,此时可作为节点核心区抗剪承载力计算的标志。
4 节点受剪承载力分析
4.1 节点核心区剪力与剪切变形
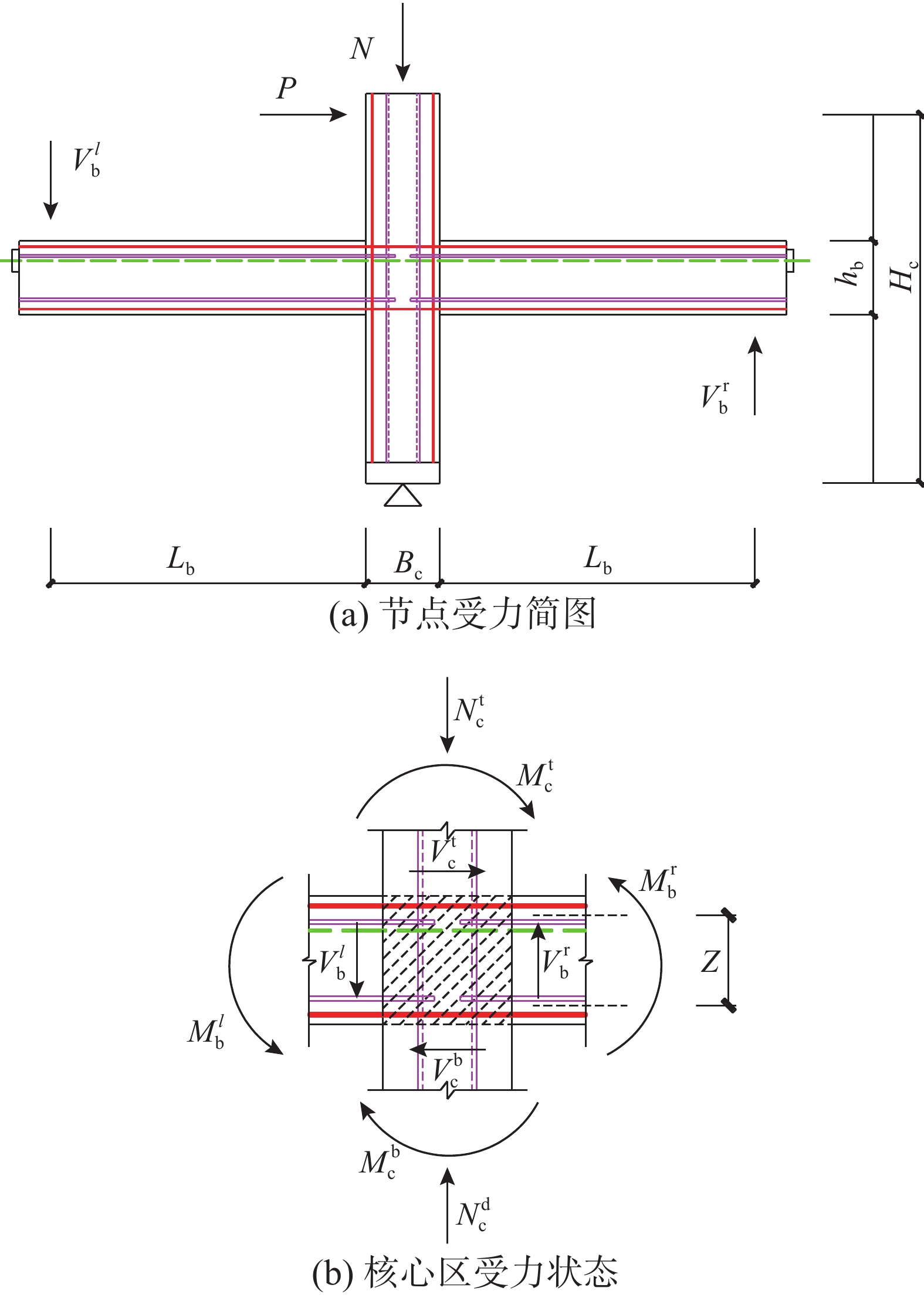
图16为节点核心区剪力计算示意图。由于试验采用自平衡装置施加柱顶轴力,未考虑二阶效应的影响,有限元模型与其一致,因此根据图16(a)可得到力矩平衡方程式(7),将式(7)代入式(8),通过采集有限元模型节点的柱顶水平荷载P,即可求得节点核心区剪力Vj。图16(a) 和图16(b)中,
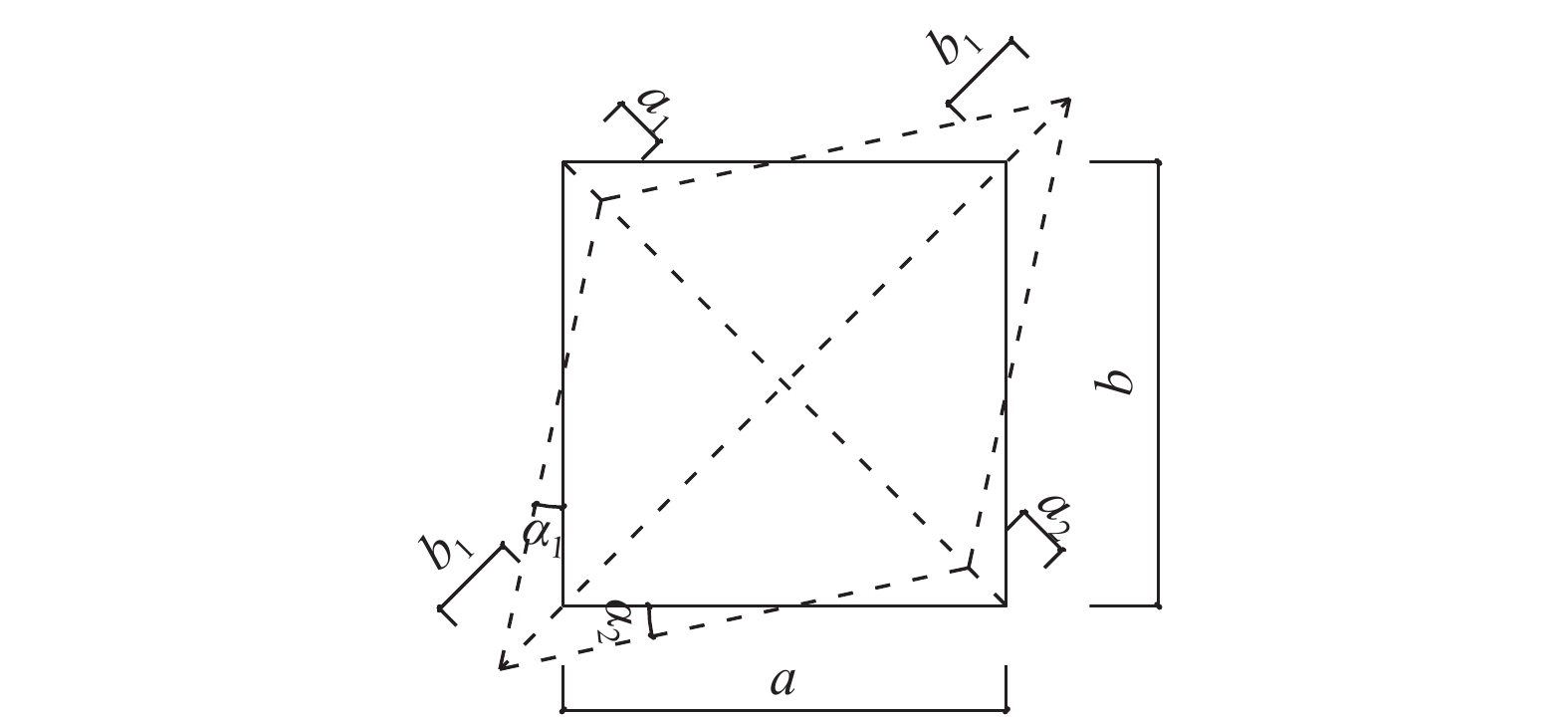
M_{\rm{b}}^l 、M_{\rm{b}}^{\rm{r }} 分别为左、右梁端弯矩;M_{\rm{c}}^{\rm{t }} 、M_{\rm{c}}^{\rm{b }} 分别为左、右梁端弯矩;V_{\rm{b}}^l 、V_{\rm{b}}^{\rm{r }} 分别为左、右梁端剪力;V_{\rm{c}}^{\rm{t }} 、V_{\rm{c}}^{\rm{b}} 分别为上、下柱端剪力;N_{\rm{c}}^{\rm{t }} 、N_{\rm{c}}^{\rm{b}} 分别为上、下柱端轴力;Hc为上、下柱反弯点间的高度,取柱底铰接点到柱顶加载点之间的距离;Z为梁端截面拉、压合力点之间的距离,可取梁上部钢筋和型钢上翼缘合力点至梁下部钢筋和型钢下翼缘合力点之间的距离;hb为梁截面高度。V_{\rm{b}}^l{L_{\rm{b}}}{\rm{ + }}V_{\rm{b}}^{\rm{r}}{L_{\rm{b}}} = P{H_{\rm{c}}}\qquad\quad\qquad\qquad\quad\quad\quad\quad\quad (7) \begin{split}& {V_{\rm{j}}} = \frac{{( {M_{\rm{b}}^l{\rm{ + }}M_{\rm{b}}^{\rm{r}}} )}}{Z}\left(1 - \frac{Z}{{{H_{\rm{c}}} - {h_{\rm{b}}}}}\right) = \\&\frac{{V_{\rm{b}}^l{L_{\rm{b}}}{\rm{ + }}V_{\rm{b}}^{\rm{r}}{L_{\rm{b}}}}}{Z}\left(1 - \frac{Z}{{{H_{\rm{c}}} - {h_{\rm{b}}}}}\right) = \frac{{P{H_{\rm{c}}}}}{Z}\left(1 - \frac{Z}{{{H_{\rm{c}}} - {h_{\rm{b}}}}}\right) \end{split} (8) 在水平位移的加载下,核心区将由矩形转变为菱形,如图17所示。通过采集有限元模型核心区对角线方向上的变形量,可按式(9)计算核心区的剪切变形。
\gamma = {\alpha _{\rm{1}}}{\rm{ + }}{\alpha _{\rm{2}}}{\rm{ = }}\frac{{\sqrt {{a^2} + {b^2}} }}{{2ab}}({a_1} + {a_2} + {b_1} + {b_2}) (9) 式中:γ为试件核心区的剪切角;α1、α2分别为变形后的菱形边与原矩形边的夹角;a1、a2、b1、b2分别为核心区对角线上的缩短和伸长量。
4.2 参数分析
为研究预应力型钢混凝土梁-钢管混凝土叠合柱框架节点核心区的受剪承载力,本文建立了不同轴压比n0、预应力度λ、钢管配钢率ρss和核心区配箍率ρsv下的有限元分析模型,考察了不同参数对节点核心区受剪承载力的影响,提出了此类组合框架节点核心区的受剪承载力计算公式。表2列出了分析参数的变化范围,表中备注分别对应于采用的预应力筋、钢管截面、核心区箍筋配置。
表 2 分析参数Table 2. Analytical parameters考察参数 参数变化范围 备注 轴压比n0 0.1;0.3;0.5;0.7;0.9 预应力度λ 0;0.4;0.44;0.48 无预应力筋;2- 
2-6

钢管配钢率ρss 4.40%;5.17%;5.95% 


配箍率ρsv 0.42%;0.76%;1.21% 


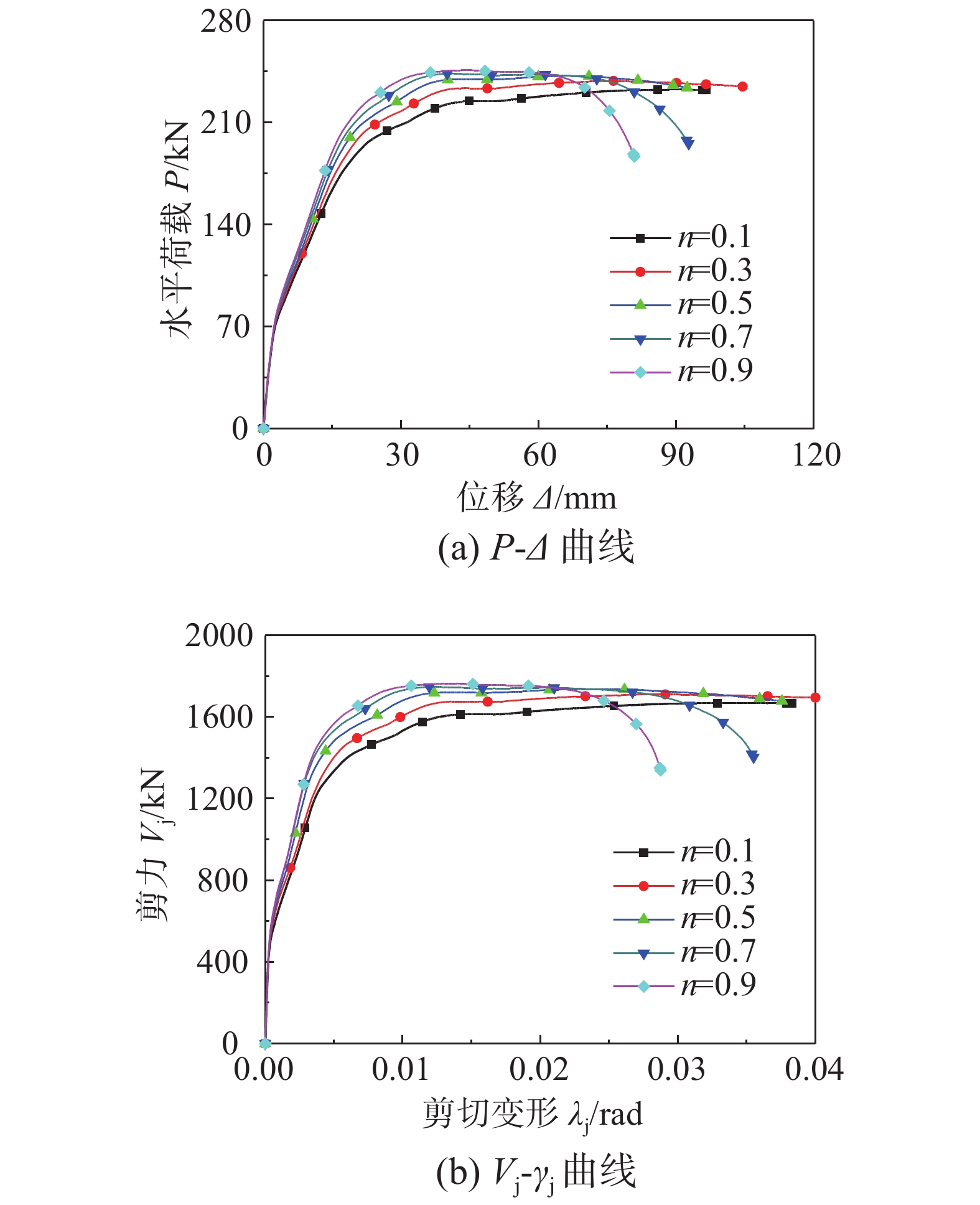
4.2.1 轴压比
图18(a)和图18(b)分别给出了轴压比n0对框架节点柱顶水平荷载-位移(P-Δ)和节点核心区剪力-剪切变形(Vj-γj)的影响。从图18可见,随着轴压比的增加,柱顶水平荷载和核心区剪力峰值均在增加,且当轴压比小于0.5时增加幅度较为明显,在轴压比小于0.5时增加幅度不大;随着轴压比的增加,水平荷载峰值对应的位移和核心区峰值剪力对应的剪切变形在逐渐减小,节点试件延性越低。
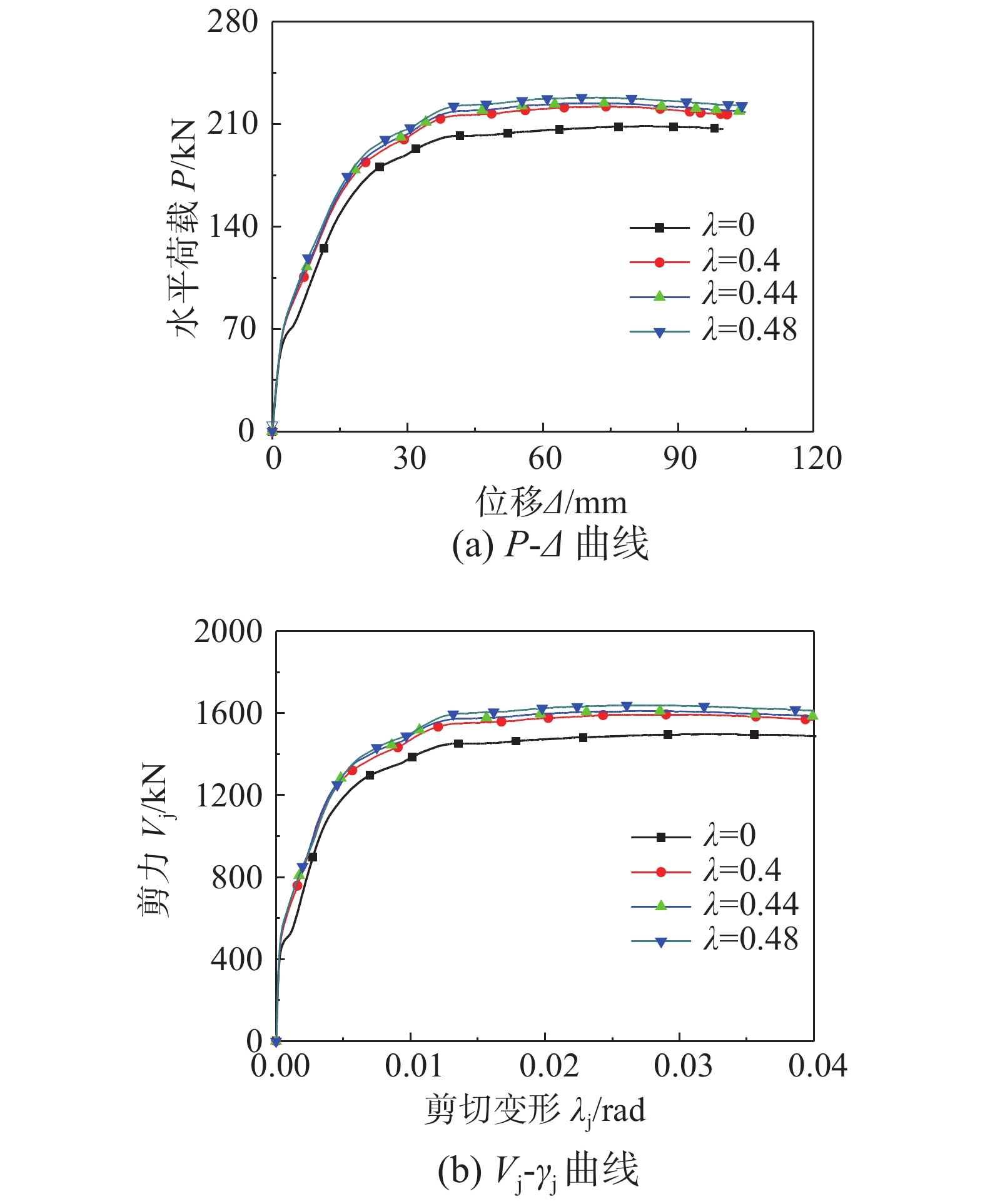
4.2.2 预应力度
图19(a)和图19(b)分别给出了预应力度λ对柱端水平荷载-位移(P-Δ)以及节点核心区剪力-剪切变形(Vj-γj)的影响。可以看出,在节点开裂后,不施加预应力的节点试件抗侧刚度明显小于预应力试件,随着预应力度λ的增加,节点试件抗侧刚度和剪切刚度增加幅度不大,柱顶水平荷载峰值和节点核心区剪力峰值相应增加,不同预应力度下的试件柱顶水平荷载-位移和核心区剪力-剪切变形曲线相似。
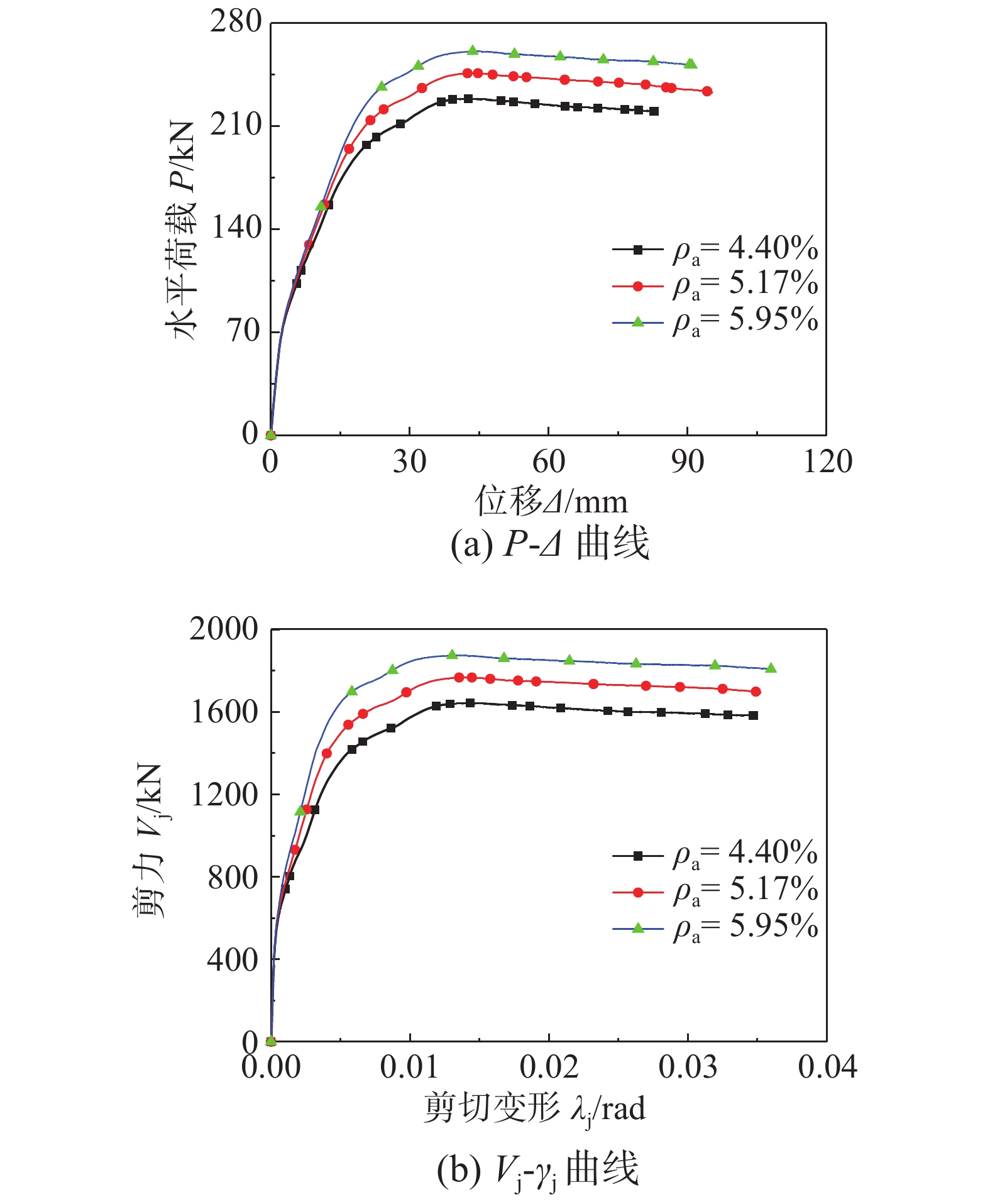
4.2.3 钢管配钢率
图20(a)和图20(b)分别为核心区钢管配钢率ρss对柱端水平荷载-位移(P-Δ)以及节点核心区剪力-剪切变形(Vj-γj)的影响。可见,随着钢管配钢率的增加,柱顶水平荷载和节点核心区剪力的峰值得到较大程度的提高,表明钢管配钢率对节点核心区抗剪承载力有较为显著的影响;然而,钢管配钢率对节点试件的延性影响不大。
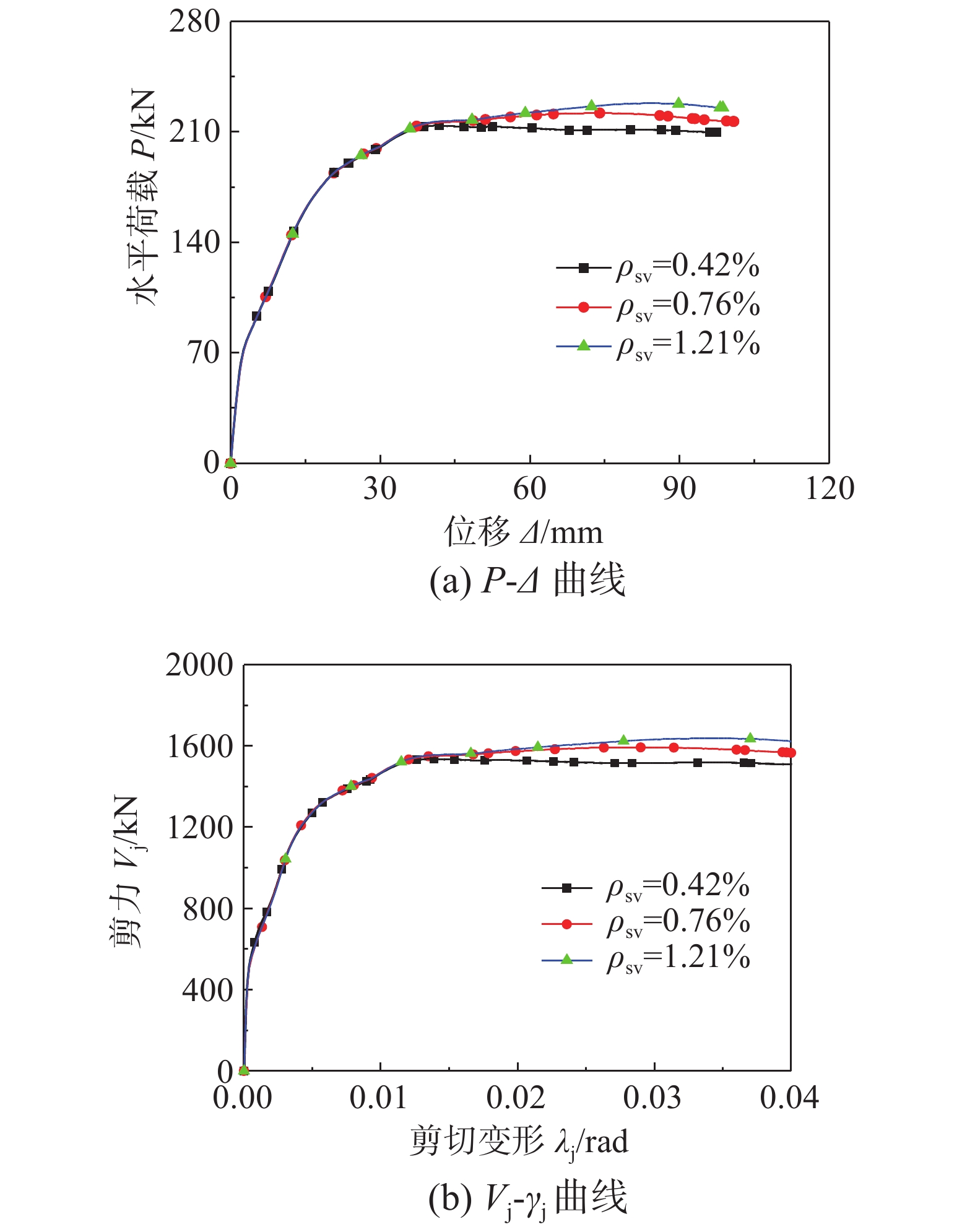
4.2.4 配箍率
图21为核心区配箍率ρsv对柱顶水平荷载-位移(P-Δ)以及节点核心区剪力-剪切变形(Vj-γj)曲线的影响。可以看出,随着核心区配箍率的增加,柱顶水平荷载和核心区剪力的峰值及延性均略有提高。
4.3 节点抗剪承载力计算
依据前述分析并参考文献[27],忽略与钢管相连的部分工字钢腹板的影响,节点核心区抗剪承载力Vj可基本由核心区钢管、核心区箍筋、混凝土(包括钢管内和钢管外)以及预应力筋四部分贡献叠加而成。其中,核心区钢管与箍筋对节点抗剪承载力的贡献Vss和Vs,可分别由式(10)和式(11)确定。
{V_{{\rm{ss}}}} = 0.58{f_{{\rm{ss}}}}{A_{{\rm{ss}}}}\qquad\quad (10) {V_{\rm{s}}} = \frac{{{f_{{\rm{yv}}}}{A_{{\rm{svj}}}}({h_{{\rm{b0}}}} - a_{\rm{s}}^{\prime})}}{s} (11) 式中:fss、fyv分别为钢管和箍筋的抗拉屈服强度;Ass、Asvj分别为核心区钢管和箍筋的截面面积;hb0为梁截面有效截面高度;
a_{\rm{s}}' 为梁受压钢筋到混凝土受压边缘的距离;s为核心区箍筋间距。预应力对任一节点i的核心区抗剪承载力的贡献
V_{{\rm{p(}}i{\rm{)}}}^{} ,可通预应力节点核心区抗剪承载力V_{{\rm{j(}}i{\rm{)}}}^{\rm{p}} 与相同条件下但不含预应力筋的节点核心区抗剪承载力V_{{\rm{j(}}i{\rm{)}}}^0 之差求得,按式(12)计算:{V_{{\rm{p(}}i{\rm{)}}}} = V_{{\rm{j(}}i{\rm{)}}}^{\rm{p}} - V_{{\rm{j(}}i{\rm{)}}}^{\rm{0}} (12) 经前述计算发现,预应力对节点核心区抗剪承载力的贡献Vp,与有效预压力Np和轴压比n0有关,因此,根据计算结果拟合得到了Vp的计算公式。
\begin{split} {V_{\rm{p}}} = &0.45{N_{\rm{p}}} + 0.8{N_{\rm{p}}}{n_{\rm{0}}} - 5.3 - 222.9{n_{\rm{0}}} + \\& 395.9{n_{\rm{0}}}^2 - 0.61{N_{\rm{p}}}{n_0}^2 - 175.9{n_{\rm{0}}}^3 \end{split} (13) 式中:Np=σpeAp,σpe、Ap分别为有效预应力和预应力筋截面面积。
任一预应力节点i试件中,混凝土对核心区抗剪承载力的贡献Vc(i),可按式(14)计算:
{V_{{\rm{c}}(i)}} = {V_{{\rm{j}}(i)}} - {V_{{\rm{s}}(i)}} - V_{{\rm{ss}}(i)}^{} - V_{{\rm{p}}(i)}^{} (14) 基于参数分析结果,核心区混凝土对节点抗剪承载力的贡献Vc,可由式(15)确定。
{V_{\rm{c}}} = {\rm{0}}{\rm{.2}}{f_{\rm{c}}}{b_{\rm{j}}}{h_{\rm{j}}} + 0.01N (15) 式中:N为柱顶施加的轴力;bj、hj分别为节点核心区截面宽度和高度。
综上,节点核心区抗剪承载力Vj可按式(16)计算:
\begin{split} {V_{\rm{j}}} =& {V_{\rm{c}}} + {V_{{\rm{ss}}}} + {V_{\rm{s}}} + {V_{\rm{p}}} = \\& 0{\rm{.2}}{f_{\rm{c}}}{b_{\rm{j}}}{h_{\rm{j}}} + 0.01N + \frac{{{f_{{\rm{yv}}}}{A_{{\rm{svj}}}}({h_{{\rm{bo}}}} - {a}_{\rm{s}}^{\prime})}}{s} + \\&0.58{f_{{\rm{ss}}}}{A_{{\rm{ss}}}} + 0.45{N_{\rm{p}}} + 0.8{N_{\rm{p}}}{n_{\rm{0}}} - 5.3 - 222.9{n_{\rm{0}}} + \\& 395.9{n_{\rm{0}}}^2 - 0.61{N_{\rm{p}}}{n_0}^2 - 175.9{n_{\rm{0}}}^3 \end{split} (16) 为使式(16)更好地应用于工程设计,本文对预应力对受剪承载力的贡献Vp进行调整,取其计算结果的下包线,可得Vp=0.315Np,从而得到节点核心区抗剪承载力Vj的实用计算公式:
\begin{split} {V_{\rm{j}}} =& {\rm{0}}{\rm{.2}}{f_{\rm{c}}}{b_{\rm{j}}}{h_{\rm{j}}} + 0.01N + \frac{{{f_{{\rm{yv}}}}{A_{{\rm{svj}}}}({h_{{\rm{bo}}}} - {a}_{\rm{s}}^{\prime})}}{s} + \\& 0.58{f_{{\rm{ss}}}}{A_{{\rm{ss}}}} + 0.315{N_{\rm{p}}} \end{split} (17) 4.4 试验与计算结果的比较
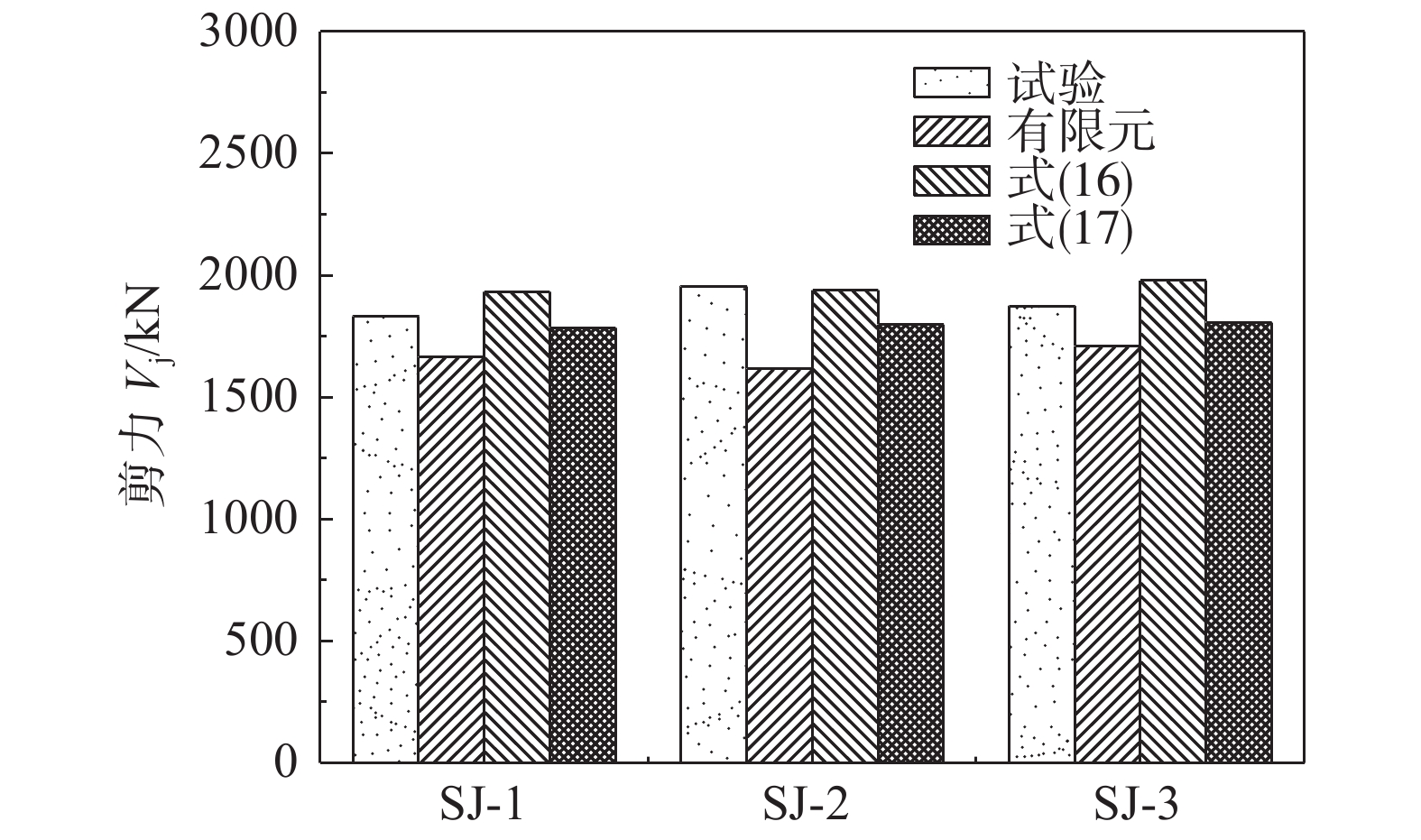
图22对比了本文3个节点试件核心区受剪承载力试验、有限元分析、式(16)和式(17)的计算结果(Vjtest、Vjcal、Vj(16)和Vj(17))。表3给出了具体的对比数值。可以发现本文3个试件的有限元分析结果均比试验值低,但大量模拟分析统计得到的式(16)与实测结果更为吻合。
目前,关于预应力型钢混凝土梁-钢管混凝土叠合柱节点抗剪承载力的研究鲜有报道,本文暂对比了式(17)与节点核心区发生剪切破坏的钢筋混凝土梁-钢管混凝土叠合柱节点的试验结果[28](见表3中的试件CCS1和CCS2)。可以看出,采用式(17)计算的抗剪承载力均大于文献[28]的实测结果,其原因可能是型钢上、下翼缘和钢管内加劲环板对混凝土的约束作用使混凝土的抗剪承载力得到了提高。
通过前述对比可以看出,式(17)与试验结果的比值Vj(17)/Vjtest平均值为1.03,标准差为0.11,表明本文提出的节点抗剪承载力实用计算公式可用于工程设计。
5 结论
通过建立预应力型钢混凝土梁-钢管混凝土叠合柱节点的有限元模型,并开展水平荷载下力学性能分析,可得如下结论:
(1)单调荷载下的有限元计算结果与试验吻合较好,节点试件核心区混凝土从屈服开始就形成了斜压杆,直至混凝土压碎。
(2)当节点试件水平荷载达到峰值点时,核心区钢管、箍筋及预应力筋均已屈服,核心区混凝土被压碎,此时可作为节点核心区抗剪承载力计算的标志。
(3)提高轴压比、预应力度、核心区钢管配钢率和配箍率均可一定程度提高节点核心区的受剪承载力,但过高的轴压比将降低节点的延性。
(4)提出了预应力型钢混凝土梁-钢管混凝土核心柱节点核心区的抗剪承载力计算公式,可用于工程设计。
-
表 1 预应力筋的参数
Table 1 Parameters of prestressing tendons
比例极限应变εp1(%) 屈服应变εp2(%) 极限应变εp3(%) 比例极限应力fp1 屈服应力fp2 0.65 0.93 5.2 0.78 fp3 0.87 fp3 表 2 分析参数
Table 2 Analytical parameters
考察参数 参数变化范围 备注 轴压比n0 0.1;0.3;0.5;0.7;0.9 预应力度λ 0;0.4;0.44;0.48 无预应力筋;2- 
2-6

钢管配钢率ρss 4.40%;5.17%;5.95% 


配箍率ρsv 0.42%;0.76%;1.21% 


-
[1] 傅传国, 李玉莹, 孙晓波, 等. 预应力及非预应力型钢混凝土框架受力及抗震性能试验研究[J]. 建筑结构学报, 2010, 31(8): 15 − 21. Fu Chuanguo, Li Yuyin, Sun Xiaobo, et al. Experimental study on seismic performance of prestressed and non-prestressed steel reinforced concrete frames [J]. Journal of Building Structures, 2010, 31(8): 15 − 21. (in Chinese)
[2] 熊学玉, 高峰. 预应力型钢混凝土框架试验研究及分析[J]. 四川大学学报(工程科学版), 2011, 43(6): 1 − 8. Xiong Xueyu, Gao Feng. Experimental investigation and analysis on large scale prestressed steel reinforced concrete frame [J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(6): 1 − 8. (in Chinese)
[3] 朱丽华, 潘鑫波, 吉翠茹, 等. 自复位圆钢管混凝土柱-钢梁连接节点足尺试验研究[J]. 工程力学, 2019, 36(12): 218 − 225. Zhu Lihua, Pan Xinbo, Ji Cuiru, et al. A full-scale test on self-reset circular concrete-filled steel tubular column to steel beam connections [J]. Engineering Mechanics, 2019, 36(12): 218 − 225. (in Chinese)
[4] 倪威康, 王万祯, 贾真, 等. 变截面方钢管轻骨料混凝土边柱-钢箱梁折线隔板贯通节点破坏机理和承载力研究[J]. 工程力学, 2019, 36(10): 122 − 133. Ni Weikang, Wang Wanzhen, Jia Zhen, et al. Study on the failure mechanism and strength of linear strengthened diaphragm-through joints of LWA concrete-filled square steel tubular side columns with variable cross sections and steel box beams [J]. Engineering Mechanics, 2019, 36(10): 122 − 133. (in Chinese)
[5] 王琨, 袁沈峰, 曹大富, 等. 配置核心钢管的钢筋混凝土柱-钢骨混凝土梁组合框架抗震性能试验研究[J]. 建筑结构学报, 2013, 34(6): 103 − 112. Wang Kun, Yuan Shenfeng, Cao Dafu, et al. Test on seismic performanceof frame structure of steel reinforced concrete beam and steel-tube encased concrete column [J]. Journal of Building Stmctures, 2013, 34(6): 103 − 112. (in Chinese)
[6] 王琨, 袁沈峰, 智海祥, 等. 配置核心钢管的钢筋混凝土柱-钢骨混凝土梁组合框架力学性能非线性分析[J]. 工程力学, 2016, 33(10): 197 − 207, 217. Wang Kun, Yuan Shenfeng, Zhi Haixiang, et al. Nonlinear analysis on mechanical performance of frame structures composed of steel reinforced concrete beams and steel-tube reinforced concrete columns [J]. Engineering Mechanics, 2016, 33(10): 197 − 207, 217. (in Chinese)
[7] 纪晓东, 张明亮, 刘平纪, 等. 钢管混凝土组合柱累积损伤性能试验研究[J]. 建筑结构学报, 2013, 34(12): 35 − 44. Ji Xiaodong, Zhang Mingliang, Liu Pingji, et al. Experimental study of cumulative damage performance of steel tube-reinforced concrete composite columns [J]. Journal of Building Structures, 2013, 34(12): 35 − 44. (in Chinese)
[8] 郭全全, 赵羽西, 李芊, 等. 钢管混凝土叠合柱偏心受压性能试验研究[J]. 建筑结构学报, 2013, 34(12): 103 − 111. Guo Quanquan, Zhao Yuxi, Li Qian, et al. Experimental study on eccentric compressive property of steel tube-reinforced concrete columns [J]. Journal of Building Structures, 2013, 34(12): 103 − 111. (in Chinese)
[9] An Y F, Han L H. Behavior of concrete encased CFST columns under combined compression and bending [J]. Journal of Constructional Steel Research, 2014, 101: 314 − 330. doi: 10.1016/j.jcsr.2014.06.002
[10] Chen J Y, Li W, Han L H, et al. Structural behaviour of concrete-encased CFST box stub columns under axial compression [J]. Journal of Constructional Steel Research, 2019, 158: 248 − 262. doi: 10.1016/j.jcsr.2019.03.021
[11] Li Y J, Li G, Hou C, et al. Long-term experimental behavior of concrete-encased CFST with preload on the inner CFST [J]. Journal of Constructional Steel Research, 2019, 155: 355 − 369. doi: 10.1016/j.jcsr.2019.01.001
[12] Hou C C, Han L H, Wang F C, et al. Study on the impact behaviour of concrete-encased CFST box members [J]. Engineering Structures, 2019, 198: 109536. doi: 10.1016/j.engstruct.2019.109536
[13] 廖飞宇, 尧国皇, 李永进. 钢管混凝土叠合柱-钢梁节点的有限元分析[J]. 工业建筑, 2016, 46(9): 152 − 157, 102. Liao Feiyu, Yao Guohuang, Li Yongjin. Finite element analysis of concrete encased CFST column to steel beam joints [J]. Building Structures, 2016, 46(9): 152 − 157, 102. (in Chinese)
[14] 钱炜武, 李威, 韩林海, 等. 带楼板钢管混凝土叠合柱-钢梁节点抗震性能数值分析[J]. 工程力学, 2016, 33(增刊): 95 − 100. Qian Weiwu, Li Wei, Han Linhai, et al. Analytical behaviour of concrete-encased concrete-filled steel tubular column to steel beam joints with RC slabs [J]. Engineering Mechanics, 2016, 33(Suppl): 95 − 100. (in Chinese)
[15] 钱炜武, 李威, 韩林海, 等. 往复荷载作用下钢管混凝土叠合柱-钢梁连接节点力学性能研究[J]. 土木工程学报, 2017, 50(7): 27 − 38. Qian Weiwu, Li Wei, Han Linhai, et al. Behavior of concrete-encased concrete-filled steel tubular column to steel beam joint under cyclic loading [J]. China Civil Engineering Journal, 2017, 50(7): 27 − 38. (in Chinese)
[16] 聂建国, 王宇航, 陶慕轩, 等. 钢管混凝土叠合柱-钢筋混凝土梁外加强环节点抗震性能试验研究[J]. 建筑结构学报, 2012, 12(7): 88 − 97. Nie Jianguo, Wang Yuhang, Tao Muxuan, et al. Experimental study on seismic behavior of laminated steel tube column-concrete beam joint with outer stiffening ring [J]. Journal of Building Structures, 2012, 12(7): 88 − 97. (in Chinese)
[17] 赵剑, 马永超, 庄金平. 钢管混凝土叠合柱-钢筋混凝土梁节点滞回性能有限元分析[J]. 福建建筑, 2016, 214(4): 45 − 47. Zhao Jian, Ma Yongchao, Zhuang Jinping. FEM analysis on cyclic behavior of joints with concrete encased CFST column and RC beams [J]. Fujian Architecture & Construction, 2016, 214(4): 45 − 47. (in Chinese)
[18] 邓志恒, 王晓燕, 张喜德, 等. 钢管混凝土核心柱预应力梁框架节点试验研究[J]. 工业建筑, 2006, 36(9): 71 − 74. doi: 10.3321/j.issn:1000-8993.2006.09.019 Deng Zhiheng, Wang Xiaoyan, Zhang Xide, et al. Experimental research on design method for frame joints of concrete-filled steel tubular core columns and prestressed concrete beams [J]. Industrial Construction, 2006, 36(9): 71 − 74. (in Chinese) doi: 10.3321/j.issn:1000-8993.2006.09.019
[19] 滕智明, 邹离湘. 反复荷载下钢筋混凝土构件的非线性有限元分析[J]. 土木工程学报, 1996, 29(2): 19 − 27. doi: 10.3321/j.issn:1000-131X.1996.02.003 Teng Zhiming, Zou Lixiang. Nonlinear finite element analysis of RC members under reversed cyclic loading [J]. China Civil Engineering Journal, 1996, 29(2): 19 − 27. (in Chinese) doi: 10.3321/j.issn:1000-131X.1996.02.003
[20] 韩林海. 钢管混凝土结构-理论与实践 [M]. 第2版. 北京: 科学出版社. 2007. Han Linhai. Concrete-filled steel tube structure- theory and practice [M]. 2rd Edition. Beijing: Science Press, 2007. (in Chinese)
[21] An Y F, Han L H. Performance of concrete-encased CFST stub columns under axial compression [J]. Journal of Constructional Steel Research, 2014, 93(2): 62 − 76.
[22] GB 50010−2010, 混凝土结构设计规范 [S]. 北京: 中国建筑工业出版社, 2015. GB 50010−2010, Concrete structure design code [S]. Beijing: China Building Industry Press, 2015. (in Chinese)
[23] 张昊宇, 郑文忠. 1860级低松弛钢绞线高温下力学性能[J]. 哈尔滨工业大学学报, 2007, 39(6): 861 − 865. doi: 10.3321/j.issn:0367-6234.2007.06.006 Zhang Haoyu, Zheng Wenzhong. Mechanical property of steel strand at high temperature [J]. Journal of Harbin Institute of Technology, 2007, 39(6): 861 − 865. (in Chinese) doi: 10.3321/j.issn:0367-6234.2007.06.006
[24] Li W, Han L H. Seismic performance of CFST column to steel beam joints with RC slab: Analysis [J]. Journal of Constructional Steel Research, 2011, 67(1): 127 − 139. doi: 10.1016/j.jcsr.2010.07.002
[25] 庄茁. 基于ABAQUS的有限元分析和应用 [M]. 北京: 清华大学出版社, 2009 Zhuang Zhuo. Finite element analysis and application of ABAQUS [M]. Beijing: Tsinghua University Press, 2009. (in Chinese)
[26] 王琨, 智海祥, 曹大富, 等. 预应力型钢混凝土梁-钢管混凝土叠合柱框架节点抗震性能试验研究[J]. 建筑结构学报, 2018, 39(12): 29 − 38. Wang Kun, Zhi Haixiang, Cao Dafu, et al. Test on hysteretic behavior of prestressed steel reinforced concrete beam to steel-tube reinforced concrete column joints [J]. Journal of Building Structures, 2018, 39(12): 29 − 38. (in Chinese)
[27] CECS188: 2005, 钢管混凝土叠合柱结构技术规程 [S]. 北京: 中国计划出版社, 2005. CECS188: 2005, Technical specification for steel tube-reinforced concrete column structure [S]. Beijing: China Planning Press, 2005. (in Chinese)
[28] 钱稼茹, 江源. 钢筋混凝土梁-钢管混凝土组合柱节点抗震性能试验[J]. 建筑结构, 2009, 39(9): 39 − 42, 48. Qian Jiaru, Jiang Yuan. Tests on seismic behavior of RC beam-composite steel tube confined concrete column joints [J]. Building Structures, 2009, 39(9): 39 − 42, 48. (in Chinese)
-
期刊类型引用(20)
1. 王彦冰,李孟鸽. 高强材料对方钢管混凝土柱滞回性能的影响分析. 广东建材. 2025(01): 22-24 .  百度学术
百度学术
2. 王飞朋,苗杰,乔文正. 受压过程对长龄期自密实棱柱体混凝土抗压强度影响研究. 混凝土. 2025(01): 65-68 .  百度学术
百度学术
3. 张志秋,陈适才,戎树伟,王经臣. 不同腰筋锚固钢管RC柱型钢组合梁节点抗震性能分析. 建筑科学. 2025(03): 65-76 .  百度学术
百度学术
4. 潘钻峰,葛雄,曾滨,许庆. 预应力混凝土梁-型钢混凝土柱新型框架节点受剪承载力计算方法. 工程力学. 2024(04): 29-38 .  本站查看
本站查看
5. 程军,许志坤,吴庆雄,袁辉辉. 界面焊接环向钢筋的钢管混凝土叠合柱抗剪性能研究. 工程力学. 2024(S1): 142-149 .  本站查看
本站查看
6. 王秋维,景烜光,景瑞颖. 内置型钢增强钢管约束钢筋混凝土柱节点抗震性能研究. 防灾减灾工程学报. 2024(04): 849-858 .  百度学术
百度学术
7. 杨航东. 装配式钢管混凝土叠合柱-钢筋混凝土梁节点抗震性能试验研究. 工业建筑. 2024(09): 133-140 .  百度学术
百度学术
8. 姚刚峰,熊学玉,肖启晟. 基于ABAQUS的SRC梁受剪承载力预测及连续梁数值研究. 建筑结构. 2024(22): 86-92 .  百度学术
百度学术
9. 侯勉望. 钢管混凝土叠合柱-钢筋混凝土梁节点抗震性能试验——以地铁车站为例. 华北地震科学. 2024(04): 26-34 .  百度学术
百度学术
10. 陈圣刚,高峰,耿娇,苑辉. 预应力型钢混凝土双坡框架抗震性能试验研究. 建筑结构学报. 2023(02): 110-118 .  百度学术
百度学术
11. 郑玉辉,钟炜辉,谭政,孟宝,段仕超,宋晓燕. 基于整体效能的不等跨钢框架抗倒塌冗余设计. 建筑结构学报. 2023(02): 96-109 .  百度学术
百度学术
12. 扈文凯. 钢管混凝土叠合柱在建筑工程中的应用分析. 居舍. 2022(05): 39-41+105 .  百度学术
百度学术
13. 张艳霞,刘梓洋,徐斌,孙宇. 矩形钢管混凝土柱-混凝土梁穿筋节点力学性能试验研究. 工程力学. 2022(04): 138-150 .  本站查看
本站查看
14. 彭大恒. 型钢混凝土转换梁在城市轨道交通高架车站中的应用. 建筑技术开发. 2022(12): 9-11 .  百度学术
百度学术
15. 李瀚源,李兴高,崔迪. 沉管隧道半刚性管节节段接头力学性能数值模拟. 地下空间与工程学报. 2022(04): 1166-1176 .  百度学术
百度学术
16. 任兆兵. 银川绿地中心型钢混凝土梁柱节点性能非线性分析. 钢结构(中英文). 2022(09): 8-16 .  百度学术
百度学术
17. 吴保强. 型钢混凝土组合结构梁柱节点抗震性能有限元分析. 建筑科技. 2022(04): 34-38 .  百度学术
百度学术
18. 刘军,徐东平. 叠合柱在文体中心项目中的应用. 建设机械技术与管理. 2022(06): 131-134 .  百度学术
百度学术
19. 赵飞. 预应力混凝土梁与型钢混凝土柱中节点受剪性能研究. 建筑科技. 2022(05): 34-40 .  百度学术
百度学术
20. 刘勇,魏珍中,郑玉超,焦晋峰. 预应力钢管桁架叠合楼板结构在变电站中应用探索和实践. 山东电力技术. 2021(02): 39-43 .  百度学术
百度学术
其他类型引用(8)



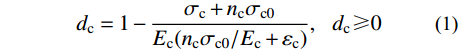
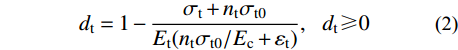
 下载:
下载: