SEISMIC UNIFORM DAMAGE-TARGETED DESIGN OF RC FRAME STRUCTURES
-
摘要: 地震均匀损伤失效模式是指结构在强震下各楼层的损伤大小相同、侧向变形近似,并具有全局化的耗能机制,是结构较理想的破坏模式。提出了考虑土-结构动力相互作用影响的RC框架结构地震均匀损伤优化设计方法。以结构层间位移角均匀化为目标,以梁柱构件截面配筋为优化变量,考虑材料成本约束和配筋率等约束,融合结构层间位移角分布和梁柱构件转角大小,提出了基于优化准则法的RC框架结构均匀损伤优化设计方法。基于非线性温克尔地基梁模型(BNWF),建立了能够考虑土-结构相互作用的RC框架结构分析模型。以两个5层和12层结构为例,研究了收敛参数对收敛速度和收敛稳定性的影响规律,分析了优化过程中各楼层配筋转移情况,对比了优化前、后结构的梁柱转角大小和层间位移角分布。结果表明,该文优化方法可使结构的损伤分布更加均匀,降低结构的最大层间位移角,提高结构的抗震能力。Abstract: The seismic failure mode of uniform damage refers to that the structure has a uniform damage and story drift along the height and develops a global energy dissipation mechanism, and it is an ideal and expected failure mode. A uniform damage-based seismic optimization design approach for RC frame structures considering the soil-structure interaction is proposed. By taking the uniformity of maximum inter-story drift ratio (IDR) as the design objective, the seismic optimization design approach was developed. Moreover, the optimization procedure accounted for the IDR distribution and component rotation demands. The component’s sectional reinforcements were selected as the design variables, and the material cost and the reinforcement ratio were considered as the design constraints. Based on the Beam on Nonlinear Winkler Foundation (BNWF) model, the numerical model of the RC frame structure considering soil-structure interaction was established. Two RC frame structures with 5 and 12 stories were employed as the prototype structures. The effects of convergence parameters on the convergence speed and stability were investigated. The transfer of story reinforcements in the optimization was studied. The change of component rotation and IDR distribution after the optimization was analyzed. The analytical results indicate that the developed approach can achieve a uniform IDR distribution and a smaller maximum IDR, thus improving the seismic performance.
-
震害调查和理论研究表明,基于现有抗震方法设计的结构在强震下的位移响应通常是不均匀分布的[1-2],即结构的某些局部构件产生损伤,而其他构件处于弹性或低损伤状态,这将导致结构的材料性能未能充分发挥。地震动的往复效应将使局部损伤逐渐累积并加剧,结构由于损伤过大而使得变形和损伤主要集中于某些局部楼层。由于损伤的不断累积、结构的变形不断加大,最终可能导致结构在该层形成薄弱层失效机制,结构的抗震潜能未得到充分发挥,未能形成全局化、整体化的耗能机制。结构材料若从损伤较低部位转移到损伤较大部位或将损伤严重部分进行加强,损伤严重的构件损伤将降低,而损伤轻微的构件损伤将变大,最终将使得结构获得近似均匀侧向变形的损伤状态。此时,结构各部位的材料不仅得到了充分利用,由于结构各部位均能耗能,结构的抗震响应有望降低,结构的抗倒塌性能大幅提高,这就是等变形或均匀损伤失效模式的基本理念[2-4]。
“均匀化”理念早已植根结构弹性优化设计中,渐近结构优化方法是实现这一理念的典型手段[5]。考虑结构在强震下的非线性特征,各楼层侧向变形的“均匀化”目前已经成为结构抗震优化设计的核心目标。基于均匀损伤失效模式原理,Chan和Zou[6]提出了一种RC框架结构两阶段的优化设计方法:小震弹性优化RC构件尺寸大小、大震Pushover分析优化截面配筋。Hajirasouliha等[7]采用Park-Ang双参数损伤指标提出了一种适用于RC框架结构的均匀损伤优化设计方法;但当构件处于弹性状态时,Park-Ang损伤指数的不连续性使得优化方法的适用性受限。徐龙河等[8]提出了基于性能的钢框架结构失效模式识别和多目标优化方法。李忠献等[9]提出了以整体结构的损伤指数为优化的约束方程和目标函数,通过修正结构柱参数来实现结构均匀损伤失效模式的优化方法。吕大刚等[10]采用可靠度方法对钢筋混凝土结构最可能的失效模式进行了分析。郑山锁等[11]对型钢混凝土框架的地震失效模式进行了识别和优化。孙爱伏等[12]发展了通过加强薄弱层来实现高层钢结构均匀损伤的抗震能力提升方法。白久林等[13-16]对均匀损伤失效模式进行了系列研究,分别提出了钢框架均匀损伤优化设计方法[13]、基于Pushover分析的均匀损伤优化设计方法[14-15]、基于地震动输入的结构地震失效模式分析与优化设计方法[16]和结构均匀损伤失效模式可控设计方法[16-17]。
必须注意的是,已有的地震均匀损伤优化设计,未能很好地考虑地震动不确定性、土-结构动力相互作用(SSI)等对优化的影响,未能量化考虑结构整体损伤和局部构件损伤与均匀损伤之间的相互关系,使得均匀损伤优化设计的应用范围受限。基于此,本文提出了一种考虑完备的RC框架结构地震均匀损伤失效模式优化设计方法。基于优化准则法,构建了优化的目标函数、优化变量、约束条件和均匀损伤优化算法。以两个5层和12层的RC框架结构为例,建立了考虑SSI效应的结构分析模型,对比分析了优化前、后结构的抗震性能。研究表明,本文所提优化方法能实现结构的地震均匀损伤,降低结构的最大层间位移角,提高结构的抗震性能,为结构抗震设计的发展提供了一种新的手段。
1 均匀损伤优化设计
优化准则法是土木工程结构诸多优化设计方法中的一种,其预先规定一组优化设计所必须满足的准则,然后根据这些准则建立达到优化设计的迭代公式,求出满足全部约束条件并使目标函数取最小值的设计变量近似解[18]。优化准则法简便、易于操作,不需要计算梯度,且优化过程与优化变量的数目无关,一般通过数十次迭代便能达到收敛条件[19]。考虑到地震均匀损伤优化设计需要计算结构的非线性响应,计算量大,且优化的变量较多,本文采用优化准则法来进行设计。
本文的优化设计有两个假设:1)构件具有足够的箍筋可确保不发生剪切破坏;2)梁柱节点为刚性连接,节点不会发生破坏。这两个假设便是结构抗震设计时“强剪弱弯、强节点弱构件”设计准则。
1.1 目标函数
本文的优化设计是基于均匀损伤的思想,将结构损伤分布的均匀程度作为优化目标函数。对于剪切型RC框架结构,其层间变形的大小与楼层的损伤密切相关。特别地,当RC框架进入屈服状态后,层间位移角通常被用来直接度量楼层的损伤大小,是衡量结构抗震性能最重要的参数之一。因此,层间位移角竖向分布的均匀性是均匀损伤优化设计的核心,进而优化目标函数可采用:
f=covIDRcovIDR−original (1) 式中,covIDR-original和covIDR分别为优化前、后结构最大层间位移角分布的变异系数。随着优化的进行,层间位移角分布逐渐趋于均匀,目标函数越来越小,进而结构的损伤也趋于均匀,最终实现均匀损伤设计的目标。
1.2 优化变量
对于RC框架结构,在结构高度和跨度一定的情况下,影响结构抗震性能的主要参数是梁柱的截面尺寸和截面配筋。由于RC构件截面尺寸与小震下结构的弹性刚度有关,其一般提前确定。因此,本文的优化变量仅选取截面配筋作为优化变量,梁柱的截面尺寸则保持不变。对于柱构件,由于截面采用对称配筋,柱截面配筋仅有一个设计变量。对于梁构件,梁上端钢筋和梁下端钢筋分别抵抗由竖向重力荷载和抗震荷载产生的最大负弯矩和最大正弯矩,因此梁设计变量为梁上部钢筋和梁下部钢筋两部分。为简化计算,假定梁下部钢筋面积与梁上部钢筋面积成比例关系,且近似取两者比值为0.5,这使得梁截面配筋的设计变量仅为一个。
1.3 约束条件
1) 在实际结构中,工程成本由于业主要求、抗震性能要求等可能出现材料成本的变化。本文考虑在优化过程中,材料成本(仅考虑梁柱钢筋和混凝土)为:
Ci=(1+η)⋅C0 (2) 式中:C0为初始材料造价;Ci为第i次迭代的材料造价;η为材料成本变化率。在本文的后续分析中,考虑成本不变、成本减少5%和成本增加5%三种情况,且假定钢筋材料成本为混凝土的25倍。
2) 梁柱构件需满足最大和最小配筋率要求。最小配筋率和最大配筋率可根据规范要求获得。
ρcmin⩽ (3) 式中:ρc、ρcmin和ρcmax分别为柱端截面配筋率、最小配筋率和最大配筋率;ρbtop、ρbt min和ρbt max分别为梁端上部截面配筋率、最小配筋率和最大配筋率;ρbbot、ρbb min和ρbb max分别为梁端下部截面配筋率、最小配筋率和最大配筋率。
3) 梁构件需满足正常使用极限状态的要求,在竖向荷载下需保持弹性状态。当某些梁在竖向荷载下屈服时,可根据钢筋应变按式(4)进行迭代使其满足弹性状态:
{[ {\left( {{A_{{\rm{sb}}}}} \right)_i^j} ]_1} = \frac{{\left( {{\varepsilon _{{\rm{steel}}}}} \right)_i^j}}{{{\varepsilon _{\rm y}}}} \cdot {[ {\left( {{A_{{\rm{sb}}}}} \right)_i^j} ]_0} (4) 式中:
{\varepsilon _{\rm{y}}} 和\left( {{\varepsilon _{{\rm{steel}}}}} \right)_i^j 分别为钢筋屈服应变和梁中钢筋应变;{[ {\left( {{A_{{\rm{sb}}}}} \right)_i^j} ]_0} 和{[ {\left( {{A_{{\rm{sb}}}}} \right)_i^j} ]_1} 分别为屈服前梁中钢筋面积和新的钢筋面积。1.4 收敛条件
本文的收敛条件为:连续两步目标函数之差的绝对值小于误差限制时则判定为收敛,如式(5)所示。在优化的过程中,可能会出现不收敛的情况。此时规定:超过30步仍未达到收敛时则在30步时停止。
\left\{ {\begin{aligned} & { \left| {{f_{i - 1}} - {f_i}} \right| \leqslant {e_0}} \\& {\left| {{f_{i + 1}} - {f_i}} \right| \leqslant {e_0} } \end{aligned}} \right. (5) 式中:fi为第i次迭代的目标函数;e0为误差限值,取值为0.01。
1.5 优化设计
本文的地震均匀损伤优化设计是基于优化准则法来开展的,主要包括“分析-重新设计”的基本过程,具体优化步骤如下:
1) 确定初始的结构配置参数,并建立结构的非线性有限元模型。
2) 选择合理的多条地震动作为结构输入,并对结构进行大震作用下的非线性时程分析。记录每条地震动下结构的最大层间位移角(IDR)分布和梁柱转角(θ)分布,并对其进行统计分析,获得整个结构的层间位移角平均值IDRave、结构柱端转角平均值(θc)ave和梁端转角平均值(θb)ave。
3) 根据收敛准则进行判断。若收敛,则停止优化,此时的结构为最优设计,实现了均匀损伤的目标。否则按步骤4)继续运行优化程序。需注意的是进行第一次优化时,不需进行判别。
4) 对结构进行重新设计。当收敛准则不满足要求时,结构的层间位移角一般是不均匀分布的。根据“均匀损伤”的基本定义,梁柱截面钢筋将从层间位移角较小的楼层转移到层间位移角较大的楼层。此外,结构的层间变形还与梁柱构件的局部变形有直接关系。因此,本文在构建优化设计时,同时考虑结构的宏观(层间位移角)和微观(梁柱转角)损伤指标。梁柱截面新的配筋可根据式(6)~式(8)获得:
{[ {\left( {{A_{\rm{c}}}} \right)_i^j} ]_{n + 1}} = {\left( {\frac{{{\rm{ID}}{{\rm{R}}_i}}}{{{\rm{ID}}{{\rm{R}}_{{\rm{ave}}}}}}} \right)^\alpha } \cdot {\left[ {\frac{{\overline {{{\left( {{\theta _{\rm{c}}}} \right)}_i}} }}{{{{\left( {{\theta _{\rm{c}}}} \right)}_{{\rm{ave}}}}}}} \right]^\gamma } \cdot {[ {\left( {{A_{\rm{c}}}} \right)_i^j} ]_n}\qquad (6) {[ {( {{A_{{\rm{btop}}}}} )_i^j} ]_{n + 1}} = {\left( {\frac{{{\rm{ID}}{{\rm{R}}_i}}}{{{\rm{ID}}{{\rm{R}}_{{\rm{ave}}}}}}} \right)^\alpha } \cdot {\left[ {\frac{{\overline {{{\left( {{\theta _{\rm{b}}}} \right)}_i}} }}{{{{\left( {{\theta _{\rm{b}}}} \right)}_{{\rm{ave}}}}}}} \right]^\gamma } \cdot {[ {( {{A_{{\rm{btop}}}}} )_i^j} ]_n} (7) {( {{A_{{\rm{bbot}}}}} )_i^j} = 0.5 \cdot {( {{A_{{\rm{btop}}}}} )_i^j} \qquad\qquad\qquad\qquad\qquad\;\;\;\; (8) 式中:n为迭代步数;i为楼层;j为该层的第j个梁柱构件;IDRi为第i层的层间位移角;
\overline{{\left({\theta}_{{c}}\right)}_{{i}}} 和\overline{{\left({\theta}_{{b}}\right)}_{{i}}} 分别为第i层的柱端和梁端转角平均值;Ac、Abtop和Abbot分别为柱截面配筋以及梁截面顶部和底部配筋;α和γ为收敛参数,取值一般在0~1,本文对收敛参数的取值进行详细分析。根据式(6)~式(8)可以发现,当梁柱构件所在楼层的层间位移角比其平均值大、梁柱构件的转角也比转角平均值大时,梁柱构件的配筋将会得到加强,此时梁柱构件的地震损伤有望降低。反之,当层间位移角和梁柱转角较小时,梁柱钢筋将会减少,梁柱构件地震损伤将会变大。通过对“损伤大的构件加强、损伤小的构件削弱”的优化设计,结构的地震损伤实现均匀分布,且结构会形成全局耗能机制,结构的整体损伤有望降低。
5) 在得到新的梁柱截面配筋之后,按式(2)~式(4)进行材料成本、配筋率等约束条件限制,获得优化后的结构模型。整个优化的流程如图1所示。
需要说明的是,均匀损伤抗震设计这一思路可以推广到竖向、平面不规则的高层建筑结构中,将结构材料重新分布,使得结构的整体抗震性能得到最大程度的发挥。
2 结构分析模型
为检验本文所提出的均匀损伤优化设计方法的有效性,选取两个5层和12层考虑土-结构相互作用(SSI)影响的RC框架结构进行分析和验证。
2.1 结构基本参数
两个RC框架的立面图和梁柱构件的截面尺寸如图2所示。初始结构按照我国抗震设计规范进行[20]。5层结构采用C30混凝土、12层结构采用C40混凝土。两个结构均采用HRB400钢筋,位于场地类别为II类、设计地震分组为第一组的场地上,结构的抗震设防烈度为8度(0.2 g)。地基土为黏性土,粘聚力和摩擦角分别为25 kPa和20°,容重为17.5 kN/m3,剪切模量为5×104 kPa,泊松比为0.3。基础形式考虑为浅基础,根据上部荷载和地基土条件,设计得到的基础参数如表1所示。
表 1 基础参数Table 1. Footing parameter/m 基础参数 5层 12层 内柱 外柱 内柱 外柱 长度Lf 1.9 1.4 3.2 2.4 宽度Bf 1.9 1.4 3.2 2.4 高度Hf 0.5 0.5 1.5 1.5 埋深Df 1.6 1.6 3.6 3.6 2.2 结构分析模型
采用OpenSees软件来建立结构的有限元分析模型[21]。上部梁柱构件采用基于力的集中塑性铰单元(beamWithHinges),其中塑性铰长度取截面高度。为考虑混凝土开裂等对构件刚度的影响,对单元中间弹性部分的刚度进行一定的折减。根据FEMA356的规定[22],梁的有效刚度取0.5倍弹性刚度,柱的有效刚度取0.7倍弹性刚度。截面采用可考虑轴力-弯矩耦合效应的纤维截面模型。混凝土采用Concrete01模型;钢筋采用Steel02模型。
下部浅基础采用非线性Winkler地基梁模型(BNWF)来模拟土-结构相互作用的影响[23]。如图3所示,BNWF模型由竖向的多个q-z弹簧(模拟基础的沉降、摇摆和隆起)和水平的p-x弹簧(模拟被动土压力)和t-x弹簧(模拟基础与地基之间的摩擦力)组成。由于BNWF模型具有:1)各个弹簧模型的骨架曲线已根据试验数据进行了全面校准;2)可捕获土体的屈服和退化(材料非线性),以及基础的沉降、间隙和滑动(几何非线性);3)竖向弹簧可改变刚度和间距以增加模型的通用性的显著特点,其已成为土-浅基础-结构相互作用体系地震分析的首选模型。
在OpenSees模型中,q-z、p-x和t-x弹簧均采用零长度单元来连接刚性地基与表征基础的弹性梁柱单元(elastic beam column element)。土体性能通过具有不同滞回性能的弹簧来模拟,三种弹簧的滞回曲线如图4所示。其中q-z弹簧采用QzSimple2材料来模拟,其具有不对称的滞回响应,即受压强度高、拉伸强度较低。在基础端部水平布置的p-x和t-x弹簧,分别选用PxSimple1材料和TxSimple1材料来模拟。PxSimple1材料具有捏缩的滞回曲线,能考虑卸载时基础与地基之间的间隙和被动土压力的影响。TxSimple1材料具有饱满的滞回性能,可较好地模拟与基础滑动相关的摩擦行为。BNWF模型的参数可根据基础数据和地基土参数计算确定。
2.3 地震输入模型
本文从PEER强震地震数据库中选取了10条天然地震动[24],地震动的详细信息如表2所示。10条地震动的选取是基于PEER的调幅方法,即将所选地震动的反应谱中位值与我国抗震设计规范反应谱最大程度地吻合。10条地震动调幅到大震水平(PGA=400 cm/s2)下的反应谱及其中位值与规范谱的对比如图5所示。可以看出两者具有很好的吻合度。结构分析时,阻尼采用Rayleigh阻尼(阻尼比为5%),考虑结构的重力二阶P-Δ效应。将10条地震动调幅到大震水平,对结构进行非线性动力分析,根据抗震响应参数进行结构的优化迭代。
表 2 10条地震动信息Table 2. 10 ground motion records编号 NGA 地震名称 震级 台站 分量 PGA/g GM1 163 Imperial Valley-06, 1979 6.53 Calipatria Fire Station H-CAL315 0.078 GM2 172 Imperial Valley-06, 1979 6.53 El Centro Array #1 H-E01230 0.134 GM3 1762 Hector Mine, 1999 7.13 Amboy 21081360 0.150 GM4 186 Imperial Valley-06, 1979 6.53 Niland Fire Station H-NIL360 0.069 GM5 51 San Fernando, 1971 6.61 2516 Via Tejon PV PVE65 0.026 GM6 719 Superstition Hills-02, 1987 6.54 Brawley Airport B-BRA225 0.156 GM7 737 Loma Prieta, 1989 6.93 Agnews State Hospital AGW000 0.172 GM8 800 Loma Prieta, 1989 6.93 Salinas - John & Work SJW160 0.091 GM9 832 Landers, 1992 7.28 Amboy ABY000 0.115 GM10 93 San Fernando, 1971 6.61 Whittier Narrows Dam WND143 0.100 3 分析结果
3.1 收敛参数的敏感性分析
在本文建立的优化设计程序中,收敛参数α和γ的取值将直接影响优化速度和收敛效果,因此需对收敛参数进行敏感性分析。图6给出了在成本不变的约束条件下,不同收敛参数对优化结果的影响。从图6中可知,随着优化的不断进行,目标函数有减小的趋势,且随着收敛参数数值的增加,收敛速度越快,所需要的迭代步数较少。当α=γ=0.5时,5层结构时能顺利收敛,12层结构则不能收敛。当α=γ=1.0时,两个结构均不能收敛。
图7给出了5层结构成本增加5%和12层结构成本降低5%时,收敛参数的取值对优化结果的影响。从图7中可以看出,在成本增减约束条件下,不同收敛参数对优化结果的影响与成本不变时大致相同。总体趋势上,随着收敛参数的增大,收敛速度会加快,但最终收敛值大致相同。特别地,两个结构在收敛参数α=γ=1.0时均不收敛。同时,从图7(a)中可以看出,当α=γ=0.1时,由于目标函数仍不断减小,即结构仍向着均匀损伤的方向发展,在优化迭代30步后仍未达到式(5)的收敛条件,此时以30步作为收敛条件。此外,对12层结构,当α=γ=0.5时(图7(b)),优化虽能收敛,但收敛值与α、γ为0.1和0.2时明显偏大,表明此时优化程度不高、收敛效果不好。此外还可发现,在收敛参数α和γ取值为0.1和0.2时,不同收敛参数获得的最终优化结果大致相同。这表明结构的最终优化结果和损伤分布的均匀程度是大致相同的,与收敛参数的取值关系不大。综合考虑收敛的稳定性、收敛速度,本文建议在地震均匀损伤优化时,收敛参数α和γ取值均为0.2。
3.2 优化前、后结构性能对比
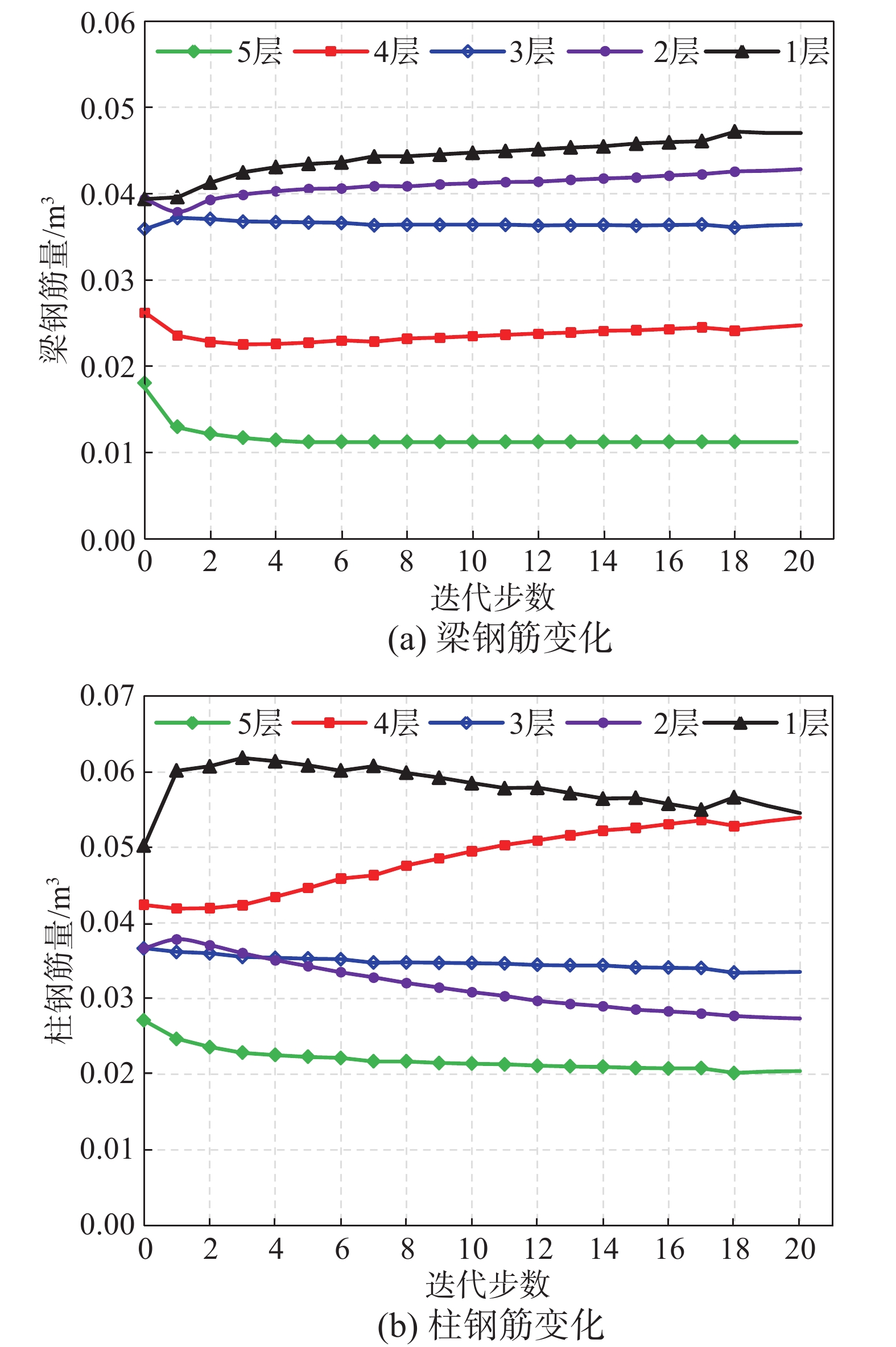
以5层结构为例,图8给出了结构在等造价优化过程中梁柱钢筋的变化情况。从图8中可以看出,随着优化的进行,各层梁柱钢筋均发生了变化。对于梁构件,1层和2层梁在整个优化过程中,其配筋逐渐增加;3层梁配筋总体上未发生变化;4层配筋先减小后又轻微地增加;5层梁配筋逐渐减小直至达到最小配筋率要求。对于柱构件,1层柱配筋先增加后逐渐减少,且达到优化状态时的配筋比初始结构有一定增加;2层钢筋先略微增加后一直逐渐减小;3层和5层钢筋在优化过程中一直减小而4层钢筋在优化过程中一直增加。12层结构也有类似的分析结论。表3给出了5层结构规范设计和优化设计结构的梁柱纵筋对比。从表3中可以看出,对于柱构件,优化设计底层柱和4层柱的配筋率相比规范设计有明显的增大;对于梁构件,优化设计结构的中下部楼层的配筋率有较为明显的增加。对于本文所提的优化设计方法,正是由于结构中梁柱构件配筋的相互转移,才使得结构的损伤逐渐趋于均匀。
表 3 5层结构规范设计和优化设计得到的梁柱纵筋对比Table 3. Comparison of longitudinal steel reinforcement ratio of the 5-story structure between code-based design and near optimum design楼层 原始设计 优化设计 柱配筋率/(%) 梁配筋率/(%) 柱配筋率/(%) 梁配筋率/(%) 边柱 内柱 边跨 中跨 边柱 内柱 边跨 中跨 1 1.52 1.52 0.95 0.95 1.65 1.65 1.30 1.30 2 1.28 1.75 0.95 0.95 0.95 1.31 1.19 1.19 3 1.28 1.75 1.44 1.44 1.17 1.60 1.49 1.49 4 2.27 2.27 0.99 0.99 2.89 2.89 1.01 1.01 5 1.45 1.45 0.55 0.55 1.09 1.09 0.34 0.34 需注意的是,梁柱转角作为构件的局部损伤指标,在本文被用来建立均匀损伤优化设计程序。为量化分析优化前、后结构的梁柱转角大小,以12层结构为例,图9给出了等造价优化结构与原始结构的梁柱转角中位值的对比。从图9(a)中可以看出,优化设计使得梁端转角分布更加均匀,同时降低了梁端转角的最大值。对于柱端转角(图9(b)),在优化前、后的转角值均较小,这表明结构柱主要处于弹性状态,确保了结构的“强柱弱梁”破坏机制;同时通过优化设计,结构柱在强震作用下将获得更小的柱端转角。
为验证优化前、后结构的均匀损伤分布情况,图10给出了成本不变、成本增加和成本减少三种情况下结构在多条地震动下层间位移角的中位值分布情况。从图10中可以看出,原始结构的层间位移角呈现出中下部楼层较大、上部楼层较小的情况,表明上部楼层的材料并未得到充分利用。经过均匀损伤优化设计后,无论材料成本是否变化,各楼层的材料得到了充分利用,结构的层间位移角均趋向于均匀化。具体来说,5层结构通过优化设计使得层间位移角的变异系数从25.2%下降到4.05%(成本−5%)、2.04%(成本不变)和0.84%(成本+5%),而12层结构对应的变异系数从35.21%分别下降到14.73%、11.48%和8.02%。需注意的是,经过均匀损伤优化后的12层结构上部楼层的层间位移角仍较小,未实现均匀化,这是由于达到收敛条件时的梁柱截面配筋均已达到最小配筋率要求,不能再进一步减少配筋。此外,随着材料成本的增加,层间位移角逐渐变小,这一现象在12层结构中表现得更加明显。在成本不变、成本减少5%和成本增加5%的约束条件下,5层结构的最大层间位移角从1.39%分别下降至1.27%和1.21%,而12层结构从1.44%降低至1.32%和1.23%。由此可以看出,本文所提的均匀损伤优化设计方法,在不同成本条件下均能实现结构地震损伤均匀分布的目标,且优化设计将降低结构的最大层间位移角,提高了结构的抗震性能。
4 结论
基于均匀损伤的思想,本文提出了RC框架结构抗震优化设计方法。以两个5层和12层的钢筋混凝土结构为例,研究了收敛参数、成本约束条件等对优化过程和优化结果的影响,得到以下主要结论:
(1) 本文所提的均匀损伤优化设计方法,综合考虑了结构整体损伤与局部损伤分布,能实现结构材料合理有效地从损伤轻微部位向损伤严重部位转移,形成结构的全局耗能机制。
(2) 收敛参数α和γ对收敛速度和收敛的稳定性均有影响。通过对收敛参数的敏感性分析,建议收敛参数α、γ取值为0.2。
(3) 本文所发展的优化方法在不同的材料成本约束下,均能实现结构损伤的均匀分布,且能降低结构的最大层间位移角,提高结构的整体抗震性能。
-
表 1 基础参数
Table 1 Footing parameter
/m 基础参数 5层 12层 内柱 外柱 内柱 外柱 长度Lf 1.9 1.4 3.2 2.4 宽度Bf 1.9 1.4 3.2 2.4 高度Hf 0.5 0.5 1.5 1.5 埋深Df 1.6 1.6 3.6 3.6 表 2 10条地震动信息
Table 2 10 ground motion records
编号 NGA 地震名称 震级 台站 分量 PGA/g GM1 163 Imperial Valley-06, 1979 6.53 Calipatria Fire Station H-CAL315 0.078 GM2 172 Imperial Valley-06, 1979 6.53 El Centro Array #1 H-E01230 0.134 GM3 1762 Hector Mine, 1999 7.13 Amboy 21081360 0.150 GM4 186 Imperial Valley-06, 1979 6.53 Niland Fire Station H-NIL360 0.069 GM5 51 San Fernando, 1971 6.61 2516 Via Tejon PV PVE65 0.026 GM6 719 Superstition Hills-02, 1987 6.54 Brawley Airport B-BRA225 0.156 GM7 737 Loma Prieta, 1989 6.93 Agnews State Hospital AGW000 0.172 GM8 800 Loma Prieta, 1989 6.93 Salinas - John & Work SJW160 0.091 GM9 832 Landers, 1992 7.28 Amboy ABY000 0.115 GM10 93 San Fernando, 1971 6.61 Whittier Narrows Dam WND143 0.100 表 3 5层结构规范设计和优化设计得到的梁柱纵筋对比
Table 3 Comparison of longitudinal steel reinforcement ratio of the 5-story structure between code-based design and near optimum design
楼层 原始设计 优化设计 柱配筋率/(%) 梁配筋率/(%) 柱配筋率/(%) 梁配筋率/(%) 边柱 内柱 边跨 中跨 边柱 内柱 边跨 中跨 1 1.52 1.52 0.95 0.95 1.65 1.65 1.30 1.30 2 1.28 1.75 0.95 0.95 0.95 1.31 1.19 1.19 3 1.28 1.75 1.44 1.44 1.17 1.60 1.49 1.49 4 2.27 2.27 0.99 0.99 2.89 2.89 1.01 1.01 5 1.45 1.45 0.55 0.55 1.09 1.09 0.34 0.34 -
[1] Ou J P, Li H. The regional engineering damage and reconstruction strategy in Wenchuan earthquake of China [J]. Journal of Earthquake and Tsunami, 2011, 5(2): 189 − 216. doi: 10.1142/S1793431111000929
[2] Chao S H, Goel S C, Lee S S. A seismic design lateral force distribution based on inelastic state of structures [J]. Earthquake Spectra, 2007, 23(3): 547 − 569. doi: 10.1193/1.2753549
[3] Hajirasouliha I, Moghaddam H. New lateral force distribution for seismic design of structures [J]. Journal of Structural Engineering, 2009, 135(8): 906 − 915. doi: 10.1061/(ASCE)0733-9445(2009)135:8(906)
[4] Leelataviwat S, Goel S C, Božidar S. Energy-based seismic design of structures using yield mechanism and target drift [J]. Journal of Structural Engineering, 2002, 128(8): 1046 − 1054. doi: 10.1061/(ASCE)0733-9445(2002)128:8(1046)
[5] Liu X, Yi W J, Li Q S, et al. Genetic evolutionary structural optimization [J]. Journal of Constructional Steel Research, 2008, 64(3): 305 − 311. doi: 10.1016/j.jcsr.2007.08.002
[6] Chan C M, Zou X K. Elastic and inelastic drift performance optimization for reinforced concrete buildings under earthquake loads [J]. Earthquake Engineering and Structural Dynamics, 2004, 33(8): 929 − 950. doi: 10.1002/eqe.385
[7] Hajirasouliha I, Asadi P, Pilakoutas K. An efficient performance-based seismic design method for reinforced concrete frames [J]. Earthquake Engineering and Structural Dynamics, 2012, 41(4): 663 − 679. doi: 10.1002/eqe.1150
[8] 徐龙河, 吴耀伟, 李忠献, 等. 基于性能的钢框架结构失效模式识别及优化[J]. 工程力学, 2015, 32(10): 44 − 51. Xu Longhe, Wu Yaowei, Li Zhongxian, et al. Performance-based seismic failure mode identification and optimization for steel frame structures [J]. Engineering Mechanics, 2015, 32(10): 44 − 51. (in Chinese)
[9] 李忠献, 王虹, 吕杨, 等. 钢筋混凝土框架结构地震失效模式优化[J]. 天津大学学报(自然科学与工程技术版), 2014, 47(4): 364 − 370. Li Zhongxian, Wang Hong, Lü Yang, et al. Failure mode optimization of reinforced concrete frames under earthquake excitations [J]. Journal of Tianjin University (Science and Technology), 2014, 47(4): 364 − 370. (in Chinese)
[10] 吕大刚, 宋鹏彦, 陈志恒. 钢筋混凝土框架结构基于可靠度的最可能倒塌失效模式分析[J]. 工程力学, 2012, 29(5): 156 − 160, 173. Lü Dagang, Song Pengyan, Chen Zhiheng. Analysis of the most likely collapse modes of RC frame structures based on reliability theory [J]. Engineering Mechanics, 2012, 29(5): 156 − 160, 173. (in Chinese)
[11] 郑山锁, 孙龙飞, 司楠, 等. 型钢混凝土框架结构失效模式的识别和优化[J]. 振动与冲击, 2014, 33(4): 167 − 172. doi: 10.3969/j.issn.1000-3835.2014.04.030 Zheng Shansuo, Sun Longfei, Si Nan, et al. Recognition and optimization for failure modes of SRC frame structures [J]. Journal of Vibration and Shock, 2014, 33(4): 167 − 172. (in Chinese) doi: 10.3969/j.issn.1000-3835.2014.04.030
[12] 孙爱伏, 侯爽, 欧进萍. 高层钢结构基于均匀损伤设计的整体抗震能力提高方法[J]. 地震工程与工程振动, 2012, 32(2): 74 − 81. Sun Aifu, Hou Shuang, Ou Jinping. A method for increasing the integral seismic capacity of tall steel buildings based on uniform-damage seismic design [J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(2): 74 − 81. (in Chinese)
[13] 白久林, 杨乐, 欧进萍. 基于等损伤的钢框架结构抗震性能优化[J]. 工程力学, 2015, 32(6): 76 − 83. Bai Jiulin, Yang Le, Ou Jinping. Aseismic performance optimization of steel frame structures based on uniform damage concept [J]. Engineering Mechanics, 2015, 32(6): 76 − 83. (in Chinese)
[14] 白久林, 金双双, 欧进萍. 钢筋混凝土框架结构强柱弱梁整体失效模式可控设计[J]. 工程力学, 2017, 34(8): 51 − 59. Bai Jiulin, Jin Shuangshuang, Ou Jinping. Strong-column weak-beam global seismic failure mode control-based design of reinforced concrete frame structures [J]. Engineering Mechanics, 2017, 34(8): 51 − 59. (in Chinese)
[15] Bai J L, Yang T, Ou J P. Improved performance-based plastic design for RC moment resisting frames: Development and a comparative case study [J]. International Journal of Structural Stability and Dynamics, 2018, 18(4): 1 − 24.
[16] Bai J L, Jin S S, Ou J P. An efficient method for optimizing the seismic resistance of reinforced concrete frame structures [J]. Advances in Structural Engineering, 2019: 1 − 17.
[17] Bai J L, Jin S S, Zhang C, et al. Seismic optimization design for uniform damage of reinforced concrete moment-resisting frames using consecutive modal pushover analysis [J]. Advances in Structural Engineering, 2016, 19(8): 1313 − 1327. doi: 10.1177/1369433216642045
[18] 张炳华, 侯旭. 土建结构优化设计 [M]. 上海: 同济大学出版社, 1998. Zhang Binua, Hou Xu. Optimization design for civil building structures [M]. Shanghai: Tongji University Press, 1998. (in Chinese)
[19] Spillers W R, MacBain K M. Structural optimization [M]. New York: Springer, 2009.
[20] GB 50011−2010, 建筑抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2010. GB 50011−2010, Code of seismic design of buildings [S]. Beijing: China Architecture and Building Press, 2010. (in Chinese)
[21] OpenSees (2013), Open system for earthquake engineering simulation, Version 2.4.2 [CP]. Pacific Earthquake Engineering Research Center, University of California, Berkeley,2013. <http://opensees.berkeley.edu>.
[22] FEMA356, Pre-standard and commentary for the seismic rehabilitation of buildings [S]. Washing D C: U.S. Federal Emergency Management Agency, 2000.
[23] Raychowdhury P. Nonlinear winkler-based shallow foundation model for performance assessment of seismically loaded structures [M]. San Diego: University of California, 2008.
[24] PEER(2005), PEER ground motion database [DB]. CA: Pacific Earthquake Engineering Research Center, University of California, Berkeley, 2005. <http://peer.berkeley.edu/nga/> .
-
期刊类型引用(8)
1. 吴山,何浩祥,兰炳稷. 面向均匀损伤的RC框架结构抗震优化设计方法. 工程力学. 2024(04): 210-221 .  本站查看
本站查看
2. 王玉奎,刘哲锋,张丹,胡张齐. RC梁构件基于能量的抗震设计方法研究. 工程力学. 2023(11): 218-226 .  本站查看
本站查看
3. 覃思中,廖文杰,林元庆,陆新征. AN EFFICIENT ASSESSMENT METHOD FOR INTELLIGENT DESIGN RESULTS OF SHEAR WALL STRUCTURE BASED ON MECHANICAL PERFORMANCE, MATERIAL CONSUMPTION, AND EMPIRICAL RULES. 工程力学. 2023(12): 148-159 .  本站查看
本站查看
4. 白久林,冯明富,李文学,陈辉明,刘明辉,金双双. 防屈曲支撑-RC框架新型开孔钢板剪力键连接节点抗震性能研究. 工程力学. 2022(06): 110-121 .  本站查看
本站查看
5. 任重翠,李建辉,唐意,刘军进,严亚林,郝玮,孙超. 风震联合作用下高层建筑主体结构和玻璃幕墙的性能研究. 工程力学. 2022(07): 58-69 .  本站查看
本站查看
6. 马利,朱雷,曹敏,杨世华,吴辉贤. 框架结构排缸的刚性分析和结构优化. 化工与医药工程. 2022(03): 49-53 .  百度学术
百度学术
7. 白久林,孙博豪,金双双. 适用于滞变性能退化结构体系抗震设计的新型侧向力模式. 振动与冲击. 2021(20): 223-231 .  百度学术
百度学术
8. 秦鹏,郑宏宇,黄琦. 基于抗震RC框架梁节点设计问题的研究进展. 建筑技术开发. 2020(21): 27-28 .  百度学术
百度学术
其他类型引用(3)



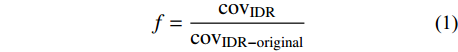
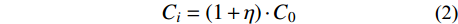

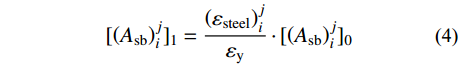
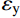

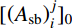
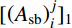

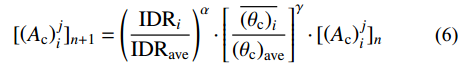
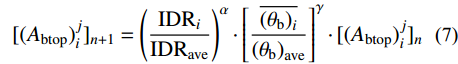

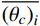
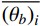

 下载:
下载: