EXPERIMENTAL STUDY ON THE MECHANICAL PERFORMANCE OF ANGLE SHEAR CONNECTORS WITH AND WITHOUT CONCRETE GAPS
-
摘要: 对于采用角钢连接件的钢壳沉管隧道结构，上翼缘板和角钢相连部位不利于混凝土流通、振捣和排气，浇筑时易产生混凝土脱空现象。基于实际工程和规范建议设计了9组足尺推出试件，包含3种脱空深度(0 mm、10 mm及20 mm)。为了减少试验本身的离散性，每组均有3个试件，共计27个试件。试验中所有试件均发生混凝土压溃破坏，相比于无脱空试件，脱空试件的混凝土压溃区域更小且角钢变形更大。相比于无脱空试件，脱空深度为10 mm和20 mm时，连接件的承载力折减可达16.5%和37.5%，刚度折减可达48.4%和70.6%。比对文献中62组试件以及文中3组试件的试验结果发现，Kiyomiya和Kimura提出的回归公式具有较高的准确度和较小的离散性，日本《钢-混凝土三明治结构设计指南》的公式则比较保守；此外基于现有试验数据通过参数回归的方式，提出了新的角钢连接件承载力计算公式，该公式具有更好的精度和适用性。在该文中提出的回归公式和混凝土脱空力学模型的基础上，提出了考虑混凝土脱空的角钢连接件承载力修正公式，通过文献中3组试件及该文6组试件进行验证，结果表明该修正公式具有较高的准确度和较小的离散性。Abstract: Because it is difficult for the flow, vibration and gas exhaust of concrete, gaps may exist near the welded regions of angle shear connectors. Based on the engineering practice and standard provisions, a test on nine groups of full-scale push-out specimens of three different gap depths (0, 10 mm and 20 mm) was conducted. To reduce the discreteness, there were three duplicate specimens in each group. All specimens failed in concrete crushing in the test. Compared with the specimens without a gap, the crushing area was smaller and the deformation of the angle steel was larger in the specimens with a gap. The concrete gap had a significant influence on the strength and stiffness of the angle shear connectors. Compared with that of the specimens without a gap, the strength was decreased by 16.5% and 37.5% and the stiffness was decreased by 48.4% and 70.6% for the specimens with a gap of 10 mm and 20 mm, respectively. Different formulas in the literature were verified based on 62 groups of specimens in other papers and 3 groups of specimens in the current test. The formula proposed by Kiyomiya and Kimura was found to have good accuracy and small discreteness, while the formula proposed by 《Design Code for Steel-Concrete Sandwich Structures》in Japan was conservative. A new shear strength empirical formula was proposed based on the existing experimental data, which showed better accuracy and applicability. Based on the new shear strength formula and a mechanical model considering the concrete gap, a shear strength corrected formula for angle shear connectors with concrete gaps was proposed. The proposed corrected formula was verified based on 3 groups of specimens in other papers and 6 groups of specimens in the current test and was found to have good accuracy and small discreteness.
-
由于具有对水上航运影响小、占地及拆迁量少、受恶劣天气影响小等优点，沉管隧道越来越多代替桥梁成为穿越江河海湾的工具[1]，沉管隧道主要可以分为混凝土沉管隧道和钢壳沉管隧道两大类。钢壳具有自重轻的优点并且可以作为混凝土浇筑的模板，实现混凝土水上浮态浇筑，大大减少水上托运工作量[2]。同时钢壳具有较好的延性、防水性，可以提高隧道整体结构的延性和耐久性，此外硬化混凝土还可以约束钢壳的屈曲，因此钢壳沉管隧道在近些年得到越来越广泛的应用[2-3]。
典型的钢壳沉管隧道横截面如图1所示，由多个双钢板墙面组成，其中典型墙面构造如图1(b)所示，包括上、下翼缘板，隔板以及连接件等组件，其中相邻纵横隔板相交构成单元区格[3]。钢壳的上、下翼缘板和纵横隔板分别起到加强结构抗弯和抗剪性能的作用。由于钢壳本身可以抵抗弯矩和剪力，考虑到施工的便利性，钢壳沉管隧道内往往不会放置钢筋[3]。
连接件是保证钢和混凝土共同工作的关键，常见形式的连接件包括栓钉连接件和PBL连接件[4]。针对传统的栓钉和PBL连接件，近些年仍有学者对其展开试验及理论研究[5-7]，但对角钢连接件的研究近些年则相对较少。相比于栓钉连接件，角钢连接件具有较好的疲劳性能和较高的承载力和刚度[8]。通常PBL连接件需要在钢板上开孔且贯穿钢筋需要放置于孔内，角钢连接件施工仅需要进行通常焊接即可，施工相对便捷。如图2所示，角钢连接件除了具有传递剪力的作用以外，还可以提高相连翼缘的惯性矩，减少施工阶段翼缘的面外鼓屈。此外当混凝土硬化后，角钢连接件还可以为受压侧钢板提供面外约束，约束受压钢板的屈曲。由于具有上述优点，角钢连接件在钢壳沉管隧道中得到广泛的应用[3, 8]。
沉管隧道所处水体温度变化一般较小，温度导致的混凝土收缩也相对较小，类似于钢管混凝土，钢壳的包裹使混凝土处于密闭保水养护状态，干燥收缩和碳化收缩量很小[9]，大面积脱空在沉管隧道中较为少见。
由于浇筑方向的原因，浇筑上表面混凝土会存在浇筑不密实情况，产生如图3所示的孔隙及孔洞现象，日本的现场浇筑试验表明脱空面积约为总面积的5%[10]。浇筑试验还表明，流动性越好的混凝土产生的脱空缺陷会越小，但即使采用高流动性混凝土，隧道上表面仍会出现不规则分布的孔洞，大部分孔洞的深度均在5 mm以内，少部分为10 mm~20 mm[8]。
![]()
图 3 钢壳沉管隧道上表面混凝土缺陷Figure 3. Concrete imperfections on top surface of steel-shell immersed tunnels由于角钢连接件根部存在倒角，不利于浇筑时的排气与振捣，在实际浇筑过程中，在连接件根部可能会产生如图4所示的大尺寸脱空。相关研究表明，当脱空深度达到20 mm时，连接件承载力折减可达31%[11]。
1 研究现状及总结
1.1 角钢连接件力学性能研究现状
Hiroshi和Kiyomiya[12]通过推出试验研究了角钢连接件的受剪性能，推出试件中角钢连接件存在三种破坏机制：连接件剪断、混凝土劈裂破坏及混凝土压溃破坏，其中大多试件发生混凝土劈裂或压溃破坏。研究结果表明，影响连接件承载力的主要因素为连接件腹板厚度以及混凝土抗压强度，文章基于试验数据的回归给出了承载力计算的经验公式[12]：
Vu=88√tw√f′c (1) 式中：Vu/(N/mm)为单位长度抗剪承载力；tw/mm为连接件腹板厚度；
f′c /(N/mm2)为混凝土圆柱体抗压强度。Chuah等[13]通过推出试验研究了型钢连接件的受剪性能，结果表明，当多个型钢连接件共同受剪时，连接件间距减小会导致单个连接件的抗剪承载力下降。Ueda[14]通过推出试验研究了型钢连接件的受剪性能，试验表明当型钢连接件相连翼缘板变薄时，连接件的抗剪承载力会下降。基于上述研究结果，日本《钢-混凝土三明治结构设计指南》给出了角钢连接件的抗剪承载力计算公式[15]：
Vu=5.6hsc√f′ck1k2k3⩽ (2) 式中：hsc/mm为连接件高度；Vb/(N/mm)为连接件根部钢材或焊缝单位长度抗剪承载力； k1代表连接件高厚比影响系数；k2代表相连翼缘厚度影响系数；k3代表连接件间距影响系数。
Soty和Shima[16]通过单侧钢板组合梁试验研究了角钢连接件的受剪性能，研究发现组合梁中角钢连接件存在三种破坏机制：混凝土劈裂破坏、混凝土压溃破坏及混凝土剪切破坏。试验结果表明，当连接件发生混凝土压溃破坏和剪切破坏时，承载力更高且延性更好[16]。文献[16]中基于极限平衡法推导了连接件抗剪承载力，得出抗剪承载力和
\sqrt {f_{\rm{c}}'} 成正比的结论，表明混凝土抗压强度对角钢连接件的抗剪承载力有显著影响[16]。Saidi等[17]试验研究了双钢板组合梁中角钢连接件的受力性能，测量了角钢腹板不同高度处的曲率值。文献[17]将角钢连接件的腹板等效为埋在混凝土中的地基梁，并对角钢腹板的变形及曲率值进行理论推导。试验和理论结果均表明，腹板根部处曲率最大，该处混凝土的压应力也为最大[17]。
1.2 混凝土缺陷影响研究现状
Kiyomiya和Kimura[11]通过试验研究了混凝土浇筑缺陷对角钢连接件抗剪承载力的影响。如图5所示，可以根据脱空位置和剪力方向的关系将脱空分为正面脱空、背面脱空及双面脱空三种形式。试验结果表明，背面脱空对抗剪承载力基本没有影响[11]，这是由于连接件在受剪过程中主要和剪力方向的正面混凝土块发生挤压，因此背面脱空对连接件影响受剪性能影响较小。当正面脱空深度为10 mm、20 mm、30 mm时，试件的抗剪承载力分别折减14%、31%、36%[11]。
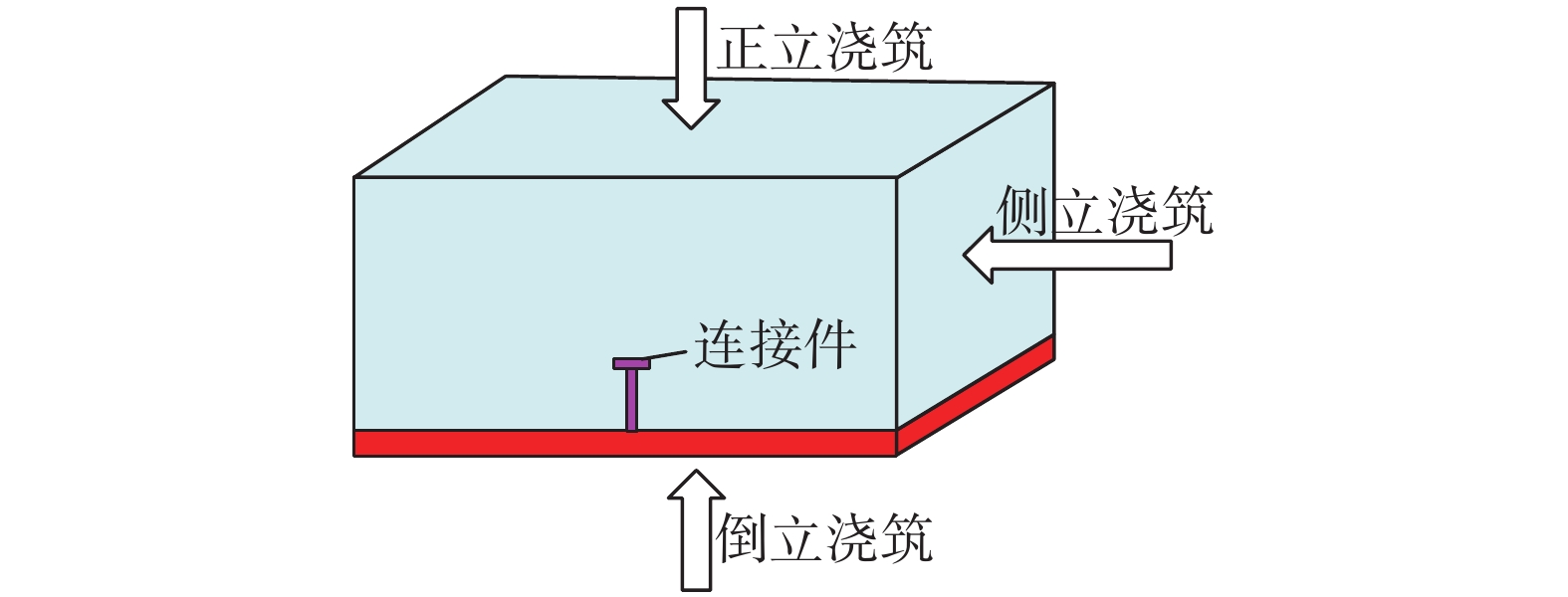
如图6所示，刘玉擎等[18-19]研究了浇筑方向对栓钉连接件受力性能的影响。试验结果表明，不同浇筑状态对栓钉和开孔板连接件抗剪承载力影响不大，受到混凝土离析等因素的影响，侧立浇筑会显著降低栓钉连接件和开孔板连接件的抗剪刚度，从而影响连接件正常使用阶段受力性能[16-17]。
此外，由于混凝土收缩徐变及温度变化的原因[20]，钢管混凝土中混凝土脱空较为普遍，因此针对钢管混凝土结构的混凝土脱空研究也相对较多。脱空主要通过影响钢和混凝土间共同工作性能从而降低构件及结构的承载力，脱空范围越大及深度越大时，钢管混凝土结构的力学性能下降越显著[21-22]。
1.3 现有研究总结及本文思路
现有针对角钢连接件力学性能研究相对较少，且主要集中在日本，试验中的大尺寸试件也相对较少。为了使角钢连接件更好地适用于中国的结构，本文在参考《热轧型钢》(GB/T 706−2008)[23]的基础上，采用大尺寸角钢设计试验连接件，并通过推出试验研究角钢连接件的力学性能。
目前研究混凝土脱空对角钢力学性能影响的文献也很少，且试件尺寸单一、主要考虑抗剪承载力，忽视了连接件尺寸的影响以及抗剪刚度这一指标。本文通过对不同尺寸和不同脱空深度的连接件展开试验，研究连接件受剪过程的剪力-相对位移全曲线，来更好地评估混凝土脱空对连接件力学性能的影响。
2 试验设计
2.1 试件尺寸
根据《热轧型钢》(GB/T 706−2008)[23]中角钢尺寸以及实际的脱空情况[10]，本文共设计了9组试件，包含3种连接件尺寸以及3种脱空深度。三种尺寸连接件型号分别为L150×90×10 (L150)、L180×110×10 (L180)以及L200×125×12 (L200)，混凝土脱空深度分别为0 mm(无脱空)、10 mm及20 mm。每种连接件尺寸均对应三种脱空深度，共计9组试件。为了减少骨料分布等因素导致的离散性[24-25]，每组推出试验均包含3个试件，共计27个试件。
为了防止加载时受压钢板出现屈曲，加载时角钢相连型钢采用箱形截面。考虑到一般钢壳沉管隧道中不会放置钢筋，推出试件采用素混凝土以更好模拟实际工程。研究表明只有剪力方向的正面混凝土对连接件性能存在显著影响[11]，因此本文在设置脱空时仅考虑正面脱空这一形式，考虑最不利影响，脱空沿角钢全长布置，其中脱空深度和长度之比为1∶10。试件的尺寸及脱空布置如图7所示。
试件混凝土采用等级为C40的混凝土，钢材采用标号为Q345的钢材，角钢和加载型钢间采用角焊缝连接，通过构造和检测保证角焊缝的强度要大于相连的角钢腹板，以免在焊缝处发生破坏。混凝土脱空通过填充低弹模的EVA材料进行模拟，推出试件实物如图8所示。
2.2 材料参数
为了保证材料参数的准确，推出试验和150 mm立方体试块单轴压缩试验同期进行，立方体抗压强度按规范选取3个试块抗压强度的平均值[26]。为了测量角钢板件的钢材强度测试，取同一批次的钢板标准试件进行标准拉伸试验[27]。此外为了减少离散性，每种厚度的钢板均包含4个试件。取试件的平均值作为该厚度钢板的力学性能指标。角钢共有10 mm和12 mm两种厚度的钢板，钢板材性参数见表1。
表 1 角钢材性参数Table 1. Material parameters of angle steels板厚/mm 屈服强度/
(N/mm2)屈服应变/
(×10−6)极限强度/
(N/mm2)延伸率/
(%)10 365 1764 503 28.5 12 380 2125 532 26.4 由于浇筑批次和加载时间导致的差异，各组试件混凝土强度存在一定差异，试件的混凝土强度指标见表2。
表 2 各组推出试件的关键参数Table 2. Key parameters of push-out specimens in each group组名 角钢型号 脱空深度/mm 立方体抗压强度/(N/mm2) L150-0 L150×90×10 0 51.9 L150-10 L150×90×10 10 48.9 L150-20 L150×90×10 20 51.9 L180-0 L180×110×10 0 55.8 L180-10 L180×110×10 10 51.1 L180-20 L180×110×10 20 51.1 L200-0 L200×125×12 0 48.9 L200-10 L200×125×12 10 51.1 L200-20 L200×125×12 20 51.1 注：由于每组均包含3个试件，之后描述同一组的三个试件时，分别在组名后添加−1、−2和−3加以区分。 2.3 加载及量测
如图9所示，推出试验采用量程为5000 kN的液压千斤顶进行加载。为了保证结构处于静力响应状态，加载速度为0.02 mm/s，当载荷下降到0.85倍峰值载荷时停止加载[28]。钢和混凝土间的界面滑移和角钢变形均为研究中常用的相对位移量[16-17]，其中界面滑移(滑移)和角钢变形(变形)的定义如图10所示。考虑到测量的准确性，如图9所示，分别采用4个位移计对界面滑移和角钢变形进行测量，各试件的滑移和变形值取四个位移计的平均值。
Saidi等[17]通过在角钢腹板贴应变片的方式测量角钢的曲率，结果表明受剪过程中连接件腹板类似于埋在混凝土内的地基梁。现有研究尚未在角钢翼缘板布置应变片，为了进一步研究角钢连接件的受力特征，如图11所示，本试验除了在角钢腹板两侧上布置一定数量的应变片外，还在角钢翼缘两侧布置一定数量的应变片。
3 试验结果
3.1 破坏形式及抗剪承载力
9组试验共计27个试件均表现为混凝土压溃破坏，以L150角钢为例，三种脱空深度的连接件典型破坏模式如图12所示。试件加载至破坏过程中，首先在角钢肢尖处产生应力集中并导致斜向裂缝(虚线线条)，之后角钢内侧混凝土发生压溃，压溃过程产生纵横向裂缝(实线线条)，最终角钢根部混凝土发生压溃破坏，试件达到抗剪承载力。从图12可以看出，脱空深度越大时，混凝土压溃区域(红色线条范围)越小。
值得注意的是，由于钢结构加工以及混凝土浇筑等原因导致同一个试件两侧连接件存在一定的力学性能差异，加载过程中构件破坏时均是单侧混凝土先发生破坏，此时另一侧混凝土还未完全发生破坏，因此推出试件的实际承载力实际上是要略小于两侧连接件的承载力之和，这也是导致同一组试件的承载力存在差异的主要原因。
9组试件在受剪破坏时，角钢均呈现一定程度的弯折。以L150角钢为例，三种脱空深度的试件的北侧角钢变形如图13所示。从图13可以看出，由于脱空区域没有混凝土支撑，相比于无脱空试件，脱空试件的角钢腹板在根部的变形更大且在脱空深度处存在明显弯折。
各组试件的抗剪承载力的结果见表3，可以看出脱空试件的承载力显著小于无脱空试件。此外，对于不同型号的大尺寸角钢连接件，脱空高度对抗剪承载力的影响规律相似，脱空深度越大，承载力折减越明显。其中当脱空深度达到10 mm时，承载力折减最大可达16.5%，当脱空深度达到20 mm时，承载力折减最大可达37.5%。此外，本试验测得的脱空影响规律和日本文献[11]结果基本一致。
表 3 各组试件抗剪承载力Table 3. Shear strength of specimens in each group组名 抗剪承载力/kN 平均值/kN 折减率/(%) −1 −2 −3 L150-0 1302 1298 982 1194 − L150-10 810 1121 1062 998 16.5 L150-20 691 722 877 763 36.1 L180-0 894 1301 1121 1105 − L180-10 781 1113 1041 978 11.5 L180-20 − 792 589 691 37.5 L200-0 1152 1088 802 1014 − L200-10 812 796 1211 940 7.3 L200-20 747 661 753 720 29.0 注：折减率表示脱空深度不为0的试件(脱空试件)相对于脱空深度为0(无脱空)的承载力降低比率；其中L180-20-1试件由于加载中存在问题而剔除数据。 3.2 载荷-相对位移曲线
将各组的三个试件的载荷-滑移曲线进行平均处理后得到各组试件的剪力-滑移曲线，剪力滑移结果如图14所示。各组试件达到极限承载力时的滑移均在3 mm以内；在到达0.5倍极限载荷之前，试件的剪力-滑移曲线均基本保持直线；0.8倍极限载荷之后剪力-滑移曲线逐渐变缓，极限载荷之后曲线下降较快，在无脱空组曲线降幅更为显著，说明试件偏向脆性破坏。从图14可以明显看出，脱空会显著降低连接件承载力和刚度，但同时脱空会增大极限承载力时试件的滑移，由于滑移的很大贡献来自于角钢根部的变形，且脱空试件的角钢变形更大，因此脱空试件达到抗剪承载力时的滑移更大。
![]()
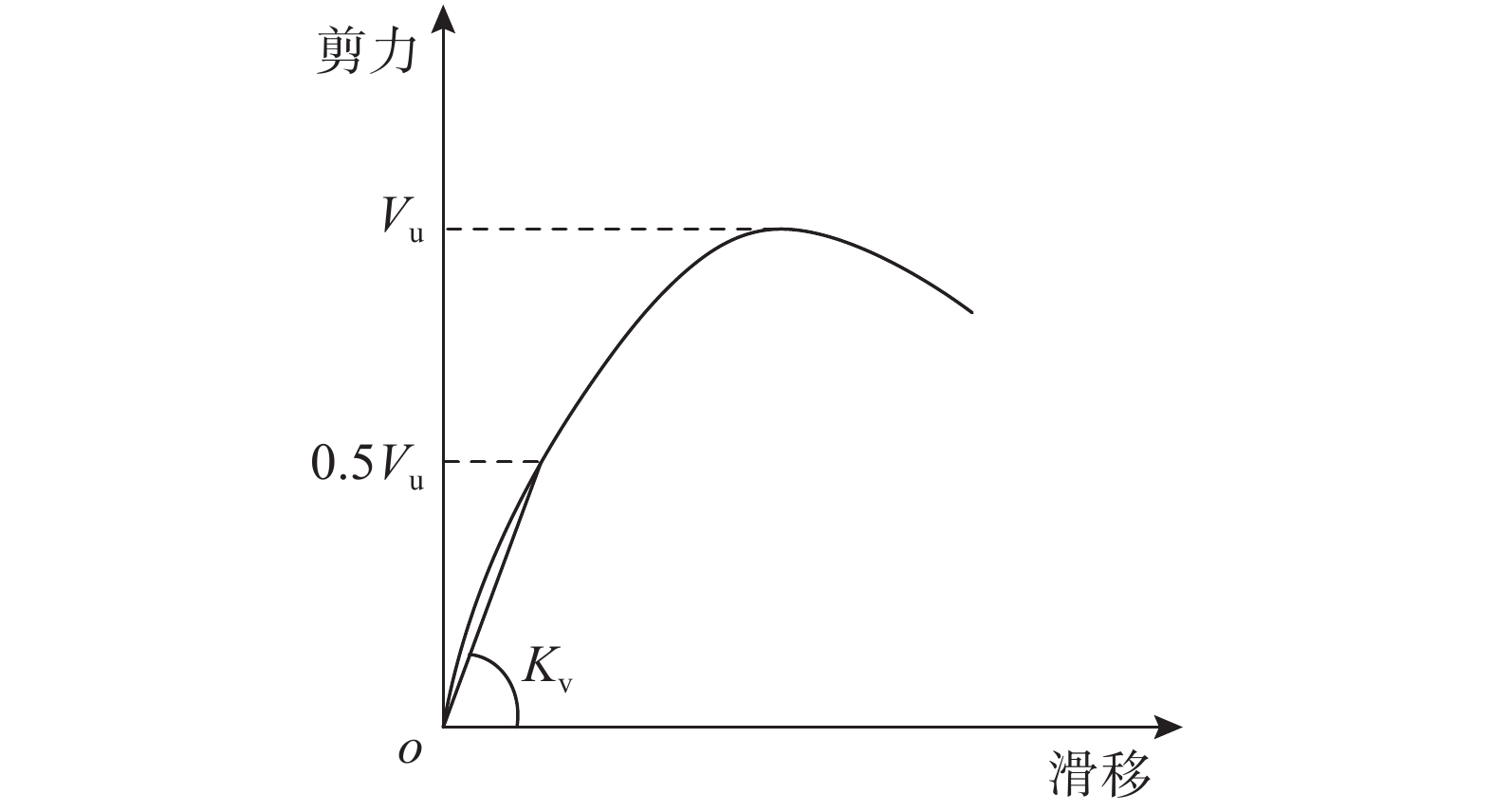
图 14 不同型号角钢的试件剪力-滑移曲线Figure 14. Shear force-slip curves of specimens with different shapes of angle steel连接件正常使用状态下的剪力一般为其承载力的0.5倍左右，如图15所示，可以考虑将连接件的抗剪刚度定义为0.5倍峰值载荷时的割线刚度Kv[29]。图16表示各组试件的抗剪刚度，其中斜纹方块、横纹方块以及竖纹方块分别代表脱空深度为0 mm、10 mm及20 mm。从图16可以看出，脱空对不同型号的角钢连接件均有影响：脱空深度达到10 mm时，连接件刚度折减最大可达48.4%；脱空深度达到20 mm时，连接件刚度折减最大可达70.6%。通过对比表3和图16的数据可以发现，脱空对连接件刚度的影响比对承载力的影响更大，说明脱空对正常使用阶段会存在更大影响。
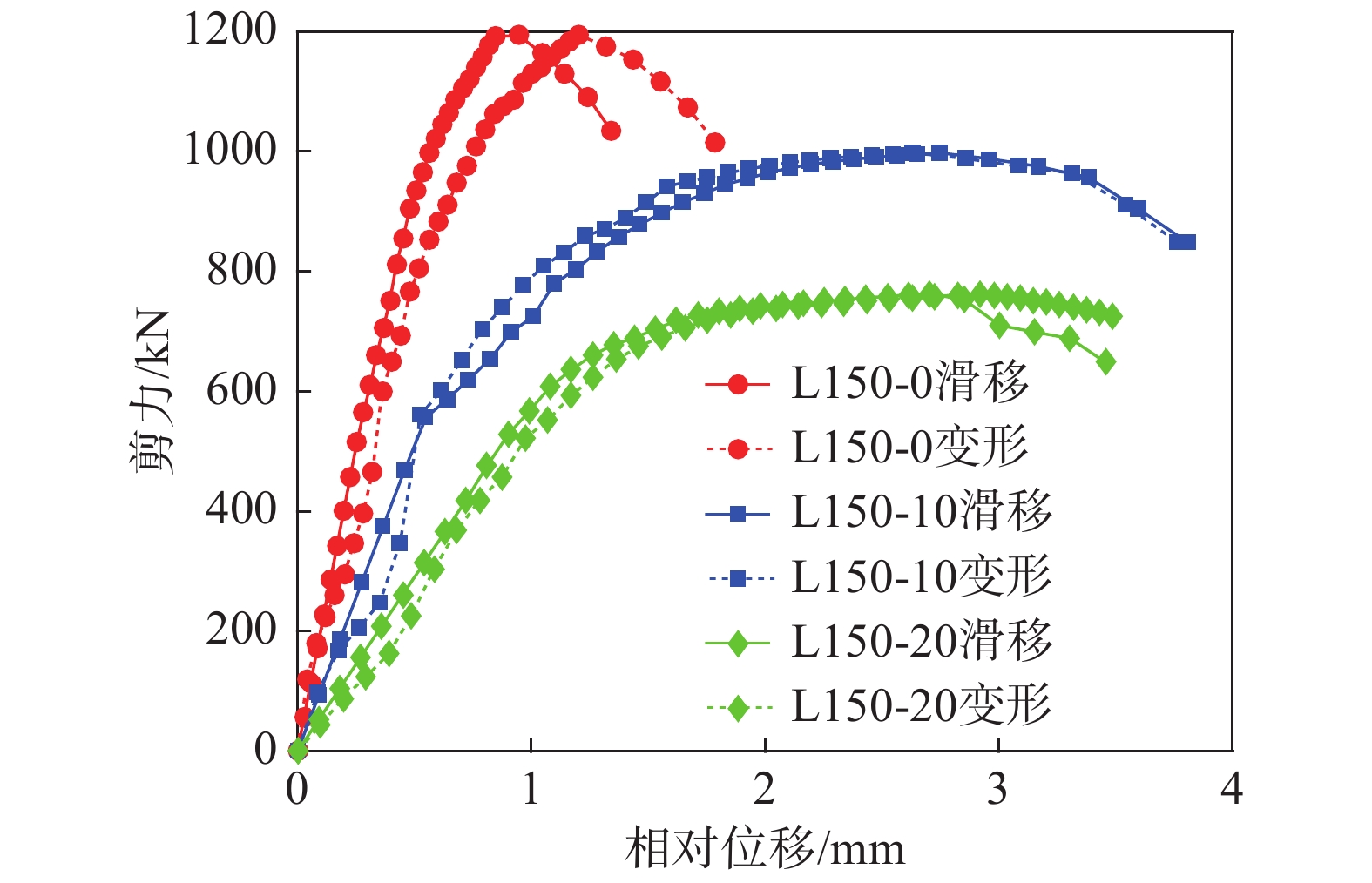
除了测量界面滑移以外，本试验还测量了角钢变形。以L150角钢为例，三种脱空深度的曲线对比如图17所示，试验中剪力-滑移和剪力-变形曲线差别不大，说明滑移量和变形量在加载过程中基本是一致的。参照图10，滑移和变形的结果差异主要来自于角钢后方混凝土的变形，试验过程中角钢后方混凝土基本没有变形，因此二者结果基本没有差异，两种测量手段均可作为角钢连接件的相对位移衡量指标。
3.3 角钢曲率分布
峰值载荷时，9组试件的南侧角钢应变分布如图18所示，实线段为腹板的曲率分布，虚线段为翼缘的曲率分布，且曲率点均标在受拉侧，L-180-20-1组的数据由于加载问题以及应变片失效而剔除。
![]()
图 18 各组试件角钢曲率分布 /(×10−6 mm−1)Figure 18. Distributions of curvatures of angle steel in each group从各组试件的腹板曲率可以看出，腹板根部曲率均较大，说明腹板根部承受较大的弯矩，但曲率数据表明各组试件的腹板均未进入屈服状态，进一步说明试件破坏是由混凝土压溃导致的。腹板根部曲率变化幅度较大表示该处弯矩变化幅度较大，由于剪力和弯矩的导数关系可知连接件根部承受较大的剪力。由于曲率变化方向发生改变，说明剪力沿腹板高度存在变向，且剪力变向位置大约在1/4腹板高度处。此外，所有试件分别在1/8和3/4左右高度处出现反弯点。
通过对比可以看出，脱空试件在腹板两个反弯点之间的曲率值显著大于无脱空试件。如图19所示，由于根部混凝土的压应力和根部剪力的方向相反，压应力的支撑可以减少由剪力导致的腹板变形，当存在混凝土脱空时，底部混凝土将无法提供压应力支撑，此时剪力将导致腹板产生更大的变形，因此腹板中部的曲率值会增大。
从各组试件的翼缘曲率可以看出，各组角钢翼缘的曲率均远小于腹板的曲率，说明角钢翼缘在连接件受剪过程中的贡献相对较小。由于翼缘主要的作用是限制腹板顶端的变形，而腹板顶变形主要集中在底端，顶端变形相对较小，因此翼缘发挥的作用也相对较小。从受剪力学性能以及经济性的角度出发，或许可以考虑适当削减角钢翼缘的用量。
4 理论分析
4.1 角钢连接件承载力计算
现有针对角钢连接件的研究多在日本进行，且计算公式多为经验回归公式，为了更好地衡量现有公式的准确性，本文收集了62组来自其他文献推出试验的数据[11-12]，加上本试验3组无脱空试件的数据，共计65组试件。65组试件均发生混凝土压溃破坏，说明一般构造条件下很难发生连接件剪断这一情况。考虑到公式的适用性，本文采用式(1)和式(2)对收集试件的承载力进行计算。需要注意的是，日本试验中大多采用的是圆柱体抗压强度，试验中若采用立方体试块，需要进行换算，对于标准试块，圆柱体抗压强度可以取为0.8倍的立方体抗压强度[30]。
从图20可以看出，大部分角钢连接件单位长度抗剪承载力在1 kN/mm~2.5 kN/mm，通过整理数据发现对于大尺寸连接件，其单位长度抗剪承载力基本都在1.5 kN/mm以上。图20中的平均值和变异系数是计算值和试验值比值的统计指标，通过图20可以看出，Hiroshi和Kiyomiya[12]提出的式(1)能较好地衡量角钢连接件的抗剪承载力，大部分计算结果都在15%误差线以内，只有少数小尺寸连接件的计算结果超出15%误差线。此外，日本《钢-混凝土三明治结构设计指南》中式(2)计算结果偏于保守，会在一定程度上低估角钢连接件的承载力。
![]()
图 20 现有角钢连接件抗剪承载力公式验证Figure 20. Verifications of existing shear strength formulas for angle shear connectors考虑到现有的角钢连接件承载力计算公式都是基于试验数据的参数回归的结果，因此本文在收集了已有文献[11-12]以及本试验中更多数据的基础上，拟采用参数回归的方法提出新的更适用性的角钢连接件承载力计算公式。通过对现有公式(式(1)和式(2))的分析，影响角钢连接件承载力的因素主要为连接件厚度tw、混凝土抗压强度
{f_{{\rm{c}}}^{\prime}} 及连接件高度hsc，经过回归得到角钢连接件的承载力计算公式如下：{V_{\rm{u}}} = 71{\left( {{t_{\rm{w}}}} \right)^{0.34}}{\left( {f_{{\rm{c}}}^{\prime }} \right)^{0.46}}{\left( {{h_{{\rm{sc}}}}} \right)^{0.16}} (3) 采用回归式(3)对现有试件的承载力计算结果与试验结果对比如图21所示，图中的平均值和变异系数是计算值和试验值的比值的统计指标，可以看出本文的拟合公式同样具有良好的精度。此外，相比于Hiroshi和Kiyomiya[12]提出的式(1)，拟合公式还可以进一步考虑连接件高度的影响。考虑到连接件受剪破坏多由混凝土压溃控制，破坏过程偏脆性，在对连接件承载力进行计算时需要适当增加安全储备。
![]()
图 21 角钢连接件抗剪承载力拟合公式验证Figure 21. Verifications of shear strength empirical formula for angle shear connectors4.2 考虑脱空后的承载力计算公式
目前仅有Kiyomiya和Kimura通过试验研究了脱空对角钢连接件抗剪承载力的影响[11]，样本量少而且缺少定量计算缺陷影响的公式。
研究表明，角钢连接件主要通过混凝土的压应力来抵抗剪力[11]：当存在脱空时，可以认为底部承压混凝土消失，导致失去一定的混凝土压应力，从而降低了连接件的抗剪承载力，如图22 (a)所示；由于工程脱空通常不超过20 mm[10]，可以假定存在脱空时混凝土压应力分布保持不变，混凝土脱空导致的承载力损失来源于无脱空试件和脱空试件的压应力图差，在该脱空深度he范围内可以认为混凝土压应力为常数σc，如图22 (b)所示。
考虑到极限状态下底部混凝土压应力状态较为复杂，本文通过回归计算σc，并且认为σc和混凝土圆柱体抗压强度
f_{\rm{c}}' 成正比。如图22 (b)所示，脱空导致的承载力损失Vde为无脱空试件承载力Vu和脱空试件承载力Vue的差值，根据之前假定可得Vde表达式：{V_{{\rm{de}}}} = {V_{\rm{u}}} - {V_{{\rm{ue}}}} = \alpha {f_{{\rm{c}}}^{\prime }}{h_{\rm{e}}} (4) 式中：Vue和Vde的单位均为N/mm；he的单位为mm；无量纲常数α为压应力σc和
{f_{c}^{\prime }} 的比值。已有脱空试件包括Kiyomiya和Kimura的3组试件[11]以及本试验的6组试件，共计9组试件。4.1节的计算结果表明，本文基于现有试验数据回归得到的式(3)能较好计算无脱空试件的抗剪承载力Vu。通过对脱空试件结果进行整理回归，结合本文提出的压应力图差模型，可以得到脱空试件的承载力表达式：
{V_{{\rm{ue}}}} = 71{\left( {{t_{\rm{w}}}} \right)^{0.34}}{\left( {f_{{\rm{c}}}^{\prime }} \right)^{0.46}}{\left( {{h_{{\rm{sc}}}}} \right)^{0.16}} - 0.85{f_{{\rm{c}}}^{\prime }}{h_{\rm{e}}} (5) 通过式(5)计算9组脱空试件的抗剪承载力，公式计算值和试验值对比见图23，图中的平均值和变异系数同样是计算值和试验值的比值的统计指标。从图23可以看出，本文基于式(3)和混凝土脱空力学模型提出的修正式(5)可以较好计算存在混凝土脱空时的角钢连接件抗剪承载力。
![]()
图 23 考虑混凝土脱空的角钢连接件抗剪承载力公式验证Figure 23. Verifications of shear strength formula for angle shear connectors with concrete gaps5 结论
本文通过文献分析、推出试验及理论推导的方式对角钢连接件的力学性能以及混凝土脱空对钢连接件的影响进行了研究。在收集了一定数量的现有试验数据的基础上，通过分析文献公式和推导理论模型，对角钢连接件抗剪承载力及考虑脱空影响时的承载力计算提供了相应的建议。主要结论如下：
(1) 9组连接件推出试验均发生混凝土压溃破坏，其中脱空会导致角钢根部产生弯折，并使得混凝土压溃区域变小，从而影响连接件力学性能。
(2)脱空会显著削弱角钢连接件的抗剪承载力和抗剪刚度，脱空对刚度的削弱比对承载力的削弱更为显著。脱空深度为10 mm和20 mm时，试验测得承载力折减可达16.5%和37.5%，刚度折减可达48.4%和70.6%。但同时脱空会增大连接件在极限承载力时的滑移，一定程度上可以提高连接件的变形能力。
(3) 连接件腹板根部的曲率及曲率变化幅度均较大，说明受剪时腹板根部承受较大的弯矩及剪力。当存在脱空时，角钢腹板中部的曲率会明显增大，这主要是由于缺少底部混凝土支撑。角钢翼缘的曲率显著小于角钢腹板，这表明角钢翼缘在受剪时作用相对较小，在抗剪设计中可以适当削减翼缘用料。
(4) 基于文献的65组试件以及本试验的3组试件，本文对现有角钢连接件计算公式的精度进行了检验，结果表明Hiroshi和Kiyomiya[12]提出的回归公式具有较高的准确度和较小的离散性。此外本文基于现有试验数据采用参数回归的方式提出了新的承载力计算公式，结果表明该公式同样具有良好的精度和更好的适用性。同时考虑到连接件破坏由混凝土压溃控制，具有较强的脆性，使用公式可以适当给予安全储备。
(5) 基于本文的参数回归公式和混凝土脱空力学模型，本文提出了考虑脱空的角钢连接件承载力计算公式，并通过文献[11]中的3组试件以及本试验6组试件的结果进行标定和比对，发现该公式具有较高的准确度和较小的离散性。
-
![]()
图 3 钢壳沉管隧道上表面混凝土缺陷
Figure 3. Concrete imperfections on top surface of steel-shell immersed tunnels
![]()
图 14 不同型号角钢的试件剪力-滑移曲线
Figure 14. Shear force-slip curves of specimens with different shapes of angle steel
![]()
图 18 各组试件角钢曲率分布 /(×10−6 mm−1)
Figure 18. Distributions of curvatures of angle steel in each group
![]()
图 20 现有角钢连接件抗剪承载力公式验证
Figure 20. Verifications of existing shear strength formulas for angle shear connectors
![]()
图 21 角钢连接件抗剪承载力拟合公式验证
Figure 21. Verifications of shear strength empirical formula for angle shear connectors
![]()
图 23 考虑混凝土脱空的角钢连接件抗剪承载力公式验证
Figure 23. Verifications of shear strength formula for angle shear connectors with concrete gaps
表 1 角钢材性参数
Table 1 Material parameters of angle steels
板厚/mm 屈服强度/
(N/mm2)屈服应变/
(×10−6)极限强度/
(N/mm2)延伸率/
(%)10 365 1764 503 28.5 12 380 2125 532 26.4 
下载: 导出CSV
表 2 各组推出试件的关键参数
Table 2 Key parameters of push-out specimens in each group
组名 角钢型号 脱空深度/mm 立方体抗压强度/(N/mm2) L150-0 L150×90×10 0 51.9 L150-10 L150×90×10 10 48.9 L150-20 L150×90×10 20 51.9 L180-0 L180×110×10 0 55.8 L180-10 L180×110×10 10 51.1 L180-20 L180×110×10 20 51.1 L200-0 L200×125×12 0 48.9 L200-10 L200×125×12 10 51.1 L200-20 L200×125×12 20 51.1 注：由于每组均包含3个试件，之后描述同一组的三个试件时，分别在组名后添加−1、−2和−3加以区分。
下载: 导出CSV
表 3 各组试件抗剪承载力
Table 3 Shear strength of specimens in each group
组名 抗剪承载力/kN 平均值/kN 折减率/(%) −1 −2 −3 L150-0 1302 1298 982 1194 − L150-10 810 1121 1062 998 16.5 L150-20 691 722 877 763 36.1 L180-0 894 1301 1121 1105 − L180-10 781 1113 1041 978 11.5 L180-20 − 792 589 691 37.5 L200-0 1152 1088 802 1014 − L200-10 812 796 1211 940 7.3 L200-20 747 661 753 720 29.0 注：折减率表示脱空深度不为0的试件(脱空试件)相对于脱空深度为0(无脱空)的承载力降低比率；其中L180-20-1试件由于加载中存在问题而剔除数据。
下载: 导出CSV
-
[1] 宋建, 陈百玲. 沉管隧道穿越江河海湾的优越性[J]. 现代隧道技术, 2005, 42(3): 28 − 30. doi: 10.3969/j.issn.1009-6582.2005.03.006 Song Jian, Chen Bailing. Advantages of immersed tube tunnel option in river- or gulf-crossing [J]. Modern Tunneling Technology, 2005, 42(3): 28 − 30. (in Chinese) doi: 10.3969/j.issn.1009-6582.2005.03.006
[2] Grantz W C. Steel-shell immersed tunnels—Forty years of experience [J]. Tunnelling and Underground Space Technology, 1997, 12(1): 23 − 31. doi: 10.1016/S0886-7798(96)00063-6
[3] Akimoto K, Hashidate Y, Kitayama H, et al. Immersed tunnels in Japan: Recent technological trends [C]//Proceedings of the 2002 Interntional Symposium on Underwater Technology (Cat. No. 02EX556). IEEE, 2002: 81 − 86.
[4] Shariati A, RamliSulong N H, Shariati M. Various types of shear connectors in composite structures: A review [J]. International Journal of Physical Sciences, 2012, 7(22): 2876 − 2890.
[5] 王威, 赵春雷, 苏三庆, 等. 带栓钉波形钢板混凝土组合构件粘结滑移性能与承载力试验研究[J]. 工程力学, 2019, 36(9): 108 − 119. Wang Wei, Zhao Chunlei, Su Sanqing, et al. Experimental study on bond-slip behavior and bearing capacity of corrugated steel plate concrete composite member with stud [J]. Engineering Mechanics, 2019, 36(9): 108 − 119. (in Chinese)
[6] 汪维安, 李乔, 赵灿晖, 等. 混合结构 PBL 剪力键的荷载-滑移特征曲线研究[J]. 工程力学, 2015, 32(3): 57 − 65. Wang Weian, Li Qiao, Zhao Canhui, et al. Study on load-slip characteristic curve of perfobond shear connectors in hybrid structures [J]. Engineering Mechanics, 2015, 32(3): 57 − 65. (in Chinese)
[7] 杨勇, 陈阳. PBL 剪力连接件抗剪承载力试验研究[J]. 工程力学, 2018, 35(9): 89 − 96. doi: 10.6052/j.issn.1000-4750.2017.05.0365 Yang Yong, Chen Yang. Experimental study on the shear capacity of PBL shear connectors [J]. Engineering Mechanics, 2018, 35(9): 89 − 96. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.05.0365
[8] Shariati M, Sulong N H R, Suhatril M, et al. Comparison of behaviour between channel and angle shear connectors under monotonic and fully reversed cyclic loading [J]. Construction and Building Materials, 2013, 38: 582 − 593. doi: 10.1016/j.conbuildmat.2012.07.050
[9] 魏文期, 陈政清. 茅草街大桥钢管混凝土收缩徐变试验研究[J]. 兰州铁道学院学报, 2003, 22(3): 62 − 65. Wei Wenqi, Chen Zhenqing. A test research on shrinkage and creep for micro-expansive concrete filled steel tubular of Maocaojie bridge [J]. Journal of Lanzhou Railway University, 2003, 22(3): 62 − 65. (in Chinese)
[10] 小門武, 鈴木雄三, 輪湖建雄, 等. 沈埋トンネル·フルサンドイッチ構造部への充填を対象とした粉体系高流動コンクリートの諸特性について[J]. コンクリート工学年次論文報告集, 1995, 17(1): 191 − 196. Komon T, Suzuki Y, Wako T, et al. Characteristics of powder type high fluidity concrete for filling into submerged tunnel full sandwich structure[J]. Annual Report on Concrete Engineering, 1995, 17(1): 191 − 196. (in Japanese)
[11] Kiyomiya O, Kimura H. Mechanical properties of shear key by angle [J]. Proceedings of the Japan Concrete Institute, 1996, 18(2): 1385 − 1390.
[12] Hiroshi Y, Kiyomiya O. Load carrying capacity of shear connectors made of shape steel in steel-concrete composite members [R]. Japan: Technical Note of the Port and Habour Reasearch Institute Ministry of Transport, 1987.
[13] Chuah C L, Shima H, Virach R. Load-displacement relationship of plate shape shear connector in steel-concrete composite structures [J]. Doboku Gakkai Ronbunshu, 1991, 1991(433): 223 − 229.
[14] Ueda T. Strength of steel plate shear connector [C]//Proceedings of the 2nd Symposium on Research and Application of Composite Constructions, JSCE, 1990: 149 − 156.
[15] Hajime O, Yoshio K, et al. JSCE Research Subcommittee on Steel-Concrete Sandwich Structures. Design code for steel-concrete sandwich structures – Draft [J]. Concrete Library of JSCE, 1992, 20: 1 − 21.
[16] Soty R, Shima H. Formulation for shear force–relative displacement relationship of L-shape shear connector in steel–concrete composite structures [J]. Engineering Structures, 2013, 46: 581 − 592. doi: 10.1016/j.engstruct.2012.09.003
[17] Saidi T, Furuuchi H, Ueda T. The transferred shear force-relative displacement relationship of the shear connector in steel-concrete sandwich beam and its model [J]. Doboku Gakkai Ronbunshuu E, 2008, 64(1): 122 − 141. doi: 10.2208/jsceje.64.122
[18] 刘玉擎, 武建敏, 蒋劲松. 使用状态对焊钉连接件抗剪性能影响的试验研究[J]. 橋樑建設, 2007(6): 23 − 25. Liu Yuqing, Wu Jianmin, Jiang Jinsong. Experimental study of influence of service conditions on shearing behavior of welded stud connectors [J]. Bridge Construction, 2007(6): 23 − 25. (in Chinese)
[19] 刘玉擎, 周伟翔, 蒋劲松. 开孔板连接件抗剪性能试验研究[J]. 橋樑建設, 2006(6): 1 − 4. Liu Yuqing, Zhou Weixiang, Jiang Jinsong. Experimental study of shearing behavior of perforated plate connector [J]. Bridge Construction, 2006(6): 1 − 4. (in Chinese)
[20] 王伟. 钢管混凝土脱空机理研究[D]. 重庆: 重庆交通大学, 2008. Wang Wei. Research on cavity mechanism of concrete filled steel tube [D]. Chongqing: Chongqing Jiao Tong University, 2008. (in Chinese)
[21] Liao F Y, Han L H, He S H. Behavior of CFST short column and beam with initial concrete imperfection: Experiments [J]. Journal of Constructional Steel Research, 2011, 67(12): 1922 − 1935. doi: 10.1016/j.jcsr.2011.06.009
[22] Xue J Q, Briseghella B, Chen B C. Effects of debonding on circular CFST stub columns [J]. Journal of Constructional Steel Research, 2012, 69(1): 64 − 76. doi: 10.1016/j.jcsr.2011.08.002
[23] GB/T 706−2008, 热轧型钢 [S]. 北京: 中国标准出版社, 2008. GB/T 706−2008, Hot rolled steel [S]. Beijing: China Standard Press, 2008. (in Chinese)
[24] European Committee for Standardization (CEN). Eurocode 4: Design of composite steel and concrete structures [S]. Part 2: Composite Bridges, 1994.
[25] Manabe Y, Fujiyama C, Kisaku T, et al. Influence of coarse aggregates on the shear resistance of perfobond rib shear connector [J]. Procedia Engineering, 2014, 95: 454 − 464. doi: 10.1016/j.proeng.2014.12.205
[26] GB/T 50107−2010, 混凝土强度检验评定标准 [S]. 北京:中国建筑工业出版社, 2010. GB/T 50107−2010, Standard for test and evaluation of concrete compression strength [S]. Beijing: China Building Industry Press, 2010. (in Chinese)
[27] GB/T 228−2002, 金属材料室温拉伸试验方法 [S]. 北京: 中国标准出版社, 2010. GB/T 228−2002, Metallic material room temperature tensile test method [S]. Beijing: China Standard Press, 2010. (in Chinese)
[28] Maleki S, Mahoutian M. Experimental and analytical study on channel shear connectors in fiber-reinforced concrete [J]. Journal of Constructional Steel Research, 2009, 65(8/9): 1787 − 1793. doi: 10.1016/j.jcsr.2009.04.008
[29] Wang Y C. Deflection of steel-concrete composite beams with partial shear interaction [J]. Journal of Structural Engineering, 1998, 124(10): 1159 − 1165. doi: 10.1061/(ASCE)0733-9445(1998)124:10(1159)
[30] Guo Z. Principles of reinforced concrete [M]. Oxford: Butterworth-Heinemann, 2014.
-
期刊类型引用(6)
1. 谢献忠，张淳淇，林文欣，彭剑. 输电线路共振舞动机理试验研究. 工程力学. 2023(10): 71-80 . 
本站查看
2. 霍冰，刘习军，张锐. 高阶扭转模态耦合下覆冰导线的稳定性和影响因素分析. 工程力学. 2020(02): 241-249 . 本站查看
3. 陈浩，何晓凤，王丙兰，李哲. 基于集合预报的两种输电线路舞动概率预测方法. 科学技术与工程. 2020(34): 14078-14084 . 百度学术
4. 张志强，黄增浩. 配网线路覆冰断线力学特性及加固措施分析. 电力科学与工程. 2019(03): 52-58 . 百度学术
5. 晏致涛，黄珏，李清，李梦丽，杨晓辉. 真型大跨输电线路的舞动模拟与失谐控制. 四川建筑科学研究. 2019(05): 52-57 . 百度学术
6. 谢献忠，胡霞，彭剑. 多档输电线非线性建模及面内自由振动分析. 应用力学学报. 2017(06): 1097-1101+1220 . 百度学术
其他类型引用(7)
计量
- 文章访问数: 652
- HTML全文浏览量: 226
- PDF下载量: 78
- 被引次数: 13
