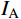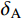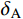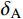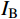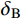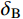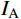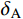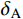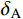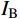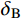COMPLEX MODE SUPERPOSITION METHOD OF HYBRID STRUCTURE SEISMIC RESPONSES BASED ON DYNAMIC CHARACTERISTICS
-
摘要: 混合结构由不同阻尼特性的材料组成,确定其阻尼矩阵存在困难。分块Rayleigh阻尼模型由于数学上的简易性,被广泛用于构建混合结构的阻尼矩阵,但分块Rayleigh阻尼模型的计算精度与参考频率的选择方法直接相关。针对参考频率的选择问题,依据结构动力响应的组成和特点,提出了一种确定Rayleigh阻尼系数的计算方法,进而实现基于分块Rayleigh阻尼模型的复模态叠加法。求解结构的瞬态反应时,根据结构前两阶振型的自振频率确定阻尼系数;求解结构的稳态反应时,选择结构的基频、与外激励频率接近的结构自振频率确定阻尼系数。依据地震波的频谱特性,提出了基于地震波卓越频率的分块Rayleigh阻尼模型,并结合地震加速度的分段线性假定,建立了混合结构的复模态叠加法。在此基础上,利用三角级数展开得到组成地震波的谐波频率,进一步提出了基于谐波频率的分块Rayleigh阻尼模型和对应的复模态叠加法。算例分析结果表明:所提方法误差更小,且克服了传统方法因振型选择不唯一导致的计算结果具有不确定性的问题;与基于地震波卓越频率的复模态叠加法相比,基于谐波频率的复模态叠加法计算量更大,但计算精度更高、适用范围更广。
-
关键词:
- 混合结构 /
- Rayleigh阻尼 /
- 复模态叠加法 /
- 瞬态反应 /
- 稳态反应
Abstract: The damping matrix of a hybrid structure of different material damping characteristics is difficult to determine. By the aid of mathematical simplicity, Rayleigh damping model is widely used in the construction of damping matrix of a hybrid structure. But the calculation precision of Rayleigh damping model is affected by the choice of reference frequencies. Thusly, a calculation method of Rayleigh damping coefficients is proposed based on the characteristics of structural dynamic responses. The corresponding complex mode superposition method is also realized. The damping coefficients are determined based on the natural frequencies of the first two modes when the structural transient responses are calculated. The damping coefficients are determined based on fundamental frequency and certain frequency when the structural steady state responses are calculated. The certain frequency is the natural frequency close to external excitation frequency. According to the spectrum characteristics of seismic wave, a Rayleigh damping model is obtained based on the predominant frequency of seismic wave. Combined with the linear assumption of earthquake acceleration, a complex mode superposition method of hybrid structure is realized. The harmonic frequencies of seismic wave could be obtained by trigonometric series. Another Rayleigh damping model is developed based on the harmonic frequencies, and the corresponding complex mode superposition method is proposed. The cases show that the proposed method could avoid the arbitrariness of selective modes based on traditional methods. The calculation error of the proposed method is small. Compared with the complex mode superposition method based on the predominant frequency of seismic wave, the computational amount of complex mode superposition method based on the harmonic frequencies is larger, but with higher calculation accuracy and wider range of application. -
由不同阻尼特性材料组成的工程结构称为混合结构,目前已经广泛应用到机械工程、航空航天工程、土木工程等领域。混合结构是非比例阻尼体系,对应的阻尼矩阵不再满足经典阻尼条件,如何求解混合结构的动力响应是抗震分析中亟待解决的问题。解决该问题的常见方法是,采用应变能法[1-4]、近似解耦法[5-6]、复频率法[7-8]、Rayleigh阻尼法[9-11]等计算出等效阻尼比,进而基于传统的实模态叠加法计算结构动力响应。上述方法的思路是将混合结构简化为等效的单一材料比例阻尼体系,这容易导致一定的误差,计算精度难以保证。Foss[12]将运动方程扩展为状态方程组,进而提出了状态空间法。依据状态空间法,可实现混合结构的复模态叠加法,在复数域中求得运动方程的精确解[13-16]。复模态叠加法计算结果的正确性依赖于阻尼矩阵的合理构造,但在结构地震反应分析中,合理地构造出能正确反映结构真实情况的阻尼矩阵是十分困难的[17]。
Rayleigh阻尼模型假定结构的阻尼矩阵是质量矩阵和刚度矩阵的线性组合[18],由于数学处理上的简易性,使其得到了广泛的应用。Clough等[19]将子结构的阻尼矩阵假定为Rayleigh阻尼矩阵,进而组装得到混合结构的分块Rayleigh阻尼矩阵。保证分块Rayleigh阻尼模型合理性的关键在于如何确定阻尼系数。阻尼系数的计算方法不合理将带来较大误差[20-22]。针对如何确定Rayleigh阻尼系数的问题,国内外学者进行了系统研究,Idriss等[23]仅采用结构的基本频率确定阻尼系数,Yoshida等[24]提出了在主要频率范围内计算阻尼系数的方法,Hudson等[25]依据结构的基本频率和地震波的卓越频率确定阻尼系数,邹德高等[26]、李哲等[27]在考虑结构基本频率和地震波卓越频率的基础上,进一步修正了阻尼系数的计算方法,许紫刚等[28]提出基于基本频率、地震波卓越频率与形心频率的平均值确定阻尼系数。为考虑整个振动频率范围内阻尼系数的影响,王田友等[29]依据结构的基本频率和输入振动的频率范围确定两个振型,并用于计算阻尼系数,潘旦光等[30-32]以结构位移反应峰值的误差为目标函数,采用最小二乘法确定阻尼系数。
上述方法依据结构体系的振动特性和/或外激励的频谱特性确定阻尼系数,本文在上述研究的基础上,提出了基于结构动力响应特性确定阻尼系数的新思路。Rayleigh阻尼系数一般通过选择两个重要振型的自振频率和振型阻尼比进行确定,为保持这一工程常用方法的简便性,同时解决振型选择方式不唯一导致地震响应计算结果存在不确定性的问题,本文提出了一种基于动力特性确定Rayleigh阻尼系数的计算方法,即在求解瞬态反应时,根据结构的前两阶振型确定阻尼系数;求解稳态反应时,根据结构的基本振型和外激励频率确定阻尼系数,可有效避免传统方法计算阻尼系数时振型选择的不唯一性,从而构建出对应的分块Rayleigh阻尼矩阵,实现了混合结构的复模态叠加法。事实上,非比例阻尼模型计算过程需涉及复振型,这样才能更符合工程问题的本质特性[33],相比基于等效阻尼比的实模态叠加法,本文提出的基于动力特性的混合结构地震响应复模态叠加法可考虑工程结构中不同阻尼特性材料导致的非比例阻尼特性。
1 基于动力特性的阻尼矩阵构建
1.1 黏性阻尼模型的复模态叠加法
基于黏性阻尼模型的时域运动方程为:
{\boldsymbol{M\ddot x}}(t) + {\boldsymbol{C\dot x}}(t) + {\boldsymbol{Kx}}(t) = - {\boldsymbol{MI}}g(t) (1) 式中:
{\boldsymbol{M}} 为质量矩阵;{\boldsymbol{K}} 为刚度矩阵;{\boldsymbol{I}} 为与地震动输入有关的向量(N \times 1 ),与g(t) 方向相同的位移自由度元素为1。由
{\boldsymbol{M}} 和{\boldsymbol{K}} 可计算得到结构的无阻尼自振频率,进一步依据分块Rayleigh阻尼模型[19],阻尼矩阵可表示为:{\boldsymbol{C}} = \sum\limits_{i = 1}^s {({\alpha _i}{{\boldsymbol{M}}_i} + {\beta _i}{{\boldsymbol{K}}_i})} (2) 式中:s为材料类型的数目;
{{\boldsymbol{M}}_i} 为第i种材料对应的质量矩阵;{{\boldsymbol{K}}_i} 为第i种材料对应的刚度矩阵;{\alpha _i} 和{\beta _i} 为第i种材料对应的Rayleigh阻尼系数。\left\{ \begin{aligned} & {\alpha _i} = \frac{{{\omega _m}{\omega _n}(2{\xi _{{\rm{e}}i}}{\omega _m} - 2{\xi _{{\rm{e}}i}}{\omega _n})}}{{{\omega _m^2} - {\omega _n^2}}} \\& {\beta _i} = \frac{{2{\xi _{{\rm{e}}i}}{\omega _m} - 2{\xi _{{\rm{e}}i}}{\omega _n}}}{{{\omega _m^2} - {\omega _n^2}}} \end{aligned} \right. (3) 式中:
{\omega _m} 为第m阶振型的自振频率;{\omega _n} 为第n阶振型的自振频率;{\xi _{{\rm{e}}i}} 为第i种材料对应子结构的材料阻尼系数产生的振型阻尼比[9, 34-35]。对于混合结构,阻尼矩阵不再保持与质量矩阵、刚度矩阵的比例关系,因此式(1)不可采用实模态叠加法进行解耦计算。为实现式(1)的模态解耦,同时避免强迫解耦引起的计算误差,需要基于状态空间法,以实现混合结构的复模态叠加法。
引入辅助方程:
{\boldsymbol{M\dot x}}(t) - {\boldsymbol{M\dot x}}(t) = 0 (4) 将式(1)和式(4)结合,可得:
{\boldsymbol{P\dot y}}(t) + {\boldsymbol{Qy}}(t) = {\boldsymbol{F}} (5) 式中:
{\boldsymbol{P }}= \left[ {\begin{array}{*{20}{c}} {\boldsymbol{C}}&{\boldsymbol{M}} \\ {\boldsymbol{M}}&{\boldsymbol{0}} \end{array}} \right] ;{\boldsymbol{Q }}= \left[ {\begin{array}{*{20}{c}} {\boldsymbol{K}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{ - {\boldsymbol{M}}} \end{array}} \right] ;{\boldsymbol{y}}(t)= \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}(t)} \\ {{\boldsymbol{\dot x}}(t)} \end{array}} \right] ;{\boldsymbol{F }}= \left[ {\begin{array}{*{20}{c}} { - {\boldsymbol{MI}}g(t)} \\ {\boldsymbol{0}} \end{array}} \right] 。式(5)对应的复特征值为:
\left\{ \begin{aligned} & {\lambda _j} = - {\sigma _j} + {\rm{i}}{\omega _{{\rm{d}}j}} \\& {\lambda _j^*} = - {\sigma _j} - {\rm{i}}{\omega _{{\rm{d}}j}} \end{aligned} \right.\;\;\;\;,j = 1,2, \cdots ,N (6) 对应于2N个复特征值的复特征向量为:
{{\boldsymbol{\varPhi }}_j}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\phi }}_j}}&{{{\boldsymbol{\phi }}_j^*}} \\ {{\lambda _j}{{\boldsymbol{\phi }}_j}}&{{\lambda _j^*}{{\boldsymbol{\phi }}_j^*}} \end{array}} \right]\;\;,j = 1,2, \cdots ,N (7) 式中:
{{\boldsymbol{\phi}} _j} 为N维复向量;{{\boldsymbol{\phi}} _j^*} 为{{\boldsymbol{\phi}} _j} 的共轭向量。令:
{\omega _j^2} = \frac{{{{\boldsymbol{\phi }}_j^{\rm{R}}}{\boldsymbol{K}}{{\boldsymbol{\phi }}_j}}}{{{{\boldsymbol{\phi }}_j^{\rm{R}}}{\boldsymbol{M}}{{\boldsymbol{\phi }}_j}}}\;\;\;\; (8) 2{\xi _j}{\omega _j} = \frac{{{{\boldsymbol{\phi }}_j^{\rm{R}}}{\boldsymbol{C}}{{\boldsymbol{\phi }}_j}}}{{{{\boldsymbol{\phi }}_j^{\rm{R}}}{\boldsymbol{M}}{{\boldsymbol{\phi }}_j}}} (9) 式中,
{{\boldsymbol{\phi}} _j^{\rm{R}}} 为{{\boldsymbol{\phi}} _j} 的共轭转置向量。由式(6)、式(8)和式(9)可得:
\left\{ \begin{array}{l} {\sigma _j} = {\xi _j}{\omega _j} \\ {\omega _{{\rm{d}}j}} = {\omega _j}\sqrt {1 - {\xi _j^2}} \\ \end{array} \right. (10) 位移向量
{\boldsymbol{x}}(t) 可由复特征向量线性表示:{\boldsymbol{x}}(t) = \sum\limits_{j = 1}^N [ {{\boldsymbol{\phi }}_j}{y_j}(t) + {{\boldsymbol{\phi }}_j^*}{y_j^*}(t)] (11) 利用复特征向量的正交性,可得:
{\dot y_j}(t) - {\lambda _j}{y_j}(t) = - {\gamma _j}g(t),\;\;j = 1,2, \cdots ,N (12) 其中:
{\gamma _j} = \frac{{{{\boldsymbol{\phi }}_j^{\rm{T}}}{\boldsymbol{MI}}}}{{{{\boldsymbol{\phi }}_j^{\rm{T}}}{\boldsymbol{C}}{{\boldsymbol{\phi }}_j} + 2{\lambda _j}{{\boldsymbol{\phi }}_j^{\rm{T}}}{\boldsymbol{M}}{{\boldsymbol{\phi }}_j}}} (13) 标准单自由度方程为:
{\ddot q_j}(t) + 2{\xi _j}{\omega _j}{\dot q_j}(t) + {\omega _j^2}{q_j}(t) = g(t) (14) 依据式(12)和式(14),可得:
{y_j}(t) = - {\gamma _j}[{\dot q_j}(t) + ({\xi _j}{\omega _j} + {\rm{i}}{\omega _{{\rm{d}}j}}){q_j}(t)] (15) 由式(11)和式(15)可得到结构的位移、速度和加速度:
\left\{ \begin{aligned} & {\boldsymbol{x}}(t) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_j}{{\dot q}_j}(t) + {{\boldsymbol{B}}_j}{q_j}(t)] \\[-2pt]& {\boldsymbol{\dot x}}(t) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_j}{{\ddot q}_j}(t) + {{\boldsymbol{B}}_j}{{\dot q}_j}(t)] \\[-2pt]& {\boldsymbol{\ddot x}}(t) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_j}{{\dddot q}_j}(t) + {{\boldsymbol{B}}_j}{{\ddot q}_j}(t)] \end{aligned} \right. (16) 其中:
\left\{ \begin{aligned} & {{\boldsymbol{A}}_j} = - 2 Re [{\gamma _j}{{\boldsymbol{\phi }}_j}] \\ & {{\boldsymbol{B}}_j} = 2 Re [{\lambda _j^*}{\gamma _j}{{\boldsymbol{\phi }}_j}] \end{aligned} \right. (17) 1.2 基于动力特性的阻尼矩阵构造
混合结构复模态叠加法的正确性依赖于合理的阻尼矩阵,目前常用的阻尼矩阵构造方法为分块Rayleigh阻尼模型。Rayleigh阻尼模型的实质是选择两个重要的振型,以便使计算的结构动力响应逼近结构的实际响应。结构承受地面运动激励时需要考虑瞬态反应和稳态反应[19],因此本文依据瞬态反应和稳态反应的特性分别确定对结构动力响应贡献最大的两个振型,进而构建出阻尼矩阵。
考虑到地震波可以分解为一系列简谐波,因此首先分析谐波作用下基于黏性阻尼模型的时域运动方程,对应的方程形式为:
{\ddot q_j}(t) + {\omega _j^2}{q_j}(t) + 2{\xi _j}{\omega _j}{\dot q_j}(t) = {p_0}\sin \theta t (18) 式中:
{p_0} 为谐波的振幅;\theta 为谐波频率。令:
{q_j}(t) = {q_{{\rm{c}}j}}(t) + {q_{{\rm{p}}j}}(t) (19) 式中:
{q_{{\rm{c}}j}}(t) 为式(18)对应的齐次方程通解;{q_{{\rm{p}}j}}(t) 为式(18)对应的非齐次方程特解。结构的位移响应可表示为:
{\boldsymbol{x}}(t) = {{\boldsymbol{x}}_{\rm{c}}}(t) + {{\boldsymbol{x}}_{\rm{p}}}(t) (20) 式中:
{{\boldsymbol{x}}_{\rm{c}}}(t) 为结构的瞬态反应;{{\boldsymbol{x}}_{\rm{p}}}(t) 为结构的稳态反应。与结构瞬态反应相对应的是齐次运动方程通解,式(18)对应的齐次方程为:
{\ddot q_{{\rm{c}}j}}(t) + {\omega _j^2}{\dot q_{{\rm{c}}j}}(t) + 2{\xi _j}{\omega _j}{q_{{\rm{c}}j}}(t) = 0 (21) 式(21)的通解为:
{q_{{\rm{c}}j}}(t) = {{\rm{e}}^{ - {\xi _j}{\omega _j}t}}[{D_j}\cos ({\omega _{{\rm{d}}j}}t) + {E_j}\sin ({\omega _{{\rm{d}}j}}t)] (22) 其中:
\left\{ \begin{split} & {D_j} = {q_{{\rm{c}}j}}({t_0}) \\& {E_j} = \frac{1}{{{\omega _{{\rm{d}}j}}}}{q_{{\rm{c}}j}}({t_0}) + \frac{{{\xi _j}{\omega _j}}}{{{\omega _{{\rm{d}}j}}}}{{\dot q}_{{\rm{c}}j}}({t_0}) \end{split} \right. (23) 由式(23)可知,当
{\xi _j} 较小时,\dfrac{{{\xi _j}{\omega _j}}}{{{\omega _{{\rm{d}}j}}}} 可忽略不计,随着振型阶数的增加,{\omega _{{\rm{d}}j}} 逐渐增大,\dfrac{1}{{{\omega _{{\rm{d}}j}}}} 逐渐减小,{q_{{\rm{c}}j}}(t) 逐渐减小。此外,振型参与系数{\gamma _j} 随着振型阶数的增加而减小。因此,在结构的瞬态反应{{\boldsymbol{x}}_{\rm{c}}}(t) 中,最重要的两个振型为第一阶振型和第二阶振型。结构稳态反应对应的是非齐次运动方程特解,式(18)的特解为:
{q_{{\rm{p}}j}}(t) = {F_j}\cos (\theta t) + {G_j}\sin (\theta t) (24) 其中:
\left\{ \begin{aligned} & {F_j} = \frac{{2{p_0}{\xi _j}{\omega _j}\theta }}{{{{({\omega _j^2} - {\theta ^2})^2}} + {{(2{\xi _j}{\omega _j}\theta )^2}}}} \\ & {G_j} = \frac{{ - {p_0}({\omega _j^2} - {\theta ^2})}}{{{{({\omega _j^2} - {\theta ^2})^2}} + {{(2{\xi _j}{\omega _j}\theta )^2}}}} \end{aligned} \right. (25) 令:
{\beta _j} = \frac{\theta }{{{\omega _j}}} (26) 式(24)进一步转化为:
{q_{{\rm{p}}j}}(t) = \frac{{{p_0}}}{{{\omega _j^2}}}\frac{{2{\xi _j}{\beta _j}\cos (\theta t) - (1 - {\beta _j^2})\sin (\theta t)}}{{(1 - {\beta _j^2}) + {{(2{\xi _j}{\beta _j})^2}}}} (27) 对应的振幅可表示为:
H = \frac{{{p_0}}}{{{\omega _j^2}}}\frac{1}{{\sqrt {(1 - {\beta _j^2}) + {{(2{\xi _j}{\beta _j})^2}}} }} (28) 随着振型阶数的增加,
{\omega _j} 逐渐增大,振幅的幅值H逐渐减小,{q_{{\rm{p}}j}}(t) 逐渐减小,同时振型参与系数{\gamma _j} 也逐渐减小;当阻尼比{\xi _j} 较小,2{\xi _j}{\beta _j} 的大小可忽略不计,{\beta _j} 接近1时,振幅的幅值趋近于无穷大,此时结构发生共振现象。因此,在结构的稳态反应{{\boldsymbol{x}}_{\rm{p}}}(t) 中,最重要的两阶振型分别为第一阶振型以及与外激励频率接近的振型。综上,本文提出了基于结构线弹性响应分离的经典思路构造分块Rayleigh阻尼矩阵的新方法,即针对瞬态反应部分,选择与第一阶振型和第二阶振型对应的自振频率、振型阻尼比构造分块Rayleigh阻尼矩阵;针对稳态反应部分,选择第一阶振型以及与外激励频率接近振型所对应的自振频率、振型阻尼比构造分块Rayleigh阻尼矩阵。
2 基于地震波卓越频率的混合结构复模态叠加法
2.1 基于地震波卓越频率的阻尼矩阵
地震波作用下基于分块Rayleigh阻尼矩阵模型的齐次运动方程为:
{\boldsymbol{M}}{{\boldsymbol{\ddot x}}_{\rm{c}}}(t) + {{\boldsymbol{C}}_{\rm{c}}}{{\boldsymbol{\dot x}}_{\rm{c}}}(t) + {\boldsymbol{K}}{{\boldsymbol{x}}_{\rm{c}}}(t) = {\boldsymbol{0}} (29) 瞬态反应对应的阻尼矩阵可表示为:
{{\boldsymbol{C}}_{\rm{c}}} = \sum\limits_{i = 1}^s {({\alpha _{{\rm{c}}i}}{{\boldsymbol{M}}_i} + {\beta _{{\rm{c}}i}}{{\boldsymbol{K}}_i})} \;\qquad (30) 依据1.2节分析,求解齐次方程通解时,选取第一阶振型和第二阶振型对应的自振频率和振型阻尼比,可计算出阻尼系数为:
\left\{ \begin{aligned} & {\alpha _{{\rm{c}}i}} = \frac{{{\omega _1}{\omega _2}(2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _2})}}{{{\omega _1^2} - {\omega _2^2}}} \\& {\beta _{{\rm{c}}i}} = \frac{{2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _2}}}{{{\omega _1^2} - {\omega _2^2}}} \end{aligned} \right. (31) 式中:
{\omega _1} 为第一阶振型的自振频率;{\omega _2} 为第二阶振型的自振频率;{\xi _{{\rm{e}}i}} 为第i种材料对应子结构的材料阻尼系数产生的振型阻尼比[9, 34-35]。地震波作用下基于分块Rayleigh阻尼矩阵的非齐次运动方程为:
{\boldsymbol{M}}{{\boldsymbol{\ddot x}}_{\rm{p}}}(t) + {{\boldsymbol{C}}_{\rm{p}}}{{\boldsymbol{\dot x}}_{\rm{p}}}(t) + {\boldsymbol{K}}{{\boldsymbol{x}}_{\rm{p}}}(t) = - {\boldsymbol{MI}}g(t) (32) 稳态反应对应的阻尼矩阵可表示为:
{{\boldsymbol{C}}_{\rm{p}}} = \sum\limits_{i = 1}^s {({\alpha _{{\rm{p}}i}}{{\boldsymbol{M}}_i} + {\beta _{{\rm{p}}i}}{{\boldsymbol{K}}_i})} (33) 依据1.2节分析,求解非齐次方程特解时,选择第一阶振型、与外激励频率接近振型对应的自振频率和振型阻尼比。目前确定阻尼系数的计算方法较多[23-32],本文对比了利用结构基频确定阻尼系数的方法、利用最小二乘法确定阻尼系数的方法、利用结构基频和地震波卓越频率确定阻尼系数的方法。选择不同的方法并不影响以下理论推导过程,为了更清楚地展示本文方法的核心思路、保持计算的简便性,并考虑同时利用结构振动特性和地震动特性,本文首先选择依据结构的第一阶振型自振频率、地震波卓越频率确定阻尼系数,进一步可得:
\left\{ \begin{aligned} & {\alpha _{{\rm{p}}i}} = \frac{{{\omega _1}{\omega _n}(2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _n})}}{{{\omega _1^2} - {\omega _n^2}}} \\& {\beta _{{\rm{p}}i}} = \frac{{2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _n}}}{{{\omega _1^2} - {\omega _n^2}}} \end{aligned} \right.\qquad\;\;\;\;\;\; (34) 式中:
{\omega _n} 为第n阶振型的自振频率,且{\omega _n} 是最接近{\omega _{\rm{e}}} 的自振频率;{\omega _{\rm{e}}} 为地震动的卓越频率。当n=1时,规定分块Rayleigh阻尼矩阵可依据前两阶振型进行确定,因此将式(34)进一步修正为:
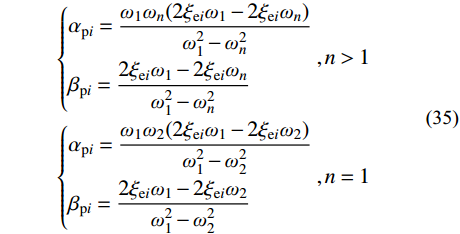
\begin{array}{l} \left\{ \begin{aligned} & {\alpha _{{\rm{p}}i}} = \frac{{{\omega _1}{\omega _n}(2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _n})}}{{{\omega _1^2} - {\omega _n^2}}} \\& {\beta _{{\rm{p}}i}} = \frac{{2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _n}}}{{{\omega _1^2} - {\omega _n^2}}} \end{aligned} \right.{\rm{ }},n > 1 \\ \left\{ \begin{aligned} & {\alpha _{{\rm{p}}i}} = \frac{{{\omega _1}{\omega _2}(2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _2})}}{{{\omega _1^2} - {\omega _2^2}}} \\& {\beta _{{\rm{p}}i}} = \frac{{2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _2}}}{{{\omega _1^2} - {\omega _2^2}}} \\\end{aligned} \right.{\rm{ }},n = 1 \end{array} (35) 综上,由式(35)可确定阻尼系数,进而得到了基于地震波卓越频率的分块Rayleigh阻尼矩阵。
2.2 基于地震波卓越频率的复模态叠加法
采用数值积分方法进行计算时,按照时间步长
\Delta t 对输入地震动加速度记录进行离散,任意时刻可表示为{t_k} = k\Delta t(k = 0,1,2,\cdots ) ,利用{t_k} 时刻结构的动力响应,计算{t_{k + 1}} 时刻的响应。由式(16)可知,求解混合结构的加速度响应需要计算方程式(14)中单自由度结构的加加速度(即{q_j}(t) 的三阶微分),因此传统的时域逐步积分计算方法将不再适用,本文采用瞬态反应与稳态反应分离的时域数值方法计算结构的动力响应。式(14)对应的齐次方程为:
{\ddot q_{{\rm{c}}j}}(t) + {\omega _{{\rm{c}}j^2}}{q_{{\rm{c}}j}}(t) + 2{\xi _{{\rm{c}}j}}{\omega _{{\rm{c}}j}}{\dot q_{{\rm{c}}j}}(t) = 0 (36) 式中:
{\omega _{{\rm{c}}j}} 为对应瞬态反应的第j阶振型无阻尼自振频率;{\xi _{{\rm{c}}j}} 为对应瞬态反应的第j阶振型阻尼比。求解式(36),可得:
\begin{split} {q_{{\rm{c}}j}}({t_{k + 1}}) =& {{\rm{e}}^{ - {\xi _{{\rm{c}}j}}{\omega _{{\rm{c}}j}}\Delta t}}[{D_j}\cos ({\omega _{{\rm{c,d}}j}}\Delta t) + \\&{E_j}\sin ({\omega _{{\rm{c,d}}j}}\Delta t)] \end{split} (37) 其中:
\left\{ \begin{aligned} & {D_j} = {q_{{\rm{c}}j}}({t_k}) \\& {E_j} = \frac{{{q_{{\rm{c}}j}}({t_k}) + {\xi _j}{\omega _j}{{\dot q}_{{\rm{c}}j}}({t_k})}}{{{\omega _{{\rm{d}}j}}}} \end{aligned} \right.\qquad\quad (38) 假定输入地震波加速度在时间步长内线性变化[36-37],可得:
g(\tilde t) = g({t_k}) + \frac{{g({t_{k + 1}}) - g({t_k})}}{{\Delta t}}\tilde t (39) 其中:
\tilde t = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;,t = {t_k} \\ \Delta t\;\;\;\;\;\;,t = {t_{k + 1}} \\ \end{array} \right.\qquad\quad (40) 式(39)代入式(14),可得到非齐次方程为:
\begin{split} & {\ddot q_{{\rm{p}}j}}(t) + {\omega _{{\rm{p}}j}^2}{q_{{\rm{p}}j}}(t) + 2{\xi _{{\rm{p}}j}}{\omega _{{\rm{p}}j}}{\dot q_{{\rm{p}}j}}(t) =\\& \qquad g({t_k}) + \frac{{g({t_{k + 1}}) - g({t_k})}}{{\Delta t}}\tilde t \end{split} (41) 式中:
{\omega _{{\rm{p}}j}} 为对应稳态反应的第j阶振型无阻尼自振频率;{\xi _{{\rm{p}}j}} 为对应稳态反应的第j阶振型阻尼比。求解式(41),可得:
\begin{split} {q_{{\rm{p}}j}}(t) =& \frac{1}{{{\omega _{{\rm{p}}j}^2}}}\frac{{g({t_{k + 1}}) - g({t_k})}}{{\Delta t}}\tilde t +\\& \frac{1}{{{\omega _{{\rm{p}}j}^2}}}g({t_k}) - \frac{{2{\xi _{{\rm{p}}j}}}}{{{\omega _{{\rm{p}}j}^3}}}\frac{{g({t_{k + 1}}) - g({t_k})}}{{\Delta t}} \end{split} (42) 由式(16)和式(42)可得:
\left\{ \begin{aligned} & {{\boldsymbol{x}}_{\rm{p}}}({t_k}) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{p}}j}}{{\dot q}_{{\rm{p}}j}}({t_k}) + {{\boldsymbol{B}}_{{\rm{p}}j}}{q_{{\rm{p}}j}}({t_k})] \\& {{{\boldsymbol{\dot x}}}_{\rm{p}}}({t_k}) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{p}}j}}{{\ddot q}_{{\rm{p}}j}}({t_k}) + {{\boldsymbol{B}}_{{\rm{p}}j}}{{\dot q}_{{\rm{p}}j}}({t_k})] \end{aligned} \right. (43) 进一步,
\left\{ \begin{aligned} & {{\boldsymbol{x}}_{\rm{c}}}({t_k}) = {\boldsymbol{x}}({t_k}) - {{\boldsymbol{x}}_{\rm{p}}}({t_k}) \\& {{{\boldsymbol{\dot x}}}_{\rm{c}}}({t_k}) = {\boldsymbol{\dot x}}({t_k}) - {{{\boldsymbol{\dot x}}}_{\rm{p}}}({t_k}) \end{aligned} \right. (44) 依据复特征向量的正交性,可由
{{\boldsymbol{x}}_{\rm{c}}}({t_k}) 和{{\boldsymbol{\dot x}}_{\rm{c}}}({t_k}) 得到{q_{{\rm{c}}j}}({t_k}) 和{\dot q_{{\rm{c}}j}}({t_k}) ,进而得到{q_{{\rm{c}}j}}({t_{k + 1}}) 和{\dot q_{{\rm{c}}j}}({t_{k + 1}}) 。{t_{k + 1}} 时刻结构的动力响应:\left\{ \begin{aligned} & {\boldsymbol{x}}({t_{k + 1}}) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{c}}j}}{{\dot q}_{{\rm{c}}j}}({t_{k + 1}}) + {{\boldsymbol{B}}_{{\rm{c}}j}}{q_{{\rm{c}}j}}({t_{k + 1}})] +\\& \qquad\qquad \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{p}}j}}{{\dot q}_{{\rm{p}}j}}({t_{k + 1}}) + {{\boldsymbol{B}}_{{\rm{p}}j}}{q_{{\rm{p}}j}}({t_{k + 1}})] \\& {\boldsymbol{\dot x}}({t_{k + 1}}) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{c}}j}}{{\ddot q}_{{\rm{c}}j}}({t_{k + 1}}) + {{\boldsymbol{B}}_{{\rm{c}}j}}{{\dot q}_{{\rm{c}}j}}({t_{k + 1}})] + \\& \qquad\qquad \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{p}}j}}{{\ddot q}_{{\rm{p}}j}}({t_{k + 1}}) + {{\boldsymbol{B}}_{{\rm{p}}j}}{{\dot q}_{{\rm{p}}j}}({t_{k + 1}})] \\& {\boldsymbol{\ddot x}}({t_{k + 1}}) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{c}}j}}{{\dddot q}_{{\rm{c}}j}}({t_{k + 1}}) + {{\boldsymbol{B}}_{{\rm{c}}j}}{{\ddot q}_{{\rm{c}}j}}({t_{k + 1}})] + \\& \qquad\qquad\sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{p}}j}}{{\dddot q}_{{\rm{p}}j}}({t_{k + 1}}) + {{\boldsymbol{B}}_{{\rm{p}}j}}{{\ddot q}_{{\rm{p}}j}}({t_{k + 1}})] \end{aligned} \right. (45) 重复式(36)~式(45),可实现基于地震波卓越频率的混合结构复模态叠加法。
3 基于地震波的谐波频率的混合结构复模态叠加法
3.1 基于谐波频率的阻尼矩阵
对于频带较宽的地震波,卓越频率不能有效地表现地震波的主要频谱特性,为此本文对基于地震波卓越频率的阻尼矩阵进行改进,将输入地震波加速度采用三角级数展开,得:
g(t) = {J_0} + \sum\limits_{l = 1}^{{N_{\rm{s}}}/2} {{J_l}\sin ({\theta _l}t) + \sum\limits_{l = 1}^{{N_{\rm{s}}}/2} {{K_l}\cos ({\theta _l}t)} } (46) 与基于地震波卓越频率的瞬态分析相同,地震波作用下基于分块Rayleigh阻尼矩阵的齐次运动方程为式(29),瞬态反应对应的阻尼矩阵可由式(30)和式(31)确定。
地震波作用下基于分块Rayleigh阻尼矩阵的非齐次运动方程为:
{\boldsymbol{K}}{{\boldsymbol{x}}_{{\rm{p0}}}}(t) = - {\boldsymbol{MI}}{J_0}\;\;\;\qquad\qquad\qquad (47) \begin{split} & {\boldsymbol{M}}{{\boldsymbol{\ddot x}}_{{\rm{p}}l}}(t) + {{\boldsymbol{C}}_{{\rm{p}}l}}{{\boldsymbol{\dot x}}_{{\rm{p}}l}}(t) + {\boldsymbol{K}}{{\boldsymbol{x}}_{{\rm{p}}l}}(t) = \\&\qquad - {\boldsymbol{MI}}[{J_l}\sin ({\theta _l}t) + {K_l}\cos ({\theta _l}t)] \end{split} (48) 其中:
{{\boldsymbol{x}}_{\rm{p}}}(t) = {{\boldsymbol{x}}_{{\rm{p}}0}}(t) + \sum\limits_{l = 1}^{NN} {{{\boldsymbol{x}}_{{\rm{p}}l}}(t)} (49) 稳态反应的阻尼矩阵可表示为:
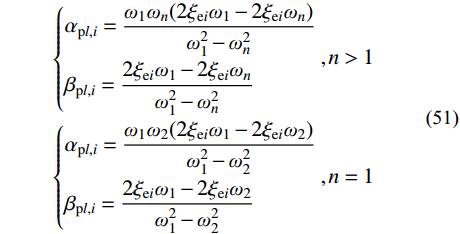
{{\boldsymbol{C}}_{{\rm{p}}l}} = {\alpha _{{\rm{p}}l}}{\boldsymbol{M}} + {\beta _{{\rm{p}}l}}{\boldsymbol{K}} (50) 阻尼系数可表示:
\begin{array}{l} \left\{ \begin{aligned} & {\alpha _{{\rm{p}}l,i}} = \frac{{{\omega _1}{\omega _n}(2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _n})}}{{{\omega _1^2} - {\omega _n^2}}} \\ & {\beta _{{\rm{p}}l,i}} = \frac{{2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _n}}}{{{\omega _1^2} - {\omega _n^2}}} \end{aligned} \right.{\rm{ }},n > 1 \\ \left\{ \begin{aligned} & {\alpha _{{\rm{p}}l,i}} = \frac{{{\omega _1}{\omega _2}(2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _2})}}{{{\omega _1^2} - {\omega _2^2}}} \\ & {\beta _{{\rm{p}}l,i}} = \frac{{2{\xi _{{\rm{e}}i}}{\omega _1} - 2{\xi _{{\rm{e}}i}}{\omega _2}}}{{{\omega _1^2} - {\omega _2^2}}} \end{aligned} \right.{\rm{ }},n = 1 \end{array} (51) 式中,
{\omega _n} 为第n阶振型的自振频率,且{\omega _n} 是最接近{\theta _l} 的自振频率。综上,由式(51)可确定阻尼系数,进而得到基于谐波频率的分块Rayleigh阻尼矩阵。
3.2 基于谐波频率的复模态叠加法
为实现基于谐波频率的复模态叠加法,首先计算齐次运动方程对应的通解
{{\boldsymbol{x}}_{\rm{c}}}(t) ,与基于地震波卓越频率的复模态叠加法相同,解耦后的齐次方程为式(36),求解可得:{q_{{\rm{c}}j}}(t) = {{\rm{e}}^{ - {\xi _{{\rm{c}}j}}{\omega _{{\rm{c}}j}}t}}[{D_j}\cos ({\omega _{{\rm{c,d}}j}}t) + {E_j}\sin ({\omega _{{\rm{c,d}}j}}t)] (52) 其中:
\left\{ \begin{aligned} & {D_j} = {q_{{\rm{c}}j}}({t_0}) \\& {E_j} = \frac{{{q_{{\rm{c}}j}}({t_0}) + {\xi _j}{\omega _j}{{\dot q}_{{\rm{c}}j}}({t_0})}}{{{\omega _{{\rm{d}}j}}}} \end{aligned} \right. (53) 计算非齐次运动方程对应的特解
{{\boldsymbol{x}}_{\rm{p}}}(t) ,求解式(45),可直接得到{{\boldsymbol{x}}_{{\rm{p0}}}}(t) 。求解式(46),依据复模态叠加法可得:
\begin{split} & {\ddot q_{{\rm{p}}l,j}}(t) + {\omega _{{\rm{p}}l,j}^2}{q_{{\rm{p}}l,j}}(t) + 2{\xi _{{\rm{p}}l,j}}{\omega _{{\rm{p}}l,j}}{\dot q_{{\rm{p}}l,j}}(t) =\\& \qquad{J_l}\sin ({\theta _l}t) + {K_l}\cos ({\theta _l}t) \end{split} (54) 令,
{q_{{\rm{p}}l,j}}(t) = {P_{{\rm{p}}l,j}}\sin ({\theta _l}t) + {Q_{{\rm{p}}l,j}}\cos ({\theta _l}t) (55) 将式(55)代入式(54),可得:
\left\{ \begin{aligned} & {P_{{\rm{p}}l,j}} = \frac{{({\omega _{{\rm{p}}l,j}^2} - {\theta _l^2}){J_l} + 2{\xi _{{\rm{p}}l,j}}{\omega _{{\rm{p}}l,j}}{\theta _l}{K_l}}}{{{{({\omega _{{\rm{p}}l,j}^2} - {\theta _l^2})^2}} + 4{\xi _{{\rm{p}}l,j}^2}{\omega _{{\rm{p}}l,j}^2}{\theta _l^2}}} \\& {Q_{{\rm{p}}l,j}} = \frac{{({\omega _{{\rm{p}}l,j}^2} - {\theta _l^2}){K_l} - 2{\xi _{{\rm{p}}l,j}}{\omega _{{\rm{p}}l,j}}{\theta _l}{J_l}}}{{{{({\omega _{{\rm{p}}l,j}^2} - {\theta _l^2})^2}} + 4{\xi _{{\rm{p}}l,j}^2}{\omega _{{\rm{p}}l,j}^2}{\theta _l^2}}} \end{aligned} \right. (56) 由式(16)和式(55)可得:
{{\boldsymbol{x}}_{{\rm{p}}l}}(t) = \sum\limits_{j = 1}^N [ {{\boldsymbol{A}}_{{\rm{p}}l,j}}{\dot q_{{\rm{p}}l,j}}(t) + {{\boldsymbol{B}}_{{\rm{p}}l,j}}{q_{{\rm{p}}l,j}}(t)] (57) 结构的动力响应为:
\left\{ \begin{aligned} & {\boldsymbol{x}}(t) = {{\boldsymbol{x}}_{\rm{c}}}(t) + {{\boldsymbol{x}}_{{\rm{p}}0}}(t) + \sum\limits_{l = 1}^{{N_{\rm{s}}}/2} {{{\boldsymbol{x}}_{{\rm{p}}l}}(t)} \\& {\boldsymbol{\dot x}}(t) = {{{\boldsymbol{\dot x}}}_{\rm{c}}}(t) + {{{\boldsymbol{\dot x}}}_{{\rm{p}}0}}(t) + \sum\limits_{l = 1}^{{N_{\rm{s}}}/2} {{{{\boldsymbol{\dot x}}}_{{\rm{p}}l}}(t)} \\& {\boldsymbol{\ddot x}}(t) = {{{\boldsymbol{\ddot x}}}_{\rm{c}}}(t) + {{{\boldsymbol{\ddot x}}}_{{\rm{p}}0}}(t) + \sum\limits_{l = 1}^{{N_{\rm{s}}}/2} {{{{\boldsymbol{\ddot x}}}_{{\rm{p}}l}}(t)} \end{aligned} \right. (58) 关于初值的确定,由式(58)可得:
\left\{ \begin{aligned} & {{\boldsymbol{x}}_{\rm{c}}}({t_0}) = {\boldsymbol{x}}({t_0}) + {{\boldsymbol{x}}_{{\rm{p}}0}}({t_0}) + \sum\limits_{l = 1}^{{N_{\rm{s}}}/2} {{{\boldsymbol{x}}_{{\rm{p}}l}}({t_0})} \\& {{\boldsymbol{x}}_{\rm{c}}}({t_0}) = {\boldsymbol{x}}({t_0}) + {{\boldsymbol{x}}_{{\rm{p}}0}}({t_0}) + \sum\limits_{l = 1}^{{N_{\rm{s}}}/2} {{{\boldsymbol{x}}_{{\rm{p}}l}}({t_0})} \end{aligned} \right. (59) 依据复特征向量的正交性,可由
{{\boldsymbol{x}}_{\rm{c}}}({t_0}) 和{{\boldsymbol{\dot x}}_{\rm{c}}}({t_0}) 得到{q_{{\rm{c}}j}}({t_0}) 和{\dot q_{{\rm{c}}j}}({t_0}) ,完成初值的确定,进而实现基于谐波频率的混合结构复模态叠加法。4 试验校核与计算分析
将由不同阻尼特性材料组成的悬臂板试件作为试验对象采用图1所示的试验测试系统,通过振动台控制系统对试件的基底施加随机激励,同时采用多普勒振动测试系统测量试件的动力响应。振动测试系统可直接采集试件的速度响应,需根据采集频率进行相应的积分或微分处理才能得到构件的位移或加速度响应,为避免后期的数据再处理导致的误差,本文仅分析了试件的速度响应,以验证本文方法的正确性。
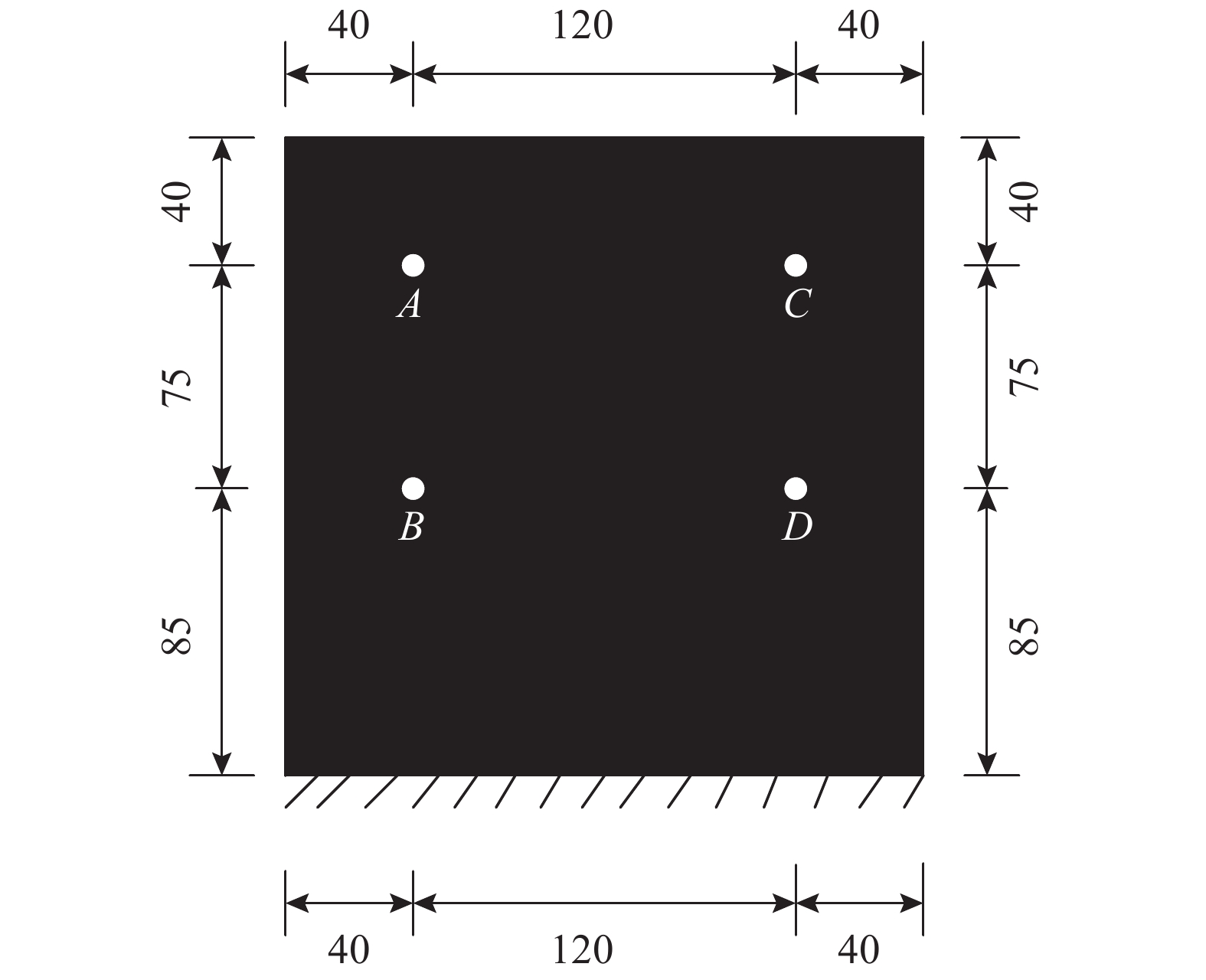
悬臂板试件的具体尺寸如图2所示,拾振点的位置如图3所示,考虑到4个拾振点的位置是对称分布的,本文仅选取拾振点A和拾振点B的动力响应进行分析、对比。试验选取尺寸和材料相同的2个试件(CP-1和CP-2)进行测试,试件的材料参数如表1所示,子结构的振型阻尼比为对应材料损耗因子的1/2[38-40],基层结构的振型阻尼比为0.0015,阻尼层结构的振型阻尼比为0.295。采用数值模拟,由试件的整体质量矩阵和整体刚度矩阵通过模态分析可得到试件的前5阶振型的无阻尼自振频率为15.26 Hz、35.58 Hz、90.13 Hz、118.54 Hz和132.41 Hz。
表 1 试件的材料参数Table 1. Material parameters of specimen材料参数 基层材料 阻尼层材料 Q235钢板 Air++3104阻尼胶片 弹性模量/Pa 2.1 \times {10^{11}} 4.0 \times {10^7} 密度/(kg/m3) 7500 1600 泊松比 0.30 0.49 损耗因子 0.003 0.59 4.1 试件CP-1的试验结果和计算结果对比
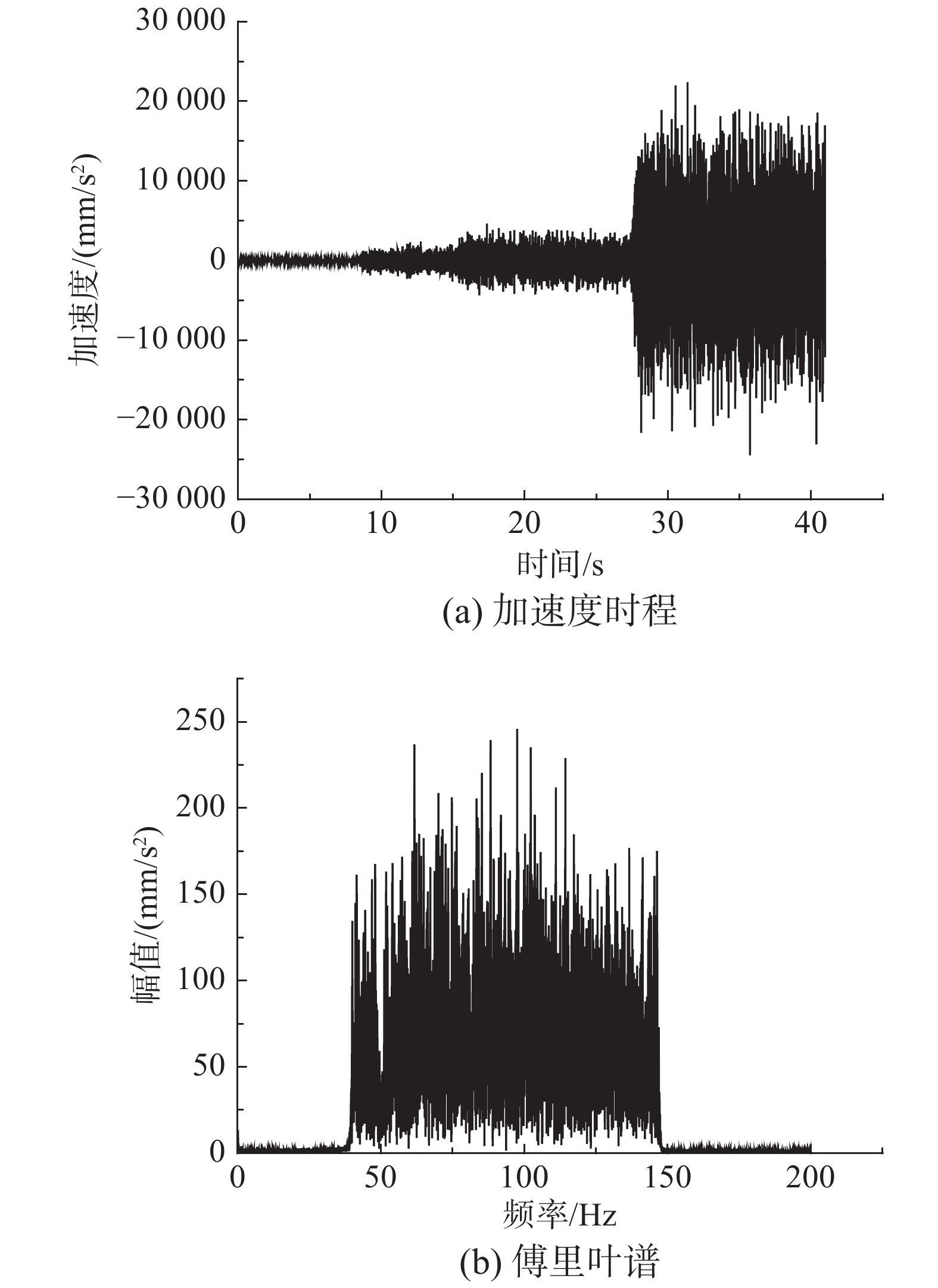
利用振动台控制系统,对试件CP-1施加随机激励,其振动频率的范围为100 Hz~150 Hz。由信号采集系统可得到随机激励的加速度时程(见图4(a))和对应的傅里叶谱(见图4(b))。分别采用基于第一阶振型和第二阶振型的复模态叠加法(CRS)、本文提出的基于地震波卓越频率的复模态叠加法(CRZ)和基于地震波的谐波频率的复模态叠加法(CRX)计算试件CP-1在随机激励作用下的速度时程,并将其分别与多普勒振动测试系统测量的试件速度响应时程(CP-1-Test)进行对比,结果如图5所示。如表2所示,对比拾振点A的速度峰值
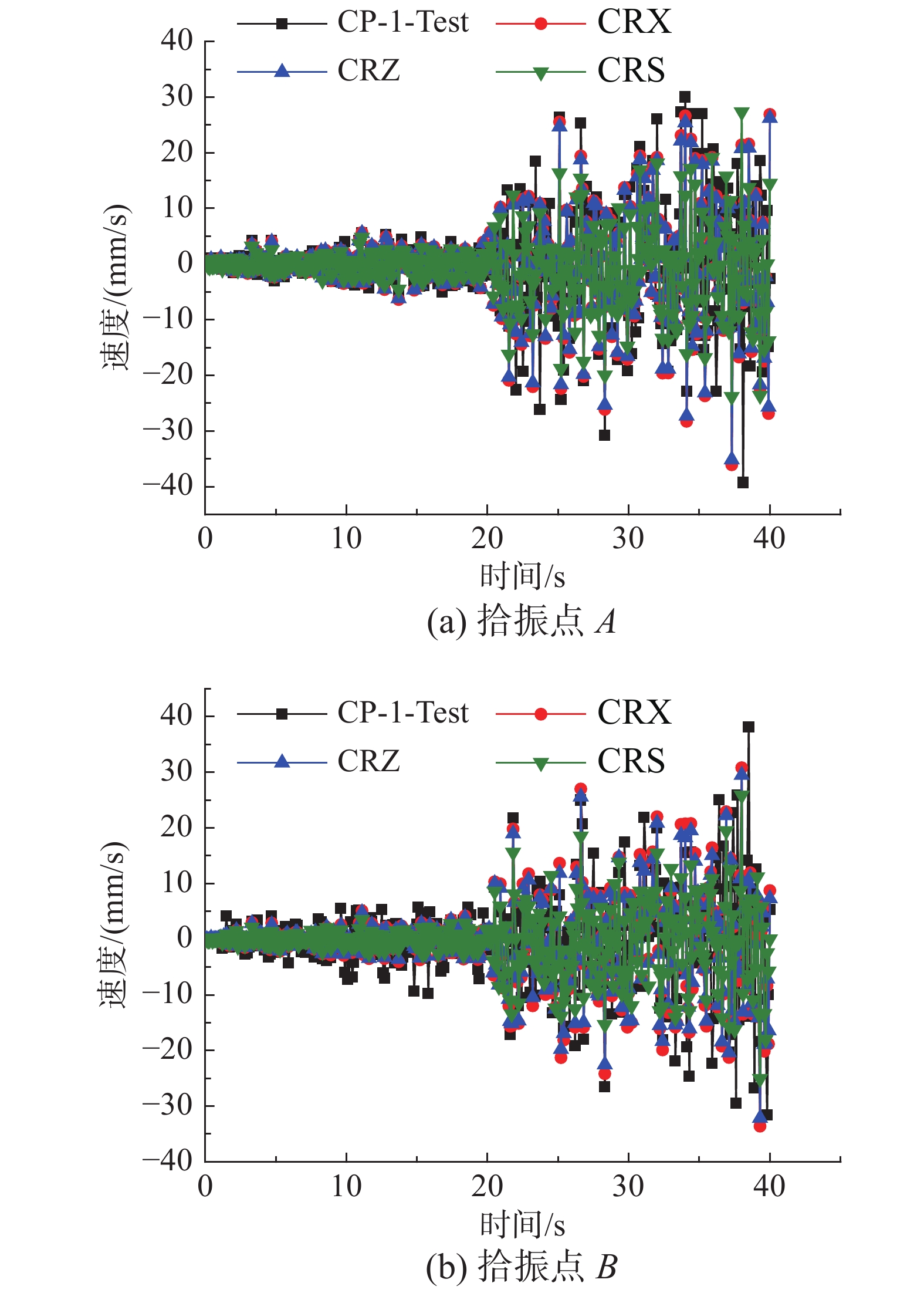
{I_{\rm{A}}} ,CRS的相对误差{\delta _{\rm{A}}} 为39.33%,CRZ的相对误差{\delta _{\rm{A}}} 为10.49%,CRX的相对误差{\delta _{\rm{A}}} 为8.16%;对比拾振点B的速度峰值{I_{\rm{B}}} ,CRS的相对误差{\delta _{\rm{B}}} 为32.19%,CRZ的相对误差{\delta _{\rm{B}}} 为15.78%,CRX的相对误差{\delta _{\rm{B}}} 为11.90%。结果表明,相比CRS,考虑了地震动频谱特征影响的CRZ和CRX的计算精度更高;对于窄频带的外激励,相比CRZ,CRX的计算精度并没有明显提高,但CRX的计算量较大。因此,对于窄频带的外激励,应优先选用CRZ。表 2 试件CP-1的动力响应对比Table 2. Comparisons of dynamic responses of specimen CP-1速度 CP-1-Test CRS CRZ CRX {I_{\rm{A}}}/(mm/s) 39.2692 23.8258 35.1506 36.0660 {\delta _{\rm{A}}}/(%) − 39.3300 10.4900 8.1600 {I_{\rm{B}}}/(mm/s) 38.1542 25.8730 32.1342 33.6120 {\delta _{\rm{B}}}/(%) − 32.1900 15.7800 11.9000 4.2 试件CP-2的试验结果和计算结果对比
利用振动台控制系统对试件CP-2施加频带较宽的随机激励,其振动频率的范围为40 Hz~150 Hz。由信号采集系统可得到随机激励的加速度时程(见图6(a))和对应的傅里叶谱(见图6(b))。分别采用CRS、CRZ和CRX计算试件CP-2在随机激励作用下的速度时程,并分别与多普勒振动测试系统得到的速度时程(CP-2-Test)进行对比,结果如图7所示。如表3所示,对比拾振点A的速度峰值
{I_{\rm{A}}} ,CRS的相对误差{\delta _{\rm{A}}} 为23.45%,CRZ的相对误差{\delta _{\rm{A}}} 为13.11%,CRX的相对误差{\delta _{\rm{A}}} 为7.92%;对比拾振点B的速度峰值{I_{\rm{B}}} ,CRS的相对误差{\delta _{\rm{B}}} 为47.50%,CRZ的相对误差{\delta _{\rm{B}}} 为19.28%,CRX的相对误差{\delta _{\rm{B}}} 为11.15%。结果表明,与试件CP-1的分析结果相同,CRZ和CRX的计算精度相比CRS明显更高。与试件CP-1不同的是,随着外激励频带增宽,CRX的计算精度比CRZ明显增高。因此,CRZ计算量更小、适用范围受限,CRX的计算精度更高,具有更宽泛的适用范围,在对计算精度有要求时,建议采用CRX。表 3 试件CP-2的动力响应对比Table 3. Comparisons of dynamic responses of specimen CP-2速度 CP-2-Test CRS CRZ CRX {I_{\rm{A}}}/(mm/s) 63.4593 48.5796 55.1387 58.4345 {\delta _{\rm{A}}}/(%) − 23.4500 13.1100 7.9200 {I_{\rm{B}}}/(mm/s) 75.2177 39.4871 60.7179 66.8291 {\delta _{\rm{B}}}/(%) − 47.5000 19.2800 11.1500 5 算例分析
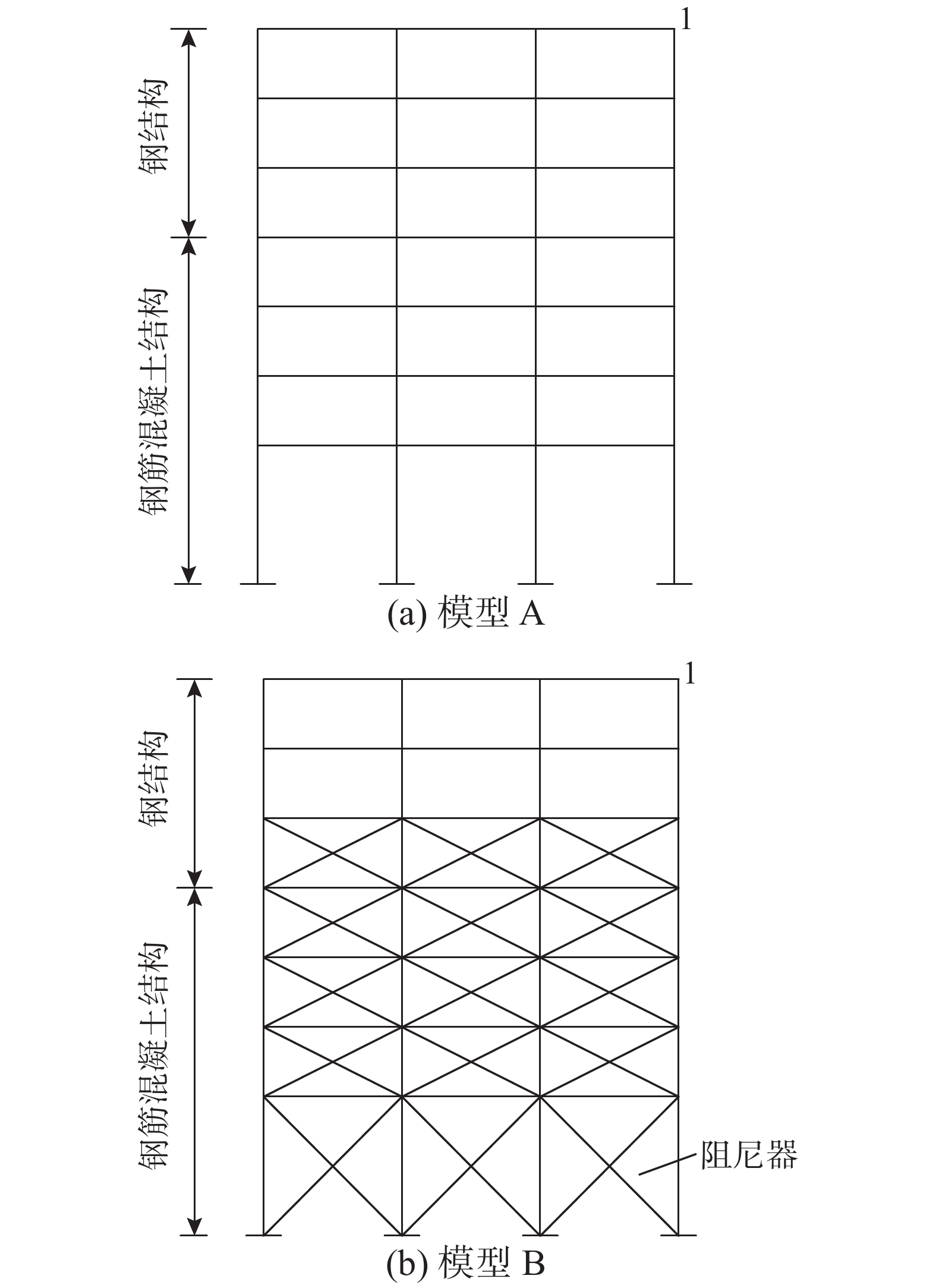
如图8所示,模型A和模型B是由不同阻尼特性材料组成的7层平面框架,1层~4层均为钢筋混凝土结构、5层~7层为钢结构。框架底层高度皆为6 m、其余各层层高均为3 m,跨度均为6 m,钢筋混凝土柱、梁的截面尺寸分别为400 mm×500 mm、300 mm×400 mm,钢柱、梁的截面尺寸分别为HM400 mm×300 mm×10 mm×16 mm、HM300 mm×200 mm×8 mm×12 mm,各楼层集中质量皆为2 0000 kg。与模型A相比,模型B的唯一区别是增设了X型阻尼器,材料参数见表4。
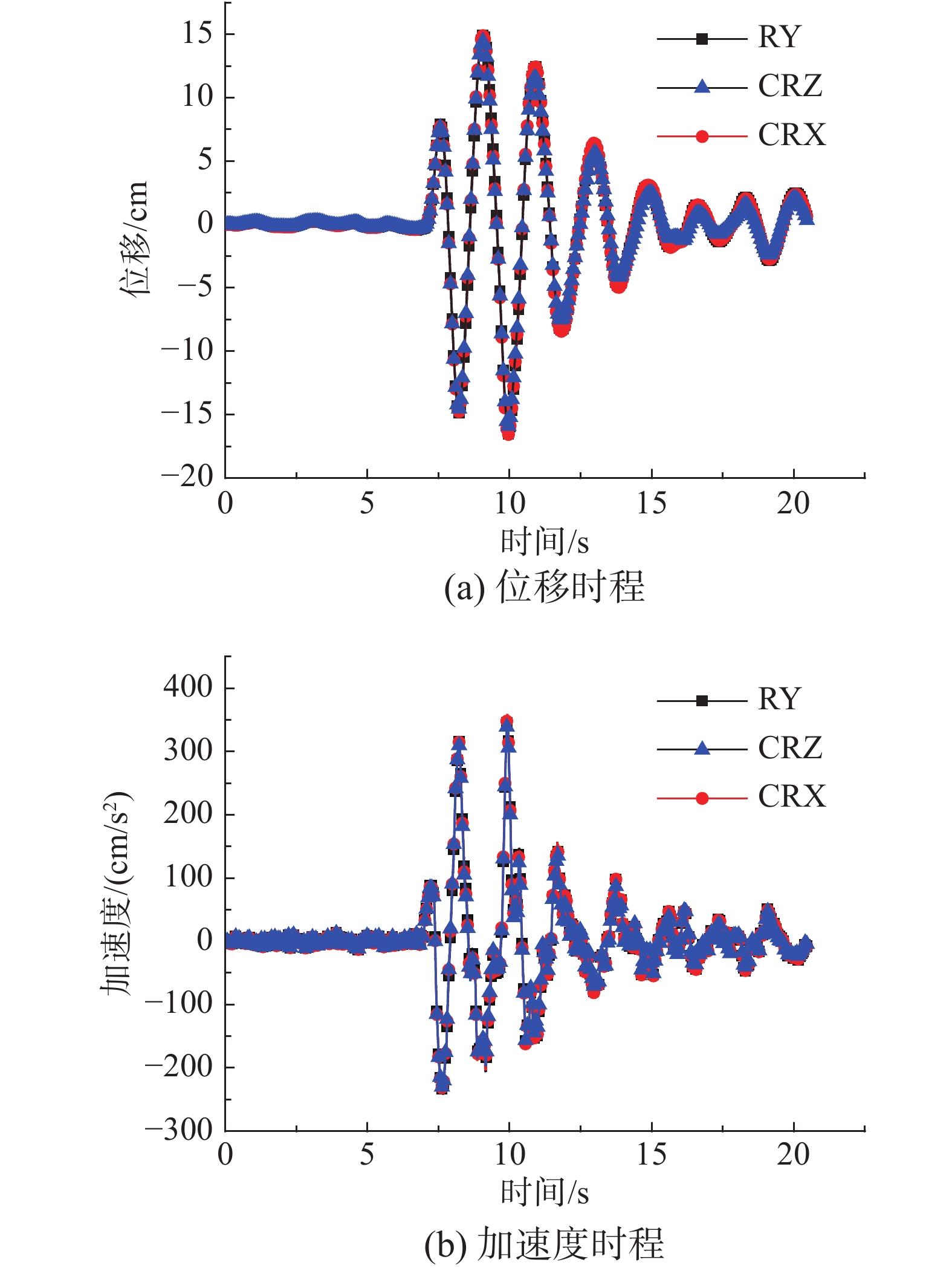
表 4 不同材料的参数Table 4. Parameters of different materials材料类别 弹性模量/Pa 密度/(kg/m3) 阻尼比 钢筋混凝土 3.5 \times {10^{10}} 2500 0.05 钢材 2.0 \times {10^{11}} 7900 0.02 阻尼器 1.0 \times {10^{11}} 5000 0.40 地震动输入选取天津地震波和迁安地震波,对应的加速度时程和傅里叶幅值谱分别如图9和图10所示。其中,天津地震波的频带较窄,迁安地震波的频带较宽。分别采用基于应变能法的实模态叠加法(RY)[1-4]、CRZ和CRX计算模型A、模型B在地震波作用下结构顶层节点1(位置见图8)的动力响应,结果如图11、图12、图13和图14所示。
对于模型A,天津地震波作用下,RY、CRZ和CRX计算得到的顶层动力响应时程近似相等(见图11)。相比RY,CRZ的位移峰值相对误差为3.65%,加速度峰值相对误差为2.47%;CRX的位移峰值相对误差为0.35%,加速度峰值相对误差为在0.30%(见表5)。迁安地震波作用下,RY和CRX计算得到的顶层加速度时程近似相等,但CRZ计算得到的动力响应时程明显不同(见图12)。相比RY,CRZ的位移峰值相对误差为19.78%,加速度峰值相对误差为14.96%;CRX的位移峰值相对误差为0.27%,加速度峰值相对误差为在0.18%(见表5)。因此,对于非比例阻尼特性较小的混合结构,RY和CRX的计算结果近似相等,而CRZ仅适用于计算窄频带地震波作用下结构动力响应。
表 5 模型A的顶层响应对比Table 5. Comparisons of top floor responses of Model A响应 天津地震波 迁安地震波 RY CRZ CRX RY CRZ CRX 位移峰值/cm 16.5223 15.9200 16.5802 1.1064 0.8875 1.1094 相对误差/(%) − 3.6500 0.3500 − 19.7800 0.2700 加速度峰值/
(cm/s2)356.7642 347.9600 357.8498 97.1007 111.6260 96.9218 相对误差/(%) − 2.4700 0.3000 − 14.9600 0.1800 对于模型B,天津地震波作用下,CRZ和CRX计算得到的顶层动力响应时程近似相等,RY计算得到的动力响应时程明显不同(见图13)。相比RY,CRZ的位移峰值相对误差为12.85%,加速度峰值相对误差为22.11%;CRX的位移峰值相对误差为10.19%,加速度峰值相对误差为在17.16%(见表6)。迁安地震波作用下,RY、CRZ和CRX计算得到的模型B顶层加速度时程明显不同(见图14)。相比RY,CRZ的位移峰值相对误差为22.21%,加速度峰值相对误差为11.58%;CRX的位移峰值相对误差为12.12%,加速度峰值相对误差为在11.98%(见表6)。因此,对于非比例阻尼特性较大的混合结构,RY与CRZ、CRX的计算结果差异较大。与模型A的规律相同,窄频带地震波作用下,CRZ和CRX的计算结果近似相等,随着地震波频带的增宽,CRZ与CRX的计算结果差异增大。
表 6 模型B的顶层响应对比Table 6. Comparisons of top floor responses of Model B响应 天津地震波 迁安地震波 RY CRZ CRX RY CRZ CRX 位移峰值/cm 0.5488 0.6193 0.6047 0.2666 0.2074 0.2989 相对误差/(%) − 12.8500 10.1900 − 22.2100 12.1200 加速度峰值/
(cm/s2)184.2694 225.0049 215.8834 162.0321 143.2617 181.4360 相对误差/(%) − 22.1100 17.1600 − 11.5800 11.9800 综上,对于非比例阻尼特性较小的混合结构,RY与CRZ、CRX的计算结果近似相等,随着混合结构非比例阻尼特性增大,RY与CRZ、CRX的计算结果差异增大。与试验结果的规律相同,CRZ的计算量小,但仅适用于窄频带地震波作用下结构动力响应的计算;CRX的计算精度更高,且适用于宽频带地震波作用下结构动力响应的计算,但计算量大。
6 结论
针对基于Rayleigh阻尼模型的地震反应分析过程中阻尼系数确定方法存在的问题,本文提出了基于动力特性确定Rayleigh阻尼系数的新方法,经过理论推导和试验校核得到以下结论:
(1)求解地震波作用下结构的瞬态反应时,依据结构的前两阶振型确定阻尼系数;求解地震波作用下结构的稳态反应时,依据结构的基本振型、与地震波卓越频率接近的振型确定阻尼系数,得到基于地震波卓越频率的分块Rayleigh阻尼模型。结合输入地震波加速度时程在时间步长内线性变化的假定,提出了相应的混合结构复模态叠加法。
(2)卓越频率仅能反映窄频带地震波的频谱特性。对于具有明显宽带频谱特性的地震波,借助快速傅里叶变换,将输入地震波加速度表示为一系列谐波的叠加组合,得到每一条谐波的频率。求解地震波作用下结构的稳态反应时,依据结构的基本振型、与谐波频率接近的振型确定阻尼系数,得到基于谐波频率的分块Rayleigh阻尼模型,建立了对应的混合结构复模态叠加法。
(3)试验结果和计算对比分析表明,基于动力响应特性确定Rayleigh阻尼系数的计算方法避免了传统方法存在的振型选择不唯一导致的计算结果不确定的问题,且计算结果误差较小;与基于地震波卓越频率的复模态叠加法相比,基于谐波频率的复模态叠加法计算量更大,但计算精度更高、适用范围更广。
-
表 1 试件的材料参数
Table 1 Material parameters of specimen
材料参数 基层材料 阻尼层材料 Q235钢板 Air++3104阻尼胶片 弹性模量/Pa 2.1 \times {10^{11}} 4.0 \times {10^7} 密度/(kg/m3) 7500 1600 泊松比 0.30 0.49 损耗因子 0.003 0.59 表 2 试件CP-1的动力响应对比
Table 2 Comparisons of dynamic responses of specimen CP-1
速度 CP-1-Test CRS CRZ CRX {I_{\rm{A}}}/(mm/s) 39.2692 23.8258 35.1506 36.0660 {\delta _{\rm{A}}}/(%) − 39.3300 10.4900 8.1600 {I_{\rm{B}}}/(mm/s) 38.1542 25.8730 32.1342 33.6120 {\delta _{\rm{B}}}/(%) − 32.1900 15.7800 11.9000 表 3 试件CP-2的动力响应对比
Table 3 Comparisons of dynamic responses of specimen CP-2
速度 CP-2-Test CRS CRZ CRX {I_{\rm{A}}}/(mm/s) 63.4593 48.5796 55.1387 58.4345 {\delta _{\rm{A}}}/(%) − 23.4500 13.1100 7.9200 {I_{\rm{B}}}/(mm/s) 75.2177 39.4871 60.7179 66.8291 {\delta _{\rm{B}}}/(%) − 47.5000 19.2800 11.1500 表 4 不同材料的参数
Table 4 Parameters of different materials
材料类别 弹性模量/Pa 密度/(kg/m3) 阻尼比 钢筋混凝土 3.5 \times {10^{10}} 2500 0.05 钢材 2.0 \times {10^{11}} 7900 0.02 阻尼器 1.0 \times {10^{11}} 5000 0.40 表 5 模型A的顶层响应对比
Table 5 Comparisons of top floor responses of Model A
响应 天津地震波 迁安地震波 RY CRZ CRX RY CRZ CRX 位移峰值/cm 16.5223 15.9200 16.5802 1.1064 0.8875 1.1094 相对误差/(%) − 3.6500 0.3500 − 19.7800 0.2700 加速度峰值/
(cm/s2)356.7642 347.9600 357.8498 97.1007 111.6260 96.9218 相对误差/(%) − 2.4700 0.3000 − 14.9600 0.1800 表 6 模型B的顶层响应对比
Table 6 Comparisons of top floor responses of Model B
响应 天津地震波 迁安地震波 RY CRZ CRX RY CRZ CRX 位移峰值/cm 0.5488 0.6193 0.6047 0.2666 0.2074 0.2989 相对误差/(%) − 12.8500 10.1900 − 22.2100 12.1200 加速度峰值/
(cm/s2)184.2694 225.0049 215.8834 162.0321 143.2617 181.4360 相对误差/(%) − 22.1100 17.1600 − 11.5800 11.9800 -
[1] Hwang J S, Chang K C, Tsai M H. Composite damping ratio of seismically isolated regular bridges [J]. Engineering Structures, 1997, 19(1): 55 − 62. doi: 10.1016/S0141-0296(96)00040-5
[2] 薛彦涛, 韦承基, 孙仁范,等. 采用不同材料加层时结构阻尼比计算方法(应变能法)[J]. 工程抗震与加固改造, 2008, 30(2): 91 − 95. doi: 10.3969/j.issn.1002-8412.2008.02.019 Xue Yantao, Wei Chengji, Sun Renfan, et al. Calculation method for damping ration of different story added structures (strain energy method) [J]. Earthquake Resistant Engineering and Retrofitting, 2008, 30(2): 91 − 95. (in Chinese) doi: 10.3969/j.issn.1002-8412.2008.02.019
[3] Wang J. Intrinsic damping: Modeling techniques for engineering systems [J]. Journal of Structural Engineering, 2009, 135(3): 282 − 291. doi: 10.1061/(ASCE)0733-9445(2009)135:3(282)
[4] Lu Z, He X, Zhou Y. Studies on damping behavior of vertically mixed structures with upper steel and lower concrete substructures [J]. The Structural Design of Tall and Special Buildings, 2017, 26: e1392. DOI: 10.1002/tal.1392
[5] 王昌盛,郑会华,李重稳,等. 非经典阻尼隔震结构近似实空间解耦分析[J]. 华中科技大学学报(自然科学版), 2015, 43(1): 45 − 49. Wang Changsheng, Zheng Huihua, Li Chongwen, et al. Analyze non-classical damping isolation structure by approximate decoupling in real spaces [J]. Journal Huazhong University of Science Technology (Natural Science Edition), 2015, 43(1): 45 − 49. (in Chinese)
[6] 黄维, 钱江, 梁飞飞,等. 竖向混合结构阻尼矩阵近似解耦计算的误差分析[J]. 中南大学学报(自然科学版), 2015, 46(4): 1454 − 1460. Huang Wei, Qian Jiang, Liang Feifei, et al. Errors of approximate decoupling analysis for vertically mixed structures [J]. Journal of Central South University (Science and Technology), 2015, 46(4): 1454 − 1460. (in Chinese)
[7] 黄本才. 组合结构振动的等效阻尼比[J]. 上海力学, 1998, 19(2): 141 − 145. Huang Bencai. Equivalent modal damping ratios of vibration in composite structures [J]. Shanghai Journal of Mechanics, 1998, 19(2): 141 − 145. (in Chinese)
[8] 黄维, 钱江, 周知. 竖向混合结构模态阻尼比计算研究[J]. 振动与冲击, 2014, 33(13): 13 − 18. Huang Wei, Qian Jiang, Zhou Zhi. Equivalent modal damping ratio for vertically mixed structures [J]. Journal of Vibration and Shock, 2014, 33(13): 13 − 18. (in Chinese)
[9] Papageorgiou A V, Gantes C J. Equivalent modal damping ratios for concrete/steel mixed structures [J]. Computers and Structures, 2010, 88(19/20): 1124 − 1136. doi: 10.1016/j.compstruc.2010.06.014
[10] 黄维, 钱江, 周知. 基于Rayleigh阻尼模型的竖向混合结构设计阻尼比研究[J]. 工程力学, 2015, 32(10): 60 − 67. Huang Wei, Qian Jiang, Zhou Zhi. Research on equivalent damping ratio of vertically mixed structures based on Rayleigh damping model [J]. Engineering Mechanics, 2015, 32(10): 60 − 67. (in Chinese)
[11] Wei H, Jiang Q, Zhi Z, et al. An approach to equivalent damping ratio of vertically mixed structures based on response error minimization [J]. Soil Dynamics and Earthquake Engineering, 2015, 72: 119 − 128. doi: 10.1016/j.soildyn.2015.02.008
[12] Foss K A. Coordinates which uncouple the equations of motion of damped linear dynamic systems [J]. Journal of Applied Dynamics, 1958, 25(9): 361 − 364.
[13] Zhou X, Yu R, Dong D. Complex mode superposition algorithm for seismic responses of non-classically damped linear MDOF system [J]. Journal of Earthquake Engineering, 2004, 8(4): 597 − 641.
[14] Chen H, Tan P, Zhou F. An improved response spectrum method for non-classically damped systems [J]. Bulletin of Earthquake Engineering, 2017, 15: 4375 − 4397. doi: 10.1007/s10518-017-0144-4
[15] Suarez L E, Gaviria C A. Dynamic properties of a building with viscous dampers in non-proportional arrangement [J]. Structural Engineering and Mechanics, 2015, 55(6): 1241 − 1260. doi: 10.12989/sem.2015.55.6.1241
[16] De Domenico D, Ricciardi G. Dynamic response of non-classically damped structures via reduced-order complex modal analysis: Two novel truncation measures [J]. Journal of Sound and Vibration, 2019, 452: 169 − 190. doi: 10.1016/j.jsv.2019.04.010
[17] Kenan Y S, Koruk H. Development and validation of a composite finite element with damping capability [J]. Composite Structures, 2013, 97(2): 136 − 146.
[18] Rayleigh J W. The theory of sound [M]. 2nd ed. New York: Dover, 1945.
[19] Clough R W, Penzien J. Dynamics of structures [M]. 3rd ed. Berkeley, California, USA: Computers and structures, Inc., 2003.
[20] Erduran E. Evaluation of Rayleigh damping and its influence on engineering demand parameter estimates [J]. Earthquake Engineering and Structural Dynamics, 2012, 41(14): 1905 − 1919. doi: 10.1002/eqe.2164
[21] 潘旦光, 高莉莉. Rayleigh阻尼系数解法比较及对结构地震反应影响[J]. 工程力学, 2015, 32(6): 192 − 199. Pan Danguang, Gao Lili. Comparison of determination methods for Rayleigh damping coefficients and effects on seismic responses of structures [J]. Engineering Mechanics, 2015, 32(6): 192 − 199. (in Chinese)
[22] 胡成宝, 王云岗, 凌道盛. 瑞利阻尼物理本质及参数对动力响应的影响[J]. 浙江大学学报(工学版), 2017, 51(7): 1284 − 1290. doi: 10.3785/j.issn.1008-973X.2017.07.003 Hu Chengbao, Wang Yungang, Ling Daosheng. Physical essence and influence of model parameters on dynamic response of Rayleigh damping [J]. Journal of Zhejiang University (Engineering Science), 2017, 51(7): 1284 − 1290. (in Chinese) doi: 10.3785/j.issn.1008-973X.2017.07.003
[23] Idriss I M, Lysmer J, Hwang R, et al. QUAD4: A computer program for evaluating the seismic response of soil structures by variable damping finite element procedures [R]. Berkeley: University of California, 1973.
[24] Yoshida N, Kobayashi S, Suetomi I, et al. Equivalent linear method considering frequency dependent characteristics of stiffness and damping [J]. Soil Dynamics and Earthquake Engineering, 2002, 22(3): 205 − 222. doi: 10.1016/S0267-7261(02)00011-8
[25] Hudson M, Idriss I M, Beikae M. A computer program to evaluate the seismic response of soil structures using finite element procedures and incorporating a compliant base [D]. Berkeley: University of California, 1994.
[26] 邹德高, 徐斌, 孔宪京. 瑞利阻尼系数确定方法对高土石坝地震反应的影响研究[J]. 岩土力学, 2011, 32(3): 797 − 803. doi: 10.3969/j.issn.1000-7598.2011.03.026 Zou Degao, Xu Bin, Kong Xianjing. Study of influence of different methods for calculating Rayleigh damping coefficient on high earth-rock dam seismic response [J]. Rock and Soil Mechanics, 2011, 32(3): 797 − 803. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.03.026
[27] 李哲, 王贡献, 胡勇,等. 改进的瑞利阻尼系数计算方法在岸桥结构地震反应分析中的应用[J]. 华南理工大学学报(自然科学版), 2015, 43(6): 103 − 109, 121. Li Zhe, Wang Gongxian, Hu Yong, et al. Coefficient to seismic response analysis of quay crane structure [J]. Journal of South China University of Technology, 2015, 43(6): 103 − 109, 121. (in Chinese)
[28] 许紫刚, 杜修力, 许成顺,等. 地下结构地震反应分析中场地瑞利阻尼构建方法比较研究[J]. 岩土力学, 2019, 40(12): 1 − 11. Xu Zigang, Du Xiuli, Xu Chengshun, et al. Comparative study of determination methods for Rayleigh damping coefficients of site in seismic responses analysis of underground structures [J]. Rock and Soil Mechanics, 2019, 40(12): 1 − 11. (in Chinese)
[29] 王田友, 丁浩民, 楼梦麟. 关于轨道交通所致建筑振动的计算方法和阻尼矩阵的讨论[J]. 振动与冲击, 2008, 27(11): 77 − 79, 100. doi: 10.3969/j.issn.1000-3835.2008.11.018 Wang Tianyou, Ding Haomin, Lou Menglin. Discussion on the methods of estimating structural vibration from railway lines and the determination of damping matrix [J]. Journal of Vibration and Shock, 2008, 27(11): 77 − 79, 100. (in Chinese) doi: 10.3969/j.issn.1000-3835.2008.11.018
[30] 潘旦光. 直接确定Rayleigh阻尼系数的一种优化方法[J]. 工程力学, 2013, 30(9): 16 − 21. Pan Danguang. An optimization method for the direct determination of Rayleigh damping coefficients [J]. Engineering Mechanics, 2013, 30(9): 16 − 21. (in Chinese)
[31] 潘旦光. 地震反应分析中Rayleigh阻尼系数的优化解[J]. 工程力学, 2013, 30(11): 15 − 20, 27. Pan Danguang. An optimization solution for Rayleigh damping coefficients in seismic response analysis [J]. Engineering Mechanics, 2013, 30(11): 15 − 20, 27. (in Chinese)
[32] Pan D, Chen G, Wang Z. Suboptimal Rayleigh damping coefficients in seismic analysis of viscously-damped structures [J]. Earthquake Engineering and Engineering Vibration, 2014, 13(4): 653 − 670. doi: 10.1007/s11803-014-0270-9
[33] 刘福顺, 王卫英. 一种粘滞阻尼体系阻尼矩阵识别新方法[J]. 工程力学, 2011, 28(5): 233 − 238, 244. Liu Fushun, Wang Weiying. A damping matrix identification method for vicious damping structures [J]. Engineering Mechanics, 2011, 28(5): 233 − 238, 244. (in Chinese)
[34] 李小军, 侯春林, 潘蓉,等. 阻尼矩阵选取对核电厂结构地震响应的影响分析[J]. 振动与冲击, 2015, 34(1): 110 − 116. Li Xiaojun, Hou Chunlin, Pan Rong, et al. Effect of damping matrix selection on seismic response of nuclear power plant structures [J]. Journal of Vibration and Shock, 2015, 34(1): 110 − 116. (in Chinese)
[35] Papageorgiou A V, Gantes C J. Equivalent uniform damping ratios for linear irregularly damped concrete/steel mixed structures [J]. Soil Dynamics and Earthquake Engineering, 2011, 31(3): 418 − 430.
[36] 谢礼立, 于双久. 强震观察与分析原理 [M]. 北京: 地震出版社, 1982. Xie Lili, Yu Shuangjiu. Observation and analysis of strong earthquake [M]. Beijing: Seismological Press, 1982. (in Chinese)
[37] 张晓志, 谢礼立, 于海英. 地震动反应谱的数值计算精度和相关问题[J]. 地震工程与工程振动, 2004, 24(6): 15 − 20. doi: 10.3969/j.issn.1000-1301.2004.06.003 Zhang Xiaozhi, Xie Lili, Yu Haiying. Precision problems in calculating response spectra by using numerical method [J]. Earthquake Engineering and Engineering Vibration, 2004, 24(6): 15 − 20. (in Chinese) doi: 10.3969/j.issn.1000-1301.2004.06.003
[38] 廖振鹏. 工程波动理论导论 [M]. 北京: 科学出版社, 2002. Liao Zhenpeng. Introduction to wave motion theories in engineering [M]. Beijing: Science Press, 2002. (in Chinese).
[39] Lage Y, Cachão H, Reis L, et al. A damage parameter for HCF and VHCF based on hysteretic damping [J]. International Journal of Fatigue, 2014, 62(7): 2 − 9.
[40] Lin R M, Zhu J. On the relationship between viscous and hysteretic damping models and the importance of correct interpretation for system identification [J]. Journal of Sound and Vibration, 2009, 325(1/2): 14 − 33. doi: 10.1016/j.jsv.2009.02.051
-
期刊类型引用(16)
1. 甄春博,刘世豪,张爱锋,邢世柱,张润泽. 基于缺口应力法的船舶焊接结构疲劳强度分析. 上海交通大学学报. 2025(04): 458-465 .  百度学术
百度学术
2. 郑三龙,陈见乙,赵基超,王鹏飞,陈冰冰. 钛制半管夹套焊接结构疲劳试验及寿命评估. 压力容器. 2024(09): 1-8 .  百度学术
百度学术
3. 刘逸,张开林,邵帅,刘家林. 基于多轴疲劳评估方法的高原机车构架强度计算. 电力机车与城轨车辆. 2023(02): 1-5 .  百度学术
百度学术
4. 李涛,汪洋,甘进,邵永波. 超声冲击处理焊接节点疲劳性能改善及寿命预测方法研究进展. 建筑钢结构进展. 2023(06): 58-67 .  百度学术
百度学术
5. 龚宝明,刘强,赵洋洋,宋宗贤,邓彩艳. 薄板焊接接头疲劳性能的缺口应力法研究. 天津大学学报(自然科学与工程技术版). 2023(09): 903-910 .  百度学术
百度学术
6. 武陇岗,王瑞杰,刘飞,覃秋雷,常亚光,王钟德. AZ31B/TA15异种材料电阻点焊接头的疲劳寿命预测. 材料热处理学报. 2022(03): 168-176 .  百度学术
百度学术
7. 隋鹏超,刘宏杰,曾超. 发动机支架焊接结构疲劳寿命预测. 内燃机与动力装置. 2022(02): 105-110 .  百度学术
百度学术
8. 陈鹏,王朋松,辛涛,霍海龙,王聚光,张宏亮. 地铁道岔滑床板失效仿真及结构优化. 中南大学学报(自然科学版). 2022(06): 2361-2369 .  百度学术
百度学术
9. 曹蕾蕾,王严,王留涛,宋绪丁,郭城臣. 大型焊接结构疲劳寿命评估研究综述. 机械强度. 2022(06): 1443-1454 .  百度学术
百度学术
10. 王严,郭城臣,樊浩. 基于子模型技术的焊接接头疲劳强度评估. 机电工程技术. 2021(02): 51-54 .  百度学术
百度学术
11. 李钰,陈迪,张亦波,宋颖刚,熊峻江. 谱载下密封角盒螺栓及长桁端头疲劳寿命估算的逐次累计求和算法. 工程力学. 2020(04): 217-226 .  本站查看
本站查看
12. 童乐为,任珍珍,景爽,牛立超. 高强度结构钢系列的疲劳裂纹扩展速率试验研究. 工程力学. 2020(12): 191-201+212 .  本站查看
本站查看
13. 丁鹏龙,牛佳佳,暴文帅,夏立乾,王涛. 基于缺口应力法的焊接纵梁疲劳数值模拟. 材料开发与应用. 2020(05): 76-80 .  百度学术
百度学术
14. 王元清,顾浩洋,廖小伟. 钢结构角焊缝抗剪疲劳性能的试验研究. 工程力学. 2018(04): 61-68 .  本站查看
本站查看
15. 郭琪,黄欣,韩庆华,邢颖,黄健. 铸钢节点对接焊缝有效缺口应力分析. 土木建筑与环境工程. 2018(03): 23-30 .  百度学术
百度学术
16. 严仁军,何丰,谌伟. 基于缺口应力法的焊接接头疲劳强度评估. 武汉理工大学学报(交通科学与工程版). 2017(05): 766-769+775 .  百度学术
百度学术
其他类型引用(31)





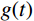
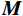
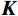
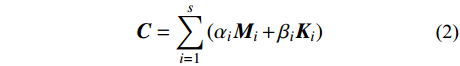
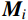
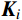
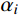
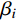
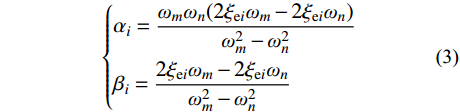
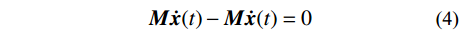
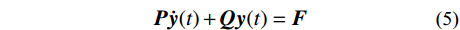
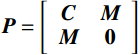
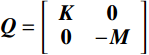
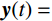
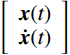
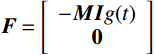
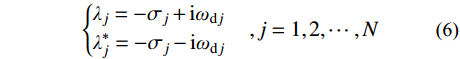
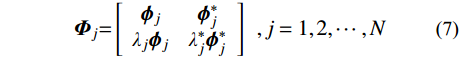
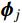
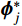
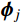
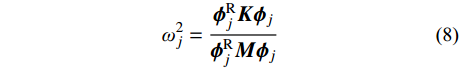
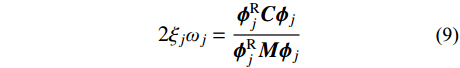
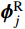
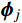
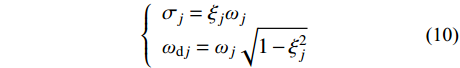
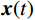
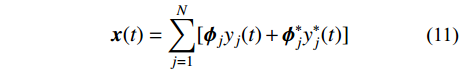
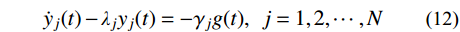
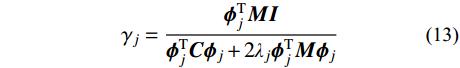
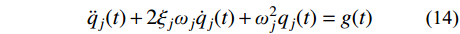
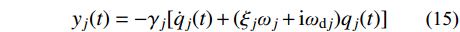
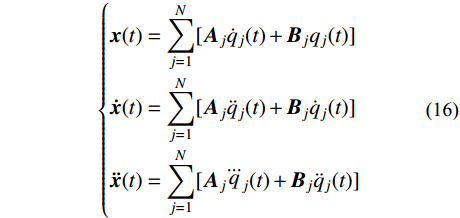
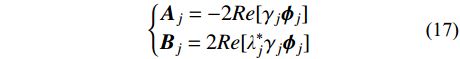
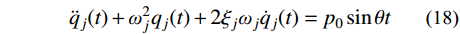
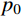
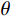
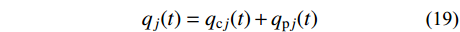
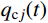
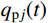
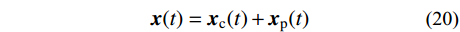
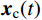
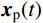
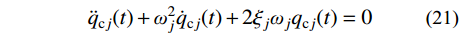
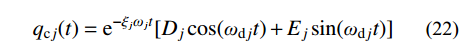
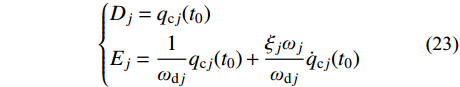
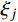
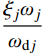
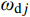
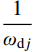
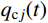
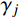
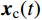

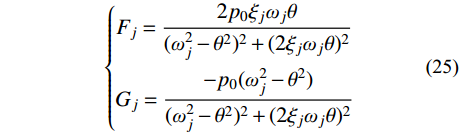
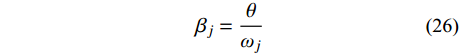
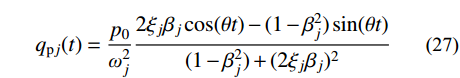
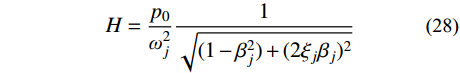
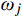
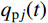
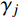
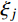
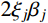
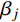
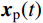
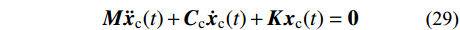
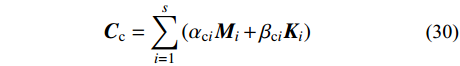
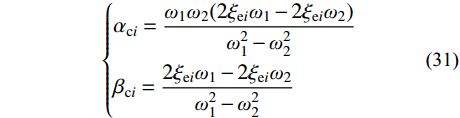
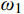
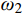
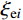
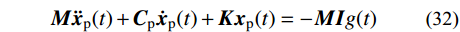
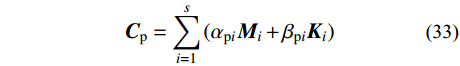
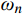
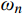
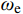
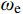
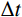

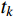
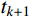
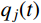
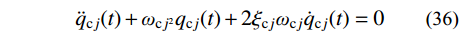
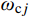
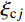
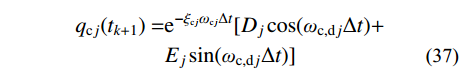
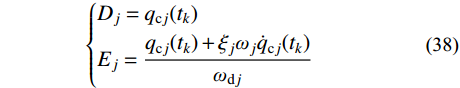
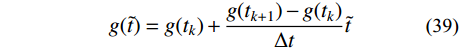
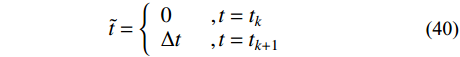
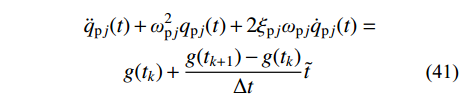
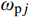
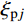
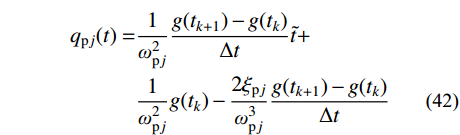
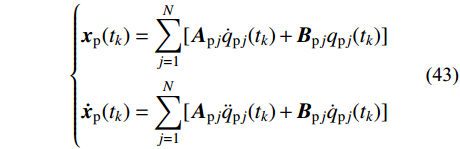
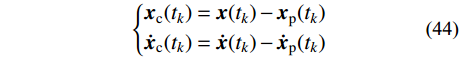
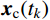
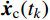
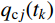
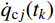
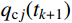
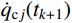
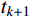
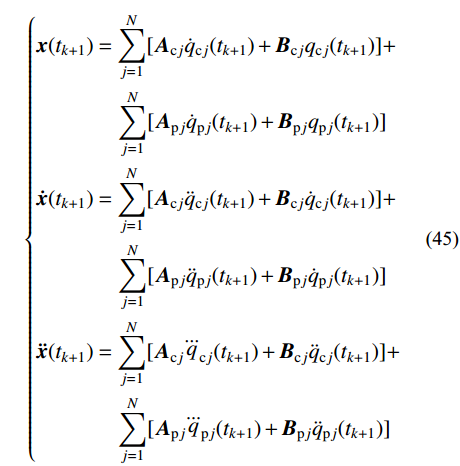
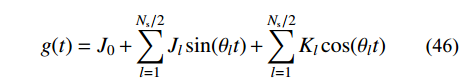
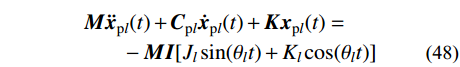
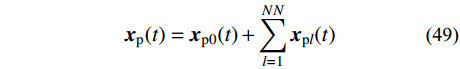
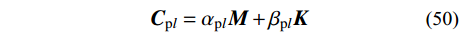
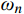
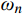
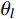
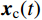

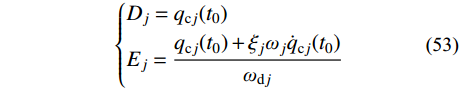
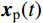
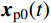
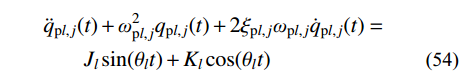
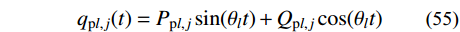
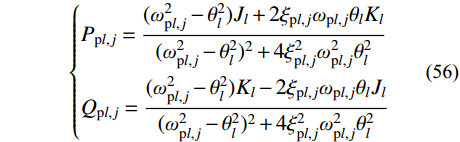
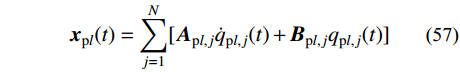
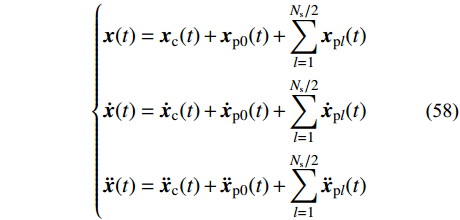
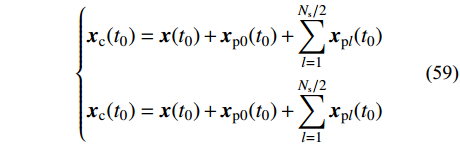
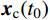
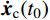
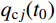
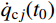

 下载:
下载: