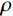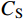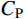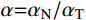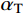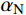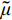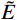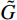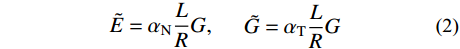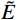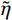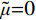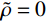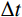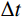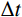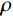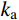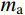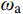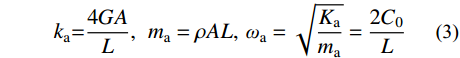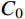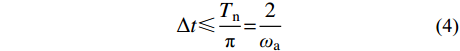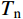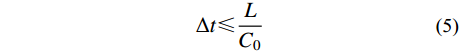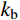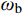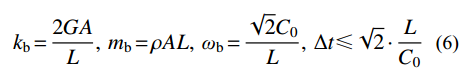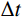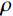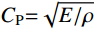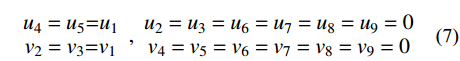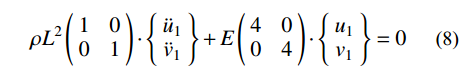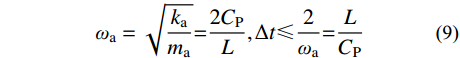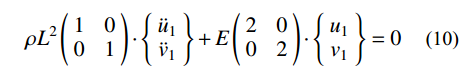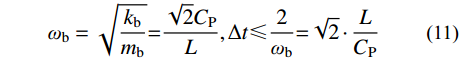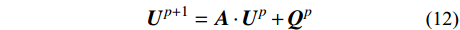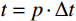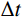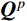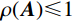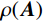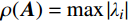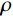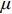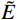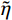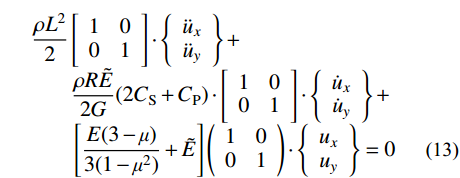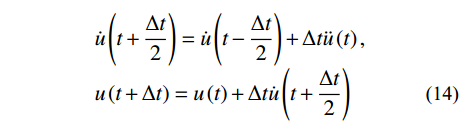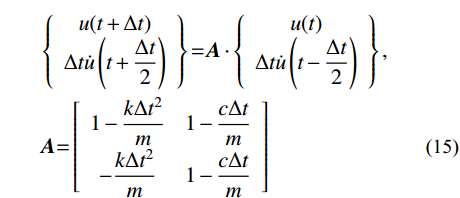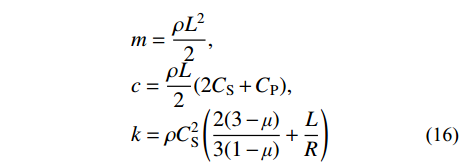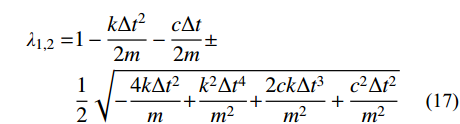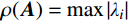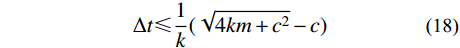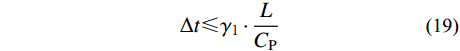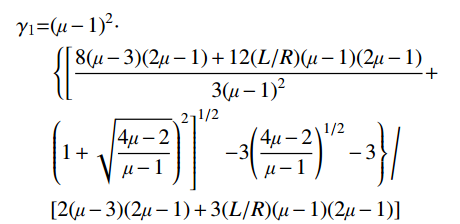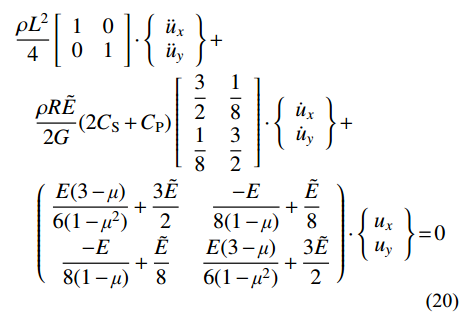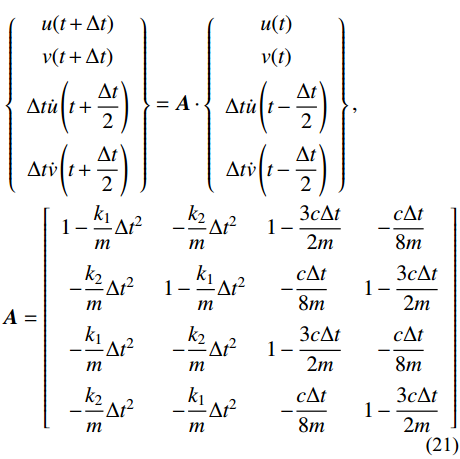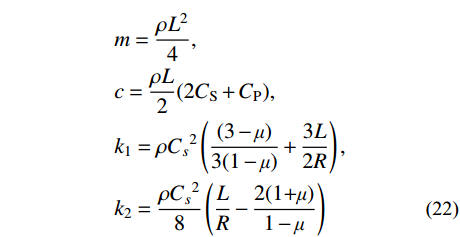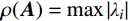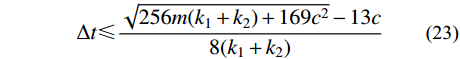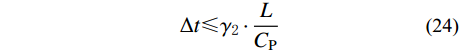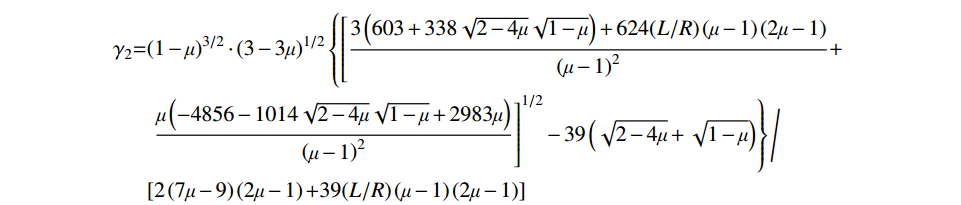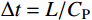STABILITY ANALYSIS OF EXPLICIT ALGORITHMS WITH VISCO-ELASTIC ARTIFICIAL BOUNDARY ELEMENTS
-
摘要: 在土-结构地震反应或近场地震波动问题的分析中，常采用粘弹性人工边界单元将无限域问题转化为近场有限域问题进行计算。由于粘弹性人工边界单元的材料参数和单元尺寸与内部介质单元不同，采用显式时域逐步积分算法时，人工边界区与内部系统的数值稳定条件存在差异，但目前尚未有针对性的分析方法和研究成果，影响了显式数值稳定条件的确定和稳定积分时间步长的正确选取。针对二维粘弹性人工边界单元，该文提出一种分析显式时域逐步积分算法稳定性的方法：建立可代表人工边界区域特征的，包含人工边界单元的若干局部子系统，对各子系统的传递矩阵进行分析，给出采用显式时域逐步积分算法时各子系统的稳定条件解析解。通过对各子系统的稳定条件进行对比分析，获得了采用粘弹性人工边界单元时，显式时域逐步积分算法的统一稳定性条件。当内部介质区也满足该稳定条件时，这一条件成为使整体系统数值计算稳定的充分条件，可用于指导数值分析中离散时间步长的选取。Abstract: In the analysis of soil-structure seismic response or of near-field seismic wave propagations, the visco-elastic artificial boundary elements are often applied to transfer the infinite-domain problem into a finite-domain problem. Since the material parameters and the size of the visco-elastic artificial boundary elements are different from those of the internal medium elements, there are differences in the numerical stability conditions between the artificial boundary domain and the internal domain when the explicit time domain step-by-step integration algorithm is used. At present, however, there are no appropriate analysis methods and research results to determine the explicit numerical stability conditions and the stable integration time steps. In this study, we propose a stability analysis method for explicit time-domain stepwise integration algorithm when using the two-dimensional visco-elastic artificial boundary elements. Firstly, several typical local subsystems of the artificial boundaries are established. The transfer matrix of each subsystem is analyzed, and the analytical solutions of the stability conditions for each subsystem are obtained. By comparing the stability conditions of the subsystems and the internal medium system, a uniform stability condition of explicit time domain stepwise integration algorithm is obtained when using the visco-elastic artificial boundary elements. When the internal medium areas also satisfy this stability condition, this condition becomes a sufficient condition for the stability calculation of the overall system and can be used to deciding the stable discrete time step in the numerical analysis.
-
采用数值方法计算土-结构地震反应或近场波动问题时，需要从半无限介质中切取出有限的近场区域进行计算，同时需在截断边界处设置人工边界来模拟外行散射波向无穷远的辐射效应[1-4]。较为常见的粘弹性人工边界[5]计算精度较高但前处理操作较为复杂，需遍历所有边界节点施加弹簧-阻尼器系统，在此基础上发展了粘弹性人工边界单元技术[6-7]，它是沿边界法线向外延伸的一层单元，通过赋予该层单元等效物理参数即可模拟粘弹性人工边界对于外行散射波的吸收作用。由于该方法具有良好的计算精度和鲁棒性，且前处理过程简单，在实际工程计算中得到较多的应用[8-12]。
随着人工边界技术的不断发展，针对人工边界条件的稳定性研究逐渐得到重视[13-14]，目前针对此类问题的主要研究方法包括：Trefethen等[15]提出的GKS定理—基于偏微分方程初边值问题有限差分格式的稳定性理论，给出初边值问题多层线性差分格式稳定的充要条件；Liao等[16]研究了离散模型中稳态波动的完备解，给出了多次透射边界的稳定性条件；Kamel等[17]和关慧敏等[18]通过传递矩阵谱半径分析积分格式的稳定性。理论研究表明，如果不全面考虑逐步积分过程中人工边界节点与内部节点运动方程的耦合效应，稳定性准则可能会失效。
由于粘弹性人工边界或粘弹性人工边界单元本身均为物理上稳定的系统，将其引入计算系统中，并不影响整体的物理稳定条件。但采用显式时域逐步积分方法进行计算时，受粘弹性人工边界单元粘性阻尼、刚度及几何尺寸的影响，整体计算模型的数值积分稳定性条件将发生改变，目前尚未给出明确而实用的含粘弹性人工边界条件影响的显式算法稳定性准则，影响了数值分析时稳定时间步长的判断和选取，进一步限制了粘弹性人工边界单元在显式动力分析中的应用。因此目前在引入粘弹性人工边界单元进行波动问题分析时，多采用隐式的无条件稳定的时域逐步积分算法，以避免显式算法带来的数值稳定性问题。隐式算法需要求解联立方程组，计算效率不高，并不适合大规模波动问题计算。随着显式时域逐步积分算法在工程结构和大范围场地分析问题中的广泛应用[19-22]，有必要对含有粘弹性人工边界单元的系统进行显式时域逐步积分算法稳定性研究。
本文考虑人工边界和内部单元节点的运动耦合效应，利用传递矩阵的谱半径分析时域逐步积分格式(中心差分)的稳定性，给出不同位置处局部节点系统显式时域逐步积分算法稳定条件的解析解，通过各子系统稳定性条件及内部介质稳定性条件的对比分析，给出考虑粘弹性人工边界条件影响的整体耦合系统显式时域逐步积分算法的稳定性条件。
1 粘弹性人工边界单元等效物理参数及尺寸设置
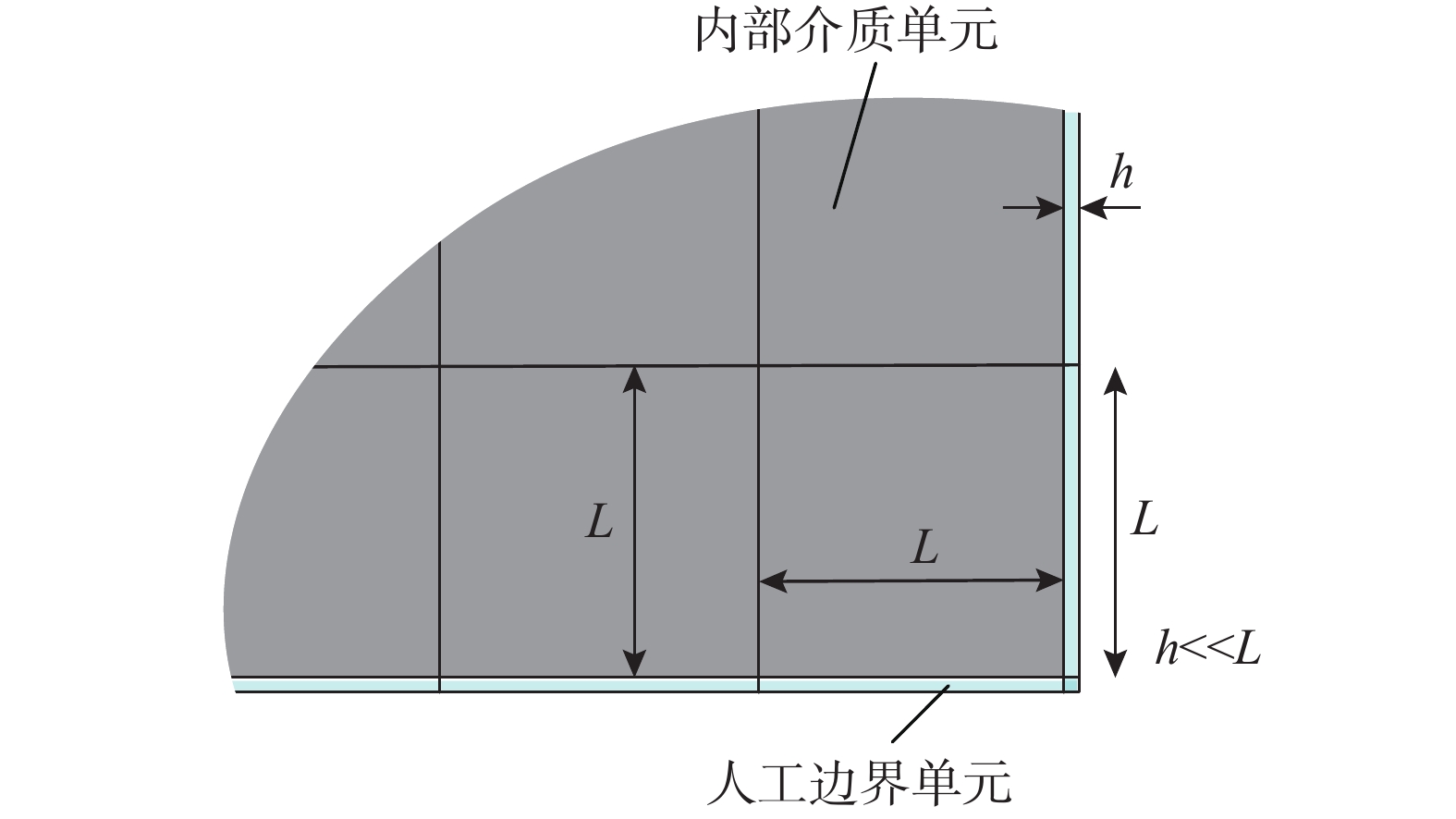
粘弹性人工边界单元是在模型截断边界处沿法线向外延伸的一层单元(见图1)，人工边界单元的厚度为h，质量密度为0，单元最外层节点固定。通过赋予单元等效物理参数来模拟粘弹性人工边界。二维粘弹性人工边界单元等效弹性模量
˜E 、等效泊松比˜μ 和等效阻尼系数˜η 分别为[2]：{˜E=αNhGR⋅(1+˜μ)(1−2˜μ)1−˜μ,˜μ=α−22(α−1),˜η=ρR2G(CSαT+CPαN) (1) 其中：设G为内部介质剪切模量；
ρ 为介质质量密度；CS 和CP 分别为介质S波和P波波速；R为散射波源至边界节点的距离；α=αN/αT ，αT 与αN 分别为切向与法向粘弹性人工边界参数，对于二维粘弹性人工边界，其推荐值分别为0.5和1，根据式(1)，此时˜μ 为0。尽管粘弹性人工边界单元等效刚度矩阵的推导过程引入了边界单元厚度h远小于宽度L的假设，如图1所示，刘晶波等[6]和谷音等[7]通过进一步的研究表明，边界单元厚度的鲁棒性良好，可灵活取值而对精度影响很小。由于显式算法的稳定条件受模型中的最小单元尺寸制约，在实际计算分析中，建议将边界单元的宽度设定为与内部单元尺寸一致，以排除边界单元尺寸对整体稳定性的影响，如图2所示。此时粘弹性人工边界单元等效弹性模量
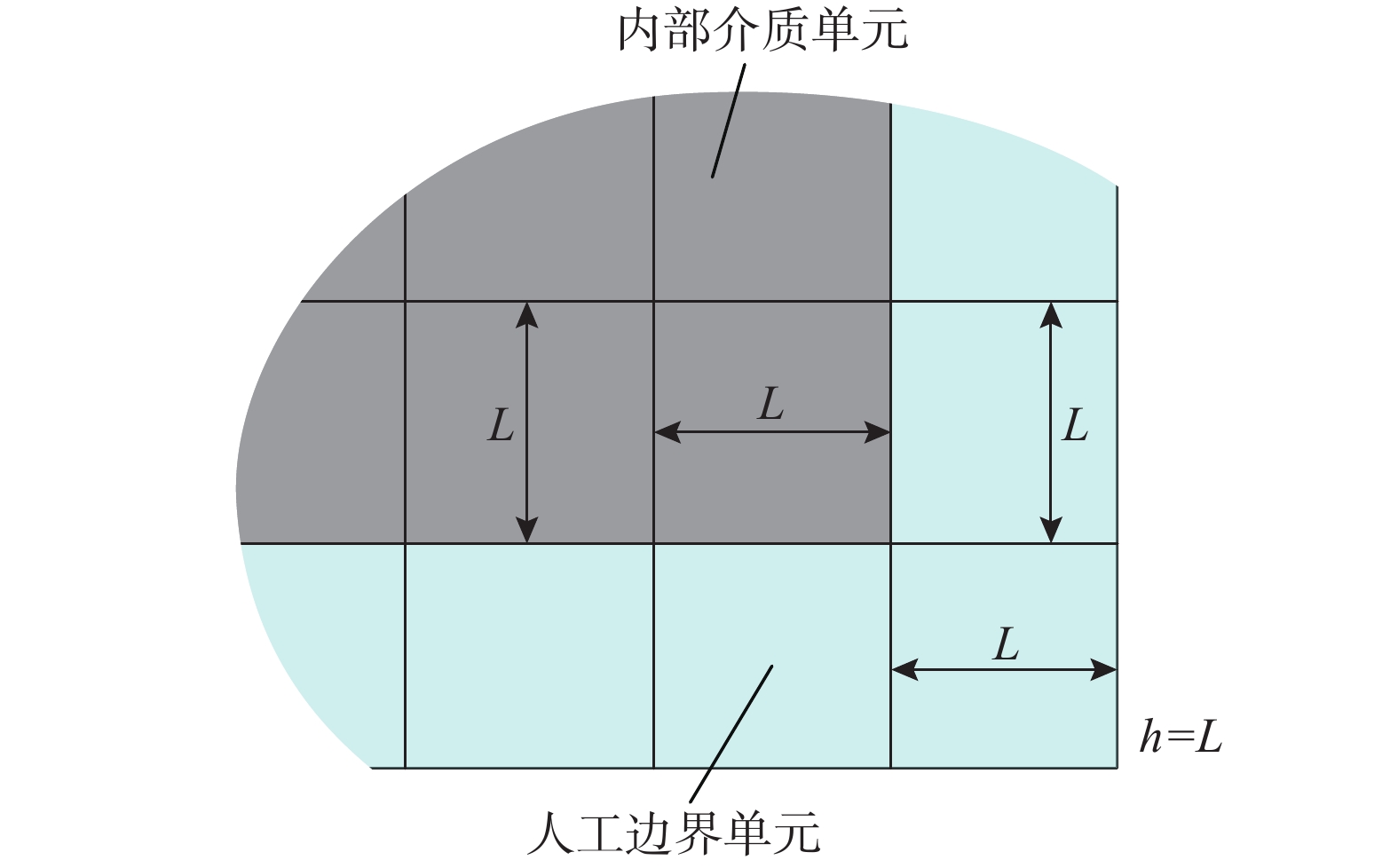
˜E 、等效剪切模量˜G 可以写为：˜E=αNLRG,˜G=αTLRG (2) ![]()
图 2 适用于显式算法的人工边界单元Figure 2. Artificial boundary elements adapted to explicit algorithms使用通用有限元软件对粘弹性人工边界单元赋予材料参数时，由于是各向同性介质，输入等效弹性模量
˜E 即可。另外还包括式(1)计算得到的等效阻尼系数˜η ，以及泊松比(˜μ=0 )和质量密度(˜ρ=0 )。由于大多数软件不支持将密度设为0，可采用近似0的小数代替。2 显式时域逐步积分算法稳定性分析方法
时域逐步积分算法稳定性分析的目的是获得时域逐步积分计算时满足稳定性要求的时间离散步长
Δt 。最大的稳定时间步长Δt 与单元的尺寸和系统的物理性质有关。为此在进行稳定性分析时，通常采用均匀介质和均匀离散化网格模型，如图3所示。当实际力学模型介质非均匀，单元尺寸不相同时，可以根据最小尺寸的单元或综合考虑单元尺寸及其介质性质来确定整体计算模型的稳定离散时间步长
Δt 。算法的稳定性通常可采用以下几种分析方法：① 不考虑自由边界和人工边界的影响，取无限计算区域模型，采用冯诺依曼方法进行稳定性分析。这一方法可以获得内部系统的数值计算稳定条件，但无法考虑含人工边界条件时系统的稳定性。
② 取实际的计算模型，考虑人工边界的影响，通过对整体系统时域逐步积分方法的传递矩阵进行特征值分析，以获得考虑耦合人工边界条件影响的整体系统的数值计算稳定性条件。但由于涉及到整体模型传递矩阵的建立和分析，这一方法在实际工作中通常是不可行的，特别是对大规模的计算问题。
③ 为对透射人工边界的数值计算稳定性进行有效分析，Kamel等[17]和关慧敏等[18]提出了一种对含透射人工边界条件子系统的传递矩阵进行特征值分析，以获得波动问题中透射人工边界稳定性的分析方法。由于分析中采用的子系统为沿人工边界切向(宽度方向)上若干排节点和沿法向(深度方向)上若干排节点组成的节点系，子系统自由度较多，仅能靠数值方法对人工边界的稳定性进行分析和判断，未给出具有解析形式的更易于使用的人工边界稳定性准则。
从以上有限元离散模型数值积分稳定性准则的研究工作中可以发现以下两个特点：1)算法的稳定性与模型的截止频率(系统最高阶自振频率)有关。2)截止频率相应的振型呈现局部节点系相邻节点交错振动的形态。由以上两个特点可以判断，整体系统的截止频率可通过对局部子系统模型的分析得到，进一步可通过局部子系统模型的数值稳定性分析，获得整体系统的数值稳定性条件。
首先以一维剪切梁问题为例证明以上判断。图4为一维剪切梁的离散模型及最高阶振型示意图，梁的剪切模量为G，密度为
ρ ，横截面面积为A，单元长度为L。取两个子系统进行分析。子系统a：取振型两节点之间的子系统，两端施加约束，由于约束是施加于振型节点(振幅为零)之上，因此并不改变剪切梁有限元模型的自振频率，如图5(a)所示；子系统b：取两个单元，在两端施加约束，此时子系统的自振频率与原系统的截止频率不相同，如图5(b)所示。一维子系统a的刚度
ka 、质量ma 和自振频率ωa 分别为：ka=4GAL,ma=ρAL,ωa=√Kama=2C0L (3) 其中，
C0 为剪切波速。根据子系统的刚度和质量，可以建立子系统a的单自由度运动方程，当采用中心差分法进行时域逐步积分计算时，一维子系统a的数值稳定条件为：
Δt⩽Tnπ=2ωa (4) 其中，
Tn 为子系统的自振周期，将式(3)中第三式代入式(4)，得到子系统数值积分稳定性条件为：Δt⩽LC0 (5) 式(5)即为一维连续介质波动有限元分析时中心差分算法的稳定性条件，可见采用子系统a获得的局部稳定性条件即为连续介质整体模型的稳定性条件。
一维子系统b的刚度
kb 、质量mb 、自振频率ωb 和中心差分稳定性条件分别为：kb=2GAL,mb=ρAL,ωb=√2C0L,Δt⩽√2⋅LC0 (6) 对比式(5)和式(6)，可以发现一维子系统b的稳定性条件比实际整体模型的稳定条件更为宽松，但仍然可以给出稳定时间积分步长
Δt 的一个上限估计。对于二维平面问题，令介质密度为
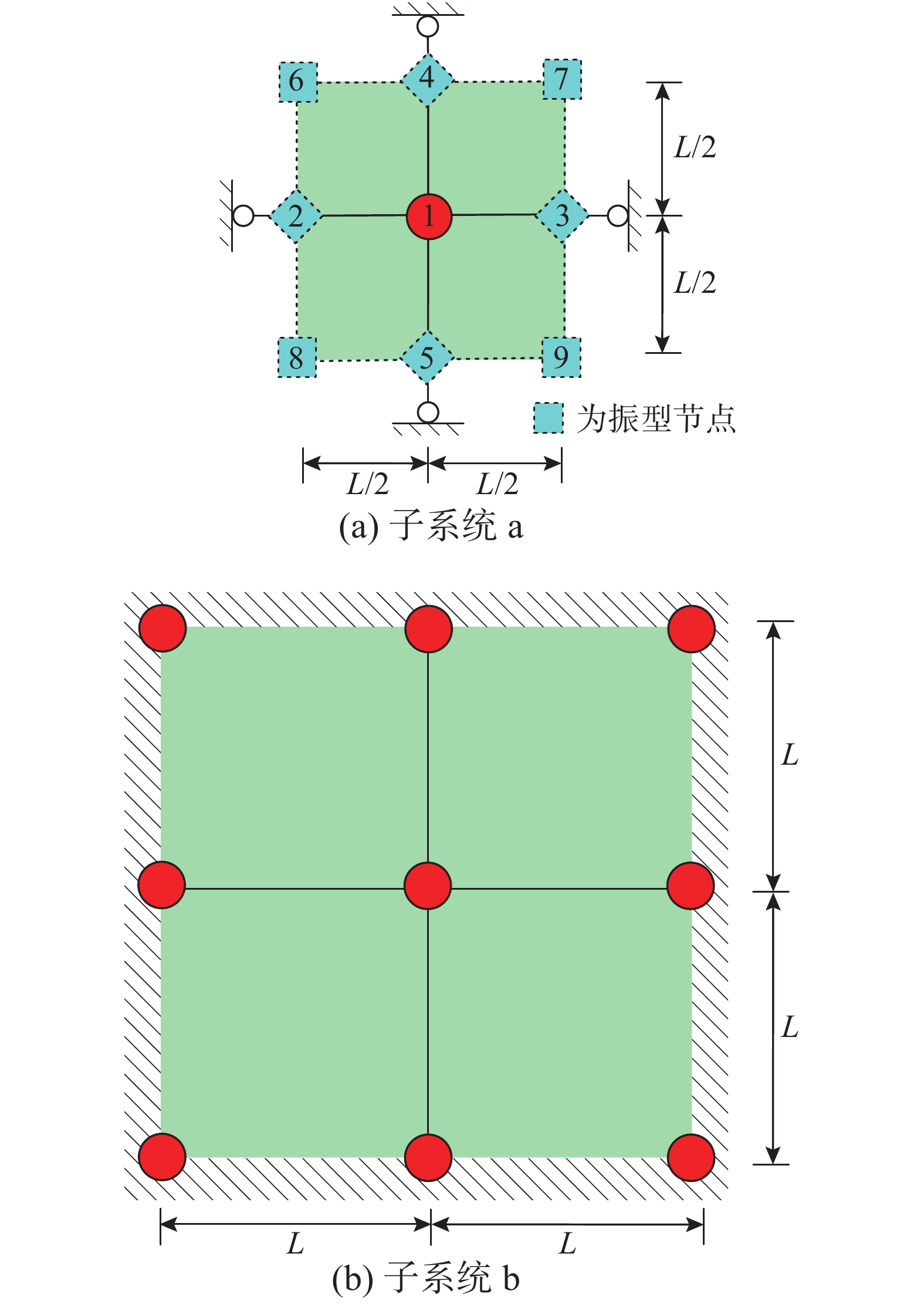
ρ ，弹性模量E，泊松比为0，P波波速为CP=√E/ρ 。采用正方形网格离散化，单元为4节点等参元，边长为L。有限元模型如图6所示，其中虚线及虚节点为系统截止频率相应的振型，该振型呈现出正交、双向“竹竿舞”的形态，每行(列)节点在振动过程中保持直线，单元的中心点为振型的节点，位移恒等于0。![]()
图 6 二维节点系统最高阶振型图Figure 6. Highest-order modal pattern of two-dimensional nodes system同样取两个子系统进行分析，二维问题局部子系统由4个单元构成，如图7(a)和图7(b)所示。其中二维子系统a的4个角点为振型节点，位移为0，4个边点的位移条件可由振型和4边形等参元的性质确定，子系统a对应的边界条件为：
u4=u5=u1v2=v3=v1,u2=u3=u6=u7=u8=u9=0v4=v5=v6=v7=v8=v9=0 (7) 其中，u、v分别为x和y方向的位移，下标对应图7(a)中的节点编号。则二维子系统a运动方程为：
ρL2(1001)⋅{¨u1¨v1}+E(4004)⋅{u1v1}=0 (8) 二维子系统a自振频率和中心差分稳定条件为：
ωa=√kama=2CPL,Δt⩽2ωa=LCP (9) 式(9)即为二维波动问题有限元分析时中心差分算法的稳定性条件，可见同样可以由子系统a的局部稳定性分析获得二维有限元模型数值算法的整体稳定性条件。
二维子系统b由4个单元构成，在周边节点施加固定约束，子系统b运动方程为：
ρL2(1001)⋅{¨u1¨v1}+E(2002)⋅{u1v1}=0 (10) 二维子系统b自振频率和中心差分稳定条件为：
ωb=√kbmb=√2CPL,Δt⩽2ωb=√2⋅LCP (11) 同样，二维子系统b给出了整体有限元模型稳定时间积分步长的上限估计。
一维和二维子系统分析的结果表明：1)若能较为准确地判断系统截止频率对应的振动模态(振型)，则可以利用最高振型的特点和振型节点的分布规律，从整体系统中分离出由阵型节点所包围的局部子系统，对振型节点施加约束条件，然后对该子系统进行稳定性分析，获得的局部子系统稳定性条件即为整体模型的数值稳定条件；2)若不能准确判断截止频率对应振动模态和相应振型节点的位置，也可选取一个能体现整体有限元模型特征的最小的子系统，对该子系统的边界节点施加约束，通过分析获得子系统的数值稳定性条件，从而获得整体系统稳定性判据中各物理量的关系式，且该条件是整体系统稳定性条件的一个逼近。再通过扩展数值算例进行修正，确定合适的系数，即可得到整体系统的数值积分稳定性条件。
当采用粘弹性人工边界单元时，内部系统的数值稳定条件已知，但难以确定人工边界区截止频率对应的振型，因而仅能采用类似于b型的子系统进行数值计算的稳定性分析。
对非均质子系统进行稳定性分析时，可根据显式逐步积分算法格式，将系统运动方程写成如下形式：
{{\boldsymbol{U}}^{p + 1}} = {\boldsymbol{A}} \cdot {{\boldsymbol{U}}^p} + {{\boldsymbol{Q}}^p} (12) 式中：向量U由子系统各节点的加速度、速度和位移组成；Q是外力向量；A是传递矩阵，与时空离散步长及系统的力学参数有关；上标p是自然数，
t = p \cdot \Delta t ；\Delta t 为时间步长。积分格式的稳定性问题与外力向量
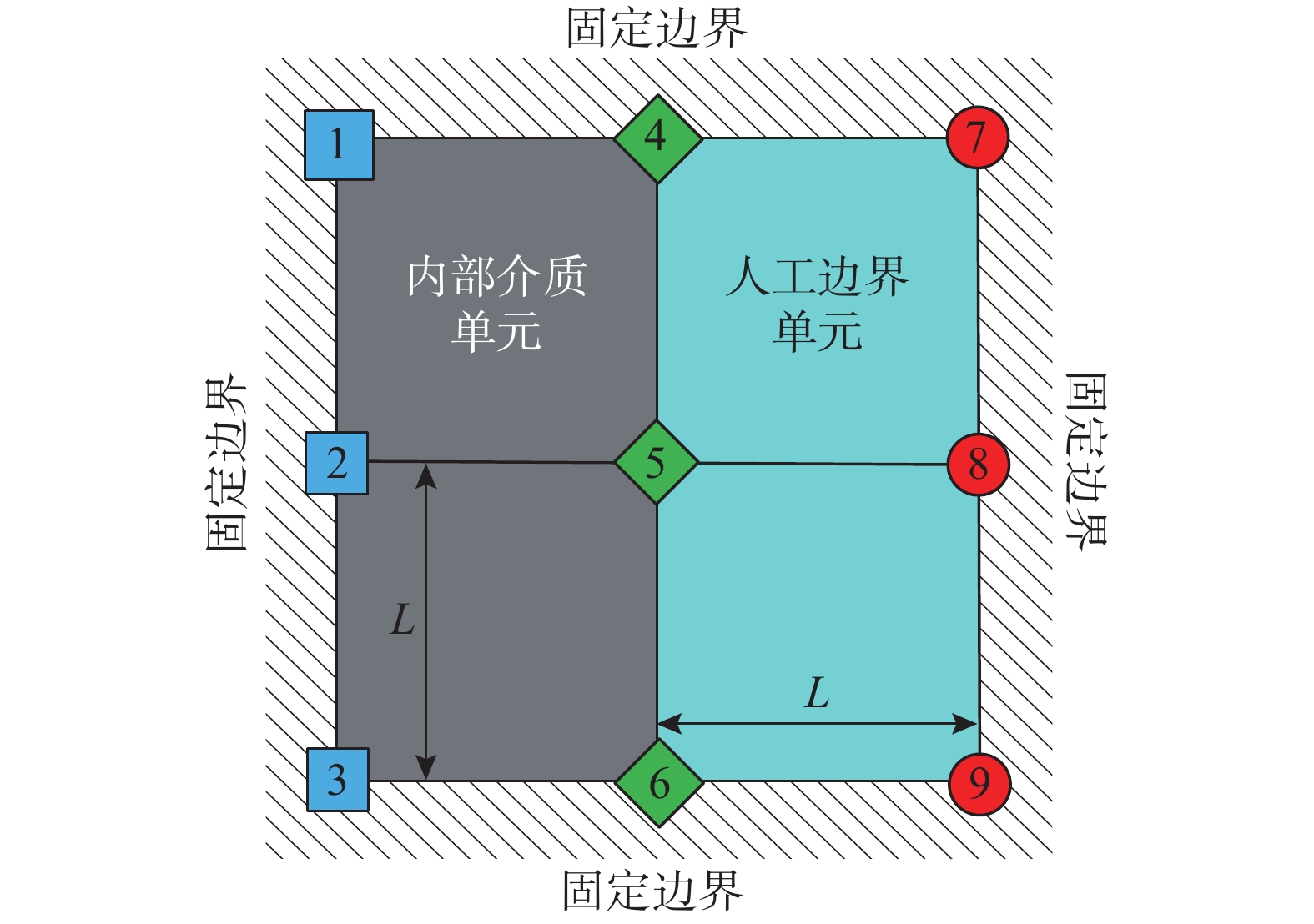
{{\boldsymbol{Q}}^p} 无关。如果满足下列两条件，则积分格式(12)是稳定[23]：条件1：\rho ({\boldsymbol{A}}) \leqslant 1 ，\rho ({\boldsymbol{A}}) 是传递矩阵A的谱半径，即\rho ({\boldsymbol{A}}) = \max \left| {{\lambda _{i}}} \right| ；条件2：如果A具有多重特征值，则该特征值的模小于1。因而可将子系统的稳定性分析归结为传递矩阵A的形成及谱半径计算，按上述条件即可建立稳定性准则。3 人工边界子系统稳定性分析
采用粘弹性人工边界单元时，人工边界区的子系统有两种形式，一种在侧面或底面切取，如图8所示，另一种在角点处切取，切取边界可设置固定边界(见图9)或自由边界(见图10)。
3.1 侧边固定边界子系统稳定性分析
侧边固定边界子系统由两个粘弹性人工边界单元和两个内部介质单元组成，如图8所示。设内部介质单元的弹性模量为E，剪切模量为G，密度为
\rho ，泊松比为\mu ，且无阻尼；粘弹性人工边界单元弹性模量为\tilde E ，阻尼系数为\tilde \eta ，泊松比为0，密度为0，单元边长均为L。四节点正方形平面单元的集中质量矩阵、刚度矩阵、阻尼矩阵分别见文献[6]和文献[24]，按节点编号进行矩阵组装后得到子系统中5号节点运动方程如下：\begin{split} & \frac{{\rho {L^2}}}{2}\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] \cdot \left\{ {\begin{array}{*{20}{c}} {{{\ddot u}_x}} \\ {{{\ddot u}_y}} \end{array}} \right\} +\\[-3pt]& \qquad\frac{{\rho R\tilde E}}{{2G}}(2{C_{\rm{S}}} + {C_{\rm{P}}}) \cdot \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] \cdot \left\{ {\begin{array}{*{20}{c}} {{{\dot u}_x}} \\ {{{\dot u}_y}} \end{array}} \right\} + \\[-3pt]& \qquad\left[ {\frac{{E(3 - \mu )}}{{3(1 - {\mu ^2})}} + \tilde E} \right]\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right) \cdot \left\{ {\begin{array}{*{20}{c}} {{u_x}} \\ {{u_y}} \end{array}} \right\} = 0 \end{split} (13) 观察式(13)可知，x和y方向运动方程是解耦的且形式相同，因此可只对其中一个方向的运动方程进行稳定性分析。显式时域逐步积分格式(中心差分[25]如下：
\begin{split} & \dot u\left(t + \frac{{\Delta t}}{2}\right) = \dot u\left(t - \frac{{\Delta t}}{2}\right) + \Delta t\ddot u\left(t\right) ,\\[-3pt]& u\left(t + \Delta t\right) = u\left(t\right) + \Delta t\dot u\left(t + \frac{{\Delta t}}{2}\right) \end{split} (14) 将式(1)代入式(13)后，根据式(14)将式(13)展开，写成传递矩阵形式：
\begin{split} & \left\{ {\begin{array}{*{20}{c}} {u(t + \Delta t)} \\ {\Delta t\dot u\left(t + \dfrac{{\Delta t}}{2}\right)} \end{array}} \right\}{\rm{ = }}{\boldsymbol{A}} \cdot \left\{ {\begin{array}{*{20}{c}} {u(t)} \\ {\Delta t\dot u\left(t - \dfrac{{\Delta t}}{2}\right)} \end{array}} \right\},\\ & {\boldsymbol{A}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {1 - \dfrac{{k\Delta {t^2}}}{m}}&{1 - \dfrac{{c\Delta t}}{m}} \\ { - \dfrac{{k\Delta {t^2}}}{m}}&{1 - \dfrac{{c\Delta t}}{m}} \end{array}} \right] \end{split} (15) 其中：
\begin{split} & m = \frac{{\rho {L^2}}}{2} ,\\[-3pt] & c = \frac{{\rho L}}{2}(2{C_{\rm{S}}} + {C_{\rm{P}}}) ,\\[-3pt] & k = \rho {C_{\rm{S}}^2}\left( {\frac{{2(3 - \mu )}}{{3(1 - \mu )}} + \frac{L}{R}} \right) \end{split} (16) 传递矩阵的特征值为：
\begin{split} {\lambda _{1,2}} = &1 - \frac{{k\Delta {t^2}}}{{2m}} - \frac{{c\Delta t}}{{2m}} \pm \\ & \frac{1}{2}\sqrt { - \frac{{4k\Delta {t^2}}}{m}{\rm{ + }}\frac{{{k^2}\Delta {t^4}}}{{{m^2}}}{\rm{ + }}\frac{{2ck\Delta {t^3}}}{{{m^2}}} + \frac{{{c^2}\Delta {t^2}}}{{{m^2}}}} \end{split} (17) 根据
\rho ({\boldsymbol{A}}) = \max \left| {{\lambda _{i}}} \right| ，将式(17)代入并整理，得出稳定性条件的表达式：\Delta t \leqslant \frac{1}{k}(\sqrt {4km + {c^2}} - c) (18) 将式(16)代入式(18)后，整理得到：
\Delta t \leqslant {\gamma _{{\text{1}}}} \cdot \frac{L}{{{C_{\rm{P}}}}} (19) 其中：
\begin{split} {\gamma _{{\text{1}}}}{\rm{ = }}&{(\mu - 1)^2}\cdot\\& \left\{ {\left[ {\frac{{8(\mu - 3)(2\mu - 1) + 12(L/R)(\mu - 1)(2\mu - 1)}}{{3{{(\mu - 1)}^2}}} + } \right.} \right.\\& {\left. {{{\left( {1 + \sqrt {\frac{{4\mu - 2}}{{\mu - 1}}} } \right)}^2}} \right]^{1/2}}\left. { - 3{{\left( {\frac{{4\mu - 2}}{{\mu - 1}}} \right)}^{1/2}} - 3} \right\}\Bigg/\\& [2(\mu - 3)(2\mu - 1) + 3(L/R)(\mu - 1)(2\mu - 1)] \end{split} 式(19)即为侧边局部人工边界子系统稳定性条件的解析表达形式，观察可知该子系统的稳定性条件与内部介质压缩波速、泊松比、单元尺寸和模型大小有关。
3.2 角点固定边界子系统稳定性分析
角点处固定边界子系统中由3个粘弹性人工边界单元和1个内部介质单元组成，如图9所示。将四节点正方形平面单元质量、阻尼和刚度矩阵按节点编号组装后得到5号节点的运动方程如下：
\begin{split} & \dfrac{{\rho {L^2}}}{4}\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] \cdot \left\{ {\begin{array}{*{20}{c}} {{{\ddot u}_x}} \\ {{{\ddot u}_y}} \end{array}} \right\} +\\&\quad \dfrac{{\rho R\tilde E}}{{2G}}(2{C_{\rm{S}}} + {C_{\rm{P}}})\left[ {\begin{array}{*{20}{c}} {\dfrac{3}{2}}&{\dfrac{1}{8}} \\ {\dfrac{1}{8}}&{\dfrac{3}{2}} \end{array}} \right] \cdot \left\{ {\begin{array}{*{20}{c}} {{{\dot u}_x}} \\ {{{\dot u}_y}} \end{array}} \right\}{\rm{ + }} \\& \quad\left( {\begin{array}{*{20}{c}} {\dfrac{{E(3 - \mu )}}{{6(1 - {\mu ^2})}} + \dfrac{{3\tilde E}}{2}}&{\dfrac{{ - E}}{{8(1 - \mu )}} + \dfrac{{\tilde E}}{8}} \\ {\dfrac{{ - E}}{{8(1 - \mu )}} + \dfrac{{\tilde E}}{8}}&{\dfrac{{E(3 - \mu )}}{{6(1 - {\mu ^2})}} + \dfrac{{3\tilde E}}{2}} \end{array}} \right) \cdot \left\{ {\begin{array}{*{20}{c}} {{u_x}} \\ {{u_y}} \end{array}} \right\} = 0 \end{split} (20) 由于该运动方程的坐标耦联，需对整体方程进行稳定性分析。将式(1)代入式(20)，然后根据式(14)将式(20)展开，写成如下传递矩阵的形式：
\begin{split} & \left\{ {\begin{array}{*{20}{c}} {u(t + \Delta t)} \\ {v(t + \Delta t)} \\ {\Delta t\dot u\left(t + \dfrac{{\Delta t}}{2}\right)} \\ {\Delta t\dot v\left(t + \dfrac{{\Delta t}}{2}\right)} \end{array}} \right\} = {\boldsymbol{A}} \cdot \left\{ {\begin{array}{*{20}{c}} {u(t)} \\ {v(t)} \\ {\Delta t\dot u\left(t - \dfrac{{\Delta t}}{2}\right)} \\ {\Delta t\dot v\left(t - \dfrac{{\Delta t}}{2}\right)} \end{array}} \right\}, \\& {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {1 - \dfrac{{{k_1}}}{m}\Delta {t^2}}&{ - \dfrac{{{k_2}}}{m}\Delta {t^2}}&{1 - \dfrac{{3c\Delta t}}{{2m}}}&{ - \dfrac{{c\Delta t}}{{8m}}} \\ { - \dfrac{{{k_2}}}{m}\Delta {t^2}}&{1 - \dfrac{{{k_1}}}{m}\Delta {t^2}}&{ - \dfrac{{c\Delta t}}{{8m}}}&{1 - \dfrac{{3c\Delta t}}{{2m}}} \\ { - \dfrac{{{k_1}}}{m}\Delta {t^2}}&{ - \dfrac{{{k_2}}}{m}\Delta {t^2}}&{1 - \dfrac{{3c\Delta t}}{{2m}}}&{ - \dfrac{{c\Delta t}}{{8m}}} \\ { - \dfrac{{{k_2}}}{m}\Delta {t^2}}&{ - \dfrac{{{k_1}}}{m}\Delta {t^2}}&{ - \dfrac{{c\Delta t}}{{8m}}}&{1 - \dfrac{{3c\Delta t}}{{2m}}} \end{array}} \right] \end{split} (21) 其中：
\begin{split} & m = \frac{{\rho {L^2}}}{4},\\&{c = \frac{{\rho L}}{2}(2{C_{\rm{S}}} + {C_{\rm{P}}})} , \\& {k_1} = \rho {C_s}^2\left( {\frac{{(3 - \mu )}}{{3(1 - \mu )}} + \frac{{3L}}{{2R}}} \right),\\&{k_2} = \frac{{\rho {C_s}^2}}{8}\left( {\frac{L}{R} - \frac{{2(1{\rm{ + }}\mu )}}{{1 - \mu }}} \right) \end{split} (22) 计算传递矩阵的特征值，根据
\rho ({\boldsymbol{A}}) = \max \left| {{\lambda _{i}}} \right| ，得出稳定性条件的表达式：\Delta t \leqslant \frac{{\sqrt {256m({k_1} + {k_2}) + 169{c^2}} - 13c}}{{8({k_1} + {k_2})}} (23) 将式(22)代入式(23)后，整理得到：
\Delta t \leqslant {\gamma _{{\text{2}}}} \cdot \frac{L}{{{C_{\rm{P}}}}} (24) 其中：
\begin{split} {\gamma _2}{\rm{ = }}&{\left( {1 - \mu } \right)^{3/2}} \cdot {(3 - 3\mu )^{1/2}}\left\{ {\left[ {\frac{{3\left( {603 + 338\sqrt {2 - 4\mu } \sqrt {1 - \mu } } \right) + 624(L/R)\left( {\mu - 1} \right)\left( {2\mu - 1} \right)}}{{{{\left( {\mu - 1} \right)}^2}}} + } \right.} \right.\\& \left. {{{\left. {\frac{{\mu \left( { - 4856 - 1014\sqrt {2 - 4\mu } \sqrt {1 - \mu } + 2983\mu } \right)}}{{{{\left( {\mu - 1} \right)}^2}}}} \right]}^{1/2}} - 39\left( {\sqrt {2 - 4\mu } + \sqrt {1 - \mu } } \right)} \right\}\Bigg/\\& [2\left( {7\mu - 9} \right)\left( {2\mu - 1} \right){\rm{ + }}39(L/R)\left( {\mu - 1} \right)\left( {2\mu - 1} \right)] \end{split} 式(24)即为角点处局部系统稳定性条件的解析表达形式，观察可知影响角点局部人工边界子系统稳定性的参数与侧边相同，但各自贡献不同。
3.3 角点自由边界子系统稳定性分析
为进一步研究角点处自由边界子系统的稳定性，如图10所示。研究对象为编号为1、2、4、5的四个节点。子系统中既有单元内部节点，也包含边界处节点。将四节点正方形平面单元质量、阻尼和刚度矩阵按节点编号组装后，可得到子系统的刚度、质量和阻尼矩阵，均为8×8阶对称矩阵。将整体运动方程按照式(14)中心差分格式展开，得到16×16阶传递矩阵。该传递矩阵无法得出解析形式的稳定性条件，可代入参数计算数值解。考虑稳定性条件受系统截止频率影响，自由边界子系统截止频率要低于固定边界子系统，由此判断后者稳定性条件应比前者严格，下一节将进行验证。
4 稳定性条件比较
为比较3种人工边界子系统的数值计算稳定条件，采用两组参数进行分析，具体参数见表1。
表 1 两组参数值(无量纲)Table 1. Two sets of parameter values (dimensionless)序号 \rho {C_{\rm{S}}} {C_{\rm{P}}} \mu L R 第1组 2500 500 935 0.3 2 158 第2组 2000 300 534 0.27 5 152 侧边固定和角点固定子系统的稳定条件可由式(19)和式(24)获得，角点自由边界子系统的稳定条件可采用数值方法获得。3种子系统谱半径的计算结果见图11。当谱半径小于等于1时，数值计算满足稳定性条件，由图11可以直观地比较两组参数条件下3种子系统的稳定条件。
表2中对3种局部子系统和内部系统满足稳定性条件的临界时间步长进行了定量比较。内部系统的稳定性条件(
\Delta t = L/{C_{\rm{P}}} )未考虑粘弹性人工边界单元对数值算法的影响，最为宽松；侧边和角点子系统考虑了粘弹性人工边界单元质量、等效刚度和阻尼对稳定性的影响，稳定性条件要比无人工边界单元时更为严格。四周固定的角点处边界节点只共享1/4内部单元质量，其子系统截止频率最高，因此稳定性条件最为严格。以上3种子系统数值积分稳定条件的对比表明，采用粘弹性人工边界单元时，系统数值积分的稳定条件由角点区控制。表 2 稳定性条件比较(无量纲)Table 2. Comparison of stability conditions (dimensionless)序号 侧边子系统
(固定边界)角点子系统
(固定边界)角点子系统
(自由边界)内部系统
稳定性第1组 0.00163 0.000623 0.00118 0.0021 第2组 0.00691 0.00265 0.00459 0.0094 5 算例验证
5.1 均匀半空间模型
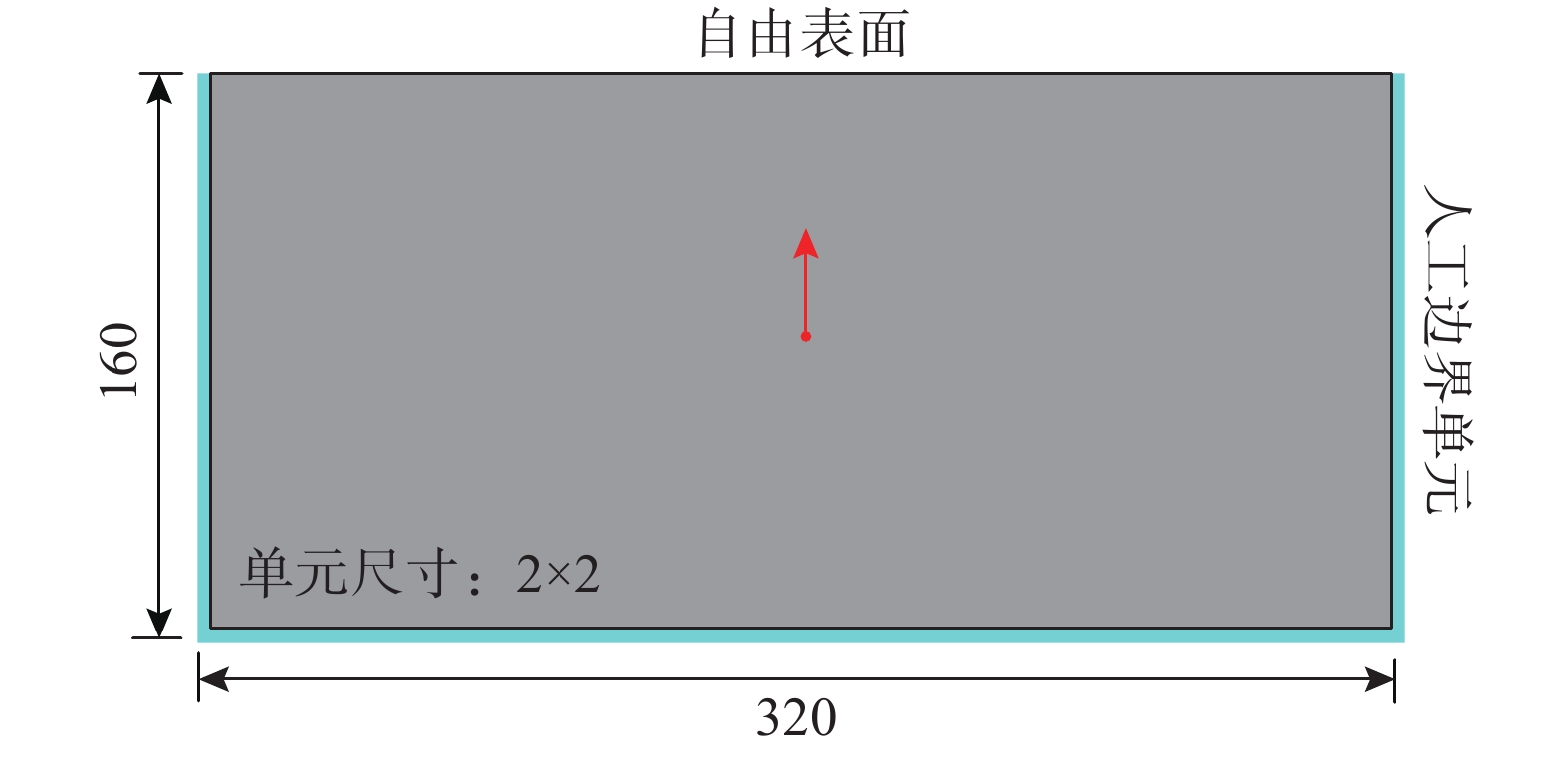
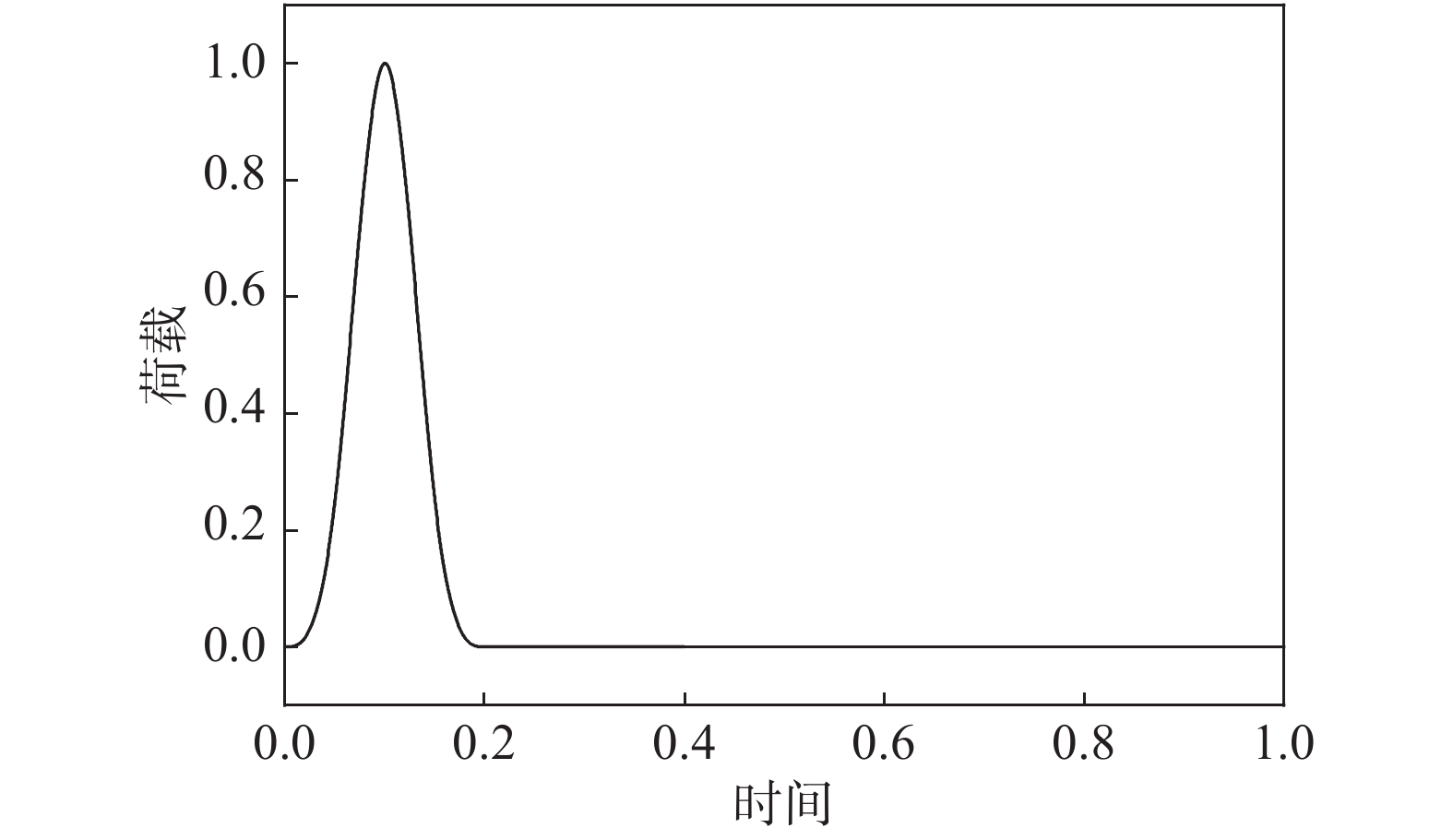
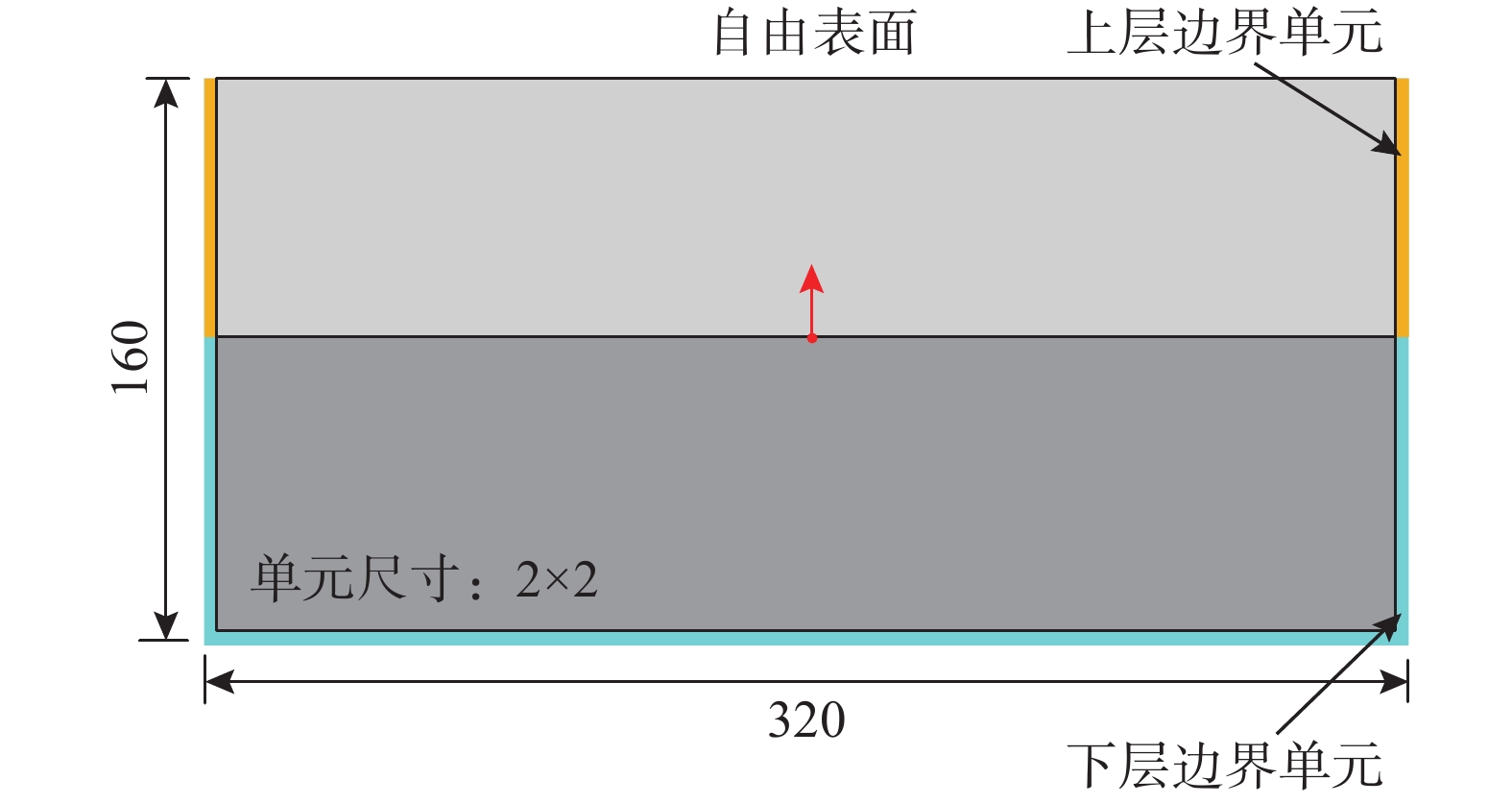
为验证以上稳定性分析的准确性，按第一组参数建立有限元近场模型，模型尺寸为320×160，内部介质密度为2500，剪切波速为500，泊松比为0.3，网格尺寸为2×2，模型侧边和底边最外层单元是粘弹性人工边界单元，如图12所示。采用持时为0.2的脉冲作为动力荷载，施加于模型中点处，时程曲线如图13所示。分别按照内部介质数值稳定条件(∆t=0.0021)、侧边子系统稳定条件(∆t=0.00163)、固定边界角点子系统稳定条件(∆t=0.00623)，采用固定时间步长的显示时域逐步积分算法对整体模型进行计算。
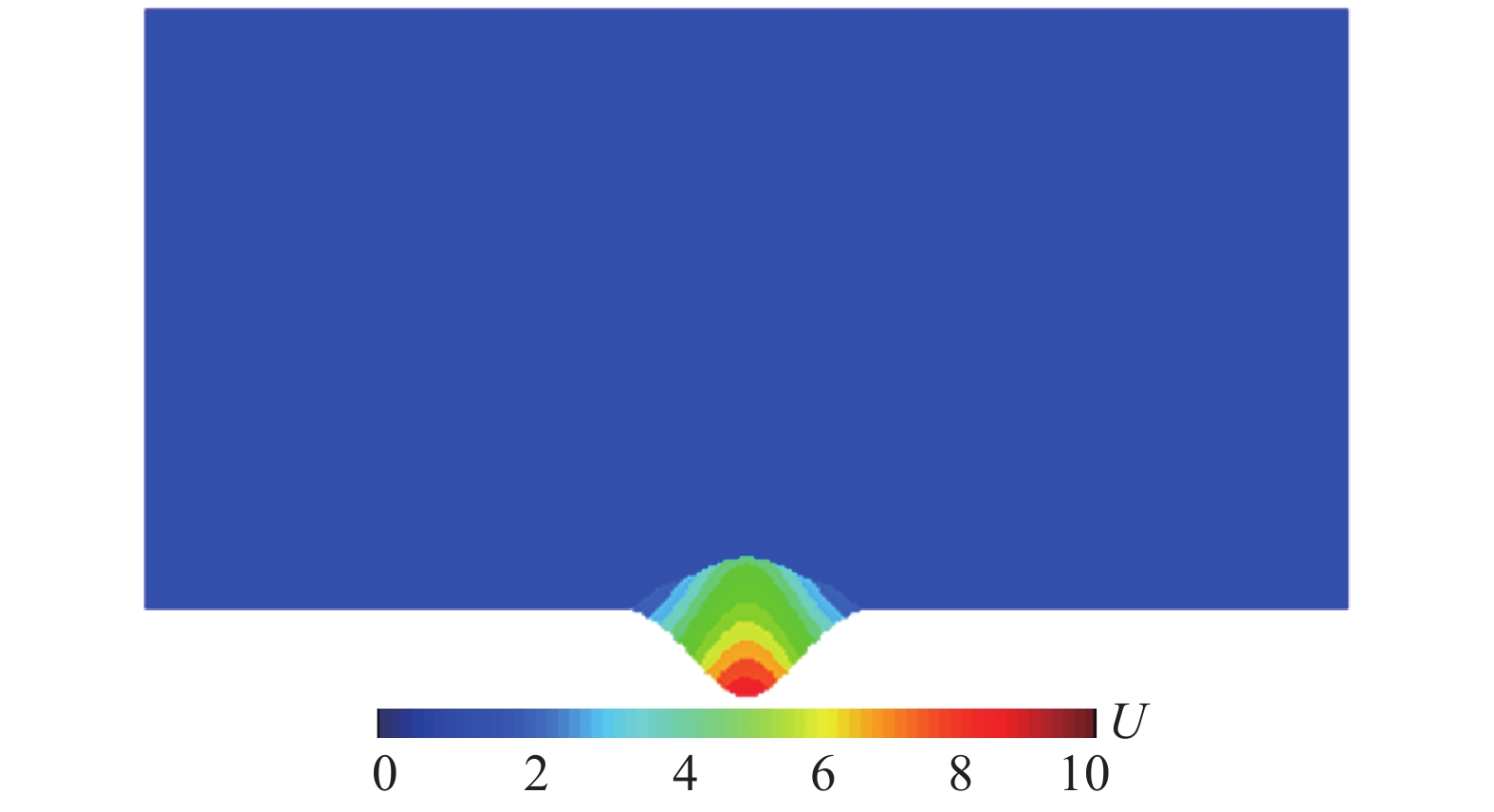
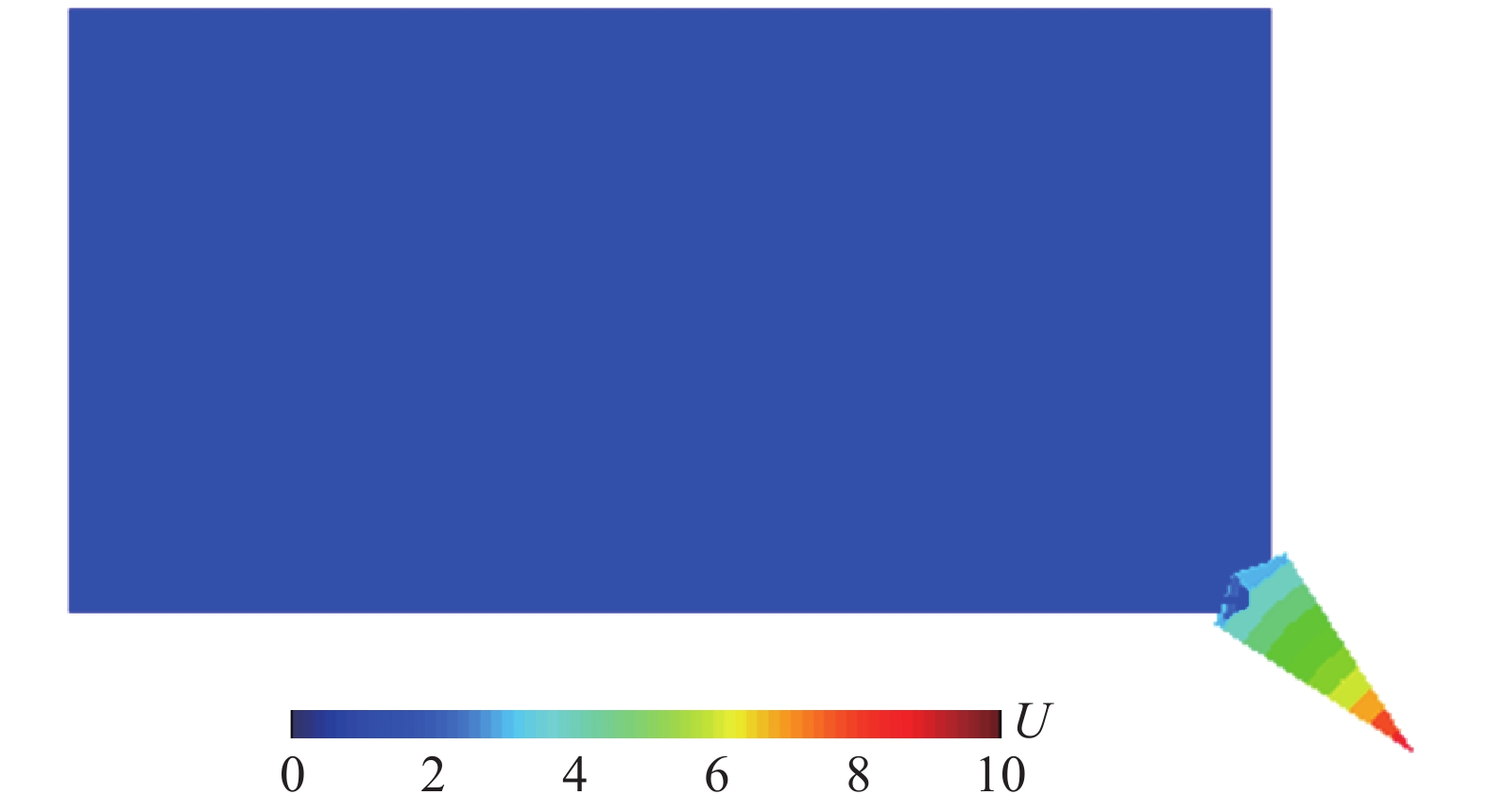
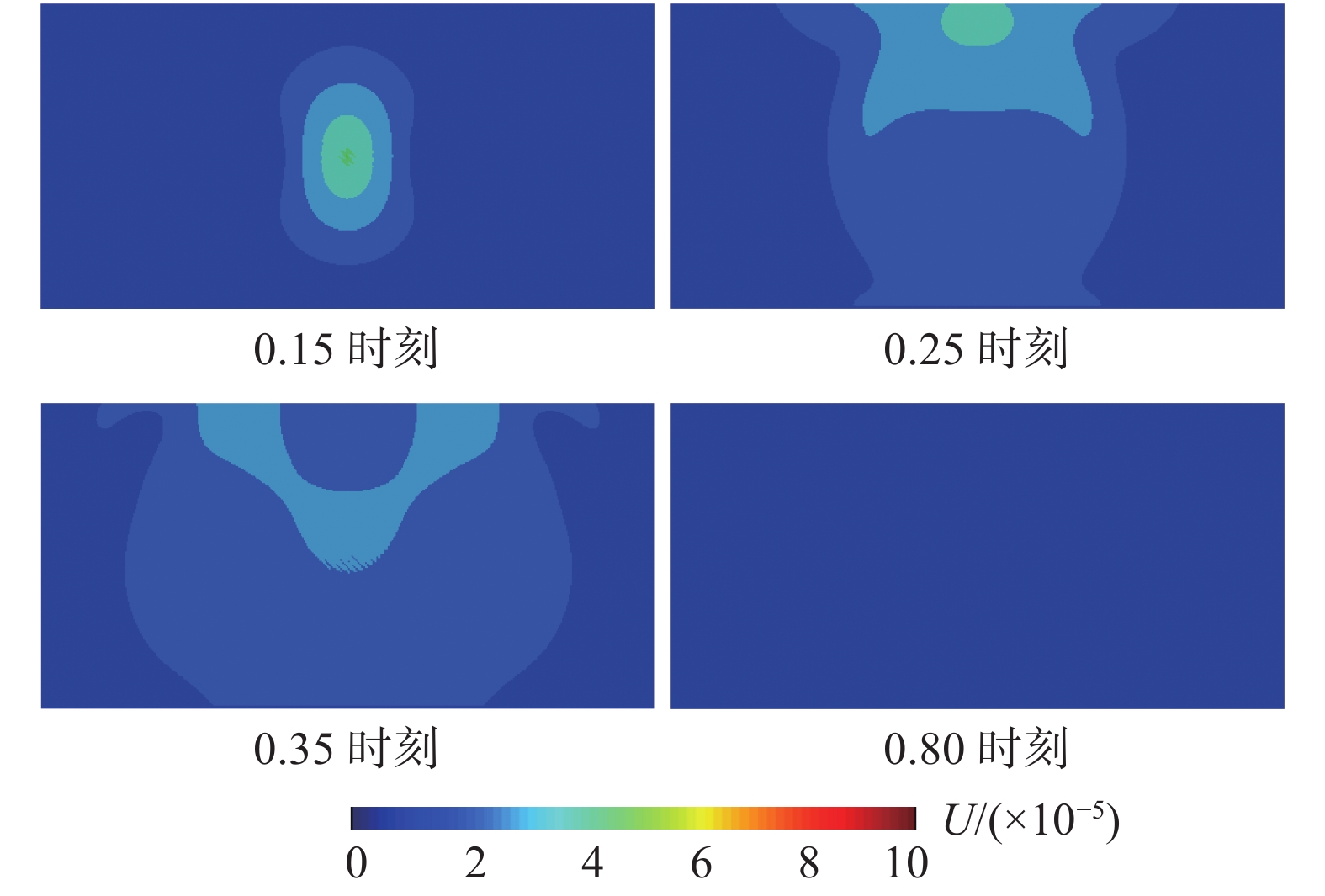
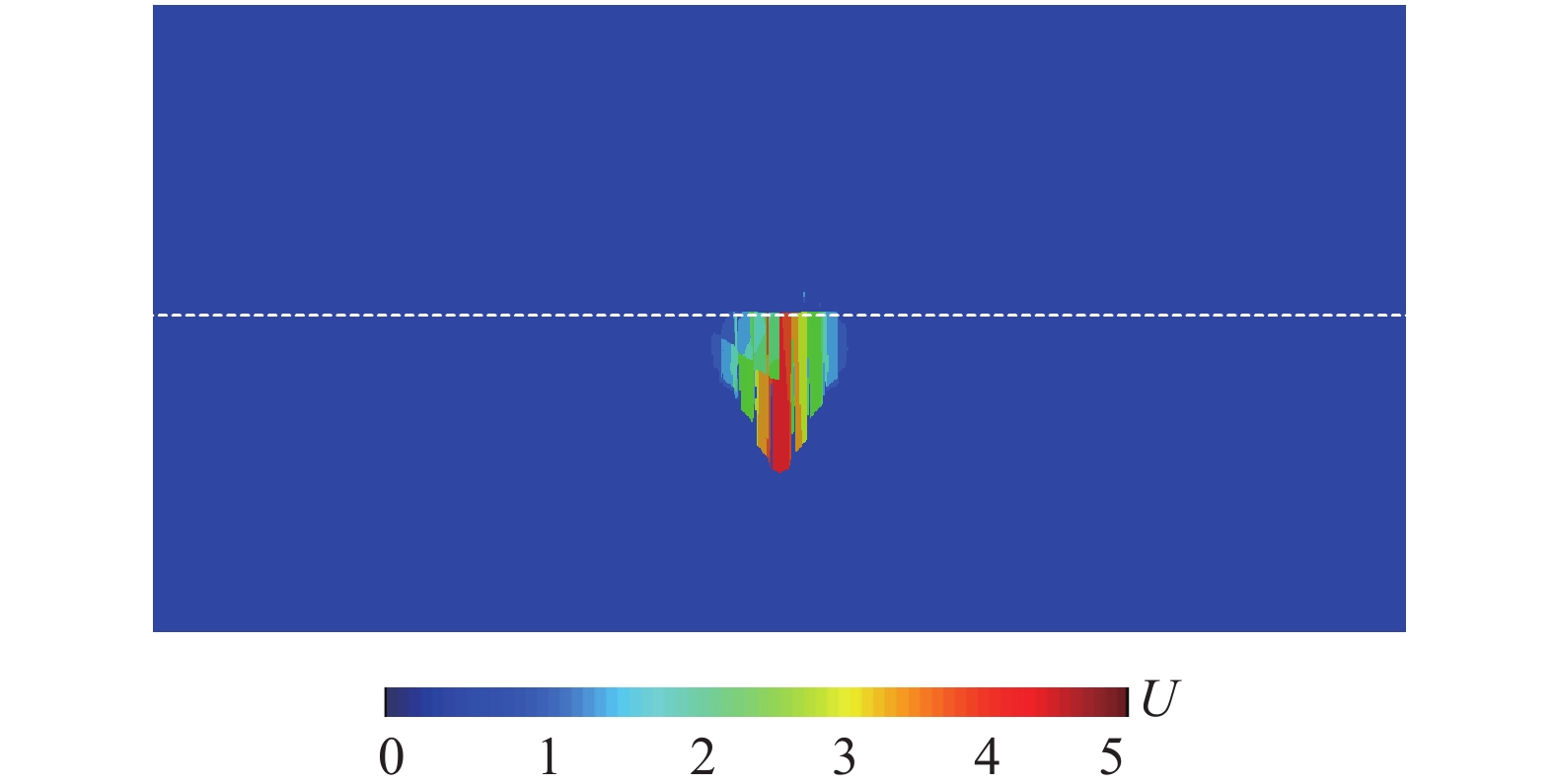
按照内部介质数值稳定条件(∆t=0.0021)计算时，由于不满足侧边(底边)子系统稳定条件，因此P波传播到距离波源最近的底边节点时发生失稳，如图14所示；按照侧边子系统稳定条件(∆t=0.00163)计算时，由于不满足角点处子系统稳定条件，波动传播到模型角点处时发生失稳，如图15所示，其中U为介质中的位移，以上两种稳定条件均无法完成整体有限元模型的计算。
![]()
图 14 按内部稳定条件计算时底边失稳状态(0.11时刻)Figure 14. The unstable state of the bottom edge when calculated according to internal stability conditions (time 0.11)按照角点处子系统稳定条件(∆t=0.000623)计算时，可顺利完成整体模型的动力显式计算，粘弹性人工边界单元很好模拟了外行波向无穷远的辐射，结果如图16所示。此外，通过进一步的计算分析发现，当整体稳定条件取值略大于角点子系统稳定条件时(例如∆t=0.00085)，模型角点处也发生失稳，失稳状态与图15相同。
![]()
图 15 按侧边子系统稳定条件计算时角点失稳状态(0.19时刻)Figure 15. The unstable state of the bottom edge when calculated according to the stability conditions of side subsystem (time 0.19)![]()
图 16 按角点子系统稳定条件计算结果Figure 16. Results calculated by the stability conditions of the corner subsystem以上计算分析验证了采用粘弹性人工边界单元时，整体模型显式数值积分算法的稳定性由角点区域控制，式(24)给出的角点处子系统稳定条件是整体模型数值稳定的充分条件。
5.2 成层半空间模型
为满足实际场地计算需要，对成层半空间算例进行验证。成层半空间有限元模型尺寸为320×160，上半部分内部介质密度2000，剪切波速300，泊松比0.27，下半部分内部介质密度为2500，剪切波速为500，泊松比为0.3，整体模型网格尺寸为2×2，模型侧边和底边最外层单元是粘弹性人工边界单元，如图17所示。脉冲荷载施加于模型中心，如图13所示。
表3给出了成层半空间局部子系统和内部系统满足稳定性条件的临界时间步长。模型中的上层介质只有侧边子系统，无角点子系统，下层介质两者均存在。
表 3 成层半空间稳定性条件比较(无量纲)Table 3. Comparison of stability conditions in layered half space (dimensionless)子系统
成层介质侧边子系统 角点子系统 内部系统稳定性 上层介质 0.0028 − 0.0037 下层介质 0.00163 0.000623 0.0021 经比较发现，上层介质中满足内部系统稳定条件的时间步长(∆t=0.0037)大于侧边子系统稳定时间步长(∆t=0.0028)。而二者均比下层介质内部系统稳定的时间步长 (∆t=0.0021)要宽松。因此，当采用上层介质稳定性条件对整体模型计算时，首先发生失稳的是下层介质的内部系统，如图18所示。
![]()
图 18 按上层介质稳定条件计算时下层介质内部系统失稳状态(0.1时刻)Figure 18. The unstable state of the internal system in lower media when calculated according to the stability conditions in upper media (time 0.1)采用下层介质内部系统稳定条件(∆t=0.0021)计算时，整体系统失稳状态与图14相同；采用下层介质侧边子系统稳定条件计算时(∆t=0.00163)，失稳状态和图15相同。
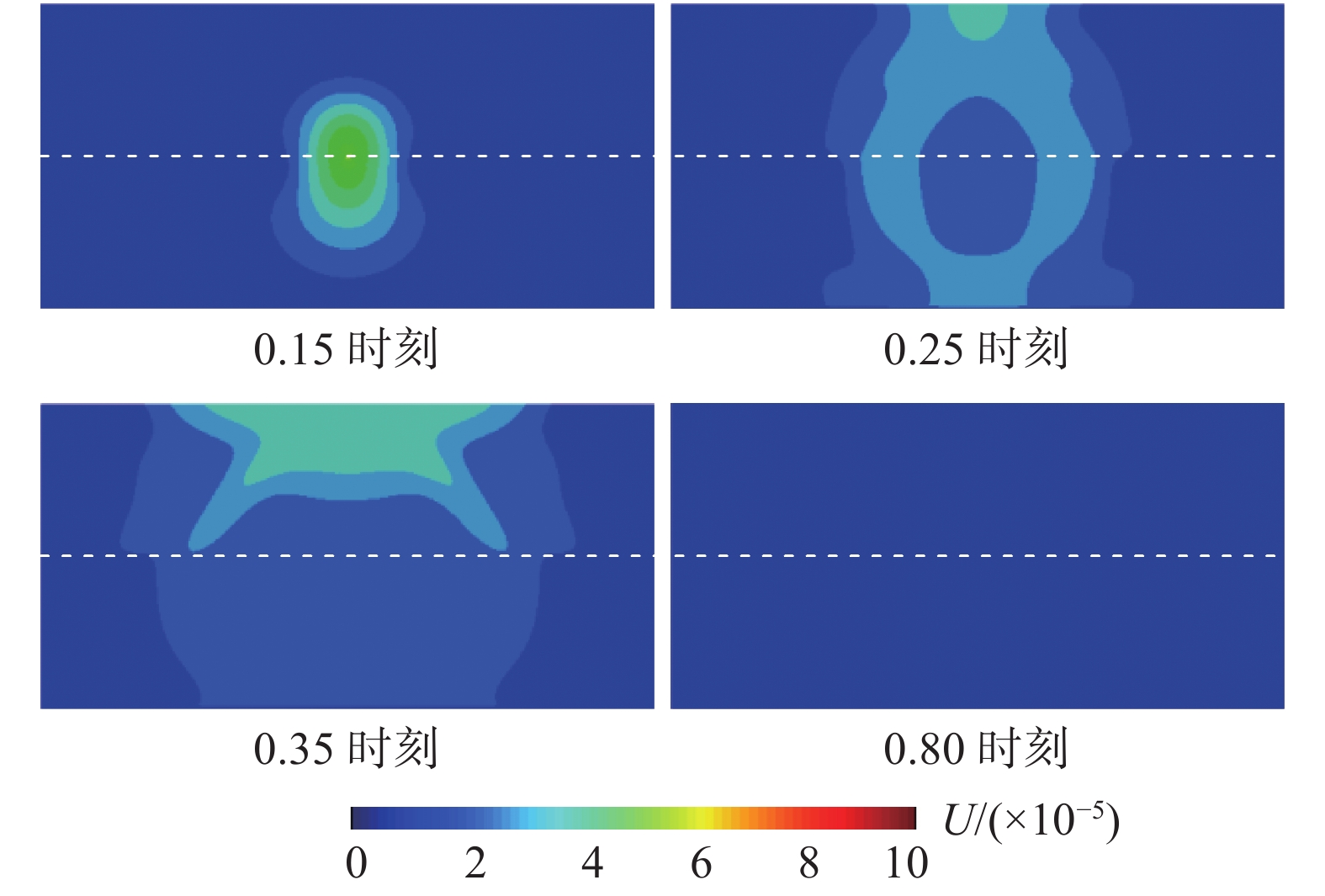
按照下层角点子系统稳定条件(∆t=0.000623)计算时，可顺利完成整体模型的动力显式计算，分层介质中，粘弹性人工边界单元也可很好地模拟外行波向无穷远的辐射，结果如图19所示。成层半空间算例进一步验证了采用粘弹性人工边界单元时，整体模型显式数值积分算法的稳定性仍然由角点区域控制。
![]()
图 19 按下层介质角点子系统稳定条件计算结果Figure 19. Results calculated by the stability conditions of the corner subsystem in lower media6 结论与展望
本文将整体模型数值稳定性问题合理转移到若干局部子系统中，充分考虑粘弹性人工边界单元和内部单元节点间的运动耦合效应，通过传递矩阵谱半径分析方法推导出各局部子系统显式时域逐步积分(中心差分)数值稳定条件的解析解和数值解。通过计算软件验证理论分析的可靠性。具体结论如下：
(1) 对于大规模数值计算问题，可选取局部的子系统并对其进行显式时域逐步积分算法的稳定性分析，该稳定性条件与整体系统稳定性条件相同或近似。
(2) 采用粘弹性人工边界单元时，受人工边界单元质量、刚度和阻尼影响，整体系统的稳定性条件与内部介质的稳定性条件不同，前者的稳定性条件更为严格，需使用更小的积分步长以满足整体系统的数值稳定。
(3) 采用粘弹性人工边界单元时，整体模型显式数值积分算法的稳定性由角点区域控制，本文给出了角点处子系统数值积分的稳定性条件，该稳定性条件是整体模型数值积分稳定的充分条件。此外，本文给出的稳定性条件是以正方形平面单元为对象推导的，同样适用于矩形平面单元，由于系统稳定条件受最小单元尺寸影响，可使用矩形单元的最小边长作为参数计算稳定性条件。
下一步展望：
(1) 对于三维粘弹性人工边界单元，同样可以利用本文提出的传递矩阵谱半径分析方法对显式时域逐步积分算法的稳定性条件进行分析，三维问题涉及的局部子结构更为特殊，传递矩阵的生成和特征值求解更加复杂，需进一步开展研究。
(2) 相比隐式算法，显式算法的解耦特性对于求解大范围复杂工程场地问题更有优势。本文的研究成果为在显式算法中合理使用粘弹性人工边界单元提供了理论依据。可在此基础上进一步开展分析和研究，以改善使用粘弹性人工边界单元时显式算法的稳定性，提高大范围工程场地问题的计算效率。
-
![]()
图 2 适用于显式算法的人工边界单元
Figure 2. Artificial boundary elements adapted to explicit algorithms
![]()
图 6 二维节点系统最高阶振型图
Figure 6. Highest-order modal pattern of two-dimensional nodes system
![]()
图 14 按内部稳定条件计算时底边失稳状态(0.11时刻)
Figure 14. The unstable state of the bottom edge when calculated according to internal stability conditions (time 0.11)
![]()
图 15 按侧边子系统稳定条件计算时角点失稳状态(0.19时刻)
Figure 15. The unstable state of the bottom edge when calculated according to the stability conditions of side subsystem (time 0.19)
![]()
图 16 按角点子系统稳定条件计算结果
Figure 16. Results calculated by the stability conditions of the corner subsystem
![]()
图 18 按上层介质稳定条件计算时下层介质内部系统失稳状态(0.1时刻)
Figure 18. The unstable state of the internal system in lower media when calculated according to the stability conditions in upper media (time 0.1)
![]()
图 19 按下层介质角点子系统稳定条件计算结果
Figure 19. Results calculated by the stability conditions of the corner subsystem in lower media
表 1 两组参数值(无量纲)
Table 1 Two sets of parameter values (dimensionless)
序号 \rho {C_{\rm{S}}} {C_{\rm{P}}} \mu L R 第1组 2500 500 935 0.3 2 158 第2组 2000 300 534 0.27 5 152 
下载: 导出CSV
表 2 稳定性条件比较(无量纲)
Table 2 Comparison of stability conditions (dimensionless)
序号 侧边子系统
(固定边界)角点子系统
(固定边界)角点子系统
(自由边界)内部系统
稳定性第1组 0.00163 0.000623 0.00118 0.0021 第2组 0.00691 0.00265 0.00459 0.0094
下载: 导出CSV
表 3 成层半空间稳定性条件比较(无量纲)
Table 3 Comparison of stability conditions in layered half space (dimensionless)
子系统
成层介质侧边子系统 角点子系统 内部系统稳定性 上层介质 0.0028 − 0.0037 下层介质 0.00163 0.000623 0.0021
下载: 导出CSV
-
[1] Zhao M, Wu L, Du X, et al. Stable high-order absorbing boundary condition based on new continued fraction for scalar wave propagation in unbounded multilayer media [J]. Computer Methods in Applied Mechanics & Engineering, 2018, 334(1): 111 − 137.
[2] Li Huifang, Zhao Mi, Wu Lihua, et al. A stable high-order absorbing boundary based on continued fraction for scalar wave propagation in 2D and 3D unbounded layers [J]. Engineering Computations, 2019, 36(7): 2445 − 2479.
[3] Wang P, Zhao M, Du X. Simplified Formula for Earthquake-Induced Hydrodynamic Pressure on Round-Ended and Rectangular Cylinders Surrounded by Water [J]. Journal of Engineering Mechanics, 2019, 145(2): 04018137.
[4] 王丕光, 赵密, 李会芳, 等. 一种高精度圆柱形人工边界条件: 水-柱体相互作用问题[J]. 工程力学, 2019, 36(1): 88 − 95. doi: 10.6052/j.issn.1000-4750.2017.10.0787 Wang Piguang, Zhao Mi, Li Huifang, et al. A high-accuracy cylindrical artificial boundary condition: water-cylinder interaction problem [J]. Engineering Mechanics, 2019, 36(1): 88 − 95. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.10.0787
[5] 刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6): 46 − 51. doi: 10.3969/j.issn.1000-4750.2005.06.008 Liu Jingbo, Wang Zhenyu, Du Xiuli, et al. There-dimensional visco-elastic artificial boundaries in time domain for wave motion problems [J]. Engineering Mechanics, 2005, 22(6): 46 − 51. (in Chinese) doi: 10.3969/j.issn.1000-4750.2005.06.008
[6] 刘晶波, 谷音, 杜义欣. 一致粘弹性人工边界及粘弹性边界单元[J]. 岩土工程学报, 2006, 28(9): 1070 − 1075. doi: 10.3321/j.issn:1000-4548.2006.09.004 Liu Jingbo, Gu Yin, Du Yixin. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070 − 1075. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.09.004
[7] 谷音, 刘晶波, 杜义欣. 三维一致粘弹性人工边界及等效粘弹性边界单元[J]. 工程力学, 2007, 24(12): 31 − 37. doi: 10.3969/j.issn.1000-4750.2007.12.006 Gu Yin, Liu Jingbo, Du Yixin. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element [J]. Engineering Mechanics, 2007, 24(12): 31 − 37. (in Chinese) doi: 10.3969/j.issn.1000-4750.2007.12.006
[8] 宝鑫, 刘晶波, 王东洋, 等. P波垂直入射下海域岛礁场地动力反应分析[J]. 工程力学, 2019, 36(增刊 1): 1 − 7. Bao Xin, Liu Jingbo, Wang Dongyang, et al. Seismic response analysis of offshore reef site under incident P wave [J]. Engineering Mechanics, 2019, 36(Suppl 1): 1 − 7. (in Chinese)
[9] Bao X, Liu J, Wang D, et al. Modification research of the internal substructure method for seismic wave input in deep underground structure-soil systems [J]. Shock and Vibration, 2019(2019): 1 − 13.
[10] Liu J, Bao X, Wang D, et al. The internal substructure method for seismic wave input in 3D dynamic soil-structure interaction analysis [J]. Soil Dynamic and Earthquake Engineering, 2019, 127: 1 − 12.
[11] Liu J, Bao X, Wang D, et al. Seismic response of the reef-seawater system under incident SV wave [J]. Ocean Engineering, 2019, 180: 199 − 210. doi: 10.1016/j.oceaneng.2019.03.068
[12] Bao X, Liu J, Li S, et al. Seismic response analysis of the reef-seawater system under obliquely incident P and SV waves [J]. Ocean Engineering, 2020, 200: 107021. doi: 10.1016/j.oceaneng.2020.107021
[13] Mahrer K D. Numerical time step instability and Stacey's and Clayton-Engquist's absorbing boundary conditions [J]. Bulletin of the Seismological Society of America, 1990, 80(1): 213 − 217.
[14] 关慧敏, 廖振鹏. 时域局部人工边界的稳定性分析方法概述[J]. 世界地震工程, 1997, 13(2): 1 − 7. Guan Huimin, Liao Zhenpeng. A summary on the methods for the stability analysis of artificial local boundaries in time domain [J]. World Information on Earthquake Engineering, 1997, 13(2): 1 − 7. (in Chinese)
[15] Trefethen L N. Instability of difference models for hyperbolic initial boundary value problems [J]. Communications on Pure and Applied Mathematics, 1984, 37(3): 329 − 367. doi: 10.1002/cpa.3160370305
[16] Liao Z P, Liu J B. Numerical instabilities of a local transmitting boundary [J]. Earthquake Engineering & Structural Dynamics, 1992, 21(1): 65 − 77.
[17] Kamel A H. A stability checking procedure for finite-difference schemes with boundary conditions in acoustic media [J]. Bulletin of the Seismological Society of America, 1989, 79(5): 1601 − 1606.
[18] 关慧敏, 廖振鹏. 局部人工边界稳定性的一种分析方法[J]. 力学学报, 1996, 28(3): 1601 − 1606. Guan Huimin, Liao Zhenpeng. A method for the stability analysis of local artificial boundaries [J]. Acta Mechanica Sinica, 1996, 28(3): 1601 − 1606. (in Chinese)
[19] Zhao M, Li H, Cao S, et al. An explicit time integration algorithm for linear and non-linear finite element analyses of dynamic and wave problems [J]. Engineering Computations, 2018, 36(1): 161 − 177.
[20] Soares D. Nonlinear dynamic analysis considering explicit and implicit time marching techniques with adaptive time integration parameters [J]. Acta Mechanica, 2018, 229(5): 1 − 20.
[21] 文颖, 陶蕤. 基于加速度泰勒展开的动力学方程显式积分方法[J]. 工程力学, 2018, 35(11): 26 − 34. doi: 10.6052/j.issn.1000-4750.2017.08.0661 Wen Ying, Tao Rui. An explicit time-domain integration scheme for solving equations of motion in structural dynamics based on a truncated Taylor expansion of acceleration [J]. Engineering Mechanics, 2018, 35(11): 26 − 34. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.08.0661
[22] 赵鹏举, 于晓辉, 陆新征. 基于显式算法的RC框架结构抗地震倒塌能力分析[J]. 工程力学, 2020, 37(3): 77 − 87. Zhao Pengju, Yu Xiaohui, Lu Xinzheng. Collapse capacity assessment of RC frame structures using explicit algorithm [J]. Engineering Mechanics, 2020, 37(3): 77 − 87. (in Chinese)
[23] Hughes T J R. Analysis of transient algorithms with particular reference to stability behavior [M]. Computational Methods for Transient Analysis. North-Holland Computational Methods in Mechanics v1 Amsterdam, Nethand, 1983: 67 − 155.
[24] 王勖成, 邵敏. 有限单元法基本原理和数值方法 [M]. 北京: 清华大学出版社, 1997: 66 − 67. Wang Xucheng, Shao Min. Basic principle and numerical method of finite element method [M]. Beijing: Tsinghua University Press, 1997: 66 − 67. (in Chinese)
[25] ABAQUS Analysis User’s Manual (version 6.14) [R]. ABAQUS, INC., 2013.
-
期刊类型引用(22)
1. 康厚军，钱登宇，苏潇阳，张晓宇，丛云跃. 刚构体系斜拉桥塔柱计算长度系数求解方法研究. 工程力学. 2025(01): 44-52 . 
本站查看
2. 张高明，王甫来，申朝旭，孙华东，岳煜斐，周航，刘枫，刘畅. 青岛胶东国际机场列车振动现场实测及分析研究. 铁道标准设计. 2025(01): 220-227 . 百度学术
3. 柳国环，费琦翔. 边界-土-多跨桥梁系统的分区独立内部子结构地震波输入法及验证. 中国公路学报. 2025(03): 331-342 . 百度学术
4. 周鹏发，申玉生，高登，张熙，黄海峰，高波. 基于混合有限元的显式时域完美匹配层研究. 岩土力学. 2025(05): 1605-1619+1631 . 百度学术
5. 李建波，杨波，李志远，丁志新. 基于CAS法的核电工程异形水箱分布质量计算模型. 工程力学. 2024(02): 160-170+193 . 本站查看
6. 黄宇峰，卢文波，王高辉，陈明，严鹏. 远场水下爆炸冲击作用下重力坝动力稳定性的简化时程分析方法. 工程力学. 2024(03): 73-81 . 本站查看
7. 巴振宁，鲁世斌，付继赛，梁建文，芦燕. 基于FK-FE混合方法的位错点源作用下全过程结构地震反应模拟. 工程力学. 2024(04): 184-198 . 本站查看
8. 谷坤生，周剑，戴福初，张路青. 地震P波倾斜入射下单面坡动力响应分析. 地球物理学报. 2024(06): 2350-2363 . 百度学术
9. 刘晶磊，陈岩，陈丰泽，李秀欣，梅名彰，尹姜鳗. 地基中混凝土排桩主动隔振研究. 地震工程与工程振动. 2024(03): 164-173 . 百度学术
10. 宝鑫，刘晶波，李述涛，陆喜欢，王菲. 地下结构整体式反应位移法的改进. 工程力学. 2023(01): 76-86 . 本站查看
11. 刘晶波，宝鑫，李述涛，王菲，王栋. 采用粘弹性人工边界时显式算法稳定性的改善研究. 工程力学. 2023(05): 20-31 . 本站查看
12. 陈龙明，李述涛，陈叶青，宝鑫. 爆炸荷载多尺度分析方法在仿真计算中的应用. 北京理工大学学报. 2023(05): 460-469 . 百度学术
13. 李述涛，魏万里，陈叶青，陈龙明. 基于体积填充法的弹体侵爆一体毁伤效应研究. 振动与冲击. 2023(12): 194-204 . 百度学术
14. 李雪菊，潘旦光，石树中. 地震作用下二维场地模态叠加等效线性化方法. 工程力学. 2023(10): 179-189 . 本站查看
15. 张佳文，李明超，韩帅，闫文钰. 基于波场分离的不规则地形下地震波输入方法. 工程力学. 2023(11): 69-80+109 . 本站查看
16. 杜碧涛，刘远明，陈会宇，陈庆芝，陈林全，滕召磊. 岩溶区铁路列车荷载对新建下穿隧道动力响应规律. 科学技术与工程. 2023(30): 13134-13142 . 百度学术
17. 刘爽，闫少敏，裴旺. 基于谐响应的三维场地地震动频域研究. 山东交通学院学报. 2023(04): 142-152 . 百度学术
18. 刘晶波，宝鑫，李述涛，王菲. 采用黏弹性人工边界时显式算法稳定性条件. 爆炸与冲击. 2022(03): 124-137 . 百度学术
19. 陈国兴，夏高旭，王彦臻，金丹丹. 琼州海峡海床地震反应特性的一维非线性分析. 工程力学. 2022(05): 75-85 . 本站查看
20. 丁祖德，陈誉升，资昊. 隧道地震响应中的人工边界和地震动输入方法研究. 地震工程与工程振动. 2022(03): 52-61 . 百度学术
21. 章旭斌，谢志南. 波动谱元模拟中透射边界稳定性分析. 工程力学. 2022(10): 26-35 . 本站查看
22. 李昊晨，田松峰，丁闪闪. 水泥余热发电机组空冷岛振动问题分析与处理. 电力科学与工程. 2021(08): 73-78 . 百度学术
其他类型引用(15)
计量
- 文章访问数: 750
- HTML全文浏览量: 131
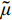
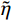
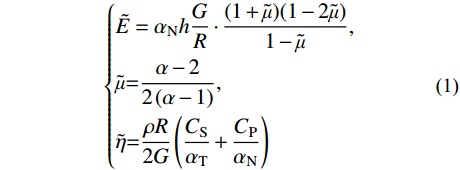
- PDF下载量: 137
- 被引次数: 37
