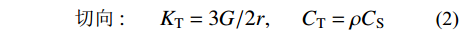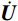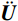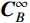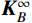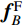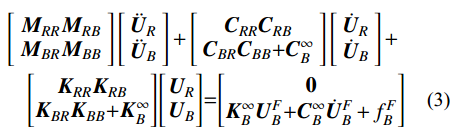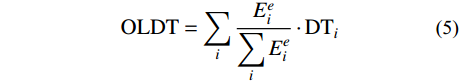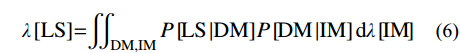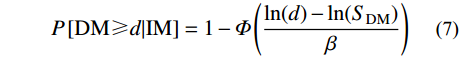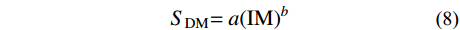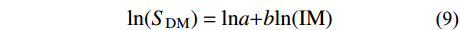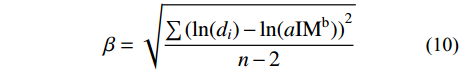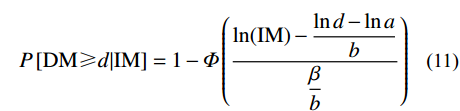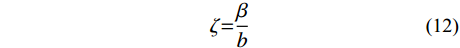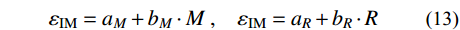SEISMIC INTENSITY MEASURES FOR THE DAMAGE EVALUATION OF CIRCULAR TUNNELS
-
摘要: 地震动强度指标是影响结构地震风险评估准确性的重要参数,在基于性能的地震工程研究框架中发挥着重要作用。合理的地震动强度指标可以使结构地震反应预测结果更加准确。为研究适用于圆形隧道损伤评价的地震动强度指标,该文基于整体式非线性动力时程分析方法,建立圆形隧道-围岩相互作用二维有限元分析模型,采用FEMA-P695推荐的近场无脉冲及远场地震动作为输入,并以衬砌横断面整体压缩损伤指数和拉伸损伤指数作为结构损伤指标评估衬砌损伤状态,对比分析了工程中常用的20种地震动强度指标在圆形隧道损伤评价中的适用性。研究结果表明:基于有效性、实用性、有益性和充分性判别准则,适用于圆形隧道损伤评价的最优地震动强度指标为持续最大加速度SMA,其次为加速度谱强度ASI。Abstract: The seismic intensity measure (IM) is a key parameter affecting the accuracy of seismic risk assessment, which plays an important role in the performance-based earthquake engineering framework. A reasonable IM can make the prediction of structural seismic responses more accurate. To study on seismic IMs which are suitable for the damage evaluation of circular tunnels, a two-dimensional finite element model was established for the nonlinear dynamic time history analyses of circular tunnel-surrounding rock interaction. The near-field ground motions without velocity pulses and far-field ground motions recommended by FEMA-P695 were used as the input in the numerical model. The overall lining damage indices in compression and in tension were used as the engineering damage measures to estimate the damage states of the lining. The applicability of 20 ground motion IMs commonly used in the engineering practice were investigated. The results show that based on the criteria of efficiency, practicality, proficiency and sufficiency, the best seismic IM for the damage evaluation of circular tunnels is the sustained maximum acceleration (SMA), and the second best is the acceleration spectrum intensity (ASI).
-
Keywords:
- circular tunnels /
- intensity measure /
- efficiency /
- practicality /
- proficiency /
- sufficiency
-
自从1989年Loma Prieta 地震和1994年Northridge地震以后,基于性能的地震工程(performance based earthquake engineering, PBEE) 抗震设计方法在结构抗震设计和研究中得到广泛应用[1-2]。在PBEE框架中,地震动强度指标(intensity measure, IM)作为联系地震危险性分析和结构地震反应分析的桥梁,是影响计算结果准确性的重要部分。由于地震动记录的随机性和结构破坏状态的复杂性,如何确定一个能综合反映地震动强度大小的指标用于结构抗震分析,一直是结构工程抗震分析领域所面临的一个难点和热点,同时也是实现基于性能抗震设计亟待解决的一个基本问题。
近年来,国内外学者针对不同地震动强度指标与结构响应之间的相关性开展了一系列研究。Riddell[3]在研究中将IM分为加速度相关型、速度相关型和位移相关型三类,选用单自由度体系作为研究对象,对23个IM和4个结构地震响应量进行分析,结果表明:没有一个指标同时适用于三个反应谱敏感区,加速度型IM适用于加速度敏感区,速度型IM适用于速度敏感区,位移型IM适用于位移敏感区。叶列平等[4]基于已有学者的研究成果,总结归纳现有主要的33个IM,基于弹塑性单自由度体系和多自由度体系的代表性响应指标,分析了不同IM与不同结构地震响应指标之间的相关性,研究结果表明:1)以地震动峰值加速度(PGA)为代表的第一类指标对短周期结构的相关程度较高,对中长期结构的相关程度较低;2)以地震动峰值速度(PGV)为代表的第二类指标对中周期结构的相关程度较高;3)以地震动峰值位移(PGD)为代表的第三类指标对长周期结构的相关性较高。张艺欣等[5]基于12榀高层钢筋混凝土结构的增量动力分析结果,首先计算了谱加速度指标在不同周期下的有效性和充分性,考察二者与高阶振型和非线性软化效应的相关性,进而分析反应谱的控制周期值,并据此提出适用于该类结构的多周期平均谱加速度指标。其他学者同样对各类型地面结构展开了大量研究,如桥梁[6-7]、房屋[8-10]、高耸结构[11]、水坝[12]、储液罐[13]等结构。但对于地下结构,特别是隧道结构等开展的研究相对较少。地下结构由于受到周围围岩土体的约束,地震反应特性与地上结构存在明显不同,地下结构的地震响应主要受控于周围围岩土体的变形,因此,对于各类型IM在地下结构的适用性有待考证。
本文采用FEMA-P695[14]中推荐的22组远场地震动和14组近场无脉冲地震动记录,建立圆形隧道-围岩相互作用二维有限元模型,研究地震动强度指标与结构损伤指标之间的关系,基于地震动强度指标判别准则如有效性、实用性、有益性和充分性对工程中常用的20个地震动强度指标进行比较分析,优选出适用于圆形隧道损伤评价的地震动强度指标。
1 地震动强度指标
地震动强度指标是用来描述地震动中强度特性的指标,学者基于不同的认识角度提出了各种类型的强度指标。在本文研究中比较分析工程中常用的20种强度指标。这些指标大致分为两类:1)仅考虑地震动信息的,如PGA、PGV、PGD等;2)与结构特性相关的,如伪加速度反应谱峰值(PSA),伪速度反应谱峰值(PSV)等。仅考虑地震动信息强度指标可以进一步分为加速度型、速度型、位移型及其他。与结构特性相关强度指标可以进一步分为与反应谱单值相关的和反应谱时间段积分相关的两种类型。本文采用的20种强度指标具体信息如表1所示,其中:a(t)、 v(t)、 d(t)分别为地震动加速度、速度、位移时程;Sa、 Sv分别表示加速度反应谱、速度反应谱;PSa、 PSv分别表示伪加速度反应谱、伪速度反应谱;ttot是地震动持时,t5和t95分别表示5%和95% AI强度的时刻,td=t95−t5表示有效强震持时。
表 1 分析中采用的地震动强度指标Table 1. Intensity measures in analyses强度指标类型 分类型 编号 名称 定义 仅考虑地震动信息型 加速度型 1 峰值加速度 PGA=max|a(t)| 2 Arias强度 AI=π2g∫ttot0a(t)2dt 3 累计绝对速度 CAV=∫ttot0|a(t)|dt 4 均方根加速度 arms=√∫t95t5a(t)2dt/td 5 特征强度 IC=arms1.5t0.5d 6 持续最大加速度[15] 加速度时程中第三个最大值(SMA) 速度型 7 峰值速度 PGV=max|v(t)| 8 均方根速度 vrms=√∫t95t5v(t)2dt/td 9 能量密度指标 SED=∫ttot0v(t)2dt 10 复合指标 IF=PGV×t0.25d 11 持续最大速度[15] 速度时程中第三个最大值(SMV) 位移型 12 峰值位移 PGD=max|d(t)| 13 均方根位移 drms=√∫t95t5d(t)2dt/td 其他 14 峰值速度平方与峰值加速度比 PGV2/PGA 考虑结构特性型 与反应谱单值相关 15 伪加速度谱峰值 PSA=maxPSa 16 伪速度谱峰值 PSV=maxPSv 与反应谱时间段积分相关 17 加速度谱强度 ASI=∫0.50.1PSadT 18 速度谱强度 VSI=∫2.50.1SvdT 19 Housner强度 HI=∫2.50.1PSvdT 20 有效峰值加速度 EPA=mean∫0.50.1SadT/2.5 2 地震动选取及有限元模型的建立
2.1 地震动记录的选取
本研究采用FEMA-P695中推荐的22组远场地震动和14组近场无脉冲地震动作为计算模型的输入荷载,将每组地震动含有的两条水平向分量分别输入计算模型共计72条,采用的远场及近场地震动伪加速度反应谱如图1所示。近断层地震动在1994年Northridge地震和1995年Kobe地震之后受到广泛关注。近场地震动与远场地震动相比具有三个主要特征:速度脉冲[16]、方向性效应[17]和竖向效应[18]。近场速度脉冲型地震动可能导致结构的大位移和大变形,与近场无脉冲及远场地震动存在显著差异。因此,本文仅研究在无脉冲型地震动作用下适用于圆形隧道损伤评价的强度指标。
应当特别指出的是,本研究中采用的是无缩放的原始地震动记录进行非线性动力时程分析,因为简单的地震动振幅缩放可能会在地震动强度指标和结构地震响应中给出错误的相关关系[19]。
2.2 有限元模型的建立
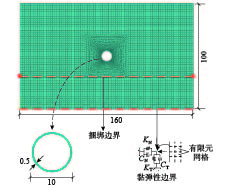
本文采用通用有限元程序ABAQUS进行圆形隧道横断面在地震动作用下动力时程分析。如图2所示,有限元模型宽160 m、高100 m。圆形隧道半径5 m,衬砌内径4.5 m,衬砌厚度0.5 m,中心位于地表以下50 m。衬砌采用混凝土塑性损伤本构,围岩采用摩尔-库仑本构,围岩和衬砌单元均采用平面应变4节点减缩积分单元(CPE4R)。本文暂不考虑围岩-结构之间的黏结、滑移和脱开,接触面采用绑定约束。根据数值模拟的精度要求,对围岩进行离散化处理,按照单元尺寸小于1/10~1/8的最小波长的要求[20],在这里取围岩单元网格尺寸为2 m。表2列出了研究中使用的混凝土和围岩材料参数。
表 2 衬砌及围岩的材料参数Table 2. Mechanical parameters of concrete and rock mass材料 本构 输入参数 数值 混凝土 塑性损伤 密度ρ/(kg/m3) 2500 弹性模量E/GPa 30 泊松比µ 0.2 剪胀角Ψ/(°) 30 偏心率η 0.1 应力比σcc/σc 1.16 拉伸屈服应力σt/MPa 1.26 压缩屈服应σco/MPa 5.82 单轴抗压强度fc/MPa 20 围岩 摩尔-库仑 密度ρ/(kg/m3) 2900 弹性模量E/GPa 7.5 泊松比µ 0.28 内摩擦角θ/(°) 45 黏聚力c/kPa 110 计算模型采用的边界条件如下:上部边界自由,底部采用黏弹性人工边界[21],黏弹性人工边界的弹簧K-阻尼C元件参数如式(1)和式(2)所示。式中,ρ为围岩土体密度;CP和CS分别为P波和S波波速;长度r 可取为近场结构几何中心到该人工边界线或面的距离。模型两侧采用捆绑边界(TDOF)[22]。其中,捆绑边界将数值模型的两个侧边界相同高度处的节点进行捆绑约束,强制侧边界上所对应点的位移相同,使得两侧边界等高度处节点在地震动作用下发生一致运动。
法向:KN=2G/r,CN=ρCP (1) 切向:KT=3G/2r,CT=ρCS (2) 本文仅考虑水平地震作用,整个分析过程分为两个步骤以便对隧道结构的地震反应进行更真实的模拟。第1步:进行地应力平衡,再现重力作用下隧道衬砌结构和围岩的初始应力场;第2步:基于文献[21, 23]的方法,对于离散化的有限元模型,将地震动转化为等效节点荷载作用于模型底部边界进行动力分析,方程如式(3)所示。式中下标R、B分别表示有限区域内的自由度和人工边界的自由度;U、
˙U 及¨U 分别表示位移、速度及加速度矢量;K、C及M分别表示刚度矩阵、阻尼矩阵及质量矩阵;C∞B 、K∞B 及fFB 分别表示黏弹性边界处的阻尼矩阵、刚度矩阵及自由场等效荷载向量。[MRRMRBMBRMBB][¨UR¨UB]+[CRRCRBCBRCBB+C∞B][˙UR˙UB]+[KRRKRBKBRKBB+K∞B][URUB]=[0K∞BUFB+C∞B˙UFB+fFB] (3) 3 结构损伤指标
结构损伤指标(damage measure, DM)是表征结构地震反应和损伤的一个参数。合理的DM取决于结构形式及其本身特性,可能需要2个或者多个DM(均由相同的非线性分析产生)来评估不同的结构反应特性、极限状态或者失效模式[24]。最大层间位移比、最大屋顶位移比和最大楼层加速度等DM常用于地上结构损伤评估。然而,对于适用于地下结构的DM尚无普遍共识。Park和Ang[25] 提出一种损伤模型,将钢筋混凝土的潜在损伤描述为最大变形和吸收滞回能量的函数。本文选择采用两个整体结构损伤指数即衬砌整体压缩损伤指数(OLDC)和衬砌整体拉伸损伤指数(OLDT)来表征衬砌损伤状态,计算公式如式(4)、式(5)所示[26]。两个整体结构损伤指数OLDC和OLDT是以能量耗散为加权函数,得到混凝土衬砌的压缩和拉伸损伤的加权平均值。在式(4)和式(5)中,Eie表示第i个单元的耗散能,
DCie和DTie分别是压缩和拉伸状态下第i个单元的损伤指数。OLDC和OLDT以标量值反映了圆形隧道横截面衬砌损伤,比较容易与标量型IM进行统计回归分析。 OLDC=∑iEei∑iEei⋅DCei (4) OLDT=∑iEei∑iEei⋅DTi (5) 4 地震动强度指标合理性的评价
在PBEE框架中描述了结构在给定地点超过给定极限状态的概率。超过给定极限状态(LS)的年超越频率(λ[LS])如式(6)所示[27]:
λ[LS]=∬ (6) 式(6)引入了两个中间变量:1)结构损伤指标(DM),例如:最大层间位移比,最大屋顶位移比等;2)地震动强度指标(IM),例如PGA、SMA等。在等式(6)中,P[LS|DM]表示在给定DM值的情况下超越极限状态的条件概率。在等式(6)中,概率地震需求模型(PSDM),P[DM|IM]表示在给定IM值的情况下超越特定结构损伤指标的条件概率。最后,λ[IM]表示超过给定IM值的平均年超越概率,通常是概率地震危险性分析计算的结果。
概率地震需求模型是一个数学表达式,它将地震动IM与结构特定DM联系起来,用来预测结构在特定地震动IM下超过结构特定DM的概率。Cornell等[28]介绍了概率地震需求模型的基本公式如下:
P\left[ {{\rm{DM}} \geqslant d|{\rm{IM}}} \right] = 1 - \varPhi \left( {\frac{{\ln(d) - \ln({S_{{\rm{DM}}}})}}{\beta }} \right) (7) 式中:结构损伤指标DM在一定地震动IM下超过特定结构损伤d的概率服从对数正态分布如式(7)所示;Φ(·)是标准正态分布函数;SDM是结构DM估计的平均值;β表示对数正态标准差。Cornell等[27]指出损伤指标DM的统计平均值SDM与地震动强度指标IM之间近似满足幂函数关系,其关系表述如式(8)所示,该关系式得到了国内外研究人员的广泛认可。
{{{S}}_{{\rm{DM}}}}{ = a}{({{{\rm{IM}}}})^b} (8) 对式(8)两边同时取自然对数,得到下式:
{\rm{ln(}}{S_{\rm{DM}}}{\rm{) = ln}}a{\rm{ + }}b{\rm{ln(}}{\rm{IM}}{\rm{)}} (9) 基于前人的研究,本文基于有效性[29]、实用性[7]、有益性[7]和充分性[30]四个判别准则研究适用于圆形隧道损伤评价的地震动强度指标。
4.1 有效性(efficiency)
有效性描述了在确定的地震动强度指标下以DM衡量结构反应的离散程度,采用一个有效的地震动强度指标来选择地震动记录能够显著地减少计算所需要的地震动记录条数及非线性动力计算次数同时获得同等置信度的分析结果。
由于ln(SDM)和ln(IM)满足一元线性回归模型,可以采用最小二乘法对计算得到的ln(di)和ln(IMi)进行线性回归分析得到式(9)中的常数lna和b,di为第i条地震动荷载作用下非线性动力时程分析得到的DM值,IMi为第i条地震动记录的IM值。有效性通过线性回归的残差标准差的大小进行评判。这里以β表示残差标准差可以通过下式进行计算:
\beta = \sqrt {\frac{{\sum {{{(\ln({d_i}) - \ln(a{\rm{I{M}}^b}))}^2}} }}{{n - 2}}} (10) 残差ε表示非线性动力计算得到DM与线性回归分析预测的DM之间的差异,残差标准差β越小表示IM指标越有效。
4.2 实用性(practicality)
实用性是指DM与IM之间是否存在直接相关关系,若某一地震动强度指标实用性不强,表明DM几乎不受该IM指标变化的影响。可以采用式(9)中的回归参数b来衡量实用性,当b值接近于零时表明该IM指标对DM的影响可以忽略,b值越大表明该IM指标实用性越强[7]。
4.3 有益性(proficiency)
为了解决基于有效性和实用性判别准则出现矛盾的情况,综合考虑有效性和实用性,提出了有益性判别准则,并将其作为选择地震动IM的主要评判准则[7]。有益性强的地震动IM具有更小的不确定性系数ζ。将式(9)代入式(7)中即可导出ζ:
P\left[ {{\rm{DM}} \geqslant d|{\rm{IM}}} \right] = 1 - \varPhi \left( {\frac{{\ln({\rm{IM}}) - \dfrac{{\ln d - \ln a}}{b}}}{{\dfrac{\beta }{b}}}} \right) (11) 经过替换后,这种形式的概率地震需求模型表达式可以推出有益性的衡量指标ζ,定义如下:
\zeta {\rm{ = }}\frac{\beta }{b} (12) 4.4 充分性(sufficiency)
充分性表示在地震动强度参数一定的情况下,结构在地震作用下的反应与地震动衰减关系中的特征参数(震级M和震中距R)具有相对独立性。在式(6)描述PBEE框架中结构在给定地点超越给定极限状态中,如果IM指标不充分,P[DM|IM]需要修改为P[DM|IM, M, R]。通过对残差ε和M、R分别进行单参数线性回归分析得到充分性,回归方程如下式所示:
{\varepsilon _{{{{\rm{IM}}}}}} = {a_{{M}}} + {b_{{M}}} \cdot M\;,\;\;\;\;{\varepsilon _{{{{\rm{IM}}}}}} = {a_{{R}}} + {b_{{R}}} \cdot R (13) 采用P值法对斜率b=0这一假设进行显著性检验来衡量充分性。P值是用来判定假设检验结果的一个参数,P值被定义为在回归分析中拒绝原假设的概率,原假设为斜率b=0。斜率b的P值越小说明IM指标越不充分,说明M、R对DM的残差ε有影响。本文采用显著性水平为5%进行假设检验[31],如果显著性水平P值大于5%时,通常认为该IM指标具有充分性。
5 分析计算结果和讨论
基于选取的72条地震动记录及建立的圆形隧道有限元模型,本节将第1节提出的20种地震动强度指标进行有效性、实用性、有益性和充分性研究,具体分析步骤如下:
1)基于整体式非线性动力时程分析方法,计算第i条地震动记录下有限元模型的DMi;
2)计算相应的第i条地震动记录的各个IMi值;
3)计算全部地震动(72条)的DM和IM值,可得到72个离散点(IMi, DMi),将其绘制在lnIM-lnDM坐标系中,进行线性回归分析,计算出斜率b值、残差ε和残差标准差β;
4)根据第3)步计算出残差ε,对残差ε和震级M和断层距R进行线性回归分析,并采用P值检验法计算出针对于斜率b=0假设的P值大小;
根据上述第3)步的结果可以计算有效性、实用性、有益性,第4)步的结果计算充分性,以下分别从有效性、实用性、有益性和充分性四个方面对所得结果进行阐述和讨论。
5.1 有效性分析
图3给出了圆形隧道结构损伤指标OLDC对四个地震动IM(ASI、SMA、drms和Ic)在对数坐标系中的线性回归图。图中对比了四个IM的有效性,同时显示出了计算数据点、线性回归方程和残差标准差。从图3可以看出,drms的离散性(β=1.18)大于ASI(β=0.79)、SMA(β=0.8)和Ic(β=0.78)。
图4给出了由线性回归分析得到的各个IM指标基于圆形隧道结构损伤指标OLDC和OLDT的残差标准差。如图4所示,对于圆形隧道结构损伤指标OLDC,各IM指标的残差标准差的范围为0.78~1.18。Ic、ASI、SMA、arms和AI在20个IM中具有最小的残差标准差,其数值分别为0.78、0.79、0.8、0.82和0.82。同时,从图4可以看出,PGD、drms和SED是有效性最差的IM指标,其残差标准差分别为1.18、1.18和1.1。另外,从图4可以看出,对于圆形隧道结构损伤指标OLDT,各IM指标的残差标准差的范围为1.47~1.95。ASI、Ic、arms和AI在表1所列举的20个IM中具有最小的残差标准差,其数值分别为1.47、1.53、1.57和1.58。PGD、drms, PGV2/PGA和SED是有效性最差的IM,其残差标准差分别为1.95、1.95、1.94和1.92。
从上述分析可以看出,综合考虑圆形隧道结构损伤指标OLDC和OLDT,ASI和Ic是最有效的IM,drms和SED是有效性最差的IM。
5.2 实用性分析
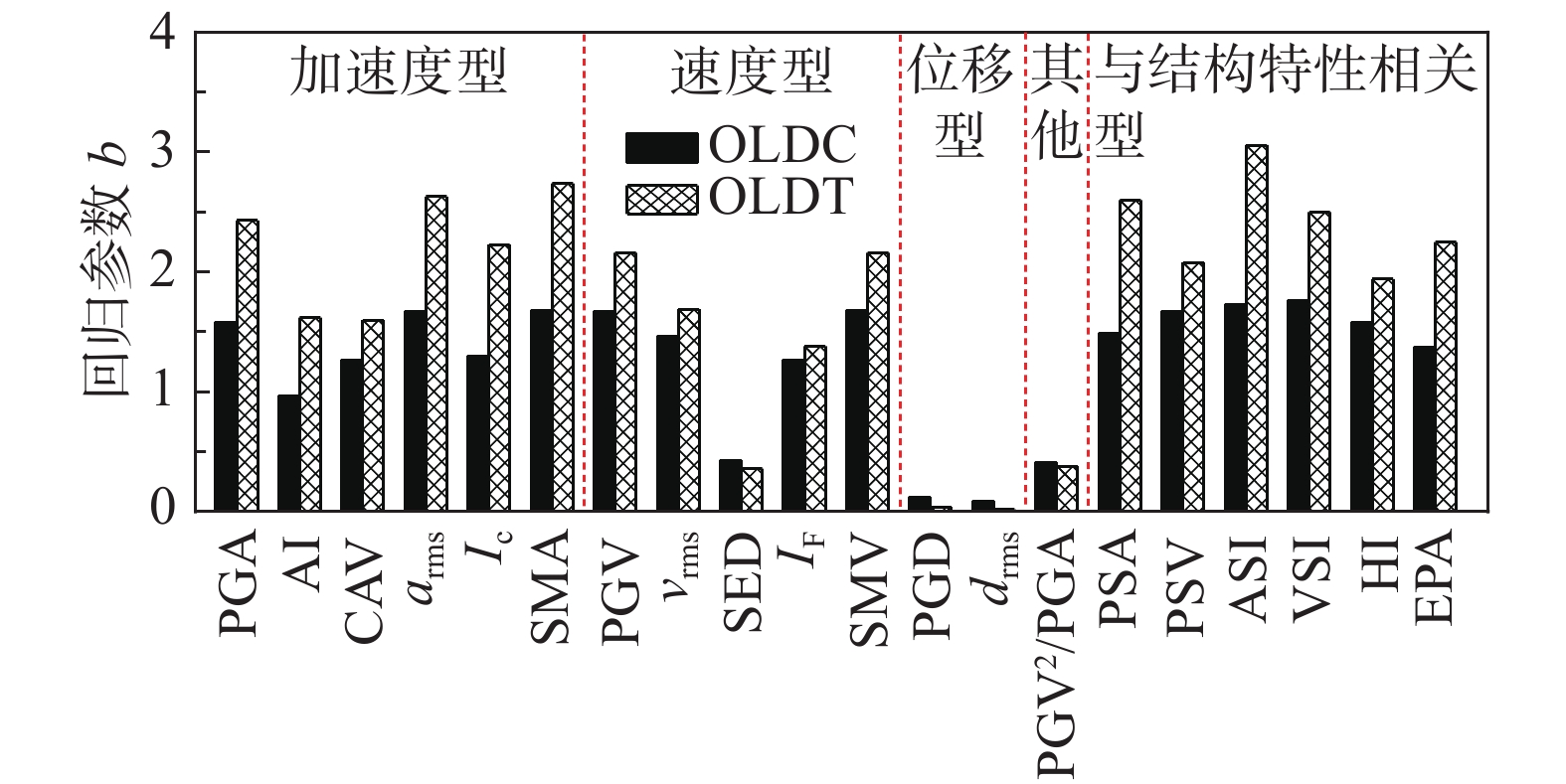
如前所述,各IM的实用性大小可以采用公式(9)中的回归参数b来衡量实用性,b值越大表明该IM指标实用性越强。各IM实用性参数b值如图5所示,从图5可以看出,对于圆形隧道结构损伤指标OLDC,VSI是最实用的IM,其次是ASI、SMA、SMV、PGV和arms,而drms是实用性最差的IM。然而,对于圆形隧道结构损伤指标OLDT,ASI是最实用性最强的IM,其次是SMA、arms和PSA;而drms是实用性最差的IM,其次是PGD。总体来看,加速度型IM和与结构特性相关型IM实用性较强,其他类型IM实用性较弱。综上所述,综合考虑结构损伤指标OLDC及OLDT,ASI是最实用IM,其次是SMA。
5.3 有益性分析
如前所述,有益性的表达式如式(12)所示。在图5可以看到地震动强度指标SED、PGD、drms和PGV2/PGA回归参数b相对较小,将会导致不确定性系数ζ出现极值,因此,这些数值将不在图中绘制。除去上述四个地震动IM,其余IM的ζ值如图6所示。从图6可以看出,对于圆形隧道结构损伤指标OLDC,ASI是有益性最强的IM,其次是SMA、VSI和arms。对于圆形隧道结构损伤指标OLDT,ASI是有益性最强的IM,其次是SMA、arms和PSA。总体来看,加速度型IM和与结构特性相关型IM有益性较强,其他类IM有益性较弱。综上所述,综合考虑结构损伤指标OLDC及OLDT,ASI是有益性最强IM,其次是SMA。
5.4 充分性分析
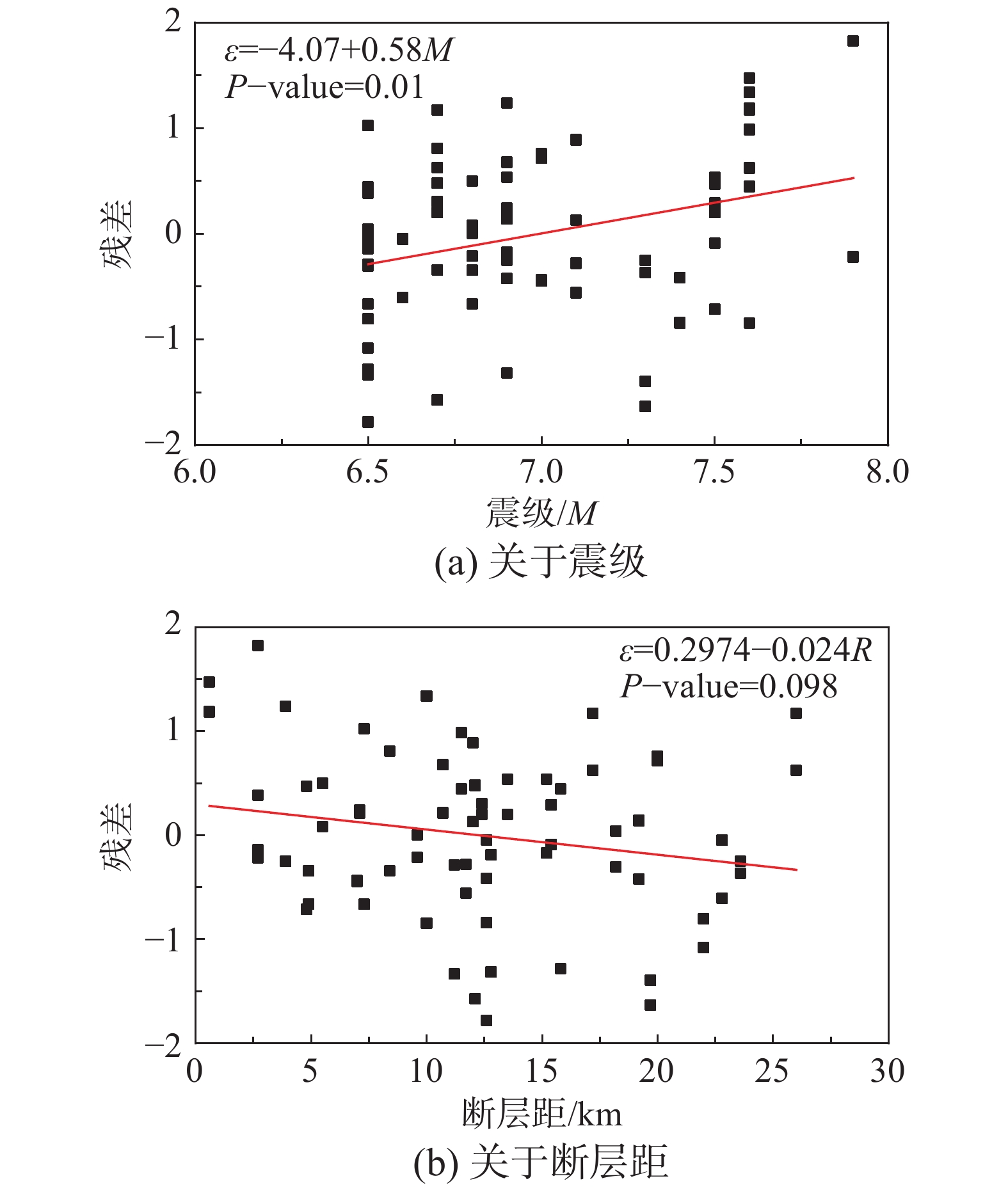
图7描述了ASI指标基于圆形隧道结构损伤指标OLDC关于震级M和断层距R的充分性。图中显示出了回归直线方程及P值。从图中可以看出,ASI指标关于震级M和断层距R的P值分别为0.01和0.098,从而可以得出ASI关于M是不充分的,而关于R是充分的。
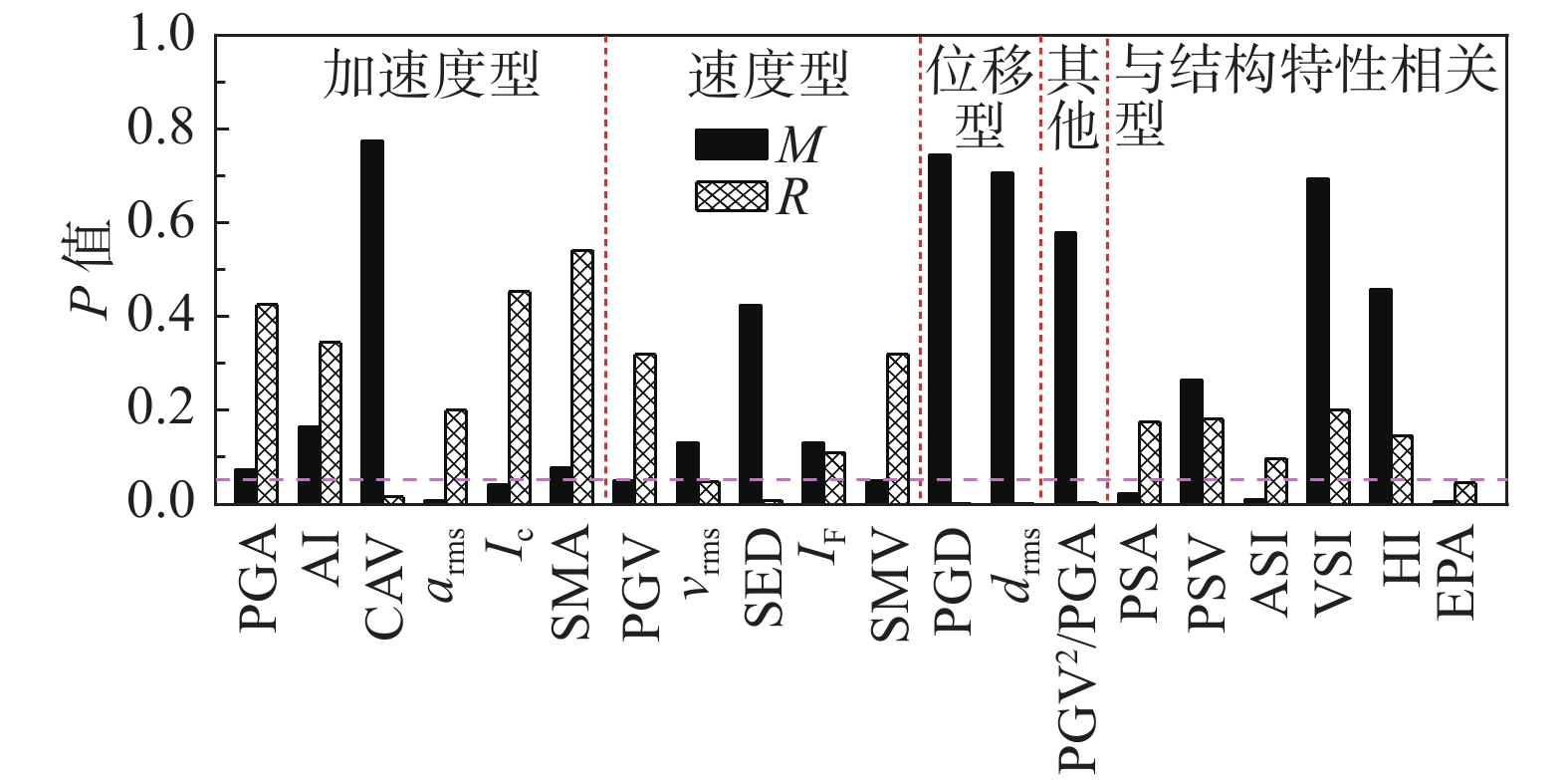
图8、图9分别给出了基于圆形隧道结构损伤指标OLDC和OLDT各IM的P值。P值等于0.05在图中用点划线绘制,如前所述,P值大于等于0.05的IM被认为是具有充分性的。图8所示,对于圆形隧道结构损伤指标OLDC,VSI是最充分的IM,其次是HI、SMA和AI,而EPA是充分性最差的IM。图9中,对于圆形隧道结构损伤指标OLDT,除了PGV和SMV,大部分IM针对于M和R都是具有充分性的,Ic是最充分的IM,其次是SMA和PGA。综上所述,综合考虑隧道结构损伤指标OLDC和OLDT,VSI、HI、SMA、AI是针对于震级M和断层距R充分性较强的地震动强度指标。
6 结论
本文基于有效性、实用性、有益性和充分性判别准则研究适用于圆形隧道损伤评价的地震动强度指标。为了进行对比分析,本文研究了20个工程中常用的地震动强度指标(例如PGA、PGV、PGD等)。基于通用有限元软件ABAQUS建立数值模型,采用FEMA P695中推荐的72条远场及近场无脉冲地震动进行计算,对地震动强度指标IM及结构损伤指标DM进行回归分析,得出以下结论:
(1)基于不同的工程需求,在上述判别准则下,采用不同的结构损伤指标DM来描述结构地震动反应会优选出不同的地震动指标IM。
(2)通常认为加速度型IM和与结构特性相关型IM只适用于地上结构,并不适用于描述地下结构地震响应。根据本文模型算例分析,基于有益性判别准则,加速度型IM和与结构特性相关型IM明显优于其他类型IM。
(3)基于有效性、充分性、有益性和实用性判别准则,在20个对比分析的IM中没有一个IM在四项判别准则中均保持最佳。然而,由于有益性判别准则综合考虑了有效性和实用性,在地震动IM优选过程中应作为首要判别准则,充分性判别标准应作为次要判别准则。因此,基于本文分析结果,综合考虑有益性和充分性判别准则,可以得出在远场及近场无脉冲地震动作用下,最适用于圆形隧道损伤评价的地震动强度指标是SMA,其次为ASI。
(4)在本文分析中,结构损伤指标仅考虑隧道结构地震响应OLDC和OLDT,后续研究中应考虑更容易被工程直观运用的结构响应量,如隧道衬砌最大弯矩、隧道直径变化率等。同时,隧道结构的地震响应与场地条件、结构埋深和结构-围岩土体柔度比等因素相关,在后续的研究中还需要针对这些因素进行相关研究以得到普适性的结论。
-
表 1 分析中采用的地震动强度指标
Table 1 Intensity measures in analyses
强度指标类型 分类型 编号 名称 定义 仅考虑地震动信息型 加速度型 1 峰值加速度 {\rm{PGA}}{ { = {\rm{max} } } }\left| {a(t)} \right| 2 Arias强度 {\rm{AI}}{\rm{ = } }\dfrac{\pi }{ {2g} }\displaystyle \int_0^{t_{\rm{tot} } } {a{ {(t)}^2} } {\rm{d} }t 3 累计绝对速度 {\rm{CAV}}{\rm{ = } }\displaystyle \int_0^{t_{\rm{tot} } } {\left| {a(t)} \right|} {\rm{d} }t 4 均方根加速度 {a_{\rm{rms}}}{\rm{ = }}\sqrt {\displaystyle \int_{{t_5}}^{{t_{95}}} {a{{(t)}^2}{\rm{d}}t{\rm{/}}{t_{\rm{d}}}} } 5 特征强度 { { {I} }_{\rm{C} } }{\rm{ = } }{a_{\rm{rms} } }^{1.5}{t_{\rm{d} } ^{0.5}} 6 持续最大加速度[15] 加速度时程中第三个最大值(SMA) 速度型 7 峰值速度 {\rm{PGV}}{ { = {\rm{max} } } }\left| {v(t)} \right| 8 均方根速度 { { {v} }_{ {\rm{rms} } } }{\rm{ = } }\sqrt {\displaystyle \int_{ {t_5} }^{ {t_{95} } } {v{ {(t)}^2}{\rm{d} }t{\rm{/} }{t_{\rm d} } } } 9 能量密度指标 {\rm{SED}}{\rm{ = } }\displaystyle \int_0^{t_{\rm{tot} } } {v{ {(t)}^2} } {\rm{d} }t 10 复合指标 { { {I} }_{\rm {F} } }{\rm{ = } }{\rm{PGV}} \times {t_{\rm{d} }^{0.25} } 11 持续最大速度[15] 速度时程中第三个最大值(SMV) 位移型 12 峰值位移 { {{\rm{PGD}} = {\rm{max} } } }\left| {d(t)} \right| 13 均方根位移 { { {d} }_{ {\rm{rms} } } }{\rm{ = } }\sqrt {\displaystyle \int_{ {t_5} }^{ {t_{95} } } {d{ {(t)}^2}{\rm{d}}t{\rm{/} }{t_{ \rm{d} } } } } 其他 14 峰值速度平方与峰值加速度比 { {{\rm{PG} }{ { {V}}} }^2}{ {{\rm{/PGA}}} } 考虑结构特性型 与反应谱单值相关 15 伪加速度谱峰值 { {{\rm{PSA}} = {\rm{max} } } }P{S_{ \rm{a} } } 16 伪速度谱峰值 { {{\rm{PSV}} = {\rm{max} } } }P{S_{\rm{v} } } 与反应谱时间段积分相关 17 加速度谱强度 { {{\rm{ASI}} = } }\displaystyle \int_{0.1}^{0.5} { { {P} }{ { {S} }_{ \rm{a} } } } {\rm{d} }T 18 速度谱强度 { {{\rm{VSI}} = } }\displaystyle \int_{0.1}^{2.5} { { { {S} }_{ \rm{v} } } } {\rm{d} }T 19 Housner强度 { {{\rm{HI}} = } }\displaystyle \int_{0.1}^{2.5} {P{S_{\rm{v} } } } {\rm{d} }T 20 有效峰值加速度 { {{\rm{EPA}} = } }{\rm{mean} }\displaystyle \int_{0.1}^{0.5} { { { {S} }_{ \rm{a} } } } {\rm{d} }T/2.5 表 2 衬砌及围岩的材料参数
Table 2 Mechanical parameters of concrete and rock mass
材料 本构 输入参数 数值 混凝土 塑性损伤 密度ρ/(kg/m3) 2500 弹性模量E/GPa 30 泊松比µ 0.2 剪胀角Ψ/(°) 30 偏心率η 0.1 应力比σcc/σc 1.16 拉伸屈服应力σt/MPa 1.26 压缩屈服应σco/MPa 5.82 单轴抗压强度fc/MPa 20 围岩 摩尔-库仑 密度ρ/(kg/m3) 2900 弹性模量E/GPa 7.5 泊松比µ 0.28 内摩擦角θ/(°) 45 黏聚力c/kPa 110 -
[1] Hamburger R, Rojahn C, Moehle J, et al. The ATC-58 project: Development of next-generation performance-based earthquake engineering design criteria for buildings [C]// 13th World Conference on Earthquake Engineering. Paper No. 1819. Vancouver, BC, Canada: Canadian Association for Earthquake Engineering, 2004.
[2] 吕大刚, 刘洋, 于晓辉. 第二代基于性能地震工程中的地震易损性模型及正逆概率风险分析[J]. 工程力学, 2019, 36(9): 1 − 11. Lv Dagang, Liu Yang, Yu Xiaohui. Seismic fragility models and forward-backward probabilistic risk analysis in second-generation performance-based earthquake engineering [J]. Engineering Mechanics, 2019, 36(9): 1 − 11. (in Chinese)
[3] Riddell R. On ground motion intensity indices [J]. Earthquake Spectra, 2007, 23(1): 147 − 173. doi: 10.1193/1.2424748
[4] 叶列平, 马千里, 缪志尾. 结构抗震分析用地震动强度参数的研究[J]. 地震工程与工程振动, 2009, 29(4): 9 − 22. Ye Lieping, Ma Qianli, Miao Zhiwei. Study on earthquake intensities for seismic analysis of structures [J]. Journal of Earthquake Engineering and Engineering Virbration, 2009, 29(4): 9 − 22. (in Chinese)
[5] 张艺欣, 郑山锁, 秦卿, 等. 适用于高层RC结构的谱加速度指标分析[J]. 工程力学, 2017, 34(10): 149 − 157. Zhang Yixin, Zheng Shansuo, Qin Qing, et al. Analysis spectra acceleration as an intensity measure adapted to RC high-rise buildings [J]. Engineering Mechanics, 2017, 34(10): 149 − 157. (in Chinese)
[6] Zhong J, Jeon J S, Shao Y H, Chen L C. Optimal intensity measures in probabilistic seismic demand models of cable-stayed bridges subjected to pulse-like ground motions [J]. Journal of Bridge Engineering, 2019, 24(2): 1 − 17.
[7] Padgett J E, Nielson B G, DesRoches R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios [J]. Earthquake Engineering and Structural Dynamics, 2008, 37: 711 − 725. doi: 10.1002/eqe.782
[8] Kostinakis K, Athanatopoulou A, Morfidis K. Correlation between ground motion intensity measures and seismic damage of 3D R/C buildings [J]. Engineering Structures, 2015, 82: 151 − 167. doi: 10.1016/j.engstruct.2014.10.035
[9] Elenas A. Correlation between seismic acceleration parameters and overall structural damage indices of buildings [J]. Soil Dynamics Earthquake Engineering, 2000, 20: 93 − 100. doi: 10.1016/S0267-7261(00)00041-5
[10] 卢啸, 陆新征, 叶列平. 超高层建筑地震动强度指标探讨[J]. 土木工程学报, 2012, 45(增刊 1): 292 − 296. Lu Xiao, Lu Xinzheng, Ye Lieping. Discussion on the ground motion intensity measures for super high-rise buildings [J]. China Civil Engineering Journal, 2012, 45(Suppl 1): 292 − 296. (in Chinese)
[11] 邱意坤, 周长东, 张光伟. 三维地震动作用下适用于高耸结构的地震动强度指标[J]. 工程力学, 2020, 37(3): 98 − 107. Qiu Yikun, Zhou Changdong, Zhang Guangwei. An earthquake intensity measure for high-rise structures under three-dimensional earthquake ground motions [J]. Engineering Mechanics, 2020, 37(3): 98 − 107. (in Chinese)
[12] Hariri-Ardebili M A, Saouma V E. Probabilistic seismic demand model and optimal intensity measure for concrete dams [J]. Structural Safety, 2016, 59: 67 − 85. doi: 10.1016/j.strusafe.2015.12.001
[13] Bakalis K, Kohrangi M, Vamvatsikos D. Seismic intensity measures for above-ground liquid storage tanks [J]. Earthquake Engineering and Structural Dynamics, 2018, 47: 1844 − 1863. doi: 10.1002/eqe.3043
[14] FEMA P695. Quantification of building seismic performance factors [R]. Federal Emergency Management Agency, Washington, D.C, 2009.
[15] Kramer S L. Geotechnical earthquake engineering [M]. Washington: Prentice-hall, 1996.
[16] Hall J F, Heaton T H, Halling M W, et al. Near-source ground motion and its effects on flexible buildings [J]. Earthquake Spectra, 1995, 11(4): 569 − 605. doi: 10.1193/1.1585828
[17] 胡进军. 近断层地震动方向性效应及超剪切破裂研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2009. Hu Jinjun. Directivity effect of near-fault ground motion and super-shear rupture [D]. Harbin: Institute of Engineering Mechanics China Earthquake Administration, 2009. (in Chinese)
[18] Li H, Yi W J, Yuan X X. Fuzzy-valued intensity measures for near-fault pulse-like ground motion[J]. Comput-Aided Civil and Infrastruct Engineering , 2013, 28: 780-795.
[19] Davalos H, Miranda E. Evaluation of bias on the probability of collapse from amplitude scaling using spectral-shape-matched records [J]. Earthquake Engineering and Structural Dynamics, 2019, 48: 970 − 986.
[20] Ma C, Lu D C, Du X L. Seismic performance upgrading for underground structures by introducing sliding isolation bearings [J]. Tunnelling and Underground Space Technology, 2018, 74: 1 − 9. doi: 10.1016/j.tust.2018.01.007
[21] Zhao M, Gao Z D, Wang L T, et al. Obliquely incident earthquake input for soil-structure interaction in layered half space [J]. Earthquakes and Structures, 2017, 13(6): 573 − 588.
[22] Zienkiewicz O C , Bicanic N, Shen F Q. Earthquake Input Definition and the Trasmitting Boundary Conditions [M]. Vienna: International Centre for Mechanical Sciences (Courses and Lectures), 1989.
[23] 刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报, 1998, 31(3): 55 − 64. Liu Jingbo, Lü Yandong. A direct method for analysis of dynamic soil-structure interaction [J]. China Civil Engineering Journal, 1998, 31(3): 55 − 64. (in Chinese)
[24] Vamvatsikos D, Cornell C A. Incremental dynamic analysis [J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491 − 514. doi: 10.1002/eqe.141
[25] Park Y J, Ang A H S. Mechanistic seismic damage model for reinforced concrete [J]. Journal of Structural Engineering, 1985, 111: 722 − 739. doi: 10.1061/(ASCE)0733-9445(1985)111:4(722)
[26] Chen Z Y, Wei J S. Correlation between ground motion parameters and lining damage indices for mountain tunnels [J]. Natural Hazards, 2012, 65: 1683 − 1702.
[27] Cornell C A, Krawinkler H. Progress and challenges in seismic performance assessment [R]. PEER Center News, 2000, 3: 1 − 3.
[28] Cornell C A, Jalayer F, Hamburger R O, Fouth DA. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines [J]. Journal of Structural Engineering, 2002, 128(4): 526 − 533. doi: 10.1061/(ASCE)0733-9445(2002)128:4(526)
[29] Shome N, Cornell C A. Probabilistic seismic demand analysis of nonlinear structures [D]. California: Stanford University, 1999.
[30] Luco N, Cornell C A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions [J]. Earthquake Spectra, 2007, 23: 357 − 392. doi: 10.1193/1.2723158
[31] 贾俊平, 何晓群, 金勇进. 统计学[M]. 北京: 中国人民大学出版社, 2015. Jia Junping, He Xiaoqun, Jin Yongjin. Statistics [M]. Beijing: Renmin University of China Press, 2015. (in Chinese)
-
期刊类型引用(12)
1. 汪亦显,薛鹏徽,郑俊,柴金飞,陈天艳,邓能伟,欧可,郭盼盼. 高渗透压岩体力学研究进展及其跨海工程应用. 交通科学与工程. 2025(01): 1-19 .  百度学术
百度学术
2. 王述红,侯钦宽,雍睿,钟祯. 结构面抗剪强度各向异性研究中试样获取方法有效性分析. 工程力学. 2023(01): 168-179 .  本站查看
本站查看
3. 何忱,姚池,姜清辉,周创兵. 基于改进刚体弹簧方法的岩石破坏过程三维模拟. 岩石力学与工程学报. 2023(01): 183-193 .  百度学术
百度学术
4. 刘伟吉,阳飞龙,董洪铎,程润,祝效华. 异形PDC齿混合切削破碎花岗岩特性研究. 工程力学. 2023(03): 245-256 .  本站查看
本站查看
5. 谭文辉,刘慧敏,梁爽,张亚飞,王培涛. 节理岩体的等效“层理”方法及其工程应用. 矿业研究与开发. 2023(04): 116-124 .  百度学术
百度学术
6. 鲁旭荣,邓爽,吴占廷. 基于巴顿强度准则的某露天矿边坡岩体结构面抗剪强度研究. 科学技术创新. 2023(23): 169-173 .  百度学术
百度学术
7. 刘伟吉,向畅,谭宾,祝效华,胡海,李枝林. 局部高温诱导致裂非均质花岗岩机理研究. 工程力学. 2023(10): 222-236 .  本站查看
本站查看
8. 李国枭,王航龙,彭俊,王林飞,代碧波. 基于Hoek-Brown准则的层理岩石强度模型研究. 岩土力学. 2023(12): 3541-3550 .  百度学术
百度学术
9. 刘伟吉,王燕飞,郭天阳,罗云旭,祝效华. 单齿切削破碎非均质花岗岩微宏观机理研究. 工程力学. 2022(06): 122-133 .  本站查看
本站查看
10. 夏晨,戚承志,利学,周卓群. 裂纹面动摩擦作用对脆性材料动力破坏的影响. 工程力学. 2022(12): 50-59 .  本站查看
本站查看
11. 赖新河,赖宏伟,卢玉丽. X型裂隙破裂试验及数值模拟研究. 水利科技与经济. 2020(03): 13-17 .  百度学术
百度学术
12. 姬晨濛,戚承志. Ⅱ型Ⅲ型动态裂纹尖端断裂过程区近似评估方法. 工程力学. 2020(07): 223-229 .  本站查看
本站查看
其他类型引用(13)



 下载:
下载: