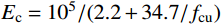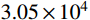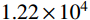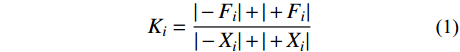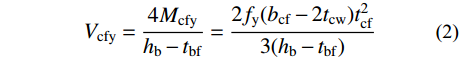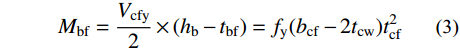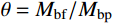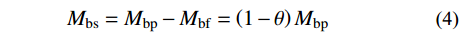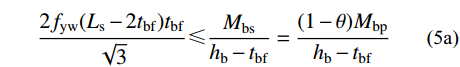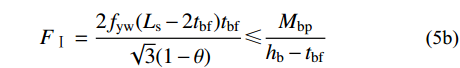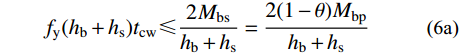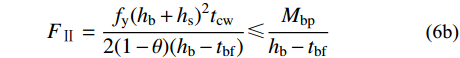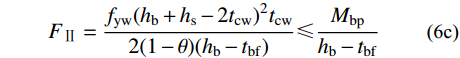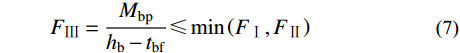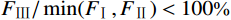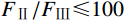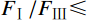EXPERIMENTAL RESEARCH ON SEISMIC PERFORMANCE OF WCFT COLUMN-STEEL BEAM JOINTS
-
摘要: 提出了壁式钢管混凝土(WCFT)柱与钢梁连接的侧板式节点。为研究其抗震性能,设计了3个侧板式节点足尺试件进行拟静力试验,分析试件的破坏形态、滞回曲线、骨架曲线、延性、耗能能力、刚度退化和节点域应变。试验结果表明:3个节点试件的节点域均处于弹性阶段,满足侧板水平及竖向强度比的侧板式节点试件破坏形态为梁端塑性铰破坏,发生梁端塑性铰破坏的节点试件具有较好的变形和耗能能力;侧板水平或竖向强度比不足100%的侧板式节点试件呈现脆性破坏特征。在试验研究的基础上,结合梁端内力传导机制提出了侧板式节点在节点域外的三种破坏模式及相应判别公式,与试验结果基本吻合,从而为工程设计提供参考。Abstract: Side-plate joints for walled concrete-filled steel tubular column and steel beam are proposed. In order to study the seismic performance of the joint, the quasi-static tests of three full-size side-plate joint specimens were carried out. The failure pattern, hysteretic curve, skeleton curve, ductility, energy dissipation capacity, stiffness degradation and strain of the joint panel were analyzed. The results are as follows. The joint panels of three specimens remain elastic; the plastic hinge failure occurs at the beam end of side-plate joint specimens meeting the horizontal and vertical strength ratio requirements; the joint specimens with plastic hinge occurring at beam ends have good deformation performance and energy dissipation capacity, while the side-plate joints whose horizontal or vertical strength ratios are less than 100% undergo brittle failure. Based on the experimental study and the internal force transmission mechanism at beam ends, three failure modes of side-plate joint outside the joint panel and corresponding discriminant formulas were put forward, which were basically consistent with the experimental results and could be used as reference for engineering design.
-
钢管混凝土柱具有承载力和刚度大、经济性优、便于施工等特性,在冶金、电力及建筑诸多行业获得广泛运用[1-2]。在钢管混凝土柱和钢梁连接节点形式中,内隔板式连接节点[3-5]、隔板贯通式连接节点[6-7]和外加强环板式连接节点[8-9]具有较好的经济性和抗震性能。《钢管混凝土结构技术规范》[10]和《矩形钢管混凝土结构技术规程》[11]将隔板式及外加强环板式连接节点作为钢管混凝土柱与钢梁的推荐连接形式。
虽然钢管混凝土柱经济性和抗震性能较好,但在工程运用时通常会凸出建筑墙体并影响建筑功能。为解决在室内凸出柱的问题,西安建筑科技大学郝际平等[12-16]提出在多高层钢结构建筑中,运用大高宽比壁式钢管混凝土柱(walled concrete-filled steel tubular column,WCFT column),下文简称WCFT柱。图1所示为典型WCFT柱截面形式。WCFT柱截面宽度较小,WCFT柱-钢梁节点采用隔板式连接不利于内部混凝土浇灌,且内隔板加工复杂容易出现焊接损伤缺陷[17],而外环板式节点局部环板突出墙面会影响建筑美观和装修布置。
针对WCFT柱-钢梁连接节点存在的问题,本文作者提出了适用于WCFT柱与钢梁连接的侧板式节点,进行了一组WCFT柱强轴方向与钢梁侧板式节点足尺试件的双向等幅低周往复加载试验,研究节点的破坏形态、滞回性能、耗能能力和延性性能等,旨在为WCFT柱-钢梁侧板式节点在实际工程中的设计和运用提供参考。
1 WCFT柱-钢梁节点设计
结合重庆市某装配式钢结构住宅项目,本文选取框架结构的中柱节点作为研究对象。依据《钢结构设计标准》[18]和《建筑抗震设计规范》[19],在满足“强柱弱梁”的设计要求下,确定钢梁和WCFT柱截面以及加工制作足尺试件。试件为典型的平面十字型节点,假定柱反弯点位置位于半层处,梁反弯点位置位于跨中,梁柱长度尺寸均取至反弯点处。
侧板式节点构成如图2所示:钢梁翼缘高度上下一定范围内,WCFT柱腹板方向设置内嵌式侧板,侧板沿钢梁长度方向外伸形成悬臂段,钢梁翼缘侧面与侧板外伸悬臂段焊接,钢梁翼缘正面与WCFT柱翼缘壁焊接,钢梁腹板和WCFT柱翼缘壁焊接。
2 试验概况
2.1 试件设计
本文共制作3个十字型侧板式节点足尺试件。试件柱子长度2.6 m,柱顶至底座销轴中心点距离2.9 m,外部钢管采用5块钢板拼装成双腔矩形截面,截面尺寸550 mm×180 mm×8 mm;节点每侧钢梁长度1.6 m,采用焊接H形钢截面H400 mm×180 mm×8 mm×14 mm,节点区柱截面尺寸及侧板外伸尺寸列于表1;钢材材料均为Q235B;WCFT柱内填充C25级商品细石混凝土,施工时由柱顶预留孔灌入。
表 1 试件主要尺寸Table 1. Main dimensions of specimens试件编号 节点区柱/mm 侧板外伸尺寸/mm JD-1 550×180×12×12 −300×500×12 JD-2 550×180×12×12 −300×500×12 JD-3 550×180×12×12 −240×500×12 注: JD-1节点区柱腹板和外伸侧板为完整板件;JD-2节点区柱翼缘外伸,柱腹板与外伸侧板断开,采用坡口焊与柱翼缘焊接。 结合试验室装置条件,按照轴压比为0.3计算柱顶竖向荷载,加载过程中通过稳压装置保持竖向荷载恒定,试件加载装置和测点布置图如图3和图4所示。试件轴压比采用试验轴压比
n=N/ (fcmAc+fymAs) ,N为施加在钢管混凝土柱顶的恒定竖向荷载,fcm为混凝土轴心抗压强度试验平均值,fym为钢材屈服强度试验平均值,Ac为截面混凝土面积,As为截面钢材面积。2.2 材性试验
试件不同钢板按《金属材料 拉伸试验 第1部分:室温试验方法》[20]的规定进行材性试验,试验主要结果平均值列于表2。根据《普通混凝土力学性能试验方法标准》[21]规定,在试件浇筑时制作150 mm立方体标准试块,与试件相同条件下养护28 d测得混凝土立方体抗压强度平均值32.25 MPa,弹性模量按《混凝土结构设计规范》[22]规定的公式
Ec=105/(2.2+34.7/fcu) 确定,Ec取3.05×104 MPa,剪切模量Gc按0.4Ec为1.22×104 MPa。表 2 钢材材性主要试验结果Table 2. Main steel properties板件规格 fy/MPa fu/MPa δ/(%) E/MPa fu/fy 钢柱(8 mm) 371.67 520.00 24.97 188667 1.40 钢柱(12 mm) 375.00 493.33 30.59 217000 1.32 钢梁翼缘 383.33 535.00 30.18 210667 1.40 钢梁腹板 380.40 513.70 24.67 175700 1.35 注:fy为屈服强度;fu为极限强度;δ为伸长率;E为弹性模量。 2.3 加载制度
在试件加载过程中首先在柱顶施加预定竖向荷载,然后在柱顶施加低周水平往复荷载。柱顶水平加载方式采用荷载-位移混合法[23],试验加载前利用有限元分析软件ABAQUS预测各个试件的屈服荷载,加载时试件到达屈服荷载前采用荷载控制,屈服后采用位移控制。荷载控制阶段各级荷载往复1次,位移控制阶段各级位移往复3次,直至试件破坏,试件加载制度如图5所示。
3 试验现象及破坏形态
3.1 试件现象
JD-1达到36 mm往复荷载时,应变数据采集箱显示钢梁翼缘较多点位均已达到屈服应变,荷载-位移曲线亦出现了轻微拐点,表明试件此时进入塑性,开始位移加载。在2.5δy(90 mm)循环过程中,东侧梁端腹板出现轻微变形和鼓曲;在3.5δy循环过程中,东侧侧板外的钢梁上下翼缘均出现屈曲,且腹板鼓曲发展明显;在4δy(144 mm)循环过程的第1圈,柱两侧钢梁翼缘腹板均出现明显屈曲,承载力下降至极限承载力的80%以下,停止试验,破坏形态如图6所示。
JD-2在弹性加载阶段,未出现明显现象。在加载达到40 mm循环过程时,荷载-位移曲线出现了轻微拐点,且部分钢梁翼缘应变片数据已到达屈服应变值,由此判定试件进入塑性状态。在塑性加载阶段,按照0.5倍的屈服位移δy加载即每级增加20 mm。在1.5δy(60 mm)循环过程中,第1圈拉至60 mm时钢梁翼缘和腹板均无明显现象,但西南角钢梁下翼缘与柱连接处焊缝开裂;第2圈推至60 mm时东南角柱壁与侧板连接处下侧焊缝开裂,且裂缝迅速开展,开裂长度达到15 cm,停止试验,破坏形态如图7所示。
当JD-3达到屈服荷载时,进入36 mm的循环过程。在塑性加载阶段,按照0.5倍屈服位移δy加载即每级增加18 mm。在1.5δy(54 mm)循环过程中,柱和侧板均无现象出现,但西北角梁上翼缘、东南角梁下翼缘与侧板连接处焊缝开裂,并迅速开展,且柱顶水平荷载无法继续维持,试验停止,破坏形态如图8所示。
在三个试件停止加载后,将核心区柱腹板和柱翼缘板切开,发现所有试件的核心区混凝土完整性均很好,表面没有形成肉眼可见的水平或斜向裂纹,如图9所示。
3.2 破坏形态
JD-1在试验过程中,侧板外钢梁腹板首先发生了微鼓曲,随后钢梁上、下翼缘发生屈曲,随着位移加载钢梁的塑性变形和屈曲不断发展,形成了塑性铰。梁端由于侧板的存在,将塑性铰位置由核心区外移,有效的保护了节点核心区,最后在距柱翼缘边约0.8倍~1.0倍梁高区域形成了塑性铰,导致试件承载能力降低。WCFT柱没有发生明显的局部鼓曲和塑性变形,且节点域混凝土没有出现可见损伤,节点域柱腹板也未发生破坏。表明侧板式节点JD-1满足强节点抗震构造要求[19]。
相比JD-1,JD-2节点核心区柱翼缘板外伸,柱腹板与外伸侧板在柱翼缘位置断开,分别采用坡口焊与柱翼缘板焊接。JD-2在弹性阶段没有出现明显现象,进入1.5倍屈服位移循环加载过程后,外伸侧板与柱翼缘板间的焊缝开裂,且裂缝迅速开展,JD-2节点随后失去承载力。JD-1和JD-3节点核心区柱腹板和外伸侧板加工为完整板件,两者区别在于JD-3侧板外伸段长度为JD-1长度的80%。JD-3在弹性阶段没有出现明显现象,进入1.5倍屈服位移循环加载过程后,梁端受拉翼缘与侧板外伸段之间的焊缝开裂,且裂缝迅速开展,柱顶水平荷载无法继续维持,JD-3发生破坏。
侧板受柱壁板和梁翼缘的边界约束较强,三个试件侧板均未发生剪切屈曲。钢梁上、下翼缘传递给侧板的轴力形成力偶,使侧板承受一定的弯矩。结合试验现象可知,JD-1的破坏形态为侧板外梁端塑性铰破坏,JD-2为柱翼缘板位置的侧板竖向受弯破坏,JD-3为侧板外伸部分与梁翼缘之间的水平焊缝受拉破坏。
4 试验结果及分析
4.1 滞回曲线
滞回曲线可反应结构抗震性能各项指标,通过对往复荷载作用下柱顶位移及荷载的监测,得到图10所示的荷载-位移滞回曲线。根据图10可得:
1) 各试件在进入屈服之前,滞回环面积很小,曲线形状均为尖梭形。JD-1在屈服后,随着塑性变形的增大,滞回环面积不断增大;峰值荷载之后,滞回环面积增大幅度较为平稳,钢梁端部逐渐进入塑性,节点刚度不断减小,滞回环较为饱满,且无明显的捏缩现象,曲线表现为梭形。
2) 与JD-1相比,JD-2柱腹板和外伸侧板与外伸柱翼缘板焊接,JD-3侧板外伸段长度为JD-1的80%。JD-2和JD-3弹性阶段滞回曲线形状与JD-1相似,三个试件均呈现尖梭形。所有试件在弹性阶段均出现捏缩,这是由于在梁端与链杆的销轴连接节点中,孔径比销轴直径略大,导致滞回曲线在位移零点出现微小滑移。JD-2和JD-3在进入屈服位移加载的第一级循环出现焊缝开裂,且焊缝快速开展,试件无法继续承载,导致滞回曲线中断。
4.2 骨架曲线
试件柱顶水平荷载-位移骨架曲线如图11所示,用“通用弯矩屈服法”确定屈服荷载Py和屈服位移Δy[23],骨架曲线荷载下降至85%峰值荷载Pp时对应位移为极限位移Δu[24]。定义层间位移角θu为柱顶水平极限位移Δu与柱有效高度的比值。试件得到的推、拉两个方向荷载差异值较小,本文确定特征点处位移和荷载取平均值。三个试件特征点处位移、荷载及层间位移角详见表3。
1) 所有节点试件的骨架曲线前期基本上呈一阶线性增长,且该阶段3个试件节点骨架曲线斜率非常接近。这表明三个侧板式节点试件初始刚度基本一致;与JD-1和JD-3相比,JD-2节点核心区柱翼缘板外伸,柱腹板与外伸侧板在柱翼缘位置断开,外伸侧板通过坡口焊与柱翼缘板焊接,JD-3侧板外伸段长度为JD-1长度的80%,说明侧板外伸长度和侧板与柱腹板的连接方式对侧板式节点初始刚度影响均较小。
2) JD-2和JD-3峰值荷载均大于JD-1的屈服荷载,分别为JD-1峰值荷载的91.3%和96.4%。这表明JD-2和JD-3亦进入了节点的屈服阶段,但未有效发挥钢材的应变硬化潜能。
表 3 主要试验结果Table 3. Main test results试件编号 Py/kN Δy/mm Pp/kN Δu/mm θu JD-1 369.10 44.02 452.60 132.73 1/22 JD-2 − − 413.19 59.71 1/49 JD-3 − − 391.05 53.67 1/54 注:JD-2和JD-3进入塑性后不久发生破坏,无法根据“通用弯矩屈服法”确定屈服荷载,峰值荷载Pp、极限位移Δu和层间位移角θu取其骨架曲线终点数据。 4.3 变形能力和耗能分析
文献[19]规定:对多层、高层钢结构弹塑性层间位移角限值为1/50,由表3中数据可知,JD-1极限位移对应的层间位移角为1/22,超过规定限值的2倍。JD-2和JD-3极限层间位移角分别为1/49和1/54,亦与弹塑性位移角限值接近。
节点延性亦是体现其变形能力的重要指标,JD-2和JD-3在进入塑性阶段不久就发生破坏,试件丧失继续承载的能力,呈现脆性破坏的特征。根据表3数据计算得到,JD-1位移延性系数为3.02,说明合理设计的侧板式节点试件延性较好。
本文采用等效粘滞阻尼系数he来评价节点试件耗能能力的优劣[24]。图12为JD-1的等效粘滞阻尼系数曲线,可以看出,随着循环加载等级的提升,he逐渐增大,说明滞回环在循环位移加载下面积逐渐增大,破坏时JD-1的he为0.47,说明该节点试件具有较强的耗能能力。
4.4 刚度退化
为了进一步研究荷载-位移曲线变化规律,本文选用峰值刚度Ki来判断结构在累计损伤的影响下刚度退化情况,其计算方法见式(1)。节点试件各循环级的峰值刚度退化曲线如图13所示,横轴为各循环加载级的位移,纵轴为Ki/K0,其中K0为试件初始刚度。从图中可以看出,JD-1的刚度退化比较均匀且平缓,没有明显的刚度陡降,由此可以说明JD-1的耗能能力较为稳定。
Ki=|−Fi|+|+Fi||−Xi|+|+Xi| (1) 式中:Ki为第i个循环的刚度值;+Fi为第i个循环正峰值点荷载值;-Fi为第i个循环反峰值点荷载值;+Xi为第i个循环正峰值点位移值;-Xi为第i次个循环反峰值点位移值。
4.5 节点域应变分析
为了分析试件节点域的应力分布情况,提取JD-1柱腹板中心点的应变,如图14所示,JD-2和JD-3应变与JD-1前期基本相似。JD-1最大应变值为1.3×10−3,应变测量结果未达到钢材塑性应变值。结合图9显示的试件核心区混凝土最终状态,表明所有试件在达到峰值荷载时,节点域仍处于弹性阶段,未发生破坏,满足“强节点弱构件”的抗震构造要求。
5 节点受力机理
5.1 节点破坏模式分析
侧板式节点梁端翼缘力偶通过2种路径传递给节点核心区:第一种是经侧板外伸段与钢梁翼缘焊缝,传递至节点核心区柱腹板侧;第二种是通过梁端翼缘与柱翼缘的焊缝,传递至节点核心区柱翼缘侧。因此,除节点域剪切破坏外,侧板式节点存在以下3种破坏模式:Ⅰ) 侧板外梁端塑性铰破坏;Ⅱ) 柱翼缘板位置侧板竖向受弯破坏;Ⅲ) 侧板外伸部分与梁翼缘之间的水平焊缝受拉破坏。
图15所示为侧板式节点的梁端内力图,其中Mbp为梁全截面塑性弯矩,Ls为侧板外伸长度,hb为钢梁高度,hs为超出梁上翼缘部分的侧板高度。根据虚功原理,柱翼缘侧屈服时其承担的剪力值Vcfy为:
Vcfy=4Mcfyhb−tbf=2fy(bcf−2tcw)t2cf3(hb−tbf) (2) 式中:Mcfy为节点核心区柱翼缘侧屈服弯矩;fy为钢材屈服强度;tbf为钢梁翼缘厚度;bcf为柱翼缘侧截面宽度;tcw为柱腹板侧厚度;tcf为柱翼缘侧厚度。
单侧钢梁由翼缘部分传递的梁端弯矩值Mbf为:
Mbf=Vcfy2×(hb−tbf)=fy(bcf−2tcw)t2cf (3) 当钢梁端部弯矩到达全截面塑性弯矩Mbp时,令柱翼缘部分承担的弯矩比例
θ=Mbf/Mbp ,由侧板部分传递的梁端弯矩Mbs为:Mbs=Mbp−Mbf=(1−θ)Mbp (4) 侧板水平焊缝强度验算:
2fyw(Ls−2tbf)tbf√3⩽ \tag{5b}{F_{\text{Ⅰ}}} = \frac{{2{f_{\rm{yw}}}({L_{\rm{s}}} - 2{t_{\rm{bf}}}){t_{\rm{bf}}}}}{{\sqrt 3 ( {1 - \theta } )}} \leqslant \frac{{{M_{\rm{bp}}}}}{{{h_{\rm{b}}} - {t_{\rm{bf}}}}}\quad\quad\quad 侧板竖向受弯强度验算:
\tag{6a}{f_{\rm{y}}}( {{h_{\rm{b}}} + {h_{\rm{s}}}} ){t_{\rm{cw}}} \leqslant \frac{{2{M_{\rm{bs}}}}}{{{h_{\rm{b}}} + {h_{\rm{s}}}}} = \frac{{2( {1 - \theta } ){M_{\rm{bp}}}}}{{{h_{\rm{b}}} + {h_{\rm{s}}}}}\;\;\; \tag{6b}{F_{{\text{Ⅱ}}}} = \frac{{{f_{\rm{y}}}{{( {{h_{\rm{b}}} + {h_{\rm{s}}}} )}^2}{t_{\rm{cw}}}}}{{2( {1 - \theta } )( {{h_{\rm{b}}} - {t_{\rm{bf}}}} )}} \leqslant \frac{{{M_{\rm{bp}}}}}{{{h_{\rm{b}}} - {t_{\rm{bf}}}}}\quad\quad\;\; \tag{6c}{F_{{\text{Ⅱ}}}} = \frac{{{f_{\rm{yw}}}{{( {{h_{\rm{b}}} + {h_{\rm{s}}} - 2{t_{\rm{cw}}}} )}^2}{t_{\rm{cw}}}}}{{2( {1 - \theta } )( {{h_{\rm{b}}} - {t_{\rm{bf}}}} )}} \leqslant \frac{{{M_{\rm{bp}}}}}{{{h_{\rm{b}}} - {t_{\rm{bf}}}}} 钢梁翼缘强度:
{F_{{\text{Ⅲ}}}} = \frac{{{M_{\rm{bp}}}}}{{{h_{\rm{b}}} - {t_{\rm{bf}}}}} \leqslant \min \left( {{F_{\text{Ⅰ}}},{F_{\text{Ⅱ}}}} \right)\qquad\qquad\quad 式中:Ls为超出柱翼缘部分的侧板外伸长度,考虑焊缝起落弧缺陷,计算焊缝长度时扣除2倍焊件厚度;bbf为钢梁翼缘宽度;fyw为对接焊缝抗拉强度;式(6b)适用于核心区柱腹板和外伸侧板加工为完整板件的节点形式;式(6c)适用于核心区柱腹板与外伸侧板在柱翼缘位置断开,采用坡口焊与柱翼缘板焊接的节点形式。
当
{F_{{\text{Ⅲ}}}}/\min ({F_{\!\!\text{Ⅰ}}},{F_{{\text{Ⅱ}}}}) < 100\text{%} 时,侧板外梁端受弯破坏或发生屈曲,出现模式Ⅰ的破坏形态;当{F_{{\text{Ⅱ}}}}/{F_{{\text{Ⅲ}}}} \leqslant 100 %时,柱翼缘板位置的侧板竖向受弯强度不足,出现模式Ⅱ的破坏形态;当{F_{\!\!\text{Ⅰ}}}/{F_{{\text{Ⅲ}}}} \leqslant 100\text{%} 时,侧板外伸部分的水平焊缝强度不足,出现模式Ⅲ的破坏形态。5.2 试验对比分析
结合5.1节理论分析,可得到JD-1~JD-3试件的强度比及预测破坏模式列于表4。对比三个试件的试验现象,表4中的预测破坏模式与试验吻合较好。此外,当钢梁端部弯矩到达全截面塑性弯矩Mbp时,根据理论计算得到三个试件的理论柱顶极限承载力为457.42 kN,表5中给出的是三个节点试件试验的最大承载力,JD-1试验的极限承载力与理论值非常接近。此外,结合表4和表5还可以发现,表4中理论计算的强度比值与JD-1~JD-3试验得到的承载力比值亦吻合较好。
表 4 试件强度比及预测破坏模式Table 4. Strength ratios of specimens and expected failure mode试件编号 {F_{\simfont\text{Ⅰ}} }/{F_{ {\simfont\text{Ⅲ} } } }/(\text{%} ) {F_{\simfont\text{Ⅱ} } }/{F_{\simfont\text{Ⅲ} } }/(\text{%}) 预测破坏模式 JD-1 110 121 破坏模式Ⅰ JD-2 110 88 破坏模式Ⅱ JD-3 85 121 破坏模式Ⅲ 表 5 柱顶承载力指标Table 5. Bearing capacity index at the top of column试件编号 JD-1 JD-2 JD-3 加载方向 正 负 正 负 正 负 柱顶承载力/kN 461.2 −460.6 429.0 −399.9 389.1 −393.0 承载力比/(%) 100.8 100.7 93.8 87.4 85.1 85.9 注:承载力比为试验柱顶极限承载力与理论计算承载力之间的比值。 6 结论
本文提出了适用于WCFT柱与钢梁连接的侧板式节点,设计了3个足尺节点试件进行拟静力试验研究,通过试验研究和节点受力机理的分析,得出以下结论:
(1) 侧板式节点形式在节点域外存在3种破坏模式:Ⅰ) 侧板外梁端塑性铰破坏;Ⅱ) 柱翼缘板位置侧板竖向受弯破坏;Ⅲ) 侧板外伸部分与梁翼缘之间的水平焊缝受拉破坏。
(2) 发生破坏模式Ⅰ的侧板式节点试件在距离柱翼缘边0.8倍~1.0倍梁高的区域形成典型梁端塑性铰,节点域处于弹性阶段,节点位移延性系数3.02,峰值荷载时弹塑性层间位移角1/22,等效粘滞阻尼系数0.47,节点试件表现出较好的变形能力和耗能性能。
(3) 发生破坏模式Ⅱ和破坏模式Ⅲ的侧板式节点试件在屈服后位移加载的第一级循环荷载下发生破坏,未充分发展塑性变形,滞回环总面积小,节点试件呈现脆性破坏的特征。
(4) 结合侧板式节点在节点域外的三类破坏模式,建立相应的判别公式。通过与试验的对比,判别公式预测的破坏模式和承载力与试验结果吻合较好,可为WCFT柱-钢梁侧板式节点的工程设计提供参考。
(5) 综合分析节点试件的破坏形态、滞回曲线、骨架曲线、变形能力和耗能能力可以发现,通过合理设计,WCFT柱-钢梁连接的侧板式节点具有较理想的抗震性能,可用于装配式钢结构建筑。
-
表 1 试件主要尺寸
Table 1 Main dimensions of specimens
试件编号 节点区柱/mm 侧板外伸尺寸/mm JD-1 550×180×12×12 −300×500×12 JD-2 550×180×12×12 −300×500×12 JD-3 550×180×12×12 −240×500×12 注: JD-1节点区柱腹板和外伸侧板为完整板件;JD-2节点区柱翼缘外伸,柱腹板与外伸侧板断开,采用坡口焊与柱翼缘焊接。 表 2 钢材材性主要试验结果
Table 2 Main steel properties
板件规格 fy/MPa fu/MPa δ/(%) E/MPa fu/fy 钢柱(8 mm) 371.67 520.00 24.97 188667 1.40 钢柱(12 mm) 375.00 493.33 30.59 217000 1.32 钢梁翼缘 383.33 535.00 30.18 210667 1.40 钢梁腹板 380.40 513.70 24.67 175700 1.35 注:fy为屈服强度;fu为极限强度;δ为伸长率;E为弹性模量。 表 3 主要试验结果
Table 3 Main test results
试件编号 Py/kN Δy/mm Pp/kN Δu/mm θu JD-1 369.10 44.02 452.60 132.73 1/22 JD-2 − − 413.19 59.71 1/49 JD-3 − − 391.05 53.67 1/54 注:JD-2和JD-3进入塑性后不久发生破坏,无法根据“通用弯矩屈服法”确定屈服荷载,峰值荷载Pp、极限位移Δu和层间位移角θu取其骨架曲线终点数据。 表 4 试件强度比及预测破坏模式
Table 4 Strength ratios of specimens and expected failure mode
试件编号 {F_{\simfont\text{Ⅰ}} }/{F_{ {\simfont\text{Ⅲ} } } }/(\text{%} ) {F_{\simfont\text{Ⅱ} } }/{F_{\simfont\text{Ⅲ} } }/(\text{%}) 预测破坏模式 JD-1 110 121 破坏模式Ⅰ JD-2 110 88 破坏模式Ⅱ JD-3 85 121 破坏模式Ⅲ 表 5 柱顶承载力指标
Table 5 Bearing capacity index at the top of column
试件编号 JD-1 JD-2 JD-3 加载方向 正 负 正 负 正 负 柱顶承载力/kN 461.2 −460.6 429.0 −399.9 389.1 −393.0 承载力比/(%) 100.8 100.7 93.8 87.4 85.1 85.9 注:承载力比为试验柱顶极限承载力与理论计算承载力之间的比值。 -
[1] 韩林海. 钢管混凝土结构-理论与实践 [M]. 第三版. 北京: 科学出版社, 2016 . Han Linhai. Concrete filled steel tubular structures- Theory and practice [M]. 3rd ed. Beijing: Science Press, 2016. (in Chinese)
[2] 聂建国, 樊健生. 广义组合结构及其发展展望[J]. 建筑结构学报, 2006, 27(6): 1 − 8. doi: 10.3321/j.issn:1000-6869.2006.06.001 Nie Jianguo, Fan Jiansheng. The development and prospect of generalized composite structures [J]. Journal of Building Structures, 2006, 27(6): 1 − 8. (in Chinese) doi: 10.3321/j.issn:1000-6869.2006.06.001
[3] Sasaki S, Teraoka M, Fujiwara T. Structural behavior of concrete-filled square column with partial-penetration weld corner seam to steel H-beam connections [C]//Proceedings of the 4th Pacific Structural Steel Conference: Volume 2, Structural Connections. Singapore: Pergamon Press, 1995: 33 − 40.
[4] 吕西林, 李学平, 余勇. 方钢管混凝土柱与钢梁连接的设计方法[J]. 同济大学学报, 2002, 30(1): 1 − 4. Lü Xilin, Li Xueping, Yu Yong. Design method for connections between concrete-filled square tubular columns and steel beams [J]. Journal of Tongji University, 2002, 30(1): 1 − 4. (in Chinese)
[5] 周天华, 聂少锋, 卢林枫, 等. 带内隔板的方钢管混凝土柱-钢梁节点设计研究[J]. 建筑结构学报, 2005, 26(5): 23 − 29. doi: 10.3321/j.issn:1000-6869.2005.05.004 Zhou Tianhua, Nie Shaofeng, Lu Linfeng, et al. Design of concrete-filled square tube column and steel beam joint with internal diaphragms [J]. Journal of Building Structures, 2005, 26(5): 23 − 29. (in Chinese) doi: 10.3321/j.issn:1000-6869.2005.05.004
[6] Qin Ying, Chen Zhihua, Bai Jingjing, et al. Test of extended thick-walled through-diaphragm connection to thick-walled CFT column [J]. Steel and Composite Structures, 2016, 20(1): 1 − 20. doi: 10.12989/scs.2016.20.1.001
[7] 秦希, 王伟. 隔板贯通式全螺栓节点抗连续性倒塌性能数值模拟分析[J]. 振动与冲击, 2015, 34(10): 68 − 75. Qin Xi, Wang Wei. Numerical simulation for progressive collapse behavior of through diaphragm bolted beam-column joints [J]. Journal of Vibration and Shock, 2015, 34(10): 68 − 75. (in Chinese)
[8] 聂建国, 秦凯, 肖岩. 方钢管混凝土柱节点的试验研究及非线性有限元分析[J]. 工程力学, 2006, 23(11): 99 − 108. doi: 10.3969/j.issn.1000-4750.2006.11.017 Nie Jianguo, Qin Kai, Xiao Yan. Experimental investigation and nonlinear finite element analysis on the behavior of concrete-filled square steel tubular column connections [J]. Engineering Mechanics, 2006, 23(11): 99 − 108. (in Chinese) doi: 10.3969/j.issn.1000-4750.2006.11.017
[9] 刘晓刚, 樊健生, 陶慕轩, 等. 钢管混凝土柱-钢梁节点核心区受剪承载力计算对比研究[J]. 建筑结构学报, 2012, 32(2): 85 − 92. Liu Xiaogang, Fan Jiansheng, Tao Muxuan, et al. Comparison and analysis on design method of shear capacity of panel zone between CFT column and steel beam [J]. Journal of Building Structures, 2012, 32(2): 85 − 92. (in Chinese)
[10] GB 50936−2014, 钢管混凝土结构技术规范 [S]. 北京: 中国建筑工业出版社, 2014. GB 50936−2014, Technical code for concrete filled steel tubular structures [S]. Beijing: China Architecture & Building Press, 2014. (in Chinese)
[11] CECS 159:2004, 矩形钢管混凝土结构技术规程 [S]. 北京: 中国计划出版社, 2004. CECS 159:2004, Technical specification for structures with concrete-filled rectangular steel tube members [S]. Beijing: China Planning Press, 2004. (in Chinese)
[12] 郝际平, 孙晓岭, 薛强, 等. 绿色装配式钢结构建筑体系研究与应用[J]. 工程力学, 2017, 34(1): 1 − 13. doi: 10.6052/j.issn.1000-4750.2016.08.ST14 Hao Jiping, Sun Xiaoling, Xue Qiang, et al. Research and application of fabricated steel structure building system [J]. Engineering Mechanics, 2017, 34(1): 1 − 13. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.08.ST14
[13] 孙晓岭, 郝际平, 薛强, 等. 壁式钢管混凝土柱抗震性能试验研究[J]. 建筑结构学报, 2018, 39(6): 92 − 101. Sun Xiaoling, Hao Jiping, Xue Qiang, et al. Experimental study on seismic behavior of walled concrete-filled steel tubular columns [J]. Journal of Building Structures, 2018, 39(6): 92 − 101. (in Chinese)
[14] 孙晓岭. 壁式钢管混凝土柱抗震试验与力学性能研究 [D]. 西安: 西安建筑科技大学, 2018. Sun Xiaoling. Seismic test and research on the behavior of walled concrete-filled steel tubular columns [D]. Xi’an: Xi’an University of Architecture & Technology, 2018. (in Chinese)
[15] 西安建筑科技大学. 一种多腔体拼接型钢混凝土组合柱 [P]. 中国: 201620469224.1, 2016.09. 01. Xi’an University of Architecture & Technology. A multi-core concrete filled steel tube composite column [P]. CN: 201620469224.1, 2016.09. 01. (in Chinese)
[16] 西安建筑科技大学. 支撑平推装配的多腔钢管混凝土组合柱支撑框架体系 [P]. 中国: 201620468549.8, 2016.09. 01. Xi’an University of Architecture & Technology. Multi-core concrete filled steel tube frame-braced systems assembled by flat pushing brace [P]. CN: 201620468549.8, 2016.09. 01. (in Chinese)
[17] 徐礼华, 凡红, 刘胜兵, 等. 钢管混凝土柱-钢梁节点抗震性能试验研究与有限元分析[J]. 工程力学, 2008, 25(2): 122 − 131. Xu Lihua, Fan Hong, Liu Shengbing, et al. Experimental studies on seismic behavior of connection between concrete-filled steel square tubular column and steel beam [J]. Engineering Mechanics, 2008, 25(2): 122 − 131. (in Chinese)
[18] GB 50017−2017, 钢结构设计标准 [S]. 北京: 中国建筑工业出版社, 2017. GB 50017−2017, Standard for design of steel structures [S]. Beijing: China Architecture & Building Press, 2017. (in Chinese)
[19] GB 50011−2010, 建筑抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2016. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: China Architecture & Building Press, 2016. (in Chinese)
[20] GB/T 228.1−2010, 金属材料 拉伸试验 第1部分: 室温试验方法 [S]. 北京: 中国标准出版社, 2011. GB/T 228.1−2010, Metallic materials-Tensile testing-Part 1: Method of test at room temperature [S]. Beijing: China Standard Press, 2011. (in Chinese)
[21] GB/T 50081−2002, 普通混凝土力学性能试验方法标准 [S]. 北京: 中国建筑工业出版社, 2003. GB/T 50081−2002, Standard for test method of mechanical properties on ordinary concrete [S]. Beijing: China Architecture & Building Press, 2003. (in Chinese)
[22] GB 50010−2010, 混凝土结构设计规范 [S]. 北京: 中国建筑工业出版社, 2015. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2015. (in Chinese)
[23] 李俊华, 章子华, 池玉宇. 火灾后型钢混凝土梁柱节点抗震性能试验研究[J]. 工程力学, 2017, 34(7): 162 − 171. Li Junhua, Zhang Zihua, Chi Yuyu. Experimental study on seismic performance of steel reinforced concrete beam-column joints after exposure to fire [J]. Engineering Mechanics, 2017, 34(7): 162 − 171. (in Chinese)
[24] JGJ/T 101−2015, 建筑抗震试验规程 [S]. 北京: 中国建筑工业出版社, 2015. JGJ/T 101−2015, Specification for seismic test of buildings [S]. Beijing: China Architecture & Building Press, 2015. (in Chinese)




 下载:
下载: