STUDY ON TIME-FREQUENCY CHARACTERISTICS OF WIND-INDUCED VIBRATION OF NON-STANDARD CIRCULAR STAYED CABLES
-
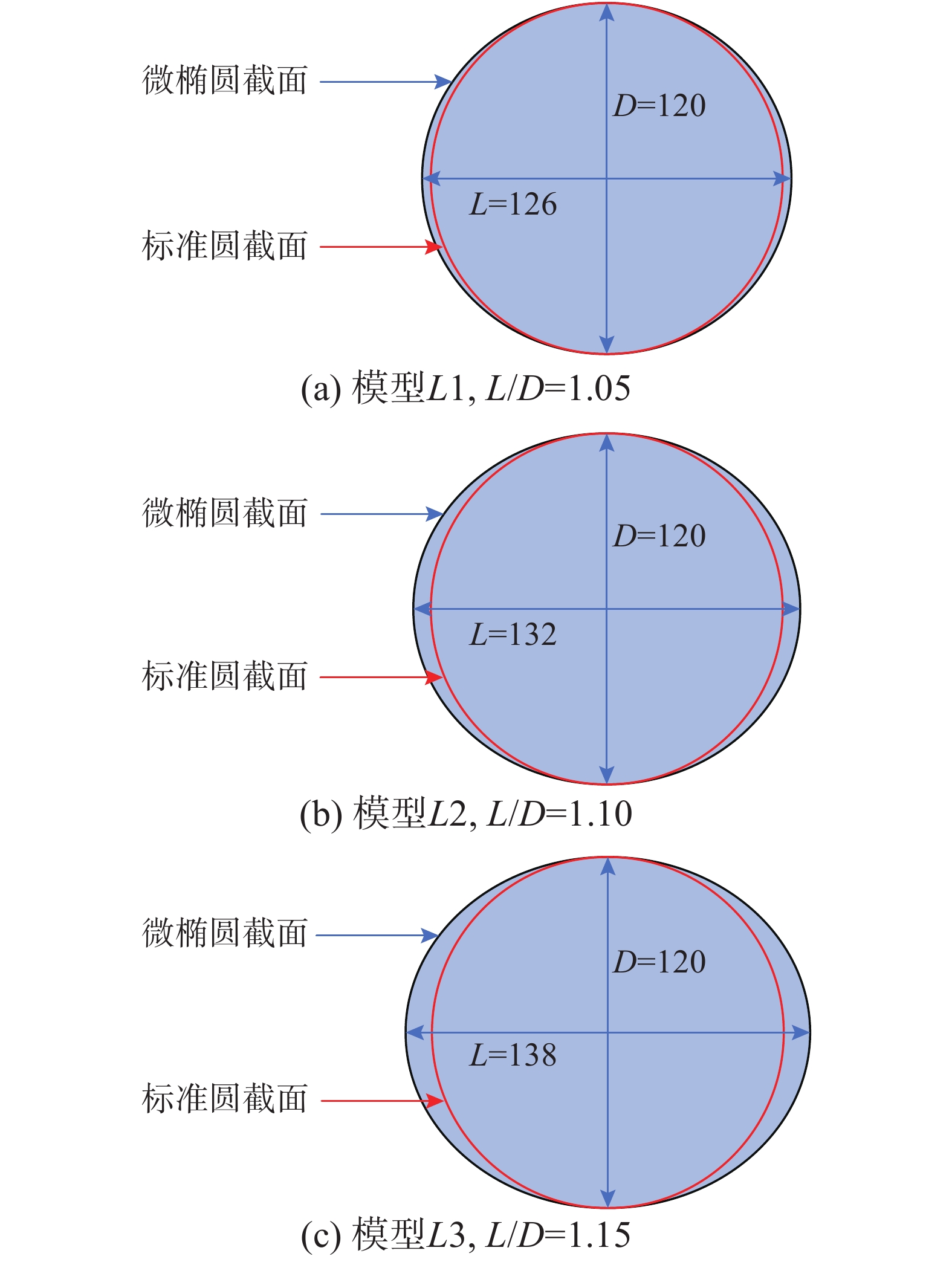
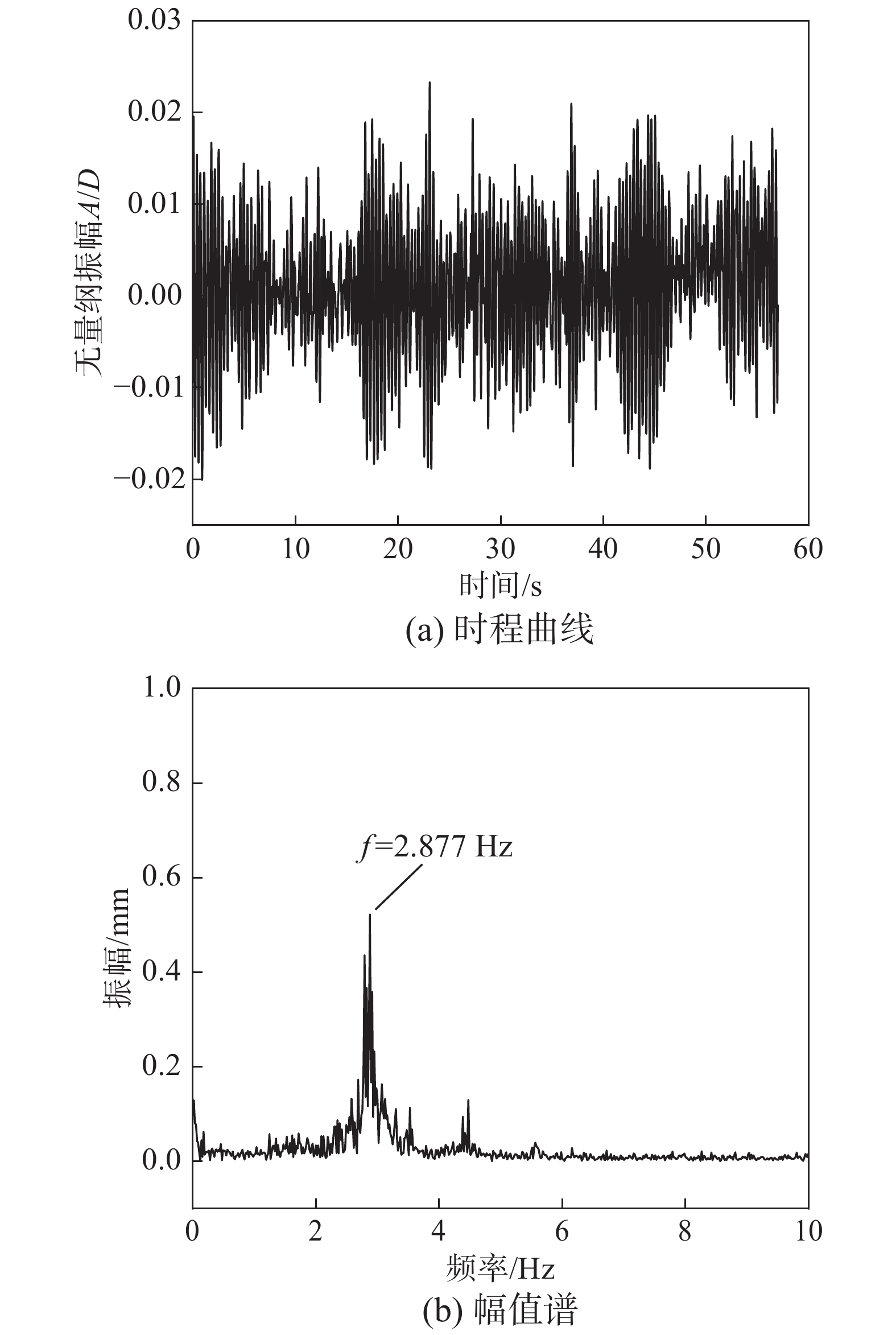
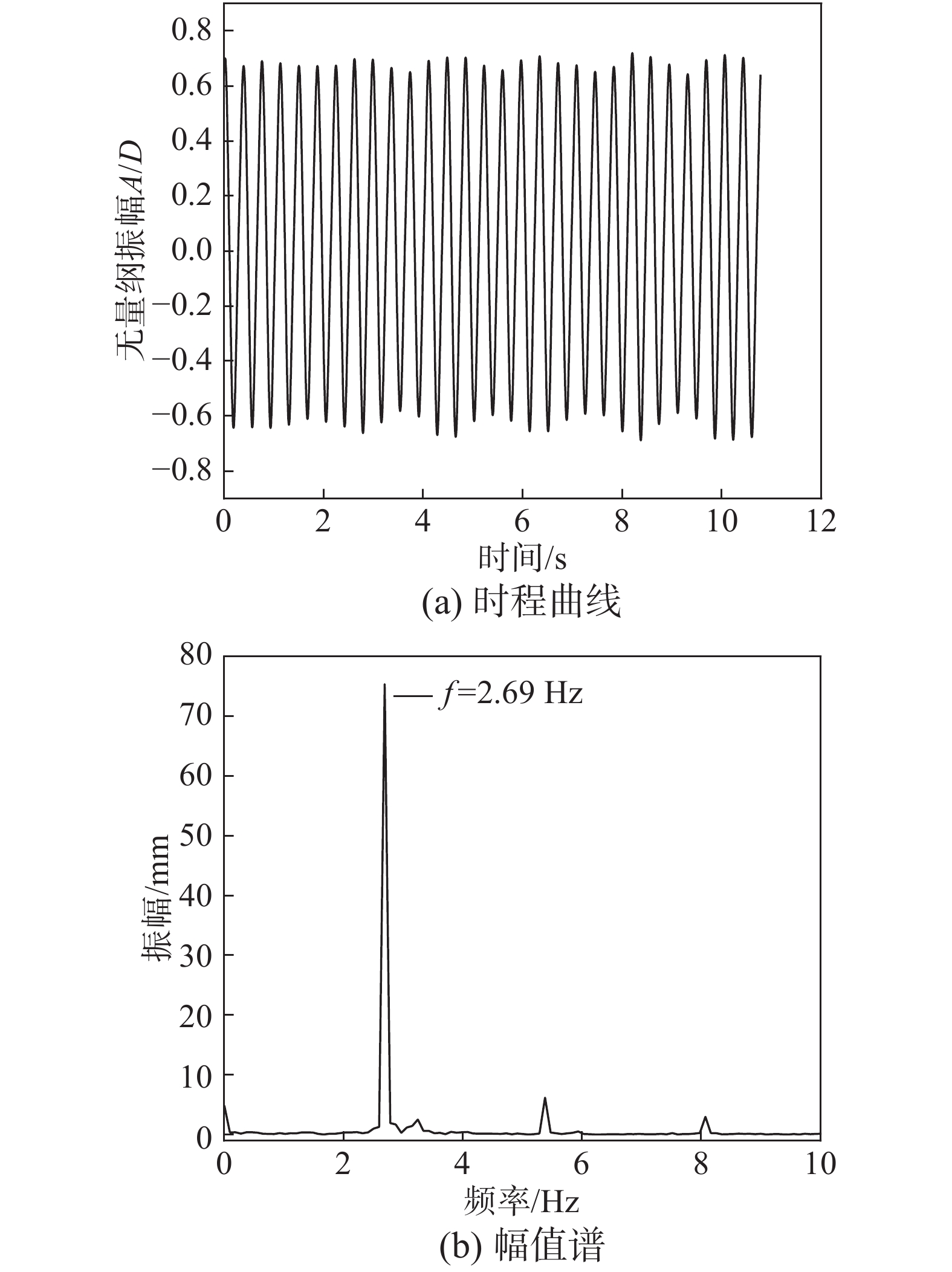
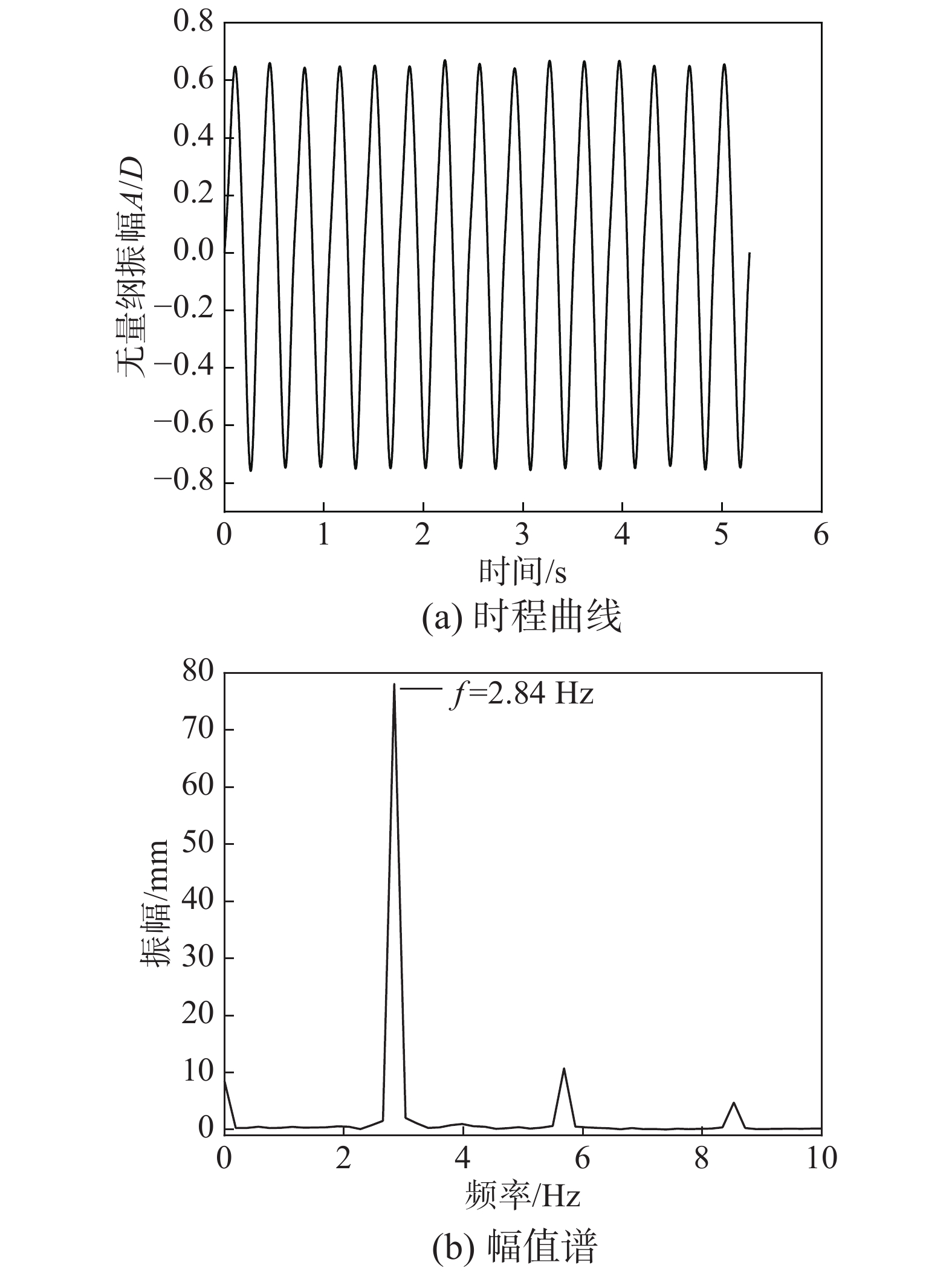
摘要: 明确斜拉索的气动特性对于保证桥梁的安全性和经济性具有重要意义,服役期的斜拉索在各种作用下,截面可能由标准圆变为非标准圆,因此,有必要对非标准圆斜拉索的风致振动特性进行研究。以长短轴之比分别为1.05、1.10、1.15的椭圆柱体模型为研究对象,利用风洞测振试验,研究非标准圆斜拉索的风致振动时频特征。结果表明:非标准圆斜拉索风致振动时程整体上可以分为两类,一类是类似于简谐运动的非常稳定的周期性运动,另一类则随时间变化不特别稳定,一段时间内振幅较小,另一时间段内振幅则较大;在绝大多数工况下,风致振动为第一类振动,振幅较大且非常稳定;模型的振动频率基本上在自振频率附近波动,当模型出现大幅振动时,振动频率开始偏离自振频率,这是因为大幅风致振动可能使得模型系统产生了气动负刚度或气动质量,进而使得振动频率降低。Abstract: It is of great significance to obtain the aerodynamics of stay cables to improve the safety and economy of bridges. However, under various effects, the cross-sections of stay cables during service might tend to be non-standard circle. It is necessary to investigate the wind-induced vibration characteristics of the non-standard circular stay cables. Three elliptical cylinders were used, with major-minor ratios of 1.05, 1.10 and 1.15, to investigate the time-frequency characteristics of vibration of non-standard circular stay cables. The results show that the time histories of the observed vibrations could be classified into two categories. One is a very stable periodic motion, which is similar to the simple harmonic motion. While the other is not particularly stable, with small amplitude in one period and large amplitude in another period. In most test cases, wind-induced vibration lies in the first category of vibration, more stable and with larger amplitude. The vibration frequency of the model is generally around the natural frequency. When the vibration is violent, the vibration frequency begins to deviate from the natural frequency. The cause might be the additional negative aerodynamic stiffness or mass induced by the large-amplitude vibration.
-
桥梁是城市交通网络的重要组成部分,对当地的政治、经济、文化等方面都有着重要的意义,在国民经济建设中占有举足轻重的地位。随着公路交通运输量的增长,车辆轴载及车辆密度的增大相当迅速,随着时间的推移,结构材料出现陈旧老化、桥梁养护不当等种种因素会导致已建桥梁的承载能力有所下降,从而影响桥梁的运营安全。因此,准确、定量地了解亚健康桥梁的实际状态十分重要。
亚健康桥梁主要有结构耐久性差、结构通行能力不足、结构安全性存在潜在风险三类。本文研究的是结构承载能力不满足设计要求,存在潜在安全风险的亚健康桥梁。
目前旧桥评定最常用的方法为静动荷载试验法,但根据国内现行规范,只能评定桥梁是否满足设计承载能力要求,而缺乏对亚健康桥梁剩余承载能力评估,也不能定量提出限载要求[1]。在实际工程中,桥梁管养单位为避免安全事故发生,大多数情况下采取保守的方式对亚健康桥梁进行限载,甚至禁止通行。然而无论限载或者禁行均会给使用者带来不便,且所造成的民怨进一步会对决策者带来舆论压力,同时,过度的限载或禁行容易造成资源浪费。因此,决策者面对亚健康桥梁的处理常常陷入两难的境地,如何既安全又充分利用亚健康桥梁,有待深究。
桥梁承载能力的研究现状主要分为三大类:模型试验研究、现场静动载实验研究和现场实桥破坏性实验研究。模型试验一般需加载至破坏以研究桥梁破坏全过程及其极限状态,其目的有两个:验证设计理论和确定复杂结构的受力状态[2-5]。早在18世纪中期德国工程师Gleiberman首次使用模型试验验证设计可靠性,1846年英国罗伯特·斯坦弗森为修正不列颠桥的设计完成了1∶6桥梁结构模型试验,与此同时,我国于二十世纪五六十年代模型试验研究也逐渐拉开序幕,并在近十年取得飞速进步。静动载试验是目前运用最广泛的评定桥梁承载能力的一种方法[6-7]。研究桥梁最理想的途径为实桥原位破坏性试验,但是由于实桥破坏性试验风险大、成本高,所以在这方面实验机会非常稀少。
本文将以简支混凝土T梁的上部结构梁体构件为研究对象,结合桥梁荷载试验结果,综合考虑了挠度、应变、基频等因素,直观有效地评估梁式桥临界使用承载能力。
1 理论分析
在支承条件不变的情况下,桥梁结构的承载能力最终由材料的抗力决定,以钢筋混凝土桥梁为例,在确保钢筋不被拉断,混凝土未被压溃,即钢筋、混凝土的应变均小于其极限拉、压应变,且桥梁下部结构基本完好的前提下,若要合理使用亚健康桥梁的剩余承载能力,则必须控制应力应变的最大值,避免构件失效。
在运营过程中,桥梁可能因为材料退化、超重车通行、船舶撞击等,使梁体构件出现开裂、混凝土剥落、钢筋锈蚀等病害,造成有效截面的削弱,进而承载能力下降,此时,认为桥梁进入了亚健康状态[8]。由于加固需要数月甚至数年的时间进行方案论证,若在此期间仍允许桥梁按实际通行荷载运营,则可能使桥梁进一步损坏,甚至发生安全事故,因此,通过限制通行车辆,减少外荷载的方式,是最快捷、最有效和最常用的亚健康桥梁安全保障措施。
桥梁在受到过大的外荷载作用后,将出现上述的病害,并在设计荷载作用下,处于非线弹性状态。根据大量荷载试验数据,梁体开裂后,其中性轴将上移,由于钢筋的作用,梁体只裂未断,开裂的梁体处于另外一种力平衡状态,并可以继续有限度承载。开裂桥梁在轻荷载作用下,已经受损的构件的受力行为仍近似处于线弹性状态,即该状态下应力与应变的关系符合虎克定律
σ=Eε [9],则应变ε在常系数弹性模量E下,与应力σ 成正比例。而应力σ 与弯矩M、惯性矩I的关系为:σ=My/I 。因此,可得简支梁由弯矩产生的应变为:ε=My/EI (1) 构件开裂的直接原因是应力过大,因此,为避免梁体进一步受损,受力关键点在开裂后的力平衡体系中,其应变不能大于设计荷载作用下的应变
εc ,进而推算使用内力M'。然而,结构受损开裂后惯性矩I'显然小于开裂前的I;而由于中性轴上移,y'也发生了变化。如何定义开裂后的I'和y'是我们接下来研究的内容。1.1 根据桥梁基频推算桥梁刚度折减系数
现通过改变截面形状,削弱惯性矩的方式,模拟病害对构件产生的承载能力削减效果,并求得其刚度折减系数。通过利用试验荷载作用下,实测的挠度、应变、基频值等,与对应的计算理论值,可推算出桥梁的刚度折减系数。
结构频率的改变能够反映其刚度的变化[10],故通过建立有限元模型推算出简支T梁桥的理论计算频率
fstat ,再通过动载试验得到桥梁实测频率fe。根据《公路桥涵设计通用规范》(JTG D60−2015)[11],简支梁冲击力引起正弯矩效应时频率与结构弹性模量E、结构计算跨径l、结构跨中截面抗弯惯性矩Ic、结构跨中处的单位长度质量mc的关系公式为: f=π2l2√EIcmc (2) 由式(2)可以得出桥梁的基频平方与刚度EI成正比。现有fe和fstat分别为基频的实测值和理论计算值,令
ηf=(fe/fstat) ,则:βf=ηf2=(fe/fstat)2 (3) 因此,由式(3)可以得出当前桥梁的实际刚度与理论计算刚度的比值
βf 为ηf 的平方。1.2 根据挠度推算桥梁刚度折减系数
对简支梁桥跨中挠度,如果是多个竖向荷载作用下,可通过叠加原理求得挠度[12],挠度示意图如图1、图2所示,挠度公式为式(4)。
Sstat=qx24EI(l3−2lx+x) (4) 当
0⩽ ,{S_{\rm{stat}}} = \dfrac{{Pbx}}{{6EI}}({l^3} - {x^2} + {b^2}) 当
a \!\leqslant \!x \!\leqslant \!l ,{S_{\rm{stat}}}\! =\! \dfrac{{Pbx}}{{6EI}}\left[\dfrac{l}{b}{(x \!- \!a)^3} \!+\! {(l \! -\! b)^2}x \!-\! {x^3}\right] 由式(4)得出桥梁的挠度值与刚度EI成反比。通过桥梁静载试验测得挠度实测值Se和计算值Sstat,令
{\eta _{\rm{s}}} = {S_{\rm{e}}}/{S_{\rm{stat}}} ,因此得:{\beta _{\rm{s}}} = {\eta _{\rm{s}}}^{ - 1} = {S_{\rm{stat}}}/{S_{\rm{e}}} (5) 因此,由式(5)可以得出当前的实际刚度与理论计算刚度的比值
{\beta _{\rm{s}}} 为{\eta _{\rm{s}}} 的倒数。为了保证桥梁计算的可靠性,通过取挠度与基频刚度比最小值推出桥梁的刚度比β。即:
\beta = \min({\beta _{\rm{f}}},\;{\beta _{\rm{s}}}) (6) 推算出实际刚度,即削减后的刚度B'与原刚度B0=I0E0的关系式为B'=βB0=I0βE0。
桥梁因为开裂、材料性能退化等因素,截面的抗弯惯性矩I出现变化。因此,对于折减后的抗弯惯性矩
{I{'}} = B'/E ,并考虑弹性模量E随时间变化的影响[13],则推出:{I{'}} = \frac{{{I_0}{\beta _{\rm{}}}{E_0}}}{E} (7) 以受正弯矩的T形截面为例,其抗弯惯性矩折减的主要原因是截面下缘开裂,因此,应通过削弱腹板高度,以实现开裂后I'抗弯惯性矩的折减。同理,受负弯矩影响,且出现梁体上缘开裂的矩形和T截面应削减翼板厚度;而受剪力影响,且腹板斜向开裂的截面应该均匀削弱各板厚度,以实现抗弯惯性矩的折减。按比例削弱后,截面的质心也会出现变化,其带来的影响也不能忽略。
通过有限元软件建立桥梁模型,设定在桥梁处于线弹性状态下计算得出的桥梁试验荷载下理论计算应变为该截面控制应变
\varepsilon _{\rm{c}} ,并以此内力值作为亚健康桥梁的临界使用内力。为模拟亚健康桥梁的受损状态,以上述方法对构件的截面的参数进行调整,达到截面折减的目的。折减后的抗弯惯性矩I' 和新质心位置y' 代入计算机模型,若以同样的荷载作用在桥上时,桥梁产生的应力(应变)将会增大。为避免截面受力过大而出现进一步损坏,通过调整车辆荷载值,减少梁体内力,并使梁体应变小于上述的截面控制应变
\varepsilon _{\rm{c}} ,在此内力值下的荷载为亚健康桥梁的通行荷载限制值,所有通过该桥的车辆不能超过此荷载。从而确定亚健康桥梁的实际使用承载能力和限载指标,使桥梁在限载指标下能安全运营,而且,不会出现进一步损坏。2 数值案例分析及验证
为验证上述方法的有效性,选取广州市二沙岛西桥作为验证对象,结合桥梁荷载试验历年检测报告,评估二沙岛西桥实际使用承载能力。
2.1 验证对象的概况
本次验证对象为二沙岛西桥15 m跨简支T梁。上部结构由14片T梁现浇而成;T梁梁高1.1 m,其中支点、四分点、跨中断面各有一根横隔梁,共5根。横隔梁与T梁间采用整体方式连结。设计荷载为:汽车−超20级,挂车−120,人群荷载为3.5 kN/m2,混凝土标号为C30。其截面构造如图3所示。
2.2 静载试验
首先计算出结构在设计活载作用下的荷载效应,然后根据控制截面内力影响线,计算出试验所需的试验荷载。试验理论计算采用Midas_civil桥梁分析软件进行有限元分析,选取具有代表性的桥跨进行试验,有限元模型如图4所示。
对桥梁按图5的载位进行加载,在试验荷载作用下,控制截面的理论控制弯矩值、试验荷载弯矩值及荷载试验效率系数见表1;桥梁挠度测点和跨中截面应变测点布置分别如图6和图7所示。
表 1 控制截面弯矩值及加载效率汇总表Table 1. Summary of bending moment value and loading ratio of control section跨中载位 设计活载
内力值/(kN·m)试验荷载
内力值/(kN·m)加载效率/(%) 载位1 231 39.62 载位2 583 361 61.92 载位3 574 98.46 2.3 2008年荷载试验数据分析
首次试验的日期是2008年6月19日。本次荷载试验的数据如表2所示。
表 2 2008年变形测点的实测值和计算值比较Table 2. Comparison of tested result and FEA results of deformation measuring points in 2008/mm 测点号 数值类型 试验工况 最大弹性挠度 实测值/计算值(Se/Sstat) 满载 卸载 3# 实测值 −6.9 −0.1 −6.8 1.11 计算值 −6.1 0.0 −6.1 3-1# 实测值 −9.2 −0.3 −8.9 1.19 计算值 −7.5 0.0 −7.5 3-2# 实测值 −5.4 0.0 −5.4 1.26 计算值 −4.3 0.0 −4.3 在各级试验荷载工况的作用下,在满载试验荷载作用下15 m试验桥跨挠度校验系数及应变校验系数均不能满足《大跨径混凝土桥梁的试验方法》中关于钢筋混凝土桥梁的要求:
\beta < \dfrac{{{S_{\rm{e}}}}}{{{S_{\rm{stat}}}}} \leqslant \alpha 式中:α=1.10;β=0.60。
因此,该桥15 m跨简支T梁桥承载能力和正常使用性能不能满足设计荷载等级的要求。
2.4 使用承载力和限载指标的评估
2008年的检测结论显示,二沙岛西桥的承载能力不能满足设计荷载等级要求。因此,为保障在加固补强之前的安全运营,必须评估其使用承载能力和确定其限载指标。以下是基于该桥2008年的理论计算和实测数据,对限载指标的推算过程。
1)根据桥梁基频推算刚度衰减程度
根据式(3),可以得出桥梁的基频平方与刚度正比。该桥的实测频率为5.00 Hz、理论计算频率为4.79 Hz,其比值为0.96,因此,当前的实际刚度与理论计算刚度的比值为0.92,如表3所示。
表 3 通过实测基频而得出刚度比值Table 3. Stiffness ratio by fundamental frequency result{f_{\rm{e}}}实测值
频率/Hz{f_{\rm{stat}} }计算值
频率/Hz频率比值
{\eta _{\rm{f}}} = ({f_{\rm{e}}}/{f_{\rm{stat}} })刚度比值
{\beta _{\rm{f}}}{\rm{ = } }{\eta _{\rm{f}}}^24.79 5.00 0.96 0.92 2)根据静载挠度推算刚度衰减程度
根据式(4),可以得出桥梁的挠度与刚度成反比。该桥的实测弹性挠度与理论计算频率的比值为0.94~1.26,平均值为1.19,因此,当前的实际刚度与理论计算刚度的比值为0.84,如表4所示。
3)临界使用承载能力与限载指标的确定
根据试验数据,该桥仍具有一定的弹性,并根据式(6),将刚度折减系数β定为0.84。通过调整截面的形状,得出折减后的抗弯惯性矩I',并考虑弹模E随时间变化的影响,进而实现折减初始刚度B0,并达到折减后刚度B'=βB0的效果。简支T梁桥的抗弯惯性矩折减主要原因是截面下缘开裂超限,因此,应通过从T梁下缘为起点,向上削减其高度,以实现抗弯惯性矩的折减。按比例削弱后,截面的质心也会出现变化。二沙岛西桥原T梁截面高度为1.10 m,经过削减计算后,截面高度调整为0.98 m,质心位置上移0.12 m,具体如图8所示。
表 4 通过实测挠度得出刚度比值Table 4. Stiffness ratio by deflection result测点 数值类型 满载 卸载 最大弹性挠度 实测值/计算值(ηs=Se/Sstat) 3# 实测值 −6.91 −0.10 −6.81 1.11 计算值 −6.11 0.00 −6.11 3-1# 实测值 −9.20 −0.30 −8.90 1.19 计算值 −7.50 0.00 −7.50 3-2# 实测值 −5.40 0.00 −5.40 1.26 计算值 −4.30 0.00 −4.30 将削弱后抗弯惯性矩和质心位置,重新输入有限元模型,再进行反馈分析计算。同样的设计荷载的作用下所产生的应变,如表5所示。超出了理论值的上限。因此,如果不对该桥进行限载,仍以设计荷载通行,则该桥的裂缝将继续发展,承载能力也将进一步削弱。
为保障桥梁安全,避免桥梁进一步损坏或发生安全事故,必须对通行荷载进行限制,因此,需要控制关键截面的应力。现将各个关键截面的应变,均控制在小于等于试验荷载作用下应变测点计算结果的范围内。在该状态下,其内力为临界使用承载能力的内力,详见表6。最后,按设计荷载的车队,通过影响线加载,在不超过临界使用承载能力的内力的前提下,最重的车不能超过33.4 t,详见表7。
2.5 限载措施有效性验证
自2008年荷载试验检测后,管养单位根据检测报告的建议,对二沙岛西桥实施限载措施,禁止30 t以上车辆通行。限载通行若干年后,该桥分别于2014年及2017年再次进行荷载试验。从表8、表9、表10可以发现,该桥跨中截面的关键测点3#、3-1#和3-2#,其最大弹性挠度实测值分别在6.17~6.72、8.25~8.50、5.50~5.90;两年的实测值与计算比值分别为1.01~1.28和1.10~1.37。
表 5 衰减后试验荷载作用下应变测点计算结果Table 5. Strain value of FE model under the reduced test load/με 测点编号 试验工况1 试验工况2 试验工况3 1#T梁 97 188 214 2#T梁 112 205 257 3#T梁 164 233 307 4#T梁 157 220 322 5#T梁 94 166 313 6#T梁 65 123 269 7#T梁 43 83 192 表 6 33.4 t重车荷载作用下应变测点的计算值Table 6. Strain value of FE model under the 33.4 t heavy vehicle load/με 测点编号 控制值 1#T梁 209 2#T梁 201 3#T梁 227 4#T梁 268 5#T梁 143 6#T梁 145 7#T梁 129 表 7 33.4 t重车荷载作用下控制断面的使用弯矩{M_{\rm{d}}} 汇总表 /(kN·m)Table 7. Summary of service bending moment of control section under 33.4 t heavy vehicle load测点编号 控制值 支点 0.0 四分之一跨 171.4 跨中 212.6 四分之三跨 168.1 支点 0.0 从图9和表11可以发现,自从2008年对该桥进行限载后,根据2014年和2017年两次荷载试验实测结果,其挠度校验系数略微波动,年平均变化率分别为−6%和1%,变化均控制在10%范围内。桥梁虽然已经处于亚健康状态,但是,其承载能力在10年间未出现明显退化,病害未出现明显发展,桥梁状况保持稳定。说明限载措施使处于亚健康的桥梁既可以继续有限度通行,又有效地防止了外荷载对其进一步损伤。
表 8 2014年变形测点的实测值和计算值比较Table 8. Comparison of FEA result and test result of deformation measuring points in 2014/mm 测点 数值 试验工况 最大弹性
挠度实测值/计算值(ηs=Se/Sstat) 满载 卸载 3# 实测值 −6.47 0.30 −6.17 1.01 计算值 −6.11 0.00 −6.11 3-1# 实测值 −8.55 0.30 −8.25 1.10 计算值 −7.50 0.00 −7.50 3-2# 实测值 −5.70 0.20 −5.50 1.28 计算值 −4.30 0.00 −4.30 表 9 2017年变形测点的实测值和计算值比较Table 9. Comparison of FEA result and test result of deformation measuring points in 2017/mm 测点 数值 试验工况 最大弹性
挠度实测值/计算值(ηs=Se/Sstat) 满载 卸载 3# 实测值 −6.52 0.2 −6.72 1.10 计算值 −6.11 − −6.11 3-1# 实测值 −8.40 0.1 −8.50 1.13 计算值 −7.50 − −7.50 3-2# 实测值 −5.90 0.0 −5.90 1.37 计算值 −4.30 − −4.30 表 10 在试验工况下变形测点挠度校验系数比较Table 10. Comparison of deflection calibration coefficients of deformation measuring points under test conditions测点 实测值/计算值(Se/Sstat) 2008年 2014年 2017年 3# 1.11 1.01 1.10 3-1# 1.19 1.10 1.13 3-2# 1.26 1.28 1.37 表 11 与2008年相比较历年挠度校验系数比较变化幅度一览表Table 11. Rangeability of deflection calibration coefficient over the years compared with 2008测点 校验系数变化率/(%) 2014年 2017年 3# −10 −1 3-1# −9 −6 3-2# 2 11 二沙岛西桥的承载能力不满足汽-超20的正常使用极限状态,应降级使用[14-15]。参考《上海城市桥梁限载标准》(SZ-C-E02−2007)。桥梁设计荷载为汽-超20的正常使用状态应限载40 t,汽-20的正常使用状态应限载30 t[16],因此,该桥的限载吨位宜在30 t~40 t之间。而方法计算得出的限载吨位为33.4 t,正在此区间内,说明此限载措施合理。
3 结论
本文展现了截面折减法反馈计算法如何应用于简支T梁限载指标的确定,并经过对验证对象近十年的情况跟踪和反复试验,研究和验证该方法的有效性。研究结果得出以下结论:
(1)截面折减反馈计算法能有效地定量确定损伤极限状态下的桥梁临界使用承载能力和限载吨位,使限载范围从30 t~40 t,精确至33.4 t;
(2)针对简支T梁跨中附近出现竖向裂缝的病害特征,采取削减计算模型T梁腹板高度的方法该病害进行仿真模拟,提出需针对不同病害而选择适当截面削弱方式的反馈分析方法,使其计算结果更具有代表性;
(3)挖掘了常规的桥梁静动试验挠度、应变、基频等数据,使其除了检验桥梁承载能力是否满足设计荷载要求外,还可以定量分析限载吨位,监测桥梁承载能力的退化情况。
-
表 1 模型参数
Table 1 The parameters of test models
模型 自振频率f/Hz 阻尼比\xi /(%) S_{\rm{c}} = { {4\pi m\xi } / {\rho {D^2} } } L1 2.93 0.22 10.46 L2 2.91 0.25 11.50 L3 2.92 0.24 10.53 -
[1] Simiu E, Scanlan R H. Wind effects on structures: fundamentals and applications to design [M]. New York: John Wiley, 1996.
[2] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005. Chen Zhengqing. Bridge wind engineering [M]. Beijing: China communication press, 2005. (in Chinese)
[3] Matsumoto M, Saitoh T, Kitazawa M, et al. Response characteristics of rain-wind induced vibration of cablestayed bridges [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(57): 323 − 333.
[4] Flamand O. Rain-wind induced vibration of cables [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2/3): 353 − 362. doi: 10.1016/0167-6105(94)00113-R
[5] Gu M, Du X Q. Experimental investigation of rain-wind-induced vibration of cables in cable-stayed bridges and its mitigation [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93: 79 − 95. doi: 10.1016/j.jweia.2004.09.003
[6] Ge Y J, Chang Y, Xu L S, et al. Experimental investigation on spatial attitudes, dynamic characteristics and environmental conditions of rain-wind-induced vibration of stay cables with high-precision raining simulator [J]. Journal of Fluid and Structures, 2018, 76: 60 − 83. doi: 10.1016/j.jfluidstructs.2017.09.006
[7] 李永乐, 卢伟, 陶启宇. 斜拉桥拉索风-雨致振动特性风洞试验研究[J]. 实验流体力学, 2007, 21(4): 36 − 40. doi: 10.3969/j.issn.1672-9897.2007.04.008 Li Yongle, Lu Wei, Tao Qiyu. Study on rain-wind induced vibration of cables in cable-stayed bridges by wind tunnel test [J]. Journal of Experiments in Fluid Mechanics, 2007, 21(4): 36 − 40. (in Chinese) doi: 10.3969/j.issn.1672-9897.2007.04.008
[8] 李明水, 何向东. 斜拉索风雨振动及制振措施的风洞试验研究[J]. 实验流体力学, 2010, 24(6): 11 − 15. doi: 10.3969/j.issn.1672-9897.2010.06.003 Li Mingshui, He Xiangdong. Wind tunnel investigation on rain/wind-induced vibration and its mitigation means of stay cables [J]. Journal of Experiments in Fluid Mechanics, 2010, 24(6): 11 − 15. (in Chinese) doi: 10.3969/j.issn.1672-9897.2010.06.003
[9] 何旭辉, 陈政清, 李春光, 等. 斜拉索风雨振非平稳风场特性分析[J]. 振动与冲击, 2011, 30(10): 54 − 60. doi: 10.3969/j.issn.1000-3835.2011.10.012 He Xuhui, Chen Zhengqing, Li Chuiguang, et al. Nonstationary wind characteristics analysis for wind-rain induced vibration of stay cables [J]. Journal of Vibration and Shock, 2011, 30(10): 54 − 60. (in Chinese) doi: 10.3969/j.issn.1000-3835.2011.10.012
[10] 陈文礼. 斜拉索风雨激振的试验研究与数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2009. Chen Wenli. Experimental investigation and numerical simulation of rain-wind induced vibration of stay cables [D]. Haerbin: Harbin Institute of Technology, 2009. (in chinese)
[11] 陈文礼, 李惠. 斜拉索风雨振-实验与数值模拟混合子结构方法[J]. 哈尔滨工业大学学报, 2011, 43(8): 6 − 10. doi: 10.11918/j.issn.0367-6234.2011.08.002 Chen Wenli, Li Hui. Hybrid approach combining experiment and CFD numerical Simulation for rain-wind-induced vibration of a stay cable [J]. Journal of Harbin Institute of Technology, 2011, 43(8): 6 − 10. (in Chinese) doi: 10.11918/j.issn.0367-6234.2011.08.002
[12] Cheng S H, Larose G L, Savage M G. Experimental study on the wind-induced vibration of a dry inclined cable—Part I: Phenomena [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(12): 2231 − 2253. doi: 10.1016/j.jweia.2008.01.008
[13] Cheng S H, Irwin P A, Tanaka H. Experimental study on the wind-induced vibration of a dry inclined cable—Part II: Proposed mechanisms [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(12): 2254 − 2272. doi: 10.1016/j.jweia.2008.01.007
[14] Macdonald J H G, Larose G L. Two-degree-of-freedom inclined cable galloping—Part 1: General formulation and solution for perfectly tuned system [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(3): 291 − 307. doi: 10.1016/j.jweia.2007.07.002
[15] Jakobsen J B, Andersen T L, Macdonald J H G. Wind-induced response and excitation characteristics of an inclined cable model in the critical Reynolds number range [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 110: 100 − 112. doi: 10.1016/j.jweia.2012.04.025
[16] Matteoni G, Georgakis C T. Effects of bridge cable surface roughness and cross-sectional distortion on aerodynamic force coefficients [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104(5): 104 − 187.
[17] Matteoni G, Georgakis C T. Effects of surface roughness and cross-sectional distortion on the wind-induced response of bridge cables in dry conditions [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 136: 89 − 100. doi: 10.1016/j.jweia.2014.11.003
[18] Benidir A, Flamand O, Gaillet L, et al. Impact of roughness and circularity defect on bridge cables stability [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 137(2): 1 − 13.
[19] Bendir A, Flamand O, Dimitriadis G. The impact of circularity defects on bridge stay cable dry galloping stability [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 181: 14 − 26. doi: 10.1016/j.jweia.2018.08.009
[20] 毕继红, 乔浩玥, 关健, 等. 带有纵向肋条斜拉索的风雨激振减振机理研究[J]. 工程力学, 2018, 35(4): 168 − 175. doi: 10.6052/j.issn.1000-4750.2017.01.0043 Bi Jihong, Qiao Haoyue, Guan Jian, et al. Mechanism study of vibration reduction for rain-wind induced vibration of stay cable with ribs [J]. Engineering Mechanics, 2018, 35(4): 168 − 175. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.01.0043
[21] 刘庆宽, 孙一飞, 张磊杰, 等. 凹痕对斜拉桥斜拉索气动性能影响研究[J]. 工程力学, 2019, 36(增刊 1): 272 − 277. doi: 10.6052/j.issn.1000-4750.2018.05.S053 Liu Qingkuan, Sun Yifei, Zhang Leijie, et al. Study on the influence of dent on aerodynamic performance of stay cables of cable-stayed bridge [J]. Engineering Mechanics, 2019, 36(Suppl 1): 272 − 277. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.S053
[22] 郑云飞, 刘庆宽, 战启芳, 等. 螺旋线参数对斜拉索气动特性影响的试验研究[J]. 工程力学, 2020, 37(增刊 1): 301 − 306. doi: 10.6052/j.issn.1000-4750.2019.04.S057 Zheng Yunfei, Liu Qingkuan, Zhan Qifang, et al. Experimental study on helical line paraments' effect on aerodynamic characteristics of stay cables [J]. Engineering Mechanics, 2020, 37(Suppl 1): 301 − 306. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S057
[23] 郑云飞, 刘庆宽, 刘小兵, 等. 端部状态对斜拉索节段模型气动特性的影响[J]. 工程力学, 2017, 34(增刊 1): 192 − 195. doi: 10.6052/j.issn.1000-4750.2016.03.S036 Zheng Yunfei, Liu Qingkuan, Liu Xiaobing, et al. Influence of end conditions on aerodynamic force of section models for stay-cables [J]. Engineering Mechanics, 2017, 34(Suppl 1): 192 − 195. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.03.S036
-
期刊类型引用(3)
1. 陆俊宏,黎家玮,李金涛,吴宜峰. 服役15年大跨跨海预应力混凝土梁桥荷载试验及结构性能评价. 北京建筑大学学报. 2024(01): 100-108 .  百度学术
百度学术
2. 吴晓宇. 病害公路桥梁通行管理问题及解决对策探析. 工程建设与设计. 2022(13): 285-287 .  百度学术
百度学术
3. 雷雨恒,任亮,李宏男,尤润州,魏易博. 基于逆有限元法的形状还原传感阵列及桥梁挠度监测试验. 工程力学. 2022(11): 89-96 .  本站查看
本站查看
其他类型引用(1)
















 下载:
下载: