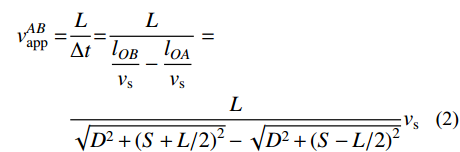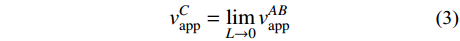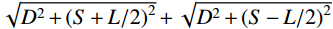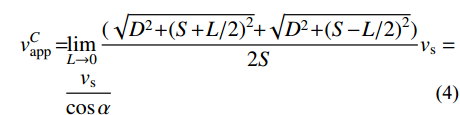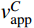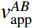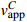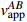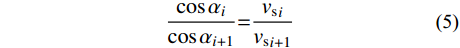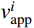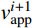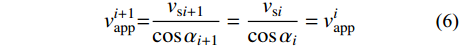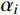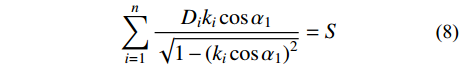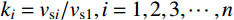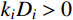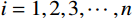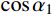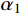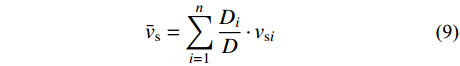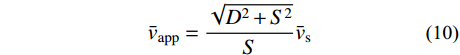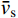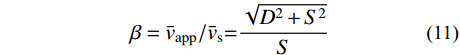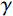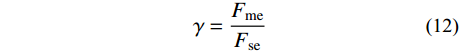视波速确定方法与行波效应研究

范重; 张康伟; 张郁山; 刘涛; 张宇; 赵作周; 葛红斌; 黄进芳

doi:10.6052/j.issn.1000-4750.2020.05.S010

视波速确定方法与行波效应研究

范重^1, ,,
张康伟^{1, 2,},
张郁山^3,,
刘涛^1,,
张宇^1,,
赵作周^2,,
葛红斌^4,,
黄进芳^4,

1.
中国建筑设计研究院，北京 100044
2.
清华大学土木工程系，北京 100084
3.
中国地震灾害防御中心，北京 100029
4.
福建兆翔机场建设公司，厦门 361006

基金项目: 中国建设科技集团股份有限公司科技创新基金项目(W2016043)

详细信息

作者简介:
张康伟(1996−)，男，山东人，硕士生，主要从事大跨度结构研究(E-mail: 1218732853@qq.com)

张郁山(1974−)，男，河北人，研究员，博士，博导，主要从事地震工程领域研究(E-mail: hyszhang@163.com)

刘　涛(1991−)，男，湖南人，工学硕士，从事大跨度结构设计研究(E-mail: 2016130@cadg.cn)

张　宇(1988−)，男，山西人，工学硕士，主要从事大跨度结构设计研究(E-mail: 201430@cadg.cn)

赵作周(1967−)，男，山东人，副教授，博士，博导，主要从事结构工程抗震研究(E-mail: zzzhao@tsinghua.edu.cn)

葛红斌(1969−)，男，福建人，工程硕士，主要从事机场工程技术研究(E-mail: 13950001889@139.com)

黄进芳(1980−)，男，福建人，工程师，工学学士，主要从事建筑结构技术研究(E-mail: hjfdzyx@163.com)

通讯作者:
范　重(1959−)，男，北京人，教授级高工，博士，主要从事建筑结构设计研究(E-mail: fanz@cadg.cn)

中图分类号: P315.3
计量
- 文章访问数: 987
- HTML全文浏览量: 200
- PDF下载量: 107
出版历程
- 收稿日期: 2020-05-08
- 修回日期: 2021-01-24
- 网络出版日期: 2021-01-31
- 刊出日期: 2021-06-01

STUDY ON APPARENT WAVE VELOCITY CALCULATION METHOD AND ON TRAVELLING WAVE EFFECT

1.
China Architecture Design & Research Institute, Beijing 100044, China
2.
Department of Civil Engineering, Tsinghua University, Beijing 100082, China
3.
China Earthquake Disaster Prevention Center, Beijing 100029, China
4.
Fujian Zhaoxiang Airport Construction Co., Ltd, Xiamen 361006, China

摘要

摘要: 通过对地震波在单一土层和不同土层之间传播规律的研究，提出基于岩土层剪切波速的视波速计算方法，并给出多土层视波速简化计算公式，便于工程应用。对于均质土层，地面某点的视波速仅与该点震源深度、震中距和土层的剪切波速有关，视波速恒大于剪切波速。采用结构中点的视波速取代根据其两端点得到的视波速，可以避免结构各方向长度不同的影响，计算简便，误差可以忽略不计。在震源深度范围内，地壳厚度通常远大于覆盖层厚度，多土层的等效剪切波速与震源所在岩层剪切波速较为接近，场地类别对视波速的影响较小。算例结果表明，文中给出的多土层视波速简化计算方法，与视波速方程数值解的误差一般在5%以内。根据95%构件内力影响系数的最大值确定地震行波效应的放大系数，可以避免由于构件内力过小引起行波效应异常增大。厦门新机场分析结果表明，考虑多点激励地震效应后，航站楼结构底部总剪力变化很小；虽然框架柱、支承屋盖钢管柱和大跨度屋盖杆件内力的平均值减小，但部分构件内力可增大约5%~10%。
- 超长结构 /
- 震源深度 /
- 震中距 /
- 视波速 /
- 多点激励 /
- 地震响应
Abstract: By studying the propagation pattern of seismic waves in a single soil layer and between different soil layers, a calculation method for apparent wave velocity based on the shear wave velocity of rock/soil layers was proposed. A simplified calculation formula of the apparent wave velocity for multiple soil layers was also developed for the engineering application convenience. For a homogeneous soil layer, the apparent wave velocity at a certain point on the ground is only related to the focal depth, to epicenter distance and to shear wave velocity, then the apparent wave velocity is always greater than the shear wave velocity. Using the apparent wave velocity at the midpoint of the structure instead of the apparent wave velocity obtained at its two ends can avoid the influence of the different lengths of the structure in all directions, the calculation is simple and the error can be ignored. In the depth range of the source, the thickness of Earth Crust is usually much larger than that of the overburden layer. The equivalent shear-wave velocity of multiple soil layers is close to the shear wave velocity of the rock layer where the source is located, and the site category has little effect on the apparent wave velocity. The results of the calculation examples show that the error of the simplified calculation method for the apparent wave velocity of multiple soil layers is generally within 5% of the numerical solution of the apparent wave velocity equation. According to the maximum value of internal force effect coefficients of 95% components to determine the amplification factor of the seismic traveling wave effect can avoid the abnormal increase of the traveling wave effect caused by the internal force of a little components being too small. The analytical results of Xiamen New Airport show that: after considering the multi-support seismic excitation, the change of the total shear force at the terminal structure bottom is very small; although the mean value of internal forces for frame columns, for steel pipe columns supporting roof and for long-span roof members decrease, the internal forces of some structural members can increase about 5%~10%.
- super-long structure /
- focal depth /
- epicenter distance /
- apparent wave velocity /
- multiple support excitation /
- seismic response

HTML全文

在进行结构抗震设计时，时程分析方法主要用于考虑发生地震时地面运动随时间变化的特征，通常假定所有竖向构件底部输入的地震时程记录完全相同，称为一致激励。地震波从震源向周边土体传播过程中，受到行波效应以及非均匀地形等地质条件的影响，场地各点地震动的同步性存在明显差异。因此，当结构单元长度很大时，地震传播速度的影响不能忽略，需要补充多点激励地震响应分析。

欧洲桥梁规范规定，当桥的长度大于200 m并且位于不连续或明显不同的地貌特征时，或者桥长大于600 m时，应考虑地震运动的空间变化^[1]。我国《建筑抗震设计规范》^[2]中规定，当结构长度大于300 m时，应分别按照单点一致输入与多点多向输入进行抗震计算。随着近年来我国大型公共建筑的迅速发展，单体结构总长度已经突破400 m~500 m，行波效应对结构整体变形与构件内力的影响不能忽略，多维多点激励已经成为超长结构抗震设计中重点关注的问题之一。

在行波效应地震响应分析中，视波速大小对计算结果影响显著。迄今为止，在我国《建筑抗震设计规范》^[2]等相关设计标准中，尚无对视波速取值的具体规定。许多学者针对结构的具体情况，在视波速取值方面进行了有益的探索。在针对具体工程进行行波效应分析时，主要基于场地土层的等效剪切波速，视波速取值区间通常在0.15 km/s~0.50 km/s范围内，并补充少量1.0 km/s及以上视波速进行校核分析，以充分考虑行波效应对结构的不利影响^[3-11]。范重等^[12-13]在行波效应分析时，将0.5 km/s~1.5 km/s作为视波速的取值范围，并对视波速的影响因素进行了研究。陆宣行等^[14]、苏亮等^[15]在研究行波效应时，结合基岩中的波速，采用了1 km/s~2 km/s的较高视波速。

迄今，在进行行波效应分析时，对视波速取值并无统一认识，大部分学者倾向于以建筑场地覆盖层的等效剪切波速为基础，选取相应的视波速区间进行地震响应分析，以获得偏于安全的计算结果。

本文通过对地震波在单一土层和不同土层之间传播规律的研究，提出根据多土层剪切波速确定视波速的精确方法，并给出多土层视波速简化计算方法，便于工程应用。通过对建设场地进行工程地质勘察以及地震安全性评估，确定厦门新机场各土层的剪切波速、震源深度和震中距等参数，在此基础上确定用于行波效应分析的视波速。通过在柱底输入位移时程进行多维多点激励，在地震加速度时程积分过程中消除了位移时程曲线基线的漂移，同时避免了超低频响应的影响。提出的行波效应计算结果的处理方法，能够有效避免极少数构件内力增幅过大的不利影响。通过研究多点激励对结构底部剪力、扭转位移比、下部主体结构构件内力和大跨度屋盖杆件应力比的影响及其规律，确定各类构件多点激励的内力放大系数。本文内容可供超长结构行波效应分析时参考。

1 视波速确定方法

1.1 地质构造、剪切波速与震源距离

1.1.1 地质构造

绝大多数地震是由地壳运动引起的。地壳位于地球构造的最外层，大陆地壳主要成分为上层的花岗岩质层与下层的玄武岩质层，平均厚度为30 km~40 km。海洋地壳厚度小于大陆地壳，最小厚度只有几公里，主要成分为玄武岩^[1]。

地壳外侧为完整、坚硬的基岩层。基岩厚度一般不超过150 m，可作大型建筑工程的地基，是地壳与上部土层之间的过渡区域^[16-17]。

地表以下土体经过长期风化与沉积，土层地质情况差异很大。我国地域辽阔，土层厚度从几米到数十米，多则达数百米^[18]。覆盖层土体通常呈层状分布，从地表的软弱土层逐渐过渡为下部的坚硬土层。对工程建设具有直接影响的建筑场地覆盖层，为地面至剪切波速大于500 m/s的土层顶面。

1.1.2 剪切波速

根据地震波介质质点振动方向和波的行进方向，可将地震波分为纵波(P波)、横波(S波)、瑞雷波(Rayleigh波)和勒夫波(Love波)^[1]。其中，P波又称为压缩波，在地壳中的传播速度最快，波速大于6.0 km/s。S波的质点振动方向与地震波的行进方向垂直，又被称为剪切波，可引起结构左右与前后振动，对结构破坏性较强，是结构行波效应分析时考虑的主要地震作用。剪切波在地壳中的传播速度低于压缩波的传播速度，两者满足如下换算关系^[1]：

${v_{\rm{s}}} = \frac{1}{{1.7}}{v_{\rm{p}}}$

(1)

式中，v_s与v_p分别为剪切波与压缩波的波速。

基岩层位于建筑场地覆盖层与地壳之间，进一步可划分为全风化岩层、强风化岩层、中风化岩层和微风化岩层，为地壳的高速覆盖层，剪切波速介于地壳剪切波速与建筑场地覆盖层剪切波速之间。根据我国《岩土工程勘察规范》^[19]，基岩波速与其风化程度有关，见表1。由表1可知，随着风化程度提高，基岩的波速显著降低。

表 1 基岩波速比与风化程度的关系

Table 1. Relationship between wave velocity ratio and weathering degree of bedrock

风化程度	野外特征	波速比K_v
未风化	岩质新鲜，偶见风化痕迹	0.9~1.0
微风化	结构基本未变，仅沿节理面有渲染或变色，有少量风化裂隙	0.8~0.9
中风化	结构部分破坏，沿节理面有次生矿物，风化裂隙发育，岩体被切割成岩块	0.6~0.8
强风化	结构大部分破坏，矿物成分显著变化，风化裂隙很发育，岩体破碎	0.4~0.6
全风化	结构基本破坏，但尚可辨认，有残余结构强度	0.2~0.4
注：波速比K_v为风化岩石与新鲜岩石压缩波速度之比。

下载: 导出CSV

| 显示表格

场地覆盖土层剪切波的波速较低，软弱土层的剪切波速低于150 m/s。随着土层埋深加大，其密实性逐渐增强，坚硬土层的剪切波速可达500 m/s。

场地各岩层剪切波速的常见范围如表2所示。

表 2 场地覆盖土层的剪切波速

Table 2. Shear wave velocity of site overburden

土层名称	剪切波速v_s /(km·s⁻¹)
软弱土	≤0.15
中软土	0.15~0.25
中硬土	0.25~0.50
基岩	0.5~3.4
地壳	3.4~4.2

下载: 导出CSV

| 显示表格

1.1.3 震源深度与震中距

对震源深度的研究结果^[20]表明，全球75%以上地震的震源深度均小于60 km，对人员生命财产有重大影响地震的震源深度一般在10 km~30 km左右，位于地壳厚度范围内的活动断裂，是引发浅源构造地震的主要原因。

我国东部地区平均震源深度为(13±6) km，西部为(18±8) km，东部比西部平均偏浅5 km，我国大陆平均震源深度为(16±7) km^[21]。

位于发震断裂两侧10 km范围以内，应按照我国《建筑抗震设计规范》^[2]的要求计入近场效应的影响，对地震动参数进行放大。距离震源250 km~300 km半径以外的区域，地震的影响通常已经很小。

1.2 单一土层视波速计算

地震波从震源出发，经过土层传播到地面，此时假设土层为均质、单一土层，地震波不发生折射、反射、耗散等情况，剪切波波速v_s保持恒定，如图1所示。对于某一总长度为L的结构，其左、右端点分别为A和B，中点为C，其震中距为S。地震波到达A、B两点的时间差为Δt，采用视波速表征在地面观测得到地震波在A、B点之间的传播速度，定义在A、B两点之间的视波速v_app为：

$\begin{split} v_{{\rm{a}}{\rm{pp}}}^{AB} =& \dfrac{L}{{\Delta t}}{\rm{ = }}\dfrac{L}{{\dfrac{{{l_{OB}}}}{{{v_{\rm{s}}}}} - \dfrac{{{l_{OA}}}}{{{v_{\rm{s}}}}}}} = \\ & \dfrac{L}{{\sqrt {{D^2} + {{(S + L/2)}^2}} - \sqrt {{D^2} + {{(S - L/2)}^2}} }}v_{\rm{s}} \end{split}$

(2)

图 1 地震波在单一土层中传播图示

Figure 1. Illustration of seismic wave propagation in a single soil layer

下载: 全尺寸图片幻灯片

当结构单元长度L趋近于0时，A、B两点之间的视波速逐渐趋向于中点C的视波速。此时，建筑中点C的视波速可通过对式(2)取极限确定：

$v_{{\rm{app}}}^C = \mathop {\lim }\limits_{L \to {\rm{0}}} v_{{\rm{app}}}^{AB}$

(3)

此时，可将式(3)的分子分母同乘 $\sqrt {{D^2} + {{(S + L/2)}^2}} + \sqrt {{D^2} + {{(S - L/2)}^2}}$ ，可得：

$\begin{split} v_{{\rm{a}}{\rm{pp}}}^C \!= \!\!& \mathop {\lim }\limits_{L \to {\rm{0}}} \frac{{{\rm{(}}\sqrt {{D^2} \!+\! {{(S \!+\! L/2)}^2}} \! \!+\!\! \sqrt {{D^2} \!+\! {{(S \!-\! L/2)}^2}} {\rm{)}}}}{{2S}}{v_{\rm{s}}}= \!\\& \frac{{{v_{\rm{s}}}}}{{\cos \alpha }} \end{split} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$

(4)

由式(4)可知，对于均质土层来说，建筑中点的视波速即为土层的波速除以该点与震源水平夹角α的余弦。视波速以单一土层的剪切波速为下限，震中距减小、震源深度加大，视波速随之增大。

对于具有代表性的4组震源深度D与震中距S，中点视波速 $v_{{\rm{a}}{\rm{pp}}}^C$ 与根据建筑2个端点确定的视波速 $v_{{\rm{a}}{\rm{pp}}}^{AB}$ 的相对误差δ如表3所示。由表3可知，当结构单元长度L在100 m~600 m范围内，中点视波速与端点视波速非常接近，最大误差不超过0.01%。由此可见，完全可以采用建筑中点视波速代替传统根据建筑两个端点距离确定的视波速，结构单元长度对视波速的影响可以忽略不计。

表 3 中点视波速

$v_{{\rm{a}}{\rm{pp}}}^C$ 与端点视波速

$v_{{\rm{a}}{\rm{pp}}}^{AB}$ 的相对误差δ

Table 3. Relative error δ of Midpoint apparent wave velocity

$v_{{\rm{a}}{\rm{pp}}}^C$ and Endpoint apparent wave velocity

$v_{{\rm{a}}{\rm{pp}}}^{AB}$

/(%)

结构长度L/m	D=5 km S=200 km	D=10 km S=50 km	D=20 km S=10 km	D=30 km S=5 km
100	0.0000	0.0000	−0.0002	−0.0001
200	0.0000	0.0000	−0.0008	−0.0005
300	0.0000	0.0000	−0.0018	−0.0012
400	0.0000	0.0000	−0.0032	−0.0021
500	0.0000	0.0000	−0.0050	−0.0033
600	0.0000	−0.0001	−0.0072	−0.0047
注：δ= $(v_{ {\rm{a} }{\rm{pp}}}^C - v_{ {\rm{a} }{\rm{pp}}}^{AB})/v_{ {\rm{a} }{\rm{pp}}}^{AB} \times 100\text{%}$ 。

下载: 导出CSV

| 显示表格

1.3 地震波在不同土层之间的传播

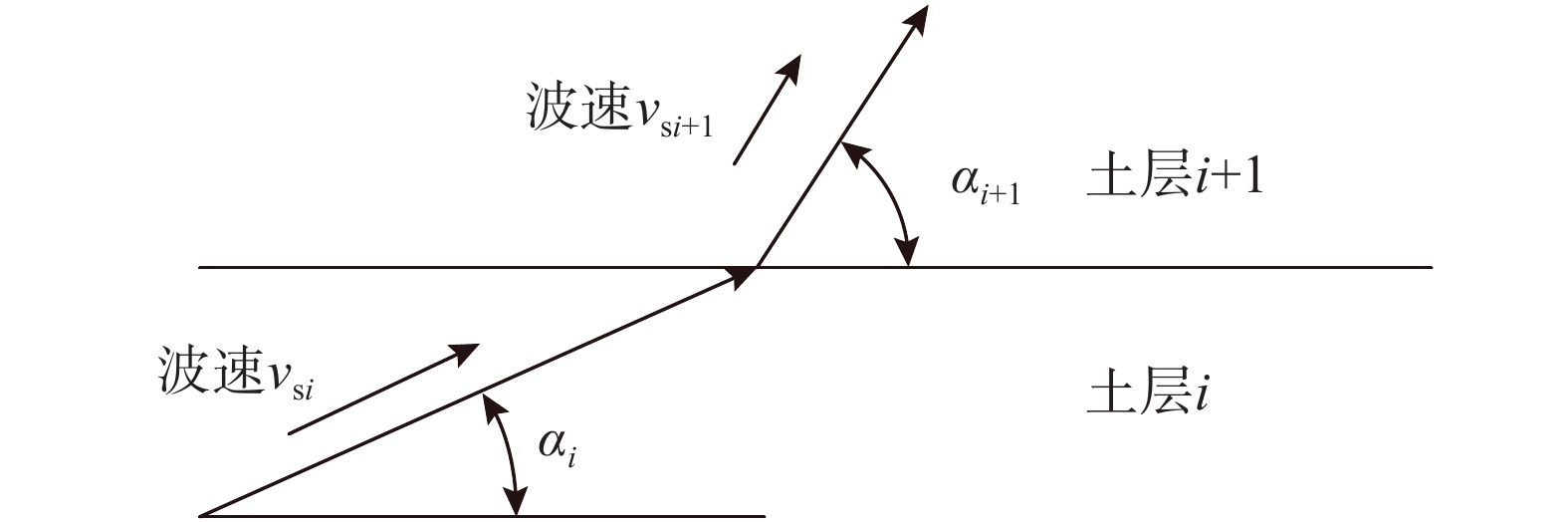
当地震波传播到不同土层界面时，会发生折射现象。设地震波以波速v_si、入射角α_i传播，以波速v_si+1、出射角α_i+1继续行进，地震波传播示意如图2所示。由斯奈尔定理^[1]可知，入射角α_i的余弦与出射角α_i+1的余弦之比等于剪切波速v_si与v_si+1之比，即：

$\frac{{\cos {\alpha _i}}}{{\cos {\alpha _{i + 1}}}}{\rm{ = }}\frac{{{v_{\rm{s}}}_i}}{{{v_{\rm{s}}}_{i + 1}}}$

(5)

图 2 相邻土层之间地震波传播示意

Figure 2. Illustration of seismic wave propagation between adjacent soil layers

下载: 全尺寸图片幻灯片

定义折射前视波速为 $v_{{\rm{a}}{\rm{pp}}}^i$ ，折射后视波速为 $v_{{\rm{a}}{\rm{pp}}}^{i + 1}$ ，由式(4)和式(5)可知：

$v_{{\rm{a}}{\rm{pp}}}^{i + 1}{\rm{ = }}\frac{{{v_{{\rm{s}}i + 1}}}}{{\cos {\alpha _{i + 1}}}} = \frac{{{v_{{\rm{s}}i}}}}{{\cos {\alpha _i}}} = v_{{\rm{a}}{\rm{pp}}}^i$

(6)

由式(6)可知，当地震波在不同土层之间发生折射后，虽然地震波的波速发生改变，但各土层的视波速保持不变。

1.4 多土层视波速计算

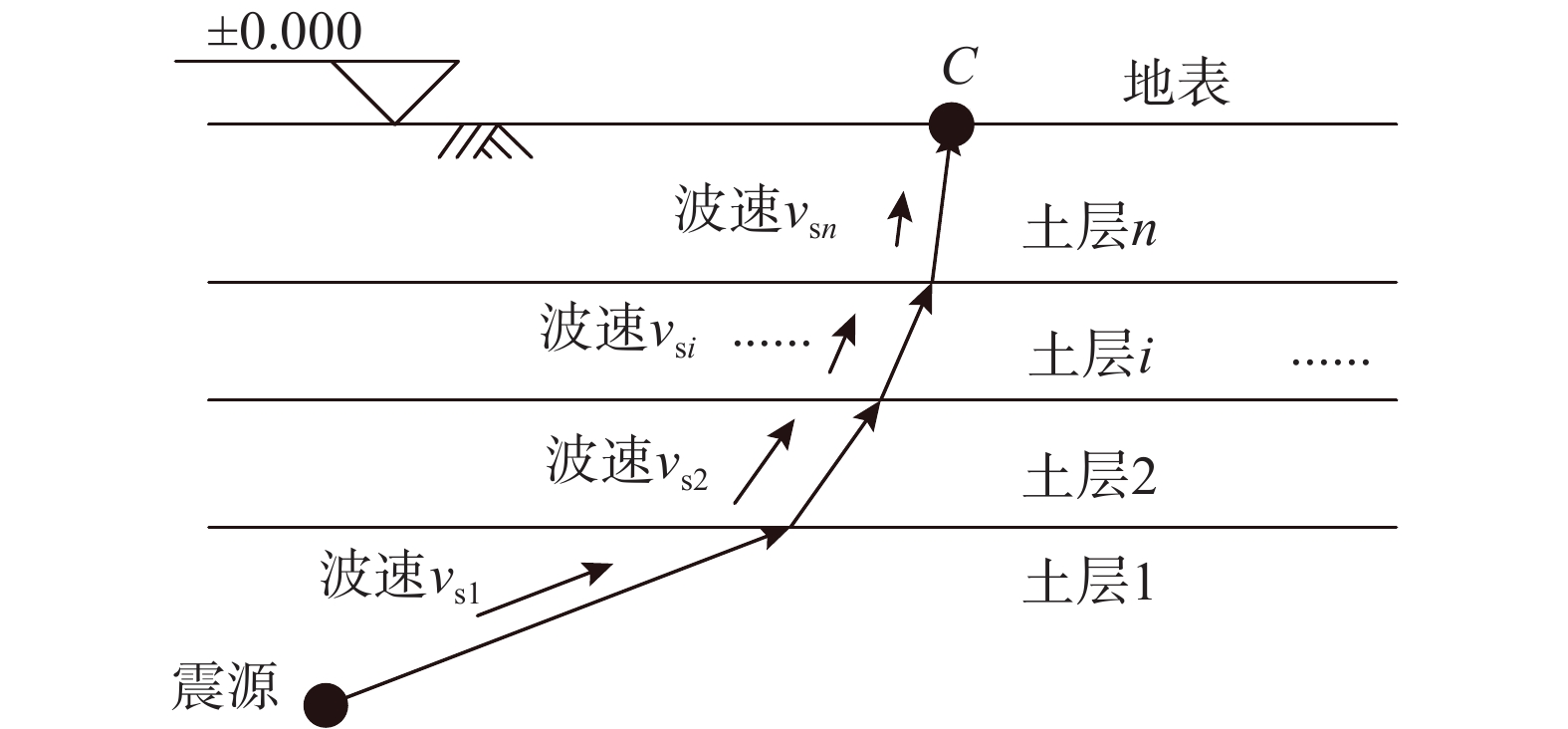
地震波从震源到达地表，需要穿过多个土层，当不考虑地震波反射的影响时，地震波的传播路径如图3所示，地震波由震源发出，以波速v_s1沿图示箭头方向传播，经过多个厚度为D_i的土层，在每层地质界面产生折射，折射后的传播角度与波速分别为α_i+1和v_si+1，最终到达地表C点。

图 3 多土层地震波传播路径示意

Figure 3. Propagation path illustration of seismic wave through multi-soil layers

下载: 全尺寸图片幻灯片

对于多土层地震波传播过程，假定在土层1中的视波速为 $v_{{\rm{app}}}^{}$ ，根据式(6)和图3，地震波从震源O传播至地表C点时，满足下列方程组：

$\left\{ \begin{split} & {v_{{\rm{app}}}} = \frac{{{v_{{\rm{s}}1}}}}{{\cos {\alpha _1}}}{\rm{ = }}\frac{{{v_{{\rm{s}}i}}}}{{\cos {\alpha _i}}}{\rm{ = }} \cdots {\rm{ = }}\frac{{{v_{{\rm{s}}n}}}}{{\cos {\alpha _n}}},\\&\qquad i = 1,2,3, \cdots ,n \\& \sum\limits_{i = 1}^n {\frac{{{D_i}}}{{\tan {\alpha _i}}}} = \sum\limits_{i = 1}^n {\frac{{{D_i}\cos {\alpha _i}}}{{\sqrt {1 - {{\cos }^2}{\alpha _i}} }}} {\rm{ = }}S \end{split} \right.$

(7)

由式(7)可知，地震波在任意土层中的传播角度 ${\alpha _i}$ 均可由在第1土层中的传播角度 ${\alpha _1}$ 表示：

$\sum\limits_{i = 1}^n {\frac{{{D_i}{k_i}\cos {\alpha _1}}}{{\sqrt {1 - {{({k_i}\cos {\alpha _1})}^2}} }}} = S$

(8)

式中， ${k}_{i}={v}_{{\rm s}i}/{v}_{{\rm s}1}, i=1,2,3, \cdots, n$ 。由于 ${k}_{i}、{D}_{i}>0$ ， $i = 1,2,3, \cdots, n$ ，由式(8)可知，该方程左侧为关于 $\cos {\alpha _1}$ 的单调递增函数，可由二分法等数值算法求得传播角度 ${\alpha _1}$ 的解。

为了分析比较方便起见，基于大量工程经验以及软土地基地质勘探资料^{[18, 22]}，并结合我国《建筑抗震设计规范》^[2]中建筑的场地类别，偏于保守地给出各类场地岩层厚度的范围，如表4所示。其中，Ⅳ类场地覆盖层总厚度为400 m，基岩厚度统一取150 m，地壳厚度均为30 km。

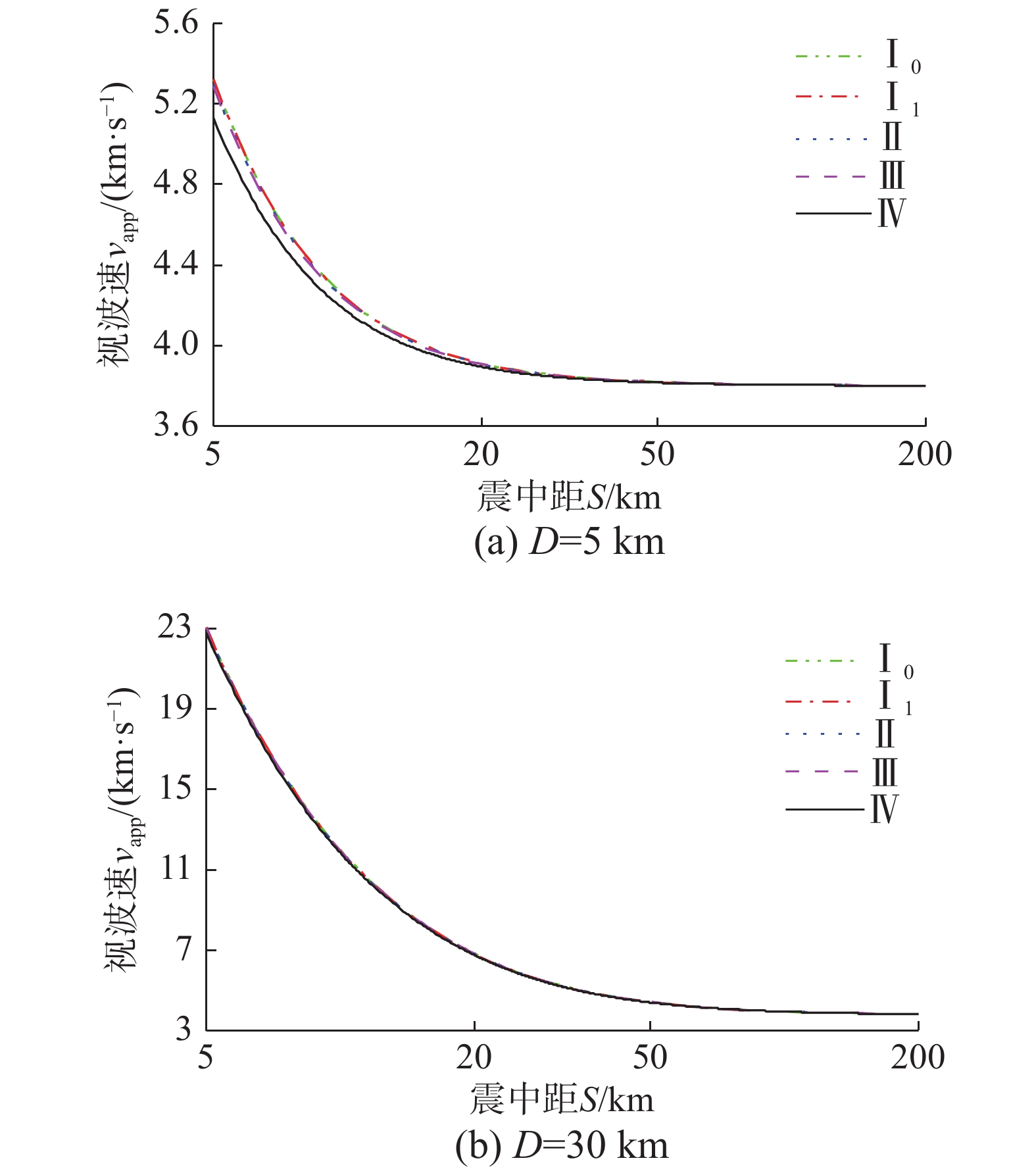
表 4 建筑场地类别与岩土层厚度

Table 4. Building site category and rock/soil thickness /km

场地类别	软弱土	中软土	中硬土	基岩	地壳
Ⅰ₀	0.000	0.000	0.000	0.150	30.00
Ⅰ₁	0.003	0.000	0.000	0.150	30.00
Ⅱ	0.000	0.030	0.020	0.150	30.00
Ⅲ	0.020	0.030	0.030	0.150	30.00
Ⅳ	0.020	0.030	0.350	0.150	30.00

下载: 导出CSV

| 显示表格

对于表4所示各建筑场地类别，当确定震中距S和震源深度D后，即可由式(8)与式(6)计算得到视波速。

各建筑场类别的视波速随震中距和震源深度的变化情况如图4所示。由图4可知：当震源深度较浅(D=5 km)时，在距震中30 km范围内视波速显著增大；除Ⅳ类场在震中距小于20 km范围内的视波速较小外，Ⅰ~Ⅲ类场地视波速的差异很小。当震源深度较深(D=30 km)时，震中距较小处的视波速可达地壳剪切波速的数倍；随着震中距增大，视波速逐渐降低；场地类别对视波速的影响进一步减小。视波速的下限值为3.80 km/s，接近于地壳的剪切波速。

图 4 视波速与震中距和震源深度的关系

Figure 4. Relationship between apparent wave velocity and epicentral distance and focal depth

下载: 全尺寸图片幻灯片

1.5 多土层视波速简化计算

考虑到前述视波速精确求解过程的复杂性，提出一种将多土层地质条件简化为均质土层地质条件的简化计算方法。首先，根据加权平均得到震源至地表多土层的剪切波速代表值：

${\bar v_{\rm{s}}} = \sum\limits_{i = 1}^n {\frac{{{D_i}}}{D} \cdot {v_{{\rm{s}}i}}} \qquad$

(9)

参照式(4)，可得等效均质土层的视波速 ${\bar v_{{\rm{app}}}}$ ：

${\bar v_{{\rm{app}}}} = \frac{{\sqrt {{D^2} + {S^2}} }}{S}{\bar v_{\rm{s}}}$

(10)

为了检验视波速简化方法的误差，选取不同震源深度D和震中距S进行计算分析，考察不同覆盖层厚度对土层剪切波速的影响，视波速简化算法的误差见表5。

从表5可知，除Ⅳ类场地浅源、远距地震(D=5 km，S=200 km)情况外，简化计算方法的误差不超过5%。由此可知，简化方法的计算结果与精确数值解较为接近，且均为负偏差，结构响应较大，偏于安全。

表 5 视波速简化计算方法的误差估计

Table 5. Error estimation of apparent wave velocity by Simplified Calculation Method /(%)

场地类别	D=5 km, S=200 km	D=10 km, S=50 km	D=20 km, S=10 km	D=30 km, S=5 km
Ⅰ₀	−1.46	−0.68	−0.05	0.00
Ⅰ₁	−1.52	−0.71	−0.05	0.00
Ⅱ	−2.39	−1.13	−0.09	−0.01
Ⅲ	−2.95	−1.40	−0.12	−0.01
Ⅳ	−8.72	−4.17	−0.41	−0.04
注：误差为 $({\bar v_{{\rm{app}}} } - {v_{{\rm{app}}} })/{v_{{\rm{app}}} } \times 100\text{%}$ 。

下载: 导出CSV

| 显示表格

1.6 视波速影响因素分析

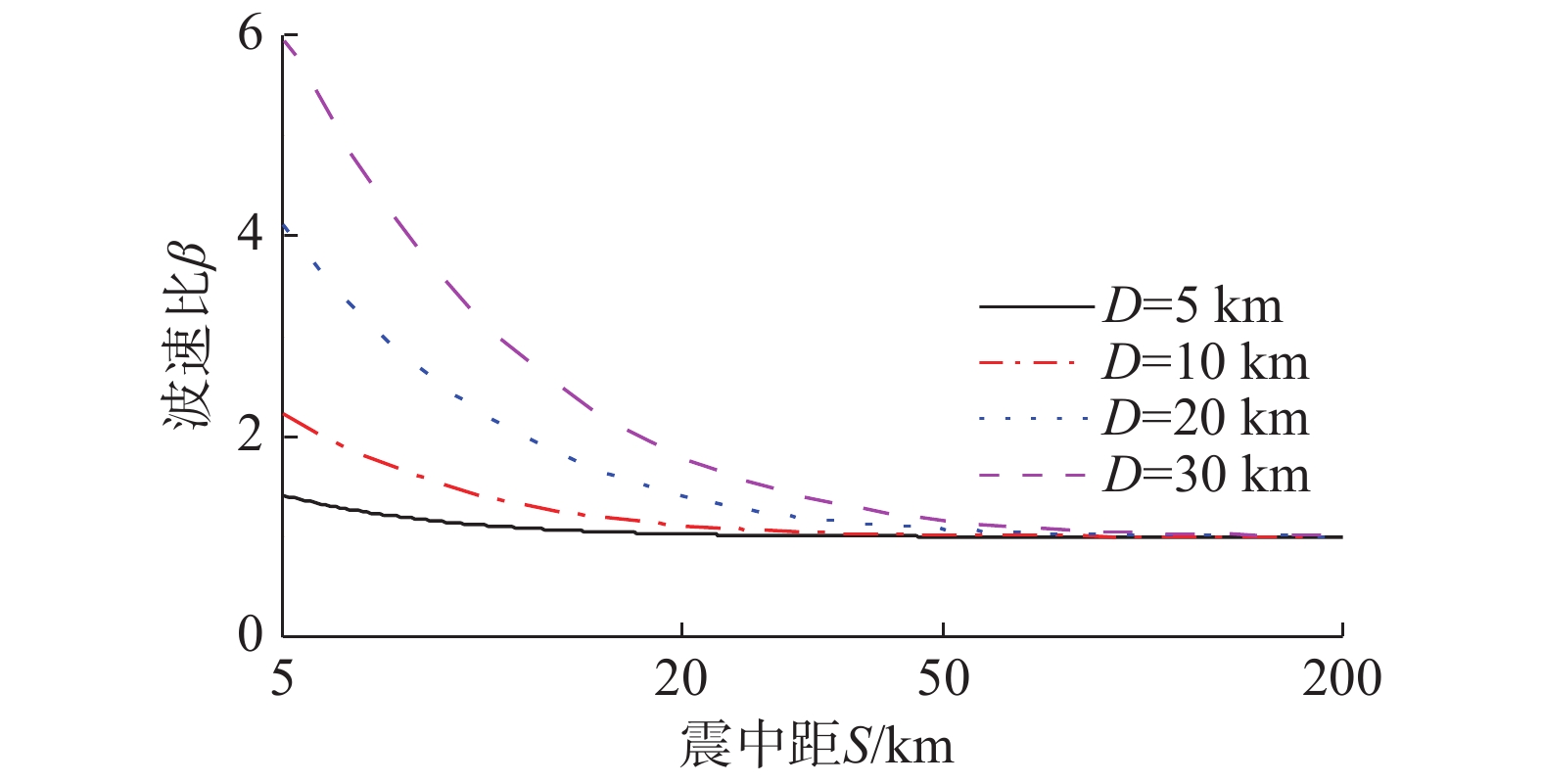
根据前述分析可知，结构单元长度对视波速影响很小，可以忽略不计。由式(10)可知，当已知场地的地质条件后，视波速主要与震源深度D、震中距S和剪切波速代表值有关。为了方便分析起见，本文将视波速 ${\bar v_{\rm app}}$ 与震源深度范围土层剪切波速代表值 ${\bar v_{\rm{s}}}$ 之比定义为波速比：

$\beta = {\bar v_{{\rm{app}}}}/{\bar v_{\rm{s}}}{\rm{ = }}\frac{{\sqrt {{D^2} + {S^2}} }}{S}$

(11)

由式(11)可知，视波速比与场地类别无关。波速比β随震源深度D与震中距S的变化情况如图5和表6所示。由图5和表6可知，当震源深度D保持不变时，β随震中距S增大而减小，但不小于1.0；当震中距S保持不变时，β随震源深度D增大而增大。在震中距S=5 km~200 km、震源深度D=5 km~30 km范围内，波速比β=1.00~6.08。

图 5 视波速比与震源深度和震中距的关系

Figure 5. Relationship between apparent wave velocity ratio and focal depth and epicenter distance

下载: 全尺寸图片幻灯片

表 6 常见地震工况的视波速比β

Table 6. Apparent wave velocity ratio β in common seismic conditions

震源深度D/km	震中距S/km
震源深度D/km	5	10	20	50	100	200
5	1.41	1.12	1.03	1.00	1.00	1.00
10	2.24	1.41	1.12	1.02	1.00	1.00
20	4.12	2.24	1.41	1.08	1.02	1.00
30	6.08	3.16	1.80	1.17	1.04	1.01

下载: 导出CSV

| 显示表格

2 场地地质构造与视波速确定

2.1 工程概况

厦门新机场工程选址位于福建省厦门市翔安区大嶝岛及与小嶝岛之间的部分海域，建设用地除部分利用大嶝岛外，主要以吹砂填海为主。场址距厦门本岛市中心直线距离约25 km，距泉州约44 km，距漳州约72 km，距台湾省金门岛约15 km。

厦门新机场为区域性枢纽机场、国际货运口岸、对台重要通道。厦门新机场近期规划占地面积约14.24 km²，建设2条远距平行跑道，T1航站楼设计年旅客吞吐量为4500万人次，货邮吞吐量75万吨，飞机起降量37万架次。

T1航站楼建筑三重屋檐造型源于闽南风格建筑中大厝的元素，如图6所示。航站楼主楼地下1层，地上3层，局部带有夹层，结构最大高度约45.0 m。

图 6 厦门新机场

Figure 6. Xiamen New Airport

下载: 全尺寸图片幻灯片

T1航站楼(含指廊)两个方向的最大尺寸分别为1300 m和980 m，其中主楼平面尺寸为468 m×354 m。故此，根据我国《建筑抗震设计规范》^[2]的要求，需要考虑地震行波效应的影响。

2.2 场地地震动参数

2.2.1 覆土层厚度与剪切波速

厦门新机场拟建场地位于大嶝岛的东南部，原为近岸孤岛，因泥砂淤积而变大，多为沙滩沙丘，属砂质海岸地貌，基底由燕山期花岗岩组成。现已吹填海砂成陆，经过超载预压+塑料排水板地基处理，地貌类型属滨海滩涂，场地地形整体较为平坦^[23]。

根据我国《建筑抗震设计规范》^[2]，拟建场地抗震设防烈度为7度(0.15 g)，设计地震分组为第三组，建筑场地类别为Ⅱ类，特征周期T_g=0.45 s。根据《厦门新机场工程场地地震安全性评价报告(修改稿)》^[24]，场地平均等效剪切波速为178.6 m/s，覆土层平均厚度为35.0 m。

2.2.2 震源深度

利用仪器记录区域内1970年1月−2017年12月M≥2.0地震共1913次，震源深度统计^[24]见表7，地震震源深度主要分布在1.0 km~20 km范围，占地震总数92.1%，在5 km~15 km范围尤为集中，占总数的67.0%，说明工程所在区域的震源深度较浅，属于地壳内浅源构造地震。不同震级震源深度分布情况见表8，区域内各震级地震平均深度为11.4 km，4级以上地震的平均深度为15.2 km。

表 7 区域范围内地震震源深度分布

Table 7. Depth distribution of earthquake sources within the region

深度/km	地震个数	百分比/(%)	深度/km	地震个数	百分比/(%)
0~5	198	10.4	20~25	102	5.3
5~10	897	46.9	25~30	34	1.8
10~15	384	20.1	30以上	14	0.7
15~20	284	14.8

下载: 导出CSV

| 显示表格

表 8 区域范围内不同震级震源深度分布

Table 8. Depth distribution of earthquake sources with different magnitudes in the region

震级M	平均深度 /km	地震个数
2.0~2.9	11.1	1553
3.0~3.9	12.1	324
≥4.0	15.2	36

下载: 导出CSV

| 显示表格

2.2.3 震中距

近场范围内有记载的破坏性地震(M≥4.7)4次，位于工程场址东北部和东南部，如表9所示，平均震中距为26.25 km。近场现今地震活动较弱，主要位于东南部近海一带，地震震中分布呈零星状。

表 9 近场区破坏性地震统计

Table 9. Destructive earthquake statistics in the near field

序号	发震时间	震中位置/(°)		参考地名	震级	震中烈度	距离/ km	计算烈度	影响烈度
序号	年月日	北纬	东经	参考地名	震级	震中烈度	距离/ km	计算烈度	影响烈度
1	1538.10.*	24.7	118.5	晋江安海	4_3/4	Ⅵ	21	4.6	Ⅴ
2	1691.05.*	25.0	118.7	晋江安海	4_3/4	Ⅵ	14	4.9	Ⅴ
3	1906.3.28	24.3	118.6	厦门海外	6_1/4		35	6.5	Ⅶ
4	1906.3.29	24.3	118.6	厦门海外	5_1/2		35	5.3	Ⅴ

下载: 导出CSV

| 显示表格

2.2.4 地壳结构与波速

场地剪切波速测试采用单孔检层法^[24]，覆土层平均厚度为35.0 m，场地20 m深度的平均等效剪切波速为178.6 m/s，20 m~35 m深度的平均等效剪切波速为279.3 m/s。

根据福建省邵武－平潭地壳结构剖面^[25]，厦门新机场地壳结构分为上、中、下三层，地壳厚度从闽西北的33 km过渡至闽东的29 km。

根据实测P波的波速^[25]，根据式(1)可以得到拟建场地P波和S波波速平均值，见表10。

表 10 场地地壳厚度、P波与S波的波速

Table 10. Crust thickness, P wave and S wave velocity of the site

地层名称	土层厚度 D_i/km	平均厚度 ${\bar D_i}$ /km	纵波波速 ${v_{\rm{p} } }$ /(km·s⁻¹)	平均纵波波速 ${\bar v_{\rm{p} }}$ /(km·s⁻¹)	平均横波波速 ${\bar v_{\rm{s} } }$ /(km·s⁻¹)
上地壳	1.84~4.63	3.235	5.00~5.90	5.45	3.20
中地壳	12.50~16.35	14.425	6.00~6.26	6.13	3.61
下地壳	12.42~14.38	13.400	6.37~6.82	6.60	3.88

下载: 导出CSV

| 显示表格

根据《厦门新机场工程场地地震安全性评价报告(修改稿)》^[24]，取震中距S=26.25 km，震源深度D=15.2 km，结合土层波速测试结果与地壳结构深地震探测结果，各土层及剪切波速见表11。

表 11 厦门新机场土层分布与剪切波速

Table 11. Soil layer distribution and S wave velocity of Xiamen New Airport

土层名称	土层界面深度/ km	土层厚度 D_i/km	土层剪切波速 v_s/(km·s⁻¹)
地表	0.000	−	−
低速覆盖层	0.020	0.020	0.178
中速覆盖层	0.035	0.015	0.279
高速覆盖层	0.630	0.595	1.700
上地壳	3.865	3.235	3.200
中地壳	15.200	11.335	3.610

下载: 导出CSV

| 显示表格

由式(8)与式(7)，求得视波速的精确数值解为4.07 km/s。

在进行厦门新机场行波效应分析时，以视波速v_app的精确解为基础。为了使计算结果偏于安全起见，考虑波速在±25%范围内波动，共选取3.0 km/s、4.0 km/s和5.0 km/s三种视波速。

3 行波效应计算方法

3.1 结构体系

在厦门新机场航站楼设计时，为了减小混凝土收缩以及温度应力的不利影响，将航站楼主楼3层(14.8 m标高)以下的主体结构划分成6个单元，设缝后最大结构单元平面尺寸为182 m×180 m。

航站楼主楼3层以下柱网尺寸为18 m×18 m，主体结构采用钢筋混凝土框架结构，楼盖采用现浇钢筋混凝土梁板体系。框架梁截面尺寸主要为1100 mm×1200 mm，次梁间距4.5 m×4.5 m，楼板厚度150 mm，混凝土强度等级均为C40。

支承大跨度屋盖钢管柱(14.8 m标高以上)的柱距主要为36 m×36 m。在主楼中部设置4根支承屋盖的跃层开花柱，柱距为72 m，下部采用钢管混凝土构件，上部通过铸钢节点转换为4根变截面矩形V形柱支承大跨度钢屋盖中部的船形桁架。航站楼大跨度屋盖不设结构缝，采用钢网架结构，T1航站楼主楼结构平面布置见图7，主要结构构件规格见表12。

图 7 T1航站楼主楼结构布置　/m

Figure 7. Structural layout of the Main Building for Terminal One

下载: 全尺寸图片幻灯片

表 12 航站楼主楼结构构件截面规格

Table 12. Dimensions of structural members for T1 Main Building

部位	尺寸/mm	强度等级	备注
混凝土柱	D1200~ D1600	C50	用于14.8 m标高以下
钢管柱	D1000×30~ D1500×50	Q355B、Q420C	14.8 m标高以上
开花柱下柱	D2300×60	Q355B、C50	±0.000~28.8 m标高，钢管混凝土柱
开花柱上斜柱	□1200~900× 700~500×40	Q355B	28.8 m标高以上
大跨屋盖杆件	D127×5~D500×25	Q355B	−

下载: 导出CSV

| 显示表格

3.2 地震波选取

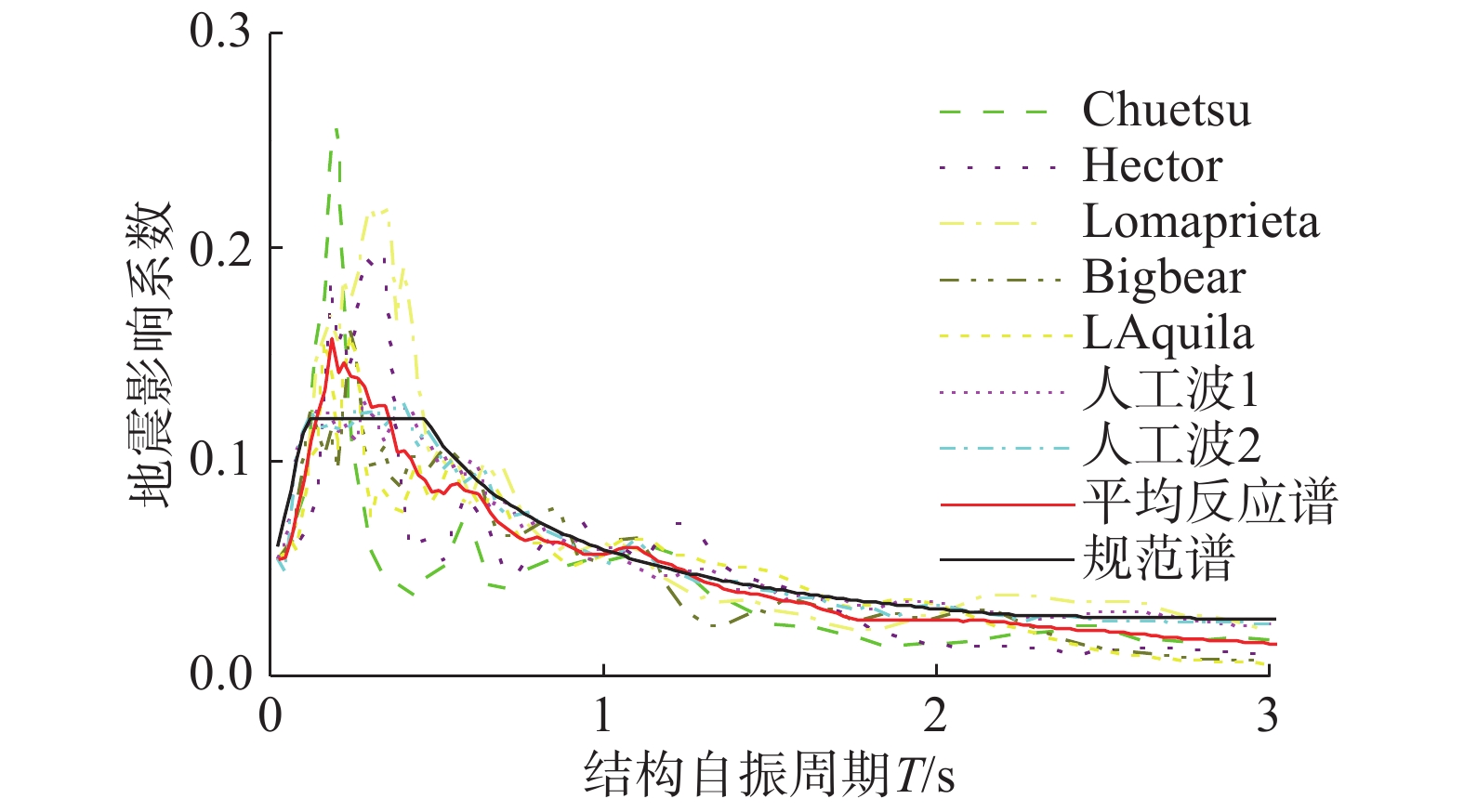
航站楼结构设计基准期为50年。本文共选取7组地震加速度时程记录，包括5组天然波和2组人工波，将地震作用的主方向、次方向和竖向分别按照1.0∶0.85∶0.65的比例进行三向激励。

7组地震波的反应谱曲线与我国《建筑抗震设计规范》^[2]反应谱曲线的对比见图8。根据计算结果，X方向地震作用时，7条波底部剪力的最小值为反应谱法的90.85%，平均值为反应谱法的104.5%；Y方向地震作用时，7条波底部剪力的最小值为反应谱法的91.9%，平均值为反应谱法的98.7%；7条波反应谱曲线在结构前三个周期点与规范谱的最大偏差平均值为−8%，满足相关要求。

图 8 地震加速度时程的反应谱与规范反应谱

Figure 8. Response spectrum of seismic waves and spectrum of Code for seismic design of buildings

下载: 全尺寸图片幻灯片

3.3 地震波输入方法

为了研究行波效应对下部多个混凝土结构单元+上部整体钢屋盖结构的影响，本文假定地震波沿建筑多个方向进行传播，分别采用三种视波速对结构柱底施加三向地震位移时程激励。

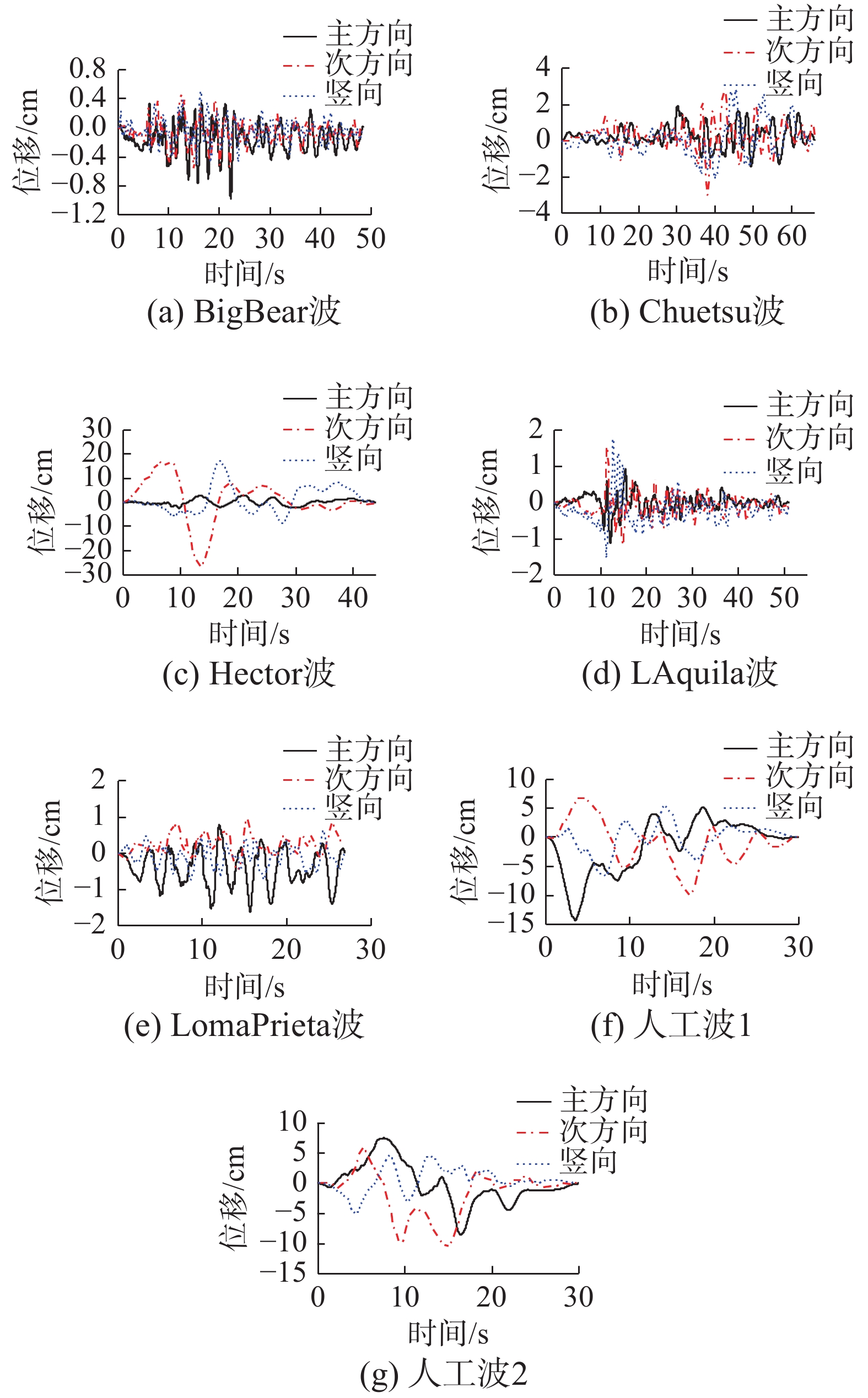
通过对7组地震加速度时程进行二次积分，得到地震位移时程。为了消除积分过程位移时程曲线发生基线漂移现象，本文采用EMD算法^[26]对位移时程进行基线归零处理，并通过控制初始条件避免超低频响应对位移时程的影响^[27]。行波效应分析采用的地震位移时程如图9所示。

图 9 地震位移时程记录

Figure 9. Seismic displacement time-history records

下载: 全尺寸图片幻灯片

3.4 地震波传播方向

考虑到在一般情况下地震传播方向的不确定性，根据本工程的特点，在360°范围内共选取8个方向角，分别进行一致输入地震激励与多点输入地震激励，考察整体结构与各类构件位移与内力的响应。

将航站楼柱底沿0°方向间隔18 m进行分组，共计27组，分别控制每组柱底地震波到达时间，如图10(a)所示。同样，将航站楼柱底沿90°方向间隔18 m进行分组，共计21组，如图10(b)所示。沿45°与135°方向每隔12.72 m进行分组，分别为38组，见图10(c)和图10(d)。

图 10 多点地震激励输入工况

Figure 10. Input cases of multiple support excitation

下载: 全尺寸图片幻灯片

3.5 计算结果处理方法

为了对多点激励和一致激励计算得到的地震力、结构变形以及构件内力等进行比较，定义多点激励计算变量的影响系数 $\gamma$ 如下：

$\gamma = \frac{{{F_{{\rm{me}}}}}}{{{F_{{\rm{se}}}}}}$

(12)

式中，F_me与F_se分别为在各地震波作用下多点激励与一致激励计算结果的最大值。

在多点地震激励作用下，极少数构件的内力影响系数可能远大于1.0，出现多点激励效应异常增大的情况。多点激励内力影响系数过大的主要原因，往往由于极少数构件在一致激励时内力很小，多点激励可能引起内力变化幅度很大。

在进行超长结构设计时，难以针对单个构件考虑行波效应的影响。通常采用统一的内力影响系数对某类构件的地震作用进行放大。为了避免极少数构件内力影响系数过大造成设计不合理，可以根据结构抗震设计理念与大量工程经验，采用95%较小内力影响系数的最大值确定该类构件地震行波效应的放大系数。

4 结构的地震响应

4.1 基底剪力

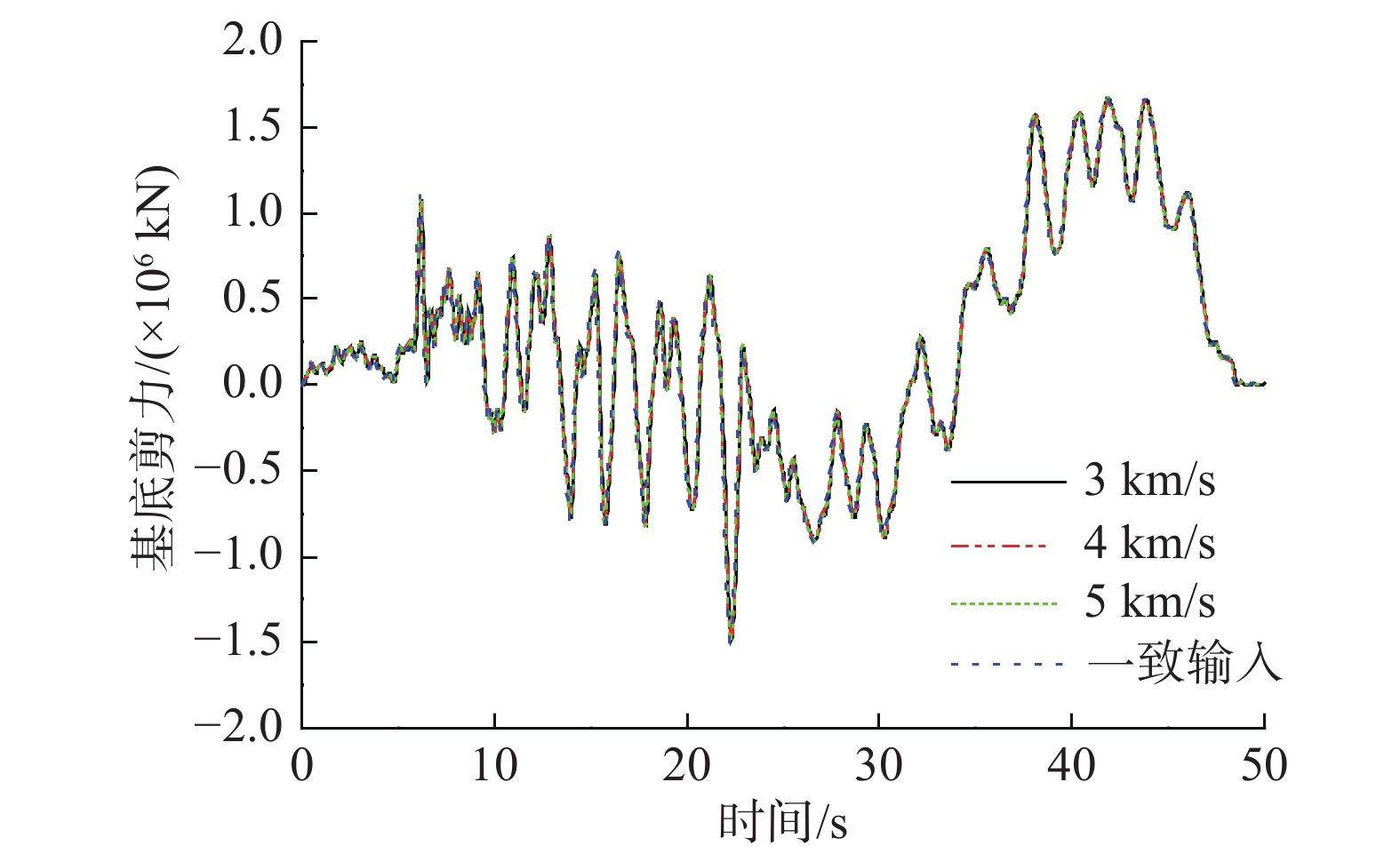
BigBear 波在0°方向作用时，厦门新机场航站楼主楼的基底剪力随时间的变化情况如图11所示。由图可知，与地震一致输入相比，考虑行波效应后基底总剪力微有减小，但差异很小，3.0 km/s、4.0 km/s和5.0 km/s三种视波速对基底总剪力的影响均很小。

图 11 0°方向地震激励时结构基底剪力的时程

Figure 11. Time-history record of base shear force at 0° direction earthquake excitation

下载: 全尺寸图片幻灯片

在7条地震波作用下，与各激励方向相应的基底剪力影响系数见表13，三种视波速的平均值分别为0.997、0.998和0.999，各激励方向差别很小。

表 13 结构基底剪力影响系数

Table 13. Effect coefficients of base shear force for the structure

激励方向/(°)	视波速v_app/(km·s⁻¹)
激励方向/(°)	3	4	5
0	0.996	0.998	0.998
180	0.997	0.998	0.999
90	0.998	0.999	0.999
270	0.996	0.998	0.998
45	0.998	0.999	0.999
225	0.998	0.998	0.999
135	0.999	1.000	1.000
315	0.997	0.998	0.998

下载: 导出CSV

| 显示表格

4.2 结构扭转位移比

采用扭转位移比反映结构的扭转效应，对6个结构单元分别提取各工况下扭转位移比时程分析结果，将多点激励与一致激励最大扭转位移的比值作为结构的扭转影响系数。2层各工况相应的结构扭转影响系数见表14。由表14可知，地震行波效应对各结构单元扭转效应总体上影响不大，扭转比最大影响系数约为1.08；结构的扭转影响系数具有随视波速降低而增大的趋势。

表 14 主体结构单元扭转比影响系数(2层)

Table 14. Effect coefficients of torsional ratios for structural units (2nd Floor)

激励方向/(°)	视波速v_app/(km·s⁻¹)	A1	A2	A3	A4	A5	A6
0	3.0	1.02	0.99	1.02	1.00	0.89	1.03
	4.0	1.02	0.99	1.01	0.98	0.88	1.04
	5.0	1.01	1.00	1.01	0.97	0.98	1.04
180	3.0	1.01	1.04	1.00	1.02	1.06	1.14
	4.0	1.00	1.00	1.00	1.02	1.06	1.01
	5.0	1.01	1.01	1.01	1.01	1.05	1.01
90	3.0	0.99	1.02	0.99	1.10	0.98	1.06
	4.0	0.99	1.01	0.99	1.08	0.97	1.03
	5.0	0.99	1.01	0.99	1.02	0.97	1.02
270	3.0	0.92	1.02	1.06	1.09	1.04	1.17
	4.0	0.92	0.99	1.02	1.07	1.02	1.06
	5.0	0.94	0.99	1.00	1.05	1.03	1.04
45	3.0	0.96	0.94	0.92	1.03	0.98	0.98
	4.0	0.96	0.98	0.93	1.03	0.97	0.96
	5.0	0.96	0.97	0.94	1.02	0.98	0.96
225	3.0	1.02	0.99	0.97	1.07	1.02	1.35
	4.0	1.02	1.00	0.98	1.03	1.00	1.33
	5.0	1.01	0.99	0.98	1.00	1.00	1.31
135	3.0	1.06	1.04	1.08	1.06	0.99	1.01
	4.0	1.01	1.02	1.08	1.03	0.99	1.00
	5.0	1.00	1.02	1.07	1.02	1.00	1.00
315	3.0	1.08	1.03	0.98	1.01	0.98	0.94
	4.0	1.04	1.02	0.98	1.00	0.99	0.93
	5.0	1.03	1.01	0.96	1.01	0.99	0.94
平均值	3.0	1.01	1.01	1.00	1.05	0.99	1.08
	4.0	0.99	1.00	1.00	1.03	0.99	1.04
	5.0	0.99	1.00	0.99	1.01	1.00	1.04

下载: 导出CSV

| 显示表格

4.3 下部主体结构框架柱

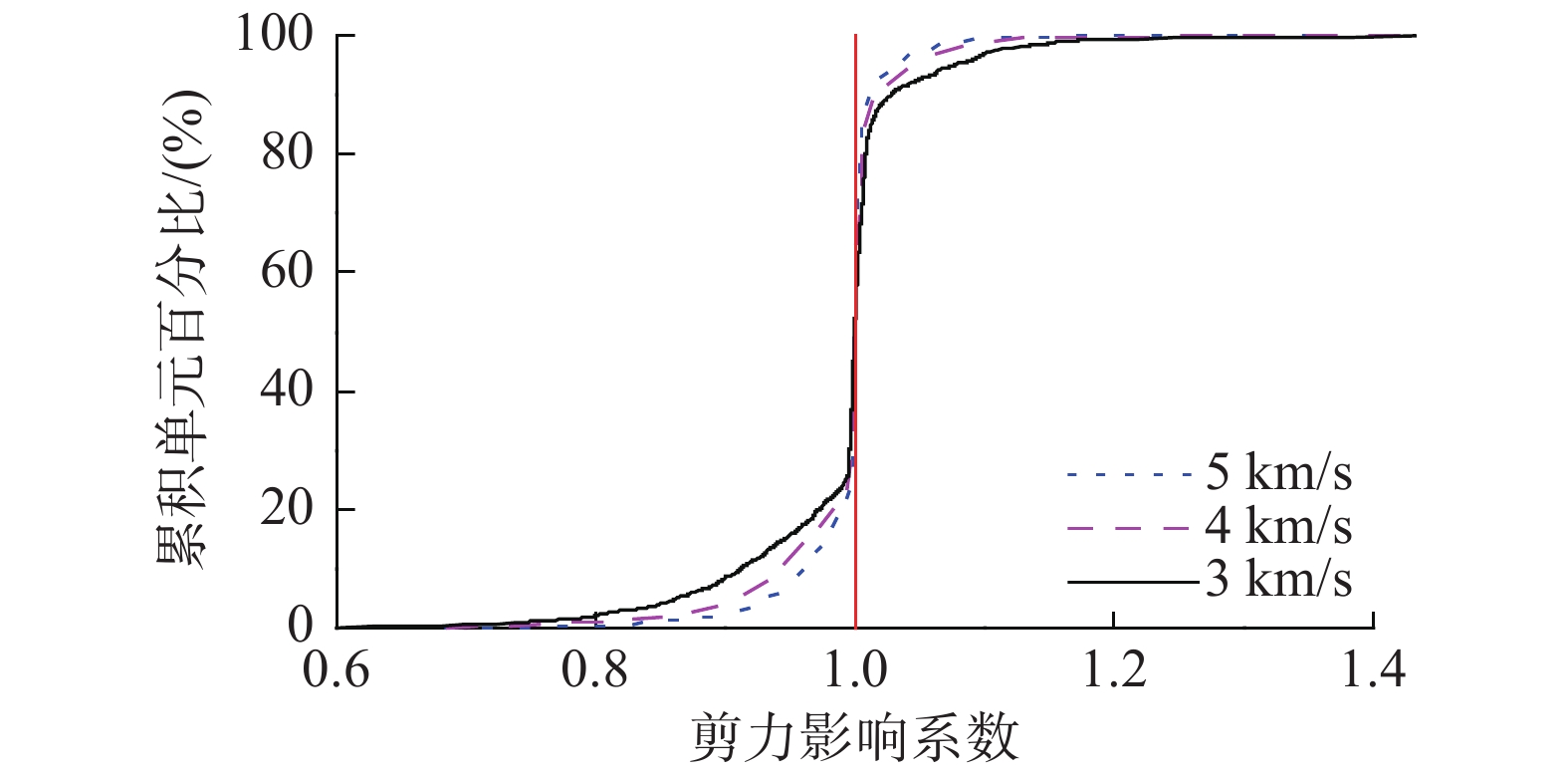
在0°方向BigBear波激励时，框架柱剪力影响系数的分布如图12所示。由图12可知，对于3.0 km/s、4.0 km/s和5.0 km/s三种视波速，框架柱剪力影响系数大部分位于1.0附近；随着视波速增大，框架柱剪力影响系数变化范围逐渐缩小，剪力影响系数接近于1.0框架柱的数量增多。

图 12 0°方向地震激励时框架柱剪力影响系数分布

Figure 12. Distribution of shear force effect coefficient of frame columns at 0°direction earthquake excitation

下载: 全尺寸图片幻灯片

在7条地震波以3.0 km/s、4.0 km/s和5.0 km/s三种视波速作用下，下部主体结构框架柱的剪力影响系数如表15所示。由表15可知，框架柱剪力影响系数的平均值分别为1.004、1.002和1.001，说明考虑行波效应时，框架柱剪力的变化幅度很小；平均有6.2%、3.9%和2.5%框架柱的剪力影响系数大于1.05，但个别构件内力增幅超过50%；95%框架柱剪力影响系数最大值的均值分别为1.062、1.041和1.030，可见随着视波速增大，行波效应对框架柱的影响逐渐减小。

表 15 框架柱剪力影响系数

Table 15. Effect coefficients of shear forces for frame columns

激励方向/(°)	视波速 v_app/(km·s⁻¹)	剪力影响系数最大值γ_V,max	95%剪力影响系数最大值95%γ_V,max	剪力影响系数平均值 $\overline \gamma_V$	$\overline \gamma_V$ >1.05 占比/(%)
0	3.0	1.456	1.087	1.005	7.6
	4.0	1.316	1.056	1.003	5.0
	5.0	1.240	1.039	1.002	3.3
45	3.0	1.275	1.066	1.004	6.5
	4.0	1.176	1.042	1.001	4.0
	5.0	1.128	1.030	1.000	2.6
90	3.0	1.197	1.044	0.999	4.1
	4.0	1.144	1.031	0.999	2.2
	5.0	1.116	1.024	0.998	1.3
135	3.0	1.273	1.041	0.999	3.7
	4.0	1.191	1.028	0.998	2.3
	5.0	1.146	1.021	0.999	1.5
180	3.0	1.497	1.071	1.004	7.0
	4.0	1.349	1.042	1.002	4.4
	5.0	1.265	1.030	1.001	2.6
225	3.0	1.541	1.074	1.010	8.5
	4.0	1.389	1.051	1.006	5.7
	5.0	1.300	1.037	1.004	3.9
270	3.0	1.405	1.059	1.007	6.9
	4.0	1.282	1.043	1.004	4.4
	5.0	1.209	1.034	1.003	3.1
315	3.0	1.414	1.053	1.003	5.2
	4.0	1.303	1.036	1.002	3.4
	5.0	1.242	1.027	1.001	2.2
平均值	3.0	1.382	1.062	1.004	6.2
	4.0	1.269	1.041	1.002	3.9
	5.0	1.206	1.030	1.001	2.5

下载: 导出CSV

| 显示表格

BigBear波在0°方向以4.0 km/s的视波速进行激励时，剪力影响系数大于1.05的框架柱位置见图13。由图13可知，对行波效应较为敏感的框架柱主要分布在各主体结构单元的周边，特别是平面的远端。

图 13 0°方向地震激励时框架柱剪力影响系数大于1.05构件的分布

Figure 13. Distribution of shear force effect coefficient greater than 1.05 for frame columns at 0° direction earthquake excitation

下载: 全尺寸图片幻灯片

4.4 支承屋盖钢管柱

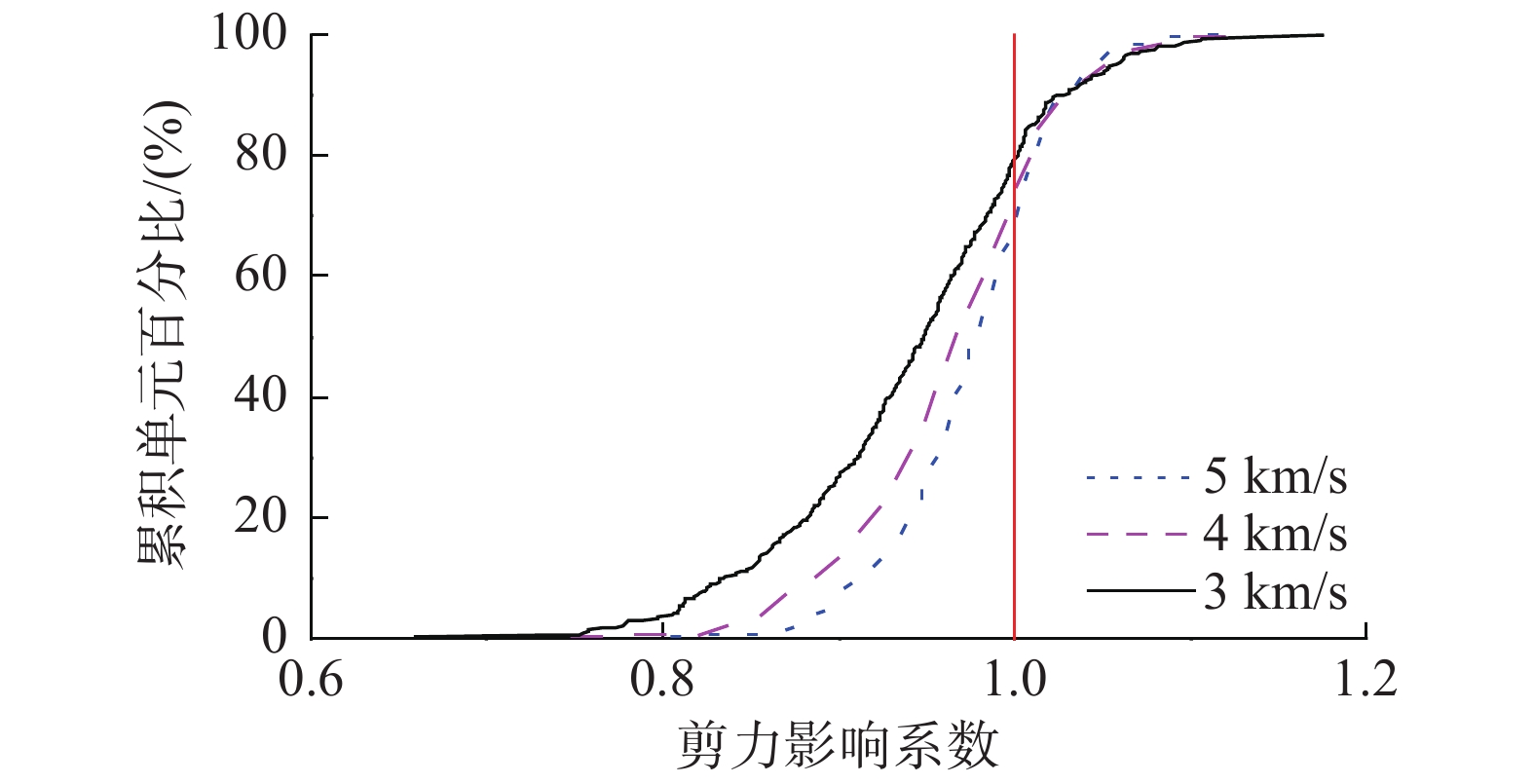
BigBear波在0 º方向进行激励时，支承屋盖钢管柱剪力影响系数的分布情况如图14所示。由图14可知，对于3.0 km/s、4.0 km/s和5.0 km/s三种视波速，剪力影响系数的均值均小于1.0，其值域范围分别为0.66~1.18、0.75~1.13和0.81~1.12。随着视波速增大，其峰值逐渐降低，值域范围缩小，剪力影响系数接近于1.0构件的数量增多。

图 14 0°方向地震激励时支承屋盖钢管柱剪力影响系数分布

Figure 14. Distribution of shear force effect coefficients of supporting roof steel columns at 0°direction Earthquake Excitation

下载: 全尺寸图片幻灯片

在3.0 km/s、4.0 km/s和5.0 km/s三种视波速作用下，14.8 m标高以上支承屋盖钢管柱行波效应的剪力影响系数见表16。由表16可知，支承屋盖钢管柱剪力影响系数的平均值分别为0.980、0.988和0.992，平均有6.5%、5.0%和3.7%钢管柱的剪力影响系数大于1.05，说明考虑行波效应时钢管柱地震剪力总体上略有减小，但个别构件内力增幅超过20%，95%钢管柱剪力影响系数最大值的均值分别为1.057、1.047和1.039。随着视波速增大，钢管柱剪力影响系数的峰值逐渐降低。

表 16 支承屋盖钢管柱剪力影响系数

Table 16. Effect coefficients of shear forces for supporting roof steel columns

激励方向/(°)	视波速v_app/ (km·s⁻¹)	剪力影响系数最大值γ_V,max	95%剪力影响系数最大值95%γ_V,max	剪力影响系数平均值 $\overline \gamma_V$	$\overline \gamma_V$ >1.05 占比 /(%)
0	3.0	1.190	1.053	0.977	6.1
	4.0	1.146	1.043	0.987	5.2
	5.0	1.124	1.039	0.992	4.0
45	3.0	1.215	1.070	0.988	8.1
	4.0	1.165	1.058	0.993	6.7
	5.0	1.133	1.047	0.996	5.0
90	3.0	1.271	1.070	0.993	8.8
	4.0	1.191	1.055	0.997	6.3
	5.0	1.142	1.045	0.999	5.0
135	3.0	1.197	1.055	0.986	6.3
	4.0	1.152	1.046	0.992	4.6
	5.0	1.129	1.038	0.996	3.5
180	3.0	1.289	1.051	0.972	5.5
	4.0	1.219	1.043	0.983	4.3
	5.0	1.173	1.036	0.988	3.4
225	3.0	1.190	1.060	0.972	6.5
	4.0	1.150	1.049	0.982	5.2
	5.0	1.126	1.040	0.987	3.7
270	3.0	1.204	1.058	0.978	6.4
	4.0	1.156	1.047	0.986	4.8
	5.0	1.121	1.038	0.990	3.4
315	3.0	1.155	1.039	0.976	3.9
	4.0	1.125	1.033	0.985	2.6
	5.0	1.103	1.028	0.990	1.7
平均值	3.0	1.214	1.057	0.980	6.5
	4.0	1.163	1.047	0.988	5.0
	5.0	1.131	1.039	0.992	3.7

下载: 导出CSV

| 显示表格

BigBear波在0°方向激励时，支承屋盖钢管柱剪力影响系数大于1.05构件的分布见图15。由图15可知，剪力影响系数大于1.05钢管柱的数量较少，主要集中在结构单元相邻部位以及各结构单元的周边。

图 15 0°方向地震激励时支承屋盖钢管柱剪力影响系数大于1.05构件的分布

Figure 15. Distribution of shear force effect coefficient greater than 1.05 for supporting roof steel columns at 0°direction earthquake excitation

下载: 全尺寸图片幻灯片

4.5 开花柱

在行波效应分析时得到开花柱的剪力影响系数见表17。由表17可知，在3.0 km/s、4.0 km/s和5.0 km/s三种视波速作用下，开花柱剪力影响系数平均值分别为0.977、0.986和0.991，说明考虑行波效应时开花柱剪力水平总体略有降低，但平均有2.4%、2.0%和2.1%开花柱的剪力影响系数均值大于1.05，最大值为1.07。95%开花柱剪力影响系数最大值的均值分别为1.022、1.021和1.020，说明考虑行波效应时，开花柱内力的峰值稍有增大。

表 17 开花柱剪力影响系数

Table 17. Effect coefficients of shear forces for V-shaped columns

激励方向/(°)	视波速v_app/ (km·s⁻¹)	剪力影响系数最大值γ_V,max	95%剪力影响系数最大值95%γ_V,max	剪力影响系数平均值 $\overline \gamma_V$	$\overline \gamma_V$ >1.05 占比/(%)
0	3.0	1.070	1.017	0.972	2.1
	4.0	1.057	1.016	0.983	2.1
	5.0	1.049	1.018	0.989	2.1
45	3.0	1.043	1.028	0.973	3.6
	4.0	1.035	1.024	0.983	3.6
	5.0	1.030	1.021	0.988	3.6
90	3.0	1.056	1.029	0.979	2.9
	4.0	1.048	1.030	0.987	2.9
	5.0	1.044	1.027	0.991	2.9
135	3.0	1.054	1.018	0.980	2.1
	4.0	1.045	1.016	0.989	2.1
	5.0	1.038	1.016	0.993	2.1
180	3.0	1.041	1.011	0.979	1.4
	4.0	1.036	1.014	0.988	1.4
	5.0	1.031	1.015	0.992	2.1
225	3.0	1.041	1.024	0.977	2.1
	4.0	1.032	1.019	0.986	0.7
	5.0	1.029	1.017	0.991	0.7
270	3.0	1.059	1.033	0.979	4.3
	4.0	1.045	1.031	0.986	2.1
	5.0	1.037	1.027	0.990	2.9
315	3.0	1.032	1.015	0.978	0.7
	4.0	1.030	1.017	0.987	0.7
	5.0	1.029	1.018	0.992	0.7
平均值	3.0	1.049	1.022	0.977	2.4
	4.0	1.041	1.021	0.986	2.0
	5.0	1.036	1.020	0.991	2.1

下载: 导出CSV

| 显示表格

4.6 大跨钢屋盖

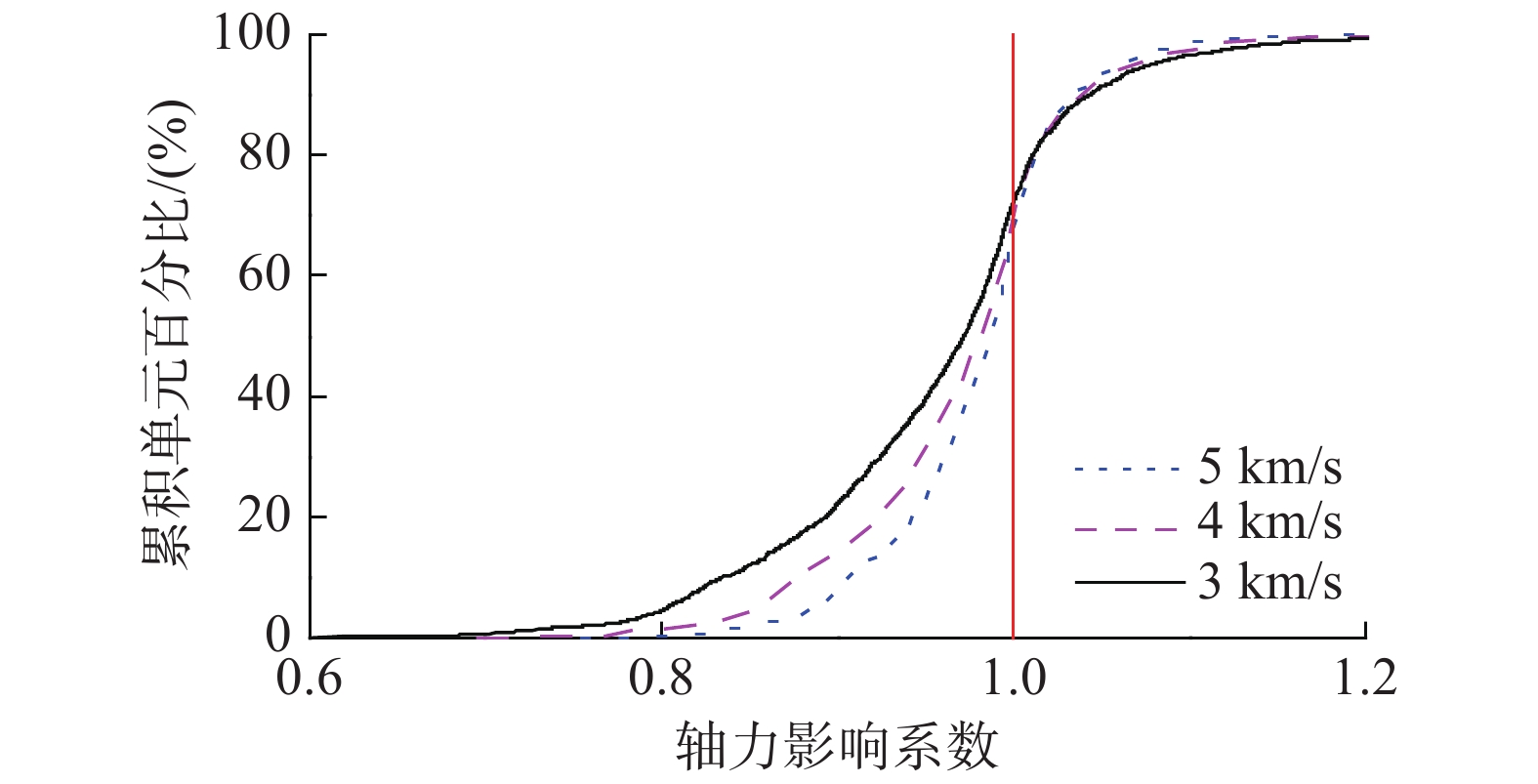
BigBear波在0º方向进行激励时，大跨度钢屋盖杆件轴力影响系数的分布如图16所示。由图16可知，对于3.0 km/s、4.0 km/s和5.0 km/s三种视波速，轴力影响系数的平均值均略小于1.0，其值域范围分别为0.56~1.39、0.69~1.32和0.75~1.27。随着视波速增大，其峰值逐渐降低，值域范围缩小，轴力影响系数接近于1.0的构件数量增多。

图 16 0°方向地震激励时大跨度钢屋盖杆件轴力影响系数分布

Figure 16. Distribution of axial force effect coefficients of steel roof components at 0°direction earthquake excitation

下载: 全尺寸图片幻灯片

行波效应分析时得到大跨度钢屋盖杆件的轴力影响系数见表18。由表18可知，在3.0 km/s、4.0 km/s和5.0 km/s三种视波速作用时，屋盖杆件内力影响系数的平均值分别为0.988、0.993和0.995，说明考虑行波效应时屋盖杆件轴力总体上微有减小，但最大值可达1.485。95%屋盖杆件轴力影响系数的均值分别为1.057、1.046和1.039，增幅随着视波速增大而逐渐减小。

表 18 大跨度钢屋盖杆件轴力影响系数

Table 18. Effect coefficients of axial forces for large span steel roof components

激励方向/(°)	视波速v_app/ (km·s⁻¹)	轴力影响系数最大值γ_N,max	95%轴力影响系数最大值95%γ_N,max	轴力影响系数平均值 $\overline\gamma_N$	$\overline\gamma_N$ >1.05 占比/(%)
0	3.0	1.287	1.057	0.985	6.4
	4.0	1.229	1.048	0.991	5.2
	5.0	1.188	1.041	0.994	4.2
45	3.0	1.316	1.059	0.988	6.3
	4.0	1.248	1.047	0.992	4.9
	5.0	1.205	1.040	0.995	3.8
90	3.0	1.286	1.057	0.991	6.5
	4.0	1.227	1.046	0.995	5.0
	5.0	1.184	1.038	0.997	3.8
135	3.0	1.324	1.058	0.994	6.9
	4.0	1.253	1.047	0.997	5.3
	5.0	1.205	1.039	0.998	4.1
180	3.0	1.485	1.061	0.986	6.5
	4.0	1.366	1.047	0.991	4.9
	5.0	1.292	1.039	0.994	3.9
225	3.0	1.395	1.067	0.988	7.2
	4.0	1.305	1.055	0.993	5.9
	5.0	1.246	1.046	0.995	4.8
270	3.0	1.360	1.057	0.990	6.1
	4.0	1.266	1.046	0.993	4.8
	5.0	1.207	1.038	0.995	3.7
315	3.0	1.211	1.036	0.983	3.9
	4.0	1.167	1.030	0.989	3.1
	5.0	1.138	1.026	0.992	2.1
平均值	3.0	1.333	1.057	0.988	6.2
	4.0	1.258	1.046	0.993	4.9
	5.0	1.208	1.039	0.995	3.8

下载: 导出CSV

| 显示表格

4.7 影响系数取值分析

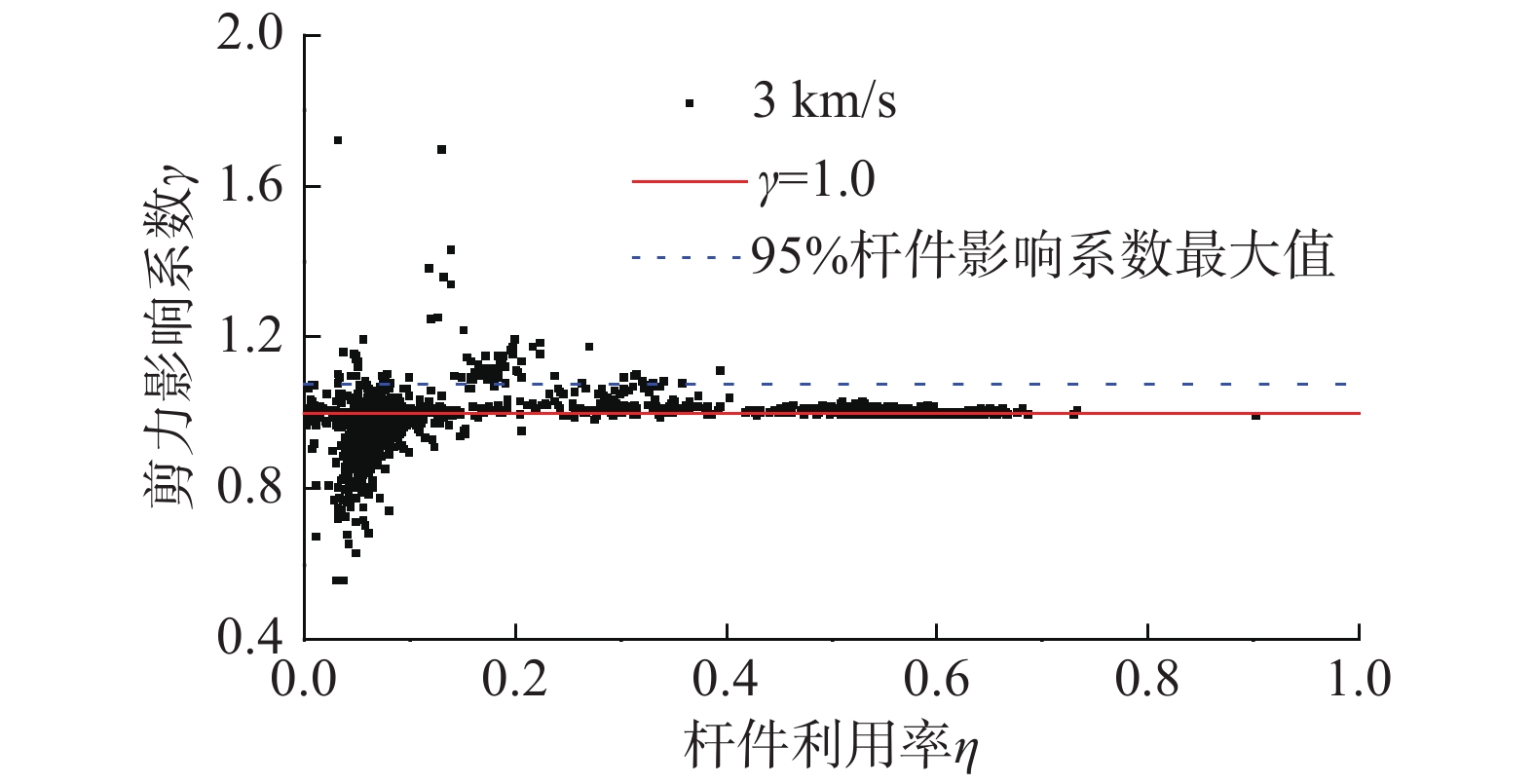
需要考虑地震行波效应影响的超长结构，通常建筑规模很大，构件数量很多。为了避免极少数构件行波效应影响系数过大引起对整体结构地震作用进行不必要的放大，本文选取涵盖95%构件内力影响系数的最大值作为地震行波效应放大系数，以保证设计结构的安全性。为说明这一做法的合理性，对计算结果进行验证。定义构件利用率η为在地震工况下构件的内力与其承载力之比。

在0°方向BigBear波激励时，下部混凝土结构框架柱的剪力影响系数与构件利用率的关系如图17所示。由图17可知，框架柱在地震作用下的利用率均不大于1.0，剪力影响系数与构件利用率的关系呈喇叭形分布，剪力影响系数与1.0偏差较大的值均位于构件利用率较低(η≤0.3)的范围，剪力影响系数小于1.0构件的数量多于剪力影响系数大于1.0构件的数量。这表明，当构件承载力冗余度很大时，即使行波效应非常显著，行波效应仍然不起控制作用。

图 17 0°方向地震激励时框架柱剪力影响系数与材料利用率的关系

Figure 17. Relationship between shear force effect coefficient and material utilization ratios of frame columns at 0° direction earthquake excitation

下载: 全尺寸图片幻灯片

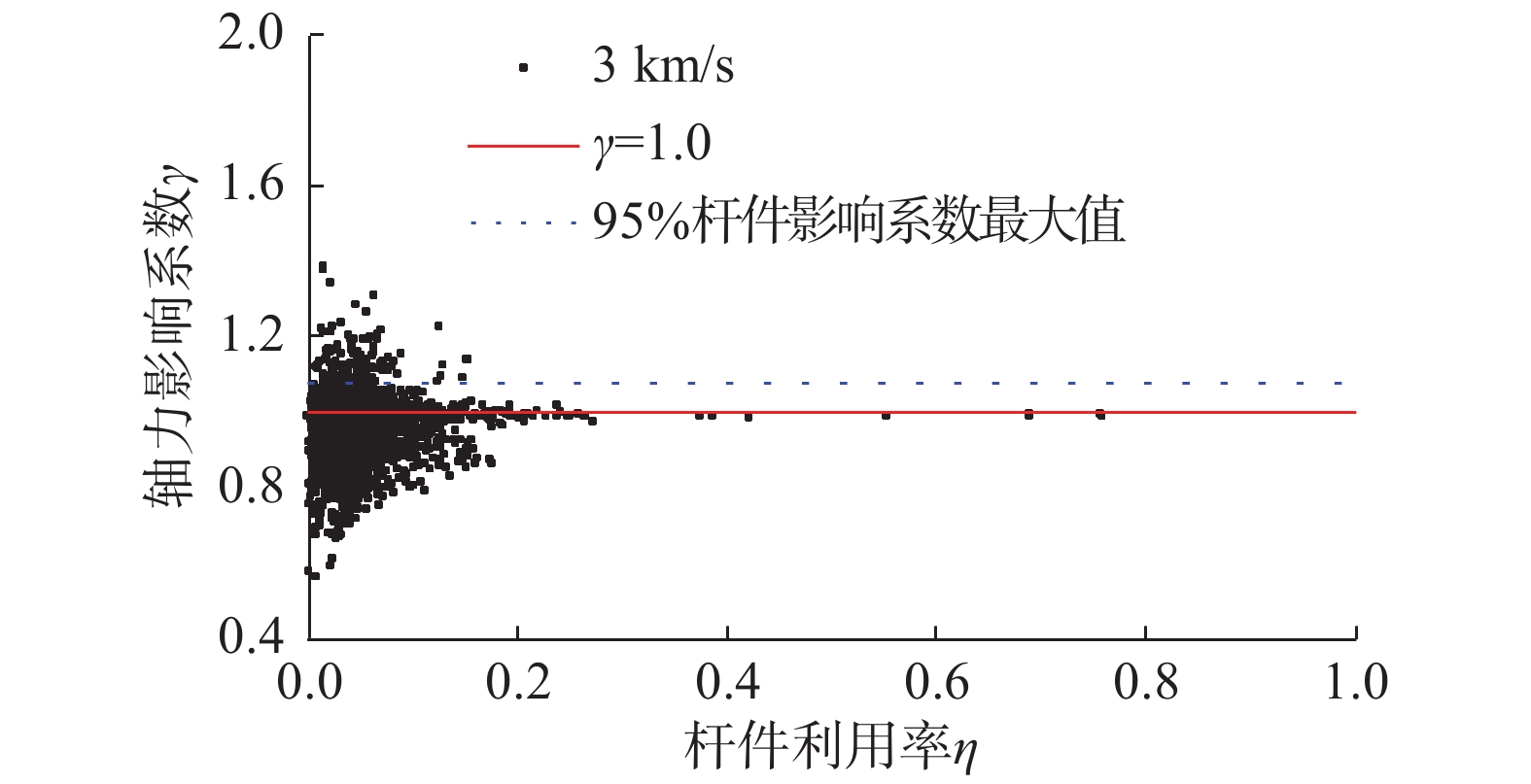
在0°方向BigBear波激励时，大跨度钢屋盖杆件轴力的影响系数与构件利用率的关系如图18所示。由图18可知，在地震作用工况，屋盖杆件的利用率均不大于1.0，轴力影响系数与杆件利用率的关系呈喇叭形分布，且轴力影响系数小于1.0杆件的数量多于轴力影响系数大于1.0杆件的数量。5%轴力影响系数较大的杆件，其构件利用率η均低于0.2。从此可知，行波效应显著的杆件通常承载力冗余度很大，当统一取用较小的内力影响系数时，可以保证结构的安全性。

图 18 0°方向地震激励时大跨度钢屋盖杆件轴力影响系数与材料利用率的关系

Figure 18. Relationship between axial force effect coefficients of steel roof components at 0° direction earthquake excitation

下载: 全尺寸图片幻灯片

5 结论

本文通过对地震波在单一土层和不同土层之间传播规律的研究，提出了基于岩土层剪切波速的视波速计算方法和适用于工程的简化计算公式，并以厦门机场为例分析了行波效应对于大跨度结构的影响，主要结论如下：

(1) 对于均质土层，地面某点的视波速仅与震源深度、震中距和该土层的剪切波速有关，视波速恒大于剪切波速。

(2) 采用结构中点的视波速取代根据其两个端点得到的视波速，可以避免结构各方向长度不同的影响，计算简便，误差可忽略不计。

(3) 在震源深度范围内，地壳厚度远大于覆盖层厚度，多土层的等效剪切波速与震源所在岩层剪切波速较为接近。

(4) 算例结果表明，本文给出的多土层视波速简化计算公式，与视波速方程数值解的误差一般在5%以内。

(5) 场地类别对视波速的影响较小，视波速的下限值接近于地壳的剪切波速。

(6) 采用柱底位移时程输入进行多维多点激励时，根据受多点激励影响较小的95%构件确定其内力影响系数，在保证结构安全的同时，可以避免由于构件内力过小引起行波效应异常增大。

(7) 厦门新机场分析结果表明，考虑多点激励地震效应后，结构底部总剪力变化很小，下部主体结构扭转比最大增幅为8%，框架柱和钢管柱剪力增幅不大于10%，开花柱剪力增幅不超过5%，大跨度屋盖杆件轴力增大幅度在10%以内。

图 1 地震波在单一土层中传播图示

Figure 1. Illustration of seismic wave propagation in a single soil layer

下载: 全尺寸图片幻灯片

图 2 相邻土层之间地震波传播示意

Figure 2. Illustration of seismic wave propagation between adjacent soil layers

下载: 全尺寸图片幻灯片

图 3 多土层地震波传播路径示意

Figure 3. Propagation path illustration of seismic wave through multi-soil layers

下载: 全尺寸图片幻灯片

图 4 视波速与震中距和震源深度的关系

Figure 4. Relationship between apparent wave velocity and epicentral distance and focal depth

下载: 全尺寸图片幻灯片

图 5 视波速比与震源深度和震中距的关系

Figure 5. Relationship between apparent wave velocity ratio and focal depth and epicenter distance

下载: 全尺寸图片幻灯片

图 6 厦门新机场

Figure 6. Xiamen New Airport

下载: 全尺寸图片幻灯片

图 7 T1航站楼主楼结构布置　/m

Figure 7. Structural layout of the Main Building for Terminal One

下载: 全尺寸图片幻灯片

图 8 地震加速度时程的反应谱与规范反应谱

Figure 8. Response spectrum of seismic waves and spectrum of Code for seismic design of buildings

下载: 全尺寸图片幻灯片

图 9 地震位移时程记录

Figure 9. Seismic displacement time-history records

下载: 全尺寸图片幻灯片

图 10 多点地震激励输入工况

Figure 10. Input cases of multiple support excitation

下载: 全尺寸图片幻灯片

图 11 0°方向地震激励时结构基底剪力的时程

Figure 11. Time-history record of base shear force at 0° direction earthquake excitation

下载: 全尺寸图片幻灯片

图 12 0°方向地震激励时框架柱剪力影响系数分布

Figure 12. Distribution of shear force effect coefficient of frame columns at 0°direction earthquake excitation

下载: 全尺寸图片幻灯片

图 13 0°方向地震激励时框架柱剪力影响系数大于1.05构件的分布

Figure 13. Distribution of shear force effect coefficient greater than 1.05 for frame columns at 0° direction earthquake excitation

下载: 全尺寸图片幻灯片

图 14 0°方向地震激励时支承屋盖钢管柱剪力影响系数分布

Figure 14. Distribution of shear force effect coefficients of supporting roof steel columns at 0°direction Earthquake Excitation

下载: 全尺寸图片幻灯片

图 15 0°方向地震激励时支承屋盖钢管柱剪力影响系数大于1.05构件的分布

Figure 15. Distribution of shear force effect coefficient greater than 1.05 for supporting roof steel columns at 0°direction earthquake excitation

下载: 全尺寸图片幻灯片

图 16 0°方向地震激励时大跨度钢屋盖杆件轴力影响系数分布

Figure 16. Distribution of axial force effect coefficients of steel roof components at 0°direction earthquake excitation

下载: 全尺寸图片幻灯片

图 17 0°方向地震激励时框架柱剪力影响系数与材料利用率的关系

Figure 17. Relationship between shear force effect coefficient and material utilization ratios of frame columns at 0° direction earthquake excitation

下载: 全尺寸图片幻灯片

图 18 0°方向地震激励时大跨度钢屋盖杆件轴力影响系数与材料利用率的关系

Figure 18. Relationship between axial force effect coefficients of steel roof components at 0° direction earthquake excitation

下载: 全尺寸图片幻灯片

表 1 基岩波速比与风化程度的关系

Table 1 Relationship between wave velocity ratio and weathering degree of bedrock

风化程度	野外特征	波速比K_v
未风化	岩质新鲜，偶见风化痕迹	0.9~1.0
微风化	结构基本未变，仅沿节理面有渲染或变色，有少量风化裂隙	0.8~0.9
中风化	结构部分破坏，沿节理面有次生矿物，风化裂隙发育，岩体被切割成岩块	0.6~0.8
强风化	结构大部分破坏，矿物成分显著变化，风化裂隙很发育，岩体破碎	0.4~0.6
全风化	结构基本破坏，但尚可辨认，有残余结构强度	0.2~0.4
注：波速比K_v为风化岩石与新鲜岩石压缩波速度之比。

下载: 导出CSV

表 2 场地覆盖土层的剪切波速

Table 2 Shear wave velocity of site overburden

土层名称	剪切波速v_s /(km·s⁻¹)
软弱土	≤0.15
中软土	0.15~0.25
中硬土	0.25~0.50
基岩	0.5~3.4
地壳	3.4~4.2

下载: 导出CSV

表 3 中点视波速 $v_{{\rm{a}}{\rm{pp}}}^C$ 与端点视波速 $v_{{\rm{a}}{\rm{pp}}}^{AB}$ 的相对误差δ

Table 3 Relative error δ of Midpoint apparent wave velocity $v_{{\rm{a}}{\rm{pp}}}^C$ and Endpoint apparent wave velocity $v_{{\rm{a}}{\rm{pp}}}^{AB}$ /(%)

结构长度L/m	D=5 km S=200 km	D=10 km S=50 km	D=20 km S=10 km	D=30 km S=5 km
100	0.0000	0.0000	−0.0002	−0.0001
200	0.0000	0.0000	−0.0008	−0.0005
300	0.0000	0.0000	−0.0018	−0.0012
400	0.0000	0.0000	−0.0032	−0.0021
500	0.0000	0.0000	−0.0050	−0.0033
600	0.0000	−0.0001	−0.0072	−0.0047
注：δ= $(v_{ {\rm{a} }{\rm{pp}}}^C - v_{ {\rm{a} }{\rm{pp}}}^{AB})/v_{ {\rm{a} }{\rm{pp}}}^{AB} \times 100\text{%}$ 。

下载: 导出CSV

表 4 建筑场地类别与岩土层厚度

Table 4 Building site category and rock/soil thickness /km

场地类别	软弱土	中软土	中硬土	基岩	地壳
Ⅰ₀	0.000	0.000	0.000	0.150	30.00
Ⅰ₁	0.003	0.000	0.000	0.150	30.00
Ⅱ	0.000	0.030	0.020	0.150	30.00
Ⅲ	0.020	0.030	0.030	0.150	30.00
Ⅳ	0.020	0.030	0.350	0.150	30.00

下载: 导出CSV

表 5 视波速简化计算方法的误差估计

Table 5 Error estimation of apparent wave velocity by Simplified Calculation Method /(%)

场地类别	D=5 km, S=200 km	D=10 km, S=50 km	D=20 km, S=10 km	D=30 km, S=5 km
Ⅰ₀	−1.46	−0.68	−0.05	0.00
Ⅰ₁	−1.52	−0.71	−0.05	0.00
Ⅱ	−2.39	−1.13	−0.09	−0.01
Ⅲ	−2.95	−1.40	−0.12	−0.01
Ⅳ	−8.72	−4.17	−0.41	−0.04
注：误差为 $({\bar v_{{\rm{app}}} } - {v_{{\rm{app}}} })/{v_{{\rm{app}}} } \times 100\text{%}$ 。

下载: 导出CSV

表 6 常见地震工况的视波速比β

Table 6 Apparent wave velocity ratio β in common seismic conditions

震源深度D/km	震中距S/km
震源深度D/km	5	10	20	50	100	200
5	1.41	1.12	1.03	1.00	1.00	1.00
10	2.24	1.41	1.12	1.02	1.00	1.00
20	4.12	2.24	1.41	1.08	1.02	1.00
30	6.08	3.16	1.80	1.17	1.04	1.01

下载: 导出CSV

表 7 区域范围内地震震源深度分布

Table 7 Depth distribution of earthquake sources within the region

深度/km	地震个数	百分比/(%)	深度/km	地震个数	百分比/(%)
0~5	198	10.4	20~25	102	5.3
5~10	897	46.9	25~30	34	1.8
10~15	384	20.1	30以上	14	0.7
15~20	284	14.8

下载: 导出CSV

表 8 区域范围内不同震级震源深度分布

Table 8 Depth distribution of earthquake sources with different magnitudes in the region

震级M	平均深度 /km	地震个数
2.0~2.9	11.1	1553
3.0~3.9	12.1	324
≥4.0	15.2	36

下载: 导出CSV

表 9 近场区破坏性地震统计

Table 9 Destructive earthquake statistics in the near field

序号	发震时间	震中位置/(°)		参考地名	震级	震中烈度	距离/ km	计算烈度	影响烈度
序号	年月日	北纬	东经	参考地名	震级	震中烈度	距离/ km	计算烈度	影响烈度
1	1538.10.*	24.7	118.5	晋江安海	4_3/4	Ⅵ	21	4.6	Ⅴ
2	1691.05.*	25.0	118.7	晋江安海	4_3/4	Ⅵ	14	4.9	Ⅴ
3	1906.3.28	24.3	118.6	厦门海外	6_1/4		35	6.5	Ⅶ
4	1906.3.29	24.3	118.6	厦门海外	5_1/2		35	5.3	Ⅴ

下载: 导出CSV

表 10 场地地壳厚度、P波与S波的波速

Table 10 Crust thickness, P wave and S wave velocity of the site

地层名称	土层厚度 D_i/km	平均厚度 ${\bar D_i}$ /km	纵波波速 ${v_{\rm{p} } }$ /(km·s⁻¹)	平均纵波波速 ${\bar v_{\rm{p} }}$ /(km·s⁻¹)	平均横波波速 ${\bar v_{\rm{s} } }$ /(km·s⁻¹)
上地壳	1.84~4.63	3.235	5.00~5.90	5.45	3.20
中地壳	12.50~16.35	14.425	6.00~6.26	6.13	3.61
下地壳	12.42~14.38	13.400	6.37~6.82	6.60	3.88

下载: 导出CSV

表 11 厦门新机场土层分布与剪切波速

Table 11 Soil layer distribution and S wave velocity of Xiamen New Airport

土层名称	土层界面深度/ km	土层厚度 D_i/km	土层剪切波速 v_s/(km·s⁻¹)
地表	0.000	−	−
低速覆盖层	0.020	0.020	0.178
中速覆盖层	0.035	0.015	0.279
高速覆盖层	0.630	0.595	1.700
上地壳	3.865	3.235	3.200
中地壳	15.200	11.335	3.610

下载: 导出CSV

表 12 航站楼主楼结构构件截面规格

Table 12 Dimensions of structural members for T1 Main Building

部位	尺寸/mm	强度等级	备注
混凝土柱	D1200~ D1600	C50	用于14.8 m标高以下
钢管柱	D1000×30~ D1500×50	Q355B、Q420C	14.8 m标高以上
开花柱下柱	D2300×60	Q355B、C50	±0.000~28.8 m标高，钢管混凝土柱
开花柱上斜柱	□1200~900× 700~500×40	Q355B	28.8 m标高以上
大跨屋盖杆件	D127×5~D500×25	Q355B	−

下载: 导出CSV

表 13 结构基底剪力影响系数

Table 13 Effect coefficients of base shear force for the structure

激励方向/(°)	视波速v_app/(km·s⁻¹)
激励方向/(°)	3	4	5
0	0.996	0.998	0.998
180	0.997	0.998	0.999
90	0.998	0.999	0.999
270	0.996	0.998	0.998
45	0.998	0.999	0.999
225	0.998	0.998	0.999
135	0.999	1.000	1.000
315	0.997	0.998	0.998

下载: 导出CSV

表 14 主体结构单元扭转比影响系数(2层)

Table 14 Effect coefficients of torsional ratios for structural units (2nd Floor)

激励方向/(°)	视波速v_app/(km·s⁻¹)	A1	A2	A3	A4	A5	A6
0	3.0	1.02	0.99	1.02	1.00	0.89	1.03
	4.0	1.02	0.99	1.01	0.98	0.88	1.04
	5.0	1.01	1.00	1.01	0.97	0.98	1.04
180	3.0	1.01	1.04	1.00	1.02	1.06	1.14
	4.0	1.00	1.00	1.00	1.02	1.06	1.01
	5.0	1.01	1.01	1.01	1.01	1.05	1.01
90	3.0	0.99	1.02	0.99	1.10	0.98	1.06
	4.0	0.99	1.01	0.99	1.08	0.97	1.03
	5.0	0.99	1.01	0.99	1.02	0.97	1.02
270	3.0	0.92	1.02	1.06	1.09	1.04	1.17
	4.0	0.92	0.99	1.02	1.07	1.02	1.06
	5.0	0.94	0.99	1.00	1.05	1.03	1.04
45	3.0	0.96	0.94	0.92	1.03	0.98	0.98
	4.0	0.96	0.98	0.93	1.03	0.97	0.96
	5.0	0.96	0.97	0.94	1.02	0.98	0.96
225	3.0	1.02	0.99	0.97	1.07	1.02	1.35
	4.0	1.02	1.00	0.98	1.03	1.00	1.33
	5.0	1.01	0.99	0.98	1.00	1.00	1.31
135	3.0	1.06	1.04	1.08	1.06	0.99	1.01
	4.0	1.01	1.02	1.08	1.03	0.99	1.00
	5.0	1.00	1.02	1.07	1.02	1.00	1.00
315	3.0	1.08	1.03	0.98	1.01	0.98	0.94
	4.0	1.04	1.02	0.98	1.00	0.99	0.93
	5.0	1.03	1.01	0.96	1.01	0.99	0.94
平均值	3.0	1.01	1.01	1.00	1.05	0.99	1.08
	4.0	0.99	1.00	1.00	1.03	0.99	1.04
	5.0	0.99	1.00	0.99	1.01	1.00	1.04

下载: 导出CSV

表 15 框架柱剪力影响系数

Table 15 Effect coefficients of shear forces for frame columns

激励方向/(°)	视波速 v_app/(km·s⁻¹)	剪力影响系数最大值γ_V,max	95%剪力影响系数最大值95%γ_V,max	剪力影响系数平均值 $\overline \gamma_V$	$\overline \gamma_V$ >1.05 占比/(%)
0	3.0	1.456	1.087	1.005	7.6
	4.0	1.316	1.056	1.003	5.0
	5.0	1.240	1.039	1.002	3.3
45	3.0	1.275	1.066	1.004	6.5
	4.0	1.176	1.042	1.001	4.0
	5.0	1.128	1.030	1.000	2.6
90	3.0	1.197	1.044	0.999	4.1
	4.0	1.144	1.031	0.999	2.2
	5.0	1.116	1.024	0.998	1.3
135	3.0	1.273	1.041	0.999	3.7
	4.0	1.191	1.028	0.998	2.3
	5.0	1.146	1.021	0.999	1.5
180	3.0	1.497	1.071	1.004	7.0
	4.0	1.349	1.042	1.002	4.4
	5.0	1.265	1.030	1.001	2.6
225	3.0	1.541	1.074	1.010	8.5
	4.0	1.389	1.051	1.006	5.7
	5.0	1.300	1.037	1.004	3.9
270	3.0	1.405	1.059	1.007	6.9
	4.0	1.282	1.043	1.004	4.4
	5.0	1.209	1.034	1.003	3.1
315	3.0	1.414	1.053	1.003	5.2
	4.0	1.303	1.036	1.002	3.4
	5.0	1.242	1.027	1.001	2.2
平均值	3.0	1.382	1.062	1.004	6.2
	4.0	1.269	1.041	1.002	3.9
	5.0	1.206	1.030	1.001	2.5

下载: 导出CSV

表 16 支承屋盖钢管柱剪力影响系数

Table 16 Effect coefficients of shear forces for supporting roof steel columns

激励方向/(°)	视波速v_app/ (km·s⁻¹)	剪力影响系数最大值γ_V,max	95%剪力影响系数最大值95%γ_V,max	剪力影响系数平均值 $\overline \gamma_V$	$\overline \gamma_V$ >1.05 占比 /(%)
0	3.0	1.190	1.053	0.977	6.1
	4.0	1.146	1.043	0.987	5.2
	5.0	1.124	1.039	0.992	4.0
45	3.0	1.215	1.070	0.988	8.1
	4.0	1.165	1.058	0.993	6.7
	5.0	1.133	1.047	0.996	5.0
90	3.0	1.271	1.070	0.993	8.8
	4.0	1.191	1.055	0.997	6.3
	5.0	1.142	1.045	0.999	5.0
135	3.0	1.197	1.055	0.986	6.3
	4.0	1.152	1.046	0.992	4.6
	5.0	1.129	1.038	0.996	3.5
180	3.0	1.289	1.051	0.972	5.5
	4.0	1.219	1.043	0.983	4.3
	5.0	1.173	1.036	0.988	3.4
225	3.0	1.190	1.060	0.972	6.5
	4.0	1.150	1.049	0.982	5.2
	5.0	1.126	1.040	0.987	3.7
270	3.0	1.204	1.058	0.978	6.4
	4.0	1.156	1.047	0.986	4.8
	5.0	1.121	1.038	0.990	3.4
315	3.0	1.155	1.039	0.976	3.9
	4.0	1.125	1.033	0.985	2.6
	5.0	1.103	1.028	0.990	1.7
平均值	3.0	1.214	1.057	0.980	6.5
	4.0	1.163	1.047	0.988	5.0
	5.0	1.131	1.039	0.992	3.7

下载: 导出CSV

表 17 开花柱剪力影响系数

Table 17 Effect coefficients of shear forces for V-shaped columns

激励方向/(°)	视波速v_app/ (km·s⁻¹)	剪力影响系数最大值γ_V,max	95%剪力影响系数最大值95%γ_V,max	剪力影响系数平均值 $\overline \gamma_V$	$\overline \gamma_V$ >1.05 占比/(%)
0	3.0	1.070	1.017	0.972	2.1
	4.0	1.057	1.016	0.983	2.1
	5.0	1.049	1.018	0.989	2.1
45	3.0	1.043	1.028	0.973	3.6
	4.0	1.035	1.024	0.983	3.6
	5.0	1.030	1.021	0.988	3.6
90	3.0	1.056	1.029	0.979	2.9
	4.0	1.048	1.030	0.987	2.9
	5.0	1.044	1.027	0.991	2.9
135	3.0	1.054	1.018	0.980	2.1
	4.0	1.045	1.016	0.989	2.1
	5.0	1.038	1.016	0.993	2.1
180	3.0	1.041	1.011	0.979	1.4
	4.0	1.036	1.014	0.988	1.4
	5.0	1.031	1.015	0.992	2.1
225	3.0	1.041	1.024	0.977	2.1
	4.0	1.032	1.019	0.986	0.7
	5.0	1.029	1.017	0.991	0.7
270	3.0	1.059	1.033	0.979	4.3
	4.0	1.045	1.031	0.986	2.1
	5.0	1.037	1.027	0.990	2.9
315	3.0	1.032	1.015	0.978	0.7
	4.0	1.030	1.017	0.987	0.7
	5.0	1.029	1.018	0.992	0.7
平均值	3.0	1.049	1.022	0.977	2.4
	4.0	1.041	1.021	0.986	2.0
	5.0	1.036	1.020	0.991	2.1

下载: 导出CSV

表 18 大跨度钢屋盖杆件轴力影响系数

Table 18 Effect coefficients of axial forces for large span steel roof components

激励方向/(°)	视波速v_app/ (km·s⁻¹)	轴力影响系数最大值γ_N,max	95%轴力影响系数最大值95%γ_N,max	轴力影响系数平均值 $\overline\gamma_N$	$\overline\gamma_N$ >1.05 占比/(%)
0	3.0	1.287	1.057	0.985	6.4
	4.0	1.229	1.048	0.991	5.2
	5.0	1.188	1.041	0.994	4.2
45	3.0	1.316	1.059	0.988	6.3
	4.0	1.248	1.047	0.992	4.9
	5.0	1.205	1.040	0.995	3.8
90	3.0	1.286	1.057	0.991	6.5
	4.0	1.227	1.046	0.995	5.0
	5.0	1.184	1.038	0.997	3.8
135	3.0	1.324	1.058	0.994	6.9
	4.0	1.253	1.047	0.997	5.3
	5.0	1.205	1.039	0.998	4.1
180	3.0	1.485	1.061	0.986	6.5
	4.0	1.366	1.047	0.991	4.9
	5.0	1.292	1.039	0.994	3.9
225	3.0	1.395	1.067	0.988	7.2
	4.0	1.305	1.055	0.993	5.9
	5.0	1.246	1.046	0.995	4.8
270	3.0	1.360	1.057	0.990	6.1
	4.0	1.266	1.046	0.993	4.8
	5.0	1.207	1.038	0.995	3.7
315	3.0	1.211	1.036	0.983	3.9
	4.0	1.167	1.030	0.989	3.1
	5.0	1.138	1.026	0.992	2.1
平均值	3.0	1.333	1.057	0.988	6.2
	4.0	1.258	1.046	0.993	4.9
	5.0	1.208	1.039	0.995	3.8

下载: 导出CSV

参考文献(27)

[1]	胡聿贤. 地震工程学[M]. 第2版. 北京: 地震出版社, 2006. Hu Yuxian. Earthquake engineering [M]. 2nd ed. Beijing: Seismological Press, 2006. (in Chinese)
[2]	GB 50011−2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2016. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: Architecture & Building Press, 2016. (in Chinese)
[3]	柯江华, 甄伟, 盛平, 等. 天狮大学城市体育场结构设计[J]. 建筑结构, 2016, 46(17): 14 − 18. Ke Jianghua, Zhen Wei, Sheng Ping, et al. Structural design of city stadium of tianshi college [J]. Building Structure, 2016, 46(17): 14 − 18. (in Chinese)
[4]	张林振, 郁银泉, 蒋航军, 等. 石家庄站站棚结构设计[J]. 建筑结构, 2016, 46(19): 30 − 34. Zhang Linzhen, Yu Yinquan, Jiang Hangjun, et al. Structural design of the main station building of Shijiazhuang Railway Station [J]. Building Structure, 2016, 46(19): 30 − 34. (in Chinese)
[5]	沈顺高, 张微敬, 朱丹, 等. 大跨度机库结构多点输入地震反应分析[J]. 土木工程学报, 2008, 41(1): 17 − 21. Shen Shungao, Zhang Weijing, Zhu Dan, et al. Seismic response analysis of two long-span hangars under multiple support excitations [J]. China Civil Engineering Journal, 2008, 41(1): 17 − 21. (in Chinese)
[6]	王秋杰, 曾锃, 张俊发, 等. 行波效应对大跨空间结构竖向构件的影响分析[J]. 工程抗震与加固改造, 2018, 40(3): 59 − 63. Wang Qiujie, Zeng Zeng, Zhang Junfa, et al. The Seismic analysis of large-span spatial structures considering the traveling wave effects [J]. Earthquake Resistant Engineering and Retrofitting, 2018, 40(3): 59 − 63. (in Chinese)
[7]	陈尚鸿, 祁皑, 王素裹, 等. 多维多点输入下大跨度连体高层结构地震反应振动台阵试验研究[J]. 工程力学, 2014, 31(6): 212 − 217. doi: 10.6052/j.issn.1000-4750.2013.03.0134 Chen Shanghong, Qi Ai, Wang Suguo, et al. Experimental study of long-span connected structure under multi-dimensional and multi-support earthquake excitations [J]. Engineering Mechanics, 2014, 31(6): 212 − 217. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.03.0134
[8]	陈志华, 赵博, 王元清, 等. 多点输入下大跨弦支筒壳结构地震响应分析[J]. 土木工程学报, 2014, 47(增刊 1): 59 − 64. Chen Zhihua, Zhao Bo, Wang Yuanqing, et al. Seismic response analysis of large span cable supported barrel vault to multi-support excitations [J]. China Civil Engineering Journal, 2014, 47(Suppl 1): 59 − 64. (in Chinese)
[9]	吴兵, 傅学怡, 孟美莉, 等. 深圳火车北站多维多点输入地震反应分析[J]. 建筑结构, 2013, 43(增刊1): 272 − 276. Wu Bing, Fu Xueyi, Mong Meili, et al. Seismic response analysis of station building of Shenzhen North Station under multi-dimension and multi-support seismic excitation [J]. Building Structure, 2013, 43(Suppl1): 272 − 276. (in Chinese)
[10]	赵鹏飞, 刘枫, 汤荣伟, 等. 多点输入反应谱中耦合系数的研究[J]. 地震工程学报, 2014, 30(2): 102 − 110. Zhao Pengfei, Liu Feng, Tang Rongwei, et al. Research on the coherency coefficients in the multi-support response spectrum [J]. World Earthquake Engineering, 2014, 30(2): 102 − 110. (in Chinese)
[11]	刘枫, 杜义欣, 赵鹏飞, 等. 武汉火车站多点输入地震反应时程分析[J]. 建筑结构, 2009, 39(1): 11 − 15. Liu Feng, Du Yixin, Zhao Pengfei, et al. Time-history analysis of Wuhan Railway Station under multi-support seismic excitation [J]. Building Structure, 2009, 39(1): 11 − 15. (in Chinese)
[12]	范重, 柴丽娜, 张宇, 等. 超长结构地震行波效应影响因素研究[J]. 建筑结构学报, 2018, 39(8): 119 − 129. Fan Zhong, Chai Lina, Zhang Yu, et al. Study on influent factors of super-long structures under seismic traveling wave action [J]. Journal of Building Structures, 2018, 39(8): 119 − 129. (in Chinese)
[13]	范重, 刘学林, 张宇, 等. 航站楼复杂超长结构行波效应分析[J]. 建筑科学与工程学报, 2019, 36(1): 56 − 66. doi: 10.3969/j.issn.1673-2049.2019.01.007 Fan Zhong, Liu Xuelin, Zhang Yu, et al. Study on traveling wave effect of complicated super-long structures for terminal buildings [J]. Journal of Architecture and Civil Engineering, 2019, 36(1): 56 − 66. (in Chinese) doi: 10.3969/j.issn.1673-2049.2019.01.007
[14]	陆宣行, 熊学玉, 方义庆. 国家会展中心大跨预应力混凝土框架水平地震行波效应影响分析[J]. 建筑结构, 2018, 48(8): 60 − 64. Lu Xuanxing, Xiong Xueyu, Fang Yiqing. Traveling wave effect analysis of large-span prestressed concrete frame structure of National Exhibition and Convention Center under horizontal earthquake [J]. Building Structure, 2018, 48(8): 60 − 64. (in Chinese)
[15]	苏亮, 董石麟. 水平行波效应下周边支承大跨度单层球面网壳的地震反应[J]. 空间结构, 2006, 12(3): 24 − 30. doi: 10.3969/j.issn.1006-6578.2006.03.005 Su Liang, Dong Shilin. Seismic response of a large span single layer reticular dome with surrounding columns considering horizontal wave passage effect [J]. Spatial Structures, 2006, 12(3): 24 − 30. (in Chinese) doi: 10.3969/j.issn.1006-6578.2006.03.005
[16]	尚彦军, 史永跃, 金维俊, 等. 花岗岩风化壳分带与岩体基本质量分级关系探讨[J]. 岩石力学与工程学报, 2008, 27(9): 1858 − 1864. doi: 10.3321/j.issn:1000-6915.2008.09.014 Shang Yanjun, Shi Yongyue, Jin Weijun, et al. Discussion on relationship between weathering crust zonation and basic quality classification of rock mass [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(9): 1858 − 1864. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.09.014
[17]	聂德新, 韩爱果, 巨广宏. 岩体风化的综合分带研究[J]. 工程地质学报, 2002(1): 20 − 25. doi: 10.3969/j.issn.1004-9665.2002.01.004 Nie Dexin, Han Aiguo, Ju Guanghong. Study on integrated zoning of weathering degree of rock mass [J]. Journal of Engineering Geology, 2002(1): 20 − 25. (in Chinese) doi: 10.3969/j.issn.1004-9665.2002.01.004
[18]	徐永林, 熊里军. 上海地表软土层、细砂层的地震波反应[J]. 中国地震, 2003(1): 84 − 88. doi: 10.3969/j.issn.1001-4683.2003.01.010 Xu Yonglin, Xiong Lijun. The seismic reflection of soft layer and fine sand layer of earth's surface in Shanghai region [J]. Earthquake Research in China, 2003(1): 84 − 88. (in Chinese) doi: 10.3969/j.issn.1001-4683.2003.01.010
[19]	GB 50021−2001(2009), 岩土工程勘察规范[S]. 北京: 中国建筑工业出版社, 2009. GB 50021−2001(2009), Code for investigation of geotechnical engineering [S]. Beijing: China Architecture & Building Press, 2009. (in Chinese)
[20]	张敏政. 地震工程的概念和应用[M]. 北京: 地震出版社, 2015: 27 − 28. Zhang Mingzheng. The concept and application of earthquake engineering [M]. Beijing: Seismological Press, 2015: 27 − 28. (in Chinese)
[21]	张国民, 李丽, 马宏生, 等. 中国大陆地震震源深度及其构造含义[J]. 科学通报, 2002, 47(9): 663 − 668, 721-722. doi: 10.3321/j.issn:0023-074X.2002.09.004 Zhang Guoming, Li Li, Ma Hongsheng, et al. Focal depth of earthquakes in mainland China and Its tectonic implications [J]. Chinese Science Bulletin, 2002, 47(9): 663 − 668, 721-722. (in Chinese) doi: 10.3321/j.issn:0023-074X.2002.09.004
[22]	夏峰, 宋成科, 孟庆筱, 等. 天津地区覆盖层土动力学参数统计分析[J]. 地震工程学报, 2015, 37(1): 48 − 54. doi: 10.3969/j.issn.1000-0844.2015.01.0048 Xia Feng, Song Chengke, Meng Qingxiao, et al. Analysis of soil dynamic parameters of overburden in the Tianjin area [J]. China Earthquake Engineering Journal, 2015, 37(1): 48 − 54. (in Chinese) doi: 10.3969/j.issn.1000-0844.2015.01.0048
[23]	翰林(福建)勘察设计有限公司. 厦门新机场工程-航站区工程(T1航站楼主楼)岩土工程详细勘察报告(K2016-C016A)[R]. 福建: 翰林(福建)勘察设计有限公司, 2017. 1. Hanlin (Fujian) Survey and Design Co., Ltd. Detailed survey report on geotechnical engineering of Xiamen New Airport project-terminal area project (main building of Terminal T1) [R]. Fujian: Hanlin (Fujian) Survey and Design Co., Ltd, 2017. 1. (in Chinese)
[24]	中国地震灾害防御中心. 厦门新机场工程场地地震安全性评价报告(修改稿)[R]. 北京: 中国地震灾害防御中心, 2019. 7. China Earthquake Disaster Prevention Center. Earthquake disaster evaluation report of Xiamen New Airport engineering site (Revised) [R]. Beijing: China Earthquake Disaster Prevention Center, 2019. 7. (in Chinese)
[25]	福建省地震局. 福建及台湾海峡地壳结构深地震测深探测报告[R]. 福州: 福建省地震局, 2011. Fujian Earthquake Agency. Deep survey report of deep seismic of crustal structure in Fujian and Taiwan Strait [R]. Fuzhou: Fujian Earthquake Agency, 2011. (in Chinese)
[26]	吴先敏, 牛超, 卞晶, 等. 地震波基线漂移校正及结构地震响应分析[J]. 水资源与水工程学报, 2019, 30(2): 186 − 190, 197. Wu Xianmin, Niu Chao, Bian Jing, et al. Baseline drift correction of seismic wave and response analysis of the structure earthquake [J]. Journal of Water Resources and Water Engineering, 2019, 30(2): 186 − 190, 197. (in Chinese)
[27]	Zhang Yushan, Zhao Fengxin. Artificial ground motion compatible with specified peak ground displacement and target multi-damping response spectra [J]. Nuclear Engineering and Design, 2010(240): 2571 − 2578.

施引文献(35)

期刊类型引用(18)

1.	黄月超，周强，吴鸿，黄鸿楷，李悦. 考虑行波效应的大跨悬索桥地震响应研究. 世界桥梁. 2025(01): 64-70 . 百度学术
2.	李昊杰，杜轲，郑超，马加路，聂桂波. 地震动方向性效应和行波效应对不同档距塔线体系的动力响应影响. 震灾防御技术. 2025(01): 185-196 . 百度学术
3.	胡进军，盛兆琦，谢礼立，邹育麟. 跨断层工程输入地震动模拟及地震响应. 地震工程与工程振动. 2024(01): 1-13 . 百度学术
4.	巴振宁，鲁世斌，付继赛，梁建文，芦燕. 基于FK-FE混合方法的位错点源作用下全过程结构地震反应模拟. 工程力学. 2024(04): 184-198 . 本站查看
5.	Linpeng Qin，Yun Wang，Chang Chen，Yongxiang Wei，Chunqi Liao，Yi Zhang，Chao Wang，Wentao Wan，Quanyang Shao. Resonance Analysis in a High-Rise Building: Combined Translational and Rotational Measurements. Journal of Earth Science. 2024(03): 1069-1074 . 必应学术
6.	李梓捷，余鑫培，潘涛，林晨豪，周华俊，付波. 西部（重庆）科学城科学会堂结构行波效应响应分析. 浙江建筑. 2024(04): 26-31 . 百度学术
7.	刘泽龙，李素贞，黄耀华. 基于低频简化频散方程的充流管道泄漏固体声波波速计算方法. 工程力学. 2024(09): 155-166+190 . 本站查看
8.	丁阳，石运东，宗亮，尤碧施，刘倩，程俊森，徐松涛. 枢纽车站结构地震响应特征. 工程力学. 2023(04): 1-11 . 本站查看
9.	钟紫蓝，张亚波，侯本伟，韩俊艳，杜修力. 考虑交叉管线影响的城市供水管网地震响应分析及震害评估. 岩土工程学报. 2023(05): 964-975 . 百度学术
10.	范重，刘学林，刘涛，高嵩，柴会娟，韩文凯，杨鸿越，王金金，杨苏，刘家名. 济南遥墙机场T2航站楼超长结构温度及行波效应研究. 建筑结构学报. 2023(09): 1-13 . 百度学术
11.	孙海林，王海波，田宇，霍文营，余蕾，杨永睿，陆颖，施泓. 贵阳某体育场大跨度悬挑罩棚结构设计研究. 建筑结构学报. 2023(09): 51-61 . 百度学术
12.	卢林彤，李孝雄，庄海洋，吴琪. 宽河谷非均匀工程场地非线性地震反应空间变异特征研究. 地震工程与工程振动. 2023(04): 216-225 . 百度学术
13.	吕迎新，王宇. 大跨度弦支穹顶结构多维多点随机地震响应分析. 世界地震工程. 2023(04): 177-184 . 百度学术
14.	杨斌斌，赵勇，魏建峰，吴国勤. 某国际会展中心地震多点激励时程分析. 工程建设. 2023(12): 27-33+49 . 百度学术
15.	周泰翔，贾军波，邓扬，李爱群. 悬浮隧道结构体系与动力响应研究进展. 工程力学. 2022(04): 15-28+85 . 本站查看
16.	禹海涛，李心熙，袁勇，马超. 沉管隧道纵向地震易损性分析方法. 中国公路学报. 2022(10): 13-22 . 百度学术
17.	夏心红，方辉，毛健宇，王四清，董冰. 长沙黄花国际机场T2航站楼出发大厅抗震性能分析. 建筑结构. 2022(22): 1-6+34 . 百度学术
18.	杨军永，朱从民，朱瑞元. 行波激励下大跨越输电线路纵向地震响应分析. 南方电网技术. 2021(12): 72-77 . 百度学术

其他类型引用(17)

资源附件(0)

图(18) / 表(18)

计量

文章访问数: 987
HTML全文浏览量: 200
PDF下载量: 107
被引次数: 35

1 视波速确定方法
1.1 地质构造、剪切波速与震源距离
1.1.1 地质构造
1.1.2 剪切波速
1.1.3 震源深度与震中距
1.2 单一土层视波速计算
1.3 地震波在不同土层之间的传播
1.4 多土层视波速计算
1.5 多土层视波速简化计算
1.6 视波速影响因素分析
2 场地地质构造与视波速确定
2.1 工程概况
2.2 场地地震动参数
2.2.1 覆土层厚度与剪切波速
2.2.2 震源深度
2.2.3 震中距
2.2.4 地壳结构与波速
3 行波效应计算方法
3.1 结构体系
3.2 地震波选取
3.3 地震波输入方法
3.4 地震波传播方向
3.5 计算结果处理方法
4 结构的地震响应
4.1 基底剪力
4.2 结构扭转位移比
4.3 下部主体结构框架柱
4.4 支承屋盖钢管柱
4.5 开花柱
4.6 大跨钢屋盖
4.7 影响系数取值分析
5 结论

1 视波速确定方法
1.1 地质构造、剪切波速与震源距离
1.1.1 地质构造
1.1.2 剪切波速
1.1.3 震源深度与震中距
1.2 单一土层视波速计算
1.3 地震波在不同土层之间的传播
1.4 多土层视波速计算
1.5 多土层视波速简化计算
1.6 视波速影响因素分析
2 场地地质构造与视波速确定
2.1 工程概况
2.2 场地地震动参数
2.2.1 覆土层厚度与剪切波速
2.2.2 震源深度
2.2.3 震中距
2.2.4 地壳结构与波速
3 行波效应计算方法
3.1 结构体系
3.2 地震波选取
3.3 地震波输入方法
3.4 地震波传播方向
3.5 计算结果处理方法
4 结构的地震响应
4.1 基底剪力
4.2 结构扭转位移比
4.3 下部主体结构框架柱
4.4 支承屋盖钢管柱
4.5 开花柱
4.6 大跨钢屋盖
4.7 影响系数取值分析
5 结论

参考文献(27)

施引文献(35)

资源附件(0)

视波速确定方法与行波效应研究

通讯作者: 范 重(1959−)，男，北京人，教授级高工，博士，主要从事建筑结构设计研究(E-mail: fanz@cadg.cn)

计量

出版历程

STUDY ON APPARENT WAVE VELOCITY CALCULATION METHOD AND ON TRAVELLING WAVE EFFECT

1 视波速确定方法

1.1 地质构造、剪切波速与震源距离

1.1.1 地质构造

1.1.2 剪切波速

1.1.3 震源深度与震中距

1.2 单一土层视波速计算

1.3 地震波在不同土层之间的传播

1.4 多土层视波速计算

1.5 多土层视波速简化计算

1.6 视波速影响因素分析

2 场地地质构造与视波速确定

2.1 工程概况

2.2 场地地震动参数

2.2.1 覆土层厚度与剪切波速

2.2.2 震源深度

2.2.3 震中距

2.2.4 地壳结构与波速

3 行波效应计算方法

3.1 结构体系

3.2 地震波选取

3.3 地震波输入方法

3.4 地震波传播方向

3.5 计算结果处理方法

4 结构的地震响应

4.1 基底剪力

4.2 结构扭转位移比

4.3 下部主体结构框架柱

4.4 支承屋盖钢管柱

4.5 开花柱

4.6 大跨钢屋盖

4.7 影响系数取值分析

5 结论

期刊类型引用(18)

其他类型引用(17)

计量

出版历程

目录

1 视波速确定方法

1.1 地质构造、剪切波速与震源距离

1.1.1 地质构造

1.1.2 剪切波速

1.1.3 震源深度与震中距

1.2 单一土层视波速计算

1.3 地震波在不同土层之间的传播

1.4 多土层视波速计算

1.5 多土层视波速简化计算

1.6 视波速影响因素分析

2 场地地质构造与视波速确定

2.1 工程概况

2.2 场地地震动参数

2.2.1 覆土层厚度与剪切波速

2.2.2 震源深度

2.2.3 震中距

2.2.4 地壳结构与波速

3 行波效应计算方法

3.1 结构体系

3.2 地震波选取

3.3 地震波输入方法

3.4 地震波传播方向

3.5 计算结果处理方法

4 结构的地震响应

4.1 基底剪力

4.2 结构扭转位移比

4.3 下部主体结构框架柱

4.4 支承屋盖钢管柱

4.5 开花柱

4.6 大跨钢屋盖

4.7 影响系数取值分析

5 结论

通讯作者:
范　重(1959−)，男，北京人，教授级高工，博士，主要从事建筑结构设计研究(E-mail: fanz@cadg.cn)