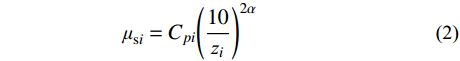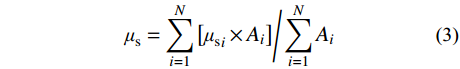女儿墙对平屋面阵列光伏板风荷载的影响

王彩玉; 马文勇; 韩晓乐; 高飞

doi:10.6052/j.issn.1000-4750.2020.06.S039

女儿墙对平屋面阵列光伏板风荷载的影响

王彩玉^1,,
马文勇^{1, 2, 3, ,},
韩晓乐^1,,
高飞^4,

1.
石家庄铁道大学土木工程学院，石家庄 050043
2.
河北省风工程和风能利用工程技术创新中心，石家庄 050043
3.
石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043
4.
河北鲲能电力工程咨询有限公司，石家庄 053700

基金项目: 河北省教育厅重点项目(ZD2018063)

详细信息

作者简介:
王彩玉(1995−)，女，河北人，硕士生，主要从事结构的风荷载、风致振动与控制研究(E-mail: wcy15613163287@163.com)

韩晓乐(1992−)，男，河北人，硕士生，主要从事结构设计研究(E-mail: hanxiaole07@163.com)

高　飞(1980−)，男，河北人，高工，学士，主要从事电力结构抗风设计研究(E-mail: 55278378@qq.com)

通讯作者:
马文勇(1981−)，男，陕西人，教授，博士，主要从事结构的风荷载、风致振动与控制研究(E-mail: ma@stdu.edu.cn)

中图分类号: TU312+.1
计量
- 文章访问数: 683
- HTML全文浏览量: 262
- PDF下载量: 74
出版历程
- 收稿日期: 2020-05-31
- 修回日期: 2021-01-13
- 网络出版日期: 2021-03-23
- 刊出日期: 2021-06-09

EFFECT OF PARAPET ON WIND LOAD OF FLAT ROOF ARRAY SOLAR PANNEL

WANG Cai-yu^1,,
MA Wen-yong^{1, 2, 3, ,},
HAN Xiao-le^1,,
GAO Fei^4,

1.
School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
2.
Innovation Center for Wind Engineering and Wind Energy Technology of Hebei Province, Shijiazhuang 050043, China
3.
State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
4.
Kunneng Electric Power Engineering Consulting CO., LTD, Shijiazhuang 053700, China

摘要

摘要: 风荷载是光伏支架最主要的设计荷载之一，目前对于屋顶上的光伏支架取值尚没有统一的标准。通过刚性模型测压风洞试验的方法，对不同女儿墙高度下平屋面阵列光伏板上风荷载分布进行分析。结果表明：对于平屋面上光伏板，无女儿墙时，光伏板的整体体型系数距离屋面边缘越近所承受的风荷载越大；女儿墙高度的增加可以有效减小平屋面光伏板所受到的风吸力。当女儿墙高度大约为0.42倍的光伏板高度时，其最大负压对应的折减系数可以达到50%以上；当女儿墙高度大于该高度后，女儿墙高度的增加对减小光伏板的风荷载效应趋于稳定。
- 光伏阵列 /
- 平屋面 /
- 女儿墙 /
- 风洞试验 /
- 体型系数
Abstract: Wind loading is one of the most important loads in the design of solar panels. The wind load acting on the solar panel on the roof of buildings is not clear so far. To illustrate the wind load distribution on a solar panel array on a flat roof with parapet, the wind pressure was measured by using the rigid model pressure test in a wind tunnel. The test results show that: the most unfavorable pressure coefficient occurs near the edge of the roof without a parapet; the pressure on the solar panel significantly decreases as the height of the parapet increase; when the ratio of the height of the parapet to the height of the solar panel is approximately 0.42, the most unfavorable negative pressure coefficient weakens up to 50%; and with further increase in the parapet height, the variation of the pressure coefficient with the parapet height has an inconsiderable reduction.
- solar panel array /
- flat roof /
- parapet /
- wind tunnel test /
- pressure coefficient

HTML全文

光伏阵列的风致损毁时有发生，风荷载是其结构设计最主要的荷载。目前对于光伏支架风荷载取值的研究和规定主要集中在地面上安装的光伏发电系统^[1-5]。对于安装在屋顶上的分布式太阳能光伏支架的风荷载取值仍然不明确^[6-7]。由于屋面坡度、女儿墙高度和建筑物^[8]等对光伏板风荷载会产生很大的影响，如何考虑这种影响是屋面安装的分布式太阳能光伏支架设计存在的主要问题之一，该问题不仅是光伏支架抗风安全需要关注的问题，也直接影响到发电的成本和效益。

光伏阵列中，光伏板之间的相互干扰会对其风荷载产生显著的影响，这种影响在风洞试验和数值模拟中都得到了验证^[9]。从静风荷载的角度看，这种干扰主要体现为上游光伏板对下游光伏板的遮挡效应，跟光伏板的尺寸和间距有很大关系^[10]。当这种光伏阵列安装在屋顶上时，光伏板上的风荷载不仅受到光伏板自身的相互干扰，还受到建筑本身绕流状态的影响^[11]，其风荷载的分布更为复杂。尤其是屋面边缘形状的改变对光伏板风荷载的影响很大，王京学等^[12]的研究成果充分说明，改变屋面流动的措施对改变光伏阵列的风荷载分布和取值有重要的意义。在实际的屋顶光伏阵列应用中，光伏板常常被安装在有女儿墙的平屋面上。由于女儿墙高度对结构顶部绕流影响很大^[13]，其中锥形涡等结构角部的典型流通特征都会受到女儿墙的影响^[14]。因此，女儿墙高度对屋顶光伏阵列的风荷载取值会有显著的影响，目前这种影响规律尚不明确。另外，由于女儿墙本身对屋顶光伏阵列也会形成遮挡效应，合理的女儿墙高度可能会显著的减小屋面光伏阵列的风荷载，因此，从减小风荷载的角度寻找合理的女儿墙高度对光伏支架设计也有很强的指导意义。

为了明确女儿墙高度对平屋面光伏阵列风荷载的影响规律，本文通过刚性模型测压风洞试验，研究了女儿墙高度对光伏支架风荷载的影响，给出了女儿墙影响下光伏支架的风荷载折减效应和不同女儿墙高度下的光伏阵列风荷载建议。

1 试验概况

1.1 模型介绍

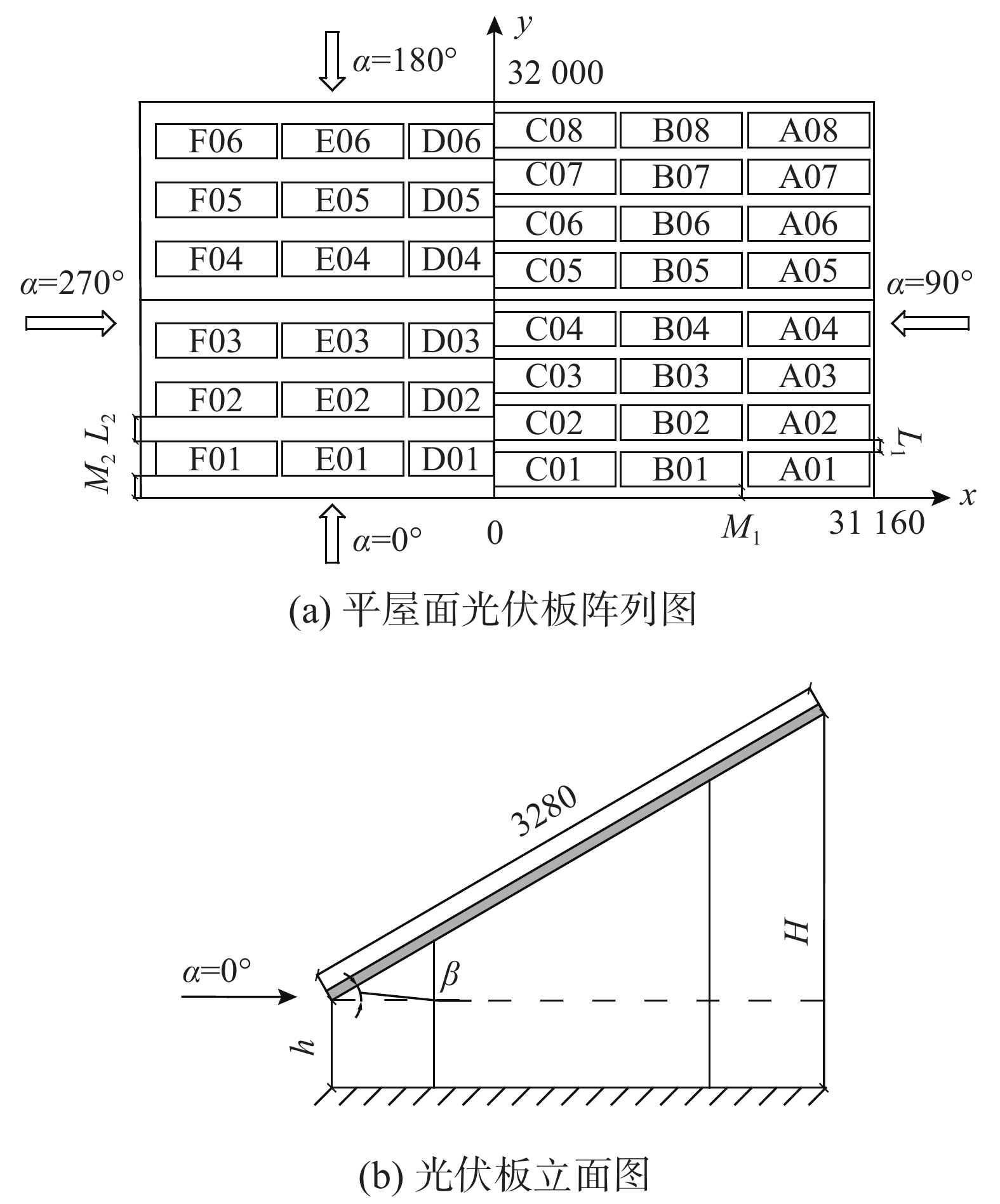
研究采用刚性模型测压风洞试验，试验在石家庄铁道大学风洞实验室低速试验段进行，试验断面宽4.4 m，高3 m，该试验段最大风速为30 m/s。研究对象为平屋面阵列光伏板，建筑尺寸为60 m×32 m×18 m，屋面共布置了42组光伏板，见图1(a)。利用模型的对称性，考虑了两种光伏板间距和距屋面边缘的距离。其中，光伏板距离屋面边缘M₁=900 mm，M₂=1800 mm；光伏板之间的间距L₁=1000 mm，L₂=2000 mm；α为风向角，取值0°~180°，以15°为间隔，共13个风向角工况。太阳能光伏板立面图见图1(b)，其中，h为光伏板离地高度，取500 mm；H光伏板整体高度2140 mm；β为光伏板倾角，取值30°。试验缩尺比为1∶50。

图 1 试验模型

Figure 1. Test mode

下载: 全尺寸图片幻灯片

试验中女儿墙高度分别取0 mm(无女儿墙)、180 mm、360 mm、900 mm、1800 mm、2700 mm、3600 mm、4500 mm，屋顶光伏板的实际高度H为2140 mm，为便于比较分析，定义RH为女儿墙高度与光伏板高度的比值，文中RH依次为0、0.08、0.17、0.42、0.84、1.26、1.68、2.1。

每组太阳能光伏板上下表面布置测压孔同步测试上下表面压力，共40个测压点，屋面阵列光伏板表面共布置1680个测压点。试验采用A类风场^[15]，自由来流风速为12 m/s。压力扫描阀采样频率为331.2 Hz，采样时间为30 s。

1.2 参数定义

平均风压系数：

${C_{p{{i}}}} = \frac{{{P_i} - {P_{\rm{s}}}}}{{{P_{\rm{t}}} - {P_{\rm{s}}}}} = \frac{{2({P_i} - {P_{\rm{s}}})}}{{\rho U_R^2}}$

(1)

式中：C_p_i为测点i在不同风向角下的平均风压系数；P_t为参考点高度处总压；P_s为参考点高度处静压；P_i为测点i在不同风向角下的压力；ρ为空气密度；U_R为参考点高度处的平均风速，为了便于使用基本风压等参数，高度选择R=10 m。

体型系数：

${\mu _{{\rm{s}}i}} = {C_{pi}}{\left(\frac{{10}}{{{{\textit{z}}_i}}}\right)^{2\alpha }}\qquad\qquad$

(2)

式中：μ_s_i为测点i的体型系数；Z_i为测点i处的高度；α为地面粗糙度指数，A类风场α取值0.12。

为了计算不同工况下的风荷载变化规律，给出了净风压的面积加权均值，即整体体型系数μ_s，A_i为测点i的附属面积。

${\mu _{\rm{s}}} = \sum\limits_{{i=1}}^N {\left[ {{\mu _{\rm{s}}}_i \times {A_i}} \right]} \Bigg/\sum\limits_{i = 1}^{{N}} {{A_i}}$

(3)

2 无女儿墙时屋面光伏板体型系数及取值建议

2.1 无女儿墙时屋面光伏板整体体型系数

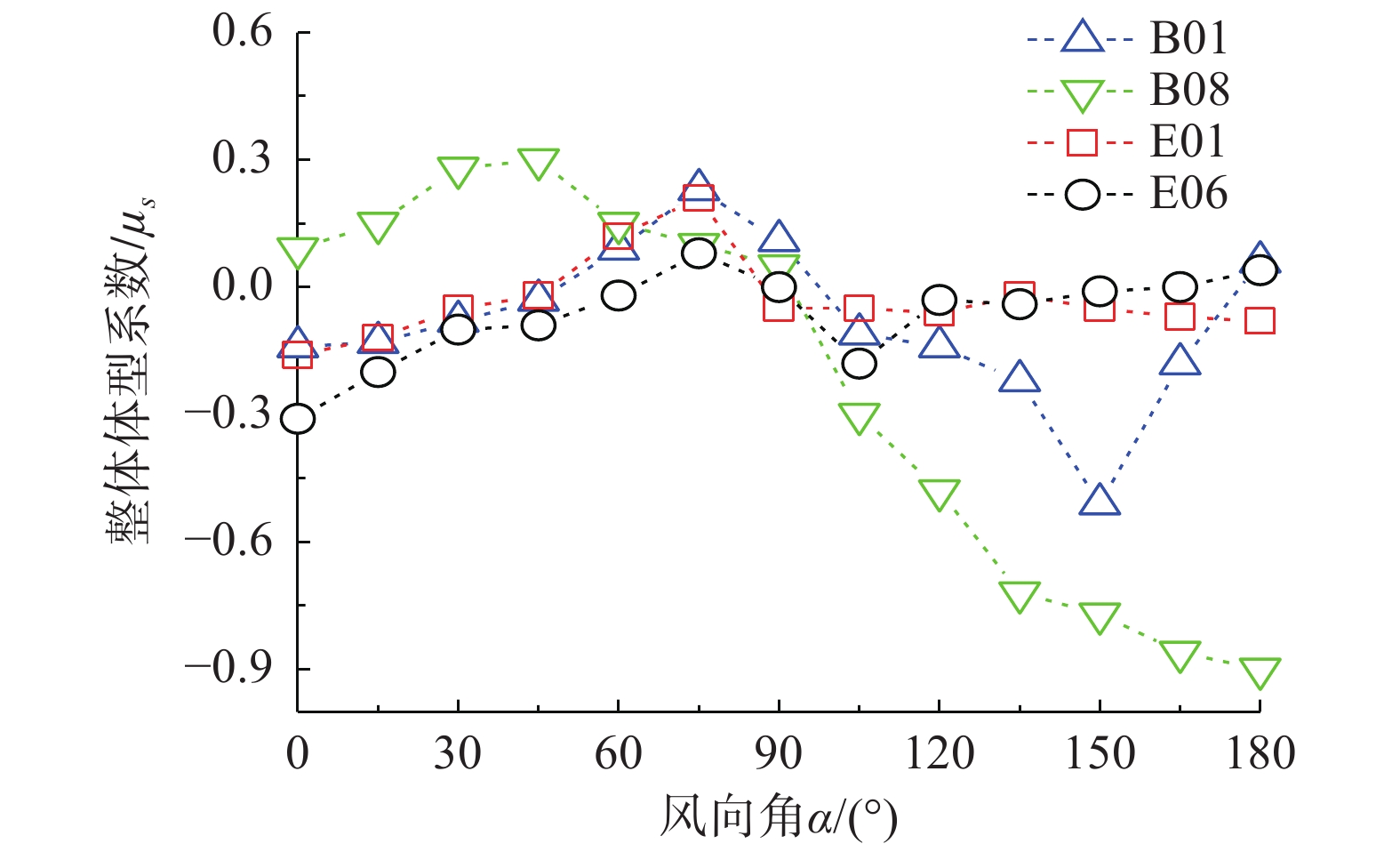
为便于比较，距屋面边缘900 mm的阵列光伏板上选择编号B01、B08；距离屋面边缘1800 mm的阵列光伏板上选择编号E01、E06，其整体体型系数随风向角变化见图2。图2中可以看到，在0°和180°风向角下，距离女儿墙900 mm的光伏板B01和B08的整体体型系数(绝对值)大于距离女儿墙1800 mm的光伏板E01和E06的整体体型系数(绝对值)，说明光伏板距离女儿墙越近，承受的风荷载越大，这主要是由结构边缘流体分离加速引起的。

图 2 屋面光伏板整体体型系数随风向角变化

Figure 2. The overall shape coefficient of the roof solar panel varies with the wind angle

下载: 全尺寸图片幻灯片

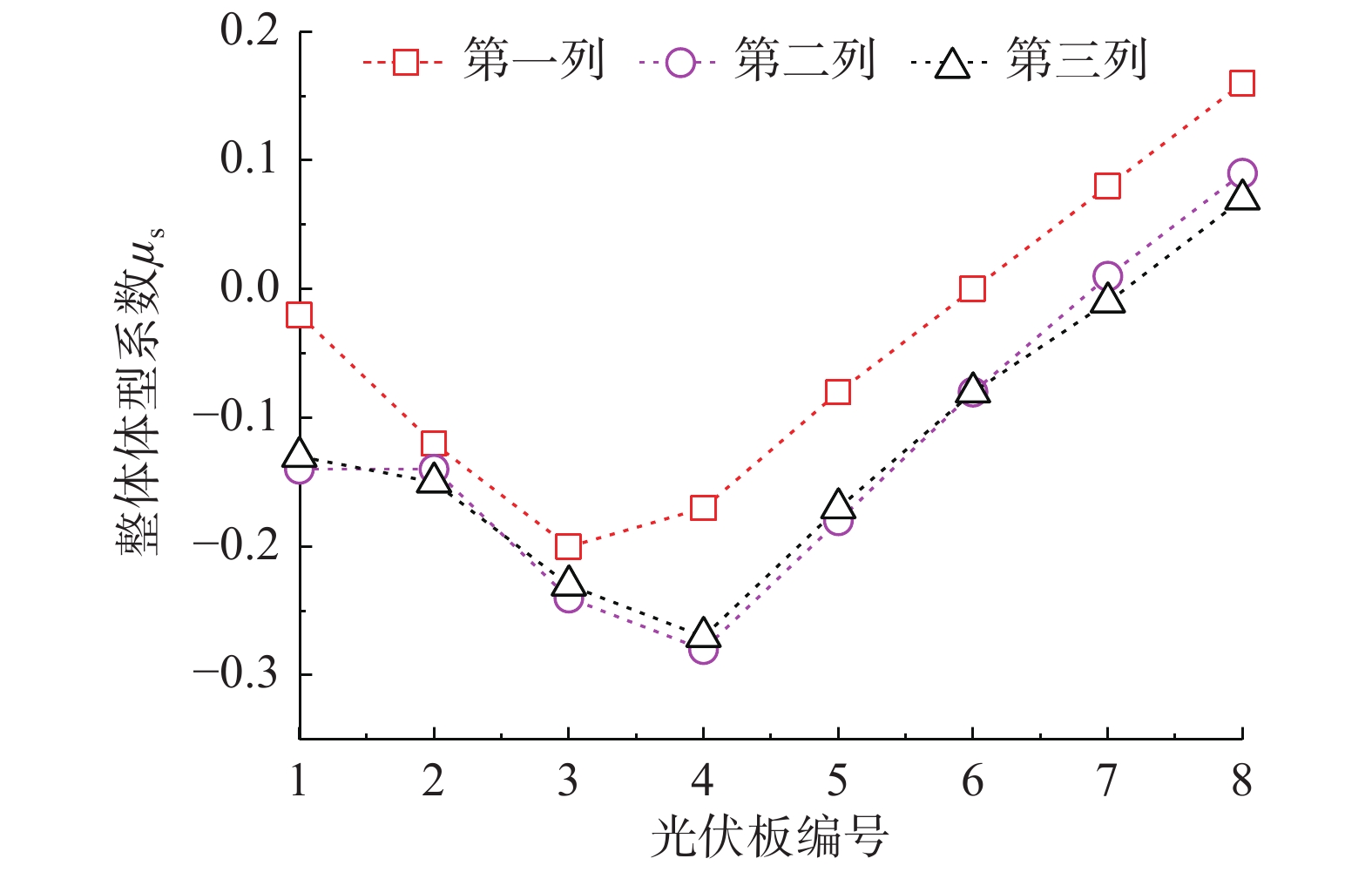
如图1(a)所示，编号A01~A08为第一列，编号B01~B08为第二列，编号C01~C08为第三列，并从1~8依次排序。图3给出了前三列屋面光伏板在倾角为30°时整体体型系数分布。以第一列光伏板为例，编号A01光伏板在风向角0°下整体体型系数为−0.02，表现为风吸力，这与地面光伏支架的正向体型系数不同，主要由于来流接触建筑时，受到建筑物的阻挡分离，编号A01光伏板整体处在分离流以内，整体体型系数出现负值，光伏板距离屋面边缘达到一定距离，分离效应减弱，风荷载表现为风压力。

图 3 三列光伏板整体体型系数随位置变化

Figure 3. The overall shape coefficient of three-row solar panels varies with position.

下载: 全尺寸图片幻灯片

2.2 无女儿墙时屋面光伏板风荷载取值建议

由于建筑结构的扰流作用，屋面上光伏板与地面上光伏板风荷载取值不同。图4给出了屋面光伏板第一列~第三列在各个风向角统计意义下的最大正压和最强负压，屋面边缘位置处光伏支架风压在−1.14~0.58，屋面中间位置处光伏支架风压在−0.5~0.5。

图 4 光伏板在全风向角下的最大正压和最强负压

Figure 4. Maximum positive pressure and maximum negative pressure of solar panel at full wind angle.

下载: 全尺寸图片幻灯片

对于30°倾角的光伏板，无女儿墙时，平屋顶上边缘位置处光伏板体型系数风吸力取−1.2，风压力取+0.6；中间位置光伏板体型系数风吸力取−0.5，风压力取+0.5。

3 女儿墙高度对体型系数的影响及取值建议

3.1 女儿墙高度整体体型系数的影响

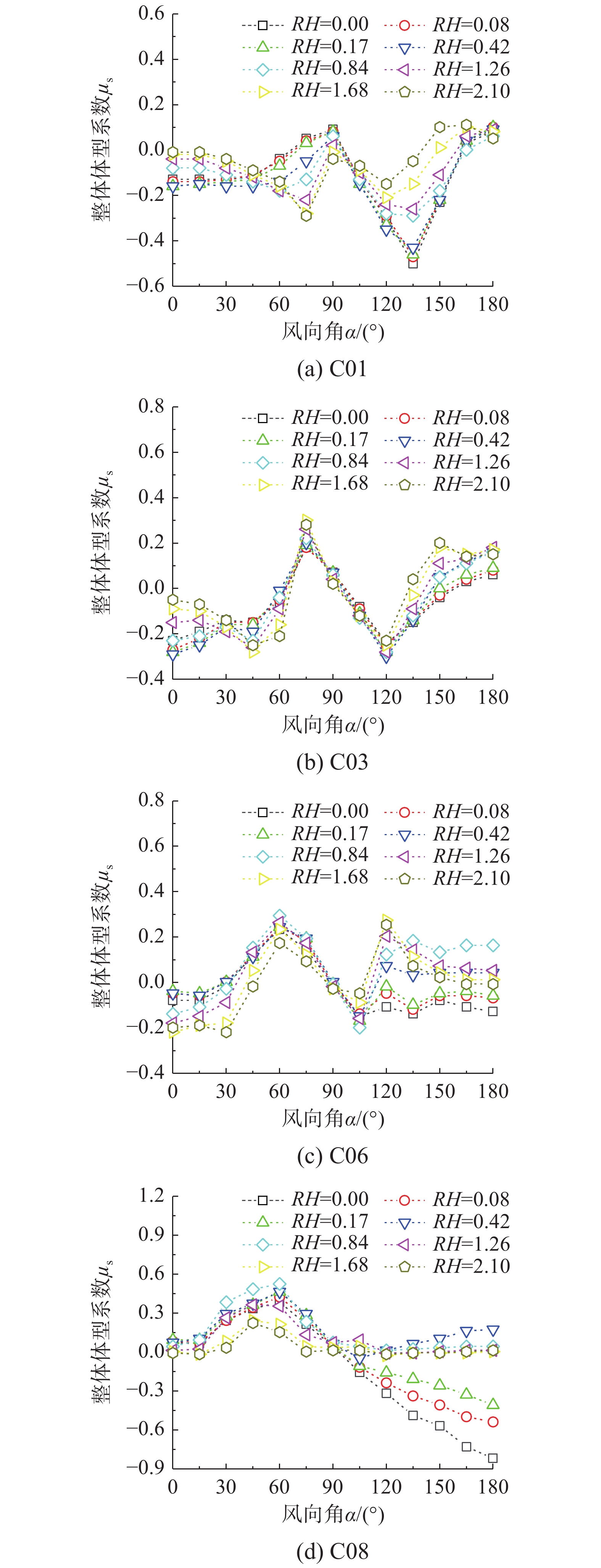
图5为第一列光伏板A01、A03、A06和A08在不同女儿墙高度下整体体型系数随风向角的变化。图5(a)可以看出A01光伏板在风向角0°~90°，RH<0.84时，整体体型系数先增大后减小，最大正压值出现在45°，RH>0.84时光伏板的风荷载很小；在风向角90°~180°，最强负压出现在165°，整体体型系数(绝对值)随女儿墙高度增加逐渐减小，女儿墙高度影响比较明显的RH值在0.42~0.84，整体体型系数由正值逐步转为负值。图5(b)可以看出A03光伏板在风向角0°~75°，不同RH值对应的整体体型系数随风向角均先增大后减小，最大正压出现在45°；风向角在75°~135°，随着RH值的增大，光伏板承受风荷载增加；风向角在135°~180°，最强负压出现在150°和165°。图5(c)可以看出光伏板在0°~90°风向角下，最不利风向角为15°；在90°~180°风向角下，RH值越大，整体体型系数绝对值越小，光伏板所受风荷载越小。图5(d)可以看出光伏板在风向角0°~60°，最大正压在15°；风向角在90°~180°，RH>0.42时，整体体型系数基本趋向于0，RH值介于0~0.42，整体体型系数为负值，并随着女儿墙高度降低，光伏板承受的风吸力有明显增大。

图 5 第一列光伏板整体体型系数随风向角变化

Figure 5. The overall shape coefficient of the first row of solar panels varies with the wind angle

下载: 全尺寸图片幻灯片

对于平屋面上第一列光伏板，女儿墙高度增加对边缘位置光伏板风荷载影响较大。位于迎风向第一个位置A01光伏板在风向角0°~90°随女儿墙高度增加体型系数变化明显；对处于背风向位置的A08在风向角90°~180°随女儿墙高度减小整体体型系数绝对值有显著增大，说明女儿墙可以有效减小平屋面光伏板所受到的风压力与风吸力；位于中间位置的太阳能光伏板，随女儿墙高度的增加体型系数有一定程度减小，但影响不明显。

图6为第二列光伏板B01、B03、B06和B08在不同女儿墙高度下整体体型系数随风向角的变化。图6(a)给出了B01光伏板在风向角0°~45°，体型系数值在−0.2~0；在风向角45°~105°，RH<0.84时，光伏板体型系数由负值转为正值；在风向角105°~150°，女儿墙越大，所承受的风吸力越小；在风向角150°~180°，光伏板所受风荷载由风吸力转为风压力。图6(b)给出了B03光伏板在风向角0°~180°在不同RH值下体型系数变化规律，可以看出，RH值越大，整体体型系数绝对值越小，但总体变化趋势保持一致。图6(c)给出了B06光伏板在风向角0°~75°整体体型系数先增大后减小，风向角45°时风压力最大；在风向角105°~180°，RH<0.42时光伏板承受风吸力，RH>0.42时，光伏板承受风压力。图6(d)给出了B08光伏板在风向角0°~90°，不同RH值光伏板整体体型系数变化趋势一致先增大后减小趋向于0；在风向角90°~180°，RH<0.42时，光伏板承受风吸力，并且RH值越小，风吸力越大。RH=0.42时，整体体型系数由负值转为正值。当RH>0.42时，整体体型系数基本保持不变，取值趋近于0。

图 6 第二列光伏板整体体型系数随风向角变化

Figure 6. The overall shape coefficient of the second row of solar panels varies with the wind angle

下载: 全尺寸图片幻灯片

对于屋面第二列光伏板，女儿墙高度增加对边缘位置处影响很大，编号B01光伏板在0°~90°变化与第一列相同位置处光伏板相比整体体型系数变化幅度逐渐减小；对于编号B08光伏板在90°~180°整体体型系数随女儿墙高度增加发生明显变化，风吸力显著减小并逐渐趋近0。

图7为第三列光伏板C01、C03、C06和C08在不同女儿墙高度下整体体型系数随风向角的变化情况。图7(a)给出了C01光伏板在风向角0°~60°，整体体型系数在−0.2~0；在90°~180°的RH值越大，整体体型系数绝对值越小，光伏板承受的风吸力越小。图7(b)给出了C03光伏板在风向角0°~180°不同RH值下整体体型系数变化规律，可以看出不同RH值下光伏板承受风荷载作用规律相同，且变化范围不大。图7(c)给出了C06光伏板在风向角0°~105°，不同RH变化趋势基本相同；在105°~180°，RH<0.42时，整体体型系数为负值表现为风吸力，且RH值越小光伏板所受风吸力越大。RH≥0.42时，整体体型系数为正值表现为风压力。图7(d)给出了C08光伏板在风向角0°~90°，RH值在0~1.26整体体型系数变化趋势相同；在90°~180°，RH<0.42时，光伏板承受风吸力，且RH值越小所受风吸力越大。RH≥0.42时，整体体型系数趋近于0，光伏板几乎不承受风荷载。

图 7 第三列光伏板整体体型系数随风向角变化

Figure 7. The overall shape coefficient of the third row of solar panels varies with the wind angle

下载: 全尺寸图片幻灯片

对于第三列屋面阵列太阳能光伏板在不同RH下整体体型系数随风向角变化可以看出，不同位置处的光伏板对于女儿墙高度的敏感程度不同。编号C01光伏板整体体型系数对女儿墙高度比较敏感的风向角是45°~90°和105°~180°；编号C03光伏板整体体型系数随女儿墙高度几乎不发生改变；编号C06光伏板整体体型系数对女儿墙高度比较敏感的风向角是105°~180°；编号C08光伏板整体体型系数对女儿墙高度比较敏感的风向角是90°~180°。

总的来说，女儿墙的高度对光伏板风荷载的影响很大，这种影响也与光伏板在屋面上的位置有关。随着女儿墙高度增加，作用在光伏板上的风荷载方向和大小均会发生变化。从试验结果看RH超过0.42后，女儿墙高度对光伏板风荷载的影响随着女儿墙高度的增加减弱。

3.2 有女儿墙时屋面光伏板风荷载取值建议

女儿墙高度对屋顶光伏板风荷载的影响主要考虑整体体型系数最大值和最小值，表1为不同RH值下光伏板的最大正压和最大负压。

表 1 不同RH值下屋面阵列光伏板整体体型系数最值

Table 1. The maximum value of overall shape coefficient of roof array solar panels under different RH values

RH值	全部光伏板体型系数		中心(不考虑边缘)光伏板体型系数
RH值	最大正压	最大负压	最大正压	最大负压
0.00	0.58	−1.14	0.38	−0.50
0.08	0.60	−1.00	0.38	−0.46
0.17	0.53	−0.94	0.41	−0.48
0.42	0.47	−0.54	0.39	−0.47
0.84	0.51	−0.52	0.47	−0.52
1.26	0.45	−0.46	0.45	−0.46
1.68	0.38	−0.40	0.38	−0.40
2.10	0.32	−0.35	0.32	−0.35

下载: 导出CSV

| 显示表格

女儿墙高度增加可以有效减小平屋面阵列光伏板整体体型系数，对于倾角为30°的平屋面光伏支架，女儿墙高度小于0.5(试验高度为0.42，考虑到应用方便，偏于保守的取0.5)倍光伏板高度时，随着女儿墙高度增加光伏板整体体型系数减小很快；女儿墙高度为0.5倍~1倍光伏板高度时，光伏板整体体型系数风吸力为−0.6，风压力为+0.6；女儿墙高度为2倍光伏板高度时，整体体型系数风吸力取−0.4，风压力取+0.4；女儿墙高度为1倍~2倍光伏板高度时，可以采用线性插值。

4 结论

通过刚性模型测压风洞试验获得不同女儿墙高度对平屋面阵列光伏板整体体型系数变化数值。女儿墙可以有效减小平屋面光伏板所受到的风吸力，其中当女儿墙高度为光伏板高度一半(试验结果为0.42)以上时，折减效应非常显著。屋顶上光伏阵列的风荷载取值需要综合考虑女儿墙高度和光伏板位置的影响，边缘位置处光伏板比屋面中心位置处光伏板承受荷载大。

对于平屋面上倾角30°，无女儿墙时，屋面边缘光伏板正压体型系数可取+0.6，负压体型系数取−1.2，中间位置正压体型系数取+0.5，负压取−0.6；女儿墙高度为大于0.5倍光伏板高度时，位于边缘和中心区域的光伏支架，正压体型系数和负压体型系数绝对值接近，正压体型系数取+0.6，负压体型系数取−0.6；当为2倍光伏板高度时，光伏板风压力取+0.35，风吸力取−0.4。

图 1 试验模型

Figure 1. Test mode

下载: 全尺寸图片幻灯片

图 2 屋面光伏板整体体型系数随风向角变化

Figure 2. The overall shape coefficient of the roof solar panel varies with the wind angle

下载: 全尺寸图片幻灯片

图 3 三列光伏板整体体型系数随位置变化

Figure 3. The overall shape coefficient of three-row solar panels varies with position.

下载: 全尺寸图片幻灯片

图 4 光伏板在全风向角下的最大正压和最强负压

Figure 4. Maximum positive pressure and maximum negative pressure of solar panel at full wind angle.

下载: 全尺寸图片幻灯片

图 5 第一列光伏板整体体型系数随风向角变化

Figure 5. The overall shape coefficient of the first row of solar panels varies with the wind angle

下载: 全尺寸图片幻灯片

图 6 第二列光伏板整体体型系数随风向角变化

Figure 6. The overall shape coefficient of the second row of solar panels varies with the wind angle

下载: 全尺寸图片幻灯片

图 7 第三列光伏板整体体型系数随风向角变化

Figure 7. The overall shape coefficient of the third row of solar panels varies with the wind angle

下载: 全尺寸图片幻灯片

表 1 不同RH值下屋面阵列光伏板整体体型系数最值

Table 1 The maximum value of overall shape coefficient of roof array solar panels under different RH values

RH值	全部光伏板体型系数		中心(不考虑边缘)光伏板体型系数
RH值	最大正压	最大负压	最大正压	最大负压
0.00	0.58	−1.14	0.38	−0.50
0.08	0.60	−1.00	0.38	−0.46
0.17	0.53	−0.94	0.41	−0.48
0.42	0.47	−0.54	0.39	−0.47
0.84	0.51	−0.52	0.47	−0.52
1.26	0.45	−0.46	0.45	−0.46
1.68	0.38	−0.40	0.38	−0.40
2.10	0.32	−0.35	0.32	−0.35

下载: 导出CSV

参考文献(15)

[1]	牛斌, 张超, 侯巍, 等. 基于CFD方法的地面光伏阵列风压时程特性研究[J]. 太阳能学报, 2016, 37(7): 1774 − 1779. doi: 10.3969/j.issn.0254-0096.2016.07.024 Niu Bin, Zhang Chao, Hou Wei, et al. Study on wind pressure time-history characteristics of ground photovoltaic array based on CFD method [J]. Journal of Solar Energy, 2016, 37(7): 1774 − 1779. (in Chinese) doi: 10.3969/j.issn.0254-0096.2016.07.024
[2]	马文勇, 孙高健, 刘小兵, 等. 太阳能光伏板风荷载分布模型试验研究[J]. 振动与冲击, 2017, 36(7): 8 − 13. Ma Wenyong, Sun Gaojian, Liu Xiaobing, et al. Tests for wind load distribution model of solar panels [J]. Journal of Vibration and Shock, 2017, 36(7): 8 − 13. (in Chinese)
[3]	Ayodeji A O, Horia H, Kamran S. Experimental investigation of wind effects on a standalone photovoltaic (PV) module [J]. Renewable Energy, 2015, 78: 657 − 665. doi: 10.1016/j.renene.2015.01.037
[4]	马文勇, 柴晓兵, 刘庆宽, 等. 底部阻塞对太阳能光伏板风荷载的影响研究[J]. 建筑结构, 2019, 49(2): 129 − 134. Ma Wenyong, Chai Xiaobing, Liu Qingkuan, et al. Study on effect of bottom flow obstruction on wind load of solar photovoltaic panels [J]. Building Structure, 2019, 49(2): 129 − 134. (in Chinese)
[5]	肖福勤, 陈作钢, 代燚, 等. 漂浮式光伏电站方阵环境载荷计算方法研究[J]. 工程力学, 2020, 37(3): 245 − 256. doi: 10.6052/j.issn.1000-4750.2019.04.0230 Xiao Fuqin, Chen Zuogang, Dai Yi, et al. Numerical method study on environmental loads of floating photovoltaic power array [J]. Engineering Mechanics, 2020, 37(3): 245 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.0230
[6]	Cao J, Yoshida A, Saha P K, et al. Wind loading characteristics of solar arrays mounted on flat roofs [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 214 − 225. doi: 10.1016/j.jweia.2013.08.014
[7]	Radu A, Axinte E. Wind forces on structures supporting solar collectors [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1989, 32(1/2): 93 − 100. doi: 10.1016/0167-6105(89)90020-2
[8]	李嘉阳, 童乐为, 吴建明, 等. 建筑屋面光伏阵列风场的模拟[J]. 工业建筑, 2018, 48(8): 155 − 162. Li Jiayang, Tong Lewei, Wu Jianming, et al. Simulation of wind field around photovoltaic array on roofs [J]. Industrial Construction, 2018, 48(8): 155 − 162. (in Chinese)
[9]	韩晓乐. 太阳能光伏阵列风荷载取值研究[D]. 石家庄: 石家庄铁道大学, 2016. Han Xiaole. Study on wind load of solar photovoltaic array [D]. Shijiazhuang: Shijiazhuang Tiedao University, 2016. (in Chinese)
[10]	黄伯城, 马文勇, 刘庆宽. 串列光伏板体型系数遮挡效应研究[C]. 济南: 全国结构工程学术会议, 2016: 326 − 329. Huang Bocheng, Ma Wenyong, Liu Qingkuan. Study on the effect of shielding tandem photovoltaic panels shape coefficient [C]. Ji’nan: National Conference on Structural Engineering, 2016: 326 − 329. (in Chinese)
[11]	李正农, 范晓飞, 蒲鸥, 等. 建筑物风沙流场与荷载的风洞试验研究[J]. 工程力学, 2020, 37(1): 152 − 158, 182. doi: 10.6052/j.issn.1000-4750.2019.02.0067 Li Zhengnong, Fan Xiaofei, Pu Ou, et al. Wind tunnel test on wind-sand flow field and wind-sand load of buildings [J]. Engineering Mechanics, 2020, 37(1): 152 − 158, 182. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.02.0067
[12]	王京学, 杨庆山, 刘敏, 等. 平屋盖及双坡屋盖光伏系统风荷载特性试验研究[J]. 建筑结构学报, 2018, 39(10): 21 − 28. Wang Jingxue, Yang Qingshan, Liu Min, et al. Experimental research on characteristics of wind loads of solar arrays mounted on flat and gable roof [J]. Journal of Building Structures, 2018, 39(10): 21 − 28. (in Chinese)
[13]	龚敏, 欧添雁. 单个屋面光伏组件风载体型系数风洞试验研究[J]. 安徽建筑, 2015, 22(6): 183 − 184, 196. Gong Min, Ou Tianyan. Research on wind tunnel test of shape coefficient of wind load for photovoltaic module with single roof [J]. Anhui Architecture, 2015, 22(6): 183 − 184, 196. (in Chinese)
[14]	李寿科, 肖飞鹏, 张雪, 等. 女儿墙对平屋面低矮建筑风荷载特性的影响[J]. 建筑结构, 2020, 50(7): 74 − 79. Li Shouke, Xiao Feipeng, Zhang Xue, et al. Effect of parapet-wall on wind load of flat roof low-rise building [J]. Building Structure, 2020, 50(7): 74 − 79. (in Chinese)
[15]	GB 50009−2012, 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012. GB 50009−2012, Load code for the design of building structures [S]. Beijing: Chinese Building Industry Press, 2012. (in Chinese)

施引文献(27)

期刊类型引用(16)

1.	肖林发，林恒，王永祥，陈华鹏. Q960D高性能钢疲劳裂纹扩展影响因素分析. 材料科学与工程学报. 2024(03): 394-404 . 百度学术
2.	杨育梅，王正鹏，雷芳明. 超导带材涂层结构边缘脱粘后的电磁应力分析. 工程力学. 2024(08): 250-256 . 本站查看
3.	黄家能，詹光曹，王义惠，许智平，周汝锦，朱丽娜，戴品强. Nb微合金化Q345qD钢的连续冷却转变行为. 福建冶金. 2024(05): 36-39 . 百度学术
4.	李武安，常义，孙小川. 断裂力学在桥梁领域的应用与发展. 科技创新与应用. 2024(34): 101-106 . 百度学术
5.	虞庐松，王庚，王力，周晓夫，顾皓玮，李子奇. 高寒环境温度下钢管混凝土柱抗震性能试验研究. 地震工程学报. 2024(06): 1251-1258 . 百度学术
6.	黄家能，詹光曹，王义惠，许智平，周汝锦，朱丽娜，戴品强. 铌微合金化Q345qD钢的热变形行为及热加工图. 江西冶金. 2024(06): 449-455 . 百度学术
7.	杨育梅，马蓉蓉，雷芳明. 临界电流密度的非均匀性对超导薄板电磁力学特性的影响. 工程力学. 2023(09): 247-256 . 本站查看
8.	周如江，于培师，吴连生，韦朋余，赵宇翔，赵军华. 低温环境下TC4ELI钛合金三维疲劳裂纹扩展模型. 机械工程材料. 2023(12): 87-92 . 百度学术
9.	黄俊，伍曾，张荣茂，马薇. 60Si2Mn弹簧钢疲劳裂纹扩展规律研究. 铸造技术. 2022(08): 690-693 . 百度学术
10.	郑杰瑜，王艺陶，刘俊杰，胡嘉骏，吴剑国，廖小伟. 焊接节点低温疲劳试验与低温主S-N曲线的构建. 海洋工程. 2021(06): 126-135 . 百度学术
11.	王元清，顾浩洋，廖小伟. 钢结构角焊缝低温抗剪疲劳性能的试验研究. 工程力学. 2020(01): 73-79+134 . 本站查看
12.	王天鹏，张建仁，肖宏彬. 低温环境下桥梁用结构钢疲劳寿命估算方法. 自然灾害学报. 2020(01): 64-71 . 百度学术
13.	王珂，秦闯，崔彭飞，张剑，李永正. 钛合金室温与低温疲劳裂纹扩展速率试验研究. 舰船科学技术. 2020(11): 30-33+49 . 百度学术
14.	潘远洲，何天虎，辛灿杰，关明智. 高温超导带材低/变温疲劳性能测试系统的研制. 工程力学. 2020(11): 248-256 . 本站查看
15.	童乐为，任珍珍，景爽，牛立超. 高强度结构钢系列的疲劳裂纹扩展速率试验研究. 工程力学. 2020(12): 191-201+212 . 本站查看
16.	甘宏运，何钢. 桥梁施工裂缝成因及处理措施研究. 交通世界. 2019(28): 86-87+126 . 百度学术