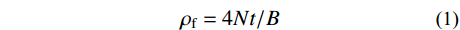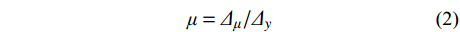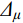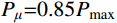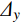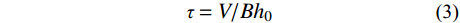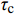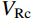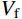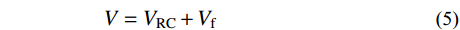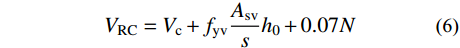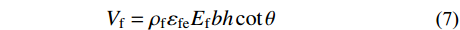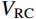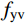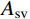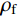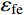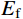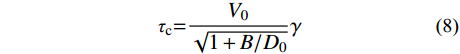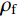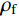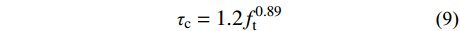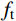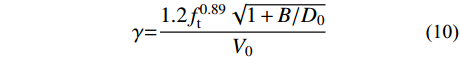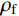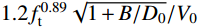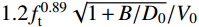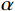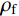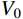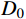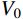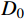MESO-SCALE ANALYSIS OF SIZE EFFECT ON ASEISMIC BEHAVIOR OF REINFORCED CONCRETE SQUARE COLUMNS STRENGTHENED WITH CFRP
-
摘要: 为研究CFRP加固钢筋混凝土方柱在地震作用下的破坏模式,该文考虑混凝土材料的非均质性、钢筋-混凝土间的粘结滑移作用,建立了CFRP加固钢筋混凝土方柱三维细观数值模型。在验证数值模型与试验结果吻合良好的基础上,扩展工况探讨了轴压比、CFRP体积配置率对CFRP加固钢筋混凝土方柱抗震性能及名义抗剪强度尺寸效应的影响。结果表明:一定轴压比范围内柱的承载力随轴压比增大而提高,但其延性会降低;该文工况中,CFRP加固钢筋混凝土柱的名义抗剪强度随试件尺寸增大呈降低趋势,存在着明显尺寸效应行为;在经典材料层次尺寸效应律基础上,提出了CFRP加固混凝土方柱名义抗剪强度尺寸效应理论公式(适用范围轴压比小于0.4),模拟结果证实了公式的合理性。
-
关键词:
- CFRP加固混凝土方柱 /
- 抗震性能 /
- 轴压比 /
- 体积配置率 /
- 尺寸效应
Abstract: In order to study the failure mechanism of RC columns strengthened by CFRP subjected to axial and cyclic lateral loads, a three-dimensional meso numerical model of reinforced concrete square columns strengthened with CFRP is established, considering the heterogeneity of concrete materials and the bond slip between reinforcement and concrete. On the grounds of the good agreement between the meso-scale simulation results with the available experimental results, the section size of the specimens is enlarged. Furthermore, the effects of axial compression ratio, volume allocation rate of CFRP on the aseismic performance and size effect on shear strength of reinforced concrete short columns strengthened with CFRP are explored. The results show that: the bearing capacity of specimens increases as the increase of axial compression ratio, but the ductility decreases; increasing the volume allocation ratio of CFRP has a limited effect on the increase of bearing capacity, which will enhance the ductility of columns; with the increase of specimen size, the nominal shear strength of columns tends to decrease, and there exists size effect behavior. -
在地震灾害发生时,钢筋混凝土柱同时承受竖向荷载以及水平荷载,是一种偏压剪构件,此时柱子往往发生脆性剪切破坏,从而导致整个结构受到灾难性破坏[1-3]。纤维增强复合材料(fiber reinforced polymer,FRP)具有轻质高强、不易腐蚀、施工方便等优点,因此采用FRP加固混凝土柱的方法引起了广泛关注,经研究发现FRP材料可以增强柱子的侧向约束作用从而显著提高柱子的延性以及耗能能力。
顾冬生等[4]试验研究了直径为360 mm的CFRP加固钢筋混凝土圆柱在高轴压比情况下的抗震性能以及影响因素——CFRP体积配置率对其抗震性能的影响,研究结果表明:高轴压比情况下CFRP加固钢筋混凝土短柱能显著提高其抗震性能,并对柱子的破坏形态有显著影响。陈勤和李静[5]对CFRP约束混凝土柱在往复荷载作用下的力学性能进行了有限元研究,发现CFRP的约束作用可以缓解混凝土柱裂缝的开展,提高柱的延性但CFRP的增强作用并不随CFRP的加固层数线性增长。张大长和吴智深[6]采用试验和模拟2种方法研究了CFRP加固钢筋混凝土柱的抗震性能,通过研究CFRP加固钢筋混凝土柱的荷载-变形关系、柱子反弯点和柱脚处的混凝土的变化、钢筋以及CFRP的应力-应变的发展,进一步证实了CFRP材料能够有效地提高钢筋混凝土柱的抗震性能。Shamim等[7]试验探究了GFRP和CFRP 2种FRP材料分别对混凝土圆柱加固后的抗震性能,发现CFRP或GFRP加固后的构件,其变形能力、抗压强度均显著增强,耗能能力也明显提高。邓宗才等[8]研究了FRP布约束氯离子腐蚀混凝土结构的抗震性能,研究结果显示,由于FRP的横向约束作用存在,组合结构的刚度与承载力在后期加载过程中退化较为缓慢,构件的延性得到了极大提高。崔宇强[9]通过试验方法研究了CFRP加固钢筋混凝土柱(截面尺寸最大为450 mm)的受压性能和抗震性能的尺寸效应行为,结果表明对于归一化后的荷载-位移骨架曲线,在相同的轴压比和单位位移条件下,钢筋混凝土柱和CFRP加固钢筋混凝土柱的水平荷载随着构件尺寸的增大而逐渐减小,即存在尺寸效应现象。
受到试验条件和经济成本等的限制,目前对于FRP约束混凝土柱抗震性能的研究一般是基于小尺寸构件进行探讨的。实际上,由于混凝土材料的非均质性和拟脆性,混凝土材料和钢筋混凝土构件的力学性能均存在着尺寸效应现象[10]。研究小尺寸试件得出的理论结果并不一定具有普遍的指导意义,在工程实践中可能会高估大尺寸试件的承载能力,进而产生严重后果。因此,本文采用细观数值模拟方法,建立CFRP加固钢筋混凝土方柱三维细观数值模型,研究其在地震作用下的破坏模式、滞回曲线及延性水平,探讨轴压比、CFRP体积配置率及试件尺寸对钢筋混凝土方柱的抗震性能的影响机制与规律。此外,对CFRP加固钢筋混凝土柱抗震性能及抗剪强度尺寸效应行为进行更加深入的研究,提出CFRP加固混凝土方柱名义抗剪强度尺寸效应理论修正公式,为CFRP加固钢筋混凝土结构合理的设计方案提供一定的支持。
1 CFRP加固钢筋混凝土方柱细观模型
1.1 3D细观模型建立
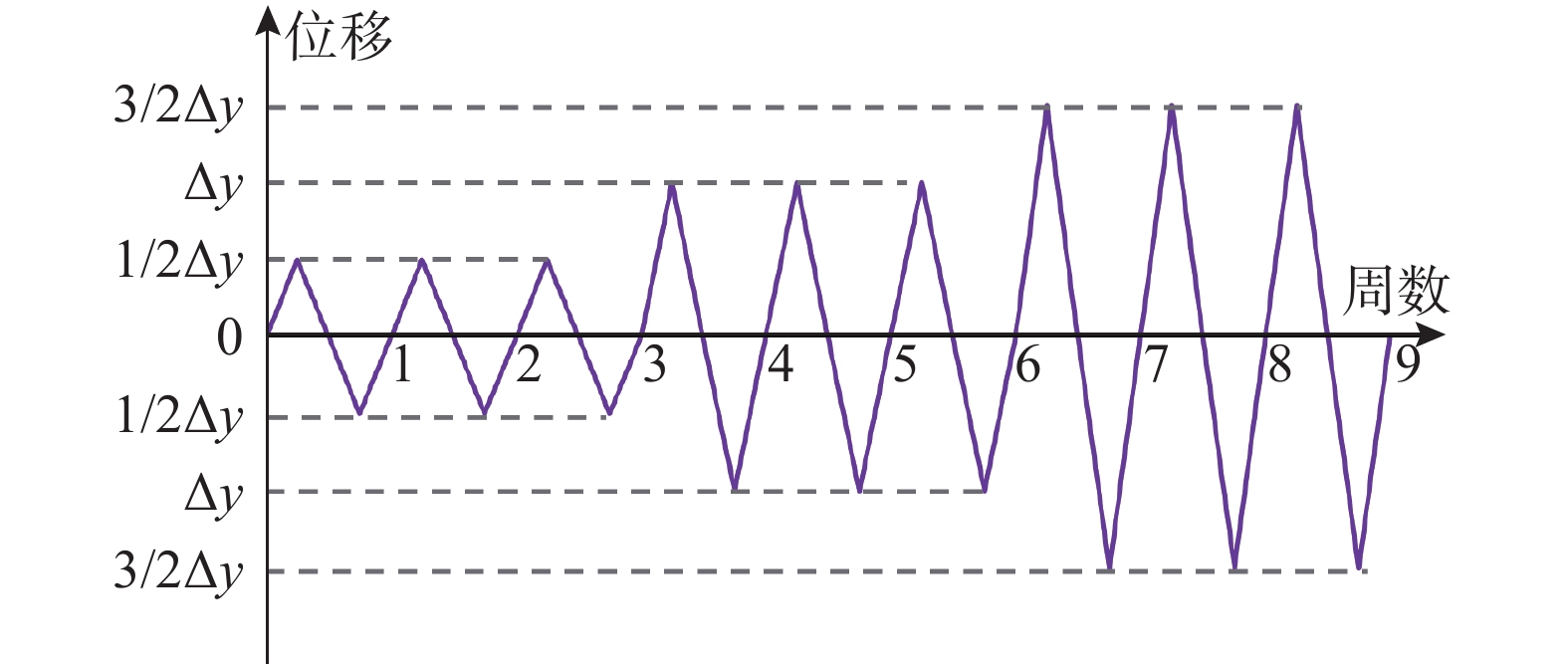
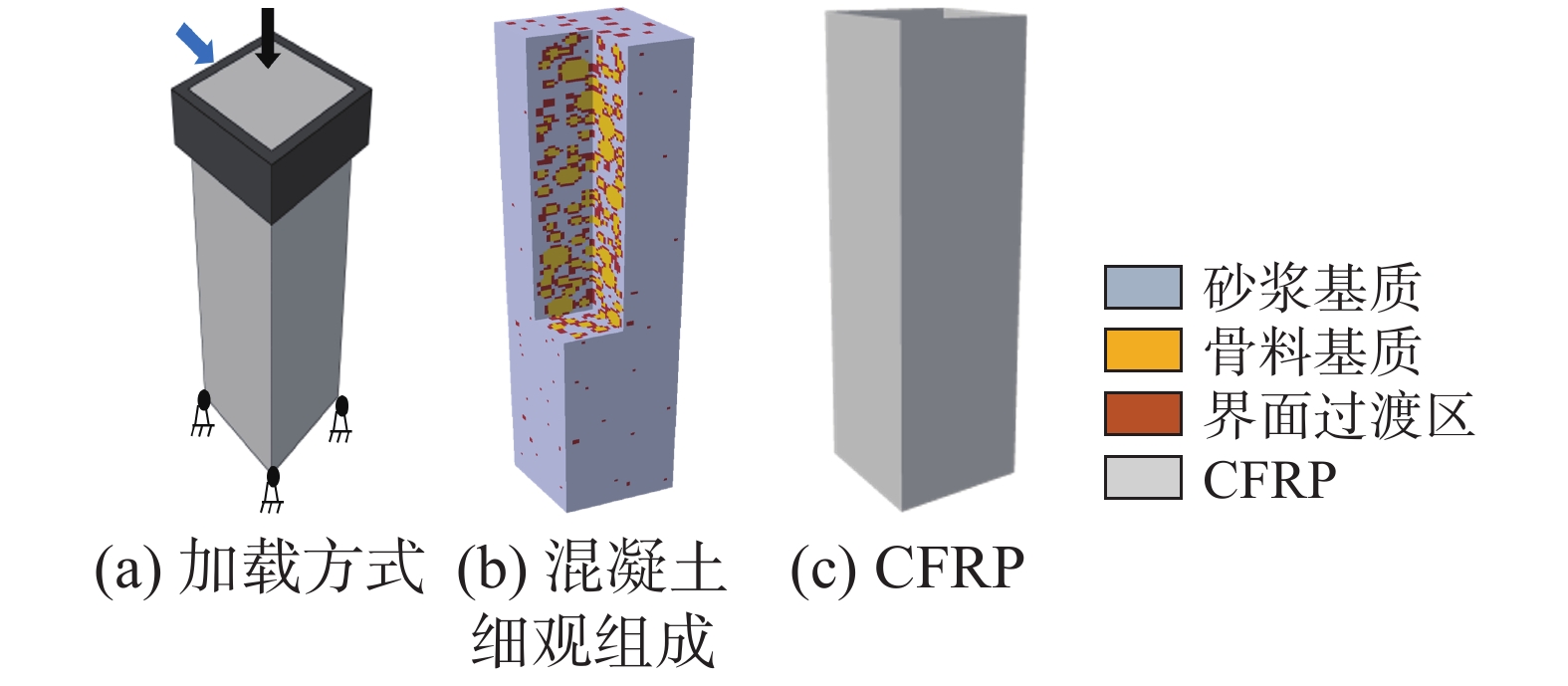
本文建立细观尺度模型,将混凝土看成骨料颗粒、砂浆及界面过渡区(ITZ) 3者组成的非均质材料[11-12]。参考文献[13]工作,将骨料假定为球形,混凝土采用二级配,即最小等效粒径为12 mm,最大等效粒径为30 mm,骨料体积分数约为45%。利用Fortran编程,将骨料颗粒随机投入到砂浆基质中。由于计算效率受限,本文将骨料颗粒周围2 mm的薄层设定为界面过渡区[14],进而生成素混凝土柱三维细观模型。将有限元网格在三维结构上进行投影,并将各项组分在网格中的相对位置判定单元类型(即骨料单元、砂浆基质单元以及ITZ单元),赋予相应的材料属性。插入钢筋笼,进而生成CFRP加固钢筋混凝土方柱细观模型,如图1所示,其中混凝土3种组分均采用8节点六面体减缩积分单元划分、CFRP采用壳单元进行划分,钢筋采用梁单元进行离散,网格单元平均尺寸为2 mm。柱子底部为固定约束,在柱上面施加预定的轴向荷载值,然后对柱上部施加侧向低周水平循环往复荷载,如图2所示,其中
Δy 为CFRP加固钢筋混凝土柱的屈服位移。1.2 本构关系
由于骨料强度较高,一般不产生较大的变形,故本文将骨料颗粒设置为弹性体,对于砂浆基质及界面过渡区,参照Jin等[15]的工作,采用塑性损伤本构模型[16]来描述其力学性能,钢筋材料质地均匀,故采用理想弹塑性本构模型来描述其力学行为。
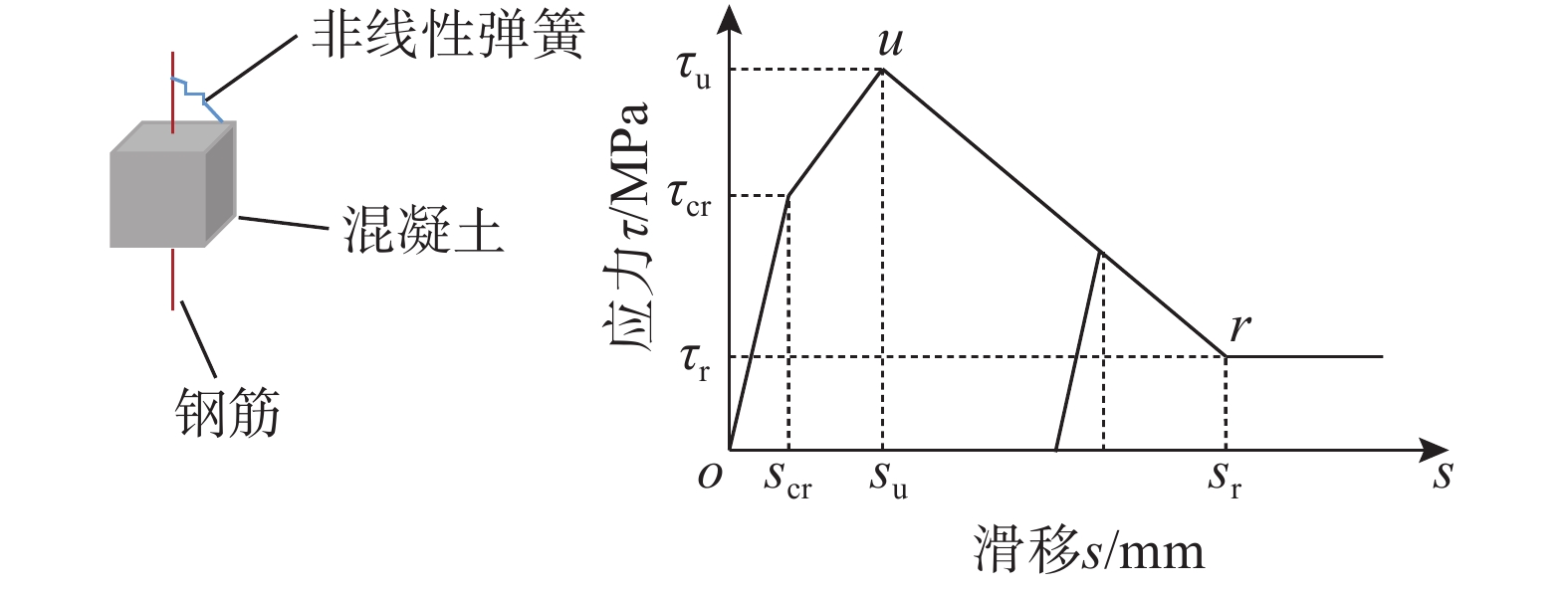
本文采用《混凝土结构设计规范》(GB 50010−2010)[17]建议的钢筋-混凝土粘结滑移(τ-s)本构关系模型(如图3)来描述钢筋与混凝土之间的相互作用,其中各关键点的确定方法见表1。
表 1 粘结-滑移本构参数Table 1. Parameters utilized in the bond-slip model关键点 开裂 峰值 残余 应力 τ/MPa τcr=2.5ft τu=3ft τr=ft 滑移 s/mm scr,l=0.025d su,l=0.04d sr,l=0.55d 试验[18]证明:FRP在破坏前表现为线弹性特征,这里设定CFRP为理想弹脆性材料,其破坏准则为:纤维达到其有效断裂应变时,试件失效,不可再承受荷载。另外,为简化计算,参考文献[19],CFRP与混凝土之间假定为理想粘结,即不产生剥离破坏。
1.3 数值模拟方法的验证
基于以上分析方法,选取崔宇强[9]试验中的S1L0N1、S1L1N1和S2L2N1试件的参数展开细观模拟工作,将试验结果与模拟结果进行对比,发现模拟得到的破坏形态及骨架曲线均与试验结果吻合度较高,因此验证了本文参数选取的合理性以及模拟方法的准确性和可行性。下面描述数值模拟方法验证工作的具体细节。
试验中3种试件的轴压比均为0.15,其中S1L0N1和S1L1N1两个试件的截面尺寸均为150 mm,S1L0N1试件作为对照试件,未进行CFRP布加固处理;而S1L1N1试件加固1层CFRP布。S2L1N2试件截面尺寸为200 mm, 加固2层CFRP布。试验中混凝土立方块轴心抗压强度为51.65 MPa,方柱剪跨比为3,纵筋选用HRB400级钢筋,配筋率为1.0%,箍筋选用HPB300级钢筋,其体积配箍率为0.5%。CFRP的单层厚度为0.167 mm,其弹性模量为240 GPa,其极限断裂应变为1.61%,试验中对核心混凝土采取侧面全包的方式。
数值计算中采用的混凝土细观组分及钢筋力学参数如表2所示。其中,试验实测数据以“*”表征,通过开展大量标准立方体混凝土试块单轴压缩试验确定的界面力学参数用“^”表示,将表2各参数代入所建模型中,结果得到的立方块的轴心抗压强度为52.3 MPa,与试验结果51.65 MPa基本吻合,初步说明本文参数选取是合理的。
表 2 混凝土细观组分及钢筋力学参数Table 2. Mechanical parameters of the three meso components of concrete and reinforcing bars utilized组分 粗骨料 砂浆基质 界面过渡区 纵筋 箍筋 抗压强度σc/MPa − *53.1 ^48.2 − − 抗拉强度σt/MPa − *5.2 ^4.7 − − 弹性模量E/GPa *60 *42.5 ^38.4 *210 *200 泊松比ν *0.2 *0.2 ^0.2 *0.3 *0.3 屈服强度fy/MPa − − − *380.71 *419.09 配筋率ρ/(%) − − − *1 *0.5 注:*为试验实测值[9];^为反复试算取值。 图4为未加固钢筋混凝土柱模拟结果与试验破坏形态[9]的对比。模拟中未加固柱首先在塑性铰区出现裂缝,随荷载增加,裂缝逐渐向四周扩散延伸,破坏时塑性铰至柱底端出现呈“X”型破坏的裂缝,构件根部混凝土亦被压碎。图5是CFRP加固钢筋混凝土柱模拟结果与试验破坏形态[9]的对比,从图5中可以看出,加载初期,首先在塑性铰区形成微裂缝,接着裂缝不断延伸,最后根部混凝土被压碎,CFRP被拉断。由图4和图5可以看出模拟结果与试验结果基本吻合。此外,可以发现CFRP能改善钢筋混凝土柱在地震作用下的破坏形态,柱子呈现由脆性的剪压破坏转变为延性较好的塑性铰区混凝土压碎破坏。
图6给出的是模拟结果与试验[9]得到的骨架曲线对比情况,可以看出模拟得到的骨架曲线形式、走向以及峰值荷载、峰值位移均与试验曲线[9]一致。
综上所述,模拟得到的破坏形态以及骨架曲线均与试验结果吻合度较高,说明本文参数选取的合理性以及模拟方法的准确性和可行性。
2 CFRP加固混凝土方柱抗震性能
在上述已验证的细观模型和数值方法的基础上,为了探讨CFRP体积配置率、轴压比对CFRP加固钢筋混凝土方柱抗震性能及其尺寸效应的影响,本文设计了CFRP加固钢筋混凝土柱在2种轴压比以及5种体积配置率情况下的CFRP加固钢筋混凝土柱。其中CFRP的体积配置率表示为[20]:
ρf=4Nt/B (1) 式中:N为CFRP层数;t为CFRP单层厚度;B为试件截面宽度。
表3给出了试件的几何参数(表中尺寸单位以mm计量),以“SC-200-0.4-1”为例解释其含义,其中字母“S”为方柱(square),字母“C”为循环加载 (cyclic loading),数字“200”代表柱子截面尺寸为200 mm,数字“0.4”表明柱子轴压比为0.4,数字“1”至“3”代表3种不同的CFRP体积配置率。
表 3 CFRP加固钢筋混凝土柱几何参数Table 3. Geometrical parameters of the RC columns strengthened with CFRP试件名称 截面宽度B/mm 柱高H/mm 轴压比n 体积配置率 ρf /(%) SC-200-0.4-1 200 600 0.4 0.000 SC-200-0.4-2 200 600 0.4 0.334 SC-200-0.4-3 200 600 0.4 1.336 SC-200-0.6-1 200 600 0.6 0.000 SC-200-0.6-2 200 600 0.6 0.334 SC-200-0.6-3 200 600 0.6 1.336 SC-400-0.4-1 400 1200 0.4 0.000 SC-400-0.4-2 400 1200 0.4 0.334 SC-400-0.4-3 400 1200 0.4 1.336 SC-400-0.6-1 400 1200 0.6 0.000 SC-400-0.6-2 400 1200 0.6 0.334 SC-400-0.6-3 400 1200 0.6 1.336 SC-800-0.4-1 800 2400 0.4 0.000 SC-800-0.4-2 800 2400 0.4 0.334 SC-800-0.4-3 800 2400 0.4 1.336 SC-800-0.6-1 800 2400 0.4 0.000 SC-800-0.6-2 800 2400 0.4 0.334 SC-800-0.6-3 800 2400 0.4 1.336 2.1 荷载-位移曲线分析
图7给出的是模拟获取的CFRP加固钢筋混凝土方柱的滞回曲线。可以看出,对于未进行CFRP加固的钢筋混凝土方柱,在加载初期,位移与荷载呈线性关系,其滞回曲线基本为直线,形成的滞回环所包围的面积很小,柱子的刚度基本没有变化,继续施加荷载,当荷载达到柱子屈服荷载后,荷载不再随位移线性增长,滞回曲线开始出现捏缩现象。3种不同尺寸CFRP加固钢筋混凝土方柱的承载力、极限位移均不同程度提高,此外,相较于未加固钢筋混凝土柱,其滞回环包围的面积增大,吸收的能量亦增多,有效地改善了钢筋混凝土柱的抗震性能。
2.2 骨架曲线分析
图8给出的是CFRP加固钢筋混凝土方柱骨架曲线,对于未加固的钢筋混凝土柱,其骨架曲线达到峰值荷载后迅速下降表现出明显的脆性破坏,当柱子截面尺寸为200 mm时,轴压比对钢筋混凝土的极限承载力、延性均影响较小。当柱的截面尺寸为400 mm或800 mm时,轴压比越小,极限承载力越大,且骨架曲线下降段越缓慢。对于CFRP加固的钢筋混凝土柱,其骨架曲线形式与未约束柱的曲线形式类似,承载力和变形能力均有不同程度提高。
2.3 延性能力分析
采用位移延性系数μ描述试件的延性能力,即:
μ=Δμ/Δy (2) 式中:
Δμ 为构件在Pμ=0.85Pmax 所对应的位移;Δy 为构件在屈服荷载时对应的位移[21]。图9给出的是在2种轴压比、3种体积配置率的情况下,柱子的位移延性系数μ随试件截面尺寸B的变化规律。从图9中可以看出位移延性系数呈现随试件截面尺寸增大而减小的趋势,且随试件截面尺寸增大这种趋势逐渐变缓。试件截面尺寸相同的试件,其位移延性系数随轴压比增大而减小,由此可知,随轴压比和截面尺寸增加,柱子的变形能力变弱,延性显著降低。此外,随CFRP体积配置率增大,相同截面尺寸的柱子延性有所提高,这是因为CFRP对核心混凝土提供有效约束,减缓了内部裂缝发展速度和柱子的横向膨胀。
3 名义抗剪强度尺寸效应分析
3.1 轴压比对名义抗剪强度尺寸效应影响
图10给出的是轴压比对柱子名义抗剪强度尺寸效应的影响,其中名义抗剪强度表示为:
τ=V/Bh0 (3) 式中:V为试件抗剪承载力;B为试件截面宽度;h0为试件有效高度。从图10可以看出,在同一种体积配置率情况下,随轴压比增大,3种不同尺寸柱子的名义抗剪强度均有不同程度提高,这说明一定范围内轴压比增大能提高柱子的名义抗剪强度。还可以发现,在两种轴压比下,随柱子截面尺寸增大,名义抗剪强度均呈下降趋势,即存在尺寸效应现象。
Bažant和Kim[22]提出了剪切强度尺寸效应理论公式:
τc=V0√1+B/D0 (4) 式中:
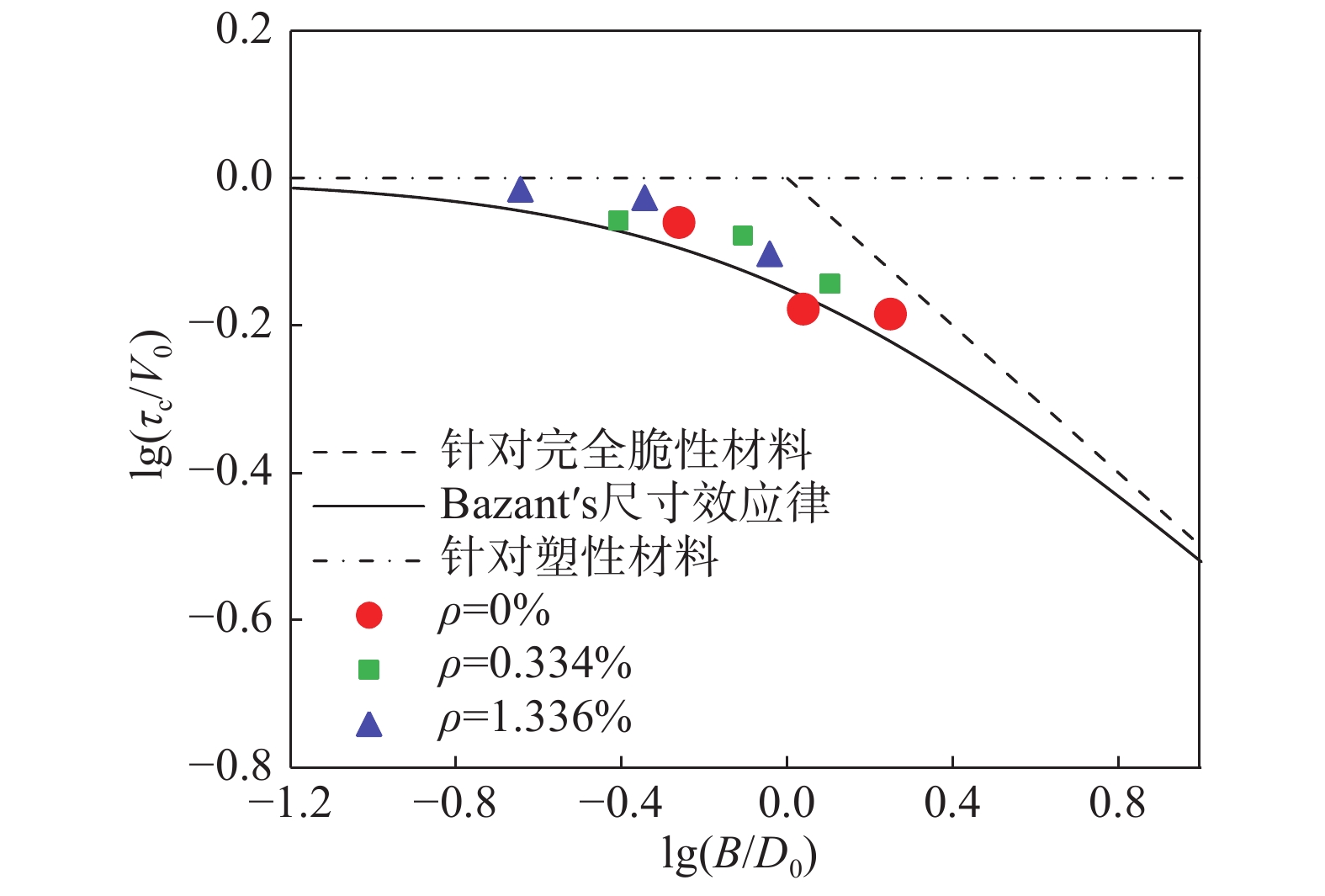
τc 为混凝土柱名义剪切强度;V0和D0是与混凝土有关的经验系数;B是试件截面尺寸(这里为柱的横截面宽度)。为了分析轴压比对混凝土柱的尺寸效应的影响,添加了未加固混凝土柱轴压比分别为0.2、0.4、0.6的工况,将模拟结果与线弹性断裂力学理论(LEFM),塑性强度理论(strength criterion)以及Bažant尺寸效应律进行了拟合对比,得到如图11(a)所示的曲线,其中相关系数为R2=0.92。可以发现相同尺寸试件在轴压比分别为0.2和0.4两种情况下的数据点基本重合,而轴压比为0.6的试件的数据点则比较分散。可以得出轴压比小于0.4时,轴压比对试件名义抗剪强度尺寸效应影响较小。
另外,将崔宇强[9]试验中的数据(柱子的截面宽度分别为150 mm、300 mm和450 mm且剪跨比均为3;3种不同尺寸的柱子在轴压比为0.15、0.3和0.45情况下发生剪切破坏)整理分析如图11(b)所示,可以得出相似的结论,也同时从另一侧面验证本文模拟结果的合理性。
3.2 体积配置率对名义抗剪强度尺寸效应影响
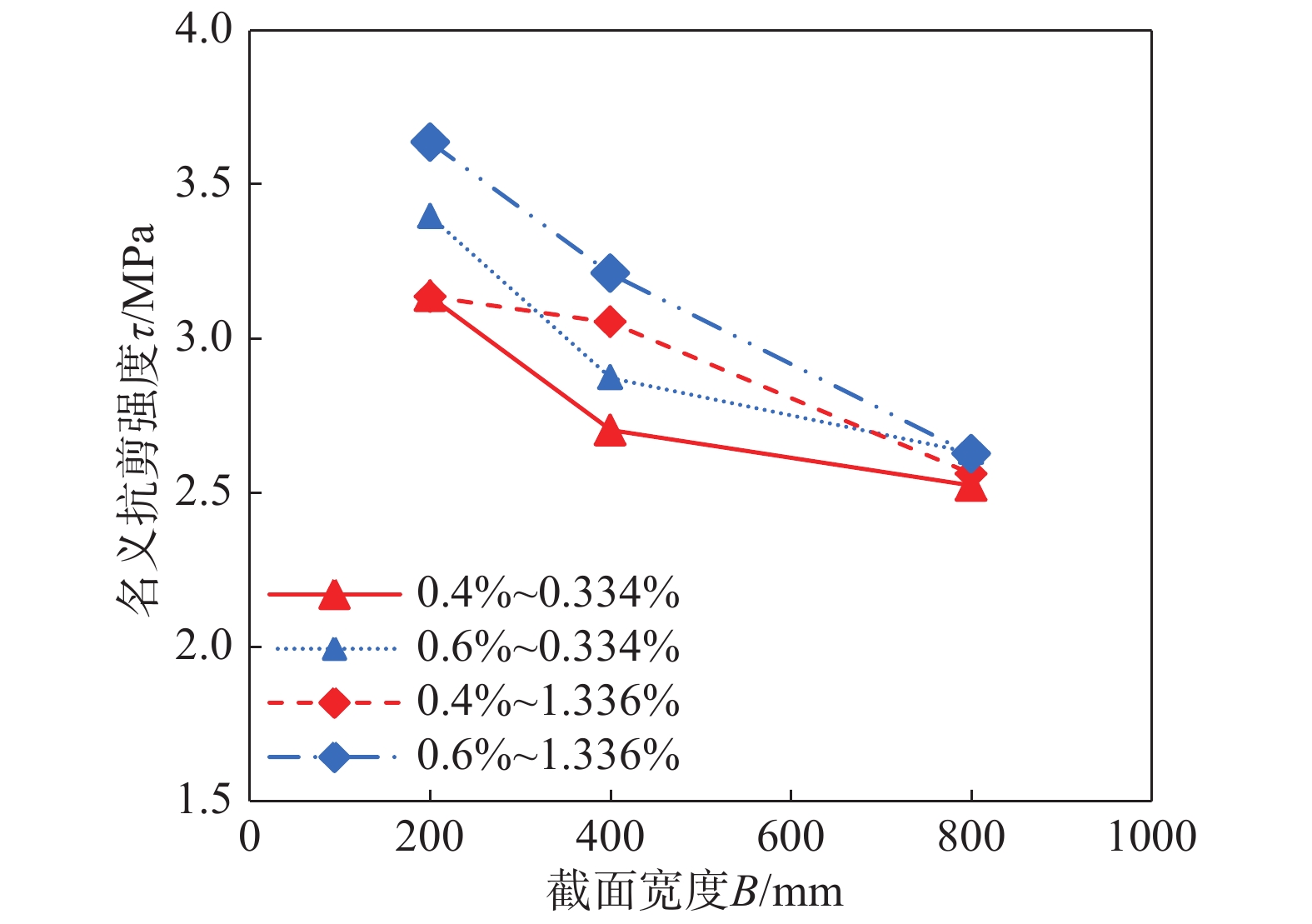
图12描述的是18根CFRP加固钢筋混凝土方柱名义抗剪强度随试件截面尺寸的变化规律。
从图12可以看到,在2种轴压比下,CFRP加固混凝土方柱的名义抗剪强度均随CFRP体积配置率增大而增强。当轴压比为0.4时,中尺寸试件和大尺寸试件的名义抗剪强度随体积配置率增大增幅比较明显;当轴压比为0.6时,随体积配置率增大,中尺寸试件的名义抗剪强度增长幅度最为显著,说明CFRP加固钢筋混凝土柱可以不同程度地提高混凝土柱的抗剪强度。总体来说,名义抗剪强度随柱子截面尺寸增大呈下降趋势,即存在尺寸效应。
由3.1节结果可知,当轴压比小于0.4时,轴压比对不同尺寸柱子的名义抗剪强度尺寸效应行为基本没有影响,故将轴压比为0.4的CFRP约束混凝土方柱的名义抗剪强度数值进行了回归分析,如图13所示。可以发现随着体积配置率的增大,CFRP加固钢筋混凝土的柱的尺寸效应行为有所削弱。
3.3 现有规范名义抗剪强度计算分析
国内外很多学者[23-24]普遍认为,CFRP加固混凝土柱的抗剪承载力包括钢筋混凝土柱受剪承载力
VRc (包括箍筋和轴力的抗剪贡献)和CFRP材料抗剪贡献Vf ,即:V=VRC+Vf (5) VRC=Vc+fyvAsvsh0+0.07N (6) Vf=ρfεfeEfbhcotθ (7) 式中:
VRC 的计算方法参考《混凝土结构设计规范》(GB 50010−2010)[17];fyv 为箍筋抗拉强度设计值;Asv 是箍筋截面面积;s为箍筋间距;N为轴力设计值;ρf 为CFRP体积配置率;εfe 为CFRP有效拉应变;Ef 为CFRP弹性模量;θ为柱子斜裂缝与其轴线的夹角,一般取45°。图14所示给出了采用式(5)~式(7)计算得到的名义抗剪强度与本文模拟结果的对比情况。可以看出,现有公式计算得到的名义抗剪强度值与模拟结果相比相对保守,保证了一定的强度储备安全系数。但CFRP约束钢筋混凝土方柱的抗剪强度存在尺寸效应,现有公式未考虑尺寸效应的影响,故柱子强度储备安全系数随试件尺寸增大呈现降低趋势。
4 剪切强度尺寸效应理论公式
4.1 半经验-半理论公式建立
由第3节的分析可得:1)试件的轴压比小于0.4时,随轴压比增大,CFRP加固钢筋混凝土柱的承载力显著提高,但轴压比对试件的尺寸效应行为基本没有影响;2)随CFRP体积配置率增大,CFRP加固钢筋混凝土柱承载力提高,同时名义抗剪强度尺寸效应行为削弱。
基于上述认识,在材料层面尺寸效应律的基础上,考虑CFRP体积配置率对CFRP加固混凝土方柱名义抗剪强度的影响,可建立轴压比小于0.4时CFRP加固混凝土方柱名义抗剪强度尺寸效应的理论公式。名义抗剪强度τc可表达为:
τc=V0√1+B/D0γ (8) 式中,γ定义为尺寸效应削弱系数,描述CFRP 体积配置率对CFRP加固混凝土方柱名义抗剪强度尺寸效应的影响。
4.2 半经验-半理论公式参数确定
如4.1节所述,CFRP的存在限制了混凝土内部裂缝的发展,增强了混凝土柱的延性,削减了其尺寸效应行为。图15描述的是尺寸效应削弱系数γ与CFRP体积配置率
ρf 的关系,其中:1)当CFRP体积配置率
ρf 为0时(即无约束混凝土柱),由于没有CFRP约束作用存在,故试件的尺寸效应行为无变化。因此,此时的尺寸效应削弱系数γ=1。2)当CFRP体积配置率很大时,CFRP对核心混凝土的约束作用很强,其抗剪强度尺寸效应行为被极大削弱,混凝土柱的抗剪强度不断趋近于混凝土材料的抗剪强度。本文选用文献[25]提出的混凝土材料抗剪强度与抗拉强度的关系计算,即:
τc=1.2f0.89t (9) 式中,
ft 为混凝土抗拉强度。联立式(8)~式(9)得:γ=1.2f0.89t√1+B/D0V0 (10) 3)当CFRP体积配置率
ρf >0时,随着CFRP约束作用的增强,混凝土柱抗剪强度的尺寸效应行为逐渐被削弱。实际上,这种行为可以采用渐近函数来表征。这里,本文采用图15所示的双曲正切函数来描述尺寸效应的削弱行为,它是一条在数值上渐近于1.2f0.89t√1+B/D0/V0 的非线性变化曲线。因此,尺寸效应削弱系数可表达为:γ=(A−1)tanh(αρf)+1 (11) 式中:A为
1.2f0.89t√1+B/D0/V0 ;α 为调节系数,反映削弱系数γ随体积配置率ρf 变化对尺寸效应行为影响速率。4.3 半经验-半理论公式验证
式(8)和式(11)有
V0 、D0 和α3个参数需要确定。以最小尺寸的素混凝土柱作为基准试件,对不同尺寸素混凝土柱的结果进行分析,可以得到V0 =3.67,D0 =364。对于尺寸效应调节系数α,式(11)是一个超越方程,很难得到系数α的解析解,本文利用反复试算方法得到α的近似解。经过大量的试算研究,发现当调节系数α的值为42或43时,理论值与模拟值吻合较好,本文中取α=43。
在此基础上,将模拟结果与本文中建立的半经验-半理论公式计算值进行对比,如图15所示。可以发现两者吻合度较高,证明了本文所建的半经验-半理论公式的正确性。
5 结论
本文建立了三维细观数值分析模型,研究了试件尺寸、轴压比及CFRP体积配置率对CFRP加固钢筋混凝土柱的失效模式和抗震性能的影响。结合轴压比、CFRP体积配置率对尺寸效应的影响机制,提出了考虑横向约束作用影响的CFRP加固混凝土方柱名义抗剪强度尺寸效应理论公式(适用范围轴压比小于0.4)。
得到的结论主要为:
(1)本工况中试件破坏形态为压剪破坏,在CFRP加固钢筋混凝土方柱破坏过程中,CFRP充分发挥其抗拉强度高的优点,起到了较强的约束作用。
(2)截面尺寸相同、CFRP体积配置率相同的试件,随轴压比增大,承载力提高,延性降低,滞回曲线捏缩效应明显。
(3)轴压比相同、CFRP体积配置率一致的试件,随试件截面尺寸增大,名义抗剪强度降低,存在明显尺寸效应行为。随CFRP体积配置率增大,延性增强,构件的承载力有不同程度的提高,尺寸效应行为有所削弱。
需要注意的是,本文建立的半经验-半理论公式只考虑了轴压比小于0.4的情况,对于轴压比大于0.4的情况其尺寸效应规律更加复杂,将在以后的工作中继续探讨。
-
表 1 粘结-滑移本构参数
Table 1 Parameters utilized in the bond-slip model
关键点 开裂 峰值 残余 应力 τ/MPa τcr=2.5ft τu=3ft τr=ft 滑移 s/mm scr,l=0.025d su,l=0.04d sr,l=0.55d 表 2 混凝土细观组分及钢筋力学参数
Table 2 Mechanical parameters of the three meso components of concrete and reinforcing bars utilized
组分 粗骨料 砂浆基质 界面过渡区 纵筋 箍筋 抗压强度σc/MPa − *53.1 ^48.2 − − 抗拉强度σt/MPa − *5.2 ^4.7 − − 弹性模量E/GPa *60 *42.5 ^38.4 *210 *200 泊松比ν *0.2 *0.2 ^0.2 *0.3 *0.3 屈服强度fy/MPa − − − *380.71 *419.09 配筋率ρ/(%) − − − *1 *0.5 注:*为试验实测值[9];^为反复试算取值。 表 3 CFRP加固钢筋混凝土柱几何参数
Table 3 Geometrical parameters of the RC columns strengthened with CFRP
试件名称 截面宽度B/mm 柱高H/mm 轴压比n 体积配置率 ρf /(%) SC-200-0.4-1 200 600 0.4 0.000 SC-200-0.4-2 200 600 0.4 0.334 SC-200-0.4-3 200 600 0.4 1.336 SC-200-0.6-1 200 600 0.6 0.000 SC-200-0.6-2 200 600 0.6 0.334 SC-200-0.6-3 200 600 0.6 1.336 SC-400-0.4-1 400 1200 0.4 0.000 SC-400-0.4-2 400 1200 0.4 0.334 SC-400-0.4-3 400 1200 0.4 1.336 SC-400-0.6-1 400 1200 0.6 0.000 SC-400-0.6-2 400 1200 0.6 0.334 SC-400-0.6-3 400 1200 0.6 1.336 SC-800-0.4-1 800 2400 0.4 0.000 SC-800-0.4-2 800 2400 0.4 0.334 SC-800-0.4-3 800 2400 0.4 1.336 SC-800-0.6-1 800 2400 0.4 0.000 SC-800-0.6-2 800 2400 0.4 0.334 SC-800-0.6-3 800 2400 0.4 1.336 -
[1] 马颖, 张勤, 贡金鑫. 钢筋混凝土柱弯剪破坏恢复力模型骨架曲线[J]. 建筑结构学报, 2012, 33(10): 116 − 125. Ma Ying, Zhang Qin, Gong Jinxin. Skeleton curves of restoring force model of reinforced concrete columns failed in flexure-shear [J]. Journal of Building Structures, 2012, 33(10): 116 − 125. (in Chinese)
[2] Thanh Ngoc Tran C, Li B. Ultimate Displacement of Reinforced Concrete Columns with Light Transverse Reinforcement [J]. Journal of Earthquake Engineering, 2013, 17(2): 282 − 300.
[3] Huang L, Xu L, Chi Y, Xu H. Experimental investigation on the seismic performance of steel–polypropylene hybrid fiber reinforced concrete columns [J]. Construction and Building Materials, 2015, 87: 16 − 27.
[4] 顾冬生, 吴刚, 吴智深, 等. CFRP加固高轴压比钢筋混凝土短圆柱抗震性能试验研究[J]. 工程抗震与加固改造, 2006(6): 71 − 77. doi: 10.3969/j.issn.1002-8412.2006.06.014 Gu Dongsheng, Wu Gang, Wu Zhishen, et al. Experimental study on seismic performance of RC short circular columns strengthened with CFRP composites under high-level compression [J]. Earthquake Resistant Engineering and Retrofitting, 2006(6): 71 − 77. (in Chinese) doi: 10.3969/j.issn.1002-8412.2006.06.014
[5] 陈勤, 李静. 往复荷载作用下CFRP约束混凝土柱力学性能有限元分析[J]. 工业建筑, 2011, 41(增刊 1): 763 − 767. Chen Qin, Li Jing. Finite element analysis on mechanical behavior of CFRP-confined concrete column under cyclic loading [J]. Industrial Construction, 2011, 41(Suppl 1): 763 − 767. (in Chinese)
[6] 张大长, 吴智深. CFRP纤维布加固RC柱的有限元分析模型[J]. 复合材料学报, 2005(4): 156 − 164. doi: 10.3321/j.issn:1000-3851.2005.04.027 Zhang Dachang, Wu Zhishen. Finite element analytical models for reinforced concrete columns reinforced with CFRP sheets [J]. Acta Materiae Compositae Sinica, 2005(4): 156 − 164. (in Chinese) doi: 10.3321/j.issn:1000-3851.2005.04.027
[7] Shamim A S, Grace Y. Seismic behavior of concrete columns confined with steel and fiber reinforced polymers [J]. ACI Structural Journal, 2002, 99(1): 72 − 80.
[8] 邓宗才, 李建辉, 张小冬. 混杂FRP 加固腐蚀混凝土柱抗震性能试验[J]. 北京工业大学学报, 2009, 35(10): 1356 − 1363. Deng Zongcai, Li Jianhui, Zhang Xiaodong. Seismic behavior of RC corroded columns strengthened with hybrid FRP. [J]. Journal of Beijing University of Technology, 2009, 35(10): 1356 − 1363. (in Chinese)
[9] 崔宇强. CFRP加固钢筋混凝土柱受压性能和抗震性能的尺寸效应研究[D]. 北京: 北京建筑大学, 2018. Cui Yuqiang. Research of size effect on compressive and seismic behavior of CFRP reinforced concrete column. [D]. Beijing: Beijing University of Engineering and Architecture, 2018. (in Chinese)
[10] 杜修力, 金浏. 细观分析方法在混凝土物理/力学性质研究方面的应用[J]. 水利学报, 2016, 47(3): 355 − 371. Du Xiuli, Jin Liu. Applications of meso-scale analysis methods on the study of the physical/mechanical properties of concrete [J]. Journal of Hydraulic Engineering, 2016, 47(3): 355 − 371. (in Chinese)
[11] Kim S M, Abu Al-Rub R K. Meso-scale computational modeling of the plastic-damage response of cementitious composites [J]. Cement and Concrete Research Ceram, 2011, 41(3): 339 − 358.
[12] Yılmaz O, Molinari J F. A mesoscale fracture model for concret [J]. Cement and Concrete Research Ceram, 2017, 97: 84 − 94.
[13] Wriggers P, Moftah S O. Mesoscale models for concrete: Homogenisation and damage behavior [J]. Finite Element in Analysis and Design, 2006, 42(7): 623 − 636.
[14] Song Z, Lu Y. Mesoscopic analysis of concrete under excessively high strain rate compression and implications on interpretation of test data [J]. International Journal of Impact Engineering, 2012, 46: 41 − 55.
[15] Jin Liu, Yu Wenxuan, Su Xiao, et al. Effect of cross-section size on the flexural failure behavior of RC cantilever beams under low cyclic and monotonic lateral loadings [J]. Engineering Structures, 2018, 156: 567 − 586.
[16] Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechanics, 1998, 124(8): 892 − 900.
[17] GB 50010−2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture and Building Press, 2010. (in Chinese).
[18] 陆新征, 冯鹏, 叶列平. FRP布约束混凝土方柱轴心受压性能的有限元分析[J]. 土木工程学报, 2003(2): 46 − 51. doi: 10.3321/j.issn:1000-131X.2003.02.009 Lu Xinzheng, Feng Peng, Ye Lieping. Behavior of FRP-confined concrete square columns under uniaxial loading. [J]. Civil Engineering Journal, 2003(2): 46 − 51. (in Chinese) doi: 10.3321/j.issn:1000-131X.2003.02.009
[19] Elsanadedy H M, Al-Salloum Y A, Alsayed S H, Iqbal R A. Experimental and numerical investigation of size effects in FRP-wrapped concrete columns [J]. Construction and Building Materials, 2012, 29: 56 − 72.
[20] 陈思同. GFRP布约束钢筋混凝土圆柱轴压下尺寸效应研究[D]. 大庆: 东北石油大学, 2016. Chen Sitong. Study on the size effect of axial compression performance of reinforced concrete circular column confined by GFRP [D]. Daqing: Northeast Petroleum University, 2016. (in Chinese).
[21] 王全凤, 沈章春, 杨勇新, 等. HRB400级钢筋混凝土短柱抗震试验研究[J]. 建筑结构学报, 2008, 29(2): 114 − 117. doi: 10.3321/j.issn:1000-6869.2008.02.017 Wang Quanfeng, Shen Zhangchun, Yang Yongxin, et al. Seismic behavior of HRB400 reinforcement concrete short columns [J]. Journal of Building Structures, 2008, 29(2): 114 − 117. (in Chinese) doi: 10.3321/j.issn:1000-6869.2008.02.017
[22] Bažant Z P, Kim J K. Size effect in shear failure of longitudinally reinforced beams [J]. Journal of the American Concrete Institute, 1984, 81(5): 456 − 468.
[23] 叶列平, 赵树红, 李全旺, 等. CFRP布加固混凝土柱的斜截面受剪承载力计算[J]. 建筑结构学报, 2000(2): 59 − 67. doi: 10.3321/j.issn:1000-6869.2000.02.008 Ye Lieping, Zhao Shuhong, Li Quanwang, et al. Calculation of shear strength of concrete column strengthened with carbon fiber reinforced plastic sheet [J]. Journal of Building Structures, 2000(2): 59 − 67. (in Chinese) doi: 10.3321/j.issn:1000-6869.2000.02.008
[24] 谢剑, 陈胜云, 赵彤. 碳纤维布增强钢筋混凝土柱受剪承载力的试验研究与理论分析[C]. 昆明: 第二届全国土木工程用纤维增强复合材料(FRP)应用技术学术交流会论文集, 2002: 144 − 149. Xie Jian, Chen Shengyun, Zhao Tong. Experimental study and theoretical analysis on shear capacity of reinforced concrete columns reinforced with carbon fiber sheets [C]. Kunming: Proceedings of the second National Symposium on fiber reinforced polymer (FRP) application technology in Civil Engineering , 2002: 144 − 199. (in Chinese)
[25] 张琦, 过镇海. 砼抗剪强度和剪切变形的研究[J]. 建筑结构学报, 1992, 13(5): 17 − 24. Zhang Qi, Guo Zhenhai. Investigation on shear strength and shear strain of concrete [J]. Journal of Building Structures, 1992, 13(5): 17 − 24. (in Chinese)
-
期刊类型引用(14)
1. 王珏. 基于CFRP法的厂房钢筋混凝土结构加固改造及抗震性能分析. 散装水泥. 2024(02): 125-127 .  百度学术
百度学术
2. 韩辰悦,胡时,庞建勇. 加固用喷射型工程水泥基复合材料循环冲击动力学特性. 公路交通科技. 2024(07): 142-152 .  百度学术
百度学术
3. 刘恺亮,黄锐,周芬,杨晓. 碳纤维聚合物筋约束钢纤维混凝土柱双轴弯曲性能研究1). 力学与实践. 2024(04): 740-748 .  百度学术
百度学术
4. 龚文平,赵晓宇,李馨馨,赵超. 基于细观模拟的土石混合体固结特性研究. 工程力学. 2024(10): 118-127 .  本站查看
本站查看
5. 庞建勇,韩辰悦,胡时. 环绕黏结CFRP-ECC修复混凝土的动态力学和能量特性. 公路交通科技. 2024(09): 87-96 .  百度学术
百度学术
6. 宋彧,李少雄. 新型体外预应力加固混凝土框架柱抗震性能研究. 甘肃科学学报. 2023(01): 37-42 .  百度学术
百度学术
7. 樊敬涛. 钢筋混凝土框架柱加固方案设计与施工要点分析. 工程技术研究. 2023(09): 168-171 .  百度学术
百度学术
8. 宋博,金浏,陈凤娟,杜修力. 基于改进MCFT的GFRP-RC梁抗剪承载力分析. 工程力学. 2023(08): 36-46 .  本站查看
本站查看
9. 寇大伦. CFRP护套加固的低强钢筋混凝土柱数值建模研究. 建筑技术. 2023(16): 1955-1959 .  百度学术
百度学术
10. 李硕,赵作周. 震损RC柱FRP加固后抗震性能数值模拟分析. 工程力学. 2023(10): 89-98 .  本站查看
本站查看
11. 枚东华. 低循环反复荷载下腐蚀钢筋混凝土柱抗震行为. 山西建筑. 2023(24): 34-36+45 .  百度学术
百度学术
12. 冯德銮,梁仕华. 一个基于细观物理机制的土石混合料抗剪强度理论模型. 工程力学. 2022(06): 134-145 .  本站查看
本站查看
13. 金浏,祝华杰,杜修力. 结构尺寸对RC柱剪扭复合受力抗震性能影响分析. 振动工程学报. 2022(05): 1211-1221 .  百度学术
百度学术
14. 曲爽,梁晨. 基于Abaqus的CFRP布加固钢筋混凝土短梁的抗弯性能. 计算机辅助工程. 2022(04): 50-54+61 .  百度学术
百度学术
其他类型引用(8)




 下载:
下载: