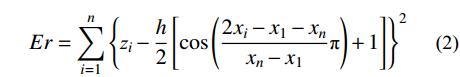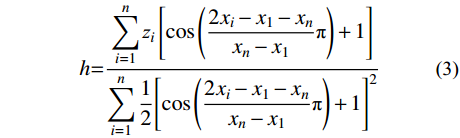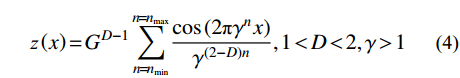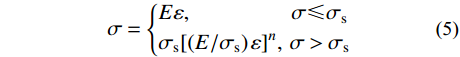EFFECTS OF INTERFACE FRACTAL PARAMETERS ON NORMAL CONTACT STIFFNESS
-
摘要: 基于最小二乘法将分形表面简化为三角函数的叠加，采用弹塑性有限元方法计算界面的接触刚度，定量表征了法向接触压力、法向接触变形及法向接触刚度的关系，研究结果揭示了粗糙面分形维数和特征尺度参数对法向接触刚度的影响机制。结果表明：存在基体最优建模厚度，可有效提高粗糙面接触刚度的计算效率；法向接触刚度随法向接触变形及法向接触压力的增加呈现非线性增加趋势；表面分形维数和特征尺度参数对法向接触刚度影响显著，法向接触刚度随分形维数增加而增加，但随特征尺度参数增加而减小。Abstract: In this study, the complex rough surface is simplified as the superposition of a series of trigonometric curves based on the least square method. In order to calculate the interface contact stiffness, the optimal substrate modeling thickness is determined by the elastic-plastic finite element method. The relationship between normal contact pressure and normal contact deformation and normal contact stiffness is quantitatively investigated. The mechanism of fractal dimension and characteristic scale parameters of rough surface on normal contact stiffness is revealed. The results show that there is an optimal thickness of the substrate, which can effectively improve the calculation efficiency of the contact stiffness of the rough surface. The normal contact stiffness increases nonlinearly with the increase of normal contact deformation and normal contact pressure. The surface fractal dimension and characteristic scale parameters have significant effects on the normal contact stiffness, and the normal contact stiffness increases with the increase of the fractal dimension. However, the normal contact stiffness decreases with the increase of characteristic scale parameters.
-
粗糙界面接触刚度是影响机械力学性能的重要因素之一，复杂机械的界面接触刚度可达整体静态刚度的60%~80%[1]。界面接触刚度受接触荷载、表面粗糙度和基体力学性能的显著影响[2-4]，研究界面接触刚度与这些因素间的关系，对优化机械界面设计、保障复杂机械工作性能具有重要的工程意义。
界面建模是研究界面接触刚度的基础，通常采用半球形[5-9]、椭球形[10-11]和正弦形[12-20]对粗糙表面简化建模。基于Hertz的球体弹性接触解[21]和Hisakado[22]的表面形貌测量，Greenwood和Williamson[5]采用孤立弹性球形微凸体描述了粗糙表面的微观形貌，首次建立了粗糙表面的接触理论模型(GW模型)。结合微凸体塑性变形体积恒定假设，Chang等[6]推导出球形微凸体的弹-塑性接触规律，将GW弹性接触模型推广至弹-塑性接触统计模型(CEB模型)。Zhao等[7]采用样板曲线描述了微凸体从弹性向完全塑性转化的过程，进一步构建了粗糙表面的弹塑性接触模型(ZMC模型)。Horng[10]将CEB球形弹-塑性接触模型推广至椭球形弹-塑性接触模型。Jeng和Wang[11]将ZMC球形弹塑性接触模型推广至椭球形弹塑性接触模型，研究了塑性指数对粗糙面平均间距和真实接触面积的影响。此类理论模型被广泛地应用于界面接触性能预测。
另一方面，数值计算由于高效、便捷的特点被广泛地应用于界面接触刚度的研究。Kogut和Etsion[8]采用有限元方法模拟了球形微凸体的弹塑性变形演化过程，建立了微凸体的弹塑性变形模型(KE模型)。Zhao等[9]在弹塑性球形微凸体接触有限元模型中考虑了幂律硬化和肩-肩接触影响，建立了法向接触刚度统计模型。Liu和Proudhon[12]将正弦微凸体变形演化划分为弹性变形和塑性变形阶段。随后，Liu和Proudhon[13]又将正弦微凸体变形划分为五个阶段来进一步精确描述正弦微凸体变形演化过程。Song等[14]、Liu[15]和Yastrebov[16]在有限元模型中分别采用4.0倍、6.6倍和7.2倍的基体厚度-微凸体宽度比研究界面的接触行为。为了考虑微凸体相互作用和基体力学性能的影响，姜英杰等[23]研究了高度和宽度随机分布的粗糙界面接触刚度，结果表明界面接触特性受微凸体分布影响显著。Gao等[17]研究表明：波状表面基体厚度大于3倍波长宽度时，基体可近似为半空间体。因此，合理简化粗糙表面模型、揭示力学机理的同时有效提高计算效率，对粗糙界面接触行为的研究具有重要意义。
本文基于最小二乘法采用三角函数叠加来表征粗糙表面，建立具有不同特征尺度参数和分形维数的界面接触有限元模型，确定基体最优建模厚度。通过弹塑性有限元计算研究法向接触压力、法向接触变形和法向接触刚度的关系，揭示分形维数和特征尺度参数对法向接触刚度的影响。
1 粗糙表面建模
1.1 三角函数叠加建模
粗糙表面测量表明正弦形接触比球形接触能更好地模拟粗糙表面微凸体接触[18-20]，三角函数叠加建模比球形建模更接近真实情况[24]。此外，由于正弦形微凸体底部与基体平滑连接，可以有效避免应力集中，因此三角函数叠加建模在微凸体塑性变形有限元模拟中具有更好的适应性[20]。Zhang等[20]以轮廓高度0位线为参考，将0位线以上的粗糙轮廓简化为三角函数，如图1所示。数学方程为：
z=f(x)=h2[cos(2x−x1−xnλπ)+1] (1) 式中：x1和xn为三角函数曲线与参考线交点；h为三角函数曲线高度；λ为三角函数曲线波长。
采用最小二乘法基于最小均方差获取最优拟合函数，以此建立粗糙表面的最优简化模型[25]。三角函数曲线与粗糙表面间的最小均方差可表示为：
Er=n∑i=1{zi−h2[cos(2xi−x1−xnxn−x1π)+1]}2 (2) 式(2)中，微凸体的高度h由∂Er/∂h=0求得：
h=n∑i=1zi[cos(2xi−x1−xnxn−x1π)+1]n∑i=112[cos(2xi−x1−xnxn−x1π)+1]2 (3) 通常采用分割三角函数的方法提高拟合精度。将三角函数谷值坐标zv与峰值坐标zp的比值定义为谷峰比，即zv/p=zv/zp。当谷峰比小于临界值zc时，将原有三角函数划分为两个三角函数，以此提高拟合精度。现有研究结果显示，当zc=0.30时，使用双三角函数比单三角函数具有更高的拟合精度[26]。
1.2 粗糙表面简化流程图
采用谷峰比的临界比值zc作为将单个微凸体原始粗糙表面简化为两个三角函数单元的判据。第一步，根据参考线与轮廓上离散点之间的关系，将分布在参考线同侧的离散点作为一个微凸体，确定每个微凸体的起始点和结束点；第二步，基于第一步确定的微凸体单元，将满足谷峰比zv/p≤0.30的微凸体划分为两个微凸体。此时，当离散点高度z(i)>z(i+1)且z(i)>z(i−1)时，则z(i)为峰值点；当离散点高度z(i)<z(i+1)且z(i)<z(i−1)，则z(i)为谷值点。以此，如图2所示将粗糙表面简化三角函数叠加。其中，将粗糙面单个微凸体单元划分为两个微凸体单元的方法如图2中虚线框所示。
1.3 粗糙表面的获取与简化
根据粗糙表面的分形特征，Weierstrass-Mandelbrot(WM)分形函数[27-28]由于其处处连续但不可导和自放射性等特征被广泛应用于拟合粗糙表面[27, 29-31]。WM分形函数为：
z(x)=GD−1∑n=nmin (4) 式中：z(x)为粗糙表面的轮廓高度；x为表面轮廓的测量位置；G为粗糙表面的特征尺度参数，与轮廓曲线粗糙度的幅值有关；D为二维粗糙表面的分形维数，与轮廓曲线粗糙度的横向密度有关；γ为控制表面起伏密度的参量，对于服从正态分布的表面，通常取γ=1.50(用来提供相位的随机性和高频谱密度的特性)；γn为随机轮廓曲线的空间频率，其大小对应于粗糙表面上单个微凸体波长的倒数γn=1/ln；nmin为与曲线结构的最低截止频率指数；nmax为最高截止频率指数。在实际应用中，表面轮廓的最高截止频率也是有限的[32]。
根据现有研究，本文选取特征尺度参数G=10−12 m~10−9 m和频率指数n=20~40来研究机械界面接触刚度[28, 32-33]。根据最高截止频率指数nmax和采样间隔l的关系[34]，可以确定采样间隔为0.05 μm。如图2所示粗糙表面简化流程图以及式(4)，可以得到典型的粗糙表面三角函数拟合结果如图3所示(分形维数D=1.40和特征尺度参数G=1.0×10−9 m)。根据文献[27, 29, 35]可知，采用三角函数叠加构建的粗糙表面轮廓具有显著的分形特征，仍然为分形表面。本文对于构建得到的分形表面采用原始的分形维数D和特征尺度参数G表示。
![]()
图 3 分形维数D=1.40和特征尺度参数G=1.0×10−9 m的粗糙表面和简化的正弦曲线表面Figure 3. Rough profile with fractal dimension D=1.40 and characteristic length scale G=1.0×10−9 m and simplified sinusoidal profile2 粗糙表面的有限元模拟方法
2.1 材料参数
金属材料一般具有明显的弹塑性力学行为，通常采用幂率硬化定律描述金属的塑性行为[36]，其应力-应变本构关系如下[37]：
\sigma = \left\{ \begin{aligned} & E\varepsilon, \qquad\qquad\quad{\sigma \leqslant {\sigma _{\rm{s}}}}\\& {\sigma _{\rm{s}}}{\left[ {\left( {{E / {{\sigma _{\rm{s}}}}}} \right)\varepsilon } \right]^n},\;{\sigma > {\sigma _{\rm{s}}}} \end{aligned}\right. (5) 式中：E为材料弹性模量；σs为屈服强度；n为硬化指数。通常硬化指数0≤n≤1。当n=0时，表示材料为理想弹塑性；当n=1时，表示材料为弹性。本研究中，粗糙表面的材料为18CrMo4钢。其中，弹性模量E=197.60 GPa；屈服强度σs=469 MPa；泊松比ν=0.29和硬化指数n=0.15[9]。
2.2 粗糙界面接触的有限元模型
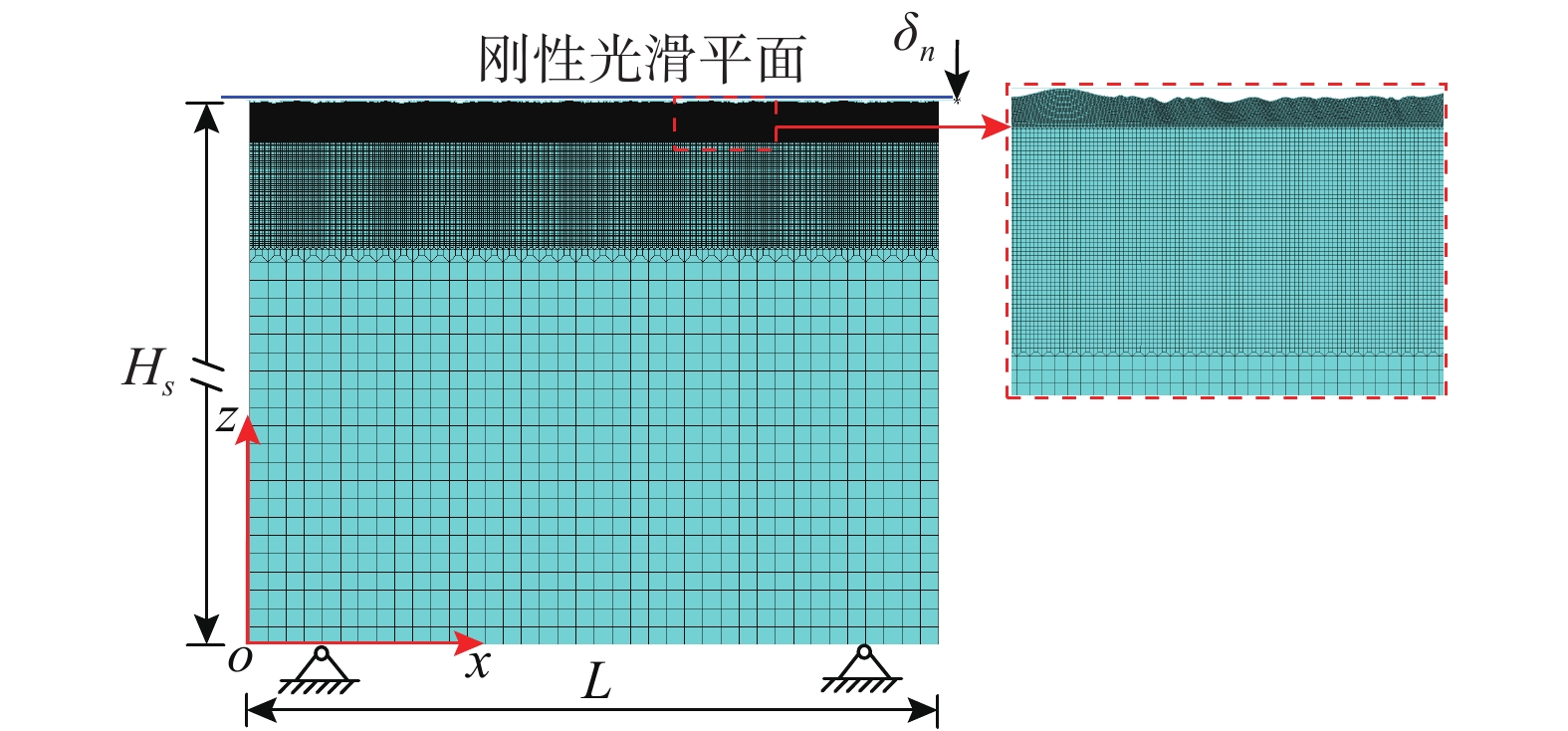
通常将三维表面进行降维处理来研究机械表面形貌[38-39]。此时，粗糙界面接触可简化为平面应变问题[40]。本文采用有限元软件ANSYS建立粗糙表面有限元模型。如图4所示为分形维数D=1.40和特征尺度参数G=1.0×10−9 m的粗糙表面与刚性光滑平板接触有限元模型。粗糙表面长度为L=3.0 mm，粗糙面以下基体厚度为Hs=5.0 mm。采用八节点PLANE183平面应变单元对粗糙表面和基体进行离散化，接触单元(CONTA172)和刚性二节点目标单元(TARGE169)模拟接触。
![]()
图 4 分形维数D=1.40和特征尺度参数G=1.0×10−9 m的粗糙表面与刚性光滑平板接触的有限元模型Figure 4. Finite element model of contact between a rigid smooth plate and a rough surface with fractal dimension D=1.40 and characteristic length scale G=1.0×10−9 m本模型接触算法采用增广拉格朗日法计算无摩擦、无粘附接触问题。粗糙界面接触有限元模型边界条件如下：1) 约束基体底部所有节点x方向位移和z方向位移，即Ux (x, 0)=Uz (x, 0)=0；2) 粗糙表面两边x方向位移和z方向位移自由，即Ux (0, z)和Ux (3, z)自由；3) 使用接触向导，在刚性光滑平板最右端生成控制节点(Pilot节点)控制刚性光滑平板自由度；4) 在Pilot节点上施加将竖向位移δn。
为了验证网格敏感性和边界条件正确性，定义相对误差Ep=(|PTH−PFE|/PTH)×100%，其中，PTH和PFE分别是理论计算荷载和有限元计算荷载，PTH=(δs/Hs)×(E/(1−ν2))。光滑表面上承受屈服荷载时，有限元模型计算的荷载和理论计算荷载的最大相对误差为1.46%。结果表明：本研究边界条件合理、网格尺寸满足计算精度要求。
3 结果与讨论
细观微凸体广泛存在于实际机械接触表面，如图5所示。机械界面接触性能不仅与微凸体有关，也与基体的力学行为有关。因此，确定最优的基体分析厚度，不仅能精确地反映接触面力学行为，更能提高计算效率(在保证计算精度时，减少基体划分时网格数量)，在界面接触有限元数值模拟中尤为重要。本研究将参考线以下基体Hs分为基体最优建模厚度Hs,1和基体厚度Hs,2，如图5(b)。以18CrMo4钢表面承受屈服荷载(即法向接触压力Pn=469 MPa)时，Von Mises应力分布规律确定基体最优建模厚度Hs,1。
3.1 特征尺度参数G对基体最优建模厚度Hs,1的影响
图6所示为不同特征尺度参数G的表面内Von Mises应力分布图。从图6(a)~图6(d)可知，当分形维数D=1.40且表面法向接触压力Pn=469 MPa时，受微凸体随机几何分布特性影响，Von Mises应力在接触表面附近区域整体复杂分布。对于单个微凸体，Von Mises应力从与刚性光滑平板接触的峰值点向微凸体底部逐渐减小，直到与基体内Von Mises应力相等。图6进一步显示，未接触区域基体内也会出现应力分布，这是由于相邻微凸体相互挤压，底部基体内应力相互影响形成的。
从图6可知，随着特征尺度参数G的增加，微凸体底部的应力从相邻微凸体相互影响变为相邻多个微凸体相互影响，如从图6(b)~图6(c)。随着特征尺度参数G的增加，表面微凸体底部应力相互影响范围增加，如图6(c)和图6(d)。在接触区域附近应力分布不均匀，基体大部分区间内应力等于469 MPa。这说明特征尺度参数G对应力分布的均匀性有影响，表明表面下基体存在两个明显的区域，即应力均匀区域和不均匀区域。根据应力分布的均匀情况，确定应力不均匀区域为基体最优建模厚度Hs,1。因此，选取粗糙表面的参考线与469 MPa的等值线间最小厚度作为基体最优建模厚度Hs,1。从图6可知，当分形维数D一定时，随着特征尺度参数G的增加，表面下应力不均匀分布的深度增加，基体最优建模厚度Hs,1增加。在本研究中，对于特征尺度参数分别为G=1.0×10−12 m、1.0×10−11 m、1.0×10−10 m和1.0×10−9 m的粗糙表面，基体最优建模厚度Hs,1分别为0.14 mm、0.18 mm、0.45 mm和0.74 mm。
![]()
图 6 在表面法向接触压力Pn=469 MPa时，具有相同分形维数D=1.40和不同特征尺度参数G的表面下Von Mises应力等值线云图Figure 6. The Von Mises stress contour map of surface with the same fractal dimension D=1.40 and different characteristic length scale G under normal contact pressure Pn=469 MPa3.2 分形维数D对基体最优建模厚度Hs,1的影响
图7所示为不同分形维数D的表面内Von Mises应力分布图。从图7可知，对于特征尺度参数G=1.0×10−9 m和不同分形维数D的表面，当表面法向接触压力Pn=469 MPa时，随着分形维数D的增加，微凸体底部的应力从相邻多个微凸体相互影响变为相邻微凸体相互影响，如从图7(b)~图7(c)。随着分形维数D的增加，表面微凸体底部应力相互影响范围减小，并且应力不向表面中心下方聚集，如图7(c)和图7(d)。在接触区域附近应力分布不均匀，基体大部分区间内应力等于469 MPa。这说明分形维数D对应力分布的均匀性有影响，表明表面下基体存在两个明显的区域，即应力均匀区域和不均匀区域。从图7可知，当特征尺度参数G一定时，随着分形维数D的增加，表面下应力不均匀分布的深度减小，基体最优建模厚度Hs,1减小。采用类似的定义方法可知，对于具有相同特征尺度参数G=1.0×10−9 m和分形维数分别为D=1.40、1.50、1.60和1.70的粗糙表面，基体最优建模厚度Hs,1分别为0.74 mm、0.37 mm、0.15 mm和0.09 mm。
![]()
图 7 在法向接触压力Pn=469 MPa时，具有相同特征尺度参数G=1×10−9 m和不同分形维数D的表面下Von Mises应力等值线云图Figure 7. The Von Mises stress contour map of surface with the same characteristic length scale G=1×10−9 m and different fractal dimension D under normal contact pressure Pn=469 MPa3.3 特征尺度参数G对界面接触行为的影响
3.1节讨论了特征尺度参数G对最优建模厚度Hs,1的影响，本部分在表面接触行为中考虑基体变形的影响。具有相同分形维数D=1.40和不同特征尺度参数G的表面接触行为如图8所示。从图中可知，法向接触压力Pn随着法向接触变形δn增加而非线性增加。在相同的法向接触变形δn下，法向接触压力Pn随着特征尺度参数G而减小。图8(b)所示为法向接触刚度Kn和法向接触压力Pn的关系。从图中可知，法向接触刚度Kn随着法向接触压力Pn增加而非线性增加。在相同法向接触压力Pn下，法向接触刚度Kn随着特征尺度参数G的增加而减小，这一规律与前人研究[33, 41-42]一致。这是因为特征尺度参数G的增加意味着表面粗糙度Ra增加[35, 43]，Ra是轮廓曲线的算术平均值以上微凸体高度的平均值[28]。对于相同分形维数D和不同特征尺度参数G的表面，随着特征尺度参数G增加，粗糙轮廓形状不变，但整个粗糙轮廓的粗糙幅值增加[28-29]。
![]()
图 8 相同分形维数D=1.40下，特征尺度参数G对表面接触行为的影响Figure 8. Influence of characteristic length scale G on contact behavior of surface with the same fractal dimension D=1.40图8(c)所示为在不同法向接触压力Pn和相同分形维数D下，特征尺度参数G对表面法向接触刚度Kn的影响。法向接触压力Pn分别取0.2σy、0.4σy、0.6σy、0.8σy和1.0σy，σy为材料的屈服强度。从图中可知，法向接触刚度Kn随着特征尺度参数G的增加而非线性减小。在相同特征尺度参数G下，法向接触刚度Kn随着法向接触压力Pn的增加而增加。
3.4 分形维数D对界面接触行为的影响
3.2节讨论了分形维数D对最优建模厚度Hs,1的影响，本部分在表面接触行为中考虑基体变形的影响。具有相同特征尺度参数G=1×10−9 m和不同分形维数D的粗糙界面接触行为如图9所示。图9(a)所示为法向接触压力Pn和法向接触变形δn的关系。从图中可知，法向接触压力Pn随着法向接触变形δn的增加而非线性增加。在相同法向接触变形δn下，法向接触压力Pn随着分形维数D的增加而增加。图9(b)所示为法向接触刚度Kn和法向接触压力Pn的关系。从图中可知，法向接触刚度Kn随着法向接触压力Pn的增加而非线性增加。在相同法向接触压力Pn下，法向接触刚度Kn随着分形维数D的增加而增加，这一规律与前人研究[33, 41, 44]一致。这是因为分形维数D的增加意味着表面粗糙度Ra减小[35]。对于相同特征尺度参数G和不同分形维数D的表面，随着分形维数D的增加，粗糙表面轮廓沿横向挤压，轮廓变得越来越密集和复杂，但整个表面的轮廓粗糙幅值减小，表面变得越来越光滑[28-29, 45]。
![]()
图 9 相同特征尺度参数G=1×10−9 m，分形维数D对表面接触行为的影响Figure 9. Influence of fractal dimension D on contact behavior of surface with the same characteristic length scale G=1×10−9 m图9(c)所示为不同法向接触压力Pn和相同特征尺度参数G下，分形维数D对表面法向接触刚度Kn的影响。法向接触压力Pn分别取0.2σy、0.4σy、0.6σy、0.8σy和1.0σy，σy为材料的屈服强度。从图中可知，法向接触刚度Kn随着分形维数D的增加而非线性增加。在相同的分形维数D下，法向接触刚度Kn随着法向接触压力Pn的增加而增加。
3.5 有限元结果和理论模型对比
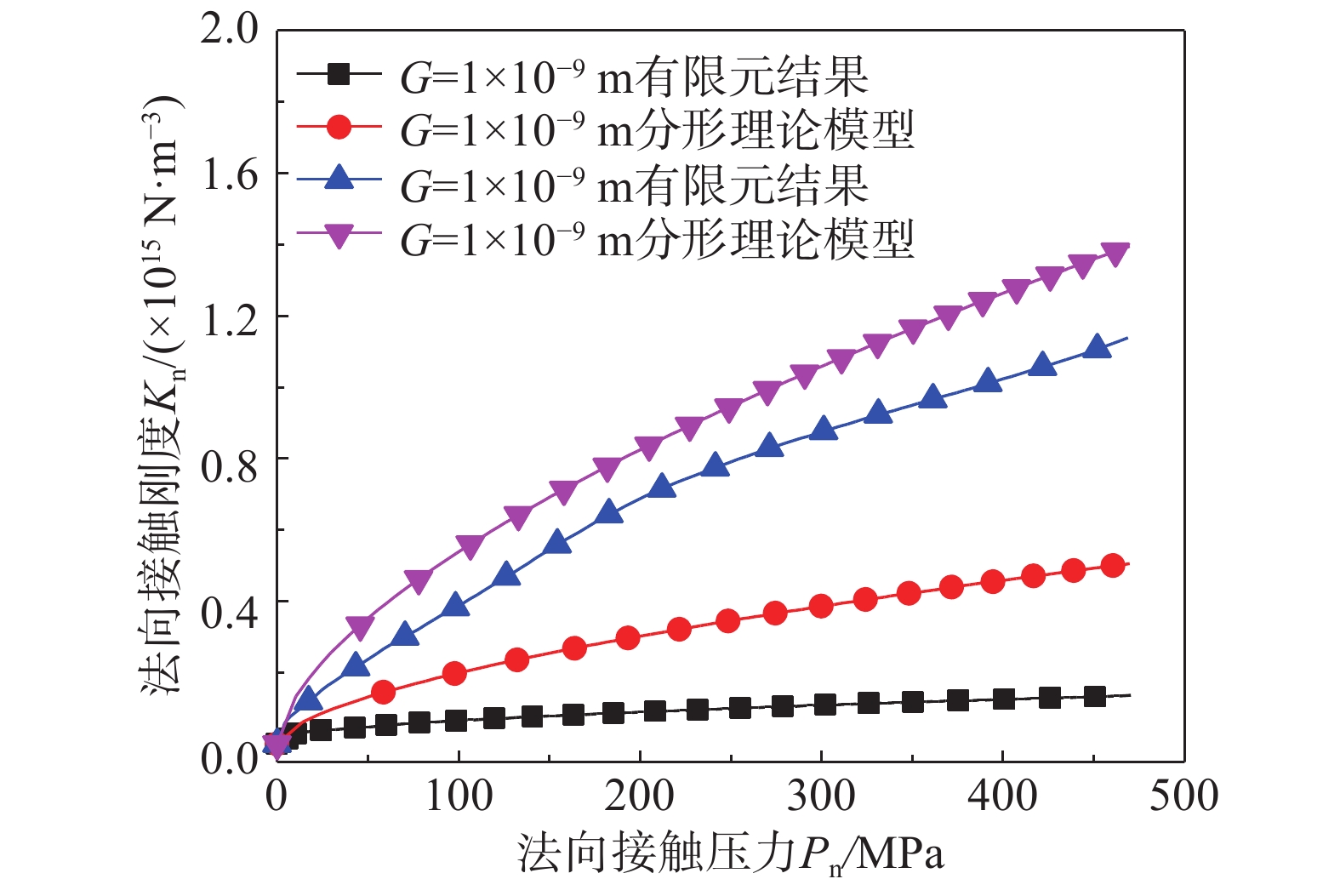
将本文有限元结果与文献[44]中建立的不考虑微凸体相互作用和基体变形的弹塑性法向接触刚度分形理论模型(简称分形理论模型)进行了对比，如图10所示。从图10可知，对于具有相同分形维数D和不同特征尺度参数G的表面，在相同的法向接触压力Pn下，分形理论模型计算的法向接触刚度Kn比有限元计算的法向接触刚度Kn大。造成此现象的原因是分形理论模型没有考虑微凸体相互作用和基体变形的影响[33, 46]。同时，特征尺度参数G=1×10−11 m的表面其有限元结果与分形理论模型结果比特征尺度参数G=1×10−9 m的表面更接近。原因是特征尺度参数G=1×10−9 m的表面受到微凸体相互作用和基体变形影响比特征尺度参数G=1×10−11 m的表面更大，而分形理论模型没有考虑微凸体相互作用和基体变形。另外，Wang等[33]的研究也表明不考虑微凸体相互作用和基体变形的接触刚度比试验结果大，考虑微凸体相互作用的接触刚度模型与试验吻合性更好，说明本文考虑的基体变形和微凸体相互作用是不可忽略的。
![]()
图 10 具有分形维数D=1.40，特征尺度参数分别为G=1×10−11 m和G=1×10−9 m表面，有限元模型结果和分形理论模型结果对比Figure 10. Comparison between finite element model and fractal theoretical model for surface with fractal dimension D=1.40, characteristic scale parameter G=1×10−11 m and G=1×10−9 m respectively4 结论
本文建立了粗糙表面与刚性光滑平板接触有限元模型，基于接触面下Von Mises应力分布特征，提出了基体最优建模厚度Hs,1。基于基体最优建模厚度Hs,1研究了不同分形维数和特征尺度参数条件下粗糙表面的接触行为。进一步讨论了分形维数和特征尺度参数对法向接触刚度的影响。主要得到以下几个结论：
(1)对于具有相同分形维数D和不同特征尺度参数G的粗糙表面，或者相同特征尺度参数G和不同分形维数D的粗糙表面，均存在基体最优建模厚度Hs,1。基体最优建模厚度可以在相同计算精度下有效提高计算效率。
(2)在相同法向接触压力Pn下，表面的法向接触刚度Kn随着特征尺度参数G的增加而非线性减少。
(3)在相同法向接触压力Pn下，表面的法向接触刚度Kn随着分形维数D的增加而非线性增加。
-
![]()
图 3 分形维数D=1.40和特征尺度参数G=1.0×10−9 m的粗糙表面和简化的正弦曲线表面
Figure 3. Rough profile with fractal dimension D=1.40 and characteristic length scale G=1.0×10−9 m and simplified sinusoidal profile
![]()
图 4 分形维数D=1.40和特征尺度参数G=1.0×10−9 m的粗糙表面与刚性光滑平板接触的有限元模型
Figure 4. Finite element model of contact between a rigid smooth plate and a rough surface with fractal dimension D=1.40 and characteristic length scale G=1.0×10−9 m
![]()
图 6 在表面法向接触压力Pn=469 MPa时，具有相同分形维数D=1.40和不同特征尺度参数G的表面下Von Mises应力等值线云图
Figure 6. The Von Mises stress contour map of surface with the same fractal dimension D=1.40 and different characteristic length scale G under normal contact pressure Pn=469 MPa
![]()
图 7 在法向接触压力Pn=469 MPa时，具有相同特征尺度参数G=1×10−9 m和不同分形维数D的表面下Von Mises应力等值线云图
Figure 7. The Von Mises stress contour map of surface with the same characteristic length scale G=1×10−9 m and different fractal dimension D under normal contact pressure Pn=469 MPa
![]()
图 8 相同分形维数D=1.40下，特征尺度参数G对表面接触行为的影响
Figure 8. Influence of characteristic length scale G on contact behavior of surface with the same fractal dimension D=1.40
![]()
图 9 相同特征尺度参数G=1×10−9 m，分形维数D对表面接触行为的影响
Figure 9. Influence of fractal dimension D on contact behavior of surface with the same characteristic length scale G=1×10−9 m
-
[1] Burdekin M, Back N, Cowley A. Analysis of the local deformations in machine joints [J]. Journal of Mechanical Engineering Science, 1979, 21(1): 25 − 32. doi: 10.1243/JMES_JOUR_1979_021_006_02
[2] Lundberg O E, Nordborg A, Arteaga I L. The influence of surface roughness on the contact stiffness and the contact filter effect in nonlinear wheel-track interaction [J]. Journal of Sound and Vibration, 2016, 366: 429 − 446. doi: 10.1016/j.jsv.2015.12.026
[3] Li P Y, Zhai Y F, Huang S K, et al. Investigation of the contact performance of machined surface morphology [J]. Tribology International, 2017, 107: 125 − 134. doi: 10.1016/j.triboint.2016.07.007
[4] Marache A, Riss J, Gentier S. Experimental and modelled mechanical behaviour of a rock fracture under normal stress [J]. Rock Mechanics and Rock Engineering, 2008, 41(6): 869 − 892. doi: 10.1007/s00603-008-0166-y
[5] Greenwood J A, Williamson J B P. Contact of nominally flat surfaces [J]. Proceedings the Royal of Society A-Mathematical, Physical & Engineering Sciences, 1966, 295: 300 − 319.
[6] Chang W R, Etsion I, Bogy D B. An elastic-plastic model for the contact of rough surfaces [J]. Journal of Tribology, 1987, 109(2): 257 − 263. doi: 10.1115/1.3261348
[7] Zhao Y W, Maietta D M, Chang L. An asperity Microcontact model incorporating the transition from elastic deformation to fully plastic flow [J]. Journal of Tribology, 2000, 122(1): 86 − 93. doi: 10.1115/1.555332
[8] Kogut L, Etsion I. Elastic-plastic contact analysis of a sphere and a rigid flat [J]. Journal of Applied Mechanics, 2002, 69(5): 657 − 662. doi: 10.1115/1.1490373
[9] Zhao B, Zhang S, Wang P, et al. Loading-unloading normal stiffness model for power-law hardening surfaces considering actual surface topography [J]. Tribology International, 2015, 90: 332 − 342. doi: 10.1016/j.triboint.2015.04.045
[10] Horng J H. An elliptic elastic-plastic asperity microcontact model for rough surfaces [J]. Journal of Tribology, 1998, 120(1): 82 − 88. doi: 10.1115/1.2834194
[11] Jeng Y R, Wang P Y. An elliptical microcontact model considering elastic, elastoplastic, and plastic deformation [J]. Journal of Tribology, 2003, 125(2): 232 − 240. doi: 10.1115/1.1537744
[12] Liu M, Proudhon H. Finite element analysis of frictionless contact between a sinusoidal asperity and a rigid plane: Elastic and initially plastic deformations [J]. Mechanics of Materials, 2014, 77: 125 − 141. doi: 10.1016/j.mechmat.2014.06.009
[13] Liu M, Proudhon H. Finite element analysis of contact deformation regimes of an elastic-power plastic hardening sinusoidal asperity [J]. Mechanics of Materials, 2016, 103: 78 − 86. doi: 10.1016/j.mechmat.2016.08.015
[14] Song H, Van der Giessen E, Liu X. Strain gradient plasticity analysis of elasto-plastic contact between rough surfaces [J]. Journal of the Mechanics and Physics of Solids, 2016, 96: 18 − 28. doi: 10.1016/j.jmps.2016.07.008
[15] Liu M. Finite element analysis of large contact deformation of an elastic-plastic sinusoidal asperity and a rigid flat [J]. International Journal of Solids and Structures, 2014, 51(21/22): 3642 − 3652.
[16] Yastrebov V A, Durand J, Proudhon H, et al. Rough surface contact analysis by means of the finite element method and of a new reduced model [J]. Comptes Rendus Mecanique, 2011, 339(7/8): 473 − 490.
[17] Gao Y F, Bower A F, Kim K S, et al. The behavior of an elastic-perfectly plastic sinusoidal surface under contact loading [J]. Wear, 2006, 261(2): 145 − 154. doi: 10.1016/j.wear.2005.09.016
[18] Shah S, Krithivasan V, Jackson R L. An electro-mechanical contact analysis of a three-dimensional sinusoidal surface against a rigid flat [J]. Wear, 2011, 270(11/12): 914 − 921.
[19] Jackson R L, Krithivasan V, Wilson W E. The Pressure to cause complete contact between elastic-plastic sinusoidal surfaces [J]. Proceedings of the Institution of Mechanical Engineers Part J Journal of Engineering Tribology, 2008, 222(7): 857 − 863. doi: 10.1243/13506501JET429
[20] Zhang S, Song H, Sandfeld S, et al. Discrete Greenwood-Williamson modeling of rough surface contact accounting for three-dimensional sinusoidal asperities and asperity interaction [J]. Journal of Tribology, 2019, 141(12): 121401. doi: 10.1115/1.4044635
[21] Hertz H. On the contact of elastic solids [J]. Journal Fur Die Reine Und Angewandte Mathematik, 1882, 92: 156 − 171.
[22] Hisakado T. Surface roughness and deformation of contact asperities a rough and a flat surface [J]. Wear, 1975, 35: 53 − 61. doi: 10.1016/0043-1648(75)90141-6
[23] 姜英杰, 黄伟强, 孙志勇, 等. 零件真实粗糙表面构建及微观接触性能分析[J]. 机械设计与制造, 2018, 8: 8 − 14. doi: 10.3969/j.issn.1001-3997.2018.08.003 Jiang Yingjie, Huang Weiqiang, Sun Zhiyong, et al. The analysis of micro contact performance based on established real rough surface of parts [J]. Machinery Design & Manufacture, 2018, 8: 8 − 14. (in Chinese) doi: 10.3969/j.issn.1001-3997.2018.08.003
[24] Poon C Y, Bhushan B. Comparison of surface roughness measurements by stylus profiler, AFM and non-contact optical profiler [J]. Wear, 1995, 190(1): 76 − 88. doi: 10.1016/0043-1648(95)06697-7
[25] Ciulli E, Ferreira L A, Pugliese G, et al. Rough contacts between actual engineering surfaces part: simple models for roughness description [J]. Wear, 2008, 264(11): 1105 − 1115.
[26] Wen Y Q, Tang J Y, Zhou W, et al. An improved simplified model of rough surface profile [J]. Tribology International, 2018, 125: 75 − 84. doi: 10.1016/j.triboint.2018.04.025
[27] Majumdar A, Bhushan B. Fractal model of elastic-plastic contact between rough surfaces [J]. Journal of Tribology, 1991, 113(1): 1 − 11. doi: 10.1115/1.2920588
[28] Yuan Y, Cheng Y, Liu K, et al. A revised Majumdar and Bushan model of elastioplastic contact between rough surfaces [J]. Applied Surface Science, 2017, 425: 1138 − 1157. doi: 10.1016/j.apsusc.2017.06.294
[29] Jiang S Y, Zheng Y J, Zhu H. A contact stiffness model of machined plane joint based on fractal theory [J]. Journal of Tribology, 2010, 132: 011401. doi: 10.1115/1.4000305
[30] Majumdar A, Bhushan B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J]. Journal of Tribology, 1990, 112(2): 205 − 216. doi: 10.1115/1.2920243
[31] Yan W, Komvopoulos K. Contact analysis of elastic-plastic fractal surfaces [J]. Journal of Applied Physics, 1998, 84(7): 3617 − 3624. doi: 10.1063/1.368536
[32] Liou J L, Tsai C M, Lin J F. A microcontact model developed for sphere- and cylinder-based fractal bodies in contact with a rigid flat surface [J]. Wear, 2010, 268: 431 − 442. doi: 10.1016/j.wear.2009.08.033
[33] Wang R Q, Zhu L D, Zhu C X. Research on fractal model of normal contact stiffness for mechanical joint considering asperity interaction [J]. International Journal of Mechanical Sciences, 2017, 134: 357 − 369. doi: 10.1016/j.ijmecsci.2017.10.019
[34] 王余松, 张学良, 温淑华, 等. 分形粗糙表面特征长度尺度参数小波识别法[J]. 机械工程学报, 2018, 54(5): 185 − 192. doi: 10.3901/JME.2018.05.185 Wang Yusong, Zhang Xueliang, Wen Shuhua, et al. Wavelet method identifying the characteristic length scale parameter of fractal rough surface [J]. Journal of Mechanical Engineering, 2018, 54(5): 185 − 192. (in Chinese) doi: 10.3901/JME.2018.05.185
[35] 葛世荣, Tonder K. 粗糙表面的分形表征与分形表达研究[J]. 摩擦学学报, 1997, 17(1): 73 − 80. doi: 10.3321/j.issn:1004-0595.1997.01.011 Ge Shirong, Tonder K. The fractal behavior and fractal characterization of rough surfaces [J]. Tribology, 1997, 17(1): 73 − 80. (in Chinese) doi: 10.3321/j.issn:1004-0595.1997.01.011
[36] 梅杰, 张博文, 张春云, 等. 幂强化弹塑性材料平面应变反问题[J]. 工程力学, 2020, 37(1): 248 − 256. doi: 10.6052/j.issn.1000-4750.2019.01.0086 Mei Jie, Zhang Bowen, Zhang Chunyun, et al. The inverse problem of plane strain in power-hardening elasticoplasticity materials [J]. Engineering Mechanics, 2020, 37(1): 248 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.01.0086
[37] Ramberg W, Osgood W R. Description of stress-strain curves by three parameters [J]. National Advisory Committee for Aeronautics Technical Note, 1943, 902: 1 − 28.
[38] Thomas T R, Rosén B G, Amini N. Fractal characterisation of the anisotropy of rough surfaces [J]. Wear, 1999, 232(1): 41 − 50. doi: 10.1016/S0043-1648(99)00128-3
[39] 缪小梅, 黄筱调. 基于有限元法的磨削表面微凸体的弹塑性接触模型[J]. 组合机床与自动化加工技术, 2015, 10: 61 − 68. Miao Xiaomei, Huang Xiaodiao. Elastic-plastic single point contact model of ground surface based on finite element method [J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015, 10: 61 − 68. (in Chinese)
[40] Kubin W K, Pletz M, Daves W, et al. A new roughness parameter to evaluate the near-surface deformation in dry rolling/sliding contact [J]. Tribology International, 2013, 67: 132 − 139. doi: 10.1016/j.triboint.2013.07.007
[41] Liu P, Zhao H, Huang K, et al. Research on mormal contact stiffness of rough surface considering friction based on fractal theory [J]. Applied Surface Science, 2015, 349: 43 − 48. doi: 10.1016/j.apsusc.2015.04.174
[42] 温淑花, 张学良, 武美先, 等. 结合面法向接触刚度分形模型建立与仿真[J]. 农业机械学报, 2009, 40(11): 197 − 202. Wen Shuhua, Zhang Xueliang, Wu Meixian, et al. Fractal model and simulation of normal contact stiffness of joint interfaces and its simulation [J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(11): 197 − 202. (in Chinese)
[43] 贺林, 朱均. 粗糙表面接触分形模型的提出与发展[J]. 摩擦学学报, 1996, 16(4): 375 − 384. He Lin, Zhu Jun. Fractal model for contact of rough surfaces [J]. Tribology, 1996, 16(4): 375 − 384. (in Chinese)
[44] Zhang D Y, Xia Y, Scarpa F, et al. Interfacial contact stiffness of fractal rough surfaces [J]. Scientific Reports, 2017, 7(1): 12874.
[45] 原园, 成雨, 张静. 基于分形的三维粗糙表面弹塑性接触力学模型与试验验证[J]. 工程力学, 2018, 35(6): 209 − 221. Yuan Yuan, Cheng Yu, Zhang Jing. Fractal based elastoplastic mechanics model for contact with rough surface and its experimental verification [J]. Engineering Mechanics, 2018, 35(6): 209 − 221. (in Chinese)
[46] Ciavarella M, Greenwood J A, Paggi M. Inclusion of "interaction" in the Greenwood and Williamson contact theory [J]. Wear, 2008, 265: 729 − 734. doi: 10.1016/j.wear.2008.01.019
下载:
计量
- 文章访问数: 512
- HTML全文浏览量: 158
- PDF下载量: 89
