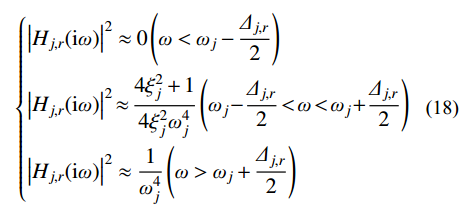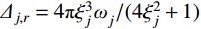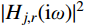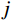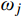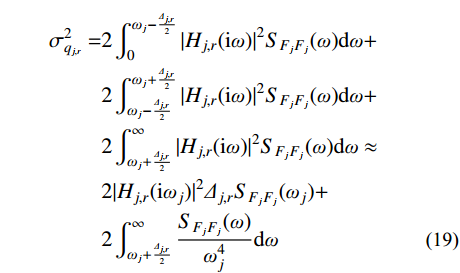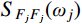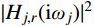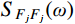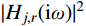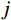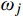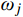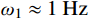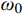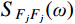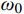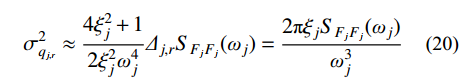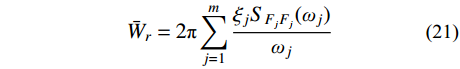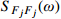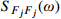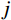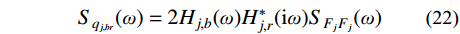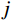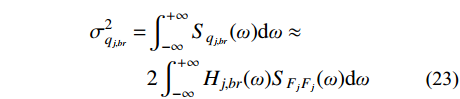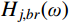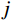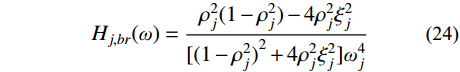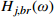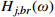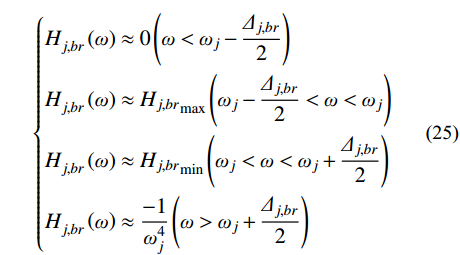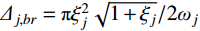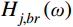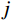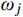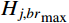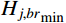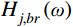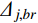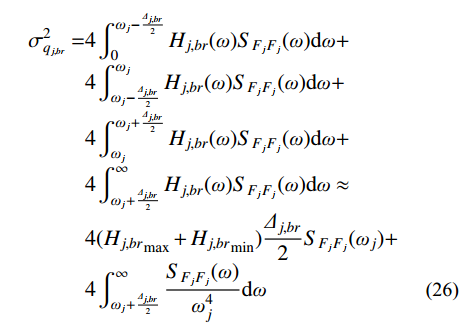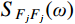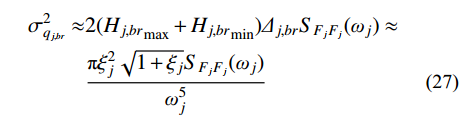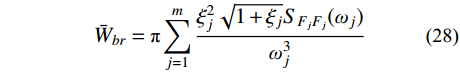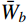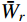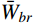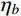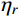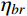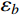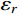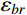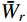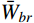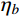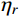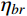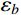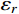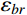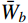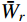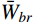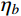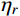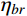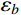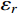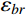A METHOD FOR DETERMINING THE CHARACTERISTIC OF FLUCTUATING WIND-INDUCED RESPONSE OF LARGE-SPAN ROOFS
-
摘要: 基于结构脉动风振响应计算的三分量(背景、共振及其耦合项)完全组合思路,提出一种大跨屋盖结构脉动风振响应特性预测方法,据此实现结构脉动风振总响应的高效精准计算。引入应变能的概念,综合考虑结构所有节点上三分量响应对脉动风振总响应的贡献,定义各响应分量应变能预测系数,为了避免直接计算各响应分量具体数值,根据大跨屋盖结构各响应分量传递函数和风荷载谱特征,对各响应分量表达式进行简化处理,实现只需借助几个简单的风荷载参数和结构动力特性参数就能方便地得到各响应分量应变能预测系数。根据各响应分量应变能预测系数取值情况,将大跨屋盖结构脉动风振响应特性划分为I~VI类,在此基础上,制定与风振响应特性类型相对应的脉动风振总响应组合求解策略。以国家网球中心莲花球场屋盖结构为例,进行结构脉动风振响应特性类型预测以及风振响应组合计算。结果表明:所提方法能够方便地预测结构脉动风振响应特性类型;据此组合计算的脉动风振总响应与精确值吻合较好。Abstract: Based on the idea of fully combining the three components of fluctuating wind-induced response (background, resonant and their coupling term), a method for determining the characteristic of fluctuating wind-induced response of large-span roofs is proposed, which is used to calculate the fluctuating wind-induced response accurately and efficiently. The concept of strain energy is introduced, and the contributions of each fluctuating wind-induced response component to the total response at all structural nodes are considered and the strain energy prediction coefficients of each response component are defined. In order to avoid directly calculating the specific value of each response component, the expression of each response component is simplified according to the characteristics of the transfer function and wind load spectrum of each response component, so that the strain energy prediction coefficients could be obtained by a few wind load parameters and structural dynamic characteristic parameters. According to the value of strain energy prediction coefficients, the characteristic categories of fluctuating wind-induced response of large-span roofs are divided into I-VI; on this basis, the combining principle for the total fluctuating wind-induced response is developed. Taking the Lotus court roof as an example, the characteristic type of fluctuating wind-induced response is determined and the total fluctuating wind-induced response is obtained. The results indicate that the proposed method can determine the characteristic type of fluctuating wind-induced response conveniently, and the combined total response is in good agreement with the accurate value.
-
近年,为了满足建筑功能多样性的需要,造型复杂、形态各异、高标准的现代大跨屋盖结构不断涌现[1-4],与传统屋盖结构相比,该类大跨屋盖结构在风荷载作用下所表现的脉动风振响应特性更加复杂多样,而如何合理判定结构脉动风振响应特性,并据此高效精准进行结构脉动风振响应计算是亟待解决的问题。
围绕这一问题,国内外不少学者进行了研究,比如,Harris[5]由结构在脉动风荷载作用下的总均方响应与准静力响应的比值定义了脉动风振响应特性参数R,根据R值将结构划分为小型静力结构、中型静力结构、大型静力结构和动力结构四类,并针对不同类型结构采用与之对应的风振响应计算方法。在Harris研究基础上,Cook[6]又将其中的动力结构细分为一般动力结构和气动弹性结构两类。Solari[7]将结构脉动风致共振响应占总响应的比例大小作为判定结构脉动风振响应特性的指标参数,据此将结构划分为三类,并建议分别采用所提出的简单方法、详细方法和严格方法计算相应的阵风荷载因子。周晅毅[8]对大跨屋盖结构进行风振响应分析时,根据结构刚度大小将其分为刚性屋盖结构、非大变形柔性屋盖结构和大变形柔性屋盖结构三类,据此决定风振响应计算中是否忽略脉动风的动力放大效应以及结构与来流的耦合效应。张建胜等[9]以结构真实脉动风振响应与假定的点状刚性结构脉动风振响应比值作为指标,对大跨屋盖结构脉动风振响应特性进行分类。在张建胜研究基础上,武岳和常虹[10]研究发现,结构自振频率、矢跨比和约束形式三个参数对单层柱面网壳结构脉动风振响应特性影响显著。
1967年Davenport[11]提出将结构脉动风振总响应分为背景响应和共振响应分别计算,该思路由于具有明确的物理意义而得到了广泛应用和发展[12-15]。基于此,有学者提出根据脉动风致背景响应和共振响应的比例关系对大跨屋盖结构风振响应特性进行分类,据此分类结果实现大跨屋盖结构脉动风振响应分析的简化[16-17]。上述研究为合理判定现代复杂大跨屋盖结构脉动风振响应特性并准确高效计算其脉动风振响应提供了清晰思路,但在实际操作过程中仍有一些关键问题需要进一步深入研究,主要包括:1)大跨屋盖结构的脉动风振响应除了背景分量、共振分量外,二者的耦合效应有时也不能忽略,因此按照响应分量比例关系对结构脉动风振响应特性进行分类时,如何兼顾背景、共振耦合项分量的贡献,对于完善分类结果非常关键;2)根据背景、共振及其耦合项分量比例关系判定大跨屋盖结构脉动风振响应特性之前,需要首先计算得到各响应分量的具体数值,这就使得目前方法只能实现大跨屋盖结构风效应分析中等效静力风荷载的高效精准计算,如何在避免对各响应分量具体值计算基础上,全面实现包括风振响应在内的大跨屋盖结构风效应高效精准分析还需要深入研究。
本文将针对上述需要深入研究的关键问题,基于大跨屋盖结构脉动风振背景、共振响应及其耦合项完全组合法(下文称为三分量完全组合法)求解思路,提出一种大跨屋盖结构脉动风振响应特性简便预测方法,其目标就是在进行脉动风振响应三分量完全组合求解之前,不再需要计算各响应分量具体数值,只借助几个简单的风荷载参数与结构动力特性参数,就可以完成大跨屋盖结构风振响应特性的合理判定,从而精准选定相应的分量进行风振响应组合计算。
1 脉动风振响应三分量完全组合
大跨屋盖结构在脉动风荷载作用下的运动方程为:
M¨Xd(t)+C˙Xd(t)+KXd(t)=LPd(t) (1) 式中:
M 、C 和K 分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;¨Xd(t) 、˙Xd(t) 和Xd(t) 分别为加速度、速度和位移响应;Pd(t) 为测压点处的脉动风荷载列向量;L 表示测压点与节点间等效力转换矩阵。综合考虑结构模态频率大小以及模态空间分布与脉动风荷载空间分布的相关性强弱,选取
m 阶主要参振模态进行风振响应计算[18],根据模态叠加原理,则式(1)中的结构位移响应可以表示为:Xd(t)=m∑j=1ϕjqj(t)=m∑j=1ϕj[qj,b(t)+qj,r(t)] (2) 式中:
ϕj 和qj(t) 分别为结构第j 阶模态向量和模态坐标;qj,b(t) 和qj,r(t) 分别为结构第j 阶模态坐标背景分量和共振分量。根据随机振动理论,由式(2)可以得到结构某一自由度i上的总响应方差:
σ2x,i=σ2x,b,i+σ2x,r,i+σ2x,br,i (3) 式中:
σ2x,b,i 和σ2x,r,i 分别为由qj,b(t) 和qj,r(t) 得到的结构第i自由度上背景响应方差和共振响应方差;σ2x,br,i 为背景、共振响应耦合项方差,通常由二者的相关系数ρx,br,i 求得:σ2x,br,i=2ρx,br,iσx,b,iσx,r,i (4) 式(3)为脉动风振响应三分量完全组合结果,由于
ρx,br,i 的计算需要涉及繁琐的双重求和与积分运算,因此在工程实践中常常将背景、共振响应耦合项省略。已有研究表明[19-20],对于大跨屋盖结构风振响应计算,省略背景、共振响应耦合项有时不能得到理想的结果。更进一步地,若在风振响应计算之前,能够同时对背景、共振响应及其耦合项对总脉动风振响应的贡献程度分别进行预测,即进行结构风振响应特性类型判定,就可以实现各分量合理取舍基础上的风振响应高效精准组合计算。
2 脉动风振响应各分量应变能贡献
为综合考虑结构所有自由度上脉动风振背景、共振响应及其耦合项对总响应的贡献,引入应变能的概念。
脉动风荷载在结构背景响应上做功表示为:
Wb(t)=12XTd,b(t)KXd,b(t)=12m∑j=1ω2jq2j,b(t) (5) 式中:
Xd,b(t) 为结构所有自由度上瞬时位移响应背景分量组成的列向量;ωj 为结构第j 阶模态频率;“T”表示向量转置。对
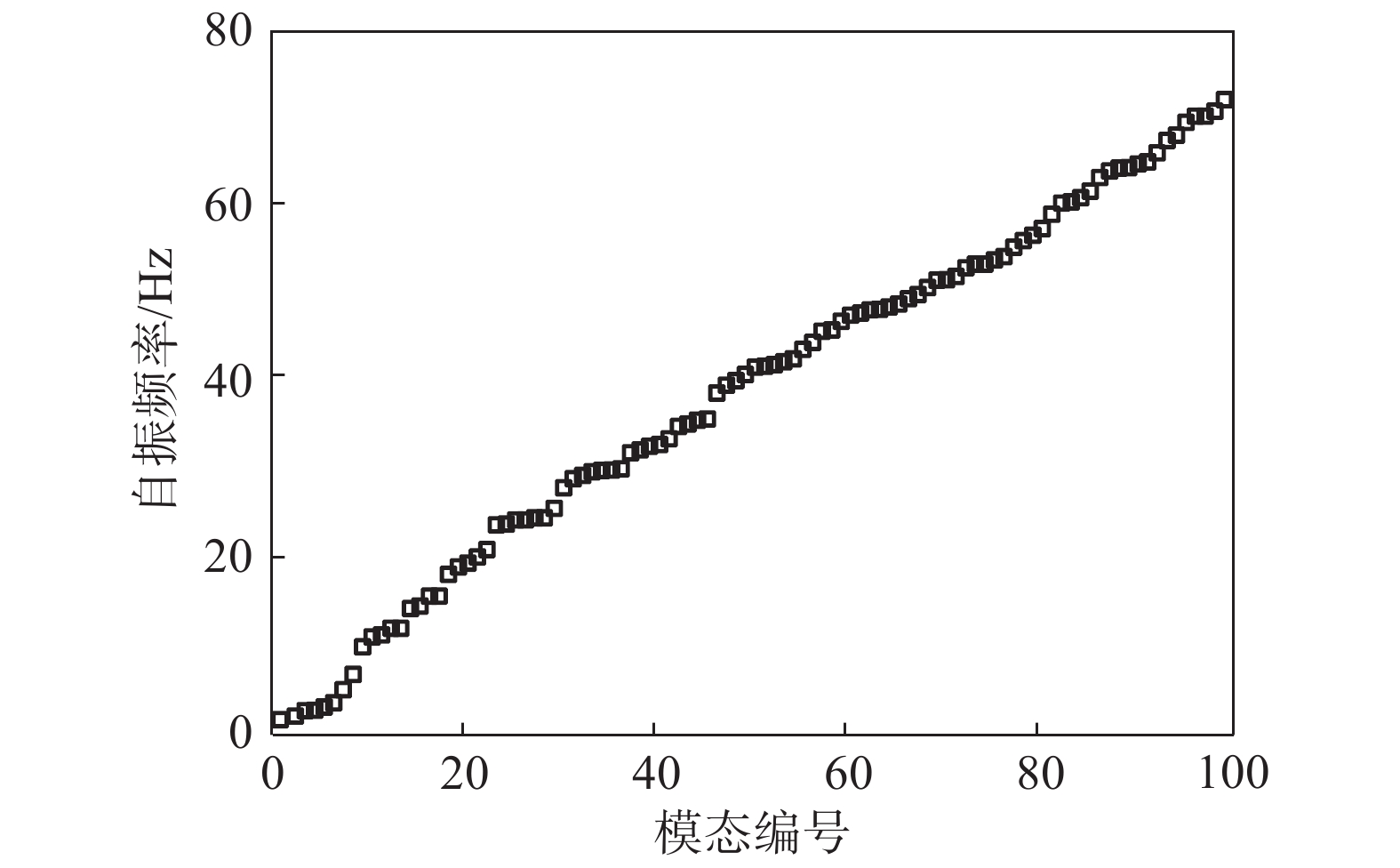
Wb(t) 取数学期望,得到具有统计意义的背景响应应变能:ˉWb=12m∑j=1ω2jσ2qj,b (6) 式中,
σ2qj,b 为结构第j 阶模态坐标方差背景分量。脉动风荷载在结构共振响应上做功表示为:
Wr(t)=12XTd,r(t)KXd,r(t)+12˙XTd,r(t)M˙Xd,r(t)=12m∑j=1[ω2jq2j,r(t)+˙q2j,r(t)] (7) 式中:
Xd,r(t) 为结构所有自由度上瞬时位移响应共振分量组成的列向量;“⋅ ”表示取一阶导数。对
Wr(t) 取数学期望,得到具有统计意义的共振响应应变能:ˉWr=12m∑j=1(ω2jσ2qj,r+σ2˙qj,r) (8) 式中,
σ2qj,r 为结构第j 阶模态坐标方差共振分量。脉动风荷载在结构背景、共振响应耦合项上做功表示为:
Wbr(t)=12XTd,br(t)KXd,br(t)+12˙XTd,br(t)M˙Xd,br(t)=12m∑j=1[ω2jq2j,br(t)+˙q2j,br(t)] (9) 式中:
Xd,br(t) 为结构所有自由度上瞬时位移响应背景、共振耦合项分量组成的列向量;qj,br(t) 为结构第j 阶模态坐标的背景、共振耦合项分量。对
Wbr(t) 取数学期望,得到具有统计意义的背景、共振响应耦合项应变能:ˉWbr=12m∑j=1(ω2jσ2qj,br+σ2˙qj,br) (10) 式中,
σ2qj,br 为结构第j 阶模态坐标方差背景、共振耦合项分量。将各响应分量应变能对结构总响应应变能的贡献定义为分量预测系数,作为风振响应计算中能否省略该响应分量的判定依据。
由式(6)~式(10)可得背景、共振响应及其耦合项分量预测系数:
ηk=ˉWkˉWtotal (11) 式中:
ˉWtotal=ˉWb+ˉWr+ˉWbr ;k 分别取b 、r 和br 。如前所述,要确定式(11)表示的预测系数,需要首先计算得到各响应分量具体值,而在进行脉动风振响应三分量组合计算之前,各响应分量值是未知的,此时也就无法根据式(11)表示的预测系数对各响应分量直接做出取舍,因此还需要对上述脉动风振响应各分量应变能进行简化处理。
3 脉动风振响应各分量应变能简化处理
3.1 背景分量应变能
根据随机响应谱分析方法,结构第
j 阶模态响应谱背景分量为:Sqj,b(ω)=Hj,b(ω)Hj,b(ω)SFjFj(ω) (12) 式中:
Hj,b(ω)=1/ω2j 为结构第j 阶模态响应背景分量频响函数;SFjFj(ω)=ϕTjLTSpp(ω)Lϕj 为结构第j 阶模态力谱,其中Spp(ω) 为测压点脉动风荷载谱矩阵。根据式(12),由方差与谱密度的关系可得结构第
j 阶模态响应方差背景分量:σ2qj,b=∫+∞−∞Sqj,b(ω)dω=1ω4j∫+∞−∞SFjFj(ω)dω=σ2FjFjω4j (13) 式中,
σ2FjFj 为结构第j 阶模态力方差。将式(13)代入式(6),可得由结构动力特性参数和风荷载参数表示的背景响应分量应变能:
ˉWb=12m∑j=1σ2FjFjω2j (14) 3.2 共振分量应变能
同样,根据随机响应谱分析方法,结构第
j 阶模态响应谱共振分量为:Sqj,r(ω)=Hj,r(iω)H∗j,r(iω)SFjFj(ω) (15) 式中:
Hj,r(iω)=(ω/ωj)2−2iζjω/ωjω2j[1−(ω/ωj)2+2iζjω/ωj] 为结构第j 阶模态响应共振分量频响函数,其中i 为虚数单位;ζj 为结构第j 阶模态阻尼比;“∗ ”表示复数取共轭。根据式(15),由方差与谱密度的关系可得结构第
j 阶模态响应方差共振分量:σ2qj,r=∫+∞−∞Sqj,r(ω)dω=∫+∞−∞|Hj,r(iω)|2SFjFj(ω)dω (16) 式中,
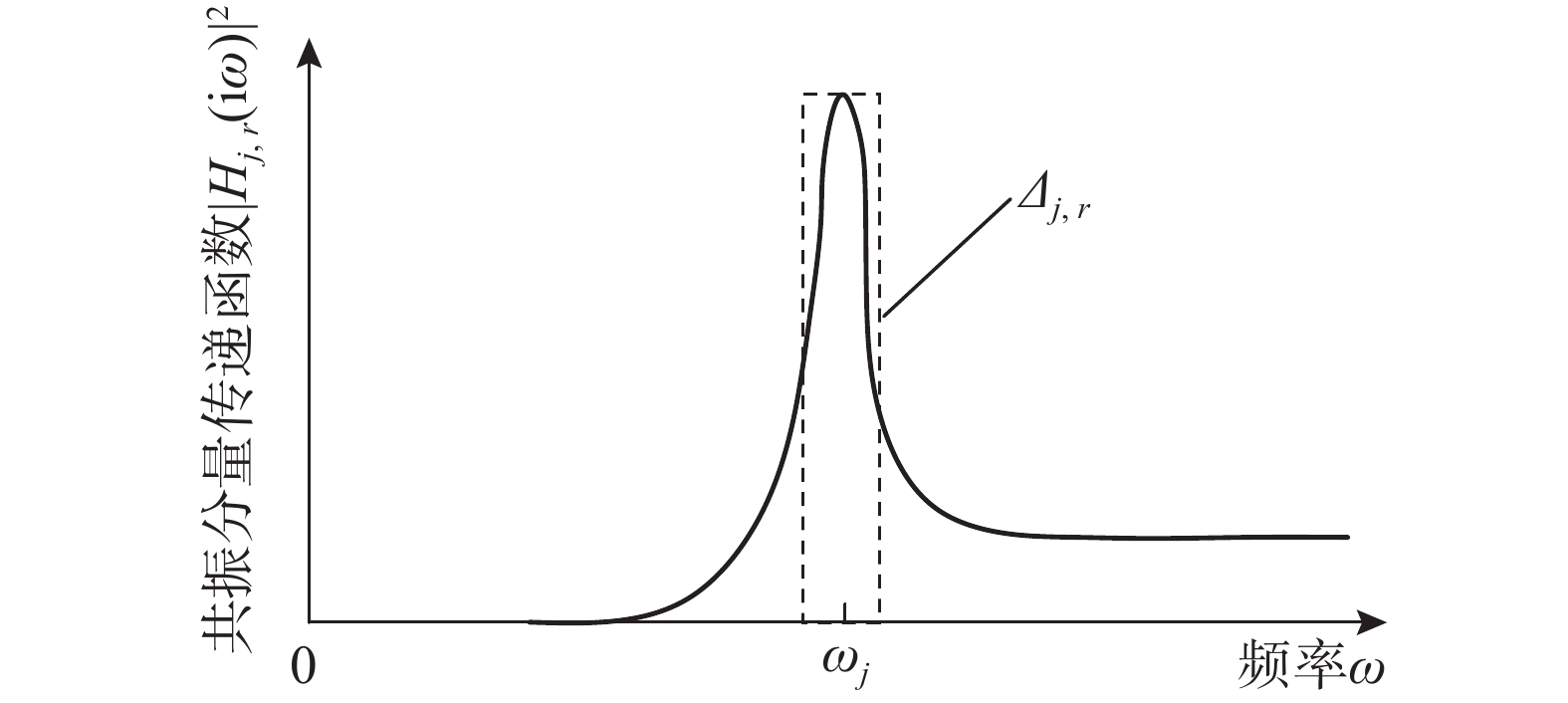
|Hj,r(iω)|2=Hj,r(iω)H∗j,r(iω) 为结构第j 阶模态响应共振分量传递函数。其在频域内的分布如图1所示,表达式为:|Hj,r(iω)|2=[ρ2j(1−ρ2j)−4ρ2jξ2j]2+4ρ2jξ2j[(1−ρ2j)2+4ρ2jξ2j]2ω4j (17) 式中,
ρj=ωωj 。根据图1模态响应共振分量传递函数的分布形式,可以将式(17)近似分段表示为:
{|Hj,r(iω)|2≈0(ω<ωj−Δj,r2)|Hj,r(iω)|2≈4ξ2j+14ξ2jω4j(ωj−Δj,r2<ω<ωj+Δj,r2)|Hj,r(iω)|2≈1ω4j(ω>ωj+Δj,r2) (18) 式中,
Δj,r=4πξ3jωj/(4ξ2j+1) 为|Hj,r(iω)|2 在结构第j 阶自振频率ωj 附近的等效宽度,可以由白噪声谱下的方差与窄带白噪声下的方差相等得到。此时,式(16)可以近似表示为:
σ2qj,r=2∫ωj−Δj,r20|Hj,r(iω)|2SFjFj(ω)dω+2∫ωj+Δj,r2ωj−Δj,r2|Hj,r(iω)|2SFjFj(ω)dω+2∫∞ωj+Δj,r2|Hj,r(iω)|2SFjFj(ω)dω≈2|Hj,r(iωj)|2Δj,rSFjFj(ωj)+2∫∞ωj+Δj,r2SFjFj(ω)ω4jdω (19) 式中,
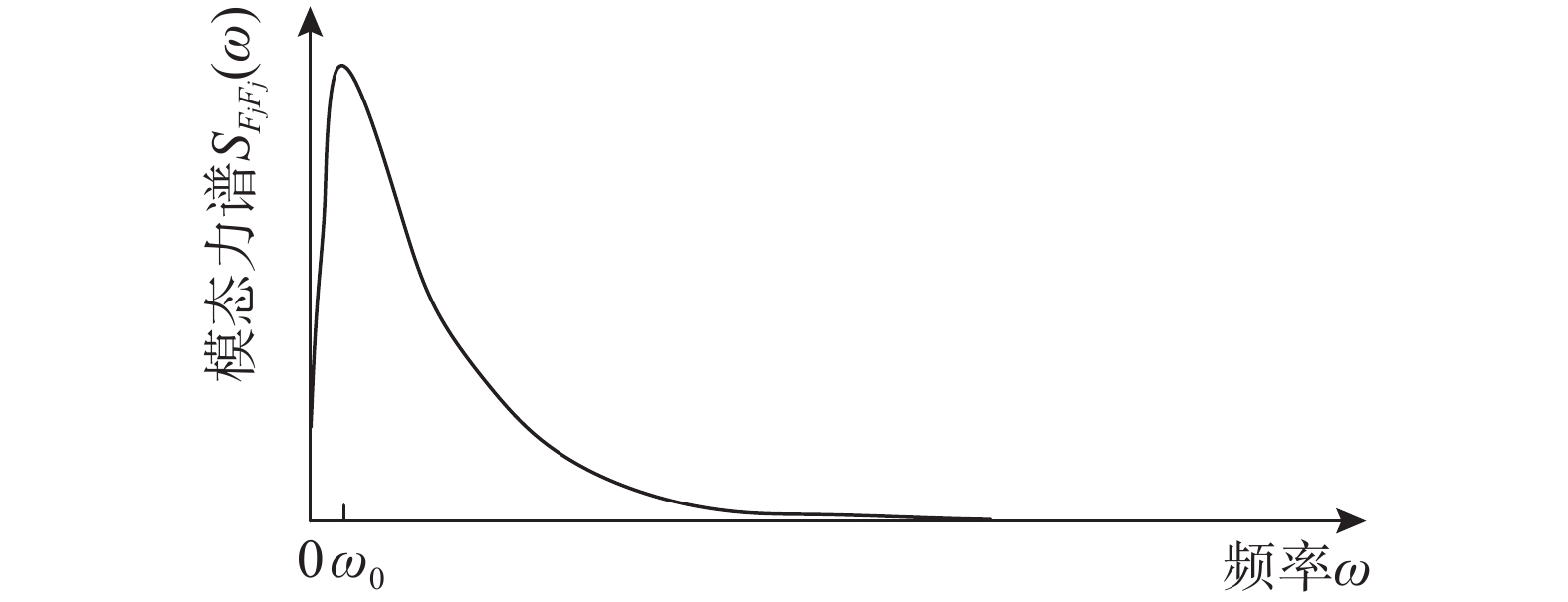
SFjFj(ωj) 和|Hj,r(iωj)|2 分别为SFjFj(ω) 和|Hj,r(iω)|2 在结构第j 阶自振频率ωj 处的值。对于大跨屋盖结构,其自振频率
ωj (一般首阶自振频率ω1≈1Hz )通常远大于风荷载主频率ω0 (一般为0.025 Hz~0.1 Hz),而SFjFj(ω) 在风荷载主频率ω0 附近有一峰值,其后在高频段迅速衰减,其分布如图2所示,据此可以将式(19)进一步简化为:σ2qj,r≈4ξ2j+12ξ2jω4jΔj,rSFjFj(ωj)=2πξjSFjFj(ωj)ω3j (20) 将式(20)代入式(8),可得由结构动力特性参数和风荷载参数表示的共振响应分量应变能:
ˉWr=2πm∑j=1ξjSFjFj(ωj)ωj (21) 3.3 背景、共振耦合项分量应变能
同样,根据随机响应谱分析方法,结构第
j 阶模态响应谱背景、共振耦合项分量为:Sqj,br(ω)=2Hj,b(ω)H∗j,r(iω)SFjFj(ω) (22) 根据式(22),由方差与谱密度的关系可得结构第
j 阶模态响应方差背景、共振耦合项分量:σ2qj,br=∫+∞−∞Sqj,br(ω)dω≈2∫+∞−∞Hj,br(ω)SFjFj(ω)dω (23) 式中,
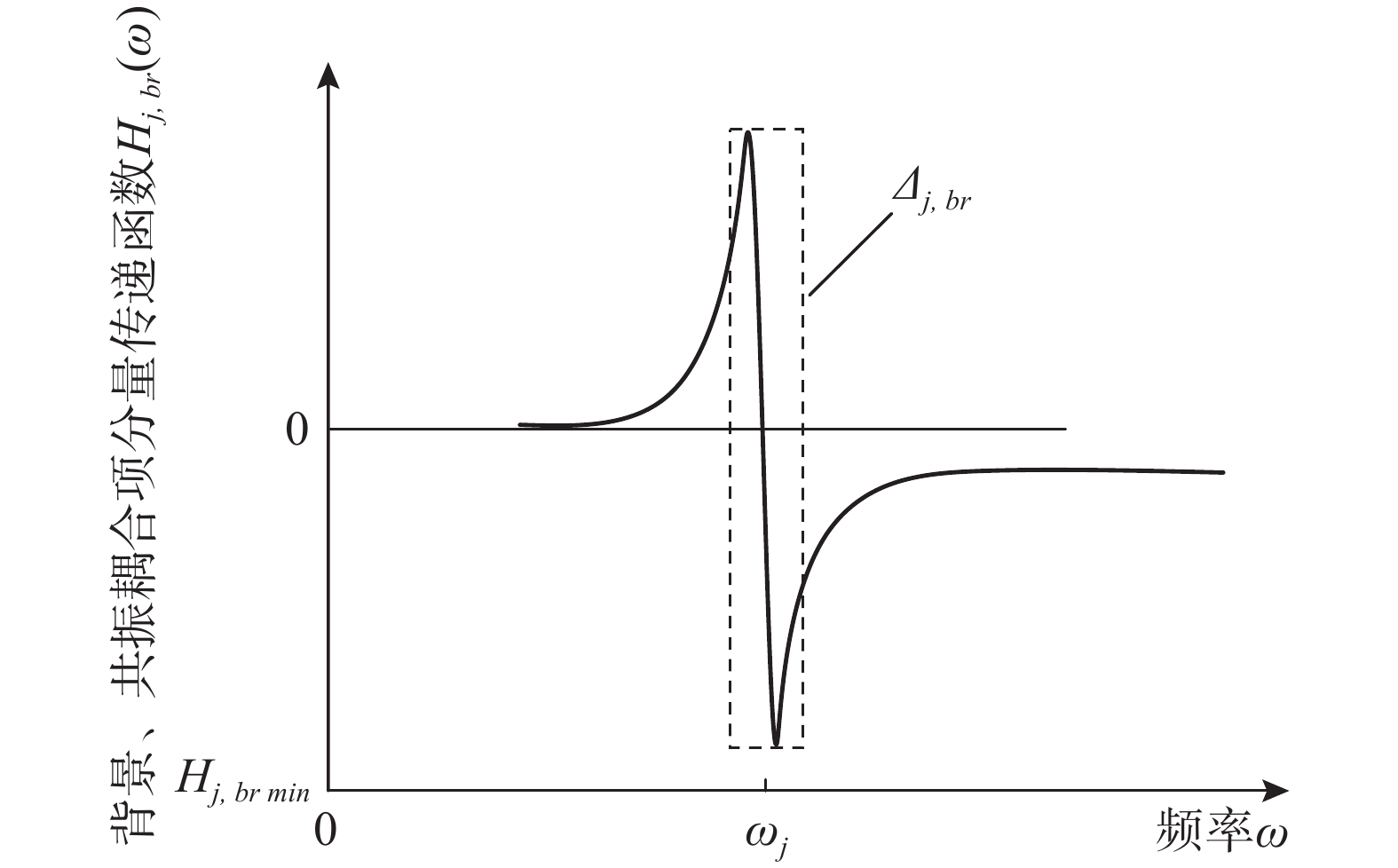
Hj,br(ω) 为结构第j 阶模态响应背景、共振耦合项分量传递函数,其在频域内分布如图3所示,表达式为:Hj,br(ω)=ρ2j(1−ρ2j)−4ρ2jξ2j[(1−ρ2j)2+4ρ2jξ2j]ω4j (24) 根据图3模态响应背景、共振耦合项分量传递函数的分布形式,可以将式(24)近似分段表示为:
{Hj,br(ω)≈0(ω<ωj−Δj,br2)Hj,br(ω)≈Hj,brmax (25) 式中:
{\varDelta _{j,br}} = {{\pi \xi _j^2\sqrt {1 + {\xi _j}} } / {2{\omega _j}}} 为H_{j,br}^{}\left( \omega \right) 在结构第j 阶自振频率{\omega _j} 附近的等效宽度;{H_{j,br}}_{\max } 、{H_{j,br}}_{\min } 分别为H_{j,br}^{}\left( \omega \right) 在等效宽度{\varDelta _{j,br}} 内的最大值和最小值。此时,式(23)可以近似表示为:
\begin{split} \sigma _{{q_{j,br}}}^2 =& 4\int_0^{{\omega _j} - \frac{{{\varDelta _{j,br}}}}{2}} {{H_{j,br}}(\omega ){S_{{F_j}{F_j}}}(\omega ){\rm{d}}\omega } + \\[-2pt]& 4\int_{{\omega _j} - \frac{{{\varDelta _{j,br}}}}{2}}^{{\omega _j}} {{H_{j,br}}(\omega ){S_{{F_j}{F_j}}}(\omega ){\rm{d}}\omega } + \\[-2pt]& 4\int_{{\omega _j}}^{{\omega _j} + \frac{{{\varDelta _{j,br}}}}{2}} {{H_{j,br}}(\omega ){S_{{F_j}{F_j}}}(\omega ){\rm{d}}\omega } + \\[-2pt]& 4\int_{{\omega _j} + \frac{{{\varDelta _{j,br}}}}{2}}^\infty {{H_{j,br}}(\omega ){S_{{F_j}{F_j}}}(\omega ){\rm{d}}\omega } \approx \\[-2pt]& 4 ( {{H_{j,br}}_{\max } + {H_{j,br}}_{\min }} )\frac{{{\varDelta _{j,br}}}}{2}{S_{{F_j}{F_j}}}({\omega _j}) + \\[-2pt]& 4\int_{{\omega _j} + \frac{{{\varDelta _{j,br}}}}{2}}^\infty {\frac{{{S_{{F_j}{F_j}}}(\omega )}}{{\omega _j^4}} {\rm{d}}\omega } \end{split} (26) 同样,考虑到图2所示
{S_{{F_j}{F_j}}}(\omega ) 在高频段的衰减特点,可将式(26)进一步简化表示为:\begin{split} \sigma _{{q_{j,br}}}^2 \approx & 2( {{H_{j,br}}_{\max } + {H_{j,br}}_{\min }} ){\varDelta _{j,br}}{S_{{F_j}{F_j}}}({\omega _j}) \approx \\& \frac{{\pi \xi _j^2\sqrt {1 + {\xi _j}} {S_{{F_j}{F_j}}}({\omega _j})}}{{\omega _j^5}} \end{split} (27) 将式(27)代入式(10),可得由结构动力特性参数和风荷载参数表示的背景、共振响应耦合项分量应变能:
{\bar W_{br}} = \pi \sum\limits_{j = 1}^m {\frac{{\xi _j^2\sqrt {1 + {\xi _j}} {S_{{F_j}{F_j}}}({\omega _j})}}{{\omega _j^3}}} (28) 4 脉动风振响应特性类型预测判定标准及实施步骤
4.1 预测判定标准
至此,由式(14)、式(21)和式(28)分别得到了由结构动力特性参数和风荷载参数表示的各响应分量应变能
{\bar W_b} 、{\bar W_r} 和{\bar W_{br}} ,将其代入式(11)便可以得到各响应分量预测系数{\eta _b} 、{\eta _r} 和{\eta _{br}} ,同时制定相应的误差限{\varepsilon _b} 、{\varepsilon _r} 和{\varepsilon _{br}} ,此误差限取值可以按照工程精度要求由工程经验综合确定。若某响应分量预测系数小于其相应的误差限,说明该分量对总响应的贡献较小,风振响应计算可以将其忽略,否则需要计及。据此将大跨屋盖结构风振响应特性划分为I~VI类,如表1所示。表 1 大跨屋盖结构脉动风振响应特性预测表Table 1. Criterion of fluctuating wind-induced response characteristic for large-span roofs类型 预测系数 类型描述 {\eta _b} {\eta _r} {\eta _{br}} I {\eta _b} < {\varepsilon _b} − {\eta _{br}} < {\varepsilon _{br}} 弱耦合柔性
(共振分量)II {\eta _b} < {\varepsilon _b} − {\eta _{br}} > {\varepsilon _{br}} 强耦合柔性
(共振、耦合分量)III − {\eta _r} < {\varepsilon _r} {\eta _{br}} < {\varepsilon _{br}} 弱耦合刚性
(背景分量)IV − {\eta _r} < {\varepsilon _r} {\eta _{br}} > {\varepsilon _{br}} 强耦合刚性
(背景、耦合分量)V {\eta _b} > {\varepsilon _b} {\eta _r} > {\varepsilon _r} {\eta _{br}} < {\varepsilon _{br}} 弱耦合刚柔适中
(背景、共振分量)VI {\eta _b} > {\varepsilon _b} {\eta _r} > {\varepsilon _r} {\eta _{br}} > {\varepsilon _{br}} 强耦合刚柔适中
(背景、共振、耦合分量)注:“类型描述”列括弧中为风振响应计算需要计及的响应分量。 4.2 实施步骤
本文所提大跨屋盖结构脉动风振响应特性预测法的基本思路为:以应变能评价各响应分量对总响应的贡献程度,并结合各响应分量的简化处理,得到只需要结构动力特性参数和风荷载参数表示的各响应分量预测系数,借此系数对结构脉动风振响应特性进行预测并判定类型,从而有效兼顾大跨屋盖结构脉动风振响应的计算效率和计算精度。具体步骤为:
1)首先对大跨屋盖结构进行动力特性分析,得到各阶模态的自振频率、模态分布,同时由经验确定模态阻尼比;根据结构模型风洞试验获取的屋盖表面风荷载信息得到模态荷载方差和模态荷载功率谱。
2)将步骤1)中所得结构动力特性参数和风荷载参数代入式(14)、式(21)和式(28),计算各响应分量的应变能
{\bar W_b} 、{\bar W_r} 和{\bar W_{br}} 。3)由式(11)分别计算各响应分量预测系数
{\eta _b} 、{\eta _r} 和{\eta _{br}} ,并与按照工程精度要求由工程经验综合确定的误差限{\varepsilon _b} 、{\varepsilon _r} 和{\varepsilon _{br}} 进行比较,由比较结果依据表1综合预测判定结构脉动风振响应特性类型,在此基础上,舍去对结构总响应贡献较小的分量,组合贡献较大的分量得到脉动风振总响应。5 算例分析
按照本文所提大跨屋盖结构脉动风振响应特性预测方法,以国家网球中心莲花球场屋盖结构为例,对其脉动风振响应特性进行预测,根据预测结果计算结构脉动风振响应,并与三分量完全组合法计算结果(精确值)进行对比,验证所提方法的有效性。
5.1 工程概况
国家网球中心莲花球场屋盖结构整体形如“莲花”,由12个“z”形花瓣单元组成,单元之间开有较大洞口,结构新颖,造型独特,如图4所示。“z”形花瓣单元挑蓬屋盖最高点标高23.0 m,悬挑长度21.6 m,并设置约3°的倾角以方便排水,该屋盖体型特殊,表面钝体绕流特性明显,属于重要且复杂的风敏感结构,其风效应分析所需的结构表面风荷载需要借助风洞试验获取。
5.2 风荷载确定及自振特性分析
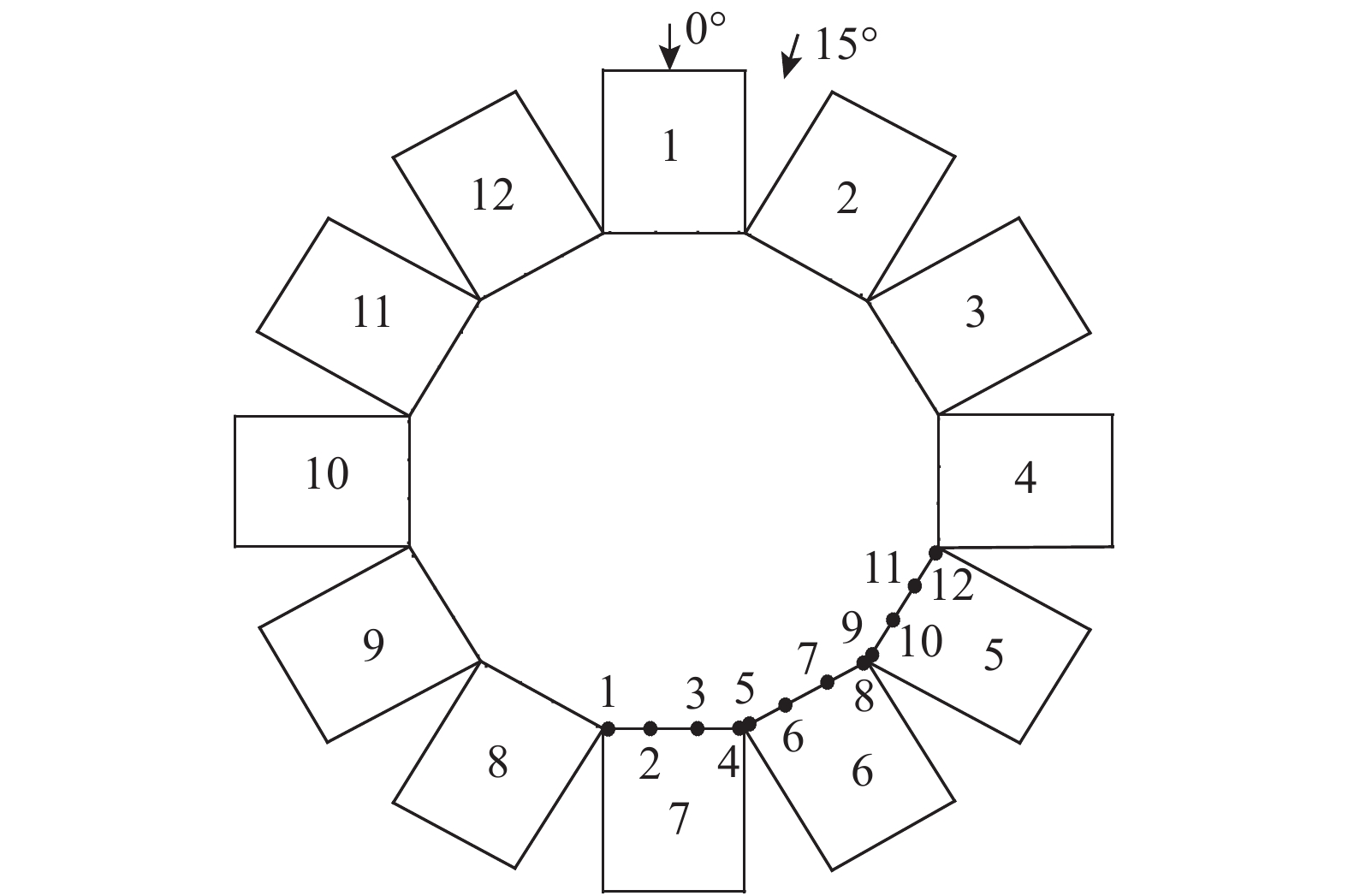
屋盖模型风洞试验在某低速风洞中进行,试验模型按照1∶120进行缩尺设计,采用有机玻璃和ABS板制作而成,满足刚性模型测压试验所需的刚度和强度要求。考虑到结构的对称性,仅在模型第3和第4单元布置测压点,每个单元上、下表面共布置78个测点(模型单元编号及测点布置如图5所示),采样频率为400 Hz,每个测点采集3900个数据,数据处理时将上、下表面测点风荷载值进行叠加,试验名义风速为15 m/s,地面粗糙度类别为B类。试验过程中,在0°~360°范围内每隔7.5°风向角测试并采集数据1次,其中以正北方向定义为0°风向角,顺时针增大,如图5所示。
如4.2节所述,若对结构进行脉动风振响应特性预测及风振响应计算,需要结构动力特性参数,为此建立了屋盖结构有限元模型,进行动力特性分析,提取了前100阶模态的自振频率、模态分布等信息,其中前100阶模态自振频率分布如图6所示。由图6可见,该屋盖结构频率分布较密集,风振响应计算需要考虑多模态参振。
5.3 风振响应特性预测及风振响应分析
如前所述,该屋盖结构风振响应计算需要考虑多模态参振,因此,综合考虑结构模态频率大小以及模态空间分布与脉动风荷载空间分布的相关性强弱[18],从5.2节结构动力特性分析提取的屋盖结构前100阶模态中选取第1阶、第2阶、第4阶、第3阶、第6阶等共17阶为主要参振模态。
利用5.2节屋盖模型风洞试验0°风向角时的风荷载测压数据,以及所选取的17阶主要参振模态信息(模态阻尼比统一取0.035),按照本文所提方法,由式(14)、式(21)和式(28),计算得到各响应分量应变能
{\bar W_b} 、{\bar W_r} 、{\bar W_{br}} ,并将其代入式(11)计算得到各响应分量预测系数{\eta _b} 、{\eta _r} 和{\eta _{br}} ,分别为0.402、0.561和0.037,取误差限{\varepsilon _b} 、{\varepsilon _r} 和{\varepsilon _{br}} 均为0.05,由表1预测该屋盖为V类弱耦合刚柔适中结构,因此其风振响应计算只需计及背景分量和共振分量。根据本文方法预测得到的屋盖结构脉动风振响应特性类型,基于随机振动理论,计算了结构背景响应和共振响应,并对其组合得到结构总脉动风振位移响应极值,其中峰值因子按照极值超越理论得到[21],同时与传统的三分量完全组合法计算结果(精确值)进行比较,选取内环屋盖上12个典型节点(该位置处于屋盖迎风前缘,为风荷载敏感区域)的计算结果示于表2,其中所选12个典型节点位置及编号如图7所示。
表 2 典型节点脉动风振位移响应极值Table 2. Fluctuating wind-induced extreme displacement response of key nodes节点号 响应极值/mm 精确值/mm 误差/(%) 1 8.537 8.325 2.546 2 9.279 9.001 3.088 3 9.599 9.201 4.325 4 9.215 8.925 3.249 5 9.284 8.896 4.361 6 7.783 7.497 3.815 7 7.970 7.797 2.219 8 7.439 7.096 4.833 9 7.826 7.503 4.304 10 7.206 6.946 3.743 11 7.296 6.855 6.433 12 6.258 6.003 4.248 由表2可见,根据本文对该屋盖结构脉动风振响应特性类型预测结果,省略背景、共振耦合项分量,只组合背景和共振分量得到的脉动风振位移响应极值,与三分量完全组合结果(精确值)相比,除11号节点误差为6.433%外,其余所选典型节点的误差基本在2%~5%,说明本文方法能够有效预测结构脉动风振响应特性,据此组合得到的结构脉动风振总响应具有较好的精度。
6 结论
针对大跨屋盖结构风振响应特性的多样性以及传统三分量完全组合法求解风振响应的复杂性,提出了一种大跨屋盖结构脉动风振响应特性预测方法,为合理取舍风振响应三分量,并对其高效精准组合得到总响应提供依据。主要结论有:
(1)引入应变能的概念,基于风振响应各分量应变能比例关系,综合考虑了结构所有节点上响应分量对总响应的贡献,据此可以实现对大跨屋盖结构脉动风振响应特性类型的判定。
(2)根据各响应分量传递函数和风荷载谱特性,通过对各响应分量表达式的简化处理,能够避免直接计算各响应分量具体值,只需借助风荷载参数和结构动力特性参数,就可以方便预测各响应分量对总响应的贡献。
(3)采用所提方法,对国家网球中心莲花球场屋盖结构脉动风振响应特性进行预测,根据预测结果,对相应的响应分量进行组合计算。结果表明,所提方法能够有效预测结构脉动风振响应特性,据此组合计算的脉动风振总响应具有较好的精度。
-
表 1 大跨屋盖结构脉动风振响应特性预测表
Table 1 Criterion of fluctuating wind-induced response characteristic for large-span roofs
类型 预测系数 类型描述 {\eta _b} {\eta _r} {\eta _{br}} I {\eta _b} < {\varepsilon _b} − {\eta _{br}} < {\varepsilon _{br}} 弱耦合柔性
(共振分量)II {\eta _b} < {\varepsilon _b} − {\eta _{br}} > {\varepsilon _{br}} 强耦合柔性
(共振、耦合分量)III − {\eta _r} < {\varepsilon _r} {\eta _{br}} < {\varepsilon _{br}} 弱耦合刚性
(背景分量)IV − {\eta _r} < {\varepsilon _r} {\eta _{br}} > {\varepsilon _{br}} 强耦合刚性
(背景、耦合分量)V {\eta _b} > {\varepsilon _b} {\eta _r} > {\varepsilon _r} {\eta _{br}} < {\varepsilon _{br}} 弱耦合刚柔适中
(背景、共振分量)VI {\eta _b} > {\varepsilon _b} {\eta _r} > {\varepsilon _r} {\eta _{br}} > {\varepsilon _{br}} 强耦合刚柔适中
(背景、共振、耦合分量)注:“类型描述”列括弧中为风振响应计算需要计及的响应分量。 表 2 典型节点脉动风振位移响应极值
Table 2 Fluctuating wind-induced extreme displacement response of key nodes
节点号 响应极值/mm 精确值/mm 误差/(%) 1 8.537 8.325 2.546 2 9.279 9.001 3.088 3 9.599 9.201 4.325 4 9.215 8.925 3.249 5 9.284 8.896 4.361 6 7.783 7.497 3.815 7 7.970 7.797 2.219 8 7.439 7.096 4.833 9 7.826 7.503 4.304 10 7.206 6.946 3.743 11 7.296 6.855 6.433 12 6.258 6.003 4.248 -
[1] 沈世钊, 武岳. 结构形态学与现代空间结构[J]. 建筑结构学报, 2014, 35(4): 1 − 10. Shen Shizhao, Wu Yue. Structural morphology and modern space structures [J]. Journal of Building Structures, 2014, 35(4): 1 − 10. (in Chinese)
[2] 周勐, 樊健生, 刘宇飞, 等. 北京大兴国际机场航站楼核心区钢网格结构日照非均匀温度场研究[J]. 工程力学, 2020, 37(5): 46 − 54, 73. doi: 10.6052/j.issn.1000-4750.2019.07.0374 Zhou Meng, Fan Jiansheng, Liu Yufei, et al. Analysis on non-uniform temperature field of steel grids of Beijing Daxing international airport terminal building core area considering solar radiation [J]. Engineering Mechanics, 2020, 37(5): 46 − 54, 73. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.07.0374
[3] 林拥军, 沈艳忱, 李明水, 等. 大跨翘曲屋盖风压分布的风洞试验与数值模拟[J]. 西南交通大学学报, 2018, 53(2): 226 − 233. doi: 10.3969/j.issn.0258-2724.2018.02.002 Lin Yongjun, Shen Yanchen, Li Mingshui, et al. Evaluation of wind pressure distribution for large-span warpage roof via wind tunnel testing and numerical simulation [J]. Journal of Southwest Jiaotong University, 2018, 53(2): 226 − 233. (in Chinese) doi: 10.3969/j.issn.0258-2724.2018.02.002
[4] 李宇, 王阳, 叶黎鹏, 等. 椭球形多曲面组合屋盖结构风荷载特性研究[J]. 广西大学学报(自然科学版), 2020, 45(1): 121 − 127. Li Yu, Wang Yang, Ye Lipeng, et al. Study on wind load characteristics of ellipsoidal multi-surface composite roof structure [J]. Journal of Guangxi University (Natural Science Edition), 2020, 45(1): 121 − 127. (in Chinese)
[5] Harris R I. The classification of structures for assessment and codification of wind effects [C]// Wind Engineering: Proceedings of the Fifth International Conference. Fort Collins, Colorado, USA: Elsevier Ltd, 1982, 2: 1257 − 1269.
[6] Cook N J. The Designer's guide to wind loading of building structures [M]. London, UK: Butterworths, 1985.
[7] Solari G. Design wind loads [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1983, 11(83): 345 − 358.
[8] 周晅毅. 大跨度屋盖结构的风荷载及风致响应研究 [D]. 上海: 同济大学, 2004. Zhou Xuanyi. Study on wind load and wind-induced response of large-span roof [D]. Shanghai: Tongji University, 2004. (in Chinese)
[9] 张建胜, 武岳, 吴迪. 结构抗风设计敏感性分析[J]. 振动工程学报, 2011, 24(6): 682 − 688. doi: 10.3969/j.issn.1004-4523.2011.06.016 Zhang Jiansheng, Wu Yue, Wu Di. Wind-sensitivity in design of structures [J]. Journal of Vibration Engineering, 2011, 24(6): 682 − 688. (in Chinese) doi: 10.3969/j.issn.1004-4523.2011.06.016
[10] 武岳, 常虹. 单层柱面网壳结构抗风敏感度研究[J]. 振动工程学报, 2016, 29(2): 284 − 290. Wu Yue, Chang Hong. Wind-sensitivity of single-layer latticed cylindrical shells [J]. Journal of Vibration Engineering, 2016, 29(2): 284 − 290. (in Chinese)
[11] Davenport A G. Gust loading factors [J]. Journal of Structural Division, 1967, 93(3): 11 − 34.
[12] Zhou Y, Kareem A, Gu M. Equivalent static buffeting wind loads on structure [J]. Journal of Structural Engineering, 2000, 126(8): 989 − 992. doi: 10.1061/(ASCE)0733-9445(2000)126:8(989)
[13] 李璟, 韩大建. 屋盖风振响应功率谱及背景与共振响应的分离[J]. 工程力学, 2010, 27(6): 65 − 71. Li Jing, Han Dajian. Power spectra of wind-induced response and separation of background response from resonant response for roof structures [J]. Engineering Mechanics, 2010, 27(6): 65 − 71. (in Chinese)
[14] 李玉学, 杨庆山, 田玉基, 等. 大跨屋盖结构多目标等效静力风荷载[J]. 工程力学, 2016, 33(6): 85 − 92. doi: 10.6052/j.issn.1000-4750.2014.10.0890 Li Yuxue, Yang Qingshan, Tian Yuji, et al. Multiple targets equivalent static wind load for long-span roofs [J]. Engineering Mechanics, 2016, 33(6): 85 − 92. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.10.0890
[15] Su N, Peng S T, Hong N N. Analyzing the background and resonant effects of wind-induced responses on large-span roofs [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 183(1): 114 − 126.
[16] 陈波, 杨庆山, 武岳. 大跨屋盖结构抗风类型划分方法及应用[J]. 北京交通大学学报, 2011, 35(4): 66 − 72. doi: 10.3969/j.issn.1673-0291.2011.04.013 Chen Bo, Yang Qingshan, Wu Yue. Classification and application of wind-resistant type of long-span roof structures [J]. Journal of Beijing Jiaotong University, 2011, 35(4): 66 − 72. (in Chinese) doi: 10.3969/j.issn.1673-0291.2011.04.013
[17] Wang X H, Huang Z Y, Chen B, et al. Equivalent static wind loads on plate-like flat roofs: Data-based closed form [J]. Journal of Structural Engineering, 2020, 146(6): 0002643.
[18] 李玉学, 杨庆山, 田玉基. 大跨屋盖结构风振响应主要参振模态确定方法研究[J]. 计算力学学报, 2010, 27(6): 1049 − 1054. doi: 10.7511/jslx20106016 Li Yuxue, Yang Qingshan, Tian Yuji. Research on the method for selecting dominant modes of wind-induced response for large-span roofs [J]. Chinese Journal of Computational Mechanics, 2010, 27(6): 1049 − 1054. (in Chinese) doi: 10.7511/jslx20106016
[19] 柯世堂, 葛耀君. 基于一致耦合法某大型博物馆结构风致响应精细化研究[J]. 建筑结构学报, 2012, 33(3): 111 − 117. Ke Shitang, Ge Yaojun. Refined research on wind-induced response of roof structure of a large museum based on consistent coupled method [J]. Journal of Building Structures, 2012, 33(3): 111 − 117. (in Chinese)
[20] 李寿科, 李寿英, 孙洪鑫. 考虑背景共振耦合效应的完全三分量法在大跨屋盖风致响应中的应用[J]. 应用力学学报, 2015, 32(6): 1048 − 1054. Li Shouke, Li Shouying, Sun Hongxin. Refined three-component method for determining wind induced response of large span roofs [J]. Chinese Journal of Applied Mechanics, 2015, 32(6): 1048 − 1054. (in Chinese)
[21] 张相庭. 结构风工程理论·规范·实践[M]. 北京: 建筑工业出版社, 2006. Zhang Xiangting. Wind engineering theory·code·practice [M]. Beijing: China Architecture and Building Press, 2006. (in Chinese)
-
期刊类型引用(3)
1. 李宏男,张鸿志,李庆伟,付兴. FAST馈源舱结构气动力特性及耦联系统风振响应研究. 工程力学. 2025(06): 33-45 .  本站查看
本站查看
2. 翟露阳,韩佳颖,沈永利. 脉动风作用下船舶风载荷数值仿真. 天津理工大学学报. 2024(03): 17-23 .  百度学术
百度学术
3. 李波,胡涛,田玉基,刘悦,卢啸,张范,宋晓峰,白凡. 北京2022年冬奥会内场主火炬抗风性能研究. 工程力学. 2024(10): 43-48 .  本站查看
本站查看
其他类型引用(4)




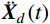
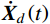
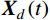
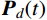
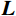
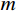
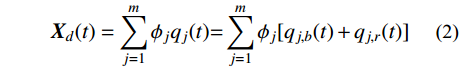
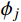
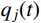
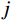
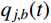
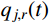
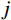
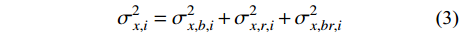
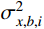
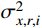
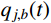
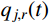
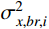
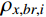
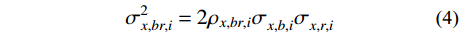
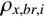
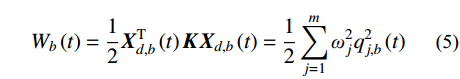
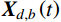
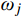
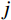
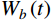
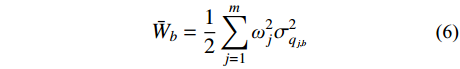
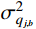
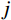
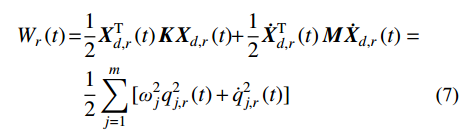
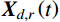

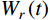
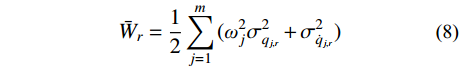
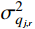
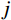
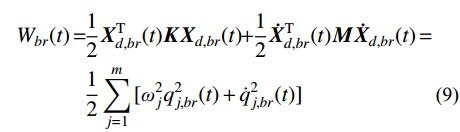
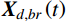
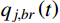
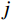
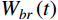
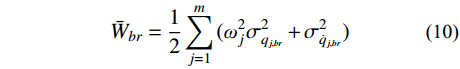
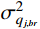
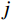
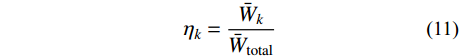
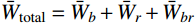
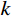
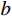
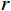
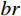
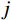
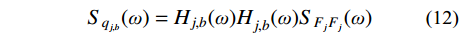
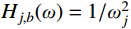
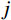
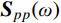
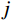
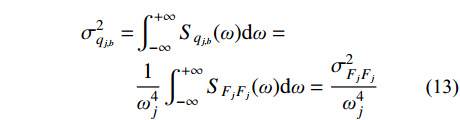
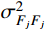
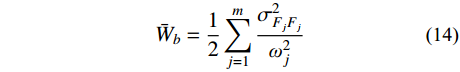
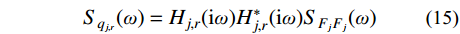
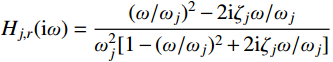
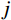
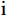
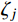
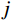

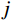
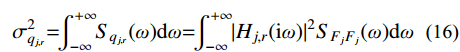
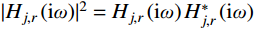
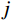
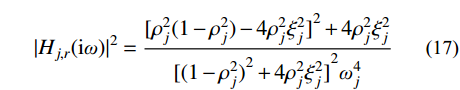
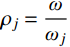
 下载:
下载: