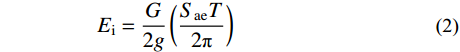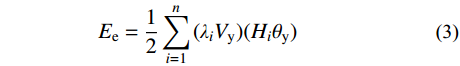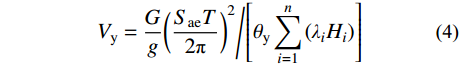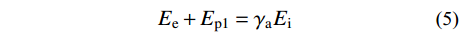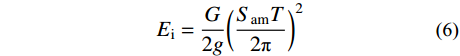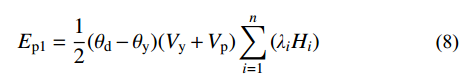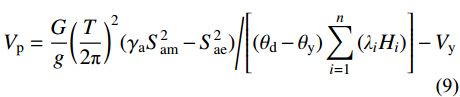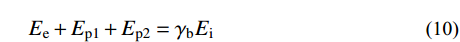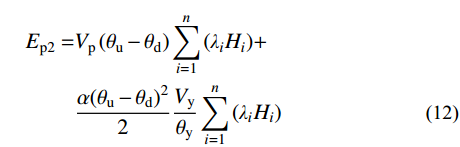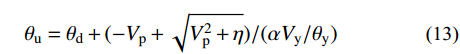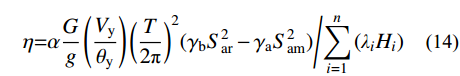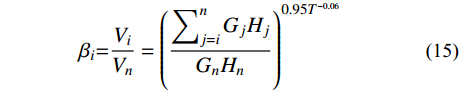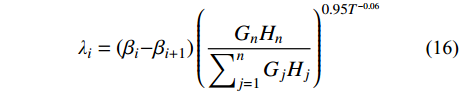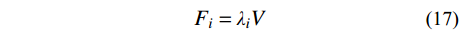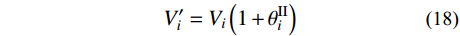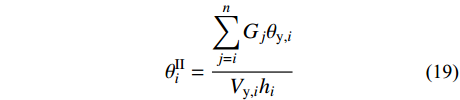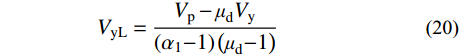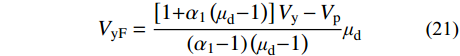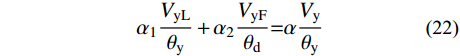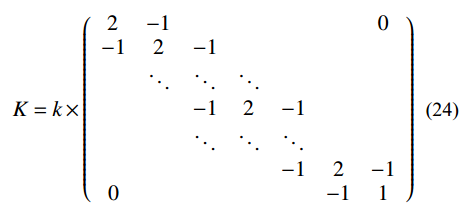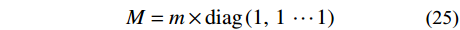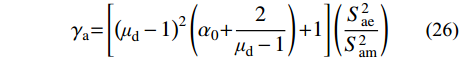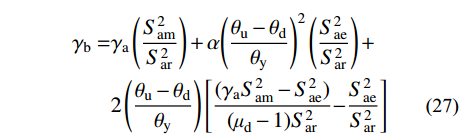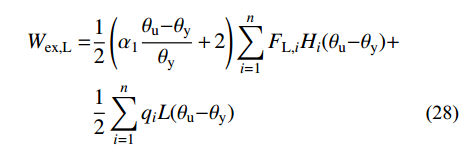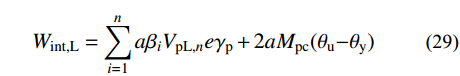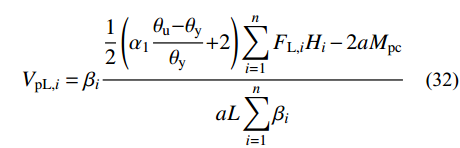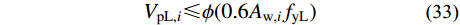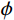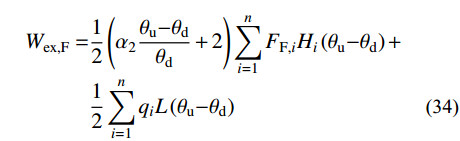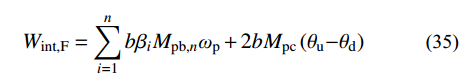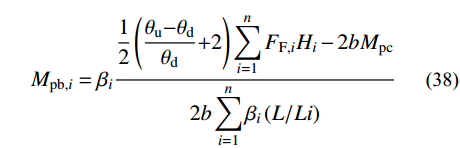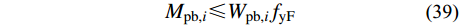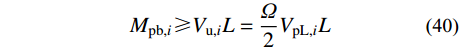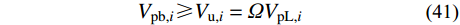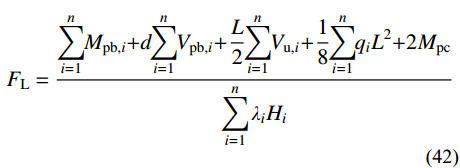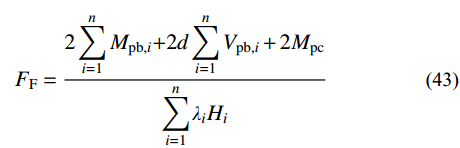PERFORMANCE-BASED PLASTIC DESIGN METHOD FOR HIGH STRENGTH STEEL FRAMED-TUBES WITH END-PLATE CONNECTED SHEAR LINKS
-
摘要: 含端板螺栓连接耗能梁段的高强钢框筒结构(SFTSs)可以有效改善传统钢框筒结构的抗震性能,且可实现震后功能可快速恢复,是一种新型的高层可恢复功能结构。由于现行规范的抗震设计方法无法准确预测和控制结构的弹塑性性能,可能会使结构损伤集中于个别楼层出现薄弱层。为了设计具有理想失效模式的SFTSs,建立该结构体系“小震不坏,中震及大震可修,巨震不倒”的四水准抗震设防性能指标。考虑不同地震水准作用下的性能目标,采用三线型的能力曲线对传统的基于能量平衡的塑性设计方法进行改进,且考虑结构高阶振型和屈服后刚度的影响,提出了SFTSs基于性能的塑性设计方法。采用建议的设计方法设计了一个30层的结构算例,并基于OpenSees对结构算例进行弹塑性时程分析。结果表明:采用提出的设计方法设计的结构算例能够实现结构预期的失效模式以及不同地震水准作用下的性能目标,结构具有良好的抗震性能,验证了所提出的基于性能的塑性设计方法的有效性,可以为SFTSs的工程设计提供参考。Abstract: High-strength steel framed-tube structures with end-plate connected shear links (SFTSs) is an innovative high-rise earthquake-resilient structural system. It improves the seismic performance of conventional steel framed-tube structures and achieves rapid post-earthquake repairability. Since the traditional seismic design method based on the current code cannot accurately predict and control the inelastic performance of the structure, the damage of the structure may be concentrated on individual floors, thus forming a weak layer. To design a structure with an ideal failure mode, we propose a specific four-level seismic fortification objective for SFTSs, which requires no damage under frequent earthquakes, replaceable under the design and rare earthquakes, and collapse prevention under very rare earthquakes. A trilinear capacity curve considering multiple performance objectives under different seismic levels was adopted in the proposed performance-based plastic design method of SFTSs. The effects of higher mode shapes and post-yield stiffness were also considered. A 30-story SFTS model was designed according to the proposed method. Nonlinear time history analyses of the model were performed under 20 selected ground motions using OpenSees. The results demonstrate that the model designed with the proposed design method exhibited the intended failure mode and achieved the performance objectives under the different seismic levels, indicating excellent seismic performance of the model. The effectiveness of the proposed performance-based plastic design method of SFTSs was verified, which can be applied to the practical engineering design of SFTSs.
-
Keywords:
- steel framed-tube /
- shear link /
- plastic design /
- performance objective /
- failure mode /
- seismic performance
-
随着社会经济的发展和科技水平的进步,结构抗震设防目标由传统的“小震不坏、中震可修、大震不倒”三水准抗震设防目标向震后结构功能可快速恢复转变[1-2]。实现结构震后功能可恢复成为地震工程的研究热点和前沿,即要求结构具有主体构件损伤小、残余变形小且损伤构件可更换的特点[3-4]。
鉴于传统钢框筒结构抗震性能较差且震后不易修复的问题,连鸣和苏明周等[5-6]提出了含端板螺栓连接耗能梁段的高强钢框筒结构(High-strength steel frame tube structures with end plate-connected shear links,SFTSs),即在裙梁跨中位置合理布置一定数量的剪切型耗能梁段,耗能梁段采用屈服强度较低且变形能力较好的钢材,其余构件(裙梁及框筒柱等)采用高强度钢材,耗能梁段与裙梁采用易于拆卸的端板螺栓连接。为了研究SFTSs的抗震性能和可更换能力,笔者研究团队[7-8]对SFTSs子结构进行了两阶段的循环加载试验研究,且对不同耗能梁段布置方式的SFTSs进行了弹塑性时程分析[9],研究结果表明大震下SFTSs主要通过耗能梁段发生塑性变形耗散地震能量,其余构件保持弹性或者部分发展塑性,且可以实现耗能梁段的更换,大震下结构最大残余层间侧移角远小于0.5%,符合功能可恢复结构的要求。
随着结构抗震设计理论研究的不断发展,国内外研究学者建议了多种抗侧力结构体系基于性能的设计方法。周颖等[3-4]针对自复位剪力墙结构整体变形能力强及残余变形小的特点,提出了自复位剪力墙结构四水准抗震设防目标下基于位移的抗震设计方法。Goel等[10]基于预选的失效模式和能量平衡方程发展了基于性能的塑性设计方法(Performance-based plastic design,PBPD),该方法被很多学者用于钢板剪力墙结构[11]、偏心支撑钢框架结构[12]、防屈曲支撑-钢筋混凝土框架结构[13]以及基于剪切耗能机制的斜交网格结构[14]等不同结构体系中。由于传统的PBPD假设结构的能力曲线为双线型,无法合理反映含保险丝结构的多性能水平,故Yang等[15]考虑结构在不同地震水准作用下的性能目标,提出了等效能量塑性设计法(Equivalent energy design procedure,EEDP),并将其用于含保险丝的功能可恢复结构中。Shoeibi等[16]将含保险丝的功能可恢复结构分为耗能体系和非耗能体系,并将其能力曲线等效为双折线,采用PBPD进行设计。Zhai等[17]考虑结构高阶振型和屈服后刚度的影响,提出了改进的PBPD,并将其应用于含耗能跨的双重钢框架结构体系中,研究结果表明改进的PBPD可以较好地应用于含耗能保险丝的结构体系,从而实现结构在不同地震水准作用下的性能目标。
然而,目前大部分国家现行的抗震设计规范采用基于强度的抗震设计方法(Force-based seismic design,FBSD)[18-19],通过弹性理论计算结构的地震反应,并对结构在弹塑性阶段的变形进行验算,不能合理反映结构的倒塌失效机制和极限状态。采用FBSD不能准确预测和控制结构的弹塑性性能,可能导致结构无法实现理想的失效模式,损伤集中于个别楼层,从而出现薄弱层,不能保证结构性能的充分发挥。为了较好地对可恢复功能结构进行设计,需考虑不同地震水准作用下结构的性能目标。SFTSs作为一种新型的高层可恢复功能结构,需要提出高于传统抗震结构的抗震性能目标,并提出其基于性能的设计方法,考虑结构在不同地震水准作用下的性能目标,保障结构具有可控的失效机制。
由于可恢复功能结构体系具有比传统抗震结构更高的抗震性能,周颖等[3-4]结合我国第五代《中国地震动区划图》[20]和《建筑隔震设计标准》(征求意见稿)[21]提出了具有更高抗震性能的四水准抗震设防目标,可以为可恢复功能结构的设计提供参考。故本文结合SFTSs的变形特征和失效机制,提出了“小震不坏,中震及大震可修,巨震不倒”的四水准抗震设防性能指标;考虑结构高阶振型和屈服后刚度的影响,对传统的PBPD进行改进,提出了适用于SFTSs基于性能的塑性设计方法;采用建议的设计方法设计了一个30层的算例,并建立了该算例的OpenSees数值模型,选取20条地震波对其进行不同地震水准作用下的弹塑性时程分析,对本文建议的基于性能的塑性设计方法的有效性进行验证。
1 SFTSs的耗能机制及四水准抗震设防性能指标
1.1 SFTSs的耗能机制
传统钢框筒结构是由外围密柱深梁、楼板与内部少量柱形成的筒体结构,该结构具有抗侧刚度大、抗扭性能好及建筑布置灵活等优点,是一种性能优良的抗侧力结构体系[22]。需要注意的是,本文研究的钢框筒结构为外筒单筒结构,水平荷载全部由外围的密柱深梁承担,内部少量柱为承重构件,不参与结构抗侧工作。但是由于外围框架柱距较小,使得裙梁跨高比较小,限制了梁端塑性铰的发展,一旦结构遭遇较大的地震作用,抗侧力结构构件可能损伤严重,不易于实现结构功能的震后可快速恢复。考虑到裙梁跨高比较小,沿裙梁跨度的剪力需求较大,裙梁跨中的弯矩需求较小,在传统钢框筒结构的裙梁跨中位置合理设置可更换的剪切型耗能梁段作为损伤元,对结构的弹性刚度影响较小。布置耗能梁段的裙梁通过耗能梁段发生剪切变形耗能代替裙梁端部形成塑性铰耗能,改变了传统钢框筒结构的耗能机制。图1给出了SFTSs的结构平面布置图、结构立面布置图以及耗能梁段与裙梁采用的端板螺栓连接示意图,其中耗能梁段的布置位置和布置数量对结构性能影响较大,本文采用图1所示的耗能梁段布置方式,该布置方式的合理性在文献[9]中进行了详细的分析论证。
1.2 SFTSs的四水准抗震设防性能指标
对于设计合理的SFTSs,在水平荷载作用下,整体结构理想的失效模式为首先耗能梁段发生剪切变形进入塑性,且耗能梁段进一步发展塑性行为形成剪切铰耗散地震能量,随着荷载作用的增强,不含耗能梁段跨(以下简称“Frame跨”)的裙梁端部屈服形成弯曲塑性铰继续耗散地震能量,最终直至结构柱底形成塑性铰失效,结构的能力曲线表现为明显的三线型,如图2所示。其中耗能梁段作为第一阶段的主要耗能构件,Frame跨的裙梁在第二阶段参与耗能,可以有效防止结构在极罕遇地震作用下发生倒塌。
由于可恢复功能结构体系具有比传统抗震结构更高的抗震性能,传统的三水准抗震设防目标无法体现可恢复功能的优越性,本文结合SFTSs的变形特征和失效机制,提出SFTSs“小震不坏,中震及大震可修,巨震不倒”的四水准抗震设防目标。多遇地震(第一水准,即小震)作用下,所有结构构件均保持弹性状态;设计地震(第二水准,即中震)作用下,部分耗能梁段开始进入塑性;罕遇地震(第三水准,即大震)作用下,所有耗能梁段均进入塑性充分耗能;极罕遇地震(第四水准,即巨震)作用下,Frame跨的裙梁端部开始屈服。设计地震和罕遇地震作用下,耗能梁段不断发展塑性,可以通过更换损伤严重的耗能梁段实现结构功能的可快速恢复。其中采用的四水准地震动参考第五代《中国地震动区划图》[20]和《建筑隔震设计标准》(征求意见稿)[21]进行取值,表1列出了四水准地震动水平影响系数最大值αmax。
表 1 四水准地震动水平影响系数最大值αmaxTable 1. Maximum values of horizontal seismic influence coefficients for four-level ground motion抗震性能水准分级 6度 7度 8度 9度 多遇地震 0.04 0.08(0.12) 0.16(0.24) 0.32 设计地震 0.12 0.23(0.34) 0.45(0.68) 0.90 罕遇地震 0.28 0.50(0.72) 0.90(1.20) 1.40 极罕遇地震 0.36 0.70(1.00) 1.35(2.00) 2.70 注:括号中数值分别为设计基本地震加速度为0.15 g和0.30 g的地区。 为了实现SFTSs的性能化设计,采用层间侧移角和残余层间侧移角对SFTSs进行性能指标的量化,如表2所示,可用于结构的抗震性能及可能换能力评估。表中分别给出了传统三水准和建议的四水准抗震设防性能指标,建议的四水准抗震设防目标要高于传统的三水准设防目标。其中层间侧移角的指标量化参考《建筑抗震设计规范》[18]和笔者研究团队[23-24]对SFTSs的弹塑性时程分析结果,残余层间侧移角的量化参考SEAOC[25]对不同性能等级的层间残余侧移角限值的规定。
表 2 性能指标量化Table 2. Quantification of performance indexes性能指标 水准分级 多遇地震 设计地震 罕遇地震 极罕遇地震 层间侧移角 三水准 1/250 − 1/50 四水准 1/300 1/150 1/75 1/50 残余层间侧移角 三水准 − − − 四水准 − 0.3% 0.5% 0.75% 2 基于性能的塑性设计方法
2.1 性能目标及设计基底剪力
传统的PBPD[10]采用预先确定的目标位移和屈服机制来控制结构的弹塑性变形,将结构的能力曲线等效为双线型,根据能量平衡原理即将结构单向推覆至目标位移所需的外力功等于理想弹塑性单自由度体系达到相同状态所需的能量确定结构的设计基底剪力,如图3(a)所示。
类似于传统的PBPD,本文建议的基于性能的塑性设计方法基于能量平衡原理,假定地震输入能Ei可以通过弹性多自由度体系吸收的能量进行估计,结构实际耗散的能量通过对结构输入能进行修正得到。图3(b)为本文采用的能量平衡概念,假定结构能力曲线为三线型,可以较好地反映结构的多性能目标,横坐标为结构顶点侧移角,纵坐标为结构基底剪力。下面分别对不同性能目标下结构能量平衡关系进行分析,计算结构的屈服基底剪力Vy、塑性设计基底剪力Vp和极限顶点侧移角θu。
2.1.1 屈服基底剪力
多遇地震作用下,即结构处于OA阶段,所有结构构件均保持弹性状态,结构能量平衡关系表示为式(1),即地震输入能Ei等于结构的弹性振动Ee,根据Housner[26]和Akiyama[27]的研究,其可分别表示为式(2)和式(3),联立可得结构的屈服基底剪力Vy如式(4)所示。
Ee=Ei (1) Ei=G2g(SaeT2π) (2) Ee=12n∑i=1(λiVy)(Hiθy) (3) Vy=Gg(SaeT2π)2/[θyn∑i=1(λiHi)] (4) 式中:G为结构重力荷载代表值;T为结构基本周期;g为重力加速度;Sae为多遇地震作用下结构的谱加速度(=αg);n为结构总层数;λi为结构第i层的侧向力分布系数,可根据结构侧向力分布模式得到;Hi为结构第i层距地面的高度;θy为结构屈服顶点侧移角,由设计人员根据性能目标预选。
2.1.2 塑性设计基底剪力
罕遇地震作用下,即结构处于OAB阶段,耗能梁段充分发展塑性,结构能量平衡关系表示为式(5),其中地震输入能Ei和结构的弹性振动Ee表示为式(6)和式(7),结构实际耗散的能量可以表示为γaEi,γa为罕遇地震作用下的能量修正系数,将在2.4节进行介绍。Ep1为能力曲线AB段包围的面积,可根据虚功原理得到,如式(8)所示。需要注意的是,SFTSs在循环荷载作用下的滞回曲线非常饱满[7],无任何捏缩现象,根据文献[13, 16]可知,此处无需对结构的滞回耗能Ep1进行修正。联立可得结构的塑性设计基底剪力Vp,如式(9)所示。
Ee+Ep1=γaEi (5) Ei=G2g(SamT2π)2 (6) Ee=G2g(SaeT2π)2 (7) Ep1=12(θd−θy)(Vy+Vp)n∑i=1(λiHi) (8) Vp=Gg(T2π)2(γaS2am−S2ae)/[(θd−θy)n∑i=1(λiHi)]−Vy (9) 式中:Sam为罕遇地震作用下结构的谱加速度;θd为结构在罕遇地震作用下的顶点侧移角,由设计人员根据性能目标预选。
2.1.3 极限顶点侧移角
极罕遇地震作用下,即结构处于OABC阶段,耗能梁段充分发展塑性,且Frame跨裙梁端部也进入塑性,结构能量平衡关系表示为式(10),其中地震输入能Ei和结构的弹性振动Ee表示为式(11)和式(7),结构实际耗散的能量可以表示为γbEi,γb为极罕遇地震作用下的能量修正系数,将在2.4节进行介绍。Ep2为能力曲线BC段包围的面积,可根据虚功原理得到,如式(12)所示,故可得到结构的极限顶点侧移角θu,如式(13)所示。
Ee+Ep1+Ep2=γbEi (10) Ei=G2g(SarT2π)2 (11) Ep2=Vp(θu−θd)n∑i=1(λiHi)+α(θu−θd)22Vyθyn∑i=1(λiHi) (12) θu=θd+(−Vp+√V2p+η)/(αVy/θy) (13) η=αGg(Vyθy)(T2π)2(γbS2ar−γaS2am)/n∑i=1(λiHi) (14) 式中:Sar为极罕遇地震作用下结构的谱加速度;α为结构的屈服后刚度,即能力曲线BC段斜率。
2.2 侧向力分布
目前我国规范采用的侧向力分布模式基于多自由度体系的弹性基本振型响应,罕遇地震作用下,规范建议的侧向力分布模式不能反映弹塑性阶段结构由于弹塑性变形引起的内力重分布,且也不能合理的反映结构高阶振型的影响。张浩等[28]通过对设计合理的SFTS结构算例进行弹塑性时程分析,建议了结构弹塑性状态的侧向力分布模式,能够较为准确的估计结构在弹塑性状态的层剪力分布,且能够考虑结构高阶振型的影响。定义结构第i层的层剪力分布系数βi为第i层的层剪力Vi与顶层层剪力Vn的比值,即可得到结构的侧向力系数λi,如下所示:
βi=ViVn=(∑nj=iGjHjGnHn)0.95T−0.06 (15) λi=(βi−βi+1)(GnHn∑nj=1GjHj)0.95T−0.06 (16) 故可得到结构第i层侧向力Fi为:
Fi=λiV (17) 式中,V为设计基底剪力。
考虑到SFTSs用于高层结构中,故需考虑P-Δ效应对结构的影响,参考《钢结构设计标准》[29]按下式对得到的各楼层剪力和层剪力分布系数进行修正:
V′i=Vi(1+θIIi) (18) θIIi=n∑j=iGjθy,iVy,ihi (19) 式中,hi为结构第i层高度。
2.3 设计基底剪力的分配
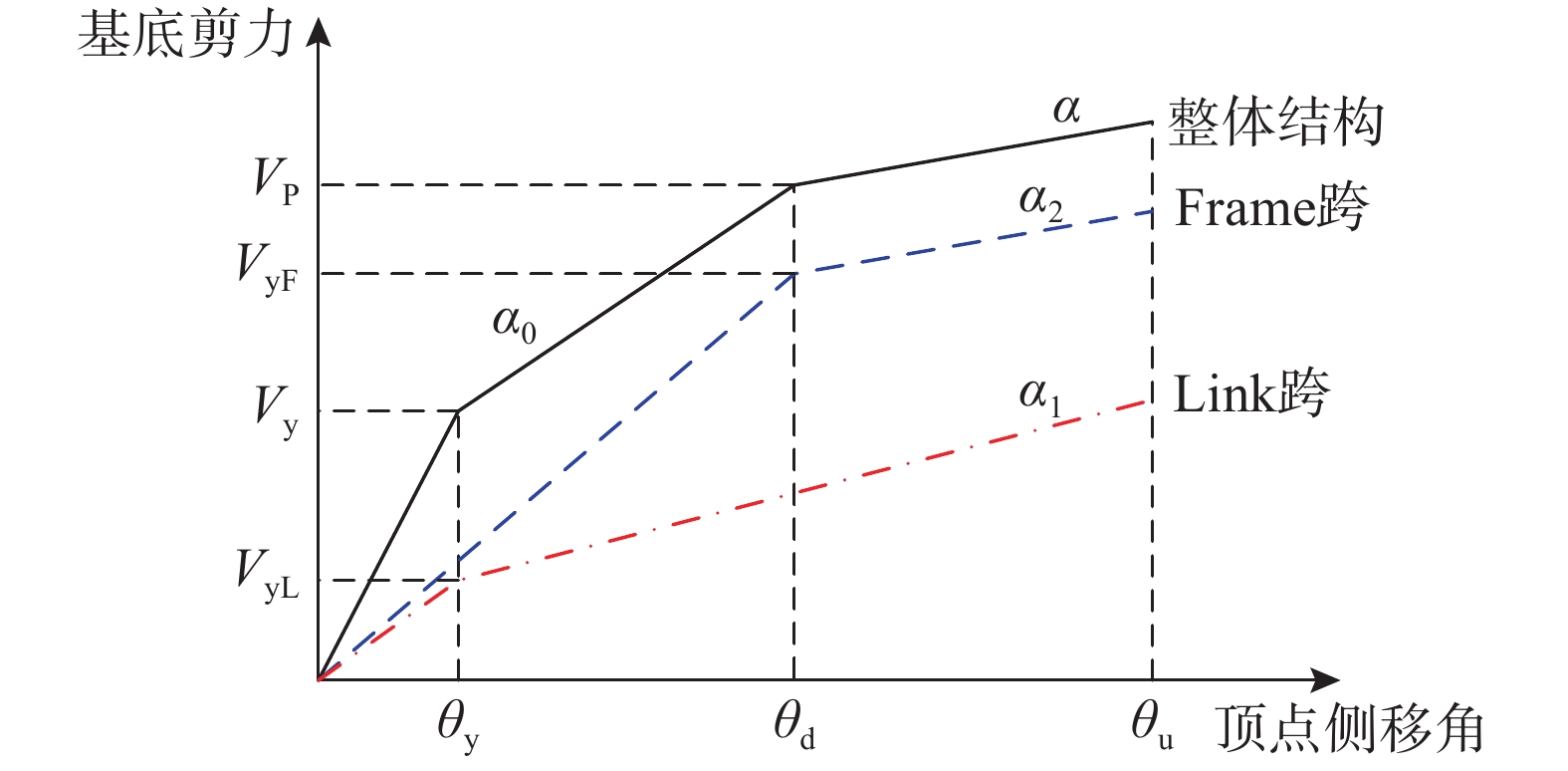
得到结构的屈服基底剪力Vy和塑性设计基底剪力Vp后,需要将其分配到含耗能梁段跨(以下简称“Link跨”)和Frame跨,进行结构构件的设计。图4为结构总基底剪力、Link跨和Frame跨的基底剪力-顶点侧移角之间的关系,根据整体结构A点和B点的基底剪力均等于Link跨和Frame跨的基底剪力之和,可以得到Link跨和Frame跨的设计基底剪力VyL和VyF,如式(20)和式(21)所示:
VyL=Vp−μdVy(α1−1)(μd−1) (20) VyF=[1+α1(μd−1)]Vy−Vp(α1−1)(μd−1)μd (21) 式中:μd为结构延性系数,可表示为μd=θd/θy;α1为Link跨结构的屈服后刚度,根据SFTSs子结构拟静力试验骨架曲线可得,α1可取0.2。然后可以根据式(22)得到结构整体的屈服后刚度α。
α1VyLθy+α2VyFθd=αVyθy (22) 式中,α2为Frame跨结构的屈服后刚度,由文献[5]中分别对不含耗能梁段和含耗能梁段的钢框筒子结构有限元分析骨架曲线可知,α2可取0.2。
2.4 能量修正系数
由传统PBPD可得,结构设计基底剪力与能量修正系数取值密切相关。Yang等[15]通过对大量单自由度体系进行时程分析建议了能量修正系数与结构周期T的关系,Li等[30]通过引入高阶振型能量修正系数对其进行修正,并将其用于高层斜交网格结构的EEDP设计中。Zhai等[17]考虑高阶振型和屈服后刚度的影响,通过对多自由度体系进行时程分析得到了结构周期T为1.0 s和2.0 s时,不同性能目标下结构的能量修正系数。本文参考Li等[30]和Zhai等[17]的方法,分别计算罕遇地震和极罕遇地震作用下的能量修正系数γa和γb。
能量修正系数γa将弹性和弹塑性多自由度体系在多遇地震和罕遇地震之间的能量联系在一起,能量修正系数γb将弹性和弹塑性多自由度体系在多遇地震和极罕遇地震之间的能量联系在一起。按照《建筑抗震设计规范》[18]的规定选取20条地震波对多自由度体系进行时程分析。
建立多自由度集中质量模型,假定楼层集中质量m和刚度k沿结构高度均匀分布且各层相同,根据式(23)~式(25)即可得到结构层刚度k。
|K−(2π/T)2M|=0 (23) K=k×(2−10−12−1⋱⋱⋱−12−1⋱⋱⋱−12−10−11) (24) M=m×diag(1,1⋯1) (25) 式中,K和M分别为多自由度集中质量模型的刚度矩阵和质量矩阵。
能量修正系数的计算流程如下:
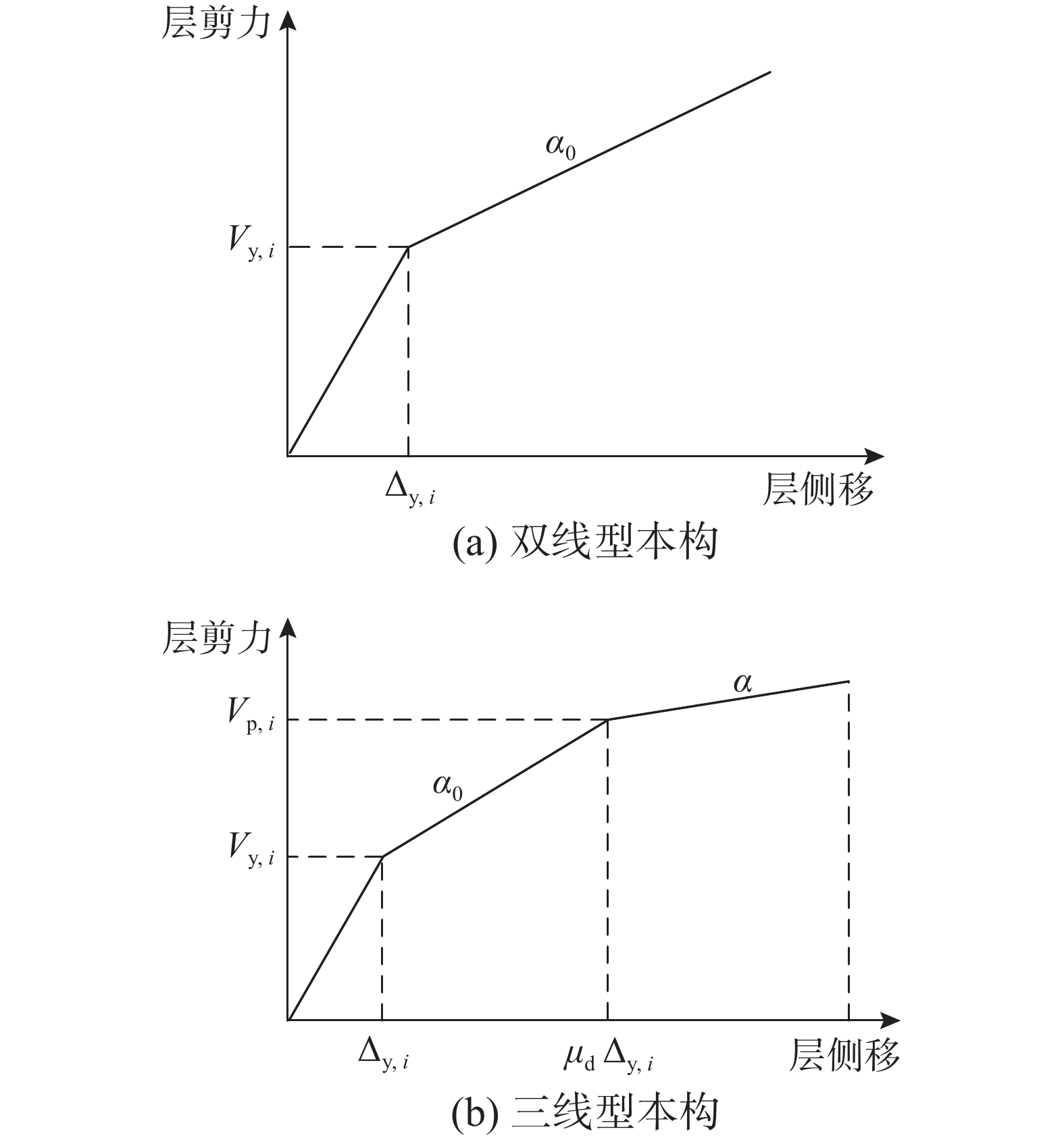
1) 将所有地震波调幅至多遇地震作用对应的加速度峰值,对多自由度弹性集中质量模型进行弹性时程分析,得到结构第i层的屈服层剪力Vy,i和屈服层间侧移Δy,i以及结构顶点侧移角θy;
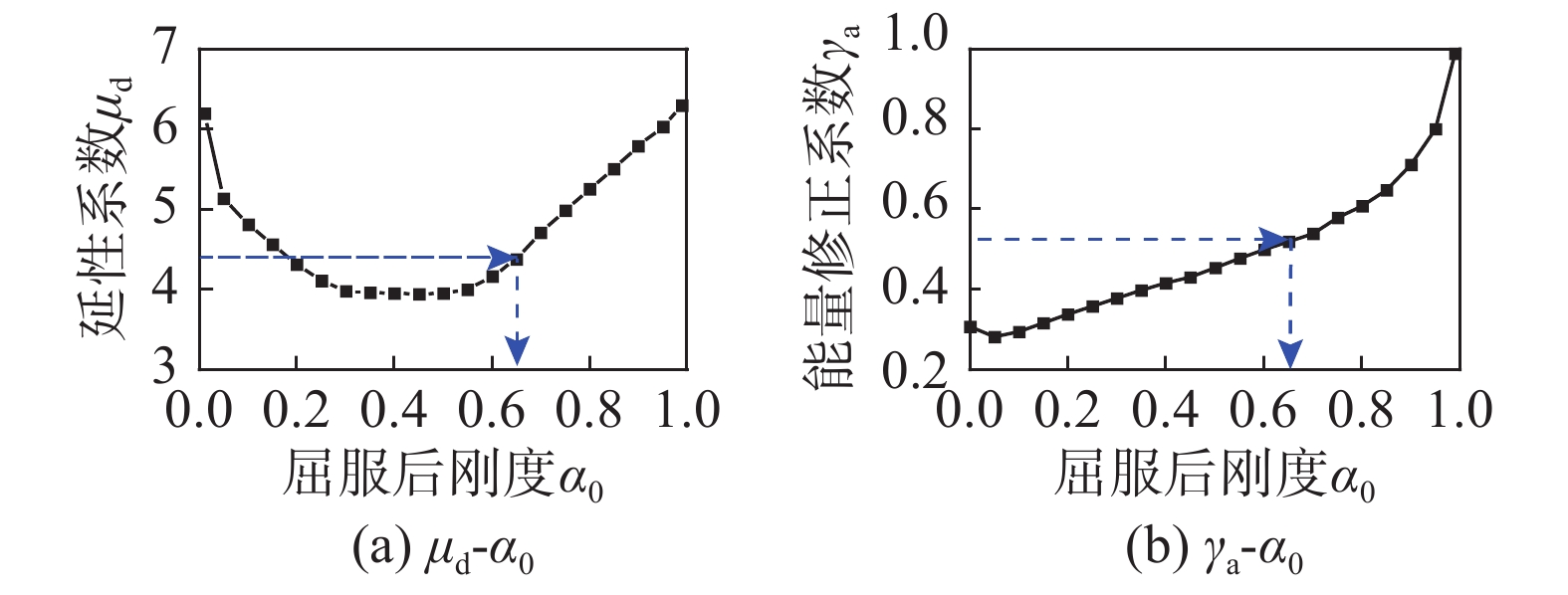
2) 根据1)的分析结果指定结构各楼层剪力-侧移关系为如图5(a)所示的双线型本构,将所有地震波调幅至罕遇地震对应的加速度峰值,对多自由度非线性集中质量模型进行非线性时程分析,得到结构顶点侧移角θd,根据式(26)即可得到能量修正系数γa,在0~1之间变化α0,即可得到α0、μd和γa之间的关系,取20条地震波时程分析的平均值;
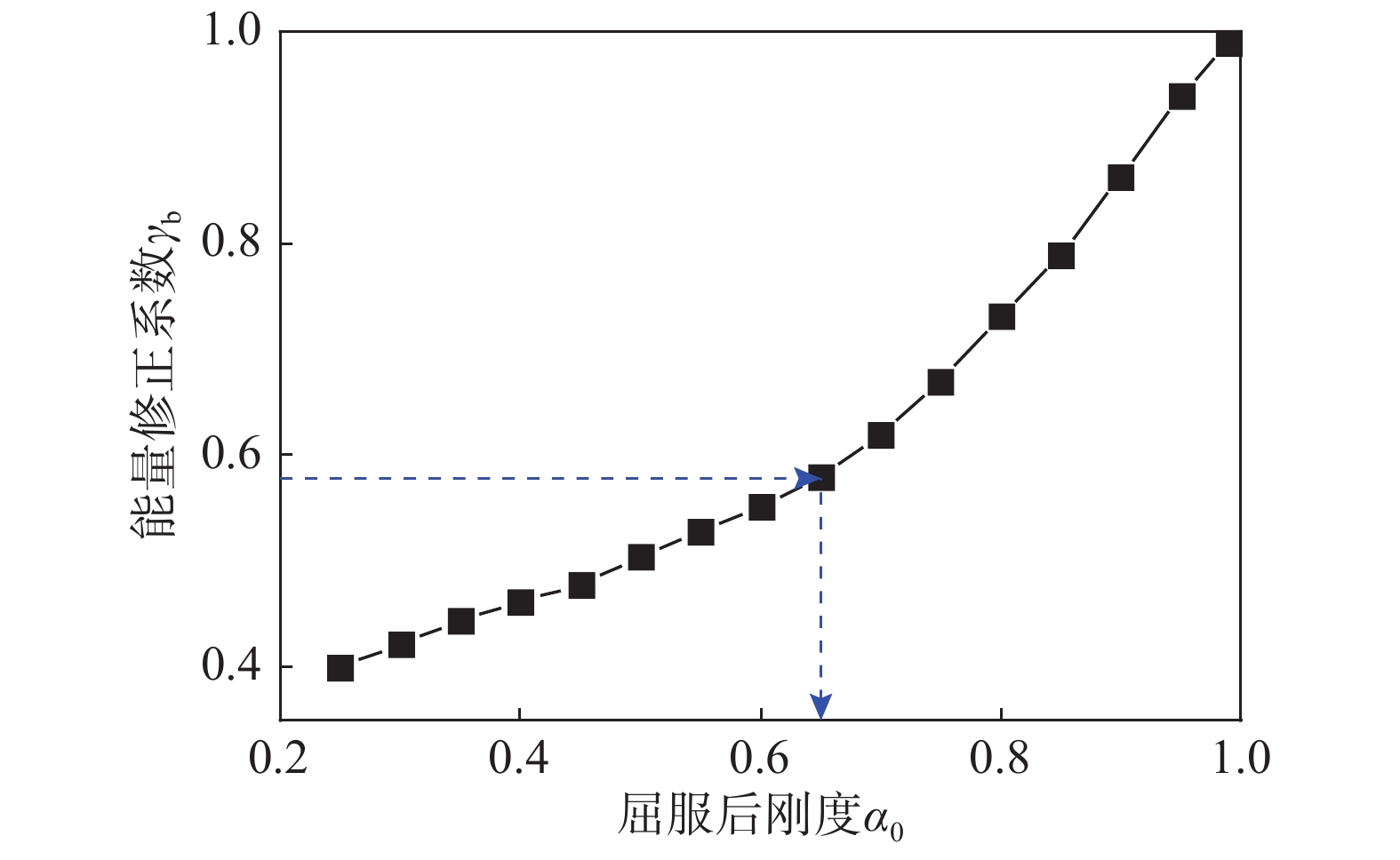
γa=[(μd−1)2(α0+2μd−1)+1](S2aeS2am) (26) 3) 根据1)和2)的分析结果指定结构楼层剪力-侧移为如图5(b)所示的三线型本构,将所有地震波调幅至极罕遇地震作用对应的加速度峰值,对多自由度非线性集中质量模型进行非线性时程分析,得到结构顶点侧移角θu,根据式(27)即可得到能量修正系数γb,从而得到α0与γb之间的关系,取20条地震波时程分析的平均值:
γb=γa(S2amS2ar)+α(θu−θdθy)2(S2aeS2ar)+2(θu−θdθy)[(γaS2am−S2ae)(μd−1)S2ar−S2aeS2ar] (27) 时程分析采用Rayleigh阻尼,阻尼比取0.05。图6和图7给出了第4节算例的能量修正系数γa和γb的计算结果,即T为3.5 s(n=30),α取0.2。
2.5 耗能构件的设计
2.5.1 耗能梁段的设计
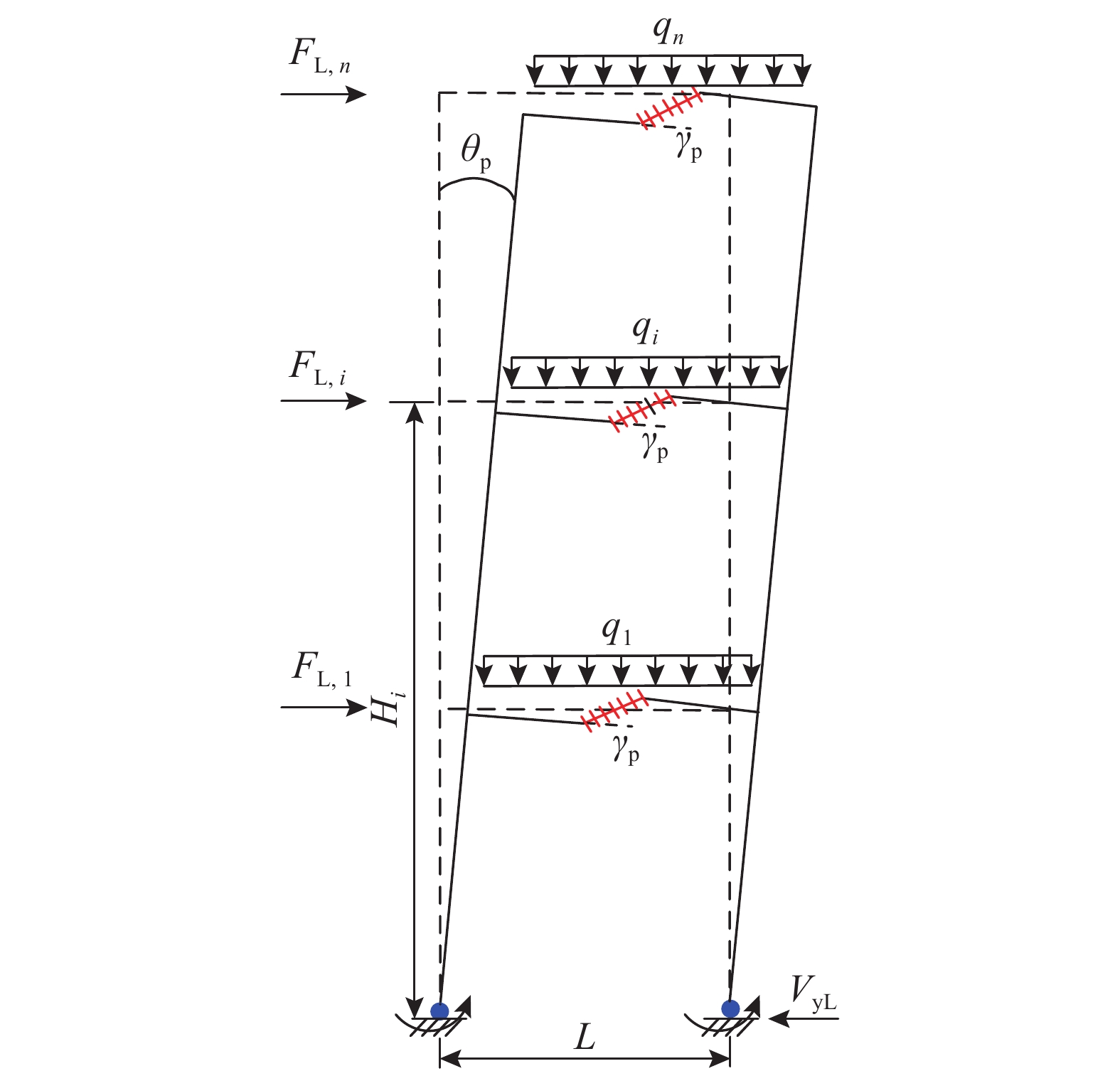
耗能构件主要包括Link跨的耗能梁段和Frame跨的裙梁。Link跨的理想失效模式如图8所示,假定Link跨层剪力服从层剪力分布规律,根据虚功原理可得第i层耗能梁段的塑性承载力需求VpL,i,计算如下所示:
Wex,L=12(α1θu−θyθy+2)n∑i=1FL,iHi(θu−θy)+12n∑i=1qiL(θu−θy) (28) Wint,L=n∑i=1aβiVpL,neγp+2aMpc(θu−θy) (29) FL,i=λiVyL (30) γp=(θu−θy)L/e (31) VpL,i=βi12(α1θu−θyθy+2)n∑i=1FL,iHi−2aMpcaLn∑i=1βi (32) 式中:Wex,L和Wint,L分别为Link跨的外力功和内力功,由于结构在水平荷载作用下发生反对称变形,故竖向荷载做功为零;FL,i为Link跨每层的层侧向力;e为耗能梁段长度;L为Link跨跨度;Mpc为底层柱的塑性受弯承载力;a为Link跨的跨数。
得到第i层耗能梁段的塑性承载力需求后,即可按照式(33)对耗能梁段进行塑性设计。
VpL,i⩽ (33) 式中:
\phi 为系数,取0.9;Aw,i为第i层耗能梁段腹板面积需求;fyL为耗能梁段钢材屈服强度。2.5.2 Frame跨裙梁的设计
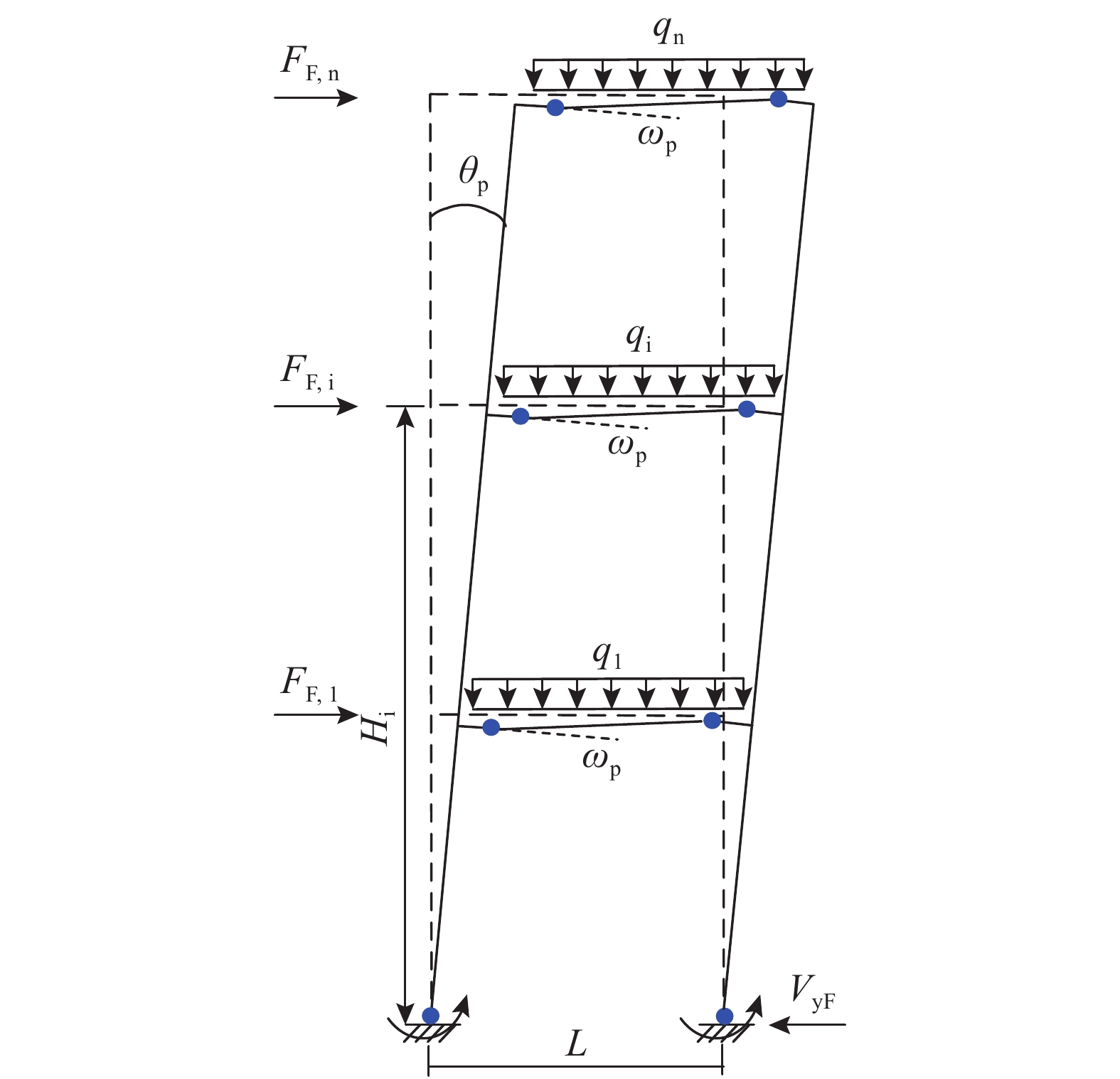
Frame跨的理想失效模式如图9所示,假定Frame跨层剪力服从层剪力分布规律,根据虚功原理可得第i层裙梁截面的塑性受弯承载力需求Mpb,i,计算如下所示:
\begin{split} {W_{{\rm{ex,F}}}} = & \frac{1}{2}\left( {{\alpha _2}\frac{{{\theta _{\rm{u}}}{\rm{ - }}{\theta _{\rm{d}}}}}{{{\theta _{\rm{d}}}}} + 2} \right)\sum\limits_{i = 1}^n {{F_{{\rm{F,}}i}}} {H_i}\left( {{\theta _{\rm{u}}}{\rm{ - }}{\theta _{\rm{d}}}} \right){\rm{ + }}\\[-3pt]&\frac{1}{2}\sum\limits_{i = 1}^n {{q_i}L\left( {{\theta _{\rm{u}}}{\rm{ - }}{\theta _{\rm{d}}}} \right)} \end{split} (34) {W_{{\rm{int,F}}}} = \sum\limits_{i = 1}^n {b{\beta _i}} {M_{{\rm{pb,}}n}}{\omega _{\rm{p}}} + 2b{M_{{\rm{pc}}}}\left( {{\theta _{\rm{u}}}{\rm{ - }}{\theta _{\rm{d}}}} \right)\qquad (35) {F_{{\rm{F,}}i}} = {\lambda _i}{V_{{\rm{yF}}}}\qquad\qquad\qquad\qquad\qquad\qquad\qquad (36) {\omega _{\rm{p}}} = {{\left( {{\theta _{\rm{u}}}{\rm{ - }}{\theta _{\rm{d}}}} \right)}/ {\left( {{L /{{L_i}}}} \right)}}\qquad\qquad\qquad\qquad\qquad (37) {M_{{\rm{pb,}}i}} = {\beta _i}\dfrac{{\dfrac{1}{2}\left( {\dfrac{{{\theta _{\rm{u}}}{\rm{ - }}{\theta _{\rm{d}}}}}{{{\theta _{\rm{d}}}}}{\rm{ + }}2} \right)\displaystyle\sum\limits_{i = 1}^n {{F_{{\rm{F,}}i}}{H_i} - 2b{M_{{\rm{pc}}}}} }}{{2b\displaystyle\sum\limits_{i = 1}^n {{\beta _i}\left( {L/Li} \right)} }} (38) 式中:Wex,F和Wint,F分别为Frame跨的外力功和内力功;FF,i为Frame跨每层的层侧向力;ωp为裙梁塑性转角,可由层间侧移角得到,如式(37)所示,其中Li为裙梁端部塑性铰之间的距离,取0.9L[12],L为Frame跨跨度;b为Frame跨的跨数。
得到第i层裙梁截面的塑性受弯承载力需求Mpb,i后,即可按照式(39)对裙梁进行塑性设计。
{M_{{\rm{pb,}}i}} \leqslant {W_{{\rm{pb,}}i}}{f_{{\rm{yF}}}} (39) 式中:Wpb,i为第i层裙梁的塑性截面模量;fyF为裙梁钢材屈服强度。
2.6 非耗能构件的设计
2.6.1 Link跨裙梁的设计
为了保证Link跨主要通过跨中设置的剪切型耗能梁段屈服耗散地震能量,其两端的裙梁不屈服,按照能力设计法对Link跨裙梁进行设计,计算如下:
{M_{{\rm{pb,}}i}} \geqslant {V_{{\rm{u,}}i}}L = \frac{\varOmega }{2}{V_{{\rm{pL,}}i}}L (40) {V_{{\rm{pb,}}i}} \geqslant {V_{{\rm{u,}}i}} = \varOmega {V_{{\rm{pL,}}i}}\quad (41) 式中:Mpb,i和Vpb,i分别为裙梁的塑性抗弯承载力和塑性抗剪承载力;Ω为耗能梁段的超强系数,取1.5[31]。
2.6.2 中柱的设计
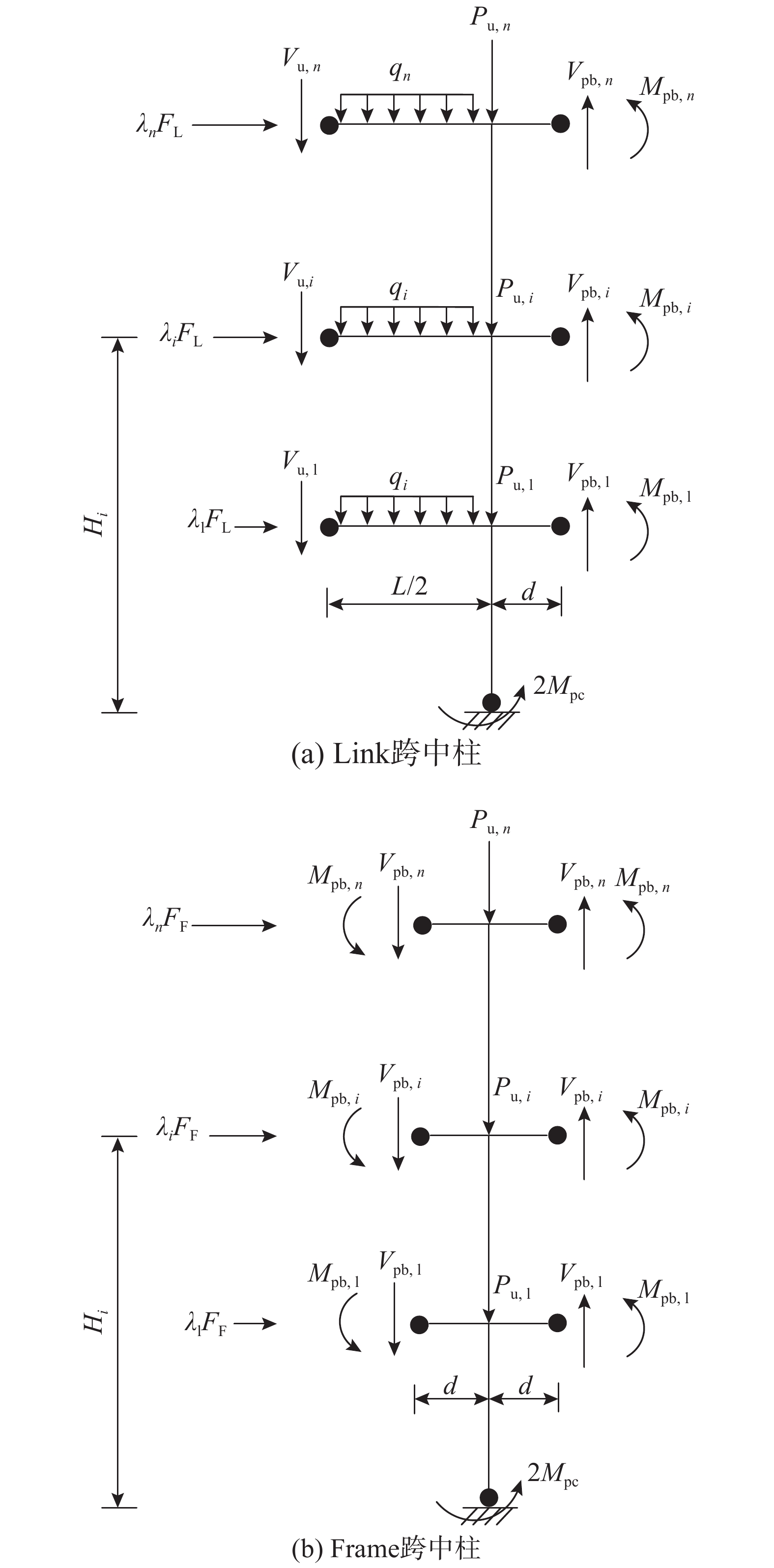
根据理想屈服机制,结构达到极限状态时,柱必须能抵抗设计重力荷载和最大指定屈服构件预期强度的组合,同时考虑钢材的应变硬化和超强,Link跨各层耗能梁段均达到极限抗剪承载力Vu,i,Frame跨裙梁端部形成塑性铰,对应的塑性弯矩和剪力分别为Mpb,i和Vpb,i,底层柱脚形成塑性铰,对应的塑性弯矩为2Mpc,可以得到中柱隔离体如图10所示,图10(a)为Link跨中柱隔离体,图10(b)为Frame跨中柱隔离体,图中d为裙梁端部塑性铰至框架柱中心的距离,可取0.05L。假定作用在隔离体上的侧向力Fi服从式(16)的分布,根据隔离体底层柱脚弯矩平衡,可以得到极限状态时图10(a)和图10(b)的需求平衡侧向力之和FL和FF分别为式(42)和式(43):
{F_{\rm{L}}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^n \!\!{{M_{{\rm{pb,}}i}}{\rm{ + }}} d\!\!\displaystyle\sum\limits_{i = 1}^n \!\!{{V_{{\rm{pb,}}i}} \!+\! \dfrac{L}{2}\!\!\displaystyle\sum\limits_{i = 1}^n \!\!{{V_{{\rm{u,}}i}} \!+\! \dfrac{1}{8}\!\!\displaystyle\sum\limits_{i = 1}^n\!\! {{q_i}{L^2}{\rm{ + 2}}{M_{{\rm{pc}}}}} } } }}{{\displaystyle\sum\limits_{i = 1}^n {{\lambda _i}{H_i}} }} (42) {F_{\rm{F}}} = \frac{{2\displaystyle\sum\limits_{i = 1}^n {{M_{{\rm{pb,}}i}}{\rm{ + }}} 2d\displaystyle\sum\limits_{i = 1}^n {{V_{{\rm{pb,}}i}} + 2{M_{{\rm{pc}}}}} }}{{\displaystyle\sum\limits_{i = 1}^n {{\lambda _i}{H_i}} }}\qquad\qquad\; (43) 得到侧向力分布后,可先估计中柱截面尺寸,然后在结构设计软件中建立图10所示的隔离体,并施加如图所示的外荷载,根据现行规范验算柱截面。角柱、内框梁和内柱的设计可以参考文献[32]进行设计,此处不再赘述。
3 基于性能的塑性设计方法流程
采用本文建议的设计方法对SFTSs进行结构设计的具体流程如下:
1) 根据设计条件确定结构设计参数,包括楼层总数n、重力荷载代表值Gi、层高hi,预估结构基本周期T,指定Link跨和Frame跨的屈服后刚度α1和α2;
2) 按照建议的四水准抗震设防性能指标确定地震强度和性能目标,计算不同地震水准对应的谱加速度Sae、Sam和Sar,并预选结构的屈服顶点侧移角θy和罕遇地震作用下的顶点侧移角θd;
3) 计算结构延性系数μd,确定结构能量修正系数γa;
4) 计算层剪力分布系数βi和层侧向力分布系数λi,从而计算结构的屈服基底剪力Vy和塑性设计基底剪力Vp;
5) 考虑P-Δ效应对结构的影响,修正层剪力分布系数βi和层剪力;
6) 计算Link跨设计基底剪力VyL和Frame跨的设计基底剪力VyF;
7) 计算结构的屈服后刚度α,确定结构能量修正系数γb,验算结构极限顶点侧移角θu;
8) 根据Link跨和Frame跨的层侧向力对耗能构件进行塑性设计,然后对非耗能构件进行弹性设计,截面设计时需满足《建筑抗震设计规范》[18]和《钢结构设计标准》[29]对截面板件宽厚比的规定。
4 算例设计及有限元分析
采用上文所述方法设计一个30层的结构算例,并对其进行Pushover分析和非线性时程分析,验证本文建议的设计方法的有效性。
4.1 算例设计
算例层高均为3.3 m,结构平面和立面布置图见图1。抗震设防烈度为8度,设计地震基本加速度为0.2 g,设计地震分组为第一组,建筑场地类别为Ⅱ类,耗能梁段采用Q235钢,其余构件采用Q460钢。表3为算例的基本设计参数,表4为算例截面信息,其中耗能梁段长度均为600 mm,长度比e/(Mp/Vp)在1.03~1.15变化,保证耗能梁段为剪切型。
表 4 算例构件截面Table 4. Member sections of model/mm 层数 耗能梁段 Link跨裙梁 Frame跨裙梁 中柱 角柱 内柱 内框梁 29~30 H230×150×6×10 H370×160×10×14 H400×160×8×12 H460×280×16×20 □430×22 □250×20 H650×250×14×20 27-28 H230×180×10×14 H410×180×12×16 H420×200×10×14 H480×300×20×24 □460×26 □320×22 H650×250×14×20 24~26 H270×180×12×16 H440×220×16×20 H430×200×16×20 H530×320×22×26 □510×26 □360×24 H650×250×14×20 21~23 H290×200×14×18 H490×220×16×20 H480×220×16×20 H560×340×22×26 □525×28 □420×30 H650×250×14×20 18~20 H330×200×14×18 H530×220×16×22 H530×220×16×20 H590×340×24×28 □545×30 □470×34 H650×250×14×20 15~17 H325×200×16×20 H560×230×18×22 H565×220×16×20 H600×380×26×30 □560×34 □520×38 H650×250×14×20 12~14 H350×200×16×20 H600×230×18×22 H560×220×18×22 H600×400×28×32 □570×36 □560×42 H650×250×14×20 9~11 H365×200×16×20 H620×230×18×22 H580×220×18×22 H610×400×28×32 □570×38 □610×44 H650×250×14×20 6~8 H380×200×16×20 H630×230×18×22 H600×220×18×22 H660×400×30×34 □610×40 □660×46 H650×250×14×20 3~5 H385×200×16×20 H640×230×18×22 H610×220×18×22 H690×420×32×36 □640×40 □710×48 H650×250×14×20 1~2 H385×200×16×20 H640×230×18×22 H610×220×18×22 H690×420×32×36 □640×40 □730×50 H650×250×14×20 4.2 有限元模型的建立
采用有限元分析软件OpenSees建立算例有限元模型。裙梁和框筒柱采用非线性梁柱单元(Nonlinear BeamColumn element)模拟,该单元可以考虑结构件的几何非线性行为,且采用1个单元即可模拟单个梁、柱构件的力学行为[33]。采用纤维截面对裙梁和柱截面进行划分,如图11虚线框内所示,其中,y轴和z轴分别为截面的局部坐标轴。由于裙梁跨高比较小,通过截面组装命令考虑裙梁的剪切刚度。裙梁和柱均采用Steel01材料,强化比为0.01。耗能梁段采用两节点连接单元(TwoNodeLink element)进行模拟,该连接单元各自由度的力学行为由相应方向上的用户自定义弹簧属性进行表征。通过给各自由度弹簧指定符合其恢复力-变形关系的单轴材料本构模型,将各自由度弹簧的恢复力曲线控制参数转化为单轴材料对应的本构参数。考虑到耗能梁段主要发生腹板平面内的变形行为,故仅指定其平面内各自由度弹簧的恢复力-变形关系。其中剪切方向采用基于Giuffré-Menegotto-Pinto本构模型[34]的Steel02材料表征,其中Stee102材料和剪切弹簧参数的对应关系以及材料具体参数取值见表5;轴向和弯曲方向分别用弹性材料表征,材料的弹性模量分别对应耗能梁段的轴向线刚度(EAL/e)和弯曲线刚度(EIL/e),E为耗能梁段钢材的弹性模量;AL和IL分别为耗能梁段的截面面积和截面惯性矩;e为耗能梁段长度。内梁和内柱采用非线性梁柱单元(Nonlinear BeamColumn element)模拟。所有柱考虑P-δ效应的影响。根据文献[7-8]可知端板螺栓连接在整个加载过程中无滑移产生,可将端板螺栓连接简化为刚接。整体结构建模时采用刚性楼板假定,忽略楼板的平面外变形。根据《高层民用建筑钢结构技术规程》[35]的规定,考虑钢筋混凝土楼板与钢梁之间有可靠连接,需要计入钢筋混凝土楼板对钢梁刚度的增大作用。在弹性分析时,模型中的内框梁由于两侧均有楼板,需对内框梁的平面内惯性矩修正为1.5Ib,裙梁仅一侧有楼板,需对裙梁的平面内惯性矩修正为1.2Ib。
表 5 Steel02材料参数Table 5. Material parameters of Steel02Steel02参数 剪切弹簧参数 取值 备注 fy 耗能梁段屈服剪力 0.6fyLAw 理论公式 E0 耗能梁段剪切刚度 GAw/e 理论公式 曲线过渡段参数 R0/cR1/cR2 18.5/0.918/0.15 参数标定 应变强化参数 b 0.003 参数标定 等向强化参数 a1/a2/a3/a4 0.03/1.0/0.03/1.0 参数标定 注:G和fyL分别为耗能梁段钢材的剪切模量和屈服强度;Aw为耗能梁段的腹板面积。 为了验证有限元模型的正确性,对文献[8]中试件HSS-FTS-A进行建模,图11为试验试件加载装置图及OpenSees有限元模型示意图。图12为有限元和试验荷载-位移滞回曲线和骨架曲线对比,表6对比了有限元和试验的初始刚度、峰值承载力和累积耗能,有限元分析得到的初始刚度与试验结果吻合较好,有限元分析得到的峰值承载力和累积耗能较试验结果高8.9%和5.7%,可能原因为加载后期有限元模型不能准确反映耗能梁段腹板裂缝引起的刚度和承载力的降低,但误差在可接受范围内。总体来讲,有限元建模方法能较为准确地模拟结构的非线性行为,可用于整体结构的抗震性能分析。
表 6 有限元与试验性能指标对比Table 6. Comparison of performance index between numerical model and test性能指标 试验 有限元 误差/(%) 初始刚度/(kN/mm) 21.72 21.75 −0.20 峰值承载力/kN 415.00 452.00 −8.90 累计耗能/kJ 583.00 616.00 −5.70 注:误差=(试验−有限元)/试验×100%。 4.3 Pushover分析
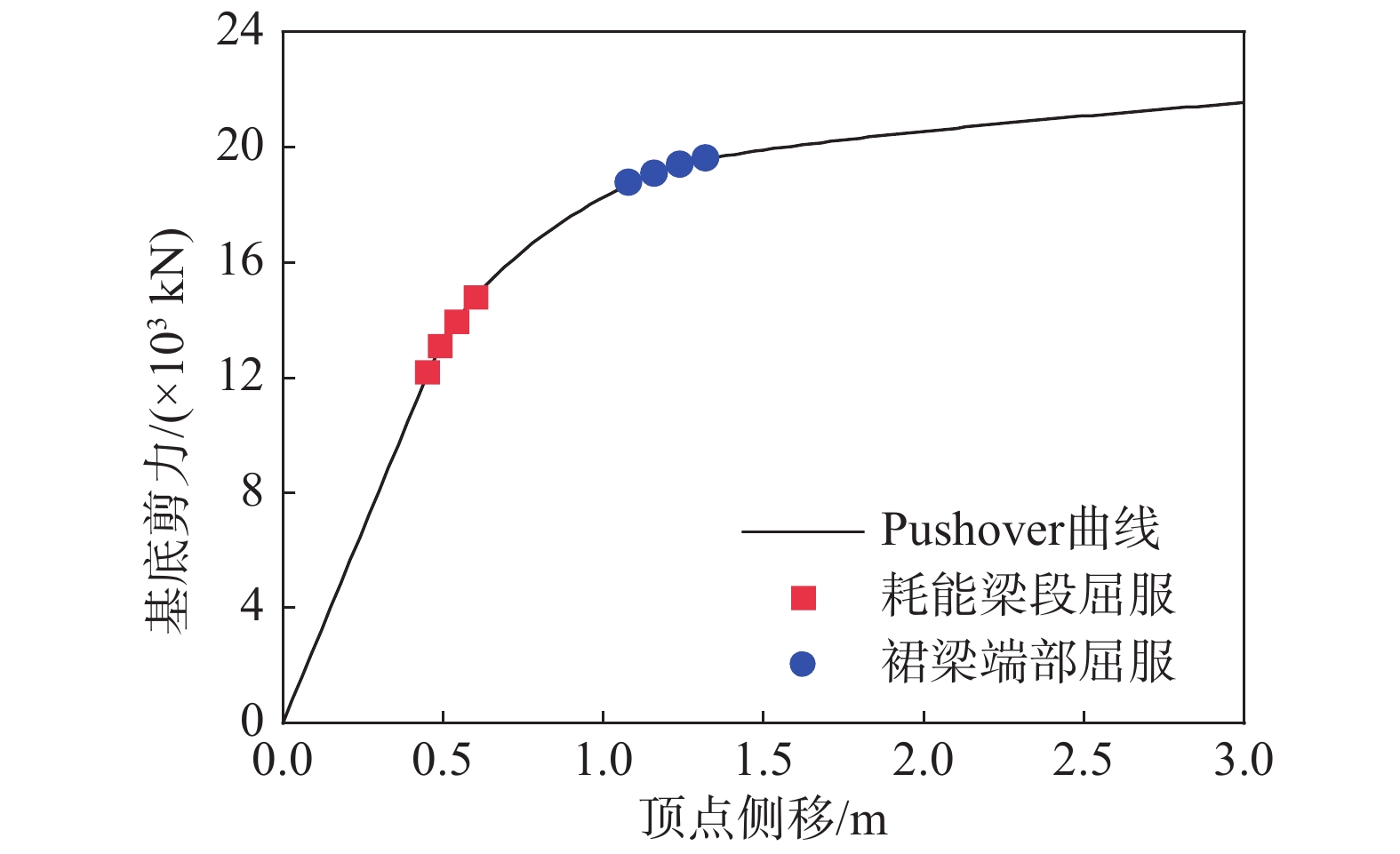
采用计算得到的层侧向力对结构进行静力弹塑性分析,图13为算例的Pushover曲线,曲线呈现明显的三线型,第一个拐点对应Link跨耗能梁段开始屈服,第二个拐点对应Frame跨裙梁端部开始屈服,与假定的结构能力曲线一致。
4.4 非线性时程分析
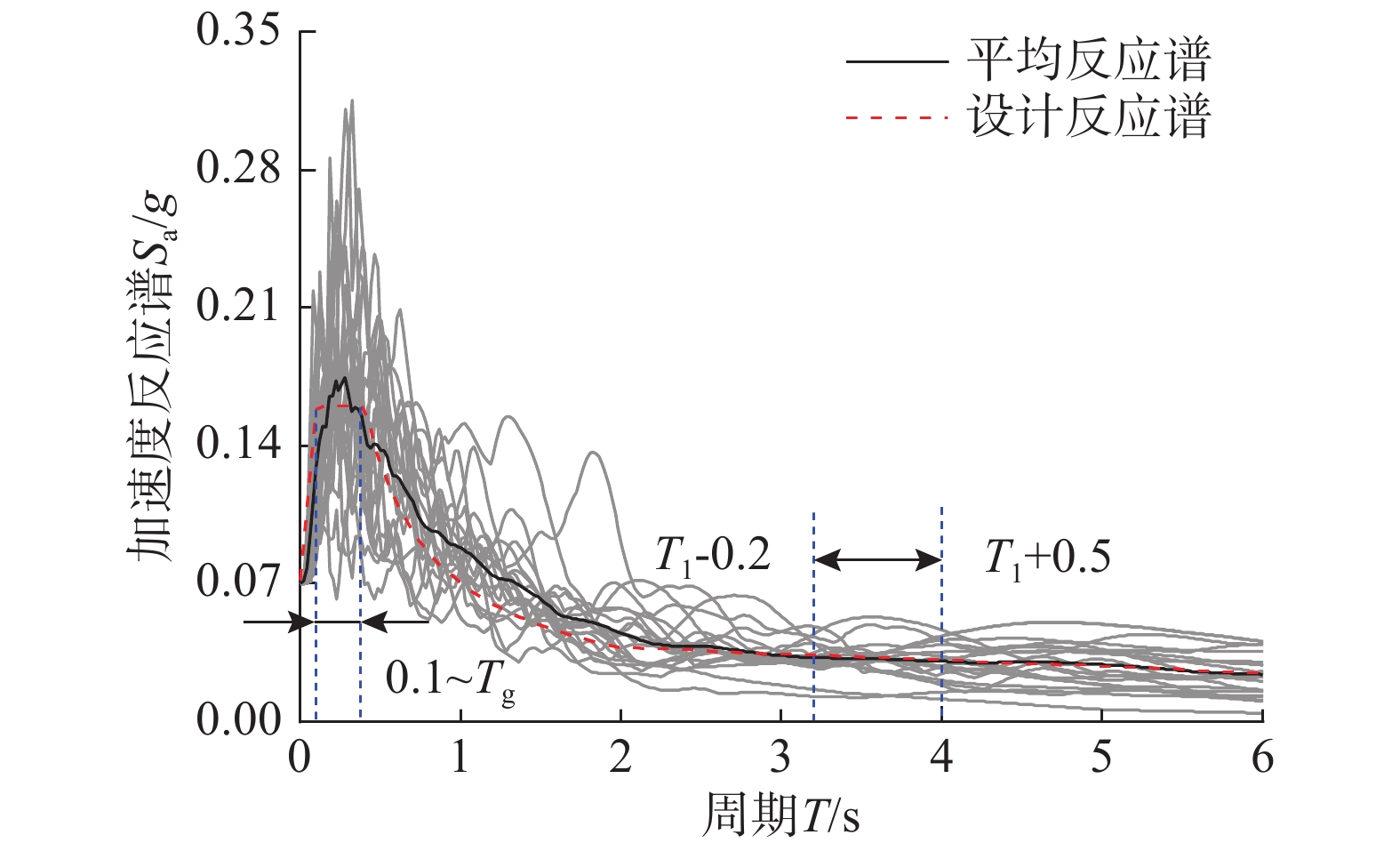
按照《建筑抗震设计规范》[18]的规定和文献[36]的建议在PEER数据库选取20条地震波,地震波频谱分析见图14。将地震波峰值加速度分别调至多遇地震、设防地震、罕遇地震和极罕遇地震对应的峰值加速度,对结构进行时程分析。
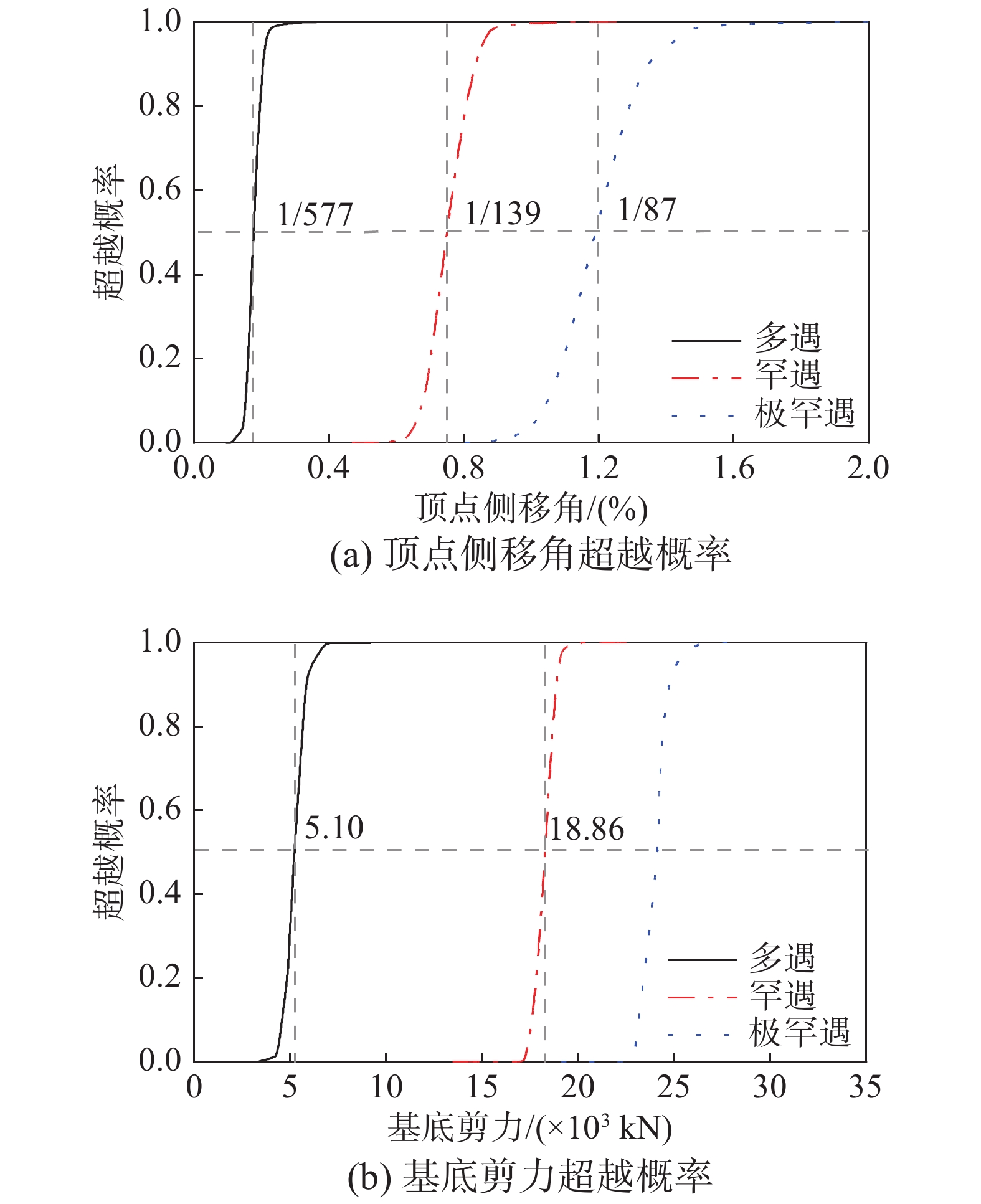
图15为设计算例在多遇地震、罕遇地震和极罕遇地震作用下结构顶点侧移角和基底剪力的超越概率曲线。算例在多遇地震、罕遇地震和极罕遇地震作用下50%超越概率对应的顶点侧移角分别为1/577、1/139和1/87,结构设计时预选的多遇地震和罕遇地震作用下的顶点侧移角分别为1/580和1/132,极罕遇地震作用下计算得到的顶点侧移角为1/76,分析结果与设计预选的顶点侧移角在多遇地震作用时吻合较好,罕遇地震和极罕遇地震下其误差分别为5.30%和14.50%,可用于对结构在非线性阶段的变形能力进行评估。算例在多遇地震和罕遇地震作用下50%超越概率对应的基底剪力分别为5095 kN和18 863 kN,结构设计采用的多遇地震和罕遇地震作用下的基底剪力分别为5204 kN和17 600 kN,分析结果与设计值吻合较好。
图16为算例在四水准地震作用下的层间侧移角分布,算例在多遇地震、设计地震、罕遇地震和极罕遇地震作用下的平均层间侧移角沿结构高度分布较为均匀,但是其中三条近场地震波在罕遇地震和极罕遇地震作用下结构底部层间侧移角偏大,超过规定的层间侧移限值,这是由于这三条地震波为近场脉冲波,使得结构在进入非线性阶段后中下部楼层层间侧移被明显放大。算例的最大平均层间侧移角分别为1/414、1/180、1/100和1/57,均满足表2中的限值规定。需要注意的是,由于实际结构层间侧移角分布不完全相同,由20条地震波分析结果可得不同地震水准作用下结构最大层间侧移角与顶点侧移角的比值约为1.5,故在预选顶点侧移角时可取(1/1.5~1/2)层间侧移限值。
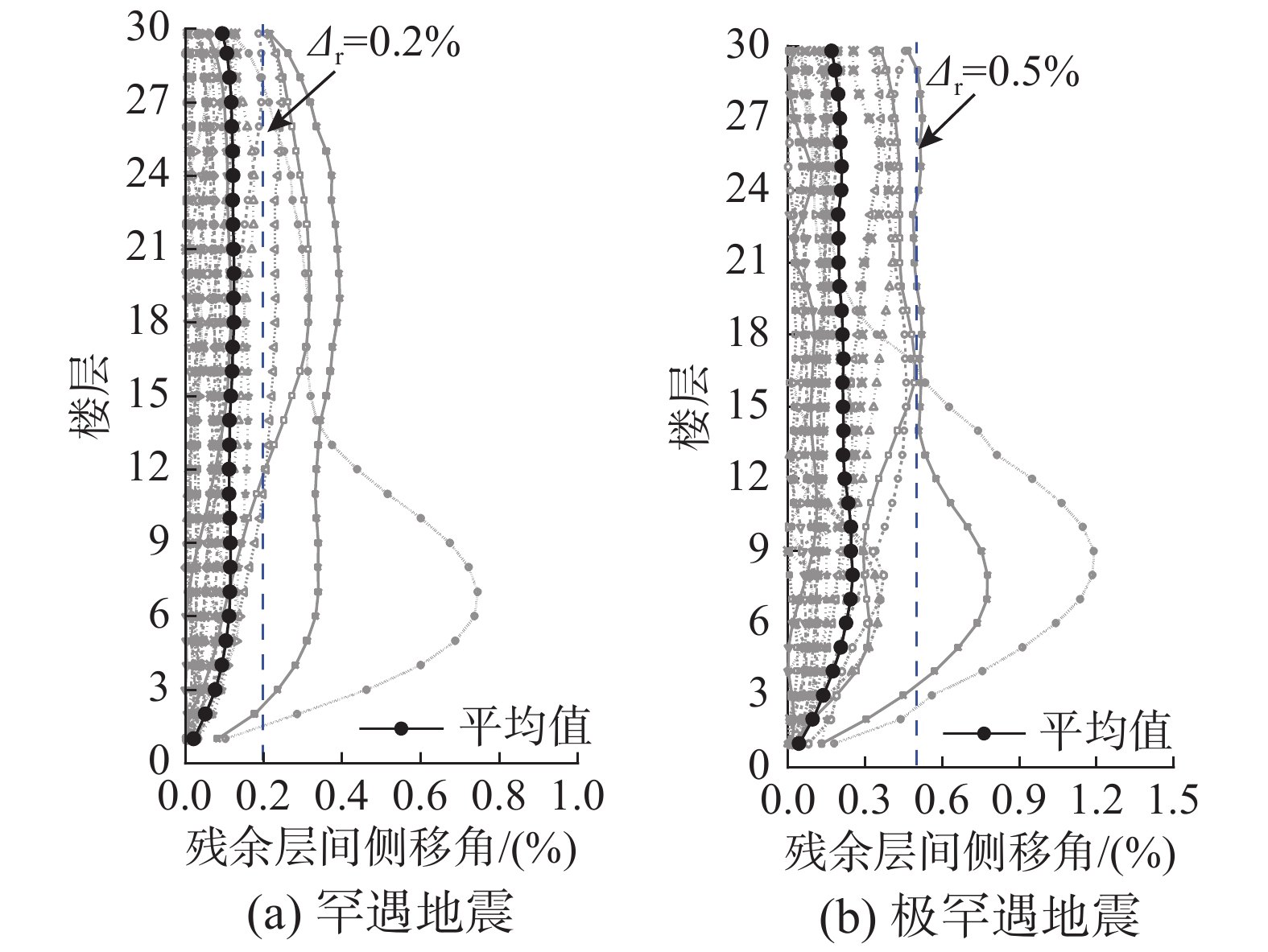
图17为算例在罕遇地震和极罕遇地震作用下的平均残余层间侧移角分布,最大平均残余层间侧移角为0.12%和0.26%,均小于表2规定的残余变形限值,且小于文献[8]中建议的可允许残余层间侧移角,表明结构可以实现震后耗能梁段的更换。
图18为算例在罕遇地震和极罕遇地震作用下的塑性铰分布,以其中一条典型地震波为例。罕遇地震作用下,几乎全部耗能梁段都进入塑性,其余构件保持弹性状态;极罕遇地震作用下,耗能梁段全部进入塑性,且多数Frame跨裙梁端部也发展了塑性,与预先假定的屈服模式一致,表明本文建议的设计方法的有效性及合理性。
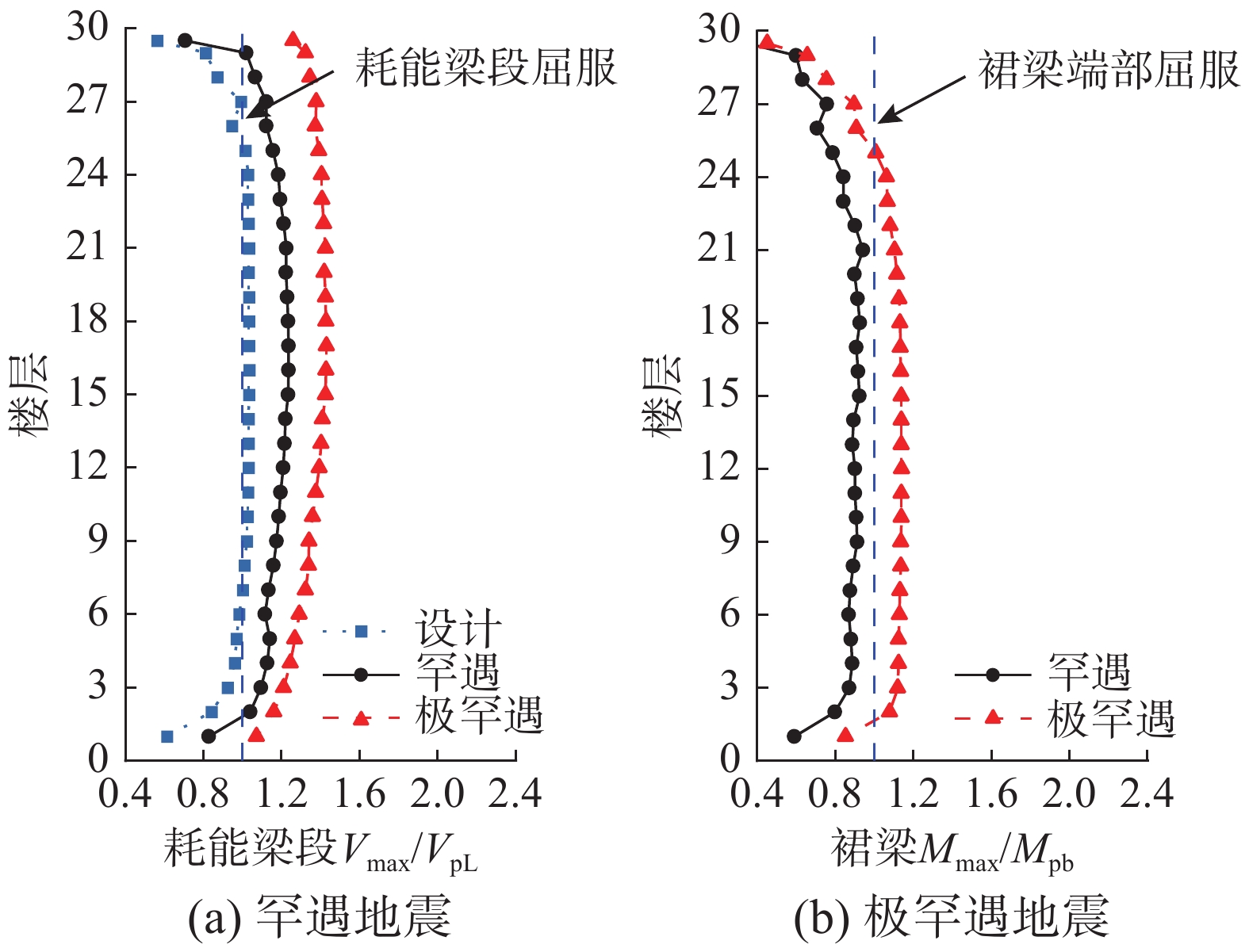
图19给出了不同地震水准作用下各层耗能梁段剪力最大值与耗能梁段塑性抗剪承载力的比值Vmax/VpL以及裙梁端部弯矩最大值与裙梁塑性抗弯承载力的比值Mmax/Mpb沿楼层的分布,可反映耗能梁段和裙梁的塑性发展程度。设计地震作用下,各层耗能梁段Vmax/VpL基本为1.0,表明耗能梁段刚进入塑性;罕遇地震作用下,各层耗能梁段Vmax/VpL约为1.2,表明耗能梁段发展了一定程度的塑性变形,各层裙梁Mmax/Mpb约为0.8,均处于弹性状态;极罕遇地震作用下,各层耗能梁段Vmax/VpL约为1.4,表明耗能梁段发展了明显的塑性变形,也证明了结构设计时耗能梁段超强系数取1.5较为合理,各层裙梁Mmax/Mpb约为1.1,表明裙梁开始屈服。通过对各构件损伤程度的分析结果表明,算例的塑性发展与预期一致。
5 结论
基于含端板螺栓连接耗能梁段的高强钢框筒结构的失效机制和变形特点,提出了适用于该结构基于性能的塑性设计方法,可以得到以下结论:
(1) 建立含端板螺栓连接耗能梁段的高强钢框筒结构这一新型功能可恢复结构体系“小震不坏,中震及大震可修,巨震不倒”的四水准抗震设防性能目标,采用层间侧移角和残余层间侧移角对其性能指标进行了量化。
(2) 将含端板螺栓连接耗能梁段的高强钢框筒结构等效为Link跨和Frame跨,假定结构能力曲线为三线型,基于能量平衡原理提出了含端板螺栓连接耗能梁段的高强钢框筒结构基于性能的塑性设计方法。
(3) 建议的基于性能的塑性设计方法可以考虑结构在不同地震水准作用下的性能目标,保证结构实现理想的失效模式,多遇地震作用下,所有构件均保持弹性状态;设计和罕遇地震作用下,耗能梁段屈服并充分发展塑性,耗散地震能量;极罕遇地震作用下,Frame跨裙梁进入塑性,保证结构不倒。
(4) 30层算例的时程分析结果表明,结构在不同地震水准作用下的实际顶点侧移角与预选的性能目标基本一致,且结构在不同地震水准作用下的最大层间侧移角和残余层间侧移角均满足性能指标限值,验证了设计方法的有效性。
(5) 极罕遇地震作用下,各层耗能梁段的塑性发展程度Vmax/VpL约为1.4,表明结构设计时耗能梁段超强系数取1.5较为合理。
-
表 1 四水准地震动水平影响系数最大值αmax
Table 1 Maximum values of horizontal seismic influence coefficients for four-level ground motion
抗震性能水准分级 6度 7度 8度 9度 多遇地震 0.04 0.08(0.12) 0.16(0.24) 0.32 设计地震 0.12 0.23(0.34) 0.45(0.68) 0.90 罕遇地震 0.28 0.50(0.72) 0.90(1.20) 1.40 极罕遇地震 0.36 0.70(1.00) 1.35(2.00) 2.70 注:括号中数值分别为设计基本地震加速度为0.15 g和0.30 g的地区。 表 2 性能指标量化
Table 2 Quantification of performance indexes
性能指标 水准分级 多遇地震 设计地震 罕遇地震 极罕遇地震 层间侧移角 三水准 1/250 − 1/50 四水准 1/300 1/150 1/75 1/50 残余层间侧移角 三水准 − − − 四水准 − 0.3% 0.5% 0.75% 表 3 算例设计参数
Table 3 Design parameters of model
表 4 算例构件截面
Table 4 Member sections of model
/mm 层数 耗能梁段 Link跨裙梁 Frame跨裙梁 中柱 角柱 内柱 内框梁 29~30 H230×150×6×10 H370×160×10×14 H400×160×8×12 H460×280×16×20 □430×22 □250×20 H650×250×14×20 27-28 H230×180×10×14 H410×180×12×16 H420×200×10×14 H480×300×20×24 □460×26 □320×22 H650×250×14×20 24~26 H270×180×12×16 H440×220×16×20 H430×200×16×20 H530×320×22×26 □510×26 □360×24 H650×250×14×20 21~23 H290×200×14×18 H490×220×16×20 H480×220×16×20 H560×340×22×26 □525×28 □420×30 H650×250×14×20 18~20 H330×200×14×18 H530×220×16×22 H530×220×16×20 H590×340×24×28 □545×30 □470×34 H650×250×14×20 15~17 H325×200×16×20 H560×230×18×22 H565×220×16×20 H600×380×26×30 □560×34 □520×38 H650×250×14×20 12~14 H350×200×16×20 H600×230×18×22 H560×220×18×22 H600×400×28×32 □570×36 □560×42 H650×250×14×20 9~11 H365×200×16×20 H620×230×18×22 H580×220×18×22 H610×400×28×32 □570×38 □610×44 H650×250×14×20 6~8 H380×200×16×20 H630×230×18×22 H600×220×18×22 H660×400×30×34 □610×40 □660×46 H650×250×14×20 3~5 H385×200×16×20 H640×230×18×22 H610×220×18×22 H690×420×32×36 □640×40 □710×48 H650×250×14×20 1~2 H385×200×16×20 H640×230×18×22 H610×220×18×22 H690×420×32×36 □640×40 □730×50 H650×250×14×20 表 5 Steel02材料参数
Table 5 Material parameters of Steel02
Steel02参数 剪切弹簧参数 取值 备注 fy 耗能梁段屈服剪力 0.6fyLAw 理论公式 E0 耗能梁段剪切刚度 GAw/e 理论公式 曲线过渡段参数 R0/cR1/cR2 18.5/0.918/0.15 参数标定 应变强化参数 b 0.003 参数标定 等向强化参数 a1/a2/a3/a4 0.03/1.0/0.03/1.0 参数标定 注:G和fyL分别为耗能梁段钢材的剪切模量和屈服强度;Aw为耗能梁段的腹板面积。 表 6 有限元与试验性能指标对比
Table 6 Comparison of performance index between numerical model and test
性能指标 试验 有限元 误差/(%) 初始刚度/(kN/mm) 21.72 21.75 −0.20 峰值承载力/kN 415.00 452.00 −8.90 累计耗能/kJ 583.00 616.00 −5.70 注:误差=(试验−有限元)/试验×100%。 -
[1] 吕西林, 武大洋, 周颖. 可恢复功能防震结构研究进展[J]. 建筑结构学报, 2019(2): 1 − 15. Lü Xilin, Wu Dayang, Zhou Ying. State-of-the-art of earthquake resilient structure [J]. Journal of Building Structures, 2019(2): 1 − 15. (in Chinese)
[2] 周颖, 吴浩, 顾安琪. 地震工程: 从抗震、减隔震到可恢复性[J]. 工程力学, 2019, 36(6): 1 − 12. doi: 10.6052/j.issn.1000-4750.2018.07.ST09 Zhou Ying, Wu Hao, Gu Anqi. Earthquake engineering: from earthquake resistance, energy dissipation, and isolation, to resilience [J]. Engineering Mechanics, 2019, 36(6): 1 − 12. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.07.ST09
[3] 周颖, 肖意, 顾安琪. 自复位支撑-摇摆框架结构体系及其基于位移抗震设计方法[J]. 建筑结构学报, 2019, 40(10): 17 − 26. Zhou Ying, Xiao Yi, Gu Anqi. Self-centering braced rocking frame systems and displacement-based seismic design method [J]. Journal of Building Structures, 2019, 40(10): 17 − 26. (in Chinese)
[4] 周颖, 田文博, 王睿, 等. 自复位剪力墙的三水准抗震设防与四水准抗震设防对比研究[J]. 建筑结构学报, 2021, 42(1): 67 − 74. Zhou Ying, Tian Wenbo, Wang Rui, et al. Comparison between three-level and four-level seismic fortifications of self-centering shear wall [J]. Journal of Building Structures, 2021, 42(1): 67 − 74. (in Chinese)
[5] Lian M, Cheng Q Q, Zhang H, et al. Numerical study of the seismic behavior of steel frame-tube structures with bolted web-connected replaceable shear links [J]. Steel and Composite Structures, 2020, 35(3): 305 − 325.
[6] 程倩倩, 苏明周, 连鸣. 带可更换剪切型耗能梁段高强钢组合框筒的结构影响系数研究[J]. 工程力学, 2020, 37(2): 145 − 158. doi: 10.6052/j.issn.1000-4750.2019.01.0127 Cheng Qianqian, Su Mingzhou, Lian Ming. Response modification factor of high strength steel fabricated framed-tube with replaceable shear links [J]. Engineering Mechanics, 2020, 37(2): 145 − 158. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.01.0127
[7] 张浩, 连鸣, 苏明周, 等. 带可更换低屈服点耗能梁段-端板连接的钢框筒结构抗震性能试验研究[J]. 土木工程学报, 2020, 53(7): 28 − 42. Zhang Hao, Lian Ming, Su Mingzhou, et al. Experimental study on seismic behavior of steel framed-tube structure with end-plate connected replaceable shear links made of low yield point steel [J]. China Civil Engineering Journal, 2020, 53(7): 28 − 42. (in Chinese)
[8] Cheng Q Q, Su M Z, Lian M, et al. Cyclic behavior of high-strength steel framed-tube structures with bolted replaceable shear links [J]. Engineering Structures, 2020, 210: 110395. doi: 10.1016/j.engstruct.2020.110395
[9] Zhang Hao, Lian Ming, Su Mingzhou. Study on the seismic performance of high-strength steel framed-tube structures with replaceable shear links [J]. Journal of Constructional Steel Research, 2020, 171: 106131.
[10] Goel S C, Liao W C, Bayat M R, et al. Performance-based plastic design (PBPD) method for earthquake-resistant structures: an overview [J]. Structural Design of Tall & Special Buildings, 2010, 19(1/2): 115 − 137.
[11] 郝际平, 袁昌鲁, 樊春雷, 等. 钢板剪力墙结构基于性能的塑性设计方法研究[J]. 工程力学, 2015, 32(7): 118 − 127. doi: 10.6052/j.issn.1000-4750.2013.12.1207 Hao Jiping, Yuan Changlu, Fan Chunlei, et al. Performance-based plastic design method for the slender unstiffened steel plate shear walls [J]. Engineering Mechanics, 2015, 32(7): 118 − 127. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.12.1207
[12] 李慎, 苏明周. 基于性能的偏心支撑钢框架抗震设计方法研究[J]. 工程力学, 2014, 31(10): 195 − 204. doi: 10.6052/j.issn.1000-4750.2014.03.0204 Li Shen, Su Mingzhou. A performance-based seismic design method for eccentrically braced steel frames [J]. Engineering Mechanics, 2014, 31(10): 195 − 204. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.03.0204
[13] Bai J L, Ou J P. Earthquake-resistant design of buckling-restrained braced RC moment frames using performance-based plastic design method [J]. Engineering Structures, 2016, 107: 66 − 79. doi: 10.1016/j.engstruct.2015.10.048
[14] Li T X, Yang T Y, Tong G S. Performance-based plastic design and collapse assessment of diagrid structure fused with shear link [J]. Structural Design of Tall & Special Buildings, 2019, 28(6): e1589.
[15] Yang T Y, Tung D P, Li Y. Equivalent energy design procedure for earthquake resilient fused structures [J]. Earthquake Spectra, 2017, 34(2): 795 − 815.
[16] Shoeibi S, Kafi M A, Gholhaki M. New performance-based seismic design method for structures with structural fuse system [J]. Engineering Structures, 2017, 132: 745 − 760. doi: 10.1016/j.engstruct.2016.12.002
[17] Zhai Z P, Guo W, Li Y Z, et al. An improved performance-based plastic design method for seismic resilient fused high-rise buildings [J]. Engineering Structures, 2019, 199: 109650. doi: 10.1016/j.engstruct.2019.109650
[18] GB 50011−2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[19] ASCE 7−10, Minimum design loads for buildings and other structures [S]. Virginia: American Society of Civil Engineers (ASCE), 2010.
[20] GB 18306−2015, 中国地震动参数区划图[S]. 北京: 中国标准出版社, 2015. GB 18306−2015, Seismic ground parameter zonation map of Chinese [S]. Beijing: China Architecture & Building Press, 2015. (in Chinese)
[21] 建筑隔震设计标准(征求意见稿)[S]. 广州: 国家标准《建筑隔震设计标准》编制组, 2017. Code of design for seismic isolated buildings (draft) [S]. Guangzhou: National Standard Establishment Group of Code of Design for Seismic Isolated Buildings, 2017. (in Chinese)
[22] 金仁和, 魏德敏. 框筒结构剪力滞后研究现状与思考[J]. 建筑钢结构进展, 2008(2): 23 − 27. Jin Renhe, Wei Demin. Current investigation and expectation on the shear lag of framed-tube structures [J]. Progress in Steel Building Structures, 2008(2): 23 − 27. (in Chinese)
[23] 程倩倩, 连鸣, 苏明周, 等. 含可更换剪切型耗能梁段的钢框筒结构抗震性能研究[J]. 建筑钢结构进展, 2020, 22(1): 35 − 46. Cheng Qianqian, Lian Ming, Su Mingzhou, et al. Seismic behavior study of steel framed-tube structure with replaceable shear links [J]. Progress in Steel Building Structures, 2020, 22(1): 35 − 46. (in Chinese)
[24] 连鸣, 韩文凯, 莫文茹, 等. 可更换剪切型耗能梁段-高强钢框筒结构抗震性能分析[J]. 建筑结构, 2020, 50(1): 74 − 82. Lian Ming, Han Wenkai, Mo Wenru, et al. Investigation on seismic performance of high-strength steel fabricated steel framed-tube structure with replaceable shear type energy-dissipated beam section [J]. Building Structures, 2020, 50(1): 74 − 82. (in Chinese)
[25] SEAOC Vision 2000, Performance based seismic engineering for building [S]. Sacramento: Structural Engineers Association of California, 1995.
[26] Housner G W. Limit design of structures to resist earthquakes [C]. Proceedings of the World Conference on Earthquake Engineering, 1956: 1−11.
[27] Akiyama H. Earthquake-resistant limit-state design of buildings [M]. Tokyo: University of Tokyo Press, 1985.
[28] Zhang H, Lian M, Su M z, et al. Lateral force distribution in the inelastic state for seismic design of high-strength steel framed-tube structures with shear links [J]. Structural Design of Tall & Special Buildings, 2020: e1801.
[29] GB 50017−2017, 钢结构设计标准[S]. 北京: 中国建筑工业出版社, 2017. GB 50017−2017, Standard for design of steel structures [S]. Beijing: China Architecture Industry Press, 2017. (in Chinese)
[30] Li T X, Yang T Y, Tong G S, et al. Performance-based seismic design and evaluation of fused steel diagrid frame [J]. Earthquake Spectra, 2018, 34(4): 1869 − 1891. doi: 10.1193/121017EQS257M
[31] 关彬林, 连鸣, 苏明周. Q235剪切型耗能梁段超强系数的建议[J]. 地震工程与工程振动, 2020, 40(3): 117 − 129. Guan Binlin, Lian Ming, Su Mingzhou. Suggestions on overstrength factors of shear links with Q235 steel [J]. Earthquake Engineering and Engineering Dynamics, 2020, 40(3): 117 − 129. (in Chinese)
[32] 关彬林, 连鸣, 苏明周. 含可更换剪切型耗能梁段的组合钢框筒截面尺寸预估方法探究[J]. 建筑钢结构进展, 2020, 22(3): 1 − 11, 21. Guan Binlin, Lian Ming, Su Mingzhou. Study on the section dimension estimation method of composite steel framed-tube structures with replaceable shear links [J]. Progress in Steel Building Structures, 2020, 22(3): 1 − 11, 21. (in Chinese)
[33] 曹徐阳, 冯德成, 王谆, 等. 基于OpenSEES的装配式混凝土框架节点数值模拟方法研究[J]. 土木工程学报, 2019, 52(4): 13 − 27. Cao Xuyang, Feng Decheng, Wang Zhun, et al. Investigation on modelling approaches for prefabricated concrete beam-to-column connections using OpenSEES [J]. China Civil Engineering Journal, 2019, 52(4): 13 − 27. (in Chinese)
[34] Filippou F C, Popov E P, Bertero V V. Effect of bond deterioration on cyclic behavior of reinforced concrete joints [C]. EERC Report 83–19, Earthquake Engineering Research Center, Berkeley, 1983.
[35] JGJ 99−2015, 高层民用建筑钢结构技术规程[S]. 北京: 中国建筑工业出版社, 2015. JGJ 99−2015, Technical specification for steel structure of tall building [S]. Beijing: China Architecture & Building Press, 2015. (in Chinese)
[36] 曲哲, 叶列平, 潘鹏. 建筑结构弹塑性时程分析中地震动记录选取方法的比较研究[J]. 土木工程学报, 2011, 44(7): 10 − 21. Qu Zhe, Ye Lieping, Pan Peng. Comparative study on methods of selecting earthquake ground motions for nonlinear time history analyses of building structures [J]. China Civil Engineering Journal, 2011, 44(7): 10 − 21. (in Chinese)
-
期刊类型引用(7)
1. 石韵,刘万鹏,苏明周,周巧玲,刘少博. 混合联肢部分外包组合剪力墙基于两阶段耗能的塑性设计方法研究. 工程力学. 2024(02): 137-150 .  本站查看
本站查看
2. 连鸣,周玉浩,李浩翔. 基于性能的含可更换耗能梁段高强钢框筒结构抗震性能研究. 西安建筑科技大学学报(自然科学版). 2024(01): 65-73 .  百度学术
百度学术
3. 李腾飞,苏明周,郭江然. 基于多目标性能的高强钢组合K形偏心支撑框架塑性设计方法研究. 建筑结构学报. 2023(01): 10-22 .  百度学术
百度学术
4. 程倩倩,连鸣,辛力,苏明周,关彬林. 含双槽钢腹板螺栓连接耗能梁段的钢框筒结构抗震性能研究. 建筑钢结构进展. 2023(01): 49-61 .  百度学术
百度学术
5. 殷占忠,杨元普,冯大哲. 带可替换腹板连接型耗能梁段的恢复力模型研究. 地震工程学报. 2023(04): 751-760 .  百度学术
百度学术
6. 马翠玲,黄镜渟. 远场地震作用下累积延性比谱的建立. 常州工学院学报. 2023(05): 13-20+34 .  百度学术
百度学术
7. 苏明周,李蕴杰,张浩,连鸣. 带端板连接可更换耗能梁段的钢框筒结构地震易损性分析. 西安建筑科技大学学报(自然科学版). 2022(04): 491-499 .  百度学术
百度学术
其他类型引用(3)




 下载:
下载: