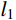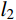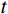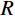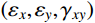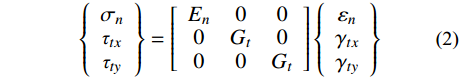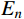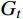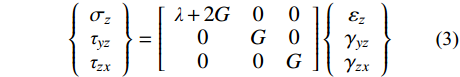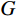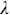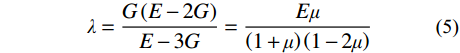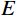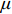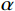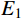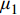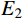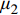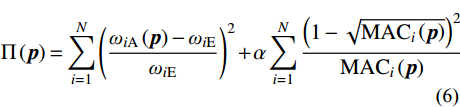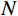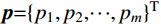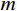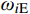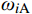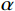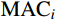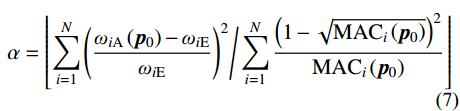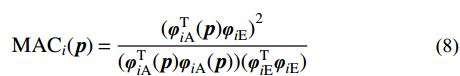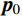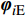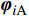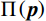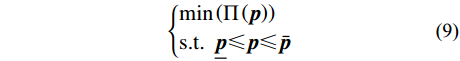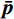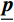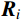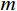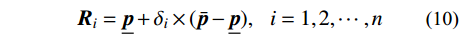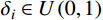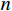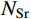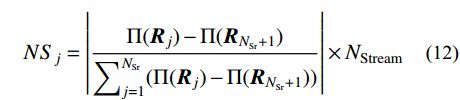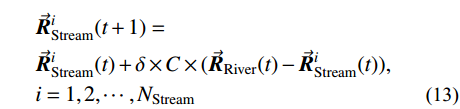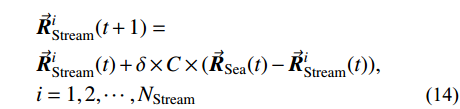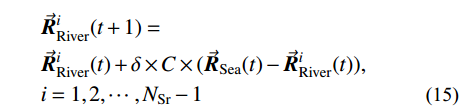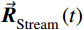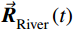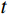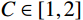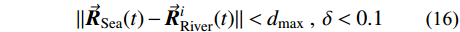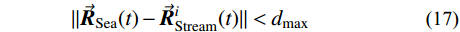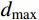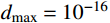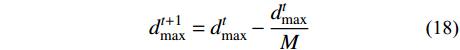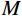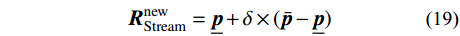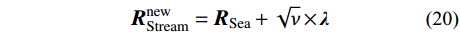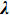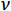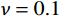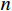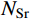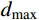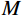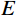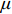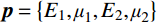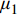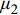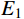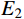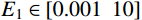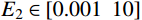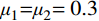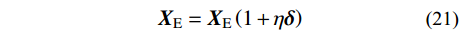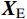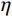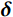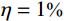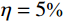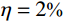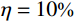基于模型修正的螺栓连接板结构动力学建模方法

郭宁; 黄庆; 曹善成; 徐超

doi:10.6052/j.issn.1000-4750.2020.07.0503

基于模型修正的螺栓连接板结构动力学建模方法

郭宁^1, ,,
黄庆^{1, 2,},
曹善成^1,,
徐超^1,

1.
西北工业大学航天学院，西安 710072
2.
湖北航天飞行器研究所，武汉 430040

基金项目: 陕西省自然科学基础研究计划项目(2020JQ-124)；国家自然科学基金项目(51705422)；国防基础科研挑战计划项目(TZ2018007)

详细信息

作者简介:
黄　庆(1993−)，男，安徽人，硕士，主要从事飞行器结构动力学研究(E-mail: huang236404@mail.nwpu.edu.cn)

曹善成(1989−)，男，山东人，副教授，博士，主要从事飞行器结构健康监测研究(E-mail: shancheng.cao@nwpu.edu.cn)

徐　超(1979−)，男，山东人，教授，博士，主要从事飞行器结构动力学与健康监测方法研究(E-mail: chao_xu@nwpu.edu.cn)

通讯作者:
郭　宁(1986−)，男，宁夏人，助理研究员，博士，主要从事飞行器结构动力学研究(E-mail: guoning@nwpu.edu.cn)

中图分类号: TB122；O327
计量
- 文章访问数: 940
- HTML全文浏览量: 344
- PDF下载量: 109
出版历程
- 收稿日期: 2020-07-22
- 修回日期: 2020-12-07
- 网络出版日期: 2020-12-22
- 刊出日期: 2021-07-14

STRUCTURAL DYNAMIC MODELING METHOD OF BOLTED JOINT PLATES BASED ON MODEL UPDATING

GUO Ning^1, ,,
HUANG Qing^{1, 2,},
CAO Shan-cheng^1,,
XU Chao^1,

1.
School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China
2.
Hubei Aerospace Flight Vehicle Institute, Wuhan 430040, China

摘要

摘要: 螺栓连接板结构是飞行器结构中应用最为广泛的可拆卸固定结合部之一。该文针对螺栓连接板结构的动力学建模展开研究：基于薄层单元理论建立螺栓连接板结构的动力学等效模型；采用固有频率误差和模态置信准则残差的加权和作为修正薄层单元材料本构参数的目标函数，并利用水循环算法对待修正参数进行全局修正；以一个双边固支五螺栓搭接板结构的动力学建模为例，来验证该文提出方法的可行性和鲁棒性。结果表明，采用该文提出的方法建立的螺栓连接结构的动力学预示模型能够准确地表征其动态特性，并且具有良好的抗噪性。
- 螺栓连接结构 /
- 薄层单元 /
- 水循环算法 /
- 模型修正 /
- 动力学建模
Abstract: The bolted joint plate structure is one of the most widely used detachable fixed joints in aircraft structures. We study the dynamic modeling of bolted-joint plates and establish the dynamic equivalent model of bolted-joint plates based on the thin-layer element theory. The weighted sum of the natural frequency error and the modal confidence criterion residual are used as the objective functions. We propose to use the water cycle algorithm to globally modify the material parameters of the thin-layer elements. By an example of a clamped-clamped five-bolt lap plate, we verify the feasibility and robustness of the proposed dynamic modeling method. The results show that the established dynamic prediction model of the bolted joint plate structure can accurately characterize its dynamic characteristics and reduces the effect of the measurement noise compared to the current dynamic modeling methods.
- bolted joint structure /
- thin-layer element /
- water cycle algorithm /
- model updating /
- dynamic modeling

HTML全文

一般情况下，影响飞行器结构动力学建模准确性的一个主要因素是其连接部位的仿真预示^[1]。螺栓连接板结构是飞行器结构中最常用最重要的一种可拆卸式连接结构形式。因此，准确建立螺栓连接板结构的动力学模型，是准确获取飞行器结构动力学特性和响应的前提之一。

目前，针对螺栓连接部件动力学建模的主要方法有：线性建模方法、非线性建模方法及薄层单元方法。线性方法是将实际的非线性连接结构近似成线性对象进行动力学分析，主要有三种方法：全固连建模方法^[2]、节点约束方法^[3]和用杆单元、弹簧单元和梁单元等模拟结构连接形式^[4-5]。线性建模方法具有工程操作简单等优点，但是不能准确地表征结构连接部位的刚度和阻尼特性，导致动响应分析结果偏差较大。非线性方法是通过假设或采用试验途径来建立连接界面的唯象力学模型。目前应用较多的界面力学模型有：Iwan模型^[6-7]、LuGre毛刷模型^[8]和Valanis模型^[9]等。上述非线性方法存在非线性机理描述有限、非线性模型参数获取难和计算耗费大等问题，还未有效地应用于工程结构分析中。薄层单元法最初是用于建立岩石与岩石界面之间的接触模型。目前已被广泛应用于连接结构建模中，Mayer和Gaul^[10]的研究表明薄层单元能够有效地模拟螺栓连接接触面的力学特性。翟学等^[11]研究了基于薄层单元法的螺栓连接结构建模和分析方法，并应用于涡扇发动机的建模。Iranzad和Ahmadian^[12]使用实验数据(固有频率、频响函数)来确定薄层单元的材料本构参数。姚星宇等^[13]给出了薄层单元法在航空发动机机匣螺栓连接结构的建模方法，并研究了薄层单元材料参数对螺栓连接刚度的影响规律。王攀和臧朝平^[14]基于螺栓连接超模型的刚度理论、赫兹接触理论以及M-B分形模型，考虑了螺栓的数量和法兰边的接触因素，建立了基于分区域薄层单元的螺栓连接简化建模方法。姜东等^[15-16]建立了基于各向同性本构关系的薄层单元理论，提出了螺栓连接结构接触面不确定性参数的识别方法。从上述的研究可以看出，采用薄层单元法建立连接结构动力学模型时薄层单元的本构参数的确定至关重要。

本文结合薄层单元理论，针对螺栓连接板结构提出了基于模型修正的动力学建模方法，其中采用薄层单元的力学行为等效模拟螺栓连接接触界面的力学行为，建立用于模型修正的初始动力学有限元模型，将不确定的薄层单元材料本构参数作为修正变量，通过模态参数构建目标函数，提出采用水循环算法(Water Cycle Algorithm, WCA)来修正薄层单元的不确定本构材料参数。

1 基于薄层单元法的螺栓连接板结构动力学建模

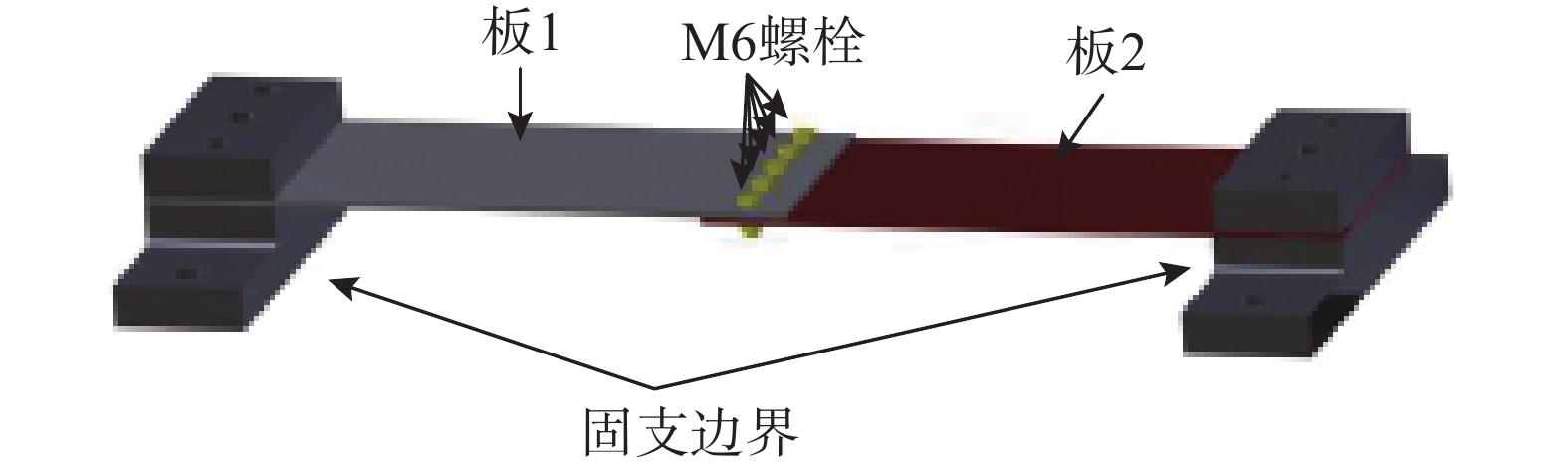
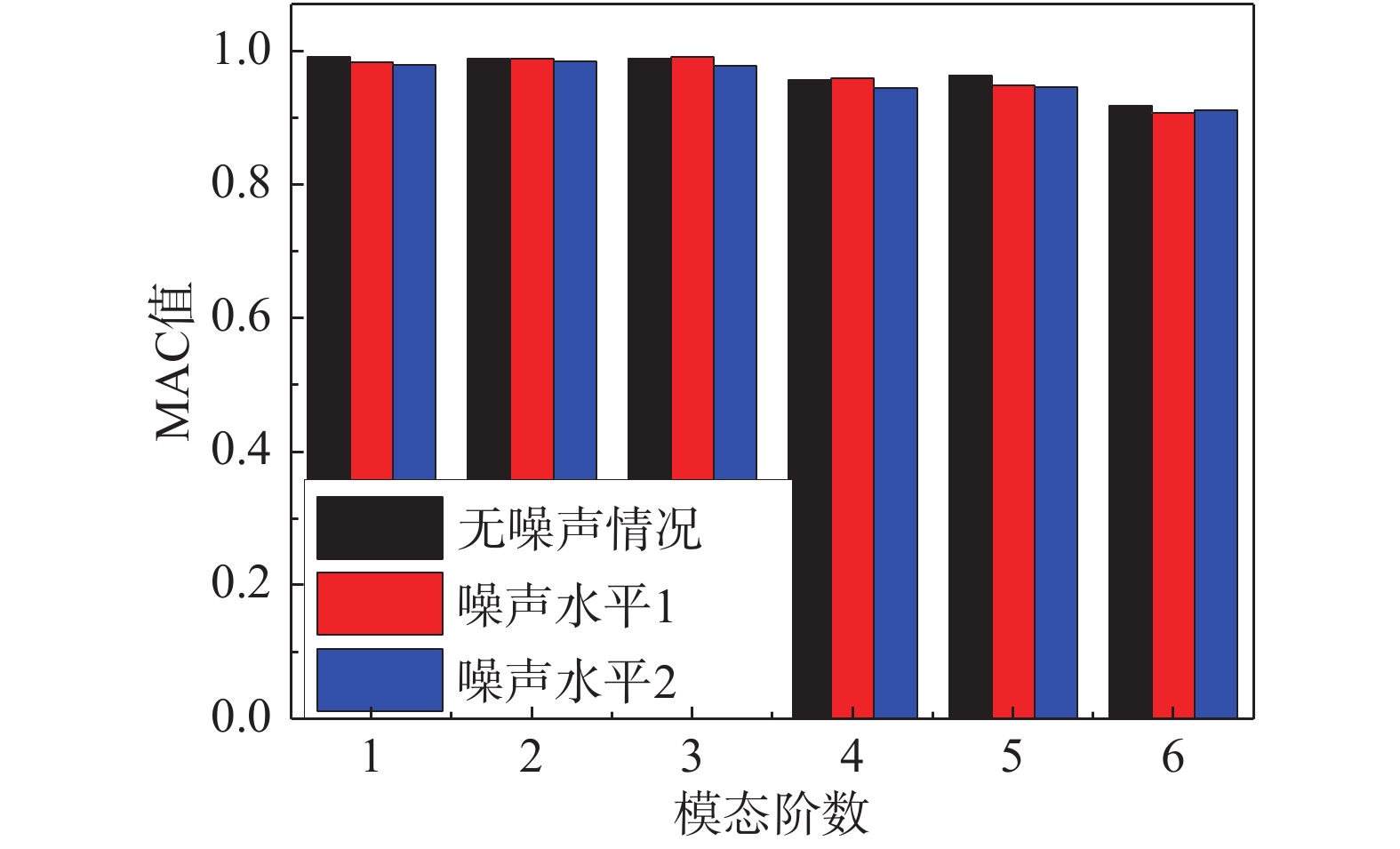
图1所示为工程中典型的螺栓连接板结构，首先采用板(壳)单元对被连接板部件进行动力学建模；继而采用一定厚度的8节点六面体实体单元(即薄层单元)来等效模拟螺栓连接力学行为；最后在薄层单元与对应接触的壳单元之间建立绑定约束关系，建立绑定约束时，需要设置绑定容差，容差应略大于两个被连接板中面之间的距离，以保证薄层单元与板(壳)单元之间能够有效的约束；螺栓的质量采用集中质量单元进行模拟。具体如图1所示。

图 1 螺栓连接板结构动力学建模

Figure 1. Dynamic modeling of bolted joint plate

下载: 全尺寸图片幻灯片

根据上述建模过程可知，螺栓连接板结构的连接界面刚度是通过薄层单元的刚度来等效的，建模过程中需要确定薄层单元的厚度以及其材料本构。薄层单元的厚度对分析结果影响较大，厚度过大则单元会有6个应变分量，难以准确体现接触界面的力学特征；厚度过小则会导致单元雅可比矩阵行列式值趋向于零，造成矩阵病态，求逆困难，无法准确计算其位移-应变关系^[15]。本文采用文献[17]中给出的薄层单元厚度计算方法，即：

$t = \frac{{{\rm{max}}\left( {{l_1},{l_2}} \right)}}{R}$

(1)

式中： ${l_1}$ 和 ${l_2}$ 分别为薄层单元的长度和宽度； $t$ 为薄层单元厚度； $R$ 的取值范围为10~100。

由于薄层单元的厚度远小于其长度和宽度，因此，可忽略薄层单元的面内应变分量 $( {{\varepsilon _x},{\varepsilon _y},{\gamma _{xy}}} )$ 。并且假设连接界面的法向和切向接触性能相互独立，且2个切向的接触性能相同，则表征界面接触性能的薄层单元本构方程可表示为^[15]：

$\left\{ {\begin{array}{*{20}{c}} {{\sigma _n}} \\ {{\tau _{tx}}} \\ {{\tau _{ty}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{E_n}}&0&0 \\ 0&{{G_t}}&0 \\ 0&0&{{G_t}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _n}} \\ {{\gamma _{tx}}} \\ {{\gamma _{ty}}} \end{array}} \right\}$

(2)

式中， ${E_n}$ 和 ${G_t}$ 分别是薄层单元的法向弹性常数和切向剪切常数。若接触面的法向与切向接触性能相互耦合，可在本构关系式(2)中通过引入耦合项来实现。

类比方程式(2)，在有限元建模中，可采用各向同性材料的本构关系近似替代薄层单元本构关系，具体为^[15]：

$\left\{ {\begin{array}{*{20}{c}} {{\sigma _{\textit{z}}}} \\ {{\tau _{y{\textit{z}}}}} \\ {{\tau _{{\textit{z}}x}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {\lambda + 2G}&0&0 \\ 0&G&0 \\ 0&0&G \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{\textit{z}}}} \\ {{\gamma _{y{\textit{z}}}}} \\ {{\gamma _{{\textit{z}}x}}} \end{array}} \right\}$

(3)

式中： $G$ 为材料剪切模量； $\lambda$ 为拉梅常数。

$G = \frac{E}{{2\left( {1 + \mu } \right)}}\;\qquad\qquad\qquad\qquad$

(4)

$\lambda = \frac{{G\left( {E - 2G} \right)}}{{E - 3G}} = \frac{{E\mu }}{{\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)}}$

(5)

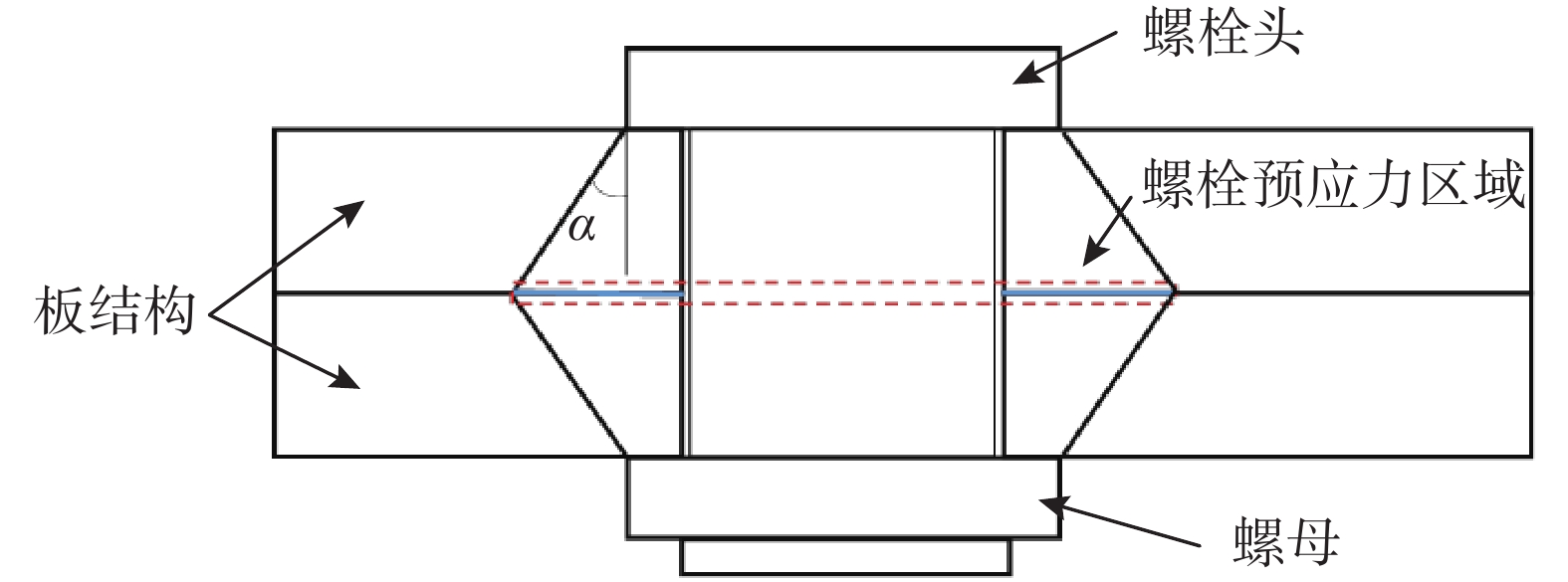
式中： $E$ 为材料弹性模量； $\mu$ 为材料泊松比。

在实际情况中，由于螺栓预应力的作用，螺栓连接界面的刚度分布并非一致，螺栓附近区域的界面连接刚度高于远离螺栓区域，因此，将薄层单元分为两部分，采用不同的材料本构参数进行建模。分区大小由螺栓预应力的作用区域大小决定，如图2所示，图中 $\alpha$ 角的取值范围为25°~33°^[18]，本文选择 $\alpha = 30^{\circ}$ 。为了进一步简化有限元建模，将圆形的螺栓预应力作用区域等效为正方形区域来进行有限元网格离散，但需要保证作用区域面积相同。

图 2 螺栓连接界面应力分布示意图

Figure 2. Stress distribution at bolted joint interface

下载: 全尺寸图片幻灯片

2 基于水循环算法的螺栓连接板结构动力学模型修正

根据第1节的分区薄层单元法建立的螺栓连接板结构动力学模型可知，需要确定的建模参数包括：螺栓预应力作用区域的薄层单元材料参数 ${E_1}$ 、 ${\mu _1}$ 以及非作用区域的薄层单元材料参数 ${E_2}$ 、 ${\mu _2}$ 。

2.1 目标函数的构建

本文利用固有频率的误差和模态置信准则残差的加权和来构建模型修正的目标函数：

${{\Pi }}\left( {{p}} \right) = \mathop \sum \limits_{i = 1}^N {\left( {\frac{{{\omega _{i{\rm{A}}}}\left( {{p}} \right) - {\omega _{i{\rm{E}}}}}}{{{\omega _{i{\rm{E}}}}}}} \right)^2} + \alpha \mathop \sum \limits_{i = 1}^N \frac{{{{\left( {1 - \sqrt {{\rm{MA}}{{\rm{C}}_i}\left( {{p}} \right)} } \right)}^2}}}{{{\rm{MA}}{{\rm{C}}_i}\left( {{p}} \right)}}$

(6)

式中： $N$ 表示实验测试模态阶数； ${{p}} \!\!=\! \!{\{ {{p_1}},{p_2}, \!\cdots \!,{{p_m}} } \}^{\rm{T}}$ 为待修正变量向量，其中，下标 $m$ 为修正变量个数； ${\omega _{i{\rm{E}}}}$ 和 ${\omega _{i{\rm{A}}}}$ 分别为实验和仿真的第i阶固有频率； $\alpha$ 为加权系数； ${\rm{MA}}{{\rm{C}}_i}$ 为第i阶模态的模态置信度。

$\alpha = \left\lfloor {\mathop \sum \limits_{i = 1}^N {{\left( {\frac{{{\omega _{i{\rm{A}}}}\left( {{{{p}}_0}} \right) - {\omega _{i{\rm{E}}}}}}{{{\omega _{i{\rm{E}}}}}}} \right)}^2}\Bigg/\mathop \sum \limits_{i = 1}^N \frac{{{{\left( {1 - \sqrt {{\rm{MA}}{{\rm{C}}_i}\left( {{{{p}}_0}} \right)} } \right)}^2}}}{{{\rm{MA}}{{\rm{C}}_i}\left( {{{{p}}_0}} \right)}}} \right\rfloor$

(7)

${\rm{MA}}{{\rm{C}}_i}( {{p}} ) = \frac{{{{( {{\bf\textit{φ}} _{i{\rm{A}}}^{\rm{T}}( {{p}} ){{\bf\textit{φ}} _{i{\rm{E}}}}} )}^2}}}{{( {{\bf\textit{φ}} _{i{\rm{A}}}^{\rm{T}}( {{p}} ){{\bf\textit{φ}} _{i{\rm{A}}}}( {{p}} )} )( {{\bf\textit{φ}} _{i{\rm{E}}}^{\rm{T}}{{\bf\textit{φ}} _{i{\rm{E}}}}} )}}\;\;\;\;\qquad\qquad\quad$

(8)

式中： $\left\lfloor \centerdot \right\rfloor$ 为取整符号； ${{{p}}_0}$ 为修正变量初始值向量； ${{\bf\textit{φ}} _{i{\rm{E}}}}$ 和 ${{\bf\textit{φ}} _{i{\rm{A}}}}$ 分别为实验和仿真的第i阶模态振型向量。

2.2 水循环优化算法

从式(6)可以看出，当目标函数 ${{\Pi }}\left( {{p}} \right)$ 取得最小值时，即可得到模型修正问题的解，即薄层单元的待确定参数。因此需要将式(6)转化为如下的最小值问题：

$\left\{ \begin{split} & {\rm{min}}\left( {{\rm{\Pi }}\left( {{p}} \right)} \right)\\& {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\underline {{p}} \leqslant {{p}} \leqslant \bar {{p}} \end{split} \right.$

(9)

式中， $\bar {{p}}$ 和 $\underline {{p}}$ 分别表示修正变量向量的上、下界向量。

本文选择水循环优化算法来执行式(9)所示的最小值优化问题。水循环优化算法是Eskandar等^[19]于2012年提出的一种新颖的优化算法，其理论受启发于大自然，是通过观察大自然水循环过程中水的流动和转换而提出的。目前，水循环算法已经被广泛地应用于各类实际工程优化问题中，如Cho和Kim^[20]将水循环算法应用于混合电磁铁的优化设计方法中，通过实验验证了该算法的性能优于常规优化算法；Ghaffarzadeh^[21]提出采用水循环算法来开发电力系统稳定器，结果表明，采用水循环算法可以在较短时间内检测出最优参数，进一步提高了电力系统的稳定性。然而，据本文作者所知，水循环算法尚未被应用到解决结构动力学模型修正的问题中。

执行水循环算法，首先要随机生成一个初始降雨层(类似于遗传算法的种群或粒子群算法中的粒子群)，其包含的个体称为雨滴(Raindrop)，代表优化问题中的一组解(类似于遗传算法的染色体或者粒子群算法中的粒子)。初始降雨层中的每个雨滴 ${{{R}}_i}$ 是在给定范围内随机产生的向量，对于本文中的 $m$ 维修正变量问题，其表达式为：

${{{R}}_i} = \underline {{p}} + {\delta _i} \times ( {\bar {{p}} - \underline {{p}} } ),\;\;\; {i = 1,2, \cdots ,n}$

(10)

式中： ${\delta _i} \in U\left( {0,1} \right)$ 为服从均匀分布的随机数； $n$ 为降雨层中的雨滴个数。

其次，将所有雨滴根据其目标函数值(即式(6))的大小划分为三个等级，其中最好的雨滴(即当前目标函数值最小的雨滴)形成海洋，较好的一些形成河流，其余的雨滴形成流向河流和海洋的溪流：

$\left[\!\! {\begin{array}{*{20}{c}} {{{{R}}_1}}\\ {{{{R}}_2}}\\ {{{{R}}_3}}\\ {{{{R}}_4}}\\ \vdots \\ {{{{R}}_n}} \end{array}} \!\!\right] = \left[\!\! {\begin{array}{*{20}{c}} {\rm {Sea}}\\ {\rm {Rive}{r_1}}\\ {\rm {Rive}{r_2}}\\ \vdots \\ {\rm {Stream}}_{N_{{\rm{Sr}}} + 1}\\ \vdots \\ {\rm {Stream}}_n \end{array}} \!\!\right] = \left[\!\! {\begin{array}{*{20}{c}} {{p_{1,1}}}&{{p_{1,2}}}& \cdots &{{p_{1,m}}}\\ {{p_{2,1}}}&{{p_{2,2}}}&{ \cdots }&{{p_{2,m}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{p_{n,1}}}&{{p_{n,2}}}& \cdots &{{p_{n,m}}} \end{array}} \!\!\right]$

(11)

式中，下标 ${N_{{\rm{Sr}}}}$ 为河流数和海洋数之和，且海洋数为1。

假定所有溪流都会汇入河流或者海洋，由于河流和海洋的流量不同，流入每条河流和海洋的溪流数量NS就不同，具体为：

$N{S_j} = \left| {\frac{{{{\Pi }}( {{{{R}}_j}} ) - {{\Pi }}( {{{{R}}_{{N_{{\rm{Sr}}}} + 1}}} )}}{{\mathop \displaystyle \sum \nolimits_{j = 1}^{{N_{{\rm{Sr}}}}} ( {{{\Pi }}( {{{{R}}_j}} ) - {{\Pi }}( {{{{R}}_{{N_{{\rm{Sr}}}} + 1}}} )} )}}} \right| \times {N_{{\rm{Stream}}}}$

(12)

式中， ${N}_{{\rm{Stream}}}$ 为溪流的数目。

然后，水循环算法进入汇流阶段。其中：一部分溪流先汇入河流，再汇入海洋；另一部分溪流则直接汇入海洋。具体汇流的表达式如下：

$\begin{split} & \vec {{R}}_{{\rm{Stream}}}^i( {t + 1} ) = \\& \vec {{R}}_{{\rm{Stream}}}^i( t ) + \delta \times C \times ( {{{\vec {{R}}}_{{\rm{River}}}}( t ) - \vec {{R}}_{{\rm{Stream}}}^i( t )} ), \\& {i = 1,2, \cdots ,{N_{{\rm{Stream}}}}} \end{split}$

(13)

$\begin{split} & \vec {{R}}_{{\rm{Stream}}}^i( {t + 1} ) = \\& \vec {{R}}_{{\rm{Stream}}}^i( t ) + \delta \times C \times ( {{{\vec {{R}}}_{{\rm{Sea}}}}( t ) - \vec {{R}}_{{\rm{Stream}}}^i( t )} ), \\& {i = 1,2, \cdots ,{N_{{\rm{Stream}}}}} \end{split} \;\;$

(14)

$\begin{split} & \vec {{R}}_{{\rm{River}}}^i( {t + 1} ) = \\& \vec {{R}}_{{\rm{River}}}^i( t ) + \delta \times C \times ( {{{\vec {{R}}}_{{\rm{Sea}}}}( t ) - \vec {{R}}_{{\rm{River}}}^i( t )} ), \\& {i = 1,2, \cdots ,{N_{{\rm{Sr}}}} - 1} \end{split} \quad$

(15)

式中： $\vec {{R}}_{{\rm{Stream}}}^{}\left( t \right)$ 、 $\vec {{R}}_{{\rm{River}}}^{}\left( t \right)$ 和 $\vec {{R}}_{{\rm{Sea}}}^{}\left( t \right)$ 分别为第 $t$ 代优化中溪流、河流和海洋的位置； $C \in \left[ {1,2} \right]$ 为位置更新的系数，本文选择 $C = 2$ 。式(13)表示溪流汇入河流的过程，以河流的位置为导向，溪流靠近河流，搜索河流位置附近空间，对比溪流与河流的目标函数值，若溪流的目标值优于河流的目标值，则彼此交换位置。同理，式(14)表示溪流直接汇入海洋的过程，式(15)表示河流汇入海洋的过程。最终海洋为最优解。

为了防止算法陷入局部最优，通过蒸发和降雨来扩大算法的搜索空间。降雨过程可根据降雨位置的不同分为两种：一种是在溪流或河流附近降雨，即随机产生溪流或河流的新个体，增大算法的搜索域；另一种是在海洋附近降雨，即在海洋附近随机产生新个体，使算法在当前最优解附近寻找更优解。可以根据以下两个条件来判断是否满足降雨条件：

$\| {{{\vec {{R}}}_{{\rm{Sea}}}}( t ) - \vec {{R}}_{{\rm{River}}}^i( t )} \| < {d_{{\rm{max}}}}\;, \;\delta < 0.1$

(16)

$\| {{{\vec {{R}}}_{{\rm{Sea}}}}( t ) - \vec {{R}}_{{\rm{Stream}}}^i( t )} \| < {d_{{\rm{max}}}}\qquad\qquad$

(17)

式中， ${d_{{\rm{max}}}}$ 为人为设置的阈值，通常在算法初始阶段取 ${d_{{\rm{max}}}} = {10^{ - 16}}$ ，且随着迭代地进行自适应减小，具体为：

$d_{{\rm{max}}}^{t + 1} = d_{{\rm{max}}}^t - \frac{{d_{{\rm{max}}}^t}}{M}$

(18)

式中， $M$ 为最大迭代次数。

如果满足式(16)，则在整个搜索空间内进行降雨，具体为：

${{R}}_{{\rm{Stream}}}^{{\rm{new}}} = {\underline {{p}} } + \delta \times ( {\bar {{p}} - {\underline {{p}} } } )$

(19)

如果满足公式(17)，则在海洋附近区域进行降雨，具体为：

${{R}}_{{\rm{Stream}}}^{{\rm{new}}} = {{{R}}_{{\rm{Sea}}}} + \sqrt \nu \times {\bf\textit{λ}}$

(20)

式中： ${\bf\textit{λ}}$ 为服从均匀分布的随机数向量； $\nu$ 为在海洋附近的搜索范围的大小，通常取 $\nu = 0.1$ 。

同其他启发式智能优化算法一样，本文选用最大迭代次数作为水循环优化算法的终止条件。

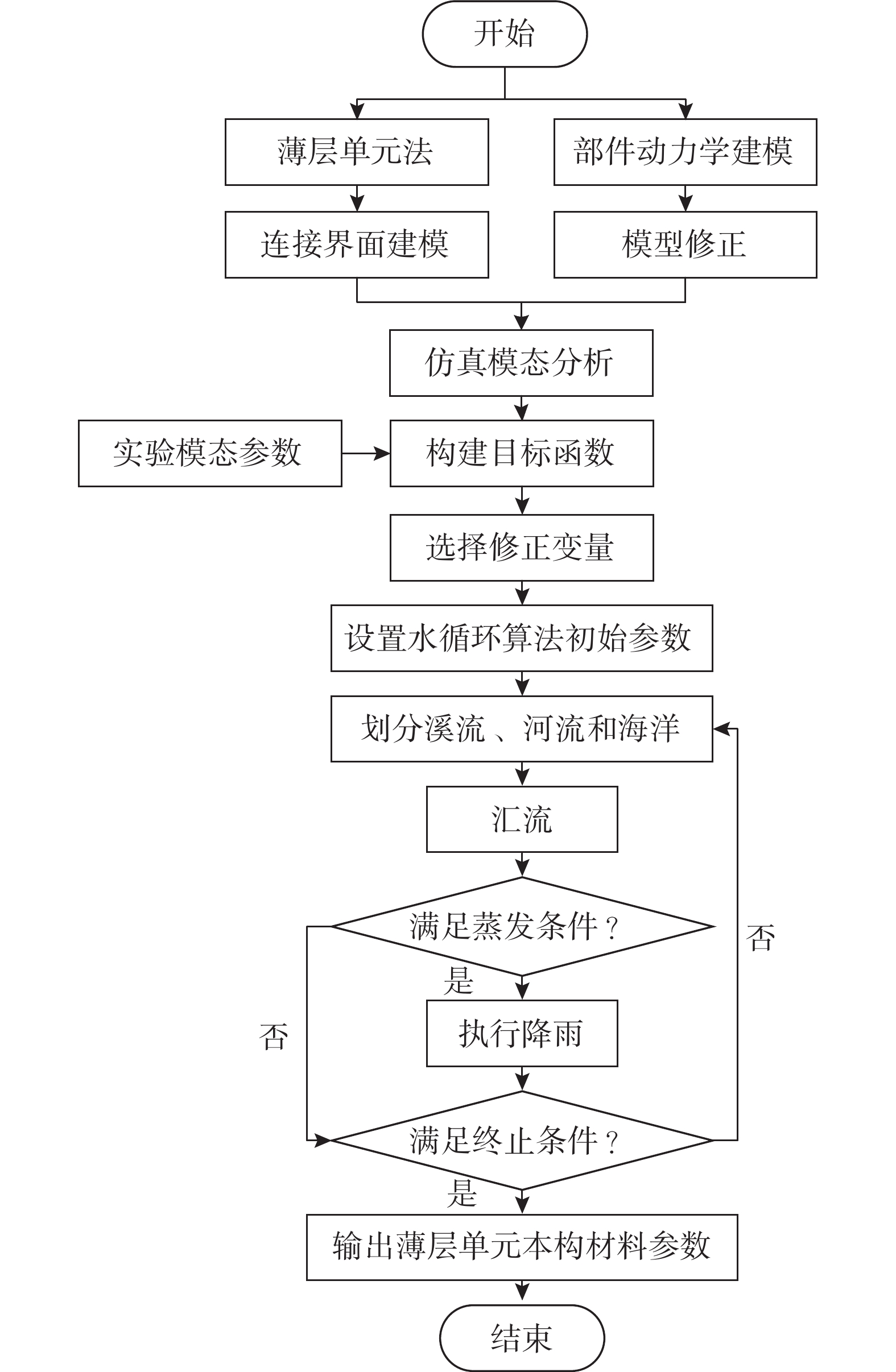
综上，结合薄层单元法和模型修正方法的螺栓连接板结构动力学建模流程如图3所示，且具体实施步骤如下：

第一步，建立部件结构的动力学模型，并对其建模参数进行修正；

第二步，采用薄层单元法建立螺栓连接板结构的初始有限元模型，并进行模态分析，提取仿真模态参数；进行螺栓连接板结构的实验模态分析，提取相应的实验模态参数；

第三步，利用实验模态参数与对应仿真模态参数，构造模型修正目标函数；

第四步，选择修正变量，给定修正范围；

第五步，设置水循环算法的初始参数，如初始雨滴数目 $n$ ，海洋加河流的数目 ${N_{{\rm{Sr}}}}$ ，溪流数目参数 ${N_{{\rm{Stream}}}}$ ，蒸发条件判断数 ${d_{{\rm{max}}}}$ ，最大迭代次数 $M$ 等；

第六步，产生初始种群，根据目标函数值划分海洋、河流和溪流，计算汇流数目，进行相应的汇流；

第七步，判断是否满足蒸发条件，如果满足，则执行降雨过程；

第八步，判断是否满足算法终止条件，如果满足，则结束算法并输出最优解；如果不满足，则返回到汇流过程，继续执行算法，直到满足终止条件为止；

第九步，输出算法最优解，即为建模所需的薄层单元的材料参数。

图 3 基于模型修正的螺栓连接板结构动力学建模流程图

Figure 3. Flow chart of dynamic modeling of bolted plate structure based on model updating

下载: 全尺寸图片幻灯片

3 实验验证

为了验证本文所提的螺栓连接板结构动力学建模方法的可行性和实用性，设计了如图4所示的两端固支五螺栓搭接板模型，其中，单板的尺寸为240 mm×120 mm×3 mm(去除边界加持区域)；搭接区域长度为40 mm。搭接板材料为铝合金，采用5个M6不锈钢螺栓进行连接，且拧紧力矩为5.2 N∙m。

图 4 五螺栓搭接板结构

Figure 4. Five-bolt lap plate

下载: 全尺寸图片幻灯片

实验结构与测试设备如图5所示，包括信号采集及模态识别系统(LMS SCADAS Mobile)、PCB力锤(灵敏度为2.267 mV/N)、PCB加速度传感器(灵敏度为100.5 mV/g)和STANLEY扭矩扳手。实验中采用“移动激励点法”进行模态测试。为了抑制由于信号截断引起的泄漏，实验测试中对输入信号(即激励信号)添加力窗，并对输出信号(即响应信号)添加指数窗。为了一定程度上消除测试噪声的影响，实验中在每个测点进行3次测量，并对3次测试响应数据进行平均。本实验所关心的结构的频带范围为1 Hz~620 Hz，包含了结构前6阶模态，实验中设定振动信号的采样频率为1280 Hz(大于最大测试频率的2倍)，频率分辨率为0.31 Hz。实验获得的结构前六阶模态结果见表1。

图 5 模态试验现场布置图

Figure 5. Layout of modal test

下载: 全尺寸图片幻灯片

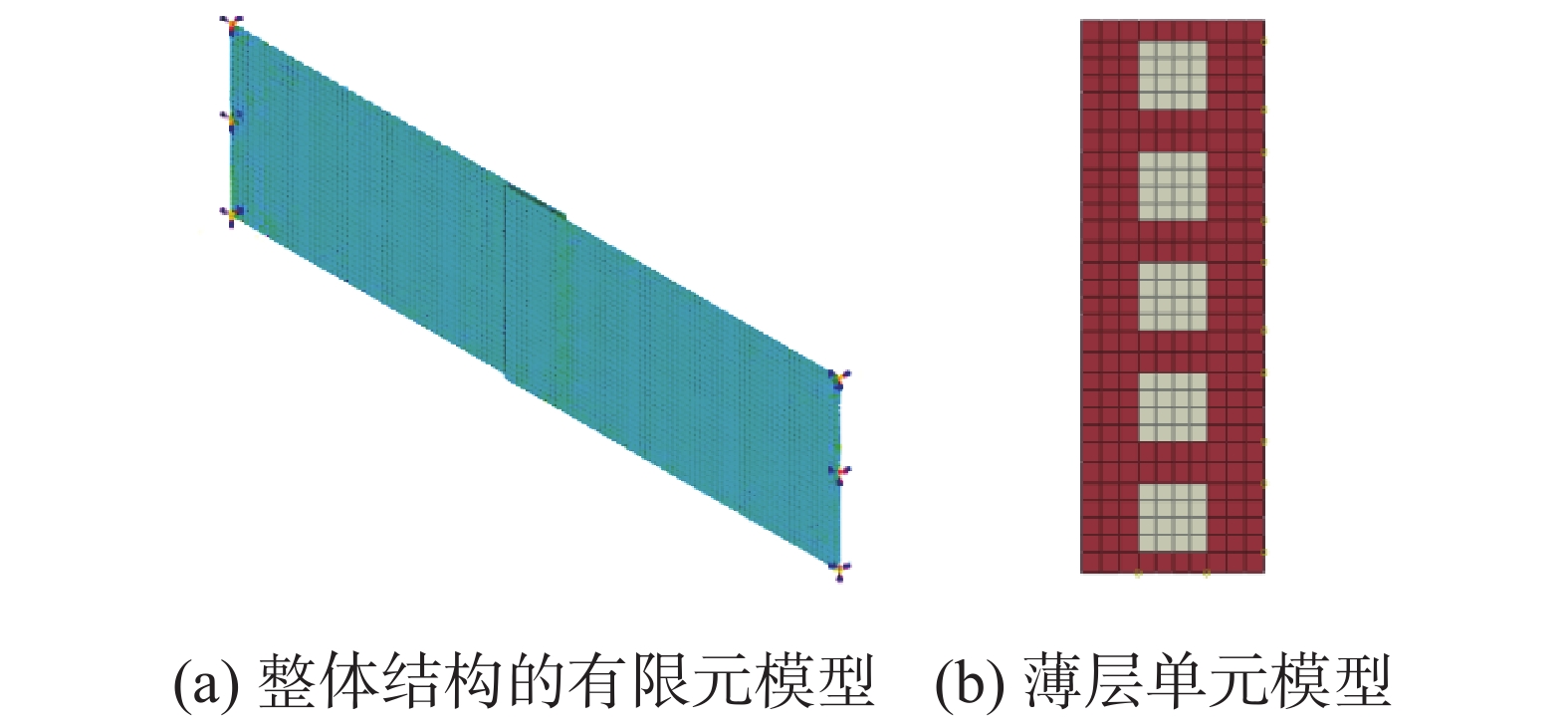
首先对部件结构(即板1和板2)的模型参数进行修正。通过对实验件进行测量，得到板1和板2的尺寸分别为240 mm×120 mm×2.96 mm和240 mm×120 mm×2.95 mm，重量分别为284 g和282 g，可计算得到结构的材料密度为2717.7×10⁻¹² t/mm³。所以仅需要对其材料弹性模量 $E$ 和泊松比 $\mu$ 进行修正。选取板1为修正结构，进行模态实验，边界条件为自由-自由，且采用4边形壳单元对单板结构进行有限元建模，修正后的材料参数见表2。

表 1 五螺栓搭接板前六阶实验模态

Table 1. First six experimental modes of five-bolt lap plate

阶数	模态频率/ Hz	振型描述
1	65.581	一弯
2	171.442	一扭
3	219.453	二弯
4	386.231	三弯
5	454.419	二扭
6	615.745	三扭

下载: 导出CSV

| 显示表格

表 2 修正后的板的材料属性

Table 2. Updated material properties of plate

弹性模量/ MPa	泊松比
6.8149×10⁴	0.285

下载: 导出CSV

| 显示表格

根据第2节中所述的螺栓连接结构的动力学建模方法，建立了如图6(a)所示的有限元模型，薄层单元采用六面体8节点实体单元，其中白色单元区域为螺栓预应力作用区域，红色单元区域为非螺栓预应力作用区域，如图6(b)所示。对结构进行有限元离散时选择的最大单元边长为4.5 mm，根据式(1)，我们选取得薄层单元厚度为0.1 mm。

图 6 五螺栓搭接板有限元模型

Figure 6. Finite element model of five-bolt lap plate

下载: 全尺寸图片幻灯片

定义设计变量集 ${{p}} = \left\{ {{E_1},{\mu _1},{E_2},{\mu _2}} \right\}$ ，每个设计变量相对于固有频率的灵敏度如图7所示。

从图7可以看出，泊松比 ${\mu _1}$ 和 ${\mu _2}$ 对低阶模态不敏感，因此，选择敏感性较强的设计变量 ${E_1}$ 和 ${E_2}$ 作为模型修正的修正变量，并分别给定修正区间为 ${E_1} \in [ {0.001}\;\;{10} ]$ 和 ${E_2} \in [ {0.001}\;\;{10} ]$ ；建模中设定 ${\mu _1}{\rm{ = }}{\mu _{\rm{2}}}{\rm{ = 0}}{\rm{.3}}$ 。

采用第2节建立的模型修正方法对修正变量进行修正，其中水循环算法的具体参数设定见表3。

图 7 设计变量对于固有频率灵敏度分析

Figure 7. Sensitivity of natural frequencies versus design parameters

下载: 全尺寸图片幻灯片

表 3 水循环算法的参数设定

Table 3. Water cycle algorithm parameters

参数	设定值
变量个数	2
雨滴数	30
位置更新系数C	2
d_max	10⁻¹⁶
最大迭代次数	40

下载: 导出CSV

| 显示表格

将修正后的参数输入有限元模型(即E₁=0.001 MPa，E₂=0.2957 MPa)，进行模态分析，并将参数修正后的模态分析结果与实验结果进行对比，详见表4。

表 4 修正后模态分析结果

Table 4. Modal analysis results after updating

阶数	固有频率/ Hz			MAC
阶数	实验值	修正结果	误差/(%)	MAC
1	65.581	66.518	1.43	0.991
2	171.442	174.337	1.69	0.988
3	219.453	222.925	1.58	0.989
4	386.231	389.427	0.83	0.957
5	454.419	450.168	0.94	0.963
6	615.745	614.248	0.24	0.918

下载: 导出CSV

| 显示表格

从表4可以看出，采用本文提出的动力学建模方法建立的螺栓连接板结构的动力学模型可以很好的预示结构的动力学特性，固有频率的最大相对误差仅为1.69%，且MAC均大于0.91，满足工程中对结构动力学建模的需求。

3.1 优化算法对比

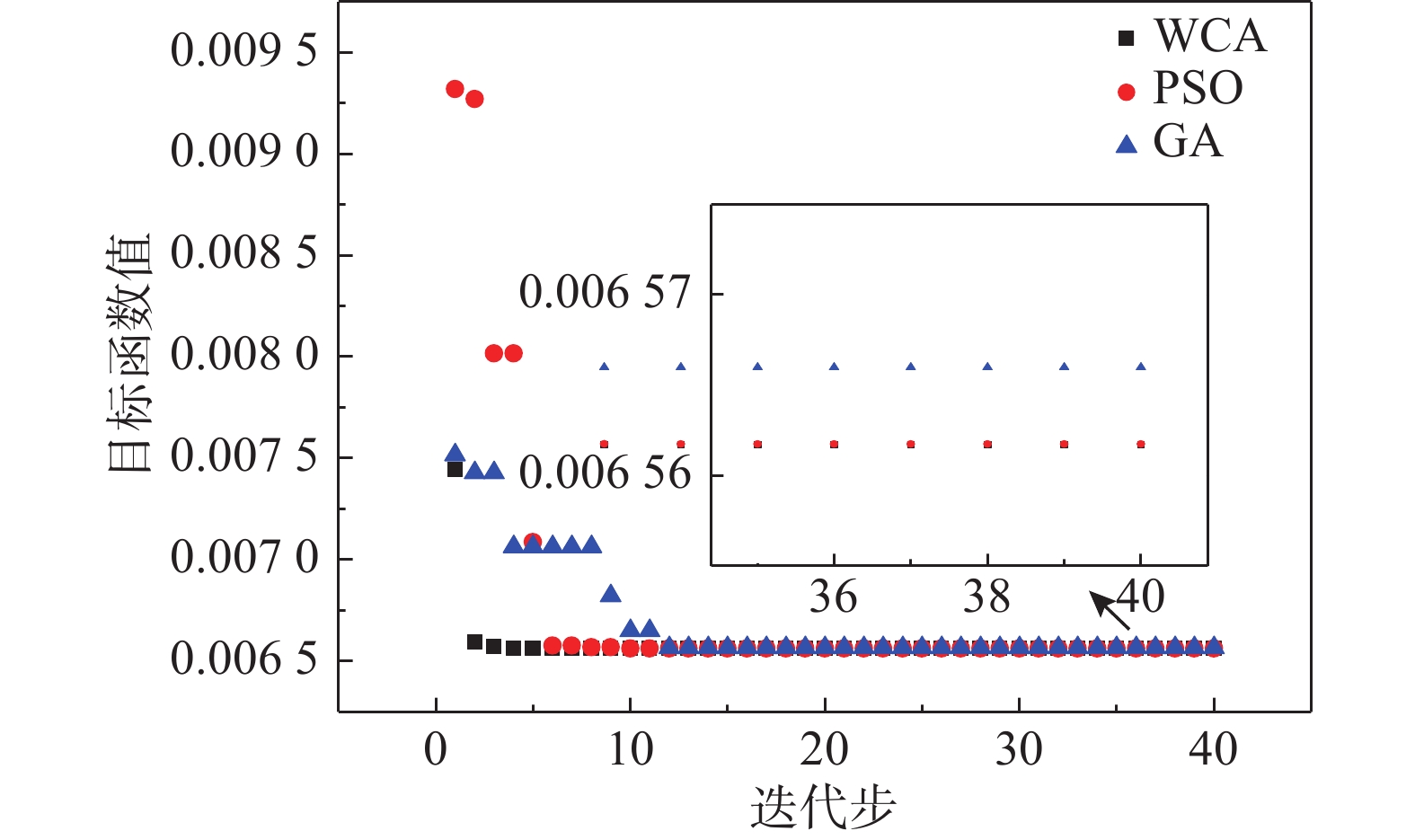
本文分别采用遗传算法^[22](Genetic Algorithm, GA)、粒子群算法^[23](Particle Swarm Optimization, PSO)和水循环算法(Water Cycle Algorithm, WCA)三种全局智能优化算法对算例中的薄层单元的参数进行修正。为了使修正结果具有可比性，将算法的种群数、粒子群数和雨滴数均设置为30，迭代次数均设置为40次。图8为分别采用三种优化算法执行模型修正问题的收敛情况对比结果。从图8中可以看出，相比遗传算法和粒子群算法，水循环算法的收敛曲线下降最快，目标函数值最小，表明水循环算法在求解结构动力学模型修正问题时具有收敛快、精度高的优点。

图 8 不同智能优化算法优化结果对比图

Figure 8. Comparison of optimization results of different intelligent optimization algorithms

下载: 全尺寸图片幻灯片

为了进一步验证水循环算法在求解最优化问题(式(9))时具有唯一性，本文在保证相同优化参数设定的前提下，重复运行求解过程10次，均得到了相同的最优解和最佳适应度值，即，E₁=0.001 MPa；E₂=0.2957 MPa；∏(p)=0.006 561 7，说明了采用水循环算法在求解结构动力学优化问题时具有很好的鲁棒性。

3.2 抗噪性验证

本节对所提动力学建模方法的抗噪性进行验证。通过对实验模态数据添加人为噪声来模拟带有测试噪声的模态参数识别结果，即：

${{{X}}_{\rm{E}}} = {{{X}}_{\rm{E}}}\left( {1 + \eta {{\delta}} } \right)$

(22)

式中： ${{{X}}_{\rm{E}}}$ 代表固有频率向量或第i阶模态振型向量； $\eta$ 为噪声水平； ${{\delta}}$ 为均值为0、方差为1，并满足标准正态分布的随机向量。

众所周知，测试噪声对识别结构的固有频率和模态振型的影响是不相同的，固有频率一般可以比较精确地识别，而模态振型的识别精度比固有频率的精度要差很多。因此，选取了两种噪声水平工况来考察本文所提出的螺栓连接板结构动力学建模方法的抗噪性，具体为：工况1(固有频率( $\eta = 1\text{%}$ )，模态振型( $\eta = 5\text{%}$ )；工况2(固有频率( $\eta = 2\text{%}$ )，模态振型( $\eta = 10\text{%}$ )。表5和表6分别给出了不同噪声水平下的固有频率和MAC值对比结果。图9示出了不同噪声水平下修正后获得的MAC值对比情况。

表 5 不同噪声水平下的固有频率对比

Table 5. Comparison of modal frequencies under different noise levels

分析工况	固有频率 / Hz
分析工况	1	2	3	4	5	6
实验值(噪声水平1)	65.74	170.26	218.02	390.84	447.09	615.59
实验值(噪声水平2)	67.15	177.04	212.73	375.90	441.02	615.23
修正后(噪声水平1)	66.60	174.50	223.14	390.24	450.42	615.09
相对误差/(%)	1.31	2.49	2.35	0.15	0.74	0.08
修正后(噪声水平2)	66.35	174.01	222.53	387.69	449.66	612.49
相对误差/(%)	1.19	1.71	4.61	3.14	1.96	0.45

下载: 导出CSV

| 显示表格

表 6 不同噪声水平下的MAC值对比

Table 6. Comparison of MAC under different noise levels

阶数	MAC
阶数	无噪声	噪声水平1	噪声水平2
1	0.991	0.984	0.979
2	0.988	0.989	0.985
3	0.989	0.991	0.978
4	0.957	0.959	0.945
5	0.963	0.949	0.946
6	0.918	0.907	0.911

下载: 导出CSV

| 显示表格

图 9 不同误差水平下修正后的MAC值对比

Figure 9. Comparison of MAC under different noise levels

下载: 全尺寸图片幻灯片

综合上述对比结果可以看出，在第一种噪声水平下，固有频率的最大相对误差仅为2.49%，MAC值均大于0.9，其最小值为0.907。在第二种噪声水平下，固有频率的最大相对误差为4.61%，MAC值均大于0.9，其最小值为0.911。上述结果表明，在两种噪声工况下建立的螺栓连接板结构的动力学有限元模型的动力学特性都和真实结构的测试结果吻合得很好，表明本文所建立的动力学建模方法具有良好的抗噪性。

4 结论

本文针对螺栓连接板的动力学建模问题，提出了一种结合薄层单元法和模型修正的建模方法。采用薄层单元法建立了用于模型修正的初始动力学模型，将薄层单元的不确定材料本构参数作为修正变量，引入水循环算法来进行优化求解。从本文的研究中可得出以下结论：

(1)相对于遗传算法和粒子群算法，采用水循环算法进行动力学模型修正，极大的提高了求解效率。

(2)采用两端固支五螺栓搭接板结构作为实验验证模型，验证了提出的螺栓连接板结构动力学建模方法是合理可行的，建立的动力学预示模型可以更好地用于进行结构的动力学分析，并且具有良好的抗噪性。

图 1 螺栓连接板结构动力学建模

Figure 1. Dynamic modeling of bolted joint plate

下载: 全尺寸图片幻灯片

图 2 螺栓连接界面应力分布示意图

Figure 2. Stress distribution at bolted joint interface

下载: 全尺寸图片幻灯片

图 3 基于模型修正的螺栓连接板结构动力学建模流程图

Figure 3. Flow chart of dynamic modeling of bolted plate structure based on model updating

下载: 全尺寸图片幻灯片

图 4 五螺栓搭接板结构

Figure 4. Five-bolt lap plate

下载: 全尺寸图片幻灯片

图 5 模态试验现场布置图

Figure 5. Layout of modal test

下载: 全尺寸图片幻灯片

图 6 五螺栓搭接板有限元模型

Figure 6. Finite element model of five-bolt lap plate

下载: 全尺寸图片幻灯片

图 7 设计变量对于固有频率灵敏度分析

Figure 7. Sensitivity of natural frequencies versus design parameters

下载: 全尺寸图片幻灯片

图 8 不同智能优化算法优化结果对比图

Figure 8. Comparison of optimization results of different intelligent optimization algorithms

下载: 全尺寸图片幻灯片

图 9 不同误差水平下修正后的MAC值对比

Figure 9. Comparison of MAC under different noise levels

下载: 全尺寸图片幻灯片

表 1 五螺栓搭接板前六阶实验模态

Table 1 First six experimental modes of five-bolt lap plate

阶数	模态频率/ Hz	振型描述
1	65.581	一弯
2	171.442	一扭
3	219.453	二弯
4	386.231	三弯
5	454.419	二扭
6	615.745	三扭

下载: 导出CSV

表 2 修正后的板的材料属性

Table 2 Updated material properties of plate

弹性模量/ MPa	泊松比
6.8149×10⁴	0.285

下载: 导出CSV

表 3 水循环算法的参数设定

Table 3 Water cycle algorithm parameters

参数	设定值
变量个数	2
雨滴数	30
位置更新系数C	2
d_max	10⁻¹⁶
最大迭代次数	40

下载: 导出CSV

表 4 修正后模态分析结果

Table 4 Modal analysis results after updating

阶数	固有频率/ Hz			MAC
阶数	实验值	修正结果	误差/(%)	MAC
1	65.581	66.518	1.43	0.991
2	171.442	174.337	1.69	0.988
3	219.453	222.925	1.58	0.989
4	386.231	389.427	0.83	0.957
5	454.419	450.168	0.94	0.963
6	615.745	614.248	0.24	0.918

下载: 导出CSV

表 5 不同噪声水平下的固有频率对比

Table 5 Comparison of modal frequencies under different noise levels

分析工况	固有频率 / Hz
分析工况	1	2	3	4	5	6
实验值(噪声水平1)	65.74	170.26	218.02	390.84	447.09	615.59
实验值(噪声水平2)	67.15	177.04	212.73	375.90	441.02	615.23
修正后(噪声水平1)	66.60	174.50	223.14	390.24	450.42	615.09
相对误差/(%)	1.31	2.49	2.35	0.15	0.74	0.08
修正后(噪声水平2)	66.35	174.01	222.53	387.69	449.66	612.49
相对误差/(%)	1.19	1.71	4.61	3.14	1.96	0.45

下载: 导出CSV

表 6 不同噪声水平下的MAC值对比

Table 6 Comparison of MAC under different noise levels

阶数	MAC
阶数	无噪声	噪声水平1	噪声水平2
1	0.991	0.984	0.979
2	0.988	0.989	0.985
3	0.989	0.991	0.978
4	0.957	0.959	0.945
5	0.963	0.949	0.946
6	0.918	0.907	0.911

下载: 导出CSV

参考文献(23)

[1]	孟光, 周徐斌, 苗军. 航天重大工程中的力学问题[J]. 力学进展, 2016, 46: 201606. doi: 10.6052/1000-0992-15-018 Meng Guang, Zhou Xubin, Miao Jun. Mechanical problems in momentous projects of aerospace engineering [J]. Advances in Mechanics, 2016, 46: 201606. (in Chinese) doi: 10.6052/1000-0992-15-018
[2]	Semke W H, Bibel G D, Jerath S, et al. Efficient dynamic structural response modelling of bolted flange piping systems [J]. International Journal of Pressure Vessels and Piping, 2006, 83(10): 767 − 776. doi: 10.1016/j.ijpvp.2006.06.003
[3]	张根辈, 臧朝平, 王晓伟, 等. 螺栓连接框架结构的有限元模型修正[J]. 工程力学, 2014, 31(4): 26 − 33. doi: 10.6052/j.issn.1000-4750.2012.11.0858 Zhang Genbei, Zang Chaoping, Wang Xiaowei, et al. Finite element model updating of a framed structure with bolted joints [J]. Engineering Mechanics, 2014, 31(4): 26 − 33. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.11.0858
[4]	Chen J, Rose T M, Trubert M, et al. Modal test/analysis correlation for the Centaur G prime launch vehicle [J]. Journal of Spacecraft and Rockets, 1987, 24(5): 423 − 429. doi: 10.2514/3.25934
[5]	Ho-Nguyen-Tan T, Kim H G. A novel scheme for modelling and analysis of spot-welded shell structures using interface shell elements [J]. Computers & Structures, 2020, 239: 106340.
[6]	Iwan W D. A distributed-element model for hysteresis and its steady-state dynamic response [J]. Journal of Applied Mechanics, 1966, 33(4): 893 − 900. doi: 10.1115/1.3625199
[7]	Li D, Xu C, Liu T, et al. A modified IWAN model for micro-slip in the context of dampers for turbine blade dynamics [J]. Mechanical Systems and Signal Processing, 2019, 121: 14 − 30. doi: 10.1016/j.ymssp.2018.11.002
[8]	Gaul L, Nitsche R. The role of friction in mechanical joints [J]. Applied Mechanics Reviews, 2001, 54(2): 93 − 106. doi: 10.1115/1.3097294
[9]	Segalman D J, Starr M J. Relationships among certain joint constitutive models [R]. Sandia National Laboratories, 2004.
[10]	Mayer M H, Gaul L. Segment-to-segment contact elements for modelling joint interfaces in finite element analysis [J]. Mechanical Systems and Signal Processing, 2007, 21(2): 724 − 734. doi: 10.1016/j.ymssp.2005.10.006
[11]	翟学, 翟庆刚, 王建军, 等. 基于有限元的螺栓连接参数化建模技术研究[J]. 推进技术, 2016, 37(7): 1364 − 1371. Zhai Xue, Zhai Qinggang, Wang Jianjun, et al. Parameterized modeling technology of bolted joints based on finite element [J]. Journal of Propulsion Technology, 2016, 37(7): 1364 − 1371. (in Chinese)
[12]	Iranzad M, Ahmadian H. Identification of nonlinear bolted lap joint models [J]. Computers & Structures, 2012, 96: 1 − 8.
[13]	姚星宇, 王建军. 航空发动机螺栓连接载荷与结构参数对连接刚度影响规律[J]. 推进技术, 2017, 38(2): 424 − 433. Yao Xingyu, Wang Jianjun. Effects of load and structure parameters of aero-engine bolted joints on joint stiffness [J]. Journal of Propulsion Technology, 2017, 38(2): 424 − 433. (in Chinese)
[14]	王攀, 臧朝平. 机匣螺栓连接分区域薄层单元建模方法[J]. 航空发动机, 2019, 45(2): 11 − 16. Wang Pan, Zang Chaoping. Modeling method of subarea thin-layer element for casing bolted joints [J]. Aeroengine, 2019, 45(2): 11 − 16. (in Chinese)
[15]	姜东, 吴邵庆, 史勤丰, 等. 基于各向同性本构关系薄层单元的螺栓连接参数识别[J]. 振动与冲击, 2014, 33(22): 35 − 40. Jiang Dong, Wu Shaoqing, Shi Qinfeng, et al. Parameter identification of bolted-joint based on the model with thin-layer elements with isotropic constitutive relationship [J]. Journal of Vibration and Shock, 2014, 33(22): 35 − 40. (in Chinese)
[16]	姜东, 吴邵庆, 史勤丰, 等. 基于薄层单元的螺栓连接结构接触面不确定性参数识别[J]. 工程力学, 2015, 32(4): 220 − 227. doi: 10.6052/j.issn.1000-4750.2013.10.0920 Jiang Dong, Wu Shaoqing, Shi Qinfeng, et al. Contact interface parameter identification of bolted structure with uncertainty using thin layer element method [J]. Engineering Mechanics, 2015, 32(4): 220 − 227. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.10.0920
[17]	Desai C S, Zaman M M, Lightner J G, et al. Thin-layer element for interfaces and joints [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1984, 8(1): 19 − 43. doi: 10.1002/nag.1610080103
[18]	Kim J, Yoon J C, Kang B S. Finite element analysis and modeling of structure with bolted joints [J]. Applied Mathematical Modelling, 2007, 31(5): 895 − 911.
[19]	Eskandar H, Sadollah A, Bahreininejad A, et al. Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems [J]. Computers & Structures, 2012, 110: 151 − 166.
[20]	Cho J H, Kim Y T. Design of hybrid magnet using advanced water cycle optimization algorithm [J]. Journal of Korean Institute of Intelligent Systems, 2019, 29(3): 189 − 196. doi: 10.5391/JKIIS.2019.29.3.189
[21]	Ghaffarzadeh N. Water cycle algorithm based power system stabilizer robust design for power systems [J]. Nephron Clinical Practice, 2015, 66(2): 91 − 96.
[22]	邓露, 钟玉婷, 杨远亮, 等. 冷弯薄壁型钢受弯构件承载力与延性优化研究[J]. 工程力学, 2021, 38(4): 93 − 101. doi: 10.6052/j.issn.1000-4750.2020.05.0327 Deng Lu, Zhong Yuting, Yang Yuanliang, et al. Optimization on bearing capacity and ductility of cold-formed thin-walled steel flexural member [J]. Engineering Mechanics, 2021, 38(4): 93 − 101. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.0327
[23]	夏志远, 李爱群, 李建慧, 等. 基于GMPSO的有限元模型修正方法验证[J]. 工程力学, 2019, 36(10): 66 − 74. doi: 10.6052/j.issn.1000-4750.2018.09.0506 Xia Zhiyuan, Li Aiqun, Li Jianhui, et al. Validation of finite element model updating methodology based on GMPSO [J]. Engineering Mechanics, 2019, 36(10): 66 − 74. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.09.0506

施引文献(15)

期刊类型引用(6)

1.	田亚雄，孙伟，杜东旭，刘宏浩. 考虑非均匀预紧的螺栓法兰连接双圆柱壳半解析动力学建模与分析. 中南大学学报(自然科学版). 2025(01): 68-79 . 百度学术
2.	崔永健，温华兵，曹植博，陈文聘，夏兆旺. 船用膜片联轴器的膜片组件简化建模方法及模态试验. 造船技术. 2024(02): 8-12 . 百度学术
3.	陈奕丰，魏莎，李旭龙，丁虎，陈立群. 基于Chebyshev多项式和区间重叠率的对接圆柱壳结构区间模型修正. 上海大学学报(自然科学版). 2024(05): 875-889 . 百度学术
4.	刘鹏韬，关天赐，王小鹏. 单螺栓连接梁的非线性连接层建模与参数识别. 振动与冲击. 2023(01): 190-197+231 . 百度学术
5.	姚星宇. 失谐螺栓连接对薄壁圆筒的动力特性影响. 北京航空航天大学学报. 2023(05): 1238-1246 . 百度学术
6.	汤涛，臧朝平，张根辈，张磊，陈俊杰. 螺栓连接梁非线性振动的定频试验研究. 机械制造与自动化. 2023(06): 28-31 . 百度学术

其他类型引用(9)

资源附件(0)

图(9) / 表(6)

计量

文章访问数: 940
HTML全文浏览量: 344
PDF下载量: 109
被引次数: 15

1 基于薄层单元法的螺栓连接板结构动力学建模
2 基于水循环算法的螺栓连接板结构动力学模型修正
2.1 目标函数的构建
2.2 水循环优化算法
3 实验验证
3.1 优化算法对比
3.2 抗噪性验证
4 结论

基于模型修正的螺栓连接板结构动力学建模方法

通讯作者: 郭 宁(1986−)，男，宁夏人，助理研究员，博士，主要从事飞行器结构动力学研究(E-mail: guoning@nwpu.edu.cn)

计量

出版历程

STRUCTURAL DYNAMIC MODELING METHOD OF BOLTED JOINT PLATES BASED ON MODEL UPDATING

1 基于薄层单元法的螺栓连接板结构动力学建模

2 基于水循环算法的螺栓连接板结构动力学模型修正

2.1 目标函数的构建

2.2 水循环优化算法

3 实验验证

3.1 优化算法对比

3.2 抗噪性验证

4 结论

期刊类型引用(6)

其他类型引用(9)

计量

出版历程

目录

1 基于薄层单元法的螺栓连接板结构动力学建模

2 基于水循环算法的螺栓连接板结构动力学模型修正

2.1 目标函数的构建

2.2 水循环优化算法

3 实验验证

3.1 优化算法对比

3.2 抗噪性验证

4 结论

通讯作者:
郭　宁(1986−)，男，宁夏人，助理研究员，博士，主要从事飞行器结构动力学研究(E-mail: guoning@nwpu.edu.cn)