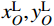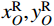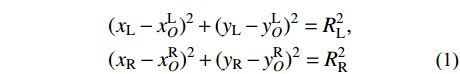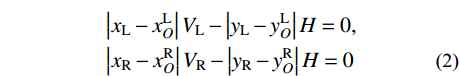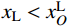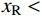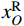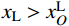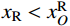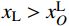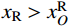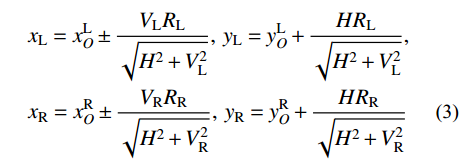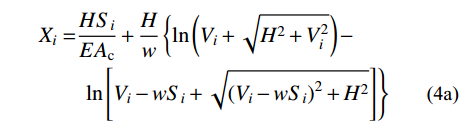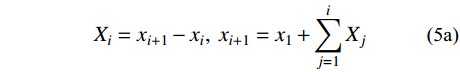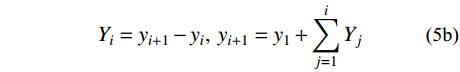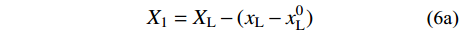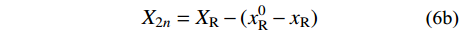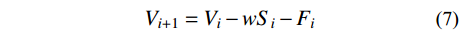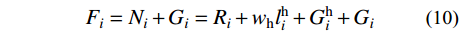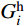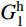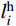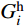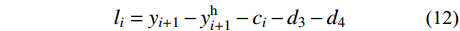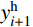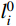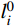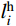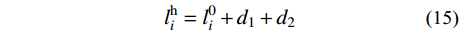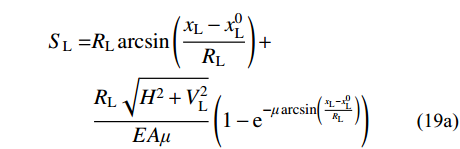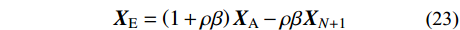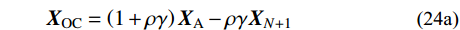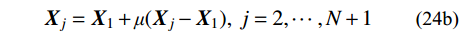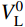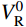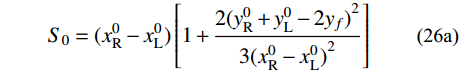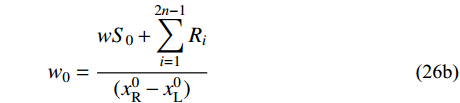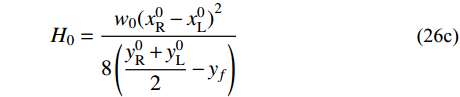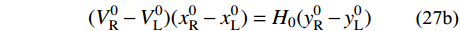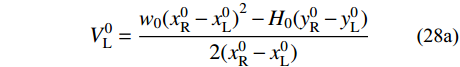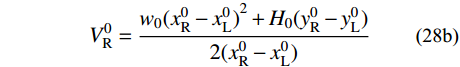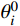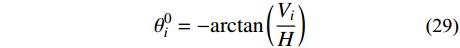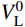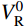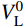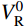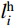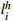HIGH-PRECISION CALCULATION METHOD FOR CONFIGURATION OF COMPLETED SUSPENSION BRIDGES WITH PIN-CONNECTED CABLE CLAMPS
-
摘要: 由于已有方法对索鞍和索夹的影响考虑不够全面,提出一种求解悬索桥目标成桥状态的高精度方法。该方法通过计入索鞍与主缆间的摩擦影响,全面考虑主缆与索鞍的接触问题,根据分段悬链线方程、闭合条件以及索鞍处主缆的力学平衡关系,分别推导得出中、边跨缆索系统的目标函数,采用Nelder-Mead算法求解函数以确定目标成桥状态。该求解过程自适应地计入了销接式索夹的影响,从而得到可靠的吊索钢丝下料长度和主缆无应力长度。以笋溪河大桥作为工程算例,将所提方法的计算结果与该桥设计值进行对比,验证了该文方法的可靠性。Abstract: Since the consideration on the saddles and clamps is not comprehensive enough in existing methods, a high-precision shape-finding method of the completed suspension bridges is proposed. This method takes the frictional effect and contact conditions between the main cable and saddles into account. According to the segmental catenary equation, the closure condition and the mechanical equilibrium relationship of the main cable at the saddle, the objective functions of mid-span and side-span systems of the main cable and saddles are derived respectively. The target configuration of a suspension bridge can be calculated by solving these objective functions using the Nelder-Mead algorithm, and then the fabrication lengths of hanger steel wires and the unstressed lengths of main cables can be credibly obtained because the influence of pin-connected cable clamps is considered into the shape-finding calculation adaptively. Finally, taking the Sunxi River Bridge as an example, the validity of this method is verified by the comparison between the calculation results and corresponding design ones of this bridge.
-
Keywords:
- bridge engineering /
- suspension bridge /
- Nelder-Mead algorithm /
- saddle /
- pin-connected cable clamp /
- main cable /
- hanger
-
悬索桥因其主缆和吊索呈柔性,展现出强烈的几何非线性行为[1]。理想成桥状态的悬索桥结构在恒载作用下应满足“塔直梁平”要求[2],且中跨主缆的跨中垂点应满足设计标高[3]。“塔直”是指主塔内不存在剪力,且塔顶主索鞍两侧主缆水平力相同;“梁平”是指主梁线形平顺,连接吊索的主梁锚点在恒载作用下处于设计位置且无下挠[4]。
以往学者对于求解悬索桥成桥状态已做了许多研究,该非线性问题的求解方法可主要分为两类:有限元法[4-6]和数值迭代法[7-13]。
有限元法通常以主缆跨中垂点高程为收敛目标,对悬索桥模型缆索单元的节点位置和初始内力进行反复迭代,直至满足收敛目标时停止计算。然而,建立悬索桥有限元模型时由于无法准确确定主缆在索鞍上的切点位置,因此难以准确模拟索鞍与主缆的接触状况,得到的主缆无应力长度与吊索钢丝下料长度很难达到设计精度需求。因此通常将有限元法作为近似方法,用于结构验算。
数值迭代法根据相邻索夹间各主缆分段在自重作用下呈悬链线的特点,采用分段悬链线方程[7]推算悬索桥的构型,该方法需已知成桥吊索力,根据主梁架设方法采用有限位移理论[4, 7, 11]易确定吊索力。唐茂林等[7]首次提出了悬索桥成桥找形的分段悬链线方法,该方法考虑了索鞍影响但未给出具体计入方式。罗喜恒[8]详述了将索鞍与主缆的相切状况计入悬索桥找形过程的方法,但未考虑索鞍与主缆间的摩擦影响。为了实现悬索桥的精确找形分析,李传习等[9]将单圆曲线索鞍位置计算的分离计算法推广到复合圆曲线索鞍位置的计算,完善了散索鞍与主缆相切状态方程;王邵瑞等[10]则推导了主索鞍与主缆的相切状态方程。Cao等[11]将吊索无应力长度自适应地计入悬索桥找形求解,但该方法没有考虑索鞍与主缆的接触状况,并且未计入索夹对吊索长度的影响。
在上述研究的基础上,笔者针对其不足之处提出了悬索桥成桥找形的高精度数值迭代法。该方法考虑了主缆与索鞍间的相切接触状况与摩擦影响,并将销接式索夹对主缆和吊索的影响自适应地计入分段悬链线方程中,构造并求解缆索系统的目标函数,最终为悬索桥的精确设计提供了解决方案。
1 计算方法
1.1 基本假定
1) 主缆和吊索是小应变的线弹性理想柔性索,忽略其弯曲刚度影响,满足虎克定律;
2) 实际工程中,悬索桥成桥时主塔中心线与塔顶主索鞍上主缆圆弧段的交点恰好是主缆固定点,该固定点也是中跨与边跨的分界点[12];
3) 实际工程中,悬索桥成桥时散索鞍(仅讨论常用的摆轴式散索鞍)转点与鞍槽内主缆固定点的连线垂直于支承面(或与支承面夹角已知),该固定点也是边跨与锚跨的分界点[12];
4) 主索鞍鞍槽是单段圆弧;散索鞍鞍槽是多段圆弧具有多个圆心,但边跨主缆在首段圆弧上[3]。
1.2 悬索桥成桥线形分析
悬索桥结构的几何参数如图1(a)所示,B、C是主索鞍,A、D是散索鞍,L1表示左边跨主缆在A、B两索鞍上切点间的水平距离;L2表示中跨主缆在B、C两索鞍上切点间的水平距离;L3表示右边跨主缆在C、D两索鞍上切点间的水平距离。如图1(b)所示,根据恒载作用下悬索桥结构内力分布情况可知,主缆位于各索夹及其吊索的上方,主梁位于其下方;根据主梁架设方法采用有限位移理论容易确定各吊索下端拉力Ri,再将Ri作为数值分析的输入,采用分段悬链线方程迭代求解缆索系统。Ni表示吊索上端拉力,受吊索自重影响,有Ni > Ri。
当悬索桥处于理想成桥状态时,主塔不应承受剪力作用,所以中、边跨内任意主缆索段内力的水平分量H都相等,应先求解中跨缆索系统得到H,再将其作为已知量求解边跨缆索系统。因此悬索桥成桥状态的数值求解按先中跨、后边跨进行,最终得到设计所需的主缆无应力长度、索夹中心(即主缆分点)坐标、索夹倾角、索鞍切点位置、吊索钢丝下料长度。由于IP点已知、鞍座位置未知的情况研究已较成熟[5-7, 10-11],故本文仅讨论鞍座位置给定的情况[3, 8]:即先假定主缆一端切点处的张力,再以主缆与另一端鞍座相切(中跨主缆还应考虑跨中垂点标高)为收敛条件,迭代求解缆索系统[3]。
1.2.1 主缆及其两端索鞍分析
图2(a)和图2(b)分别展示了中、边跨主缆及其两端索鞍示意图。根据分段悬链线理论,以2n−1副索夹的索夹中心为分界点将两端索鞍切点间的主缆划分为2n段。左、右两端索鞍上主缆圆弧段的固定点坐标分别用(
x0L ,y0L )和(x0R,y0R )表示,圆心坐标分别用(xLO,yLO )和(xRO,yRO )表示,圆弧半径分别用RL与RR表示,上述参数均为计算前的已知常量。(xL,yL)和(xR,yR)分别表示一跨主缆与其左右两端索鞍的切点坐标,主缆悬链线段和主缆圆弧段在切点处相连。切点应满足主缆圆弧段的形状方程:
(xL−xLO)2+(yL−yLO)2=R2L,(xR−xRO)2+(yR−yRO)2=R2R (1) 根据切点处向量关系,可知其坐标满足方程:
|xL−xLO|VL−|yL−yLO|H=0,|xR−xRO|VR−|yR−yRO|H=0 (2) 式中:H为主缆内力的水平分量大小;VL、VR分别为两切点处主缆拉力TL、TR的竖向分量大小;在数值运算中H、VL、VR都是仅表征力大小的正实数变量。由于主缆圆弧段圆心与切点的相对位置关系由该段主缆所属跨径(中、边跨)和所属索鞍容易确定:当计算左边跨时,
xL<xLO 且xR< xRO ;当计算中跨时,xL>xLO 且xR<xRO ;当计算右边跨时,xL>xLO 且xR>xRO 。因此联立式(1)和式(2)可得:xL=xLO±VLRL√H2+V2L,yL=yLO+HRL√H2+V2L,xR=xRO±VRRR√H2+V2R,yR=yRO+HRR√H2+V2R (3) 式中,正负号的取法由上述相对位置关系确定。
根据分段悬链线理论[7],可得中跨各主缆分段的跨度Xi (i =1,2,···,2n)和高差Yi (i =1,2,···,2n)满足:
Xi=HSiEAc+Hw{ln(Vi+√H2+V2i)−ln[Vi−wSi+√(Vi−wSi)2+H2]} (4a) Yi=wS2i−2ViSi2EAc−1w[√H2+V2i−√(Vi−wSi)2+H2] (4b) 式中:w为沿主缆无应力长度的均布自重荷载,为已知常量;Si (i =1,2,···,2n)为各主缆分段的无应力长度;Vi (i =1,2,···,2n)为各主缆分段左端点处拉力的竖向分量,V1的大小为VL;各主缆分段跨度、高差与左端点坐标的换算关系为:
Xi=xi+1−xi,xi+1=x1+i∑j=1Xj Yi=yi+1−yi,yi+1=y1+i∑j=1Yj 在一跨主缆的各分段中,X1、X2n是两索鞍上主缆切点到端索夹的跨度,需根据切点坐标计算得到;其余主缆分段的跨度Xi (i =2,3,···,2n−1)均为索夹间距,是已知常量。由于左端索夹至左端索鞍固定点的跨度XL、右端索夹至右端索鞍固定点的跨度XR是已知常量,可得X1、X2n的表达式:
X1=XL−(xL−x0L) X2n=XR−(x0R−xR) 得到X1、X2n后,若能确定H、Vi的值,则式(4a)是关于Si的一元超越方程,求解该方程得到Si后,由式(4b)可得各主缆分段的高差Yi (i =1,2,···,2n)。此外,主缆各分点处的受力平衡关系满足:
Vi+1=Vi−wSi−Fi (7) 式中,Fi (i =1,2,···,2n−1)为各主缆分点(即索夹中心)处的集中力,故F1作用点的坐标为(x2, y2)。
任意中、边跨的主缆及其两端索鞍均可用式(1)~式(7)来描述。应注意,当桥梁构型采用单跨简支悬索桥时,边跨主缆通常不设吊索;此外,当悬索桥边跨设有吊索时,也并非所有主缆分点(即索夹中心)处都布置有吊索。因此,当某索夹处无吊索布置时,则式(7)中集中力Fi等于边跨紧缆索夹的重量;当某索夹处设有吊索时,则式(7)中集中力Fi的大小还需通过分析索夹与吊索受力情况得到。
1.2.2 销接式索夹及其吊索分析
各个索夹中心(即主缆分点)的高程和倾角决定了主缆线形,因此对于悬索桥的精确设计尤为重要;此外,还需根据索夹的几何形状确定准确的吊索钢丝下料长度[14-15]。悬索桥吊索根据索夹构造可分为销接式和骑跨式,本文仅考虑采用销接式连接的情况。销接式索夹与吊索的几何参数与受力分析如图3所示,d1和d2分别是上端和下端锚头内的锚固长度;d3表示上端锚头锚口至销铰中心的距离;d4表示下端锚头锚口至主梁下锚面的距离;且d1、d2、d3、d4是吊索出厂时的已知几何参数[16-17]。
b、ai、ci是销接式索夹的几何参数,三者恰好形成直角三角形的三个边,其中b为已知常量。索夹倾角θi (i =1,2,···,2n−1)同样也是直角边b和斜边ci的夹角,由几何关系可知:
ci=bcosθi (8) 根据索夹中心(即主缆分点)处的力学平衡关系,可知索夹倾角θi满足下式:
θi=arctan(−Vi+1H)=−arctan(Vi+1H) (9) 根据图3所示的吊索受力分析可知,索夹中心处集中力Fi的表达式为:
Fi=Ni+Gi=Ri+whlhi+Ghi+Gi (10) 式中:Gi、
Ghi (i =1,2,···,2n−1)分别为索夹重量和吊索非钢丝部分重量;G1、Gh1 作用点的坐标为(x2,y2);wh为沿吊索钢丝无应力长度的均布自重荷载;lhi 为吊索钢丝下料长度;且Gi、Ghi 和wh均为已知常量,联立式(7)和式(10)可得:Vi+1=Vi−wSi−Ri−whlhi−Ghi−Gi (11) 吊索钢丝弹性部分的形状长度li (i=1,2,···,2n−1)为[16-17]:
li=yi+1−yhi+1−ci−d3−d4 (12) 式中,
yhi+1 (i =1,2,···,2n−1)表示主梁下锚面的设计高程,在理想成桥状态下为已知常量。Eh和Ah分别为吊索中钢丝部分的弹性模量与横截面积,为已知常量。根据虎克定律,吊索中钢丝弹性部分的无应力长度
l0i (i=1,2,···,2n−1)[11]为:∫l0i0Ri+whyEhAhdy+l0i=li (13) 联立式(5b)、式(12)和式(13)可得吊索钢丝弹性部分无应力长度
l0i 的表达式:l0i=[√(Ri+EhAh)2+2EhwhAh(y1+i∑j=1Yj−yhi+1−ci−d3−d4)−(Ri+EhAh)]/wh (14) 由此可得吊索钢丝下料长度
lhi 的表达式为:lhi=l0i+d1+d2 (15) 综上所述,联立式(8)、式(9)、式(11)、式(14)和式(15)可得关键控制方程:
−Htan(θi)=Vi−wSi−Ghi−Gi−whd1−whd2+EhAh−√(Ri+EhAh)2+2EhwhAh(y1+i∑j=1Yj−yhi+1−b/cosθi−d3−d4) (16) 1.2.3 中、边跨目标函数
求解中跨缆索系统时,应先确定切点坐标(xL, yL)和(xR, yR);根据式(3)可知,当H、VL、VR的值已知时得以确定切点坐标,此时式(4a)转化为关于Si (i=1,2,···,2n)的一元超越方程,解得Si后,再由式(4b)可得各主缆分段的高差Yi (i =1,2,···,2n)。由于VL=|V1|且VR= |V2n+wS2n|,式(16)转化为关于θi (i =1,2,···,2n−1)的一元超越方程;若V1已知,解方程式(16)可得θ1,再将θ1代入式(9)可得V2,依此循环直到解得θ2n−1、V2n为止,最终完成对中跨主缆各分段、各吊索内力与构形的遍历计算,得到式(1)~式(16)中所有参数的值。为保证解得的悬索桥成桥状态正确、唯一,应控制中跨缆索系统的收敛误差em,根据中跨内主缆形状与主缆内力的闭合条件可得其表达式为:
em=√(y2n+1−yR)2+(yn+1−yf)2+(|V2n−wS2n|−VR)2 (17) 式中:y2n+1、yn+1、V2n、S2n可由H、VL、VR通过式(5)、式(9)和式(16)进行循环遍历计算得出;yf是跨中垂点的设计高程,为已知常量。
求解边跨缆索系统时,主缆内力的水平分量大小H已经算出,可作为已知量;此外,各索夹中心处不一定都设有吊索。因此,在循环遍历求解过程中,由式(4a)和式(4b)得到Si和Yi后,应判断该索夹中心处是否设有吊索:若设有吊索,则计算超越方程式(16)可得θi,再由式(9)得到Vi+1;若未设吊索,则根据式(7)可得Vi+1,此时式(7)中Fi等于Gi,再由式(9)得到θi;依此循环直至解得θ2n−1、V2n为止。根据边跨内主缆形状与主缆内力的闭合条件可得控制边跨缆索系统的收敛误差es为:
es=√(y2n+1−yR)2+(|V2n−wS2n|−VR)2 (18) 根据式(17)和式(18),按收敛误差构造中、边跨缆索系统的目标函数,可得三元函数em =f(H,VL,VR)和二元函数es=g (VL,VR)。
1.2.4 主缆无应力长度
如图2所示,对任一跨内的缆索系统(无论中跨或是边跨)而言,该跨主缆无应力长度等于分段悬链线段与两端圆弧段无应力长度之和。由文献[10]的研究成果可知,主缆左端索鞍和右端索鞍上圆弧段无应力长度SL、SR的表达式为:
SL=RLarcsin(xL−x0LRL)+RL√H2+V2LEAμ(1−e−μarcsin(xL−x0LRL)) (19a) SR=RRarcsin(x0R−xRRR)+RR√H2+V2REAμ(1−e−μarcsin(x0R−xRRR)) (19b) 式中,μ为索鞍弧面与主缆的摩擦系数,取0.15[10, 18]。
因此,一跨主缆的无应力长度SSUM为:
SSUM=SL+SR+2n∑i=1Si (20) 1.3 计算步骤
将中、边跨缆索系统的目标函数em=f(H,VL,VR)、es =g (VL,VR)构造完成后,基于1.2节提及的所有已知常量,可采用优化算法求解函数:即迭代更新函数自变量,直至收敛误差em和es都趋于0为止。因此,悬索桥成桥找形的计算流程如图4所示,由此可得式(1)~式(20)中所有参数的值。
1.4 函数求解
1.4.1 优化算法
本方法按照图4所示流程,使用MATLAB完成缆索系统目标函数的构造与求解过程。由于目标函数内置循环计算,因此通过优化算法求解缆索系统的目标函数时,需要反复求解一元超越方程式(4a)和式(16),采用零值搜索算法(MATLAB中的fzero函数)可解决此问题。
本方法采用Nelder-Mead算法[19-20](MATLAB中的fminsearch函数)先后求解悬索桥中、边跨缆索系统的目标函数。该算法是基于单纯形原理的直接搜索法,用于迭代求解无约束极小值问题。该算法在求解N元复杂函数时通过输入的自变量迭代初值构造一个具有N+1个顶点的单纯形,各顶点在N维空间内的坐标值恰好就是当前迭代步中函数的自变量值,然后在迭代寻优过程中通过“标定”、“反射(ρ)”、“扩展(β)”、“收缩(γ)”和“折减(μ)”算子不断搜索更新单纯形的各顶点坐标;若某次迭代中该单纯形存在一个顶点,顶点坐标对应的函数值满足收敛条件,则计算结束。在本文计算中算法相关系数按惯例取为ρ=1、β=2、γ=0.5和μ=0.5。
在每个迭代步中,Nelder-Mead算法首先对当前单纯形进行标定,也即是对N+1个顶点进行标号排序,标定完成后各顶点坐标X j (j=1,···, N+1)的目标函数值应满足关系:F(X1)<···<F(XN)<F(XN+1)。为便于介绍该算法的迭代策略,引入XA:
{{\boldsymbol{X}}_{\rm{A}}} = \frac{1}{N}\sum\limits_{j = 1}^N {{{\boldsymbol{X}}_j}} (21) 标定完成后,采用“反射”算子由式(22)得XR。
{{\boldsymbol{X}}_{\rm{R}}} = \left({1 + {\rm{\rho }}} \right){{\boldsymbol{X}}_{\rm{A}}} - {\rm{\rho }}{{\boldsymbol{X}}_{N + 1}} (22) 若F(XR)<F(X1),则按式(23)对单纯形进行“扩展”操作:若F(XE)<F(XR),则将最差顶点的坐标XN+1替换为XR;否则,将最差顶点的坐标XN+1替换为XR。然后程序进入下一个迭代步。
{{\boldsymbol{X}}_{\rm{E}}} = \left({1 + {\rm{\rho \beta }}} \right){{\boldsymbol{X}}_{\rm{A}}} - {\rm{\rho \beta }}{{\boldsymbol{X}}_{N + 1}} (23) 若F(X1)≤F(XR)<F(XN),则将最差顶点的坐标XN+1替换为XR,程序进入下一个迭代步。
若F(XN)≤F(XR)<F(XN+1),则按式(24a)对单纯形进行“镜像收缩”操作:若F(XOC)≤ F(XR),则将最差顶点的坐标XN+1替换为XOC;否则,令最优顶点的坐标X1保持不变,按式(24b)对单纯形其他顶点进行“折减”操作。然后程序进入下一个迭代步。
\tag{24a} {{\boldsymbol{X}}_{{\rm{OC}}}} = \left({1 + {\rm{\rho \gamma }}} \right){{\boldsymbol{X}}_{\rm{A}}} - {\rm{\rho \gamma }}{{\boldsymbol{X}}_{N + 1}}\qquad\qquad \tag{24b} {{\boldsymbol{X}}_j} = {{\boldsymbol{X}}_1} + {\rm{\mu }}({{\boldsymbol{X}}_j} - {{\boldsymbol{X}}_1}),\;j = 2, \cdots ,N + 1 若F(XR)≥F(XN+1),则按式(25)对单纯形进行“朴素收缩”操作:若F(XIC)<F(XN+1),则将最差顶点的坐标XN+1替换为XIC;否则按式(24b)对单纯形进行“折减”操作。然后程序进入下一个迭代步。
{{\boldsymbol{X}}_{{\rm{IC}}}} = \left({1 - {\rm{\gamma }}} \right){{\boldsymbol{X}}_{\rm{A}}} + {\rm{\gamma }}{{\boldsymbol{X}}_{N + 1}} (25) 1.4.2 迭代初值
计算悬索桥成桥状态时,应首先采用优化算法求解中跨缆索系统的目标函数f (H,VL,VR),因此需事先给定与真实值相近的寻优初值H0、
V_{\rm{L}}^0 、V_{\rm{R}}^0 ,由于大跨悬索桥通常在主缆上布置密集吊索,那么可近似将主缆承受的外荷载等效为均布荷载,所以可采用抛物线公式近似描述中跨主缆:\tag{26a} {S_0} = (x_{\rm{R}}^0 - x_{\rm{L}}^0)\left[ {1 + \frac{{2{{(y_{\rm{R}}^0 + y_{\rm{L}}^0 - 2{y_f})}^2}}}{{3{{(x_{\rm{R}}^0 - x_{\rm{L}}^0)}^2}}}} \right] \tag{26b} {w_0} = \frac{{w{S_0} + \displaystyle \sum\limits_{i = 1}^{2n - 1} {{R_i}} }}{{(x_{\rm{R}}^0 - x_{\rm{L}}^0)}}\qquad\qquad\qquad\qquad \tag{26c} {H_0} = \frac{{{w_0}{{(x_{\rm{R}}^0 - x_{\rm{L}}^0)}^2}}}{{8\left(\dfrac{{y_{\rm{R}}^0 + y_{\rm{L}}^0}}{2} - {y_f}\right)}}\qquad\qquad\qquad\;\; 式中:S0为中跨主缆无应力长度的近似值;w0为将中跨主缆等效为抛物线后的均布自重荷载;H0为目标函数f (H,VL,VR)中自变量H的迭代初值。
根据等效后中跨主缆的力学平衡关系可得:
\tag{27a} V_{\rm{L}}^0 + V_{\rm{R}}^0 = {w_0}(x_{\rm{R}}^0 - x_{\rm{L}}^0)\qquad\qquad \tag{27b} (V_{\rm{R}}^0 - V_{\rm{L}}^0)(x_{\rm{R}}^0 - x_{\rm{L}}^0) = {H_0}(y_{\rm{R}}^0 - y_{\rm{L}}^0) 联立式(27a)与式(27b)可得VL与VR的迭代初值:
\tag{28a} V_{\rm{L}}^0 = \frac{{{w_0}{{(x_{\rm{R}}^0 - x_{\rm{L}}^0)}^2} - {H_0}(y_{\rm{R}}^0 - y_{\rm{L}}^0)}}{{2(x_{\rm{R}}^0 - x_{\rm{L}}^0)}} \tag{28b} V_{\rm{R}}^0 = \frac{{{w_0}{{(x_{\rm{R}}^0 - x_{\rm{L}}^0)}^2} + {H_0}(y_{\rm{R}}^0 - y_{\rm{L}}^0)}}{{2(x_{\rm{R}}^0 - x_{\rm{L}}^0)}} 此外,采用零值搜索法求解一元超越方程时也需设定合适的初值。式(4a)是关于一跨主缆各分段无应力长度Si (i =1,2,···,2n)的一元超越方程;因各分段跨度Xi与Si相近,可将Xi用作初值。计算一元超越方程式(16)时,因各索夹倾角θi在一跨主缆内是渐变的,且首个主缆分段左端点拉力竖向分量V1的大小为VL,已知VL为自变量,那么调整式(9)可得索夹倾角的初值
\theta _i^0 (i=1,2,···,2n−1)为:\theta _i^0 = - {\rm{arctan}}\left(\frac{{{V_i}}}{H}\right) (29) 由于同一主索鞍上两侧主缆切点处的拉力竖向分量大小相近,故仍使用中跨迭代初值
V_{\rm{L}}^0 、V_{\rm{R}}^0 分别作为左、右边跨主缆在主索鞍切点处拉力竖向分量的迭代初值。当边跨无吊索布置时,主缆在散索鞍切点处竖向力大小与在主索鞍切点处竖向力大小相近,故将目标函数g(VL,VR)中两个自变量的迭代初值取为一致;当边跨设有吊索时,此时由V_{\rm{L}}^0 或V_{\rm{R}}^0 减去边跨内所有吊索下端拉力大小之和可得散索鞍切点处主缆竖向力的迭代初值。2 实例验证
如图5所示,笋溪河大桥是典型的大跨地锚式悬索桥,主桥采用单跨660 m简支钢桁加劲梁构造。该桥缆索系统采用双幅对称布置,因篇幅限制,故仅列出单幅桥结果。
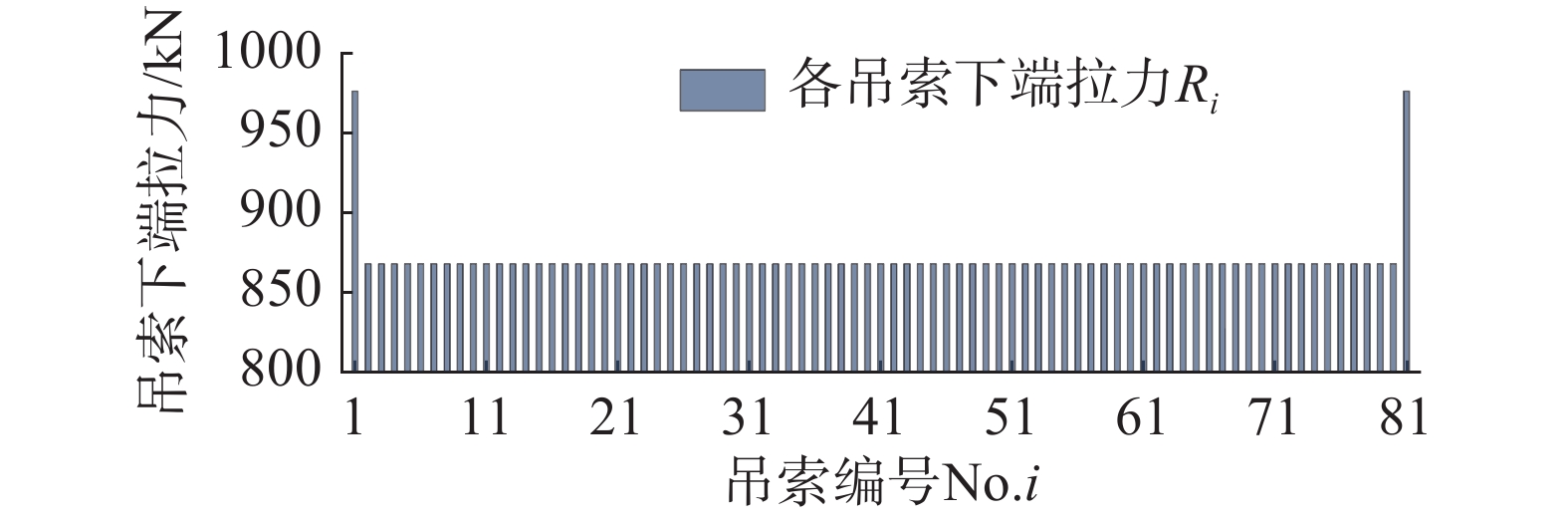
该桥主缆跨径布置为215 m+660 m+268 m。中跨设有81对销接式索夹及其吊索,端吊索到主塔中心线的间距为10 m,相邻吊索间距为8 m;各吊索下端拉力Ri (i=1,2,···,81)如图6所示,端吊索下端拉力R1=R81=976.232 kN,其余均为867.762 kN。左、右边跨分别设有21对和27对紧缆索夹,无吊索布置。
如1.2节所述,所有索夹及中跨吊索非钢丝部分的自重均已知;各索鞍上主缆圆弧段的半径、固定点坐标和圆心坐标均已知;各跨径内相邻索夹间距、端部索夹与主塔中心线的间距、端部索夹与散索鞍固定点的间距均已知。各跨缆索系统采用原点位置不同但高程相同的笛卡尔坐标系(建议按图2所示将原点坐标设于缆索系统左下角的某点处即可),以确保全桥高程的一致性。此数值算例中,该桥中跨跨中垂点的设计高程yf为122.555 m (按1985国家高程基准计则为668.668 m),是重要的迭代收敛目标。主缆的弹性模量E=200 GPa,横截面积Ac=0.1971 m2,均布自重荷载w=15.0818 kN/m。吊索钢丝部分的弹性模量Eh=200 GPa,横截面积Ah=0.0019 m2,均布自重荷载wh=0.155 kN/m。
2.1 不同优化算法收敛能力的比较
在悬索桥成桥找形中,应先求解中跨缆索系统;若计算收敛,方可继续求解边跨缆索系统。求解目标函数f (H,VL,VR)是搜索无约束极小值的问题,无论采用何种优化算法求解,其迭代初值均由式(26)~式(29)得到;然而,由于目标函数都是内置循环计算和超越方程计算的多元复杂函数,采用最速下降法、共轭梯度法和牛顿型法等有导数优化算法[19]求解时易遇到Jacobi矩阵和Hessian矩阵不正定或病态的情况,导致计算不收敛。笔者采用有导数优化算法中具代表性的拟牛顿法求解笋溪河大桥中跨缆索系统时发现:当自变量的迭代步长已达10−9量级时,收敛误差em仍停滞在101量级,计算不收敛,证明此类优化算法不收敛的情况确实存在。
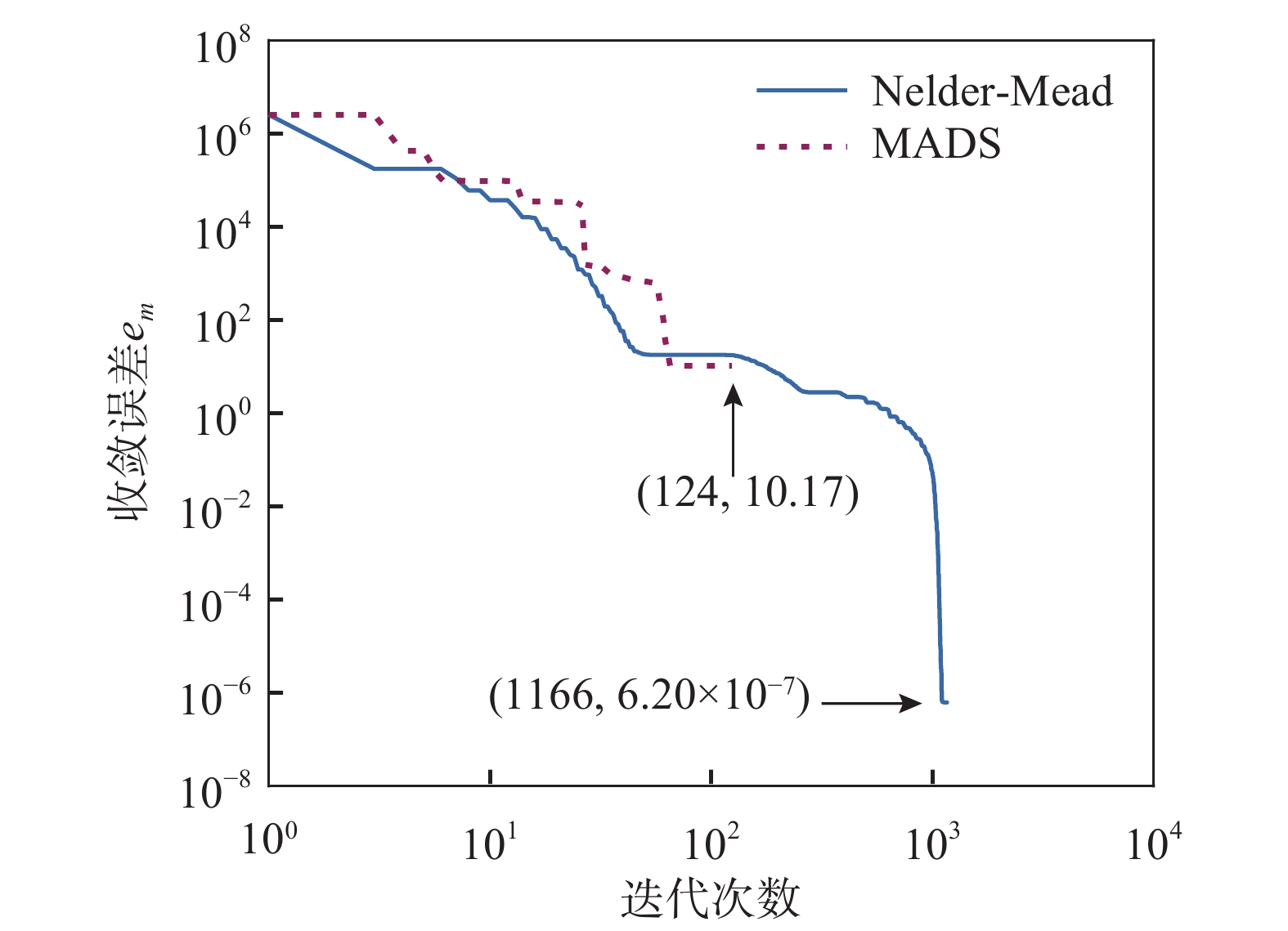
在众多用于求解无约束最小值问题的无导数优化算法[19]中,自适应网格算法(MADS)[19]和Nelder-Mead算法[19-20]是最具代表性的两种。若采用MADS求解,当收敛误差趋于0时,则计算收敛;当自变量的网格尺寸(MeshSize,类似于有导数优化算法中自变量的迭代步长)已趋于0,而收敛误差仍较大时则无法收敛。为了选取适合本方法的求解策略,笔者比较了两者的收敛能力,结果如图7所示。
当MADS进行到第124次迭代时,网格尺寸已达10−13量级,收敛误差em却停滞于101量级,计算不收敛;Nelder-Mead进行到第1166次迭代时,收敛误差em趋于10−7量级,计算收敛。根据对上述不同优化算法的比较分析结果,选取Nelder-Mead算法作为本方法的求解策略。
2.2 设计值与计算值的比较
采用Nelder-Mead算法,先求解笋溪河大桥中跨缆索系统,再求解边跨缆索系统。计算收敛时累计耗时132 s,各跨缆索系统目标函数的求解结果如表1所示。
表 1 目标函数的求解结果Table 1. Solution results of objective functions目标函数 自变量收敛结果 收敛误差em (或es) H / kN VL / kN VR / kN 中跨 1.032×105 3.945×104 4.226×104 6.203×10−7 左边跨 − 3.995×104 4.346×104 2.308×10−8 右边跨 − 3.925×104 4.363×104 3.422×10−8 为了验证本方法的计算精度,将本文方法计算结果与该桥实际设计结果进行多组比较分析;设计院采用专业桥梁分析软件TDV RM,通过建立精细化有限元模型尽可能地减小模拟误差,以主梁锚点(即连接吊索的主梁节点)和中跨主缆跨中垂点的竖向位移均趋于0作为控制目标,应用考虑松弛因子的Newton-Raphson方法进行非线性迭代计算得到该桥的实际设计结果。
图8(a)和图8(b)分别展示了该桥各销接式索夹的索夹倾角θi (i =1,2,···,81)及其计算值与设计值的误差结果。θi的计算值在[−20.375°, 22.210°]范围内,设计值在[−20.604°, 21.955°]范围内,两者的绝对误差在[0.206°, 0.255°]范围内。表2展示了各索鞍切点处的主缆切线角,其计算值与设计值间绝对误差不超过0.033°。显然,主缆分点(即索夹中心)和主缆切点处切线角的绝对误差(“计算值−设计值”)很小,这是由于切线角度都是通过计算主缆内力分量的比值而得所致。
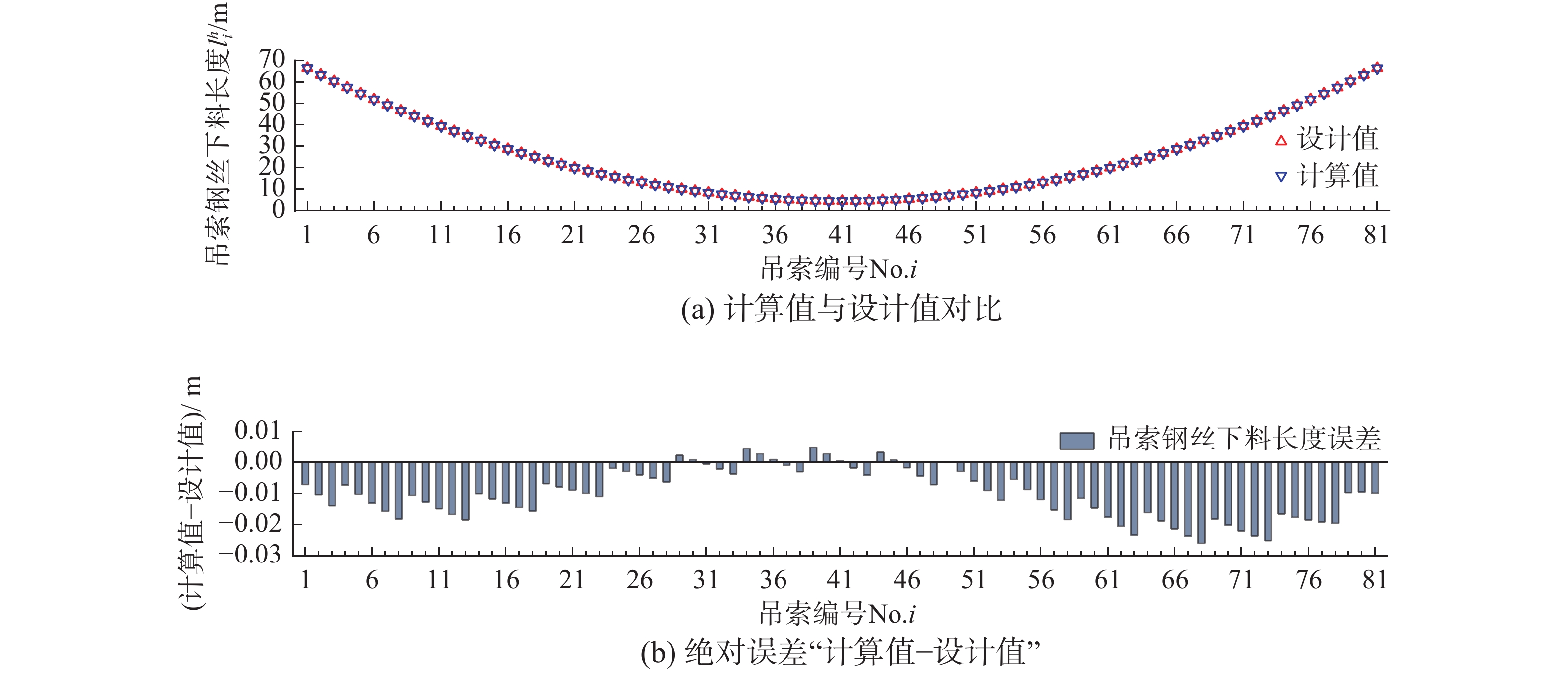
表 2 各索鞍切点处的主缆切线角Table 2. Angles at tangent points between the main cable and the saddles切线角 左边跨切点位置/(°) 中跨切点位置/(°) 右边跨切点位置/(°) 索鞍A 索鞍B 索鞍B 索鞍C 索鞍C 索鞍D 设计值 21.133 22.872 20.905 22.251 22.904 20.838 计算值 21.166 22.841 20.924 22.272 22.919 20.824 注:索鞍A和D分别代表位于主桥左右两侧的散索鞍,索鞍B和C分别代表位于主桥左、右塔顶上的主索鞍。 图9(a)和图9(b)分别展示了该桥各吊索钢丝下料长度
l_i^{\rm{h}} (i =1,2,···,81)及其计算值与设计值的误差结果,两者的绝对误差处于[−0.026 m, 0.005 m]间。左端第一根吊索(No.1)最长,其计算值与设计值分别为66.389 m和66.396 m;位于主缆跨中垂点处的吊索(No.41)最短,因跨中垂点竖向位移是两者的共同迭代收敛目标,故计算值与设计值均为4.541 m。图10(a)和图10(b)分别展示了该桥中跨主缆线形(即各索夹中心的连线)及其计算值与设计值的误差结果,两者的绝对误差处于[−0.023 m, 0.004 m]间。主缆线形由吊索形状长度和桥面线形确定,由于桥面设计高程是已知常量,而吊索钢丝伸长量相对吊索形状长度小很多,因此图9(a)和图10(a)中主缆线形和吊索钢丝无应力长度的分布规律相似。
比较图9(b)和图10(b)可知,无论主缆线形还是吊索钢丝下料长度,其绝对误差(“计算值−设计值”)均呈现由跨中向两端增大的趋势。虽然本方法与设计采用的迭代方法有所不同,但中跨主缆跨中垂点的竖向位移却是两者共同的迭代收敛目标;因此,主缆线形与吊索钢丝下料长度在远离跨中处的绝对误差相对较大,而在跨中处的绝对误差则较小。
表3分别列出了各跨主缆无应力长度设计值以及本文方法的计算结果(即“计算值”),可见两者的绝对误差较小。根据经典力学中弧面上柔性体的力学关系[21]可知,仅当摩擦系数μ已知时,结合胡克定律对该段柔性体的应变进行积分才能得到弹性伸长量的解析解,对应式(19a)和式(19b)中等号右边第二项。因此,实际工程中通常不考虑索鞍弧面与主缆的摩擦效应,取圆弧段主缆的形状长度近似作为其无应力长度。为了量化忽略圆弧段主缆弹性伸长量时所引起的误差,表3列出了不计摩擦效应时本文方法的计算结果(“计算值*”),最终发现各跨圆弧段主缆的累计伸长量均在1 cm左右,因此摩擦效应对计算结果的影响较小。
表 3 各跨主缆无应力长度Table 3. Unstressed lengths of the mid-span and side-span main cables主缆无应力长度 左边跨/m 中跨/m 右边跨/m 设计值 231.288 675.557 288.046 计算值 231.147 675.267 287.882 计算值* 231.155 675.278 287.890 3 结论
本文全面考虑了销接式索夹位形对吊索钢丝下料长度的影响、主缆与索鞍间的相切接触状况以及两者间的摩擦影响,然后构造了此类悬索桥缆索系统的目标函数。通过工程实例验证,最终得到以下结论:
(1) 针对销接式索夹的构造情况,推导了索夹倾角、吊索钢丝下料长度的表达式,然后将分段悬链线方程中常用的传统表达式(7)转化为本方法的关键控制方程式(16),由此可将销接式索夹对主缆、吊索位形的影响自适应地计入了缆索系统的目标函数求解过程中。传统的数值迭代方法通过对式(7)的近似处理(即取Fi = Ri),先计算主缆线形再根据索夹形状修正吊索钢丝下料长度;本方法只需一次性求解目标函数就能得到悬索桥理想成桥状态下各构件的位形,避免了这种二次修正误差。
(2) 基于相同的迭代初值,分别采用多种不同优化算法求解同一悬索桥工程算例的缆索系统目标函数,经对比发现:仅Nelder-Mead算法能够收敛,且该算法迭代速度较快、计算精度很高。因此,选择该优化算法作为本方法的合理求解策略。
(3) 采用本数值迭代方法求解该悬索桥工程算例后,将各项计算结果与该桥设计值进行对比,发现各项绝对误差均较小,满足实际工程的精度需求。因此,本方法为悬索桥精确设计给出了可供参考的解决方案。
-
表 1 目标函数的求解结果
Table 1 Solution results of objective functions
目标函数 自变量收敛结果 收敛误差em (或es) H / kN VL / kN VR / kN 中跨 1.032×105 3.945×104 4.226×104 6.203×10−7 左边跨 − 3.995×104 4.346×104 2.308×10−8 右边跨 − 3.925×104 4.363×104 3.422×10−8 表 2 各索鞍切点处的主缆切线角
Table 2 Angles at tangent points between the main cable and the saddles
切线角 左边跨切点位置/(°) 中跨切点位置/(°) 右边跨切点位置/(°) 索鞍A 索鞍B 索鞍B 索鞍C 索鞍C 索鞍D 设计值 21.133 22.872 20.905 22.251 22.904 20.838 计算值 21.166 22.841 20.924 22.272 22.919 20.824 注:索鞍A和D分别代表位于主桥左右两侧的散索鞍,索鞍B和C分别代表位于主桥左、右塔顶上的主索鞍。 表 3 各跨主缆无应力长度
Table 3 Unstressed lengths of the mid-span and side-span main cables
主缆无应力长度 左边跨/m 中跨/m 右边跨/m 设计值 231.288 675.557 288.046 计算值 231.147 675.267 287.882 计算值* 231.155 675.278 287.890 -
[1] 李政圜, 樊健生, 马晓伟, 等. 基于悬吊系统的钢-混凝土组合桥面系试验[J]. 工程力学, 2019(12): 134 − 144. doi: 10.6052/j.issn.1000-4750.2018.12.0722 Li Zhengyuan, Fan Jiansheng, Ma Xiaowei, et al. Test on the steel-concrete composite girder by using suspension system [J]. Engineering Mechanics, 2019(12): 134 − 144. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.12.0722
[2] Chen Z, Cao H, Ye K, et al. Improved particle swarm optimization-based form-finding method for suspension bridge installation analysis [J]. Journal of Computing in Civil Engineering, 2015, 29: 04014047. doi: 10.1061/(ASCE)CP.1943-5487.0000354
[3] 罗喜恒. 悬索桥主缆线形的鞍座影响[J]. 公路交通科技, 2005, 22(8): 36 − 48. doi: 10.3969/j.issn.1002-0268.2005.08.009 Luo Xiheng. Effect of saddle on cable shape of suspension bridges [J]. Journal of Highway and Transportation Research and Development, 2005, 22(8): 36 − 48. (in Chinese) doi: 10.3969/j.issn.1002-0268.2005.08.009
[4] Jung M R, Min D J, Kim M Y. Nonlinear analysis methods based on the unstrained element length for determining initial shaping of suspension bridges under dead loads [J]. Computer and Structures, 2013, 128: 272 − 85. doi: 10.1016/j.compstruc.2013.06.014
[5] 郭彤, 李爱群, 王浩. 基于牛顿-拉普森迭代和零阶优化算法的悬索结构找形研究[J]. 工程力学, 2007, 24(4): 142 − 146. doi: 10.3969/j.issn.1000-4750.2007.04.025 Guo Tong, Li Aiqun, Wang Hao. Research in form-finding of suspension structures based on Newton-Raphson iteration and zero order optimization arithmetic [J]. Engineering Mechanics, 2007, 24(4): 142 − 146. (in Chinese) doi: 10.3969/j.issn.1000-4750.2007.04.025
[6] 景天虎, 李青宁. 悬索桥主缆成桥线形确定的有限元新算法[J]. 世界桥梁, 2012(1): 45 − 49. Jing Tianhu, Li Qingning. New finite element algorithm for determination of geometric shape of completed bridge main cable of suspension bridge [J]. World Bridges, 2012(1): 45 − 49. (in Chinese)
[7] 唐茂林, 强士中, 沈锐利. 悬索桥成桥主缆线形计算的分段悬链线法[J]. 铁道学报, 2003(1): 87 − 91. doi: 10.3321/j.issn:1001-8360.2003.01.018 Tang Maolin, Qiang Shizhong, Shen Ruili. Segmental catenary method of calculating the cable curve of suspension bridge [J]. Journal of the China Railway Society, 2003(1): 87 − 91. (in Chinese) doi: 10.3321/j.issn:1001-8360.2003.01.018
[8] 罗喜恒. 悬索桥缆索系统的数值分析法[J]. 同济大学学报: 自然科学版, 2004(4): 26 − 31. Luo Xiheng. Numerical analysis method for cable system of suspension bridges [J]. Journal of Tongji University, 2004(4): 26 − 31. (in Chinese)
[9] 李传习, 王雷, 刘光栋, 等. 悬索桥索鞍位置的分离计算法[J]. 中国公路学报, 2005, 18(1): 63 − 68. doi: 10.3321/j.issn:1001-7372.2005.01.012 Li Chuanxi, Wang Lei, Liu Guangdong, et al. Separate calculation method on suspension bridge saddle's position [J]. China Journal of Highway and Transport, 2005, 18(1): 63 − 68. (in Chinese) doi: 10.3321/j.issn:1001-7372.2005.01.012
[10] 王邵锐, 周志祥, 高燕梅, 等. 悬索桥索鞍预偏量的牛顿-拉斐森算法[J]. 中国公路学报, 2016, 29(1): 82 − 88. doi: 10.3969/j.issn.1001-7372.2016.01.011 Wang Shaorui, Zhou Zhixiang, Gao Yanmei, et al. Newton-Raphson algorithm for pre-offsetting of cable saddle on suspension bridge [J]. China Journal of Highway and Transport, 2016, 29(1): 82 − 88. (in Chinese) doi: 10.3969/j.issn.1001-7372.2016.01.011
[11] Cao H, Qian X, Chen Z, et al. Layout and size optimization of suspension bridges based on coupled modelling approach and enhanced particle swarm optimization [J]. Engineering Structures, 2017, 146(sep. 1): 170 − 183.
[12] 罗喜恒, 肖汝诚, 项海帆. 悬索桥锚跨索股分析研究[J]. 公路交通科技, 2004, 21(12): 45 − 49. doi: 10.3969/j.issn.1002-0268.2004.12.012 Luo Xiheng, Xiao Rucheng, Xiang Haifan. Analysis study of anchor span strand for suspension bridges [J]. Journal of Highway and Transportation Research and Development, 2004, 21(12): 45 − 49. (in Chinese) doi: 10.3969/j.issn.1002-0268.2004.12.012
[13] Zhang W, Shi L, Li L, et al. Methods to correct unstrained hanger lengths and cable clamps' installation positions in suspension bridges [J]. Engineering Structures, 2018, 171(sep. 15): 202 − 213.
[14] 王晓明, 贺拴海, 段瑞芳. 空间索形自锚式悬索桥吊索张拉过程分析方法[J]. 工程力学, 2016(10): 164 − 171. doi: 10.6052/j.issn.1000-4750.2015.03.0168 Wang Xiaoming, He Shuanhai, Duan Ruifang. Hanger tensioning process analysis of self-anchored suspension bridge with spatial cables [J]. Engineering Mechanics, 2016(10): 164 − 171. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.03.0168
[15] 王晓明, 雷晓鸣, 王成树, 等. 空间索形悬索桥主缆线形施工过程空间转换控制方法[J]. 工程力学, 2017(4): 187 − 195. doi: 10.6052/j.issn.1000-4750.2015.11.0902 Wang Xiaoming, Lei Xiaoming, Wang Chengshu, et al. Spatial transformation control method of main cable alignment during construction process in suspension bridge with spatial cables [J]. Engineering Mechanics, 2017(4): 187 − 195. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.11.0902
[16] 祝长春, 王鹏, 闫朔. 海外大型悬索桥吊索长度计算及架设精度控制[J]. 公路交通科技, 2018, 35(增刊 1): 21 − 25, 39. Zhu Changchun, Wang Peng, Yan Shuo. Calculation of suspender length and control of construction precision for overseas large suspension bridge [J]. Journal of Highway and Transportation Research and Development, 2018, 35(Suppl 1): 21 − 25, 39. (in Chinese)
[17] 贾一全, 刘世忠. 刘家峡大桥吊索长度计算及索力优化[J]. 公路工程, 2015, 40(3): 42 − 45, 69. doi: 10.3969/j.issn.1674-0610.2015.03.010 Jia Yiquan, Liu Shizhong. The hanger length calculation and forces optimization analysis of Liujiaxia suspension bridge [J]. Highway Engineering, 2015, 40(3): 42 − 45, 69. (in Chinese) doi: 10.3969/j.issn.1674-0610.2015.03.010
[18] Takena K, Sasaki M, Hata K, et al. Slip behavior of cable against saddle in suspension bridges [J]. Journal of Structural Engineering, 1992, 118(2): 377. doi: 10.1061/(ASCE)0733-9445(1992)118:2(377)
[19] Audet C, Kokkolaras M. Blackbox and derivative-free optimization: theory, algorithms and applications [J]. Optimization & Engineering, 2016, 17(1): 1 − 2.
[20] Lagarias J C, Reeds J A, Wright M H, et al. Convergence properties of the Nelder-Mead simplex method in low dimensions [J]. Siam Journal on Optimization, 1998, 9(1): 112 − 147. doi: 10.1137/S1052623496303470
[21] 孟凡超. 公路桥涵设计手册. 悬索桥[M]. 北京: 人民交通出版社, 2011. Meng Fanchao. Design manual of highway bridge and culvert: suspension bridge [M]. Beijing: China Communications Press, 2011. (in Chinese)
-
期刊类型引用(6)
1. 谢献忠,张淳淇,林文欣,彭剑. 输电线路共振舞动机理试验研究. 工程力学. 2023(10): 71-80 .  本站查看
本站查看
2. 霍冰,刘习军,张锐. 高阶扭转模态耦合下覆冰导线的稳定性和影响因素分析. 工程力学. 2020(02): 241-249 .  本站查看
本站查看
3. 陈浩,何晓凤,王丙兰,李哲. 基于集合预报的两种输电线路舞动概率预测方法. 科学技术与工程. 2020(34): 14078-14084 .  百度学术
百度学术
4. 张志强,黄增浩. 配网线路覆冰断线力学特性及加固措施分析. 电力科学与工程. 2019(03): 52-58 .  百度学术
百度学术
5. 晏致涛,黄珏,李清,李梦丽,杨晓辉. 真型大跨输电线路的舞动模拟与失谐控制. 四川建筑科学研究. 2019(05): 52-57 .  百度学术
百度学术
6. 谢献忠,胡霞,彭剑. 多档输电线非线性建模及面内自由振动分析. 应用力学学报. 2017(06): 1097-1101+1220 .  百度学术
百度学术
其他类型引用(7)




 下载:
下载: