EXPERIMENTAL STUDY ON THE CREEP CHARACTERISTICS OF HIGH-STRENGTH CONCRETE FILLED HIGH-STRENGTH STEEL TUBE
-
摘要: 高强钢管高强混凝土的应用越来越广泛,但目前对于其徐变特性的试验研究较少。该文对15根不同含钢率的高强钢管高强混凝土轴压短柱进行了365 d的收缩和徐变测试,并将试验结果与常用的徐变预测模型MC90、ACI209和MC2010等进行了对比。试验结果表明:高强钢管高强混凝土的徐变系数远小于素混凝土,当加载365 d后,素混凝土的徐变系数是高强钢管高强混凝土的2倍以上;含钢率对钢管混凝土试件的徐变有一定影响,徐变系数随着含钢率的增大而减小。在对比的3种常用徐变预测模型中,MC2010模型的徐变预测结果与试验结果吻合最好,可推荐用于高强钢管高强混凝土的收缩和徐变效应计算。此外,还将高强钢管高强混凝土与普通钢管混凝土的徐变试验结果进行了对比,结果表明,钢管混凝土的徐变随着核心混凝抗压强度的增加而减小。研究成果可为高强钢管高强混凝土轴心受压构件在正常使用阶段的徐变预测及徐变变形控制提供依据。Abstract: High strength concrete filled steel tube (HS-CFST) is widely used in civil engineering, however, the studies on the creep properties of HS-CFST are rarely reported. It measured the shrinkage and creep of fifteen specimens with different steel ratios under the action of axial compression for 365 days. The experimental results were compared with the prediction ones from the creep prediction model of MC 90, ACI 209 and MC 2010. It showed that: the creep coefficients of HS-CFST specimens are far less than that of the plain concrete specimens, and by the end of 365 days, the creep coefficient of plain concrete was more than twice of that of concrete in HS-CFST. The steel ratio affects the creep of the CFST specimens. The creep coefficient decreases as the steel ratio increases. Among the three existing creep models, the MC 2010 model can well predict the creep behavior of the HS-CFST specimens. Furthermore, the creep coefficient of the HS-CFST specimens were also compared with that of the normal strength CFST, and the results showed that the creep of CFST decreases as the compressive strength of the core concrete increases. It provides a useful reference for the creep prediction and creep control of HS-CFST under the action of axial compression.
-
钢管混凝土(CFST)是一种极具潜力的组合结构形式,其充分结合了钢材和混凝土的优点。目前,随着工艺进步和各种硅灰、添加剂的使用,强度大于100 MPa的高强混凝土的制备越发容易,然而高强混凝土由于脆性大,不能直接应用于建筑与桥梁结构[1-2],为了增加其延性,可将高强混凝土与高强钢管进行组合,形成高强钢管高强混凝土(HS-CFST),充分利用高强钢管的约束作用,使核心混凝土具有一定的延性,从而满足结构使用性能的要求[3]。徐变是混凝土的重要特性,将导致混凝土结构的长期变形,并会对钢管混凝土结构产生重大的应力重分布影响[4-6]。目前,国内外很多学者对钢管普通混凝土的收缩和徐变特性进行了大量的试验研究。其中,Terrey等[7]、Uy[8]和Kwon等[9]进行了钢管混凝土试件的收缩和徐变试验,并采用ACI209徐变预测模型与试验结果进行了对比分析。Vandewalle[10]进行了变温变湿环境的混凝土收缩和徐变特性试验研究,重点研究了温湿度变化对徐变的影响。Yang等[11]进行了9个钢管普通混凝土和3个素混凝土试件分别在3种不同应力水平下的收缩和徐变试验,实测了1710 d的实测数据,并在试验结果的基础上对ACI209徐变模型进行了修正。Wang等[12]依托北盘江大桥工程,实测了该大桥所用钢管混凝土的收缩和徐变特性,并基于试验结果,对MC2010徐变模型进行了修正。还有部分学者对钢管再生骨料混凝土[13]、钢管膨胀混凝土[14]、钢管粉煤灰混凝土等[15]的收缩和徐变特性进行了试验研究。彭建新等[16]推导了钢管混凝土拱肋应力重分布计算公式,王玉银等[17]对5种常用的钢管混凝土收缩和徐变模型及3种常用的计算方法进行了对比分析,丁敏等[18]提出了适用于钢管混凝土轴心受压构件的徐变预测模型-Huo模型。曹万林等[19]对11个配筋再生混凝土棱柱体试件进行了长期轴压荷载下的徐变试验,研究了再生骨料取代率配筋对混凝土徐变特性的影响。
针对高强钢管高强混凝土的收缩和徐变特性,Ma和Wang[20]进行了8个高强钢管混凝土试件的徐变试验,实测了380 d的徐变数据,基于B3模型提出了高强钢管混凝土的徐变预测模型。Farhad [21]基于徐变试验数据库的结果,对比分析了普通和高强自密实混凝土的徐变特性,并提出了徐变预测模型。Pan等[22]评估了几种常用徐变模型如ACI 209-92[23]、JTG D62−2004[24]、B3[25]和GL 2000[26]的适用性,并在JTG D62−2004[24]徐变模型的基础上提出了一种修正模型。
综上,国内外关于高强钢管高强混凝土收缩和徐变特性的研究并不多见,由于高强混凝土的配合比与普通混凝土存在较大差异,既有的钢管普通混凝土的收缩和徐变试验结果和徐变模式能否推广应用于高强钢管高强混凝土还存在不确定性。为此,本文将进行高强钢管高强混凝土轴压短柱试件的收缩和徐变试验,实测其徐变变化规律,通过将现有的徐变预测模型的理论计算结果与试验结果进行对比,比选出适用于高强钢管高强混凝土最优的徐变预测模型,从而为研究高强钢管高强混凝土拱桥的时变力学行为提供依据。
1 混凝土收缩和徐变模型
1.1 素混凝土的收缩和徐变预测模型
国内外现有常用的素混凝土徐变预测模型主要包括如下几种:MC90模型[27]、ACI209模型[23]、B3模型[25]、GL2000模型[26]、MC2010等[28]。其中MC90模型[27]和ACI209模型[23]应用最为广泛,而MC2010模型[28]将徐变分为基本徐变和干燥徐变,特别适用于钢管核心混凝土。因此本文主要采用MC90模型[27]、ACI209模型[23]和MC2010模型[28]与试验结果进行对比分析。
1.2 钢管混凝土的收缩和徐变预测模型
对于钢管约束的核心混凝土,其工作环境与素混凝土主要存在以下2点不同:一是核心混凝土被钢管所密封,其无法与外部进行湿度的交换,也就不存在干燥收缩与干燥徐变;二是核心混凝土被钢管所约束而无法自由的变形,这也将导致混凝土和钢管的内力重分布,即钢管的应力变大,混凝土的应力变小,从而导致核心混凝土的徐变变小。因此,上述素混凝土的收缩和徐变预测模型无法直接用来预测钢管混凝土的收缩和徐变。
为了考虑钢管混凝土的密封性,通常的做法是在徐变模型计算时将相对湿度取一个大值,根据文献[29]的试验研究结果,一般取值为RH>95%。另外,如果徐变模式将徐变分为基本徐变和干燥徐变,则可以直接将干燥徐变取为0,从而只考虑基本徐变的影响。为了考虑钢管的约束作用,可以通过内力平衡条件,建立钢管和混凝土的变形协调方程来考虑其内力重分布的影响[30]。其中最常用的方法有2种[31]:一是按龄期调整的有效模量法(AAEM);二是逐步积分法(Step-by-Step)。这两种方法各有优缺点,AAEM是一种代数的方法[32],其可以理论推导徐变变形的解析表达式,便于工程设计。而逐步积分法精度更高,但需要编程实现,不利于设计和规范采用。为此,本文采用AAEM计算钢管混凝土的收缩和徐变系数表达式。文献[33]的研究结果表明,AAEM的计算精度与逐步积分法误差并不大。
当采用AAEM法进行钢管混凝土的收缩和徐变计算时,其徐变系数表达式如下[32]:
φ′(t,t0)=φ(t,t0)1+EsEc×AsAc×[1+χ×φ(t,t0)] (1) 式中:
φ(t,t0) 为素混凝土的徐变系数;Es、Ec分别为钢管和混凝土的弹性模量;As、Ac分别为钢管和混凝土的截面面积;χ(t,t0) 为老化系数,其计算公式如下[34]:χ(t,t0)=11−e−[0.09+0.686φ(t,t0)]−1φ(t,t0) (2) 2 收缩和徐变试验
2.1 模型设计
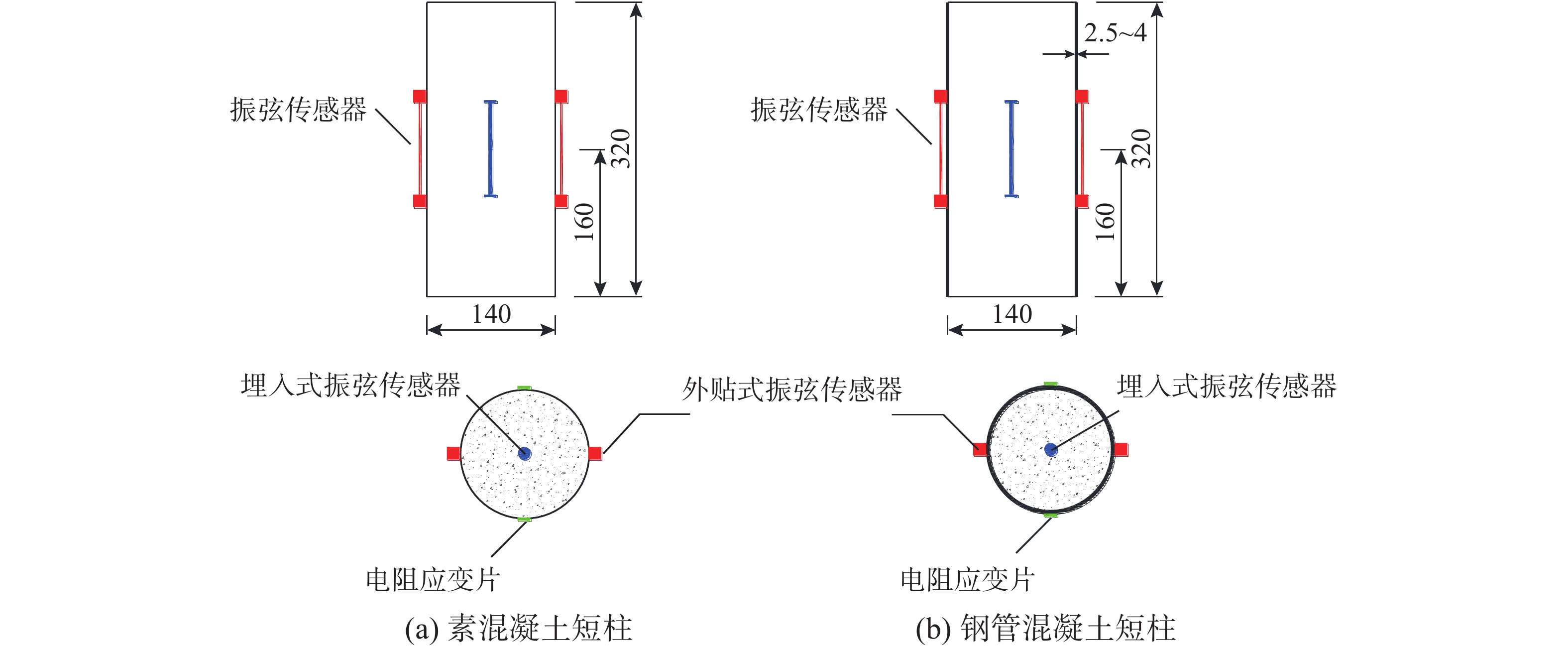
本次试验一共设计了4组共15个模型,其中A0组为素混凝土模型,包括2个高强素混凝土徐变模型和1个收缩模型;A1~A3组分别为含钢率8%、10%、12%的高强钢高强混凝土模型,分别包括3个高强钢高强混凝土徐变模型和1个收缩模型。钢管的外径为140 mm,钢管壁厚分别为2.5 mm、3.2 mm和4 mm,试件高度为320 mm。加载试件的核心混凝土应力水平即施加的长期荷载与极限荷载的比值为0.30,试件的极限荷载通过轴压短柱的承载力试验得到。试验模型参数见表1。
表 1 收缩和徐变试验模型参数表Table 1. Details of creep and shrinkage experiment specimens组别 编号 钢管厚度 含钢率/(%) 荷载值/kN 荷载强度比 测试项目 A0 A0-0-1 0 0 539 0.3 徐变 A0-0-2 0 0 539 0.3 A0-0-3 0 0 0 0 收缩 A1 A1-2.5-1 2.5 8 707 0.3 徐变 A1-2.5-2 2.5 8 707 0.3 A1-2.5-3 2.5 8 707 0.3 A1-2.5-4 2.5 8 0 0 收缩 A2 A2-3.2-1 3.2 10 738 0.3 徐变 A2-3.2-2 3.2 10 738 0.3 A2-3.2-3 3.2 10 738 0.3 A2-3.2-4 3.2 10 0 0 收缩 A3 A3-4.0-1 4 12 784 0.3 徐变 A3-4.0-2 4 12 784 0.3 A3-4.0-3 4 12 784 0.3 A3-4.0-4 4 12 0 0 收缩 2.2 材料参数
高强钢材采用Q560钢材,通过材性试验实测得到的钢材屈服强度为560 MPa,极限强度为688 MPa,弹性模量为220 GPa,泊松比为0.292,延伸率为29.0%。
核心混凝土28 d立方体强度为106.3 MPa,配合比如表2所示,实测得到的混凝土力学特性如表3所示。
表 2 试验混凝土配合比Table 2. Concrete mixing proportion for testing/(kg/m3) 水泥 水 硅粉 细骨料 粗骨料 减水剂 630 140 70 560 1040 4.2 表 3 混凝土力学性能实测值Table 3. Tested mechanical properties of concrete28 d立方体
抗压强度
fcu,28/MPa65 d立方体
抗压强度
fcu,65/MPa28 d
弹性模量
Ec,28/GPa65 d
弹性模量
Ec,65/GPa28 d
泊松比
μc,2865 d
泊松比
μc,65106.3 115.7 44.6 45.7 0.2 0.19 2.3 收缩和徐变测试装置
试验加载设备采用北京仪创YC-XB100S型混凝土徐变仪,如图1所示。加载装置由3根大直径螺杆,上、中、下3块加载钢板,压力传感器和底部弹簧组成。该装置最大加载能力为1000 kN,通过电动千斤顶施加荷载,所施加的荷载由压力传感器通过读数仪实时显示。底部弹簧的恢复力可以有效消除由于徐变变形导致的力的卸载。
在钢管表面前、后、左、右4个方向对称布置振弦传感器和应变片采集钢管应变,在核心混凝土的中央预先埋入振弦传感器用于测试混凝土应变。应变测点布置示意图如图2所示。表面式振弦传感器采用北京基康的BGK-4000x传感器,埋入式振弦传感器采用北京基康的BGK-4200x传感器,应变花采用日本TML公司生产的型号为FCA-3-11-3LJBT双轴应变花。
试验中电阻应变片采用扬州晶明JM3813静态应变采集仪进行数据采集,每台应变采集仪60个通道。振弦传感器采用扬州晶明JM3818A频率采集仪进行。JM3813与JM3818A均自带有蓄电池和存储卡,可以在断电情况下连续工作48 h,保证了测试的连续性。试验在恒温的实验室进行,通过空调将温度控制在20 ℃ ± 2 ℃以内,湿度控制在50%~70%,尽量消除温湿度的影响。
3 试验结果和分析
3.1 收缩应变
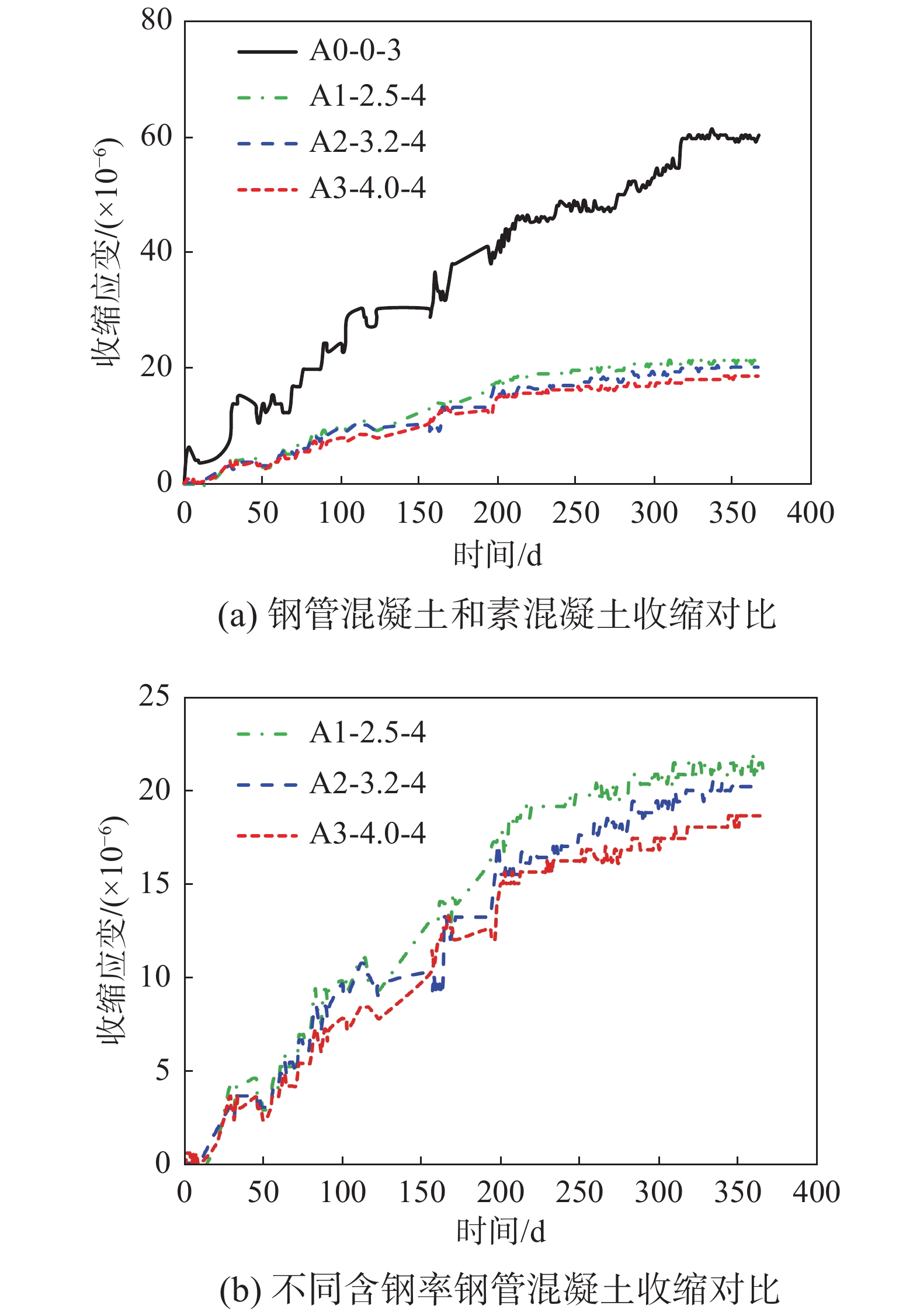
图3(a)为4个收缩试件的收缩应变随时间的变化曲线,由图可知,素混凝土的收缩应变远大于钢管混凝土的收缩应变,当加载365 d后,素混凝土的收缩应变约为钢管混凝土的3倍。无论是素混凝土还是钢管混凝土,收缩应变只是在早期增加的非常迅速,而随着时间增加,增速越来越慢,加载200 d后,钢管混凝土的收缩已基本稳定,但是素混凝土的收缩还在持续增加。图3(b)为3个不同含钢率钢管混凝土试件的收缩应变随时间的变化曲线,由图可知,含钢率对钢管混凝土的收缩基本无影响,当加载365 d后,含钢率分别为8%、10%、12%的试件的收缩应变分别为21 με、20 με和19 με,几乎相等。这主要是因为:1) 由于钢管的密封作用,核心混凝土与外部环境没有水分的交换,其收缩值非常小,导致其差距不明显;2) 三个试件的含钢率差异不大,难以对钢管混凝土的收缩产生明显影响。
3.2 徐变应变和徐变系数
素混凝土和钢管混凝土的徐变应变随时间的变化曲线如图4所示,在这些曲线中均减去了相应的收缩应变。由图可知:1) 钢管混凝土和素混凝土的徐变具有相同的趋势,徐变应变均随着时间的增加而增加,且早期增加速度较快;2) 钢管混凝土的徐变应变远小于素混凝土,当加载365 d后,A0组(素混凝土)、A1、A2和A3(钢管混凝土)组的平均徐变应变分别为464 με、 214 με、221 με和194 με,钢管混凝土的徐变应变小于素混凝土的1/2;3) A2组3个试件徐变应变的离散性较大,这主要是因为加载偏心导致。同一组中3个试件为层叠放置,加载时偏心难以避免,若偏心较大则实测应变的离散性也较大。综合三组试件结果可知,A2组的偏心更为严重,但通过对3个试件取平均值,可有效消除偏心的影响。
将徐变应变除以试件加载时刻的初始弹性应变即可得到试件的徐变系数,如图5所示。由图可知,徐变系数曲线的变化规律与徐变应变一致,在加载早期徐变系数快速增加,而后期增长缓慢。
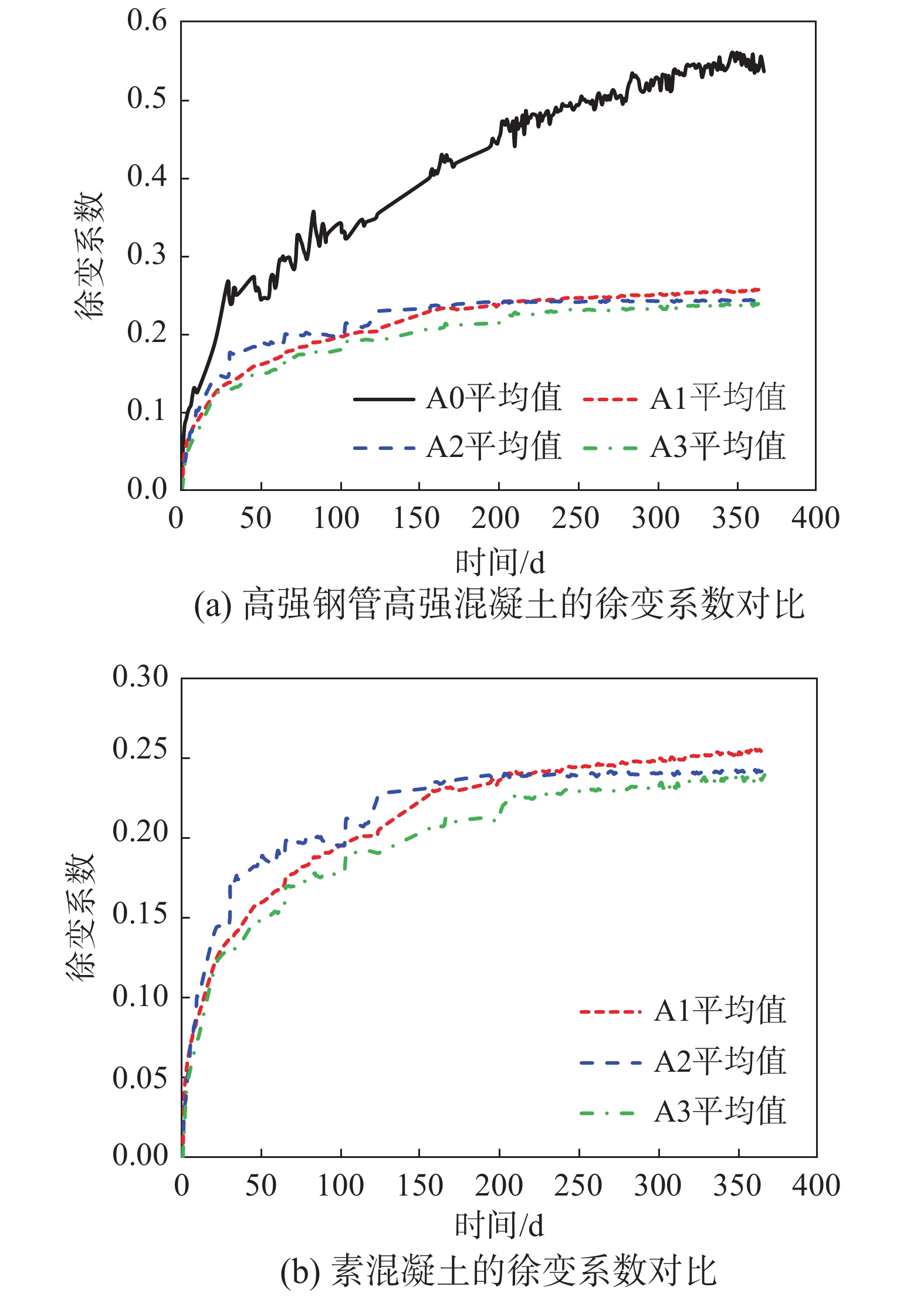
钢管混凝土与素混凝土的徐变系数对比如图6(a)所示,由图可知,钢管混凝土的徐变系数远小于素混凝土,当加载365 d后,A0、A1、A2和A3组的平均徐变系数分别为0.554、0.256、0.243和0.239,钢管混凝土的徐变系数小于素混凝土的1/2。
不同含钢率钢管混凝土试件的徐变系数对比如图6(b)所示,由图可知,徐变系数随着含钢率的增加而减小,这与理论公式是一致的,可由式(1)直观看出。但由于本次试验模型的含钢率差异不大,导致各曲线的差异不明显。
3.3 试验结果和规范模型的对比
本文将试验结果与MC90模型[27]、ACI209模型[23]和MC2010模型[28]的预测结果进行对比。在这3种徐变模型中,需要用到的设计参数如表4所示。由于钢管的密闭作用,相对湿度RH取为99%,fcm为混凝土平均抗压强度。模型预测结果为按式(1)修正后的结果。
表 4 徐变模型计算参数Table 4. The parameters for the creep models参数 取值 参数 取值 加载龄期 t0/d 52 塌落度 s/mm 30 相对湿度 RH/(%) 99 细骨料百分比 ψ/(%) 35 理论厚度 h/mm 70 含气率 α/(%) 5.6 平均抗压强度 fcm/MPa 92 图7为试验结果与3种徐变预测模型计算结果的对比。由图可知:1) 无论是试验结果还是预测结果均表现出同样的规律,即徐变在开始加载阶段增长较快,随着时间的增加而变得平缓;2) 无论是素混凝土还是钢管混凝土,在这3种徐变预测模型中,MC2010模型[28]与实测结果吻合最好,其次为MC90模型[27],ACI209模型[23]的预测结果误差最大。MC90模型[27]和ACI209模型[23]均高估了素混凝土和钢管混凝土的徐变,因此在工程设计中推荐采用MC2010模型[28]来预测素高强混凝土及高强钢管高强混凝土的收缩和徐变。
4 徐变特性对比研究
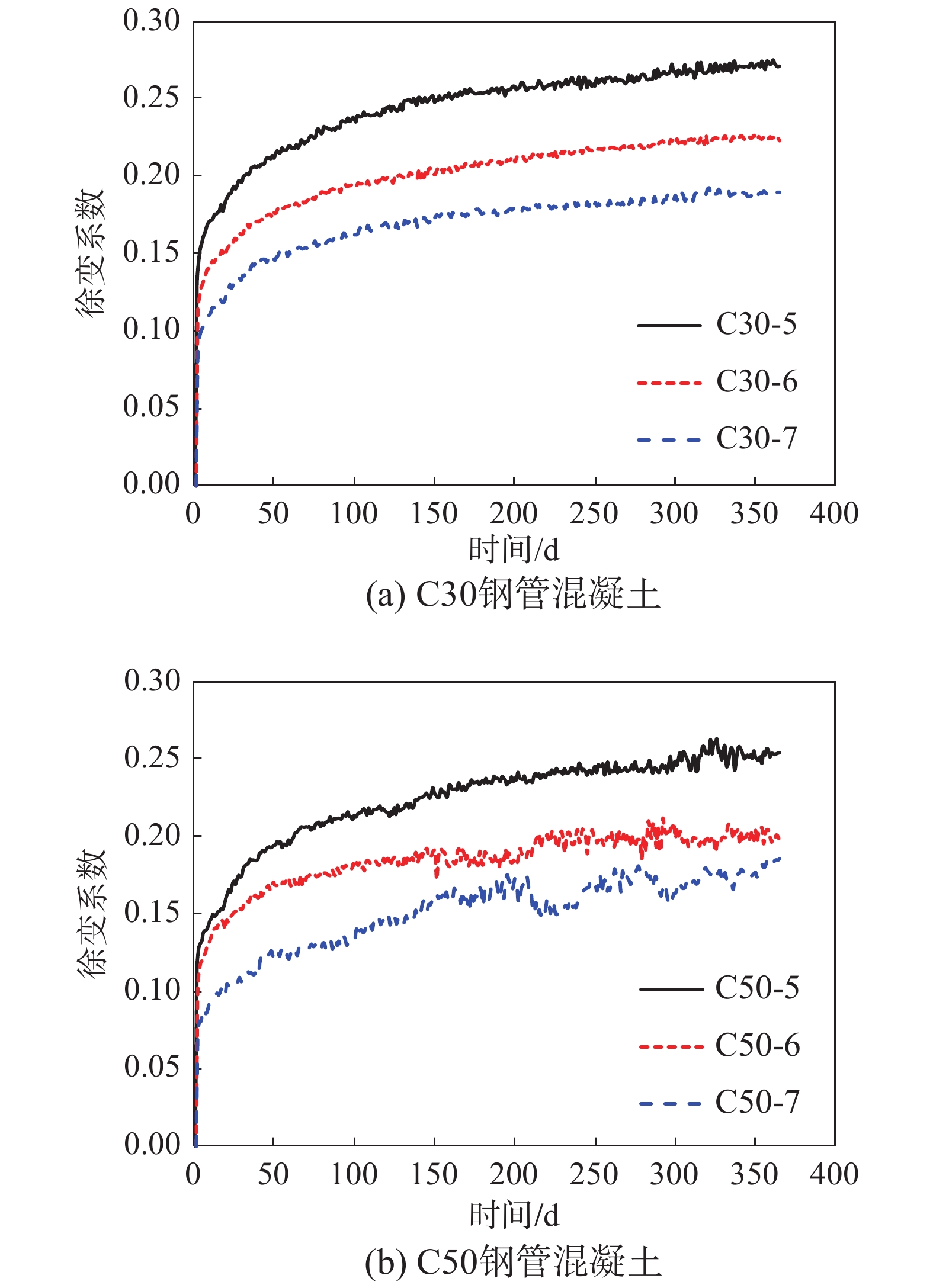
为了对比高强钢管高强混凝土与普通钢管混凝土收缩和徐变特性的不同,同时还进行了C30钢管混凝土和C50钢管混凝土短柱的徐变试验,实测了365 d的收缩和徐变值。普通钢管混凝土徐变试件的参数如表5所示,其中钢管采用的是Q235普通钢材,钢管厚度分别为5 mm、6 mm和7 mm 这3种,其他尺寸参数与高强钢管高强混凝土试件相同。
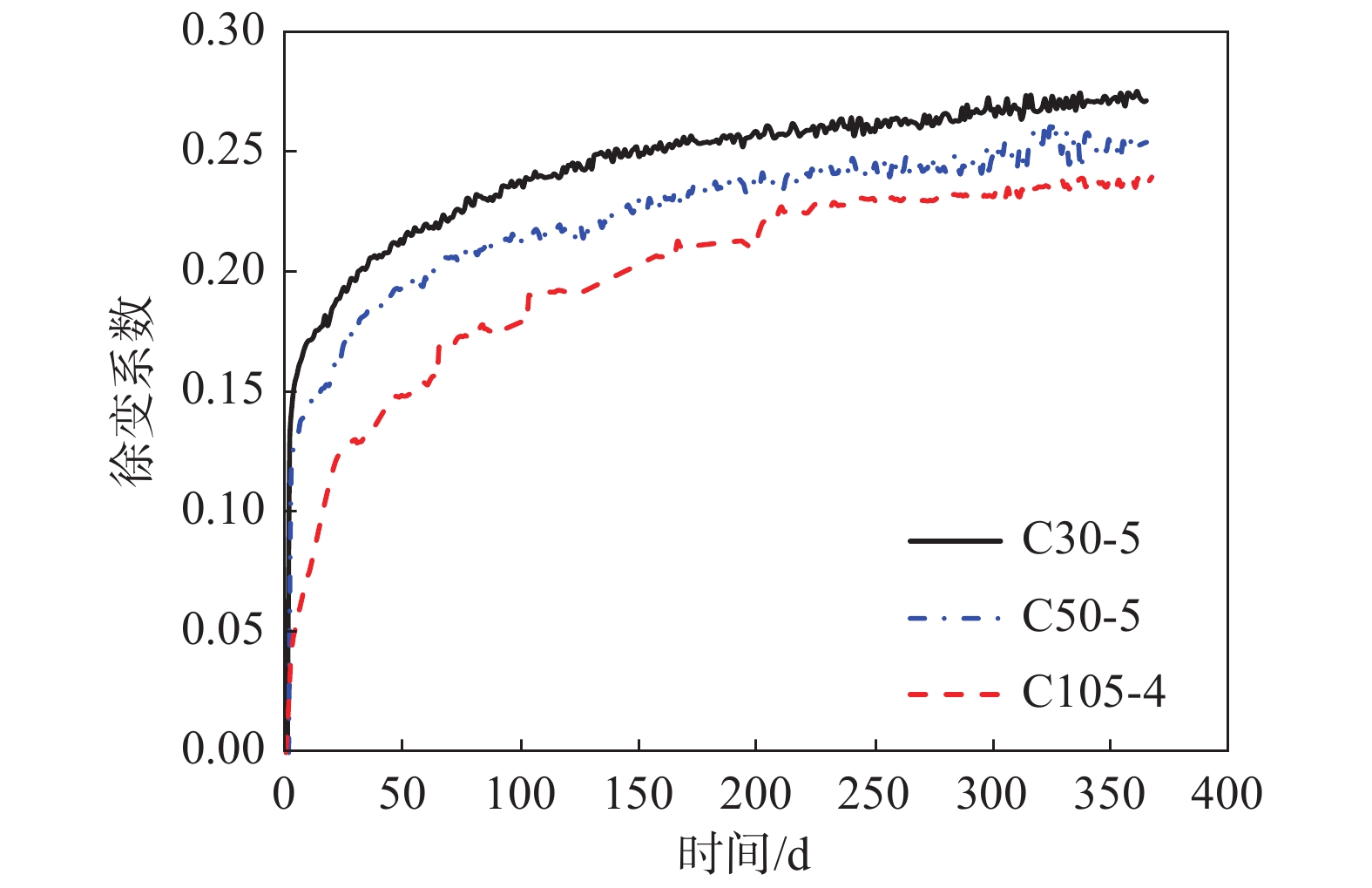
表 5 普通钢管混凝土收缩和徐变试验参数Table 5. Parameters of creep and shrinkage experiments of N-CFST specimens试件 混凝土等级 钢材等级 钢管外径/mm 钢管厚度/mm 含钢率/(%) C30-5 C30 Q235 140 5 15.9 C30-6 C30 Q235 140 6 19.6 C30-7 C30 Q235 140 7 23.4 C50-5 C50 Q235 140 5 15.9 C50-6 C50 Q235 140 6 19.6 C50-7 C50 Q235 140 7 23.4 图8为C30钢管混凝土和C50钢管混凝土的实测徐变系数随时间的变化曲线。由图8可知:1) 普通钢管混凝土与高强钢管高强混凝土的徐变系数呈现相同的规律,即徐变在加载初期增长较快,后期变得平缓,加载200 d后,混凝土的徐变开始稳定,前60 d的徐变值达到了365 d徐变值的70%;2) 钢管混凝土的徐变随着含钢率的增加而减小,3种不同含钢率试件的徐变系数曲线之间差别非常明显;3) 徐变系数随着混凝土强度的增加而减小,相同设计参数下,C50钢管混凝土的徐变系数比C30钢管混凝土的徐变系数小约10%。
为对比普通钢管混凝土与高强钢管高强混凝土收缩和徐变的异同,选用普通钢管混凝土的C30-5和C50-5试件与高强混凝土的A3(C105-4)试件进行对比分析。这3组试件的含钢率基本一致,其中C30-5和C50-5的含钢率为15.9%,C105-4的含钢率为12%。徐变系数的对比曲线如图9所示,试验参数如表6所示。由图9可知:3组试件的徐变系数曲线存在明显的区别,混凝土的徐变随着强度的提高而减小。加载365 d后,C30-5、C50-5、A3(C105-4)的徐变系数分别为0.271、0.254和0.239。需要说明的是,C30-5、C50-5和A3(C105-4)的加载龄期和含钢率并不完全一致。如果C105-4试件的加载龄期由52 d改为75 d,则其徐变将随着加载龄期的增大而减小;如果C105-4试件的含钢率由12.0%改为15.9%,则其徐变将随着含钢率的增大而进一步减小。因此如果所有参数都一致,C105钢管混凝土的徐变系数曲线与C30-5、C50-5的区别将会更加明显。这主要是因为高强混凝土的配合比和普通混凝土相比存在明显差异,高强混凝土的水灰比远小于普通混凝土,导致其徐变偏小。
表 6 高强钢管高强混凝土和普通钢管混凝土试件设计参数Table 6. Parameters of HS-CFST and N-CFST specimens试件 混凝土等级 含钢率/(%) 加载龄期/d C30-5 C30 15.9 75 C50-5 C50 15.9 75 A3(C105-4) C105 12.0 52 5 结论
本文对高强钢管高强混凝土的收缩和徐变展开了试验研究,将试验结果与现有的常用徐变预测模型MC90模型[27],ACI209模型[23]和MC2010模型[28]的预测结果进行了对比,同时对比分析了高强钢管高强混凝土和普通钢管混凝土徐变系数的差异,研究结果表明:
(1)钢管混凝土试件的收缩特性和素混凝土试件有明显不同。素混凝土试件的收缩应变远大于钢管混凝土试件的收缩应变,在加载365 d后,素混凝土的收缩约为钢管混凝土的3倍。
(2)钢管混凝土试件的徐变特性与普通混凝土试件有明显不同。由于钢管的密封和约束作用,钢管混凝土的徐变远远小于普通混凝土试件的徐变,在加载365 d后,普通混凝土的徐变系数是钢管混凝土徐变系数的2倍以上。含钢率对钢管混凝土试件的徐变有一定的影响,徐变系数随着含钢率的增加而减小。
(3)将试验结果与现有的常用徐变预测模型MC90模型,ACI209模型和MC2010模型的预测结果进行对比分析,结果表明无论是钢管混凝土试件还是素混凝土试件,采用MC2010模型预测的徐变曲线与实测结果吻合最好,其次为MC90模型,ACI209模型的预测结果误差最大。因此在工程设计中建议采用MC2010模型来预测素高强混凝土以及高强钢管高强混凝土的收缩和徐变。
(4)进行了C30和C50普通钢管混凝土试件的徐变试验,并将其与C105高强钢管混凝土试件的徐变结果进行了对比。结果表明,钢管混凝土 的徐变与混凝土的强度负相关,钢管混凝土的徐变随着混凝土强度的增加而减小,不同混凝土强度试件的实测徐变曲线存在明显区别。这主要是因为,高强混凝土的配合比和普通混凝土相比存在明显差异,高强混凝土的水灰比远小于普通混凝土,导致其徐变偏小。
-
表 1 收缩和徐变试验模型参数表
Table 1 Details of creep and shrinkage experiment specimens
组别 编号 钢管厚度 含钢率/(%) 荷载值/kN 荷载强度比 测试项目 A0 A0-0-1 0 0 539 0.3 徐变 A0-0-2 0 0 539 0.3 A0-0-3 0 0 0 0 收缩 A1 A1-2.5-1 2.5 8 707 0.3 徐变 A1-2.5-2 2.5 8 707 0.3 A1-2.5-3 2.5 8 707 0.3 A1-2.5-4 2.5 8 0 0 收缩 A2 A2-3.2-1 3.2 10 738 0.3 徐变 A2-3.2-2 3.2 10 738 0.3 A2-3.2-3 3.2 10 738 0.3 A2-3.2-4 3.2 10 0 0 收缩 A3 A3-4.0-1 4 12 784 0.3 徐变 A3-4.0-2 4 12 784 0.3 A3-4.0-3 4 12 784 0.3 A3-4.0-4 4 12 0 0 收缩 表 2 试验混凝土配合比
Table 2 Concrete mixing proportion for testing
/(kg/m3) 水泥 水 硅粉 细骨料 粗骨料 减水剂 630 140 70 560 1040 4.2 表 3 混凝土力学性能实测值
Table 3 Tested mechanical properties of concrete
28 d立方体
抗压强度
fcu,28/MPa65 d立方体
抗压强度
fcu,65/MPa28 d
弹性模量
Ec,28/GPa65 d
弹性模量
Ec,65/GPa28 d
泊松比
μc,2865 d
泊松比
μc,65106.3 115.7 44.6 45.7 0.2 0.19 表 4 徐变模型计算参数
Table 4 The parameters for the creep models
参数 取值 参数 取值 加载龄期 t0/d 52 塌落度 s/mm 30 相对湿度 RH/(%) 99 细骨料百分比 ψ/(%) 35 理论厚度 h/mm 70 含气率 α/(%) 5.6 平均抗压强度 fcm/MPa 92 表 5 普通钢管混凝土收缩和徐变试验参数
Table 5 Parameters of creep and shrinkage experiments of N-CFST specimens
试件 混凝土等级 钢材等级 钢管外径/mm 钢管厚度/mm 含钢率/(%) C30-5 C30 Q235 140 5 15.9 C30-6 C30 Q235 140 6 19.6 C30-7 C30 Q235 140 7 23.4 C50-5 C50 Q235 140 5 15.9 C50-6 C50 Q235 140 6 19.6 C50-7 C50 Q235 140 7 23.4 表 6 高强钢管高强混凝土和普通钢管混凝土试件设计参数
Table 6 Parameters of HS-CFST and N-CFST specimens
试件 混凝土等级 含钢率/(%) 加载龄期/d C30-5 C30 15.9 75 C50-5 C50 15.9 75 A3(C105-4) C105 12.0 52 -
[1] Liew Richard J Y. Design of concrete filled tubular beam-columns with high strength steel and concrete [J]. Structures, 2018, 8: 213 − 226.
[2] Xiong M X, Xiong D X, Liew Richard J Y. Axial performance of short concrete filled steel tubes with high- and ultra-high- strength materials [J]. Engineering Structures, 2017, 136: 494 − 510. doi: 10.1016/j.engstruct.2017.01.037
[3] 韦建刚, 罗霞, 陈宝春, 等. 圆高强钢管UHPC梁抗弯性能研究[J]. 工程力学, 2021, 38(1): 183 − 194. doi: 10.6052/j.issn.1000-4750.2020.03.0158 Wei Jiangang, Luo Xia, Chen Baochun, et.al. Study on bending behavior of circular UHPC filled high strength steel tube beams [J]. Engineering Mechanics, 2021, 38(1): 183 − 194. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.03.0158
[4] 胡守旺, 彭建新, 张建仁, 等. 钢管混凝土拱桥核心混凝土徐变效应可靠度分析[J]. 中国公路学报, 2017, 30(3): 185 − 190. Hu Shouwang, Peng Jianxin, Zhang Jianren, et al. Reliability analysis of core concrete creep effect on concrete-filled steel tubular arch bridge [J]. China Journal of Highway and Transport, 2017, 30(3): 185 − 190. (in Chinese)
[5] 王庆贺, 梁永泽, 张欢, 等. 考虑荷载分布的多跨连续钢-再生混凝土组合板长期性能研究[J]. 工程力学, 2021, 38(2): 198 − 210. doi: 10.6052/j.issn.1000-4750.2020.04.0242 Wang Qinghe, Liang Yongze, Zhang Huan, et al. Time-dependent behavior of multi-span continuous steel-rac composite slabs considering the loading distribution effects [J]. Engineering Mechanics, 2021, 38(2): 198 − 210. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.04.0242
[6] Shao X D, Peng J X, Li L F, et.al. Time-dependent behavior of concrete-filled steel tubular arch bridge [J]. Journal of Bridge Engineering, 2010, 15(1): 98 − 107. doi: 10.1061/(ASCE)1084-0702(2010)15:1(98)
[7] Terrey P J, Bradford M A, Gilbert R I. Creep and shrinkage of concrete in concrete-filled circular steel tubes [C]. Proceedings of 6th International Symposium on Tubular Structures, Melbourne (Grundy P, Hogate A, Wong S M (eds)). Balkema, Rotterdam, the Netherlands, 1994: 293 − 298.
[8] Uy B. Static long-term effects in short concrete-filled steel box columns under sustained loading [J]. ACI Structural Journal, 2001, 98(1): 96 − 104.
[9] Kwon S H, Kim Y Y, Kim J K. Long-term behaviour under axial service loads of circular columns made from concrete filled steel tubes [J]. Magazine of Concrete Research, 2005, 57(2): 87 − 99. doi: 10.1680/macr.2005.57.2.87
[10] Vandewalle L. Concrete creep and shrinkage at cyclic ambient conditions [J]. Cement & Concrete Composites, 2000, 22: 201 − 208.
[11] Yang M G, Cai C S, Chen Y. Creep performance of concrete-filled steel tubular (CFST) columns and applications to a CFST arch bridge [J]. Steel and Composite Structures, 2015, 19(1): 111 − 129. doi: 10.12989/scs.2015.19.1.111
[12] Wang Y B, Zhao R D, Jia Y. Creep characteristics of concrete used in long-span arch bridge [J]. The Baltic Journal of Road and Bridge Engineering, 2019, 14(1): 18 − 36. doi: 10.7250/bjrbe.2019-14.431
[13] Yang Y F, Han L H, Wu X. Concrete shrinkage and creep in recycled aggregate concrete-filled steel tubes [J]. Advances in Structural Engineering, 2008, 11(4): 383 − 396. doi: 10.1260/136943308785836772
[14] 王玉银, 耿悦, 张素梅. 钢管微膨胀混凝土轴压短柱长期变形研究[J]. 中国公路学报, 2007, 24(6): 57 − 63. Wang Yuyin, Geng Yue, Zhang Sumei. Research on long-term deformation of concrete-filled steel tubular stubs with expansive additive under axial loading [J]. China Journal of Highway and Transport, 2007, 24(6): 57 − 63. (in Chinese)
[15] Yan W T, Han B, Zhang J Q, et al. Experimental study on creep behavior of fly ash concrete filled steel tube circular arches [J]. Steel and Composite Structures, 2018, 27(2): 185 − 192.
[16] 彭建新, 邵旭东, 程翔云, 等. 钢管混凝土拱肋徐变研究[J]. 工程力学, 2007, 24(6): 79 − 85. doi: 10.3969/j.issn.1000-4750.2007.06.014 Peng Jianxin, Shao Xudong, Cheng Xiangyun, et al. Creep behavior of concrete-filled steel tubular arch rib [J]. Engineering Mechanics, 2007, 24(6): 79 − 85. (in Chinese) doi: 10.3969/j.issn.1000-4750.2007.06.014
[17] 王玉银, 耿悦, 张素梅. 钢管混凝土收缩徐变模型及计算方法对比分析[J]. 天津大学学报, 2011, 44(12): 1075 − 1082. Wang Yuyin, Geng Yue, Zhang Sumei. Comparison of concrete models and simplified analysis methods for concrete-filled steel tubular members [J]. Journal of Tianjin University, 2011, 44(12): 1075 − 1082. (in Chinese)
[18] 丁敏, 汪友弟, 代春辉, 等. 钢管混凝土轴心受压构件的徐变预测模型及其徐变性能分析[J]. 工程力学, 2017, 34(6): 166 − 176. doi: 10.6052/j.issn.1000-4750.2016.01.0022 Ding Min, Wang Youdi, Dai Chunhui, et al. Creep calculation and behavior analysis of concrete-filled steel tubular member under axial compression [J]. Engineering Mechanics, 2017, 34(6): 166 − 176. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.01.0022
[19] 曹万林, 刘亦斌, 肖建庄, 等. 配筋再生混凝土棱柱体徐变试验研究[J]. 建筑结构学报, 2020, 41(12): 141 − 147, 164. Cao Wanlin, Liu Yibin, Xiao Jianzhuang, et al. Experimental study on creep of reinforced recycled concrete prism [J]. Journal of Building Structures, 2020, 41(12): 141 − 147, 164. (in Chinese)
[20] Ma Y S, Wang Y F. Creep of high strength concrete filled steel tube columns [J]. Thin-Walled Structures, 2012, 53: 91 − 98. doi: 10.1016/j.tws.2011.12.012
[21] Farhad Aslani. Creep behaviour of normal- and high-strength self-compacting concrete [J]. Structural Engineering and Mechanics, 2015, 53(5): 921 − 938. doi: 10.12989/sem.2015.53.5.921
[22] Pan Zuanfeng, Lv Zhitao, Fu Chung C. Experimental study on creep and shrinkage of high-strength plain concrete and reinforced concrete [J]. Advances in Structural Engineering, 2011, 14(2): 235 − 247. doi: 10.1260/1369-4332.14.2.235
[23] ACI 209R-92, Prediction of creep, shrinkage, and temperature effects in concrete structures [J]. Farmington Hills, MI: ACI (American Concrete Institute), 1992.
[24] JTG D62−2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范 [S]. 北京: 人民交通出版社, 2004. JTG D62−2004, Code for design reinfoced and prestressed concrete bridges and culverts [S]. Beijing: China Communications Press, 2004. (in Chinese)
[25] Bazant, Z P, Baweja S. Creep and shrinkage prediction model for analysis and design of concrete structures: Model B3 [J]. Materials and Structures, 1995, 28(180): 357 − 365.
[26] Gardner N J, Lockman MJ. Design provisions for drying shrinkage and creep of normal-strength concrete [J]. ACI Materials Journal, 2001, 98(2): 159 − 167.
[27] CEB-FIP, Model code 1990 [S]. London: Thomas Telford Co. Ltd, 1993.
[28] CEB-FIP, Fib model code for concrete structures 2010 [S]. Berlin: Ernst & Sohn, 2013.
[29] 文智. 钢管混凝土徐变及其对承载力的影响 [D]. 广州: 广州大学, 2019. Wen Zhi. Creep of concrete-filled steel tube and its effect on bearing capacity [D]. Guangzhou: Guangzhou University, 2019. (in Chinese)
[30] 王永宝, 赵人达, 徐腾飞, 等. 钢管混凝土轴压构件徐变简化计算方法研究[J]. 公路交通科技, 2016, 33(1): 57 − 63. doi: 10.3969/j.issn.1002-0268.2016.01.009 Wang Yongbao, Zhao Renda, Xu Tengfei, et al. Study on simplified creep calculation method of CFST members under axial loading [J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 57 − 63. (in Chinese) doi: 10.3969/j.issn.1002-0268.2016.01.009
[31] Wang W N, Gong J X. New relaxation function and age-adjusted effective modulus expressions for creep analysis of concrete structures [J]. Engineering Structures, 2016, 188: 1 − 10.
[32] Bazant Z P. Prediction of concrete creep effects using age-adjusted effective modulus method [J]. ACI Materials Journal, 1972, 69(4): 212 − 217.
[33] Geng Yue, Wang Yuyin, Chen Jie. Time-dependent behaviour of steel tubular columns filled with recycled coarse aggregate concrete [J]. Journal of Constructional Steel Research, 2016, 122: 455 − 468. doi: 10.1016/j.jcsr.2016.04.009
[34] Brooks J J, Neville A M. Relaxation of stress in concrete and its relation to creep [J]. ACI Materials Journal, 1976, 73(4): 227 − 232.
-
期刊类型引用(3)
1. 吴小勇,熊琦龙,周凯. 钢筋钢丝网砂浆加固钢筋混凝土方柱耗能特性数值分析. 科学技术与工程. 2022(20): 8789-8796 .  百度学术
百度学术
2. 卜良桃,朱天宇,贺洪霞. RPC钢筋网加固足尺RC柱偏压性能试验. 沈阳建筑大学学报(自然科学版). 2022(05): 830-838 .  百度学术
百度学术
3. 高子恒,杨德健. 二次受力下HPFL加固RC方柱抗震性能影响因素分析. 河北水利电力学院学报. 2021(02): 23-29+38 .  百度学术
百度学术
其他类型引用(2)




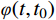
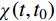
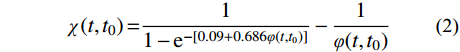
 下载:
下载: