HIGH-PRECISION ARTIFICIAL BOUNDARY CONDITION FOR SCALAR WAVE PROPAGATION IN VERTICAL STRATIFIED MEDIA
-
摘要: 为了实现含竖向成层介质以及表面不规则地形场地中标量波传播问题的高效且高精度求解,该文基于连分式展开和扩展的一致边界,建立了一种频域下折线形高精度人工边界条件。通过在每个竖向地层内引入独立的斜角坐标变换,新的人工边界条件可以用于多起伏地表地形条件。新的折线形人工边界在频域下推导,仅含有连分式阶数一个待定实参数,用于调整计算精度,该参数不随外行波的频率和传播角度改变。人工边界条件可以与内域有限元方程无缝耦合,应用简单方便。由于新边界条件的高精度,内域尺寸可以取较小甚至可以直接将人工边界加在结构周围或者地表,从而极大提高计算效率。通过典型数值算例,将人工边界计算模型与有限元大模型的解进行了对比分析,验证了该文提出的折线形人工边界条件的有效性和高精度。Abstract: To realize the efficient and high precision solution of the scalar wave propagation problem in the field with vertical stratified media and irregular surface topography, a high-precision artificial boundary condition is established based on continuous fraction expansion and the extension of consistent boundary. The proposed artificial boundary condition can be applied to sites with zigzag surfaces by introducing an independent oblique coordinate transformation in each vertical layer. The frequency-domain artificial boundary condition only has the continuous fraction order as an undetermined parameter, which can be used to adjust the calculation accuracy and is independent of frequency and incidence angle of outgoing propagating waves. The artificial boundary conditions can be seamlessly coupled with finite element methods for the inner finite domain, which is easy to use. Due to the high precision of the boundary condition, the size of the finite domain can be very small, or even directly added to the ground surface or around the structure, thus greatly improving the computational efficiency. The validity and accuracy of the artificial boundary condition are verified by comparing with the finite element model in typical numerical examples.
-
在地下结构抗震分析中,有限元法因其灵活高效的特点,被广泛用于有限域模拟。为了更有效地反映截断无限土体的辐射阻尼效应,需要引入人工边界条件[1]。人工边界的适用性和精度直接影响计算结果的精度,并通过影响计算区域的大小而影响计算效率。城市抗震防灾和重大工程项目建设中经常遇到竖向成层介质以及不规则地形场地。在我国西南部山岭地区中这种地形地质条件较为常见,如滇中引水工程中香炉山隧道穿越的含多条断裂带的复杂地形地质条件[2]。厦门市轨道交通2号线跨海盾构隧道穿越了基岩、基岩强风化、基岩全风化等多个地层[3]。不均匀介质和不规则地形场地条件引起复杂的波动反射和透射,会造成与均匀半空间场地明显不同的动力反应。复杂场地中结构动力反应研究表明,不均匀地质和不规则地形的存在会对场地和结构的动力反应产生显著影响[4-8],在地下结构抗震分析领域引起越来越多的关注。建立竖向成层介质中的高精度人工边界条件具有研究和实际意义。国内外研究者已提出大量人工边界条件[9],其中包括:粘性边界[10]、粘弹性边界[11]、透射边界[12]、无限元法[13-14]、边界元法[15-16]、Engquist-Majda边界[17]、Higdon 边界[18]、Bayliss-Turkel 边界[19]、Dirichlet-to-Neumann (DtN) 边界[20-23]、一致边界(薄层法)[24-26]、比例边界有限元法[27]、吸收层法如完美匹配层法[28-29]等。以上人工边界条件主要用于均匀介质的半空间或全空间场地以及底部固定的单层或水平成层场地。
近年来适用于水平成层半空间场地的人工边界条件得到进一步发展。2009年,蒋通和田治见宏[30]提出一致边界结合粘性边界来处理水平成层半空间介质的波传播问题,粘性边界中阻尼器的吸能效果对整体精度影响较大。2011年,Lee和 Tassoulas[31]提出一致边界结合连分式吸收层的方法;2012年,João等[32]提出采用一致边界结合完美匹配离散层来解决水平成层半空间介质的波传播问题,分析表明连分式吸收层可等效转化为完美匹配离散层,其中匹配层厚度为基于频率和外行波入射角的纯虚数。2015年,Hamdan等[33]提出采用一致边界结合旁轴边界来模拟水平成层半空间介质中波传播问题,旁轴边界采用二阶泰勒展开代替半空间的解析刚度精度较低。2020年,李会芳等[34]提出H形高精度人工边界处理水平成层半空间标量波传播问题,此边界应用简单方便且能得到高精度、高效率的求解。
基于水平成层半空间场地中人工边界条件的研究工作,本文针对含竖向成层介质以及不规则地形场地中标量波传播问题,建立了频域下折线形高精度人工边界条件。竖向成层介质的底边界采用广义一致边界来拟合,通过适当的空间变换并精确模拟两侧的半空间刚度,将原来适用于表面自由、底部固定的一致边界扩展应用于两侧开放的竖向成层介质底边界;成层介质侧边界采用基于连分式的高精度边界。由于提出边界的高精度特性,有限域可以取得尽量小,对于无内域结构仅关心地表反应的情况,可以直接将人工边界加在地表,极大地减少自由度,提高计算效率。通过在每个竖层边界上引入斜角变换,广义一致边界可以为任意折线形,适用于竖向成层、不规则地表的场地反应。
1 问题描述
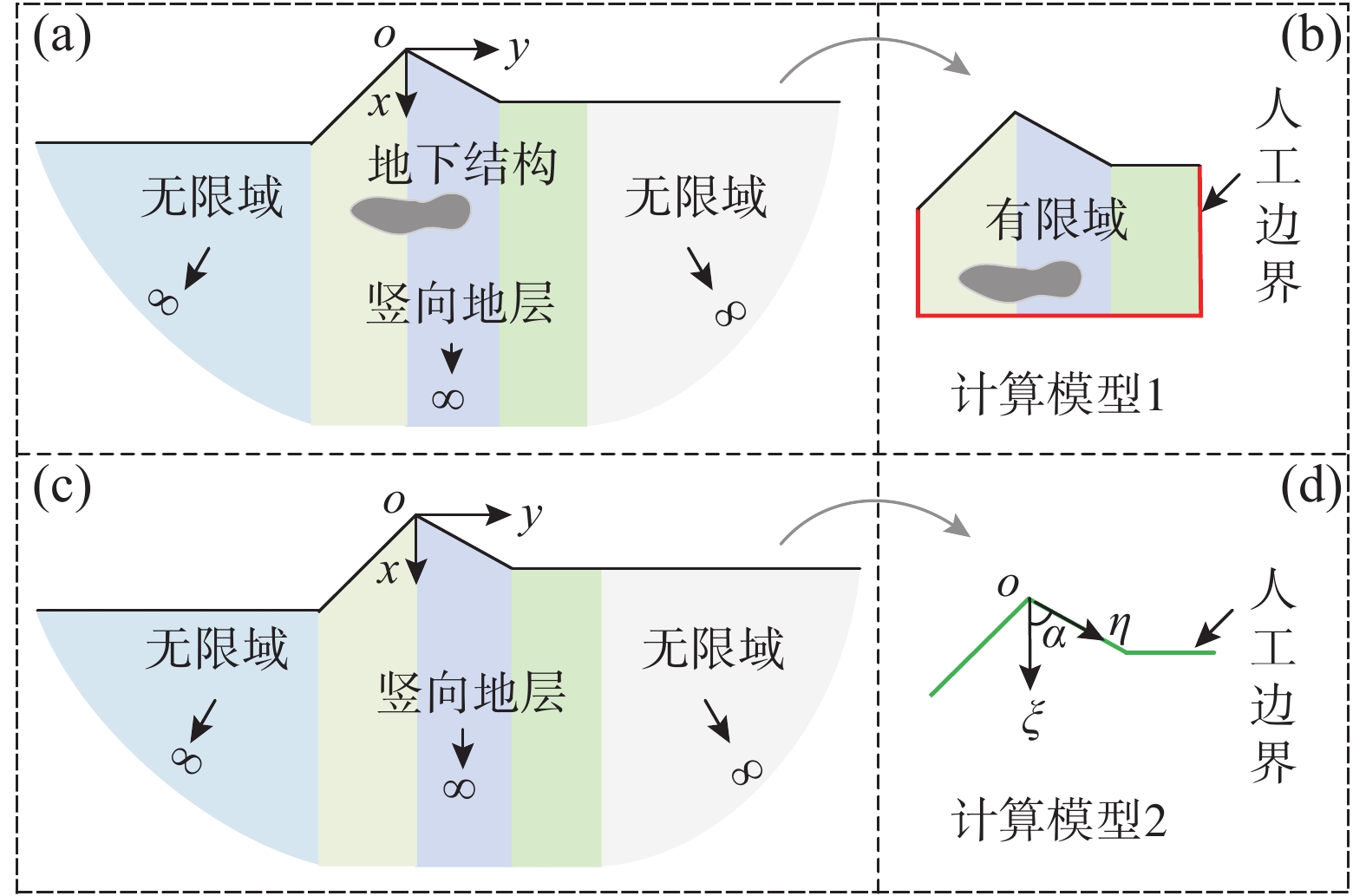
地震作用下重大基础设施结构的动力响应需考虑与周围介质的相互作用,形成无限域介质中的波传播问题。图1(a)所示为二维竖向成层半空间场地中的标量波传播问题,场地中包含任意不规则地形以及广义结构。为高效求解出平面波动问题,引入人工边界分别将竖向地层和两侧无限域截断,如图1(b)所示计算模型1由人工边界条件与内域有限元部分组成,其中有限域中可以包含任意不均匀、非线性材料以及不规则结构,采用有限元法模拟。由于提出人工边界条件的高精度,有限域尺寸可以尽量小。对于不含地下结构仅关心地面反应的情况如图1(c)所示,可以直接将人工边界加在地表,仅用折线形高精度人工边界条件来模拟竖向成层半空间场地,如图1(d)中计算模型2,最大限度减少计算自由度高效求解地表反应。
半空间场地中,左右两侧无限域以及竖向无限延伸的地层内为均匀线弹性材料。频域下标量波传播问题的控制方程为:
∂2u∂x2+∂2u∂y2=−ω2c2u (1) 式中:
u(x,y,ω) 为频域下位移;(x, y)为笛卡尔坐标系;ω 为圆频率;波速c在各层和两侧无限域内为常数,在不同层和无限域中可以取不同的值。应力向量为:
τ={τxτy}T={∂u∂x∂u∂y}T (2) 地表为自由边界条件,各竖向地层和无限域之间的交界面以及人工边界两侧均满足位移和应力连续条件。另外,满足无限远处辐射条件以及初始静止条件。
2 高精度人工边界条件
以图1(b)中计算模型1为例给出本文高精度折线形人工边界条件的实现过程。不含广义结构时,人工边界条件可加在地表处,此时计算模型中无内域和竖层侧边界,计算模型1简化为图1(d)中计算模型2。另外,计算模型1中竖层底边界可以根据结构形式、计算效率等需要设置为任意角度折线形边界。
2.1 两侧无限域连分式边界
将频域与波数域位移关系
u=˜˜ue−ikxx+ikyy 代入式(1),得到波数域内的位移方程:(k2x+k2y−ω2c2)˜˜u=0 (3) 式中:i为虚数单位;kx和ky分别为x方向和y方向波数;上标双波浪线表示x-y波数域中的变量。对于左侧无限域,为满足无穷远处辐射条件取外行波解,由式(3)得:
ky˜˜u=−ωc√1−(kxcω)2˜˜u (4) 关于y坐标进行傅里叶逆变换,将式(4)变换到y空间域和x波数域:
˜τy=iωc√1−(kxcω)2˜u=iωcS˜u (5) 则侧边无限域y方向的动力刚度为:
S=√1+z2,z=ikxcω (6) 由于侧边半空间动力刚度式(6)是关于波数平方的根式,力-位移关系式(5)和随后与内域耦合的方程不能直接转化到x空间域。下面对式(6)进行连分式展开,为了得到成对的特征根模拟波向两侧传播的特性,选取关于波数平方的连分式[34]对动力刚度式(6)进行展开。
基于平方差公式得到如下连分式形式:
S=α+β2α+(S−α)=α+β2α+β2α+β2α+⋱ (7) 当
α=1+z2/2 ,β=−z4/4 时可得到:S=1+z2/2−z4/42+z2−z4/42+z2−z4/42+z2−⋱ (8) 采用式(8)对动力刚度式(6)进行连分式展开:
{S=1+z22−z44S−11Sj=2+z2−z44S−1j+1,j=1,2,⋯,J (9) 式中:J为连分式阶数;Sj为辅助变量,
S−1J+1=0 。将式 (9)代入式(5),并引入辅助变量
Sj˜uj= −z22˜uj−1 ,其中˜u0=˜u ,˜uJ+1=0 ,得到:{S˜u=˜u+z22˜u+z22˜u1z22˜uj−1+2˜uj+z2˜uj+z22˜uj+1=0,j=1,2,⋯,J (10) 式(10)写成矩阵形式为:
{{\boldsymbol{S}}^l}{\tilde {\boldsymbol{u}}^l} = {\tilde {\bf\textit{τ}}}_y^l (11) 式中:
{\tilde {\boldsymbol{u}}^l} = {\{ {\tilde u}\;\;{{{\tilde u}_1}}\;\;{{{\tilde u}_2}}\;\; \cdots \;\;{{{\tilde u}_J}} \}^{\rm T}} ;{\tilde{\bf\textit{τ}}}_y^l = {\{ {{{\tilde \tau }_y}}\;\;0\;\;0\;\; \cdots \;\;0 \}^{\rm T}} ,{{\boldsymbol{S}}^l} = \dfrac{{k_x^2}}{{{\rm{i}}\omega }}{{\boldsymbol{E}}_1} + {\rm{i}}\omega {{\boldsymbol{E}}_2} ,{{\boldsymbol{E}}_1} = \frac{c}{2}\left[ {\begin{array}{*{20}{c}} {\rm{1}}&{\rm{1}}&0&0& \cdots &0 \\ {\rm{1}}&{\rm{2}}&{\rm{1}}&0& \cdots &0 \\ 0&{\rm{1}}&{\rm{2}}&{\rm{1}}& \cdots & \vdots \\ \vdots & \cdots & \ddots & \ddots & \ddots &0 \\ 0& \cdots &0&{\rm{1}}&{\rm{2}}&{\rm{1}} \\ 0& \cdots &0&0&{\rm{1}}&{\rm{2}} \end{array}} \right], {{\boldsymbol{E}}_2} = \frac{1}{c}\left[ {\begin{array}{*{20}{c}} 1&0&0&0& \cdots &0 \\[-2pt] 0&2&0&0& \cdots &0 \\[-2pt] 0&0&2&0& \cdots & \vdots \\[-2pt] \vdots & \cdots & \ddots & \ddots & \ddots &0 \\[-2pt] 0& \cdots &0&0&2&0 \\[-2pt] 0& \cdots &0&0&0&2 \end{array}} \right]{\text{。}} 以上为左侧无限域的人工边界条件,同理可以得到右侧无限域的人工边界条件。
2.2 竖层底部广义一致边界
将笛卡尔坐标系(x, y)中波动问题转换到局部坐标系
(\xi ,\eta ) 中,如图1所示。坐标变换关系为:\left\{ \begin{aligned} & {x = \xi + \eta \cos\alpha } \\& {y = \eta \sin \alpha } \end{aligned} \right. (12) 式(1)转换到局部坐标系下,可以写为:
\frac{1}{{{{\sin }^2}\alpha }}\left( {\frac{{{\partial ^2}u}}{{\partial {\xi ^2}}} - 2\cos \alpha \frac{{{\partial ^2}u}}{{\partial \xi \partial \eta }} + \frac{{{\partial ^2}u}}{{\partial {\eta ^2}}}} \right) = - \frac{{{\omega ^2}}}{{{c^2}}}u (13) 式中,α为竖向地层底边界与竖向x轴的夹角,各层可取不同值,图1(b)中α=90°;无内域时α为地表与x轴的夹角,如图1(d)所示。
将式(13)沿η轴离散,第j个单元的离散方程为:
- {{\boldsymbol{E}}_3}\frac{{{\partial ^2}{\boldsymbol{u}}}}{{\partial {\xi ^2}}} - {{\boldsymbol{E}}_4}\frac{{\partial {\boldsymbol{u}}}}{{\partial \xi }} + ({{\boldsymbol{E}}_5} - {\omega ^2}{{\boldsymbol{E}}_6}){\boldsymbol{u}} = {{\bf\textit{τ}}_y} (14) 式中:
{{\boldsymbol{E}}_3} = \dfrac{{\rm{1}}}{{\sin \alpha }}\int_0^{\bar \eta } {{{\boldsymbol{N}}^{\rm{T}}}} {\boldsymbol{N}}{\rm{d}}\eta = \dfrac{{\rm{1}}}{{\sin \alpha }}\dfrac{{\bar \eta }}{6}\left[ {\begin{array}{*{20}{c}} 2&1 \\ 1&2 \end{array}} \right], \begin{split} {{\boldsymbol{E}}_4} = & - \frac{{\cos \alpha }}{{\sin \alpha }}\int_0^{\bar \eta } {{{\boldsymbol{N}}^{\rm{T}}}} \frac{{\partial {\boldsymbol{N}}}}{{\partial \eta }}{\rm d}\eta + \\& \frac{{\cos \alpha }}{{\sin \alpha }}\int_0^{\bar \eta } {\frac{{\partial {{\boldsymbol{N}}^{\rm{T}}}}}{{\partial \eta }}} {\boldsymbol{N}}{\rm d}\eta = \frac{{\cos \alpha }}{{\sin \alpha }}\left[ {\begin{array}{*{20}{c}} 0&{ - 1} \\ 1&0 \end{array}} \right], \end{split} {{\boldsymbol{E}}_5} = \frac{1}{{\sin \alpha }}\int_0^{\bar \eta } {\frac{{\partial {{\boldsymbol{N}}^{\rm{T}}}}}{{\partial \eta }}\frac{{\partial {\boldsymbol{N}}}}{{\partial \eta }}{\rm d}\eta } = \frac{{\rm{1}}}{{\bar \eta \sin \alpha }}\left[ {\begin{array}{*{20}{c}} 1&{ - 1} \\ { - 1}&1 \end{array}} \right], {{\boldsymbol{E}}_6} = \frac{1}{{{c^2}}}\sin \alpha \int_0^{\bar \eta } {{{\boldsymbol{N}}^{\rm{T}}}} {\boldsymbol{N}}{\rm d}\eta = \frac{1}{{{c^2}}}\frac{{\bar \eta \sin \alpha }}{6}\left[ {\begin{array}{*{20}{c}} 2&1 \\ 1&2 \end{array}} \right], {{\bf\textit{τ}}_y} = {{\boldsymbol{N}}^{\rm{T}}}\left.\frac{{\partial {\rm{u}}}}{{\partial y}}\right| _0^{\bar \eta } = \left[ {\begin{array}{*{20}{c}} {{\tau _{y,\eta = \bar \eta }}}\\ {{\tau _{y,\eta = 0}}} \end{array}} \right] 式中,单元端点坐标
{\rm{(}}{\eta _j},{\eta _{j + 1}}) ,单元长度\bar \eta = {\eta _{j + 1}} - {\eta _j} ,{\boldsymbol{N}}(\eta ) 为线性插值函数。将式(14)变换到波数域,装配有限域底边所有单元以及两侧无限域人工边界条件式(11),可得到用于两侧开放的竖向成层介质底部广义一致边界条件,其特征值方程为:
( {{\boldsymbol{A}}k_\xi ^2 + {\rm{i}}{\boldsymbol{B}}{k_\xi } + {\boldsymbol{C}}} ){\tilde u^B} = {\boldsymbol{0}} (15) 式中:
{\boldsymbol{A}} = \left( {{{\boldsymbol{E}}_3}} \right)\ddot + \left( {\dfrac{1}{{{\rm{i}}\omega }}{{\boldsymbol{E}}_1}} \right) ;{\boldsymbol{B}}\ddot = {{\boldsymbol{E}}_4} ;{\boldsymbol{D}}\ddot = {{\boldsymbol{E}}_7} ;{\boldsymbol{C}} = ( {{\boldsymbol{E}}_5} - {\omega ^2}{{\boldsymbol{E}}_6} )\ddot + ( {{\rm{i}}\omega {{\boldsymbol{E}}_2}} ) ,\ddot + ,\ddot = 表示对应自由度运算且矩阵扩充维度,式(15)中包含有限域底边自由度及底边两端由侧向连分式引入的辅助自由度。求解式(15)得:
{\tilde {\boldsymbol{u}}^B} = {{\boldsymbol{\varPhi }}_\xi }{{\boldsymbol{E}}_\xi }{{\boldsymbol{q}}_\xi } (16) 式中:
{{\boldsymbol{E}}_\xi } 为对角阵,元素为{{\rm e}^{ - {\rm i}{k_\xi }\xi }} ;{{\boldsymbol{\varPhi }}_\xi } 为特征向量矩阵;{{\boldsymbol{q}}_\xi } 为待定常向量。将式(16)代入底边人工边界上力与位移关系,可以得到:
\begin{split} {{\boldsymbol{f}}^B} = & - {\boldsymbol{A}}\frac{{\partial {{\tilde {\boldsymbol{u}}}^B}}}{{\partial \xi }} + {\boldsymbol{D}}{\tilde {\boldsymbol{u}}^B} =\\& ( {{\rm{i}}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_\xi }{\boldsymbol{K}}_\xi ^{}{\boldsymbol{\varPhi }}_\xi ^{ - 1} + {\boldsymbol{D}}} ){\tilde {\boldsymbol{u}}^B} = {{\boldsymbol{S}}^B}{\tilde {\boldsymbol{u}}^B} \end{split} (17) 式中:
{{\boldsymbol{K}}_\xi } 为对角阵,元素为{k_\xi } ;{{\boldsymbol{S}}^B} = {\rm{i}}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_\xi }{\boldsymbol{K}}_\xi ^{}{\boldsymbol{\varPhi }}_\xi ^{ - 1} + {\boldsymbol{D}} 。式(17)为有限域底部人工边界条件,无内域时即计算模型2(地表处人工边界条件)的有限元方程。
2.3 有限域与人工边界条件耦合
将有限域侧边力位移关系的连分式展开式(11)沿竖向x轴离散,通过线性插值得到侧边人工边界条件有限元方程:
{{\boldsymbol{S}}^L}{{\boldsymbol{u}}^L} = {{\boldsymbol{f}}^L} (18) 式(18)中包含有限域左侧自由度以及各节点连分式引入的辅助自由度。其中,动力刚度向量为:
{{\boldsymbol{S}}^L} = {\rm{i}}\omega {\boldsymbol{Q}} + \frac{1}{{{\rm{i}}\omega }}{\boldsymbol{R}},\qquad\qquad\qquad\qquad\qquad\qquad\qquad {\boldsymbol{Q}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {2{{\boldsymbol{Q}}_1}}&{{{\boldsymbol{Q}}_1}}&{\boldsymbol{0}}& \cdots &{\boldsymbol{0}} \\[-2pt] {{{\boldsymbol{Q}}_1}}&{2{{\boldsymbol{Q}}_1} + 2{{\boldsymbol{Q}}_2}}&{{{\boldsymbol{Q}}_2}}& \ddots & \vdots \\[-2pt] {\boldsymbol{0}}& \ddots & \ddots & \ddots &{\boldsymbol{0}} \\[-2pt] \vdots & \ddots &{{{\boldsymbol{Q}}_{M - 2}}}&{2{{\boldsymbol{Q}}_{M - 2}} + 2{{\boldsymbol{Q}}_{M - 1}}}&{{{\boldsymbol{Q}}_{M - 1}}} \\[-2pt] {\boldsymbol{0}}& \cdots &{\boldsymbol{0}}&{{{\boldsymbol{Q}}_{M - 1}}}&{2{{\boldsymbol{Q}}_{M - 1}}} \end{array}} \right], {\boldsymbol{R}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}_1}}&{ - {{\boldsymbol{R}}_1}}&{\boldsymbol{0}}& \cdots &{\boldsymbol{0}} \\[-2pt] { - {{\boldsymbol{R}}_1}}&{{{\boldsymbol{R}}_1} + {{\boldsymbol{R}}_2}}&{ - {{\boldsymbol{R}}_2}}& \ddots & \vdots \\[-2pt] {\boldsymbol{0}}& \ddots & \ddots & \ddots &{\boldsymbol{0}} \\[-2pt] \vdots & \ddots &{ - {{\boldsymbol{R}}_{M - 2}}}&{{{\boldsymbol{R}}_{M - 2}} + {{\boldsymbol{R}}_{M - 1}}}&{ - {{\boldsymbol{R}}_{M - 1}}} \\[-2pt] {\boldsymbol{0}}& \cdots &{\boldsymbol{0}}&{ - {{\boldsymbol{R}}_{M - 1}}}&{{{\boldsymbol{R}}_{M - 1}}} \end{array}} \right], M为侧边界上节点数,上标L表示属于左侧边的物理量,
{{\boldsymbol{Q}}_m} = \dfrac{{\Delta x}}{6}{{\boldsymbol{E}}_1} ,{{\boldsymbol{R}}_m} = \dfrac{1}{{\Delta x}}{{\boldsymbol{E}}_2} 。类似地,可以得到右侧人工边界条件的有限元方程。将有限域与底部人工边界条件式(17)以及两侧人工边界条件式(18)组装,得到频域下耦合系统有限元方程:
\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{S}}_{II}}}&{{{\boldsymbol{S}}_{IB}}}&{\boldsymbol{0}} \\ {{{\boldsymbol{S}}_{BI}}}&{{{\boldsymbol{S}}_{BB}}}&{{{\boldsymbol{S}}_{BC}}} \\ {\boldsymbol{0}}&{{{\boldsymbol{S}}_{CB}}}&{{{\boldsymbol{S}}_{CC}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{u}}_I}} \\ {{{\boldsymbol{u}}_B}} \\ {{{\boldsymbol{u}}_C}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{f}}_I}} \\ {{{\boldsymbol{f}}_B}} \\ {\boldsymbol{0}} \end{array}} \right\} (19) 式中,下标I、B、C分别对应内域自由度、边界自由度以及连分式引入的辅助自由度。
3 数值算例
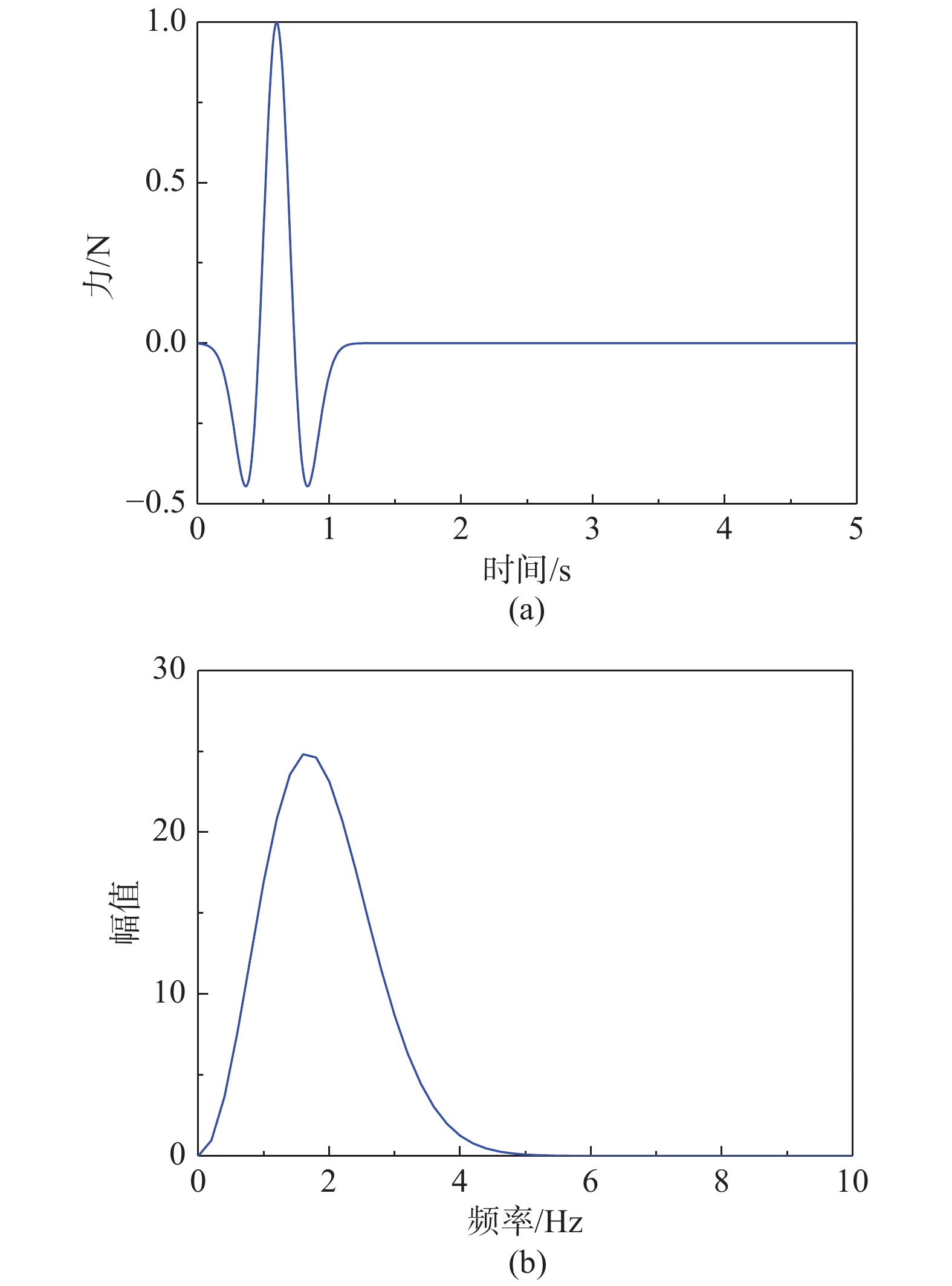
本节给出不同地形、地质条件下四种场地中波传播问题的数值算例来验证提出高精度折线形人工边界条件的有效性和精度。参考解为大区域有限元模型的时域解,模型尺寸足够大能够保证在观测时间内结果不受到截断边界处反射波的影响。同时采用了简单常用的粘弹性人工边界条件[11]进行了对比分析,说明提出的折线形人工边界条件适用于竖向成层不规则地形场地,且在计算精度上有显著改进。本文人工边界条件中连分式阶数统一取为5阶,阶数为零时可退化为旁轴近似。采用Ricker波作为荷载,其时程和频谱曲线如图2所示。
3.1 水平地表场地
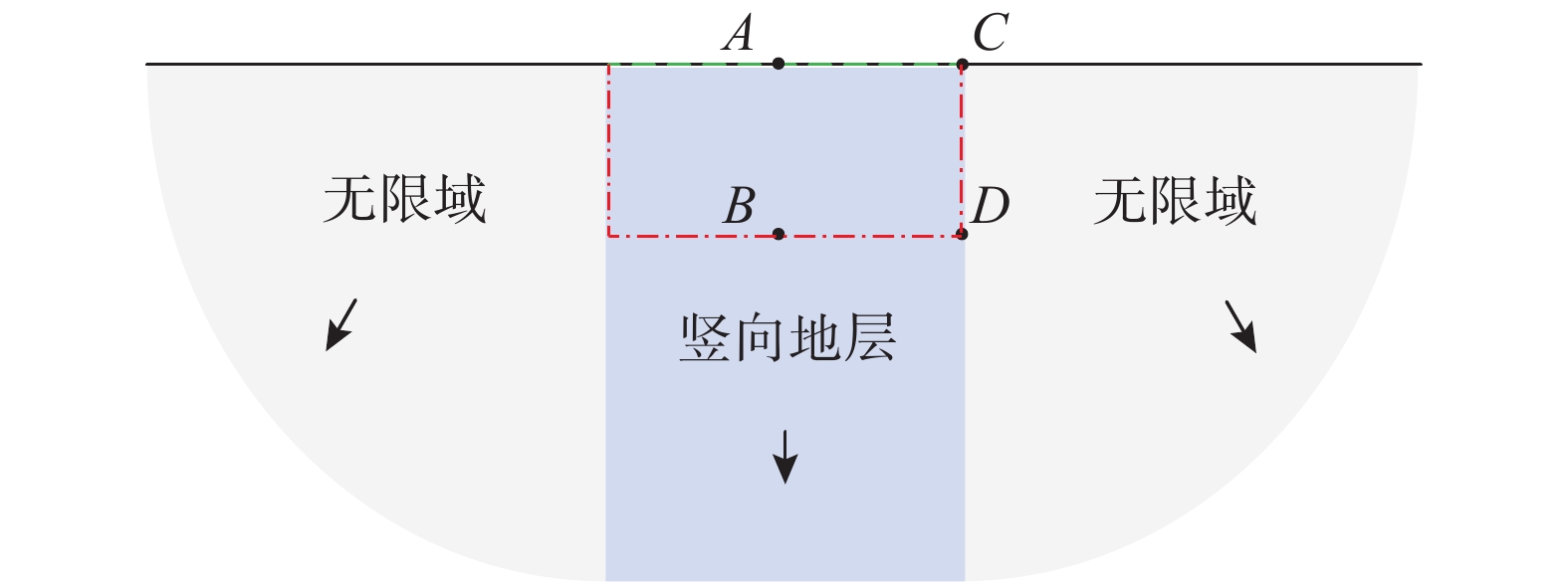
平直地表半空间场地中含有一个竖向无限延伸地层,如图3所示。中间地层的剪切波速c1 = 100 m/s,两侧无限域介质剪切波速c2 = 200 m/s。坐标原点取地表中心点A。计算中选取了两种形式的人工边界,如图3中点划线和虚线所示。加载点为点A,观察点为A(0, 0)、 B(0, −100)、 C(100, 0)、 D(100, −100)。有限元网格尺寸为2 m,计算时间步长为0.01 s。
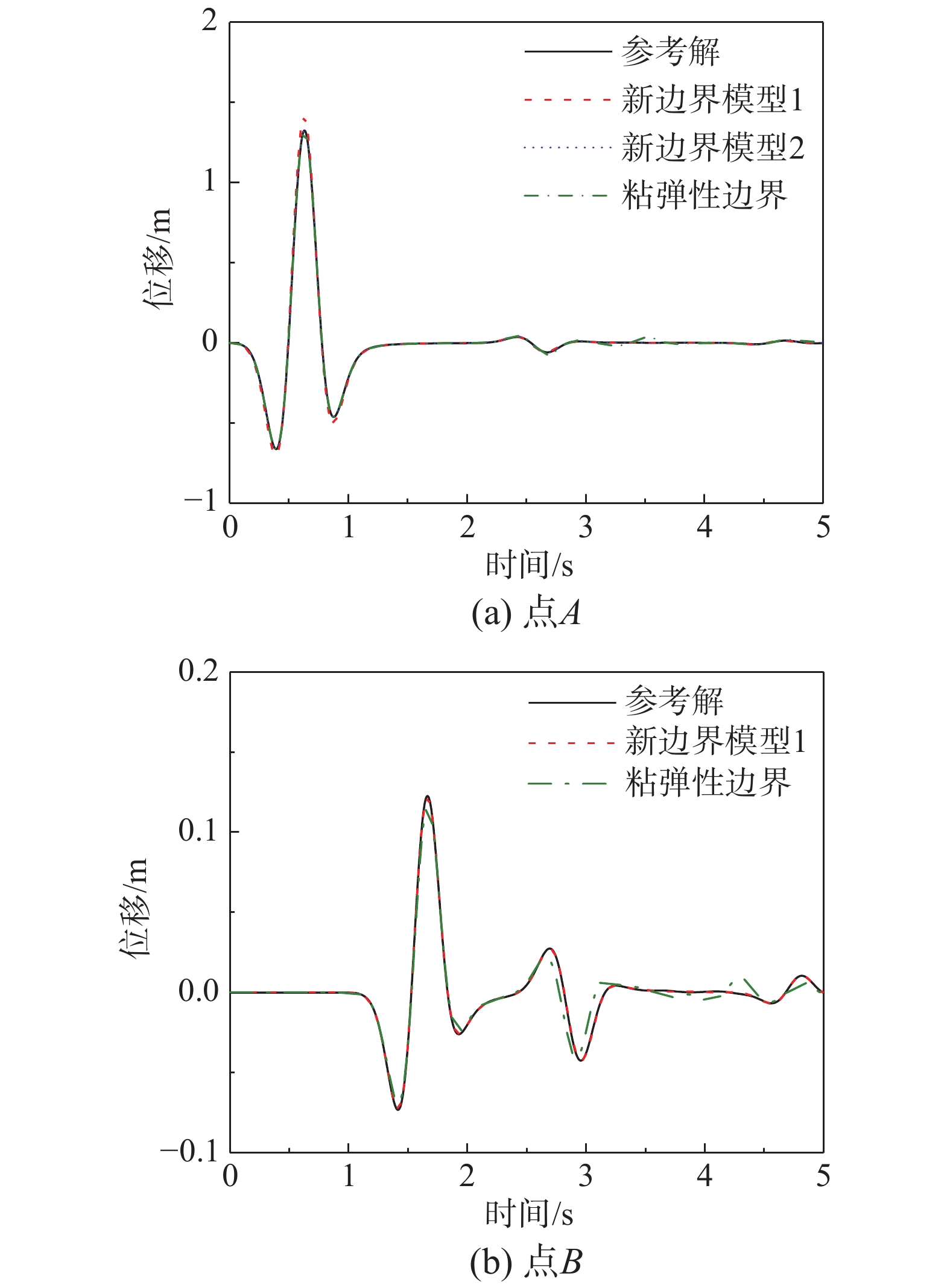
观察点的位移时程结果如图4所示。将采用新边界的两种计算模型和采用粘弹性边界的计算模型1与采用大区域有限元模型得到的参考解进行比较。其中计算模型1由人工边界条件与内域有限元部分组成,如图3中点划线所示区域;计算模型2为直接将人工边界加在地表,如图3中虚线所示。下文中图例意义相同。从图中可以看出,无论是加载点还是边界处节点以及材料交界面上节点,采用新人工边界条件的两种模型计算结果均与参考解吻合较好,而粘弹性边界模型在边界及材料交界面节点上计算误差较大。验证了新提出人工边界条件的有效性和精度。
3.2 折线地表场地
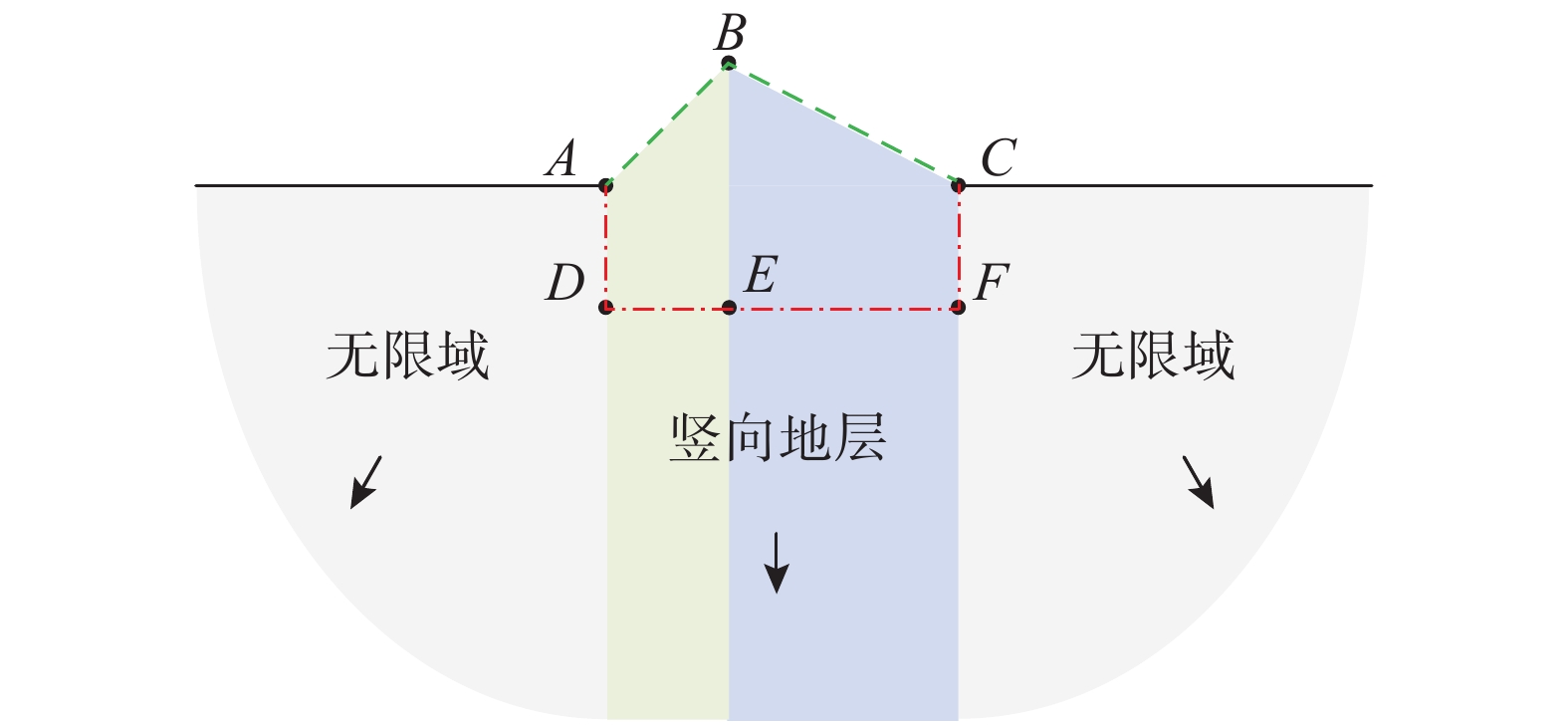
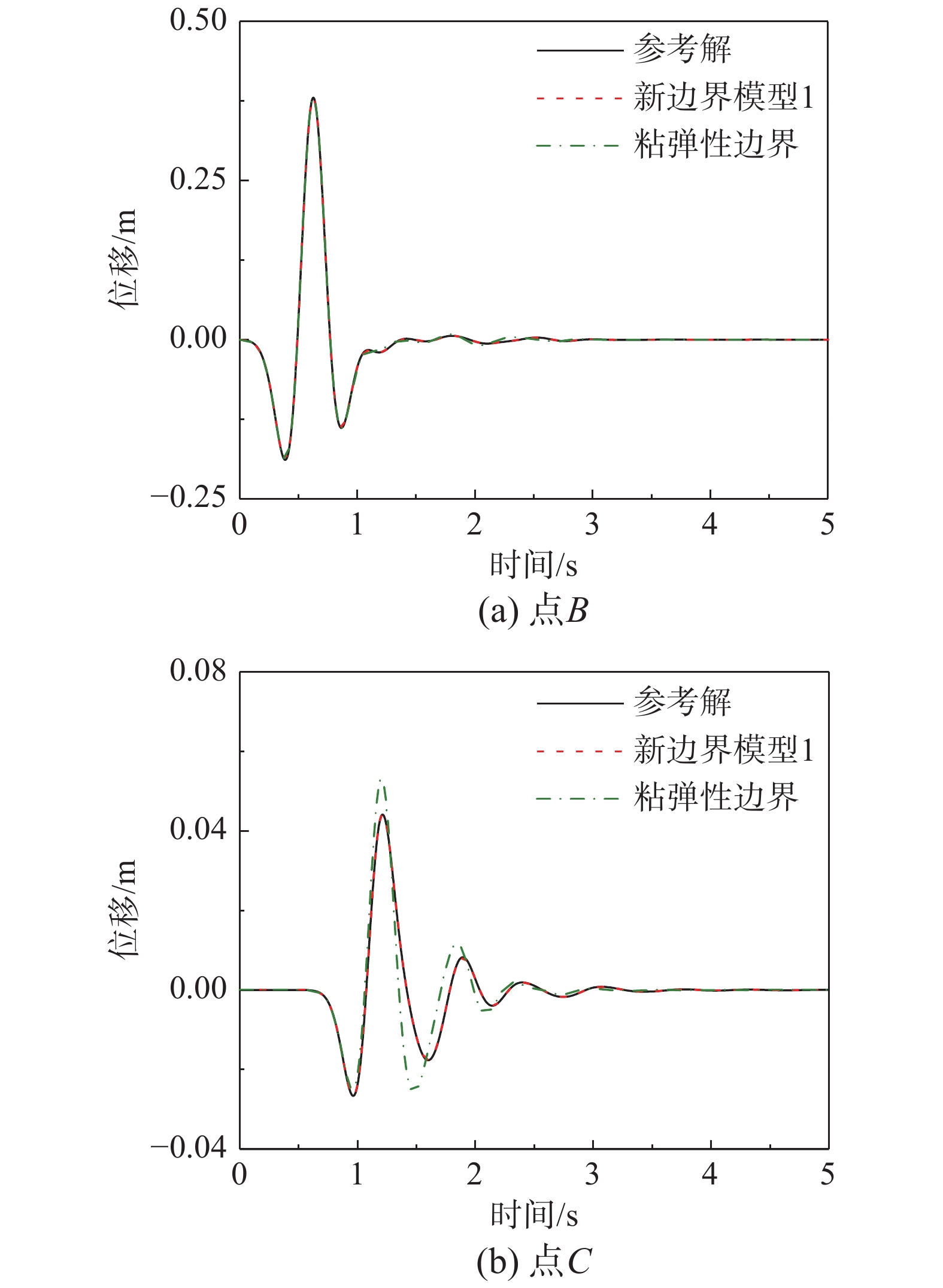
折线形地表半空间场地中含有两个竖向地层,如图5所示。左侧地层的剪切波速c1 =100 m/s,右侧地层的剪切波速c2 = 300 m/s,两侧无限域介质剪切波速c3 = 200 m/s。图5中各点坐标为A(0, 0)、B(50, 50)、C(150, 0)、D(0, −50)、E(50, −50)、F(50, −50),其中加载点为B,观察点为B、C、E、F。有限元网格尺寸为1 m~3 m,计算时间步长为0.002 s。
观察点的位移时程结果如图6所示。观察点包括地表节点、人工边界上的节点以及材料交界面处的节点。从图6中可以看出,两种新边界计算模型的位移解与参考解吻合较好,而粘弹性边界模型在边界及材料交界面节点上计算误差较大。表明提出的人工边界条件可以很好的模拟边界处和材料变化带来的反射和散射波,以及随时间空间变化的辐射效应,验证了新人工边界条件的有效性和精度。
3.3 阶梯地形场地
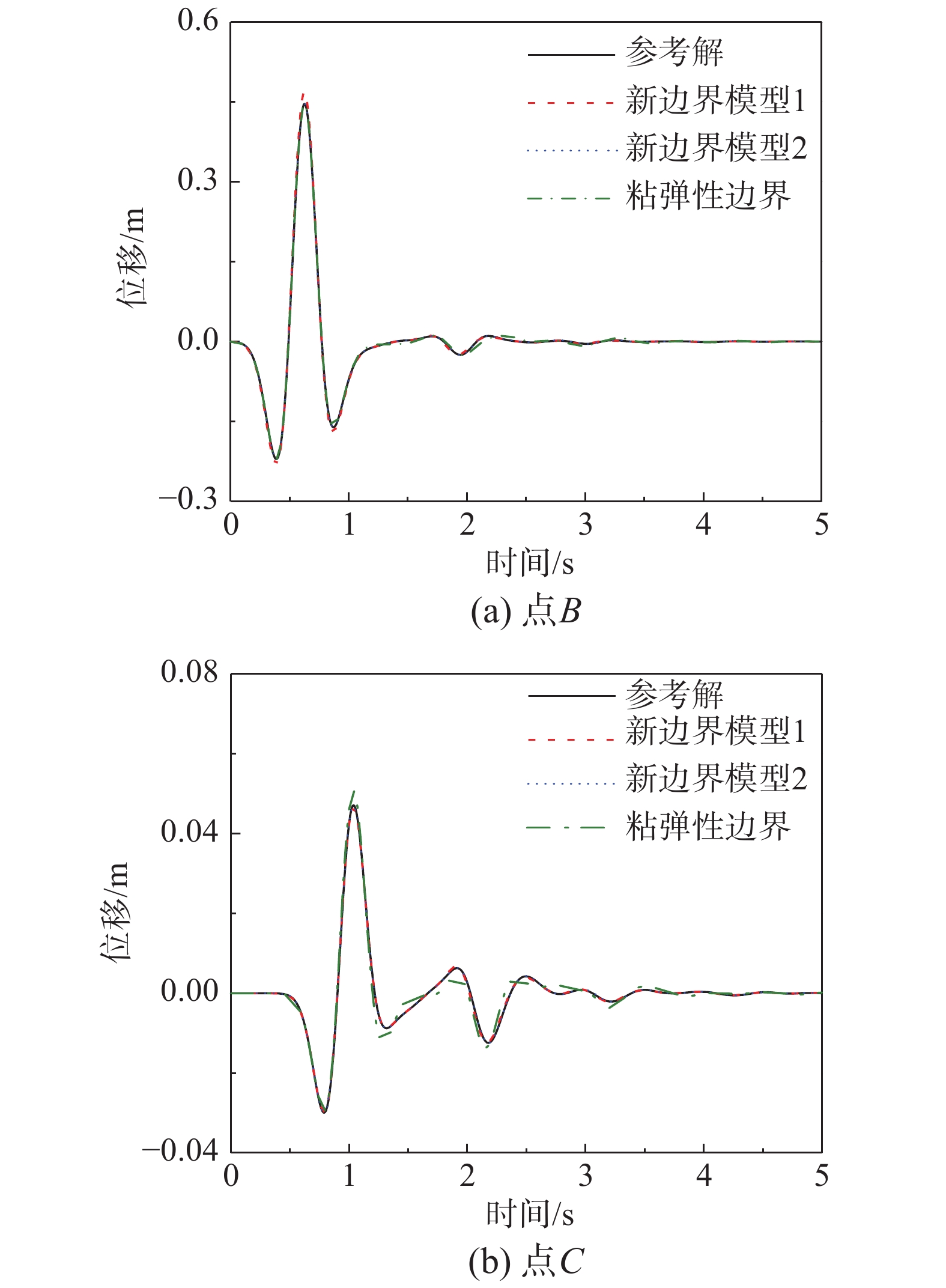
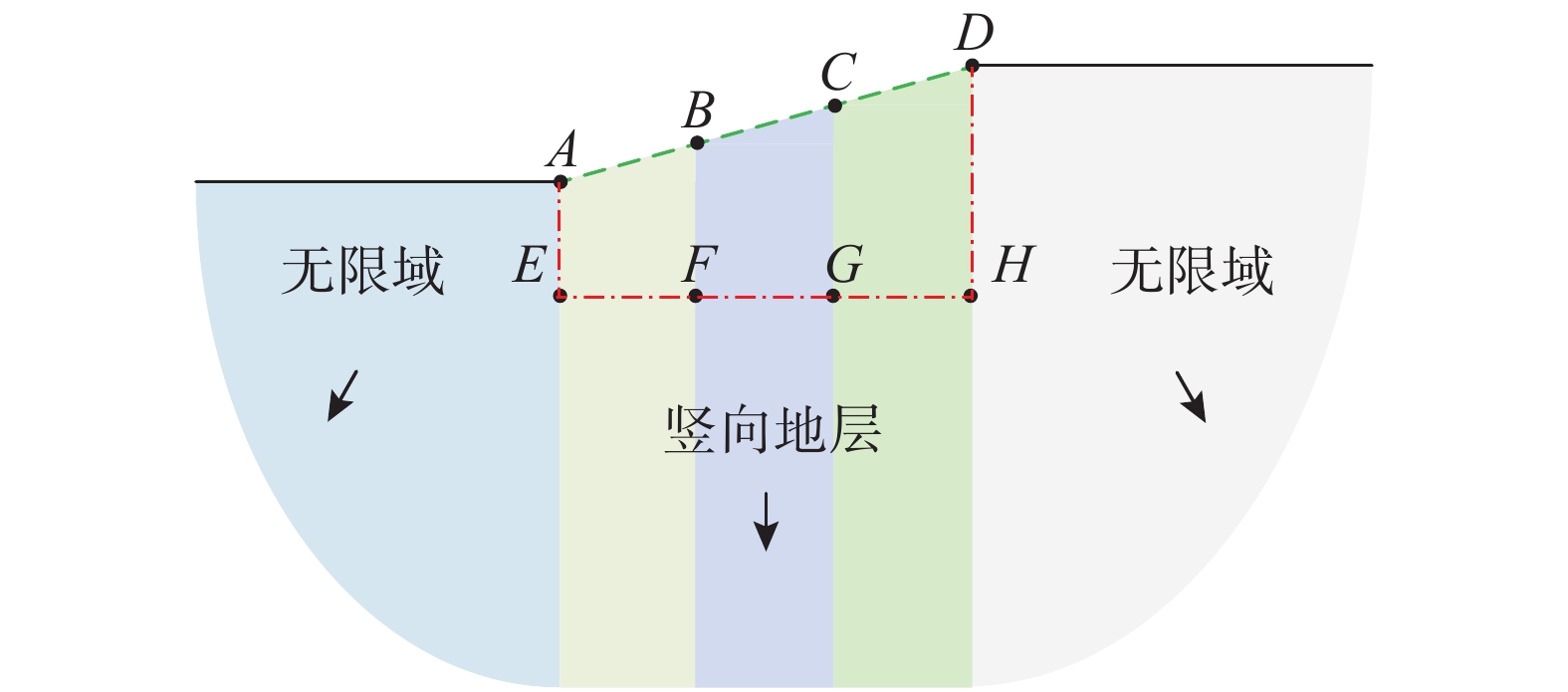
阶梯地形半空间场地中含有三个竖向地层,如图7所示。从左到右介质刚度依次增大,左侧无限域介质剪切波速cl = 100 m/s,三个竖向地层的剪切波速分别为c2 = 150 m/s、c3 = 200 m/s、c4 = 250 m/s,右侧无限域介质剪切波速c5 = 300 m/s。图7中定位点坐标为A(0, 0)、B(50, 50/3)、C(100, 100/3)、D(150, 50)、E(0, −50)、F(50, −50)、G(100, −50)、H(150,−50),其中加载点为 B,观察点为A、C、E、G。有限元网格尺寸为1 m~2.2 m,计算时间步长为0.002 s。
观察点的位移时程结果如图8所示。观察点包括地表节点、人工边界上的节点以及材料交界面处的节点。从图8中可以看出,两种新边界计算模型的位移解与参考解吻合较好,而粘弹性边界模型在边界及材料交界面节点上计算误差较大。表明新人工边界条件可以很好的吸收边界以及材料变化产生的反射和散射波,模拟无限场地的辐射效应,验证了新人工边界条件的有效性和精度。
3.4 含地下结构场地
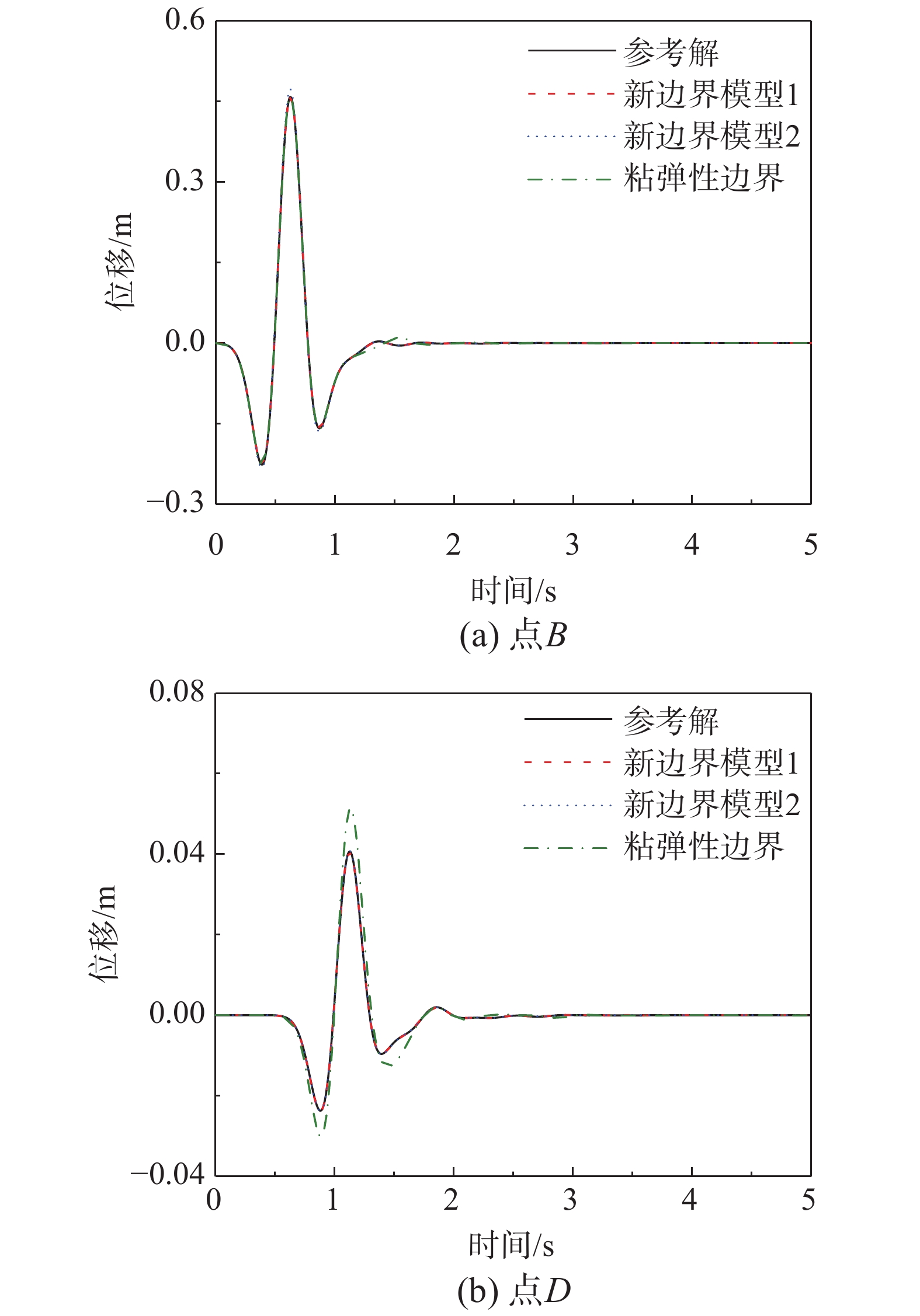
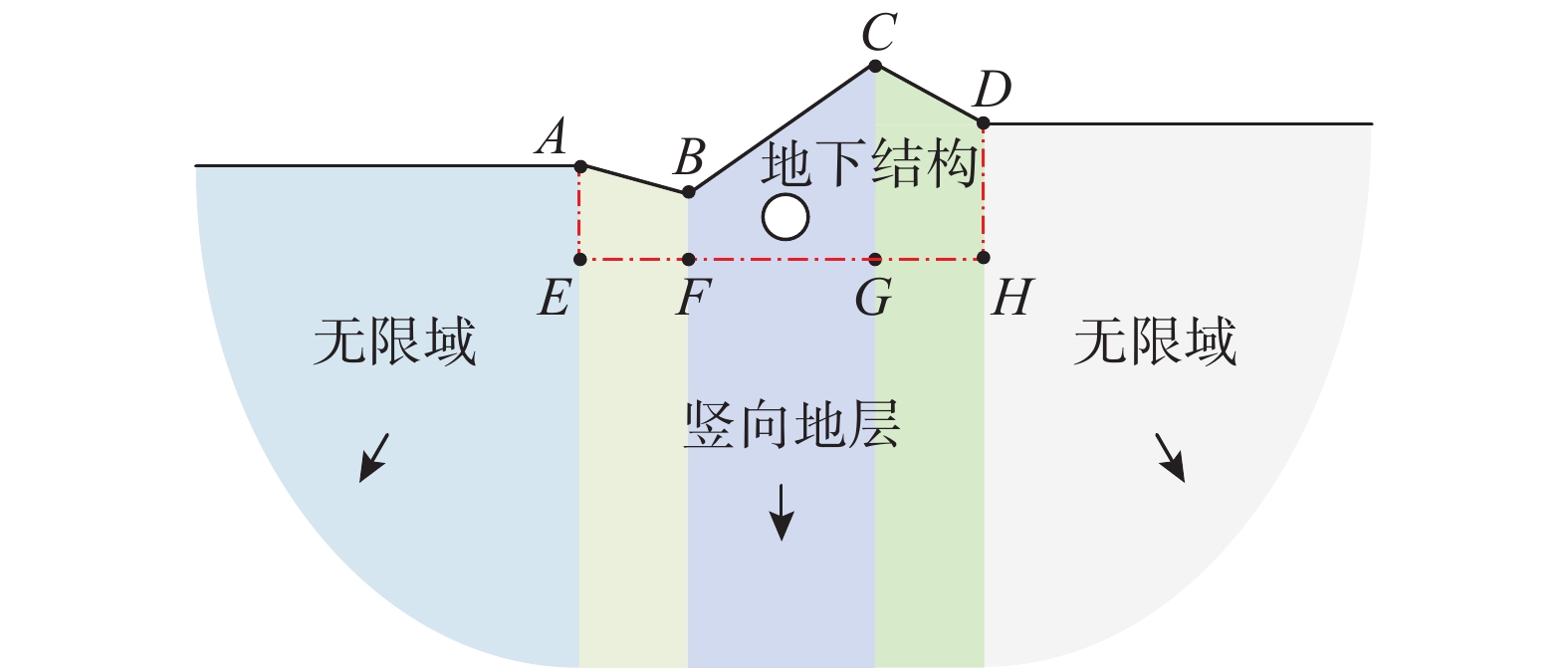
如图9所示,地下结构建立在含竖向成层介质且两侧不等高地形的半空间场地中,其地表高低起伏可模拟河谷与山坡同时存在的复杂地形,本算例分析其中的标量波传播问题。从左到右5种介质刚度依次增大,左侧无限域介质剪切波速cl = 100 m/s,三个竖向层的剪切波速分别为c2 = 150 m/s,c3 = 200 m/s,c4 = 250 m/s,右侧无限域介质剪切波速c5 = 300 m/s。因含有地下结构,计算模型2不再适用或者说误差较大,本节仅采用计算模型1与参考解比较,人工边界位置如图9中点划线所示,分别施加新边界条件和粘弹性边界条件[11]。图9中定位点坐标为A(0, 0)、B(50, −20)、C(150, 30)、D(200, 10)、E(0, −50)、F(50, −50)、G(150, −50)、H(200, −50),地下结构圆心坐标为(100, −30),半径10 m。其中加载点为 B,观察点为B、C、E、H以及地下结构上节点C1(90, −30)、C2(100, −20)。有限元网格最大尺寸小于4 m,计算时间步长为0.002 s。
观察点的位移时程结果如图10所示。观察点包括地表节点、人工边界和材料界面处的节点以及地下结构上的节点。从图10中可以看出,新人工边界条件可以很好地模拟边界处、材料界面以及地下结构带来的反射波和散射波,以及随时间空间变化的辐射效应。新边界计算模型的场地反应和结构反应均与参考解吻合较好,而粘弹性人工边界误差较大。验证了新人工边界条件的有效性和精度。
4 结论
本文针对竖向成层介质中的标量波传播问题,基于连分式展开和扩展的一致边界,建立了含竖向成层介质和地表不规则场地的折线形高精度人工边界条件。半空间场地划分为竖向成层介质以及两侧无限域。两侧无限域的人工边界条件基于动力刚度的连分式展开,引入辅助变量来模拟无限域辐射效应;竖向成层介质为广义的一致边界,两端开放与侧边连分式边界耦合,并引入斜角变换使得提出的人工边界条件可以为任意折线形。侧边界与底边界耦合后的折线形人工边界可用于竖向成层介质中标量波传播分析。数值算例结果表明,提出的高精度人工边界条件适用于多种竖向成层介质中标量波传播问题,具有较高的计算精度,极大提高计算效率。
与水平成层半空间中标量波传播问题的H形人工边界[34]相比,本文折线形人工边界条件主要是对原有方法的扩展应用。水平成层半空间模型转换到竖向成层半空间模型的过程中,多层和半空间区域的无限延伸方向以及物理边界均发生变化,人工边界的截断位置也随之改变。因此针对水平成层半空间中的人工边界条件不再直接适用,但具有重要参考价值。为进一步扩展人工边界条件的适用范围,适用于倾斜地层的人工边界条件正在研究中。
-
-
[1] Wolf J P, Song C M. Finite-element modelling of unbounded media [M]. New York: Wiley, 1996.
[2] 张新辉, 付平, 尹健民, 等. 滇中引水工程香炉山隧洞地应力特征及其活动构造响应[J]. 岩土工程学报, 2021, 43(1): 130 − 139. Zhang Xinhui, Fu Ping, Yin Jianmin, et al. In-situ stress characteristics and its active tectonic response in Xianglushan Tunnel of Yunnan Diversion Project [J]. Chinese Journal of Geotechnical Engineering, 2021, 43(1): 130 − 139. (in Chinese)
[3] 王 维. 软硬突变地层盾构隧道地震响应特性研究[D]. 成都: 西南交通大学, 2015. Wang Wei. The study of seismic response of shield tunnel crossing interface of soft and hard strata [D]. Chengdu: Southwest Jiaotong University, 2015. (in Chinese)
[4] 刘中宪, 武凤娇, 王冬. 沉积盆地-山体耦合场地对平面P波、SV波和Rayleigh波的二维散射分析[J]. 工程力学, 2016, 33(2): 160 − 171. doi: 10.6052/j.issn.1000-4750.2014.05.0396 Liu Zhongxian, Wu Fengjiao, Wang Dong. Two dimensional scattering analysis of plane P, SV, and Rayleigh waves by coupled alluvial basin-mountain terrain [J]. Engineering Mechanics, 2016, 33(2): 160 − 171. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.05.0396
[5] Ba Z, Wang Y, Liang J, et al. 3D dynamic responses of a 2D hill in a layered half-space subjected to obliquely incident plane P-, SV- and SH-waves [J]. Engineering Analysis with Boundary Elements, 2019, 105: 129 − 145. doi: 10.1016/j.enganabound.2019.04.004
[6] 李志远, 钟红, 胡志强, 等. 局部褶皱对层状地基马蹄形孔洞散射的影响分析[J]. 工程力学, 2020, 37(8): 237 − 245. doi: 10.6052/j.issn.1000-4750.2019.09.0512 Li Zhiyuan, Zhong Hong, Hu Zhiqiang, et al. Analysis of the influence of local folds on the scattering of horseshoe cavity in a layered half-space [J]. Engineering Mechanics, 2020, 37(8): 237 − 245. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.09.0512
[7] Chen X, Zhang N, Gao Y, et al. Effects of a V-shaped canyon with a circular underground structure on surface ground motions under SH wave propagation [J]. Soil Dynamics and Earthquake Engineering, 2019, 127: 105830. doi: 10.1016/j.soildyn.2019.105830
[8] 王笃国, 赵成刚. 地震波斜入射下考虑场地非线性、地形效应和土结动力相互作用的大跨连续刚构桥地震响应分析[J]. 工程力学, 2017, 34(4): 32 − 41. doi: 10.6052/j.issn.1000-4750.2015.03.0180 Wang Duguo, Zhao Chenggang. Seismic analysis of long-span continuous rigid frame bridge considering site nonlinearity, topography effect and soil-structure dynamic internation under oblique incidence [J]. Engineering Mechanics, 2017, 34(4): 32 − 41. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.03.0180
[9] Han H D, Wu X N. A survey on artificial boundary method [J]. Science China Mathematics, 2013, 56: 2439 − 2488. doi: 10.1007/s11425-013-4694-x
[10] Lysmer J. Finite dynamic model for infinite media [J]. Journal of the Engineering Mechanics Division, 1969, 95: 859 − 878. doi: 10.1061/JMCEA3.0001144
[11] 杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38: 49 − 56. doi: 10.3321/j.issn:0459-1879.2006.01.007 Du Xiuli, Zhao Mi, Wang Jinting. A stress artificial boundary in FEA for near-field wave problem [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38: 49 − 56. (in Chinese) doi: 10.3321/j.issn:0459-1879.2006.01.007
[12] Liao Z P. Extrapolation nonreflecting boundary conditions [J]. Wave Motion, 1996, 24: 117 − 138. doi: 10.1016/0165-2125(96)00010-8
[13] Astley R J. Infinite elements for wave problems: A review of current formulations and an assessment of accuracy [J]. International Journal for Numerical Methods in Engineering, 2000, 49: 951 − 976. doi: 10.1002/1097-0207(20001110)49:7<951::AID-NME989>3.0.CO;2-T
[14] Edip K, Sheshov V, Wu W, et al. Numerical modelling of saturated boundless media with infinite elements [J]. Acta Geotechnica, 2021, 16(8): 2683 − 2692. doi: 10.1007/s11440-020-01139-9
[15] Hall W S, Oliveto G. Boundary element methods for soil-structure interaction [M]. Netherlands: Springer, 2003.
[16] Sumbatyan M A, Martynova T S, Musatova N K. Boundary element methods in diffraction of a point-source acoustic wave by a rigid infinite wedge [J]. Engineering Analysis with Boundary Elements, 2021, 125(5): 157 − 167.
[17] Engquist B, Majda A. Absorbing boundary conditions for the numerical simulation of waves [J]. Mathematics of Computation, 1977, 31: 629 − 651. doi: 10.1090/S0025-5718-1977-0436612-4
[18] Higdon R L. Absorbing boundary conditions for difference approximations to the multidimensional wave equation [J]. Mathematics of Computation, 1986, 47: 437 − 459.
[19] Bayliss A, Turkel E. Radiation boundary conditions for wave-like equations [J]. Communications on Pure and Applied Mathematics, 1980, 33: 707 − 725. doi: 10.1002/cpa.3160330603
[20] Givoli D. Recent advances in the DtN FE method [J]. Archives of Computational Methods in Engineering, 1999, 6: 71 − 116. doi: 10.1007/BF02736182
[21] 赵密, 杜修力, 刘晶波. 一种高阶精度人工边界条件: 出平面外域波动问题[J]. 工程力学, 2012, 29(4): 7 − 14. Zhao Mi, Du Xiuli, Liu Jingbo. A high-order accurate artificial boundary condition: out-of-plane exterior wave problem [J]. Engineering Mechanics, 2012, 29(4): 7 − 14. (in Chinese)
[22] Zhao M, Du X L, Liu J B, et al. Explicit finite element artificial boundary scheme for transient scalar waves in two-dimensional unbounded waveguide [J]. International Journal for Numerical Methods in Engineering, 2011, 87: 1074 − 1104. doi: 10.1002/nme.3147
[23] Li H F, Zhao M, Wu L H, et al. A stable high-order absorbing boundary based on continued fraction for scalar wave propagation in 2D and 3D unbounded layers [J]. Engineering Computations, 2019, 36(7): 2445 − 2479.
[24] Kausel E, Manolis G D, Abarbanel S. The thin layer method in seismology and earthquake engineering [C]// Wave Motion in Earthquake Engineering. Southampton: WIT Press, 2000.
[25] Wu L H, Zhao M, Jeng D S, et al. A local time-domain absorbing boundary condition for scalar wave propagation in a multilayered medium [J]. Computers and Geotechnics, 2020, 128: 103809. doi: 10.1016/j.compgeo.2020.103809
[26] Zhao M, Wu L H, Du X L, et al. Stable high-order absorbing boundary condition based on new continued fraction for scalar wave propagation in unbounded multilayer media [J]. Computer Methods in Applied Mechanics and Engineering, 2018, 334: 111 − 137. doi: 10.1016/j.cma.2018.01.018
[27] Wolf J P. The scaled boundary finite element method [M]. Chichester: Wiley, 2003.
[28] Basu U. Explicit finite element perfectly matched layer for transient three-dimensional elastic waves [J]. International Journal for Numerical Methods in Engineering, 2009, 77: 151 − 176. doi: 10.1002/nme.2397
[29] Liu X, Liu Y, Ren Z, et al. Perfectly matched layer boundary conditions for frequency-domain acoustic wave simulation in the mesh-free discretization [J]. Geophysical Prospecting, 2019, 67(7): 1732 − 1744. doi: 10.1111/1365-2478.12788
[30] 蒋通, 田治见宏. 地基-结构动力相互作用分析方法: 薄层法原理及应用[M]. 上海: 同济大学出版社, 2009. Jiang Tong, Tajimi Hiroshi. Foundation-structure dynamic interaction analysis method: Principle and application of thin layer method [M]. Shanghai: Tongji University Press, 2009. (in Chinese)
[31] Lee J H, Tassoulas J L. Consistent transmitting boundary with continued-fraction absorbing boundary conditions for analysis of soil-structure interaction in a layered half-space [J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200: 1509 − 1525. doi: 10.1016/j.cma.2011.01.004
[32] João M D O B, Joonsang P, Eduardo K. Perfectly matched layers in the thin layer method [J]. Computer Methods in Applied Mechanics and Engineering, 2012, 217/218/219/220: 262 − 274. doi: 10.1016/j.cma.2011.12.006
[33] Hamdan N, Laghrouche O, Woodward P K, et al. Combined paraxial-consistent boundary conditions finite element model for simulating wave propagation in elastic half-space media [J]. Soil Dynamics and Earthquake Engineering, 2015, 70: 80 − 92. doi: 10.1016/j.soildyn.2014.12.005
[34] Li H F, Zhao M, Du X L. Accurate H-shaped absorbing boundary condition in frequency domain for scalar wave propagation in layered half-space [J]. International Journal for Numerical Methods in Engineering, 2020, 121(19): 4268 − 4291. doi: 10.1002/nme.6424
-
期刊类型引用(2)
1. 陈培见, 彭娟, 赵慧明, 沈晓明, 张桂民. 趣味“桁架”教学资源的探索和分析. 力学与实践. 2025(03)  百度学术
百度学术
2. 刘洋,付玲,刘延斌,尹莉. 细长桁架臂卸载反弹动应力分布规律及试验. 振动与冲击. 2024(15): 251-260 .  百度学术
百度学术
其他类型引用(3)



 下载:
下载: