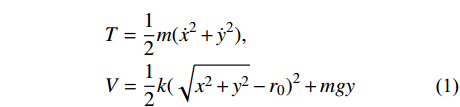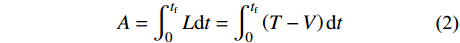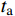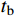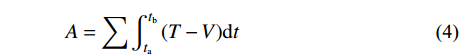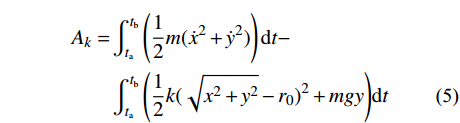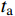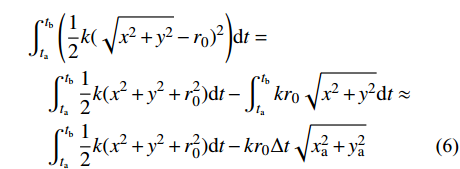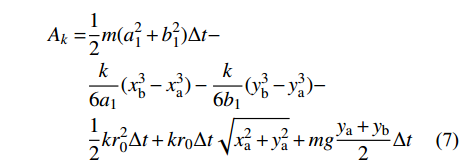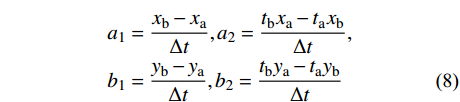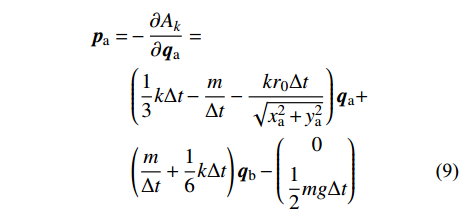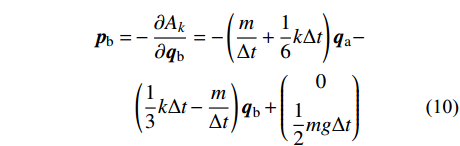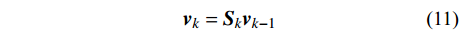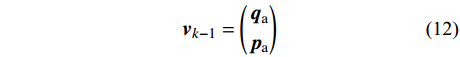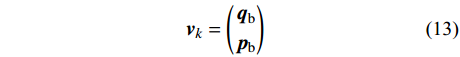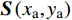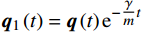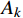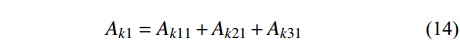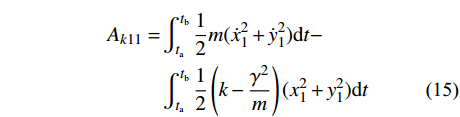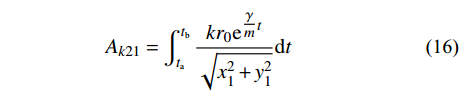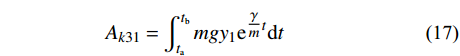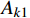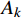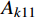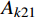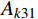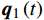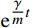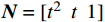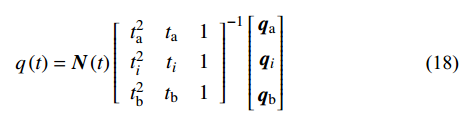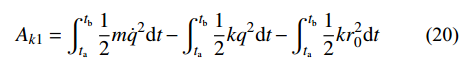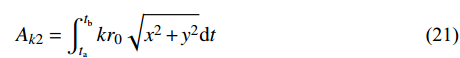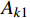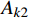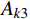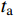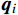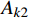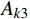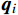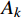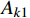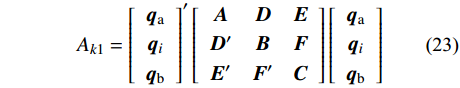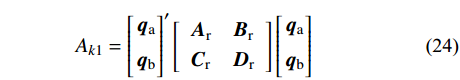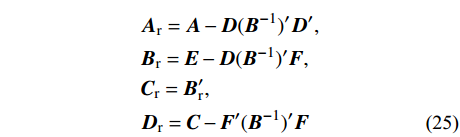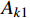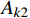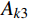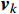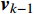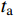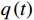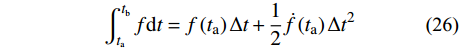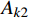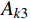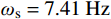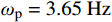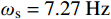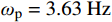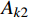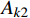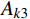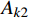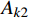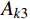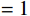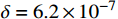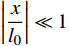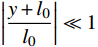A NEW DYNAMIC SOLUTION OF SPRING PENDULUM BASED ON TIME FINITE ELEMENT METHOD
-
摘要: 弹簧摆问题是一种刚柔耦合的非线性动力学问题,随着电力技术的发展,弹簧摆在高压电塔减震方面获得了大规模的应用,但其动力学仿真还存在很多不完善之处。对此该文提出了一种利用时间有限元与保辛递推算法求解弹簧摆问题的新方法。该方法通过对弹簧摆的非线性摆动问题进行了近似积分处理,并对作用量采用矩形和梯形积分的方法获得保辛递推的形式。在提高求解速度的同时,提高了长时间求解的数值稳定性。为了体现了该文方法在求解内共振系统上的速度和稳定性优势,同已有结果进行两次对比,显示本算法较传统算法的计算速度、时间稳定性与精度上均存在一定优势。最后初步讨论了采用该方法求解大摆角混沌问题的途径。Abstract: The problem of spring pendulum is a kind of rigid flexible coupling nonlinear dynamic problem. With the development of power technology, spring pendulum has been widely used in high-voltage tower damping, but its dynamic simulation still has many imperfections. It presents a new method to solve the problem of spring pendulum by using time finite element method and symplectic recursive algorithm. In this method, the nonlinear swing problem of spring pendulum is treated by approximate integration, and the Symplectic recursive form is obtained by using rectangular and trapezoidal integral methods. It also improves the numerical stability of the long-term solution. In order to reflect the speed and stability advantages of the method proposed in solving an internal resonance system, two comparisons with existing results are carried out. The results show that the algorithm proposed has some advantages in computational speed, in time stability and in accuracy compared with the traditional algorithm. Finally, the approach to solve the chaotic problem with a large swing angle is discussed.
-
Keywords:
- spring pendulum /
- time finite element /
- symplectic conservation /
- internal resonance /
- chaos
-
弹簧摆问题是一种刚柔耦合的非线性动力学问题[1],具有强耦合、强非线性等诸多特征。近年来随着国家电力建设的进一步推进,输电塔线系统的在恶劣环境下[2],特别是在地震[3],下击暴流[4]情况下的减振要求成为重点。为了研制较悬挂摆更好的减震器,催生了针对弹簧摆问题的深入研究。张鹏等[5]发现弹簧摆的减振能力优于悬挂摆,并对利用弹簧摆内共振特性设计减震器进行了探讨。霍林生等[6]、王奇等[7]、黄正等[8]在弹簧摆内共振特性上也开展了一定程度的研究。此外Wu等[9]利用弹簧摆的能量耦合特性研制了低频能量收集器。随着弹簧摆应用的深入,其模型自身的特性也受到了研究者多方面的关注。
由于弹簧摆兼具耦合性,强非线性等诸多特性,弹簧摆的运动特征受其初始位置、质点质量、弹簧刚度以及弹簧在自重作用下的长度影响很大。一般对于内共振特性的研究主要采用振动模态圆频率
ωs=√km 与摆动模态圆频率ωp=√gl0 两个重要参数的比值进行描述。在λ=ωs∶ωp= 1∶1 时系统呈现准周期运动,而在λ=ωs∶ωp=1∶2 时系统则出现明显的内共振现象,在比值更大时会出现混沌现象。于洪洁等[10]、李银山等[11]、赵聪等[12]对内共振现象与混沌现象的产生原因进行了深入研究。国际上van de Weele等[13]通过频率比和能量比研究了弹簧摆的有序与混沌的动力学过程,de Sousa等[14]研究了参数空间下的能量耦合传递情况,提出了一种应用于非线性耦合系统,揭示耦合如何介导内部能量交换,以及能量分布如何随系统参数而变化的方法。司丽荣等[15]、Rusbridge等[16]对于弹簧摆的内共振问题进行了实验,为弹簧摆在不同λ下的内共振规律提供了实验支撑。Grażyna Sypniewska-Kamińska等[17]采用给定区间逼近三角函数,并提出了基于此的多尺度法,提高了近似效果的精度。Amer等[18-19]采用多尺度法,对于含阻尼的弹簧摆运动形式进行了持续研究,分析了相关物理参数对解的影响。弹簧摆的特性决定了其求解属于非线性方程的求解。现有弹簧摆问题主要有解析法和数值两种方法,其中对于混沌弹簧摆问题的求解的解析方法采用的是基于Hamilton系统的Holmes方法[20],该方法是少数能够精确求解混沌系统的方法。李银山等[11]通过此方法求解了不同λ下弹簧摆的相图。在2000年后随着计算机技术的成熟,国内对于弹簧摆的研究多采用非线性微分方程组的数值方法[9-10]与谐波平衡法[21-22]进行求解。于洪洁等[10]详细地研究了现有不同类型非线性常微分方程组解法并给出了计算效率与计算精度。对于内共振问题计算则多采用谐波平衡法处理。这两类方法各有千秋,非线性方程组的数值解法多以Runge-Kutta法,Gear法与Adams法为基础[10],由于这类求解方法没有体现哈密顿系统本身的保守特性,因而容易产生累计误差,还容易出现系统的不稳定甚至发散的情况。而针对于谐波平衡法,其对于弹簧摆的初始位置有一定要求,一般要求
|xl0|≪1 ,|y+l0l0|≪1 。这限制了其对于在大摆角情况下的分析能力。鉴于传统方法存在一定缺陷,针对于哈密顿系统自身特性求解的时间有限元方法应运而生。由于有限元方法是基于变分原理获得的,故保辛。时间有限元最早是由Zienkiewicz等[23]提出的对于时间坐标的有限元,但并未要求保辛[24]。由于保守体系可用Hamilton体系描述,而保守体系的差分格式应当保辛[25]。故钟万勰[24]提出了保辛时间有限元的计算方法对于线性问题进行处理,体现了该方法的可靠性。吴峰等[26]利用了保辛摄动算法求解了刚-柔性杆的耦合问题,显示了保辛算法在处理小变形几何非线性问题的优势。
本文主要运用时间有限元以及矩形法作用量积分对小摆角弹簧摆进行处理,采用保辛递推,通过部分降低求解精度提高了计算速度,并能够保证积分过程的长时间稳定,保辛的特性能够避免系统误差随时间积分产生积累。
1 弹簧摆模型
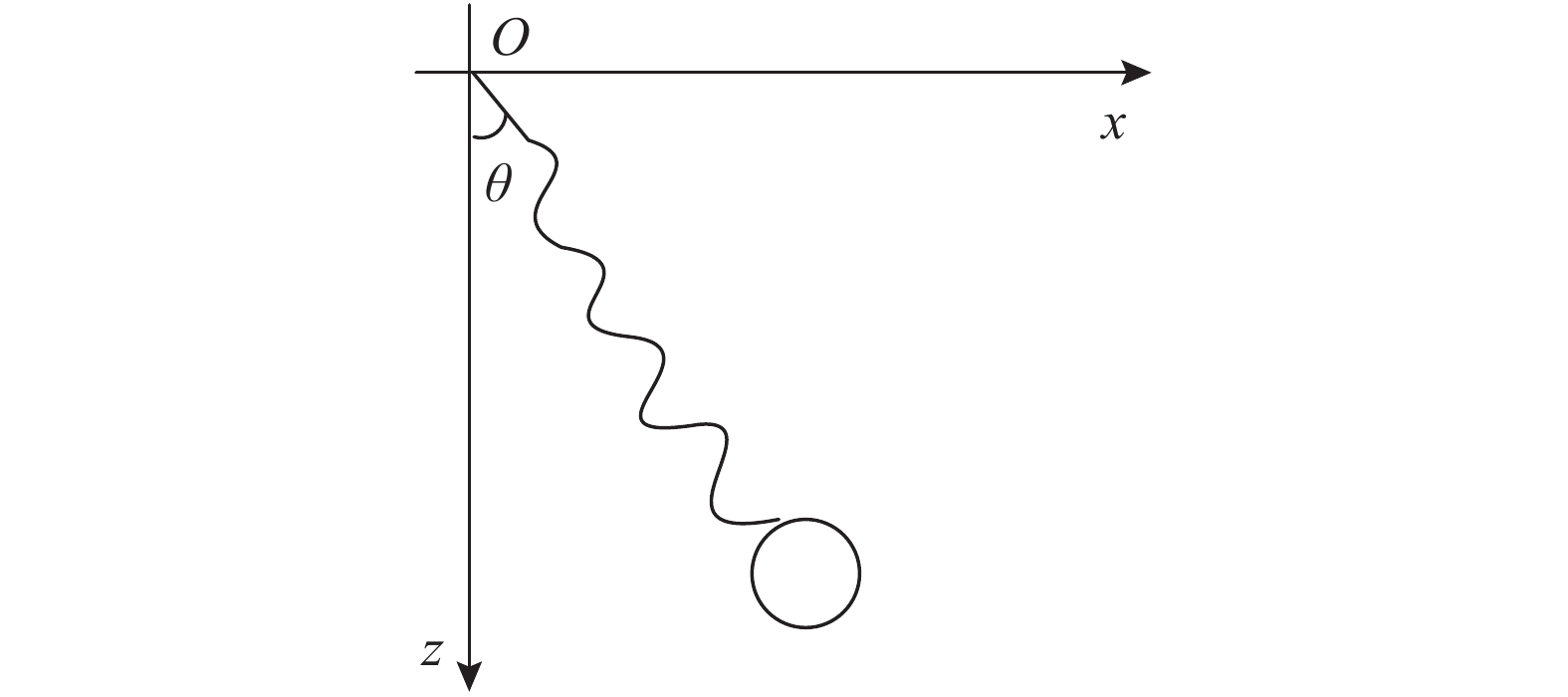
时间有限元与保辛递推求解不同于传统的微分方程求解,其从动力方程的Hamilton变分原理出发,对系统作用量进行时间离散。本文以绕支点无阻尼自由摆动的弹簧摆为对象进行研究,研究模型如图1所示。采用直角坐标系描述弹簧摆的空间位置,设定二自由度坐标分别为x与y,质点质量m,弹簧在质点自重作用下的长度为l0,弹簧自然长度为r0,弹簧劲度系数为k,重力加速度为g,单位全部采用国际单位制。
取弹簧摆的端点为原点,在此情况下建立系统动能和势能的表达式为:
T=12m(˙x2+˙y2),V=12k(√x2+y2−r0)2+mgy (1) 作用量积分,即拉格朗日函数对于时间的积分,表示为:
A=∫tf0Ldt=∫tf0(T−V)dt (2) 这时可以采用时间有限元对于该问题进行描述,对于两个自由度x, y分别在时间区段
ta ,tb 上进行线性插值可以构造一阶的时间有限元函数:{\boldsymbol{q}}\left( t \right) = {\boldsymbol{N}}\left[ \begin{gathered} {q_{\rm{a}}} \\ {q_{\rm{b}}} \\ \end{gathered} \right] = \frac{1}{{\Delta t}}\left[ \begin{gathered} \left( {{x_{\rm{b}}} - {x_{\rm{a}}}} \right)t + {t_{\rm{b}}}{x_{\rm{a}}} - {t_{\rm{a}}}{x_{\rm{b}}} \\ \left( {{y_{\rm{b}}} - {y_{\rm{a}}}} \right)t + {t_{\rm{b}}}{y_{\rm{a}}} - {t_{\rm{a}}}{y_{\rm{b}}} \\ \end{gathered} \right] (3) 进行有限元变换的目的是,时间有限元变换是保辛的,能够保证系统的能量守恒。离散化后的作用量积分可以写成:
A = \sum {\int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\left( {T - V} \right)} } {\rm d}t (4) 由于存在平方积分项,求解非线性方程组会耗费大量的时间。为了提高求解速度,本文在构造递推式时对平方积分进行线性化处理,采用矩形积分近似以求得近似解。单元作用量函数为:
\begin{split} {A_k} = &\int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\left( {\frac{1}{2}m( {{{\dot x^2}} + {{\dot y^2}}} )} \right){\rm d}t} - \\& \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\left( {\frac{1}{2}k{{( {\sqrt {{x^2} + {y^2}} - {r_0}} )^2}} + mgy} \right)} {\rm d}t \end{split} (5) 其中,主要是对于平方积分项中的部分进行处理,用于保证后文的求解过程是前项递推的,因而只保留
{t_{\rm{a}}} 时刻的相关项,采用矩形积分方法对于该方程进行部分离散,有:\begin{split} & \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\left( {\frac{1}{2}k{{( {\sqrt {{x^2} + {y^2}} - {r_0}} )^2}}} \right)} {\rm d}t = \\&\quad \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\frac{1}{2}k( {{x^2} + {y^2} + {r_0^2}} )} {\rm d}t - \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {k{r_0}\sqrt {{x^2} + {y^2}} } {\rm d}t \approx \\&\quad \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\frac{1}{2}k( {{x^2} + {y^2} + {r_0^2}} )} {\rm d}t - k{r_0}\Delta t\sqrt {{x_{\rm{a}}^2} + {y_{\rm{a}}^2}} \end{split} (6) 其余部分进行常规的有限元积分离散,有离散后的作用量格式:
\begin{split} {A_k} = &\frac{1}{2}m( {{a_1^2} + {b_1^2}} )\Delta t - \\& \frac{k}{{6{a_1}}}( {{x_{\rm{b}}^3} - {x_{\rm{a}}^3}} ) - \frac{k}{{6{b_1}}}( {{y_{\rm{b}}^3} - {y_{\rm{a}}^3}} ) - \\& \frac{1}{2}k{r_0^2}\Delta t + k{r_0}\Delta t\sqrt {{x_{\rm{a}}^2} + {y_{\rm{a}}^2}} + mg\frac{{{y_{\rm{a}}} + {y_{\rm{b}}}}}{2}\Delta t \end{split} (7) 其中:
\begin{split} & {a_1} = \frac{{{x_{\rm{b}}} - {x_{\rm{a}}}}}{{\Delta t}},{a_2} = \frac{{{t_{\rm{b}}}{x_{\rm{a}}} - {t_{\rm{a}}}{x_{\rm{b}}}}}{{\Delta t}} ,\\& {b_1} = \frac{{{y_{\rm{b}}} - {y_{\rm{a}}}}}{{\Delta t}},{b_2} = \frac{{{t_{\rm{b}}}{y_{\rm{a}}} - {t_{\rm{a}}}{y_{\rm{b}}}}}{{\Delta t}} \end{split} (8) 采用保辛迭代格式求解,首先构造对偶变量:
\begin{split} {{\boldsymbol{p}}_{\rm{a}}} = & - \frac{{\partial {A_k}}}{{\partial {{\boldsymbol{q}}_{\rm{a}}}}} = \\& \left( {\frac{1}{3}k\Delta t - \frac{m}{{\Delta t}} - \frac{{k{r_0}\Delta t}}{{\sqrt {{x_{\rm{a}}^2} + {y_{\rm{a}}^2}} }}} \right){{\boldsymbol{q}}_{\rm{a}}} + \\& \left( {\frac{m}{{\Delta t}} + \frac{1}{6}k\Delta t} \right){{\boldsymbol{q}}_{\rm{b}}} - \left( \begin{gathered} 0 \\ \frac{1}{2}mg\Delta t \\ \end{gathered} \right) \end{split} (9) \begin{split} {{\boldsymbol{p}}_{\rm{b}}} = & - \frac{{\partial {A_k}}}{{\partial {{\boldsymbol{q}}_{\rm{b}}}}} = - \left( {\frac{m}{{\Delta t}} + \frac{1}{6}k\Delta t} \right){{\boldsymbol{q}}_{\rm{a}}} - \\& \left( {\frac{1}{3}k\Delta t - \frac{m}{{\Delta t}}} \right){{\boldsymbol{q}}_{\rm{b}}} + \left( \begin{gathered} 0 \\ \frac{1}{2}mg\Delta t \\ \end{gathered} \right) \end{split} (10) 引入状态向量并写成递推形式:
{{\boldsymbol{v}}_k} = {{\boldsymbol{S}}_k}{{\boldsymbol{v}}_{k - 1}} (11) 其中:
{{\boldsymbol{v}}_{k - 1}} = \left( \begin{gathered} {{\boldsymbol{q}}_{\rm{a}}} \\ {{\boldsymbol{p}}_{\rm{a}}} \\ \end{gathered} \right) (12) {{\boldsymbol{v}}_k} = \left( \begin{gathered} {{\boldsymbol{q}}_{\rm{b}}} \\ {{\boldsymbol{p}}_{\rm{b}}} \end{gathered} \right)\;\; (13) 经过前面的矩形积分近似最终可以处理为
{\boldsymbol{S}}\left( {{x_{\rm{a}}},{y_{\rm{a}}}} \right) 的形式,可以代入初始状态向量进行递推求解。以上是针对无阻尼系统的推导,对于有阻尼系统,时间有限元也能展现其适应性。对文献[27]中提到的阻尼力与时间成正比阻尼形式,若阻尼系数不是时变参数,可采用变量代换方法求解。即令阻尼系数为γ,
{{\boldsymbol{q}}_1}\left( t \right) = {\boldsymbol{q}}\left( t \right){{\rm e}^{ - \tfrac{\gamma }{m}t}} 。利用该变换可以消除耦合项并将作用量{A_k} 转化为:{A_{k1}} = {A_{k11}} + {A_{k21}} + {A_{k31}} (14) \begin{split} {A_{k11}} = &\int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\frac{1}{2}m( {{{\dot x}_1^2} + {{\dot y}_1^2}} )} {\rm d}t - \\& \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\frac{1}{2}\left( {k - \frac{{{\gamma ^2}}}{m}} \right)( {{x_1^2} + {y_1^2}} )} {\rm d}t \end{split} (15) {A_{k21}} = \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\frac{{k{r_0}{{\rm e}^{\tfrac{\gamma }{m}t}}}}{{\sqrt {{x_1^2} + {y_1^2}} }}} {\rm d}t (16) {A_{k31}} = \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {mg{y_1}{{\rm e}^{\tfrac{\gamma }{m}t}}} {\rm d}t (17) 转化后的
{A_{k1}} 与{A_k} 形式类似,在{A_{k11}} 部分可以直接利用时间有限元方法求解;在{A_{k21}} 、{A_{k31}} 两部分可以继续通过构造梯形积分公式的形式进行积分。只需要再对求得的{{\boldsymbol{q}}_1}\left( t \right) 变量乘系数{{\rm e}^{\tfrac{\gamma }{m}t}} 即可获得原变量的解。一阶时间有限元与差分格式类似,不能显著提高有限元方法的精确度。可以通过改进时间有限元格式,增加时间有限元节点个数来提高计算精度,故而产生了二阶或者阶数更高的时间有限元。在维度更高的时间有限元推导过程中,采用矩阵形式和张量形式更为便捷,本方法中采用矩阵方法对于二阶时间有限元进行推导。
采用基函数
{\boldsymbol{N}} = [ {{t^2}}\;\;t\;\;1] 进行时间有限元插值,即:q\left( t \right) = {\boldsymbol{N}}\left( t \right){\left[ {\begin{array}{*{20}{c}} {{t_{\rm{a}}^2}}&{{t_{\rm{a}}}}&1 \\ {{t_i^2}}&{{t_i}}&1 \\ {{t_{\rm{b}}^2}}&{{t_{\rm{b}}}}&1 \end{array}} \right]^{ - 1}}\left[ \begin{gathered} {{\boldsymbol{q}}_{\rm{a}}} \\ {{\boldsymbol{q}}_i} \\ {{\boldsymbol{q}}_{\rm{b}}} \\ \end{gathered} \right] (18) {A_k} = {A_{k1}} + {A_{k2}} + {A_{k3}} (19) {A_{k1}} = \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\frac{1}{2}} m{\dot q^2}{\rm d}t - \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\frac{1}{2}} k{q^2}{\rm d}t - \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {\frac{1}{2}} k{r_0^2}{\rm d}t (20) {A_{k2}} = \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {k{r_0}\sqrt {{x^2} + {y^2}} } {\rm d}t (21) {A_{k3}} = \int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {mgy} {\rm d}t (22) 采用时间有限元法,即
{A_{k1}} 采用二阶时间有限元方法离散,{A_{k2}} 、{A_{k3}} 采用其他数值方法离散,这里要求的数值离散方法需要能够满足前文提到的递推要求,因而仅能通过{t_{\rm{a}}} 端点进行构造。在本解法中采用矩形积分方法进行离散。由于引入了中间节点
{{\boldsymbol{q}}_i} 对应,采用二阶时间有限元的推导需要进行节点凝聚以满足递推格式,而且可以推广到更高阶数的时间有限元上。需要注意,对于不采用有限元离散的非线性项部分,这部分在计算过程中不能引入中间节点进行节点凝聚的方法进行计算。因为下文给出的凝聚格式不能针对于非线性项进行处理,故而应采用两端时间节点位置进行离散。节点凝聚格式由变分原理推导,由于
{A_{k2}} 、{A_{k3}} 两作用量仅利用端点离散,与{{\boldsymbol{q}}_i} 无关,故{A_k} 的节点凝聚格式同{A_{k1}} 的相一致,可以采用齐次方程下的节点凝聚法进行推导。通过可知对于形式为:{A_{k1}} = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{q}}_{\rm{a}}}} \\ {{{\boldsymbol{q}}_i}} \\ {{{\boldsymbol{q}}_{\rm{b}}}} \end{array}} \right]'}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{A}}&{\boldsymbol{D}}&{\boldsymbol{E}} \\ {{\boldsymbol{D}}'}&{\boldsymbol{B}}&{\boldsymbol{F}} \\ {{\boldsymbol{E}}'}&{{\boldsymbol{F}}'}&{\boldsymbol{C}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{q}}_{\rm{a}}}} \\ {{{\boldsymbol{q}}_i}} \\ {{{\boldsymbol{q}}_{\rm{b}}}} \end{array}} \right] (23) 的作用量,可以转换为:
{A_{k1}} = {\left[ \begin{gathered} {{\boldsymbol{q}}_{\rm{a}}} \\ {{\boldsymbol{q}}_{\rm{b}}} \\ \end{gathered} \right]'}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{A}}_{\rm{r}}}}&{{{\boldsymbol{B}}_{\rm{r}}}} \\ {{{\boldsymbol{C}}_{\rm{r}}}}&{{{\boldsymbol{D}}_{\rm{r}}}} \end{array}} \right]\left[ \begin{gathered} {{\boldsymbol{q}}_{\rm{a}}} \\ {{\boldsymbol{q}}_{\rm{b}}} \\ \end{gathered} \right] (24) 其中:
\begin{split} & {{\boldsymbol{A}}_{\rm{r}}} = {\boldsymbol{A}} - {\boldsymbol{D}}{( {{{\boldsymbol{B}}^{ - 1}}} )'}{{\boldsymbol{D}}'} ,\\& {{\boldsymbol{B}}_{\rm{r}}} = {\boldsymbol{E}} - {\boldsymbol{D}}{( {{{\boldsymbol{B}}^{ - 1}}} )'}{\boldsymbol{F}} ,\\& {{\boldsymbol{C}}_{\rm{r}}} = {{\boldsymbol{B}}_{\rm{r}}' } ,\\& {{\boldsymbol{D}}_{\rm{r}}} = {\boldsymbol{C}} - {{\boldsymbol{F}}'}{( {{{\boldsymbol{B}}^{ - 1}}} )'}{\boldsymbol{F}} \end{split} (25) 节点凝聚可以保证本方法构造成保辛递推格式,完成递推求解。在节点凝聚后仍然需要构造对偶变量并确立保辛递推格式以完成求解。
由于该计算方法的时间有限元部分
{A_{k1}} 保辛,误差的产生主要源于梯形积分在{A_{k2}} 、{A_{k3}} 处产生的误差。这里引入代数精度的概念,根据文献[28],梯形积分仅具有一阶精度,是导致整个积分算法精度较低的一个关键因素。时间有限元又因为采用迭代算法不能在其迭代矩阵中引入非线性的{{\boldsymbol{v}}_k} ,仅可选用{{\boldsymbol{v}}_{k - 1}} 相关值进行积分,故对积分精度有一定影响。本方法中构造了一种梯形算法以提高数值积分的积分精度。该积分算法采用{t_{\rm{a}}} 时刻q\left( t \right) 及其导数构造积分格式,即:\int_{{t_{\rm{a}}}}^{{t_{\rm{b}}}} {{f} {\rm d}t} = {{f}} \left( {{t_{\rm{a}}}} \right)\Delta t + \frac{1}{2}\dot f\left( {{t_{\rm{a}}}} \right)\Delta {t^2} (26) 对于
{A_{k2}} 、{A_{k3}} 采用该方程构造积分格式,由代数精度的定义可知其具有二阶代数精度,较矩形公式有进一步的精度提高。2 模拟分析
为了检验方法的准确性,本文采用数值模拟同实验数据[15]进行对比。通过计算可知
\lambda = 2 ,处于内共振区间。同时与广泛使用的谐波平衡法[22]进行了对比,共进行2个状态下的数值模拟。2.1 无阻尼情况
通过已有文献[10-11, 21-22, 29-31],对于内共振现象的数值解法通常采用不考虑阻尼的方程进行求解。采用表1的实验参数进行了模拟,采用传递辛矩阵法,单步时间为0.002 s时的模拟结果图2、图3所示。
表 1 模拟参数1Table 1. Simulation parameters No.1因素 模拟次号 1 2 水平初位置 x0/m 0.1414 0.1960 竖直初位置 y0/m −0.9290 −0.8774 水平初动量 px0/(kg·m/s) 0.0000 0.0000 竖直初动量 Py0/(kg·m/s) 0.0000 0.0000 初始摆长 r0/m 0.6162 0.6162 振子质量 m/kg 0.0484 0.0484 弹簧刚度 k/(N/m) 2.3000 2.3000 1) 对于振幅的分析:在初始状态1下出现了明显的共振现象,而初始状态2下内共振现象不明显,这与实验现象一致,与文献[22]中提到的只有在小角度摆动才出现强烈耦合的现象是一致的,而且该共振显现的周期与幅值同文献[22]中采用高阶Runge-Kutta法的结果也一致。这说明,本算法能够对内共振现象进行初步的预测。但实验中振动幅度存在明显的衰减现象,且内共振现象发生的周期与实验不一致。认为运动过程中存在阻尼对于内共振现象的发生是有影响的,而实验过程中的阻尼主要由空气阻尼或实验器材本身阻尼影响产生。需要进行进一步分析。
2) 对于频率的分析:40 s内的平均垂直振动频率为
{\omega _{\rm s}} = 7.41\;{\rm{Hz}} ,水平振动频率{\omega _{\rm p}} = 3.65\;{\rm{Hz}} ,与实验中测定的{\omega _{\rm s}} = 7.27\;{\rm{Hz}} ,{\omega _{\rm p}} = 3.63\;{\rm{Hz}} 分别存在1.93%与0.54%的误差。相较于其进行简谐运动近似的相对偏差4.9%与5.5%有较大提高。3) 对于机械能守恒效果的分析:由于对保守系统进行分析,观察总能量的变化规律是评判算法好坏的重要指标。在该算法中能量偏差存在着周期性的变化,在计算步长为0.002 s时可以保证能量偏差与输入能量初值比维持在5‰以下。在计算过程中可以看出总能量偏差同初始能量之间的变化关系是周期性质的,而不像[10]中提到的对于微分方程求解方法的能量误差会出现发散的现象。这能够保证能量积分的相对稳定,对于长历程积分有很好适应性。
2.2 有阻尼情况
由于考虑引入阻尼力后,考虑阻尼系数γ=0.0013的情况对于表1中模拟次号1的初始状态进行分析,分析结果如下:
图5反映了含有阻尼力的摆动曲线与实验曲线更为类似,也更符合实验曲线的衰减规律。此外在增加系统阻尼的情况下,模拟轨迹出现了较之前的一些不同。首先,是阻尼系数导致振动频率的降低,增加阻尼后,两个方向振动频率分别降低至3.62 Hz与7.24 Hz,与实验计算的频率偏差分别为0.27%与0.41%,相较于不加阻尼分别提高了1.66%与0.13%,效果很好。其次,是阻尼系数的引入能够导致内共振现象发生频率产生变化,对于模拟次号1实验,内共振现象峰值出现频数由5次降低至4次,说明阻尼对内共振现象确实存在较大影响。最后,通过多次改变初始条件的值可以发现,通过使初值在一定范围(x方向不变,y方向0.01 m~0.1 m)内浮动可以发现,内共振现象的发生是依赖与初始条件的,且这种依赖现象同阻尼关系不大。在计算中可以发现,在y在区间0.05 m~0.06 m时,内共振现象很难发生,x方向与y方向几乎相对独立的进行振动。
2.3 时间有限元方法之间的对比
除一阶矩形法(仅对
{A_{k2}} 使用)外,一阶梯形(对{A_{k2}} 、{A_{k3}} 使用)法,二阶矩形法(仅对{A_{k2}} 使用)以及二阶梯形法(对{A_{k2}} 、{A_{k3}} 使用)均给出了类似的结果,并对各组结果进行比较。表2采用计算步长0.2 ms,计算总时长20 s,分别对于第一次实验和第二次实验,针对于这四种方法的运算速度以及计算精度通过下表进行比较。表 2 积分方式对于模拟效果的影响Table 2. The influence of integral method on simulation积分方法 模拟次号1 精度/(×10−5 J) 精度偏差/(%) 时间/s 时间偏差/(%) 一阶矩形 6.2154 0.000 0.9002 0.00 一阶梯形 6.2154 0.000 1.2032 33.66 二阶矩形 6.2173 0.030 1.4258 58.39 二阶梯形 6.2175 0.033 1.7018 89.05 积分方法 模拟次号2 精度/(×10−5 J) 精度偏差/(%) 时间/s 时间偏差/(%) 一阶矩形 7.8835 0.000 0.9047 0.00 一阶梯形 7.8835 0.000 1.1992 32.55 二阶矩形 7.8859 0.030 1.4203 56.99 二阶梯形 7.8863 0.036 1.5658 73.07 注:偏差是相对本列中最小量取得的,计算方法为偏差量除以最小量。 从表2可看出四种方法精度相近,采用增加阶数与增加代数精度的方法并没有显著增加计算精度,反而显著增加了计算时间。综上,采用一阶矩形法求解该问题即可获得理想的结果。
关于本方法的计算精度,整个推导过程存在2处近似,但仅采用梯形法积分是存在能量误差的。这部分会导致能量计算不够精确,是误差的主要来源。因此对总能量偏差与步长关系进行研究。
由图6可以看出,计算步长对于总能量偏差影响较大,在采用线性时间有限元的情况下在步长高于0.002 s时总能量偏差即超过5‰,因而在计算过程中需要尽量选取低于0.002 s的步长,以保证积分的准确性。
3 同其他非线性方程解法的对比
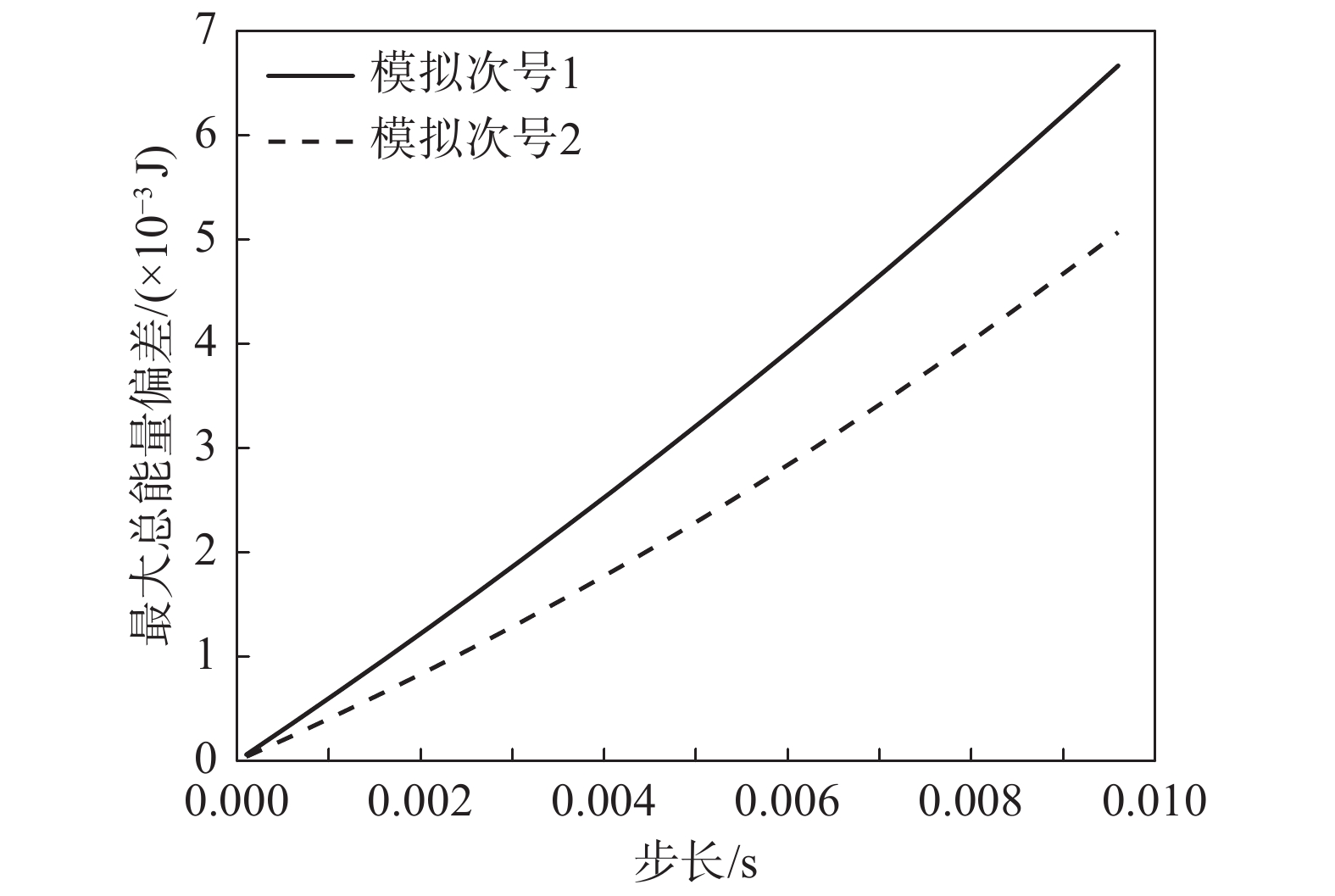
时间有限元方法在计算精度相同的情况下同其他微分方程求解算法进行对比。计算机CPU采用四核i7-4710 MQ,主频2.5G Hz,内存4 GB。在计算步长为10 μs时计算2 s计算时间为0.64 s,且收敛速度较其他数值方法有明显提高。同表3中的非线性微分方程求解方法相比较,在λ
=1 ,\delta = 6.2 \times {10^{ - 7}} 时,同4阶R-K法的计算速度类似,显著高于Ode15 s。确实在降低求解步长的情况下提高了计算速度,并保持了积分误差的稳定性。4 对强非线性问题的适应性
由于不要求
\left| {\dfrac{x}{{{l_0}}}} \right| \ll 1 ,\left| {\dfrac{{y + {l_0}}}{{{l_0}}}} \right| \ll 1 。本方法除了可以解决耦合共振问题,也可以求解几何非线性问题即大角度摆动产生的非线性问题[16, 32],本算例通过限制总能量偏差的方法求解大角度摆动问题,设计条件如表4所示。表 4 大角度摆动初始条件Table 4. Initial condition of wide-angle swing因素 模拟次号 3 水平初位置 x0/m 0.7000 竖直初位置 y0/m −0.4000 水平初动量 px0/(kg·m/s) 0.0000 竖直初动量 Py0/(kg·m/s) 0.0000 初始摆长 r0/m 0.6162 振子质量 m/kg 0.0484 弹簧刚度 k/(N/m) 2.3000 在文献[11]中提到,在两振动方向频率比为1∶2的情况下,方程的解是初值敏感的,在不同的初值条件下能够表现出准周期性或混沌的特性。这里通过模拟次号2与模拟次号3相对照以检验该算法对于混沌问题的适应性。采用传递辛矩阵法,步进时间为0.002 s时的模拟结果如下:
从图7(b)和图7(c)的比较中可以发现在不同初值下,相图x方向出现了一定的混沌特征,这与文献[11]的结论一致。但从总能能量偏差的角度可以看出能量偏差虽然较小角度摆动的能量偏差更大,但在合理范围内且并没有出现发散趋势,通过前文的模拟也可知通过减小步长可以大幅降低总能量偏差。该模拟表明了时间有限元的保辛递推算法具有非线性长时间积分下稳定的特点。
5 结论
本文通过模拟证明了时间有限元能够处理弹簧摆的内共振问题。具有收敛较快、精度较高,并在长尺度积分下保持稳定的特性。
在对时间有限元步长进行了误差分析与速度分析后发现,该方法不存在误差累积的现象,计算精度主要取决于步长,在步长为0.001 s~0.01 s的范围内最大能量偏差小于2.17%,且能够保证计算速度。一阶矩形时间有限元的计算精度与时间经济性更好。此外对于更一般的大角度非线性弹簧摆问题也进行了求解,得到了长时间积分下误差可控的模拟结果。
由于该方法体现的刚柔耦合性不需要通过相对坐标进行参与,在绝对坐标下即可实现。虽相较于保辛摄动迭代法[26]精度有所下降,但更适于绝对节点坐标法的求解。
-
表 1 模拟参数1
Table 1 Simulation parameters No.1
因素 模拟次号 1 2 水平初位置 x0/m 0.1414 0.1960 竖直初位置 y0/m −0.9290 −0.8774 水平初动量 px0/(kg·m/s) 0.0000 0.0000 竖直初动量 Py0/(kg·m/s) 0.0000 0.0000 初始摆长 r0/m 0.6162 0.6162 振子质量 m/kg 0.0484 0.0484 弹簧刚度 k/(N/m) 2.3000 2.3000 表 2 积分方式对于模拟效果的影响
Table 2 The influence of integral method on simulation
积分方法 模拟次号1 精度/(×10−5 J) 精度偏差/(%) 时间/s 时间偏差/(%) 一阶矩形 6.2154 0.000 0.9002 0.00 一阶梯形 6.2154 0.000 1.2032 33.66 二阶矩形 6.2173 0.030 1.4258 58.39 二阶梯形 6.2175 0.033 1.7018 89.05 积分方法 模拟次号2 精度/(×10−5 J) 精度偏差/(%) 时间/s 时间偏差/(%) 一阶矩形 7.8835 0.000 0.9047 0.00 一阶梯形 7.8835 0.000 1.1992 32.55 二阶矩形 7.8859 0.030 1.4203 56.99 二阶梯形 7.8863 0.036 1.5658 73.07 注:偏差是相对本列中最小量取得的,计算方法为偏差量除以最小量。 数值方法 λ=1 步长h/s 所需误差精度 ε 能量相对误差 δ 计算时间 t/s Adams 10−2 10−6 1.86×10−6 0.24 4阶R-K 10−2 10−6 8.22×10−8 0.31 Ode113 − 10−10 1.99×10−10 0.42 Ode45 − 10−10 2.28×10−8 0.64 Ode15 s − 10−10 5.44×10−7 1.50 表 4 大角度摆动初始条件
Table 4 Initial condition of wide-angle swing
因素 模拟次号 3 水平初位置 x0/m 0.7000 竖直初位置 y0/m −0.4000 水平初动量 px0/(kg·m/s) 0.0000 竖直初动量 Py0/(kg·m/s) 0.0000 初始摆长 r0/m 0.6162 振子质量 m/kg 0.0484 弹簧刚度 k/(N/m) 2.3000 -
[1] 周纪卿, 朱因远. 非线性振动 [M]. 西安: 西安交通大学出版社, 1998: 255. Zhou Jiqing, Zhu Yinyuan. Nonlinear vibration [M]. Xi’an: Xi’an Jiaotong University Press, 1998: 255. (in Chinese)
[2] 陈波, 宋欣欣, 吴镜泊. 输电塔线体系力学模型研究进展[J]. 工程力学, 2021, 38(5): 1 − 21. doi: 10.6052/j.issn.1000-4750.2020.08.ST07 Chen Bo, Song Xinxin, Wu Jingbo. Advances in mechanical models of transmission tower-line systems [J]. Engineering Mechanics, 2021, 38(5): 1 − 21. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.08.ST07
[3] 刘俊才, 田利, 张睿, 易思银. 远场地震作用下输电塔-线体系最不利输入方向预测研究[J]. 工程力学, 2020, 37(增刊): 97 − 103. doi: 10.6052/j.issn.1000-4750.2019.05.S014 Liu Juncai, Tian Li, Zhang Rui, Yi Siyin. Study on the prediction of the most adverse input direction of transmission tower-line system under far-field seismic ground motions [J]. Engineering Mechanics, 2020, 37(Suppl): 97 − 103. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.05.S014
[4] 李艺, 黄国庆, 程旭, 赵丽娜. 移动型下击暴流及其作用下高层建筑风荷载的数值模拟[J]. 工程力学, 2020, 37(3): 176 − 187. doi: 10.6052/j.issn.1000-4750.2019.04.0231 Li Yi, Huang Guoqing, Cheng Xu, Zhao Lina. The numerical simulation of moving downbursts and their induced wind load on high-rise buildings [J]. Engineering Mechanics, 2020, 37(3): 176 − 187. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.0231
[5] 张鹏, 李宏男, 田利, 张卓群. 弹簧摆的内共振原理及其对输电塔的减震作用[J]. 世界地震工程, 2016, 32(1): 210 − 218. Zhang Peng, Li Hongnan, Tian Li, Zhang Zhuoqun. Seismic vibration control of transmission tower with a spring pendulum [J]. World Earthquake Engineering, 2016, 32(1): 210 − 218. (in Chinese)
[6] 霍林生, 黄辰, 李宏男. 基于非线性能量阱的悬吊摆对输电塔振动控制的研究[J]. 防灾减灾工程学报, 2019, 39(6): 898 − 904. Huo Linsheng, Huang Chen, Li Hongnan. Vibration control of transmission towers with a suspended pendulum based on nonlinear energy sink [J]. Journal of Disaster Prevention and Mitigation Engineering, 2019, 39(6): 898 − 904. (in Chinese)
[7] 王奇, 李宏男, 张鹏. 弹簧摆碰撞减震系统计算模型研究[J]. 沈阳建筑大学学报(自然科学版), 2018, 34(2): 222 − 228. Wang Qi, Li Hongnan, Zhang Peng. Calculation model of impact vibration reducing system of spring pendulum [J]. Journal of Shenyang Jianzhu University (Natural Science), 2018, 34(2): 222 − 228. (in Chinese)
[8] 黄正, 刘石, 聂铭, 杨毅, 高庆水, 张楚. 利用球形弹簧摆对输电塔风振控制的有限质点法[J]. 振动与冲击, 2020, 39(1): 266 − 273. Huang Zheng, Liu Shi, Nie Ming, Yang Yi, Gao Qingshui, Zhang Chu. Finite particle method for wind-induced vibration control of transmission towers with spherical spring pendulum [J]. Journal of Vibration and Shock, 2020, 39(1): 266 − 273. (in Chinese)
[9] Wu Yipeng, Qiu Jinhao, Zhou Shengpeng, et al. A piezoelectric spring pendulum oscillator used for multi-directional and ultra-low frequency vibration energy harvesting [J]. Applied Energy, 2018, 231: 600 − 614. doi: 10.1016/j.apenergy.2018.09.082
[10] 于洪洁, 张靖姝, 洪嘉振. 刚柔耦合弹簧摆的复杂动力学行为[J]. 科技导报, 2013, 31(18): 32 − 38. doi: 10.3981/j.issn.1000-7857.2013.18.004 Yu Hongjie, Zhang Jingshu, Hong Jiazhen. Complex dynamical behavior of rigid-flexible coupling spring pendulum [J]. Science & Technology Review, 2013, 31(18): 32 − 38. (in Chinese) doi: 10.3981/j.issn.1000-7857.2013.18.004
[11] 李银山, 白育堃, 树学锋. 弹簧摆的内共振和混沌运动[J]. 太原理工大学学报, 1998(6): 3 − 7. Li Yinshan, Bai Yukun, Shu Xuefeng. Internal resonance and chaotic motion of a spring pendulum [J]. Journal of Taiyuan University of Technology, 1998(6): 3 − 7. (in Chinese)
[12] 赵聪, 于洪洁. 一种刚性杆-弹簧摆模型的混沌动力学行为研究[J]. 复杂系统与复杂性科学, 2016, 13(3): 97 − 102. Zhao Cong, Yu Hongjie. On the chaotic dynamic behavior of the rigid rod-spring pendulum model [J]. Complex Systems And Complexity Science, 2016, 13(3): 97 − 102. (in Chinese)
[13] van der Weele J P, de Kleine E. The order-chaos-order sequence in the spring pendulum [J]. Physica A, 1996, 228: 245 − 272. doi: 10.1016/0378-4371(95)00426-2
[14] de Sousa M C, Marcus F A, Caldas I L, Viana R L. Energy distribution in intrinsically coupled systems: The spring pendulum paradigm [J]. Physica A: Statistical Mechanics and its Applications, 2018, 509: 1110 − 1119. doi: 10.1016/j.physa.2018.06.089
[15] 司丽荣, 张竞夫. 弹簧摆内共振现象的实验研究[J]. 物理实验, 2002(3): 9 − 12. doi: 10.3969/j.issn.1005-4642.2002.03.003 Si Lirong, Zhang Jingfu. Study on the experiment of the autoparametric resonance of a spring pendulum [J]. Physics Experimentation, 2002(3): 9 − 12. (in Chinese) doi: 10.3969/j.issn.1005-4642.2002.03.003
[16] Rusbridge M G. Motion of the sprung pendulum [J]. American Journal of Physics, 1980, 48(2): 146 − 151. doi: 10.1119/1.12190
[17] Grażyna Sypniewska-Kamińska, Jan Awrejcewicz, Henryk Kamiński, Robert Salamon. Resonance study of spring pendulum based on asymptotic solutions with polynomial approximation in quadratic means [J]. Meccanica, 2020, 56(10): 1 − 8. doi: 10.1007/s11012-020-01164-8
[18] Amer T S, Bek M A, Abouhmr M K. On the vibrational analysis for the motion of a harmonically damped rigid body pendulum [J]. Springer Netherlands, 2018, 91(4): 2485 − 2502. doi: 10.1007/s11071-017-4027-7
[19] Amer T S, Bek M A, Abohamer M K. On the motion of a harmonically excited damped spring pendulum in an elliptic path [J]. Mechanics Research Communications, 2019, 95: 23 − 34. doi: 10.1016/j.mechrescom.2018.11.005
[20] Holmes P J, Marsden J E. Horseshoes and arnold diffusion for hamiltonian systems on lie groups [J]. Indiana University Mathematics Journal, 1983, 32(2): 273 − 310. doi: 10.1512/iumj.1983.32.32023
[21] 李欣业, 张华彪, 贺丽娟, 张丽娟. 内共振关系对弹簧摆动力学行为的影响[J]. 动力学与控制学报, 2011, 9(2): 152 − 157. doi: 10.3969/j.issn.1672-6553.2011.02.012 Li Xinye, Zhang Huabiao, He Lijuan, Zhang Lijuan. Influence of internal resonance on dynamics of spring pendulums [J]. Journal of Dynamics and Control, 2011, 9(2): 152 − 157. (in Chinese) doi: 10.3969/j.issn.1672-6553.2011.02.012
[22] 郑建龙, 虞献文. 弹簧摆的内共振特性分析[J]. 物理与工程, 2010, 20(2): 13 − 16. doi: 10.3969/j.issn.1009-7104.2010.02.005 Zheng Jianlong, Yu Xianwen. Analysis of the autoparametric resonance of a spring pendulum [J]. Physics and Engineering, 2010, 20(2): 13 − 16. (in Chinese) doi: 10.3969/j.issn.1009-7104.2010.02.005
[23] Zienkiewicz O C, Taylor R. The finite element method [M]. 5th ed. New York: McGraw-Hill, 2000.
[24] 钟万勰, 姚征. 时间有限元与保辛[J]. 机械强度, 2005(2): 178 − 183. doi: 10.3321/j.issn:1001-9669.2005.02.009 Zhong Wanxie, Yao Zheng. Time domain FEM and Symplectic conservation [J]. Journal of Mechanical Strength, 2005(2): 178 − 183. (in Chinese) doi: 10.3321/j.issn:1001-9669.2005.02.009
[25] 冯康, 秦孟兆. Hamilton体系的辛计算格式 [M]. 杭州: 浙江科技出版社, 2004. Feng Kang, Qin Mengzhao. Symplectic geometric algorithm for Hamiltonian systems [M]. Hangzhou: Zhejiang Science and Technology Press, 2004. (in Chinese)
[26] 吴锋, 高强, 钟万勰. 刚-柔体动力学方程的保辛摄动迭代法[J]. 应用数学和力学, 2014, 35(4): 341 − 352. doi: 10.3879/j.issn.1000-0887.2014.04.001 Wu Feng, Gao Qiang, Zhong Wanxie. Iterative symplectic perturbation method for the dynamic analysis of rigid-flexible bodies equations [J]. Applied Mathematics and Mechanics, 2014, 35(4): 341 − 352. (in Chinese) doi: 10.3879/j.issn.1000-0887.2014.04.001
[27] 石玉仁, 薛具奎. 弹簧摆的混沌行为[J]. 西北师范大学学报(自然科学版), 2001(3): 91 − 97. Shi Yuren, Xue Jukui. The chaotic behavior in spring pendulum system [J]. Journal of Northwest Normal University (Natural Science), 2001(3): 91 − 97. (in Chinese)
[28] 李庆扬, 王能超, 易大义. 数值分析 [M]. 第5版. 北京: 清华大学出版社, 2008: 97 − 100. Li Qingyang, Wang Nengchao, Yi Dayi. Numerical analysis [M]. 5th ed. Beijing: Tsinghua University Press, 2008: 97 − 100. (in Chinese)
[29] 张义灵, 蓝冬云, 张振美, 等. 基于Matlab的弹簧摆内共振与混沌运动研究[J]. 大学物理实验, 2020, 33(4): 84 − 89. Zhang Yiling, Lan Dongyun, Zhang Zhenmei, et al. Study on internal resonance and chaotic motion of spring pendulum based on Matlab [J]. Physical Experiment of College, 2020, 33(4): 84 − 89. (in Chinese)
[30] Victor F. Edneral, Alexander G. Petrov. Nonlinear oscillations of a spring pendulum at the 1∶1∶2 resonance by normal form methods [J]. Mathematics in Computer Science, 2020, 14(2): 295 − 303. doi: 10.1007/s11786-019-00427-2
[31] Petrov A G, Vanovskiy V V. Nonlinear oscillations of a spring pendulum at the 1∶1∶2 resonance: Theory, experiment, and physical analogies [J]. Proceedings of the Steklov Institute of Mathematics, 2018, 300(1): 159 − 167. doi: 10.1134/S0081543818010133
[32] Cuerno R, Rañada A F, Ruiz‐Lorenzo J J. Deterministic chaos in the elastic pendulum: A simple laboratory for nonlinear dynamics [J]. American Journal of Physics, 1992, 60(1): 73 − 79. doi: 10.1119/1.17047




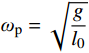
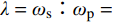
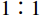
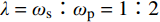
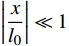
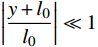
 下载:
下载: