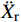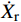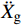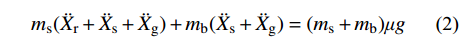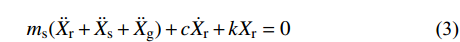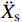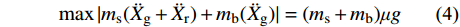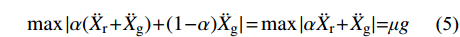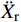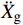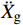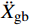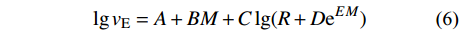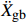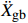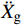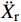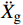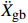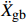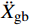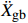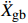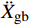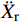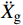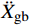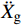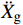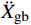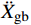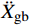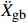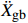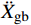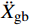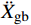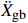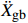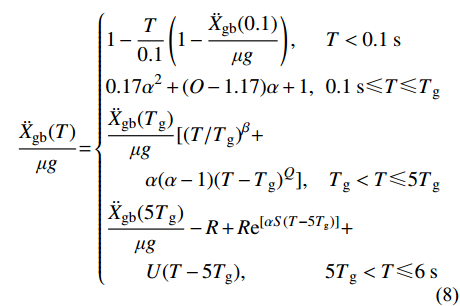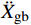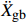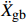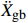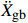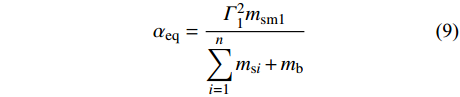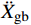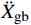A NUMERICAL STUDY ON SLIDING OCCURRENCE ACCELERATION FOR SLIDING BASE ISOLATION STRUCTURES
-
摘要: 起滑条件是影响滑移隔震结构动力响应特性的重要参数,也是滑移隔震结构性能化设计研究的理论基础。采用两自由度模型模拟滑移隔震结构,基于动力时程分析方法,分析了隔震结构参数(包括自振周期、质量比和摩擦系数)和地震动参数(包括反应谱特征周期和近断层地震动脉冲)对隔震结构起滑加速度的影响。结果表明:结构参数比地震动参数对起滑加速度的影响更明显。隔震结构的起滑加速度-自振周期曲线分为下降、水平、上升和先上升后水平4段。所选地震动集激励下,当自振周期小于1.4 s时,相同自振周期结构的起滑加速度随质量比的增大而减小;大于7.8 s时,起滑加速度随质量比的增大而增大。起滑加速度随摩擦系数的增加而等比例增大。基于分析结果,采用分段拟合方法建立了起滑加速度计算公式,公式计算结果和多自由度结构算例的时程分析结果吻合良好。研究成果可为滑移隔震结构的起滑条件研究和结构设计提供参考。Abstract: The occurrence condition of sliding is an important parameter for the dynamic response characteristics of the sliding base isolation structures, and it provides the theoretical basis to the performance based structural design of the sliding base isolation structures. A two-degree-of-freedom system model is adopted to simulate sliding base isolation structures. Base on the time history analysis method, the influence of various structural parameters (including natural period, mass ratio, and sliding friction coefficient) and ground motion parameters (including characteristic period of response spectrum and pulses of near-fault ground motion) on the sliding PGA are investigated. The results indicate that the structural parameters exhibit a stronger influence on the sliding PGA than that of the ground motion parameters. The sliding PGA versus natural period relationship curves of the isolated structures consisted of 4 segments, i.e., descend segment, horizontal segment, ascend segment, and ascend initially then keep horizontal segment. The sliding PGA decreases with increase in the mass ratio for the structures with natural periods smaller than 1.4 s, and increases with increase in the mass ratio for the structures with natural periods larger than 7.8 s subjected to the considered ground motion groups. The sliding PGA increases in an equal proportion with the increase of the sliding friction coefficient. An empirical expression to predict the sliding PGA is proposed using a piecewise linear fitting method. The calculated results of sliding PGA for the multi-degree-of-freedom structures using the proposed expression and time history analyses are in a good agreement. The results provide a basis for the following research on the sliding occurrence condition and the structure design of the sliding base isolation structures.
-
基础隔震是一种能有效减小房屋地震需求,减轻强震作用下房屋损伤的技术。基础隔震体系主要包括纯摩擦滑移隔震体系[1]、恢复力滑移隔震体系[2]、摩擦摆隔震体系[3-6]、铅芯橡胶隔震体系[7-10]和高阻尼橡胶隔震体系[11-12]等。其中,纯摩擦滑移隔震体系因其造价低廉,施工简单的优点,常应用于村镇建筑中。该体系仅需在上部结构与基础间设置一层摩擦滑移界面,其工作原理是:强震作用下,上部结构沿摩擦界面水平滑动,界面的动摩擦力限制了传递至上部结构的地震力大小,同时摩擦阻尼耗散了地震能量,从而达到减震的目的。
国内外学者针对纯摩擦滑移隔震结构的隔震性能及不同材料滑移界面的摩擦性能开展了一系列试验研究。Li[1]提出以沙粒为隔震层材料,并开展了5个滑移隔震砌体房屋模型的振动台试验,研究发现:设置隔震层能有效防止房屋在强震下倒塌。楼永林等[13]对以石墨、砾砂和石蜡为隔震层材料的隔震砖墙试件开展了振动台试验,研究发现:石墨适用性最好,带石墨隔震缝砖墙试件起滑加速度为0.2 g~0.3 g。Qamaruddin等[14]对以摩擦系数分别为0.25、0.34和0.41的石墨粉,干砂和湿砂为隔震层材料的隔震砖砌房屋及相应固定支座房屋模型开展了振动台试验,结果表明:隔震缝能有效降低房屋加速度响应。Nanda等[15-16]对绿色大理石-高密度聚乙烯、双层绿色大理石、绿色大理石-土工合成材料和绿色大理石-橡胶隔震缝界面开展了摩擦性能试验研究,结果表明:竖向压应力,滑移距离和速度对界面动摩擦系数均基本无影响,四种界面的动摩擦系数分别为0.08、0.09、0.11和0.16。荣强等[17]对聚四氟乙烯-不锈钢板滑移隔震界面开展了力学性能试验研究,结果表明:界面滑动摩擦系数随竖向压力增大而减小,随滑动速度增大而增大,涂抹硅脂明显降低摩擦系数。基于试验结果建立了新的界面摩擦力模型。
此外,国内外学者采用数值方法对纯摩擦滑移隔震结构的动力响应特性进行了研究。常用的数值模型为由上部和基础质点组成的两自由度体系。Mostaghel等[18]首次采用两自由度模型模拟滑移隔震结构,研究了简谐波激励下,模型参数及简谐波特性对隔震结构峰值加速度和滑移位移响应的影响规律。Westermo等[19]研究发现简谐波激励下,隔震结构呈现出3种周期性响应状态,即持续固定支座状态(stick-stick)、断续滑动状态(stick-slide)和持续滑动状态(slide-slide),提出了结构由持续固定支座状态转换至断续滑动状态先决条件的计算公式。Iura等[20]提出了简谐波激励下,隔震结构由断续滑动状态转换至持续滑动状态先决条件的计算公式。Hu等[21]提出了简谐波激励下,隔震结构持续滑动状态最大伪加速度响应的理论解。Mostaghel等[22]研究了在El Centro和Olympia地震动记录激励下,隔震结构的动力响应特性。毛利军等[23]对地震动激励下,不同参数隔震结构的反应谱特性开展了研究,研究表明:采用反应谱法对隔震结构进行初步设计可行,精度满足工程要求。隔震体系上部结构绝对及相对加速度、相对位移反应谱的变异系数均明显小于传统结构反应谱。
国内学者建议的村镇滑移隔震结构设计性能目标为“小震不滑,中震起滑,大震限位”。然而现有研究中,尚未见有关地震动激励下,纯滑移摩擦隔震结构由持续固定支座状态转换至断续滑动状态先决条件,即起滑条件的研究。本文采用两自由度体系模拟滑移隔震结构,以匹配于规范设计反应谱的6组地震动集为输入,研究了地震动参数和隔震结构参数对起滑加速度的影响规律。采用分段拟合的方法建立了起滑加速度计算公式。结果可供滑移隔震结构的起滑条件研究和工程设计提供参考。
1 两自由度滑移隔震结构模型及起滑加速度求解流程
采用两自由度模型模拟基础滑移隔震结构,如图1所示。该模型由通过阻尼单元及水平弹簧单元相连接的上部及基础质点组成,基础质点设置于允许水平向滑动的滑移摩擦面上,基础质点与摩擦面间摩擦力符合库仑摩擦定律。
地震动激励下,隔震结构有两种阶段。当上部及基础质点的惯性力之和小于滑移面摩擦力时,结构处于固定支座阶段。此时结构滑移位移Xs等于0,其基础质点与地面同步振动,其上部质点的动力平衡方程为:
ms(¨Xr+¨Xg)+c˙Xr+kXr=0 (1) 式中:
¨Xr ,˙Xr 和Xr分别为上部结构相对加速度、速度和位移;¨Xg 为地面运动加速度;ms为上部质点质量;c和k分别为上部结构粘滞阻尼系数和水平刚度。当上部及基础质点的总惯性力等于或大于摩擦力后,模型进入滑动阶段,此时整体模型及上部质点的动力平衡方程为:
ms(¨Xr+¨Xs+¨Xg)+mb(¨Xs+¨Xg)=(ms+mb)μg (2) ms(¨Xr+¨Xs+¨Xg)+c˙Xr+kXr=0 (3) 式中:mb为基础质点质量;
¨Xs 为滑动加速度;μ为滑移面摩擦系数;g为重力加速度。当地震动峰值加速度较小时,结构在整个地震时程中均未滑动,均处于固定支座阶段,此时结构的状态为持续固定状态;当峰值加速度足够大时,地震时程中结构交替进入固定和滑动阶段,此时结构的状态为断续滑动状态。两种状态的临界地震动峰值加速度即为起滑加速度。达到起滑状态时,结构上部与基础质点惯性力之和的峰值时程响应等于滑移面摩擦力,且此时结构滑动加速度近似为0,即:
max (4) 将式(4)两端除以ms+mb可得:
\max | {\alpha ( {{{\ddot X}_{\rm{r}}} + {{\ddot X}_{\rm{g}}}} ) + ( {1 - \alpha } ){{\ddot X}_{\rm{g}}}} | = \max | {\alpha {{\ddot X}_{\rm{r}}} + {{\ddot X}_{\rm{g}}}} |{\rm{ = }}\mu {{g}} (5) 式(5)中:α=ms/(ms+mb)为质量比;α(
{{{\ddot X}_{\rm{r}}}} +{{{\ddot X}_{\rm{g}}}} )为起滑时上部质点加速度响应对总起滑加速度的贡献;(1−α){{{\ddot X}_{\rm{g}}}} 为基础质点加速度响应的贡献。以隔震结构响应能否满足式(5)为判别依据,对所输入地震动加速度时程等比例缩放,通过二分法可求出给定参数隔震结构的起滑加速度
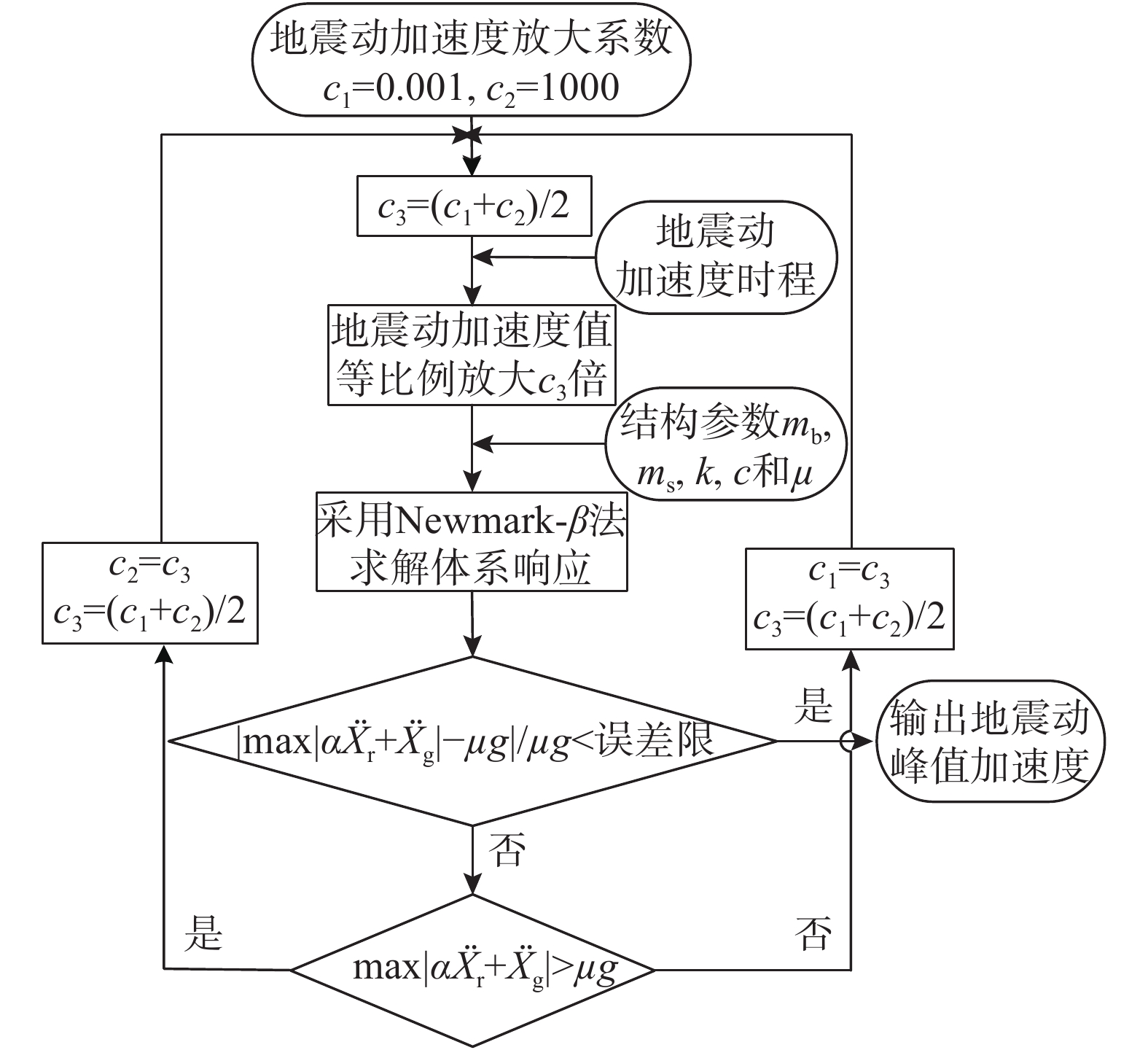
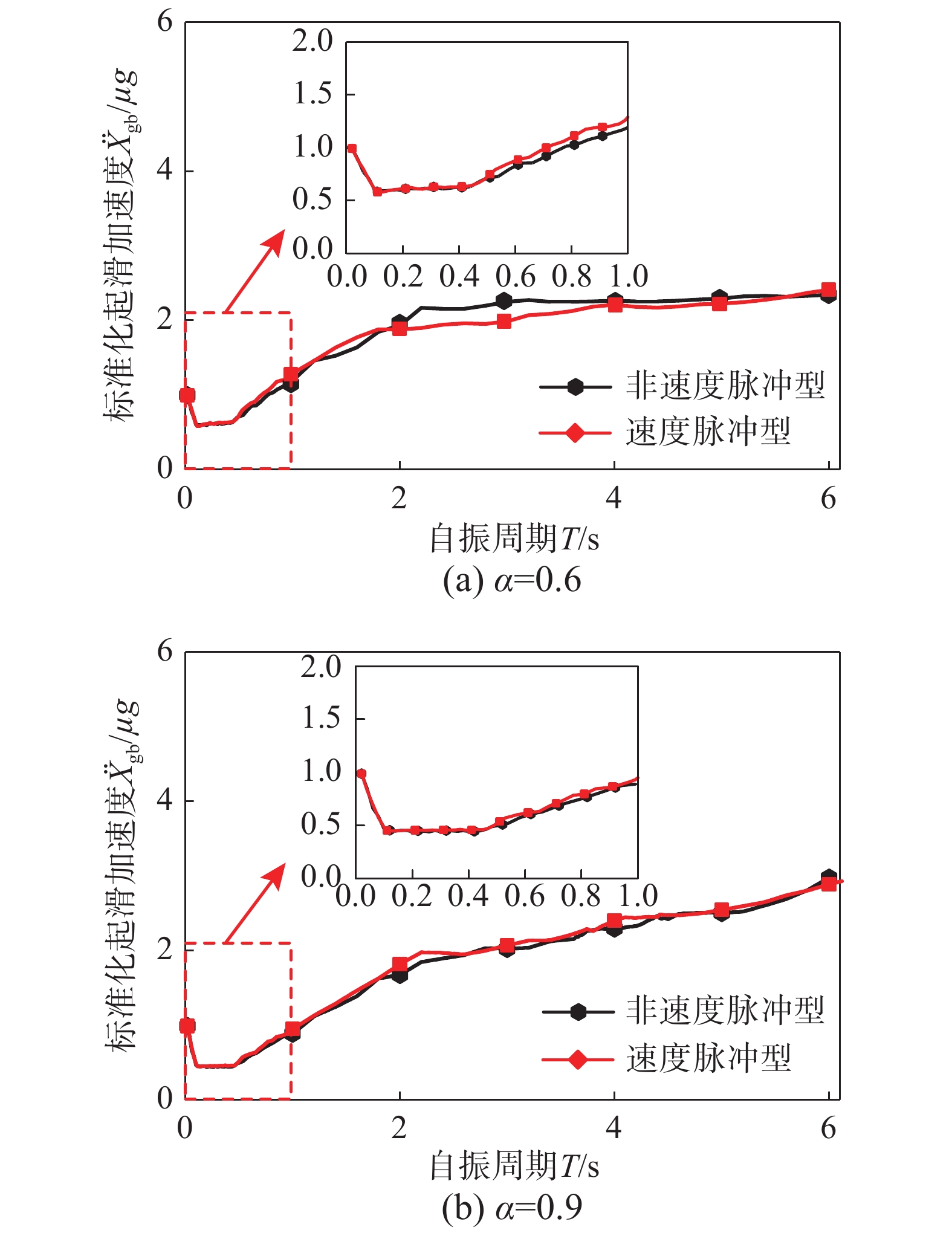
{{{\ddot X}_{{\rm{gb}}}}} 。具体流程如图2所示,根据图式流程在MATLAB软件中编制相应程序。2 地震记录选取与模型参数
采用Pant等[24]建议的方法选取共6组,每组20条匹配于中国抗震规范[25]中设计反应谱的地震记录。地震记录参数包括地震记录类型及目标反应谱特征周期,地震记录包括近断层脉冲型和非脉冲型记录,通过Baker[26]提出的方法区分。规范中影响特征周期的参数主要为设计地震分组和场地类别。本文所选取目标设计反应谱的场地类别为第Ⅰ类、第Ⅱ类和第Ⅲ类,设计地震分组为第一组、第二组和第三组。各组地震记录集的地震记录类型、目标反应谱地震分组、场地类别及特征周期列于表1。
表 1 所选地震记录参数Table 1. Parameters of the selected ground motions地震记录集编号 地震记录类型 地震分组 场地类型 特征周期/s 1 非脉冲型 第一组 Ⅱ类 0.35 2 非脉冲型 第二组 Ⅱ类 0.40 3 非脉冲型 第三组 Ⅱ类 0.45 4 非脉冲型 第三组 Ⅰ类 0.35 5 非脉冲型 第三组 Ⅲ类 0.65 6 脉冲型 第三组 Ⅱ类 0.45 地震记录选取分两步:
1) 从太平洋地震中心(PEER)强震数据库中选取6组地震记录。采用30 m覆盖层平均剪切波速Vs30作为判别场地类别的指标,基于吕红山等[27]的研究,第Ⅰ类、第Ⅱ类和第Ⅲ类场地地震记录Vs30的取值范围分别取>510 m/s、260 m/s~510 m/s和150 m/s~260 m/s。采用震级和震中距(观测点到震中的水平距离)作为判别设计地震分组的指标,Ⅱ类场地第一组、第二组和第三组地震记录震级及震中距的取值范围根据高孟潭[28]提出的衰减关系模型确定,其表达式为:
\lg {v_{\rm{E}}} = A + BM + C\lg ( {R + D{{\rm{e}}^{EM}}} ) (6) {v_{\rm{E}}} = {{{{{T}}_{\rm{g}}}{\alpha _{\rm{E}}}} / {2{\rm{\pi }}}}\qquad\qquad\qquad\qquad\; (7) 式中:vE为峰值速度;R和M分别为震中距和震级;A、B、C、D和E为回归系数,本文选用东部强震区长轴对应的系数;αE为峰值加速度,本文取目标设计反应谱对应的设计基本加速度0.15 g;Tg为反应谱特征周期。所选地震记录震级均在4级~7级,震中距在0 km~200 km,以满足衰减关系模型的适用范围。
2) 采用Hancock等[29]提出的方法对第一步中所选取地震记录进行调整以生成匹配于目标反应谱的地震记录。该方法的原理是通过在时域内对地震波加速度时程叠加小波来生成兼容于反应谱的地震波。所生成6组地震波集平均加速度反应谱与目标设计反应谱的对比如图3所示。
模型参数主要包括动摩擦系数μ、质量比α和上部结构自振周期T。前期摩擦滑移隔震体系的相关试验研究中[13-17],滑移界面动摩擦系数的取值在0.07~0.41,基于此动摩擦系数取0.05、0.15、0.25、0.35和0.45。质量比取0.6、0.7、0.8和0.9。上部结构自振周期取0.02 s~6 s内的112个周期。上部结构阻尼比取常用的0.05。
3 参数分析
3.1 上部结构自振周期的影响
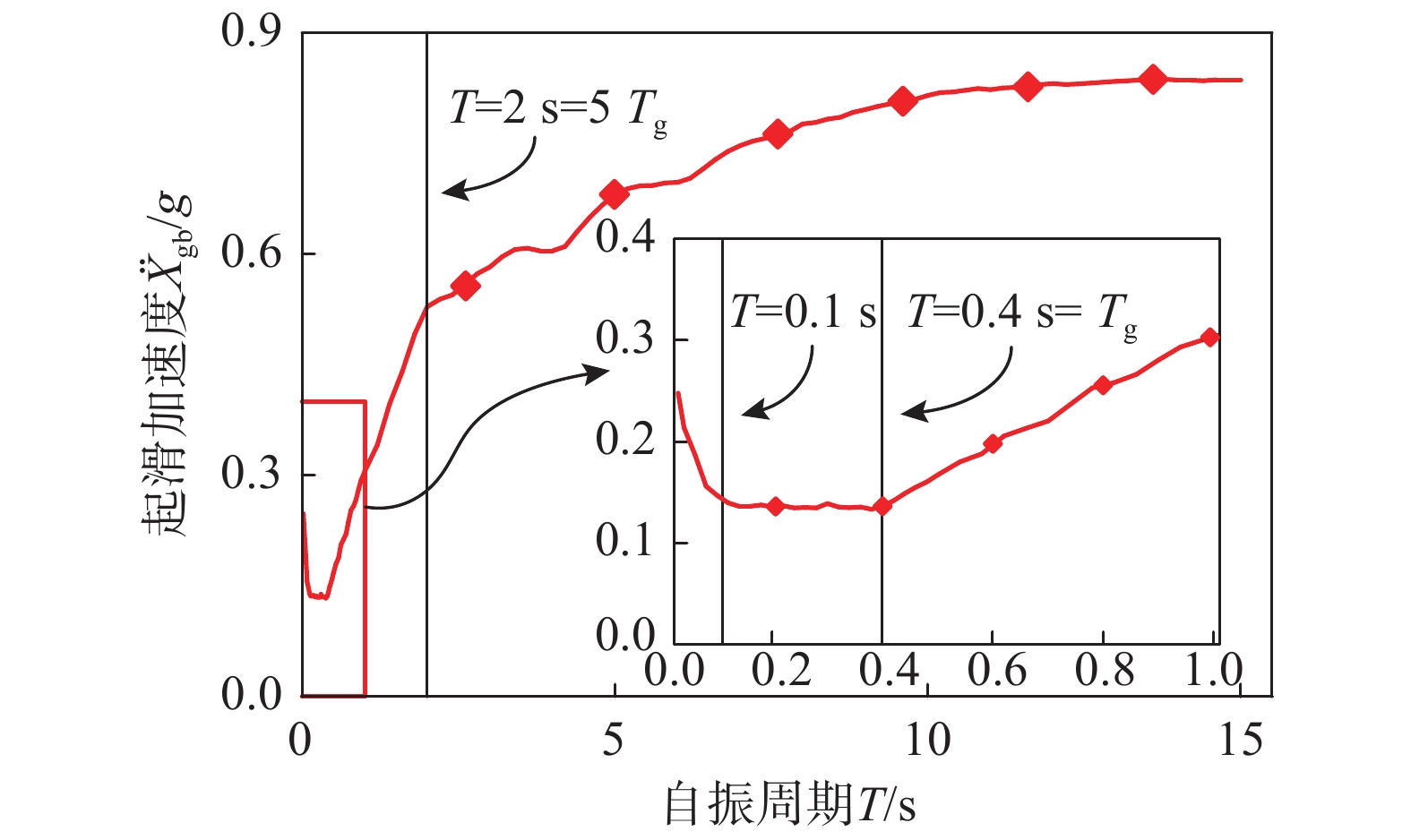
结构平均起滑加速度与自振周期典型的关系曲线如图4所示。由图可知,曲线可分为4段,各段的自振周期取值范围分别为:T=0 s~0.1 s、T=0.1 s~Tg、T=Tg~5Tg和T>5Tg。前三段分别对应于相应固定支座结构加速度设计反应谱的上升段、加速度敏感段和速度敏感段。随自振周期的增大,起滑加速度在曲线第一段内近似呈线性降低,第二段基本保持不变,第三段增大,第四段中先增大而后基本保持不变。前三段中起滑加速度值与相应固定支座结构反应谱值成反比。这是因为上部质点加速度峰值响应值越大,结构越易起滑。第四段中当自振周期较小时,起滑加速度同样与反应谱值成反比,但当自振周期足够大时,由于上部结构惯性力响应较小,起滑力主要由基础质点惯性力响应贡献,起滑加速度值与反应谱值无明显相关性,其值基本保持不变。
3.2 摩擦系数的影响
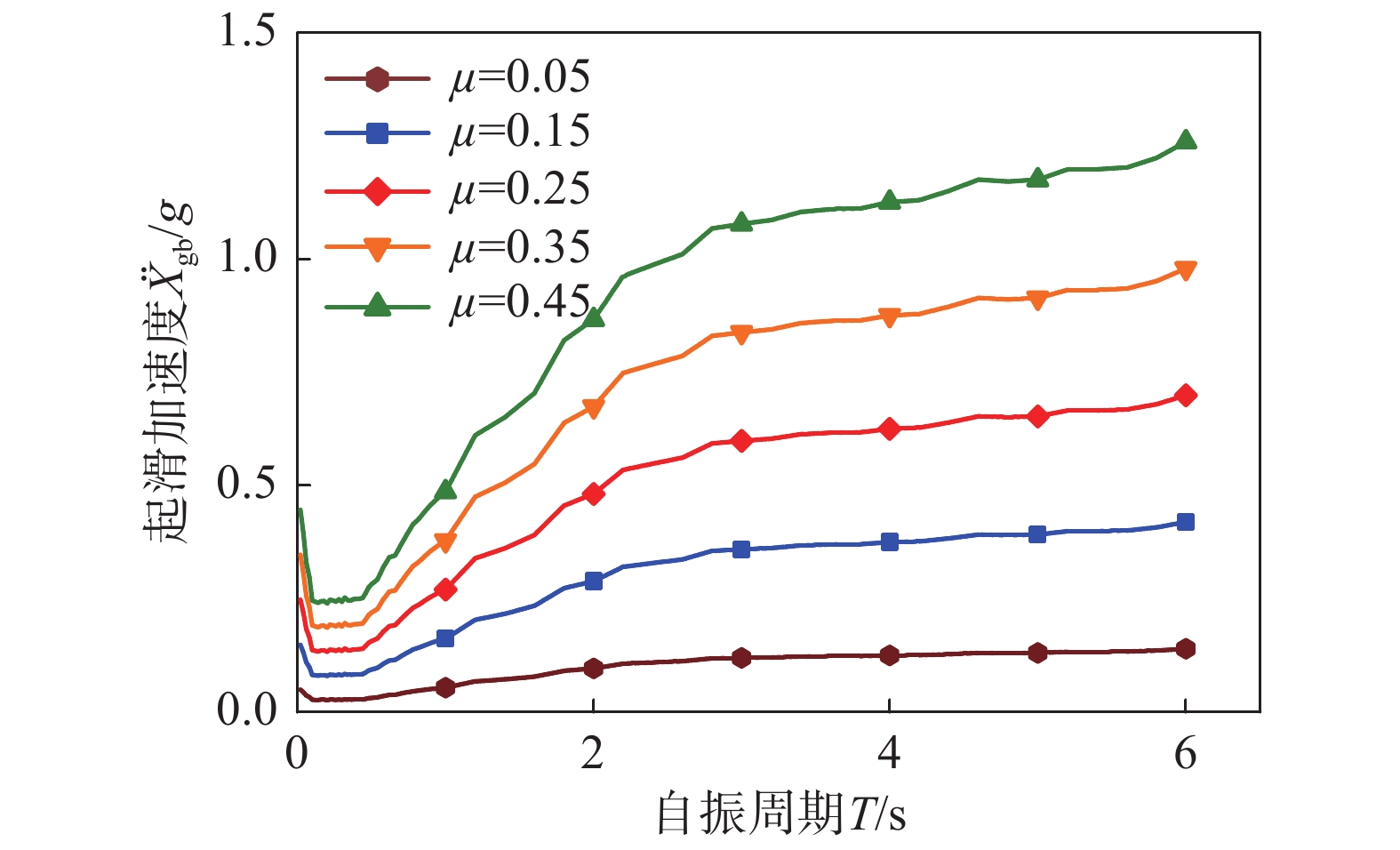
图5为在地震分组为第三组,场地类型为Ⅱ类(Tg=0.45 s)的非脉冲型地震动集激励下,4种摩擦系数隔震结构(α=0.7)平均起滑加速度−自振周期曲线的对比图。由图可知,随摩擦系数增大,起滑加速度明显增大,且两者为等比例增大。摩擦系数分别为0.05、0.15、0.25、0.35和0.45的结构,起滑加速度的比值为1∶3∶5∶7∶9。其原因是结构起滑时,结构峰值总惯性力响应(max|ms(
{{{\ddot X}_{\rm{g}}}} +{{{\ddot X}_{\rm{r}}}} )+mb{{{\ddot X}_{\rm{g}}}} |)与地面运动峰值加速度之比为常数。摩擦系数对其余参数结构起滑加速度的影响有相同规律,限于篇幅,未予给出。基于该等比例关系,为简化分析,后文中以摩擦系数和重力加速度的乘积(μg)为基准,对起滑加速度进行标准化处理。3.3 质量比的影响
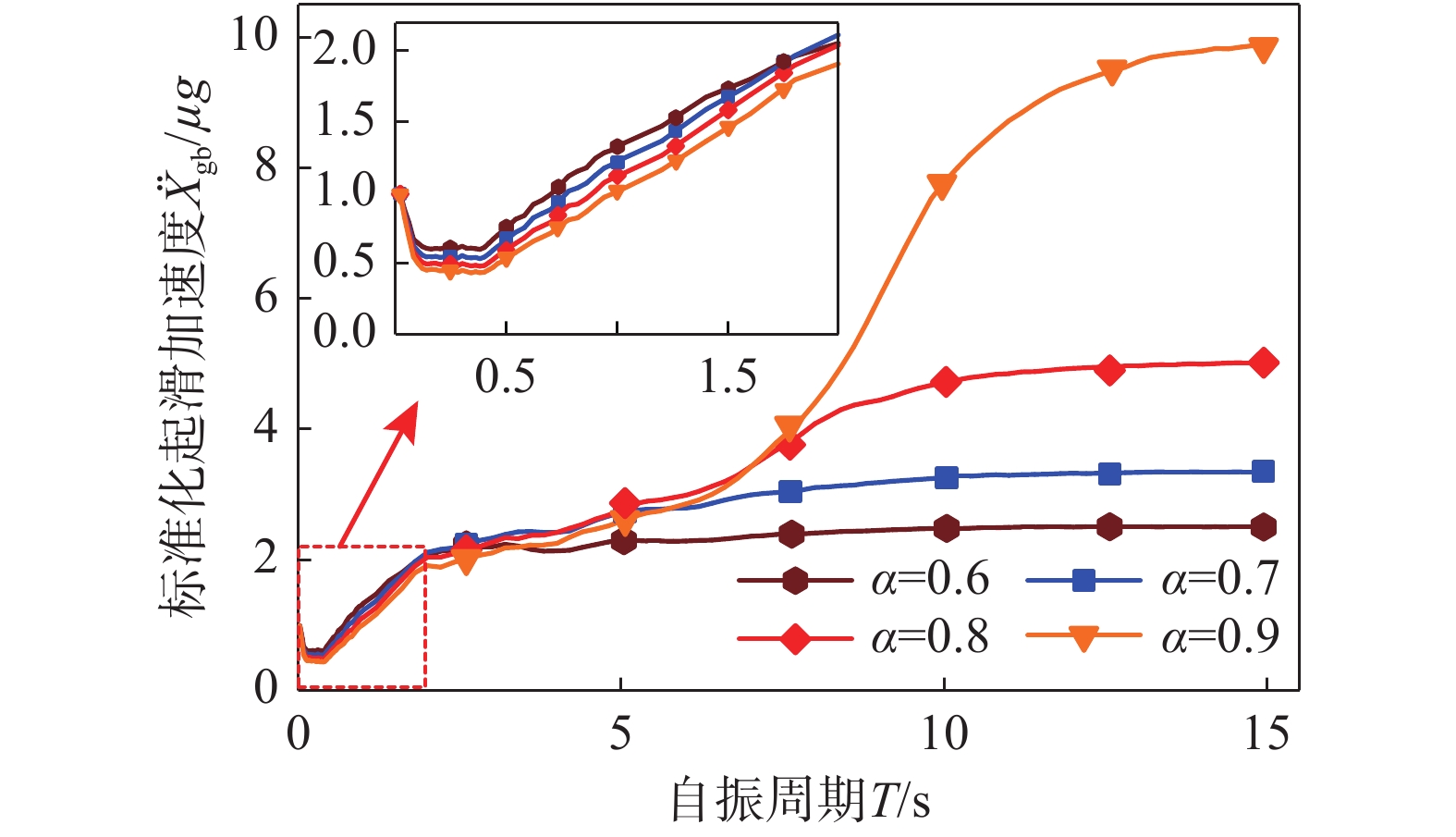
图6为在地震分组为第二组,场地类型为Ⅱ类(Tg=0.4 s)的非脉冲型地震动集激励下,4种质量比结构的平均标准化起滑加速度(
{{{\ddot X}_{{\rm{gb}}}}} /μg)−自振周期曲线对比图。由图6可知:① 当T趋近于0时,
{{{\ddot X}_{{\rm{gb}}}}} /μg趋近于1,其原因是此时上部质点近似于刚体,其相对加速度响应趋近于0,由式(4)可知,结构起滑时的地面运动峰值加速度趋近于μg;② 结构自振周期小于1.8 s时(其余地震动集激励下在1.4 s~2.3 s),起滑加速度随质量比的增大而减小。大于1.8 s后,随自振周期的增加,质量比较小结构的起滑加速度逐步小于质量比较大的同自振周期结构,自振周期分别为3.4 s、5.8 s和7 s后,质量比为0.6、0.7和0.8结构的起滑加速度小于质量比大于其的结构,当自振周期大于7 s时(其余地震动集激励下在6.5 s~7.8 s),起滑加速度随质量比的增加而增大,其原因是随自振周期增加,结构起滑时总惯性力从由上部质点惯性力控制逐渐发展为由基础质点惯性力控制,如图7所示,而上部和基础质点的惯性力分别与质量比成正比和反比;③ 当自振周期足够大时,结构起滑加速度基本由基础质点贡献,即式(5)中α({{{\ddot X}_{\rm{r}}}} +{{{\ddot X}_{\rm{g}}}} )趋于0,故此时{{{\ddot X}_{{\rm{gb}}}}} /μg趋近于max|{{{\ddot X}_{\rm{g}}}} |/max|(1−α){{{\ddot X}_{\rm{g}}}} |=1/(1−α),图中质量比为0.6、0.7、0.8和0.9的结构自振周期足够大时,其{{{\ddot X}_{{\rm{gb}}}}} /μg值分别趋近于2.50、3.33、5和10。其余参数地震动集激励下,质量比的影响规律与此相近。3.4 特征周期的影响
图8为具有不同特征周期反应谱的地震动集激励下,结构(α=0.6和0.9)平均标准化起滑加速度−自振周期曲线对比图。由于规范中设计反应谱自振周期最大值为6 s,故仅对此范围内结构的起滑加速度进行对比。图8(a)和图8(b)中地震动特征周期由地震分组控制,图8(c)和图8(d)中由场地类型控制。由图8可知:① 当T=0.02 s~Tg时,特征周期对其起滑加速度影响较小,三种地震分组及三种场地类型地震动集激励下,各自振周期结构
{{{\ddot X}_{{\rm{gb}}}}} /μg最大差值(同一周期结构在两两地震动集激励下差值的最大值)的平均值为3.1%、7.5%(α=0.6)和3.5%、9.1%(α=0.9),起滑加速度在不同场地类型地震动激励下差值相对较大是由于所选地震动集平均反应谱平台段值与平均地震动峰值加速度之比差值较大(一类、二类和三类场地的比值分别为2.5、2.46和2.22);② 当T=Tg~5Tg,特征周期越大,起滑加速度越小,与特征周期对反应谱的影响相反;③ 当T=5Tg~6 s,反应谱特征周期对起滑加速度影响较小,三种地震分组及三种场地类型地震动集激励下,各自振周期结构{{{\ddot X}_{{\rm{gb}}}}} /μg最大差值的平均值为7.6%、8.5%(α=0.6)和3.9%、2.3%(α=0.9)。质量比为0.6结构的差值相对较大是因为自振周期在此范围内时,结构起滑时上部及基础质点惯性力均未明显起控制作用。地震动时程范围内,总惯性力达到最大值时所对应时间可能与上部或基础质点独自受迫振动时峰值惯性力所对应时间均不同,故起滑加速度可能受地震动加速度时程特性影响。特征周期对质量比为0.7和0.8结构起滑加速度的影响规律与此基本相同。3.5 近断层脉冲的影响
图9为场地类型为Ⅱ类,地震分组为第三组的近断层脉冲和非脉冲型地震动集激励下,隔震结构(α=0.6,0.9)平均标准化起滑加速度−自振周期曲线对比图。由图可知:两种类型地震动集激励下,当结构自振周期在曲线前三段内(T=0.02 s~2.25 s)时,各自振周期结构
{{{\ddot X}_{{\rm{gb}}}}} /μg的平均差值为4.6%(α=0.6)和3.7%(α=0.9);当自振周期在反应谱位移敏感段内(T=2.25 s~6 s)时,受地震加速度时程特性不同的影响,{{{\ddot X}_{{\rm{gb}}}}} /μg的最大差值达到11.7%(α=0.6,T=3 s),但各自振周期隔震结构{{{\ddot X}_{{\rm{gb}}}}} /μg的平均差值较小,为5.2%(α=0.6)和2.1%(α=0.9)。表明当相应固定支座结构反应谱相同时,地震动近断层脉冲对起滑加速度影响较小。脉冲对质量比为0.7和0.8结构起滑加速度的影响规律与此基本相同。4 起滑加速度计算公式建立
基于计算所得平均标准化起滑加速度−自振周期曲线,采用分段拟合方法建立了不同参数曲线的计算公式,如下:
\frac{{{{\ddot X}_{{\rm{gb}}}}( T )}}{{\mu {{g}}}}{\rm{ = }}\left\{ \begin{aligned} & 1 - \frac{T}{{0.1}}\left( {1 - \frac{{{{\ddot X}_{{\rm{gb}}}}( {0.1} )}}{{\mu {{g}}}}} \right),\;\;\;\;\;\; T < 0.1 \;{\rm{s}}\\& {\rm{0}}{\rm{.17}}{\alpha ^2} + ( {O - {\rm{1}}{\rm{.17}}} )\alpha + 1 ,\;\;0.1 \;{\rm{s}} \leqslant T \leqslant {{T}}{}_{\rm{g}}\\& \frac{{{{\ddot X}_{{\rm{gb}}}}( {{{T}}{}_{\rm{g}}} )}}{{\mu {{g}}}}[ {{{( {{T / {{{T}}{}_{\rm{g}}}}} )}^\beta } + } \\&\qquad {\alpha ( {\alpha - 1} ){{( {T - {{T}}{}_{\rm{g}}} )}^Q}} ], \;\;\;\;{{T}}{}_{\rm{g}} < T \leqslant 5{{T}}{}_{\rm{g}} \\& \frac{{{{\ddot X}_{{\rm{gb}}}}( {{{5T}}{}_{\rm{g}}} )}}{{\mu {{g}}}} - R +R{{\rm{e}}^{[ {\alpha S( {T - 5{{{T}}_{\rm{g}}}} )} ]}} + \\&\qquad U(T - 5{{{T}}_{\rm{g}}}),\qquad\;\;\;\;\;\;\;\;5{{T}}{}_{\rm{g}} < T \leqslant 6 \;{\rm{s}} \end{aligned}\right. (8) 式中:O为地震动峰值加速度与固定支座结构加速度反应谱平台段值之比;β=0.9αP;P和Q为与特征周期和质量比有关的回归系数;R、S和U为与质量比有关的回归系数,由于α为0.8和0.9的曲线曲率随自振周期增大变化较大,故当Tg=0.65 s曲线的R、S和U取值与其余曲线一致时,其拟合公式与时程分析计算得曲线差值较大,为确保拟合公式准确性,该曲线的回归系数R、S和U独立取值。各回归系数取值列于表2。对于质量比未列于表中的结构,回归系数值可按线性插值的方法确定。对于T≤5Tg的结构,公式求得标准化起滑加速度值能满足:当α趋近于0时,结构趋近于刚体,标准化起滑加速度值趋近于1;当α趋近于1时,结构趋近于单自由度体系,标准化起滑加速度值趋近于地震动峰值加速度与相应固定支座结构加速度反应谱值之比。采用式(8)求得
{{{\ddot X}_{{\rm{gb}}}}} /μg-T曲线与动力时程分析求得曲线对比如图10所示。由图10可知,拟合公式与动力时程分析计算值吻合良好。表 2{{{\ddot X}_{{\rm{gb}}}}} /μg−T曲线拟合公式回归系数取值Table 2. Regression coefficient values of fitting formula for{{{\ddot X}_{{\rm{gb}}}}} /μg−T curves特征周期/s 质量比 P Q R S U 0.35 0.6 0.044 3.624 −0.089 0.586 0.170 0.7 −0.024 2.482 0.051 −0.070 0.205 0.8 −0.085 1.740 0.272 −1.078 0.303 0.9 −0.163 0.474 30.400 0.049 −1.235 0.40 0.6 0.071 2.223 −0.089 0.586 0.170 0.7 −0.012 1.460 0.051 −0.070 0.205 0.8 −0.083 0.755 0.272 −1.078 0.303 0.9 −0.183 0.177 30.400 0.049 −1.235 0.45 0.6 −0.049 2.583 −0.089 0.586 0.170 0.7 −0.150 2.227 0.051 −0.070 0.205 0.8 −0.257 1.924 0.272 −1.078 0.303 0.9 −0.444 1.603 30.400 0.049 −1.235 0.65 0.6 0.403 0.298 −0.089 0.586 0.170 0.7 0.253 0.404 0.051 −0.070 0.205 0.8 0.211 0.708 0.039 0.806 0.236 0.9 0.271 1.152 0.001 1.599 0.273 隔震结构设计时,可根据所提出公式求解结构在多遇地震和设计地震作用下的起滑摩擦系数,进而确定满足“小震不滑,中震起滑”设计原则的摩擦系数取值范围,以指导隔震层材料的选用。
5 算例验证
为验证拟合公式估算多自由度结构起滑加速度的准确性,以某上部结构为3层和9层的滑移隔震结构为算例进行分析。所取结构的层质量及层刚度沿高度方向均匀分布,且基础质量与层质量相等,即mb=ms1=ms2=···msn,k1=k2=···kn(n为楼层数)。层刚度均取7500 kN/mm。3层和9层结构层质量分别取1.5 t和1.86 t,以使其上部结构第一振型自振周期分别等于0.2 s和0.6 s。各阶振型的阻尼比均取0.05。采用拟合公式计算起滑加速度时,将多自由度体系等效为两自由度体系,等效体系上部结构自振周期取相应固定支座多自由度结构第一振型自振周期。质量比取相应固定支座多自由度结构第一振型参与质量与隔震结构总质量之比:
{\alpha _{{\rm{eq}}}} = \frac{{{\varGamma _1^2}{m_{{\rm{sm1}}}}}}{{\displaystyle\sum\limits_{i = 1}^{{n}} {{m_{{{{\rm{s}}i}}}} + {m_{\rm{b}}}} }} (9) 式中,Γ1和msm1分别为相应固定支座多自由度结构第一振型参与系数和第一振型主质量。根据式(9)求得3层和9层算例的等效质量比分别为0.6856和0.7665。
6组所选地震动集激励下,采用时程分析及式(8)求解出的算例平均标准化起滑加速度值列于表3。由表可知,两者差值在5%之内,表明所提出公式较合理。
表 3 公式与时程分析结果对比Table 3. Comparation between the results obtained using fitting formula and time history analyses地震动类型 非脉冲 脉冲 场地类型
地震分组Ⅱ类
一组Ⅱ类
二组Ⅱ类
三组Ⅰ类
三组Ⅲ类
三组Ⅱ类
三组{{{\ddot X}_{{\rm{gbe}}}}}/μg 3层 0.555 0.556 0.556 0.552 0.587 0.565 9层 0.828 0.709 0.673 0.823 0.587 0.686 {{{\ddot X}_{{\rm{gbt}}}}}/μg 3层 0.537 0.552 0.541 0.541 0.600 0.563 9层 0.812 0.712 0.681 0.820 0.569 0.707 Δ 3层 0.033 0.007 0.028 0.020 0.023 0.004 9层 0.020 0.004 0.011 0.004 0.030 0.030 注:{{{\ddot X}_{{\rm{gbe}}}}}/μg和{{{\ddot X}_{{\rm{gbt}}}}}/μg分别为拟合公式和时程分析计算所得标准化起滑加速度值,Δ=|{{{\ddot X}_{{\rm{gbe}}}}}/μg-{{{\ddot X}_{{\rm{gbt}}}}}/μg|/({{{\ddot X}_{{\rm{gbe}}}}}/μg)。 隔震结构设计时,若所设计隔震结构的动力特性与本文3层算例相近,且所在地区的设计基本地震加速度为0.15 g,场地类型为Ⅱ类(设计地震分组为第二组)。由式(8)算得多遇和基本烈度地震作用下结构起滑时的摩擦系数分别为0.096和0.270,则所设计房屋隔震层材料的摩擦系数选择范围在0.096~0.270。
6 结论
本文以滑移隔震结构为对象,研究了结构参数和地震波参数对其起滑加速度的影响规律,并建立了起滑加速度计算公式。所考虑参数范围内,研究结果如下:
(1) 滑移隔震结构起滑加速度-上部结构自振周期曲线由下降段、水平平稳段、上升段和先上升后水平平稳段四部分组成。前三段曲线分别对应于相应固定支座结构加速度设计反应谱的上升段、加速度敏感段和速度敏感段。自振周期趋近于0时,标准化起滑加速度(
{{{\ddot X}_{{\rm{gb}}}}} /μg)趋近于1。自振周期足够大时,{{{\ddot X}_{{\rm{gb}}}}} /μg趋近于1/(1−α)。(2) 当自振周期小于1.4 s时,相同自振周期结构的起滑加速度随质量比的减小而增大。自振周期大于7.8 s时,相同自振周期结构的起滑加速度随质量比的减小而减小。起滑加速度随摩擦系数的增加而等比例增加。
(3) 结构自振周期在设计反应谱速度敏感段内时,起滑加速度随反应谱特征周期增大而减小,特征周期对其余自振周期结构起滑加速度影响较小。当相应固定支座结构加速度反应谱较接近时,结构在脉冲型和非脉冲型地震动集激励下的起滑加速度相差较小。
(4) 基于参数分析结果,采用分段拟合的方法建立了起滑加速度计算公式。公式计算结果与多自由度结构算例时程分析计算结果吻合良好。公式可为滑移隔震结构的隔震层摩擦系数取值提供参考。
-
表 1 所选地震记录参数
Table 1 Parameters of the selected ground motions
地震记录集编号 地震记录类型 地震分组 场地类型 特征周期/s 1 非脉冲型 第一组 Ⅱ类 0.35 2 非脉冲型 第二组 Ⅱ类 0.40 3 非脉冲型 第三组 Ⅱ类 0.45 4 非脉冲型 第三组 Ⅰ类 0.35 5 非脉冲型 第三组 Ⅲ类 0.65 6 脉冲型 第三组 Ⅱ类 0.45 表 2
{{{\ddot X}_{{\rm{gb}}}}} /μg−T曲线拟合公式回归系数取值Table 2 Regression coefficient values of fitting formula for
{{{\ddot X}_{{\rm{gb}}}}} /μg−T curves特征周期/s 质量比 P Q R S U 0.35 0.6 0.044 3.624 −0.089 0.586 0.170 0.7 −0.024 2.482 0.051 −0.070 0.205 0.8 −0.085 1.740 0.272 −1.078 0.303 0.9 −0.163 0.474 30.400 0.049 −1.235 0.40 0.6 0.071 2.223 −0.089 0.586 0.170 0.7 −0.012 1.460 0.051 −0.070 0.205 0.8 −0.083 0.755 0.272 −1.078 0.303 0.9 −0.183 0.177 30.400 0.049 −1.235 0.45 0.6 −0.049 2.583 −0.089 0.586 0.170 0.7 −0.150 2.227 0.051 −0.070 0.205 0.8 −0.257 1.924 0.272 −1.078 0.303 0.9 −0.444 1.603 30.400 0.049 −1.235 0.65 0.6 0.403 0.298 −0.089 0.586 0.170 0.7 0.253 0.404 0.051 −0.070 0.205 0.8 0.211 0.708 0.039 0.806 0.236 0.9 0.271 1.152 0.001 1.599 0.273 表 3 公式与时程分析结果对比
Table 3 Comparation between the results obtained using fitting formula and time history analyses
地震动类型 非脉冲 脉冲 场地类型
地震分组Ⅱ类
一组Ⅱ类
二组Ⅱ类
三组Ⅰ类
三组Ⅲ类
三组Ⅱ类
三组{{{\ddot X}_{{\rm{gbe}}}}}/μg 3层 0.555 0.556 0.556 0.552 0.587 0.565 9层 0.828 0.709 0.673 0.823 0.587 0.686 {{{\ddot X}_{{\rm{gbt}}}}}/μg 3层 0.537 0.552 0.541 0.541 0.600 0.563 9层 0.812 0.712 0.681 0.820 0.569 0.707 Δ 3层 0.033 0.007 0.028 0.020 0.023 0.004 9层 0.020 0.004 0.011 0.004 0.030 0.030 注:{{{\ddot X}_{{\rm{gbe}}}}}/μg和{{{\ddot X}_{{\rm{gbt}}}}}/μg分别为拟合公式和时程分析计算所得标准化起滑加速度值,Δ=|{{{\ddot X}_{{\rm{gbe}}}}}/μg-{{{\ddot X}_{{\rm{gbt}}}}}/μg|/({{{\ddot X}_{{\rm{gbe}}}}}/μg)。 -
[1] Li L. Base isolation measure for aseismic buildings in China [C]// Proceedings of the 8th World Conference on Earthquake Engineering. California, America, 1984: 791 − 798.
[2] Mostaghel N, Khodaverdian M. Dynamics of resilient-friction base isolator (R-FBI) [J]. Earthquake Engineering and Structural Dynamics, 1987, 15(3): 379 − 390. doi: 10.1002/eqe.4290150307
[3] Zayas V A, Low S S, Mahin S A. A simple pendulum technique for achieving seismic isolation [J]. Earthquake Spectra, 1990, 6(2): 317 − 333. doi: 10.1193/1.1585573
[4] 曹胜涛, 李志山, 刘博. 基于显式摩擦摆单元的大规模复杂连体结构非线性时程分析[J]. 工程力学, 2019, 36(6): 128 − 137. doi: 10.6052/j.issn.1000-4750.2018.05.0259 Cao Shengtao, Li Zhishan, Liu Bo. Nonlinear time history analysis of a large-scale complex connected structure base on an explicit friction pendulum element [J]. Engineering Mechanics, 2019, 36(6): 128 − 137. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.0259
[5] 杜修力, 许紫刚, 许成顺, 等. 摩擦摆支座在地下地铁车站结构中的减震效果研究[J]. 工程力学, 2019, 36(9): 60 − 67, 88. doi: 10.6052/j.issn.1000-4750.2018.04.0225 Du Xiuli, Xu Zigang, Xu Chengshun, et al. Seismic mitigation effect analysis on friction pendulum bearing applied in the underground subway station [J]. Engineering Mechanics, 2019, 36(9): 60 − 67, 88. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.04.0225
[6] Yang T, Marafi N A, Calvi P M, et al. Accounting for spectral shape in a simplified method of analyzing friction pendulum systems [J]. Engineering Structures, 2020, 222: 111002. doi: 10.1016/j.engstruct.2020.111002
[7] Robinson W H, Tucker A G. A lead-rubber shear damper [J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1977, 10(3): 151 − 153. doi: 10.5459/bnzsee.10.3.151-153
[8] 叶昆, 张子翔, 朱宏平. 近场地震竖向分量对LRB基础隔震结构地震响应影响分析[J]. 工程力学, 2016, 33(4): 49 − 57. doi: 10.6052/j.issn.1000-4750.2014.04.0315 Ye Kun, Zhang Zixiang, Zhu Hongping. Influence of near-field vertical ground motions on the seismic response of LRB base-isolated structures [J]. Engineering Mechanics, 2016, 33(4): 49 − 57. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.04.0315
[9] Wang S J, Lin W C, Chiang Y S, et al. Mechanical behavior of lead rubber bearings under and after nonproportional plane loading [J]. Earthquake Engineering and Structural Dynamics, 2019, 48(13): 1508 − 1531. doi: 10.1002/eqe.3211
[10] Ren X X, Lu W S, Zhu Y H, et al. Compressive behavior of low shape factor lead-rubber bearings: Full-scale testing and numerical modeling [J]. Engineering Structures, 2020, 209: 110030. doi: 10.1016/j.engstruct.2019.110030
[11] Dall'Asta A, Ragni L. Experimental tests and analytical model of high damping rubber dissipating devices [J]. Engineering Structures, 2006, 28(13): 1874 − 1884. doi: 10.1016/j.engstruct.2006.03.025
[12] Murota N, Suzuki S, Mori T, et al. Performance of high-damping rubber bearings for seismic isolation of residential buildings in Turkey [J]. Soil Dynamic and Earthquake Engineering, 2021, 143: 106620. doi: 10.1016/j.soildyn.2021.106620
[13] 楼永林, 王敏权, 苏志奇. 多层砖房底部滑移减震研究[J]. 建筑结构学报, 1994, 15(1): 24 − 31. Lou Yonglin, Wang Minquan, Su Zhiqi. Study on sliding shock absorption joint layer at bottom part of multistory brick masonry structure [J]. Journal of Building Structures, 1994, 15(1): 24 − 31. (in Chinese)
[14] Qamaruddin M, Rasheeduzzafar, Arya A S, et al. Seismic response of masonry buildings with sliding substructure [J]. Journal of Structural Engineering, 1986, 112(9): 2001 − 2011. doi: 10.1061/(ASCE)0733-9445(1986)112:9(2001)
[15] Nanda R P, Agarwal P, Shrikhande M. Suitable friction sliding materials for base isolation of masonry buildings [J]. Shock and Vibration, 2012, 19(6): 1327 − 1339. doi: 10.1155/2012/106436
[16] Nanda R P, Shrikhande M, Agarwal P. Low-cost base-isolation system for seismic protection of rural buildings [J]. Practice Periodical on Structural Design and Construction, 2016, 21(1): 04015001. doi: 10.1061/(ASCE)SC.1943-5576.0000254
[17] 荣强, 盛严, 程文瀼. 滑移隔震支座的试验研究及力学模型[J]. 工程力学, 2010, 27(12): 40 − 45. Rong Qiang, Sheng Yan, Chen Wenrang. Experimental investigation and mechanical model of sliding isolation bearings [J]. Engineering Mechanics, 2010, 27(12): 40 − 45. (in Chinese)
[18] Mostaghel N, Hejazi M, Tanbakuchi J. Response of sliding structures to harmonic support motion [J]. Earthquake Engineering and Structural Dynamics, 1983, 11(3): 355 − 366. doi: 10.1002/eqe.4290110305
[19] Westermo B, Udwadia F. Periodic response of a sliding oscillator system to harmonic excitation [J]. Earthquake Engineering and Structural Dynamics, 1983, 11(1): 135 − 146. doi: 10.1002/eqe.4290110111
[20] Iura M, Matsui K, Kosaka I. Analytical expressions for three different modes in harmonic motion of sliding structures [J]. Earthquake Engineering and Structural Dynamics, 1992, 21(9): 757 − 769. doi: 10.1002/eqe.4290210902
[21] Hu H S, Nakashima M. Response of two-degree-of-freedom sliding base systems subjected to harmonic ground motions [J]. Journal of Structural Engineering, 2017, 143(2): 04016173. doi: 10.1061/(ASCE)ST.1943-541X.0001653
[22] Mostaghel N, Tanbakuchi J. Response of sliding structures to earthquake support motion [J]. Earthquake Engineering and Structural Dynamics, 1983, 11(6): 729 − 748. doi: 10.1002/eqe.4290110603
[23] 毛利军, 李爱群. 基础滑移隔震体系的地震反应谱[J]. 土木工程学报, 2004, 37(2): 58 − 66. doi: 10.3321/j.issn:1000-131X.2004.02.011 Mao Lijun, Li Aiqun. Earthquake response spectrum of sliding base seismic-isolation system [J]. China Civil Engineering Journal, 2004, 37(2): 58 − 66. (in Chinese) doi: 10.3321/j.issn:1000-131X.2004.02.011
[24] Pant D R, Constantinou M C, Wijeyewickrema A C. Re-evaluation of equivalent lateral force procedure for prediction of displacement demand in seismically isolated structures [J]. Engineering Structure, 2013, 52: 455 − 465. doi: 10.1016/j.engstruct.2013.03.013
[25] GB 50011−2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: China Architecture Industry Press, 2010. (in Chinese)
[26] Baker J W. Quantitative classification of near-fault ground motions using wavelet analysis [J]. Bulletin of the Seismological Society of America, 2007, 97(5): 1486 − 1501. doi: 10.1785/0120060255
[27] 吕红山, 赵凤新. 适用于中国场地分类的地震动反应谱放大系数[J]. 地震学报, 2007, 29(1): 67 − 76. doi: 10.3321/j.issn:0253-3782.2007.01.008 Lü Hongshan, Zhao Fengxin. The earthquake response spectra amplification factor applied to china's site condition [J]. Acta Seismologica Sinica, 2007, 29(1): 67 − 76. (in Chinese) doi: 10.3321/j.issn:0253-3782.2007.01.008
[28] 高孟潭. GB 18306−2015,《中国地震动参数区划图》宣贯教材[M]. 北京: 中国质检出版社, 2015. Gao Mengtan. Publicizing and implementing teaching materials of GB 18306−2015,《Map of seismic parameters in China》[M]. Beijing: China Zhijian Publishing House, 2015. (in Chinese)
[29] Hancock J, Watson-Lamprey J, Abrahamson N A, et al. An improved method of matching response spectra of recorded earthquake ground motion using wavelets [J]. Journal of Earthquake Engineering, 2006, 10(Supp1): 67 − 89.
-
期刊类型引用(0)
其他类型引用(1)




 下载:
下载: