MESOSCALE NUMERICAL STUDY ON THE TUNNELING-INDUCED GROUND RESPONSE IN A SANDY COBBLE STRATUM CONSIDERING THE ROCK ORIENTATION ANGLE
-
摘要: 在实际工程中,椭圆形或亚圆形的卵石以不同角度在地层中层状分布。针对卵石倾角对砂卵石地层施工力学行为的影响,将地层材料视为由卵石和土体基质组成的混合材料,建立砂卵石地层二维细观有限元模型,开展不同卵石倾角下的隧道开挖数值计算。通过围岩应力模拟值和理论值的对比,对细观分析模型的适用性进行了验证。在此基础上,从围岩应力和围岩变形两个角度,对不同倾角下的隧道开挖围岩反应进行了分析。结果表明:当卵石倾角从0°增大至90°时,围岩塑性区的形态和范围均发生变化,且拱腰处的围岩竖向应力不断增大。在给定的计算条件下,地表沉降最大值以每10°相对增幅5.17%的速度线性增加,地表沉降槽宽度系数呈现出先增加后减小的趋势,在卵石倾角为30°时取得最大值;地中沉降最大值和地中沉降槽宽度系数随深度的变化关系均可以采用幂函数形式的公式进行描述。Abstract: In engineering practice, oval or subcircular pebbles are distributed in ground at different orientation angles. It investigates the effect of the rock orientation angle on the ground response during tunneling in sandy cobble stratums, with special attention to the material meso-structure. By treating the ground material as a composite of rock blocks and soil matrix, mesoscale numerical models were established. A series of simulations were carried out to model the tunnel excavation using the mesoscale models. By comparing the ground stress between the simulation results and the theoretical values, the applicability of the mesoscale models was verified. Based on this, the ground response during tunnelling in a sandy cobble stratum is analyzed from the viewpoint of stress distribution and deformation performance. The simulation results show that, with the increase of the orientation angle from 0° to 90°, both the shape and extension of the plastic zone changes, and the vertical stress in the soil mass at the tunnel side increases gradually. Under given conditions, the maximum surface subsidence increases linearly with the increase of the rock orientation angle at a relative rate of 5.17% per 10°. The width coefficient of the surface settlement trough first increases and then decreases. When the rock orientation angle is 30°, the width coefficient of the surface settlement trough reaches the maximum value. The relationship between the maximum subsidence Smax(z) with the depth z can be described by a power function. The relationship between the width coefficient of the subsurface settlement trough i(z) with the depth z can also be described by a power function.
-
砂卵石地层是由具有一定尺寸、强度较高的岩块和强度较低的土体构成的不均匀松散岩土介质,为典型的土石混合体地层[1-3]。由于组成成分的物理力学性质差异很大,砂卵石地层表现出显著的非均质性,其材料力学行为和场地力学行为将显著地受到内部细观结构的影响。
对于单独的卵石颗粒,在三维分析时通常呈椭球形或球形,在二维分析时呈椭圆形或亚圆形。在实际地层中,由于河流的冲洪积作用及沉积作用,椭球形或亚圆形的卵石将在地层中水平分布或与水平面呈一定夹角,呈现出定向性排列的现象。卵石在地层中的沉积方向通常采用卵石长轴倾角来描述,其是指卵石长轴与水平面之间的夹角。王振峰[4]对西安地铁2号线沿线卵石进行了统计,结果表明:卵石含量随长轴倾角增加呈近似指数下降的趋势。基于数值图像技术,马辉等[5]对成都地铁1号线沿线卵石的统计也给出了相同的结论,并得到卵石长轴倾角平均值为32°。牟迪[6]对成都地铁4号线沿线卵石进行了统计,结果表明卵石长轴倾角集中在30°~60°区间。通过对三峡库区的土石混合体进行统计,张抒和唐辉明[7]指出,块石含量与块石长轴倾角间呈现出均匀分布、正态分布、伽马分布三种形式。XU等[8]研究表明:块石数目随倾角的增加呈现出“M”形的变化规律,长轴倾角集中在10°~40°与130°~170°两个区间。
目前,各国学者已在卵石倾角对材料力学行为的影响方面展开深入研究[9-11],而关于卵石倾角对场地力学行为方面的研究鲜有报道。层状岩体隧道施工力学方面的研究表明,当岩层倾角发生变化时,围岩变形的分布特征和破坏模式将发生显著变化[12-15]。因此,基于在层状岩体施工力学方面的认识,考虑砂卵石地层材料的细观结构特征,开展不同卵石倾角下的隧道开挖计算,探讨卵石倾角对围岩应力、围岩变形的影响规律,具有重要的工程意义。
当采用数值方法开展隧道开挖模拟时,目前考虑材料细观结构特征的计算模型主要分为两类:基于非连续介质力学的离散元模型[16-18]和基于连续介质力学的细观有限元模型[1, 2, 19]。离散元模型将砂卵石地层材料视为圆形或球形颗粒集合体,并结合单元体试验结果标定土体颗粒接触参数。该类模型可以再现围岩灾害发生过程,但其计算代价昂贵,计算规模有限。细观有限元模型将砂卵石地层介质视为由土体基质和块石等形成的多相材料,分别赋予各自的材料属性,并将块石的细观结构特征,如块石形状、尺寸、倾角以及空间分布形式等都进行显式地表征[1-2]。该类模型能准确地反应围岩变形发展和应力传递路径的细观机制,特别是大块石对变形模式的影响。
本文从细观角度出发,考虑地层材料的非均质性,建立砂卵石地层细观有限元分析模型,开展不同卵石倾角下的隧道开挖模拟。通过对比围岩应力计算值与理论值,对细观分析模型的适用性进行验证。结合PECK经验公式,验证高斯分布函数在描述砂卵石地层和地中沉降曲线的适用性;在此基础上,分析了沉降最大值和沉降槽宽度系数随卵石倾角的变化规律;提出地层沉降最大值、沉降槽宽度系数沿深度方向变化规律的数学描述公式,并对隧道断面变形模式进行了分析。
1 PECK经验公式
基于隧道工程实践经验和大量监测数据,PECK[20]于1969年提出地表沉降曲线可以采用高斯分布函数进行描述。地表沉降S可表述为:
S(x)=Smax (1) 式中:Smax为地表沉降最大值;i为地表沉降槽宽度系数,其物理含义为沉降曲线反弯点至隧道中心线的水平距离;x为地表任一位置至隧道中心线的水平距离。
PECK经验公式现已成为评价隧道开挖时地表变形规律的基本方法。通过现场监测和离心机模型试验,MAIR等[21]发现地中沉降曲线也可采用高斯分布函数进行描述,并将式(1)拓展至如下形式:
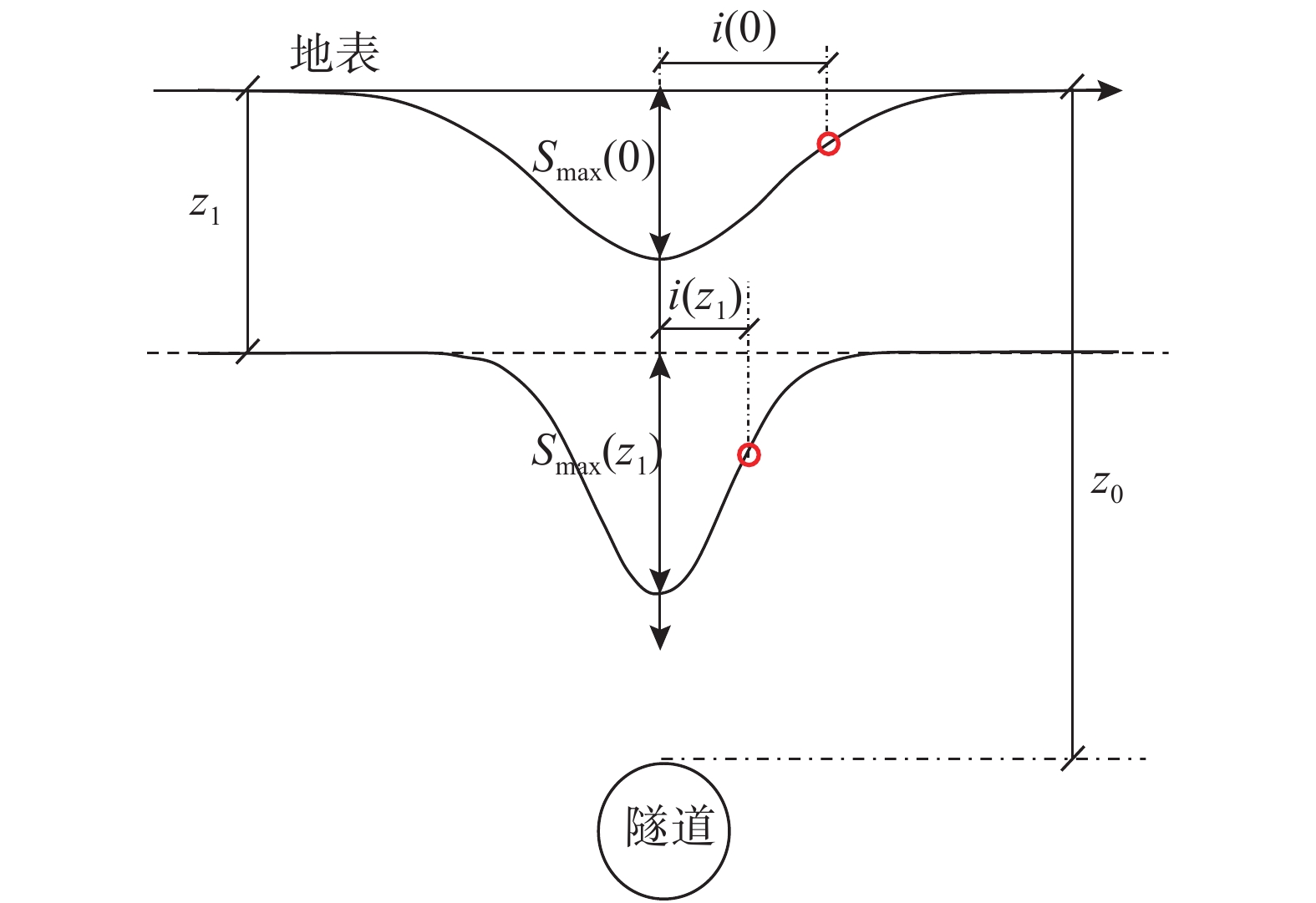
S(x,{\textit{z}}) = {S_{\max }}({\textit{z}})\exp \left[{\rm{ - }}\frac{{{x^2}}}{{2i{{({\textit{z}})}^2}}}\right] (2) 式中:Smax(z)为z深度处的地中沉降最大值;i(z)为z深度处的沉降槽宽度系数;z为地表到地中某位置处的竖向距离,如图1所示。从式(2)可以看出,当采用高斯函数描述地中沉降曲线时,存在地中沉降最大值和地中沉降槽宽度系数两个关键参数。
已有研究[22]表明:在砂卵石地层中,PECK公式的适用性与地层中的块石含量密切相关,界限含石量通常在50%左右。当地层中的块石含量小于50%时,地表和地层沉降曲线仍可采用高斯函数进行描述;当含石量大于50%时,地表沉降槽形态呈“V”型分布,采用高斯曲线描述将存在一定的误差。
2 砂卵石地层隧道开挖细观分析模型
2.1 二维细观有限元模型
考虑到计算量的限制,采用砂卵石地层二维细观有限元模型开展隧道开挖模拟。图2所示为建立的砂卵石地层隧道开挖细观分析模型,其计算区域长度为40 m、高度为30 m。隧道开挖断面为圆形,直径D为6.0 m、洞顶埋深H为12.0 m。隧道开挖方式采用全断面一步开挖,不设衬砌支护,从而可以最大程度地体现出开挖作用对围岩的影响。
在全部计算区域内,均考虑地层材料的非均质特性,将材料视为由土体与块石组成的两相介质,暂不考虑土体与卵石间界面过渡区的影响。为方便模型的建立,卵石形态均采用椭圆形描述,并采用“取与放”的方法[23-25]将卵石均匀地放置于计算区域中。椭圆形卵石具有长轴长度、扁平度和长轴倾角等细观结构因素。为避免细观因素间的耦合影响,在分析长轴倾角对隧道开挖围岩反应的影响时,将卵石扁平度及卵石长轴长度设为定值。监测路径Path-1沿竖直方向分布,位于模型的纵向对称线上,如图2所示。
2.2 工况设计
结合实际工程,研究者对卵石的细观结构特征进行了统计分析。通过对西安地铁2号线沿线卵石进行统计,王振峰[4]得到卵石扁平度的平均值为1.75,分布范围为1.0~2.50。杨期祥[26]对成都光华公园站的卵石特征进行了分析,结果表明:卵石扁平度的平均值为2.35,分布范围集中在1.30~2.60。GAO等[10]对成都地铁1号线沿线卵石进行了统计,结果表明:卵石扁平度的平均值为1.50。鉴于此,本文选取卵石的扁平度为1.50。
在卵石尺寸方面,统计结果表明,对于北京市砂卵石地层,颗粒粒径由北向南逐渐增大。其中,北京地铁7号线达官营站至湾达站区间,颗粒尺寸分布范围是20 mm~500 mm,超过200 mm的漂石含量约为15%~45%[27];地铁9号线局部区域,颗粒尺寸大于200 mm的漂石含量大于20%[26];地铁10号线西南段,颗粒尺寸集中在20 mm~300 mm,最大粒径为1630 mm,其中100 mm~200 mm的颗粒含量约占40%[28]。成都市也属于典型的砂卵石地层。其中,成都地铁1号、2号线工程,颗粒尺寸集中在20 mm~80 mm,局部区域有超过300 mm的漂石[7];地铁四号线西延线工程,颗粒尺寸分布范围为20 mm~660 mm,超过200 mm的漂石含量为4%~20%[6]。对于兰州市砂卵石地层,大粒径颗粒尺寸集中在150 mm~400 mm,最大粒径为720 mm[28]。
通过对Franciscan 的土石混合体进行研究,LINDQUIST[29]和MEDLEY[30]发现,对于隧道工程,当地层中块石尺寸小于0.05倍隧道直径时,可将地层材料视为均匀介质;而当块石尺寸大于0.05倍隧道直径时,需考虑块石细观结构特征的影响,视为非均质材料。也就是说,对于直径为6.0 m的隧道,当地层中块石粒径大约300 mm时,就需考虑其在地层中的细观分布特征。鉴于此,本文选取的卵石含量
{c_{\rm{r}}} 为45%,卵石长轴尺寸为300 mm,则卵石短轴的尺寸为200 mm。网格尺寸取为0.10 m,该模型单元数为611 340,节点数为306 371。对于所有的细观分析模型,卵石扁平度、卵石含量和长轴长度均保持不变,仅改变长轴倾角θ。在同一个模型中,所有的卵石均采用同一长轴倾角。对于隧道、地下管廊等长线型工程,其纵向跨度较大,穿越地层中的卵石倾角将随冲积方向和沉积作用程度的不同而发生变化[9]。因此,本文选取的长轴倾角θ变化范围为[0°, 90°],以10°为单位变化。
2.3 细观组分材料参数
由于块石拉/压强度较大,在隧道开挖荷载作用下通常不发生破坏,可视为弹性材料。土体基质采用经典的Mohr-Coulomb弹塑性本构模型来描述其力学性质和变形行为。砂卵石地层细观组分材料参数如表1所示。细观组分相关参数是由杜修力等[31]结合中型三轴试验标定得出的,详细的标定和验证过程见文献[31]。
表 1 砂卵石地层细观组分材料参数[31]Table 1. Material parameters for meso-constituents材料 参数 数值 卵石 密度\rho /(kg/m3) 2700 弹性模量E/GPa 50 泊松比\nu 0.20 土体基质 密度\rho /(kg/m3) 1900 黏聚力c/kPa 17.5 内摩擦角\varphi /(°) 20 剪胀角\psi /(°) 5 弹性模量E (σ3=400 kPa)/MPa 10 泊松比 \nu 0.30 2.4 边界条件
砂卵石地层隧道开挖细观分析模型的边界条件为上表面自由,底部设置水平与竖向位移约束,侧面设置法向水平位移约束。
2.5 模拟过程
模拟过程共包含2个分析步:地应力平衡分析步、隧道开挖分析步。地应力平衡分析步中,仅考虑土体自重应力的作用,通过给定有限元模型地表和底部的竖向应力值及其对应的坐标值,形成初始应力场。计算模型中其他部位的竖向应力值则根据地表和底部的差值得到,水平应力通过竖向应力乘以侧压力系数获取,侧压力系数K0 = 0.5。隧道开挖分析步中,采用“生死单元”的方法移除相应于隧道断面位置处的单元,来实现隧道的开挖模拟。
3 围岩应力结果与分析
3.1 计算值与设定值的对比
地层初始应力场是隧道开挖计算的初始条件。对于初始应力,将细观分析模型计算值与理论值进行对比,对细观分析模型的可靠性进行判断。
在本文研究中,初始应力理论值的计算公式为:
{S}_{22}={\rho }_{{\rm{e}}} g {\textit{z}}\;\;\; (3) {S_{11}} = {K_0} {S_{22}} (4) 式中:S22为竖向应力;S11为水平应力;
{\rho }_{{\rm{e}}} 为地层等效密度,{\rho }_{{\rm{e}}}{\rm{=}}{\rho }_{{\rm{r}}}\times {c}_{\rm{r}}+{\rho }_{{\rm{s}}}\times (1-{c}_{\rm{r}}) ;g为重力加速度,通常取9.8 m/s2;K0为侧压力系数,取值为0.50。图3为不同卵石倾角下,监测路径Path-1竖向应力和水平应力计算值与理论值的对比。从图可见,不同卵石倾角下围岩竖向应力与理论值均拟合较好,其值随地层深度线性增加。对于围岩水平应力,模拟值与理论值也吻合较好,且其值等于竖向应力的0.50倍,与设定值保持一致。对比结果表明,细观有限元模型能准确地描述地层中的围岩应力分布。
3.2 竖向应力云图
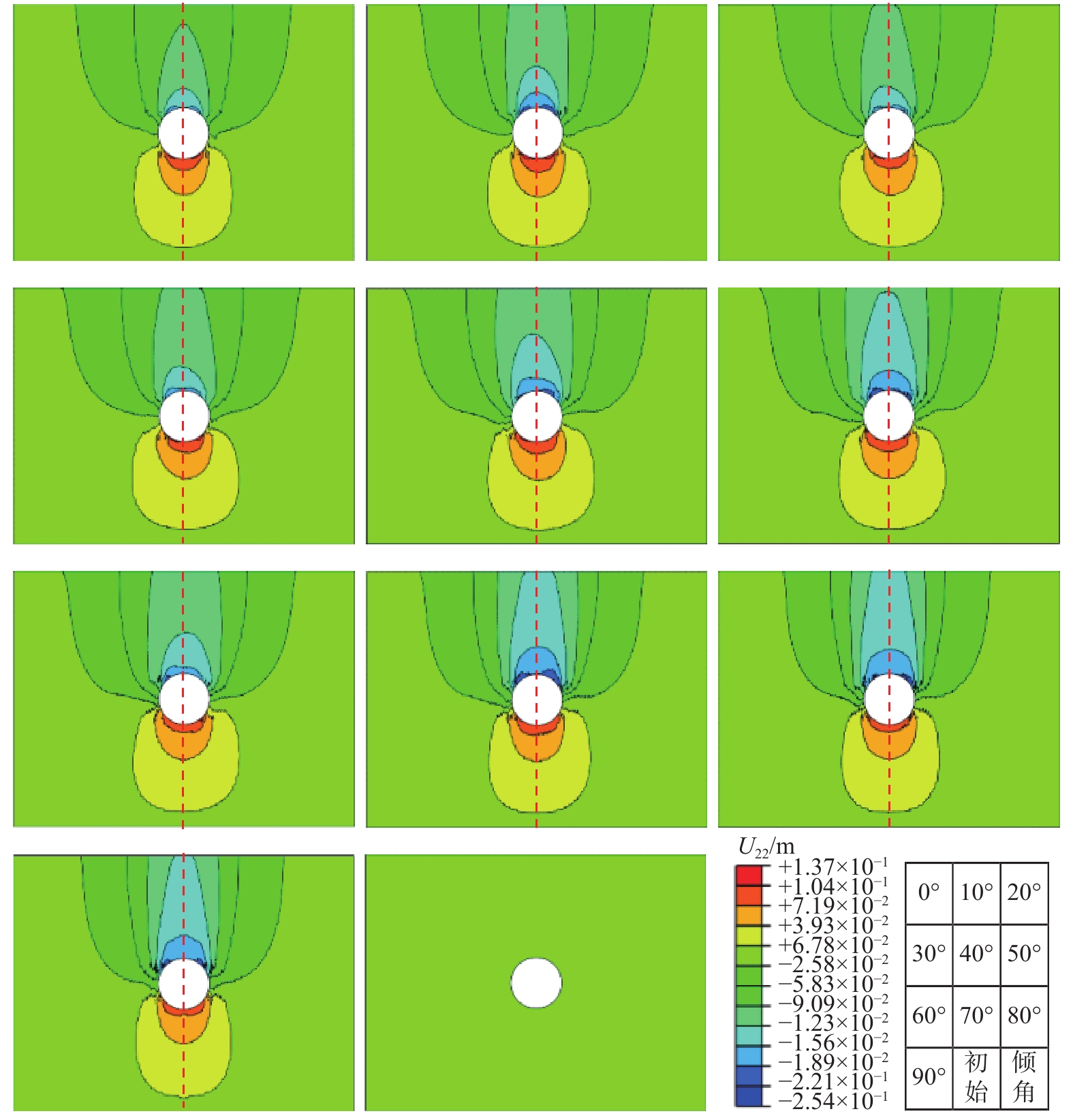
隧道开挖前后,围岩竖向应力云图如图4所示。从图4中可以看出,在隧道开挖前,竖向应力沿地层深度不断增大。当隧道开挖后,竖向应力在断面周围发生显著变化。
将不同倾角下的围岩竖向应力云图进行对比,可以发现,当卵石倾角从0°增加到90°时,拱腰处的竖向应力逐渐增大,且竖向应力增大的区域是不断扩大的,如图4中拱腰处蓝色区域所示。当卵石倾角为0°和90°时,竖向应力分布表现出对称性,当卵石倾角为10°~80°时,竖向应力呈现出不同程度的非对称性,且当卵石倾角为40°~60°时,非对称性最为明显。竖向应力云图沿顺时针方向发生偏转,向模型对称轴右侧区域倾斜。
由以上分析可知,当地层中卵石倾角发生变化时,围岩竖向应力大小和分布范围均发生显著变化。对于由卵石和土体基质组成的砂卵石地层,荷载由卵石骨架和土体基质共同承担。当卵石倾角由0°逐渐变化至90°时,其在水平方向上荷载传递面积逐渐减小,而在竖直方向上荷载传递面积逐渐增大。因而,在相同的开挖荷载作用下,拱腰处的应力将逐渐增大,围岩应力分布会呈现出显著差别。
3.3 塑性区
塑性区为围岩土体应力达到屈服状态的区域,可作为分析围岩扰动区的参考。隧道开挖后,围岩塑性区分布如图5所示。从图5中可以看出,与均质地层类似,在非均质砂卵石地层中,围岩塑性区也主要分布于开挖断面周围。隧道开挖后,围岩塑性区呈蝴蝶状,分布于隧道拱肩、拱腰及拱脚位置。
将不同倾角下的围岩塑性区进行对比,可以发现,当卵石倾角为0°和90°时,围岩塑性区呈对称分布,对称轴为过隧道中心的竖直线。当卵石倾角为0°时,拱肩、拱腰、拱脚处的分布范围分别为3.75R、1.75R和1.75R;当卵石倾角为90°时,相应的分布范围分别是4.0R、1.75R和1.75R。当卵石倾角在10°~80°时,围岩塑性区呈非对称性分布,且当卵石倾角为40°时,非对称特征最为显著。 围岩塑性区沿逆时针方向发生偏转,向模型对称轴左侧倾斜,左拱肩处的塑性区面积大于右拱肩,而左拱脚处的塑性区面积小于右拱脚,拱腰处的塑性区面积未发生显著变化。当卵石倾角为40°时,左拱肩处塑性区面积约为4.0R
\times 3.0R,右拱肩处为4.0R\times 2.0R,左拱脚处约为π\times (0.75 R) 2,右拱脚处约为π\times (1.25 R) 2。4 围岩变形结果与分析
4.1 变形云图
地层变形是地下工程施工模拟的关键问题,也是对工程环境影响评价的基础。隧道开挖前,通常认为地层中围岩变形为零。隧道开挖后,地层中的围岩变形发生显著变化。
4.1.1 竖向位移
图6为不同卵石倾角时的围岩竖向位移等值线图。从图6中可以看出,隧道开挖后,洞顶围岩表现为沉降变形,洞底围岩表现为隆起变形。将不同倾角下的围岩竖向位移进行对比,可以看出围岩竖向位移的分布形态和大小因卵石倾角的不同而存在差异。当卵石倾角为0°和90°时,围岩竖向变形呈对称分布,对称轴为过隧道中心的竖直线。当卵石倾角在10°~80°时,围岩竖向变形呈现出非对称性分布的现象。在本文给定条件下,当卵石倾角在0°~90°变化时,洞顶沉降值在156.87 mm~192.94 mm范围内变化,洞底回弹值在84.76 mm~105.65 mm 范围内变化。
4.1.2 水平位移
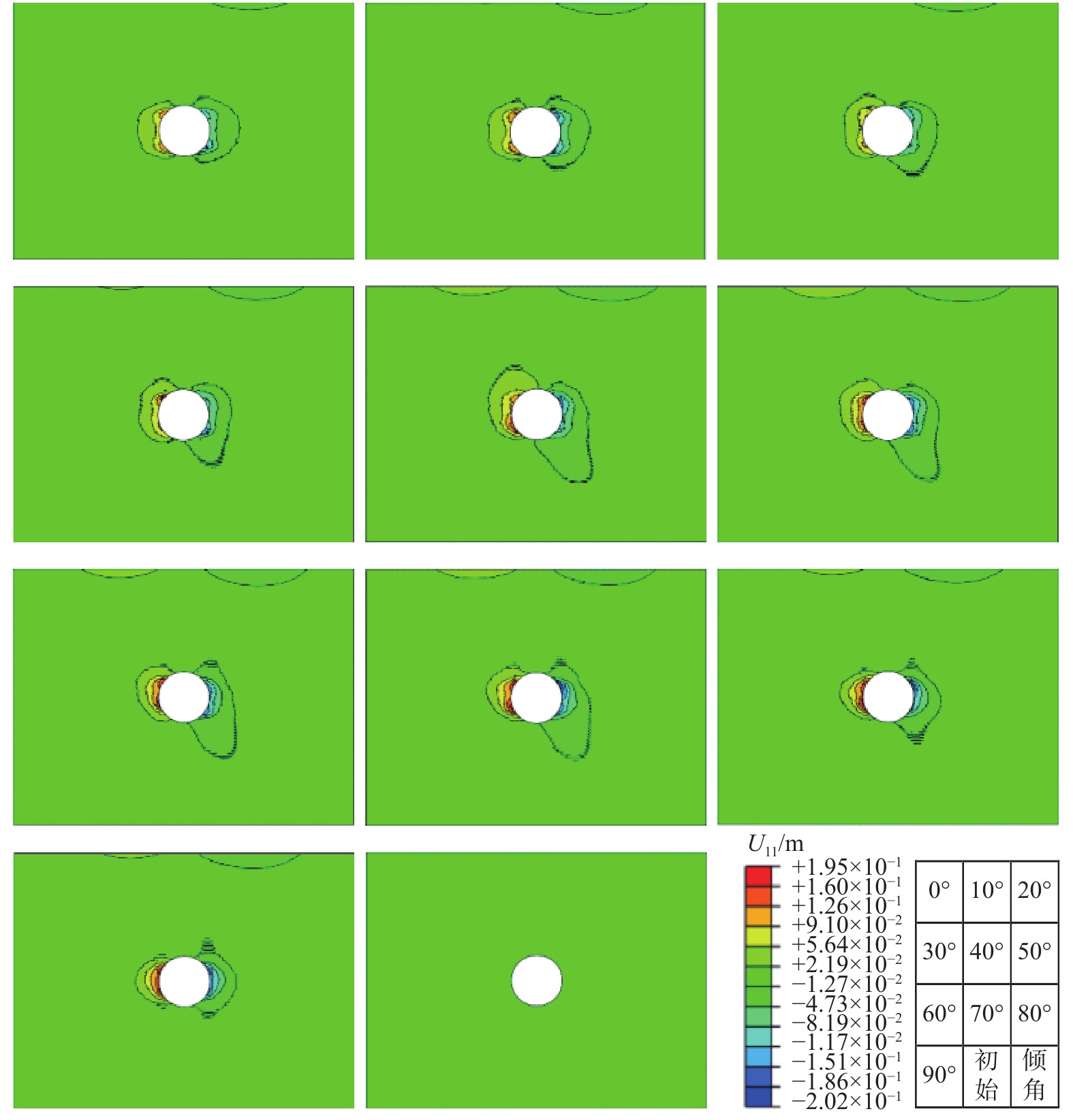
图7为不同卵石倾角时的围岩水平位移等值线图。从图7中可以看出,隧道开挖后,卵石倾角的变化对水平位移的分布形态和大小均产生影响。在本文给定条件下,当卵石倾角在0°~90°变化时,左拱腰处水平位移值在67.74 mm~148.83 mm范围内变化,右拱腰处水平位移值在67.08 mm~146.88 mm范围内变化。
4.2 地表沉降槽
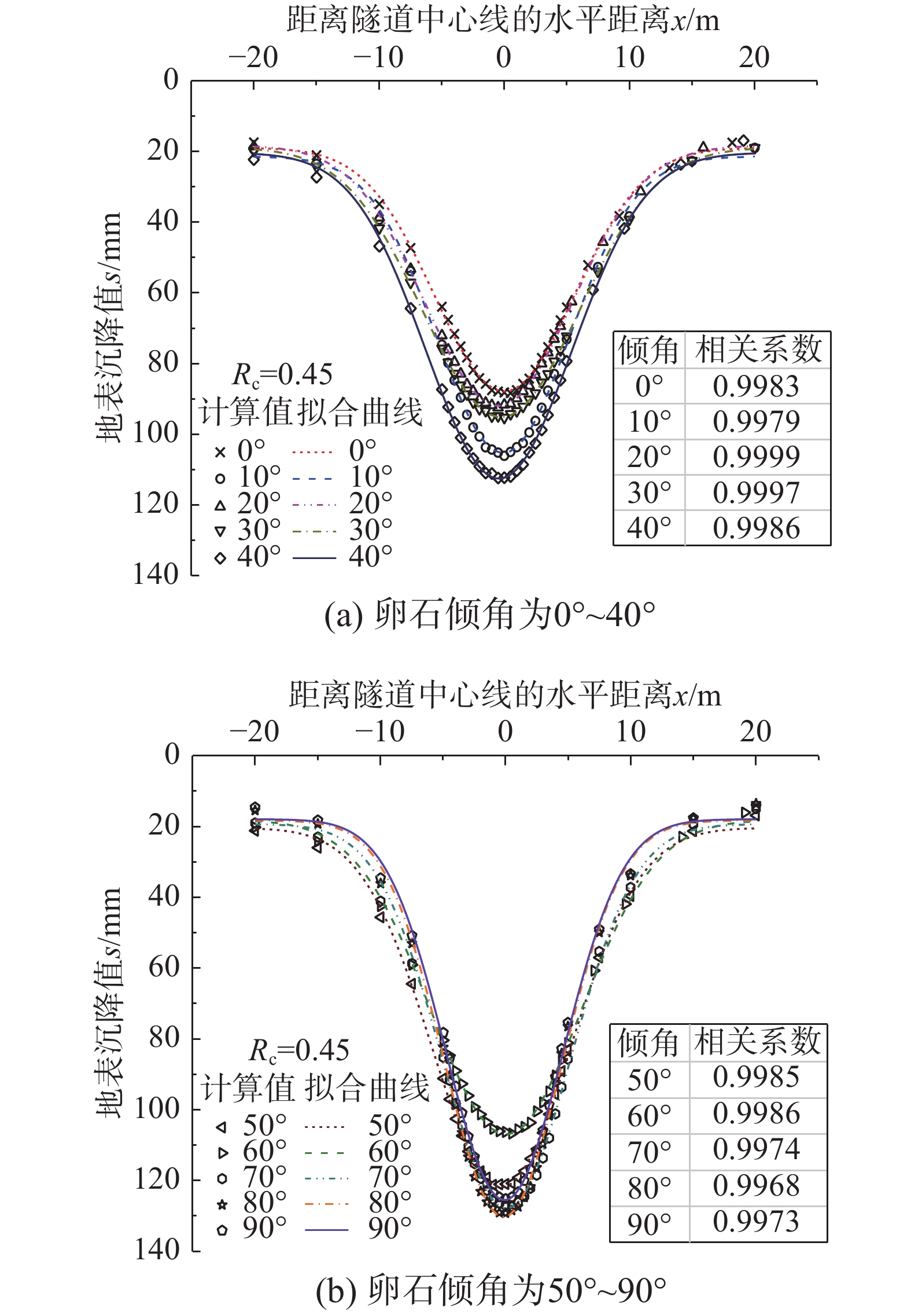
图8为不同卵石倾角下的地表沉降曲线。从图8中可以看出,当地层中的卵石倾角发生变化时,地表沉降值呈现出显著差异,沉降最大值和沉降槽宽度均有所不同。同时,沉降最大值的位置也会偏离模型竖向对称轴。将不同倾角下的地表沉降曲线采用PECK高斯公式进行拟合,如图8所示。从图8中可以看出,不同卵石倾角的地表沉降值和拟合曲线吻合较好,相关系数均达到0.99。分析结果表明:当块石含量为45%时,PECK公式可以较好地描述砂卵石地层不同卵石倾角下的隧道开挖地表沉降特征。
提取地表沉降曲线上的最大值,并根据拟合曲线得到沉降槽宽度系数,分别绘制沉降最大值、沉降槽宽度系数随卵石倾角的变化图,如图9(a)和图9(b)所示。将沉降最大值位置偏离隧道中心的水平距离定为δ,绘制δ随倾角的变化图,如图9(c)所示。
从图9(a)可以看出,当卵石倾角从0°变化到90°时,地表沉降最大值Smax(0)整体上呈现出线性增加的趋势。当卵石含量为45%时,在本文给定条件下,地表沉降最大值由88.2 mm增加至129.2 mm。该变化规律相当于卵石倾角每增大10°,沉降最大值增加4.56 mm,增幅比例为5.17%。图9(b)为地表沉降槽宽度系数i(0)随倾角的变化规律,从图中可以看出,当卵石倾角从0°增加到90°时,地表沉降槽宽度系数呈现出先增大后减小的规律,呈下开口的抛物线型变化形式。在卵石倾角为30°时,其值达到最大值;在卵石倾角为90°时,其值达到最小值。当卵石含量为45%时,地表沉降槽宽度系数在4.71 m~6.24 m范围内变化。图9(c)为不同卵石倾角下,地表沉降最大值偏移隧道中心的水平距离δ。从图中可以看出,当卵石倾角从0°增加到90°时,δ的变化形式呈现出先减小后增大的变化规律,呈上开口的抛物线形式。当卵石含量为45%时,偏移距离δ在−0.45 m~0.07 m范围内变化。相对隧道直径,偏移量δ均小于7.5%D,可忽略不计,仍可认为沉降最大值位于模型纵向对称线上。
对于平面应变条件,在重力荷载作用下,地层初始应力状态以竖向应力为大主应力,水平应力为小主应力。隧道开挖后,不同位置处的围岩应力发展路径不同,因应力重分布而产生的承压、卸载状态也不同。其中,在开挖断面周围,拱顶和洞底处的围岩土体主应力方向发生旋转,以水平应力为大主应力,竖向应力为小主应力。研究表明[32]:对于此类应力状态,当颗粒倾角或沉积方向从0°增大至90°时,材料内摩擦角呈现出单调递减的规律。因此,地表沉降值将呈现出逐渐增加的现象。
4.3 地中沉降槽
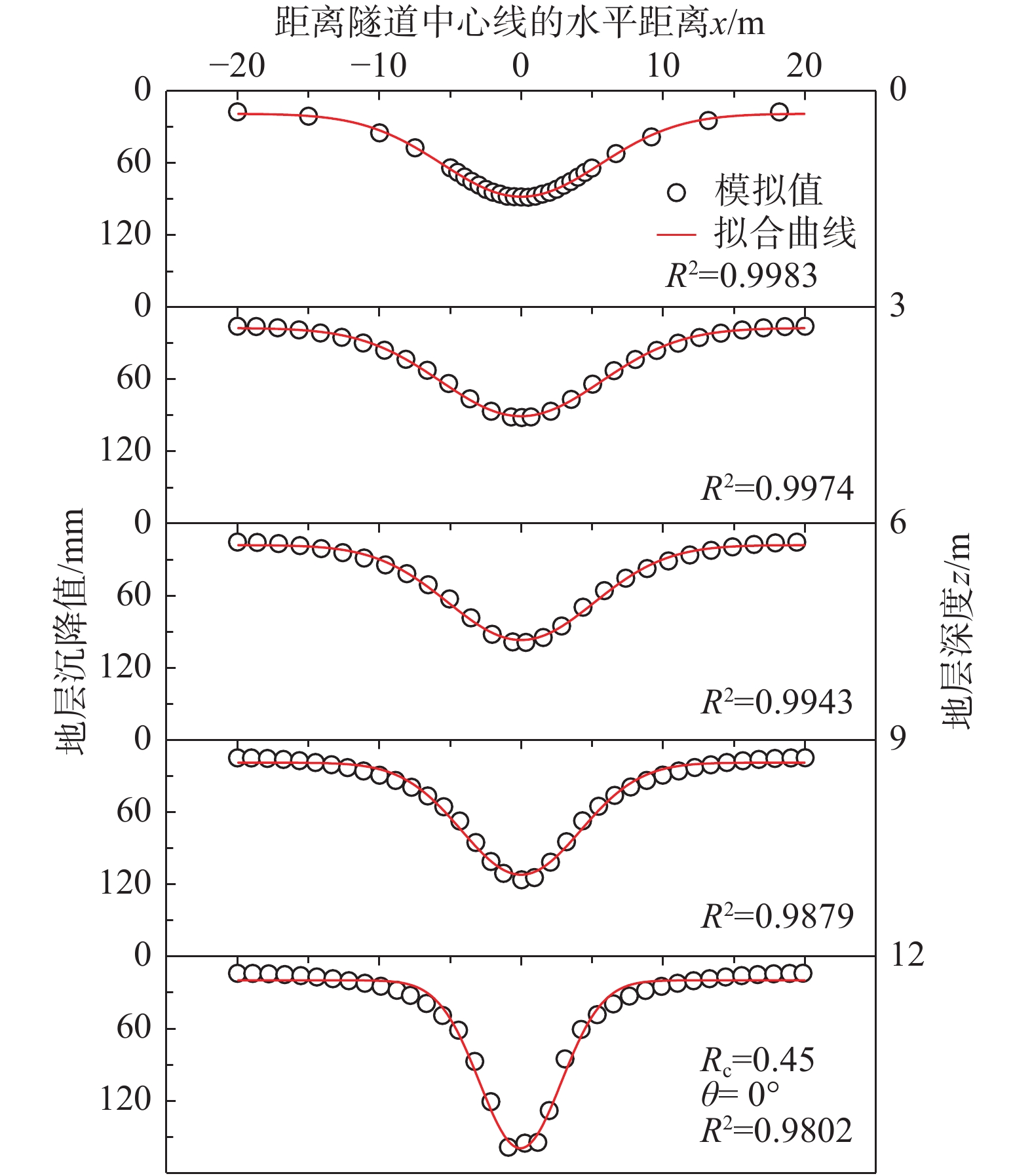
地中变形决定了隧道开挖对地下结构的影响程度,是围岩变形分析的关键问题之一。图10所示卵石含量为45%、卵石倾角为0°时的地中沉降曲线,地层深度分别为0.0 m、3.0 m、6.0 m、9.0 m和12.0 m。由图10可见,随着深度变化,地层沉降最大值和沉降槽宽度均发生变化。采用Peck高斯公式对地表沉降曲线进行拟合,可以看出,不同深度处的地层沉降曲线和拟合曲线均吻合较好,相关系数均达在0.98以上。分析结果表明:当块石含量为45%时,高斯公式可以很好地描述砂卵石地层不同深度处的地层沉降特征。
从式(2)可以看出,Smax(z)和i(z)是地中沉降变形曲线的两个关键参数,理清Smax(z)和i(z)随深度z以及卵石倾角θ的变化规律,是确定整个地层沉降变形的基础。
4.3.1 Smax(z)的变化规律及数学描述方法
提取路径Path-1上的竖向位移值Smax(z),并将其整理在(z/z0)−(Smax(z)/Smax(z0))的坐标系中。Smax(z0)为深度z0处的竖向沉降最大值,即洞顶竖向位移。图11为不同卵石倾角时,Smax(z)/Smax(z0)随深度的变化规律。由图11可见,其变化具有以下特征:
1) 在地表处(z=0),Smax(z)/Smax(z0)等于Smax(0)/Smax(z0);
2) 在洞顶处(z=z0), Smax(z)/Smax(z0)=1.0;
3) 当地层深度z从0增加至z0时,Smax(z)/Smax(z0) 呈现出非线性增加的趋势;
4) 在不同卵石倾角下,Smax(z)/Smax(z0)与深度z均表现出以上的变化特征。
基于以上认识,本文提出以下幂函数来描述Smax(z)/Smax(z0)与z/z0间的变化规律:
\frac{{{S_{\max }}({\textit{z}})}}{{{S_{\max }}({{\textit{z}}_0})}} = \left[\frac{{{S_{\max }}(0)}}{{{S_{\max }}({{\textit{z}}_0})}} - 1\right]{\left(1 - {\left(\frac{{\textit{z}}}{{{{\textit{z}}_0}}}\right)^2}\right)^n} + 1 (4) 式中,n为地中沉降最大值影响参数。
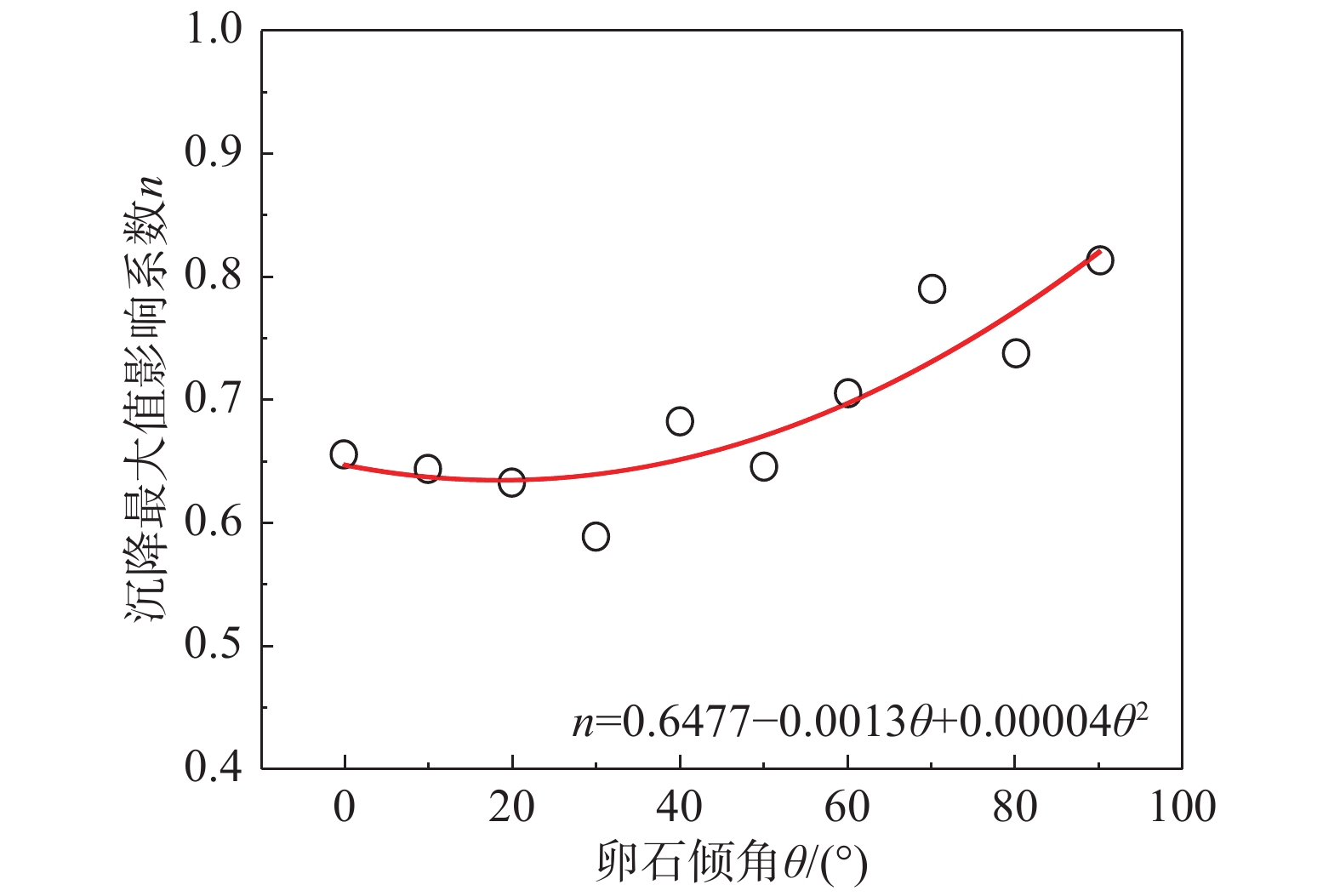
采用式(4)对Smax(z)进行拟合,如图11所示。从图11中可以看出,当不同卵石倾角下,细观模型模拟值与式(4)计算值吻合较好,相关系数均大于0.98。当卵石倾角从0°增加到90°时,n值呈现出先减小后增大的趋势,当卵石倾角为30°时取得最小值,如图12所示。当卵石含量为45%时,在本文给定条件下,n值在0.59~0.81范围内变化。
4.3.2 i(z)的变化规律及数学描述方法
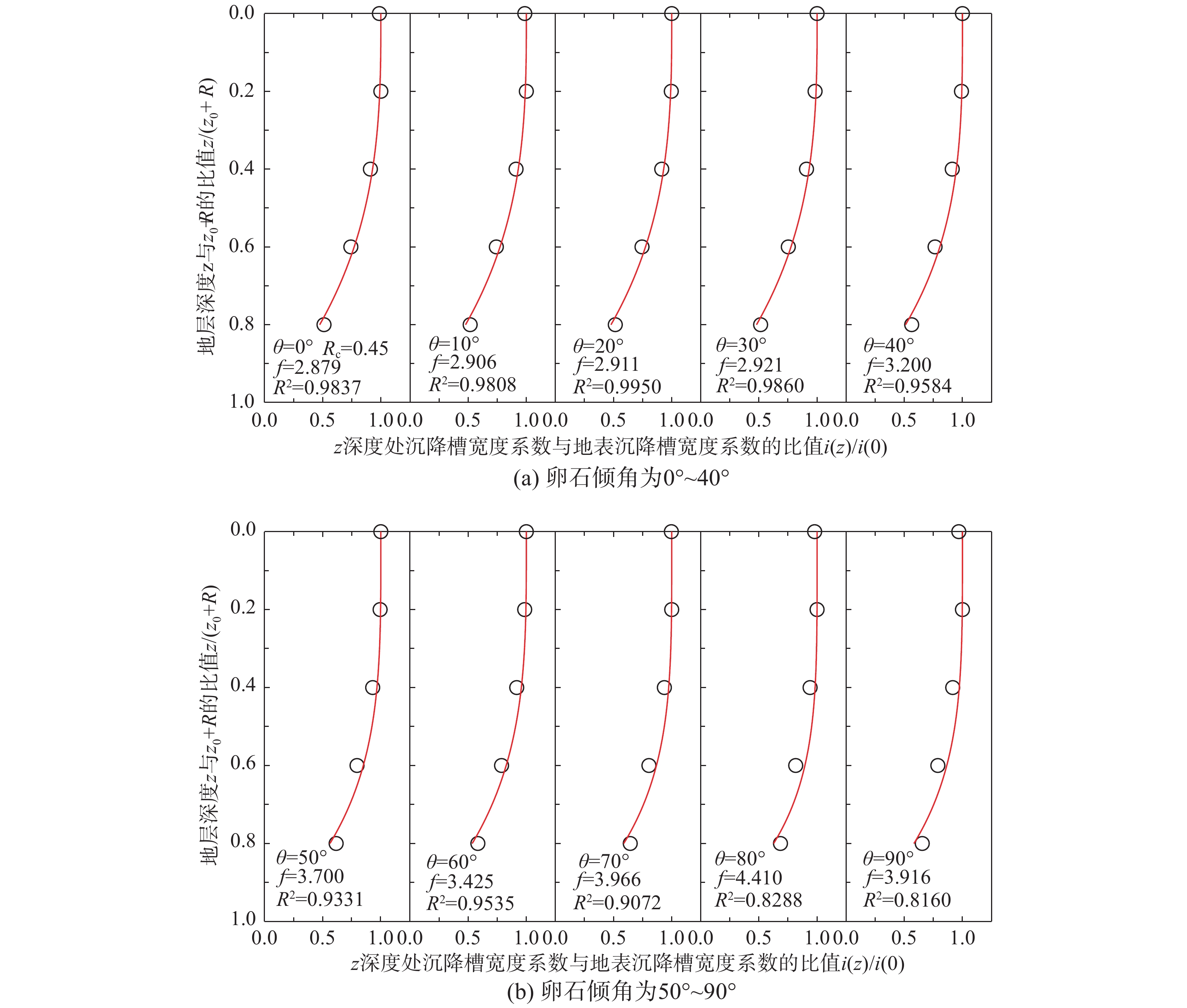
根据地中沉降槽拟合曲线,得到不同深度处沉降槽宽度系数i(z),并将其整理在(z/(z0+R))−(i(z)/i(0))的坐标系中。图12为不同卵石倾角时,i(z)/i(0)随深度的变化规律。由图可见,其变化具有以下特征:
1) 在地表处(z=0),i(z)/i(0)=1;
2) 在洞顶处(z=z0), i(z)/i(0)=i(z0)/i(0);
3) 当地层深度z从0增加至z0时,i(z)/i(0)呈现出非线性减小的趋势;
4) 在不同卵石倾角下,i(z)/i(0)与深度z均表现出以上的变化特征。
基于以上认识,本文提出以下幂函数来描述i(z)/i(0)与z/(z0+R)间的变化规律:
\frac{{i({\textit{z}})}}{{i(0)}} = 1 - {\left(\frac{{\textit{z}}}{{{{\textit{z}}_0} + R}}\right)^f} (5) 式中,f为沉降槽宽度系数影响参数。
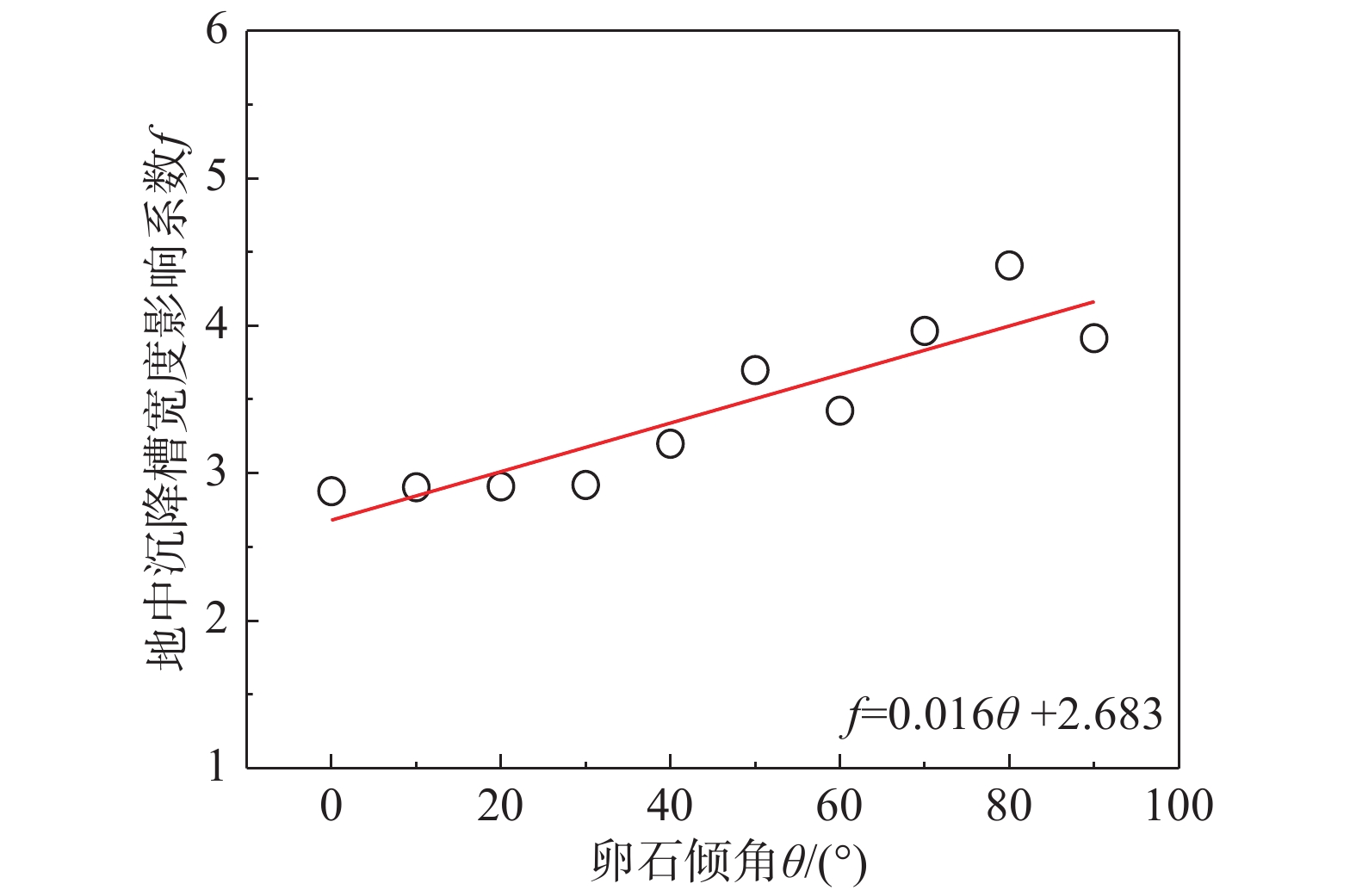
采用式(5)对i(z)进行拟合,如图13所示。由图13可见,不同卵石倾角下,细观模型模拟值与式(4)计算值吻合较好,当卵石倾角为0°~70°时,相关系数均大于0.90。当卵石倾角从0°增加到90°时,f值在整体上呈现出逐渐增大的趋势,如图14所示。当卵石含量为45%时,在本文给定条件下,f值在2.88~4.41范围内变化。
4.4 隧道断面变形模式
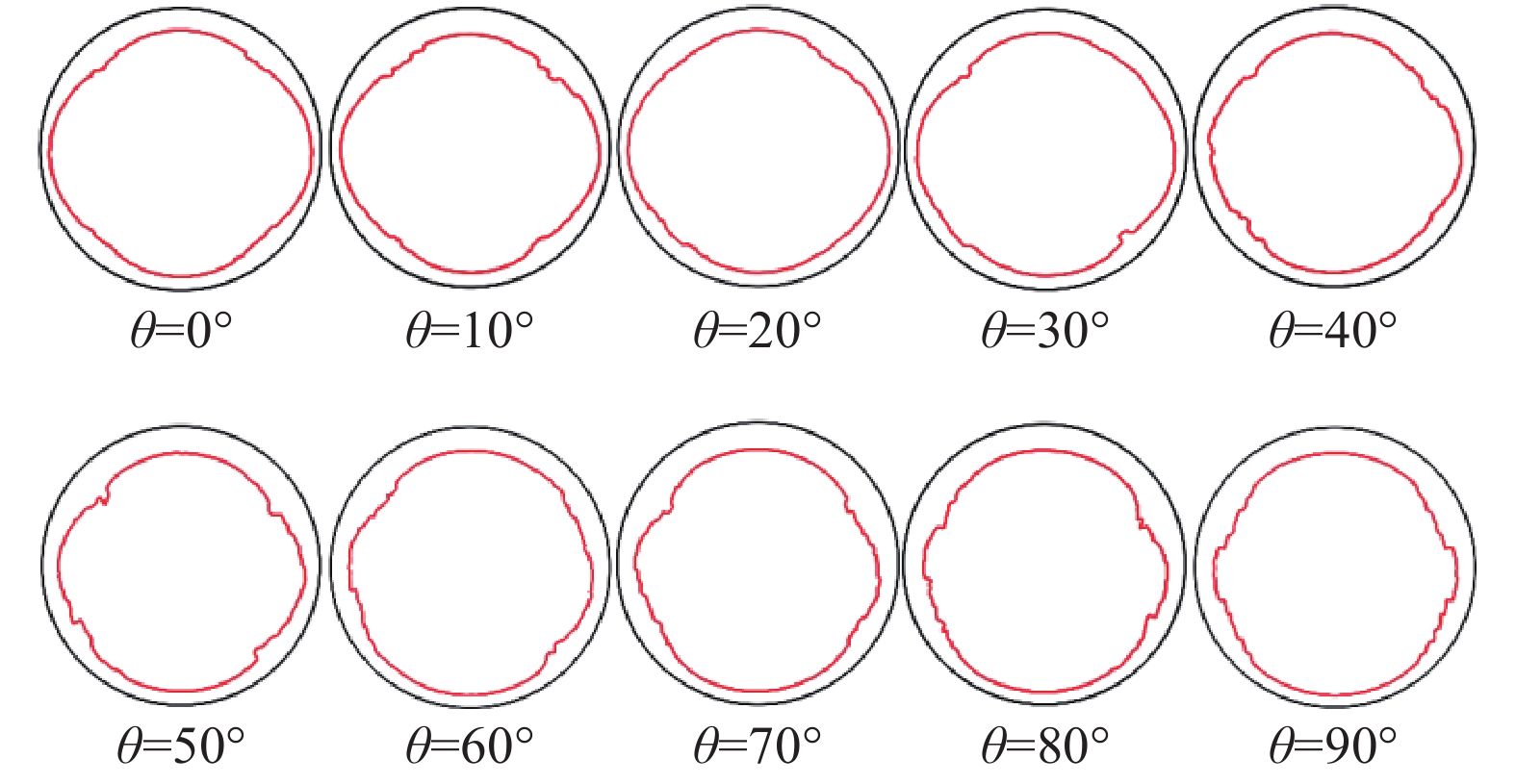
图15为不同卵石倾角时的隧道开挖断面变形图,变形系数统一取为2.0。图15中圆形代表隧道开挖前断面形状,不规则线框为隧道开挖后断面形状。由图15可见,隧道开挖后,在无支护状态下,断面向隧道中心收敛。不同于均质地层,由于卵石的存在,变形模式呈现非光滑的锯齿状。同时,从图15中可以看出卵石倾角的变化对开挖断面变形模式具有一定影响。在卵石倾角为0°和90°时,变形形态呈对称分布,对称轴为通过隧道中心的竖直线。当卵石倾角在10°~80°间变化时,变形模式沿着顺时针方向发生偏转,形态逐渐由水平扁平状向竖直扁平状发展。
5 结论
考虑地层材料的非均质性,本文开展了不同卵石倾角下的砂卵石地层隧道开挖细观有限元计算,分析了卵石倾角对围岩应力和围岩变形的影响,并分别给出了地中沉降最大值和沉降槽宽度系数与地层深度间的数学描述公式,主要结论如下:
(1) 当卵石倾角从0°变化至90°时,围岩塑性区的分布形态和分布范围会发生显著变化,拱腰处围岩的竖向应力不断增大;当卵石倾角在10°~80°时,围岩塑性区逆时针方向发生偏转,向模型对称轴左侧倾斜;围岩竖向应力云图呈非对称分布,沿顺时针方向发生偏转,向模型对称轴右侧区域倾斜。
(2) 在本文给定条件下,当卵石倾角从0°增大至90°时,地表沉降最大值以每10°增幅5.17%的速度随卵石倾角增加而线性增长;地表沉降槽宽度系数则呈现出先增大后减小的变化规律,当卵石倾角为30°时,其值取得最大值。
(3) 地中沉降最大值与地中沉降槽宽度系数随地层深度的变化均可采用幂函数形式的公式进行描述。当卵石倾角从0°增大至90°,地中沉降最大值影响参数表现出先减小后增大的抛物线型变化规律,而地中沉降槽宽度影响参数则呈现出线性增加的趋势。
(4) 由于卵石的存在,隧道断面变形模式呈非光滑的锯齿状;当卵石倾角从0°增大至90°,断面变形模式由水平扁平状向竖向扁平状发展。
本文将砂卵石地层视为由卵石和土体组成的两相介质,忽略了土石界面作用的影响。在后续研究中,将考虑界面过渡区的影响。同时,卵石倾角对围岩应力和围岩变形的影响程度需结合卵石含量、卵石尺寸、土体基质属性以及隧道几何特征等综合确定。因此,需进一步开展相关研究,对影响程度给出定量化评价方法。
-
表 1 砂卵石地层细观组分材料参数[31]
Table 1 Material parameters for meso-constituents
材料 参数 数值 卵石 密度\rho /(kg/m3) 2700 弹性模量E/GPa 50 泊松比\nu 0.20 土体基质 密度\rho /(kg/m3) 1900 黏聚力c/kPa 17.5 内摩擦角\varphi /(°) 20 剪胀角\psi /(°) 5 弹性模量E (σ3=400 kPa)/MPa 10 泊松比 \nu 0.30 -
[1] ZHANG P, JIN L, DU X L, et al. Computational homogenization for mechanical properties of sand cobble stratum based on fractal theory [J]. Engineering Geology, 2018, 232: 82 − 93. doi: 10.1016/j.enggeo.2017.11.013
[2] DU X L, ZHANG P, JIN L, et al. A multi-scale analysis method for the simulation of tunnel excavation in sandy cobble stratum [J]. Tunnelling and Underground Space Technology, 2019, 83: 220 − 230. doi: 10.1016/j.tust.2018.09.019
[3] LIN Q T, LU D C, LEI C M, et al. Model test study on the stability of cobble strata during shield under-crossing [J]. Tunnelling and Underground Space Technology, 2021, 110(9): 103807.
[4] 王振峰. 卵石地层中地铁隧道盾构施工引起的地表沉降研究[D]. 西安: 西安科技大学, 2012. WANG Zhenfeng. Study on ground surface settlement due to metro shield tunneling in sand cobble stratum [D]. Xi’an: Xi’an University of Technology, 2012. (in Chinese)
[5] 马辉, 高明忠, 张建康, 等. 卵石土等效弹性模量理论预测模型初探[J]. 岩土力学, 2011, 32(12): 3642 − 3646. doi: 10.3969/j.issn.1000-7598.2011.12.018 MA Hui, GAO Mingzhong, ZHANG Jiankang, et al. Theoretical model developed for equivalent elastic modulus estimation of cobblestone-soil matrix [J]. Rock and Soil Mechanics, 2011, 32(12): 3642 − 3646. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.12.018
[6] 牟迪. 成都地铁四号线砂卵石层分布规律及工程特性研究[D]. 成都: 西南交通大学, 2015. MOU Di. Research on distribution law and engineering properties in sand and gravel strata [D]. Chengdu: Southwest Jiaotong University, 2015. (in Chinese)
[7] 张抒, 唐辉明. 基于细观统计规律的土石混合体随机模型研究[J]. 人民长江, 2015, 46(16): 48 − 52, 79. ZHANG Shu, TANG Huiming. Research on soil-rock mixture stochastic model based on meso-structural statistical characteristics [J]. Yangtze River, 2015, 46(16): 48 − 52, 79. (in Chinese)
[8] XU W J, YUE Z Q, HU R L. Study on the meso-structure and meso-mechanical characteristics of the soil-rock mixture using digital image processing based finite element method [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45: 749 − 762. doi: 10.1016/j.ijrmms.2007.09.003
[9] 张佩, 杜修力, 金浏, 等. 卵石长轴倾角对土石混合体宏观力学性能的影响研究[J]. 工程力学, 2018, 35(8): 64 − 72. doi: 10.6052/j.issn.1000-4750.2017.05.0362 ZHANG Pei, DU Xiuli, JIN Liu, et al. Study on the orientation angel of rock long axis on the micromechanical properties of soil-rock mixture [J]. Engineering Mechanics, 2018, 35(8): 64 − 72. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.05.0362
[10] GAO M Z, ZHAO J, LI S W, et al. Theoretical model of the equivalent elastic modulus of a cobblestone-soil matrix for TBM tunneling [J]. Tunnelling and Underground Space Technology, 2016, 54: 117 − 122. doi: 10.1016/j.tust.2016.02.001
[11] 徐文杰, 胡瑞林, 岳中琦. 土-石混合体随机结构生成系统的研发及其细观结构力学数值试验研究[J]. 岩石力学与工程学报, 2009, 28(8): 1652 − 1665. doi: 10.3321/j.issn:1000-6915.2009.08.017 XU Wenjie, HU Ruilin, YUE Zhongqi. Development of random meso-structure generating system of soil-rock mixture and study of its mesostructural mechanics based on numerical test [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1652 − 1665. (in Chinese) doi: 10.3321/j.issn:1000-6915.2009.08.017
[12] CUI Z D, LIU D A, WU F Q. Influence of dip directions on the main deformation region of layered rock around tunnels [J]. Bulletin of Engineering Geology and the Environment, 2014, 73: 441 − 450. doi: 10.1007/s10064-013-0511-6
[13] WANG Z, QIAO C, SONG C, et al. Upper bound limit analysis of support pressures of shallow tunnels in layered jointed rock strata [J]. Tunnelling and Underground Space Technology, 2014, 43: 171 − 183. doi: 10.1016/j.tust.2014.05.010
[14] 马腾飞, 李树忱, 李术才, 等. 不同倾角多层节理深部岩体开挖变形破坏规律模型试验研究[J]. 岩土力学, 2016, 37(10): 2899 − 2908. MA Tengfei, LI Shuchen, LI Shucai, et al. Model experimental study of deformation and failure law in excavation of deep rock mass with multi-cleftiness of different angles [J]. Rock and Soil Mechanics, 2016, 37(10): 2899 − 2908. (in Chinese)
[15] 王志杰, 王振, 徐海岩, 等. 倾角对土砂互层地层围岩稳定性的影响研究[J]. 铁道工程学报, 2019, 9: 54 − 59, 84. doi: 10.3969/j.issn.1006-2106.2019.02.011 WANG Zhijie, LI Zhen, XU Haiyan, et al. Research on the influence of dip angle on stability of surrounding rock in sand and soil interbedded strata [J]. Journal of Railway Engineering Society, 2019, 9: 54 − 59, 84. (in Chinese) doi: 10.3969/j.issn.1006-2106.2019.02.011
[16] HE C, FENG K, FANG Y, et al. Surface settlement caused by twin-parallel shield tunnelling in sandy cobble strata [J]. Journal of Zhejiang University Science A, 2012, 13: 858 − 869.
[17] 胡敏. 砂卵石土物理力学特性及盾构施工相应的数值模拟研究[D]. 广州: 华南理工大学, 2014. HU Min. Numerical method to study the physical and mechanical characteristics of sandy pebble soil and the response caused by shield tunneling [D]. Guangzhou: South University of Technology, 2014. (in Chinese)
[18] LIU T, XIE Y, FENG Z H, et al. Better understanding the failure modes of tunnels excavated in the boulder-cobble mixed strata by distinct element method [J]. Engineering Failure Analysis, 2020: 104712.
[19] ZHANG P, DU X L, LU D C, et al. Study on the excavation disturbed zone during tunneling in sandy cobble stratum considering the material meso-structure [J]. Transportation Geotechnics, 2021, 29: 100590. doi: 10.1016/j.trgeo.2021.100590
[20] PECK R B. Deep excavation and tunneling in soft ground [C]. Proceedings of 7th International Conference on Soil Mechanics and Foundation Engineering, State of the Art Volume, Mexico. 1969: 225 − 290.
[21] MAIR R J, TAYLOR R N, BRACEGIRDLE A. Subsurface settlement profiles above tunnels in clays [J]. Geotechnique, 1993, 43(2): 315 − 320.
[22] 宋伟涛, 张佩, 杜修力. 含石量对砂卵石地层隧道开挖地表沉降影响研究[J]. 地下空间与工程学报, 2021, 17(增刊 1): 359 − 366, 374. SONG Weitao, ZHANG Pei, DU Xiuli. Research on the influence of stone content on surface settlement caused by tunnel excavation in sandy cobble stratum [J]. Chinese Journal of Underground Space and Engineering, 2021, 17(Suppl 1): 359 − 366, 374. (in Chinese)
[23] UNGER J F, ECKWARDS S. Multiscale modeling of concrete [J]. Archives of Computational Methods in Engineering, 2011, 18(3): 341 − 393. doi: 10.1007/s11831-011-9063-8
[24] 金浏, 余文轩, 杜修力, 等. 基于细观模拟的混凝土动态压缩强度尺寸效应研究[J]. 工程力学, 2019, 36(11): 50 − 61. doi: 10.6052/j.issn.1000-4750.2018.06.0363 JIN Liu, YU Wenxuan, DU Xiuli, et al. Research on size effect of dynamic compressive strength of concrete based on meso-scale simulation [J]. Engineering Mechanics, 2019, 36(11): 50 − 61. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.06.0363
[25] 金浏, 杨旺贤, 余文轩, 等. 基于细观模拟的轻骨料混凝土动态压缩破坏及尺寸效应分析[J]. 工程力学, 2020, 37(3): 56 − 65. doi: 10.6052/j.issn.1000-4750.2019.01.0012 JIN Liu, YANG Wangxian, YU Wenxuan, et al. Dynamic compressive failure and size effect in lightweight aggregate concrete based on mesoscale simulation [J]. Engineering Mechanics, 2020, 37(3): 56 − 65. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.01.0012
[26] 杨期祥. 成都地铁砂卵石层盾构开挖引起的地表沉降规律分析[D]. 成都: 西南交通大学, 2016. YANG Qixiang. Study on the regularity of surface settlement caused by shield tunneling in Chengdu sandy pebbles stratum [D]. Chengdu: Southwest Jiaotong University, 2016. (in Chinese)
[27] 李润军. 北京地铁七号线达官营站及湾达区间暗挖关键技术研究[D]. 北京: 中国矿业大学, 2014. LI Runjun. Stduy on the key technology of shallow mining in Beijing metro line.7 DaGuan Ying station and WanDa section [D]. Beijing: China University of Mining and Technology, 2014. (in Chinese)
[28] 张淑朝. 兰州地铁低含砂率强渗透性砂卵石降低土压平衡盾构扭矩及防喷涌研究[D]. 北京: 北京交通大学, 2018. ZHANG Shuchao. Research on reducing the torque and anti-spewing of EPB shield tunnelling in low sand content and strong permeability sandy pebble strata of Lanzhou subway [D]. Beijing: Beijing Jiaotong University, 2018. (in Chinese)
[29] LINDQUIST E S. The strength and deformation properties of mélange [D]. Berkley: University of California, 1994.
[30] MEDLEY E W. The engineering characterization of mélanges and similar block-in-matrix rocks (Bimrocks) [D]. Berkley: University of California, 1994.
[31] 杜修力, 张佩, 金浏. 土石混合体宏观力学性能研究的细观等效分析方法[J]. 工程力学, 2017, 34(10): 44 − 52. doi: 10.6052/j.issn.1000-4750.2016.03.0181 DU Xiuli, ZHANG Pei, JIN Liu. A mesoscopic equivalent analysis method for the study on micromechanical properties of soil-rock mixture [J]. Engineering Mechanics, 2017, 34(10): 44 − 52. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.03.0181
[32] 梁靖宇. 土的三维非正交弹塑性本构模型研究[D]. 北京: 北京工业大学, 2020. LIANG Jingyu. Study on 3D non-orthogonal elastoplastic constitutive model for soil [D]. Beijing: Beijing University of Technology, 2020. (in Chinese)
-
期刊类型引用(5)
1. 刘军,申精,张宇,丁鹏菲. 考虑卵石倾角及形状特征卵石地层几何迂曲度计算模型. 北京建筑大学学报. 2024(02): 97-104 .  百度学术
百度学术
2. 梁沈伟,王彬,荣传新,于胜民. 卸载状态下非均质圆形寒区隧道围岩弹塑性统一解. 冰川冻土. 2024(02): 650-661 .  百度学术
百度学术
3. 张治国,沃巍,朱正国,韩凯航,孙苗苗. 考虑衬砌截面协调变形约束的既有隧道受盾构下穿施工影响的Fourier能量变分解. 岩土力学. 2024(05): 1397-1411+1422 .  百度学术
百度学术
4. 邓鹏海,刘泉声,黄兴. 基于Weibull分布的非均质隧洞围岩破裂碎胀FDEM数值模拟研究. 工程力学. 2024(07): 40-59 .  本站查看
本站查看
5. 杨治军,胡金鑫,邱成虎,王文卓,曾洋. 基于离散元法的隧道穿越卵石地层稳定性研究. 土木工程与管理学报. 2024(04): 76-82 .  百度学术
百度学术
其他类型引用(5)





 下载:
下载: