RESEARCH ON COHESIVE ZONE MODEL OF THE INTERFACE BETWEEN CRTS Ⅱ TRACK SLAB AND CA MORTAR
-
摘要: 轨道板与CA砂浆层间离缝是CRTS Ⅱ型板式无砟轨道结构的主要病害之一。为描述轨道板-CA砂浆层间界面本构行为、揭示层间离缝机理,该文提出了一种改进指数型界面内聚力模型,并基于理论分析和试验数据确定了改进模型的参数取值。该模型为含有指数系数的分段函数,可以表征层间界面拉力-位移关系的非线性特征。研究结果表明:改进指数型内聚力模型可以高效计算轨道板-CA砂浆界面内聚强度、损伤萌生时界面相对位移和界面临界断裂能,结果与试验值基本一致;改进指数型模型可以较为准确地模拟轨道板-CA砂浆界面的法向和切向开裂行为。
-
关键词:
- CRTS Ⅱ 板式无砟轨道 /
- CA砂浆 /
- 界面损伤 /
- 内聚力模型 /
- 改进指数模型
Abstract: Debonding between track slab and CA mortar layer is one of the main defects of CRTS Ⅱ slab-type ballastless track system. In order to describe the constitutive behavior of the interface and reveal the mechanism of debonding, an improved exponential cohesive zone model was proposed with parameters determined based on theoretical analysis and experimental data. The proposed model is a segmentation function and adopts exponential coefficients to reflect the nonlinearity of the tension-displacement relationship of the interlayer interface. It is found that: The proposed model can efficiently calculate the interface cohesive strength, the interface relative displacement at damage initiation, and the interface critical fracture energy between track slab and CA mortar, and the results are basically consistent with the experimental results. The proposed model can simulate the normal and tangential cracking behavior of the interface between track slab and CA mortar layer with relatively high accuracy. -
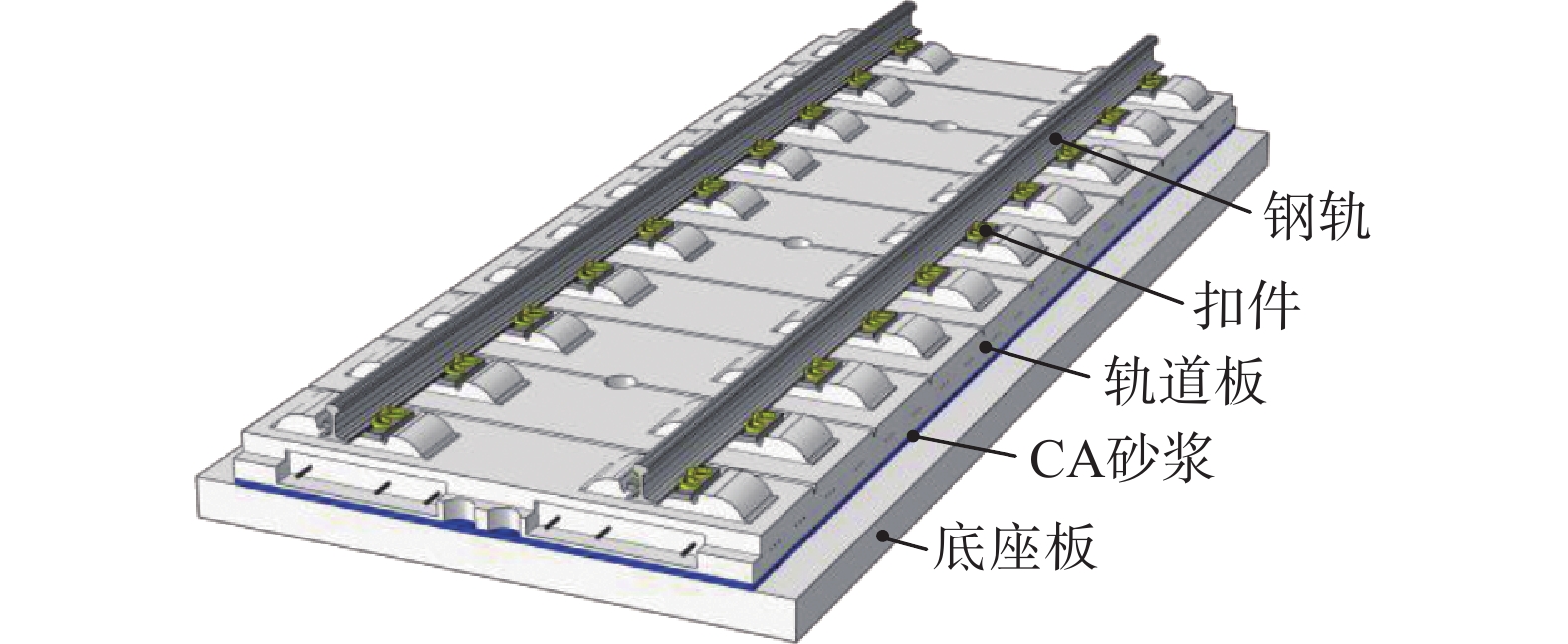
相比传统的有砟轨道结构,无砟轨道结构具有高平顺性、高耐久性、少维修的优点,已成为高速铁路轨道建设的首选结构型式[1-2]。CRTS II 型板式无砟轨道结构作为主要的无砟轨道结构型式之一,广泛应用于京津、京沪、沪昆等高铁线路。CRTS II 型板式无砟轨道结构主要由钢轨、扣件、轨道板、水泥乳化沥青(CA)砂浆层和底座板(支承层)等组成,其中,桥上CRTS II 型板式无砟轨道结构示意图如图1所示。CRTS II 型板式无砟轨道结构为竖向多层的纵连结构体系,各结构层间的界面是轨道结构最薄弱的部分之一,尤其是轨道板(底座板)与CA砂浆层之间的界面。现场调研表明,在长期温度和列车荷载作用下,CRTS II型轨道板与CA砂浆层间经常发生离缝病害[3-5],如图2所示。
目前,轨道板与CA砂浆层间离缝分析大部分基于断裂力学与损伤力学原理,采用的主要分析方法有近场动力学、扩展有限元、内聚力模型和断裂相场法等[6-9]。近场动力学基于非局部作用思想研究裂纹的萌生和发展,无法精确描述断裂的本构力函数,并且计算精度和效率低于传统有限元方法;扩展有限元可以模拟任意方向的裂纹扩展,对有限元网格改动较少,但需要在单元形状函数中增添附加函数,有限元计算成本较高;断裂相场法无须追踪裂纹表面,易于处理复杂的裂纹扩展问题,但能量泛函求解复杂。而基于能量准则的内聚力模型,通过作用在裂纹表面的张力与张开位移的等效关系来描述特定路径裂纹萌生、扩张和断裂的全过程。内聚力模型属于非强度因子主导型断裂准则,避免了计算断裂力学的复杂性。
有关内聚力本构理论,国内外学者开展了相关研究。自Barenblatt[10]和Dugdale[11]首次提出内聚力概念以来,国内外学者提出了多种内聚力模型,就拉力-位移曲线的形状而言,主要有双线性、指数型、梯形和多项式型等。其中,针对双线性和指数型内聚力模型,有关学者开展了一系列研究。Mi等[12]通过研究纤维复合材料界面拉力-位移关系,提出双线性内聚力模型。Camanho等[13]完善了双线性内聚力模型,并应用于零厚度粘结单元。与此同时,Rose 等[14]通过分析金属界面断裂能和分离位移的普遍关系,提出指数型内聚力模型。针对金属晶体排列的周期性,Rice[15]在切向上提出正弦内聚本构关系。之后,Xu和Needleman[16]基于塑性流动理论,提出耦合的指数型内聚力模型,完善了指数型内聚力模型理论。van den Bosch 等[17]改善了指数型内聚力模型,使之更好地描述混合模式下界面的脱粘过程。此外,还有学者提出并发展了梯形[18-19],多项式[20-21]等内聚力模型。其中指数型内聚力模型可表征非线性黏聚特性,相比双线性内聚力模型,指数型内聚力模型拉力-位移曲线及导数具有连续性,使其在数学求导及有限元实现方面具有一定优势。
由于内聚力模型主要用于模拟复合材料层间脱粘行为,CRTS II 型板式无砟轨道作为多层复合结构,国内学者开始将内聚力模型用于CRTS II 型板式无砟轨道层间离缝研究。有学者借助数字图像相关技术,对无砟轨道界面刚度、强度、韧性等性能进行了测试,确定了双线性内聚力模型[22-23]和指数型内聚力模型[24]参数,为研究无砟轨道离缝机理提供了重要的数据支撑。也有学者通过有限元方法,采用双线性内聚力模型[25-28]、指数型内聚力模型[29]和多项式内聚力模型[30]等研究在温度和列车荷载作用下轨道板和CA砂浆离缝过程。既有研究均采用单一内聚力模型对层间界面粘结试验数据进行分析,鲜有采用不同内聚力模型对层间界面脱粘预测效果进行对比分析。
本文基于内聚力本构理论和试验数据,分别采用双线性和指数型内聚力模型对CRTS Ⅱ 型轨道板与CA砂浆层间离缝进行预测。针对双线性和指数型模型存在的不足,提出了一种改进的指数型内聚力模型,并通过拟合既有试验数据,确定了改进指数型内聚力模型的主要参数。分析了不同模型对层间粘结的预测结果,验证了本文所提内聚力模型模拟轨道板与CA砂浆层间离缝的合理性与适用性。
1 内聚力模型
内聚力模型属于一种唯象本构模型,其拉力-位移曲线有多种形式,其中双线性和指数型应用最为广泛。
1.1 双线性内聚力模型
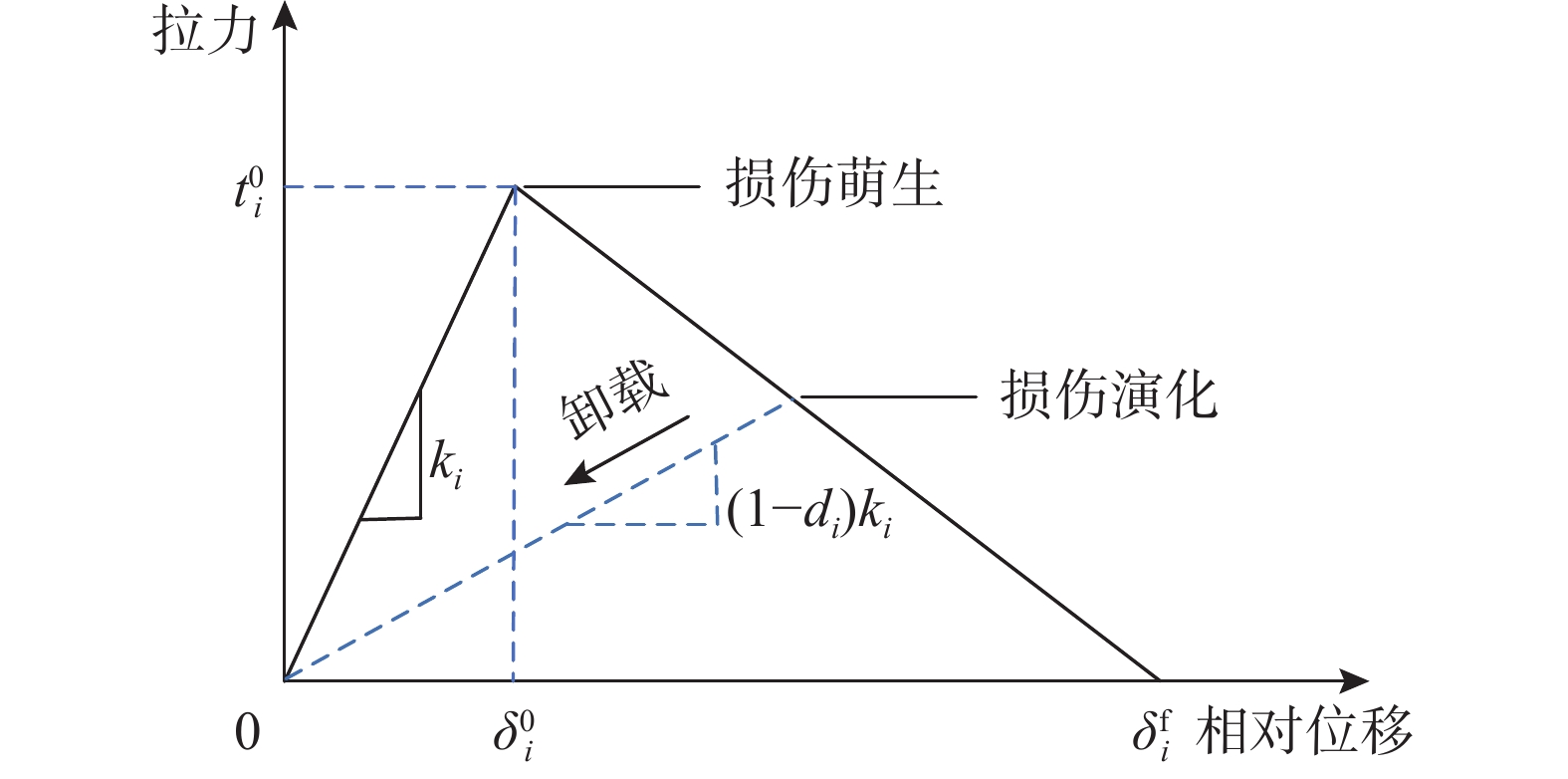
Hillerborg等[31]初次引入关于混凝土断裂能和抗拉强度的线性软化模型,之后双线性模型被用于混凝土断裂研究;Camanho等[13]基于连续损伤力学提出了双线性内聚力模型。如图3所示,单一模式下,双线性内聚力模型的拉力-位移关系为:
i=n,s,tti={kiδi,δmaxi⩽δ0i(1−di)kiδi,δ0i<δmaxi<δfi0,δmaxi⩾δfi (1) δmaxi = max{δmaxn,|δn|},且δmaxn⩾0,i=n (2) δmaxi = max{δmaxi,|δi|},i=s,t (3) 式中:
n 表示法向断裂;s 、t 分别表示横、纵切向断裂;ti 为界面应力;di 为损伤因子;ki 为界面刚度;δi 为界面相对位移值;δmaxi 为加载历史中所达到的最大界面相对位移值;δ0i 为损伤萌生时界面相对位移值;δfi 为断裂发生时界面相对位移值。根据界面内聚强度与界面相对位移的关系,界面刚度可以表示为:
ki=t0iδ0i,i=n,s,t (4) 式中,
t0i 为界面内聚强度。在开裂的初始阶段,层间界面无损伤产生,当界面相对位移达到一定程度后,层间界面开始产生损伤。界面刚度随界面相对位移的增加而减小,通过引入损伤因子
di 来定量描述界面损伤程度[31]:di=δfi(δmaxi−δ0i)δmaxi(δfi−δ0i),i=n,s,t (5) 损伤因子
di 的取值范围为0~1。当di=0 时,表明界面未伤损,层间粘结完好;而当di=1 时,表明界面完全失效,层间开裂。界面临界断裂能为拉力-位移曲线与坐标轴所围成的面积,可以表示为:
ϕn=δfnt0n2,ϕs,t=δfs,tt0s,t2 (6) 式中:
ϕn 为界面法向临界断裂能;ϕs 和ϕt 分别为横、纵界面切向临界断裂能;δfn 为断裂发生时的界面法向相对位移值;δfs 和δft 分别为断裂发生时横、纵界面切向相对位移值;t0n 为界面法向内聚强度;t0s 和t0t 分别为横、纵界面切向内聚强度。双线性内聚力模型的拉力-位移曲线上升段和下降段均为直线型。上升段的斜率表示界面的初始刚度,为一定值;界面损伤萌生后,界面刚度随着界面相对位移增加而减小,直至界面完全断开。双线性内聚力模型具有形式简洁、便于应用的特点,比较适用于研究脆性材料界面断裂行为[32]。
1.2 指数型内聚力模型
Xu和Needleman[16]为解释复合晶体材料孔隙成核、界面脱粘现象,提出了耦合的指数内聚力模型。该指数型内聚力模型的二维形式可以表示为:
ϕ(δn,δt)=ϕn+ϕnexp(−δnδ0n){[1−r+δnδ0n]1−qr−1−[q+(r−qr−1)δnδ0n]exp(−δ2t(δ0t)2)} (7) 式中:
δn 和δt 分别为界面法向和切向相对位移值;δ0n 和δ0t 分别为损伤萌生时界面法向和切向相对位移值;ϕ 为断裂过程中总的界面断裂能;其中q 和r 可以表示为:q=ϕtϕn,r=δ∗nδ0n (8) 式中,
δ∗n 为界面完全切向开裂时界面法向位移值。其中:ϕn=et0nδ0n,ϕt=√e2t0tδ0t (9) 式中,
e=exp(1) 。界面法向和切向拉力可以通过势函数(7)对界面法向和切向相对位移求偏导得到:
tn=∂ϕ(δn,δt)∂δn=−ϕnδ0nexp(−δnδ0n){δnδ0nexp(−δ2t(δ0t)2)+1−qr−1[1−exp(−δ2t(δ0t)2)][r−δnδ0n]} (10) tt=∂ϕ(δn,δt)∂δt=−ϕnδ0n(2δ0nδ0t)δtδ0t{q+(r−qr−1)δnδ0n}×exp(−δnδ0n)exp(−δ2t(δ0t)2) (11) 在纯法向和切向开裂模式下,由式(10)和式(11)可以计算得到界面法向拉力和界面切向拉力分别为:
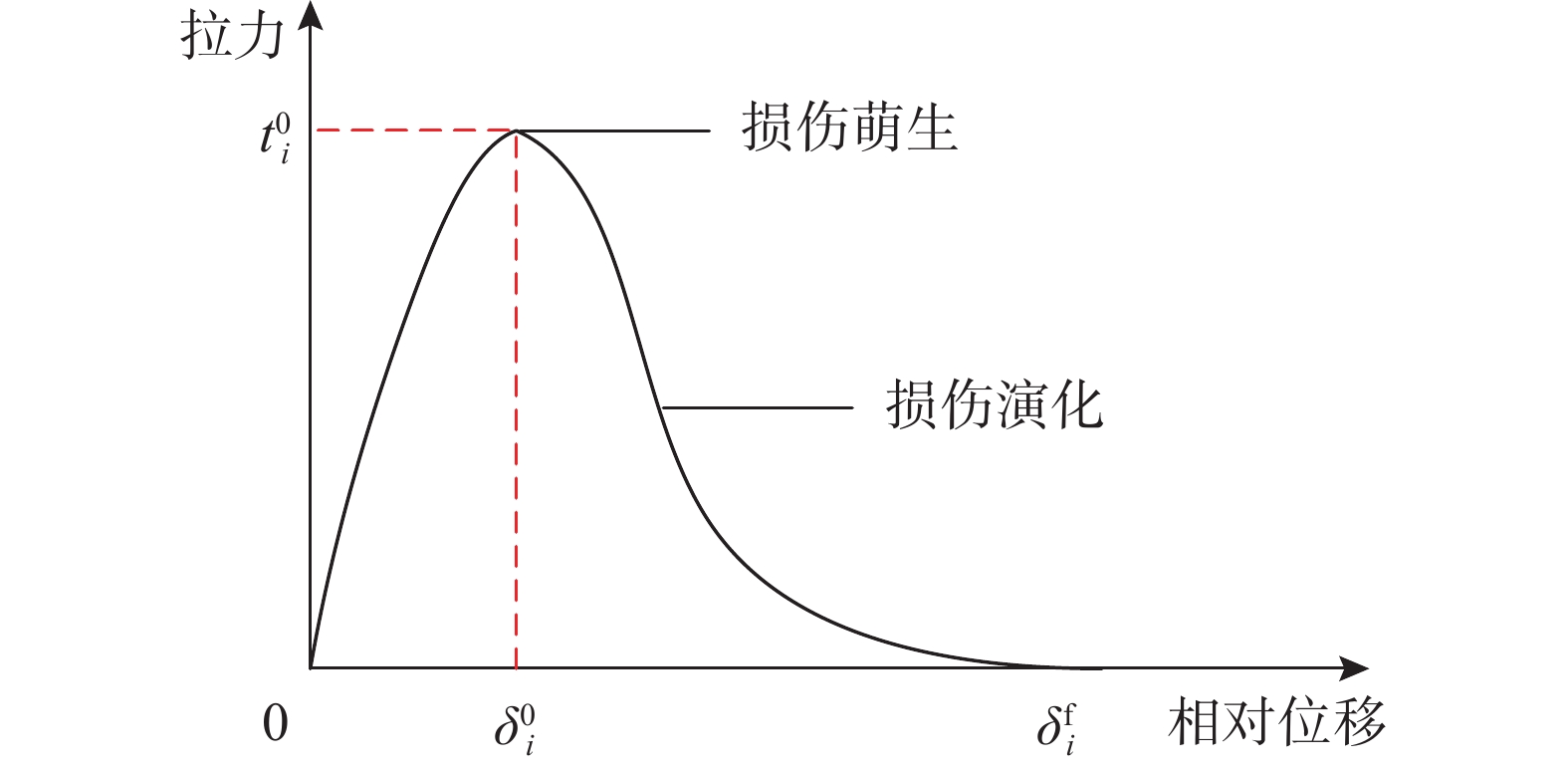
tn=et0nδnδ0nexp(−δnδ0n) (12) tt=√2et0tδtδ0texp(−(δtδ0t)2) (13) 则单一模式下,指数型内聚力模型的拉力-位移关系如图4所示。
指数型内聚力模型的拉力-位移曲线的上升段和下降段均为幂指数函数。随界面损伤的发展,界面刚度发生连续性变化,拉力-位移曲线的非线性衰减能合理描述界面刚度的软化过程[33]。
1.3 双线性和指数型内聚力模型的适用性分析
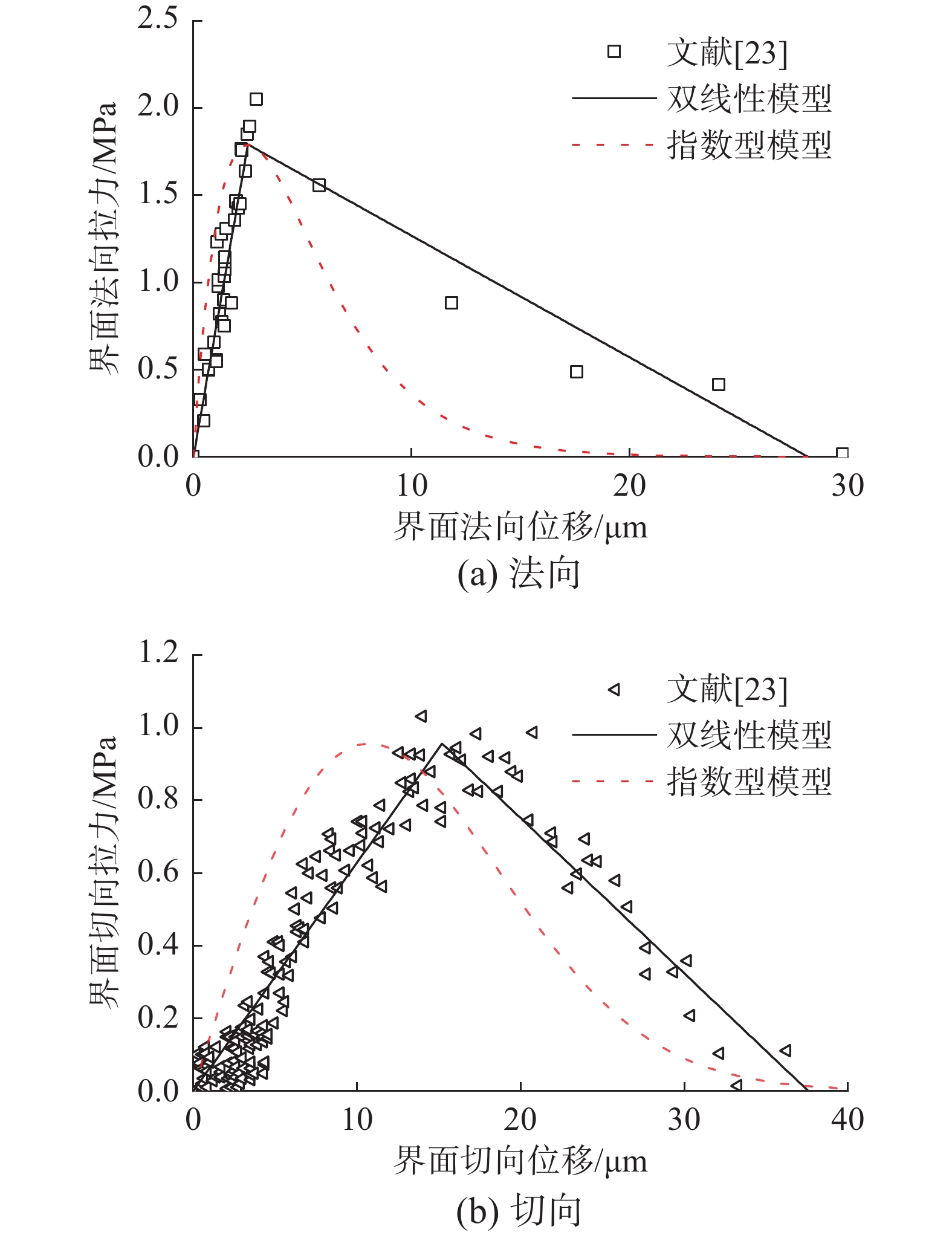
分别采用双线性内聚力模型和指数型内聚力模型对文献[23]中的轨道板与砂浆界面试验数据进行拟合,拟合方法选取最小二乘法,结果如图5所示。
由图5可知,由双线性内聚力模型拟合界面法向开裂试验数据,得到界面法向内聚强度为1.792 MPa及其对应的界面相对位移为2.5 μm,界面法向刚度为716.8 MPa/mm,界面法向临界断裂能为25.24 J/m2。由指数型内聚力模型拟合试验数据,得到界面法向临界断裂能为12.2 J/m2,远小于双线性内聚力模型计算值。这主要与指数型内聚力模型拉力-位移曲线下降段衰减速率过快有关。
由双线性内聚力模型拟合界面切向开裂试验数据,得到界面切向内聚强度为0.956 MPa及其对应的界面相对位移为15.2 μm,界面切向刚度为62.9 MPa/mm,界面切向临界断裂能为17.96 J/m2。由指数型内聚力模型拟合试验数据,得到界面切向临界断裂能为16.4 J/m2,大于双线性内聚力模型计算值,且损伤萌生时界面的相对位移较双线性模型小。这主要由指数型内聚力模型拉力-位移曲线上升段增加速率过快导致。
在复杂的荷载作用下,为了合理阐述轨道板与CA砂浆界面离缝机理,内聚力模型的选择较为关键。虽然混凝土属于准脆性材料,但在宏观断裂过程中应力和应变具有非线性的相互依赖关系[34],并且无砟轨道结构在温度和列车荷载作用下,层间界面受力较为复杂。双线性内聚力模型可能无法准确描述无砟轨道结构层间损伤行为,而指数型内聚力模型可以表征层间损伤过程中界面刚度的连续性,但指数型拉力-位移曲线的上升段和下降段的增加和衰减速率无法有效控制。所以在既有内聚力模型基础上,有必要发展指数型内聚力模型,以符合轨道板与CA砂浆层间界面损伤萌生和发展过程。
2 改进指数型内聚力模型
2.1 改进指数型内聚力模型的建立
在上述内聚力模型的基础上,本文提出了改进的指数型内聚力模型,用来描述轨道板与CA砂浆层间界面的宏观断裂行为。宏观断裂行为需要满足以下断裂边界条件:
• 当界面相对位移达到断裂发生时的界面相对位移值
δfi 时,界面会发生失效,此时:ti(δfi)=0 (14) • 拉力-位移曲线下的面积对应于界面临界断裂能,因此界面临界断裂能
ϕi 可表示为:ϕi=∫δfi0tidδi (15) • 当界面相对位移达到损伤萌生时界面相对位移值
δ0i 时,界面拉力达到最大值。此时界面拉力应满足:∂ti∂δi|δi=δ0i=0 (16) • 界面拉力最大值应等于界面内聚强度
t0i ,即:ti(δ0i)=t0i (17) 在满足以上断裂边界条件的基础上,通过引入指数系数来改善界面断裂过程中的非线性特征。本文提出了改进的指数型内聚力模型,其拉力-位移关系可表示为:
法向(i=n)ti={t0iδiδ0i,0⩽δi<δ0it0ie(δiδ0i)ni2exp[−(δiδ0i)ni2],δ0i⩽δi<δfi0,其他 (18) 切向(i=s,t)ti={t0ie(δiδ0i)ni1exp[−(δiδ0i)ni1],0⩽δi<δ0it0ie(δiδ0i)ni2exp[−(δiδ0i)ni2],δ0i⩽δi<δfi0,其他 (19) 式中:
ni1 为上升段指数系数;ni2 为下降段指数系数。改进指数型内聚力模型的拉力-位移曲线如图6所示。单一模式下界面临界断裂能可表示为:
ϕi=∫∞0tidδi,i=n,s,t (20) 在单一模式下,改进的指数型内聚力模型法向和切向下降段分别采用指数形式,通过引入指数系数,可改变下降段曲线衰减速率。且指数形式可以表征界面拉力和界面相对位移之间的非线性关系。
2.2 改进指数型内聚力模型参数确定
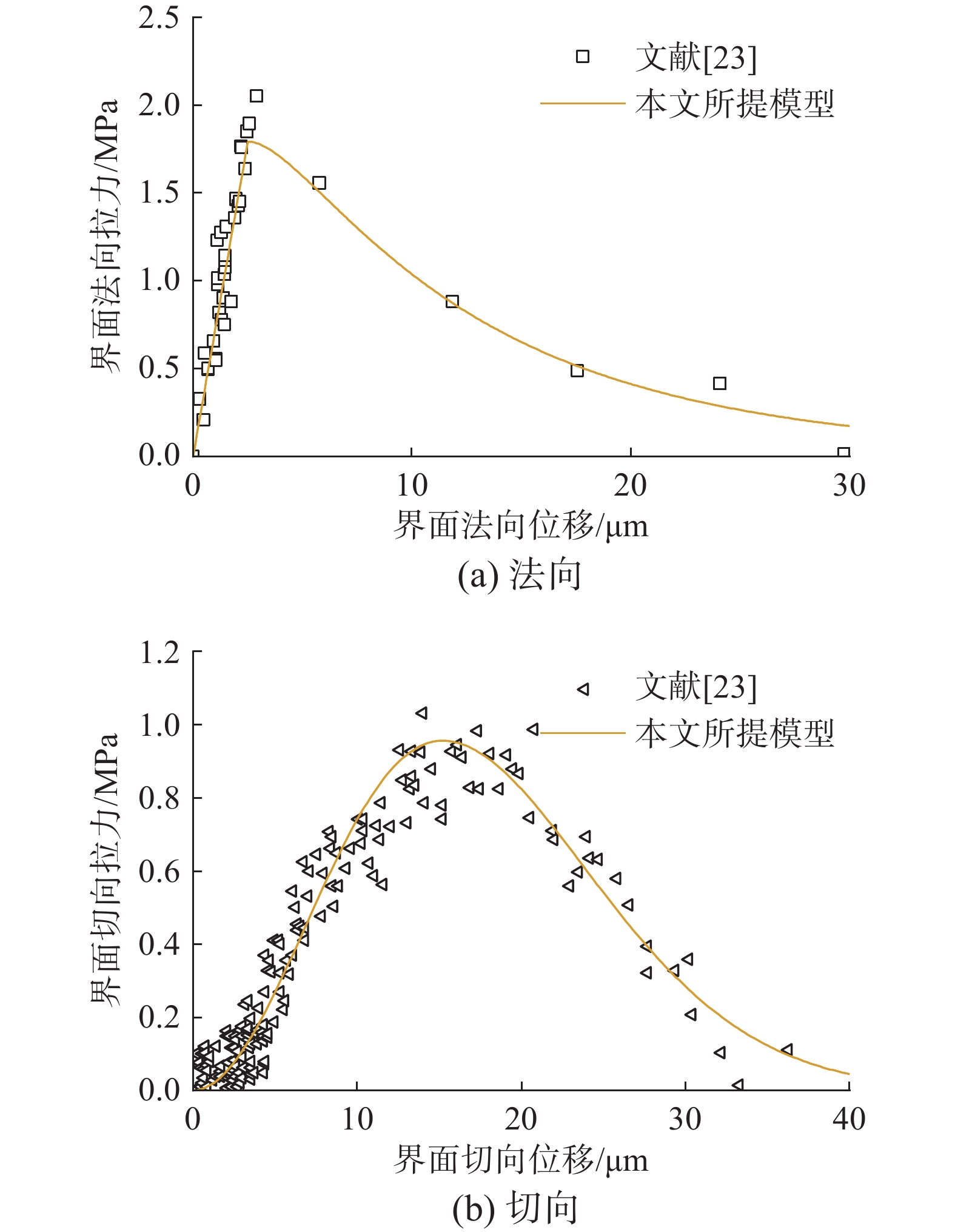
采用改进指数型内聚力模型对文献[23]的轨道板与砂浆界面试验数据进行拟合,结果见图7。采用最小二乘法分别拟合上升段和下降段试验数据,确定改进指数型内聚力模型的系数,进而可以得到界面内聚力模型参数,即:界面内聚强度、损伤萌生时界面相对位移和界面临界断裂能。
在界面法向,由拟合结果可以得到改进指数型内聚力模型上升段刚度为716.8 MPa/mm,下降段系数
nn2 为0.6429。得到界面法向内聚强度为1.792 MPa及损伤萌生时界面相对位移为2.5 μm,界面法向临界断裂能为22.54 J/m2。在界面切向,由拟合结果可以得到改进指数型内聚力模型上升段系数nt1 为1.934,下降段系数nt2 为1.822。得到界面切向内聚强度为0.956 MPa及损伤萌生时界面相对位移为15.2 μm,界面切向临界断裂能为18.7 J/m2。2.3 改进指数型内聚力模型验证
为验证改进指数型内聚力模型模拟轨道板与CA砂浆层间界面损伤开裂行为的合理性。将改进指数型内聚力模型与既有内聚力模型(双线性、指数型)进行对比,如图5和图7所示。由界面的拉力-位移曲线可以看出,改进指数型内聚力模型能较好地反映试验现象,具体对比结果如表1所示。由表1可知,由改进指数型内聚力模型计算的界面内聚强度与临界断裂能和文献[23]的计算结果比较接近,说明了改进指数型内聚力模型模拟轨道板与CA砂浆界面开裂行为的合理性。
表 1 几种内聚力模型拟合结果Table 1. Fitting results of several cohesive zone models由试验数据可知,轨道板与CA砂浆界面的拉力-位移关系具有非线性特征。描述拉力-位移非线性特征的模型主要有多项式和指数型模型,相比多项式内聚力模型,指数型内聚力模型在纯法向失效状态下可以准确保持法向拉力为0,所以指数型内聚力模型能更好地分析界面损伤。其次,指数型内聚力模型的拉力及其导数是连续函数,在应用和计算方面具有优势。本文模型是在指数型内聚力模型的基础上提出来的,因此,本文模型具有指数型模型的优点。
3 轨道板与CA砂浆层间粘结预测结果对比
为说明改进指数型内聚力模型模拟轨道板与CA砂浆界面离缝的适用性,将改进的指数型模型和目前所采用的双线性和指数型模型进行对比。参考文献[23]的无砟轨道层间粘结试验数据,分别采用双线性内聚力模型、指数型内聚力模型和本文所提模型进行拟合。具体拟合结果见图5及图7。
3.1 界面法向开裂
由图5(a)和图7(a)可知,在轨道板与CA砂浆层界面法向开裂的过程中,改进的指数型内聚力模型可以更好地拟合上升段和下降段试验数据,尤其对下降段的试验结果拟合效果较双线性内聚力模型好。由表1的拟合结果可知,本文所提模型计算的界面临界断裂能和文献[23]的试验结果比较接近,且小于双线性内聚力模型计算值。
因下降段数据点较少,本文将法向上升段和下降段预测结果绘于同一图中。采用不同内聚力模型对界面法向拉力进行预测,预测结果和试验数据对比如图8所示。
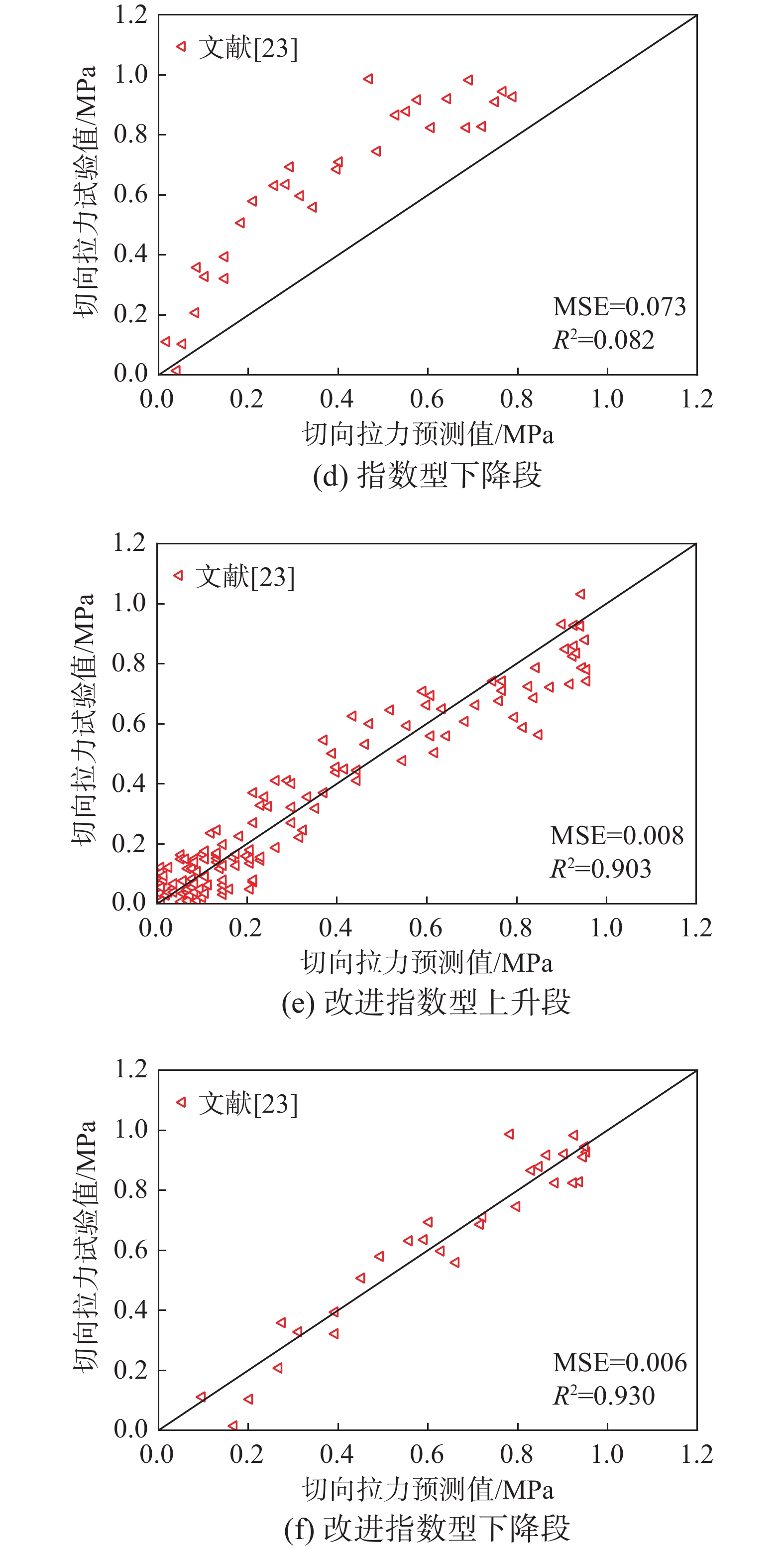
由图8可知,改进指数型模型和双线性模型对文献[23]的界面法向开裂试验数据预测效果较好,而指数型模型对文献[23]的试验数据预测偏大。采用改进的指数型内聚力模型计算的决定系数R2为0.902,均方误差(Mean Square Error, MSE)为0.028,可以较好预测试验结果;由双线性内聚力模型计算的决定系数R2为0.89,均方误差MSE为0.031,可知由改进指数型内聚力模型计算的均方误差比双线性模型小,说明改进指数型模型对界面脱粘的模拟效果好于双线性模型。而采用指数型内聚力模型计算的决定系数R2为0.243,均方误差MSE为0.214,模型预测值明显大于试验值,对试验结果预测性较差,这是由于指数型模型上升段和下降段的增加和衰减速率过快,且下降段试验数据较少,从而使多数预测值大于试验值。通过综合考虑试验结果预测的准确性和法向试验数据下降段的非线性,改进的指数型模型对试验结果的预测效果要好于双线性模型和指数型模型,采用改进的指数型模型可以较为合理地模拟轨道板与CA砂浆层间界面的法向拉力-位移关系。
3.2 界面切向开裂
由图5(b)和图7(b)可知,对于轨道板与CA砂浆层间界面切向试验结果,改进的指数型内聚力模型和双线性内聚力模型均能较好拟合试验数据。而改进指数型模型可以更好地表征界面切向损伤过程中拉力-位移关系的非线性。通过表1的拟合结果可知,本文所提模型计算的界面临界断裂能和文献[23]的试验计算值比较接近。
采用不同内聚力模型对界面切向拉力进行预测,预测结果和试验数据对比如图9所示。
为准确评估模型预测效果,本文将切向上升段和下降段预测结果分开考虑。由图9可知,改进指数型模型和双线性模型对文献[23]的界面切向开裂试验数据预测效果较好,而指数型模型对文献[23]的上升段试验数据预测偏大,对下降段试验数据预测偏小。采用改进的指数型内聚力模型计算上升段和下降段的决定系数R2分别为0.903和0.93,均方误差MSE分别为0.008和0.006,可以比较好地预测试验结果。由双线性内聚力模型计算上升段和下降段的决定系数R2分别为0.883和0.896,均方误差MSE分别为0.009和0.008,说明在模拟轨道板与CA砂浆层间界面切向开裂行为时,改进指数型模型对试验结果的预测效果要好于双线性内聚力模型。而采用指数型内聚力模型计算上升段和下降段的决定系数R2分别为−0.08和0.082,均方误差MSE分别为0.085和0.073,模型预测值和试验值的误差较大,对试验结果预测性较差。综上,改进的指数型模型对试验结果的预测效果要好于双线性模型和指数型模型,且可以较好地表征界面切向拉力-位移曲线的非线性特性。
4 结论
本文基于内聚力本构理论和试验数据,分别采用双线性和指数型内聚力模型对CRTS Ⅱ 型轨道板与CA砂浆层间离缝进行预测,分析了双线性和指数型内聚力模型的适用性。在此基础上,提出了改进的指数型内聚力模型,并确定了改进指数型内聚力模型的主要参数。最后,采用不同内聚力模型对轨道板与CA砂浆层间离缝进行预测分析。得到以下结论:
(1) 双线性内聚力模型上升段和下降段均为线性,极值点导数不连续;指数型内聚力模型上升段和下降段非线性特征难以控制。而提出的改进指数型内聚力模型则改善了既有模型的不足。
(2) 改进指数型内聚力模型采用分段函数,通过引入指数系数改善了模型的非线性特征。可以高效进行轨道板-CA 砂浆界面内聚强度、损伤萌生时界面相对位移和界面临界断裂能的计算,分析结果与试验值基本一致。
(3) 改进指数型模型能准确描述轨道板与CA砂浆界面开裂行为,预测精度高于双线性和指数型内聚力模型。改进指数型内聚力模型可更好地表征轨道板与CA砂浆层间界面法向和切向开裂行为。
-
表 1 几种内聚力模型拟合结果
Table 1 Fitting results of several cohesive zone models
-
[1] Gautier P E. Slab track: Review of existing systems and optimization potentials including very high speed [J]. Construction and Building Materials, 2015, 92: 9 − 15. doi: 10.1016/j.conbuildmat.2015.03.102
[2] Sadeghi J, Esmaeili M H. Effectiveness of track stiffness reduction in attenuation of metro induced vibrations received by historical buildings [J]. Latin American Journal of Solids and Structures, 2018, 15(11): 1 − 11.
[3] 赵国堂, 高亮, 赵磊, 等. CRTS Ⅱ 型板式无砟轨道板下离缝动力影响分析及运营评估[J]. 铁道学报, 2017, 39(1): 1 − 10. Zhao Guotang, Gao Liang, Zhao Lei, et al. Analysis of dynamic effect of gap under CRTS Ⅱ track slab and operation evaluation [J]. Journal of the China Railway Society, 2017, 39(1): 1 − 10. (in Chinese)
[4] 何川. CRTS Ⅱ 型板式无砟轨道砂浆离缝的影响及维修指标研究[D]. 成都: 西南交通大学, 2013. He Chuan. Study on influence of interface connections damage and maintenance index of the CRTS Ⅱ slab track [D]. Chendu: Southwest Jiaotong University, 2013. (in Chinese)
[5] 戴公连, 粟淼. 剪切荷载下板式无砟轨道界面黏结破坏机理[J]. 华中科技大学学报(自然科学版), 2016, 44(1): 16 − 21. Dai Gonglian, Su Miao. Mechanism of interfacial bond failure for slab ballastless track under shear loading [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(1): 16 − 21. (in Chinese)
[6] 黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 448 − 459. doi: 10.6052/1000-0992-2010-4-J2010-002 Huang Dan, Zhang Qing, Qiao Pizhong, et al. A review on peridynamics (PD) method and its applications [J]. Advances in Mechanics, 2010, 40(4): 448 − 459. (in Chinese) doi: 10.6052/1000-0992-2010-4-J2010-002
[7] 李录贤, 王铁军. 扩展有限元法(XFEM)及其应用[J]. 力学进展, 2005, 35(1): 5 − 20. doi: 10.3321/j.issn:1000-0992.2005.01.002 Li Luxian, Wang Tiejun. The extended finite element method and its applications-a review [J]. Advances in Mechanics, 2005, 35(1): 5 − 20. (in Chinese) doi: 10.3321/j.issn:1000-0992.2005.01.002
[8] 卢子兴. 复合材料界面的内聚力模型及其应用[J]. 固体力学学报, 2015, 36(增刊 1): 85 − 94. Lu Zixing. A simple review for cohesive zone models of composite interface and their applications [J]. Chinese Journal of Solid Mechanics, 2015, 36(Suppl 1): 85 − 94. (in Chinese)
[9] 张豪, 于继东, 裴晓阳, 等. 相场断裂方法发展概况[J]. 高压物理学报, 2019, 33(3): 1 − 12. Zhang Hao, Yu Jidong, Pei Xiaoyang, et al. An overview of phase field approach to fracture [J]. Chinese Journal of High Pressure Physics, 2019, 33(3): 1 − 12. (in Chinese)
[10] Barenblatt G I. The formation of equilibrium cracks during brittle fracture: general ideas and hypotheses, axially symmetric cracks [J]. Advances in Applied Mechanics, 1959, 23(3): 622 − 636.
[11] Dugdale D S. Yielding of steel sheets containing slits [J]. Journal of the Mechanics and Physics of Solids, 1960, 8(2): 100 − 104. doi: 10.1016/0022-5096(60)90013-2
[12] Mi Y, Crisfield M A, Davies G A O, et al. Progressive delamination using interface elements [J]. Journal of Composite Materials, 1998, 32(14): 1246 − 1272. doi: 10.1177/002199839803201401
[13] Camanho P P, Davila C G, De Moura M F. Numerical simulation of mixed-mode progressive delamination in composite materials [J]. Journal of Composite Materials, 2003, 37(16): 1415 − 1438. doi: 10.1177/0021998303034505
[14] Rose J H, Ferrante J, Smith J R. Universal binding energy curves for metals and bimetallic interfaces [J]. Physics Review Letters, 1981, 47(9): 675 − 678. doi: 10.1103/PhysRevLett.47.675
[15] Rice J R. Dislocation nucleation from a crack tip: an analysis based on the peierls concept [J]. Journal of the Mechanics and Physics of Solids, 1992, 40(2): 239 − 271. doi: 10.1016/S0022-5096(05)80012-2
[16] Xu X P, Needleman A. Numerical simulations of fast crack growth in brittle solids [J]. Journal of the Mechanics and Physics of Solids, 1994, 42(9): 1397 − 1434. doi: 10.1016/0022-5096(94)90003-5
[17] Bosch M J V D, Schreurs P J G, Geers M G D. An improved description of the exponential Xu and Needleman cohesive zone law for mixed-mode decohesion [J]. Engineering Fracture Mechanics, 2006, 73(9): 1220 − 1234. doi: 10.1016/j.engfracmech.2005.12.006
[18] Tvergaard V, Hutchinson J W. The influence of plasticity on mixed mode interface toughness [J]. Journal of the Mechanics and Physics of Solids, 1993, 41(6): 1119 − 1135. doi: 10.1016/0022-5096(93)90057-M
[19] 吴业飞, 陈伟球. 基于内聚力模型的FRP-混凝土粘结强度分析[J]. 工程力学, 2010, 27(7): 113 − 119. Wu Yefei, Chen Weiqiu. Cohesive zone model based analysis of bond strength between FRP and concrete [J]. Engineering Mechanics, 2010, 27(7): 113 − 119. (in Chinese)
[20] Park K, Paulino G H, Roesler J R. A unified potential-based cohesive model of mixed-mode fracture [J]. Journal of the Mechanics and Physics of Solids, 2009, 57(6): 891 − 908. doi: 10.1016/j.jmps.2008.10.003
[21] 张振宇, 万璐, 冯吉利. 带有橡胶垫层的混凝土接触特性试验及其内聚力模型[J]. 工程力学, 2018, 35(8): 55 − 66. doi: 10.6052/j.issn.1000-4750.2017.03.0239 Zhang Zhenyu, Wan Lu, Feng Jili. Characteristics of direct shear test for plain concrete joint with rubber and its cohesive zone model [J]. Engineering Mechanics, 2018, 35(8): 55 − 66. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.03.0239
[22] 王明昃. 高速铁路列车荷载-环境复合作用下双块式无砟轨道层间粘结失效行为分析[D]. 成都: 西南交通大学, 2018. Wang Mingze. Interface failure analysis of double-block ballastless track in high-speed railway under joint actions of train and environment loads [D]. Chengdu: Southwest Jiaotong University, 2018. (in Chinese)
[23] 刘学毅, 苏成光, 刘丹, 等. 轨道板与砂浆粘结试验及内聚力模型参数研究[J]. 铁道工程学报, 2017, 34(3): 22 − 28. doi: 10.3969/j.issn.1006-2106.2017.03.005 Liu Xueyi, Su Chengguang, Liu Dan, et al. Research on the bond properties between slab and CA mortar and the parameters study of cohesive model [J]. Journal of Railway Engineering Society, 2017, 34(3): 22 − 28. (in Chinese) doi: 10.3969/j.issn.1006-2106.2017.03.005
[24] Dai G L, Su M. Full-scale field experimental investigation on the interfacial shear capacity of continuous slab track structure [J]. Archives of Civil and Mechanical Engineering, 2016, 16(3): 485 − 493. doi: 10.1016/j.acme.2016.03.005
[25] 赵春发, 刘建超, 毛海和, 等. 温度梯度荷载作用下CRTS Ⅱ 型板式无砟轨道砂浆层界面损伤分析[J]. 中国科学: 技术科学, 2018, 48(1): 79 − 86. doi: 10.1360/N092017-00254 Zhao Chunfa, Liu Jianchao, Mao Haihe, et al. Interface damage analysis of CA mortar layer of the CRTS Ⅱ ballastless slab track under temperature gradient loads [J]. Scintia Sinica Technologica, 2018, 48(1): 79 − 86. (in Chinese) doi: 10.1360/N092017-00254
[26] Zhang Y R, Wu K, Gao L, et al. Study on the interlayer debonding and its effects on the mechanical properties of CRTS Ⅱ slab track based on viscoelastic theory [J]. Construction and Building Materials, 2019, 224(10): 387 − 407.
[27] 钟阳龙, 高亮, 王璞, 等. 温度荷载下CRTS II 型轨道板与CA砂浆界面剪切破坏机理[J]. 工程力学, 2018, 35(2): 230 − 238. doi: 10.6052/j.issn.1000-4750.2016.09.0753 Zhong Yanglong, Gao Liang, Wang Pu, et al. Mechanism of interfacial shear failure between CRTS II slab and CA mortar under temperature loading [J]. Engineering Mechanics, 2018, 35(2): 230 − 238. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.09.0753
[28] 陈龙, 陈进杰, 王建西. CRTS Ⅱ 型板式无砟轨道层间传力规律及离缝破坏研究[J]. 铁道学报, 2018, 40(8): 130 − 138. doi: 10.3969/j.issn.1001-8360.2018.08.017 Chen Long, Chen Jinjie, Wang Jianxi. Study on stress transfer and interface damage of CRTS Ⅱ slab ballastless track [J]. Journal of the China Railway Society, 2018, 40(8): 130 − 138. (in Chinese) doi: 10.3969/j.issn.1001-8360.2018.08.017
[29] Zhu S Y, Cai C B. Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads [J]. International Journal of Non-Linear Mechanics, 2014, 58: 222 − 232. doi: 10.1016/j.ijnonlinmec.2013.10.004
[30] 钟阳龙. CRTS Ⅱ 型无砟轨道板-砂浆层层间开裂机理及控制研究[D]. 北京: 北京交通大学, 2018. Zhong Yanglong. Research on the interface cracking of CRTS Ⅱ ballastless track slab-mortar layer and its control [D]. Beijing: Beijing Jiaotong University, 2018. (in Chinese)
[31] Hillerborg A, Modeer M, Petersson P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements [J]. Cement and Concrete Research, 1976, 6(6): 773 − 781. doi: 10.1016/0008-8846(76)90007-7
[32] Yamakov V, Saether E, Phillips D R, et al. Molecular-dynamics simulation-based cohesive zone representation of intergranular fracture processes in aluminum [J]. Journal of the Mechanics and Physics of Solids, 2006, 54(9): 1899 − 1928. doi: 10.1016/j.jmps.2006.03.004
[33] Liu P F, Islam M M. A nonlinear cohesive model for mixed-mode delamination of composite laminates [J]. Composite Structures, 2013, 106: 47 − 56. doi: 10.1016/j.compstruct.2013.05.049
[34] Elices M, Guinea G V, Gomez J, et al. The cohesive zone model: Advantages, limitations and challenges [J]. Engineering Fracture Mechanics, 2002, 69(2): 137 − 163. doi: 10.1016/S0013-7944(01)00083-2
-
期刊类型引用(3)
1. 王瑶,和振兴. 轨道板侧裂纹对车辆-轨道动力性能的影响研究. 高速铁路技术. 2025(01): 55-62 .  百度学术
百度学术
2. 张雅琴,高亮,钟阳龙,蒋函珂,黄伊琛. 夏季高温下支承层斜裂缝诱发纵连板上拱规律研究. 铁道学报. 2024(03): 165-175 .  百度学术
百度学术
3. 王平,李抒效,闫正,徐井芒,李智恒. 板间离缝对高速道岔转辙器区轨道动力响应的影响. 中南大学学报(自然科学版). 2023(12): 4946-4955 .  百度学术
百度学术
其他类型引用(6)



 下载:
下载: