基于HLRF法与修正对称秩1方法的改进可靠度方法

范文亮; 刘丞; 李正良

doi:10.6052/j.issn.1000-4750.2021.05.0379

基于HLRF法与修正对称秩1方法的改进可靠度方法

范文亮^{1, 2, ,},
刘丞^1,,
李正良^{1, 2,}

1.
重庆大学土木工程学院，重庆 400045
2.
山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045

基金项目: 中能建规划设计集团科技项目(GSKJ2-T05-2020)；国家自然科学基金项目(51678092)

详细信息

作者简介:
刘　丞(1995−)，男，重庆石柱人，博士生，主要从事可靠度分析研究 (E-mail: liucheng19950330@163.com)

李正良(1963−)，男，江苏江阴人，教授，博士，博导，主要从事结构工程和结构抗风方面研究(E-mail: lizhengl@hotmail.com)

通讯作者:
范文亮(1979−)，男，江西九江人，教授，博士，博导，主要从事结构工程、随机系统分析和可靠度分析方面的研究(E-mail: davidfwl@126.com)

中图分类号: TB114.3；TU318+.1
计量
- 文章访问数: 583
- HTML全文浏览量: 112
- PDF下载量: 154
出版历程
- 收稿日期: 2021-05-20
- 修回日期: 2021-10-31
- 录用日期: 2021-11-15
- 网络出版日期: 2021-11-15
- 刊出日期: 2022-08-31

IMPROVED RELIABILITY METHOD BASED ON HLRF AND MODIFIED SYMMETRIC RANK 1 METHOD

FAN Wen-liang^{1, 2, ,},
LIU Cheng^1,,
LI Zheng-liang^{1, 2,}

1.
School of Civil Engineering, Chongqing University, Chongqing 400045, China
2.
Key Laboratory of New Technology for Construction of Cities in Mountain Area (Chongqing University), Ministry of Education, Chongqing 400045, China

摘要

摘要: 一次可靠度方法简单、高效，但在处理强非线性功能函数时存在较大误差；已有的二次可靠度方法在提高精度的同时往往降低了效率。为此，该文中在发展改进一次可靠度方法的同时提出了更好地兼顾精度与效率的改进二次可靠度方法。将修正对称秩1方法与HLRF法的步长确定策略相结合，提出了具有较好收敛性的改进一次可靠度方法，且在基本不增加计算量的前提下获得了功能函数的近似Hessian矩阵；结合坐标旋转、单变量降维近似和非中心卡方分布，提出了与改进一次可靠度方法同效率但具有更高精度的改进二次可靠度方法；通过数值算例和工程算例验证了建议方法的广泛适用性以及精度或效率上的优势。
- 结构 /
- 可靠度方法 /
- 改进一次可靠度方法 /
- 改进二次可靠度方法 /
- 近似Hessian矩阵
Abstract: The first-order reliability method (FORM) is simple and efficient, but the error is significant when dealing with strong nonlinear functions. With existing second-order reliability methods (SORM), the calculation accuracy is improve, but the efficiency is reduced. In this research, an improved SORM, which can achieve better balance between accuracy and efficiency, is presented. The modified symmetric rank 1 method is combined with the determination of step length of the HLRF method, and an improved FORM with better convergence is proposed, in which the approximate Hessian matrix of performance function is obtained without increasing the amount of function evaluations. Combining the coordinate rotation with the univariate dimensional reduction approximation of the performance function according to its known gradient vector and Hessian matrix, and introducing the non-central chi-square distribution, the paper proposes an improved SORM with the same efficiency but higher accuracy. The wide applicability and advantages in both accuracy and efficiency of the proposed methods are verified by several numerical examples and engineering examples.
- structure /
- reliability method /
- improved first-order reliability method /
- improved second-order reliability methods /
- approximated Hessian matrix

HTML全文

在结构可靠度分析领域，研究者经常使用概率分布模型来描述目标结构的荷载、材料属性等不确定性因素。为考虑这些不确定性因素对结构性能及安全性的影响，发展准确而有效的可靠度分析方法是非常必要的。

一次可靠度方法^[1-7]是最常用的可靠度分析方法。其中的验算点法(即Hasofer-Lind-Rackwitz-Fiessler方法，简称HLRF法)以其迭代格式简单、收敛迅速，被广泛应用于求解可靠指标，且研究者针对HLRF法在面对复杂问题时常出现的迭代迂回振荡甚至不收敛的问题，发展了一系列改进的HLRF法^[8-11]。由于验算点的迭代计算在形式上可以表示为一个约束优化问题，通过引入拉格朗日乘子可得到与之等效的无约束优化方程，因此，将收敛性能更优的无约束优化方法(如拟牛顿优化方法等)引入可靠度分析是可行的研究方向。文献[12]将拟牛顿优化方法中的BFGS(Broyden-Fletcher-Goldfarb-Shanno)方法^[13]引入可靠度分析，并结合HLRF法的步长参数，提出了HLRF-BFGS方法，避免了传统方法中的步长搜索过程，改善了计算效率。

一次可靠度方法采用了功能函数在验算点处的线性近似，因此对于功能函数非线性程度较高的强非线性问题，可靠指标的精度往往很难保证。为此，在一次可靠度方法的基础上，若引入功能函数在验算点处的二次函数近似，并以此为基础计算可靠指标，则形成了二次可靠度方法^[14-18]。由于需要利用功能函数在验算点处的Hessian矩阵，若采用差分法对其计算，尽管改善了计算精度，但降低了计算效率。利用拟牛顿优化方法中对称秩1方法^[13]近似Hessian矩阵的良好特性^[19]，文献[20-21]分别将一次可靠度方法的传统优化求解结果或HLRF-BFGS方法的求解结果与对称秩1方法的近似Hessian矩阵计算相结合，给出了与一次可靠度方法具有相同效率的二次可靠度方法。然而，在利用各优化方法获得一次可靠度的结果后，上述方法均主观地将迭代过程的结果直接用于对称秩1方法中Hessian矩阵的正迭代，不能保证迭代结果的匹配性；此外，由于引入拉格朗日乘子处理约束优化问题，迭代过程中的Hessian矩阵是针对拉格朗日函数，而非功能函数，因此，严格意义上需通过拉格朗日函数的Hessian矩阵确定功能函数的Hessian矩阵。

为此，本文将修正对称秩1方法^[22]与HLRF法的步长确定策略相结合，发展了一种具有更优收敛性能的改进一次可靠度方法；其次，利用改进一次可靠度方法的迭代结果给出了功能函数的近似Hessian矩阵，保证了一次可靠度分析与Hessian矩阵近似中参数的匹配性。然后，结合坐标旋转、单变量降维近似模型与非中心卡方分布，提出了可兼顾效率和精度的改进二次可靠度方法。

1 基于修正对称秩1方法的改进一次可靠度方法

1.1 标准正态空间内可靠度问题的等价描述

假设可靠度问题的功能函数为：

$G = g\left( {\boldsymbol{X}} \right)$

(1)

式中， ${\boldsymbol{X}}=\left \{ {X_1,\;X_2,\;\cdots,\;X_n}\right \}$ 为功能函数的基本随机向量，n为随机变量的数量。

首先，可引入Nataf变换将X转换为独立的标准正态向量U，即：

${V_i} = {{{\varPhi }}^{ - 1}}\left( {{F_i}\left( {{X_i}} \right)} \right)$

(2)

${{\boldsymbol{\rho}} _{\boldsymbol{V}}} = {L^{\rm{T}}}L$

(3)

${\boldsymbol{U}} = {L^{ - 1}}{\boldsymbol{V}}$

(4)

式中：Φ⁻¹(∙)为标准正态变量的累积分布函数Φ(∙)的反函数；F_i(∙)为X_i的累积分布函数；V_i为与X_i对应的标准正态变量；ρ_V为V={V₁, V₂, ···, V_n}的等效相关系数矩阵，可根据文献[22]的高效方法确定如下：

${{\boldsymbol{\rho}} _{{\boldsymbol{X}},ij}} = \mathop \sum \limits_{k = 1}^{{\text{min}}\left( {{m_i},{m_j}} \right)} \frac{1}{{k!}}{I_{i,k}}{I_{j,k}}{( {{{\boldsymbol{\rho }}_{V,ij}}} )^k}$

(5)

${I_{i,k}} = \mathop \smallint \nolimits_{ - \infty }^\infty \left( {\frac{{F_i^{ - 1}\left( {{{\varPhi }}\left( {{v_i}} \right)} \right) - {\mu _i}}}{{{\sigma _i}}}} \right){{{{He{r}}}}_k}\left( {{v_i}} \right)\varphi \left( {{v_i}} \right){\rm{d}}{v_i}$

(6)

式中：ρ_X为X的相关系数矩阵；μ_i和σ_i分别为X的均值和标准差；Her_k(∙)为Hermite正交多项式；φ(∙)为标准正态变量的概率密度函数；m_i为方程的最高次数。表1给出了三种常用分布的m_i，其余常用分布的m_i详见文献[23]。

表 1 常用分布的m_i

Table 1. m_i for common distribution

分布类型	m_i
正态分布	1
极值I型分布	4
对数正态分布	$\max \{ 2,floor[2 + 20({\sigma _{\ln }} - 0.1)/3]\}$
注：floor $\left(A\right)$ 函数指小于 $A$ 的最大整数值。

下载: 导出CSV

| 显示表格

由上述Nataf变换，可得标准正态空间的功能函数表达式：

$G = g( {{{\boldsymbol{N}}^{ - 1}}( {\boldsymbol{U}} )} ) \triangleq h( {\boldsymbol{U}} )$

(7)

式中，N ⁻¹(∙)为Nataf变换的逆变换，与式(7)功能函数对应的可靠指标可通过如下优化问题求解，即：

$\begin{gathered} \min \;\;\;\; \frac{1}{2}{{\boldsymbol{u}}^{\rm{T}}}{\boldsymbol{u}} \\ {\rm s.t.} \;\;\;\;\;\; h({\boldsymbol{u}}) = 0 \\ \end{gathered}$

(8)

获得上述优化问题的解u^*(即验算点)后，可靠指标为：

${\beta ^{F}} = ||{{\boldsymbol{u}}^*} ||$

(9)

1.2 基于HLRF法与修正对称秩1方法的可靠度分析

引入拉格朗日乘子，可将式(8)转化为无约束优化问题，即：

$\text{min}l\left({\boldsymbol{u}},{\boldsymbol{\lambda}} \right)=\frac{1}{2}{\boldsymbol{u}}^{{\rm{T}}}\boldsymbol{u}+{{\boldsymbol{\lambda}} }^{{\rm{T}}}h\left(\boldsymbol{u}\right)$

(10)

式中， ${\boldsymbol{\lambda}}$ 为拉格朗日乘子。

1.2.1 基于修正对称秩1方法的可靠度分析

对于式(10)所示的无约束优化问题，可以采用各种优化方法求解。拟牛顿优化方法是一类具有较好收敛性能的优化方法，其中的对称秩1方法在保持良好收敛特性的同时可以获得较好的近似Hessian矩阵^[19]，修正对称秩1方法^[22]由于在优化迭代过程中更充分地利用了功能函数的函数值与一阶偏导数值，具有比对称秩1方法和BFGS方法等拟牛顿优化方法更好的收敛性能和计算效率，因此，文中引入修正对称秩1方法求解上述优化问题。

修正对称秩1方法求解式(10)的迭代公式如下：

${\boldsymbol{u}_{k + 1}} = {\boldsymbol{u}_k} + {{\boldsymbol{d}}_k}$

(11)

${{\boldsymbol{d}}_k} = - {{\bf\textit{τ}} _k}{{\boldsymbol{H}}_k}{\nabla _u}l\left( {{\boldsymbol{u}_k},{{\boldsymbol{\lambda}} _k}} \right)$

(12)

式中：u_k为第k次迭代的验算点坐标； $\nabla$ _ul(u_k, λ_k)为该验算点处拉格朗日函数的一阶偏导数值；H_k为拉格朗日函数的Hessian矩阵 $\nabla_{uu}^2$ l(u_k, λ_k)的逆矩阵；d_k为迭代步长，由搜索方向H_k $\nabla$ _ul(u_k, λ_k)及步长参数τ_k确定；τ_k可根据Wolfe定理或Armijo定理由线搜索法^{[22, 24]}确定，借鉴文献[22, 24]的思路，H_k的迭代公式如下：

${{\boldsymbol{H}}_{k + 1}} = {{\boldsymbol{H}}_k} + \frac{{( {{{\boldsymbol{S}}_k} - {{\boldsymbol{H}}_k}{{\boldsymbol{y}}_k^*}} ){{( {{{\boldsymbol{S}}_k} - {{\boldsymbol{H}}_k}{{\boldsymbol{y}}_k^*}} )}^{\rm{T}}}}}{{{{( {{{\boldsymbol{y}}_k^*}} )}^{\rm{T}}}( {{{\boldsymbol{S}}_k} - {{\boldsymbol{H}}_k}{{\boldsymbol{y}}_k^*}} )}}$

(13)

式中：S_k=u_k+1−u_k； ${\boldsymbol{y}}_k^*$ = $\nabla$ _ul(u_k+1, λ_k+1)− $\nabla$ _ul(u_k, λ_k+1)+ψ_k·S_k/( ${\boldsymbol{S}}_{\boldsymbol{k}}^{\rm{T}}$ S_k)；ψ_k=2(l(u_k,λ_k)−l(u_k+1, λ_k+1))+( $\nabla$ _ul(u_k+1, λ_k+1)+ $\nabla$ _ul(u_k, λ_k+1))^TS_k。不难发现，H_k+1的计算仅涉及功能函数在u_k与u_k+1处的函数值及一阶偏导数值。

为保持H_k在迭代更新中的正定性及稳定性，文献[20]给出了迭代保护措施，即：

$|{\boldsymbol{S}}_k^{\rm{T}}({\boldsymbol{y}}_k^* - {{\boldsymbol{H}}_k}{{\boldsymbol{S}}_k})| > \varepsilon ||{{\boldsymbol{S}}_k}||{\text{ }}||({\boldsymbol{y}}_k^* - {{\boldsymbol{H}}_k}{{\boldsymbol{S}}_k})||$

(14)

式中，ε为极小值，一般取ε=10⁻⁶~10⁻⁸。

通过上述迭代过程确定验算点u^*后，可由式(9)计算得到可靠指标。

1.2.2 基于HLRF法的步长参数

上述方法的每步迭代过程中均需由线搜索法确定τ_k，以及与之对应的λ_k+1。由于线搜索过程中涉及功能函数的调用，方法的计算效率受到影响。

值得指出的是，文献[12]证明了HLRF法是序列二次规划方法^[25]的一类特例，并推导出了在序列二次规划方法中与HLRF法对应的d_k和λ_k+1，即：

${{\boldsymbol{d}}_k} = \frac{{[ {\nabla h{{\left( {{{\boldsymbol{u}}_k}} \right)}^{\rm{T}}}{{\boldsymbol{H}}_k}{{\boldsymbol{u}}_k} - h\left( {{{\boldsymbol{u}}_k}} \right)} ]{{\boldsymbol{H}}_k}\nabla h\left( {{{\boldsymbol{u}}_k}} \right)}}{{\nabla h{{\left( {{{\boldsymbol{u}}_k}} \right)}^{\rm{T}}}{{\boldsymbol{H}}_k}\nabla h\left( {{{\boldsymbol{u}}_k}} \right)}} - {{\boldsymbol{H}}_k}{{\boldsymbol{u}}_k}$

(15)

${{\boldsymbol{\lambda}} }_{k+1}=\frac{h\left({{\boldsymbol{u}}}_{k}\right)-\nabla h{\left({{\boldsymbol{u}}}_{k}\right)}^{{\rm{T}}}{{\boldsymbol{H}}}_{k}{{\boldsymbol{u}}}_{k}}{\nabla h{\left({{\boldsymbol{u}}}_{k}\right)}^{{\rm{T}}}{{\boldsymbol{H}}}_{k}\nabla h\left({{\boldsymbol{u}}}_{k}\right)}$

(16)

式中， $\nabla$ h(∙)为函数h(∙)的梯度。

1.3 隐式功能函数的处理

由于上述方法涉及功能函数的偏导数运算，若涉及隐式功能函数，则引入前向单边差分法对其近似，即：

$\frac{{\partial h( {{{\boldsymbol{u}}^*}} )}}{{\partial {{\boldsymbol{U}}_i}}} = \frac{{h( {{\boldsymbol{u}}_{\underline i }^*,{\boldsymbol{u}}_i^* + \zeta \cdot {\boldsymbol{u}}_i^*} ) - h( {{\boldsymbol{u}}_{\underline i }^*,{\boldsymbol{u}}_i^*} )}}{{\zeta \cdot {\boldsymbol{u}}_i^*}}$

(17)

式中： ${\boldsymbol{u}}^*_i$ 为u^*中除了 ${\boldsymbol{u}}^*_i$ 外的所有元素构成的向量；ζ为差分每步的大小，通常取0.001。

综合1.1节~1.3节，即可形成一种无步长搜索的高效一次可靠度分析方法，本文将其称为基于修正对称秩1方法的改进一次可靠度方法，简称为改进一次可靠度方法或建议方法1。

1.4 改进一次可靠度方法的实现步骤

文中建议的改进一次可靠度方法的实现步骤为：

1) 计算等效相关系数，将原始空间随机向量X转换为独立标准正态向量U。

2) 确定迭代过程的初始验算点(可设u₀=0)和初始Hessian逆矩阵H₀(可设为单位阵I)，计算该验算点处功能函数值和梯度值，h(u₀)和 $\nabla$ h(u₀)。

3) 由式(15)计算第k步步长d_k。

4) 由式(11)更新第k+1步验算点u_k+1，并确定该验算点处的h(u_k+1)， $\nabla$ h(u_k+1)。

5) 若式(14)满足，则由式(13)更新修正的逆矩阵H_k+1，否则，跳过此次更新。

6) 若||u_k+1−u_k|| > ε，则跳转回步骤3)；否则，结束迭代，由式(9)计算可靠指标，并记验算点u^*= u_k+1，拉格朗日乘子λ^*=λ_k+1，以及该点对应的偏导数 $\nabla$ h(u^*)和Hessian矩阵的逆矩阵H^*。

2 功能函数的近似Hessian矩阵及改进二次可靠度方法

功能函数的Hessian矩阵计算是二次可靠度方法的重要环节。由于在第1节改进一次可靠度方法的过程中利用了Hessian矩阵的逆矩阵，尽管该逆矩阵是针对拉格朗日函数的，但仍可能在不增加功能函数调用次数的基础上获得功能函数的Hessian矩阵近似解。

2.1 基于修正对称秩1方法的功能函数近似Hessian矩阵

2.1.1 拉格朗日函数的近似Hessian矩阵

由于修正对称秩1方法中利用了Hessian逆矩阵 ${{{\boldsymbol{H}}}}_{k}$ 的迭代，但同时亦存在正矩阵的迭代，因此，可以直接在搜索验算点的迭代过程中获得Hessian矩阵的近似。此外，由于迭代过程可以给出Hessian逆矩阵的近似解，因此，亦可以通过矩阵求逆的方式得到近似的Hessian矩阵。两种方法分别介绍如下。

1)迭代法

利用改进一次可靠度方法的迭代过程结果，可以给出拉格朗日函数的Hessian矩阵的近似解，即B_k= $\nabla _{uu}^2$ l(u_k,λ_k)，的迭代公式为：

${{\boldsymbol{B}}_{k + 1}} = {{\boldsymbol{B}}_k} + \frac{{( {{{\boldsymbol{y}}_k^*} - {{\boldsymbol{B}}_k}{{\boldsymbol{S}}_k}} ){{( {{{\boldsymbol{y}}_k^*} - {{\boldsymbol{B}}_k}{{\boldsymbol{S}}_k}} )}^{\rm{T}}}}}{{{{( {{{\boldsymbol{S}}_k}} )}^{\rm{T}}}( {{{\boldsymbol{y}}_k^*} - {{\boldsymbol{B}}_k}{{\boldsymbol{S}}_k}} )}}$

(18)

将u^*处的Hessian矩阵记为B^*。

2)求逆法

直接对u^*处的拉格朗日函数的H^*进行求逆计算，即：

${{\boldsymbol{B}}}^{\text{*}}= {\left({{\boldsymbol{H}}}^{*}\right)}^{-1}$

(19)

由于对称秩1方法的自互补性^[26]，即Hessian矩阵的逆更新和求逆运算是一致的，理论上迭代法和求逆法将得到相同的B^*。

2.1.2 功能函数的近似Hessian矩阵

由式(10)可知，任意迭代步骤内，拉格朗日函数与功能函数的Hessian矩阵存在如下关系：

$\begin{split} \nabla _{uu}^2l\left( {{{\boldsymbol{u}}_k},{{\boldsymbol{\lambda}} _k}} \right) =& \nabla _{uu}^2\frac{1}{2}{{\boldsymbol{u}}_k^{\rm{T}}}{{\boldsymbol{u}}_k} + {{\boldsymbol{\lambda}} _k}\nabla _{uu}^2h\left( {{{\boldsymbol{u}}_k}} \right) =\\ & {\boldsymbol{I}} + {{\boldsymbol{\lambda}} _k}\nabla _{uu}^2h\left( {{{\boldsymbol{u}}_k}} \right) \end{split}$

(20)

于是，在u^*处功能函数的Hessian矩阵计算如下：

$\nabla _{uu}^2h\left( {{{\boldsymbol{u}}^*}} \right) = ( {{{\boldsymbol{B}}^{\text{*}}} - {\boldsymbol{I}}} )/{{\boldsymbol{\lambda}} ^*}$

(21)

2.2 基于非中心卡方分布积分的改进二次可靠度方法

2.2.1 基于正交矩阵的坐标旋转

为降低二次近似函数中交叉项的影响，一般需采用正交矩阵进行坐标旋转。常用的正交矩阵有：1) 由梯度向量正交化确定的正交矩阵^[27]；2) Hessian矩阵的特征向量矩阵^[28]；3) 上述两个矩阵的乘积^[20]。考虑到文中Hessian矩阵是近似确定的，为避免误差累积，故由梯度向量正交化确定的正交矩阵进行旋转。

将改进一次可靠度方法中得到的验算点u^*处的梯度向量 $\nabla$ h(u^*)归一化，即：

$\begin{split} {\boldsymbol{\alpha}} _u^* = &- \left( {\left[ {\frac{{\partial h\left( {\boldsymbol{U}} \right)}}{{\partial {U_1}}},\frac{{\partial h\left( {\boldsymbol{U}} \right)}}{{\partial {U_2}}}, \ldots ,\frac{{\partial h\left( {\boldsymbol{U}} \right)}}{{\partial {U_n}}}} \right] \Bigg|_{{{\boldsymbol{u}}^*}}^{\rm{T}}} \right) \Bigg/\\& \sqrt {\mathop \sum \limits_{i = 1}^n {{\left( {\frac{{\partial h\left( {\boldsymbol{U}} \right)}}{{\partial {U_i}}}{\Bigg|_{{{\boldsymbol{u}}^*}}}} \right)}^2}} \end{split}$

(22)

以 ${\boldsymbol{\alpha}}^*_u$ 为基础，可由Gram-Schmidt正交化方法构造如下正交矩阵R，即：

${\boldsymbol{R}} = \left[ {{{\boldsymbol{R}}_1}|{\boldsymbol{\alpha}} _{{u}}^*} \right]$

(23)

式中： ${\boldsymbol{\alpha}}^*_u$ 为R的第n列；R₁为n×(n−1)的矩阵，且满足 ${\boldsymbol{\alpha}}^*_u$ R₁=0。

以R为旋转矩阵，可建立如下的变换关系：

${\boldsymbol{U}} = {\boldsymbol{RY}}$

(24)

式中，Y为旋转后的标准正态向量。

结合式(7)和式(24)，可得到旋转变量Y空间的功能函数为：

${\boldsymbol{G}} = h\left( {{\boldsymbol{RY}}} \right) \triangleq q\left( {\boldsymbol{Y}} \right)$

(25)

2.2.2 功能函数单变量降维近似及高效二次近似

对于多变量函数q(Y)，以验算点为参考点对其进行单变量降维近似^[29]，可表示为：

$q\left( {\boldsymbol{Y}} \right) \approx \mathop \sum \limits_{i = 1}^n q({\boldsymbol{y}}_{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i} }^*,{Y_i}) - \left( {n - 1} \right)q\left( {{{\boldsymbol{y}}^*}} \right)$

(26)

式中：y^*=R⁻¹u^*为Y空间的验算点；Y_i为Y第i个分量； ${\boldsymbol{y}}^*_{\underline{i}}$ 为y^*中除 $y^*_i$ 外所有元素构成的向量，因此( ${\boldsymbol{y}}^*_{\underline{i}}$ ,Y_i)= $(y_1^*,\cdots ,y_{i-1}^*,Y_i,y_{i+1}^*,\cdots,y_n^*)$ 。

显然，分量函数 $({\boldsymbol{y}}^*_{\underline{i}},Y_i)$ 是关于Y_i的单变量函数，对其采用二次多项式近似：

$q( {{\boldsymbol{y}}_{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{i} }^*,{Y_i}} ) = {a_i} + {b_i}{Y_i} + {c_i}Y_i^2$

(27)

式中，待定系数a_i、b_i、c_i可由如下线性方程组确定：

$\left[ {\begin{array}{*{20}{c}} 1&{y_i^*}&{y{{_i^*}^2}} \\ 0&1&{2y_i^*} \\ 0&0&2 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_i}} \\ {{b_i}} \\ {{c_i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {q\left( {{{\boldsymbol{y}}^*}} \right)} \\ {\dfrac{{\partial q\left( {\boldsymbol{Y }}\right)}}{{\partial {Y_i}}}{|_{{{\boldsymbol{y}}^*}}}} \\ {\dfrac{{{\partial ^2}q\left( {\boldsymbol{Y}} \right)}}{{\partial Y_i^2}}{|_{{{\boldsymbol{y}}^*}}}} \end{array}} \right]$

(28)

其中：

$\frac{{\partial q\left( {\boldsymbol{Y}} \right)}}{{\partial {Y_i}}} = \mathop \sum \limits_{j = 1}^n \frac{{\partial h\left( {\boldsymbol{U}} \right)}}{{\partial {U_j}}} \times \frac{{\partial {U_j}}}{{\partial {Y_i}}}$

(29)

$\begin{split} \frac{{\partial }^{2}q({\boldsymbol{Y}})}{\partial {Y}_{i}^{2}}=& \mathop \sum \limits_{j = 1}^n\frac{{\partial }^{2}h\left({\boldsymbol{U}}\right)}{\partial {U}_{j}^{2}}\times {\left(\frac{\partial {U}_{j}}{\partial {Y}_{i}}\right)}^{2}+\mathop \sum \limits_{j = 1}^n\frac{\partial h\left({\boldsymbol{U}}\right)}{\partial {U}_{j}} \times \\& \left(\frac{{\partial }^{2}{U}_{j}}{\partial {Y}_i^2}\right)+2\times {\displaystyle \sum _{i\ne j}\frac{{\partial }^{2}h\left({\boldsymbol{U}}\right)}{\partial {U}_{i}\partial {U}_{j}}\times \frac{\partial {U}_{i}}{\partial {Y}_{i}}\times \frac{\partial {U}_{j}}{\partial {Y}_{i}}}\end{split}$

(30)

显然，方程组式(28)可解析求解。由于式(29)中的 $\partial h\left( {\boldsymbol{U}} \right)/ \partial {U_j}$ 和式(30)中的 ${\partial ^2}h\left( {\boldsymbol{U}} \right)/\partial {U_j^2}$ 、 ${\partial ^2}h\left( {\boldsymbol{U}} \right)/ \partial {U_i}\partial {U_j}$ 分别在改进一次可靠度方法以及功能函数的近似Hessian矩阵中确定，因此，由式(28)确定q( ${\boldsymbol{y}}_i^*$ ,Y_i)的二次多项式近似时无需额外调用功能函数，具有较高的效率。将各单变量分量函数的二次多项式近似代入式(27)可得到功能函数的近似二次函数，即：

$q\left( {\boldsymbol{Y}} \right) \approx \mathop \sum \limits_{i = 1}^n ({a_i} + {b_i}{Y_i} + {c_i}{Y_i^2}) - \left( {n - 1} \right)q\left( {{{\boldsymbol{y}}^*}} \right)$

(31)

2.2.3 基于非中心卡方分布积分的失效概率计算

对于形如式(31)功能函数对应的二次可靠度计算，文献[28]将其转化为两个广义卡方分布的线性组合进行计算，尽管理论上是严谨的，但是由于涉及到多个gamma函数的无穷和^[30]，应用颇为不便。为此，可将式(31)等价改写为：

$q\left( {\boldsymbol{Y}} \right) \approx \sum\limits_{i = 1}^n {{c_i}{{\left( {{Y_i} + \frac{{{b_i}}}{{2{c_i}}}} \right)}^2}} + \sum\limits_{i = 1}^n {\left( {{a_i} - \frac{{b_i^2}}{{4c_i^2}}} \right)} - \left( {n - 1} \right)q\left( {{{\boldsymbol{y}}^*}} \right)$

(32)

若式(32)存在二次项系数c_i相等的情况，且假设相等c_i出现的最多次数为s，所有这些c_i下标的集合记为Ω₀，该系数记为 ${c}_{0}$ ，在系数集合Rⁿ中其余二次项系数集合记为Ω₀的补集 ${{\bar {\boldsymbol{\varOmega}} }_{0}}$ 。若式(32)中有多个二次项系数的重复出现次数为s，只需任选一个c_i进行上述处理。于是，式(32)可进一步改写为：

$\begin{split} q\left({\boldsymbol{Y}}\right)\approx & {c}_{0}\left[\sum_{i \in {\text{Ω}}_{0}}{\left({Y}_{i}+\frac{{b}_{i}}{2{c}_{i}}\right)}^{2}\right]+\left[\sum _{i \in\overline{{\text{Ω}}_{0}}}{c}_{i}{\left({Y}_{i}+\frac{{b}_{i}}{2{c}_{i}}\right)}^{2}+\right.\\& \left. {\displaystyle \sum _{i=1}^{n}\left({a}_{i}-\frac{{b}_{i}^{2}}{4{c}_{i}^{2}}\right)}-\left(n-1\right)q\left({{\boldsymbol{y}}}^{*}\right) \right]\triangleq {c}_{0}{\boldsymbol{Z}}+{{A}}\end{split}$

(33)

其中：

${\boldsymbol{Z}}=\sum _{i\in {\text{Ω}}_{0}}{\left({Y}_{i}+\frac{{b}_{i}}{2{c}_{i}}\right)}^{2}$

(34)

${{A}}=\sum _{i\in \overline{{\text{Ω}}_{0}}}{c}_{i}{\left({Y}_{i}+\frac{{b}_{i}}{2{c}_{i}}\right)}^{2}+{\displaystyle \sum _{i=1}^{n}\left({a}_{i}-\frac{{b}_{i}^{2}}{4{c}_{i}^{2}}\right)}-\left(n-1\right)q\left({{\boldsymbol{y}}}^{*}\right)$

(35)

由于Z为s个独立同方差的正态变量的平方和，因此服从自由度为s、非中心参数 $\delta = \displaystyle \sum _{i\in {\text{Ω}}_{0}}{\left({b}_{i}/2{c}_{i}\right)}^{2}$ 的非中心卡方分布^[31]，其累积分布函数可表示为 ${F_Z}( \cdot |s,\delta )$ 。

由式(33)可知失效概率计算如下：

$\begin{split} {P_{\rm{F}}} = &P\left\{ {q\left( {\boldsymbol{Y}} \right) \lt 0} \right\} = \left\{ \begin{aligned} {P\left\{ {Z \lt - A/{c_0}} \right\} ,{c_0} \gt 0} \\ {P\left\{ {Z \gt - A/{c_0}} \right\}, {c_0} \lt 0} \end{aligned} \right. =\\ & \left\{ {\begin{aligned} &{E\left\{ {{F_Z}( - A/{c_0}|s,\delta } \right\}, \;\;\;\;\;\;\;\;\;\;{c_0} \gt 0} \\ & {1 - E\left\{ {{F_Z}( - A/{c_0}|s,\delta } \right\}, \;\;\;\;{c_0} \lt 0} \end{aligned}} \right. \end{split}$

(36)

式中：P{·}为概率函数；E{·}为数学期望。

显然，由式(32)~式(36)的推导过程中未引入任何假定和近似，可认为是精确的。式(36)中的期望运算实际上是多维积分，可采用成熟的数值积分方法，如Gauss-Hermite积分法、稀疏点集积分法和Monte Carlo法等进行计算，文中采用Monte Carlo法。

综合2.1节和2.2节，即可形成一种更好地兼顾精度与效率的二次可靠度分析方法，本文将其称为改进二次可靠度方法。

2.3 改进二次可靠度方法的实现步骤

在第1节改进一次可靠度方法的基础上，改进二次可靠度方法的实现步骤如下：

1) 基于改进一次可靠度方法的计算结果，可根据迭代法(结合式(18)、式(21))或求逆法(结合式(19)、式(21))计算功能函数的近似Hessian矩阵。

2) 根据式(22)、式(23)确定矩阵R，计算旋转后Y空间内的验算点y^*，偏导数 $\partial q\left( {\boldsymbol{Y}} \right)/\partial {Y_i}{|_{{{\boldsymbol{y}}^*}}}$ ，二阶偏导数 ${\partial ^2}q\left( {\boldsymbol{Y}} \right)/\partial {Y_i}^2{|_{{{\boldsymbol{y}}^*}}}$ 。

3) 根据式(28)计算待定系数，确定近似的二次多项式。

4) 基于式(36)求解失效概率，其中， ${F_Z} ( \cdot |s,\delta )$ 可直接调用MATLAB软件中的 ${\text{ncx2cdf}}( \cdot |s,\delta )$ 命令计算。

由于存在迭代法和求逆法两种确定Hessian矩阵的方式，文中把与之对应的改进二次可靠度方法分别称为建议方法2-1与建议方法2-2。

3 算例分析

为了验证所提出方法的有效性，文中分别对2个纯数学表达式的功能函数算例和2个具有工程背景的算例进行分析。其中，前两者视为功能函数表达式已知的显式功能函数情形，其分析次数为函数调用次数与偏导数计算次数的和；后两者视为功能函数表达式未知的隐式功能函数情形，功能函数的偏导数采用差分法计算，其分析次数为函数调用的次数。同时，为考察建议方法的精度与效率，文中将其与一次可靠度方法中的HLRF法^[5]、HLRF-BFGS方法^[12]和二次可靠度方法中的Breitung方法^[14]、拟牛顿近似方法^[21]进行对比分析。其中，文献[21]是将近似的Hessian矩阵与常用的7种二次可靠度方法分别结合的结果的均值作为最终结果，为简便，本文仅采用其与Breitung方法结合的结果。各方法精度比较时，以抽样数为10⁸的Monte Carlo法(记为MCS)结果作为标准解，各方法的误差为：

$\vartheta = \frac{{\left| {Value - MCS} \right|}}{{MCS}}$

(37)

式中：Value为对应方法的失效概率；MCS为Monte Carlo方法计算的失效概率。

算例1. 三变量功能函数

假设功能函数为^[2]：

$G\left( {\boldsymbol{X}} \right) = {X_3} - \sqrt {300X_1^2 + 1.92X_2^2}$

(38)

式中，随机变量统计特征如表2所示，表3给出了可靠度计算结果。

表 2 算例1中随机变量的统计特征

Table 2. Statistical characteristics of the random variables in Example 1

变量	概率分布	均值	变异系数
${X}_{1}$	对数正态分布	1.0	0.1600
${X}_{2}$	极值I型分布	20.0	0.1000
${X}_{3}$	韦布尔分布	48.0	0.0625

下载: 导出CSV

| 显示表格

表 3 算例1中可靠度计算结果

Table 3. computed reliability results of Example 1

方法	分析次数	可靠指标	失效概率/ (×10⁻²)	误差/(%)
MCS	1×10⁸	2.9040	0.1842	−
HLRF	21	3.0855	0.1016	44.84
HLRF-BFGS	13	3.0855	0.1016	44.84
Breitung	21+6	2.8972	0.1882	2.19
拟牛顿近似	13	2.8967	0.1886	2.36
建议方法1	11	3.0855	0.1016	44.84
建议方法2-1	11	2.8956	0.1892	2.71
建议方法2-2	11	2.8956	0.1892	2.71

下载: 导出CSV

| 显示表格

由表3结果可知，本文建议方法1相比HLRF法和HLRF-BFGS方法而言，能够更快收敛，减少了功能函数调用次数，而且达到了近乎相同的一次可靠指标精度，但是上述三种一次可靠度方法的结果精度都不理想。本文建议的改进二次可靠度方法在改进一次可靠度方法的基础上，不额外增加函数调用次数和偏导数计算次数，用更高的效率达到了与二次可靠度方法的Breitung方法、拟牛顿近似方法相近的精度。值得注意的是，建议方法2-1与建议方法2-2的效率与精度完全一致，这验证了本文所提改进二次可靠度方法在一次可靠度分析与Hessian矩阵近似过程中是自洽的。其余算例在自洽性方面都有相同结论，因此后续算例不再进行讨论。

算例2. 四变量功能函数

假设功能函数为^[28]：

$\begin{split} G\left( {\boldsymbol{X}} \right) = & - X_1^2 - X_2^2 - X_3^2 - X_4^2 + 10{X_1} +\\ & 12{X_2} + 12{X_3} + 12{X_4} - 43 \end{split}$

(39)

式中， ${X_i} \sim N(0,1)$ ，i=1, 2, 3, 4，且各变量相互独立。

表4给出了可靠度计算结果。

表 4 算例2中可靠度计算结果

Table 4. computed reliability results of Example 2

方法	分析次数	可靠指标	失效概率/(×10⁻²)	误差/(%)
MCS	1×10⁸	2.1890	1.4301	−
HLRF	8	2.0457	2.0392	42.59
HLRF-BFGS	8	2.0457	2.0392	42.59
Breitung	8+10	2.1644	1.5217	6.42
拟牛顿近似	8	2.1644	1.5217	6.42
建议方法1	8	2.0457	2.0392	42.59
建议方法2-1	8	2.2125	1.3466	5.82

下载: 导出CSV

| 显示表格

由表4结果可知，一次可靠度方法中，本文建议方法1在效率上与HLRF法、HLRF-BFGS方法相当，且该三种方法的精度都完全一致，但与MCS结果相比误差偏大。建议方法2-1在效率与建议方法1相同的情况下，提高了可靠指标精度，相比Breitung方法、拟牛顿近似方法而言误差更小。因此，本文建议的二次可靠度方法能更好地兼顾精度与效率。

算例3. 三变量工程实例

考虑Chan和Low^[32]首次提出的一个柔性矩形基础沉降问题，并对其变量类型进行修改，沉降问题的功能函数可以表示为：

$G\left( {\boldsymbol{X}} \right) = 50 - 0.5B{q_0}\frac{{1 - {\nu^2}}}{{{E_{\rm{s}}}}}m\left( {{I_1} + \frac{{1 - 2\nu}}{{1 - \nu}}{I_2}} \right){I_F}$

(40)

假设泊松比与弹性模量之间的相关系数为0.5，部分确定性参数见表5，随机变量统计特征见表6。表7给出了可靠度计算结果。

表 5 确定性参数

Table 5. deterministic parameters

基础确定性参数	数值
宽度B/m	30
长度L/m	40
嵌入深度D/m	3
地层厚度H/m	10
角数m	4
影响因素I₁	0.073
影响因素I₂	0.089
影响因素I_F	0.950

下载: 导出CSV

| 显示表格

表 6 算例3中随机变量的统计特征

Table 6. Statistical characteristics of the random variables in Example 3

变量	概率分布	均值	标准差
均布荷载 ${q}_{0}$ /kPa	对数正态分布	280.00	40.00
泊松比 $\nu$	对数正态分布	0.25	0.08
弹性模量 ${E}_{{\rm{s}}}$ /MPa	正态分布	70.00	2.50

下载: 导出CSV

| 显示表格

表 7 算例3中可靠度计算结果

Table 7. computed reliability results of Example 3

方法	分析次数	可靠指标	失效概率/ (×10⁻²)	误差/(%)
MCS	1×10⁸	3.0697	0.1071	−
HLRF	52	3.0259	0.1239	15.69
HLRF-BFGS	20	3.0259	0.1239	15.69
Breitung	52+6	3.0668	0.1082	0.98
拟牛顿近似	20	3.0390	0.1187	10.78
建议方法1	20	3.0259	0.1239	15.69
建议方法2-1	20	3.0741	0.1056	1.46

下载: 导出CSV

| 显示表格

由计算结果可知，一次可靠度方法中，建议方法1与HLRF-BFGS方法具有一致的精度与效率，相比HLRF法具有更高的效率。建议方法2-1相比Breitung方法而言在保持相近的精度的同时，具有显著的效率提高，与拟牛顿近似方法相比，尽管两种方法效率一致，但建议方法在精度上有明显的改善，进一步验证了本文建议的改进二次可靠度方法在兼顾效率和精度上的优势。

算例4. 多变量工程问题

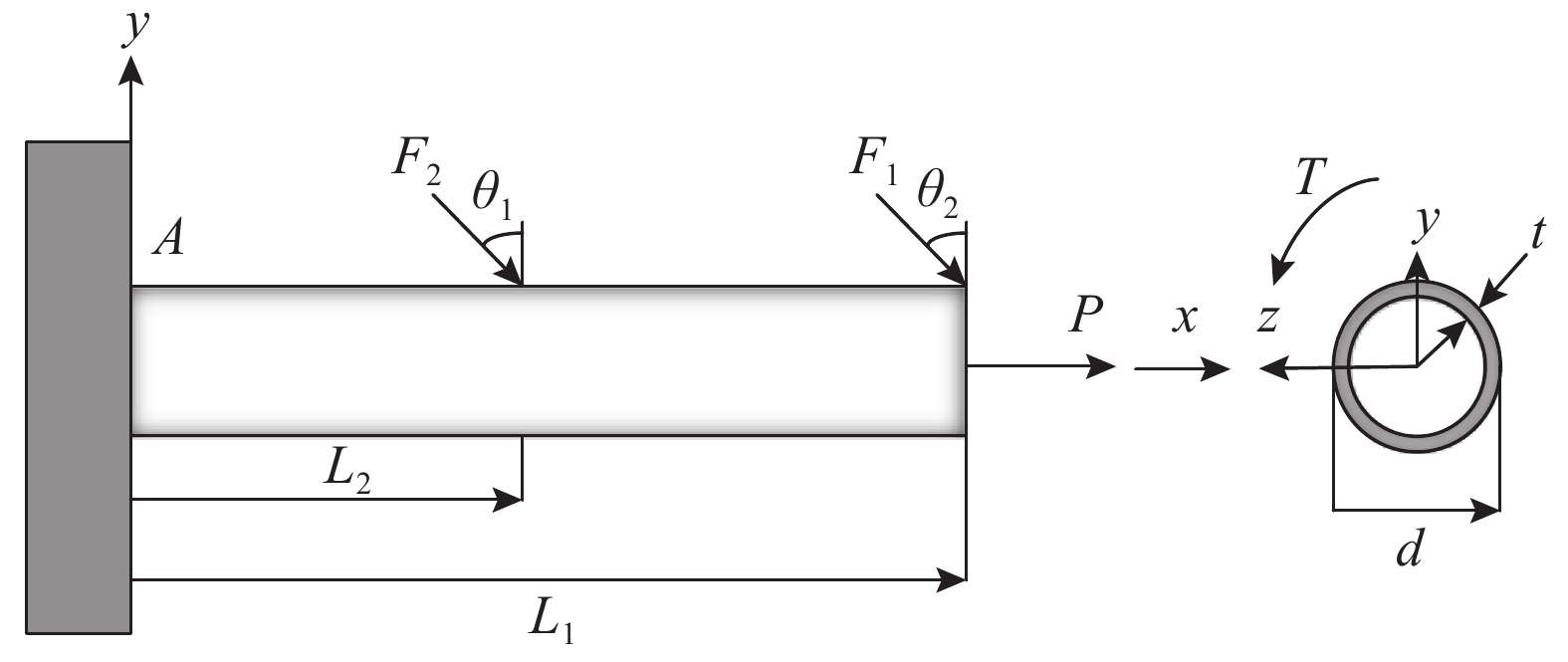
考虑文献[33]的具有9个随机变量的悬臂管工程算例，如图1所示，悬臂管在x-y平面上受集中荷载F₁、F₂，在y-z平面受轴力P与扭矩T，图1中的A点将出现最大的Von-Mises应力σ_max，将σ_max超过材料的屈服强度S_y作为失效准则，于是功能函数为：

$G\left( {\boldsymbol{X}} \right) = {S_y} - {\sigma _{{\rm{max}}}}$

(41)

图 1 悬臂管

Figure 1. Cantilever tube

下载: 全尺寸图片幻灯片

A点的最大Von-Mises应力σ_max由下式计算：

${\sigma _{\max }} = \sqrt {\sigma _x^2 + 3\tau _{x{\textit{z}}}^2}$

(42)

式中，正应力σ_x与切应力τ_xz分别为：

$\begin{split}& {\sigma _x} = \frac{{P + {F_1}\sin {\theta _1} + {F_2}\sin {\theta _2}}}{{\dfrac{\pi }{4}[ {{d^2} - {{(d - 2t)}^2}} ]}} + \\&\qquad\frac{{({F_1}{L_1}\cos {\theta _1} + {F_2}{L_2}\cos {\theta _2})d}}{{2 \times \dfrac{\pi }{{64}}[ {{d^4} - {{(d - 2t)}^4}} ]}} , \\& {\tau _{x{\textit{z}}}} = \frac{{Td}}{{4 \times \dfrac{\pi }{{64}}[ {{d^4} - {{(d - 2t)}^4}} ]}}{\text{ }} \end{split}$

(43)

算例中两个角度为定值，θ₁=5^o、θ₂=10^o。悬臂管随机变量统计特征见表8，其中，原文献中可靠指标偏低，文中对屈服强度参数进行调整以达到高可靠指标。表9给出了可靠度计算结果。

表 8 算例4中随机变量的统计特征

Table 8. Statistical characteristics of the random variables in Example 4

随机变量	均值	标准差	分布类型
壁厚t/mm	4.0	0.04	正态分布
直径d/mm	40.0	0.40	正态分布
长度L₁/mm	120.0	6.00	正态分布
长度L₂/mm	60.0	3.00	正态分布
外力F₁/kN	3.0	0.30	正态分布
外力F₂/kN	3.0	0.30	正态分布
外力P/kN	12.0	1.20	正态分布
扭转T/Nm	90.0	9.00	正态分布
屈服强度S_y/MPa	350.0	50.00	正态分布

下载: 导出CSV

| 显示表格

表 9 算例4中可靠度计算结果

Table 9. computed reliability results of Example 4

方法	分析次数	可靠指标	失效概率/ (×10⁻²)	误差/(%)
MCS	1×10⁸	3.4027	0.033 36	−
HLRF	40	3.4042	0.033 18	0.539
HLRF-BFGS	50	3.4042	0.033 18	0.539
Breitung	40+45	3.4033	0.033 29	0.209
拟牛顿近似	50	3.4015	0.033 51	0.449
建议方法1	40	3.4042	0.033 18	0.539
建议方法2-1	40	3.4025	0.033 38	0.059

下载: 导出CSV

| 显示表格

可以看出，本文建议方法1与HLRF法在效率和精度上都一致，相比HLRF-BFGS方法而言收敛更快。建议方法2-1在效率和精度上，相比已有的二次可靠度方法都有一定改善。

4 结论

本文引入拉格朗日乘子，将约束优化的可靠度问题转化为无约束优化问题，并结合修正对称秩1方法与HLRF法，提出了具有较好收敛性的改进一次可靠度方法。在此基础上，结合坐标旋转、单变量降维近似和非中心卡方分布进一步提出了改进二次可靠度方法。通过算例分析可得到如下结论：

(1)由于修正对称秩1方法的良好收敛特性和HLRF法无需迭代确定步长的特点，本文的改进一次可靠度方法继承了两者的优点，既有良好的收敛性，亦有较高的效率。

(2)由于近似的Hessian矩阵既可以基于改进一次可靠度方法的迭代过程结果确定，亦可以由最终的Hessian逆矩阵求逆获得，且能保持两者结果的一致性，因此，本文的改进二次可靠度方法在一次可靠度分析与Hessian矩阵近似过程中是自洽的。

(3)由于改进二次可靠度方法所采用的Hessian矩阵不需要额外调用功能函数，因此，本文的改进二次可靠度方法可以更好地兼顾效率与精度。

(4)由于引入差分近似偏导数，本文的建议方法均适用于显式、隐式功能函数。

图 1 悬臂管

Figure 1. Cantilever tube

下载: 全尺寸图片幻灯片

表 1 常用分布的m_i

Table 1 m_i for common distribution

分布类型	m_i
正态分布	1
极值I型分布	4
对数正态分布	$\max \{ 2,floor[2 + 20({\sigma _{\ln }} - 0.1)/3]\}$
注：floor $\left(A\right)$ 函数指小于 $A$ 的最大整数值。

下载: 导出CSV

表 2 算例1中随机变量的统计特征

Table 2 Statistical characteristics of the random variables in Example 1

变量	概率分布	均值	变异系数
${X}_{1}$	对数正态分布	1.0	0.1600
${X}_{2}$	极值I型分布	20.0	0.1000
${X}_{3}$	韦布尔分布	48.0	0.0625

下载: 导出CSV

表 3 算例1中可靠度计算结果

Table 3 computed reliability results of Example 1

方法	分析次数	可靠指标	失效概率/ (×10⁻²)	误差/(%)
MCS	1×10⁸	2.9040	0.1842	−
HLRF	21	3.0855	0.1016	44.84
HLRF-BFGS	13	3.0855	0.1016	44.84
Breitung	21+6	2.8972	0.1882	2.19
拟牛顿近似	13	2.8967	0.1886	2.36
建议方法1	11	3.0855	0.1016	44.84
建议方法2-1	11	2.8956	0.1892	2.71
建议方法2-2	11	2.8956	0.1892	2.71

下载: 导出CSV

表 4 算例2中可靠度计算结果

Table 4 computed reliability results of Example 2

方法	分析次数	可靠指标	失效概率/(×10⁻²)	误差/(%)
MCS	1×10⁸	2.1890	1.4301	−
HLRF	8	2.0457	2.0392	42.59
HLRF-BFGS	8	2.0457	2.0392	42.59
Breitung	8+10	2.1644	1.5217	6.42
拟牛顿近似	8	2.1644	1.5217	6.42
建议方法1	8	2.0457	2.0392	42.59
建议方法2-1	8	2.2125	1.3466	5.82

下载: 导出CSV

表 5 确定性参数

Table 5 deterministic parameters

基础确定性参数	数值
宽度B/m	30
长度L/m	40
嵌入深度D/m	3
地层厚度H/m	10
角数m	4
影响因素I₁	0.073
影响因素I₂	0.089
影响因素I_F	0.950

下载: 导出CSV

表 6 算例3中随机变量的统计特征

Table 6 Statistical characteristics of the random variables in Example 3

变量	概率分布	均值	标准差
均布荷载 ${q}_{0}$ /kPa	对数正态分布	280.00	40.00
泊松比 $\nu$	对数正态分布	0.25	0.08
弹性模量 ${E}_{{\rm{s}}}$ /MPa	正态分布	70.00	2.50

下载: 导出CSV

表 7 算例3中可靠度计算结果

Table 7 computed reliability results of Example 3

方法	分析次数	可靠指标	失效概率/ (×10⁻²)	误差/(%)
MCS	1×10⁸	3.0697	0.1071	−
HLRF	52	3.0259	0.1239	15.69
HLRF-BFGS	20	3.0259	0.1239	15.69
Breitung	52+6	3.0668	0.1082	0.98
拟牛顿近似	20	3.0390	0.1187	10.78
建议方法1	20	3.0259	0.1239	15.69
建议方法2-1	20	3.0741	0.1056	1.46

下载: 导出CSV

表 8 算例4中随机变量的统计特征

Table 8 Statistical characteristics of the random variables in Example 4

随机变量	均值	标准差	分布类型
壁厚t/mm	4.0	0.04	正态分布
直径d/mm	40.0	0.40	正态分布
长度L₁/mm	120.0	6.00	正态分布
长度L₂/mm	60.0	3.00	正态分布
外力F₁/kN	3.0	0.30	正态分布
外力F₂/kN	3.0	0.30	正态分布
外力P/kN	12.0	1.20	正态分布
扭转T/Nm	90.0	9.00	正态分布
屈服强度S_y/MPa	350.0	50.00	正态分布

下载: 导出CSV

表 9 算例4中可靠度计算结果

Table 9 computed reliability results of Example 4

方法	分析次数	可靠指标	失效概率/ (×10⁻²)	误差/(%)
MCS	1×10⁸	3.4027	0.033 36	−
HLRF	40	3.4042	0.033 18	0.539
HLRF-BFGS	50	3.4042	0.033 18	0.539
Breitung	40+45	3.4033	0.033 29	0.209
拟牛顿近似	50	3.4015	0.033 51	0.449
建议方法1	40	3.4042	0.033 18	0.539
建议方法2-1	40	3.4025	0.033 38	0.059

下载: 导出CSV

参考文献(33)

[1]	赵国藩. 工程结构可靠度 [M]. 北京: 水利电力出版社, 1984. Zhao Guofan. Reliability theory for engineering structures [M]. Beijing: Water Resources and Electric Power Press, 1984. (in Chinese)
[2]	贡金鑫. 工程结构可靠度计算方法[M]. 大连: 大连理工大学出版社, 2003. Gong Jinxin. Computational methods for reliability of engineering structures [M]. Dalian: Dalian University of Technology Press, 2003. (in Chinese)
[3]	Hasofer A M, Lind N C. Exact and invariant second-moment code format [J]. Journal of the Engineering Mechanics Division, 1974, 100(1): 111 − 121. doi: 10.1061/JMCEA3.0001848
[4]	Tu J, Choi K K, Park Y H. Design potential method for robust system parameter design [J]. AIAA Journal, 2001, 39(4): 667 − 677. doi: 10.2514/2.1360
[5]	Rackwitz R, Fiessler B. Structural reliability under combined random load sequences [J]. Computers & Structures, 1978, 9: 489 − 494.
[6]	秦琪, 张玄一, 卢朝辉, 等. 简化三阶矩拟正态变换及其在结构可靠度分析中的应用[J]. 工程力学, 2020, 37(12): 78 − 86, 113. doi: 10.6052/j.issn.1000-4750.2020.01.0015 Qin Qi, Zhang Xuanyi, Lu Zhaohui, et al. Simplified third-order normal transformation and its application in structural reliability analysis [J]. Engineering Mechanics, 2020, 37(12): 78 − 86, 113. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.01.0015
[7]	蒋水华, 姚池, 杨建华, 等. 基于模型修正的空间变异边坡可靠度分析方法[J]. 工程力学, 2018, 35(8): 154 − 161. doi: 10.6052/j.issn.1000-4750.2017.04.0308 Jiang Shuihua, Yao Chi, Yang Jianhua, et al. Model correction factor method based approach for reliability analysis of spatially variable slopes [J]. Engineering Mechanics, 2018, 35(8): 154 − 161. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.04.0308
[8]	Liu P L, Der Kiureghian A. Optimization algorithms for structural reliability [J]. Structural Safety, 1991, 9(3): 161 − 177. doi: 10.1016/0167-4730(91)90041-7
[9]	Santosh T V, Saraf R K, Ghosh A K. Optimum step length selection rule in modified HL–RF method for structural reliability [J]. International Journal of Pressure Vessels & Piping, 2006, 83(10): 742 − 748.
[10]	Santos S R, Matioli L C, Beck A T. New optimization algorithms for structural reliability analysis [J]. Computer Modeling in Engineering & Sciences, 2012, 83(1): 23 − 55.
[11]	亢战, 罗阳军. 计算结构可靠度指标的修正迭代算法[J]. 工程力学, 2008, 25(11): 20 − 26. Kang Zhan, Luo Yangjun. A modified iteration algorithm for structural reliability index evaluation [J]. Engineering Mechanics, 2008, 25(11): 20 − 26. (in Chinese)
[12]	Periçaro G A, Santos S R, Ribeiro A A, et al. HLRF–BFGS optimization algorithm for structural reliability [J]. Applied Mathematical Modelling, 2015, 39(7): 2025 − 2035. doi: 10.1016/j.apm.2014.10.024
[13]	Mikosch T V, Resnick S I, Robinson S M. Numerical optimization [M]. New York: Springer, 2006.
[14]	Breitung K. Asymptotic approximations for multinormal integrals [J]. Journal of Engineering Mechanics, 1984, 110(3): 357 − 366. doi: 10.1061/(ASCE)0733-9399(1984)110:3(357)
[15]	Zhang J, Du X. A Second-order reliability method with first-order efficiency [J]. Journal of Mechanical Design, 2010, 132(10): 101006. doi: 10.1115/1.4002459
[16]	Hohenbichler M, Rackwitz R. Improvement of second-order reliability estimates by importance sampling [J]. Journal of Engineering Mechanics, 1988, 114(12): 2195 − 2199. doi: 10.1061/(ASCE)0733-9399(1988)114:12(2195)
[17]	Zhang Z, Jiang C, Wang G G, et al. First and second order approximate reliability analysis methods using evidence theory [J]. Reliability Engineering & System Safety, 2015, 137: 40 − 49.
[18]	Tvedt L. Distribution of quadratic forms in normal space-application to structural reliability [J]. Journal of Engineering Mechanics, 1990, 116: 1183 − 1197.
[19]	Lim J, Lee B, Lee I. Second-order reliability method-based inverse reliability analysis using Hessian update for accurate and efficient reliability-based design optimization [J]. International Journal for Numerical Methods in Engineering, 2014, 100(10): 773 − 792. doi: 10.1002/nme.4775
[20]	Kang S B, Park J W, Lee I. Accuracy improvement of the most probable point-based dimension reduction method using the hessian matrix [J]. International Journal for Numerical Methods in Engineering, 2017, 111(3): 203 − 217. doi: 10.1002/nme.5458
[21]	Zeng P, Jimenez R, Li T. An efficient quasi-Newton approximation-based SORM to estimate the reliability of geotechnical problems [J]. Computers and Geotechnics, 2016, 76: 33 − 42. doi: 10.1016/j.compgeo.2016.02.003
[22]	Modarres F, Malik A H, Leong W J. Improved Hessian approximation with modified secant equations for symmetric rank-one method [J]. Journal of Computational and Applied Mathematics, 2011, 235(8): 2423 − 2431. doi: 10.1016/j.cam.2010.10.042
[23]	Zu Y F, Fan W L. Investigation of equivalent correlation coefficient based on the Mehler's formula [J]. Engineering Computations, 2019, 36(4): 1169 − 1200. doi: 10.1108/EC-07-2018-0316
[24]	Wei Z, Li G, Qi L. New quasi-Newton methods for unconstrained optimization problems [J]. Applied Mathematics and Computation, 2006, 175(2): 1156 − 1188. doi: 10.1016/j.amc.2005.08.027
[25]	唐贞云, 王志宇, 杜修力. 时域稳定的基础频响连续有理近似参数识别方法[J]. 工程力学, 2022, 39(4): 29 − 38. doi: 10.6052/j.issn.1000-4750.2021.01.0108 Tang Zhenyun, Wang Zhiyu, Du Xiuli. A stable parameter identification method in the time domain for the frequency response of foundations based on continuous-time rational approximation [J]. Engineering Mechanics, 2022, 39(4): 29 − 38. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.01.0108
[26]	Modarres F, Hassan M A, Leong W J. A symmetric rank-one method based on extra updating techniques for unconstrained optimization [J]. Computers & Mathematics with Applications, 2011, 62(1): 392 − 400.
[27]	Adhikari S. Reliability analysis using parabolic failure surface approximation [J]. Journal of Engineering Mechanics, 2004, 130(12): 1407 − 1427. doi: 10.1061/(ASCE)0733-9399(2004)130:12(1407)
[28]	Lee I, Yoo D, Noh Y. A novel second-order reliability method (SORM) using non-central or generalized chi-squared distributions [J]. Journal of Mechanical Design, 2012, 134(10): 100912. doi: 10.1115/1.4007391
[29]	Rahman S, Wei D. A univariate approximation at most probable point for higher-order reliability analysis [J]. International Journal of Solids and Structure, 2006, 43(9): 2820 − 2839. doi: 10.1016/j.ijsolstr.2005.05.053
[30]	Provost S B, Rudiuk E M. The exact distribution of indefinite quadratic forms in noncentral normal vectors [J]. Annals of the Institute of Statistical Mathematics, 1996, 48(2): 381 − 394. doi: 10.1007/BF00054797
[31]	Johnson N L, Kotz S, Balakrishnan N. Continuous univariate distributions, Volume 2 [M]. New Jersey: Wiley & Sons, 1994.
[32]	Chan C L, Low B K. Practical second-order reliability analysis applied to foundation engineering [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(11): 1387 − 1409. doi: 10.1002/nag.1057
[33]	Guo J, Du X. Reliability sensitivity analysis with random and interval variables [J]. International Journal for Numerical Methods in Engineering, 2009, 78(13): 1585 − 1617. doi: 10.1002/nme.2543

施引文献(13)

期刊类型引用(6)

1.	李双宝，李芳. 高温环境下发动机叶片-硬涂层阻尼结构动力学建模与分析. 中国民航大学学报. 2024(01): 30-39 . 百度学术
2.	黄梦婷，仝国军，张东健，蒲伟. 多孔双向功能梯度板瞬态热应力分析. 机械科学与技术. 2024(09): 1631-1639 . 百度学术
3.	刘知辉，牛军川，贾睿昊. 热梯度环境下梁高频振动的能量流模型. 航空学报. 2022(05): 592-604 . 百度学术
4.	王永刚，胡宇达，徐浩然. 谐变力作用功能梯度旋转圆板强非线性主共振. 工程力学. 2022(11): 31-41 . 本站查看
5.	孙梦楠，刘少华，刘京城. 顾及空间各向异性的IDW插值算法. 计算机工程与设计. 2020(04): 983-987 . 百度学术
6.	张正平. 飞行器薄壁结构热噪声响应及动强度研究. 强度与环境. 2019(01): 1-7 . 百度学术

其他类型引用(7)

资源附件(0)

图(1) / 表(9)

计量

文章访问数: 583
HTML全文浏览量: 112
PDF下载量: 154
被引次数: 13

1 基于修正对称秩1方法的改进一次可靠度方法
1.1 标准正态空间内可靠度问题的等价描述
1.2 基于HLRF法与修正对称秩1方法的可靠度分析
1.2.1 基于修正对称秩1方法的可靠度分析
1.2.2 基于HLRF法的步长参数
1.3 隐式功能函数的处理
1.4 改进一次可靠度方法的实现步骤
2 功能函数的近似Hessian矩阵及改进二次可靠度方法
2.1 基于修正对称秩1方法的功能函数近似Hessian矩阵
2.1.1 拉格朗日函数的近似Hessian矩阵
2.1.2 功能函数的近似Hessian矩阵
2.2 基于非中心卡方分布积分的改进二次可靠度方法
2.2.1 基于正交矩阵的坐标旋转
2.2.2 功能函数单变量降维近似及高效二次近似
2.2.3 基于非中心卡方分布积分的失效概率计算
2.3 改进二次可靠度方法的实现步骤
3 算例分析
4 结论

1 基于修正对称秩1方法的改进一次可靠度方法
1.1 标准正态空间内可靠度问题的等价描述
1.2 基于HLRF法与修正对称秩1方法的可靠度分析
1.2.1 基于修正对称秩1方法的可靠度分析
1.2.2 基于HLRF法的步长参数
1.3 隐式功能函数的处理
1.4 改进一次可靠度方法的实现步骤
2 功能函数的近似Hessian矩阵及改进二次可靠度方法
2.1 基于修正对称秩1方法的功能函数近似Hessian矩阵
2.1.1 拉格朗日函数的近似Hessian矩阵
2.1.2 功能函数的近似Hessian矩阵
2.2 基于非中心卡方分布积分的改进二次可靠度方法
2.2.1 基于正交矩阵的坐标旋转
2.2.2 功能函数单变量降维近似及高效二次近似
2.2.3 基于非中心卡方分布积分的失效概率计算
2.3 改进二次可靠度方法的实现步骤
3 算例分析
4 结论

参考文献(33)

施引文献(13)

资源附件(0)

基于HLRF法与修正对称秩1方法的改进可靠度方法

作者简介: 刘 丞(1995−)，男，重庆石柱人，博士生，主要从事可靠度分析研究 (E-mail: liucheng19950330@163.com) 李正良(1963−)，男，江苏江阴人，教授，博士，博导，主要从事结构工程和结构抗风方面研究(E-mail: lizhengl@hotmail.com)

通讯作者: 范文亮(1979−)，男，江西九江人，教授，博士，博导，主要从事结构工程、随机系统分析和可靠度分析方面的研究(E-mail: davidfwl@126.com)

计量

出版历程

IMPROVED RELIABILITY METHOD BASED ON HLRF AND MODIFIED SYMMETRIC RANK 1 METHOD

1 基于修正对称秩1方法的改进一次可靠度方法

1.1 标准正态空间内可靠度问题的等价描述

1.2 基于HLRF法与修正对称秩1方法的可靠度分析

1.2.1 基于修正对称秩1方法的可靠度分析

1.2.2 基于HLRF法的步长参数

1.3 隐式功能函数的处理

1.4 改进一次可靠度方法的实现步骤

2 功能函数的近似Hessian矩阵及改进二次可靠度方法

2.1 基于修正对称秩1方法的功能函数近似Hessian矩阵

2.1.1 拉格朗日函数的近似Hessian矩阵

2.1.2 功能函数的近似Hessian矩阵

2.2 基于非中心卡方分布积分的改进二次可靠度方法

2.2.1 基于正交矩阵的坐标旋转

2.2.2 功能函数单变量降维近似及高效二次近似

2.2.3 基于非中心卡方分布积分的失效概率计算

2.3 改进二次可靠度方法的实现步骤

3 算例分析

4 结论

期刊类型引用(6)

其他类型引用(7)

计量

出版历程

目录

1 基于修正对称秩1方法的改进一次可靠度方法

1.1 标准正态空间内可靠度问题的等价描述

1.2 基于HLRF法与修正对称秩1方法的可靠度分析

1.2.1 基于修正对称秩1方法的可靠度分析

1.2.2 基于HLRF法的步长参数

1.3 隐式功能函数的处理

1.4 改进一次可靠度方法的实现步骤

2 功能函数的近似Hessian矩阵及改进二次可靠度方法

2.1 基于修正对称秩1方法的功能函数近似Hessian矩阵

2.1.1 拉格朗日函数的近似Hessian矩阵

2.1.2 功能函数的近似Hessian矩阵

2.2 基于非中心卡方分布积分的改进二次可靠度方法

2.2.1 基于正交矩阵的坐标旋转

2.2.2 功能函数单变量降维近似及高效二次近似

2.2.3 基于非中心卡方分布积分的失效概率计算

2.3 改进二次可靠度方法的实现步骤

3 算例分析

4 结论

作者简介:
刘　丞(1995−)，男，重庆石柱人，博士生，主要从事可靠度分析研究 (E-mail: liucheng19950330@163.com)

李正良(1963−)，男，江苏江阴人，教授，博士，博导，主要从事结构工程和结构抗风方面研究(E-mail: lizhengl@hotmail.com)

通讯作者:
范文亮(1979−)，男，江西九江人，教授，博士，博导，主要从事结构工程、随机系统分析和可靠度分析方面的研究(E-mail: davidfwl@126.com)