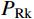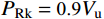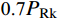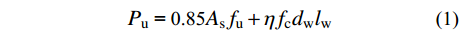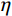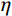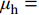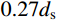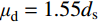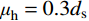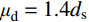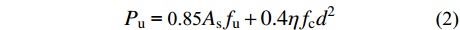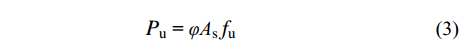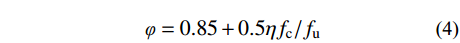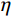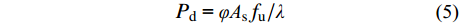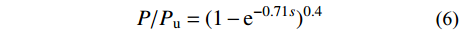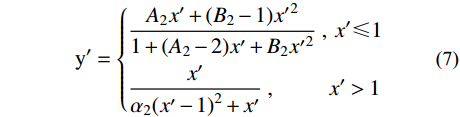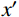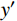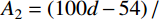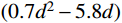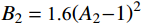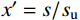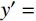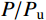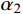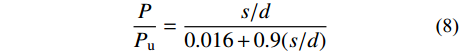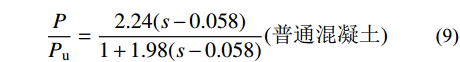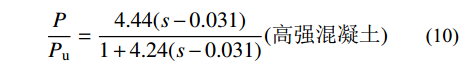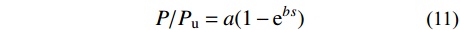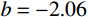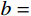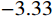STUDY ON MECHANICAL PROPERTIES OF STUD SHEAR CONNECTORS IN STEEL-UHPC COMPOSITE STRUCTURES
-
摘要: 为深入研究栓钉在超高性能混凝土(ultra-high performance concrete,UHPC)和普通混凝土(normal concrete,NC)中的力学特性及破坏形态,对8个栓钉剪力键试件进行了推出试验,详细探讨了混凝土类型、栓钉直径及长度对栓钉剪力键极限抗剪承载力的影响规律;基于有限元模型,进一步分析栓钉的极限抗拉强度、直径、长径比及混凝土强度对抗剪性能的影响,并详细研究栓钉直径、长度及混凝土强度对栓钉剪应力有效分布长度的影响。结果表明:栓钉根部附近的剪切断裂是主要的破坏形式;与NC试件相比,UHPC试件的抗剪承载力和抗剪刚度更高,但延性较低;栓钉剪应力在根部出现峰值,并沿钉帽方向迅速衰减;栓钉直径对剪应力有效分布长度影响显著。最后,根据试验结果提出了栓钉剪断破坏模式下的荷载-滑移曲线及抗剪承载力计算公式,计算结果与试验结果吻合良好,可为工程设计提供一定的参考价值。Abstract: In order to further study the mechanical properties and failure modes of studs embedded in ultra-high performance concrete (UHPC) and normal concrete (NC), a total of eight stud push-out specimens were tested and the influences of concrete type, diameter and length of stud on ultimate shear capacity were discussed. Based on the finite element model, the effects of ultimate tensile strength, diameter and length diameter ratio of stud and concrete strength on shear performance were further analyzed. The effects of diameter and length of stud and concrete strength on the effective distribution length of shear stress of stud were studied. The results show that the shear fracture near stud roots is the leading dominant failure mode. The shear capacity and shear stiffness of studs embedded in UHPC are higher than that of ordinary concrete, but the ductility is lower. The shear stress of stud peaks at the root and decreases rapidly along the direction of the nail cap. The diameter of stud has a significant effect on the effective distribution length of shear stress. Finally, according to the test results, the load-slip curve and a formula for the calculation of shear capacity under the stud shear failure mode are put forward, and the calculated results are in a good agreement with the test results, which can provide a reference for pertinent engineering design.
-
Keywords:
- bridge engineering /
- stud connector /
- push-out test /
- shear performance /
- finite element analysis
-
钢-混凝土组合梁是通过剪力连接件将钢梁和混凝土板组合而共同受力,充分发挥钢材抗拉性能和混凝土抗压性能,应用前景广阔[1]。栓钉连接件安装方便、各向抗剪性能一致,是桥梁工程中应用最广泛的一种抗剪连接件[2]。我国公路超载现象严重,传统组合梁结构的普通混凝土(normal concrete,NC)桥面板经常出现裂缝,特别是在连续组合梁的负弯矩区域混凝土开裂严重,进而腐蚀栓钉,严重影响结构承载力及耐久性[3-5]。超高性能混凝土(ultra-high performance concrete,UHPC)具有较高强度,且基体中掺入的钢纤维使其具有相当大的拉伸硬化能力和较好的延性[6-8]。将UHPC桥面板代替普通混凝土桥面板,不仅能解决传统组合梁桥面板易开裂问题,还能降低结构自重[9],使组合梁的跨径进一步增大。
目前国内外学者已采用推出试验和数值分析的方法对栓钉连接件在普通强度混凝土中的性能进行了大量研究,发现栓钉的抗剪性能主要受栓钉直径、高度、抗拉强度及混凝土强度参数的影响[10-13]。随着UHPC在组合桥面板中的应用,钢-UHPC组合结构中栓钉剪力键的力学行为备受关注。Kim等[14]对UHPC中栓钉连接件进行了推出试验,并指出在不损失抗剪强度情况下,长径比可以从4降到3.1。田启贤等[15]对高性能混凝土中短栓钉的力学性能进行了试验研究,结果表明栓钉在靠近焊缝处剪切破坏,栓钉周围混凝土无明显开裂或压溃现象,短栓钉在高性能混凝土中可以充分发挥其强度。邵旭东等[16]分析了活性粉末混凝土(reactive powder concrete, RPC)中短栓钉的剪应力沿长度方向分布情况,并与常规栓钉进行对比,发现短栓钉和长栓钉受力性能基本一致,但短栓钉抗剪效率更高。
Ollgaard等[17]进行栓钉连接件的模型推出试验研究,结果表明栓钉连接件的抗剪强度由周围的混凝土破碎破坏和栓钉剪切破坏两种破坏机制控制,提出计算栓钉连接件的抗剪承载力计算式和荷载-滑移曲线指数型方程。各国规范基于Ollgaard计算式,考虑抗力分项系数给出栓钉连接件抗剪承载力设计计算式,但仅适用于普通强度混凝土,用于计算UHPC中栓钉承载力的结果偏保守。Döinghaus等[18]发现焊接环的存在提高了高强混凝土中栓钉的抗剪强度,并提出了考虑焊缝增强效应的抗剪承载力公式。李萌等[19]用统计分析将文献[18]承载力计算式中的焊缝直径和高度统一转化为栓钉直径,极大简化了算式,提出适用于UHPC中短栓钉的抗剪承载力计算式;同时采用无量纲法得到不同直径栓钉荷载-滑移曲线计算公式,但没有考虑混凝土强度的影响。An等[20]对普通混凝土(40 MPa)和高强混凝土(100 MPa)分别给出荷载-滑移曲线计算公式,对于强度介于两者之间的混凝土试件没有给出取值方法。
综上,目前关于栓钉连接件抗剪性能的研究主要集中于传统钢-混凝土组合结构中栓钉或正交异性钢桥面+薄层UHPC组合结构中短栓钉,对钢梁+UHPC板组合结构中常规栓钉连接件的抗剪性能影响的相关研究较少,而且对栓钉抗剪承载力、荷载-滑移曲线的取值未形成统一的计算公式。本文旨在通过试验与数值分析相结合分析NC和UHPC试件破坏现象,探讨栓钉承载力和荷载-滑移曲线影响因素以及长短栓钉的应力分布特征的差异性。依据试验结果,提出适用于栓钉剪断破坏的抗剪承载力计算公式及考虑混凝土强度的栓钉荷载-滑移曲线公式,为钢-UHPC组合结构的推广应用提供一定的参考价值。
1 试验概况
1.1 试件设计
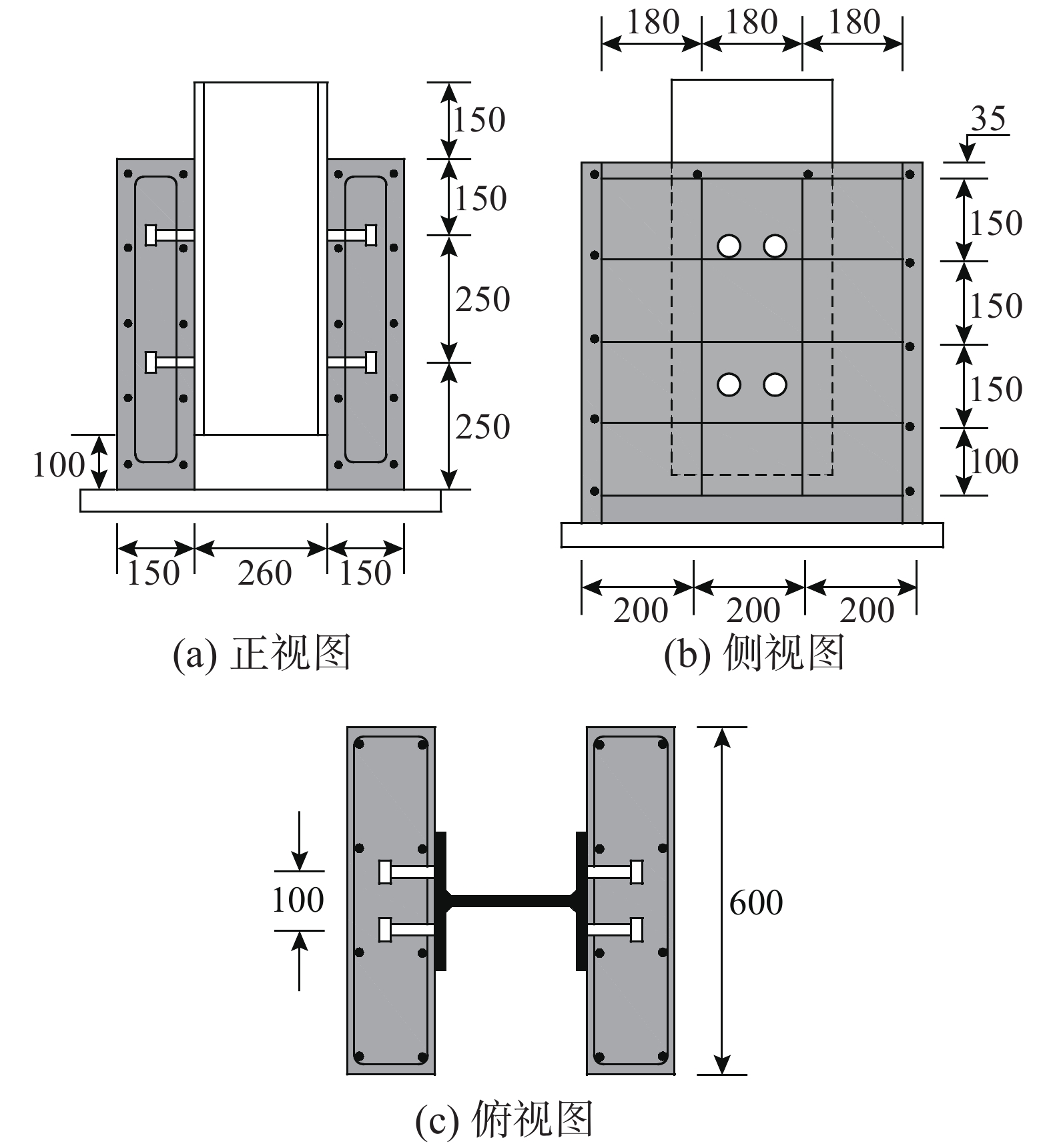
本次试验共设计8个推出试件,试件构造如图1所示。试验中混凝土采用NC和UHPC,混凝土板采用现浇的方式浇筑,高为650 mm、宽为600 mm、厚为150 mm,其层内布置有直径为8 mm的HRB400级钢筋作为配筋;H型钢梁采用Q345D桥梁钢,其截面规格为HW300×300×10×15,长度为700 mm;栓钉采用ML15,其直径有13 mm、16 mm两种,长度有80 mm、120 mm 两种,两侧各布置4个栓钉,纵横向布置间距250 mm×100 mm,试件具体参数见表1。本次试验不考虑混凝土的粘接作用,试件全部涂润滑油做脱粘处理。
表 1 推出试件构造图Table 1. Constructions of push-out specimens混凝土 栓钉长度/mm 栓钉直径/mm 试件编号 NC 80 13 NC-80-13 NC 120 13 NC-120-13 NC 80 16 NC-80-16 NC 120 16 NC-120-16 UHPC 80 13 UHPC-80-13 UHPC 120 13 UHPC-120-13 UHPC 80 16 UHPC-80-16 UHPC 120 16 UHPC-120-16 按照相关规范对常温养护的混凝土、HRB400钢筋和型钢进行力学性能试验,如图2所示。栓钉和UHPC中钢纤维的力学参数采用生产厂家提供的参数。NC和UHPC的力学性能见表2,各钢材具体材料参数见表3。
表 2 混凝土材料基本力学性能Table 2. Measured mechanical properties of concrete材料 抗压强度/MPa 抗折强度/MPa 弹性模量/GPa 泊松比 UHPC 116 30.6 46.66 0.2 NC 53 1.85 37.88 0.2 表 3 钢材材料性能Table 3. Measured mechanical properties of steel材料 弹性模量/GPa 屈服强度/MPa 抗拉强度/MPa 泊松比 Q345 206 357 476 0.3 HRB400 200 400 570 0.3 13 mm栓钉 206 380 530 0.3 16 mm栓钉 206 380 540 0.3 钢纤维 200 − 2850 0.3 1.2 试件制作
试件制作时,先将H型钢切割为700 mm的节段,并在钢板两侧相应位置采用透焊方式焊接栓钉。按设计尺寸绑扎箍筋笼与制作模板,并将焊接栓钉的H型钢与箍筋笼立模组装,然后在模具及H型钢表面涂抹润滑油,浇筑混凝土。试件制作完成后,自然条件下浇水养护28 d。试件的制作具体步骤如图3所示。
1.3 试验加载方案
试验采用500 t压力机进行加载,在混凝土板和工字钢腹板底部布置左右对称的位移计(LVDT),以测量板与钢梁之间的相对滑移,试验加载装置及LVDT的布置如图4所示。加载前在工字钢顶部焊接一块30 cm×30 cm的钢板,保证工字钢顶板受力均匀。试验正式加载前先进行预加载。正式加载时,由于相对滑移达到1 mm以前位移增量不明显,先以荷载控制加载,每级加载增量为10 kN,记录每级荷载对应的相对滑移值,位移大于1 mm后塑性变形迅速扩大,此后按照位移增量0.1 mm~0.2 mm来记录数据直到试件破坏。
2 试验现象与结果分析
2.1 试验现象
栓钉剪力键的破坏形态主要表现为栓钉剪断和混凝土结构开裂破碎两种。当栓钉直径较小、混凝土强度相对较高,破坏形式表现为栓钉剪断,并伴随着栓钉根部混凝土局部压碎;栓钉直径较大、混凝土强度相对较低,其破坏形式表现为混凝土开裂破碎。本文推出试验中试件破坏如图5所示,8个试件均为栓钉剪断破坏且断面光滑,栓钉根部混凝土局部压碎。NC试件和UHPC试件破坏形式类似,但UHPC试件混凝土表面裂缝少,UHPC板破坏面中局部压碎区域较NC更小,表明UHPC更能够充分发挥栓钉的抗剪性能。
由栓钉剪断,栓钉根部焊缝处混凝土局部压碎破坏现象可知,栓钉抗剪承载力主要由两部分组成:一是栓钉自身抗剪承载力;二是栓钉根部焊缝周边混凝土的承载力。试验过程中,试件均为脆性破坏,在荷载达到峰值前有一段较长平台期,但破坏时栓钉突然剪断并伴随着巨响。随后,荷载大幅度降低,栓钉剪断、混凝土板与工字钢分离,试件破坏,试验终止。
2.2 试验结果分析
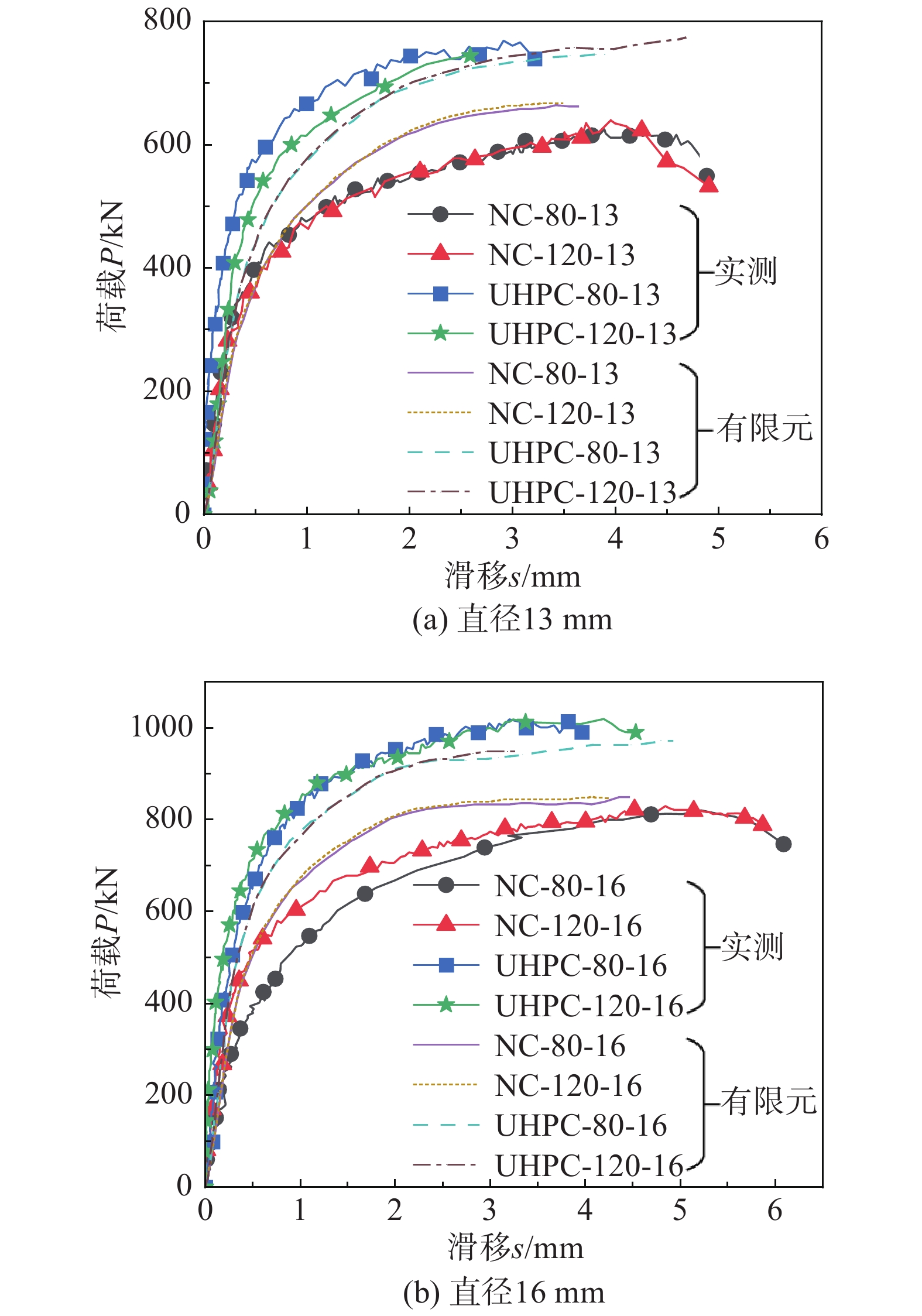
图6(a)及图6(b)分别是直径13 mm、16 mm栓钉剪力键的荷载-滑移曲线。荷载-滑移曲线分为弹性阶段、塑性阶段和破坏阶段。当荷载小于60%抗剪承载力时,荷载-滑移曲线基本处于弹性阶段;随着荷载增加,栓钉剪力键进入塑性阶段,滑移量较荷载增长更快;当荷载超过峰值时,试件突然破坏,曲线下降部分变得陡、滑、短。
从图6可知,钢-混组合结构中栓钉的抗剪承载力受混凝土强度和栓钉直径影响显著。NC试件中,直径13 mm和16 mm栓钉剪力键的平均抗剪承载力分别为 614 kN和812 kN;而UHPC试件中,抗剪承载力平均值分别为752 kN 和1016 kN。与直径13 mm栓钉剪力键相比,16 mm栓钉的抗剪承载力提高34%。相比NC剪力键,UHPC栓钉剪力键承载力提高25%,绝对值高出150 kN~200 kN,但延性降低,且栓钉剪力键破坏较早。在混凝土类型和栓钉直径相同的情况下,栓钉长度为80 mm和120 mm的试件抗剪承载力基本相等。栓钉主要通过根部与混凝土传递剪力作用,因此,栓钉长度对栓钉剪力键的抗剪承载力影响甚微,但是栓钉长度会对剪力键前期的剪切刚度造成一定的影响,这是由于栓钉剪力键的抗剪刚度与栓钉的长径比密切相关。
UHPC试件中栓钉直径为13 mm时,相对滑移值为3 mm;直径为16 mm时,相对滑移值为5 mm。NC试件中栓钉直径为13 mm时,相对滑移值为4.5 mm;直径为16 mm时相对滑移值为6.5 mm。可知,栓钉直径的增加可提高剪力键的抗滑移性能。
剪切刚度的计算通常采用基于荷载-滑移曲线的割线刚度,但各国规范关于抗剪刚度取值方法存在差异。
1) Eurocode 4[21]规范规定,栓钉抗剪刚度
K=0.7PRk/s ,其中PRk 为推出实验得到的抗剪承载力设计值,考虑0.9的折减PRk=0.9Vu ,即s为0.7PRk 对应滑移值。2) JSSC规定[22],根据实测荷载-滑移曲线,极限抗剪承载力的1/3处对应的割线为抗剪刚度。
各试件抗剪刚度值见表4,由表可以看出,栓钉直径对抗剪刚度影响较大,UHPC中栓钉的抗剪刚度比普通混凝土的栓钉大。
3 有限元分析
3.1 有限元模型建立
推出试件有限元模型如图7所示。
混凝土材料采用实体单元solid65,工字钢和栓钉采用实体单元solid45。为提高结果精度,同时节约算力,在栓钉局部位置采用细化网格的方法,局部网格尺寸为2 mm,过渡区域取3 mm,外边缘取 5 mm。栓钉与混凝土的交界面接触采用conta173接触单元,考虑摩擦,假定摩擦系数为0.3,忽略了混凝土与工字钢之间的粘接力。考虑到结构对称性,推出试件的有限元模型只模拟计算1/4的试件,对称面边界采用对称约束。
混凝土采用双线性各向同性硬化模型,参考文献[23],推出试验中混凝土开裂后应力下降对计算结果影响不大,不设置下降段,其本构关系如图8(a)所示,fct为UHPC抗拉强度,Ec为UHPC弹性模量,fc为UHPC抗压强度,fct、Ec和fc取实测值;εc1为受压曲线峰值应变,取3500 με。混凝土破坏准则采用William-Warnke五参数破坏准则。钢梁和栓钉均采用多线性各向同性硬化模型进行模拟,其本构关系分别如图8(b)和图8(c)所示,强度准则采用Mises屈服准则。钢筋采用理想弹塑性模型,其本构关系如图8(d)所示。
3.2 模型验证
推出试件的试验荷载-滑移曲线与有限元分析数值曲线对比结果如图9所示。由于试验混凝土的不均匀性和有限元法简化的混凝土本构关系,其非线性性能略有不同,但数值与试验荷载-滑移曲线变化趋势一致性较好。
有限元预测的栓钉剪力键的极限抗剪承载力与试验结果对比如表5所示,由表5可知,有限元预测的栓钉剪力键的极限抗剪承载力与试验结果的最大误差为7.0%。本文主要针对栓钉剪力键的极限抗剪承载力特性进行研究,因而可在此基础上进一步开展栓钉抗剪性能参数分析。
表 5 有限元与实测极限抗剪承载力结果Table 5. The results of finite element and measured ultimate shear capacity试件 试验结果/kN 有限元结果/kN 误差/(%) NC-80-13 618 661 7.0 NC-120-13 639 666 4.2 UHPC-80-13 768 746 2.9 UHPC-120-13 744 773 3.9 NC-80-16 820 849 3.5 NC-120-16 829 846 2.1 UHPC-80-16 1018 971 4.6 UHPC-120-16 1019 949 6.9 3.3 参数分析
混凝土强度:以直径分别为10 mm、13 mm、16 mm、19 mm、22 mm 的5种栓钉为例,计算得到的五种栓钉直径下3种强度混凝土的推出模型抗剪承载力如图10(a)所示。从图中可以看出,栓钉抗剪承载力随混凝土强度提高而提高,但承载力增速并不大。
栓钉直径:以混凝土抗压强度分别为50 MPa、80 MPa、120 MPa的试件模型为例, 计算得到的5种栓钉直径的栓钉剪力键承载力如图10(b)所示。栓钉受剪承载力随栓钉直径增加而增加,承载力变化较明显,说明栓钉面积在承载力中起到关键作用。
栓钉极限抗拉强度:以混凝土材料抗压强度50 MPa,剪力钉极限强度分别为345 MPa、420 MPa、550 MPa,剪力钉直径分别为10 mm、13 mm、16 mm、19 mm、22 mm 的推出模型为例,计算得到3种极限抗拉强度下栓钉的承载力如图10(c)所示。从图中数据可以发现,栓钉抗剪承载力随剪力钉强度增加而表现出线性增加关系。
栓钉长径比:以混凝土材料抗压强度为50 MPa,剪力钉的极限强度为550 MPa,直径为13 mm、16 mm、19 mm、22 mm的剪力连接件模型为例,12种栓钉长径比的推出试件抗剪承载力如图10(d)所示,栓钉承载力随其长径比增加有一定幅度的增加,但增加的绝对值较小,表明在一定的长径比范围内,长径比对抗剪承载力无较大影响。
3.4 短栓钉与常规栓钉的受力特点
3.4.1 不同长度栓钉荷载-位移曲线
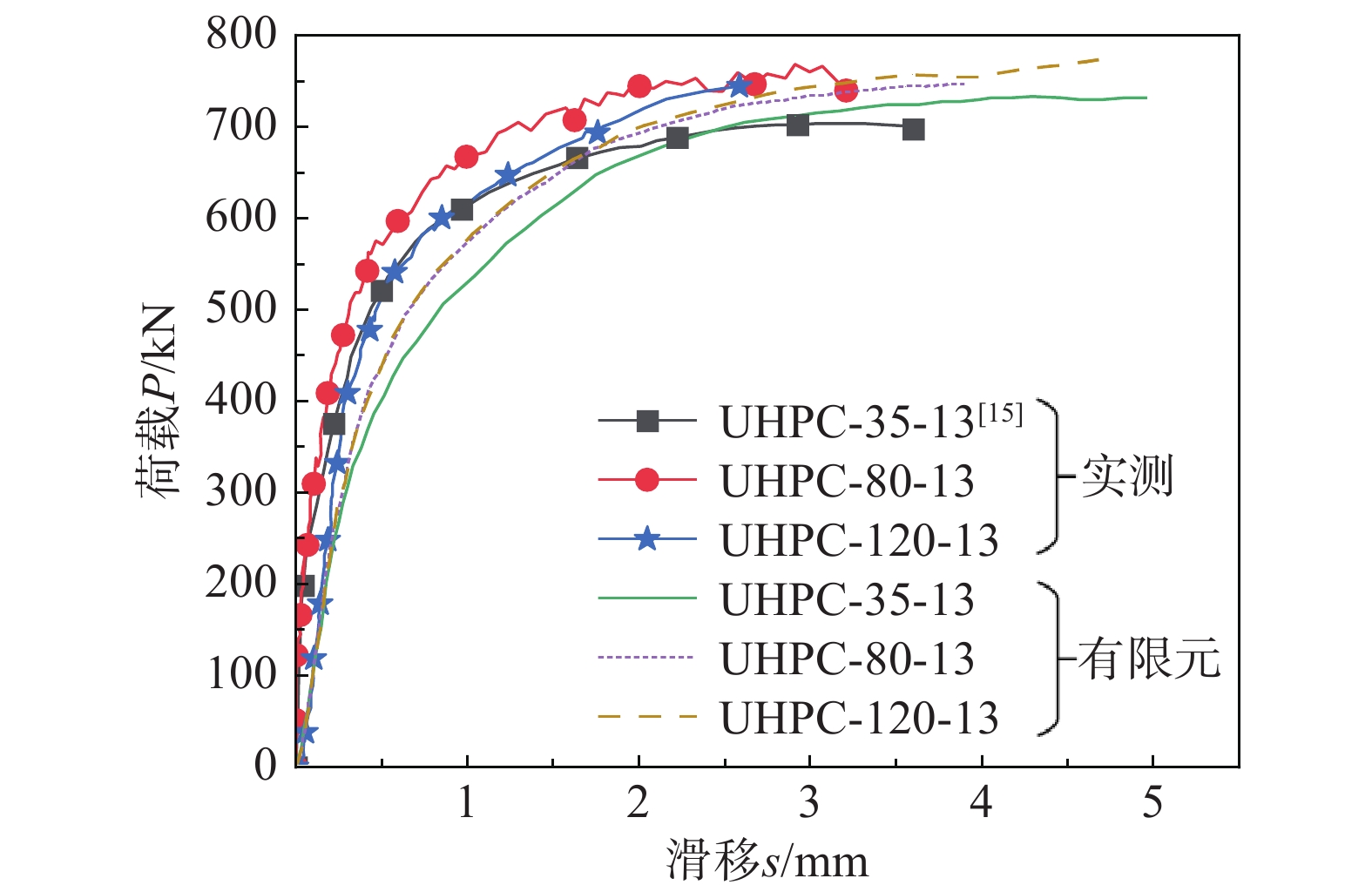
根据文献[15]中高性能混凝土试件的短栓钉的承载力结果,结合本文试验与有限元结果得到不同长度栓钉荷载-滑移曲线,其对比分析结果如图11所示。在实际应用中,若采用正交异性钢桥面板+UHPC薄层的结构,UHPC层厚度一般不超过50 mm,导致栓钉长度通常不超过35 mm。如果进一步减小铺装层厚度,栓钉焊接难度增大。根据实际应用情况可知,一般短栓钉长径比为2<l/d<4,而规范规定的常规栓钉长径比为l/d>4,因此非常有必要分析两种类型栓钉的实际受力特点及差异性。计算数据表明,栓钉直径、抗拉强度及混凝土强度一定时,栓钉长度对荷载-滑移曲线影响有限。栓钉长35 mm时极限承载力较常规栓钉略小,栓钉长80 mm和120 mm的承载力相同,表明常规栓钉存在较大部分未被充分利用。
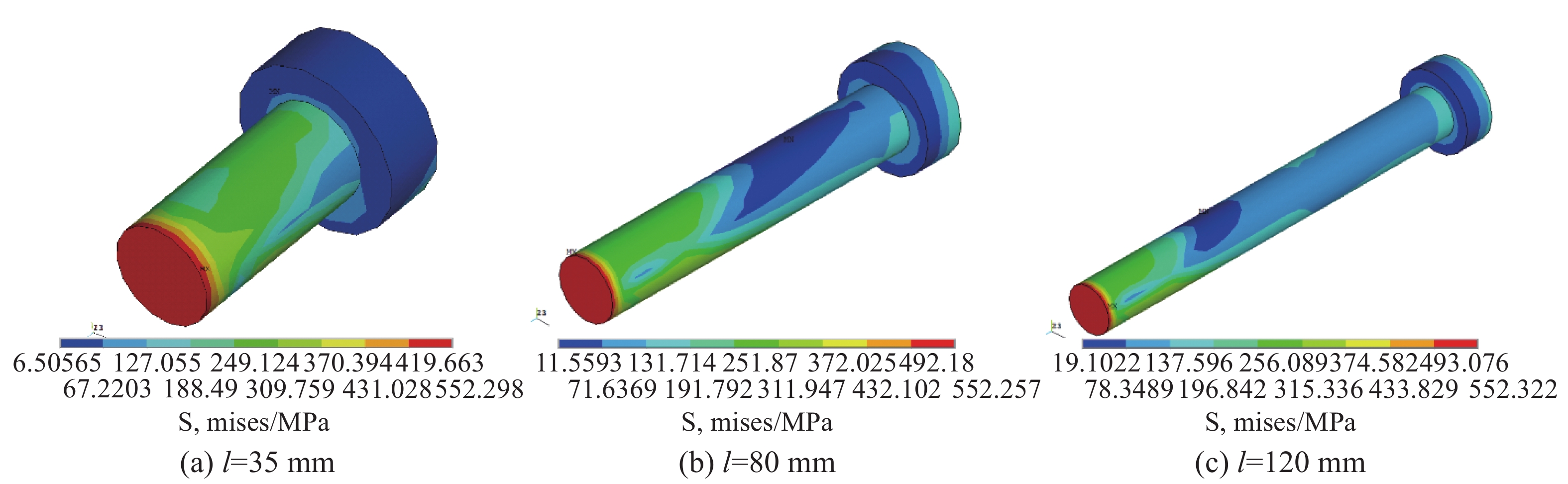
3.4.2 栓钉极限状态下Von Mises应力云图
图12~图14是栓钉在极限状态下的Von Mises应力云图。由图可知,应力主要集中于栓钉根部区域,在钉帽方向应力基本为0,相对于栓钉直径为13 mm的试件,直径为16 mm的栓钉应力分布更均匀,应力沿栓钉分布长度更大;相比于NC试件,UHPC试件中栓钉应力分布更集中。
3.4.3 栓钉剪应力沿长度方向分布图
3.4.1节分析结果表明,栓钉长度对承载力的影响不大,为深入研究栓钉剪应力的分布规律,探讨栓钉的合理的长度区间,本文将通过栓钉的有限元模型对栓钉剪应力沿长度方向的分布规律进行分析,剪应力取栓钉中心点位置数值,考虑NC和UHPC两种混凝土,栓钉长度分别取35 mm、80 mm、120 mm这3种,栓钉直径为13 mm、16 mm这2种,得到的栓钉剪应力分布如图15所示。
通过图15的数据对比可知,剪应力在栓钉上的分布均集中在根部区域,直径相同、栓钉长度不同时,不同长径比栓钉中应力分布规律基本一致。栓钉直径为13 mm时,在距离栓钉根部20 mm以内,剪应力衰减速度快,在20 mm外基本为0;直径增加到16 mm时,剪应力的分布长度有所提高,在距离栓钉根部30 mm以内,剪应力快速衰减,在30 mm之后基本为0。混凝土强度对栓钉剪应力分布规律影响较小。综上,剪应力沿栓钉有效分布长度与栓钉直径呈正相关,与长度和混凝土强度关系较小。
4 理论计算
4.1 抗剪承载力计算
表6是各国规范的承载力公式。规范公式均考虑了一定的安全系数,栓钉材料取值为屈服强度,且设计理念是栓钉剪力键承载力在混凝土承载力和栓钉自身承载力之间取较小值,这与本实验认为的两者都是承载力组成部分的观念不同。
表 6 规范中栓钉承载力公式Table 6. Formula of stud bearing capacity in code规范 计算公式 GB 50917−2013[24] Ncy=1.19Asfy(Ec/Es)0.2(fcu/fy)0.1栓钉剪断
Ncv=0.43ηAs√fcdEc混凝土破坏AASHTO[25] Ncv=0.5As√Ecf′c⩽ Eurocode 4[21] N_{\rm{v}}^{\rm{c}} = \min \left\{ { {\text{ 0} }{\text{.29} }\alpha { { {{d} } } ^{\text{2} } }\sqrt { { { {E_{\rm{c}}}f_{{\rm{ck}}}'} / { {\gamma _{\rm{v}}} } } } ,{\text{0} }{\text{.8} }{A_{\rm{s}}}{ { {f_{\rm{y}}} } / { {\gamma _{\rm{v}}} } } } \right\} 注:中国规范[24]中,N_{\rm{v}}^{\rm{c}}为剪力钉抗剪承载力;As为剪力钉截面面积;Ec、Es分别为混凝土和剪力钉弹性模量;fcu为边长为150 mm的混凝土立方体抗压强度;fcd为混凝土轴心抗压强度设计值;fy为剪力钉屈服强度。材料性能为4.6级时,取400 MPa,\eta 为群钉折减系数。f_{\rm{c}}'为圆柱体轴心抗压强度,f_{\rm{c}}' = {\text{0}}{\text{.4}}{f_{{\rm{cu}}}^{7/6}}。欧洲规范[21]中,当{{3 \lt {h_{\rm{s}}}} / {{{d}}} } < 4时,\alpha = {\text{0}}{\text{.2}}[({h_{\rm{s}}}/{{{d}}} + 1) + 1] \leqslant 1.0;当{{{h_{\rm{s}}}} / {{{d}}} } > 4时,α=1,γv=1.25,式中,f_{{\rm{ck}}}'为圆柱体标准抗压强度。 从表7的计算结果对比来看,中国《钢-混凝土组合桥梁设计规范》[24]与欧洲Eurocode 4规范[21]结果较为接近,结果偏于保守,无论是C50混凝土还是UHPC,规范值均在试验值50%左右。美国 AASHTO 规范计算方法在普通混凝土试件中更接近实际值,比值大约在68%~80%,但用于UHPC的计算则结果明显偏小,大约在56%~66%。分析表明,规范计算结果偏小的原因主要有两点:① 材料取值保守,栓钉用屈服强度fy计算而非极限抗拉强度fu;② 计算理念保守,栓钉剪断破坏时主要考虑栓钉的抗剪性能,混凝土作为系数调整或者不考虑,但实际上是混凝土与栓钉共同作用。
Döinghaus等[18]认为,带栓钉钢-混组合试件的抗剪承载力由栓钉抗剪承载力和焊缝处周边混凝土压碎破坏承载力两部分组成,提出了考虑焊缝承载力的栓钉抗剪承载力公式如下:
{P_{\rm u}}{\text{ = 0}}{\text{.85}}{A_{\rm s}}{f_{\rm u}} + \eta {f_{\rm c}}{d_{\rm w}}{l_{\rm w}} (1) 式中:As为栓钉杆身面积;fu为栓钉极限抗拉强度;fc为混凝土抗压强度;
\eta 为栓钉焊缝承载力提高系数;dw为剪力钉焊缝直径;lw为栓钉焊缝高度。式(1)存在不足之处:一是
\eta 的取值没有统一;二是焊缝尺寸参数无法统一,不方便使用。李萌等[19]对栓钉周边焊缝尺寸进行统计,得到焊缝高度与直径的平均值,考虑95%的保证率后得到相关公式;本实验统计直径13 mm和16 mm的试件焊缝高度与直径的平均值分别为:{\mu _{\rm h}} = 0.27{d_{\rm s}} 和{\mu _{\rm d}} = 1.55{d_{\rm s}} 、{\mu _{\rm h}} = 0.3{d_{\rm s}} 和{\mu _{\rm d}} = 1.4{d_{\rm s}} ,整理后得到式(2):{P_{\rm u}}{\text{ = 0}}{\text{.85}}{{{A}}_{\rm s}}{f_{\rm u}} + 0.4\eta {f_{\rm c}}{{{{d}}} ^2} (2) 式(2)考虑了栓钉直径、栓钉极限抗拉强度和混凝土抗压强度参数,并通过建立焊缝尺寸与栓钉直径的关系,间接考虑焊缝参数。为使该式的表达形式简洁,将其变为乘积形式:
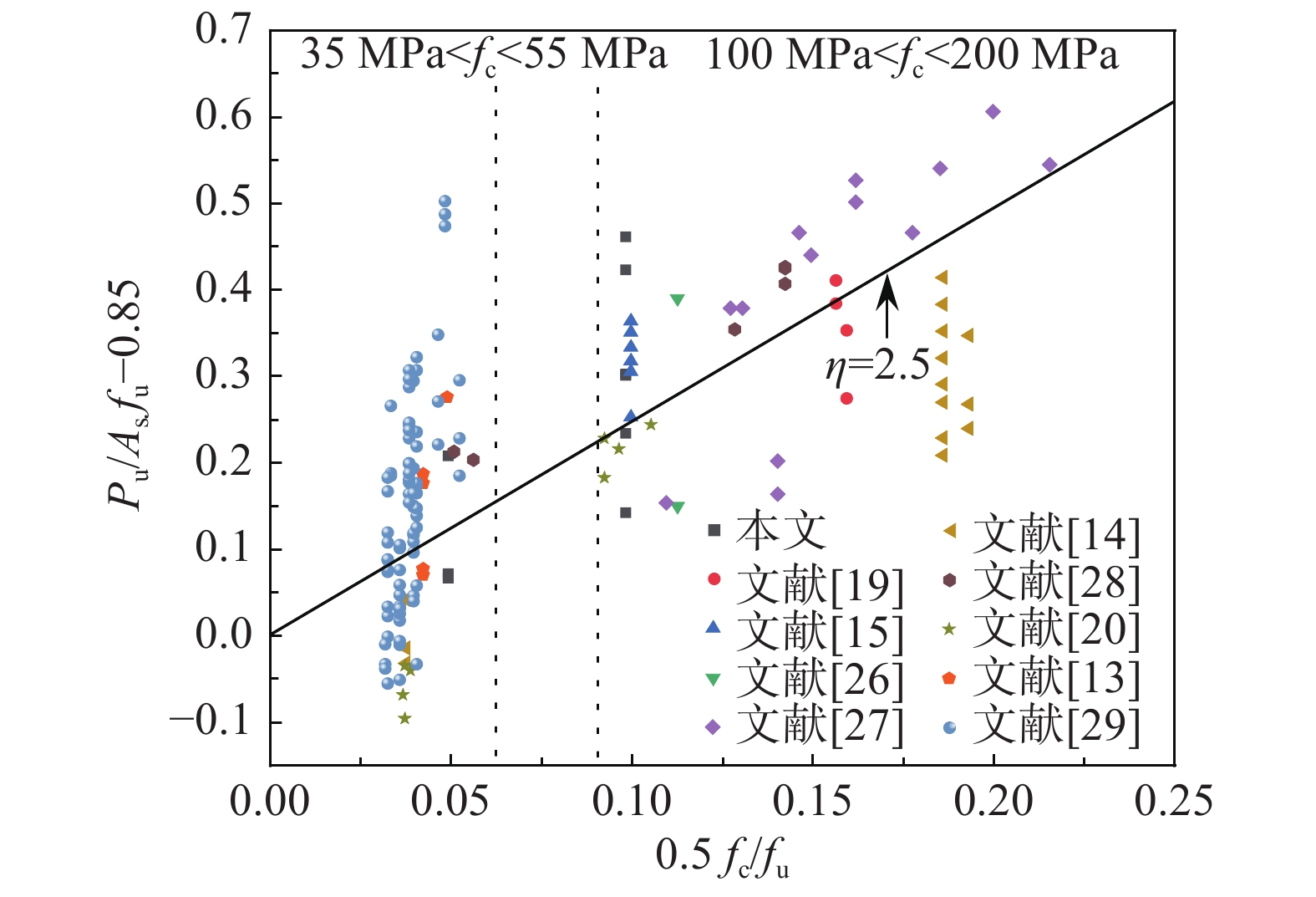
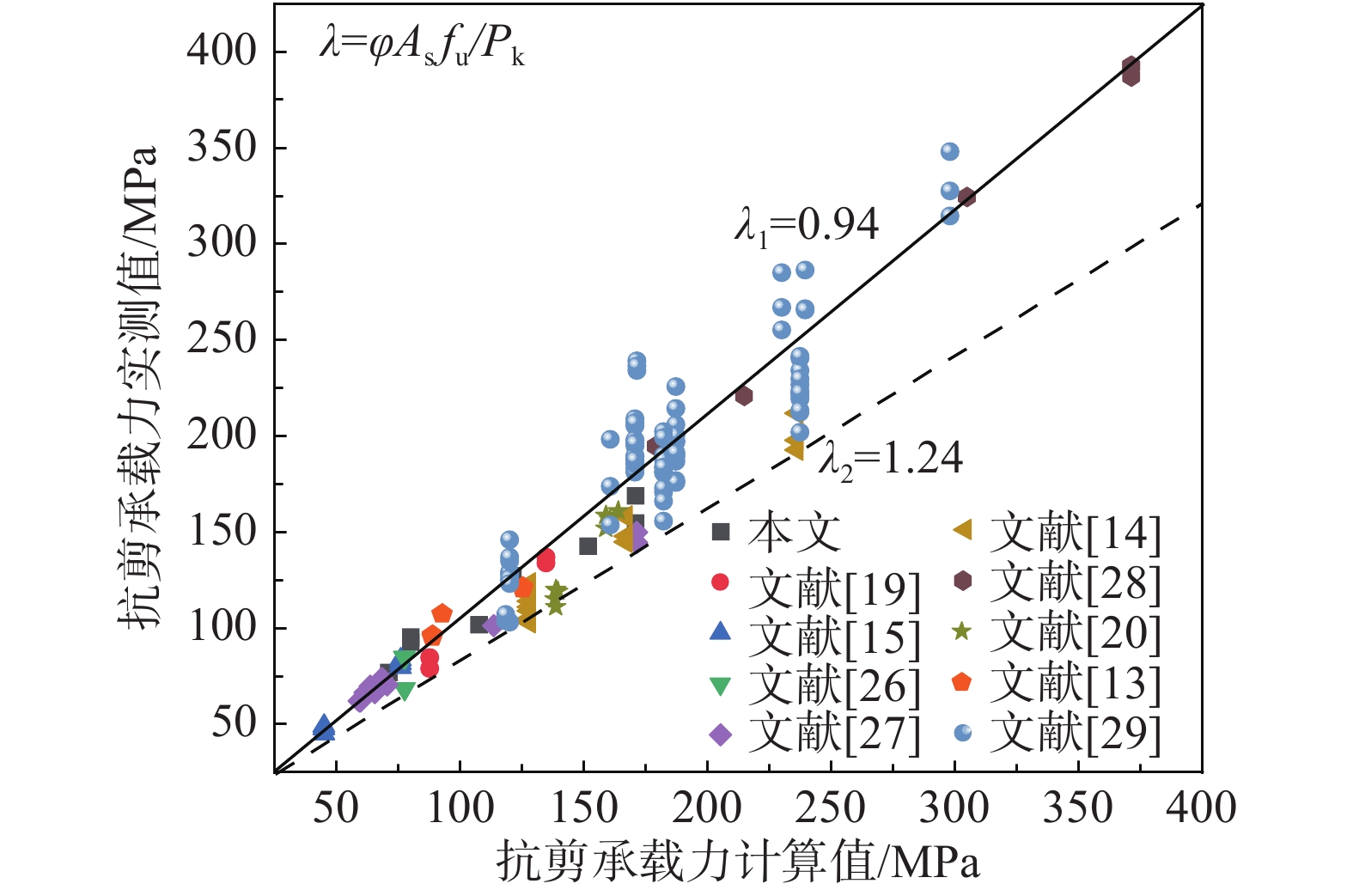
{P_{\rm u}}{\text{ = }}\varphi {{\text{A}}_{\rm s}}{f_{\rm u}} (3) \varphi = 0.85 + 0.5\eta {f_{\rm c}}/{f_{\rm u}} (4) 文献[19]的研究范围是短栓钉(2<l/d<4)和UHPC铺装结构中的栓钉,本文在其理论基础上加入常规长度栓钉(l/d>4)试件的试验数据和普通强度的混凝土试件的试验数据。试验样本115个(统计的试件破坏形式均是栓钉剪断),其中普通混凝土(35 MPa<fc<55 MPa)样本65个、高强混凝土(100 MPa<fc<200 MPa)样本50个;常规栓钉74个、短栓钉41个;汇总得到图16,图中数据拟合时精度较高。此时式(3)也适用于普通强度混凝土和常规栓钉。对于栓钉长径比,前文研究也表明栓钉长度对承载力影响不大,所以不影响公式计算精度。
将
\eta 代入式(4),可得到各材料参数已知时的栓钉承载力计算值,在考虑计算值与实测值的误差后并修正可得到承载力设计值,计算式如下:{P_{\rm d}}{\text{ = }}\varphi {{\text{A}}_{\rm s}}{f_{\rm u}}/\lambda (5) 式中:λ为抗力分项系数;Pd为实测承载力。图17中拟合得到的λ1=0.94,表明计算值与实测值误差较小。其主要原因是栓钉本身承担了绝大部分承载力,但设计时可按照偏保守取值,因此建议λ2取1.24。文献[19]得到的λ1=1,λ2=1.25,表明在破坏形式均为栓钉剪断破坏的前提下,本文提出的计算方法不仅适用于短栓钉和高强混凝土,也适用于常规栓钉和普通混凝土。
4.2 荷载-滑移曲线计算
对于栓钉剪力键,国内外学者提出了许多荷载-滑移曲线计算公式,见式(6)~式(10)。然而,大多数公式建立在普通强度混凝土,这些公式能否应用于UHPC必须通过试验进行验证。
1)文献[17]
P/{P_{\rm{u}}} = {(1 - {{\rm{e}}^{ - 0.71s} })^{0.4} } (6) 式中:P为栓钉剪力值;s为相对滑移;Pu为栓钉抗剪承载力。
2)文献[13]
{\rm{y'}} = \left\{ \begin{aligned} &\frac{{{A_2}x' + ({B_2} - {\rm{1}}){{x'}^2}}}{{1 + ({A_2} - {\rm{2}})x' + {B_2}{{x'}^2}}}\;,\;x' \leqslant 1\\& \frac{{x'}}{{{\alpha _2}{{(x' - {\rm{1}})}^2} + x'}}\;,\;\;\;\;\;\;\;\;\;\;\;x' \gt 1 \end{aligned} \right. (7) 式中:A2、B2、
{x'} 、{y'} 为参数,{A_2} = \left( {100{ {{d} } } - 54} \right)/ (0.7{ { {{d} } } ^2} - 5.8{{d} }) 、{B_2} = {\text{1}}{\text{.6}}{\left( {{A_2}{{ - 1 }}} \right)^2} 、{x'} = {s / { {s_{\rm{u}}} } } 、{y'} = {P / { {P_{\rm{u}}} } } ,su为峰值滑移;d为栓钉直径;{\alpha _{\text{2}}} 为下降段参数,取值0.15;其他参数含义同上。3)文献[19]
\frac{P}{P_{\rm{u} } } = \dfrac{ {s/{ {{d} } } } }{ {0.016 + 0.9(s/{ {{d} } } )} } (8) 4)文献[20]
\frac {P}{P_{\rm{u}}} = \dfrac{ {2.24(s - 0.058)} }{ {1 + 1.98(s - 0.058)} } (普通混凝土) (9) \frac{P}{P_{\rm{u}}} = \dfrac{ {4.44(s - 0.031)} }{ {1 + 4.24(s - 0.031)} }(高强混凝土) (10) 图18是不同影响因素下的荷载-滑移曲线各公式计算值与实测值计算结果的对比。图18(a)和图18(b)为栓钉极限抗拉强度分别为465 MPa和650 MPa情况下的拟合曲线结果对比情况,图18(c)和图18(d)为栓钉直径分别为10 mm和13 mm情况下的拟合曲线结果对比情况,这两组试件长径比2<l/d<4,归类为短栓钉。图18(e)和图18(f)为混凝土分别为NC和UHPC情况下的拟合曲线结果对比情况。结果显示,不考虑下降段更符合实际情况,无量纲荷载-滑移曲线在不同混凝土强度下误差较大。
通过对推出试件的试验值和有限元模型计算值进行拟合,荷载-滑移曲线均表现为指数函数的形式。本文考虑混凝土强度的影响,不区分混凝土材料,提出指数形式的荷载-滑移曲线公式:
P/{P_{\rm u}} = a(1 - {{\rm e}^{bs}}) (11) 通过8组试件拟合得到参数a和b的平均值,其中a=0.95;NC中
b = - 2.06 ,UHPC中b = - 3.33 。用插值法考虑混凝土强度fc,则b = - 0.023{f_{\rm c}} - 0.841 。式(11)表示承载力与滑移值的关系,考虑混凝土强度对曲线斜率的影响,针对栓钉剪断的破坏形式,适用范围广,拟合曲线与试验曲线在弹性阶段拟合效果较好,栓钉实际服役过程中主要在弹性阶段工作,具有一定的参考价值。5 结论
本文通过栓钉剪力键推出试验和有限元分析,对栓钉抗剪承载力和荷载-滑移曲线的影响因素进行研究,揭示栓钉的应力分布规律,并基于试验数据提出栓钉抗剪承载力和荷载-滑移曲线计算公式。主要结论如下:
(1) 所有推出试件的破坏形态均为栓钉剪断破坏,且断面光滑,栓钉根部混凝土局部压碎。相比NC试件,UHPC试件的极限抗剪承载能力更高,但延性降低。
(2) 栓钉连接件的抗剪承载力受混凝土强度、栓钉直径和屈服强度影响显著,栓钉长度则影响较小。适当提高混凝土强度,增大栓钉的直径和屈服强度,可提高栓钉连接件的抗剪承载力。
(3) 栓钉剪应力在根部最大,沿钉帽方向迅速衰减。栓钉剪应力有效分布长度随栓钉直径增大而增大,受栓钉长度和混凝土强度影响较小。直径13 mm和16 mm的栓钉剪应力有效分布长度分别为距离根部20 mm和30 mm范围。
(4) 现有规范中栓钉极限抗剪承载力计算公式是针对普通钢-混组合结构,若用于钢-UHPC组合结构,其结果偏保守。本文提出的栓钉承载力计算公式针对栓钉剪断破坏形式,适用于普通混凝土和高性能混凝土,具有精度高、适用范围广的特点;栓钉荷载-滑移曲线考虑混凝土强度因素,适用于栓钉剪断破坏的情况,与试验数据在弹性阶段拟合效果较好。
-
表 1 推出试件构造图
Table 1 Constructions of push-out specimens
混凝土 栓钉长度/mm 栓钉直径/mm 试件编号 NC 80 13 NC-80-13 NC 120 13 NC-120-13 NC 80 16 NC-80-16 NC 120 16 NC-120-16 UHPC 80 13 UHPC-80-13 UHPC 120 13 UHPC-120-13 UHPC 80 16 UHPC-80-16 UHPC 120 16 UHPC-120-16 表 2 混凝土材料基本力学性能
Table 2 Measured mechanical properties of concrete
材料 抗压强度/MPa 抗折强度/MPa 弹性模量/GPa 泊松比 UHPC 116 30.6 46.66 0.2 NC 53 1.85 37.88 0.2 表 3 钢材材料性能
Table 3 Measured mechanical properties of steel
材料 弹性模量/GPa 屈服强度/MPa 抗拉强度/MPa 泊松比 Q345 206 357 476 0.3 HRB400 200 400 570 0.3 13 mm栓钉 206 380 530 0.3 16 mm栓钉 206 380 540 0.3 钢纤维 200 − 2850 0.3 表 4 栓钉抗剪刚度
Table 4 Shear stiffness of single stud
/(kN/m) 表 5 有限元与实测极限抗剪承载力结果
Table 5 The results of finite element and measured ultimate shear capacity
试件 试验结果/kN 有限元结果/kN 误差/(%) NC-80-13 618 661 7.0 NC-120-13 639 666 4.2 UHPC-80-13 768 746 2.9 UHPC-120-13 744 773 3.9 NC-80-16 820 849 3.5 NC-120-16 829 846 2.1 UHPC-80-16 1018 971 4.6 UHPC-120-16 1019 949 6.9 表 6 规范中栓钉承载力公式
Table 6 Formula of stud bearing capacity in code
规范 计算公式 GB 50917−2013[24] {N}_{{\rm{y}}}^{{\rm{c}}}=1.19{A}_{{\rm{s}}}{f}_{{\rm{y}}}({E}_{{\rm{c}}}/{E}_{{\rm{s}}}{)}^{0.2}({f}_{{\rm{cu}}}/{f}_{{\rm{y}}}{)}^{0.1}栓钉剪断
N_{\rm{v}}^{\rm{c}} = {\text{0} }{\text{.43} }\eta A{}_{\rm{s}}\sqrt { {f_{{\rm{cd}}} }{E_{\rm{c}}} }混凝土破坏AASHTO[25] N_{\rm{v}}^{\rm{c}} = {\text{0} }{\text{.5} }A{}_{\rm{s}}\sqrt { {E_{\rm{c}}}f_{\rm{c}}'} \leqslant A{}_{\rm{s}}{f_{\rm{y}}} Eurocode 4[21] N_{\rm{v}}^{\rm{c}} = \min \left\{ { {\text{ 0} }{\text{.29} }\alpha { { {{d} } } ^{\text{2} } }\sqrt { { { {E_{\rm{c}}}f_{{\rm{ck}}}'} / { {\gamma _{\rm{v}}} } } } ,{\text{0} }{\text{.8} }{A_{\rm{s}}}{ { {f_{\rm{y}}} } / { {\gamma _{\rm{v}}} } } } \right\} 注:中国规范[24]中,N_{\rm{v}}^{\rm{c}}为剪力钉抗剪承载力;As为剪力钉截面面积;Ec、Es分别为混凝土和剪力钉弹性模量;fcu为边长为150 mm的混凝土立方体抗压强度;fcd为混凝土轴心抗压强度设计值;fy为剪力钉屈服强度。材料性能为4.6级时,取400 MPa,\eta 为群钉折减系数。f_{\rm{c}}'为圆柱体轴心抗压强度,f_{\rm{c}}' = {\text{0}}{\text{.4}}{f_{{\rm{cu}}}^{7/6}}。欧洲规范[21]中,当{{3 \lt {h_{\rm{s}}}} / {{{d}}} } < 4时,\alpha = {\text{0}}{\text{.2}}[({h_{\rm{s}}}/{{{d}}} + 1) + 1] \leqslant 1.0;当{{{h_{\rm{s}}}} / {{{d}}} } > 4时,α=1,γv=1.25,式中,f_{{\rm{ck}}}'为圆柱体标准抗压强度。 -
[1] 聂建国, 陶慕轩, 吴丽丽, 等. 钢-混凝土组合结构桥梁研究新进展[J]. 土木工程学报, 2012, 45(6): 110 − 122. Nie Jianguo, Tao Muxuan, Wu Lili, et al. Advances of research on steel-concrete composite bridges [J]. China Civil Engineering Journal, 2012, 45(6): 110 − 122. (in Chinese)
[2] Qi J, Hu Y, Wang J, et al. Behavior and strength of headed stud shear connectors in ultra-high performance concrete of composite bridges [J]. Frontiers of Structural and Civil Engineering, 2019, 13(5): 1138 − 49. doi: 10.1007/s11709-019-0542-6
[3] Lin W, Yoda T. Mechanical behavior of composite girders subjected to hogging moment: experimental study [J]. Journal of Japan Society of Civil Engineers Ser A1, 2011, 67(3): 583 − 596.
[4] 樊健生, 聂建国. 负弯矩作用下考虑滑移效应的组合梁承载力分析[J]. 工程力学, 2005, 22(3): 177 − 182. doi: 10.3969/j.issn.1000-4750.2005.03.031 Fan Jiansheng, Nie Jianguo. Effects of slips on load-carrying capacity of composite beams under negative bending [J]. Engineering Mechanics, 2005, 22(3): 177 − 182. (in Chinese) doi: 10.3969/j.issn.1000-4750.2005.03.031
[5] 聂建国, 樊健生. 组合梁在负弯矩作用下的刚度分析[J]. 工程力学, 2002, 19(4): 33 − 36, 28. doi: 10.3969/j.issn.1000-4750.2002.04.007 Nie Jianguo, Fan Jiansheng. Analysis of composite beam stiffness under negative bending [J]. Engineering Mechanics, 2002, 19(4): 33 − 36, 28. (in Chinese) doi: 10.3969/j.issn.1000-4750.2002.04.007
[6] Henderson I E J, Zhu X Q, Uy B, et al. Dynamic behaviour of steel–concrete composite beams with different types of shear connectors. Part II: Modelling and comparison [J]. Engineering Structures, 2015: 103.
[7] Khaloo A R, Afshari M. Flexural behaviour of small steel fibre reinforced concrete slabs [J]. Cement and Concrete Composites, 2005, 27(1): 141 − 149. doi: 10.1016/j.cemconcomp.2004.03.004
[8] 周茗如, 樊乐涛, 于景龙, 等. 基于平板法纤维混凝土早期抗裂性能试验研究[J]. 硅酸盐通报, 2016, 35(8): 2590 − 2595. Zhou Mingru, Fan Letao, Yu Jinglong, et al. Experimental study on early cracking resistance of fibre concrete based on flat plate method [J]. Bulletin of the Chinese Ceramic Society, 2016, 35(8): 2590 − 2595. (in Chinese)
[9] 刘君平, 徐帅, 陈宝春. 钢-UHPC组合梁与钢-普通混凝土组合梁抗弯性能对比试验研究[J]. 工程力学, 2018, 35(11): 92 − 98, 145. doi: 10.6052/j.issn.1000-4750.2017.06.0454 Liu Junping, Xu Shuai, Chen Baochun. Experimental study on flexural behaviors of steel-UHPC composite girder and steel-conventional concrete composite girder [J]. Engineering Mechanics, 2018, 35(11): 92 − 98, 145. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.06.0454
[10] Shim C S, Lee P G, Yoon T Y. Static behavior of large stud shear connectors [J]. Engineering Structures, 2004, 26(12): 1853 − 1860. doi: 10.1016/j.engstruct.2004.07.011
[11] Xue W C, Ding M, Wang H, et al. Static behavior and theoretical model of stud shear connectors [J]. Journal of Bridge Engineering, 2008, 13(6): 623 − 634. doi: 10.1061/(ASCE)1084-0702(2008)13:6(623)
[12] 赵根田, 侯智译, 高鹏, 等. 拟静力作用下群钉连接件抗剪性能研究[J]. 工程力学, 2020, 37(7): 201 − 213. doi: 10.6052/j.issn.1000-4750.2019.09.0513 Zhao Gentian, Hou Zhiyi, Gao Peng, et al. Study on shear performance of group stud connector under the quasi-static load [J]. Engineering Mechanics, 2020, 37(7): 201 − 213. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.09.0513
[13] 丁发兴, 倪鸣, 龚永智, 等. 栓钉剪力连接件滑移性能试验研究及受剪承载力计算[J]. 建筑结构学报, 2014, 35(9): 98 − 106. Ding Faxin, Ni Ming, Gong Yongzhi, et al. Experimental study on slip behavior and calculation of shear bearing capacity for shear stud connectors [J]. Journal of Building Structures, 2014, 35(9): 98 − 106. (in Chinese)
[14] Kim J S, Kwark J, Joh C, et al. Headed stud shear connector for thin ultrahigh-performance concrete bridge deck [J]. Journal of Constructional Steel Research, 2015, 108: 23 − 30. doi: 10.1016/j.jcsr.2015.02.001
[15] 田启贤, 杜新喜. 高性能混凝土复合铺装短栓钉推出试验研究[J]. 桥梁建设, 2016, 46(1): 40 − 46. Tian Qixian, Du Xinxi. Short stud push-out test study of high-performance concrete composite pavement [J]. Bridge Construction, 2016, 46(1): 40 − 46. (in Chinese)
[16] 邵旭东, 周环宇, 曹君辉. 钢-薄层RPC组合桥面结构栓钉的抗剪性能[J]. 公路交通科技, 2013, 30(4): 34 − 39, 64. doi: 10.3969/j.issn.1002-0268.2013.04.007 Shao Xudong, Zhou Huanyu, Cao Junhui. Shear behavior of studs of composite deck system composed of steel and ultra-thin RPC layer [J]. Highway Transportation Technology, 2013, 30(4): 34 − 39, 64. (in Chinese) doi: 10.3969/j.issn.1002-0268.2013.04.007
[17] Ollgaard J G, Slutter R G, Fisher J W. Shear strength of stud connectors in lightweight and normal weight concrete [J]. AISC Engineering Journal, 1971, 8(2): 55 − 64.
[18] Döinghaus P, Goralski C, Will N. Design rules for composite structures with high performance steel and high-performance concrete [J]. High Performance Materials in Bridges, 2003, 13: 139 − 149.
[19] 李萌, 邵旭东, 曹君辉, 等. UHPC中短栓钉抗剪性能试验及理论分析[J]. 中国公路学报, 2021, 34(8): 191 − 204. Li Meng, Shao Xudong, Cao Junhui, et al. Performance of experimental and theoretical analysis on shear short headed studs embedded in UHPC [J]. China Journal of Highway and Transport, 2021, 34(8): 191 − 204. (in Chinese)
[20] An L, Cederwall K. Push-out tests on studs in high strength and normal strength concrete [J]. Journal of Constructional Steel Research, 1996, 36(1): 15 − 29.
[21] EN 1994-1-1:2004, Eurocode 4: Design of composite steel and concrete structures. Part1-1. General rules and rules for buildings [S]. Brussels, Belgium: European Committee for Standardization, 2004.
[22] 日本鋼構造協会. 頭付きスタッドの押拔き試験方法(案)とスタッドに関する研究の現状[S]. 日本鋼構造協会, 1996. Japanese Society of Steel Construction. Standard on push-out test for headed stud (draft) [S]. Japanese Society of Steel Construction, 1996. (in Japanese)
[23] 王新敏. ANSYS工程结构数值分析 [M]. 北京: 人民交通出版社, 2007. Wang Xinmin. ANSYS numerical analysis of engineering structure [M]. Beijing: China Communications Press, 2007. (in Chinese)
[24] GB 50917−2013, 钢-混凝土组合桥梁设计规范 [S]. 北京: 中国标准出版社, 2013. GB50917−2013, Code for design of steel and concrete composite bridges [S]. Beijing: China National Standard, 2013. (in Chinese)
[25] LRFDUS-4, AASHTO LRFD bridge design specifications [S]. Washington, D C: American Association of State Highway and Transportation Officials, 2007.
[26] 孙启力, 路新瀛, 聂鑫, 等. 非蒸养UHPC-钢板结构界面的受拉和剪切性能试验研究[J]. 工程力学, 2017, 34(9): 167 − 174, 192. doi: 10.6052/j.issn.1000-4750.2016.05.0361 Sun Qili, Lu Xinying, Nie Xin, et al. Experimental research on tensile and shear behaviour of the interface between non-steam-cured UHPC and steel plate structure [J]. Engineering Mechanics, 2017, 34(9): 167 − 174, 192. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.05.0361
[27] Kruszewski D, Wille K, Zaghi A E. Push-out behavior of headed shear studs welded on thin plates and embedded in UHPC [J]. Engineering Structures, 2018, 173: 429 − 441. doi: 10.1016/j.engstruct.2018.07.013
[28] Wang J, Qi J, Tong T, et al. Static behavior of large stud shear connectors in steel-UHPC composite structures [J]. Engineering Structures, 2018, 178(1): 534 − 542.
[29] 王倩, 刘玉擎. 焊钉连接件抗剪承载力试验研究[J]. 同济大学学报(自然科学版), 2013, 41(5): 659 − 663. doi: 10.3969/j.issn.0253-374x.2013.05.004 Wang Qian, Liu Yuqing. Experimental study of shear capacity of stud connector [J]. Journal of Tongji University (Natural Science), 2013, 41(5): 659 − 663. (in Chinese) doi: 10.3969/j.issn.0253-374x.2013.05.004
-
期刊类型引用(22)
1. 时富禄, 杨思敏, 田径, 柯研, 张世顺. 采用栓钉剪力键的钢箱-UHPC界面剪切性能. 土木工程与管理学报. 2025(03)  百度学术
百度学术
2. 郝朝伟,张卫强,程寿山,陈彦江,李鹏飞. 钢-UHPC组合桥面铺装长期性能及退化成因分析. 桥梁建设. 2025(01): 56-63 .  百度学术
百度学术
3. 门进杰,杜天宇,李家富,张谦,王家琛,MUDASSAR Ali. 预埋型螺栓连接件的可拆换性能研究. 地震工程与工程振动. 2025(02): 86-96 .  百度学术
百度学术
4. 王昊,李晨阳,王凯,白光耀,任超,党王辉,牛艳伟. 组合箱梁桥混凝土横隔板与钢腹板连接段承载力试验研究. 混凝土. 2025(04): 215-222 .  百度学术
百度学术
5. 邓宗才,黄松,薛会青. 钢-UHPC轻型组合结构短栓钉抗剪性能试验研究. 天津大学学报(自然科学与工程技术版). 2024(01): 42-52 .  百度学术
百度学术
6. 方志,武霄楠,谭星宇,廖原,阳晏,唐守峰. 钢-UHPC组合桥面板横向负弯矩区受弯性能研究. 工程力学. 2024(02): 112-124 .  本站查看
本站查看
7. 吴锦鹏,吴加杰,曹志鹏,方壮城,姜海波. 钢-预制UHPC组合梁中高强螺栓剪力键群的抗剪性能试验研究. 广东公路交通. 2024(01): 19-29 .  百度学术
百度学术
8. 黄民水,张健蔚,罗金,万能,邓志航,何仲骜. 大跨度斜拉桥钢-混组合梁一维日照温度场高效数值模型构建及试验验证. 工程力学. 2024(S1): 197-205 .  本站查看
本站查看
9. 吴锦鹏,吴加杰,曹志鹏,方壮城,姜海波. 可拆卸式钢-预制UHPC组合梁中高强螺栓剪力键的抗剪性能试验. 福州大学学报(自然科学版). 2024(04): 462-470 .  百度学术
百度学术
10. 郑双杰,扶庆祝,王笛,李海锋. 外露型钢锚箱组合索塔锚固区水平传力机理. 工程力学. 2024(09): 101-110 .  本站查看
本站查看
11. 左海平,赖世锦,张钊,邓建新. ECC组合桥面板中短栓钉抗剪性能影响因素分析. 西部交通科技. 2024(09): 90-93 .  百度学术
百度学术
12. 李翠华,陈锋威,李威,彭卫兵. 采用后张预制板技术的组合梁负弯矩段长期抗裂性能研究. 工程力学. 2024(11): 67-78 .  本站查看
本站查看
13. 韩强,倪玉龙,胡梦涵,惠斌. 钢-混组合梁抗剪连接件构造型式及其力学性能研究进展. 北京工业大学学报. 2024(11): 1369-1385 .  百度学术
百度学术
14. 朱劲松,高天歌,丁婧楠. 钢-UHPC组合梁单钉连接件抗拔性能分析. 东南大学学报(自然科学版). 2023(01): 44-52 .  百度学术
百度学术
15. 修洪亮. 基于大直径栓钉界面连接的钢-UHPC组合结构推出试验研究. 钢结构(中英文). 2023(03): 34-42 .  百度学术
百度学术
16. 张世顺,田径,陈东,曾卓,聂雪飞. 预制节段UHPC梁接缝抗剪性能的有限元模拟. 工程力学. 2023(06): 85-98+256 .  本站查看
本站查看
17. 李聪,陈宝春,胡文旭,苏家战. 钢-UHPC组合板栓钉抗剪承载力、滑移与刚度计算. 工程力学. 2023(06): 110-121 .  本站查看
本站查看
18. 郑莲琼,章超勇. 钢-GPC栓钉连接界面抗剪性能. 福建工程学院学报. 2023(03): 205-211 .  百度学术
百度学术
19. 陈德宝,林志平,苏庆田,欧阳明谷,上官兵. 混合梁刚构桥钢-混结合段的构造优化与试验. 工程力学. 2023(08): 149-160 .  本站查看
本站查看
20. 马亚飞,周彪,王磊,张建仁. 承压型组合剪力键剪切性能试验与承载力计算. 工程力学. 2023(11): 120-129 .  本站查看
本站查看
21. 曹君辉,樊伟,李立峰,邵旭东,张阳,赵华. 基于UHPC的高性能桥梁结构研究与应用. 湖南大学学报(自然科学版). 2022(11): 1-32 .  百度学术
百度学术
22. 赵晓翠,张岗,王宝莹,王世超,汤陈皓,张永飞. 钢桁架-混凝土组合梁界面工作协调性及整体力学性能. 长安大学学报(自然科学版). 2022(06): 77-89 .  百度学术
百度学术
其他类型引用(40)



 下载:
下载: