薄柔H形截面双向压弯钢构件极限承载力研究

杜辉波; 程欣; 张超; 陈以一

doi:10.6052/j.issn.1000-4750.2021.05.0390

薄柔H形截面双向压弯钢构件极限承载力研究

杜辉波^1,,
程欣^1, ,,
张超^1,,
陈以一^2,

1.
太原理工大学土木工程学院，山西，太原 030024
2.
上海杉达学院工程学院，上海 201209

基金项目: 国家自然科学基金面上项目(51978437)

详细信息

作者简介:
杜辉波(1998−)，男，山西运城人，硕士生，主要从事钢结构方面的研究(E-mail: duhuibo0456@link.tyut.edu.cn)

张　超(1995−)，男，山西大同人，硕士生，主要从事钢结构方面的研究(E-mail: zhangchao0350@link.tyut.edu.cn)

陈以一(1955−)，男，浙江天台人，教授，工学博士，主要从事钢结构方面的研究(E-mail: yiyichen@tongji.edu.cn)

通讯作者:
程　欣(1986−)，女，江西景德镇人，教授，博士，主要从事钢结构方面的研究(E-mail: xchengtyut@126.com)

中图分类号: TU391
计量
- 文章访问数: 391
- HTML全文浏览量: 289
- PDF下载量: 66
出版历程
- 收稿日期: 2021-05-24
- 修回日期: 2021-08-31
- 网络出版日期: 2021-09-17
- 刊出日期: 2022-08-31

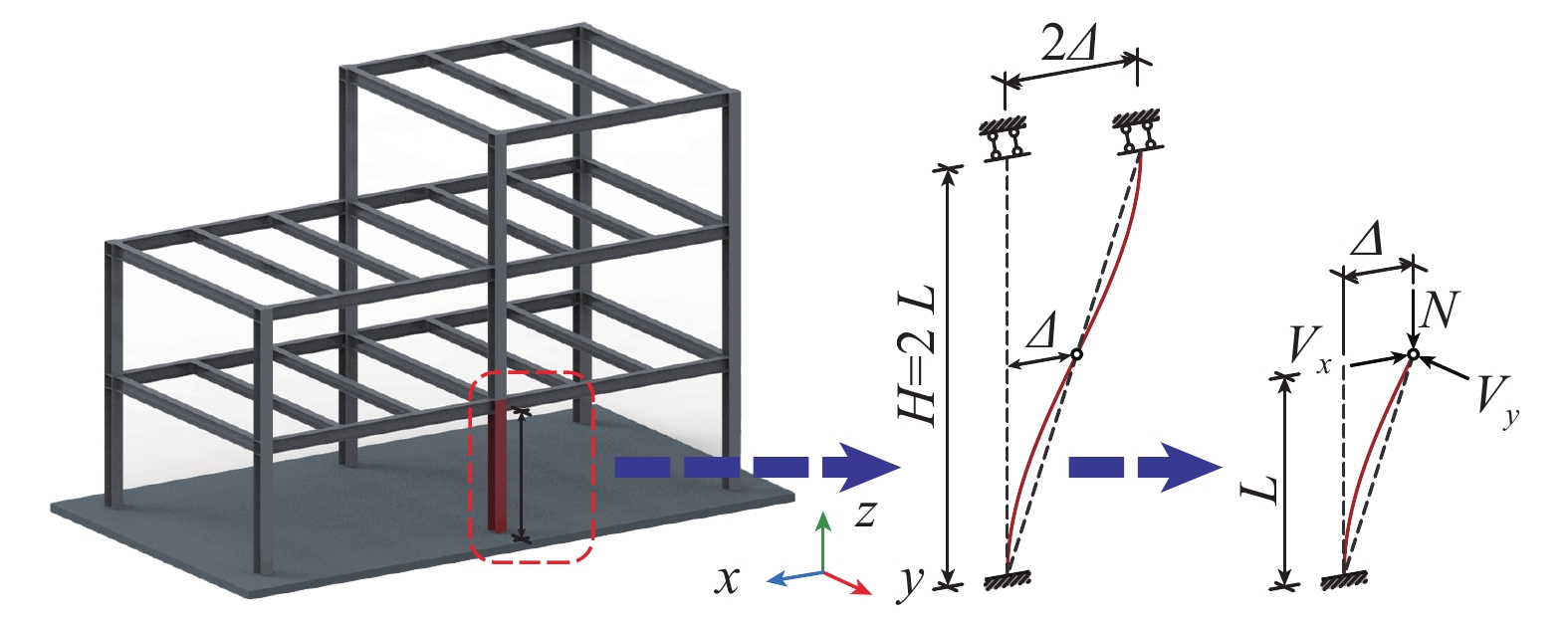
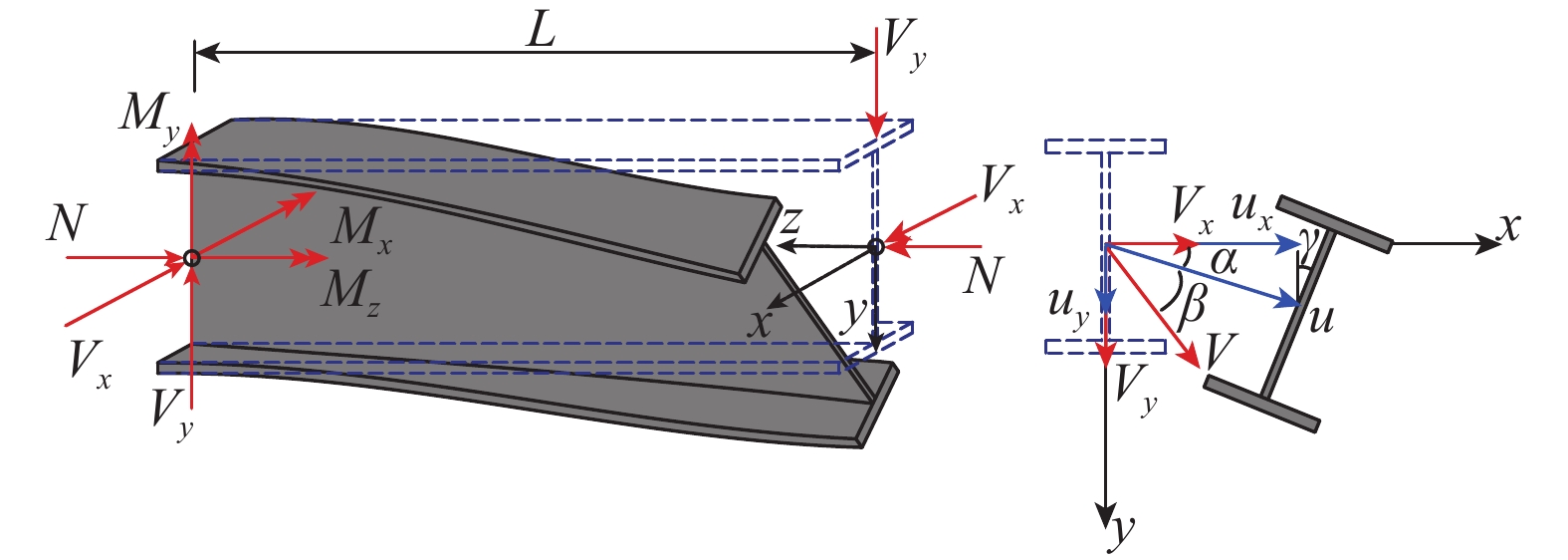
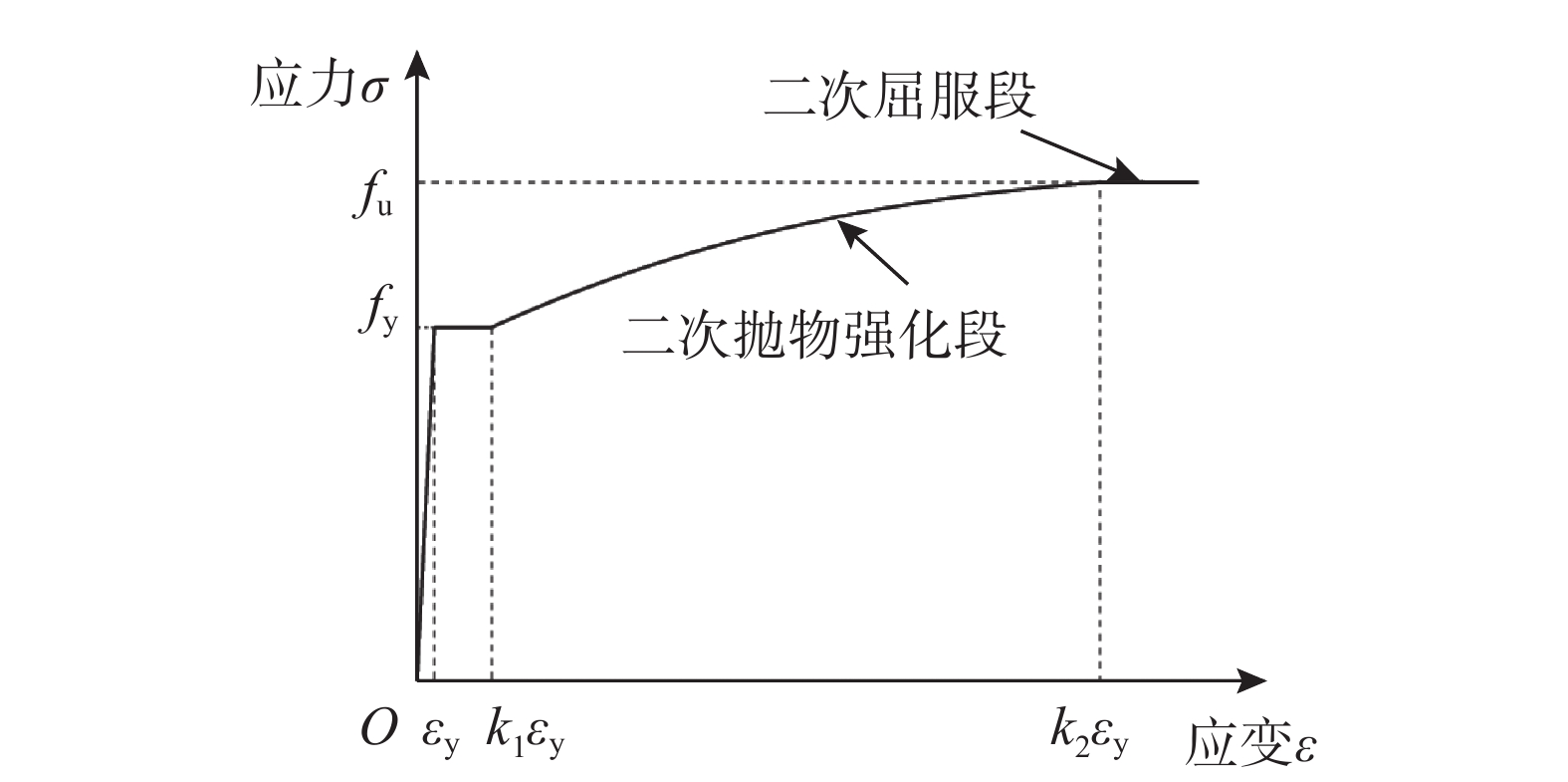
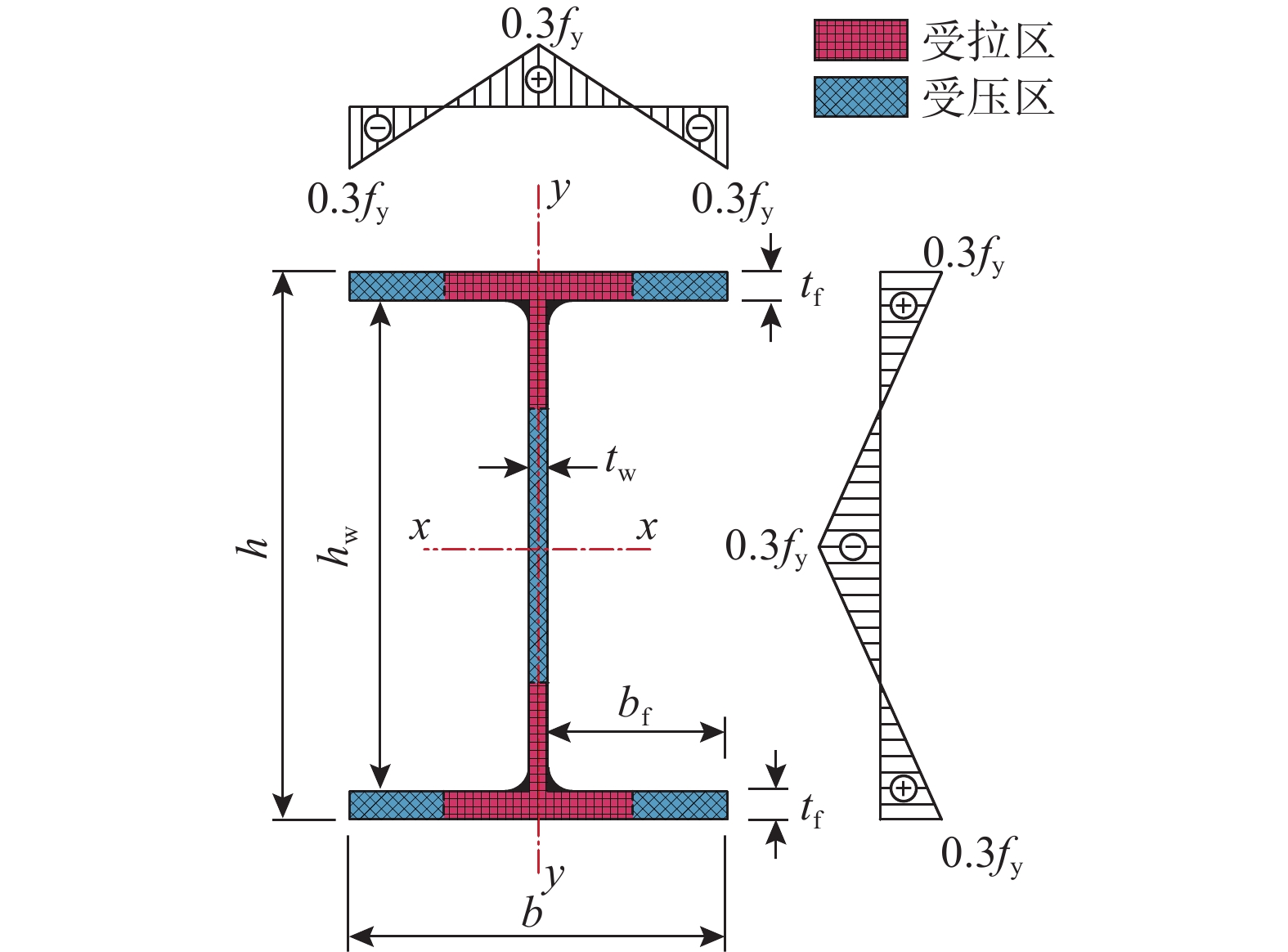
STUDY ON ULTIMATE BEARING CAPACITY OF BIAXIAL COMPRESSION-BENDING STEEL MEMBERS WITH THIN AND SLENDER H-SHAPED SECTION

1.
College of Civil Engineering, Taiyuan University of Technology, Taiyuan, Shanxi 030024, China
2.
College of Engineering, Shanghai Sanda University, Shanghai 201209, China

摘要

摘要: 为探究薄柔H形截面双向压弯构件的极限状态性能，采用ABAQUS建立了不同轴压比、腹板和翼缘宽厚比的H形截面构件在不同加载角度下的参数分析模型，分析中考虑了材料非线性、几何非线性及残余应力的影响，并基于已有试验数据验证了该模型的适用性。基于经典弹塑性稳定理论，提出了用于确定双向压弯构件极限状态的判定准则，对于塑性铰截面定义为截面出现塑性铰时达到其极限状态；对于由局部屈曲控制的薄柔截面其极限状态为屈曲起始时刻，且该准则能够准确识别出板件局部屈曲的发生。通过最小二乘法拟合得到双轴弯矩极限相关曲线，呈现出腹板和翼缘宽厚比及轴压力的复杂相关影响关系。提出了考虑材料的强化作用和板件相关作用的极限相关计算公式，能够良好地预测H形截面双向压弯构件的极限承载力，且不受截面分类的限制，具有良好的适用性。
- 极限状态判定准则 /
- H形截面 /
- 双向压弯 /
- 局部屈曲 /
- 极限相关曲线
Abstract: To investigate the ultimate behavior of H-section members with large width-thickness ratios under a combined biaxial compression-bending, the parametric analysis models of H-section members with different axial force ratios, web and flange width-thickness ratios and different loading angles were developed by ABAQUS. Material and geometric nonlinearity were considered throughout the whole analysis, and the finite element models were validated by previous laboratory test results. Based on the elastic-plastic stability theory, a criterion for determining the ultimate state of biaxial compression-bending members was proposed. For plastic-hinge sections, the ultimate state is defined as the occurrence of plastic hinge. For slender sections controlled by local buckling, the ultimate state is the initial buckling moment, with the occurrence of plate local buckling been accurately identified through the criterion. The ultimate interactive curves of biaxial bending moments were obtained by least-square method, within which complicated interactive effects of width-thickness ratios of web and flange and the axial force were noted. The ultimate interactive formula for biaxial moments considering the strain hardening effect of material and the correlation effect of plate was proposed. Not limited by section classification, the proposed method is proved to have good applicability and accuracy.
- ultimate state criterion /
- H-section /
- combined biaxial bending and compression /
- local buckling /
- ultimate interactive curve

HTML全文

图 1 截面分类方法及设计准则

注：M_pc为全截面塑性弯矩；M_ppc为部分塑性弯矩；M_ec为边缘屈服弯矩；M_u为极限抗弯承载力；f_y为屈服应力

Figure 1. Section classification method and design criterion

下载: 全尺寸图片幻灯片

图 2 悬臂构件等效原理

Figure 2. Equivalence principle of cantilever member

下载: 全尺寸图片幻灯片

图 3 受力情况及变形特点

Figure 3. Force condition and deformation features

下载: 全尺寸图片幻灯片

图 4 钢材本构模型

Figure 4. Constitutive model of structural steel

下载: 全尺寸图片幻灯片

图 5 残余应力分布及截面参数定义

Figure 5. Residual stress distribution and definition of cross-section dimensions

下载: 全尺寸图片幻灯片

图 6 网格划分与边界条件

Figure 6. Finite element meshing and boundary conditions

下载: 全尺寸图片幻灯片

图 7 加载方式

Figure 7. Loading condition

下载: 全尺寸图片幻灯片

图 8 典型试件有限元破坏模态与试验对比

Figure 8. Comparison of failure modes between finite element and test of typical specimens

下载: 全尺寸图片幻灯片

图 9 参数分析中的加载方向角

Figure 9. Loading direction angle in parametric study

下载: 全尺寸图片幻灯片

图 10 试件B-0.2-70-21-5的抗弯承载力弯矩分量发展

Figure 10. Development of moment components of B-0.2-70-21-5

下载: 全尺寸图片幻灯片

11 典型模型双向弯矩发展与极限状态

注：① σ_z,1和σ_z,5分别为有限元壳单元在上下积分面的z向应力值，拉应力为正值，压应力为负值，当σ_z,1和σ_z,5开始分岔时，表征了板件屈曲的发生；② u_e为屈服合位移，表征柱底截面受压边缘进入塑性时柱顶施加的合位移： ${u_{\text{e}}} = \dfrac{{2(1 - n){L^2}{f_{\text{y}}}}}{{3(b\cos \alpha + h\sin \alpha )E}}$ ，u为柱顶的加载合位移。

11. Development of moments about two axes and ultimate state of typical models

下载: 全尺寸图片幻灯片

图 12 典型模型双向弯矩相关关系及极限相关曲线

Figure 12. Correlation between biaxial bending moments and ultimate interactive curves of typical models

下载: 全尺寸图片幻灯片

图 13 不同轴压比下的极限相关曲线

Figure 13. Interactive curves under different axial force ratios

下载: 全尺寸图片幻灯片

图 14 现行规范与本文提出公式

Figure 14. Formulas in current codes and this paper

下载: 全尺寸图片幻灯片

15 本文提出公式的试验^[21]评价结果

15. Evaluation of the proposed formula using the test results^[21]

下载: 全尺寸图片幻灯片

16 式(6)与EC3和有限元比较结果

16. Comparison between formula (6), EC3 and FE results

下载: 全尺寸图片幻灯片

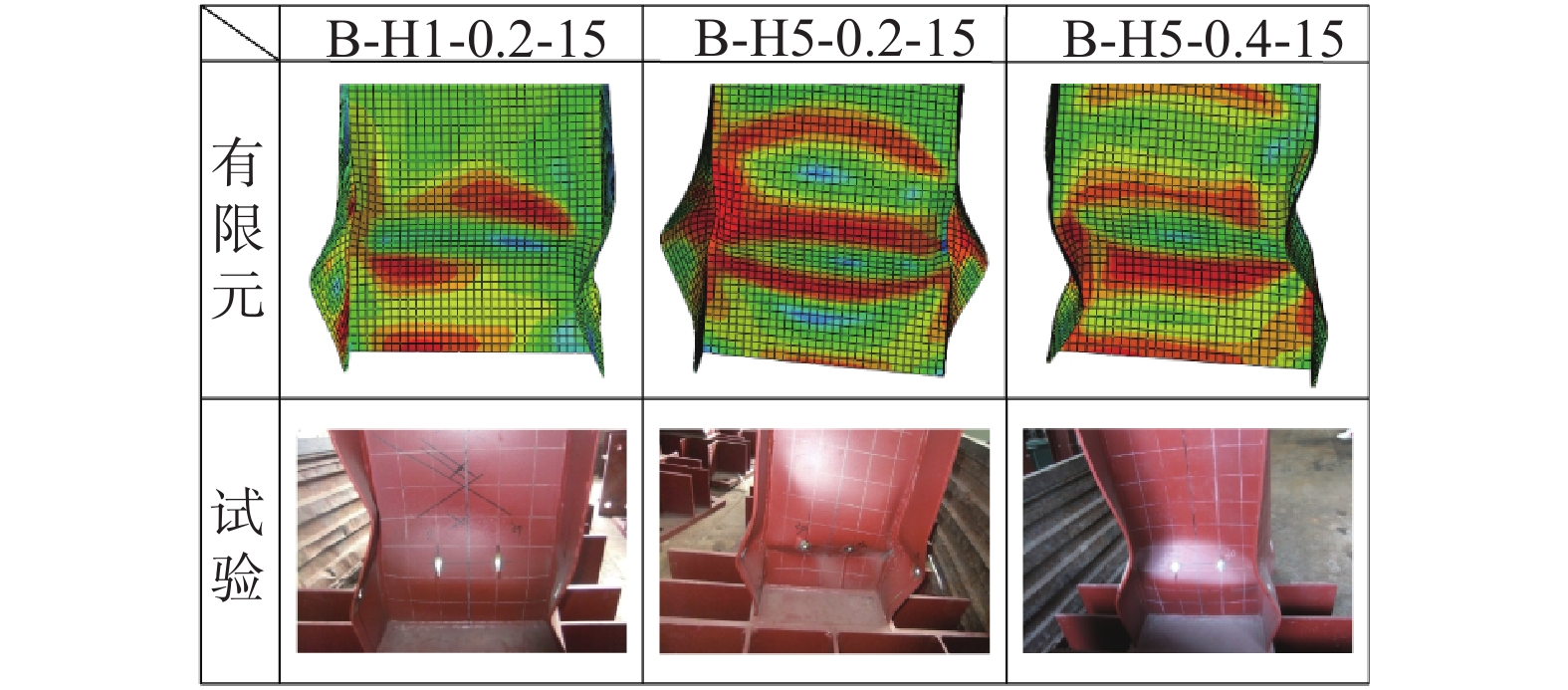
表 1 有限元结果与试验结果^[21]比较

Table 1 Comparison between finite element results and available experimental results^[21]

试件编号	r_w	r_f	M_xmax,test/ (kN·m)	M_xmax,FEA/ (kN·m)	M_xmax,test/ M_xmax,FEA	M_ymax,test/ (kN·m)	M_ymax,FEA/ (kN·m)	M_ymax,test/ M_ymax,FEA
B-H1-0.2-15	61	35	61.9	63.5	0.975	19.0	20.2	0.941
B-H2-0.2-15	117	16	79.9	87.2	0.916	20.8	20.4	1.020
B-H3-0.2-15	118	30	54.1	60.6	0.893	13.2	13.5	0.978
B-H3-0.2-30	118	30	64.5	60.9	1.059	10.2	10.2	1.000
B-H4-0.2-15	117	21	77.8	79.8	0.975	35.7	32.7	1.092
B-H4-0.2-30	117	21	103.8	94.7	1.096	26.3	27.1	0.970
B-H5-0.2-15	100	21	74.4	61.1	1.218	35.3	35.1	1.006
B-H5-0.4-15	100	21	44.8	50.2	0.892	32.9	33.1	0.994
B-H6-0.2-15	100	16	66.3	74.2	0.894	20.8	18.5	1.124
B-H7-0.2-30	42	11	130.8	128.3	1.019	30.7	27.6	1.112
B-H7-0.4-15	42	11	69.1	73.3	0.943	41.9	38.6	1.085
平均值					0.989			1.029
标准差/(%)					9.780			6.010
注： ${r_{\rm{w}}} = {h_{\rm{w}}}/{t_{\rm{w}}}\sqrt {{f_{\rm{y}}}/235}$ ， ${r_{\rm{f}}} = {b_{\rm{f}}}/{t_{\rm{f}}}\sqrt {{f_{\rm{y}}}/235}$ ；M_xmax,test和M_ymax,test分别为试验结果的强轴和弱轴弯矩分量的峰值；M_xmax,FEA和M_ymax,FEA分别为有限元结果的强轴和弱轴弯矩分量的峰值。

下载: 导出CSV

表 2 参数设置范围

Table 2 Range of parameter values

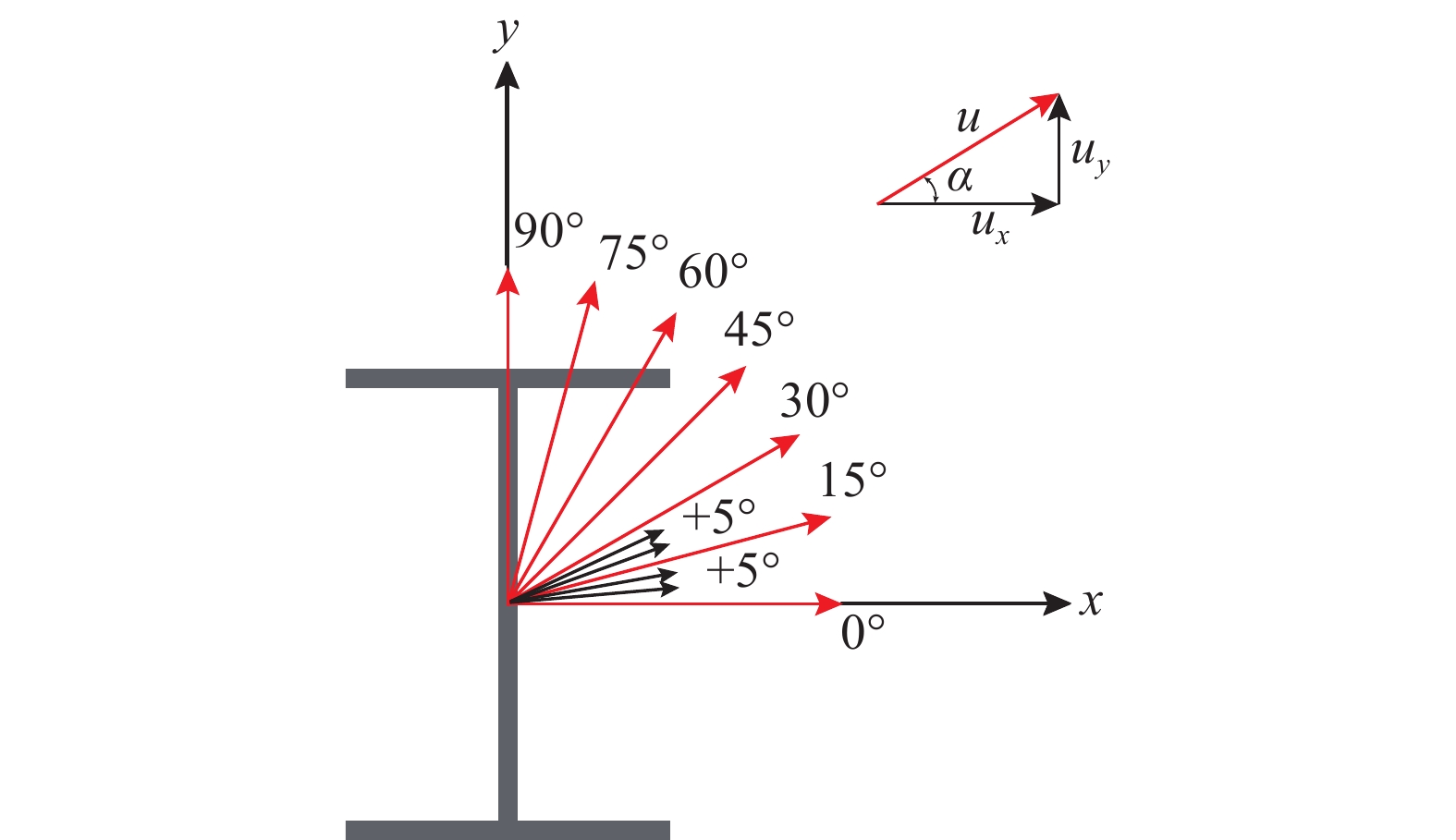
关键参数	参数值
n	0, 0.1, 0.2, 0.3, 0.4, 0.5
r_w	40, 55, 70, 85, 100, 115, 130
r_f	9, 11, 13, 15, 17, 19, 21
α/(°)	0, 5, 10, 15, 20, 25, 30, 45, 60, 75, 90

下载: 导出CSV

表 3 可靠度分析结果

Table 3 Reliability analysis results

截面分类	R_u,EC3/R_u,FEM		R_u,proposed/R_u,FEM
截面分类	平均值	标准差/(%)	平均值	标准差/(%)
I和II类	0.66	10.32	1.01	4.43
III类	0.56	13.69	0.98	4.94
IV类	0.47	14.60	0.97	7.48
I~IV类	0.50	14.97	0.98	6.99

下载: 导出CSV

参考文献(27)

[1]	陈以一, 王伟, 童乐为, 等. 装配式钢结构住宅建筑的技术研发和市场培育[J]. 住宅产业, 2012(12): 32 − 35. Chen Yiyi, Wang Wei, Tong Lewei, et al. Technology Development and Market Cultivation of Prefabricated Steel Structure Residential Building [J]. Housing Industry, 2012(12): 32 − 35. (in Chinese)
[2]	Yong C X, Zhong P T. Comparative study on the design schemes of residential steel structure [J]. Applied Mechanics and Materials, 2012, 2080: 581 − 584.
[3]	王萌, 柯小刚, 吴照章. 可更换延性耗能连接组件的钢框架节点抗震性能研究[J]. 工程力学, 2018, 35(12): 151 − 163. doi: 10.6052/j.issn.1000-4750.2017.09.0743 Wang Meng, Ke Xiaogang, Wu Zhaozhang. Seismic behavior of steel frame connections with replaceable high ductility and energy dissipation components [J]. Engineering Mechanics, 2018, 35(12): 151 − 163. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.09.0743
[4]	CEN. Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings [S]. Brussels, CEN/TC250, 2005.
[5]	GB 50017−2017, 钢结构设计规范[S]. 北京: 中国计划出版社, 2017. GB 50017−2017, Design code for steel structures [S]. Perking: China Planning Press, 2017. (in Chinese)
[6]	陈乐川, 程欣, 陈以一. 考虑局部屈曲的H形截面钢构件单轴压弯恢复力模型研究[J]. 工程力学, 2021, 38(4): 80 − 92. doi: 10.6052/j.issn.1000-4750.2020.05.0326 Chen Lechuan, Cheng Xin, Chen Yiyi. Research on restoring force model of h-section steel members under uniaxial compression and bending considering local buckling [J]. Engineering Mechanics, 2021, 38(4): 80 − 92. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.0326
[7]	程欣, 侯雪松, 李卓峰. 考虑板件相关作用的H形截面分类准则[J]. 工程力学, 2020, 37(4): 178 − 185. doi: 10.6052/j.issn.1000-4750.2019.05.0266 Cheng Xin, Hou Xuesong, Li Zhuofeng. Cross-section classification criteria of steel h-sections considering theplate interaction effect [J]. Engineering Mechanics, 2020, 37(4): 178 − 185. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.05.0266
[8]	Watanabe E, Sugiura K, Oyawa W O. Effects of multi-directional displacement paths on the cyclic behaviour of rectangular hollow steel columns [J]. Japan Society of Civil Engineers, 2000(647): 79 − 95.
[9]	Guerrero N, Marante M E, Picón R, et al. Model of local buckling in steel hollow structural elements subjected to biaxial bending [J]. Journal of Constructional Steel Research, 2006, 63(6): 779 − 790.
[10]	申红侠. 高强钢焊接薄壁箱形截面双向压弯构件的稳定承载力[J]. 建筑钢结构进展, 2020, 22(4): 57 − 67. Shen Hongxia. The stability of high-strength steel welded thin-walled box beam-columns under biaxial bending [J]. Progress in Steel Building Structures, 2020, 22(4): 57 − 67. (in Chinese)
[11]	Goto Y, Muraki M, Obata M. Ultimate state of thin-walled circular steel columns under bidirectional seismic accelerations [J]. Journal of Structural Engineering, 2009, 135(12): 1481 − 1490. doi: 10.1061/(ASCE)ST.1943-541X.0000076
[12]	Goto Y, Ebisawa T, Lu X, et al. Ultimate state of thin-walled circular steel columns subjected to biaxial horizontal forces and biaxial bending moments caused by bidirectional seismic accelerations [J]. Journal of Structural Engineering, 2014, 4(141): 4014122-1 − 4014122-12.
[13]	范峰, 聂桂波, 支旭东, 等. 圆钢管空间滞回试验及材料本构模型[J]. 土木工程学报, 2011, 44(12): 18 − 24. Fan Feng, Nie Guibo, Zhi Xudong, et al. Spatial hysteresis experiment and constitutive model for circular steel pipes [J]. China Civil Engineering Journal, 2011, 44(12): 18 − 24. (in Chinese)
[14]	Zubydan A H. Inelastic large deflection analysis of space steel frames including H-shaped cross sectional members [J]. Engineering Structures, 2013, 48: 155 − 165. doi: 10.1016/j.engstruct.2012.09.024
[15]	Baptista A M. Resistance of steel I-sections under axial force and biaxial bending [J]. Journal of Constructional Steel Research, 2012, 72: 1 − 11. doi: 10.1016/j.jcsr.2011.07.013
[16]	Cheng X, Chen Y. Ultimate strength of H-sections under combined compression and uniaxial bending considering plate interaction [J]. Journal of Constructional Steel Research, 2018, 143: 196 − 207. doi: 10.1016/j.jcsr.2017.12.019
[17]	Cheng X, Chen Y, Nethercot D A. Experimental study on H-shaped steel beam-columns with large width-thickness ratios under cyclic bending about weak-axis [J]. Engineering Structures, 2013, 49: 264 − 274. doi: 10.1016/j.engstruct.2012.10.035
[18]	Cheng X, Chen Y, Pan L. Experimental study on steel beam–columns composed of slender H-sections under cyclic bending [J]. Journal of Constructional Steel Research, 2013, 88: 279 − 288. doi: 10.1016/j.jcsr.2013.05.020
[19]	Yun X, Gardner L, Boissonnade N. Ultimate capacity of I-sections under combined loading – Part 1: Experiments and FE model validation [J]. Journal of Constructional Steel Research, 2018, 147: 408 − 421. doi: 10.1016/j.jcsr.2018.04.016
[20]	Yun X, Gardner L, Boissonnade N. Ultimate capacity of I-sections under combined loading – Part 2: Parametric studies and CSM design [J]. Journal of Constructional Steel Research, 2018, 148: 265 − 274. doi: 10.1016/j.jcsr.2018.05.024
[21]	Cheng X, Chen Y, Niu L, et al. Experimental study on H-section steel beam-columns under cyclic biaxial bending considering the effect of local buckling [J]. Engineering Structures, 2018, 174: 826 − 839. doi: 10.1016/j.engstruct.2018.08.001
[22]	石永久, 王萌, 王元清. 结构钢材循环荷载下的本构模型研究[J]. 工程力学, 2012, 29(9): 92 − 98. doi: 10.6052/j.issn.1000-4750.2010.09.0711 Shi Yongjiu, Wang Meng, Wang Yuanqing. Study on constitutive model of structural steel under cyclic loading [J]. Engineering Mechanics, 2012, 29(9): 92 − 98. (in Chinese) doi: 10.6052/j.issn.1000-4750.2010.09.0711
[23]	ECCS. Ultimate limit state calculation of sway frames with rigid joints [M]. Brussels (Belgium): ECCS General Secretariat, 1984.
[24]	胡世光, 梁炳文. 弹塑性稳定理论[M]. 北京: 国防工业出版社, 1983. Hu Shiguang, Liang Bingwen. Elastic plastic stability theory [M]. Peking: National Defense Industry Press, 1983. (in Chinese)
[25]	Hill R. A general theory of uniqueness and stability in elastic-plastic solids [J]. Journal of the Mechanics and Physics of Solids, 1958, 3(6): 236 − 249.
[26]	Bresler B. Design criteria for reinforced columns under axial load and biaxial bending [J]. Journal Proceedings, 1960, 57(11): 481 − 490.
[27]	Mohammad A, Ashraf M, Ahmed S. Behaviour and design of stainless steel slender cross-sections subjected to combined loading [J]. Thin-Walled Structures, 2016, 104: 225 − 237. doi: 10.1016/j.tws.2016.03.020

施引文献(4)

期刊类型引用(2)

1.	梁刚，陈江，李淑敏，卢俊龙. 梁柱节点弯剪型可更换耗能件抗震性能数值分析. 地震工程与工程振动. 2025(02): 173-182 . 百度学术
2.	李晓梦，韩灵杰. 冲击荷载下建筑用钢梁摩擦摇摆柱节点的抗震性能. 兵器材料科学与工程. 2025(03): 91-96 . 百度学术