拱脚沉降下3D打印拱的非线性失稳研究

文新钧; 刘爱荣; 毛吉化

doi:10.6052/j.issn.1000-4750.2021.05.S003

拱脚沉降下3D打印拱的非线性失稳研究

1.
广州大学风工程与工程振动研究中心，广东，广州 510006
2.
广州广检建设工程检测中心有限公司，广东，广州 510030

基金项目: 国家自然科学基金项目(51878188)；高等学校学科创新引智计划项目(111计划D21021)；广州市科技计划项目(20212200004)

详细信息

作者简介:
文新钧(1995−)，男，湖南人，硕士生，主要从事打印材料拱的稳定性研究(E-mail: wxjvenn@foxmail.com)

毛吉化(1978−)，男，安徽人，高工，硕士，常务副总经理，主要从事土木工程检测研究(E-mail: 1750358980@qq.com)

通讯作者:
刘爱荣(1972−)，女，山西人，教授，博士，主任，主要从事新型桥梁结构的静动力稳定性研究(E-mail: liuar@gzhu.edu.cn)

中图分类号: U441；TU31
计量
- 文章访问数: 226
- HTML全文浏览量: 137
- PDF下载量: 23
出版历程
- 收稿日期: 2021-05-25
- 修回日期: 2022-03-17
- 网络出版日期: 2022-05-05
- 刊出日期: 2022-06-05

STUDY ON NONLINEAR INSTABILITY OF 3D PRINTING ARCH UNDER SETTLEMENT OF ARCH FOOT

1.
Research Center for Wind Engineering and Engineering Vibration, Guangzhou University, Guangzhou, Guangdong 510006, China
2.
Guangzhou Guangjian Construction Engineering Testing Center Co. LTD, Guangzhou, Guangdong 510030, China

摘要

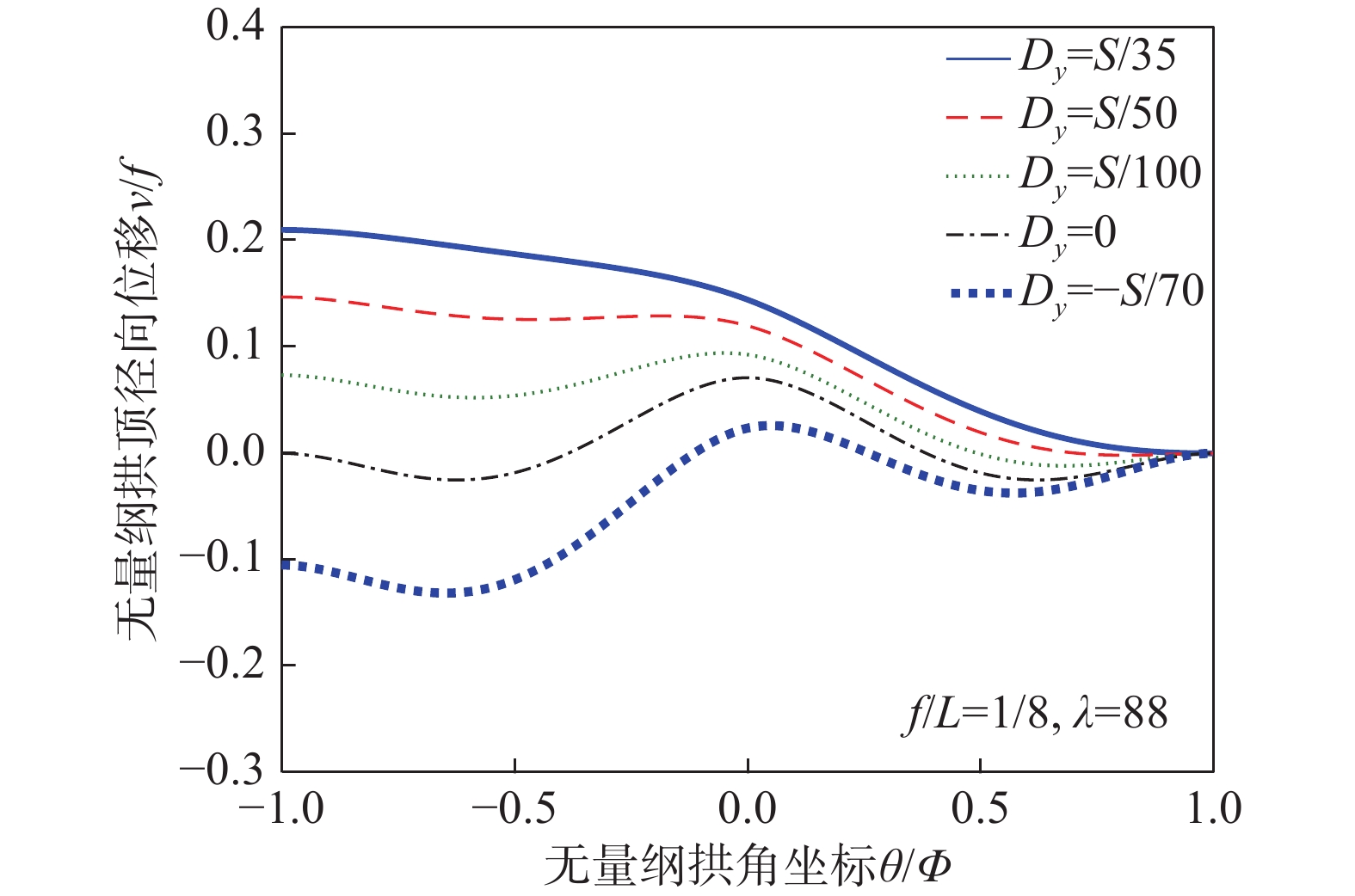
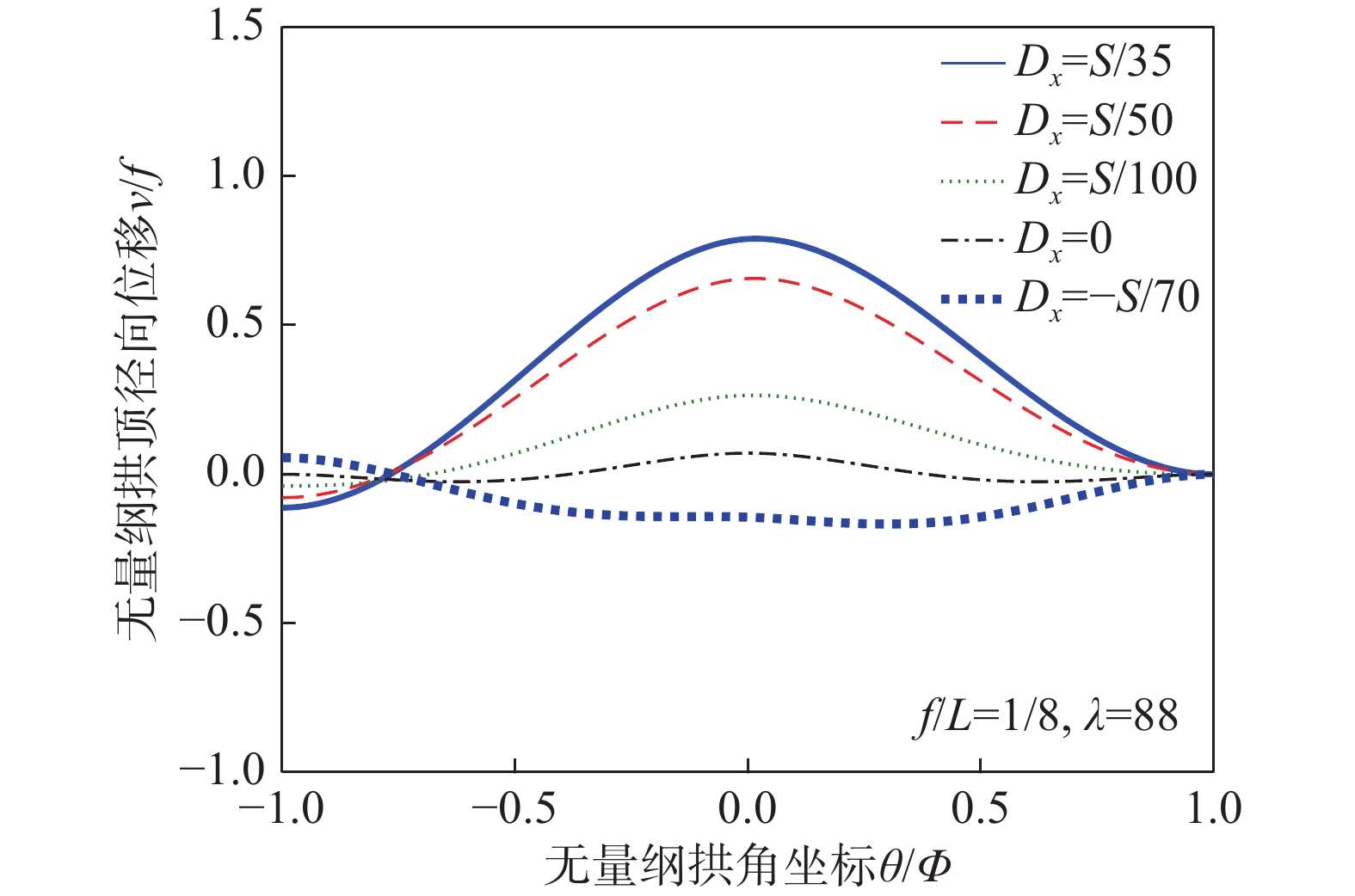
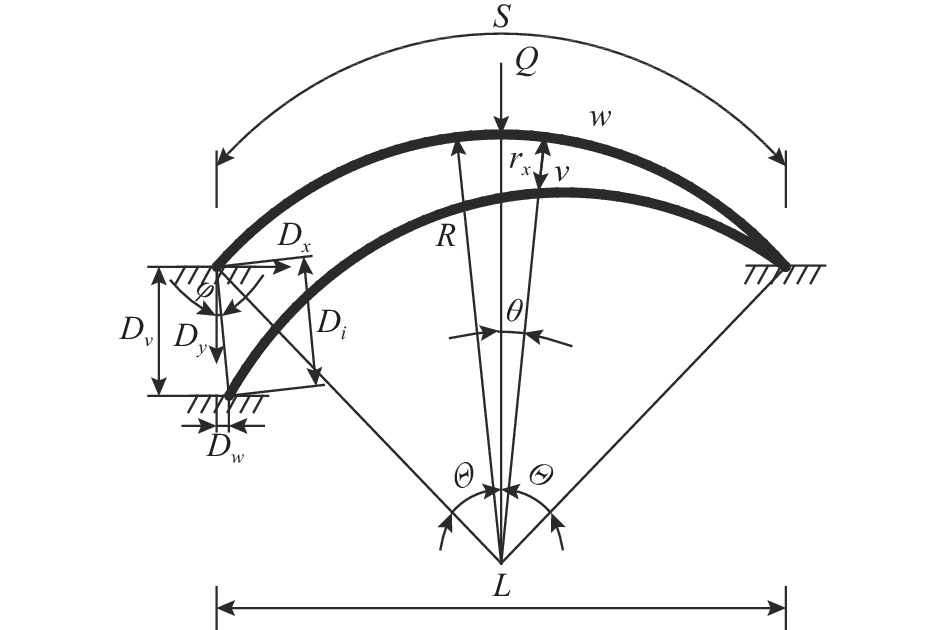
摘要: 该文以3D打印材料ABS-M30作为试验载体，开展了拱脚沉降下3D打印拱的非线性失稳研究。基于最小势能原理推导了失稳临界荷载的解析表达式，得到了拱脚竖向和水平变位下拱径向位移沿拱轴线的分布图；设计了可控制拱脚沉降的加载系统，试验得到了拱在加载过程中的平衡路径，并通过有限元模拟对解析与试验结果进行了验证；分析了拱脚沉降量、矢跨比和长细比对3D打印拱失稳临界荷载的影响。研究结果表明：非线性失稳临界荷载随着拱脚沉降量的增大而减小；在拱脚沉降量一定的前提下，非线性失稳荷载随着矢跨比的增大而增大，随着长细比的增大而减小，且长细比的影响最为显著。
- 3D打印拱 /
- 拱脚沉降 /
- 非线性面内失稳 /
- 理论推导 /
- 试验研究 /
- 有限元模拟
Abstract: Presents an investigation on nonlinear instability of 3D printing arch made of 3D printing material ABS-M30 under the settlement of arch foot. Based on the principle of minimum potential energy, the analytical expression of instability critical load is derived, and the distribution of arch radial displacement along the arch axis under vertical and horizontal displacements of arch foot is obtained. The loading system which is capable of controlling the settlement of arch foot is designed. Then the equilibrium path of arch in the loading process is obtained experimentally, which is verified by analytical and finite element simulation. Meanwhile, the influence of rise span ratio and slenderness ratio on the critical load of 3D printing arch is analyzed. The results show that the nonlinear instability load decreases with the increase of arch foot settlement; with a certain arch foot settlement, the nonlinear instability load increases with the increase of rise span ratio, while decreases with the increase of slenderness ratio which has the most significant effect on the nonlinear instability load.
- 3D printing arch /
- settlement of arch foot /
- nonlinear instability /
- analytical solution /
- experiment /
- finite element simulation

HTML全文

图 1 拱脚变位时圆弧拱受力图

Figure 1. Stress diagram of circular arch during displacement of arch foot

下载: 全尺寸图片幻灯片

图 2 拱脚竖向变位下拱径向位移沿拱轴线分布图

Figure 2. Distribution of arch radial displacement along arch axis under vertical displacement of arch foot

下载: 全尺寸图片幻灯片

图 3 拱脚水平变位下拱径向位移沿拱轴线分布图

Figure 3. Distribution of arch radial displacement along arch axis under horizontal displacement of arch foot

下载: 全尺寸图片幻灯片

图 4 加载试验全过程(以工况1为例)

Figure 4. Whole process of loading test (taking condition 1 as an example)

下载: 全尺寸图片幻灯片

图 5 拱的上下极值点试验值随着拱脚竖向变位的折线图

Figure 5. Line chart of the test value of the upper and lower extreme points of the arch with the vertical displacement of the arch foot

下载: 全尺寸图片幻灯片

图 6 拱的上下极值点试验值随着矢跨比变化的折线图

Figure 6. Line chart of the variation of the test value of the upper and lower extreme points of the arch with the rise span ratio

下载: 全尺寸图片幻灯片

图 7 拱的上下极值点试验值随着长细比变化的折线图

Figure 7. Line chart of the variation of the test value of the upper and lower extreme points of the arch with the slenderness ratio

下载: 全尺寸图片幻灯片

图 8 拱脚沉降量对失稳荷载的影响

Figure 8. Influence of arch foot settlement on instability load

下载: 全尺寸图片幻灯片

图 9 矢跨比对失稳荷载的影响

Figure 9. Influence of rise span ratio on instability load

下载: 全尺寸图片幻灯片

图 10 长细比对失稳荷载的影响

Figure 10. Influence of slenderness ratio on instability load

下载: 全尺寸图片幻灯片

表 1 试件材性试验结果

Table 1 Material property test results of test piece

项目	拉伸弹性模量/MPa	泊松比	拉伸强度/MPa
平均值	1540	0.3164	13.63
标准差	0.10	0.0040	0.17
离散系数/(%)	6.58	1.2700	1.25

下载: 导出CSV

表 2 3D打印拱试件设计参数

Table 2 Design parameters of 3D printing of arch specimen

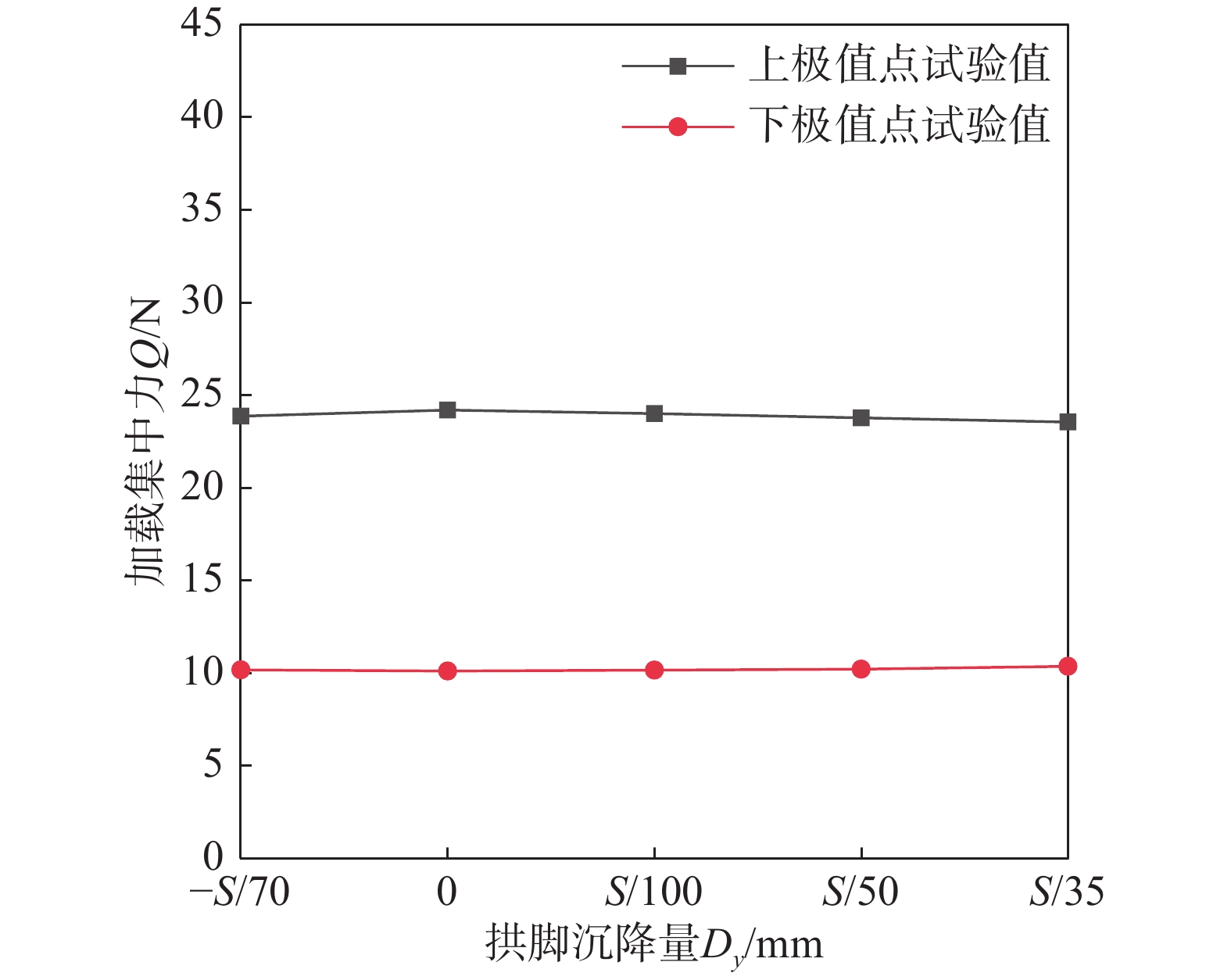
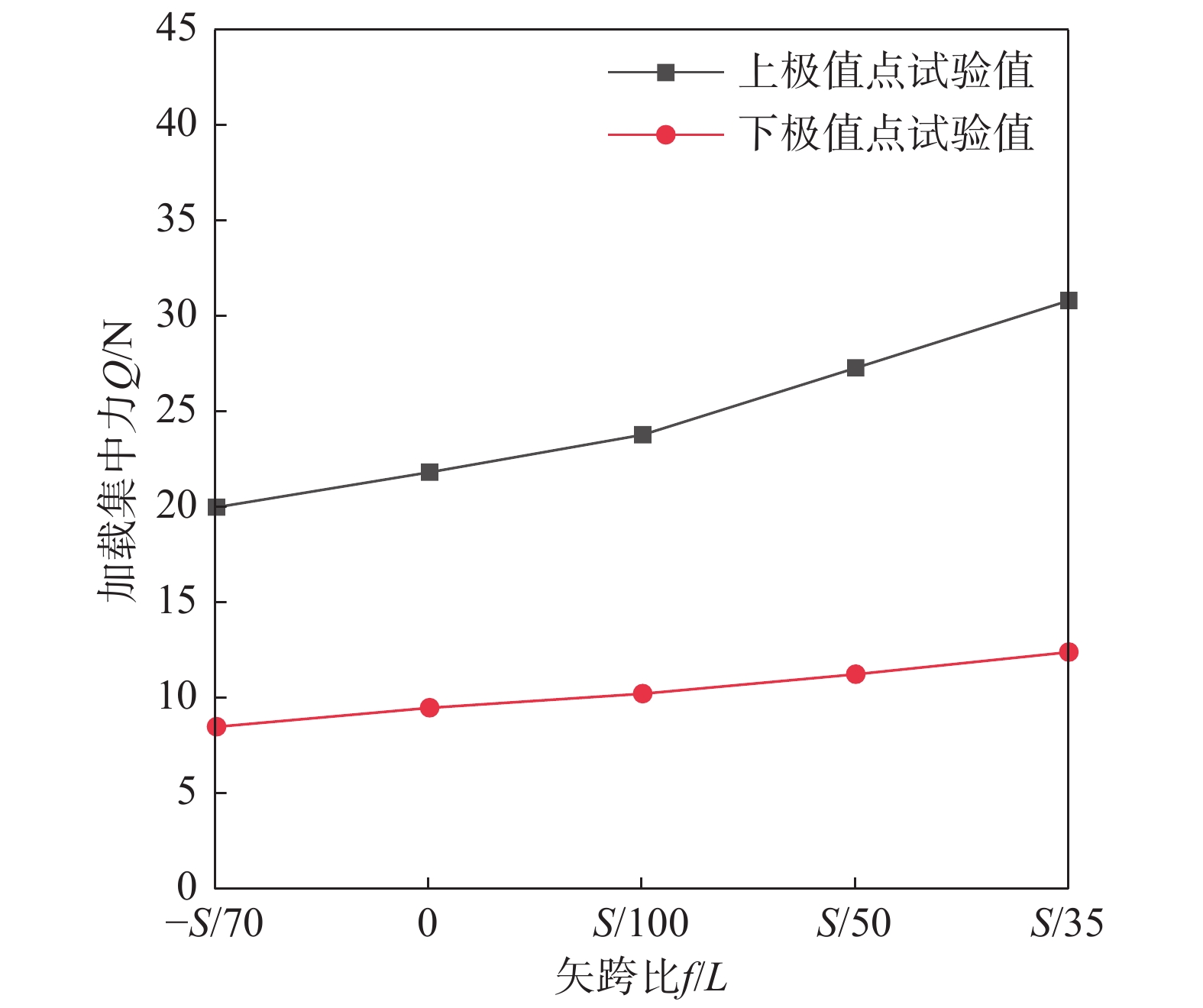
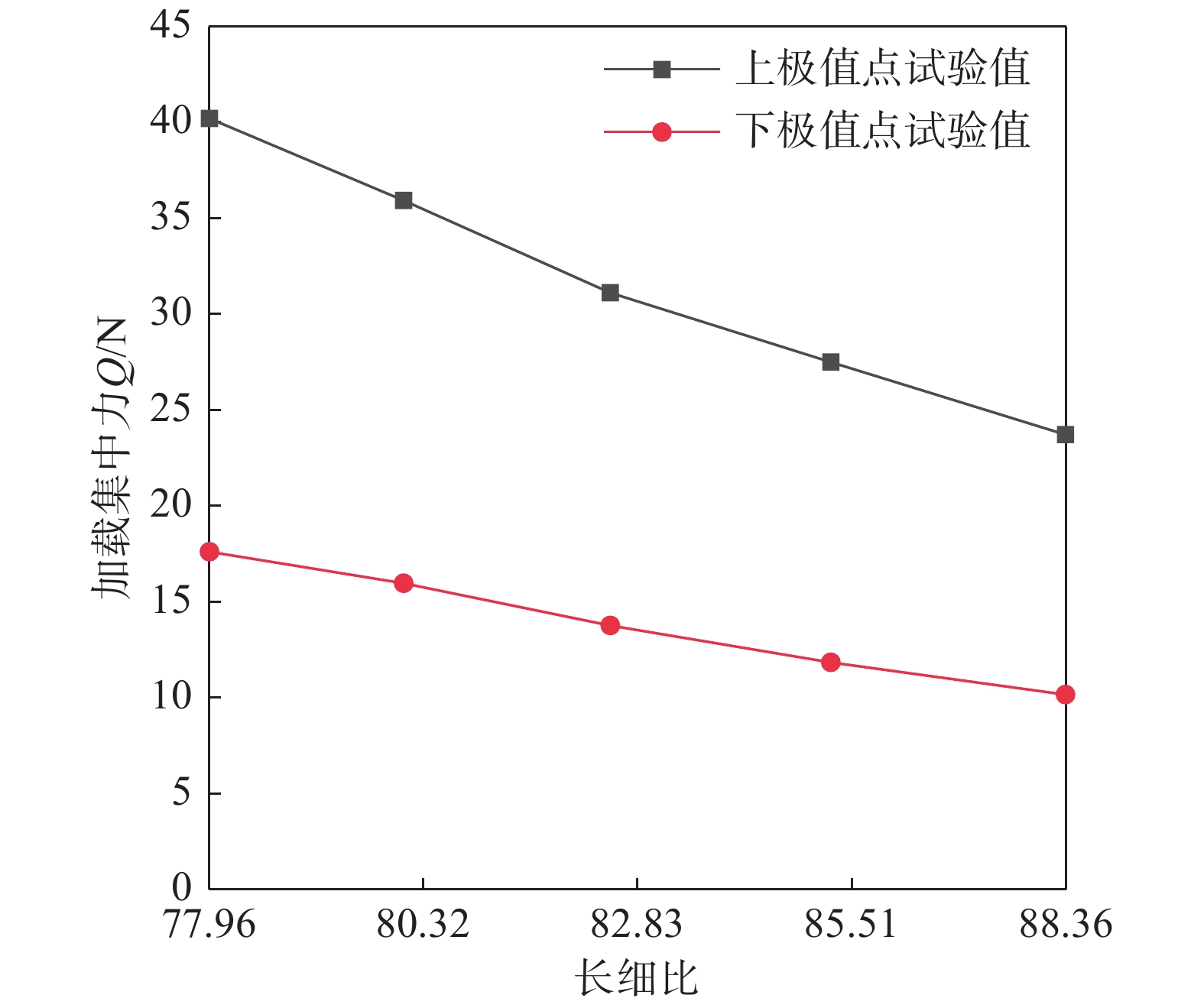
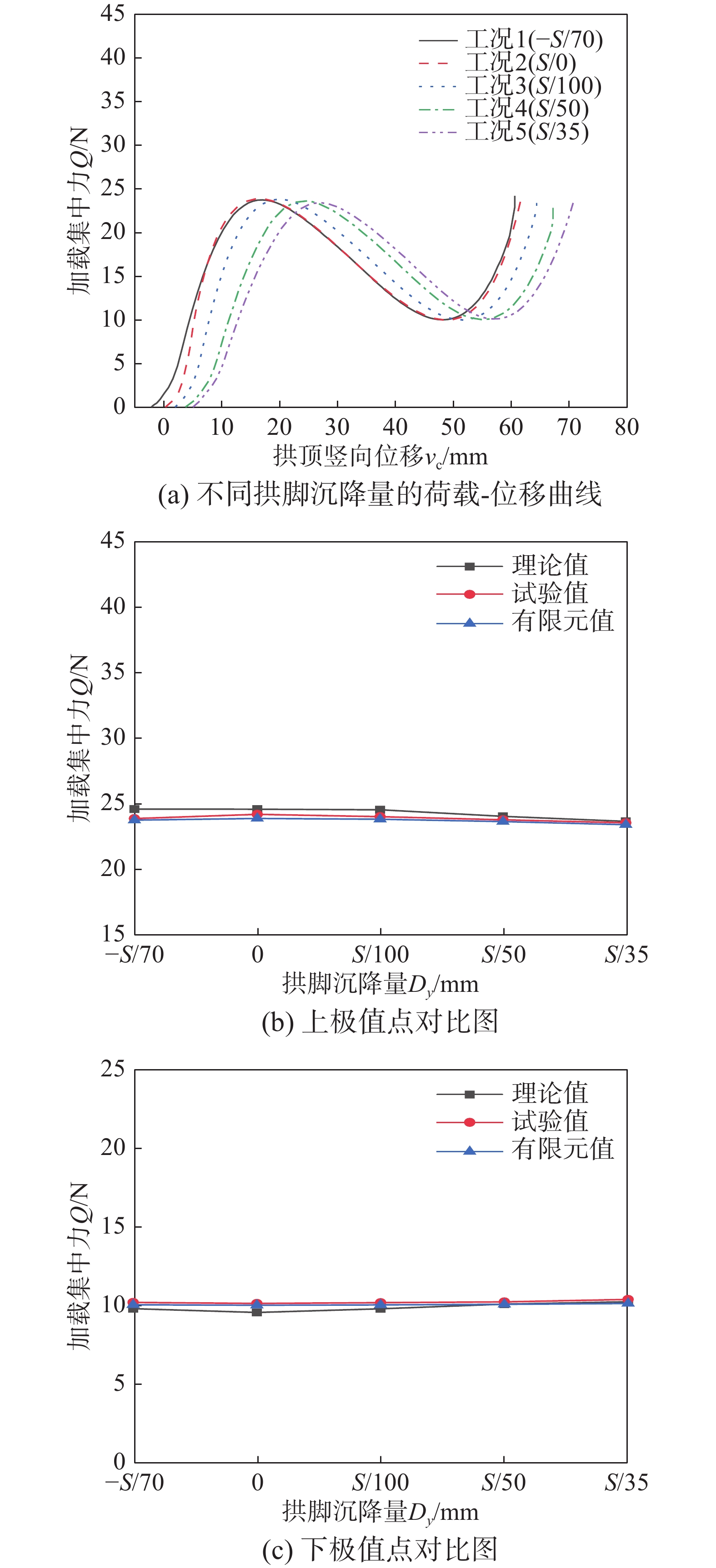
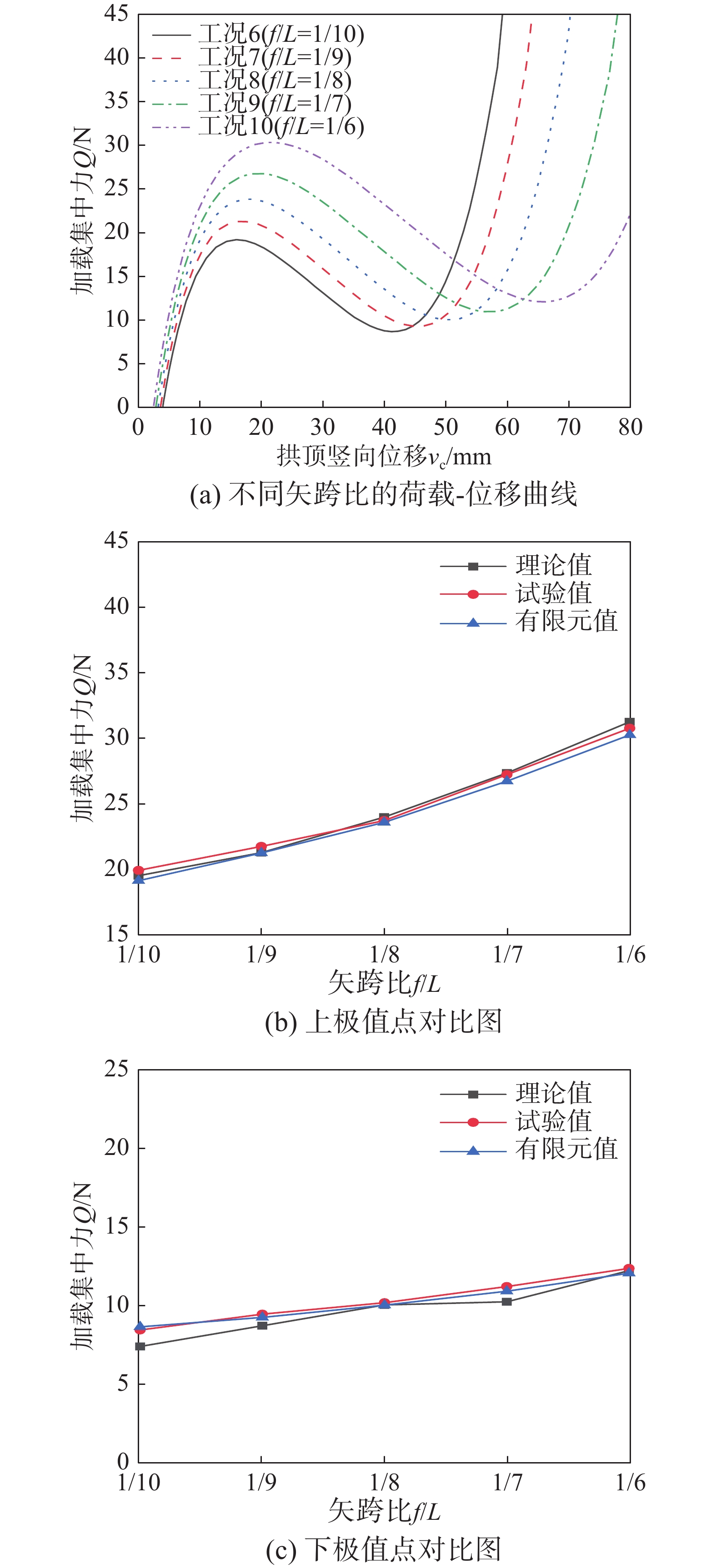
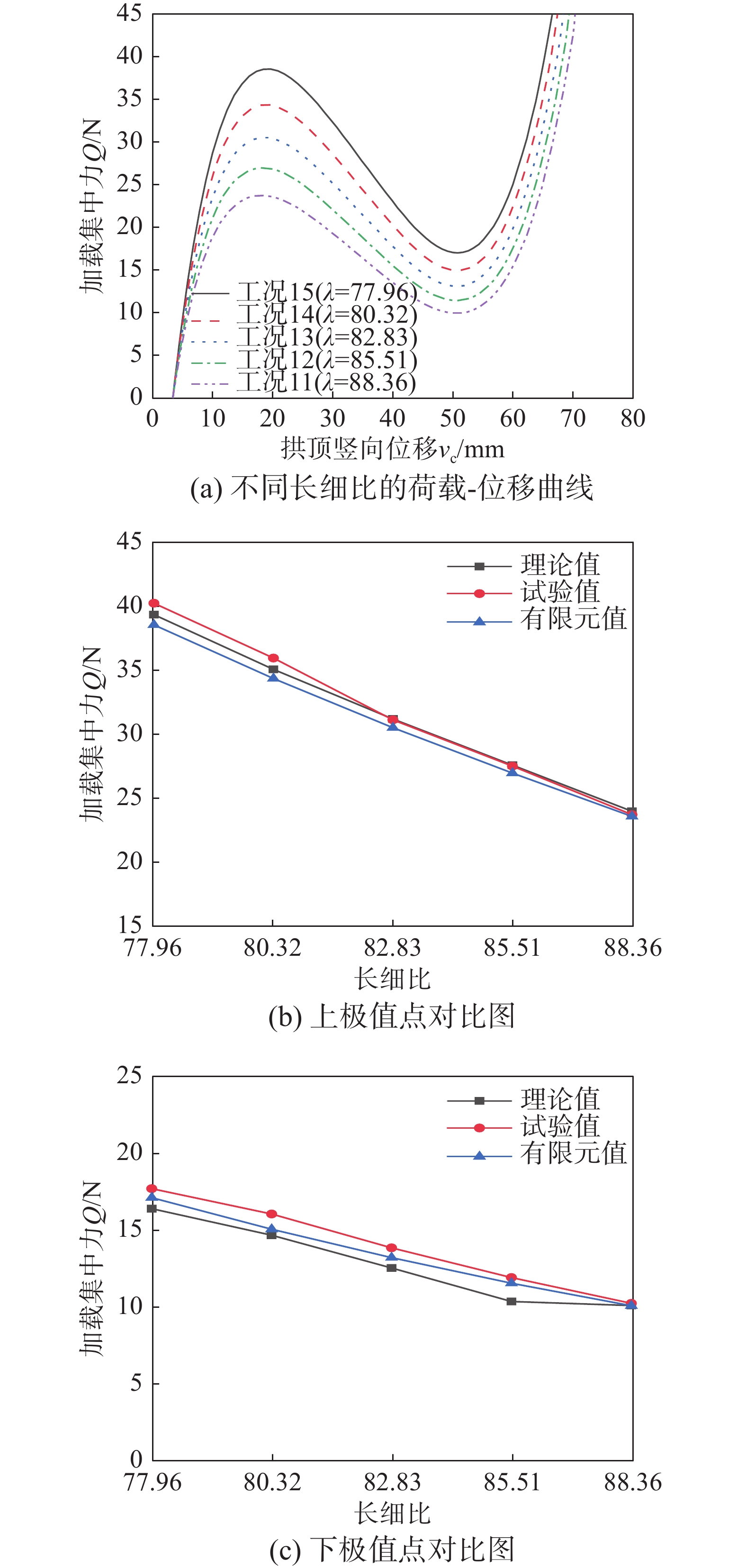
工况组	矢跨比f/L	跨径L/mm	矢高f/mm	截面宽度b/mm	截面高度h/mm	支撑截面高度b^'/mm	支撑截面高度h^'/mm	长细比λ	拱脚变位量X/mm
1	1/8	300	37.50	6.00	3.00	6.00	1.41	88.36	−4.46
2	1/8	300	37.50	6.00	3.00	6.00	1.41	88.36	0.00
3	1/8	300	37.50	6.00	3.00	6.00	1.41	88.36	3.12
4	1/8	300	37.50	6.00	3.00	6.00	1.41	88.36	6.25
5	1/8	300	37.50	6.00	3.00	6.00	1.41	88.36	8.92
6	1/10	300	30.00	6.00	3.00	6.00	1.15	70.19	6.25
7	1/9	300	33.33	6.00	3.00	6.00	1.27	78.22	6.25
8	1/8	300	37.50	6.00	3.00	6.00	1.41	88.36	6.25
9	1/7	300	42.86	6.00	3.00	6.00	1.58	101.57	6.25
10	1/6	300	50.00	6.00	3.00	6.00	1.80	119.54	6.25
11	1/8	300	37.50	6.00	3.00	6.00	1.41	88.36	6.25
12	1/8	300	37.50	6.20	3.10	6.20	1.46	85.51	6.25
13	1/8	300	37.50	6.40	3.20	6.40	1.51	82.83	6.25
14	1/8	300	37.50	6.60	3.30	6.60	1.55	80.32	6.25
15	1/8	300	37.50	6.80	3.40	6.80	1.60	77.96	6.25
注：表中负号表示拱脚向上变位量。

下载: 导出CSV

表 3 3D打印拱临界失稳荷载误差分析表

Table 3 Error analysis table of 3D printing arch critical load

误差分析项	上极值点临界荷载				下极值点临界荷载
误差分析项	理论值X₁/N	试验值X₂/N	有限元值X₃/N	误差率 ${\varDelta _1}$ /(%)	理论值Y₁/N	试验值Y₂/N	有限元值Y₃/N	误差率 ${\varDelta _2}$ /(%)
工况1	24.60	23.88	23.76	0.50	9.79	10.19	10.04	1.47
工况2	24.59	24.20	23.89	1.28	9.55	10.12	10.01	1.09
工况3	24.55	24.02	23.83	0.79	9.78	10.17	10.03	1.38
工况4	24.05	23.79	23.65	0.59	10.08	10.22	10.07	1.47
工况5	23.67	23.56	23.41	0.64	10.23	10.38	10.12	2.50
工况6	19.58	19.99	19.20	3.95	7.44	8.49	8.69	−2.36
工况7	21.34	21.82	21.32	2.29	8.76	9.49	9.29	2.11
工况8	24.05	23.79	23.65	0.59	10.08	10.22	10.07	1.47
工况9	27.41	27.29	26.79	1.83	10.28	11.25	10.95	2.67
工况10	31.32	30.82	30.31	1.65	12.26	12.40	12.10	2.42
工况11	24.05	23.79	23.65	0.59	10.08	10.22	10.07	1.47
工况12	27.65	27.57	27.03	1.96	10.34	11.90	11.53	3.11
工况13	31.25	31.18	30.57	1.96	12.52	13.83	13.19	4.63
工况14	35.12	36.00	34.41	4.42	14.65	16.03	15.04	6.18
工况15	39.39	40.28	38.59	4.20	16.38	17.68	17.09	3.34

下载: 导出CSV

参考文献(13)

[1]	Pi Y L, Bradford M A, Liu A R. Nonlinear equilibrium and buckling of fixed shallow arches subjected to an arbitrary radial concentrated load [J]. International Journal of Structural Stability and Dynamics, 2017, 17(8): 1750082. doi: 10.1142/S0219455417500821
[2]	Liu A R, Bradford M A, Pi Y L. In-plane nonlinear multiple equilibria and switches of equilibria of pinned-fixed arches under an arbitrary radial concentrated load [J]. Archive of Applied Mechanics, 2017, 87(11): 1909 − 1928. doi: 10.1007/s00419-017-1300-7
[3]	Pi Y L, Bradford M A, Tin-Loi F. Non-linear in-plane buckling of rotationally restrained shallow arches under a central concentrated load [J]. International Journal of Non-Linear Mechanics, 2008, 43(1): 1 − 17. doi: 10.1016/j.ijnonlinmec.2007.03.013
[4]	Pi Y L, Bradford M A. Nonlinear in-plane post-buckling of arches with rotational end restraints under uniform radial loading [J]. International Journal of Non-Linear Mechanics, 2009, 44(9): 975 − 989. doi: 10.1016/j.ijnonlinmec.2009.07.003
[5]	张紫祥, 刘爱荣, 黄永辉, 等. 集中荷载作用下弹性扭转约束层合浅拱的非线性面内稳定[J]. 工程力学, 2020, 37(增刊): 13 − 19, 31. doi: 10.6052/j.issn.1000-4750.2019.04.S048 Zhang Zixiang, Liu Airong, Huang Yonghui, et al. Nonlinear in-plane stability of laminated shallow arch with elastic torsional restraint under concentrated load [J]. Engineering Mechanics, 2020, 37(Suppl): 13 − 19, 31. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S048
[6]	刘璐璐, 刘爱荣, 卢汉文. T型截面拱在拱顶集中力作用下的平面外弯扭失稳[J]. 工程力学, 2020, 37(增刊): 151 − 156. doi: 10.6052/j.issn.1000-4750.2019.04.S026 Liu Lulu, Liu Airong, Lu Hanwen. Out of plane bending and torsional instability of T-section arch under concentrated force on arch crown [J]. Engineering Mechanics, 2020, 37(Suppl): 151 − 156. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S026
[7]	王德禹, 杨桂通. 支座突然沉陷时浅拱的冲击屈曲[J]. 太原工业大学学报, 1991(4): 10 − 14. Wang Deyu, Yang Guitong. Impact buckling of shallow arch when the support suddenly subsides [J]. Journal of Taiyuan University of Technology, 1991(4): 10 − 14. (in Chinese)
[8]	严建科, 许璐, 吕婷. 拱脚扰动对拱桥安全的影响分析[J]. 山西建筑, 2005, 31(4): 183 − 184. Yan Jianke, Xu Lu, Lü Ting. Analysis of influence of arch foot disturbance on arch bridge safety [J]. Shanxi Architecture, 2005, 31(4): 183 − 184. (in Chinese)
[9]	邓一三, 王燕楠. 拱脚沉陷对圆拱屈曲性能的影响[J]. 武汉大学学报(工学版), 2013, 46(6): 772 − 775. Deng Yisan, Wang Yannan. Effect of arch foot settlement on buckling behavior of circular arch [J]. Journal of Wuhan University (Engineering Edition), 2013, 46(6): 772 − 775. (in Chinese)
[10]	Lu H W, Liu L L, Liu A R, et al. Effects of movement and rotation of supports on nonlinear instability of fixed shallow arches [J]. Thin-Walled Structures, 2020, 155(1): 106909. doi: 10.1016/j.tws.2020.106909
[11]	黄赋云. 3D打印机用的数码ABS新材料[J]. 现代塑料加工应用, 2014, 26(1): 40. Huang Fuyun. New digital ABS material for 3D printer [J]. Modern plastic processing and Application, 2014, 26(1): 40. (in Chinese)
[12]	林海英, 崔博然, 刘冰河. 3D打印工程塑料力学特性分析[J]. 公路交通科技, 2017, 34(1): 149 − 153. Lin Haiying, Cui Boran, Liu Binghe. Analysis of mechanical properties of 3D printing engineering plastics [J]. Highway Transportation Technology, 2017, 34(1): 149 − 153. (in Chinese)
[13]	GB/T 1040.1−2018, 塑料拉伸性能的测定第1部分: 总则[S]. 北京: 中国标准出版社, 2018. GB/T 1040.1−2018, Plastics-Determination of tensile properties-Part 1: General principles [S]. Beijing: China Standards Press, 2018. (in Chinese)

施引文献(2)

期刊类型引用(2)

1.	汤轶丰，顾敏明，程洪福，胡伏原. 差异沉降下的拱形门径向裂纹应力强度因子解析解研究. 力学与实践. 2023(05): 1117-1127 . 百度学术
2.	兰金江，苏正雄，邱文举，吴建永，马良红. 风力发电机组塔架焊接变形超声无损检测方法. 焊接技术. 2023(11): 133-137 . 百度学术