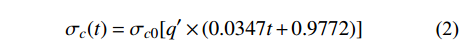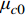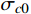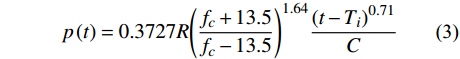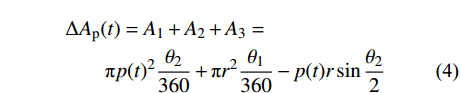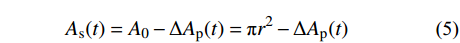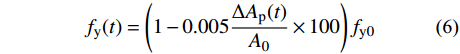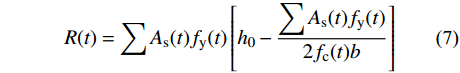RELIABILITY EVALUATION OF AN URBAN BRIDGE BASED ON DURABILITY THEORY AND LOAD LIMIT POLICY
-
摘要: 城市桥梁在户外各种不利环境因素的影响下,结构材料的耐久性能会发生退化,以致出现混凝土强度降低、钢筋锈蚀等耐久性病害,导致桥梁结构的安全性和可靠性逐渐下降。以某典型城市高架桥为例,基于混凝土结构耐久性理论和城市的限载政策,结合现场检测、实地交通调查结果,分析了桥梁结构的时变抗力和荷载效应的变化规律,最后,推算了桥梁控制截面抗弯承载能力可靠性功能函数的失效概率,并对其可靠度进行了评估。该研究方法为各地城市桥梁的可靠性评估、维修养护、交通荷载限载政策等提供借鉴和参考。Abstract: Under the attack of various aggressive environmental factors, the durability of material degrades, which leads to the reduction of concrete strength, steel bar corrosion and other durability diseases, resulting in the gradual decline of the safety and reliability of urban bridges. A typical city viaduct was taken as an example, based on the durability theory of concrete structures and the load limit policy of city, combined with the results of in-situ inspection and traffic survey, the time-varying load bearing capacity and load effect of the bridge structure were analyzed, and the failure probability was calculated by referring to the reliability function of the bridge’s control sections, and then the reliability was evaluated. The research method provides reference for the reliability assessment & maintenance of urban bridges and the formulation of traffic load limit policy.
-
我国以城市高架桥和立交为主的城市桥梁建设主要开始于20世纪80年代−90年代,通常采用钢筋混凝土或预应力混凝土的梁式桥桥型结构,设计荷载标准偏低。进入21世纪后,随着城市现代化进程的加速、汽车工业的发展,客货运输交通需求日益增长,城市桥梁面临车辆拥堵和货车超限超载的现象,运营车辆荷载效应接近甚至超过设计荷载效应。对于既有桥梁而言,由于设计时对结构材料的耐久性、结构抗力的变化并没有充分地考虑,以致不少桥梁虽然未达到设计使用年限,已出现了混凝土开裂、钢筋锈蚀等耐久性病害,显著影响了桥梁结构的安全性和可靠性。
混凝土结构的耐久性问题已引起国内外学者的关注。主要相关研究包括Ho、Lewis[1]研究了水灰比、水泥品种对混凝土碳化深度的影响,建立混凝土碳化公式。谷慧等[2]基于贝叶斯理论,提出碳化环境下的耐久性模型更新方法。潘洪科等[3]运用损伤力学理论对因钢筋锈蚀膨胀而对混凝土产生的作用效应进行数值模拟,并对结构的耐久性使用寿命进行评价和预测。牛荻涛[4]基于腐蚀电化学原理,建立了混凝土开裂前后的锈蚀量预测模型,分析了锈蚀钢筋混凝土构件的结构性能退化对承载力的影响。张建仁、王磊等[5]通过试验建立了混凝土抗压强度、锈蚀钢筋强度退化模型,提出了腐蚀钢筋混凝土梁承载力计算方法。吕金浩[6]推导了钢筋局部锈蚀后的时变面积公式,统计了城市典型车型轴重尺寸的数字特征,构建了基于材料概率模型的城市桥梁时变抗力模型。此外,为了保证既有混凝土结构在目标使用年限内的安全和正常使用,我国于2019年颁布了《既有混凝土结构耐久性评定标准》(GB/T 51355−2019)[7]。
为了缓解城市交通拥堵问题,城市内通常实施限制货车通行的交通管制政策和措施。以广州市区为例,曾先后多次调整货车限载限行政策,自2018年以来,政策规定:上下班高峰期时段禁止货车通行;每日7:00−22:00(下称限载时段),禁止核定载重质量为5 t(广州市籍号牌)、0.6 t(外地号牌)以上的货车通行。此限载政策是否能有效地保障城市桥梁的安全运营?
本文以广州市某典型城市高架桥为例,基于混凝土结构耐久性理论和既有混凝土结构耐久性评定标准,结合现场检测、实地交通调查的结果,分析了桥梁结构后续服役期的抗力和车辆荷载效应变化,计算了桥梁控制截面的抗弯承载力可靠度,最后对该桥的可靠性进行了评估。
1 工程概况
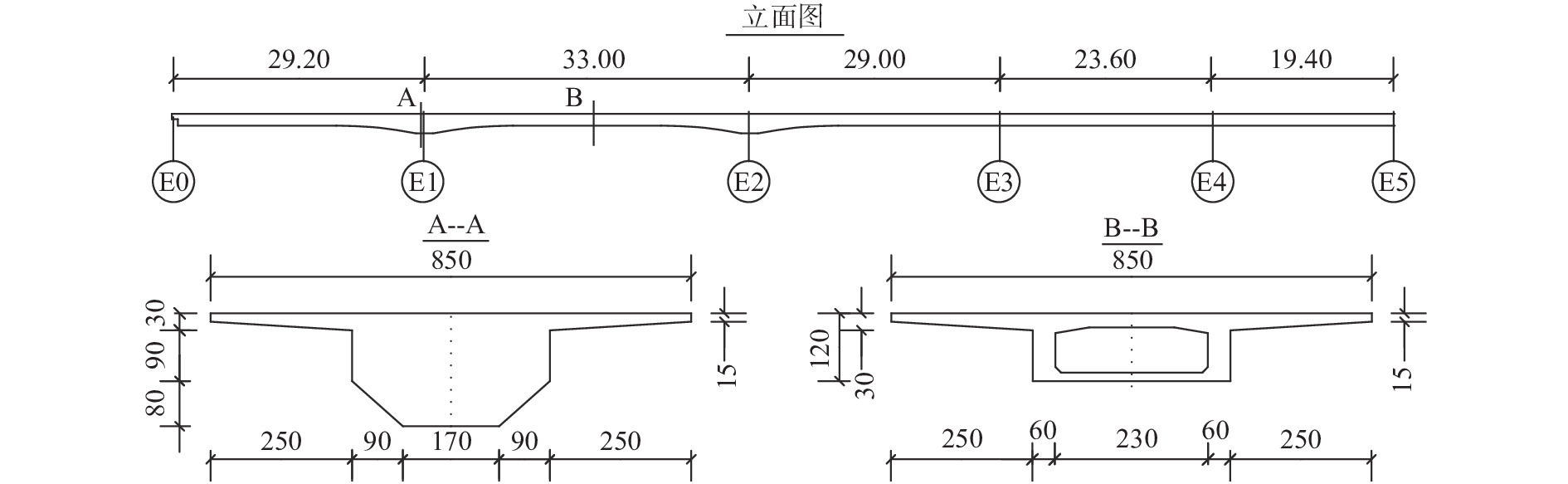
某城市高架桥为广州市城区某立交工程的匝道桥梁,上部结构采用变高单箱单室钢筋混凝土连续结构,跨径组合29.20 m+33.00 m+29.00 m+23.60 m+19.40 m =134.20 m,桥面宽8.50 m、单向双车道。上部结构及桥面铺装采用现浇C35混凝土,主钢筋型号为HRB335。设计荷载为:汽-超20、挂-120,并于1998年建成通车。2007年该桥进行了桥跨结构的混凝土抗压强度和钢筋保护层厚度检测,且在外观检查时发现多数箱梁底板和腹板普遍存在微裂缝。2018年底,该桥进行了实地交通荷载调查。桥梁上部结构布置简图如图1所示。
2 混凝土结构耐久性的时变模型
2.1 混凝土抗压强度时变模型
参考张建仁等基于混凝土碳化腐蚀理论以及实桥混凝土强度统计回归模型[5],认为混凝土的时变抗压强度fc
(t)服从正态分布,某t年该强度分布的平均值和标准差分别为: μc(t)=μc0[q×1.3781e−0.0246(lnt−1.7154)2] (1) σc(t)=σc0[q′×(0.0347t+0.9772)] (2) 式中:q和q′为模拟参数,对应的值分别为1.156和为0.981;现浇C35对应的初始平均值
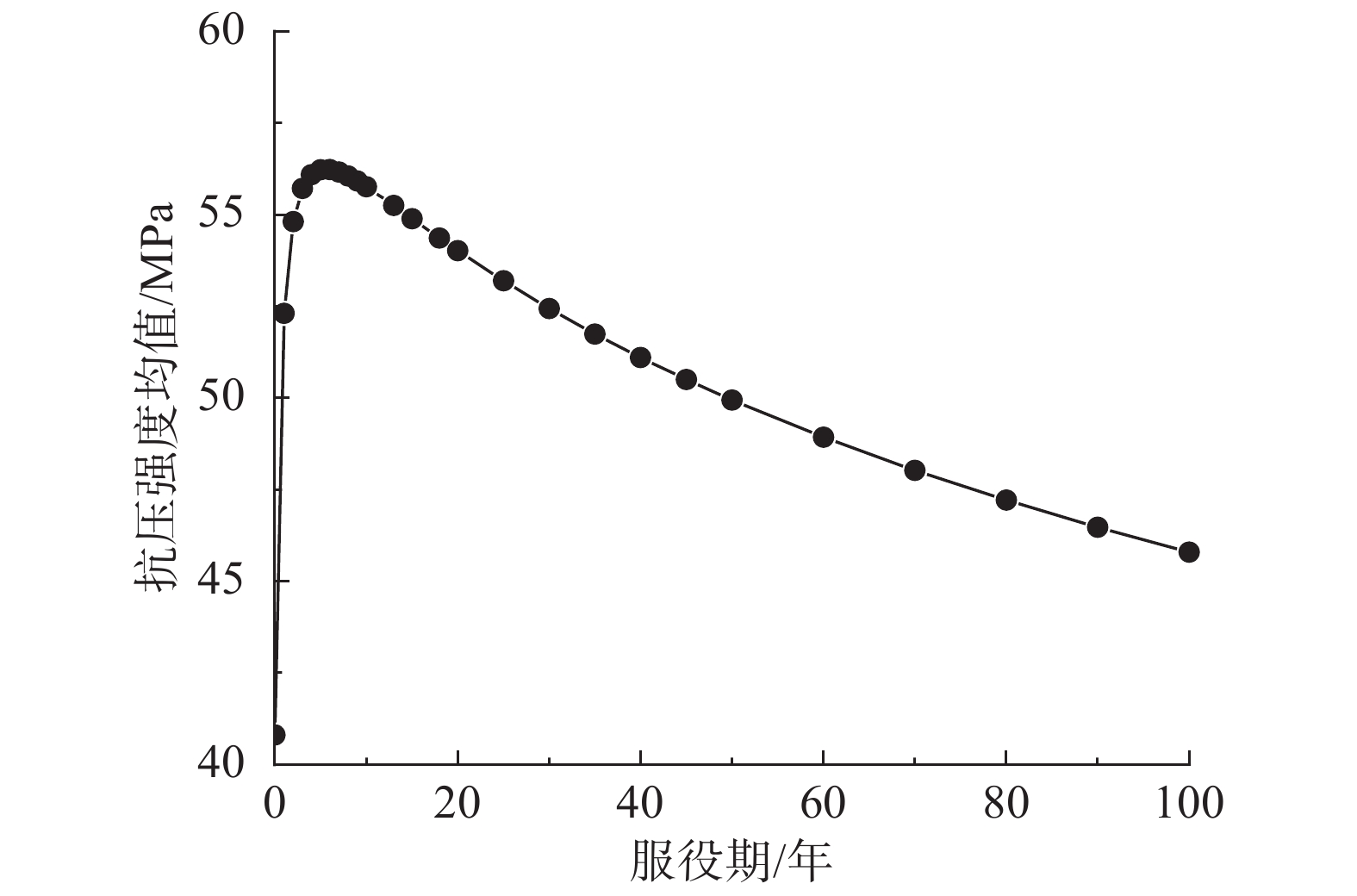
μc0 和标准差σc0 分别为32、5.2554。服役期第9年(2007年),利用式(1)、式(2)可得到t=9年的混凝土强度分布(先验分布)的平均值和标准差;而由该年度(2007年)桥跨结构的混凝土抗压强度检测结果可知,实际强度分布的平均值为54.30 和标准差4.64,并以此作为混凝土强度后验分布的特征值,按贝叶斯修正理论得到更新后混凝土强度分布模型的平均值53.10 和标准差3.80,以及更新后模拟参数q和q′的值为1.275和0.561。所得到混凝土强度均值的时变模型计算结果如图2所示,呈现服役期前6年迅速增长而后缓慢下降的趋势。2.2 钢筋初始锈蚀时间
参考既有混凝土结构耐久性评定标准(GB/T 51355−2019)[7]5.2节的公式,按一般环境考虑,钢筋初始锈蚀时间Ti与碳化系数、保护层厚度和局部环境的影响系数的乘积相关。其中,在碳化系数的影响系数Kk按环境温度、相对湿度取地区均值计算;二氧化碳浓度影响按大中城市市区的工业建筑室外环境取值(1.40);酸雨影响程度影响取中值计算(1.35),保护层厚度影响系数Kc参考2007年混凝土保护层厚度实测结果(均值18.50 mm,标准差3.92 mm)插值计算;局部环境的影响系数Km按室外淋雨、酸雨环境取局部环境系数m=4插值计算。最后得到混凝土结构钢筋开始锈蚀时间Ti为18年,如表1所示。
表 1 钢筋初始锈蚀时间的计算Table 1. Calculation of the initial corrosion time of the reinforcementKk Kc Km Ti=15.2 Kk Kc Km 1.45 1.20 0.68 18.05 2.3 钢筋局部锈蚀深度和锈蚀面积
假设钢筋沿最靠近大气的方向发生局部锈蚀,且局部锈蚀坑呈半圆形,参考文献[5],当桥梁建成服役期t年后,对于钢筋开始锈蚀时间Ti,钢筋局部锈蚀深度p(t)公式计算为:
p(t)=0.3727R(fc+13.5fc−13.5)1.64(t−Ti)0.71C (3) 式中: R为锈蚀不均匀系数,在4~8间取中值为6;fc/MPa为钢筋开始锈蚀时混凝土对应的抗压强度,按2.1节混凝土抗压强度时变模型取值;C/mm为混凝土保护层厚度。
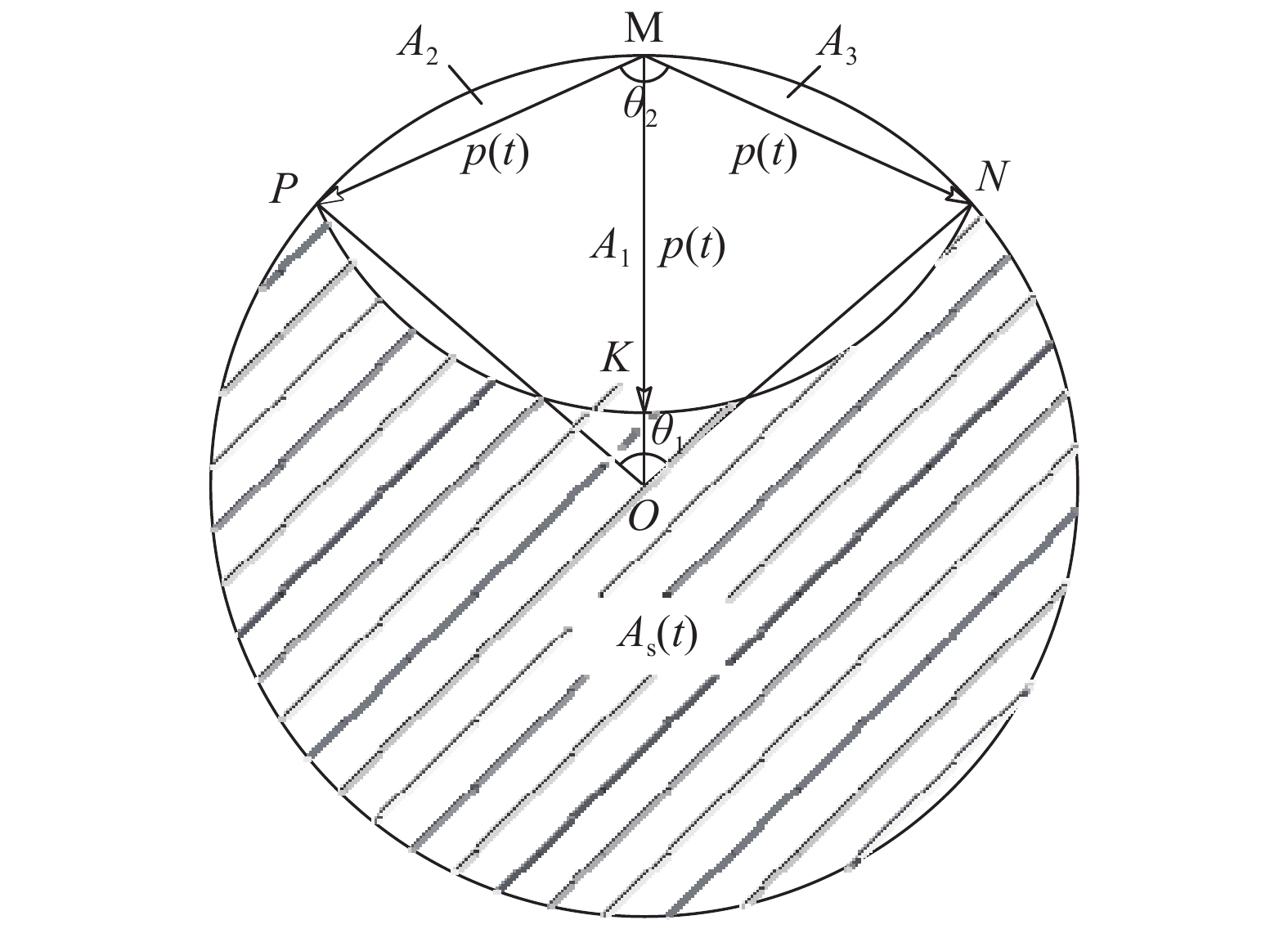
当钢筋局部锈蚀深度p(t)不大于钢筋半径r时,由几何关系可推导出钢筋损失的总面积ΔAp(t)和钢筋剩余面积As(t)的计算公式[6]:
ΔAp(t)=A1+A2+A3=πp(t)2θ2360+πr2θ1360−p(t)rsinθ22 (4) As(t)=A0−ΔAp(t)=πr2−ΔAp(t) (5) 式中:A0为钢筋原面积;A1为扇形MPKN的面积;A2为弦PM与圆弧PM所围面积;A3为弦MN与圆弧MN所围面积;θ1=∠PON,θ2=∠PMN,如图3所示。
2.4 锈蚀钢筋屈服强度时变模型
根据相关学者研究的研究结果[8-9],钢筋的时变屈服强度fy(t)与钢筋的锈蚀损失面积ΔAp(t)以及钢筋初始的面积A0的比值线性相关,相关系数参考文献[10]的取值0.005,可得相对于原钢筋屈服强度fy0的时变模型:
fy(t)=(1−0.005ΔAp(t)A0×100)fy0 (6) 2.5 桥梁主梁截面时变抗弯承载力
按一般环境混凝土结构材料耐久性变化规律,考虑混凝土抗压强度和钢筋的锈蚀面积及其抗拉强度随时间的变化,据桥梁设计规范可得到桥梁上部结构抗弯承载力的时变计算公式:
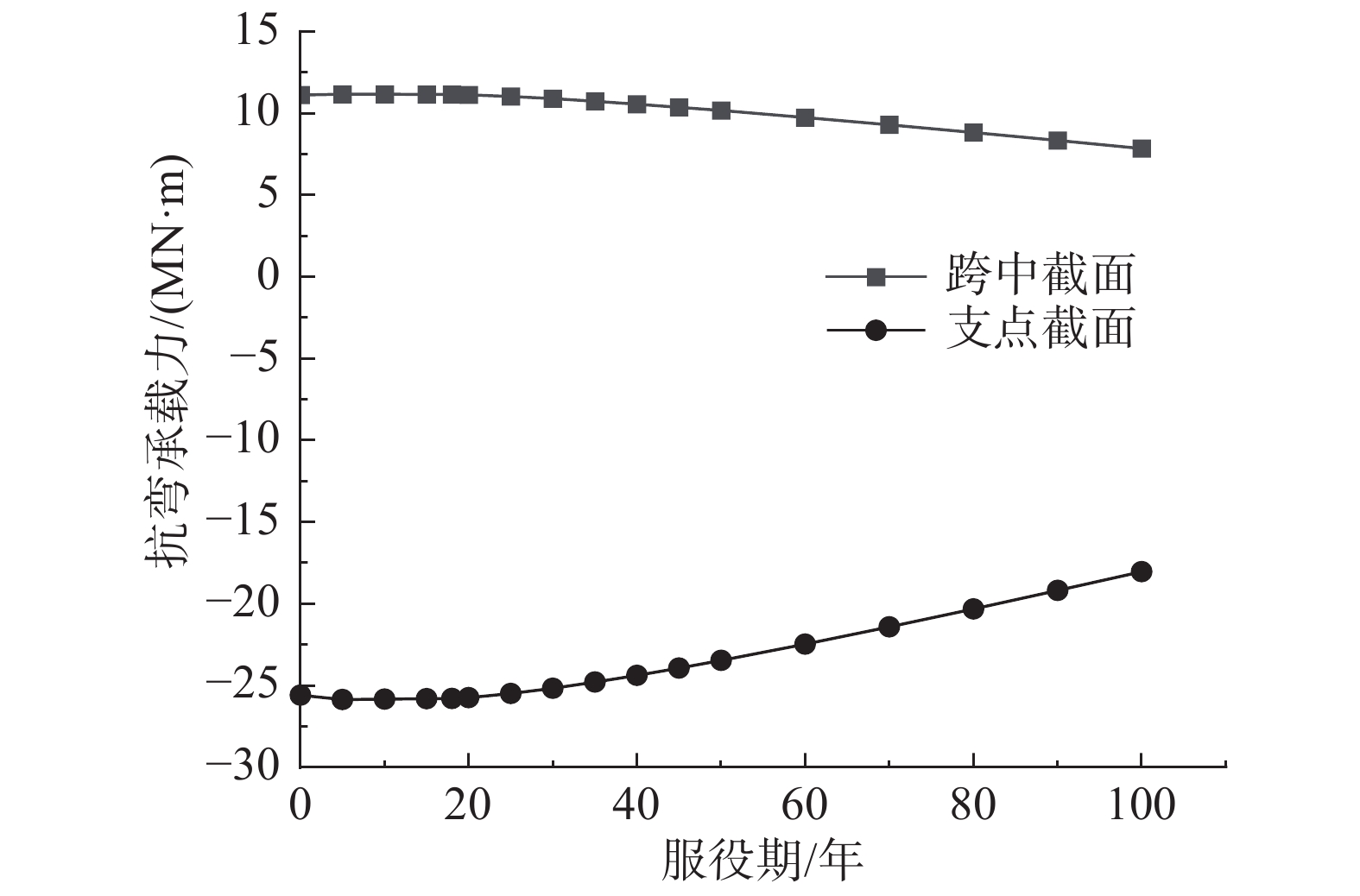
R(t)=∑As(t)fy(t)[h0−∑As(t)fy(t)2fc(t)b] (7) 经计算该桥第1跨、第2跨的支点截面(简称支点截面)、第2跨跨中截面(简称跨中截面)在设计荷载下有最大负、正弯矩值,故分别将混凝土抗压强度、钢筋屈服强度、钢筋剩余面积的时变模型代入式(7),据配筋情况计算不同服役期的抗弯承载能力,计算结果如表2、图4所示。图4显示,在混凝土强度改变和钢筋锈蚀的影响下,跨中和支点截面的抗弯承载力分别从第18年、第20年开始下降、至第100年均约减少了29%。
表 2 两控制截面抗弯承载能力的变化Table 2. Changes of the bending bearing capacity of two control sections服役期/年 承载力/(×104 kN∙m) 变化率/(%) 跨中 支点 跨中 支点 0 1.112 −2.559 0.0 0.0 10 1.116 −2.579 −0.4 −0.9 18 1.113 −2.573 −0.3 −0.8 20 1.103 −2.548 0.1 −0.6 25 1.089 −2.516 0.8 0.4 30 1.056 −2.437 2.0 1.7 40 1.017 −2.346 5.0 4.8 60 0.929 −2.140 12.4 12.2 80 0.834 −1.918 20.7 20.6 100 1.112 −2.559 29.4 29.5 3 城市交通车辆荷载效应模型
结合广州市城区货车的限载政策以及2018年该桥的实地交通调查,得到限载和非限载时段代表性交通小时的通行车辆数据。表3显示了各不同时段的运营交通荷载车型比例,限载时段与非限载时段货客车占比分别为0.01和0.39,可见,限载政策能显著影响城区交通车型的出行分布。
表 3 运营交通荷载车型分布占比Table 3. Distribution proportion of operating traffic load types/(%) 客/货车 轴数 类型 时段 限载 非限载 客车 二轴 小 85.4 52.8 中 5.6 2.7 大 8.1 5.1 货车 二轴 11 0.3 1.2 12 0.7 8.7 三轴 112 0.0 4.0 15 0.0 5.6 四轴 115 0.0 7.4 125 0.0 0.9 五轴 129 0.0 3.9 155 0.0 0.1 六轴 1129 0.0 0.2 159 0.0 7.6 根据城市中常见车辆的参数及国家对运营车辆总质量的限值 [11],其中车重按最大重量的95%且不超过规范限值,统计出城市运营典型客、货车车轴重、轴距以及前后悬的基本参数[6]。车辆间距经现场调研按拥堵状态确定,得到塞车拥堵状态下的车辆间距不拒绝服从N(1.25,0.252)的正态分布。通过控制截面内力影响线,再利用MATLAB软件和蒙特卡洛法根据车重和车型分布模型形成随机车流,进行控制截面内力影响线动态加载,得到随机车辆对桥梁控制截面产生的荷载效应。应用GEV极值分布,对调查时段随机车流下两控制截面的弯矩效应进行了模型拟合,计算结果如表4。
表 4 车辆荷载效应GEV分布的拟合参数Table 4. Fitting parameters for the vehicle load effect GEV distribution截面
位置时段 模型参数 k σ μ 支点 限载 −0.1714 522.11 1846.52 非限载 −0.2371 1601.00 5171.23 跨中 限载 −0.0116 283.20 340.47 非限载 −0.2011 940.68 1028.72 4 可靠性评估
桥梁结构可靠度分析主要分为解析法和随机模拟法,本文采用随机模拟法中的蒙特卡洛法(简称MC法),对抗力、效应模型进行随机抽样,通过统计功能函数的失效概率,求得可靠指标。按控制截面的抗弯承载能力极限状态构建功能函数:Z=R(t)−(S恒+S活) 。
功能函数中,参考文献[12]对结构抗力和恒载分布模型的规定,将已求得的时变抗力值和恒载值作为模型的均值,经查表可得到模型的标准差,即得相应时变抗力、恒载效应分布模型。
基于交通调查时段的随机车流荷载效应的分布模型,鉴于车辆的车轴重均按最大车重95%保证率计入,以调查时段荷载效应分布模型代表1个月的荷载效应最大值分布模型,假设车型分布在后续服役期基本保持不变,则利用极值理论,可推算1年车辆荷载效应最大值分布F1(x)和后继服役年间的车辆荷载效应最大值分布Fn(x),且Fn(x)= [F1(x)]n。
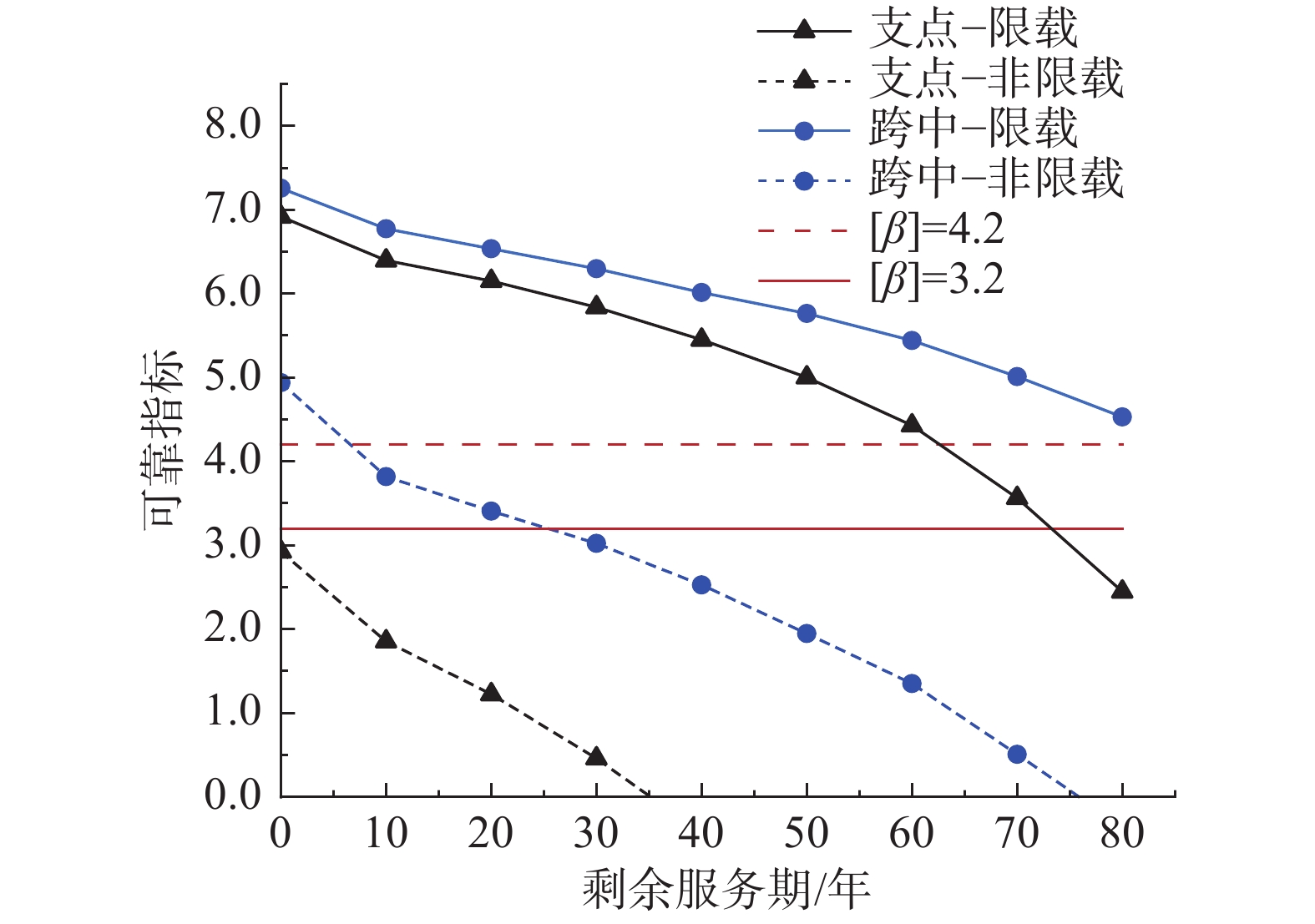
最后,利用MC法编制MATLAB程序,自2018年对于不同剩余服役期(t=0年~80年),生成随机数代入各抗力和效应的分布模型,计算相应的抗力和效应,通过功能函数运算求失效概率求得可靠指标β,如表5、图5所示。
表 5 抗弯可靠指标的计算结果Table 5. Calculation results of reliability index of bending resistance剩余服役期/年 支点截面 跨中截面 限载 非限载 限载 非限载 0 6.9 2.9 7.3 4.9 10 6.4 1.9 6.8 3.8 20 6.2 1.2 6.5 3.4 30 5.8 0.5 6.3 3.0 40 5.5 <0.0 6.0 2.5 50 5.0 <0.0 5.8 1.9 60 4.4 <0.0 5.4 1.4 70 3.6 <0.0 5.0 0.5 80 2.4 <0.0 4.5 <0.0 参考与该桥建成年份相近的《公路工程结构可靠度设计统一标准》[12],该桥属于二级安全等级,对应原延性破坏的目标可靠指标[β]为4.2;对于既有桥梁,参考文献[13]的处理方法,目标可靠指标[β]调整为3.2(下降两级差),即当可靠指标β<[β]=3.2时,认为该结构构件处于破损状态,不能满足设计基准期100年的可靠性使用要求[13]。
图5可见,按照现行的城市城区货车限行政策,考虑桥梁结构耐久性的承载能力退化后,如果按限载时段的交通荷载通行,则支点截面在第73年后将不满足现目标可靠指标3.2的要求;如果按当下的限载政策、存在货车自由通行的非限载时段,则在当下最不利交通荷载下,支点截面已经不能满足要求,跨中截面在第6年后不能满足要求。
5 结论
通过对某既有典型城市桥梁的可靠性评估,可以得到以下结论:
(1)考虑结构材料耐久性变化后,某典型桥梁在服役100年后控制截面的抗弯承载能力减少了29%;基于当前城市桥梁的限载政策,在货车自由通行的非限载时段最不利车辆荷载作用下,支点截面在当年的可靠性不能满足目标可靠指标3.2的要求,存在一定的安全隐患。
(2)建议在非限载时段,管理部门应严格控制通行货车的总重,加强定期检查和维护,以延长城市桥梁的使用寿命。
(3)基于混凝土结构耐久性,结合混凝土抗压强度现场检测结果、实地运营交通车辆荷载调查的可靠性评估方法能有效地评估各地既有城市桥梁的结构可靠性。
-
表 1 钢筋初始锈蚀时间的计算
Table 1 Calculation of the initial corrosion time of the reinforcement
Kk Kc Km Ti=15.2 Kk Kc Km 1.45 1.20 0.68 18.05 表 2 两控制截面抗弯承载能力的变化
Table 2 Changes of the bending bearing capacity of two control sections
服役期/年 承载力/(×104 kN∙m) 变化率/(%) 跨中 支点 跨中 支点 0 1.112 −2.559 0.0 0.0 10 1.116 −2.579 −0.4 −0.9 18 1.113 −2.573 −0.3 −0.8 20 1.103 −2.548 0.1 −0.6 25 1.089 −2.516 0.8 0.4 30 1.056 −2.437 2.0 1.7 40 1.017 −2.346 5.0 4.8 60 0.929 −2.140 12.4 12.2 80 0.834 −1.918 20.7 20.6 100 1.112 −2.559 29.4 29.5 表 3 运营交通荷载车型分布占比
Table 3 Distribution proportion of operating traffic load types
/(%) 客/货车 轴数 类型 时段 限载 非限载 客车 二轴 小 85.4 52.8 中 5.6 2.7 大 8.1 5.1 货车 二轴 11 0.3 1.2 12 0.7 8.7 三轴 112 0.0 4.0 15 0.0 5.6 四轴 115 0.0 7.4 125 0.0 0.9 五轴 129 0.0 3.9 155 0.0 0.1 六轴 1129 0.0 0.2 159 0.0 7.6 表 4 车辆荷载效应GEV分布的拟合参数
Table 4 Fitting parameters for the vehicle load effect GEV distribution
截面
位置时段 模型参数 k σ μ 支点 限载 −0.1714 522.11 1846.52 非限载 −0.2371 1601.00 5171.23 跨中 限载 −0.0116 283.20 340.47 非限载 −0.2011 940.68 1028.72 表 5 抗弯可靠指标的计算结果
Table 5 Calculation results of reliability index of bending resistance
剩余服役期/年 支点截面 跨中截面 限载 非限载 限载 非限载 0 6.9 2.9 7.3 4.9 10 6.4 1.9 6.8 3.8 20 6.2 1.2 6.5 3.4 30 5.8 0.5 6.3 3.0 40 5.5 <0.0 6.0 2.5 50 5.0 <0.0 5.8 1.9 60 4.4 <0.0 5.4 1.4 70 3.6 <0.0 5.0 0.5 80 2.4 <0.0 4.5 <0.0 -
[1] Ho D W S, Lewis R K. Carbonation of concrete and its prediction. cement and concrete research [J]. Cement and Concrete Research, 1987, 17(3): 489 − 504.
[2] 谷慧, 李全旺, 侯冠杰. 碳化环境下混凝土结构耐久性模型的更新方法[J]. 工程力学, 2021, 38(5): 113 − 121. doi: 10.6052/j.issn.1000-4750.2020.06.0361 Gu Hui, Li Quanwang, Hou Guanjie. Updating method for durability models of concrete structures in carbonation environment [J]. Engineering Mechanics, 2021, 38(5): 113 − 121. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0361
[3] 潘洪科, 王穗平, 祝彦知, 杨林德. 钢筋混凝土结构锈胀开裂的耐久性寿命评判与预测研究[J]. 工程力学, 2009, 26(7): 111 − 116. Pan Hongke, Wang Suiping, Zhu Yanzhi, Yang Linde. The judgment and prediction on reinforced concrete structures’ durability based on steel rustiness and concrete cracking [J]. Engineering Mechanics, 2009, 26(7): 111 − 116. (in Chinese)
[4] 牛荻涛. 混凝土结构的耐久性与寿命预测[M]. 北京: 科学出版社, 2003. Niu Ditao. Durability and life forecast of reinforced concrete structure [M]. Beijing: Science Press, 2003. (in Chinese)
[5] 张建仁, 王磊, 彭建新等. 服役钢筋混凝土桥梁时变可靠度评估与剩余寿命预测[M]. 北京: 科学出版社, 2017. Zhang Jianren, Wang Lei, Peng Jianxin, et al. Evaluation of time-variable reliability and residual life prediction for in-service reinforced concrete bridge [M]. Beijing: Science Press, 2017. (in Chinese)
[6] 吕金浩. 考虑限载政策的广州城市既有混疑土梁式桥的时变可靠度分析研究[D]. 广州: 广州大学, 2020. Lü Jinhao. Time-dependent reliability analysis of existing concrete beam bridge in Guangzhou city considering load limit policy [D]. Guangzhou, Guangzhou University, 2020.
[7] GB/T 51355−2019, 既有混凝土结构耐久性评定标准[S]. 北京: 中国建筑工业出版社, 2019. GB/T 51355−2019, Code for durability assessment of existing concrete structures [S]. Beijing: China Architecture and Building Press, 2019. (in Chinese)
[8] Stewart M G. Mechanical behaviour of pitting corrosion of flexural and shear reinforcement and its effect on structural reliability of corroding RC beams [J]. Structural Safety, 2009, 31(1): 19 − 30. doi: 10.1016/j.strusafe.2007.12.001
[9] Ma Yafei, Zhang Jianren, Wang Lei, et al. Probabilistic Prediction with Bayesian Updating for Strength Degradation of RC Bridge Beams [J]. Structural Safety, 2013, 44(2334): 102 − 109.
[10] Du Y G, Clark L A, Chan A H C. Residual capacity of corroded reinforcing bars [J]. Mag Concrete Res, 2005, 57(3): 135 − 147.
[11] GB 1589−2016, 汽车、挂车及汽车列车外廓尺寸、轴荷及质量限值[S]. 北京: 中国标准出版社, 2016. GB 1589−2016, Limits of dimensions, axle load and masses for motor vehicles, trailers and combination vehicles [S]. Beijing: China Standard Press, 2016. (in Chinese)
[12] GB/T 50283−1999, 公路工程结构可靠度设计统一标准[S]. 北京: 中国计划出版社, 1999. GB/T 50283−1999, Unified standard for reliability design of highway engineering structures [S]. Beijing: China Planning Press, 1999. (in Chinese)
[13] 赵国藩. 工程结构可靠性理论与应用[M]. 大连: 大连理工大学出版社, 1996. Zhao Guofan. Reliability theory and its applications for engineering structures [M]. Dalian: Dalian University of Technology Publishing House, 1996. (in Chinese)
-
期刊类型引用(7)
1. 寇玉冬,张利伟. 城市浅层土体水热耦合数值模拟分析. 工程与建设. 2024(06): 1249-1252+1257 .  百度学术
百度学术
2. 朱成立,李依,王策,库热西·吾尔开西,段正宇. 变温度-风速模拟条件下微润灌工况自适应调节机理. 农业机械学报. 2023(03): 347-355+362 .  百度学术
百度学术
3. 寇玉冬,刘春. 基于高精度光纤测温的水热耦合试验. 河南理工大学学报(自然科学版). 2023(03): 88-94 .  百度学术
百度学术
4. 张进平,王煜曦,刘桂宏,何铁柱,袁利娟,徐浩然,孔祥军. 通州区地热资源优化开采模式动态研究. 工程力学. 2022(06): 247-256 .  本站查看
本站查看
5. 李军,陈文涛,陈栋梁. 非饱和土体力学性质及其在采矿工程中的应用研究. 能源与环保. 2022(06): 290-295 .  百度学术
百度学术
6. 熊春宝,胡倩倩,郭颖. 孔隙率各向异性下饱和多孔弹性地基动力响应. 力学学报. 2020(04): 1120-1130 .  百度学术
百度学术
7. 张超,姜景山,王如宾,金华. 降雨非饱和入渗对土壤热量运移变化的影响. 农业工程学报. 2020(18): 118-126 .  百度学术
百度学术
其他类型引用(10)



 下载:
下载: