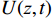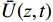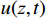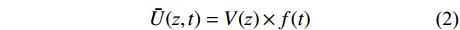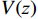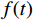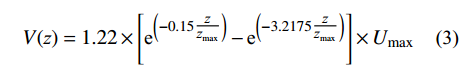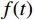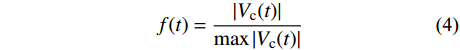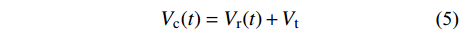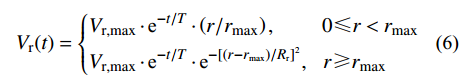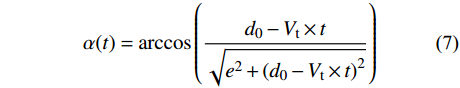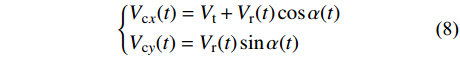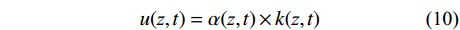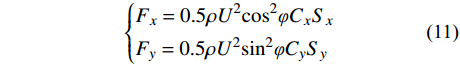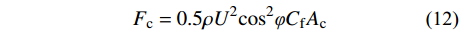Processing math: 38%

下击暴流作用下输电塔-线体系倒塌破坏研究

毕文哲, 田利

毕文哲, 田利. 下击暴流作用下输电塔-线体系倒塌破坏研究[J]. 工程力学, 2022, 39(S): 78-83. DOI: 10.6052/j.issn.1000-4750.2021.05.S012
引用本文: 毕文哲, 田利. 下击暴流作用下输电塔-线体系倒塌破坏研究[J]. 工程力学, 2022, 39(S): 78-83. DOI: 10.6052/j.issn.1000-4750.2021.05.S012
shu
BI Wen-zhe, TIAN Li. STUDY ON THE COLLAPSE FAILURE OF TRANSMISSION TOWER-LINE SYSTEM UNDER DOWNBURST[J]. Engineering Mechanics, 2022, 39(S): 78-83. DOI: 10.6052/j.issn.1000-4750.2021.05.S012
Citation: BI Wen-zhe, TIAN Li. STUDY ON THE COLLAPSE FAILURE OF TRANSMISSION TOWER-LINE SYSTEM UNDER DOWNBURST[J]. Engineering Mechanics, 2022, 39(S): 78-83. DOI: 10.6052/j.issn.1000-4750.2021.05.S012
shu

下击暴流作用下输电塔-线体系倒塌破坏研究

  • 山东大学土木工程系，山东，济南 250061

基金项目: 山东大学青年学者未来计划项目(2017WLJH33)
详细信息
    作者简介:

    毕文哲(1997−)，女，山东人，博士生，主要从事输电塔-线体系抗风研究 (E-mail: 845860312@qq.com)

    通讯作者:

    田　利(1982−)，男，山东人，教授，博士，博导，主要从事结构防灾减灾工程研究 (E-mail: tianli@sdu.edu.cn)

  • 中图分类号: TM75；TU312+.3

STUDY ON THE COLLAPSE FAILURE OF TRANSMISSION TOWER-LINE SYSTEM UNDER DOWNBURST

  • School of Civil Engineering, Shandong University, Jinan, Shandong 250061, China

摘要

    摘要
  • 摘要: 下击暴流在近地面形成的短时破坏性强风会对建筑结构造成较大威胁，尤其是输电塔-线体系等风敏感结构。依托实际工程，该文建立了输电塔-线体系有限元模型，采用确定性-随机性混合模型生成下击暴流风场，基于Tian-Ma-Qu本构模型模拟了该结构在下击暴流作用下的连续倒塌过程。结果表明，下击暴流下输电塔表现为在极短时间内的局部大变形，该区域大量斜材和少量主材相继屈曲是导致输电塔发生整体倒塌的主要原因。该输电塔的薄弱部位是第六节间，在抗下击暴流设计中应重点关注。
    Abstract: The short-term destructive strong wind formed by the downburst near the ground will pose a greater threat to building structures, especially to wind-sensitive structures such as transmission tower-line systems. Based on practical engineering, a new finite element model for the transmission tower-line system is established. The deterministic-stochastic hybrid model is used to simulate the generation of the downburst wind field. Based on the Tian-Ma-Qu material model, the progressive collapse process of the structure under the downburst is conducted. The research results demonstrate that: the transmission tower under the downburst performs its significant local deformation in a short time, the buckling of many diagonal members and several main members is the governing reason for the entire collapse of the tower. The segment 6 of the tower is considered the weakest position, to which should be particularly paid attention in the design of the structural resistance to downburst.
    • HTML全文

  • 输电塔-线体系在国民生活中扮演着重要角色，而作为典型的风敏感结构极易受到下击暴流等强风的威胁[1-2]。据相关数据统计，在美国、澳大利亚和南非等国家与气象有关的输电线路故障中，有80%以上是由下击暴流等强风引起的[3]。在我国，2005年6月，江苏泗阳发生特大飑线风灾，致华东电网“任上5237线”10基输电塔发生连续性倒塌[4]。2007年7月发生在河南的下击暴流致郑祥线6基输电塔倒塌[5]，造成了重大的社会经济损失。下击暴流区别于良态风的风速特性，使得输电塔在两者下的响应规律和失效特征存在差异，而现行的建筑规范和标准对下击暴流等强风少有涉及，因此，开展输电塔-线体系在下击暴流作用下的倒塌破坏研究，对提高输电塔抗下击暴流能力和保证电网安全具有重要意义[6]。

    近年来，国内外在输电塔抗下击暴流方面的研究趋于活跃。国外：Shehata等[7-8]基于CFD数值模拟生成下击暴流风场，以弹性和静态的方式开展了输电塔在下击暴流作用下的失效倒塌分析；Savory等[9]利用Holmes经验模型生成下击暴流风荷载时程，采用隐式直接积分法研究了输电塔的失效模式；Damatty等[10]研究了不同的下击暴流参数如相对位置、攻角和大小对输电塔内力的影响。国内：吉柏锋等[11]以输电塔一竖向主杆为研究对象，重现了其弹塑性失稳全过程，在此基础上对整体结构进行了倒塌破坏分析；王昕等[12]研究发现，下击暴流脉动成分在输电塔失效分析中不可忽略；魏文晖等[13]提出了一种能量法用于判定输电塔在下击暴流下的失效倒塌时刻，并通过分析发生塑性变形杆件的应力和空间分布研究了输电塔的失效倒塌机理。

    在现有研究的基础上，本文利用ABAQUS建立某“一塔两线”三维有限元模型，采用确定性-随机性混合模型(deterministic-stochastic hybrid model)模拟下击暴流风场，基于Tian-Ma-Qu本构模型开展下击暴流作用下输电塔的倒塌破坏分析，为输电塔抗下击暴流设计提供参考依据。

    1   输电塔-线体系有限元模型

    本文以某1000 kV特高压交流输变电线路的SZ30101JD型直线塔为研究对象，建立“一塔两线”三维有限元模型。直线塔总高87.3 m，呼高45 m，主要采用Q345和Q420钢管制成，图1给出了该直线塔的平面尺寸与杆件构成。输电线路挡距400 m，导、地线型号分别为8×JL1/LHA1-465/210和OPGW-185。

    图  1  直线塔的平面尺寸与杆件构成　/mm
    Figure  1.  Dimension and configuration of the suspension tower
    下载: 全尺寸图片 幻灯片

    图2所示为在ABAQUS中建立的该塔-线体系有限元模型，其中，输电塔采用B31梁单元进行模拟，输电线和绝缘子均采用T3D2桁架单元进行模拟，钢材的弹性模量、屈服强度、质密度和泊松比分别取值为2.01×1011 Pa，345 MPa (Q345)、420 MPa (Q420)，7800 kg/m3和0.3。输电塔与输电线的阻尼比分别取值为2%与1%。通过模态分析得到，考虑输电线影响的直线塔在纵向、横向的一阶自振频率分别为0.970 Hz与0.922 Hz。

    图  2  “一塔两线”三维有限元模型　/m
    Figure  2.  Finite element model of transmission tower-line system
    下载: 全尺寸图片 幻灯片

    2   下击暴流风荷载模拟

    2.1   下击暴流风荷载模拟原理

    本文首先采用Chen和Letchford提出的确定性-随机性混合模型[14]生成下击暴流风速时程，然后基于准定常假设计算作用于结构上的下击暴流风荷载。由于下击暴流竖向风速仅存在于雷暴中心周围较小范围内，并随离中心距离迅速减小，故本文不作考虑。

    将不同空间位置点处的下击暴流风速表达为平均风速与脉动风速之和，如式(1)所示。

    U(z,t)=ˉU(z,t)+u(z,t) (1)

    式中：U(z,t)为z高度处t时刻的总风速；ˉU(z,t)为移动平均风速；u(z,t)为脉动风速。

    对于平均风速，将其表达为竖向风速剖面与时间函数的乘积，如式(2)所示。

    ˉU(z,t)=V(z)×f(t) (2)

    式中：V(z)为最大平均风速的竖向风剖面；f(t)为时间函数，反映下击暴流平均风速随时间的变化。

    最大平均风速的竖向风剖面采用Vicroy模型，其表达式如式(3)所示。

    V(z)=1.22×[e(−0.15zzmax (3)

    式中：zmax为下击暴流最大水平风速对应的高度；Umax为下击暴流在竖向剖面的最大水平风速。

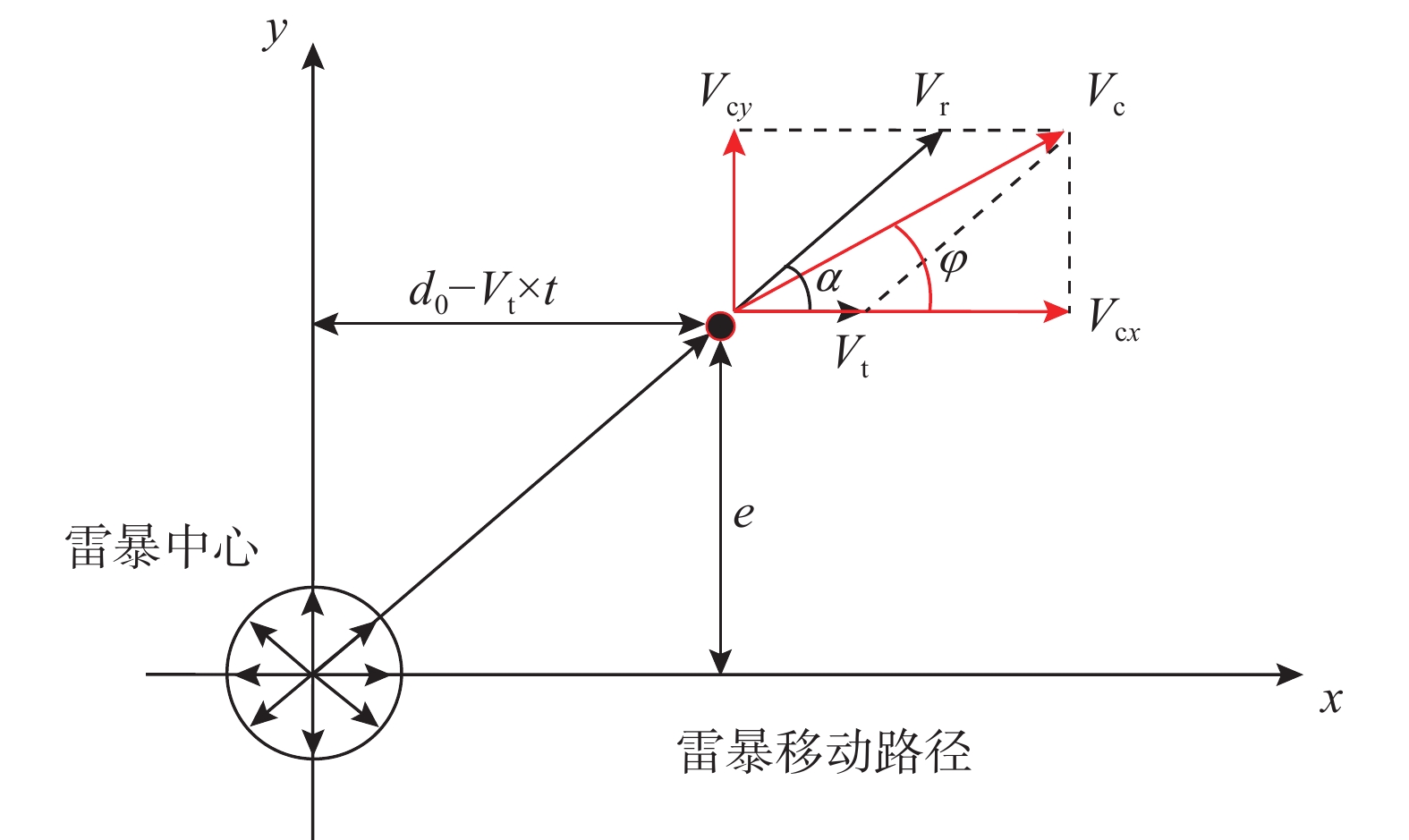
    f(t)由任意时刻的平均风速与最大平均风速的比值得到，如式(4)所示。

    f(t) = \frac{{|{V_{\rm c}}(t)|}}{{\max |{V_{\rm c}}(t)|}} (4)

    式中，下击暴流风场中任意位置处的平均风速Vc(t)等于径向风速Vr(t)和雷暴移动速度Vt的矢量和，如式(5)所示。

    {V_{\rm c}}(t) = {V_{\rm r}}(t) + {V_{\rm t}} (5)

    Vr(t)采用Holmes等[15]提出的考虑时间衰减的下击暴流径向风速剖面模型，如式(6)所示。

    {V_{\rm r}}(t) = \left\{ \begin{aligned} & {V_{{\text{r}},\max }} \cdot {{\text{e}}^{ - t/T}} \cdot \left( {r/{r_{\max }}} \right),\;\;\;\;\;\;\;\;\;\;0 \leqslant r < {r_{\max }}\\& {V_{{\text{r}},\max }} \cdot {{\text{e}}^{ - t/T}} \cdot {{\text{e}}^{ - {{\left[ {(r - {r_{\max }})/{R_{\text{r}}}} \right]}^2}}},\;\;\;r \geqslant {r_{\max }} \end{aligned} \right. (6)

    式中：r为t时刻空间点与雷暴中心的距离；Vr,max为最大径向射流速度；rmax为取得Vr,max时的位置距雷暴中心的径向距离；Rr为特征半径；T为下击暴流持续时间。

    图3为下击暴流平均风速的合成示意图，雷暴沿着x轴正方向移动引起与观测点相对位置的变化，观测点处径向风速方向不断改变，故合成风速方向也随时间变化，径向风速与移动方向的夹角为：

    \alpha (t) = \arccos \left(\frac{{{d_0} - {V_{\rm t}} \times t}}{{\sqrt {{e^2} + {{({d_0} - {V_{\rm t}} \times t)}^2}} }}\right) (7)

    将组合风速Vc(t)矢量表示为Vc(t)=[Vcx(t), Vcy(t)]，Vc(t)与雷暴运动轨迹之间的夹角记为φ(t)，则：

    \left\{ \begin{aligned} & {V_{{\rm c}x}}(t) = {V_{\rm t}} + {V_{\rm r}}(t)\cos \alpha (t) \\& {V_{{\rm c}y}}(t) = {V_{\rm r}}(t)\sin \alpha (t) \end{aligned} \right. (8)
    \varphi (t) = \arccos ({V_{{\rm c}x}}(t)/|{V_{\rm c}}(t)|) (9)
    图  3  下击暴流平均风速合成示意图
    Figure  3.  Vector diagram of average wind speed of downburst
    下载: 全尺寸图片 幻灯片

    对于脉动风速，假定其频域特性不变，将脉动风速时程表达为以平均风速为基准并且随时间变化的调制函数和给定功率谱的稳态高斯过程乘积的形式，如式(10)所示。

    u({\textit{z}},t) = \alpha ({\textit{z}},t) \times k({\textit{z}},t) (10)

    式中：α(z,t)为调制函数；k(z,t)为一个服从标准正态分布的平稳高斯随机过程，采用线性滤波法模拟生成，其自功率谱密度函数采用单位化的Davenport谱，空间相关系数采用Shiotami建议的仅与两点间距离有关的简单表达式。

    依据准定常假设和美国输电线路结构荷载导则(ASCE NO. 74-2009)[16]，下击暴流过程中作用于输电塔横向(x向)和纵向(y向)的风荷载根据式(11)计算。

    \left\{ \begin{aligned} & {F_x} = 0.5\rho {U^2}{\cos ^2}\varphi {C_x}{S_x} \\& {F_y} = 0.5\rho {U^2}{\sin ^2}\varphi {C_y}{S_y} \end{aligned}\right. (11)

    式中：ρ为空气密度，取1.226 kg/m3；Cx和Cy分别为x、y方向阻力系数；Sx和Sy分别为输电塔各段x、y方向有效迎风面积。

    作用于导线和地线上的风荷载根据式(12)计算。

    {F_{\rm c}} = 0.5\rho {U^2}{\cos ^2}\varphi {C_{\rm f}}{A_{\rm c}} (12)

    式中：Fc为导线或地线上的风荷载并垂直输电线方向；Cf为阻力系数，取1.0；Ac为迎风面积。

    2.2   塔-线体系风荷载时程模拟

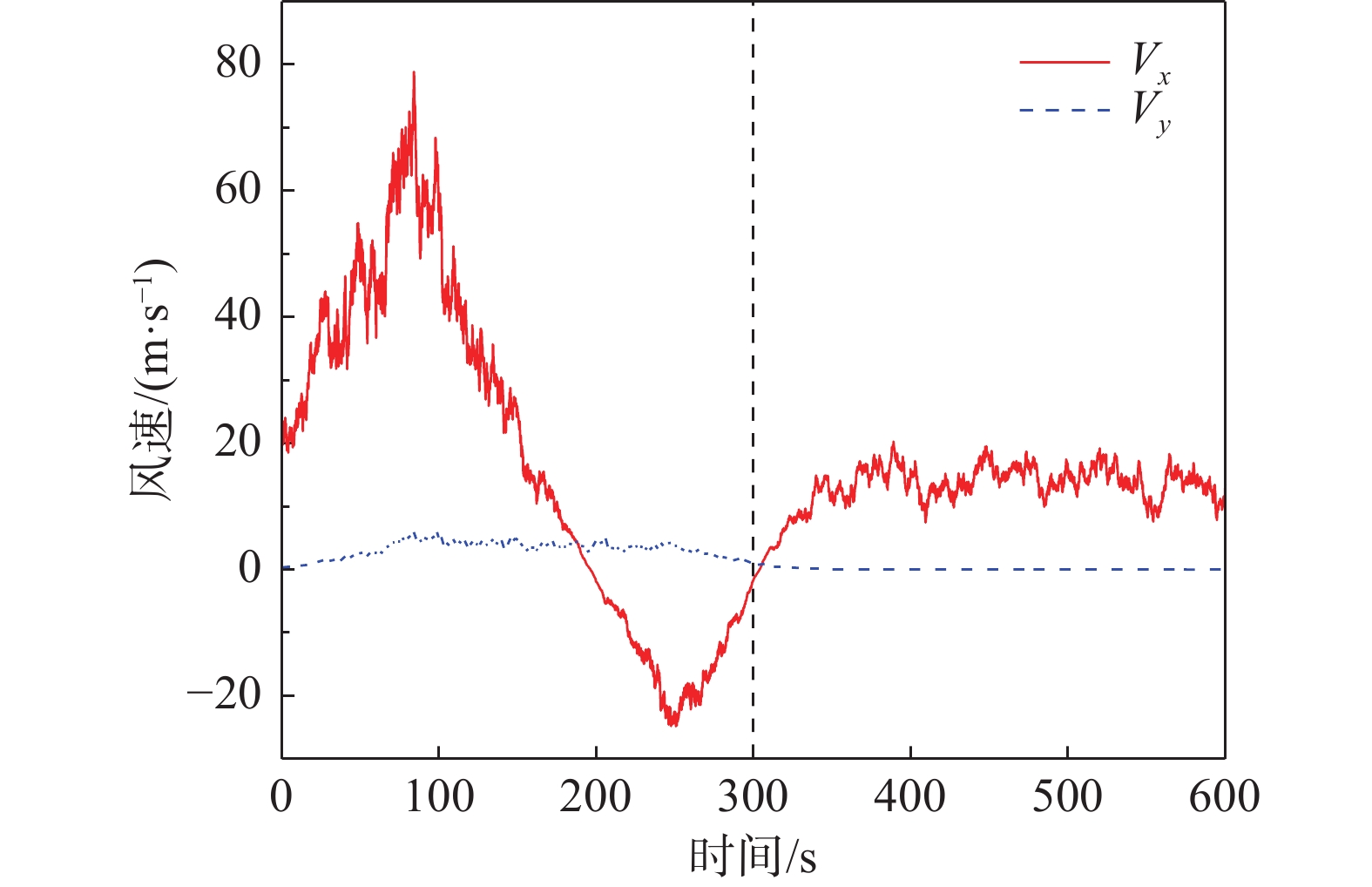
    假设输电塔-线体系与下击暴流的相对位置如图4所示，坐标原点位于雷暴中心并随着下击暴流沿垂直于输电线路的路径移动，输电塔的初始位置坐标为(2000，100)。假设一典型下击暴流过程，取Umax=60 m/s，zmax=70 m，Rr=700 m，rmax=1000 m，Vr,max=47 m/s，Vt=12 m/s，T=600 s。图5所示为塔身66.5 m高度处模拟点的下击暴流风速时程，可以看出，前300 s内，x方向风速随时间发生剧烈波动，并在80 s左右达到峰值，y方向风速远小于x方向并维持在一定范围；300 s后，x向风速约为12 m/s，与雷暴移动速度几乎相同，y向风速趋近于0，说明雷暴中心已经通过了输电塔。基于以上考虑，本文取前300 s风速时程用于后续动力分析。

    图  4  输电塔-线体系与下击暴流相对位置图　/m
    Figure  4.  Relative position between the transmission tower-line system and downburst
    下载: 全尺寸图片 幻灯片
    图  5  塔身66.5 m处模拟点下击暴流风速时程
    Figure  5.  Time history of wind speed at height of 66.5 m
    下载: 全尺寸图片 幻灯片

    为方便风荷载的施加，将输电塔分为10节段(见图1)，每跨输电线分为4段，该塔-线体系下击暴流风荷载模拟点如图4中点儿所示，所有模拟点在同一个y平面上，并对应各自的空间位置坐标。

    3   下击暴流致输电塔倒塌破坏机理研究

    3.1   本构模型和倒塌准则

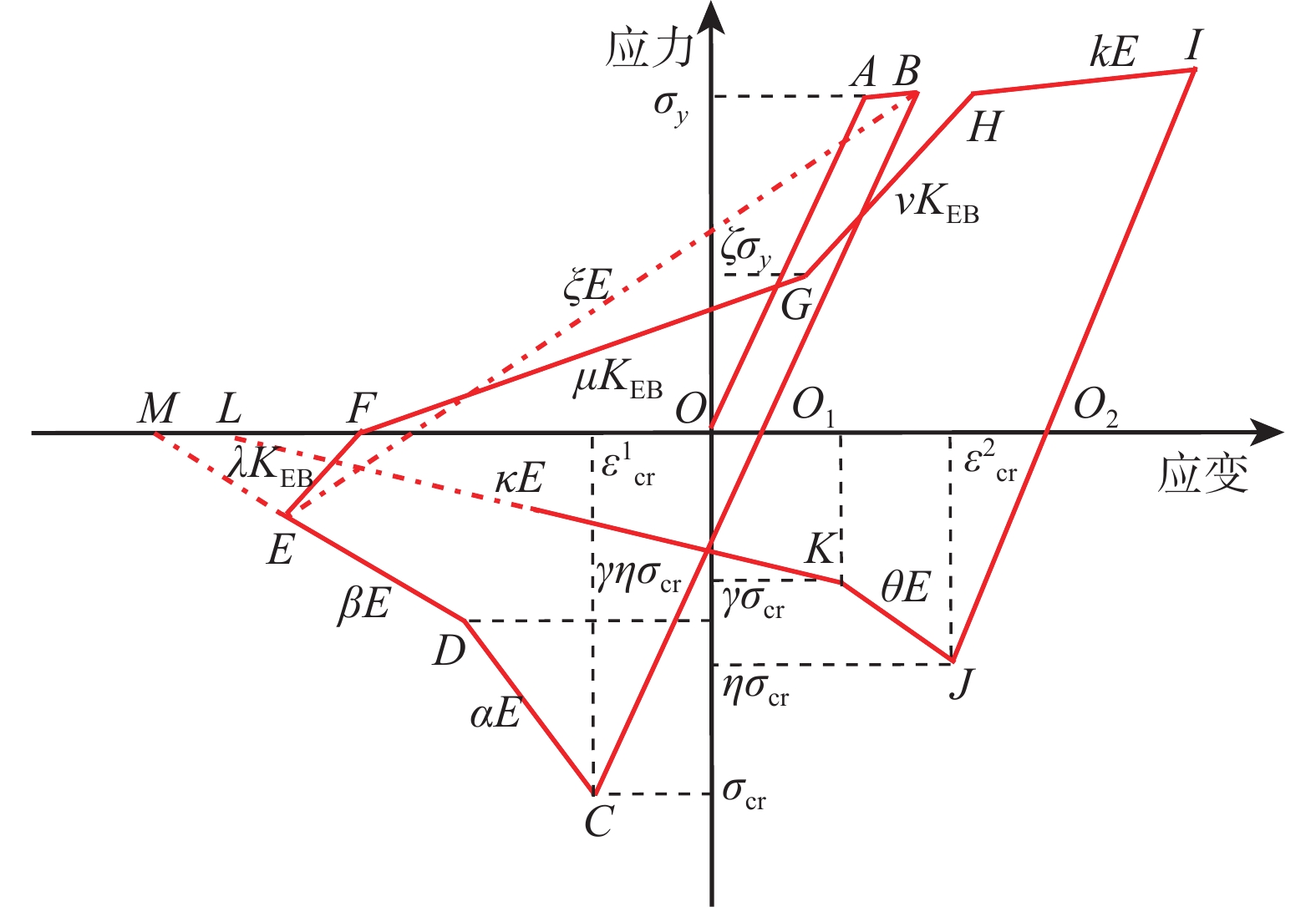
    采用Tian-Ma-Qu本构模型[17]来模拟钢材的本构关系，如图6所示。该模型将材料的力学性能分为以下几个阶段：弹性受拉阶段OA、塑性强化阶段AB和HI，受拉卸载阶段BO1和IO2，受压加载阶段O1C和O2J，初始屈曲阶段CDE，受压卸载阶段EF，受拉加载段FGH。该模型能够准确地捕捉钢材的非线性行为，较好地模拟塔-线体系在强风下倒塌时钢材的力学行为。通过用户子程序VUMAT将Tian-Ma-Qu模型关联到ABAQUS中，用于本文的倒塌模拟。

    图  6  Tian-Ma-Qu本构模型
    Figure  6.  Tian-Ma-Qu material model
    下载: 全尺寸图片 幻灯片

    在倒塌分析中引入输电塔的塔顶水平位移作为指标来量化破坏程度。倒塌准则定义[18]为：在荷载输入完成后，当塔顶水平位移急剧增加或出现发散时，可认为结构完全倒塌。

    3.2   结构倒塌模拟

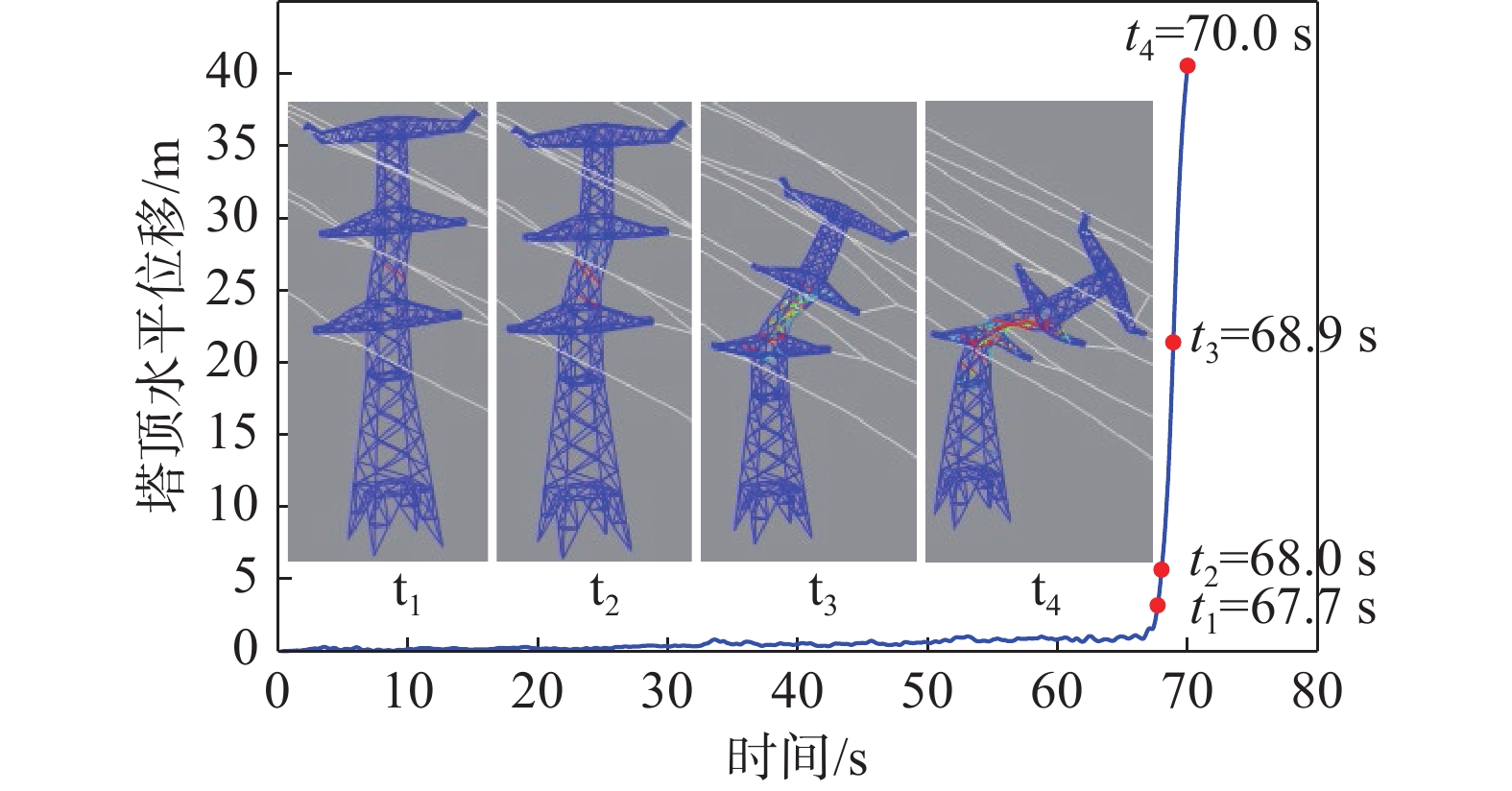
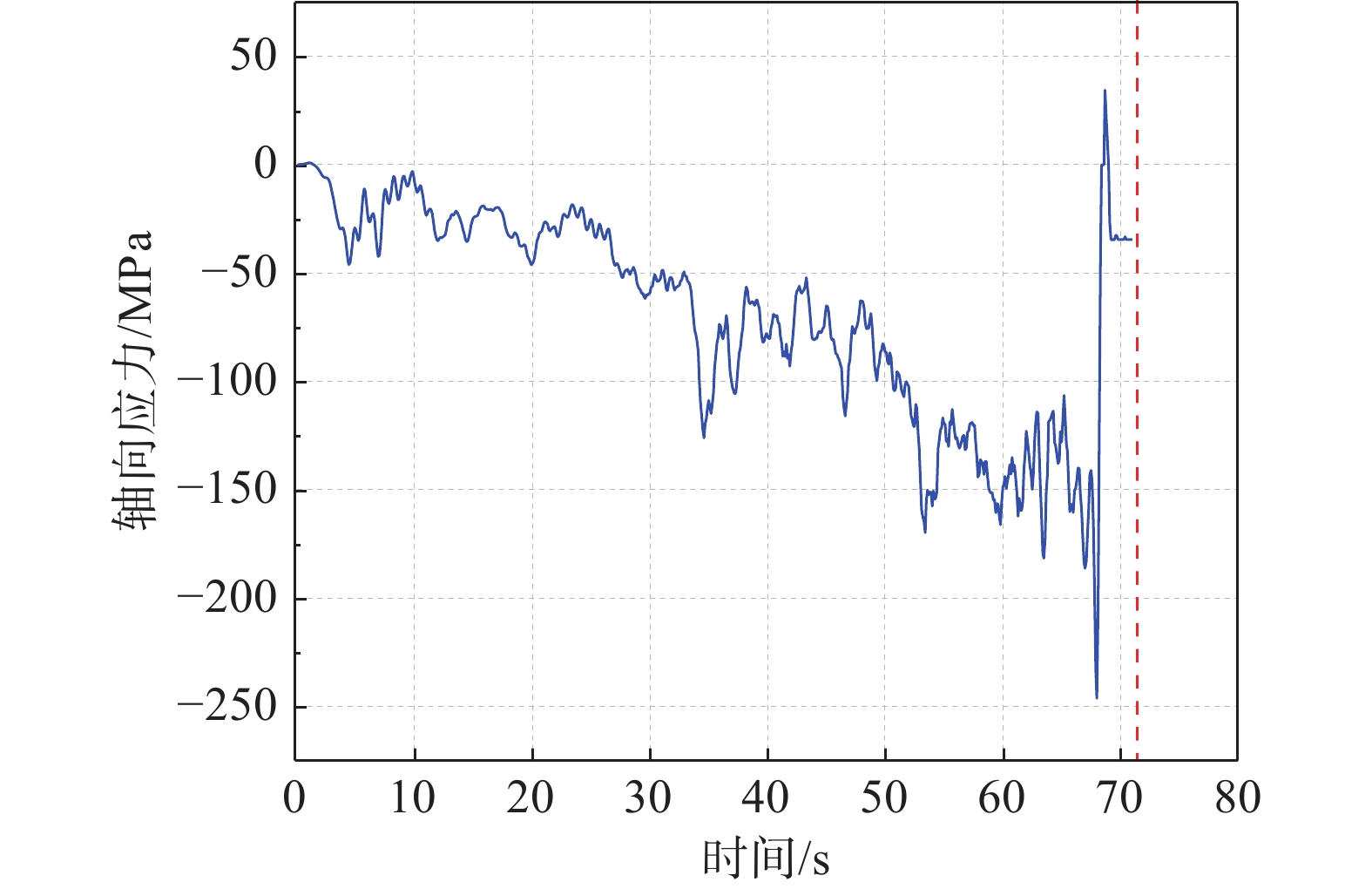
    基于Tian-Ma-Qu本构模型采用显式动力分析方法模拟输电塔-线体系在下击暴流作用下的连续倒塌过程，研究输电塔的倒塌机理、破坏特点及薄弱部位。图7为输电塔在连续倒塌过程中的塔顶水平位移时程曲线和特定时刻变形图，由屈曲引起的失效杆件在图中以红色突出显示。在初始阶段，输电塔保持完好状态，所有杆件处于弹性工作状态；当t=67.7 s时，位于第六节间的两根斜材(杆件编号488和500)同时出现失稳，图8给出了杆件488的轴向应力时程图，从图中可以看出，该杆件屈曲后的承载能力迅速降低，导致输电塔内力重分布；当t=68.0 s时，附近斜材相继发生屈曲破坏，塔体出现了轻微的变形；当t=68.9 s时，大量杆件失效，并迅速传递到第五节间和第七节间，塔顶水平位移表现出明显的发散现象；当t=70.0 s时，输电塔腰部弯折，分析中断，输电塔完全倒塌。

    图  7  塔顶水平位移时程曲线和特定时刻变形图
    Figure  7.  Time-history curves of the tip displacement and deformed shape of the tower at specific time points
    下载: 全尺寸图片 幻灯片
    图  8  杆件488轴向应力时程图
    Figure  8.  Axial force time-history curve of element488
    下载: 全尺寸图片 幻灯片

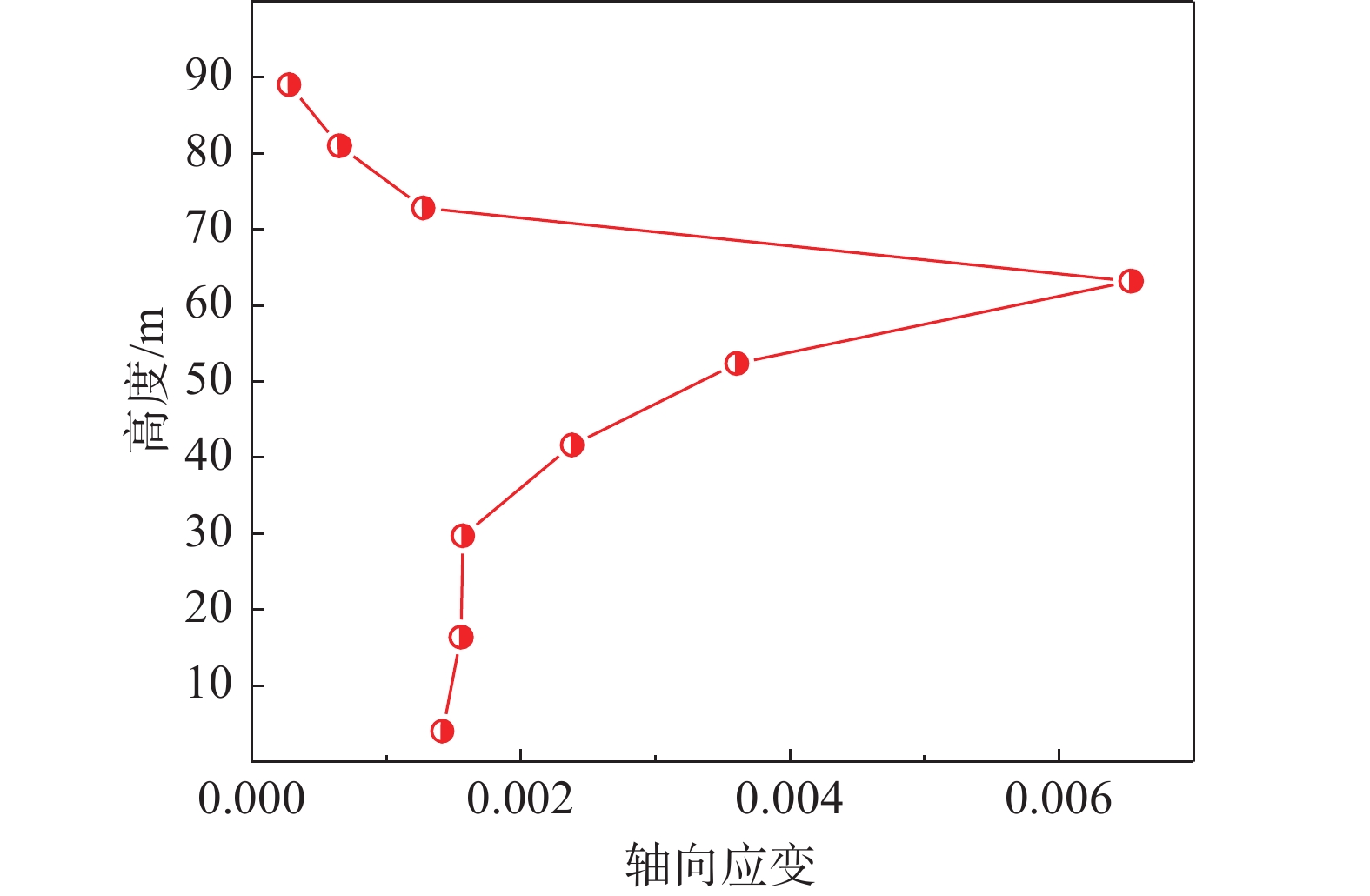
    塔身主材轴向应变和节点位移的最大值沿高度分布分别如图9、图10所示，可以看出，塔身中上部和中下部的交接部位沿高度存在轴向应变和位移的突变；其余部位呈现出中上部结构小变形、大位移和中下部结构大变形、小位移的破坏特点。此外，输电塔的破坏非常迅速，从杆件开始屈曲到输电塔完全倒塌发生在短短2 s~3 s内。

    分析结果表明：典型下击暴流对输电塔-线体系有很强的破坏力，尤其是输电线的强烈舞动通过绝缘子传递给塔身很大的内力，局部大量斜材和少量主材相继屈曲是导致输电塔发生整体倒塌的主要原因。随着雷暴强度的增加，输电塔杆件内力和变形迅速增加，最先发生失稳破坏的是第六节间的斜腹杆，杆件屈曲后的承载能力迅速降低，导致输电塔内力重分布，附近杆件的应力迅速增加；随后，破坏情况逐渐向上和向下扩展，失效杆件逐渐增多；最后，塔体主要受力杆和斜杆出现大范围破坏，塔身产生明显的局部变形，输电塔-线体系发生倒塌。

    图  9  轴向应变峰值沿高度分布图
    Figure  9.  Peak axial strain along the height of the tower
    下载: 全尺寸图片 幻灯片
    图  10  位移峰值沿高度分布图
    Figure  10.  Peak displacement along the height of the tower
    下载: 全尺寸图片 幻灯片

    整体而言，下击暴流下输电塔表现为突发性的局部大变形，该区域大量斜材和少量主材相继发生失稳破坏；引起输电塔-线体系发生倒塌的薄弱部位是离地40 m~70 m的塔身区段，该区域承受的下击暴流风荷载相对较强，在结构抗下击暴流设计中应重点关注。

    4   结论

    本文建立了输电塔-线体系的有限元模型，采用确定性-随机性混合模型生成下击暴流风场，基于Tian-Ma-Qu本构模型模拟了该结构在下击暴流作用下的连续倒塌过程，研究了输电塔的倒塌机理、破坏特点以及薄弱部位。得到以下结论：

    (1) 基于Tian-Ma-Qu本构模型开展了下击暴流下输电塔的倒塌分析。研究发现，输电线的强烈舞动引起大量斜材和少量主材相继发生屈曲是输电塔倒塌的主要原因。

    (2) 下击暴流下输电塔的破坏特点为突发性的局部大变形，具体表现为：沿高度塔身腰部存在轴向应变和位移突变，中上部结构小变形大位移和中下部结构大变形小位移以及突发性倒塌。

    (3) 输电塔的初始失效杆件多数分布在第六节间，引起输电塔-线体系发生倒塌的薄弱部位是离地40 m~70 m的塔身区段，在结构抗下击暴流设计中应重点关注。

  • 图  1   直线塔的平面尺寸与杆件构成　/mm

    Figure  1.   Dimension and configuration of the suspension tower

    下载: 全尺寸图片 幻灯片

    图  2   “一塔两线”三维有限元模型　/m

    Figure  2.   Finite element model of transmission tower-line system

    下载: 全尺寸图片 幻灯片

    图  3   下击暴流平均风速合成示意图

    Figure  3.   Vector diagram of average wind speed of downburst

    下载: 全尺寸图片 幻灯片

    图  4   输电塔-线体系与下击暴流相对位置图　/m

    Figure  4.   Relative position between the transmission tower-line system and downburst

    下载: 全尺寸图片 幻灯片

    图  5   塔身66.5 m处模拟点下击暴流风速时程

    Figure  5.   Time history of wind speed at height of 66.5 m

    下载: 全尺寸图片 幻灯片

    图  6   Tian-Ma-Qu本构模型

    Figure  6.   Tian-Ma-Qu material model

    下载: 全尺寸图片 幻灯片

    图  7   塔顶水平位移时程曲线和特定时刻变形图

    Figure  7.   Time-history curves of the tip displacement and deformed shape of the tower at specific time points

    下载: 全尺寸图片 幻灯片

    图  8   杆件488轴向应力时程图

    Figure  8.   Axial force time-history curve of element488

    下载: 全尺寸图片 幻灯片

    图  9   轴向应变峰值沿高度分布图

    Figure  9.   Peak axial strain along the height of the tower

    下载: 全尺寸图片 幻灯片

    图  10   位移峰值沿高度分布图

    Figure  10.   Peak displacement along the height of the tower

    下载: 全尺寸图片 幻灯片
    • 参考文献(18)
  • [1] 刘慕广, 王树彬, 谢壮宁, 等. 基于位移测量的输电塔等效静风荷载研究[J]. 工程力学, 2017, 34(4): 160 − 166. doi: 10.6052/j.issn.1000-4750.2015.10.0869

    Liu Muguang, Wang Shubin, Xie Zhuangning, et al. Equivalent static wind load of transmission tower based on displacement measurement [J]. Engineering Mechanics, 2017, 34(4): 160 − 166. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.10.0869
    [2] 刘俊才, 田利, 张睿, 等. 远场地震作用下输电塔-线体系最不利输入方向预测研究[J]. 工程力学, 2020, 37(增刊 1): 97 − 103. doi: 10.6052/j.issn.1000-4750.2019.05.S014

    Liu Juncai, Tian Li, Zhang Rui, et al. Study on the prediction of the most adverse input direction of transmission tower-line system under far-field seismic ground motions [J]. Engineering Mechanics, 2020, 37(Suppl 1): 97 − 103. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.05.S014
    [3]

    Dempsey D, White H B. Winds wreak havoc on lines [J]. Transmission & Distribution World, 1996, 48(6): 32 − 37.
    [4] 谢强, 张勇, 李杰. 华东电网500 kV任上5237线飑线风致倒塔事故调查分析[J]. 电网技术, 2006, 30(10): 59 − 63. doi: 10.3321/j.issn:1000-3673.2006.10.012

    Xie Qiang, Zhang Yong, Li Jie. Investigation on tower collapse of 500 kV Renshang 5237 transmission line caused by downburst [J]. Power System Technology, 2006, 30(10): 59 − 63. (in Chinese) doi: 10.3321/j.issn:1000-3673.2006.10.012
    [5]

    Fu D, Yang F, Li Q, et al. Simulations for tower collapses of 500kV Zhengxiang transmission line induced by the downburst [C]// 2010 International Conference on Power System Technology: Technological Innovations Making Power Grid Smarter, Hangzhou, China: IEEE, 2010.
    [6] 姚旦, 沈国辉, 潘峰, 等. 基于向量式有限元的输电塔风致动力响应研究[J]. 工程力学, 2015, 32(11): 63 − 70. doi: 10.6052/j.issn.1000-4750.2013.08.0795

    Yao Dan, Shen Guohui, Pan Feng, et al. Wind-induced dynamic response of transmission tower using vector-form intrinsic finite element method [J]. Engineering Mechanics, 2015, 32(11): 63 − 70. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.08.0795
    [7]

    Shehata A Y, Damatty A, Savory E. Finite element modeling of transmission line under downburst wind loading [J]. Finite Elements in Analysis & Design, 2006, 42(1): 71 − 89.
    [8]

    Shehata A Y, Damatty A. Failure analysis of a transmission tower during a microburst [J]. Wind & Structures an International Journal, 2008, 11(3): 193 − 208.
    [9]

    Savory E, Parke G, Zeinoddini M. Modelling of tornado and microburst-induced wind loading and failure of a lattice transmission tower [J]. Engineering Structures, 2001, 23(4): 365 − 375. doi: 10.1016/S0141-0296(00)00045-6
    [10]

    Damatty A E, Elawady A. Critical load cases for lattice transmission line structures subjected to downbursts: Economic implications for design of transmission lines [J]. Engineering Structures, 2018, 159(15): 213 − 226.
    [11] 吉柏锋, 瞿伟廉, 王亮, 等. 下击暴流作用下输电塔弹塑性失稳倒塌研究[J]. 中国安全科学学报, 2014, 24(12): 90 − 95.

    Ji Baifeng, Qu Weilian, Wang Liang, et al. Elastic-plastic buckling collapse analysis of transmission tower under downburst [J]. China Safety Science Journal, 2014, 24(12): 90 − 95. (in Chinese)
    [12]

    Wang X, Lou W J, Li H N, et al. Wind-induced dynamic response of high-rise transmission tower under downburst wind load [J]. Journal of Zhejiang University(Engineering Science), 2009, 43(8): 1520 − 1525.
    [13] 魏文晖, 周翔, 邓晨, 等. 基于能量法的下击暴流作用下输电塔线体系失效倒塌研究[J]. 建筑科学与工程学报, 2020, 37(6): 73 − 80.

    Wei Wenhui, Zhou Xiang, Deng Chen, et al. Research on failure and collapse of transmission tower line system under downburst action based on energy method [J]. Journal of Architecture and Civil Engineering, 2020, 37(6): 73 − 80. (in Chinese)
    [14]

    Chen L, Letchford C W. A deterministic-stochastic hybrid model of downbursts and its impact on a cantilevered structure [J]. Engineering Structures, 2004, 26(5): 619 − 629. doi: 10.1016/j.engstruct.2003.12.009
    [15]

    Holmes J D, Oliver S E. An empirical model of a downburst [J]. Engineering Structures, 2000, 22(9): 1167 − 1172. doi: 10.1016/S0141-0296(99)00058-9
    [16]

    American Society of Civil Engineers. ASCE NO. 74-2009, Guidelines for electrical transmission line structural loading [S]. Reston, USA: Library of Congress Cataloging-in-Publication Data, 2009.
    [17]

    Tian L, MA R S, Pan H Y, et al. Progressive collapse analysis of long-span transmission tower-line system under multi-component seismic excitations [J]. Advances in Structural Engineering, 2017, 20: 1920 − 1932. doi: 10.1177/1369433217700426
    [18] 清华大学, 中国建筑科学研究. CECS 392: 2014, 建筑结构抗倒塌设计规范 [S]. 北京: 中国计划出版社, 2014.

    Tsinghua University, China Academy of Building Research. CECS 392: 2014, Code for anti-collapse design of building structures [S]. Beijing: China Planning Publishing House, 2014. (in Chinese)
    • 相关文章
    • 施引文献(21)

  • 期刊类型引用(11)

    1. 杨子烨，王梦薇，匡春霖，施伟国，何畅. 强风作用下110 kV换向分支杆风振响应和薄弱位置分析. 南方能源建设. 2025(02): 48-57 . 百度学术
    2. 李正良，王邦杰，王涛. 考虑山地风场效应的耐张型悬索支撑输电结构风振响应分析. 工程力学. 2025(06): 93-104 . 本站查看
    3. 于佳宝，卓越，张佳毅，郑翀，曹枚根. 海岛大跨越输电塔线体系风振响应及动力失稳分析. 山东电力技术. 2024(01): 1-10+23 . 百度学术
    4. 汪大海，王国强，王昕，孙启刚，杨庆山，黄国庆，杨军永. 下击暴流风冲击作用下输电塔非平稳动力响应的频域方法. 工程力学. 2024(08): 152-163 . 本站查看
    5. 韩承永，吴磊，胡晨，王静峰，胡培芳，刘用. 下击暴流作用下羊角型输电塔的风振动力响应与倒塌破坏分析. 建筑钢结构进展. 2024(08): 78-86 . 百度学术
    6. 周琦，王振华. 输电塔风致倒塌破坏研究进展. 南方能源建设. 2024(06): 59-68 . 百度学术
    7. 张思祥，国震，马震，张思遥，田利. 雷诺数为10000时航空警示球对输电线的气动特性影响研究. 自然灾害学报. 2024(06): 118-129 . 百度学术
    8. 南东敏，杨会伟，王树勇，高东阳. 局部构件失效对输电塔结构的影响分析. 电力学报. 2024(05): 446-456 . 百度学术
    9. 张石，杨庆山，徐晓达. 基于北京市区实测数据的雷暴风风场时空统计特性研究. 工程力学. 2023(06): 193-203 . 本站查看
    10. 吴昊，陈勇，楼文娟. 输电塔线体系下击暴流风致倒塌研究. 低温建筑技术. 2023(08): 1-5 . 百度学术
    11. 张旭耀，李对，寇海霞，杨从新，李泽，王倩玉. 下击暴流不同高度水平最大风速对风力机气动载荷的影响. 太阳能学报. 2023(10): 370-375 . 百度学术

    其他类型引用(10)

    • 资源附件(0)
图(10)
计量
  • 文章访问数:  547
  • HTML全文浏览量:  125
  • PDF下载量:  73
  • 被引次数: 21
出版历程
  • 收稿日期:  2021-05-28
  • 修回日期:  2022-02-16
  • 网络出版日期:  2022-02-28
  • 刊出日期:  2022-06-05

目录

摘要
HTML全文

  • 1   输电塔-线体系有限元模型

  • 2   下击暴流风荷载模拟

  • 2.1   下击暴流风荷载模拟原理

  • 2.2   塔-线体系风荷载时程模拟

  • 3   下击暴流致输电塔倒塌破坏机理研究

  • 3.1   本构模型和倒塌准则

  • 3.2   结构倒塌模拟

  • 4   结论

参考文献(18)
相关文章
施引文献(21)
资源附件(0)

/

返回文章
返回

京ICP备18030614号

版权所有 © 《工程力学》编辑部

地址：北京清华大学新水利馆114室邮政编码：100084

电话：(010)62788648传真：021-64253812电子信箱：gclxbjb@tsinghua.edu.cn

本系统由北京仁和汇智信息技术有限公司开发  百度统计