历次地震灾害显示，桥梁、建筑等工程结构的钢筋混凝土(RC)柱在强震作用下可能发生弯曲破坏、弯剪破坏或剪切破坏，影响工程结构的安全性^[1-3]。因此，有必要识别RC柱地震破坏模式的重要特征参数，并建立地震破坏模式的判别方法。

目前，RC柱的地震破坏模式判别方法主要有经验判别法和机器学习判别法两大类。其中，经验判别法基于工程经验或试验数据分析，建立位移延性系数^[4]、剪跨比^[5]、抗剪需求与抗剪承载力比^[6]等特征参数与地震破坏模式之间的关系。例如，文献[7]综合考虑剪跨比、轴压比、纵筋特征参数和箍筋特征参数的影响，提出了RC柱地震破坏模式的经验判别指标；文献[8]根据抗剪需求与抗剪承载力比、剪跨比、箍筋间距与截面有效高度比来综合判别RC柱的地震破坏模式。分析表明：经验判别法具有简便实用的优点，但通常是基于工程经验或试验数据相关性分析建立的，导致特征参数与地震破坏模式之间缺乏内在联系，判别准确率不高^[9]。机器学习判别法结合试验数据和各种机器学习算法，构建特征参数与地震破坏模式之间的联系^[10]。其中，文献[11]采用随机森林算法判别RC柱的地震破坏模式；文献[12]对比分析了6种机器学习算法对于RC柱地震破坏模式的判别精度；文献[13]结合机器学习的回归算法和分类算法，建立了RC柱的地震破坏模式判别方法。然而，上述机器学习判别法存在以下缺陷：一是所建立的判别模型虽然可以构建输入特征参数与输出破坏模式之间的映射关系，但是没有建立二者之间的显式函数表达式，属于“黑盒”模型^[11-14]；二是建模过程中没有遴选特征参数，通常将全部特征参数作为模型输入变量，导致所建立的判别模型复杂程度高、计算效率低^[15]；三是难以定量分析输入特征参数对输出破坏模式的影响程度，导致模型的可解释性差。因此，有必要合理遴选RC柱地震破坏模式的最优特征参数，并建立具有明确函数表达式且简便实用的地震破坏模式判别模型。

鉴于此，本文首先基于穷举搜索策略，分别遴选了判别弯曲破坏与非弯曲破坏以及弯剪破坏与剪切破坏的最优特征参数；然后结合最优特征参数和逻辑回归算法，建立了RC柱地震破坏模式判别的两阶段逻辑回归模型(即先判别弯曲破坏和非弯曲破坏，然后判别弯剪破坏和剪切破坏)；最后通过与经典逻辑回归算法和传统经验判别方法进行对比分析，验证了该模型的有效性。

1   地震破坏模式判别的逻辑回归算法

对于第i条RC柱的地震破坏模式数据集${{\boldsymbol{D}}} = \left\{ {{{x}_i},{y_i}} \right\}$$\left(i=1,2,\cdots,m\right)$。其中：${y_i}$为第i条RC柱对应的类标签，通常利用数字1或0来分别表示${y_i}$为特定类和非特定类，即${y_i} \in \left\{ {0,1} \right\}$；${{{\boldsymbol{x}}}_i} = ( {x_i^{\left( 1 \right)},x_i^{\left( 2 \right)}, \cdots ,x_i^{\left( n \right)}} )$为第i条RC柱的n维特征参数向量(如剪跨比、轴压比、箍筋特征参数、纵筋特征参数等)；m和n分别表示地震破坏模式样本的组数和特征个数。基于逻辑回归算法^[16]，第i条RC柱属于特定类的概率为：

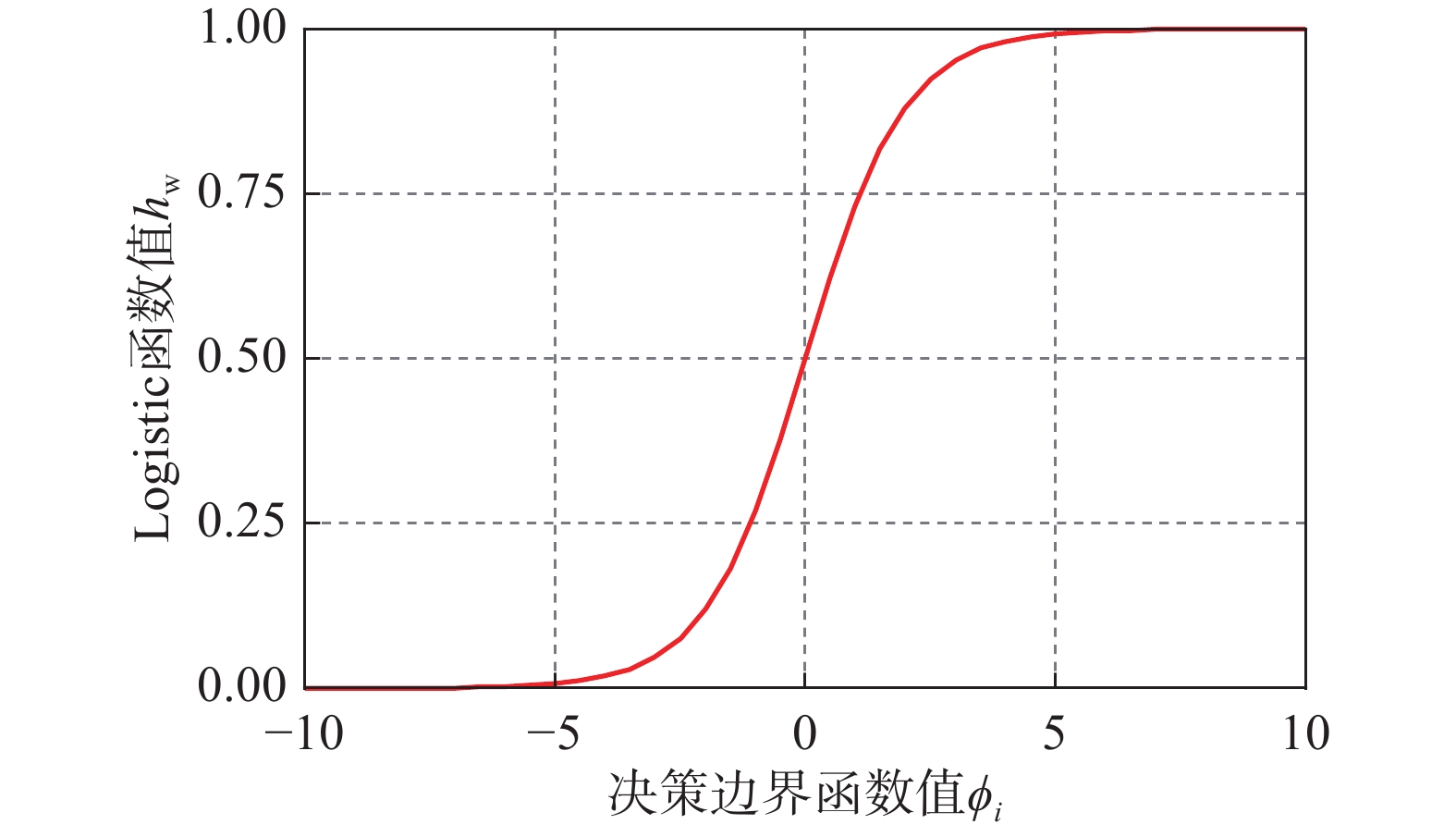
式中：$p({y_i} = 1{\left| {{\boldsymbol{x}}} \right._i})$为第i条RC柱属于特定类的概率；${\phi _i} = {{{\boldsymbol{w}}}^{\rm{T}}}{{{\boldsymbol{x}}}_i} + b$为第i条RC柱的决策边界函数；${{\boldsymbol{w}}^{{\rm{T}}} } = {\left( {{w_1},{w_2}, \cdots ,{w_n}} \right)^{{\rm{T}}} }$为特征权值向量，表征n维特征参数对分类结果的影响程度；$b$为偏置；${h_{{\rm{w}}}}({\phi _i})$为Logistic函数，可将$\left( { - \infty , + \infty } \right)$区间范围内的决策边界函数${\phi _i}$值转换为$\left( {0,1} \right)$区间范围内的概率值，其函数曲线如图1所示。

图  1  Logistic函数曲线

Figure  1.  Curve of Logistic function

下载: 全尺寸图片 幻灯片

根据逻辑回归模型^[17]，判断第i条RC柱属于特定类的几率可以定义为第i条RC柱属于与不属于特定类的概率之比。因此，由式(1)可知，第i条RC柱属于特定类的对数几率${R_{\rm{p}}}$为：

根据逻辑回归模型^[17]，当第i条RC柱属于特定类的概率大于非特定类的概率(即${R_{\rm{p}}} > 0$)时，判定类标签${y_i} = 1$；当第i条RC柱属于特定类的概率小于非特定类的概率(${R_{\rm{p}}} < 0$)时，判定类标签${y_i} = 0$。

为了求解式(2)中的参数${{\boldsymbol{w}}}$和$b$，假定m组地震破坏模式样本之间相互独立，根据式(1)可以构造逻辑回归模型的极大似然估计函数$L({\boldsymbol{w}},b)$^[18]：

进一步地，取$L({\boldsymbol{w}},b)$的对数的相反数，可以定义$L({\boldsymbol{w}},b)$的平均对数损失函数$J({\boldsymbol{w}},b)$^[17]：

根据逻辑回归模型^[17]，模型预测值与样本观测值之间的偏差$J({\boldsymbol{w}},b)$越小表明模型预测精度越高。因此，可以将确定RC柱地震破坏模式判别模型的最优参数$\hat {\boldsymbol{w}}$和$\hat b$的问题描述为：

式(5)为关于参数${{\boldsymbol{w}}}$和$b$的高阶可导连续凸函数。根据凸优化理论^[19]，基于梯度下降法和牛顿法等经典数值优化算法可以确定最优参数$\hat{\boldsymbol{ w}}$和$\hat b$，进而根据式(2)可以判别任意第i条RC柱的地震破坏模式。

2   基于穷举搜索策略的最优特征参数遴选

影响RC柱地震破坏模式的特征参数较多，包括抗剪需求与抗剪承载力比(V_p/V_n)、箍筋间距与截面有效高度比(s/h₀)、纵筋特征参数、箍筋特征参数、剪跨比和轴压比等^{[5-8, 20-21]}。然而，不同特征参数对RC柱地震破坏模式的影响程度存在明显差异。因此，本文首先基于穷举搜索策略，分别遴选了判别弯曲破坏与非弯曲破坏以及弯剪破坏与剪切破坏的最优特征参数。

2.1   地震破坏模式判别的原始特征参数

国内外学者围绕RC柱地震破坏模式的特征参数分析开展了广泛研究。其中，文献[7]研究分析了纵筋特征参数(α_l=ρ_l f_yl /$f_c'$)、轴压比(n)、箍筋特征参数(α_v=ρ_v f_yv /f_t)和剪跨比(a/h₀)对RC柱的地震破坏模式的影响，发现随着α_l和n的增大，或者α_v和a/h₀的减小，RC柱的地震破坏模式逐渐从弯曲破坏向弯剪或剪切破坏转变；文献[8]研究表明：箍筋间距与截面有效高度比(s/h₀)对RC柱的地震破坏模式具有显著影响，随着s/h₀的增大，RC柱的地震破坏模式逐渐由弯曲破坏向弯剪破坏和剪切破坏转变；文献[20]研究了α_l和a/h₀对RC柱地震破坏模式的影响，发现随着α_l增大或a/h₀减小，RC柱的地震破坏模式逐渐由弯曲破坏向剪切破坏转变；文献[5]研究发现剪跨比与RC柱的地震破坏模式具有较强相关性，对于高、中和低剪跨比，RC柱依次发生弯曲破坏、弯剪破坏和剪切破坏；文献[6]认为抗剪需求与抗剪承载力比(V_p/V_n)与RC柱的地震破坏模式密切相关，V_p/V_n越大，RC柱越容易发生剪切破坏；文献[21]分析发现，RC柱的地震破坏模式与V_p/V_n和a/h₀密切相关，V_p/V_n越大，RC柱越容易发生剪切破坏，而当V_p/V_n较小且a/h₀较大时，RC柱容易发生弯曲破坏和弯剪破坏；这里，ρ_l和ρ_v分别为配筋率和配箍率，f_yl和f_yv分别为纵筋和箍筋的屈服强度，$f_{\rm c}'$和f_t分别为混凝土圆柱体抗压强度和混凝土抗拉强度，a为剪跨，h₀为截面有效高度，s为箍筋间距，V_p为抗剪需求，V_n为抗剪承载力。综上所述，V_p/V_n、s/h₀、α_l、α_v、a/h₀和n对RC柱的地震破坏模式具有重要影响。因此，本文将上述6个特征参数选取为RC柱地震破坏模式的原始特征参数。由于上述特征参数均为无量纲量，所以可以排除量纲的影响。

为了分析上述6个特征参数对RC柱地震破坏模式的影响规律，本文从国内外文献[7, 21-42]中收集了270组矩形截面RC柱的破坏试验数据，基本信息见表1。综合考虑参考文献中报道的破坏模式、RC柱的裂缝分布形态、滞回曲线以及破坏过程中箍筋和纵筋的屈服状态等因素确定了上述270组RC柱的破坏模式。绘制不同地震破坏模式下各特征参数的半小提琴图，如图2所示。图2中，半小提琴左侧为频率分布图，右侧为小提琴图，小提琴外部形状为核密度估计图，中间白点表示均值，黑线表示标准差范围。由图2可知，当RC柱的地震破坏模式由弯曲破坏向弯剪破坏转变、由弯剪破坏向剪切破坏转变时，V_p/V_n的均值增加率分别为85.5%和32.4%，s/h₀的均值增加率分别为40.7%和44.7%，α_l的均值增加率分别为20.8%和24.1%，α_v的均值减小率分别为43.7%和25.9%，a/h₀的均值减小率分别为30.7%和30.3%，n的均值减小率和增大率分别为2.8%和4.5%。由此可见，随着特征参数V_p/V_n、s/h₀和α_l的增大，以及α_v和a/h₀的减小，RC柱的地震破坏模式逐渐由弯曲破坏逐渐向弯剪破坏和剪切破坏转变，但是不同特征参数的变化趋势不同，说明不同特征参数对地震破坏模式的影响程度存在差异。因此，有必要从地震破坏模式的原始特征参数中遴选出RC柱地震破坏模式的最优特征参数。

表  1  270组RC柱试验数据的基本信息

Table  1.  Basic information of experimental data of 270 RC columns

参考文献	试件 数量	$f_{\rm{c}}'/{\rm{MPa} }$	fyv /MPa	fyl /MPa	ρl/(%)	ρv/(%)	Vp/Vn	s/h0	αl	αv	a/h0	n
[7]	10	44	347	365	2.34	0.33~0.66	0.61~1.10	0.30~0.60	0.20	0.31~0.62	2.42~5.14	0.19~0.48
[21]	11	32	367~371	414	1.57~2.36	0.14~0.78	0.45~1.33	0.28	0.20~0.30	0.16~0.90	2.79~4.51	0.14~0.43
[22]	178	16~118	249~1424	318~587	1.01~6.03	0.07~2.24	0.08~1.79	0.11~1.27	0.06~0.51	0.08~3.82	0.56~8.90	0.00~0.80
[23]	4	31	392	402	1.69~2.65	0.11~0.21	1.23~1.61	0.39~0.78	0.23~0.35	0.14~0.27	2.34~2.35	0.20~0.30
[24]	2	20	476	345	2.00	0.28	0.59~0.74	0.62	0.35	0.54	3.12	0.10~0.20
[25]	3	13~14	524	324~372	1.00	0.13	0.83~0.91	0.60	0.25~0.28	0.33~0.34	2.39	0.23~0.24
[26]	2	31~35	455	374~450	2.45	0.32	0.56~0.70	0.25	0.27~0.36	0.44~0.47	1.73	0.00~0.19
[27]	2	31	392	409	1.69	0.14~0.21	1.22~1.37	0.41~0.62	0.23	0.18~0.27	2.47	0.20
[28]	4	20~23	364	363	2.53	0.52~0.65	0.95~1.03	0.23~0.43	0.40~0.45	0.70~0.94	2.29	0.20~0.33
[29]	1	45	425	434	1.95	0.10	1.32	0.63	0.19	0.11	3.11	0.15
[30]	2	26	400	335	2.00~3.00	0.10~0.17	1.53~1.58	0.77~1.15	0.26~0.39	0.14~0.24	1.86~1.87	0.28
[31]	4	34	273	370	3.03~3.53	0.10~0.30	0.91~1.76	0.22~1.86	0.33~0.39	0.08~0.25	1.61~3.38	0.40~0.65
[32]	2	27	375	380	2.68	0.19	1.53~1.66	0.39	0.38	0.25	1.76	0.18~0.27
[33]	3	14~18	384	340	1.69	0.28	1.02~1.14	0.30	0.32~0.43	0.46~0.53	1.82	0.20~0.30
[34]	4	28	242	384	1.90	0.34	0.77~1.06	0.42	0.26	0.28	2.51	0.00~0.11
[35]	4	32~36	270~273	370~433	3.03~3.53	0.16~0.29	0.97~1.78	0.22~0.62	0.35~0.41	0.13~0.25	1.61~3.38	0.40~0.45
[36]	3	26	398	340~447	1.69~2.26	0.43~0.85	0.82~1.21	0.20	0.22~0.39	0.60~1.18	1.21~1.82	0.23
[37]	3	25	392	350~396	1.77~2.68	0.19	1.45~1.93	0.39	0.25~0.42	0.26	1.18	0.19~0.29
[38]	11	14~28	384~587	340~447	1.69~2.26	0.08~0.43	0.95~1.76	0.19~0.62	0.27~0.43	0.19~0.60	1.17~2.25	0.15~0.30
[39]	6	23~30	393	408	2.05	0.13~0.18	1.08~1.65	0.28-0.40	0.28-0.37	0.17-0.24	1.89~2.75	0.04~0.46
[40]	2	18~21	362	536	0.99	0.07	1.08~1.14	1.13	0.25-0.29	0.10-0.11	4.51	0.20~0.40
[41]	8	23~28	430~458	438	3.10	0.24~1.27	0.22~1.70	0.23~0.45	0.49-0.58	0.39-1.97	0.56~1.13	0.09~0.30
[42]	1	29	500	320	2.05	0.13	1.41	0.40	0.22	0.21	1.94	0.35
注：$f_c'$为混凝土的圆柱体抗压强度；fyv为箍筋屈服强度；fyl为纵筋屈服强度；ρl为配筋率；ρv为配箍率；Vp/Vn为抗剪需求与抗剪承载力比；s/h0为箍筋间距与截面有效高度比；αl为纵筋特征参数；αv为箍筋特征参数；a/h0为剪跨比；n为轴压比。

下载: 导出CSV 

| 显示表格

图  2  对应不同地震破坏模式时各特征参数的半小提琴图

Figure  2.  Half violin plot of characteristic parameters for different failure modes

下载: 全尺寸图片 幻灯片

2.2   RC柱地震破坏模式的最优特征参数

根据穷举搜索策略^[15]，对于包含n个原始特征参数的RC柱地震破坏模式原始特征参数集${{\boldsymbol{a}}} = \left\{ {{a_1},{a_2}, \cdots ,{a_n}} \right\}$，存在$k = {2^n} - 1$个非空特征参数候选子集${{{\boldsymbol{a}}}_k}$。为了从k个特征参数候选子集中遴选最优特征参数子集${\hat {\boldsymbol{a}}}$，引入特征子集评价函数$f\left( {{\boldsymbol{a}_k}} \right)$，将最优特征参数子集${\hat {\boldsymbol{a}}}$的遴选问题描述为以下最优化问题：

式中，子集评价函数$f\left( {{{{\boldsymbol{a}}}_k}} \right)$为地震破坏模式判别模型的性能评价指标(如总体判别准确率)。通过式(6)，可以从k个候选特征参数子集中，遴选出地震破坏模式判别模型的性能评价指标最优时对应的特征参数子集，进而可以遴选出RC柱地震破坏模式的最优特征参数。需要说明的是，式(6)的最优化问题涉及到两阶段求解：第一阶段是计算子集评价函数$f\left( {{{{\boldsymbol{a}}}_k}} \right)$的取值，其关键是确定式(5)中的最优参数$\hat {\boldsymbol{w}}$和$\hat b$，采用的算法为梯度下降法和牛顿法；第二阶段是在2ⁿ−1个特征子集对应的子集评价函数$f\left( {{{{\boldsymbol{a}}}_k}} \right)$中选取最大值，采用的是简单排序算法。值得注意的是，穷举搜索策略属于完全搜索策略，能克服其他启发式搜索策略(如序列前向选择和序列后向选择等)陷入局部最优的弊端，适用于最优特征参数遴选问题。

3   最优特征参数遴选与地震破坏模式判别模型

由于在强烈地震作用下RC柱可能发生弯曲破坏、弯剪破坏和剪切破坏，所以RC柱的地震破坏模式判别属于多分类问题。然而，传统的逻辑回归模型属于二分类模型^[15]，所以无法直接用于RC柱的地震破坏模式判别。因此，本文提出了RC柱地震破坏模式判别的两阶段逻辑回归模型：第一阶段逻辑回归模型判别RC柱是否发生弯曲破坏或非弯曲破坏(包括弯剪破坏和剪切破坏)；第二阶段逻辑回归模型进一步针对非弯曲破坏类别判别RC柱发生弯剪破坏或剪切破坏。

3.1   两阶段地震破坏模式判别的最优特征参数

为了建立具有明确函数表达式且简便实用的RC柱地震破坏模式判别模型，基于穷举搜索策略，分别遴选了对应于第一阶段逻辑回归模型(判别弯曲破坏和非弯曲破坏)和第二阶段逻辑回归模型(判别弯剪破坏和剪切破坏)的最优特征参数。

为遴选第一阶段逻辑回归模型(判别弯曲破坏和非弯曲破坏)的最优特征参数，首先基于穷举搜索策略，利用由前述6个特征参数组成的原始特征参数集$\{ {{V_{\rm{p}}}{\text{/}}{V_{{\rm{n}}} },a{\text{/}}{h_0},s{\text{/}}{h_0},{\alpha _{{\rm{1}}} },{\alpha _{{\rm{v}}} },n} \}$生成${2^6} - 1 = 63$个特征参数候选子集；然后将逻辑回归模型的最高准确率指标作为确定最优特征参数子集的性能评价指标；最后基于第一阶段270组试验数据(弯曲破坏135组和非弯曲破坏135组)，结合十折交叉验证方法，确定第一阶段逻辑回归模型的最优特征参数子集，计算结果如图3(a)所示。由图3(a)可知，当候选特征参数子集编号k=15时(对应的特征参数子集为$\{ {{V_{\rm{p}}}{\text{/}}{V_{{\rm{n}}} },n} \}$)，逻辑回归模型达到最高判别准确率峰值点；随着k继续增加(与候选特征参数子集中特征参数数量增加保持一致)，模型判别准确率并不会明显提高，甚至反而有所降低。由此可见，第一阶段逻辑回归模型(判别弯曲破坏和非弯曲破坏)的最优特征参数子集为$\{ {{V_{\rm{p}}}{\text{/}}{V_{{\rm{n}}} },n} \}$。

为遴选第二阶段逻辑回归模型(判别弯剪破坏和剪切破坏)的最优特征参数，基于135组非弯曲破坏的试验数据(弯剪破坏62组、剪切破坏73组)，结合穷举搜索策略、逻辑回归算法和十折交叉验证方法，可以确定第二阶段的最优特征参数子集，计算结果如图3(b)所示。由图3(b)可知，当k<48时，逻辑回归模型的准确率整体上呈增大趋势，表明逻辑回归模型的判别性能受到了更多特征参数的影响；当候选特征参数子集编号k=48时(对应的特征参数子集为$\left\{ {a{\text{/}}{h_0},s{\text{/}}{h_0},{\alpha _{1} },{\alpha _{{\rm{v}}} }} \right\}$)，逻辑回归模型达到最高判别准确率，随着k的继续增大，逻辑回归模型的判别准确率无法得到明显提高，说明此时逻辑回归模型已达到最优判别性能。因此，第二阶段逻辑回归模型(判别弯剪破坏和剪切破坏)的最优特征参数子集为$\left\{ {a{\text{/}}{h_0},s{\text{/}}{h_0}, {\alpha _{1} }, {\alpha _{{\rm{v}}} }} \right\}$。

图  3  基于穷举搜索策略的最优特征参数遴选

Figure  3.  Selection of optimal characteristic parameters based on exhaustive search mechanism

下载: 全尺寸图片 幻灯片

综上所述，判别弯曲破坏与非弯曲破坏的最优特征参数为抗剪需求与抗剪承载力比和轴压比，而判别弯剪破坏与剪切破坏的最优特征参数为箍筋特征参数、纵筋特征参数、剪跨比、箍筋间距与截面有效高度比。

3.2   地震破坏模式判别的两阶段逻辑回归模型

当建立第一阶段逻辑回归模型(判别弯曲破坏和非弯曲破坏)时，对所收集的270组(弯曲破坏135组、弯剪破坏62组和剪切破坏73组)RC柱地震破坏模式试验数据进行分类，将非弯曲破坏划分为特定类(共135组数据)，将弯曲破坏划分为非特定类(共135组数据)，然后按照训练集与测试集的比例为7∶3将数据集进行分层随机抽样，最后以第一阶段所遴选的最优特征参数V_p/V_n和$n$作为输入变量，利用189组训练集样本数据(包括特定类95组和非特定类94组)，训练第一阶段逻辑回归模型：

根据式(7)，当${R_{{{\rm{p}}_1}}} < 0$时，表明RC柱发生非弯曲破坏的概率小于弯曲破坏的概率，则判别RC柱为弯曲破坏；当${R_{{{\rm{p}}_1}}} > 0$时，表明RC柱发生非弯曲破坏的概率大于弯曲破坏的概率，则判别RC柱为非弯曲破坏，进一步可以继续对该样本进行弯剪破坏和剪切破坏的判别。

当建立第二阶段逻辑回归模型(判别弯剪破坏和剪切破坏)时，将剪切破坏划分为特定类(共73组数据)，将弯剪破坏划分为非特定类(共62组数据)，然后按照训练集与测试集的比例为7∶3将数据集进行分层随机抽样，最后以第二阶段所遴选的最优特征参数a/h₀、s/h₀、$\alpha_{1}$和$\alpha_{{\rm{v}}}$为输入变量，利用94组训练集样本(包括特定类51组和非特定类43组)，训练第二阶段逻辑回归模型：

根据式(8)，当${R_{{{\rm{p}}_2}}} < 0$时，表明RC柱发生剪切破坏的概率小于弯剪破坏的概率，则判别RC柱为弯剪破坏；当${R_{{{\rm{p}}_2}}} > 0$时，表明RC柱发生剪切破坏的概率大于弯剪破坏的概率，则判别RC柱为剪切破坏。

需要说明的是，由式(7)和式(8)所建立的RC柱地震破坏模式两阶段逻辑回归模型具有以下几方面优势：一是构建了RC柱的特征参数与地震破坏模式之间的显式函数关系，克服了传统机器学习判别方法属于“黑盒”模型，导致预测结果解释性较差的缺陷；二是基于穷举搜索策略，通过合理遴选最优特征参数，在保证判别准确度的前提下简化了判别模型的函数形式，解决了传统机器学习判别方法存在的判别模型复杂程度高、计算效率低的问题；三是在两阶段逻辑回归模型的函数表达式中，其特征参数系数表征了各特征参数对地震破坏模式的影响程度。其中，系数的绝对值反映了影响程度的大小，而正负号则反映二者属于正相关和负相关。

4   对比验证分析

4.1   与经典逻辑回归算法的对比分析

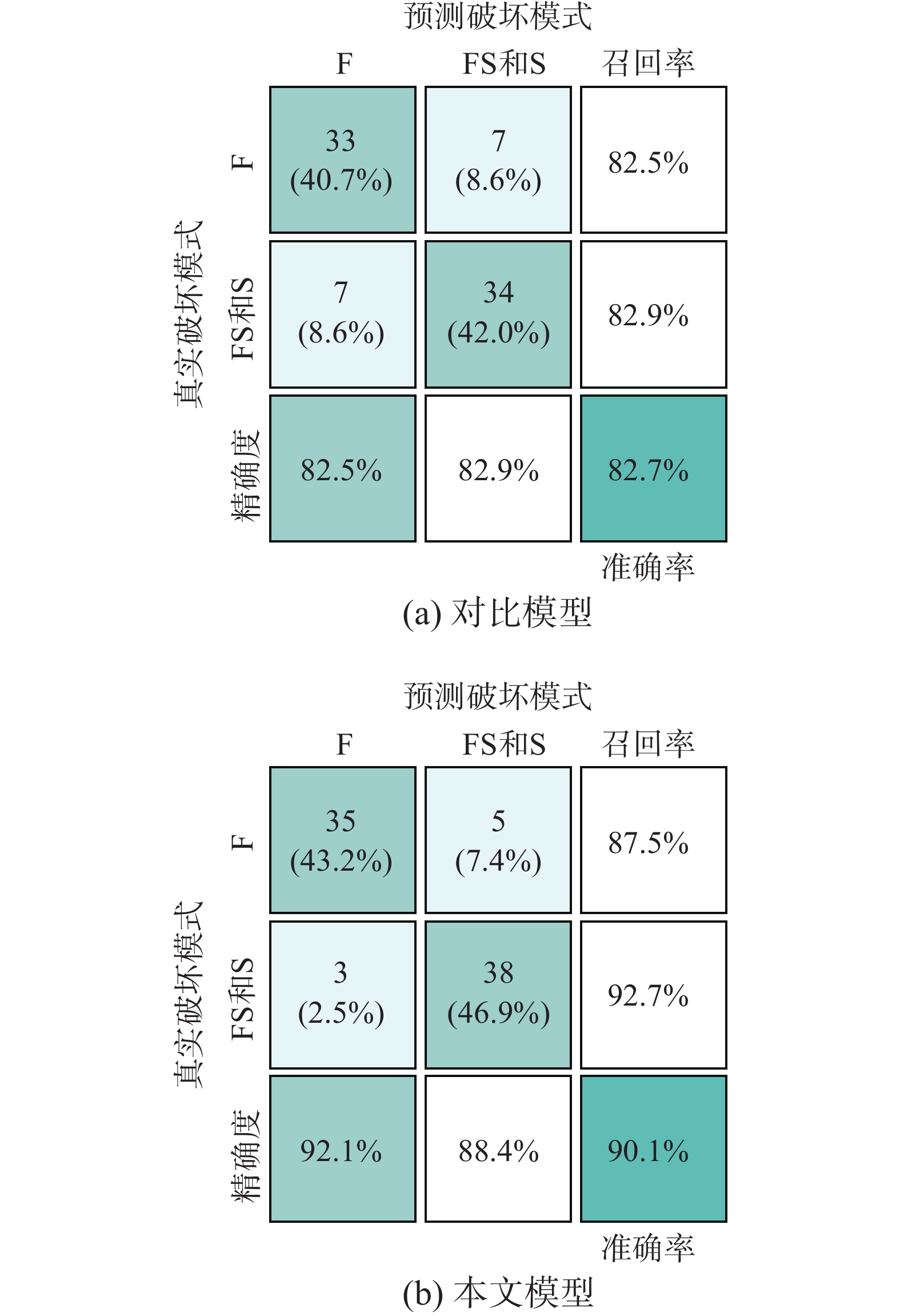
为验证本文模型的有效性，选取经典逻辑回归算法^{[15, 17]}进行对比分析。其中，经典逻辑回归算法基于原始特征参数建立两阶段逻辑回归判别模型(简称对比模型)，而本文模型基于最优特征参数建立两阶段逻辑回归判别模型(简称本文模型)。根据上述第一阶段和第二阶段判别的训练集样本数据，分别建立两个阶段的对比模型，其特征参数系数取值见表2。由表2可知，两个阶段的对比模型均与所有原始特征参数有关，所以两个阶段的对比模型均包含6个特征参数，其判别模型的函数形式均有7项，比式(7)和式(8)所描述的函数形式更加复杂。

表  2  对比模型的模型参数取值

Table  2.  Model parameters of comparative models

对比模型	Vp/Vn	a/h0	s/h0	αl	αv	n	b
第一阶段	8.97	−1.51	7.09	6.03	1.04	−1.93	−7.15
第二阶段	2.45	−3.06	14.28	11.53	−1.70	−2.34	−3.82
注：Vp/Vn为抗剪需求与抗剪承载力比；a/h0为剪跨比；s/h0为箍筋间距与截面有效高度比；αl为纵筋特征参数；αv为箍筋特征参数；n为轴压比；b为偏置。

下载: 导出CSV 

| 显示表格

根据训练集建立的第一阶段对比模型和本文模型，在测试集上的判别结果混淆矩阵如图4所示。图4中：F表示弯曲破坏，FS表示弯剪破坏，S表示剪切破坏；混淆矩阵左上角2×2矩阵中数字和百分比分别代表正确或错误判别样本的个数和比例；混淆矩阵的最后一行和最后一列分别为精确度和召回率，前者表示每一类预测结果中正确预测的样本所占的比例，后者表示每一类真实样本中正确预测的样本所占的比例，召回率和精确度越大，判别性能相对就越好，误判的样本就越少；混淆矩阵右下角的数字代表准确率，代表模型的总体判别准确度。由图4可知，对于弯曲破坏和非弯曲破坏，对比模型的正确判别数分别为33和34，而本文模型的正确判别数分别为35和38，说明对比模型对弯曲破坏和非弯曲破坏的样本数均发生较多的误判；对于弯曲破坏，对比模型的召回率和精确度均为82.5%，而本文模型的召回率和精确度分别为87.5%和92.1%；对于非弯曲破坏，对比模型的召回率和精确度均82.9%，而本文模型的召回率和精确度分别是92.7%和88.4%；由此可见，对于弯曲破坏和非弯曲破坏，本文模型的召回率和精度均明显优于对比模型；同时，对比模型的总体判别准确率是82.7%，而本文模型的总体判别准确率是90.1%，比对比模型提高9%左右，说明本文模型具有较高的判别准确率。

图  4  第一阶段判别结果混淆矩阵

Figure  4.  Confusion matrix of the 1st stage’s classification result

下载: 全尺寸图片 幻灯片

类似地，根据训练集建立的第二阶段本文模型和对比模型，在测试集上的判别结果混淆矩阵如图5所示。由图5可知，对于弯剪破坏和剪切破坏，对比模型的正确判别数分别为16和19，而本文模型的正确判别数分别为16和21，说明对比模型发生较多的误判；对于弯剪破坏，对比模型的召回率和精确度均为84.2%，而本文模型的召回率和精确度分别为84.2%和94.1%，说明本文模型的精确度更高；对于剪切破坏，对比模型的召回率和精确度均为86.4%，而本文模型的召回率和精确度分别是95.5%和87.5%，说明本文模型的召回率和精度均较好；同时，对比模型的总体判别准确率是85.4%，而本文模型的总体判别准确率是90.2%，比对比模型提高5%左右，说明本文模型具有较高的判别准确率。

图  5  第二阶段判别结果混淆矩阵

Figure  5.  Confusion matrix of the 2nd stage’s classification result

下载: 全尺寸图片 幻灯片

为了进一步综合对比分析本文模型和对比模型对于三种地震破坏模式的判别精度，计算三种地震破坏模式的F₁值，见表3。其中，F₁值定义为精确率P与召回率R的调和均值，综合考虑了精确率和召回率的影响，F₁值越大，说明判别精度越高。由表3可知，对于弯曲破坏、弯剪破坏和剪切破坏，对比模型的F₁值分别为0.83、0.84和0.86，而本文模型的F₁值分别为0.90、0.89和0.91，比对比模型均提高5%左右，说明对于三种地震破坏模式本文模型均具有更好的判别精度。

表  3  RC柱三种地震破坏模式的F₁值

Table  3.  F₁ score of three failure modes for RC column

判别模型	弯曲破坏	弯剪破坏	剪切破坏
对比模型	0.83	0.84	0.86
本文模型	0.90	0.89	0.91

下载: 导出CSV 

| 显示表格

4.2   与传统经验判别方法的对比分析

下面通过与五种传统经验判别方法(见表4)进行对比分析，以验证本文模型的有效性。对于所收集的270组RC柱地震破坏模式试验数据，五种传统经验判别方法(分别记为CM1~CM5)与本文模型的判别结果混淆矩阵如图6所示。

表  4  五种传统经验判别方法

Table  4.  Five traditional empirical classification methods

文献	简称	弯曲破坏	弯剪破坏	剪切破坏
[4]	CM1	$\mu > 6$	$2 < \mu \leqslant 6$	$\mu \leqslant 2$
[5]	CM2	$\lambda \geqslant 4$	$2 < \lambda < 4$	$\lambda \leqslant 2$
[6]	CM3	Vp/Vn≤0.6	1≥Vp/Vn>0.6	Vp/Vn>1
[7]	CM4	0<ω≤0.02	0.02<ω≤0.31	ω>0.31
[8]	CM5	ymax = y1	ymax = y2	ymax = y3
注：$\omega = 10( {n + 0.59} ){( {{{{\rho _{\text{l}}}{f_{{\text{yl}}}}}/ {{f_{\text{c}}}}}} )^2}{[ {{{( {\lambda + 0.5} )}^2} $$ ( {{{{\rho _{\text{v}}}{f_{{\text{yv}}}}} /{{f_{\text{t}}}}}} )} ]^{ - 1}}$；y1=−7.664χ+6.448λ+16.86m−19.455；y2=−0.168χ+4.942λ+21.232m−20.815；y3=−2.935χ+4.038λ+25.726m−23.226；χ=s/h0；m=Vp/Vn；ymax= max(y1, y2, y3)。

下载: 导出CSV 

| 显示表格

图  6  传统经验判别方法与本文模型的混淆矩阵

Figure  6.  Confusion matrix of traditional empirical methods and proposed model

下载: 全尺寸图片 幻灯片

由图6(a)可知，本文模型对于弯曲破坏的正确判别率、召回率和精确度分别为44.4%、88.9%和89.6%，对于弯剪破坏的正确判别率、召回率和精确度分别为16.7%、72.6%和71.4%，对于剪切破坏的正确判别率、召回率和精确度分别为23.7%、87.7%和87.7%，模型的总体判别准确率是84.8%，说明本文模型对三种地震破坏模式的判别效果均较好，对弯曲破坏、剪切破坏和弯剪破坏的召回率和精确度分别达到89%、88%和72%左右，说明对三种地震破坏模式产生的误判较少。由图6(b)可知，判别方法CM1对于弯曲破坏的正确判别率、召回率和精确度分别为17.0%、34.1%和90.2%，对于弯剪破坏的正确判别率、召回率和精确度分别为20.7%、74.2%和30.9%，对于剪切破坏的正确判别率、召回率和精确度分别为10.7%、39.7%和76.3%，模型的总体判别准确率是48.5%，说明判别方法CM1对弯曲破坏和剪切破坏样本的判别精确度相对较高，但是对弯剪破坏样本的判别精确度只有30%左右，而且对弯曲破坏和剪切破坏的召回率均不到40%，较多的弯曲破坏或剪切破坏样本被误判为弯剪破坏。由图6(c)可知，判别方法CM2对于弯曲破坏的正确判别率、召回率和精确度分别为27.0%、54.1%和83.0%，对于弯剪破坏的正确判别率、召回率和精确度分别为14.8%、64.5%和32.8%，对于剪切破坏的正确判别率、召回率和精确度分别为17.8%、65.8%和80.0%，模型的总体判别准确率是59.6%，说明判别方法CM2对弯曲和剪切破坏样本的判别精确度相对较高，但是对弯剪破坏样本的判别精确度仅为35%左右，而且对三种地震破坏模式的召回率都仅有60%左右，说明每一类地震破坏模式中都存在较多的样本被误判。由图6(d)可知，判别方法CM3对于弯曲破坏的正确判别率、召回率和精确度分别为20.4%、40.7%和80.9%，对于弯剪破坏的正确判别率、召回率和精确度分别为13.0%、56.5%和31.3%，对于剪切破坏的正确判别率、召回率和精确度分别为20.4%、75.3%和61.1%，模型的总体判别准确率是53.7%，说明判别方法CM3对弯曲破坏样本的判别精确度相对较高，但对弯剪破坏和剪切破坏样本的判别精确度都较低，分别为30%和60%左右，而且对弯曲破坏样本的召回率仅有40.0%左右，说明较多的弯曲破坏样本被误判为弯剪破坏或剪切破坏，对弯剪破坏的召回率也仅有60%左右，较多的弯剪破坏样本被误判为弯曲破坏或剪切破坏。由图6(e)可知，判别方法CM4对于弯曲破坏的正确判别率、召回率和精确度分别为20.4%、40.7%和98.2%，对于弯剪破坏的正确判别率、召回率和精确度分别为20.7%、90.3%和37.8%，对于剪切破坏的正确判别率、召回率和精确度分别为21.5%、79.5%和87.9%，模型的总体判别准确率是62.6%，说明判别方法CM4对弯曲破坏和剪切破坏样本的判别精确度相对较高，但对弯剪破坏样本判别精确度较低，而且对弯曲破坏的召回率仅有40%左右，较多的弯曲破坏样本被误判为剪切破坏或弯剪破坏。由图6(f)可知，判别方法CM5对于弯曲破坏的正确判别率、召回率和精确度分别为44.1%、88.1%和86.2%，对于弯剪破坏的正确判别率、召回率和精确度分别为15.6%、66.7%和43.8%，对于剪切破坏的正确判别率、召回率和精确度分别为11.5%、42.5%和86.1%，模型的总体判别准确率是71.1%，说明判别方法CM5对弯曲破坏和剪切样本的判别精确度相对较高，但对弯剪破坏样本的判别精确度较低，且对剪切破坏的召回率仅有40%左右，较多的剪切破坏样本被误判为弯曲破坏或弯剪破坏。

综上所述，五种传统的经验判别方法无法兼顾三种地震破坏模式的召回率。根据判别精确度可知，存在较多的弯曲破坏和剪切破坏样本被误判为弯剪破坏，从而导致判别准确率较低；而本文模型对于三种地震破坏模式都具有较高的召回率和判别精确度，相较于五种传统的经验判别方法，总体判别准确率提高20%左右。

对于多分类问题，除了采用以上准确率、精确率和召回率等性能评价指标外，可采用统计学中评估多分类一致性的Kappa系数^[43]进行评估：

式中：K_a为Kappa系数；p_o为与实际观测一致的百分比，即准确率；p_c为与理论期望一致的百分比，为每一类真实结果样本数占样本数的比例与预测结果样本数占样本数的比例的乘积之和。K_a的取值范围为[0, 1]，其一致性评价标准^[44]见表5。

本文模型与五种传统经验判别方法的K_a值见表6。由表6可知，判别方法CM1和CM3的K_a值分别为0.279和0.328，均属于[0.2, 0.4)区间取值范围内，表明该两种方法对三种地震破坏模式的判别效果较差，一致性等级评价较低，判别结果不具有实际参考价值；判别方法CM2、CM4和CM5的K_a值分别为0.400、0.469和0.539，属于[0.4, 0.6)区间取值范围内，表明该方法对三种地震破坏模式的判别准确率一般，一致性等级评价结果为中度一致性，判别结果具有一定的实际参考价值；本文模型的K_a值为0.757，属于[0.6, 0.8)区间取值范围内，表明本文方法预测结果大多数准确，一致性等级评价结果为高度一致性，具有较好的判别效果和实际参考价值。

表  5  Kappa系数一致性评价标准

Table  5.  Conformance evaluation criteria of Kappa coefficient

Ka	<0.2	[0.2, 0.4)	[0.4, 0.6)	[0.6, 8)	[0.8, 1]
一致等级评价	极低	较低	中度	高度	完全

下载: 导出CSV 

| 显示表格

表  6  不同判别方法的Kappa系数

Table  6.  Kappa coefficient of different classification methods

判别方法	CM1	CM2	CM3	CM4	CM5	本文模型
Ka	0.279	0.400	0.328	0.469	0.539	0.757

下载: 导出CSV 

| 显示表格

5   结论

基于穷举搜索策略和逻辑回归算法，提出了一种RC柱地震破坏模式判别的两阶段逻辑回归模型，并与传统判别方法进行了对比。分析结果表明：

(1)基于穷举搜索策略，遴选了RC柱地震破坏模式的最优特征参数。其中，判别RC柱发生弯曲破坏和非弯曲破坏的最优特征参数为V_p/V_n和轴压比，判别RC柱发生弯剪破坏和剪切破坏的最优特征参数为箍筋特征参数、纵筋特征参数、剪跨比和s/h₀。

(2)对于RC柱的三种地震破坏模式，本文模型对于三种地震破坏模式的判别准确率均达到90%以上，比经典逻辑回归算法的准确率提高5%左右，比传统经验判别方法的判别准确率提高20%左右。

(3)本文模型不仅构建了特征参数与地震破坏模式之间的显式函数关系，克服了传统机器学习判别方法属于“黑盒”模型，导致预测结果解释性较差的缺陷，而且通过合理遴选最优特征参数，在保证判别准确度的前提下简化了判别模型的函数形式，解决了传统机器学习判别方法存在的判别模型复杂程度高、计算效率低的问题。

(4)需要说明的是，本文方法具有广泛适用性，不仅适用于RC柱的地震破坏模式判别，同样也适用于其他三分类识别问题。