钢筋与混凝土的粘结锚固机理较为复杂，影响因素众多，针对钢筋与混凝土粘结强度的计算多为基于试验结果，采用统计分析的方式提出经验模型^[1-4]。由于该方法所建立的计算公式形式简单，易于设计人员和研究人员的使用，因此得到了广泛应用。基于一系列力学假定，采用平衡方程和协调方程建立用于确定钢筋与混凝土粘结强度的分析模型^[5-6]，是计算钢筋与混凝土粘结强度的另一途径。由于钢筋与混凝土粘结发生在混凝土内部，无法直接观测，因此很长一段时间内人们对钢筋与混凝土粘结机理的认识要晚于粘结试验的发展。Goto^[7]通过注入墨水的拉拔试验观察到了拉拔试件中的混凝土裂缝的产生和发展状态，首次揭示了变形钢筋与混凝土之间的粘接机理以及由于粘结作用导致局部裂缝的产生。Tepfers^[8]将带肋钢筋与混凝土的粘接问题视为以承受内压的厚壁圆筒，从弹性力学理论出发，结合不同状态截面的应力分布，求出了相应的粘结强度。Tepfers^[8]的方法为理论计算钢筋与混凝土的粘结强度提供了思路，但该方法假设部分开裂区域内的环向拉力为零，忽略了该区域对于径向压力的影响作用^[9]。部分学者对Tepfers^[8]模型中的开裂区域考虑因裂缝引起的混凝土软化^[10]，得到了若干综合考虑开裂区及未开裂区混凝土影响的钢筋与混凝土粘结强度理论计算方法^[11-14]，但已有的理论计算方法依然存在计算结果误差较大，及计算过程迭代分析复杂、耗时过长等缺陷。因此，可合理反应混凝土受力状态，且计算精度较好的钢筋与混凝土粘结强度理论计算方法亟待建立。

本文通过钢筋与混凝土拉式粘结试验，测试了高强度带肋钢筋与不同强度混凝土的粘结强度，分析了带肋钢筋与混凝土的粘结受力机理；基于弹性力学中的厚壁圆筒理论，采用断裂力学中的双线性软化本构对开裂区混凝土的应力状态进行描述，建立了综合考虑开裂区及未开裂区混凝土影响的粘结强度理论计算模型；研究了开裂区不同的径向位移分布对粘结强度的计算结果的影响，并将计算结果与试验结果进行对比，验证了计算模型的有效性。

1   试验概况

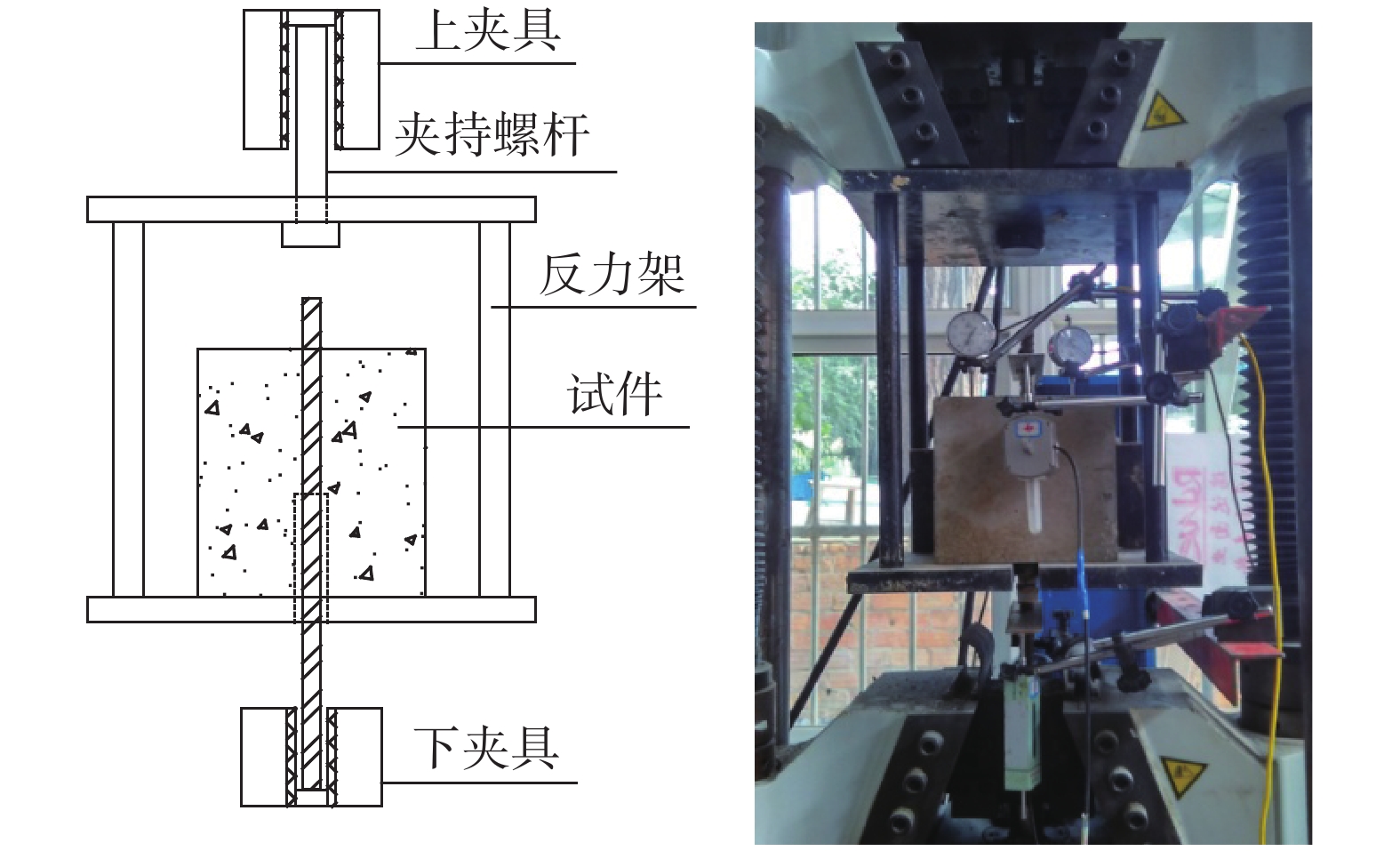
试验所用钢筋为强度等级630 MPa的热处理带肋高强钢筋。参照《混凝土结构试验方法标准》(GB 50152−92)^[15]制作和养护钢筋与混凝土拉式粘结试件，试件尺寸如图1所示。试件分为三组，每组6个试件，共18个试件。各组混凝土强度等级分别为C30、C40及C50，所有试件中钢筋公称直径均为16 mm，粘结长度均为7d(d为钢筋直径)。正式加载前对试件施加3 kN拉力，以保证试件和反力架紧密接触；预加载完成后，开始进行正式加载，先用力控制加载，加载速率为6 kN/min，加载至试件最大荷载的60%后采用位移加载，加载速率取为0.5 mm/min，直至加载结束。试验加载装置见图2，试验结果见表1所示。

图  1  试件尺寸　/mm

Figure  1.  Specimen size

下载: 全尺寸图片 幻灯片

图  2  加载装置

Figure  2.  Loading device

下载: 全尺寸图片 幻灯片

表  1  拉式粘结试验结果

Table  1.  Bond test results

试件编号	钢筋直径/mm	锚固长度/mm	保护层厚度/mm	混凝土抗压强度/MPa	混凝土抗拉强度/MPa	粘结强度均值/MPa	粘结强度标准差/MPa
T16-7d-C30	16	115	92	40.69	3.03	18.65	3.41
T16-7d-C40	16	115	92	50.32	3.41	24.94	1.83
T16-7d-C50	16	115	92	56.02	3.62	25.79	1.52

下载: 导出CSV 

| 显示表格

2   钢筋与混凝土粘结破坏机理

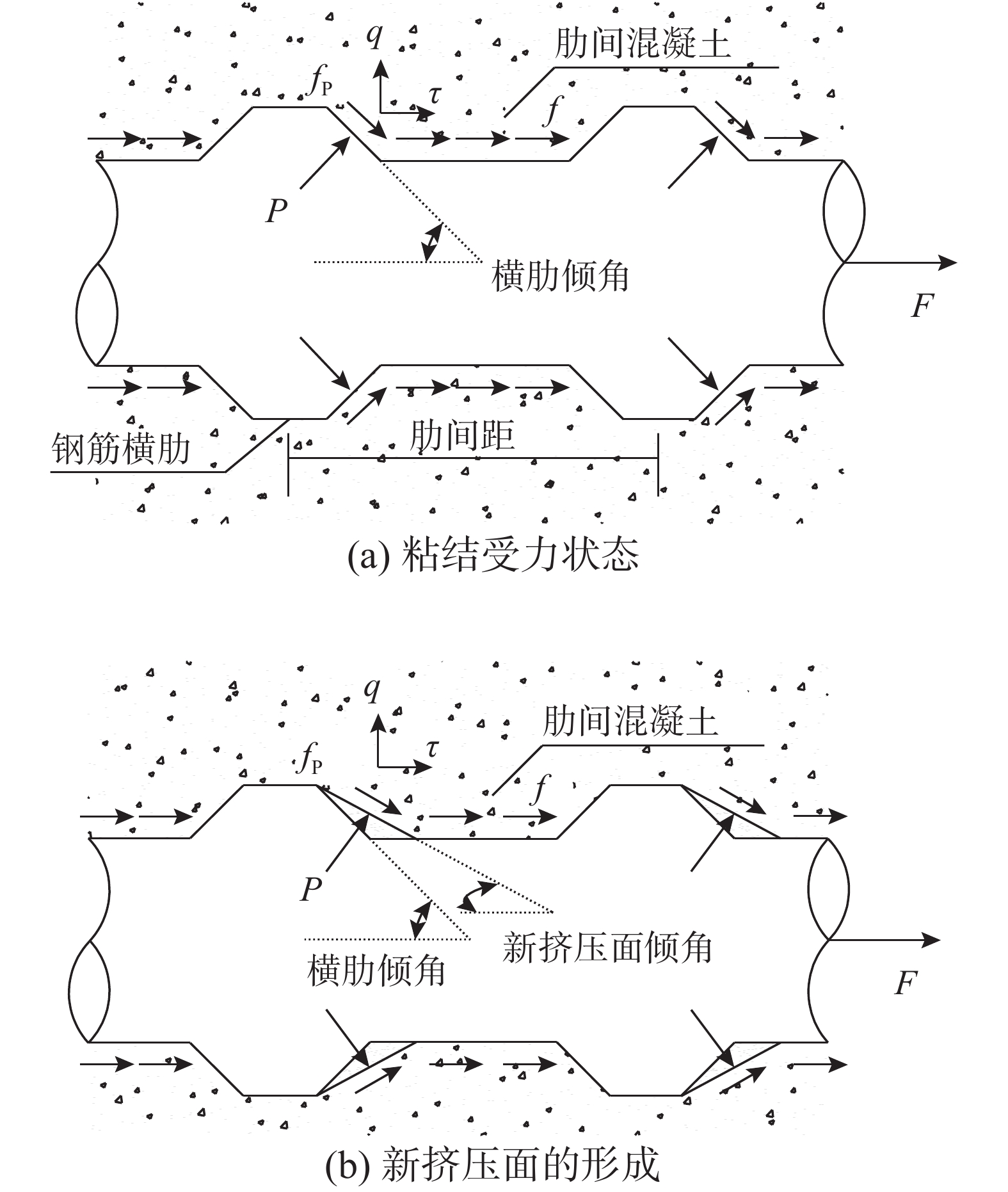
为分析带肋钢筋与混凝土粘结破坏机理，取带肋钢筋与混凝土单元进行受力分析。图3(a)为局部钢筋和混凝土粘结受力状态，当钢筋受到外力F作用时，肋间混凝土与钢筋产生摩擦力和胶结力f，由于钢筋横肋存在倾角，会与肋间的混凝土齿产生锥楔作用，钢筋会对混凝土产生垂直于横肋方向的挤压力P和沿横肋倾角的摩擦力f_p，将两者分别在纵向和径向进行投影，两者纵向产生剪应力τ，径向产生径向内压力q，其中内压力q会对钢筋周围混凝土产生径向的压应力和环向的拉应力。

当混凝土保护层较厚时，混凝土受到的环向拉应力较小，混凝土内基本不产生裂缝，或产生细小内裂缝但难以达到试件表面，试件仍保持完好。继续增大荷载，剪应力τ随之增加，肋间混凝土齿被逐渐剪坏，钢筋滑移量增大，当肋间混凝土齿完全被剪坏时，锥楔传力机制也随即消失，钢筋被缓缓拔出，形成“挂犁式”破坏。钢筋在拔出的过程中，仍具有一定的粘结力，这是因为破坏的肋间混凝土碎末充满在钢筋两肋之间，将带肋钢筋填充为以近似圆柱体，此圆柱体与周围混凝土仍有一定的摩擦力和机械咬合力。值得注意的是，钢筋在滑移过程中，其与肋间混凝土齿作用的平面并不总是横肋所在的面，这是由于肋前混凝土不断破碎，破碎的混凝土在肋前逐渐被挤压为粉末，并且紧密地积聚在肋前，这些肋前的混凝土细末会形成新的挤压力作用面(图3(b))，此作用面会随着滑移量的增加而不断变化。

当混凝土保护层较小时，在较小的荷载作用下，混凝土内部即产生较大的环向拉应力，当内部环向拉应力达到混凝土抗拉强度时，试件内部首先开裂，并快速扩展至混凝土表面，导致混凝土劈裂为2块~3块，产生劈裂破坏，劈裂破坏一般较为突然，属于典型的脆性破坏，并且在破坏时伴随较大声响。

图  3  钢筋与混凝土粘结锚固受力机理

Figure  3.  Mechanisms of bonding and anchoring between rebar and concrete

下载: 全尺寸图片 幻灯片

3   粘结强度计算模型

3.1   计算模型简化

为了方便对带肋钢筋与混凝土的粘结进行力学分析，需对粘结模型进行一定简化：

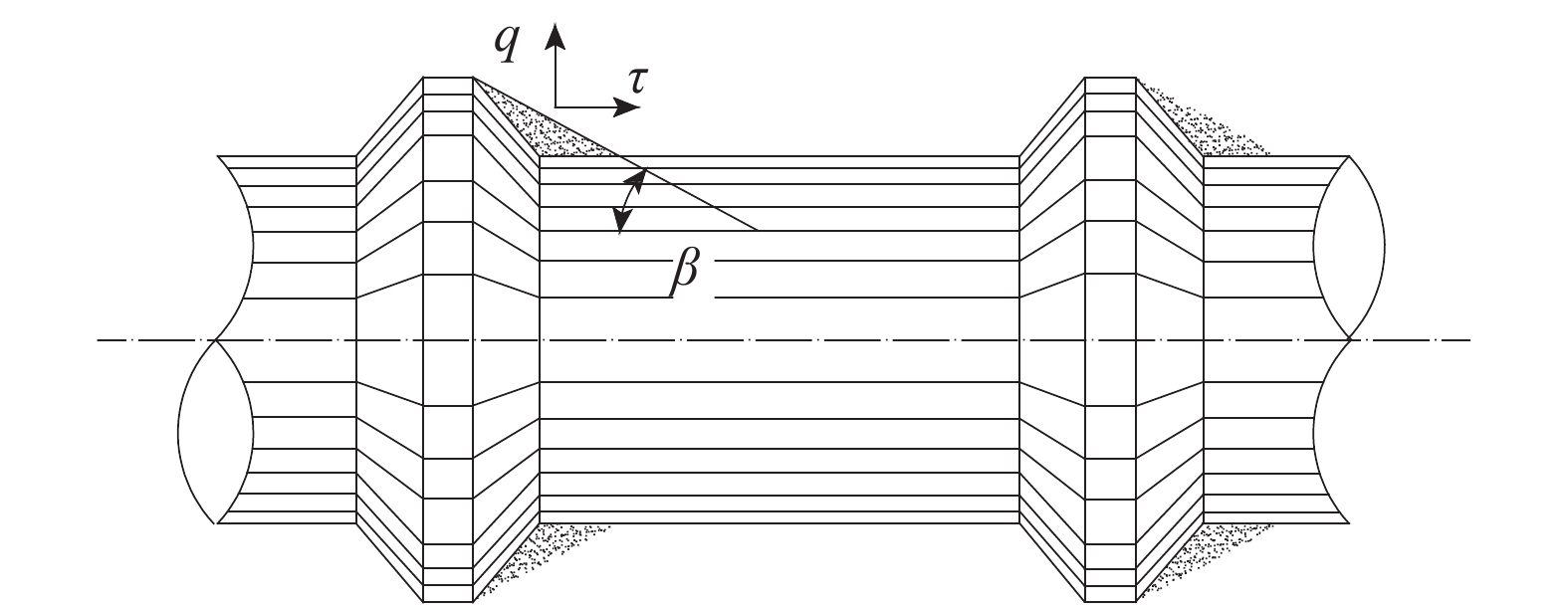
1)将带肋钢筋外形简化为以横肋最高处截面绕钢筋轴线旋转而成的等高肋钢筋，如图4；

图  4  简化计算模型

Figure  4.  Simplified analytical model

下载: 全尺寸图片 幻灯片

2)忽略钢筋纵肋的影响；

3)忽略钢筋与混凝土的化学胶结力以及肋间混凝土与钢筋的粘结力；

4)在以上简化的基础上，假设钢筋与混凝土的粘结长度内各截面处的应力状态相同，均为肋前破坏面上的应力，如图4。

3.2   粘结强度理论模型分析

将钢筋横肋挤压面上的挤压力和摩擦力分别沿钢筋轴线和垂直于钢筋轴线的方向分解，得到径向的内压力q和轴向的剪切力τ，此剪切力τ即为钢筋与混凝土之间的粘结力，τ和q应满足以下关系：

式中：μ为钢筋与混凝土的界面摩擦系数；β为挤压面与钢筋轴线的夹角。根据式(1)可知，粘结应力τ与内压力q成正比，当内压力最大时粘结应力也达到最大值。以下针对内压力进行分析。

将钢筋周围的混凝土视为承受均匀内压q的厚壁圆筒，文献[16]中给出了圆筒截面上的径向压应力、环向拉应力的解答：

式中：σ_r,r、σ_t,r为距离圆筒中心r处的径向应力、环向应力；R_b为钢筋的半径，即R_b=d/2；R_c为圆筒中心至截面边缘的距离，即R_c=R_b+c。

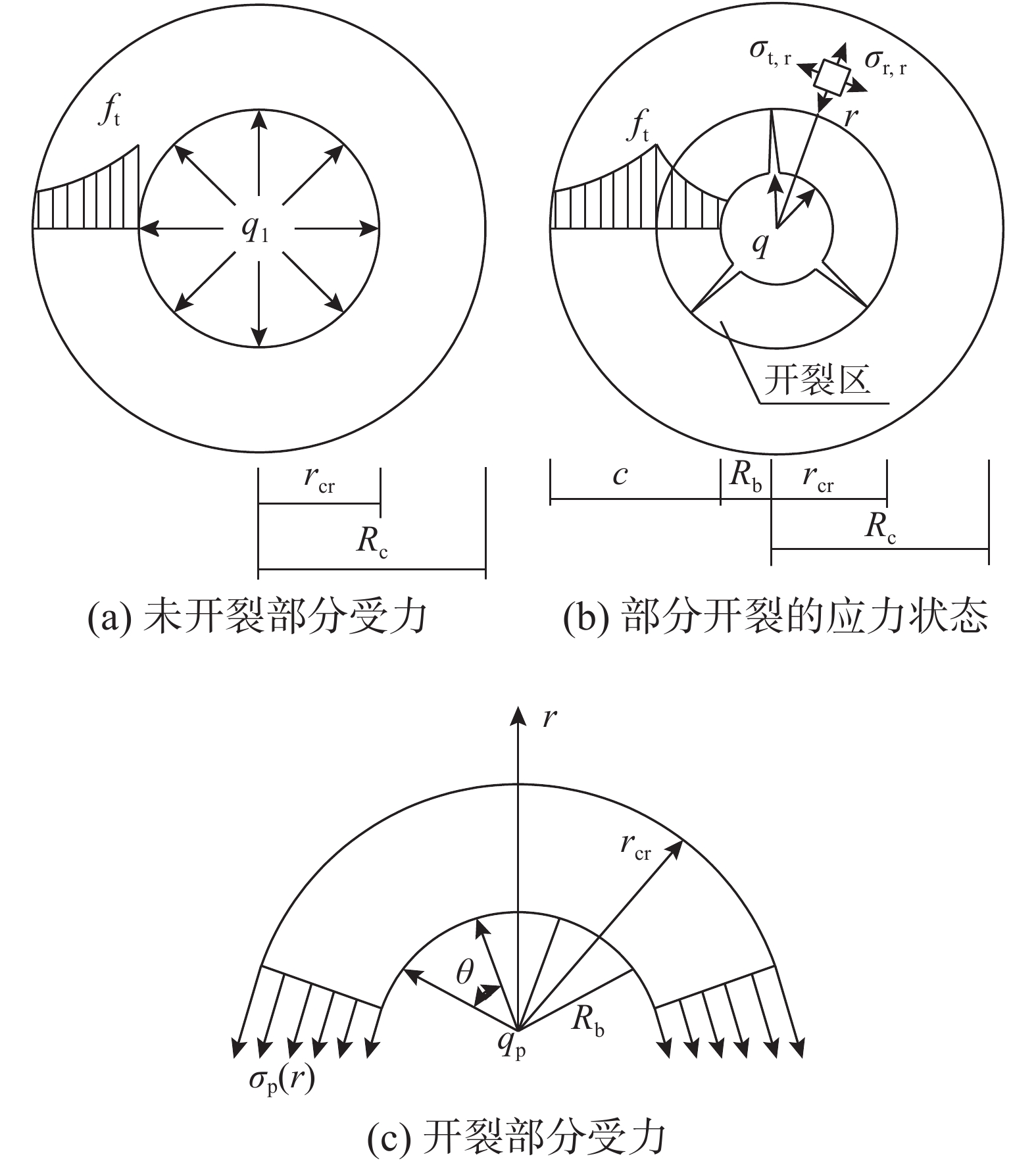
当拉力较小、截面上的混凝土尚未开裂时，截面上的应力分布满足式(2)和式(3)的关系，从式(3)可以看出，钢筋外边缘附近的混凝土受到的拉应力最大，随着拉力的增大，此处拉应力最先达到混凝土抗拉强度f_t(图5(a))，裂缝开始产生。令式(3)中r=R_b、σ_t,r=f_t即得此时的内压力q_cr：

图  5  考虑开裂区混凝土软化的计算模型

Figure  5.  Computational model considering softening of concrete in cracked zone

下载: 全尺寸图片 幻灯片

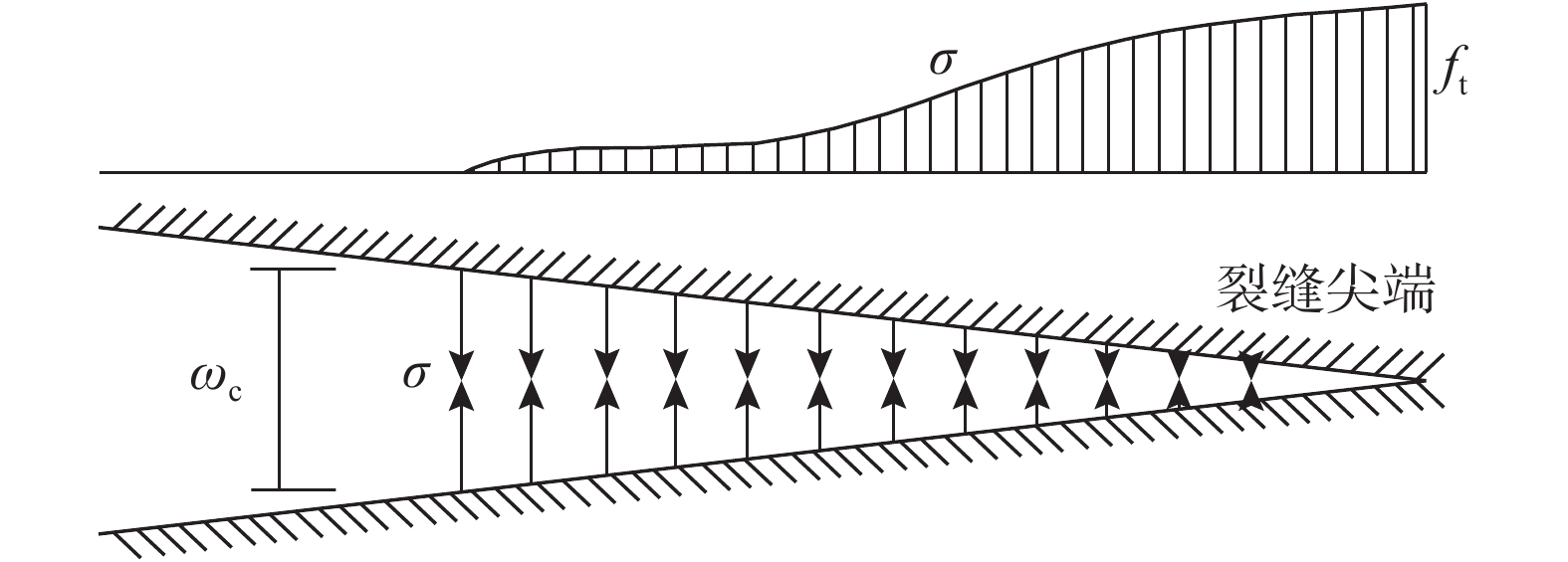
混凝土开裂后，考虑开裂区作用的截面上实际应力分布应当如图5所示，设裂缝延伸的深度为r_cr(从圆筒中心算起)，以此半径为圆的界面将截面分为两部分：在R_b<r<r_cr的范围内为开裂区；r_cr<r<R_c的范围为未开裂区。随着断裂力学的发展及其在描述混凝土等准脆性材料力学行为中的应用，大量学者发现：当混凝土表面在拉力作用下产生微裂缝时，缝间拉应力(即粘聚力σ)并非在开裂瞬间降为0，而是在裂缝宽度达到某一临界值ω_c前，混凝土仍可通过微裂缝传递部分拉应力，该作用随着裂缝宽度的增大逐渐递减为0。这一过程即为混凝土的软化效应^[13](图6)。因此，为了更准确的描述开裂区混凝土的力学行为，需对该区域混凝土的软化效应加以考虑。在r=r_cr的界面上混凝土处于开裂的临界状态，其环向拉应力等于混凝土抗拉强度f_t。为计算内压力q，将两部分分开考虑(图5(a)和图5(b))，分别计算各部分对内压力的贡献。

图  6  混凝土的软化效应

Figure  6.  Softening effect of concrete

下载: 全尺寸图片 幻灯片

外围未开裂部分的计算模型见图5(a)，设r=r_cr界面上的径向压力为q₁，此计算模型与前述式(4)的计算相同，令式(4)中R_b=r_cr，则得到q₁的计算结果为：

再对开裂部分的圆环整体由力的平衡有：

式中，q_e即为未开裂部分对q的贡献，由式(5)和式(6)得：

接下来计算开裂区域对q的贡献，取两裂缝间的混凝土部分圆环为研究对象(图5(c))，裂缝两侧的混凝土的拉应力(粘聚力)垂直于半径分布，设其分布与r的函数关系为σ_p$(r)$，则对图5(c)中的部分圆环由力的平衡有：

对式(8)运算、化简后得到q_p的计算式为：

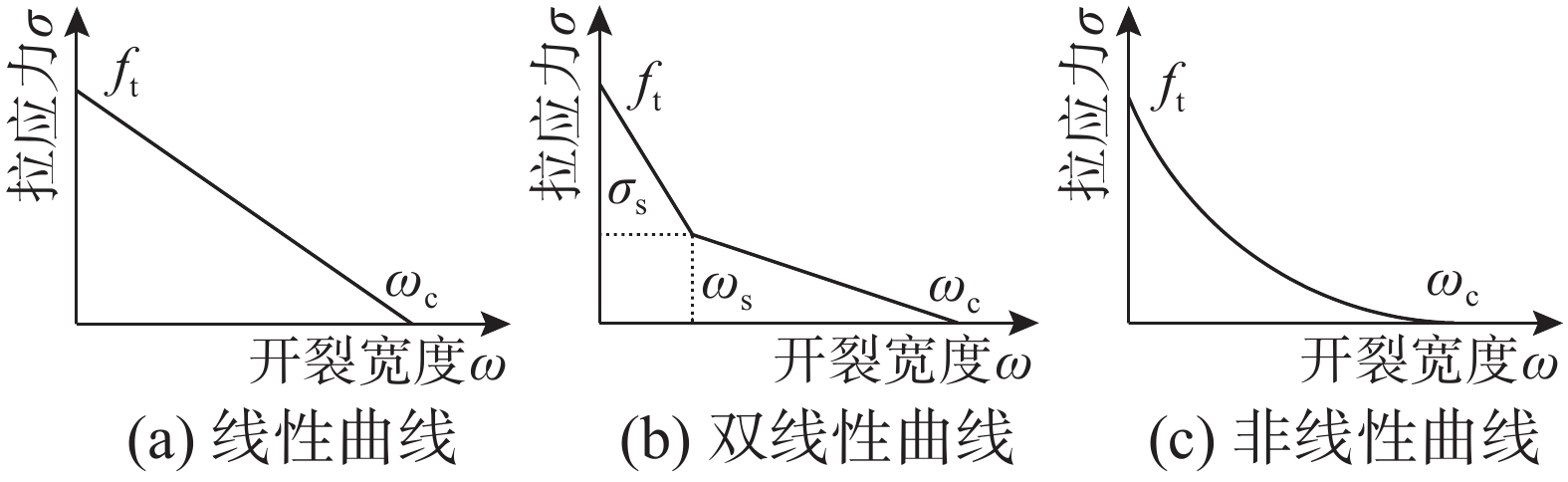
显然，为了计算出q_p，须得到σ_p(r)的具体表达式，为此需选择适当的软化本构曲线对该区域的软化行为进行描述。目前，关于描述混凝土软化关系的模型主要有两类，即Hillerborg等^[10]的虚拟裂缝模型(FCM)和Bazant等^[17]的裂缝段断裂模型(CBM)。关于虚拟裂缝模型，已经得有大量的试验和理论验证，是目前使用最广最为成熟的一种混凝土断裂模型，因此，本文以选择选择其作为描述混凝土软化的基本模型。虚拟裂缝模型中软化曲线的形式并不唯一，其描述函数有多种，包括线性函数、双线性函数、非线性函数等^[18](图7)。

图  7  不同软化曲线形式

Figure  7.  Different forms of softening curve

下载: 全尺寸图片 幻灯片

图7中直线型曲线是最早提出的一种软化曲线，其与混凝土材料软化特性的真实情况有一定差距，而非线性曲线与试验结果最为接近，但其表达式较为复杂，不利于计算分析。因此，双线性软化曲线是目前应用较多的混凝土软化本构，本文也应用双线性软化曲线进行分析，其具体表达式为：

为简化后续计算，将式(10)简化为：

式(11)中，对于特定的软化曲线而言，a、b、m、n均为常量。从图7(b)中的双线性软化曲线和式(10)可以看出，决定曲线形状的最主要参数为σ_s、ω_s和ω_c，本文采用徐世烺针对混凝土材料本身的性能所提出的建议式^[16]：

式中：G_f/(N/mm)为断裂能，即曲线与坐标轴围成的面积；d_max为骨料最大粒径，本文取为20 mm；其余符号同前。

以上给出了开裂区裂缝宽度和环向应力的关系，为求出σ_p(r)的分布，考虑截面距离圆心r处的环向纤维的伸长量δ(r)，δ(r)应等于两裂缝间的混凝土由于应力σ_p(r)产生的变形加上裂缝宽度，即：

式中，n为裂缝条数。又有：

式中：ε_θ(r)为r处的平均应变；u(r)为r处的径向位移。由此可见，为求出σ_p(r)还需考虑径向位移的分布。由于混凝土开裂的影响导致开裂区的径向位移分布与非开裂区的弹性分布不同。因此，此区域内的径向位移分布往往是通过一定的假设得到。以下采用不同的径向位移假设进行计算。

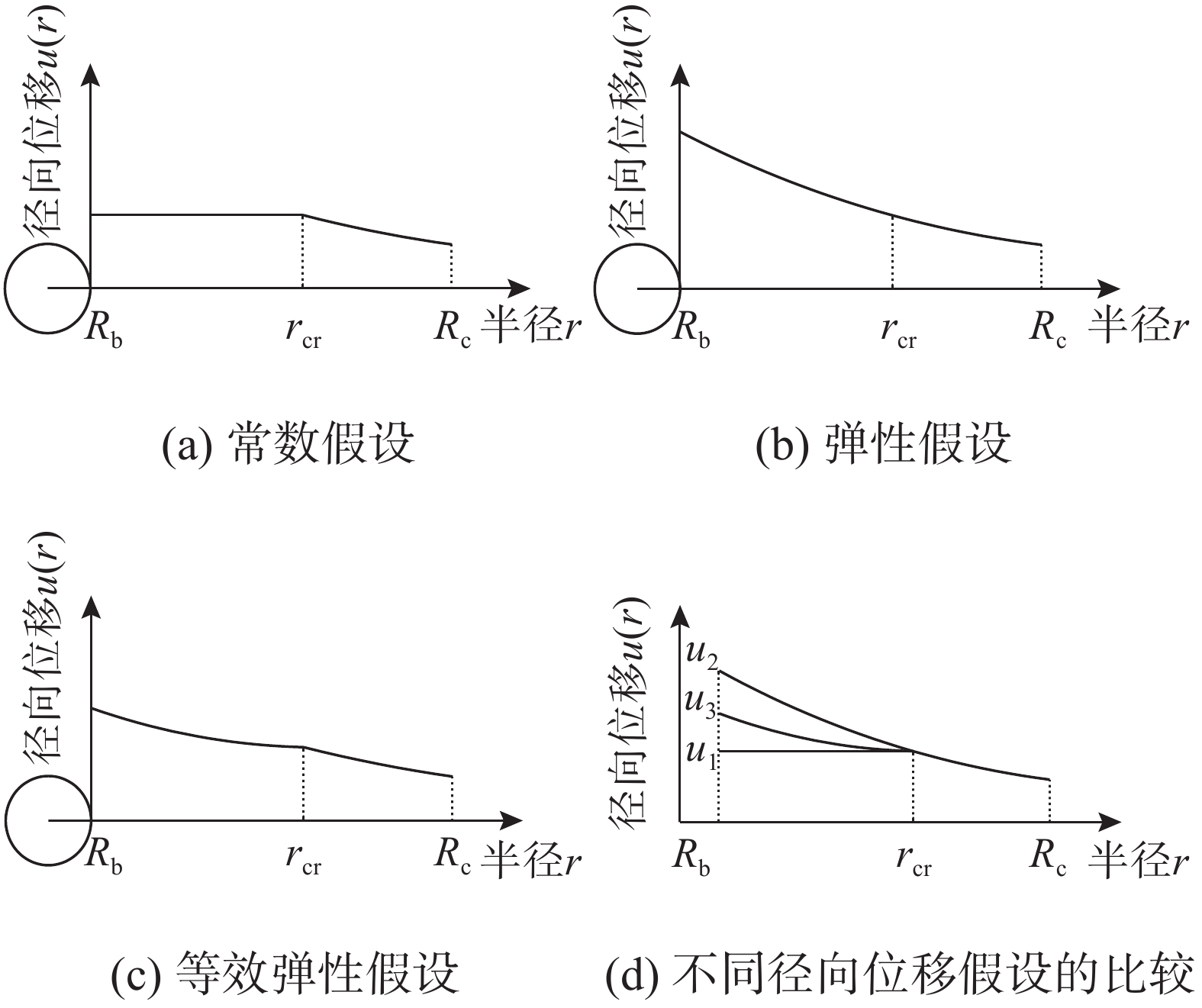
1)假设开裂区径向位移为常量，均等于开裂区与未开裂区界面(r=r_cr)上的径向位移，易知此界面上的径向位移为r_crε_cr，则：

将式(11)和式(15)代入式(13)，得：

式中：

下同。将式(16)代入式(9)，得：

将式(7)和式(18)相加，得：

可以看出q是r_cr的函数，为了求出q的最值，对r_cr求导：

令${{{\text{d}}q} \mathord{\left/ {\vphantom {{{\text{d}}q} {{\text{d}}{r_{{\text{cr}}}}}}} \right. } {{\text{d}}{r_{{\text{cr}}}}}} = {\text{0}}$，得：

求解式(21)，可以得到满足方程的r_cr唯一合理解，记为r_u1(R_b<r_u1<R_c)，将r_cr=r_u1代入式(19)得到q的最大值q_u1，再将q_u1代入式(1)即可得到极限粘结强度${\tau} _{{\text{u1}}}^{\text{c}}$。

2) 假设开裂区的径向位移分布与未开裂区的径向位移分布相同，即忽略混凝土开裂对径向位移的影响，将整个混凝土区域视为内径为R_b外径为R_c承受内压q₂的厚壁筒，则根据厚壁圆筒的位移解答有：

在开裂面上，环向拉应力等于f_t，根据式(3)，有：

由式(22)和式(23)得：

式中，“≈”的成立主要是考虑到便于运算而忽略了泊松效应。将式(24)和式(12)、式(15)代入式(13)，得：

将式(25)代入式(9)中积分，得：

对q_e和q_p求和，得：

式(27)对r_cr求导，并使${{{\text{d}}q} \mathord{\left/ {\vphantom {{{\text{d}}q} {{\text{d}}{r_{{\text{cr}}}}}}} \right. } {{\text{d}}{r_{{\text{cr}}}}}} = {\text{0}}$，得到：

式(28)的唯一合理解为r_u2(R_b<r_u2<R_c)，将r_cr=r_u2代入式(27)得到q的最大值q_u2，再将q_u2代入式(1)即可得到极限粘结强度${\tau} _{{\text{u2}}}^{\text{c}}$。以上两种关于开裂区径向位移的假定实际上分别模拟了开裂区混凝土为刚体和弹性体，是开裂区径向位移的两种极端情况，实际的径向位移应介于两者之间。

3)采用“等效弹性假设”^[19]反映开裂区径向位移分布进行计算。考虑到开裂区混凝土的径向位移与外围混凝土径向位移的不同，将整个开裂区视为一内径为R_b外径为r_cr的厚壁圆筒，设其均匀内压力为q₃，外径处的环向拉应力已知等于f_t，反算得到开裂区的径向位移分布，则根据式(22)有：

在开裂面上，环向拉应力等于f_t，根据式(3)，有：

由式(29)和式(30)并忽略泊松效应得：

将式(31)、式(12)、式(15)代入式(13)，得：

将式(32)代入式(9)，积分得：

将式(7)和式(33)相加，得：

式(34)对r_cr求导，得：

令${{{\text{d}}q} \mathord{\left/ {\vphantom {{{\text{d}}q} {{\text{d}}{r_{{\text{cr}}}}}}} \right. } {{\text{d}}{r_{{\text{cr}}}}}} = {\text{0}}$，得：

求解式(36)，可以得到满足方程的r_cr唯一合理的解，记为r_u3(R_b<r_u3<R_c)，将r_cr=r_u3代入式(34)得到q的最大值q_u3，再将q_u3代入式(1)即可得到极限粘结强度${\tau} _{{\text{u3}}}^{\text{c}}$。上述3种不同假设的径向位移分布见图8(a)~图8(c)，为进一步比较各径向位移的分布，令R_c=10R_b、r_cr=5R_b分别代入式(15)、式(24)和式(31)中计算各径向位移分布，将计算结果绘于同一坐标图中，见图8(d)。由图8及各径向位移的表达式可知，u₁(r)<u₃(r)<u₂(r)，即等效弹性假设(假设③)的径向位移分布在常数假设和弹性假设之间，与实际情况更为相符。

图  8  开裂区混凝土径向位移的不同假设

Figure  8.  Different hypotheses of radial displacement of concrete in cracked zone

下载: 全尺寸图片 幻灯片

3.3   粘结强度理论模型计算值与试验值的比较

为验证该推导过程和计算结果的正确性，除本文试验得到的3组试验数据外，按照钢筋强度等级相近(600 MPa~650 MPa级)、钢筋类型相同(月牙纹热轧带肋钢筋)、试验方法相同(拉式粘结试验方法)、混凝土类型相同(普通混凝土)的原则从既有研究中收集6组数据，并将理论计算结果将试验结果进行对比。在计算前，先对部分参数进行说明：式(1)中参数μ为摩擦系数，文献[20]中根据钢筋表面不同锈蚀程度建议了不同的摩擦系数，其中轻锈钢筋与混凝土的摩擦系数为0.26~0.30，值得注意的是根据前面的分析，由于肋前混凝土粉末的堆积，实际挤压面上的摩擦更多的是混凝土粉末之间的摩擦，该类摩擦的摩擦系数要小于钢筋与混凝土间的摩擦系数，但本文仍偏不安全地取μ为0.30；式(1)中参数β应为横肋挤压面与钢筋轴线所成角度，由于钢筋在滑移的过程中钢筋粉末在肋前堆积，使得实际β的大小要小于钢筋的横肋倾角α，而横肋倾角α一般为45°，相应的取β为25°；式(13)中n为裂缝条数，一般可取2或3，本文取为3。其余参数在前文中均已有所叙述，不再赘述。粘结强度理论计算值见表2。将以上计算得到的结果与试验值进行比较，比较结果见表3。

表  2  粘结强度的理论计算值

Table  2.  Calculation value of bond strength

试件编号	参数C1/mm	按假设①计算			按假设②计算			按假设③计算
		ru1/mm	${\tau} _{ {\text{u1} } }^{\text{c} }$/MPa		ru2/mm	${\tau} _{ {\text{u2} } }^{\text{c} }$/MPa		ru3/mm	${\tau} _{ {\text{u3} } }^{\text{c} }$/MPa
T16-7d-C30	−174.97	69.85	24.55		52.96	18.54		57.33	21.10
T16-7d-C40	168.11	69.04	27.34		51.97	20.49		56.58	23.44
T16-7d-C50	−164.15	68.55	28.84		51.38	21.52		56.13	24.69
A18-10d-C40[2]	−209.56	73.93	10.48		57.95	8.71		61.11	9.30
A18-10d-C50[2]	−207.28	73.66	11.41		57.62	9.36		60.86	10.08
A18-10d-C60[2]	−204.05	73.28	12.72		57.16	10.27		60.51	11.18
B18-20d-C60[21]	−208.86	73.85	10.77		57.85	8.91		61.04	9.54
B18-20d-C80[21]	−204.73	73.59	11.66		57.53	9.53		60.79	10.29
B18-20d-C100[21]	−201.50	72.98	13.76		56.79	11.00		60.23	12.05
注：1) 为便于对比分析，所收集数据试件编号按照本文试件编号规则重新赋予编号，例如A18-10d-C40含义为钢筋公称直径为18 mm、锚固长度为10 d、混凝土强度等级为C40的试件；2) 每组收集数据为3个试件实测值的平均值；3) 相同强度等级混凝土实测强度值存在差异，所收集数据中详细试验参数见相应文献；4) ru1、ru2、ru3分别为假设①、②、③下计算得到的裂缝深度；5) ${\tau} _{ {\text{u1} } }^{\text{c} }$、${\tau} _{ {\text{u2} } }^{\text{c} }$、${\tau} _{ {\text{u3} } }^{\text{c} }$分别为假设①、②、③下计算得到的粘结强度。

下载: 导出CSV 

| 显示表格

表  3  粘结强度理论计算值与试验值的对比

Table  3.  Comparisons between calculated and experimental values of bond strength

试件编号	试验值${\tau} _{\text{u} }^{\text{t} }$/MPa	${ {{\tau} _{ {\text{u1} } }^{\text{c} } } \mathord{/ {\vphantom { {{\tau} _{ {\text{u1} } }^{\text{c} } } {{\tau} _{\text{u} }^{\text{t} } } }} } {{\tau} _{\text{u} }^{\text{t} } } }$	${ {{\tau} _{ {\text{u2} } }^{\text{c} } } \mathord{/ {\vphantom { {{\tau} _{ {\text{u2} } }^{\text{c} } } {{\tau} _{\text{u} }^{\text{t} } } }} } {{\tau} _{\text{u} }^{\text{t} } } }$	${ {{\tau} _{ {\text{u3} } }^{\text{c} } } \mathord{/ {\vphantom { {{\tau} _{ {\text{u3} } }^{\text{c} } } {{\tau} _{\text{u} }^{\text{t} } } }} } {{\tau} _{\text{u} }^{\text{t} } } }$
T16-7d-C30	18.65	1.33	1.00	1.15
T16-7d-C40	24.94	1.10	0.82	0.95
T16-7d-C50	25.79	1.16	0.87	0.99
A18-10d-C40	8.92	1.17	0.98	1.04
A18-10d-C50	10.45	1.09	0.90	0.96
A18-10d-C60	11.56	1.10	0.89	0.97
B18-20d-C60	10.31	1.04	0.86	0.93
B18-20d-C80	11.50	1.01	0.83	0.89
B18-20d-C100	12.45	1.11	0.88	0.97
注：${ { {\tau} _{ {\text{u1} } }^{\text{c} } } \mathord{/ {\vphantom { { {\tau} _{ {\text{u1} } }^{\text{c} } } { {\tau} _{\text{u} }^{\text{t} } } } } } { {\tau} _{\text{u} }^{\text{t} } } }$、${ {{\tau} _{ {\text{u2} } }^{\text{c} } } \mathord{/ {\vphantom { {{\tau} _{ {\text{u2} } }^{\text{c} } } {{\tau} _{\text{u} }^{\text{t} } } }} } {{\tau} _{\text{u} }^{\text{t} } } }$、${ {{\tau} _{ {\text{u3} } }^{\text{c} } } \mathord{/ {\vphantom { {{\tau} _{ {\text{u3} } }^{\text{c} } } {{\tau} _{\text{u} }^{\text{t} } } }} } {{\tau} _{\text{u} }^{\text{t} } } }$分别为假设①、②、③下计算得到的粘结强度与试验实测粘结强度的比值。

下载: 导出CSV 

| 显示表格

表2中通过比较各组数据的C₁及r_u1两个参数，可以发现混凝土强度对于相关断裂参数及最大粘结强度下的裂缝扩展半径的影响均较小；比较在各径向位移假设下计算得到的裂缝深度r_u及粘结强度τ_u，可以发现，采用不同的径向位移假设时裂缝深度和粘结强度均有一定的差别，当径向位移越小，计算所得的裂缝深度就越大，最终计算的粘结强度也越大。从表3可以看出，假设①实际上给出了粘结强度的最大值，其计算值均大于试验值；假设②给出了粘结强度的最小值，除T16-7d-C30试件，其余计算值均小于试验值，各组误差均在20%以内；虽然采用假设③计算的结果与试验值最为吻合，但却过高的估计了低强度(C30)混凝土试件的粘结强度；为确保有足够的安全储备，建议采用假设②作为开裂区混凝土径向位移分布。

4   结论

本文基于带肋钢筋与混凝土粘结破坏机理分析，采用双线性软化本构对开裂区混凝土的软化行为进行描述，建立了考虑开裂及未开裂区混凝土影响的粘结强度理论计算模型，研究了开裂区不同径向位移分布对计算结果的影响，得出研究结论如下：

(1) 结合弹性力学的厚壁圆筒理论对粘结强度进行理论计算，计算时克服了以往未考虑开裂区混凝土影响的缺点，采用双线性软化本构对开裂区的软化行为进行描述，得到了综合考虑未裂区和开裂区的粘结强度的计算方法，计算结果与试验计算吻合较好。计算推导过程可为进一步理论分析粘结锚固问题提供思路。

(2) 当采用不同的开裂区径向位移模式时，粘结强度计算结果存在差异。开裂区径向位移越小，粘结强度计算值越大，实际粘结强度应在假设径向位移为常量和弹性分布之间；采用等效弹性假设作为开裂区混凝土径向位移分布时，所得计算结果与试验结果最为吻合，但却过高的估计了低强度混凝土试件的粘结强度；为确保有足够的安全储备，建议采用弹性假设作为开裂区混凝土径向位移分布。