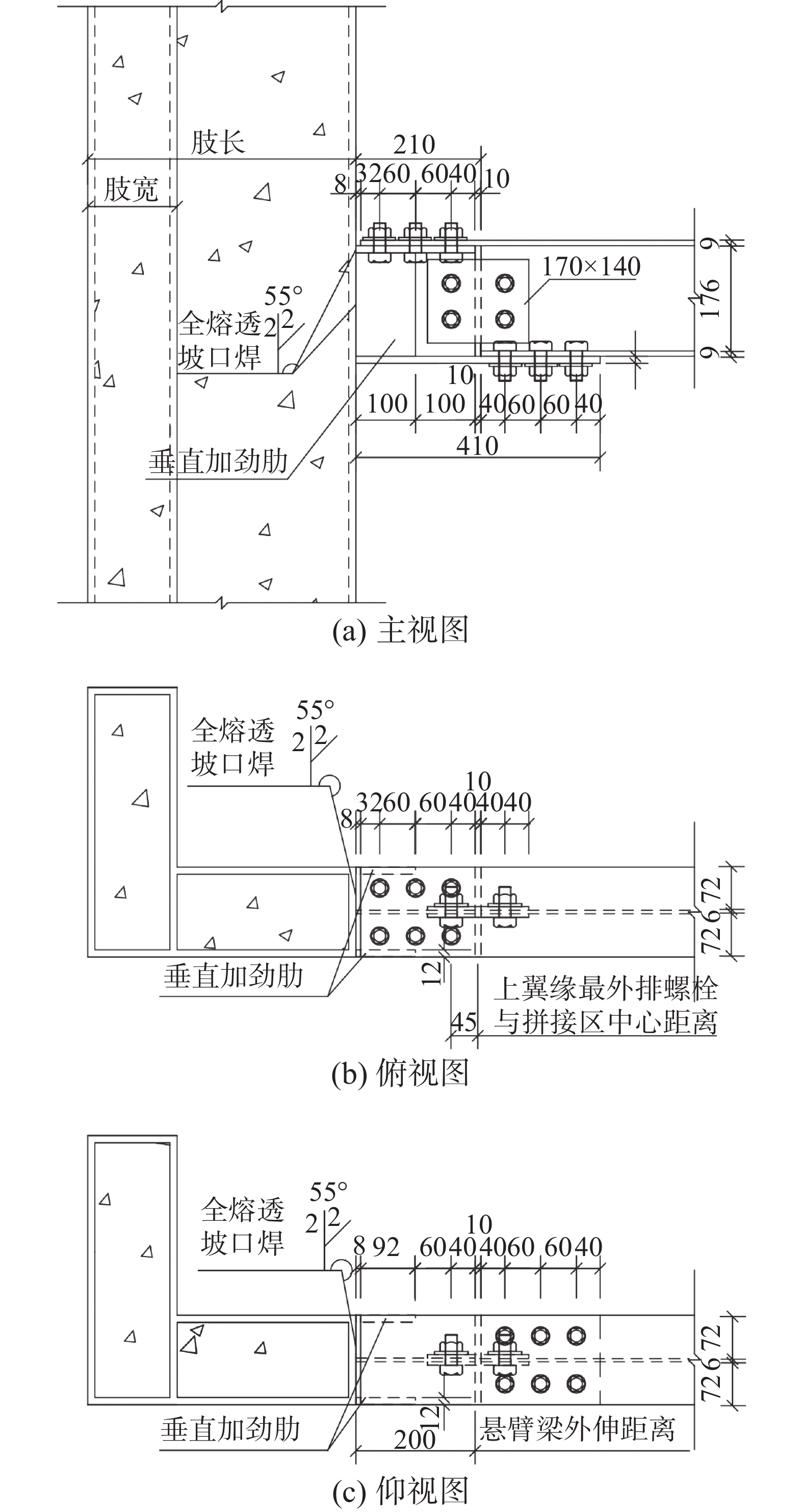
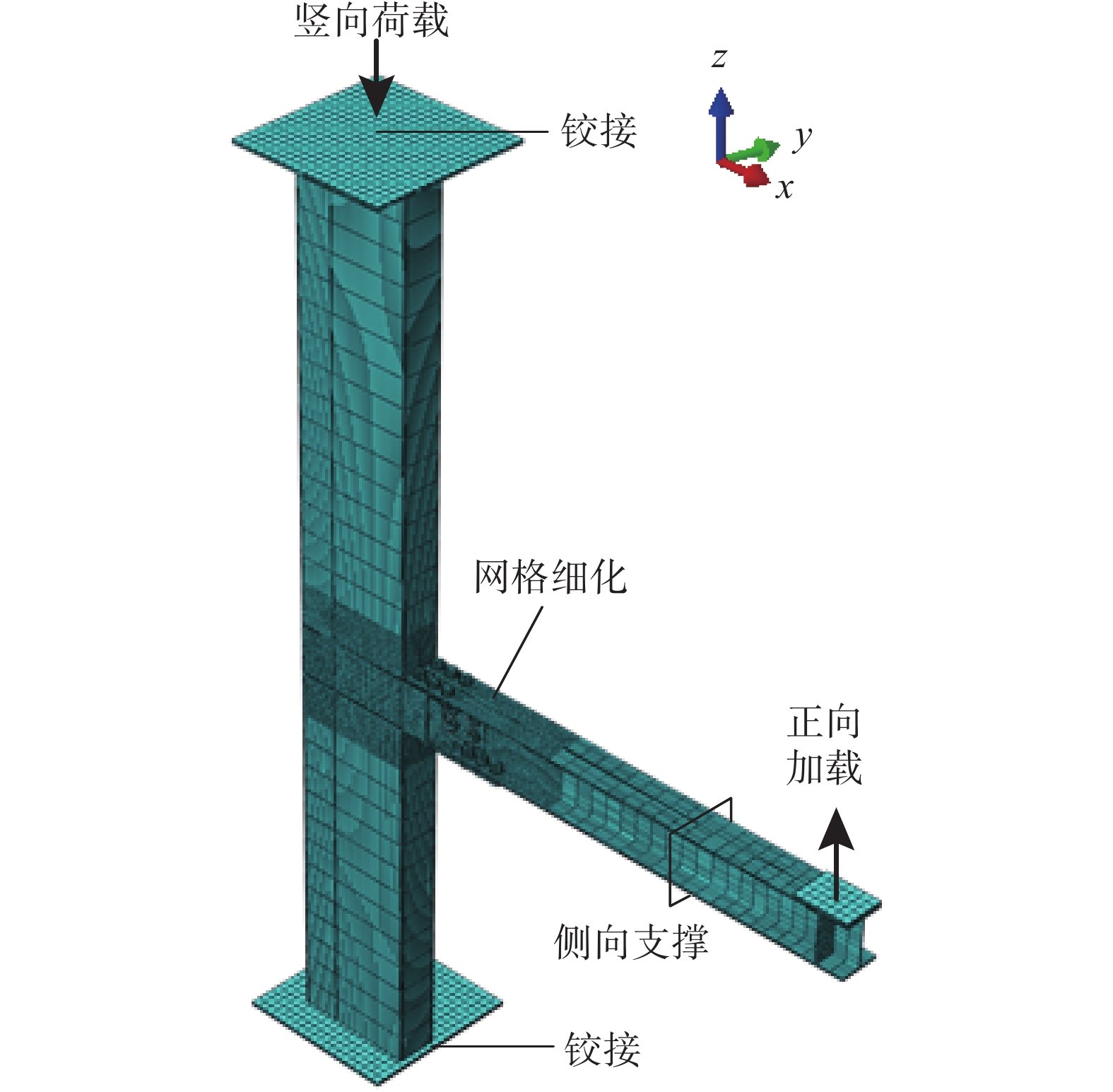
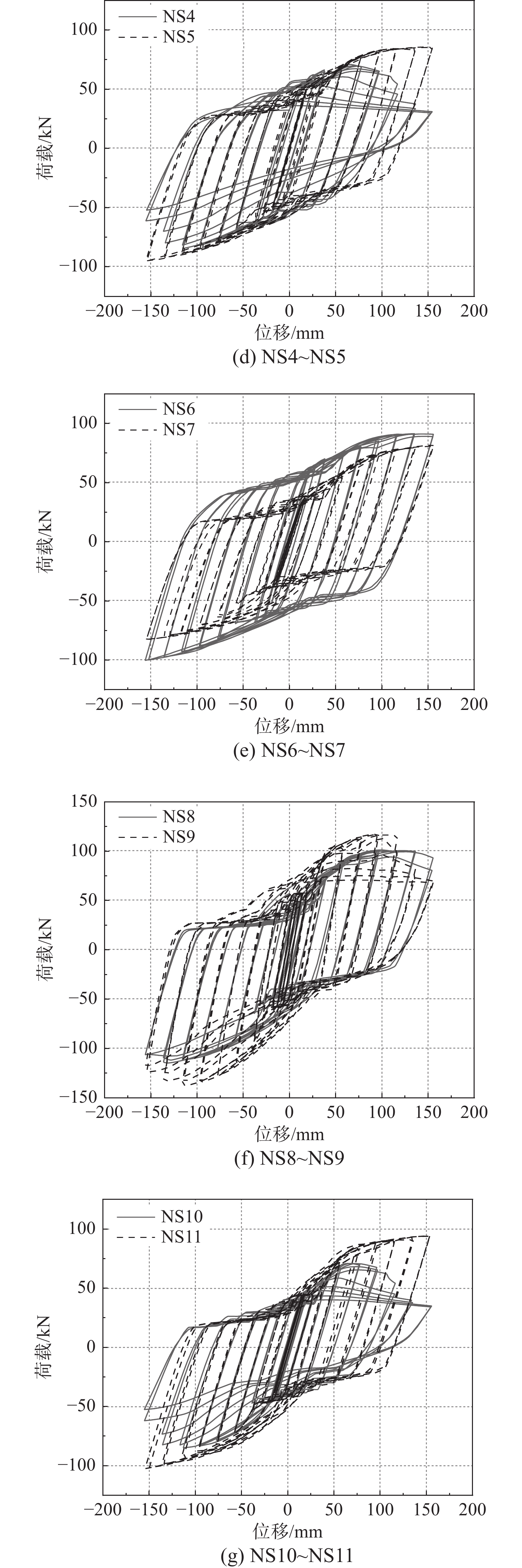
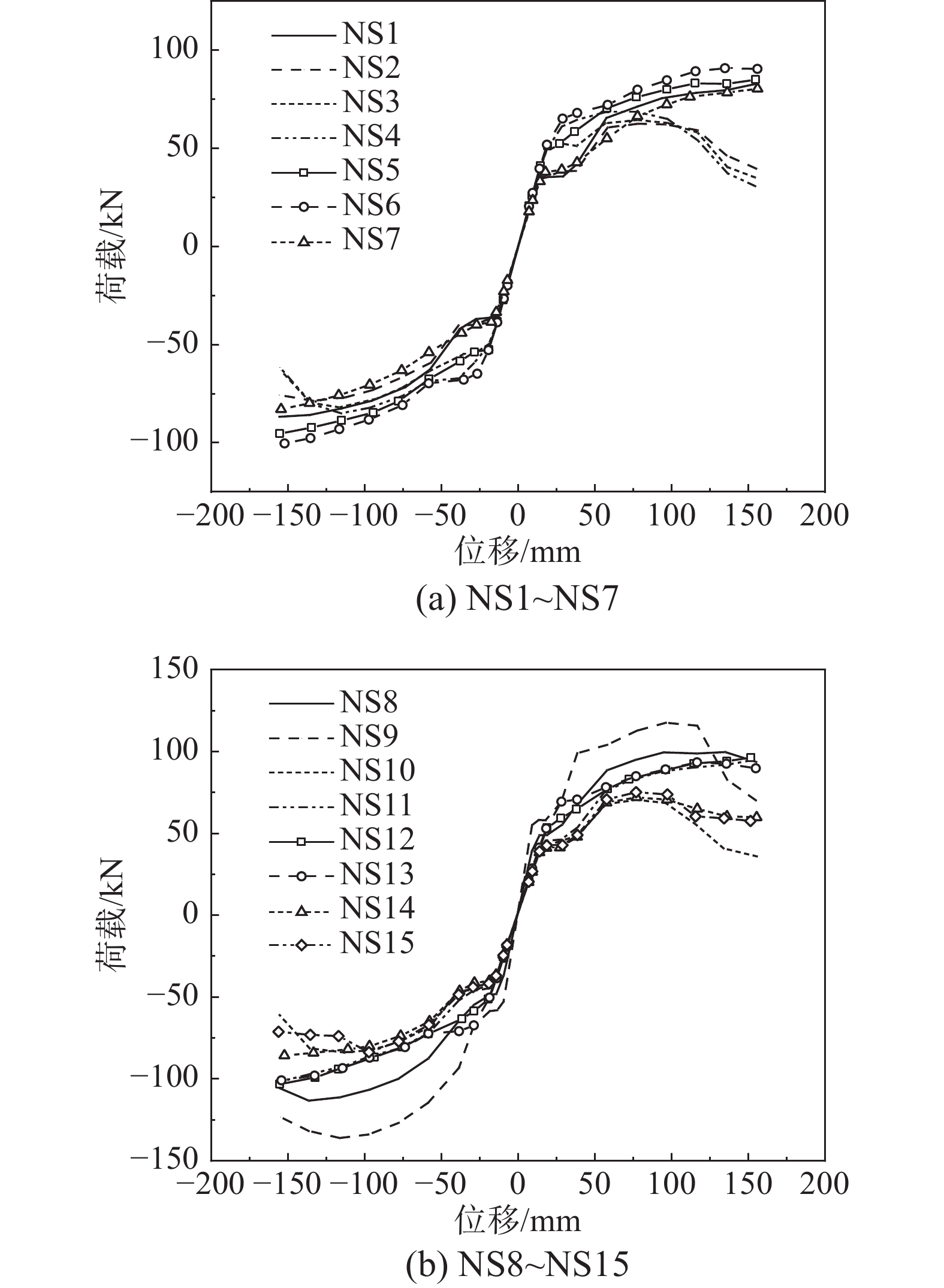
SEISMIC BEHAVIOR OF Z-SHAPED JOINT CONNECTING H-BEAM AND L-SHAPED CONCRETE-FILLED STEEL TUBULAR COLUMN
-
摘要: 对适用于装配式钢结构的钢管混凝土L形柱-H型钢梁Z字形节点的抗震性能进行研究。建立并基于节点试验结果验证了ABAQUS有限元模型,通过有限元分析获得了节点的荷载-位移曲线、骨架曲线、破坏模式和性能指标。结果表明:设置腹板拼接板、增加梁高、减小上翼缘最外排螺栓与拼接区中心距离等措施,能够提高节点的屈服荷载和峰值荷载;增加翼缘高强度螺栓数量能够提高节点的滑移荷载,但是会降低延性;增加悬臂梁外伸距离,可以提高滑移荷载、屈服荷载和峰值荷载,减少翼缘连接的高强度螺栓数量需求。基于有限元结果,验证了节点受弯承载力和极限受弯承载力计算公式的可靠性。Abstract: The seismic behavior of Z-shaped joints connecting H-section beam and L-shaped concrete-filled steel tubular column for prefabricated steel structures were studied. The ABAQUS finite element model was established and validated based on the joint test results. The load-displacement curves, skeleton curves, failure mode and performance indicators of the joint were obtained by finite element analysis. According to the finite element results, adding web splice plates, increasing the beam section height or decreasing the distances between the outmost bolts and the splicing zone center can increase the yield load and peak load of the joints. Increasing the bolt number on the flange can improve the slip load of the joint, but may reduce the ductility performance. Increasing the overhang distance of cantilever beam can improve the slip load, yield load and peak load, and reduce the required bolt number for the flange connection. Based on the finite element results, the reliability of the calculation formulas for the joint flexural capacity and ultimate flexural capacity is verified.
-
Keywords:
- Z-shaped joint /
- L-shaped column /
- beam-column connection /
- cantilever-beam /
- seismic performance
-
住宅产业化采用集约型建筑模式,将建筑构件在工厂预制完成后,运输到现场装配成房屋[1-6]。装配式建筑具备快速施工的优点,但其装配施工过程常受到现浇混凝土楼板的影响,需要研究与之配套的三板体系[7-14]。作者提出适用于装配式建筑的一种带C形钢边框-钢筋混凝土预制楼板。这种装配式楼板将C形钢作为楼板的边框,在边框内布置钢筋、浇筑混凝土,不同板块间通过断续焊接C形钢实现楼板连接,可实现不同板块间横向钢筋连续受力,使单向预制装配的楼板双向受力,从而使板间连接更加牢固,整体性更强。
1 楼板构造及装配方法
1.1 楼板构造
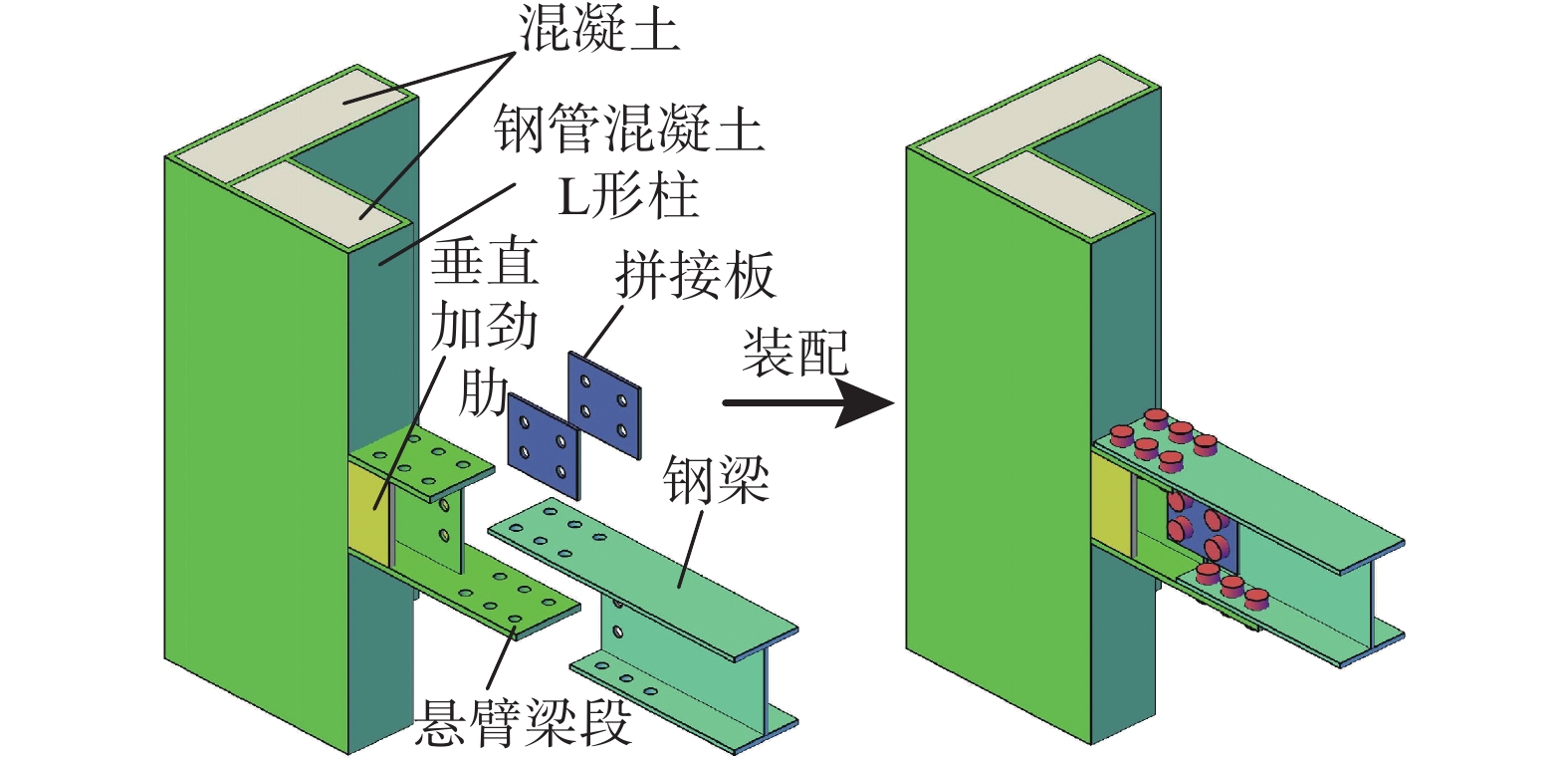
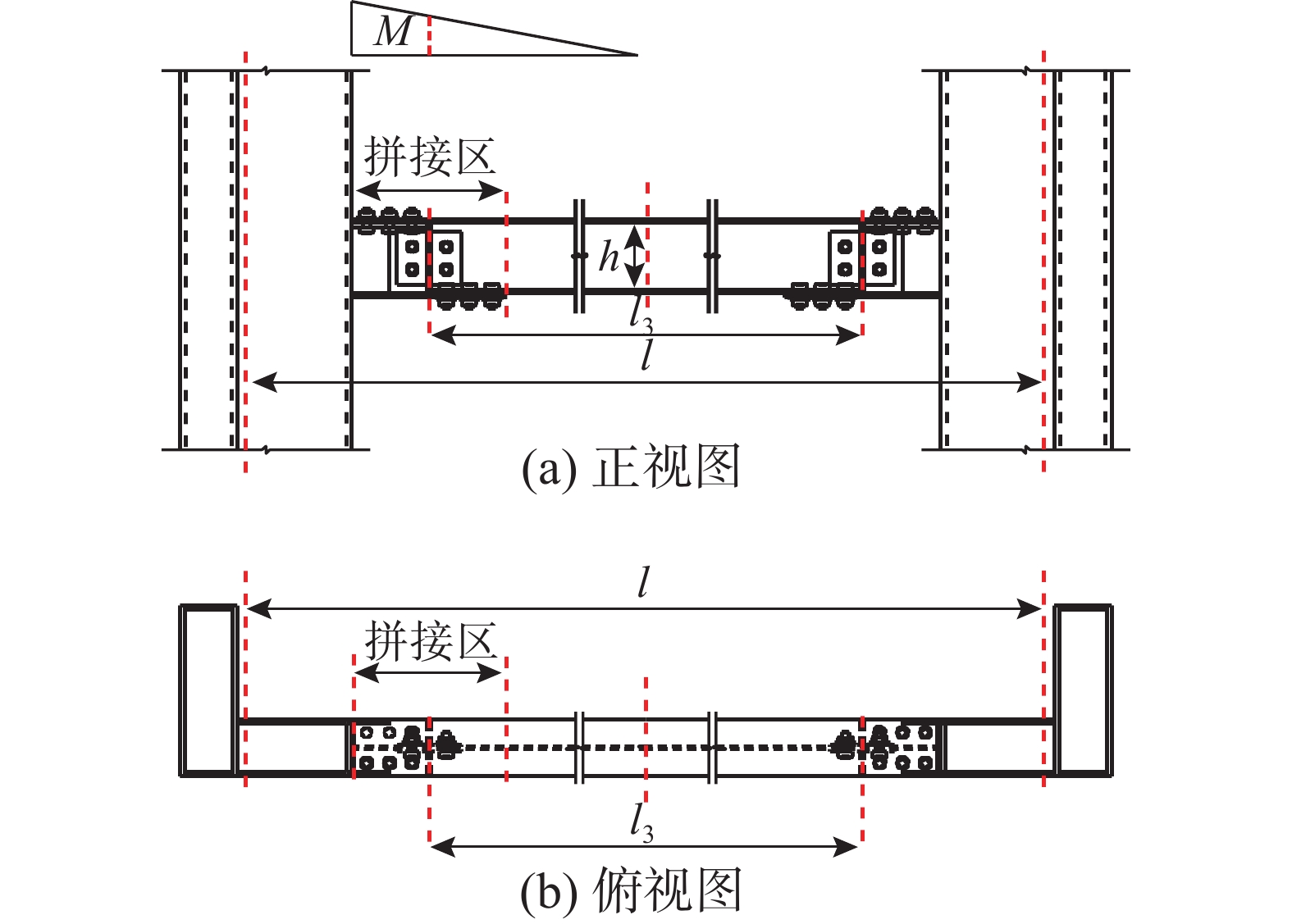
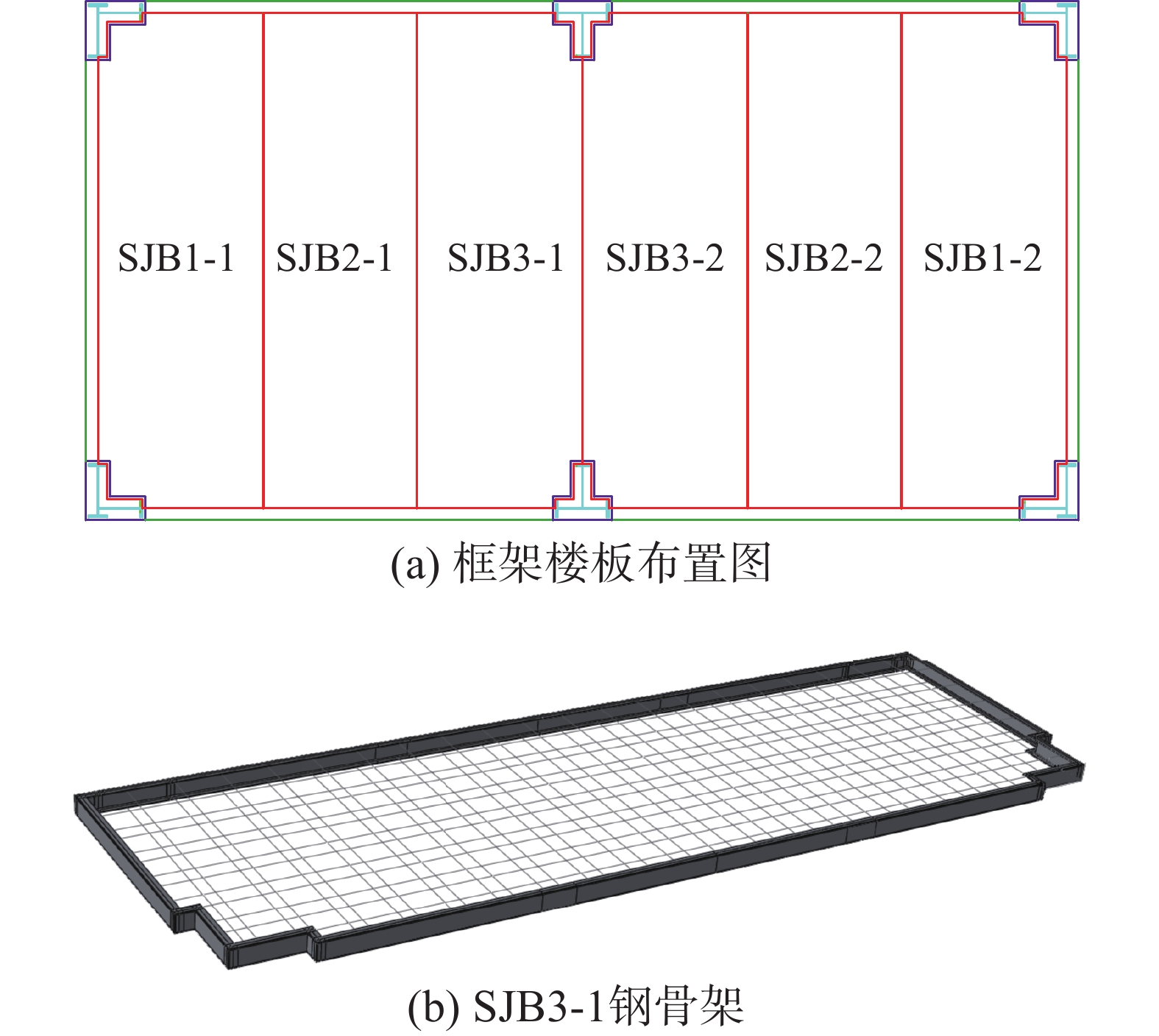
所涉及的装配式钢结构体系由梁、柱和带C形钢边框的钢筋混凝土楼板构成。梁、柱以及楼板均在工厂预制,现场仅进行节点连接。图1为应用该楼板的一种框架示意图,在一个柱距范围内,楼板由3块带C形钢边框混凝土楼板装配而成,每个楼板宽度小于2.4 m,便于运输。
带C形钢-钢筋混凝土楼板在工厂中预制时,先在楼板四周焊接C形钢边框。以SJB3-1为例,见图1(b),骨架由4块80 mm×35 mm×4 mm的Q235 C形钢焊接形成4200 mm×1396 mm的钢边框,在边框内部布置双层双向钢筋网,配筋为
 表 1 试件设计参数Table 1. Design parameters of specimens
表 1 试件设计参数Table 1. Design parameters of specimens样品编号 楼板尺寸/mm 配筋 纵向钢筋数量 SJB1-1 4200×1398×120 
6 SJB2-1 4200×1296×120 
5 SJB3-1 4200×1396×120 
6 SJB3-2 4200×1396×120 
6 SJB2-2 4200×1296×120 
5 SJB1-2 4200×1398×120 
6 1.2 梁板连接
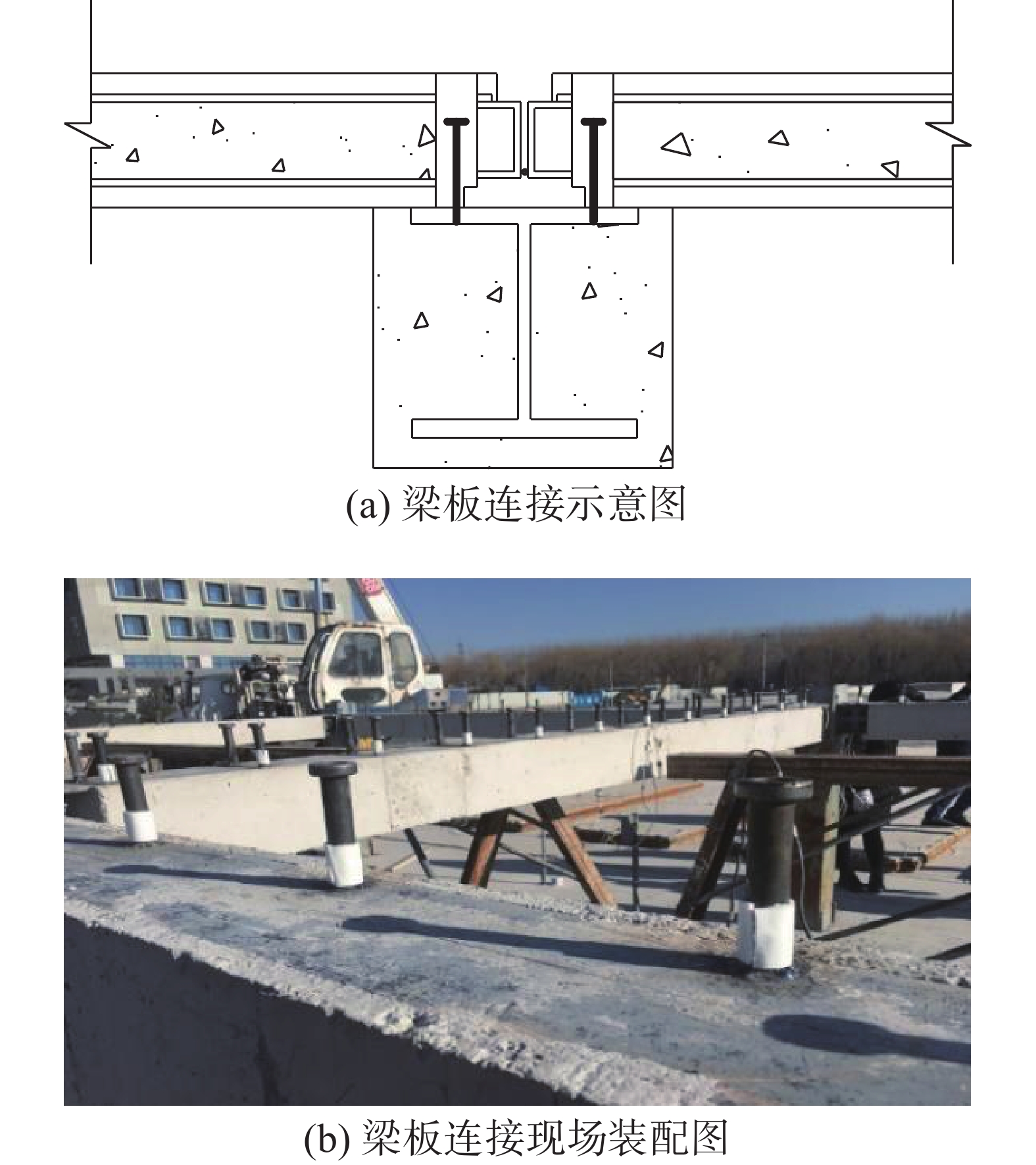
工厂预制圆钢管与楼板C形钢边框焊接形成一个整体,圆钢管间距350 mm,圆钢管下侧留有缺口,在梁上翼缘对应位置焊接栓钉。现场装配楼板时,栓钉插入到圆钢管内,之后向圆钢管内浇筑C60灌浆料,灌浆料通过圆钢管缺口流入楼板与钢梁之间的缝隙,使楼板与梁紧密结合,并增加隔音性能。梁板连接具体构造如图2。
1.3 板间连接
在楼板与楼板之间的连接处(两侧C形钢之间)缝隙上部和下部进行断续焊接(焊缝的焊脚尺寸hf=8 mm,每段焊缝长度为50 mm,间距为200 mm),随后在C形钢下翼缘外侧和板缝间涂抹抗裂砂浆,压平养护。由于板内双层横向钢筋焊接于C形钢上,通过板件连接焊缝将横向钢筋连接起来,实现楼板双向受力,增大楼板承载力,提高刚度。板间的连接具体构造如图3。
2 试验加载方案
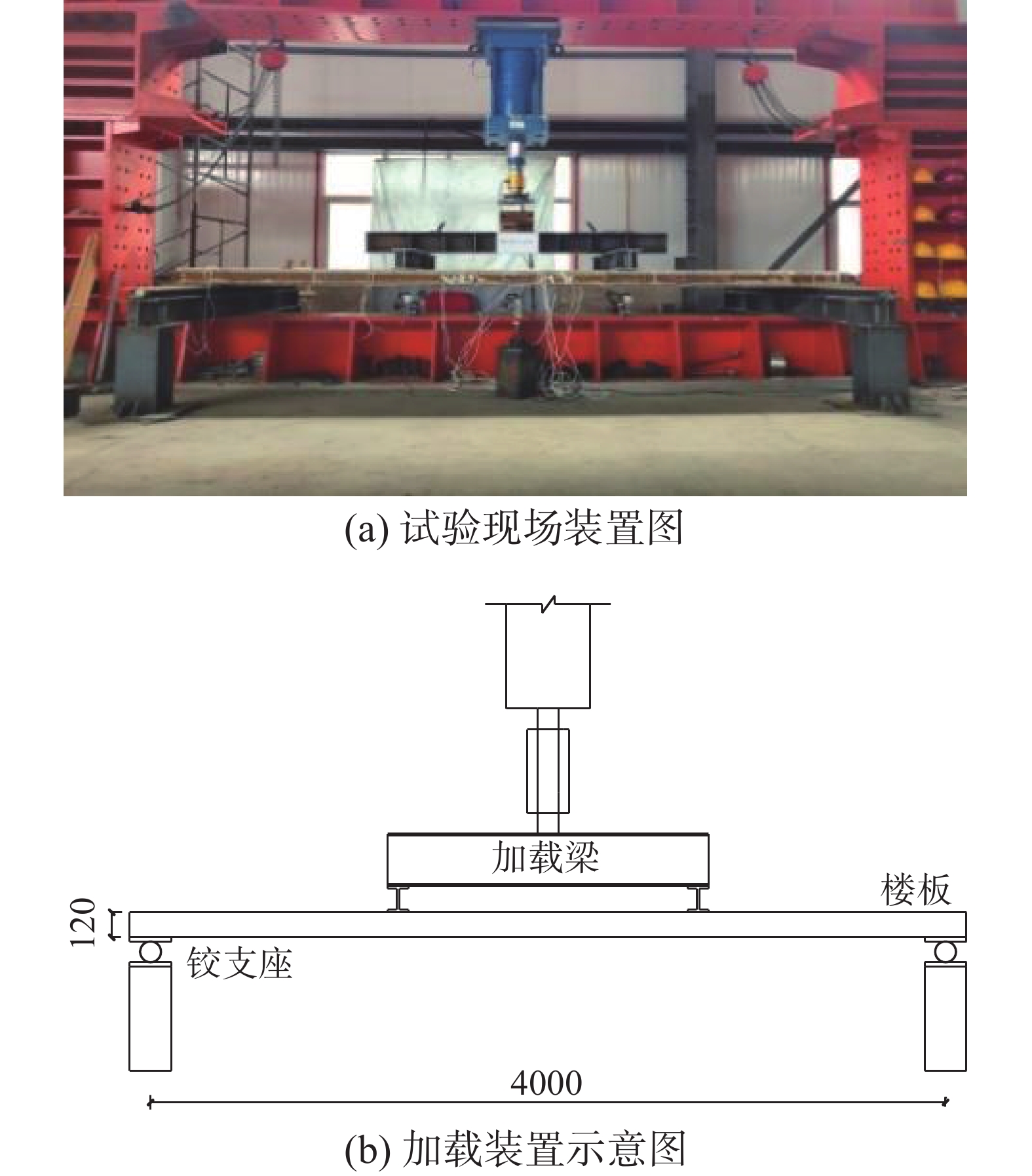
本试验采用单向板两端简支、通过100 kN千斤顶静力加载,通过一根分配梁和两根加载梁进行两点加载,加载点位于板跨三分点处。试件短边简支于墩台上,两端采用辊轴支承,试验装置如图4。以SJB1-1为例加载前考虑楼板自重(13.2 kN)、加载梁自重(2.25 kN),通过跨中等弯矩原则将上述自重折合成集中力为11.59 kN(后文所述性能指标均包含以上自重)。开始加载时取2 kN为一级;出现裂缝后,以1 kN为一级,每一级加载完毕后持荷稳定5 min并观察裂缝开展状况;楼板试件屈服后,以0.5 kN为一级,加载至试件破坏,破坏后以3 kN为一级分级卸载[15]。
3 试验结果及分析
3.1 荷载-挠度曲线
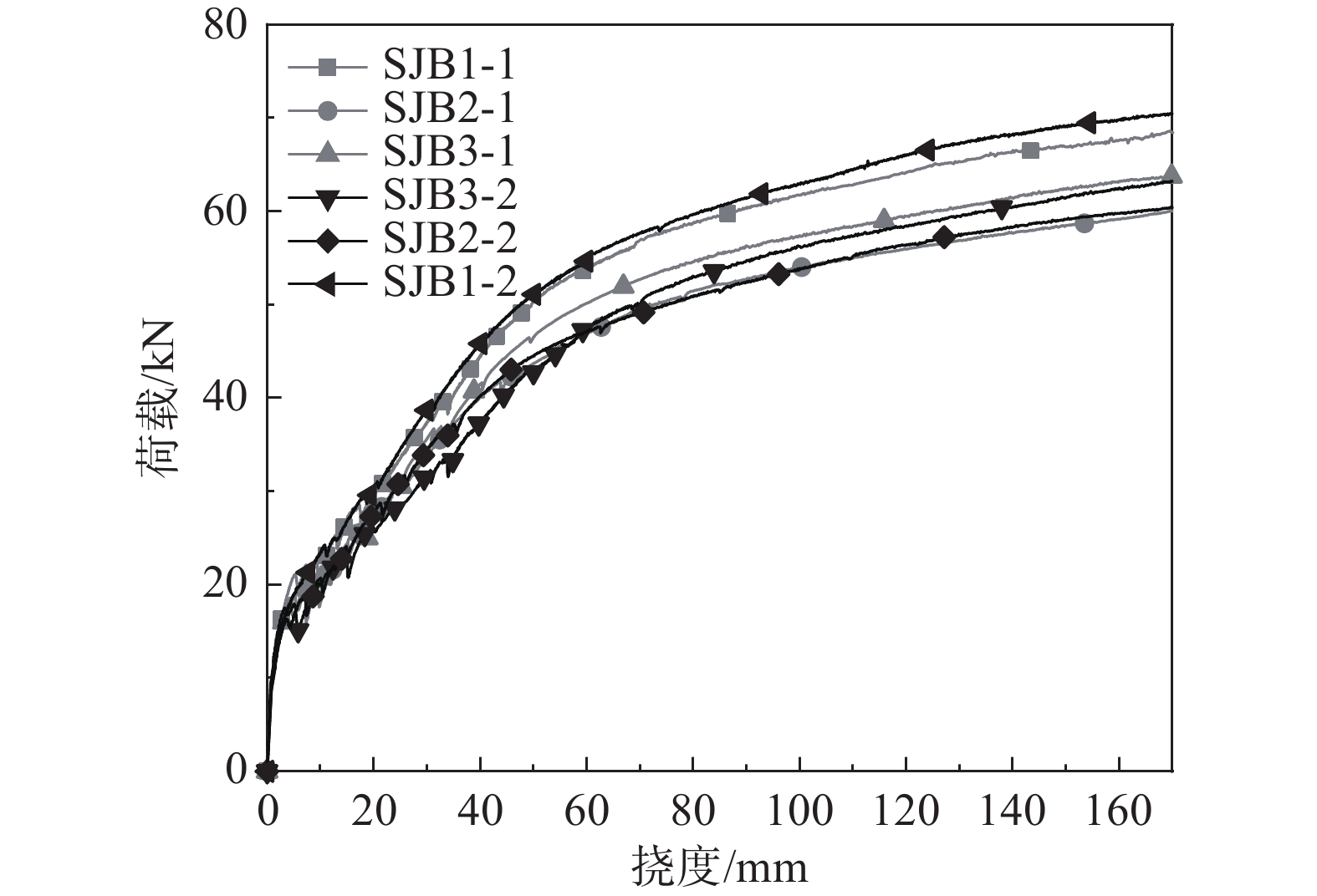
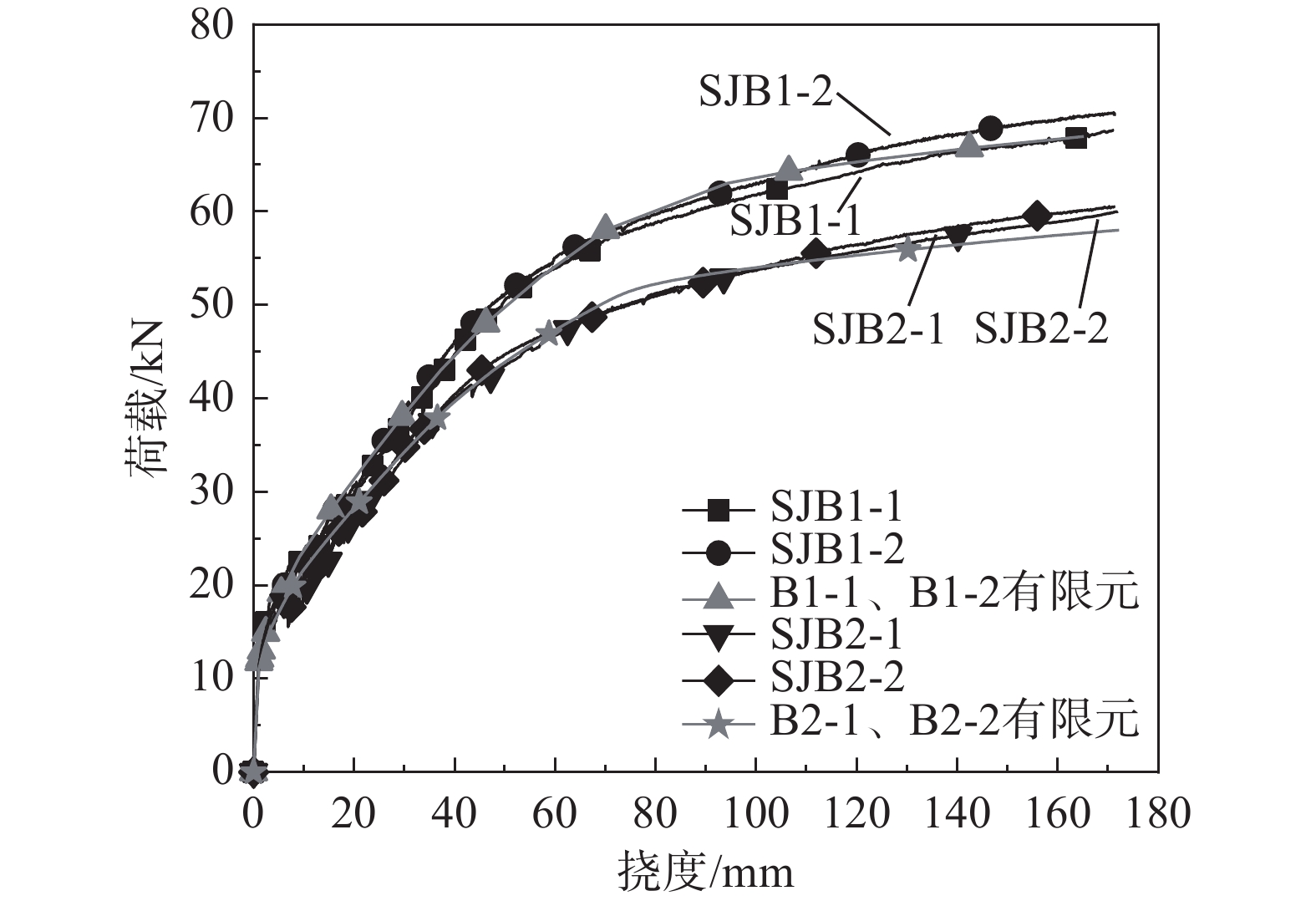
图5为楼板跨中总挠度与总外荷载的关系曲线。为避免材料性能离散的影响,将SJB1-1和SJB1-2、SJB2-1和SJB2-2、SJB3-1和SJB3-2三组中两个试件设计的完全相同,采用两者平均值。六个试件的荷载-挠度曲线(包括自重和自重产生挠度)经历了以下四个阶段:
1)未裂弹性阶段:从将楼板放置于平坦地面开始采集数据,再将楼板吊装到加载平台,将分配梁放置于带C形钢-钢筋混凝土楼板上。荷载与挠度近似成线性比例,楼板刚度较大,荷载迅速增大而挠度增长速度缓慢,曲线斜率较大;
2)混凝土开裂阶段:预制板下部的混凝土在拉力的作用下开裂,裂缝处受拉区混凝土退出工作,荷载和挠度仍近似为线性关系,但曲线斜率略有减小,楼板处于带裂缝工作阶段;
3)钢筋和C形钢屈服阶段:随着变形增加,裂缝不断向上延伸并扩展,裂缝条数也在显著增加,与此同时预制板在跨中变形加大,钢筋先屈服。由于此时边缘C形钢仍未屈服,边缘C形钢承担楼板外荷载增量,所以楼板仍有一定的刚度增量;伴随C形钢也开始屈服,此时楼板刚度降低变快;
4)破坏阶段:荷载增长非常缓慢,但跨中挠度急剧加大,在跨中L/3周围出现了几条贯通整个预制板的受拉主裂缝,楼板上表面有混凝土压碎的迹象,根据《混凝土结构试验方法标准》(GB/T 50152−2012)[16]规定的楼板破坏标志为跨中最大挠度达到楼板跨度的1/50(Pu=84 mm)。此时受拉区大部分混凝土退出工作,试件刚度迅速下降,荷载-挠度曲线接近于水平。
3.2 试件性能指标
试验得到各试件的主要性能指标见表2,其中:Pcr为混凝土开裂荷载;P1为设计承载力;Py为屈服荷载;Pu为极限荷载。从表2可看出,各试件Pcr在于14.3 kN ~16.5 kN。这是由于各板配筋和混凝土浇筑养护条件基本相同,所以混凝土开裂荷载相差不大;各试件Py/Pu分布在0.75~0.79范围内,表明带C形钢-钢筋混凝土楼板从屈服到破坏具有一定的承载力安全储备;P1/Pu分布在0.48~0.54,表明此类型楼板极限承载力较高,也表明其完全满足正常使用极限状态的要求,可保证楼板在使用过程中处于安全状态。
表 2 试件主要性能指标Table 2. Main performance indicators of the specimens试件编号 开裂荷载Pcr/kN 屈服荷载Py/kN 极限荷载Pu/kN Py/Pu 设计承载力P1/kN P1/Pu SJB1-1 16.49 46.59 59.45 0.78 30.39 0.51 SJB1-2 16.03 45.48 60.38 0.75 29.15 0.48 平均值1 16.26 46.04 59.92 0.77 29.77 0.50 SJB2-1 14.95 39.32 52.09 0.75 27.65 0.53 SJB2-2 14.34 39.89 51.52 0.77 28.05 0.54 平均值2 14.65 39.61 51.81 0.76 27.85 0.54 SJB3-1 16.40 42.29 55.31 0.76 28.49 0.52 SJB3-2 16.01 42.41 53.61 0.79 28.25 0.53 平均值3 16.20 42.35 54.46 0.78 28.37 0.52 3.3 楼板应变分析
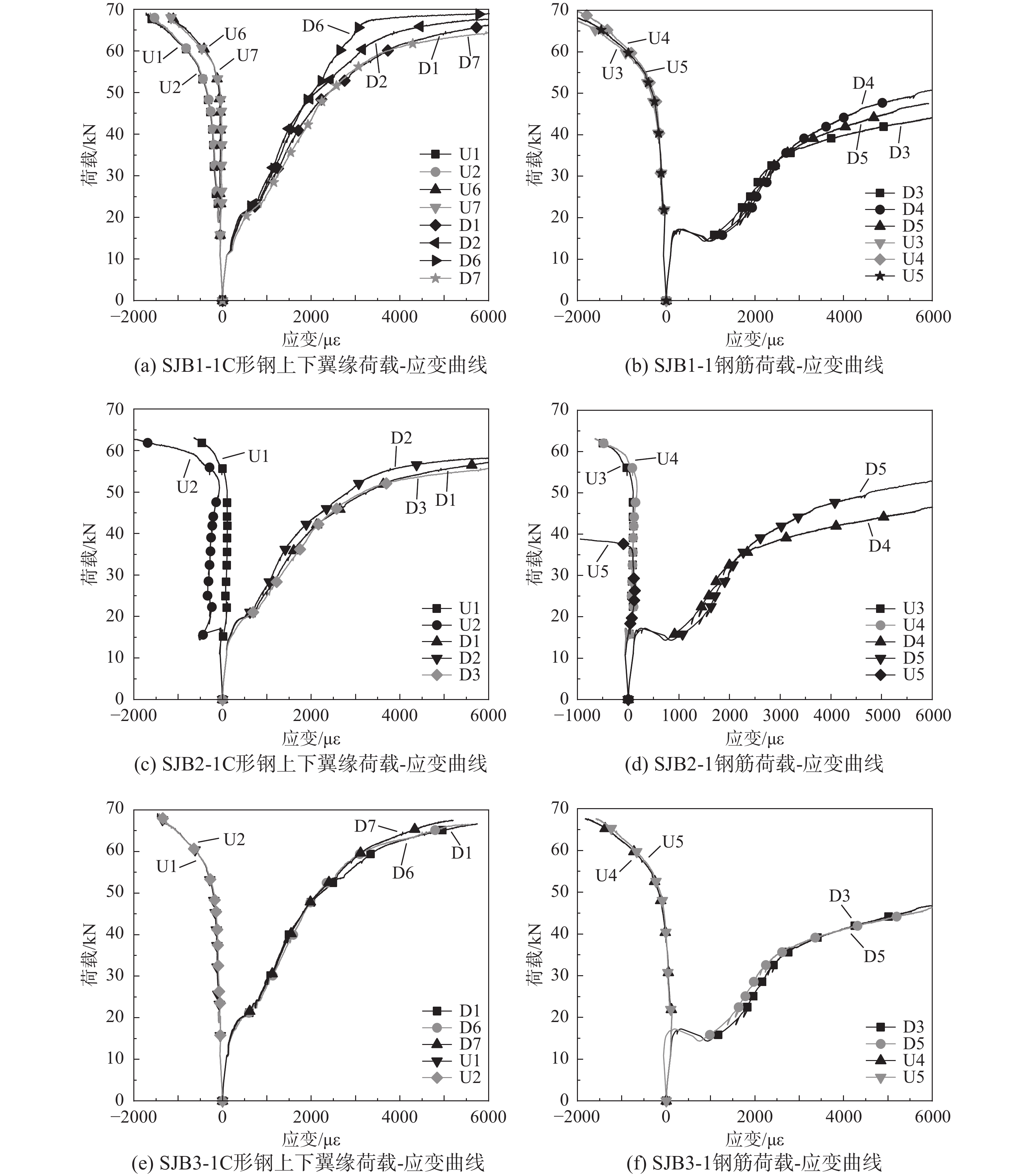
以SJB1-1、SJB2-1及SJB3-1为例说明试件在试验过程中上弦钢筋和下弦钢筋以及C形钢上下翼缘主要测点的应变变化情况。由于应变片无法监测到楼板自重对钢筋和C形钢的影响,所以对此楼板进行有限元分析,提取楼板自重及分配梁自重引起钢筋与C形钢应变加入到试验荷载-应变曲线,曲线见图6。
由图可见,钢筋和C形钢下翼缘应变变化基本可以分为四个阶段:1)未裂弹性阶段:此阶段混凝土受拉且未开裂,C形钢和钢筋应变变化缓慢;2)开裂阶段:当荷载达到15 kN左右时,C形钢应变184 με左右,钢筋应变148 με左右,曲线斜率略微变小,钢筋应变曲线出现短暂降低过程,这表明此时混凝土内已有微裂缝出现并引起楼板刚度变小,与混凝土带裂缝工作的实际工作状态相符。受拉区的拉力主要由钢筋和C形钢承担,这个阶段下弦钢筋和C形钢应变开始逐步提升;3)钢筋和C形钢屈服阶段:钢筋应变达到2200 με,钢筋屈服,此时C形钢还没有屈服,这个阶段再增加的荷载主要由C形钢承担。此时,C形钢应变变化速率略有加快,上弦钢筋应变变化缓慢,下弦钢筋应变变化速率极快;C形钢应变达到1400 με,C形钢屈服,C形钢和下弦钢筋应变变化速率极快,此时上弦钢筋应变开始快速增长;4)破坏阶段:C形钢和上、下弦钢筋应变均增长速度极快,曲线逐渐变水平,这个阶段C形钢和上下弦钢筋基本退出工作。
综上所述,由应变分析可得楼板试件性能良好,混凝土、钢筋及C形钢三者粘结良好,整体协同工作性能优良。
4 有限元模型
4.1 有限元模型
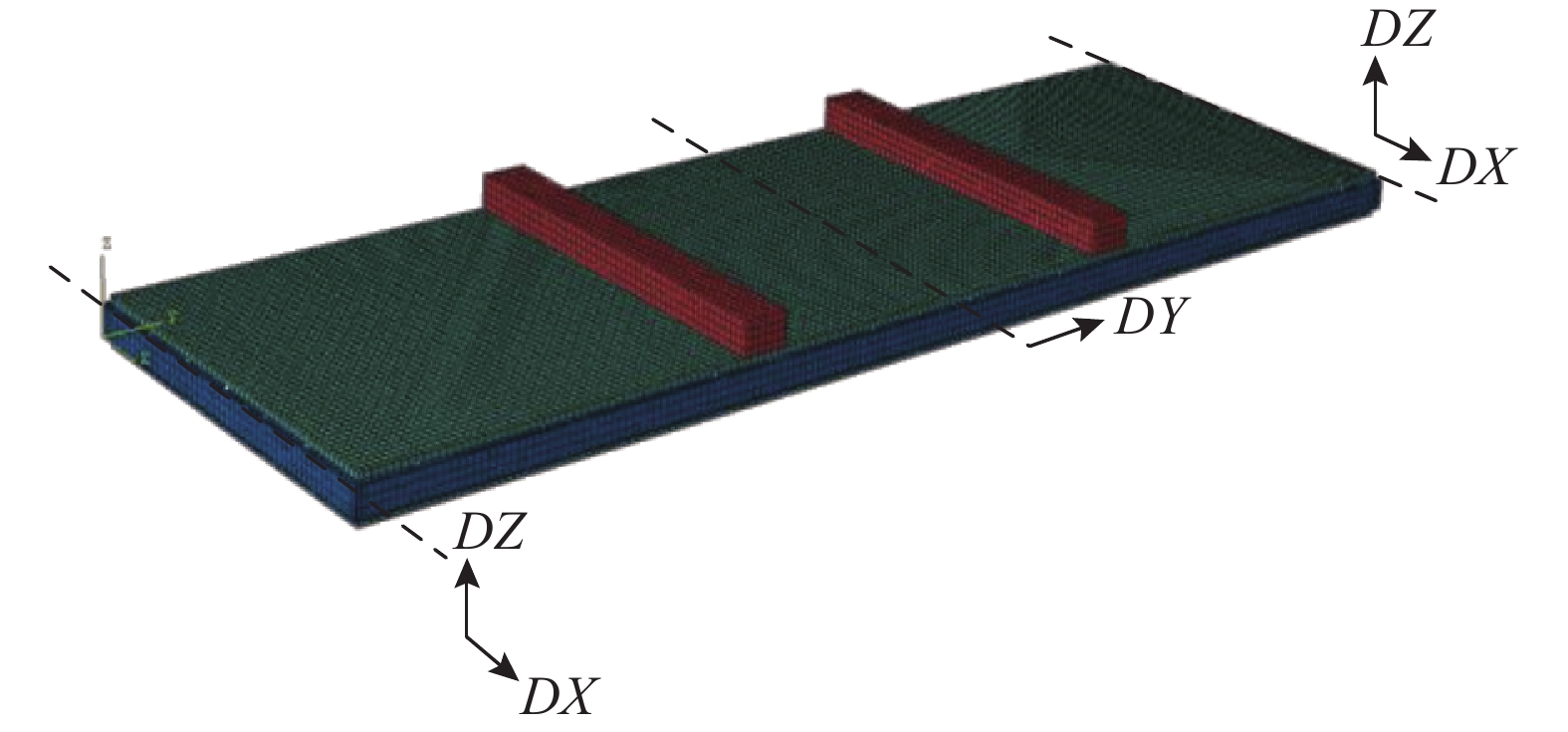
采用通用有限元软件ABAQUS对带C形钢-钢筋混凝土楼板试验试件进行模拟,材料本构关系均取自材性试验,参数见表3。试验当天进行混凝土试块抗压强度和弹性模量的试验,试验测得楼板混凝土的平均立方体抗压强度和弹性模量分别为32.07 N/mm2和3.09×104 N/mm2。典型网格见图7。将有限元与试验得到的荷载-挠度曲线结果比对于图8,有限元数据与试验数据基本吻合,表明有限元模型合理可靠。变化腹板高度、腹板厚度及翼缘宽度(腹板厚度与翼缘厚度相同)等主要几何参数开展参数分析,分析模型见表4。
表 3 材性试验主要参数Table 3. Main parameters of material property test试样类型 直径或厚度/mm 屈服强度fy/(N/mm2) 抗拉强度fu/(N/mm2) 弹性模量E/GPa 极限应变εu/(%) 钢筋 8 440.67 598.12 201.13 13.46 C形钢 4 301.88 386.54 215.72 11.25 表 4 有限元模型参数表Table 4. Parameters of finite element models试件编号 腹板高/mm 腹板厚/mm 翼缘宽/mm H1 60 4 35 H2 70 4 35 H3 80 4 35 H4 90 4 35 T1 80 4 35 T2 80 6 35 T3 80 8 35 T4 80 10 35 W1 80 4 35 W2 80 4 50 W3 80 4 65 4.2 参数分析结果
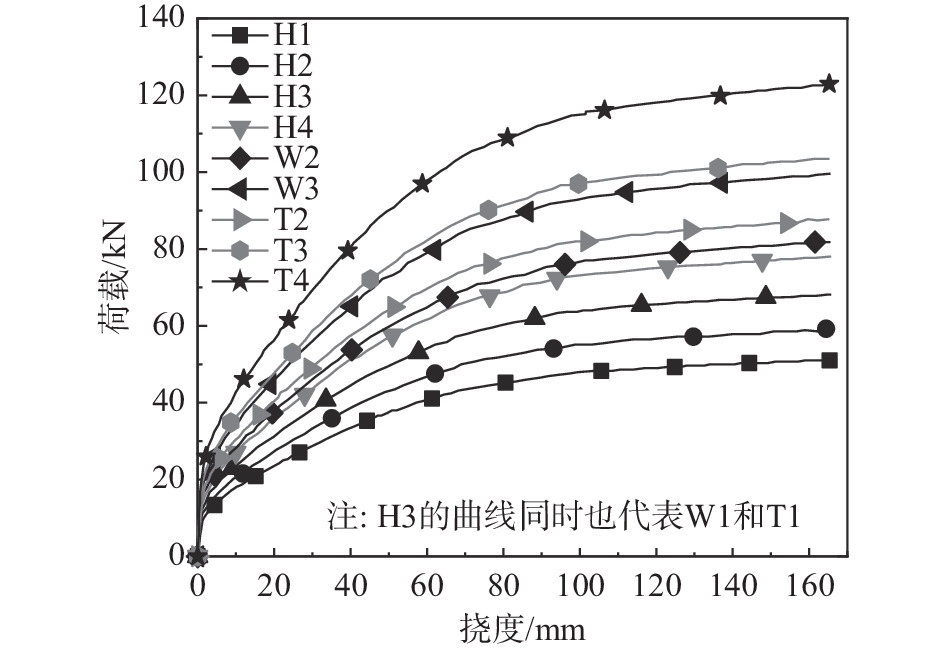
图9为带C形钢-钢筋混凝土楼板在不同参数作用下的荷载-挠度曲线,表5为不同参数下楼板模型的设计和极限承载力。具体分析结果如下:
1) C形钢的腹板高度
伴随着C形钢的腹板高度每次增加10 mm,楼板的设计承载力持续增长,变化速率先慢后快再变慢,对比这四个腹板高度,80 mm的设计承载力提升更为显著;极限承载力则随着腹板高度的增长呈线性增长趋势。同时,设计承载力的百分比变化均比极限承载力的高,说明C形钢的腹板高度对设计承载力影响更大。
试件达到设计承载力的时候均是由于挠度达到限值,此时钢筋没有屈服。增大腹板高度,对于钢筋屈服延缓效果并不明显,对C形钢的屈服有一定的延缓效果。
2) C形钢的腹板厚度
C形钢的腹板厚度每增加2 mm,楼板的设计承载力和极限承载力变化速率与腹板高度类似,设计承载力在腹板厚度为8 mm时提升速率最快,极限承载力基本呈线性增长;不同的是,极限承载力比设计承载力的百分比变化高,说明C形钢的腹板厚度对极限承载力影响更大。
与腹板高度变化不同,提高C形钢的厚度,大大延缓了钢筋的屈服和C形钢的屈服,导致极限承载力提升空间更大,楼板试件的延性更好。
3) C形钢的翼缘宽度
C形钢的翼缘宽度每增加15 mm,楼板的设计承载力就会提升25%,极限承载力提升20%,二者百分比均为线性增长。
对比三者设计承载力和极限承载力百分比变化发现,带C形钢-钢筋混凝土楼板对腹板厚度的变化更敏感,腹板厚度比腹板高度及翼缘宽度对其设计承载力和极限承载力影响更大。
表 5 不同参数下的楼板模型的设计和极限承载力Table 5. Design and ultimate resistance of floor model with different parameters项目 H1 H2 H3(T1,W1) H4 T2 T3 T4 W2 W3 设计承载力/kN 21.59 24.59 31.09 34.59 39.69 48.09 55.09 38.59 46.59 极限承载力/kN 45.87 52.65 60.37 69.82 78.10 92.63 110.10 72.24 88.82 5 计算公式
基于我国规范[15]方法,只考虑钢筋作用时承载力按式(1)~式(2)计算,其中fy为受拉钢筋屈服强度设计值;As为下弦受拉钢筋面积;h0为截面有效高度,取h0=96 mm;x为混凝土受压区高度。计算得到只考虑钢筋作用极限承载力并与试验结果对比,发现试验结果较上述结果提高了2.4倍,表明C形钢边框显著提高了楼板极限承载力。同时试验楼板达到设计承载力时钢筋均未屈服,表明C形钢的存在延缓了钢筋的屈服。
a1fcbx=fyAs (1) Mu = fyAs(h0−x2) (2) 基于参数分析结果,进一步提出带C形钢-钢筋混凝土楼板承载力的简易计算方法,见式(3),式中H、T、W分别为C形钢腹板高度、厚度和翼缘宽度,计算时单位均取 mm。表6对比了式(3)计算值和有限元模拟结果,其比值在0.95~1.05附近,表明计算公式较为准确。
M′u=3.4fyAs(h0−x2)(1+0.15H−8010)⋅(1+0.25T−802)(1+0.20W−3515) (3) 表 6 极限承载力模拟值和计算值对比Table 6. Comparison between simulated and calculated value of ultimate resistance项目 H1 H2 H4 T2 T3 T4 W2 W3 模拟结果/kN 45.87 52.65 69.82 78.10 92.63 110.10 72.24 88.82 计算结果/kN 44.32 53.81 72.80 79.14 94.96 110.79 75.97 88.63 模拟结果/计算结果 1.03 0.98 0.96 0.99 0.98 0.99 0.95 1.00 6 结论
提出一种带C形钢-钢筋混凝土预制楼板,通过对6个试件进行静力试验和有限元分析,得到如下结论:
(1)带C形钢-钢筋混凝土楼板截面形式新颖,板底平整, 施工构造简单,便于板间连接,具有较好的截面特性和受力性能,有很好的推广应用价值;
(2)试验中的6个楼板荷载-挠度曲线走势基本一致,都历经未裂弹性阶段、混凝土开裂阶段、钢筋、C形钢屈服阶段和破坏阶段。在试验加载过程中,受压区混凝土并没有出现和C形钢、钢筋滑移或者脱离的现象,钢筋、C形钢和混凝土三者粘结性能良好,整体协同工作性能优秀;
(3) 6个试件的极限荷载均为屈服荷载的1.3倍左右,可保证楼板屈服后有一定的安全储备。
(4)模拟进行参数分析,得到增大腹板高度,设计承载力百分比变化比极限承载力的高,说明腹板高度对设计承载力影响更大;增大腹板厚度,极限承载力的百分比变化比设计承载力的高,说明腹板厚度对极限承载力影响更大;腹板厚度比腹板高度及翼缘宽度对其设计承载力和极限承载力影响更大。
(5)提出了所提楼板极限承载力的简易计算公式。
-
表 1 节点编号和参数
Table 1 Number and parameters of the joints
节点
编号腹板
拼接板翼缘高强螺
栓数量垂直
加劲肋H型钢
梁高/mm悬臂梁外伸
距离/mm上翼缘最外排螺栓与拼接区
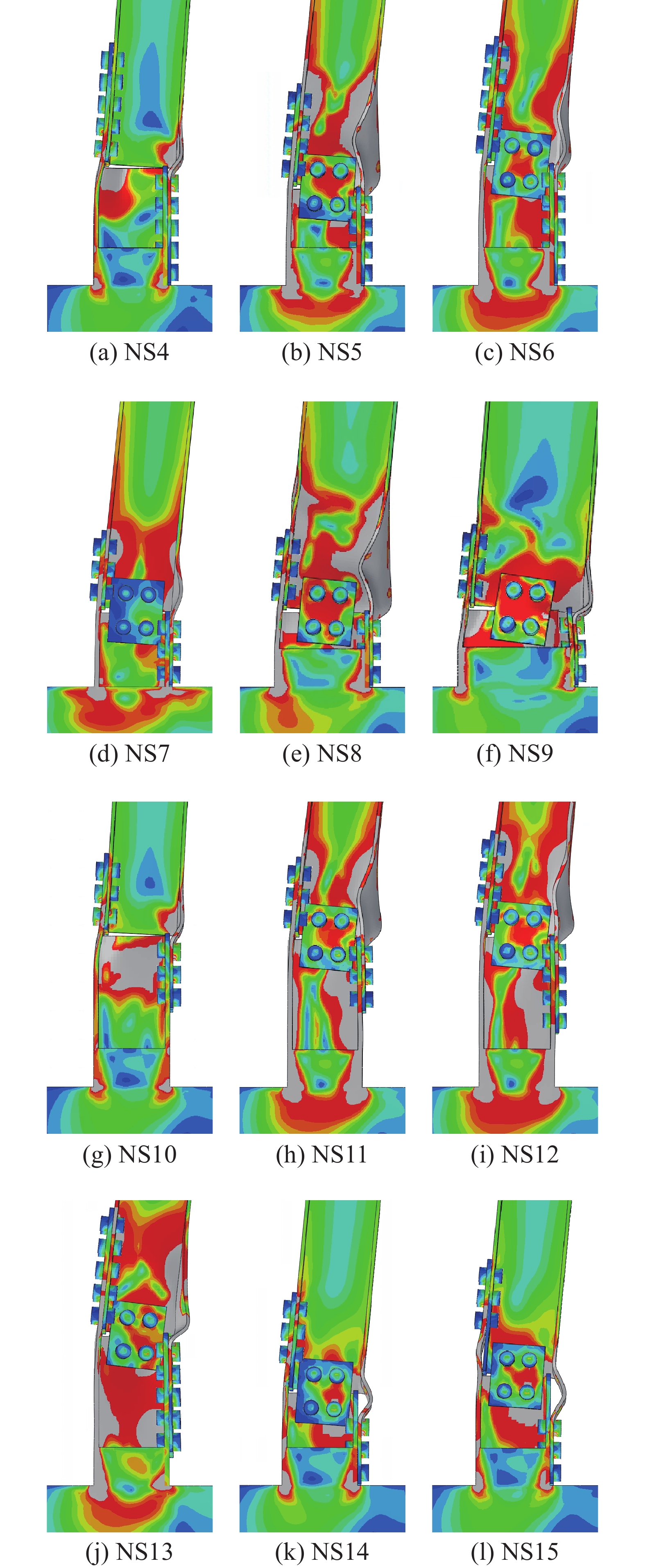
中心距离/mmNS1 √ 6 √ 194 200 45 NS2 − 6 √ 194 200 45 NS3 − 8 √ 194 260 45 NS4 − 10 √ 194 320 45 NS5 √ 8 √ 194 260 45 NS6 √ 10 √ 194 320 45 NS7 √ 6 − 194 200 45 NS8 √ 6 √ 244 200 45 NS9 √ 6 √ 294 200 45 NS10 − 6 √ 194 400 45 NS11 √ 6 √ 194 400 45 NS12 √ 8 √ 194 400 45 NS13 √ 10 √ 194 400 45 NS14 √ 6 √ 194 250 95 NS15 √ 6 √ 194 300 145 表 2 节点主要性能指标
Table 2 Primary performance indicators of the joints
节点编号 方向 滑移荷载Ps/kN 滑移位移Δs/mm 屈服荷载Py/kN 屈服位移Δy/mm 峰值荷载Pu/kN 极限位移Δu/mm 延性系数μ 极限转角θu/(%rad) NS1 正向 34.40 13.92 68.98 69.44 83.04 155.71 11.19 7.99 负向 35.01 13.87 71.47 73.38 86.65 155.70 11.23 7.98 NS2 正向 35.49 14.10 41.14 40.03 62.57 125.89 8.93 6.46 负向 36.24 14.10 60.37 60.22 78.50 155.74 11.04 7.99 NS3 正向 48.61 18.15 52.37 29.18 64.54 120.44 6.64 6.18 负向 49.56 19.18 58.03 44.07 81.83 147.11 7.67 7.54 NS4 正向 49.16 18.32 61.58 29.52 68.64 109.45 5.98 5.61 负向 49.44 18.20 67.36 42.76 84.89 143.39 7.88 7.35 NS5 正向 51.22 19.14 63.92 46.10 85.09 154.73 8.08 7.93 负向 52.46 19.23 67.19 57.47 95.28 155.38 8.08 7.97 NS6 正向 65.20 28.94 69.06 42.94 90.90 155.85 5.39 7.99 负向 64.73 26.70 69.14 52.79 100.21 152.34 5.71 7.81 NS7 正向 37.97 17.69 58.24 63.35 80.47 155.92 8.82 8.00 负向 38.36 17.56 57.90 66.08 82.81 154.62 8.80 7.93 NS8 正向 48.07 14.10 74.24 45.51 98.93 155.45 11.03 7.97 负向 48.94 14.08 87.74 57.79 114.17 155.83 11.07 7.99 NS9 正向 57.37 13.56 98.24 38.89 116.79 126.22 9.31 6.47 负向 58.90 13.37 107.09 50.60 136.98 154.51 11.55 7.92 NS10 正向 37.88 14.10 49.49 40.54 69.78 109.03 7.73 5.59 负向 38.07 14.10 68.65 57.12 84.71 145.50 10.32 7.46 NS11 正向 44.67 18.01 77.95 64.02 94.04 153.74 8.54 7.88 负向 45.38 17.92 79.63 72.24 101.30 150.39 8.39 7.71 NS12 正向 52.53 19.18 72.14 51.64 95.58 151.99 7.93 7.79 负向 52.09 19.18 74.33 60.18 104.10 155.16 8.09 7.96 NS13 正向 68.56 28.42 71.20 42.01 92.60 155.16 5.46 7.96 负向 68.18 28.62 72.65 51.39 101.79 154.07 5.38 7.90 NS14 正向 37.54 14.10 54.70 45.71 71.21 132.53 9.40 6.80 负向 37.16 14.10 68.59 63.75 86.61 152.14 10.79 7.80 NS15 正向 38.16 14.10 58.03 47.47 74.38 110.88 7.86 5.69 负向 37.78 14.10 67.84 58.03 84.58 155.97 11.06 8.00 表 3 受弯承载力模拟值与公式值对比
Table 3 Comparison of flexural capacity between simulated values and formula values
节点编号 受弯承载力模拟值
MR,FE/(kN·m)受弯承载力公式值
MR/(kN·m)MR/MR,FE 极限受弯承载力
模拟值Mu,FE/(kN·m)极限受弯承载力
公式值Mu/(kN·m)Mu/Mu,FE 正向 负向 MS1 MS2 MR 正向 负向 正向 负向 Mu1 Mu2 Mu3 Mu 正向 负向 NS1 67.1 68.3 64.8 88.3 64.8 0.97 0.95 161.9 169.0 140.9 196.1 99.1 99.1 0.61 0.59 NS2 69.2 70.7 64.8 88.3 64.8 0.94 0.92 122.0 153.1 140.9 196.1 99.1 99.1 0.81 0.65 NS3 94.8 96.6 90.0 92.0 90.0 0.95 0.93 125.9 159.6 195.9 272.6 103.4 103.4 0.82 0.65 NS4 95.9 96.4 117.6 96.1 96.1 1.00 1.00 133.8 165.5 255.8 355.9 108.0 108.0 0.81 0.65 NS5 99.9 102.3 90.0 92.0 90.0 0.90 0.88 165.9 185.8 195.9 272.6 103.4 103.4 0.62 0.56 NS6 127.1 126.2 117.6 96.1 96.1 0.76 0.76 177.3 195.4 255.8 355.9 108.0 108.0 0.61 0.55 NS7 74.0 74.8 64.8 88.3 64.8 0.87 0.87 156.9 161.5 140.9 196.1 99.1 99.1 0.63 0.61 NS8 93.7 95.4 81.5 111.0 81.5 0.87 0.85 192.9 222.6 177.2 246.6 124.7 124.7 0.65 0.56 NS9 111.9 114.8 98.2 133.8 98.2 0.88 0.85 227.7 267.1 213.5 297.1 150.2 150.2 0.66 0.56 NS10 80.4 83.0 75.0 102.2 75.0 0.93 0.90 136.1 165.2 163.1 227.0 114.8 114.8 0.84 0.69 NS11 87.1 88.5 75.0 102.2 75.0 0.86 0.85 183.4 197.5 163.1 227.0 114.8 114.8 0.63 0.58 NS12 102.4 101.6 100.0 102.2 100.0 0.98 0.98 186.4 203.0 217.5 302.7 114.8 114.8 0.62 0.57 NS13 133.7 132.9 125.0 102.2 102.2 0.76 0.77 180.6 198.5 271.9 378.4 114.8 114.8 0.64 0.58 NS14 73.2 72.5 64.8 88.3 64.8 0.88 0.89 138.9 168.9 140.9 196.1 99.1 99.1 0.71 0.59 NS15 74.4 73.7 64.8 88.3 64.8 0.87 0.88 145.0 164.9 140.9 196.1 99.1 99.1 0.68 0.60 平均值 − − − − − 0.89 − − − − − − 0.64 标准差 − − − − − 0.07 − − − − − − 0.07 -
[1] Luis F Ibarra, Helmut Krawinnkler. Global collapse of frame structures under seismic excitations [R]. Stanford, Califormia: The John A. Blume Earthquake Engineering Research Center, 2005.
[2] Miller D K. Lessons learned from the Northridge earthquake [J]. Engineering Structures, 1998, 20(4/5/6): 249 − 260. doi: 10.1016/S0141-0296(97)00031-X
[3] Nakashima M, Inoue K, Tada M. Classification of damage to steel buildings observed in the 1995 Hyogoken-Nanbu earthquake [J]. Engineering Structures, 1998, 20(4/5/6): 271 − 281. doi: 10.1016/S0141-0296(97)00019-9
[4] 张爱林, 孙勇, 刘学春, 詹欣欣, 李超. 方钢管混凝土柱-H形钢梁螺栓连接节点受力性能试验研究[J]. 建筑结构学报, 2017, 38(11): 64 − 73. Zhang Ailin, Sun Yong, Liu Xuechun, Zhan Xinxin, Li Chao. Experimental study on mechanical performance of concrete-filledsquare steel tubular columns to H-section steelbeam bolted connection [J]. Journal of Building Structures, 2017, 38(11): 64 − 73. (in Chinese)
[5] Liu X C, Zhan X X, Pu S H, et al. Seismic performance study on slipping bolted truss-to-column connections in modularized prefabricated steel structures [J]. Engineering Structures, 2018, 163: 241 − 254. doi: 10.1016/j.engstruct.2018.02.043
[6] 张伟杰, 廖飞宇, 李威. 带圆弓形脱空缺陷的钢管混凝土构件在压弯扭复合受力作用下的滞回性能试验研究[J]. 工程力学, 2019, 36(12): 121 − 133. doi: 10.6052/j.issn.1000-4750.2018.12.0713 Zhang Weijie, Liao Feiyu, Li Wei. Experimental study on the cyclic behavior of concrete-filled steel tubular (CFST) members with circular-segment gaps under combined comperssion-bending-torsion loading [J]. Engineering Mechanics, 2019, 36(12): 121 − 133. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.12.0713
[7] 徐礼华, 宋杨, 刘素梅, 李彪, 余敏, 周凯凯. 多腔式多边形钢管混凝土柱偏心受压承载力研究[J]. 工程力学, 2019, 36(4): 135 − 146. doi: 10.6052/j.issn.1000-4750.2018.02.0090 Xu Lihua, Song Yang, Liu Sumei, Li Biao, Yu Min, Zhou Kaikai. Study on the eccentric compressive bearing capacity of polygonal multi-cell concrete filled steel tubular columns [J]. Engineering Mechanics, 2019, 36(4): 135 − 146. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.02.0090
[8] 刘学春, IM MYONG HAK, 陈学森, 余少乐, 潘钧俊. L形钢管混凝土柱-H型钢梁Z字形拼接节点抗震性能研究[J]. 建筑结构, 2021, 51(23): 61 − 68. Liu Xuechun, IM MYONG HAK, Chen Xuesen, Yu Shaole, Pan Junjun. Seismic behavior of Z-shaped splicing joint between concrete-filled L-shaped steel tubular column and H-section beam [J]. Building Structure, 2021, 51(23): 61 − 68. (in Chinese)
[9] ANSI/AISC 341-16, Seismic provisions for structural steel buildings [S]. Chicago: American Institute of Steel Construction, 2016.
[10] Liu X C, He X N, Wang H X, et al. Bending-shear performance of column-to-column bolted-flange connections in prefabricated multi-high-rise steel structures [J]. Journal of Constructional Steel Research, 2018, 145: 28 − 48.
[11] Liu X C, Cui F Y, Zhan X X, et al. Seismic performance of bolted connection of H-beam to HSS-column with web end-plate [J]. Journal of Constructional Steel Research, 2019, 156: 167 − 181.
[12] 刘威. 钢管混凝土局部受压时的工作机理研究 [D]. 福州: 福州大学, 2005. Liu Wei. Research on mechanism of concrete-filled steel tubes subjected to local compression [D]. Fuzhou: Fuzhou University, 2005. (in Chinese)
[13] T/CSCS 012−2021, 多高层建筑全螺栓连接装配式钢结构技术标准 [S]. 北京: 中国建筑工业出版社, 2021. T/CSCS 012−2021, Technical standard for fully bolted assembled steel structures of multi-high-rise storey buildings [S]. Beijing: China Architecture & Building Press, 2021. (in Chinese)
-
期刊类型引用(4)
1. 王怡平,李进孝,任志凤,谢鑫宇,毛湘,刘建坤. 光伏支架基础现状与砂砾石地质下其结构优化的研究. 太阳能. 2025(05): 88-95 .  百度学术
百度学术
2. 石敬州,周凌宇,方蛟鹏,刘晓春,刘家豪,何昌杰,李分规,戴超虎,廖飞,吴睿智. 梁板融合预制装配式双拼槽钢-混组合楼板试验. 哈尔滨工业大学学报. 2024(01): 73-83 .  百度学术
百度学术
3. 巩涛,赵博,曹万林,杨兆源,徐涛,王红兵. 装配式轻钢框架组合楼盖平面外受力性能研究. 施工技术(中英文). 2024(20): 167-174 .  百度学术
百度学术
4. 陶慕轩,蒋骋昊,潘文豪. 复杂结构楼板面内力学行为研究综述与展望. 工程力学. 2024(12): 1-9 .  本站查看
本站查看
其他类型引用(4)



 下载:
下载: