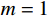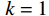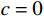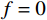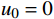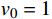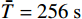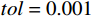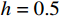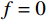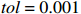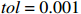AN INITIAL STUDY OF A PRIORI ESTIMATION OF STEP-SIZE FOR TIME-ELEMENTS IN SOLVING MOTION EQUATION
-
摘要: 基于单元能量投影(element energy projection,EEP)法和边值问题固端法的思想,将其扩展至运动方程问题。该文以单自由度线性元为例,采用Taylor级数渐近展开,对问题的求解进行实质性简化计算;探讨了不经有限元求解便可进行先验定量误差估计的算法;进而实现了自适应单元步长的先验估计和确定。该文给出初步算例,验证了该方法的可行性和有效性。
-
关键词:
- Galerkin有限元法 /
- 运动方程 /
- EEP超收敛 /
- 先验定量估计 /
- 自适应步长
Abstract: Based on the concept of the element energy projection (EEP) and the fix-end method, which makes a priori quantitative error estimation in finite element method (FEM) possible for boundary value problems (BVP), it extends the technique to a typical initial value problem (IVP), i.e., the motion equation. Taking the linear element with single degree of freedom as example, the possibility of a priori quantitative error estimation is discussed by using Taylor series expansion without the needs for FEM solution, which in turn achieves a priori determination of adaptive step-size for the linear time-element. Some preliminary examples are given to show the feasibility and effectiveness of the proposed method. -
结构动力响应问题是近年来的热门课题,常用的时程积分方法更是常用的重要方法,但其计算效率、收敛精度、数值稳定性等均与步长的选择和优化相关[1-2],因此自适应步长求解也成为近几年研究的难点和热点之一。就自适应求解而言,有对离散解进行误差估计并建立自适应算法[3-4]的研究,但在时域上逐点按最大模控制误差的高效自适应求解比较少见,而这恰是本文追求的目标。
袁驷教授领导的课题组依据有限元原理[5]提出的单元能量投影[6-8](element energy projection,EEP)法是一种非常有效的有限元后处理的超收敛算法,可用于逐点误差估计和精度修正。该EEP算法已应用于一维[9-10]、二维有限元[11],乃至三维有限元[12],并且提出一类基于EEP技术的线性有限元时程积分的自适应方法[13-14]。该法采用简单的线性元,构建单步法递推公式,然后运用EEP法进行超收敛计算,并对结点位移修正来提高精度并进行后验自适应求解。此外,该课题组还对边值问题提出了一种先验的自适应方法,称为固端法[15-16],该法可以不经有限元计算,通过EEP解的超收敛性进行直接误差估计,并一举给出满足精度要求的网格划分。
本文基于边值问题的固端法思想,提出一类不经有限元求解、便能得到先验EEP解的自适应步长算法。本文算法相比于文献[13]的后验法,能够在不计算有限元解的情况下,得到满足精度要求的单元步长。文中以线性元为例,给出了代表性算例,用以验证该法的有效性和高效性。算例表明,本文方法在大幅提高计算效率的同时,仍严格保障了解答精度,为其后相关的深入广泛研究提供了有效的可行性方案。
1 问题描述与有限元解
文献[13]采用线性Galerkin有限元,对运动方程进行自适应步长求解提出了整套方案,本节对此做一简要概述。
1.1 问题描述
本文考虑单自由度常系数运动方程:
{Lu≡mu″ (1) 式中:
L 为式中定义的微分算子;m 、c 和k 分别为质量、阻尼和刚度;f 为外荷载函数;u 为动位移;{u_0} 、{v_0} 分别为初始位移和速度;\bar T 为时域的上界。为了兼顾一般问题,时间自变量采用x 。为构造Galerkin弱形式,定义双线性型和线性型:
\begin{split} & a(u,v) = \int_{\,\,0}^{\,\,\bar T} {( - v'mu' + vcu' + vku)\,{\text{d}}x} ,\\& (f,v) = \int_{\,\,0}^{\,\bar T} {vf\,{\text{d}}x} + v(0)m{v_0} \end{split} (2) 记
H_u^1 为所有满足u(0) = {u_0} 且直到一阶导数均平方可积的函数空间,而H_v^1 为所有满足v(\bar T) = 0 且直到一阶导数均平方可积的函数空间,则问题(1)(见式(1))的Galerkin法归结为求解u \in H_u^1 使得:a(u,v) = (f,v),\;\forall v \in H_v^1 (3) 1.2 Galerkin有限元解
由于可以逐单元步长积分求解,不失一般性,仅考虑两端结点坐标为
(0,\;h) 的典型单元e 。采用线性单元,将试探函数u_{}^h 与检验函数v_{}^h 均取为线性函数:\begin{split} & u_{}^h = \sum\limits_{i = 1}^2 {{N_i}u_i^h} = \left( {1 - \frac{{\bar x}}{h}} \right)u_1^h + \frac{{\bar x}}{h}u_2^h \;, \\& v_{}^h = \sum\limits_{i = 1}^2 {{N_i}v_i^h} ,\; \bar x \in [0,\;h] \end{split} (4) 则Galerkin有限元解归结为求解
{u^h} \in S_u^h \subset H_u^1 使得:a({u^h},{v^h}) = (f,{v^h})\; ,\;\forall {v^h} \in S_v^h \subset H_v^1 (5) 其中,
S_u^h 和S_v^h 为通常意义下的有限元试探空间和检验空间。基于式(5),可求得单元刚度矩阵和单元等效结点荷载向量:\begin{split} & {{\boldsymbol{k}}^e} = \left( {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}} \\ {{k_{21}}}&{{k_{22}}} \end{array}} \right) = \\&\;\;\;\; \frac{1}{{6h}}\left( {\begin{array}{*{20}{c}} { - 6m - 3ch + 2k{h^2}}&{6m + 3ch + k{h^2}} \\ {6m - 3ch + k{h^2}}&{ - 6m + 3ch + 2k{h^2}} \end{array}} \right) ,\\& {{\boldsymbol{F}}^e} = \left\{ {\begin{array}{*{20}{c}} {{F_1}} \\ {{F_2}} \end{array}} \right\} \end{split} (6) 则Galerkin有限元求解归结为如下递推公式[13]:
\left\{ \begin{gathered} u_2^h = k_{12}^{ - 1}(F_1^{} - k_{11}^{}u_1^h + mv_1^ * ) \hfill \\ v_2^ * = {m^{ - 1}}(F_2^{} - {k_{22}}u_2^h - k_{21}^{}u_1^h) \hfill \\ \end{gathered} \right. (7) 其中,在第一个单元,
u_1^h 和v_1^* 分别取{u_0} 和{v_0} 。注意,{m^{ - 1}} 与步长h 无关,可以一次性求出,而k_{12}^{ - 1} 则对不同步长h 需要重新计算,对于多自由度问题更是主要的耗时计算的环节。通常情况,线性元的结点位移和单元内位移同为O({h^2}) 收敛。1.3 EEP超收敛解
EEP超收敛计算是本文误差估计的核心技术[6-8]。在得到常规有限元解答
{u^h} 后,可推导出EEP超收敛位移的计算公式[13]如下:\begin{split} u_{}^ * = &u_{}^h - \frac{h}{m}\;\left( {N_1^{}\int_0^{\bar x} {N_2^{}(f - L{u^h})\,{\text{d}}} x} + \right. \\ & \left. { N_2^{}\int_{\bar x}^h {N_1^{}(f - L{u^h})\,{\text{d}}x} } \right) \end{split} (8) 其中:上标
* 表示超收敛解。对于线性元,有限元解{u^h} 与EEP解u_{}^ * 具有相同收敛阶,同为O({h^2}) ;但研究表明,u_{}^ * 仍可用来代替精确解u 对{u^h} 进行误差估计。1.4 自适应步长公式
本文的自适应目标与文献[13]相同,即在精确解
u 未知的情况下,事先给定误差限tol ,寻求一个优化的单元步长h ,使得有限元解答{u^h} 按最大模度量,逐单元满足:\mathop {\max }\limits_e |u_{}^* - u_{}^h|\; \leqslant tol (9) 其中,
{u^h} 和u_{}^* 为当前单元步长{h_0} 上的解答。若当前解不满足式(9),则采用文献[13]的步长公式估算新的步长:h = {h_0}{\left( {\frac{{\alpha \cdot tol}}{{\mathop {\max }\limits_e \left| {u_{}^* - u_{}^h} \right|}}} \right)^{\tfrac{2}{5}}} (10) 其中,
\alpha \leqslant 1 是一个安全系数(通常取0.8)。步长公式的数学证明见文献[17]。1.5 结点位移修正
由于线性元结点收敛阶与有限元解和EEP解收敛阶均相同,而对于初值问题,结点位移的误差是发生数值耗散的最主要和关键的因素,为此文献[13]引入了基于EEP超收敛解的结点位移修正技术[18]。
将
{e^*} = u - {u^*} 代回式(1),限于第一个单元,可以得到{e^*} 的控制微分方程和初值条件:\left\{ \begin{gathered} L{e^*} = {f^*},\quad 0 < x \leqslant h \hfill \\ {e^*}(0) = 0,\quad {e^*}^\prime (0) = 0 \hfill \\ \end{gathered} \right. (11) 其中,残余荷载
{f^*} = f - L{u^*} 。对此问题,在现有的有限元步长上,再次求解{e^*} 的有限元解{\varepsilon ^h} ,并将结点2的位移修正为u_2^h + \varepsilon _2^h 。这一修正技术的突出特点是,只需用{f^*} 代替f 形成一个新荷载向量,无需求逆计算,只经回代过程即可;且如此修正后的结点位移的收敛阶由原来的O({h^{\text{2}}}) 提升为O({h^{\text{4}}}) ,使得结点位移精度翻倍,极大提升了自适应的性能和效率。1.6 自适应步长求解
综合以上可得一个自适应步长求解的完整算法[13],简要归纳为:① 用初始步长计算有限元解;② 计算EEP解并进行误差比较;③ 如果不满足要求则调整步长,并返回①;④ 如果满足要求则对右端点进行结点位移修正,并进行下一个单元计算。
2 先验法
1.6节算法是一套完整、可靠、有效的算法,其中为了自适应调整步长,采用了后验误差估计
u_{}^ * - {u^h} 。为了计算u_{}^ * - {u^h} ,需要事先计算有限元解u_{}^h ,亦即需要多次计算式(7)中的k_{12}^{ - 1} 。以下探讨一种不经有限元求逆计算k_{12}^{ - 1} 的先验误差估计并确定步长的方法,以期进一步提升求解效率。2.1 误差估计的简化
误差估计的常规做法是采用EEP解
{u^*} 代替精确解u ,亦即用{e^{*h}} = {u^*} - {u^h} 代替{e^h} = u - {u^h} 来估计有限元解{u^h} 的误差,且要求{e^{{\text{*}}h}} 满足误差限来确定临界步长。由于{e^{*h}} 在单元两端点均为0,故单元上{e^{{\text{*}}h}} 的最大值必取在单元内的极值点上。这样,确定临界步长归结为如下一组非线性代数方程组的求解,即求解x、\;h ,使得:\left\{ \begin{aligned} & {{e^{*h}}(x,\;h) = {\rm sgn} ({e^{*h}})tol} \\& {\frac{{\partial {e^{*h}}(x,h)}}{{\partial x}} = 0} \end{aligned} \right. (12) 为了能得到式(12)的先验计算结果,本文采取以下两项简化举措。
简化一,将单元上的荷载近似为常数
{f_0} 。本文取单元内中点值,即{f_0} = f({h \mathord{\left/ {\vphantom {h 2}} \right. } 2}) ,则{e^{*h}} 可简化为显式表达的三次多项式:\begin{split} & {{\hat e}^{{\text{*}}h}} = {\mkern 1mu} \frac{{6mkh{u_0} + 2{\mkern 1mu} mk{\mkern 1mu} {h^2}{v_0} + 6mch{v_0}{\mkern 1mu} - 6{\mkern 1mu} mh{f_0}}}{{2mH}}x + \\& \quad \frac{{ - 6m{\mkern 1mu} k{\mkern 1mu} {u_0} - {k^2}{h^2}{u_0} - 6{\mkern 1mu} m{\mkern 1mu} c{\mkern 1mu} {v_0} + 6{\mkern 1mu} m{f_0} + k{\mkern 1mu} {h^2}{f_0}}}{{2mH}}{x^2} + \\& \quad \frac{{{k^2}h{u_0} - 2mk{v_0} - kh{f_0}}}{{2mH}}{x^3} \end{split} (13) 其中,
H = 6h{\kern 1pt} {k_{12}} = 6m + 3ch + k{h^2} 。{\hat e^{{\text{*}}h}} 虽然是x的三次多项式,但是对于h是有理分式,其中{1 \mathord{\left/ {\vphantom {1 H}} \right. } H} 涉及{({k_{12}})^{ - 1}} 的计算,随着自由度数值的增加,计算效率随之大幅降低。事实上,若完成了{({k_{12}})^{ - 1}} 的计算,就相当于完成了有限元求解,便不能称为先验法了。简化二,将
{H^{ - 1}} 进行Taylor级数展开。记为:\begin{split} \bar H =& {H^{ - 1}} = \frac{1}{{6m}} + \frac{c}{{12{m^2}}}h + \\ & \frac{{3{c^2} - 2mk}}{{72{m^3}}}{h^2} + \frac{{4mck - 3{c^3}}}{{144{m^4}}}{h^3} + O({h^4}) \end{split} (14) 实际计算时,
\bar H 的展开式中可取2项或者3项。将
\bar H 展开式(14)代入式(13),可得到先验误差估计{\hat e^{{\text{*}}h}} 的进一步简化的表达式。2.2 先验误差估计
在计算步长的时候,首先需要求得最大误差。为了求
{\hat e^{{\text{*}}h}} 的极值,给定初始步长{h_0} ,则由({\hat e^{{\text{*}}h}})' = 0 可得一个x 的二次方程,意味着在单元上最多有2个极值点(记为{x_1} 、{x_2} ,且{x_1} \leqslant {x_2} ),均可以用公式直接求出。记
{x_{\rm m}} 为取得最大误差值\max | {{{\hat e}^{{\text{*}}h}}} | 的坐标点。若单元内只有一个极值点,则该点即为{x_{\rm m}} 。若有两个极值点,则取使绝对误差较大的{x_{\rm m}} 。2.3 先验步长计算
有了当前步长
{h_0} 上的{x_{\rm m}} ,则可令| {{{\hat e}^{{\text{*}}h}}({x_{\rm m}})} | = tol 来估算一个临界步长h 。但由于临界步长的迭代计算涉及到虚根计算,仍显复杂,本文采用效率更高的步长公式计算新的步长:h = {h_0}{\left( {\frac{{{\alpha _0} \cdot tol}}{{| {{{\hat e}^{*h}}({x_{\rm m}})} |}}} \right)^{\tfrac{2}{5}}} (15) 其中,
{\alpha _0} 为先验算法的安全系数,可以比后验公式(10)中的\alpha 更小一些,以保证先验法的有效性和安全性。与式(10)类似,先验法自适应目标为\max | {{{\hat e}^{{\text{*}}h}}} | \leqslant tol ;但是与后验法不同的是,先验法无需计算有限元解。2.4 双验法求解策略
有了先验误差估计和步长计算的手段,可以对第1.6小节中的求解方案作出改进,即:用先验法估计步长,用后验法检验步长。这样,先验法和后验法各自发挥自己所长,既提高了求解效率,又不失精度的保障。这一“双验法”自适应步长求解策略可归纳为:
a) 给定初始步长
{h_0} ;b) 用先验法检验误差,必要时调整步长
h ;c) 计算有限元解;
d) 计算EEP解并用后验法检验误差;
e) 如不满足要求则调整步长,并返回到c),满足则继续下一步;
f) 对右端点进行结点位移修正,并进行下一个单元计算。
3 数值算例
本文采用符号计算软件Maple计算有阻尼简谐运动和无阻尼自由振动的算例,以验证本法的有效性。为方便起见,本文引入误差比,即误差与误差限之比,记作
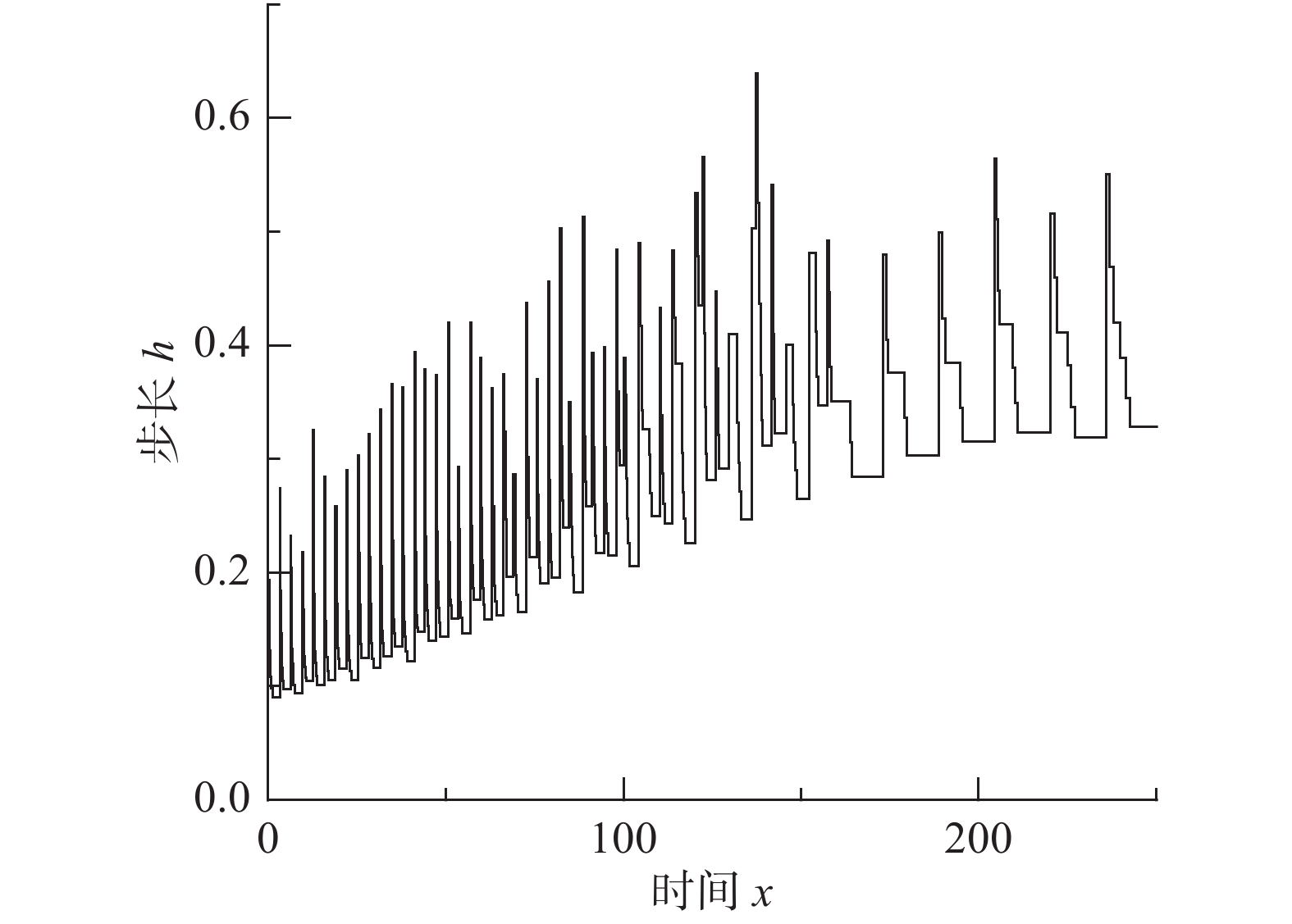
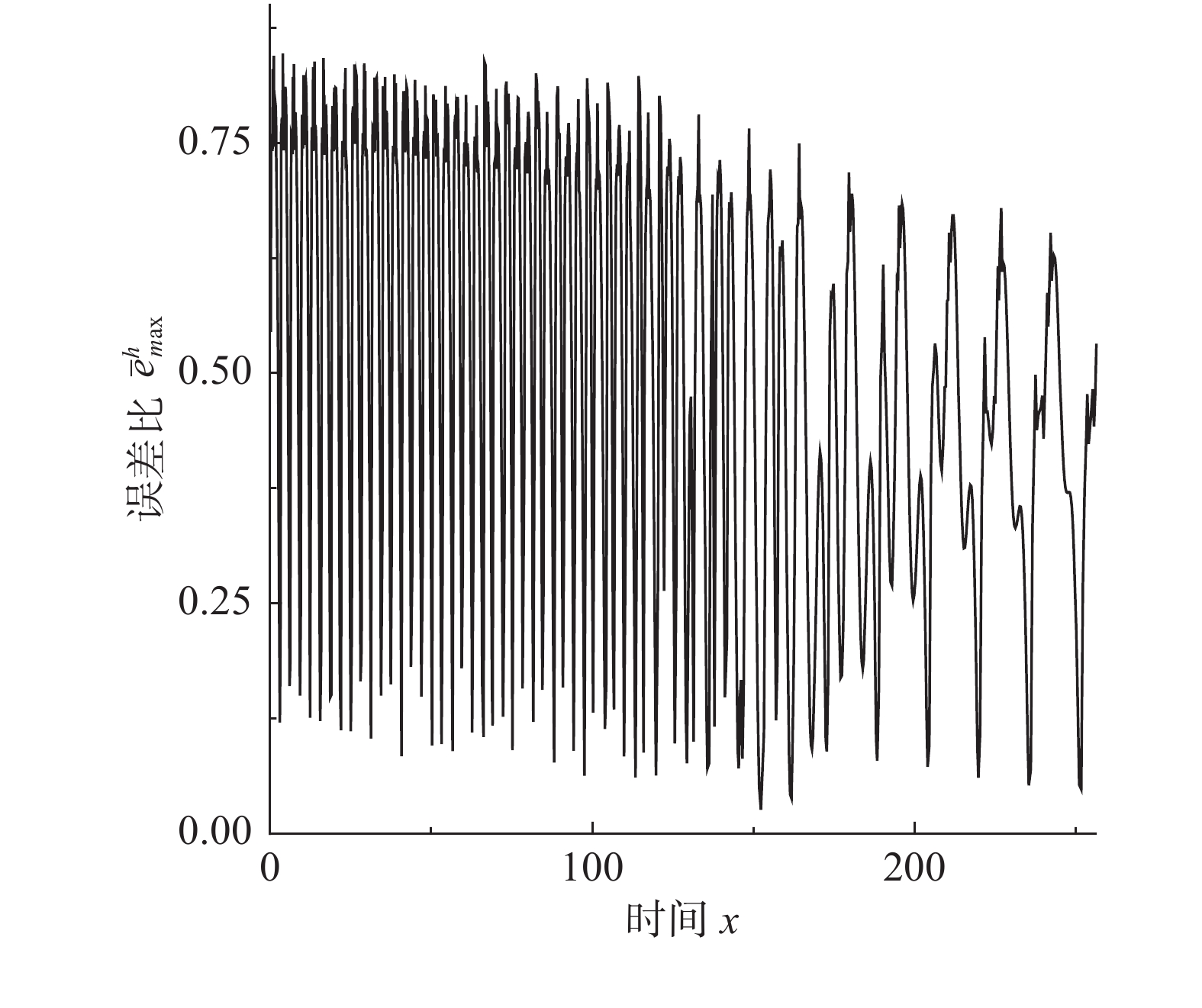
{\bar e^h} 。例1. 有阻尼简谐运动。
计算数据为:
m = 1 ,\;k = 1 ,c = 0.04 ,f = \sin (0.2x) ,{u_0} = 0 ,{v_0} = 1 ,\bar T = 256{\text{ s}} ,初始步长{h_0} = 0.5 。表1和表2分别是tol = 0.001 和0.01的相关计算结果。需要注意的是,无论是先验法还是后验法,理论上都是基于h 足够小时才足够有效,且h 越小越可靠。表1中的误差限比较小,步长h 足够小,先验法几乎可以取代后验法,而且所有单元逐点满足误差限,精度完全保证,效率大幅提高。表2中的误差限相对较大,使得h 变大,后验法矫正次数增加,但直接后验法失控率反而更高;从误差比大于1的单元数和最大误差值来看,双验法比直接后验法更加安全可靠,可以更好地满足自适应要求,这也是先验法的一种功效。在图1和图2是取Taylor级数2项,tol = 0.001 的先验法数据,可见该方法单元步长分布合理,误差得到有效控制。表 1 有阻尼简谐运动计算数据 (256 s,tol = 0.001 )Table 1. Results of damped harmonic motion (256 s,tol = 0.001 )误差估计方法 单元数 {N_{\rm{e}}} 自适应次数 {N_{{\rm{adp}}}} 先验迭代次数 {n_{{\rm{iter}}\,0}} 后验迭代次数 {n_{{\rm{iter}}\,}} 误差比大于1的单元数 {N_{{\rm{fail}}}} 最小单元长度 {h_{\,\min }} 最大单元长度 {h_{\,\max }} 直接后验 1003 373 472 0 0.09255 1.21070 求逆先验 1047 286 315 0 0 0.09050 0.75368 3项先验 1044 284 310 4 0 0.09050 0.76208 2项先验 1081 294 329 23 0 0.09048 0.63940 表 2 有阻尼简谐运动计算数据 ( 256s,tol = 0.01 )Table 2. Results of damped harmonic motion (256s,tol = 0.01 )误差估计方法 单元数 {N_{\rm{e}}} 自适应次数 {N_{{\rm{adp}}}} 先验迭代次数 {n_{{\rm{iter}}\,0}} 后验迭代次数 {n_{{\rm{iter}}\,}} 误差比大于1的单元数(最大超限值) {N_{{\rm{fail}}}} 最小单元长度 {h_{\,\min }} 最大单元长度 {h_{\,\max }} 直接后验 342 99 168 16 (1.384) 0.29528 3.18623 求逆先验 381 70 87 4 1 (1.005) 0.28098 1.30528 3项先验 364 85 128 20 2 (1.097) 0.28103 1.35135 2项先验 422 81 116 8 0 0.27923 0.99091 例2. 无阻尼自由振动。
计算数据为:
m = 1 ,\;k = 1 ,c = 0 ,f = 0 ,{u_0} = 0 ,{v_0} = 1 ,\bar T = 256{\text{ s}} ,tol = 0.001 , 初始步长h = 0.5 。由表3可知,采用直接求逆的先验法和后验法是完全等效的;这是由于本算例中f = 0 ,则荷载近似为常数以及逆矩阵的Taylor级数展开带来的误差,都未出现。此外,由于本例步长较小,故Taylor渐近展开也足够精确,可以完全替代后验法。图3和图4为Taylor级数取2项的先验法计算结果;可见,本例步长、误差分布均匀且有周期性规律。表 3 无阻尼自由振动计算数据 ( 256 s,tol = 0.001 )Table 3. Results of undamped free vibration (256 s,tol = 0.001 )误差估
计方法单元数 {N_{\rm{e}}} 自适应次数 {N_{{\rm{adp}}}} 先验迭代次数 {n_{{\rm{iter}}\,0}} 后验迭代次数 {n_{{\rm{iter}}\,}} 误差比大于1的单元数 {N_{{\rm{fail}}}} 最小单元长度 {h_{\,\min }} 最大单元长度 {h_{\,\max }} 直接后验 2790 677 677 0 0.07749 0.25854 求逆先验 2790 677 677 0 0 0.07749 0.25845 3项先验 2790 677 677 0 0 0.07749 0.25848 2项先验 2790 677 677 0 0 0.07749 0.26791 4 结论
本文以单自由度运动方程线性元为例,提出了一种先验的自适应步长算法,构建了“双验”法自适应求解策略:
(1) 该法对于给定的求解误差限,可以直接确定步长大小,从而得到合理的有限元解;
(2) 在后验法保障精度的前提下,简明高效的先验法大幅提升了自适应步长求解的效率;
(3) 典型的数值算例验证了本法的有效性,展示了本法在计算效率上的提升。
本研究为未来多自由度运动方程、高次单元等更为一般情况的自适应步长求解提供了良好的基础理论和成功的案例。
-
表 1 有阻尼简谐运动计算数据 (256 s,
tol = 0.001 )Table 1 Results of damped harmonic motion (256 s,
tol = 0.001 )误差估计方法 单元数 {N_{\rm{e}}} 自适应次数 {N_{{\rm{adp}}}} 先验迭代次数 {n_{{\rm{iter}}\,0}} 后验迭代次数 {n_{{\rm{iter}}\,}} 误差比大于1的单元数 {N_{{\rm{fail}}}} 最小单元长度 {h_{\,\min }} 最大单元长度 {h_{\,\max }} 直接后验 1003 373 472 0 0.09255 1.21070 求逆先验 1047 286 315 0 0 0.09050 0.75368 3项先验 1044 284 310 4 0 0.09050 0.76208 2项先验 1081 294 329 23 0 0.09048 0.63940 表 2 有阻尼简谐运动计算数据 ( 256s,
tol = 0.01 )Table 2 Results of damped harmonic motion (256s,
tol = 0.01 )误差估计方法 单元数 {N_{\rm{e}}} 自适应次数 {N_{{\rm{adp}}}} 先验迭代次数 {n_{{\rm{iter}}\,0}} 后验迭代次数 {n_{{\rm{iter}}\,}} 误差比大于1的单元数(最大超限值) {N_{{\rm{fail}}}} 最小单元长度 {h_{\,\min }} 最大单元长度 {h_{\,\max }} 直接后验 342 99 168 16 (1.384) 0.29528 3.18623 求逆先验 381 70 87 4 1 (1.005) 0.28098 1.30528 3项先验 364 85 128 20 2 (1.097) 0.28103 1.35135 2项先验 422 81 116 8 0 0.27923 0.99091 表 3 无阻尼自由振动计算数据 ( 256 s,
tol = 0.001 )Table 3 Results of undamped free vibration (256 s,
tol = 0.001 )误差估
计方法单元数 {N_{\rm{e}}} 自适应次数 {N_{{\rm{adp}}}} 先验迭代次数 {n_{{\rm{iter}}\,0}} 后验迭代次数 {n_{{\rm{iter}}\,}} 误差比大于1的单元数 {N_{{\rm{fail}}}} 最小单元长度 {h_{\,\min }} 最大单元长度 {h_{\,\max }} 直接后验 2790 677 677 0 0.07749 0.25854 求逆先验 2790 677 677 0 0 0.07749 0.25845 3项先验 2790 677 677 0 0 0.07749 0.25848 2项先验 2790 677 677 0 0 0.07749 0.26791 -
[1] Clough R W. Dynamics of structures [M]. New York: McGraw-Hill. 1995.
[2] 刘晶波, 杜修力. 结构动力学 [M]. 北京: 机械工业出版社, 2005. Liu Jingbo, Du Xiuli. Structural dynamics [M]. Beijing: China Machine Press, 2005. (in Chinese)
[3] Zienkiewicz C, Xie Y M. A simple error estimator and adaptive time stepping procedure for dynamic analysis [J]. Earthquake Engineering & Structural Dynamics, 1991, 20(7): 871 − 887.
[4] Lages E N, Silveira E S S, Cintra D T, Frery A C. An adaptive time integration strategy based on displacement history curvature [J]. International Journal for Numerical Methods in Engineering, 2013, 93(12): 1235 − 1254. doi: 10.1002/nme.4421
[5] Strang G, Fix G J. An analysis of the finite element method (Second Edition) [M]. Wellesley MA: Wellesley- Cambridge Press, 2008.
[6] 袁驷, 王枚. 一维有限元后处理超收敛解答计算的 EEP 法[J]. 工程力学, 2004, 21(2): 1 − 9. doi: 10.3969/j.issn.1000-4750.2004.02.001 Yuan Si, Wang Mei. An element-energy-projection method for post-computation of super-convergent solutions in one-dimensional FEM [J]. Engineering Mechanics, 2004, 21(2): 1 − 9. (in Chinese) doi: 10.3969/j.issn.1000-4750.2004.02.001
[7] 袁驷, 林永静. 二阶非自伴两点边值问题Galerkin有限元后处理超收敛解答计算的 EEP 法[J]. 计算力学学报, 2007, 24(2): 142 − 147. doi: 10.3969/j.issn.1007-4708.2007.02.004 Yuan Si, Lin Yongjing. An EEP method for post-computation of super-convergent solutions in one-dimensional Galerkin FEM for second order non-self-adjoint boundary-value problem [J]. Chinese Journal of Computational Mechanics, 2007, 24(2): 142 − 147. (in Chinese) doi: 10.3969/j.issn.1007-4708.2007.02.004
[8] Wang Mei, Yuan Si. Computation of super-convergent nodal stresses of Timoshenko beam elements by EEP method [J]. Applied Mathematics and Mechanics (English Version), 2004, 25(11): 1228 − 1240. doi: 10.1007/BF02438278
[9] Yuan Si, He Xuefeng. A self-adaptive strategy for one-dimensional FEM based on EEP method [J]. Applied Mathematics and Mechanics (English Version), 2006, 27(11): 1461 − 1474. doi: 10.1007/s10483-006-1103-1
[10] Yuan Si, Xing Qinyan, Wang Xu, Ye Kangsheng. Self-adaptive strategy for one-dimensional finite element method based on EEP method with optimal super-convergence order [J]. Applied Mathematics and Mechanics (English Version), 2008, 29(5): 591 − 602. doi: 10.1007/s10483-008-0504-8
[11] Yuan S, Wu Y, Xu J J, Yuan Z, Xing Q Y, Ye K S. A super-convergence strategy for two-dimensional FEM based on element energy projection technique [J]. Journal of Nanoelectronics and Optoelectronics, 2017, 12(11): 1284 − 1294. doi: 10.1166/jno.2017.2272
[12] Yuan S, Wu Y, Xing Q Y. Recursive super-convergence computation for multi-dimensional problems via one-dimensional element energy projection technique [J]. Applied Mathematics and Mechanics, 2018, 39(7): 1031 − 1044. doi: 10.1007/s10483-018-2345-7
[13] 袁驷, 袁全, 闫维明, 李易, 邢沁妍. 运动方程自适应步长求解的一个新进展——基于EEP超收敛计算的线性有限元法[J]. 工程力学, 2018, 35(2): 13 − 20. doi: 10.6052/j.issn.1000-4750.2017.05.ST01 Yuan Si, Yuan Quan, Yan Weiming, Li Yi, Xing Qinyan. New development of solution of equations of motion with adaptive time-step size — Linear FEM based on EEP superconvergence technique [J]. Engineering Mechanics, 2018, 35(2): 13 − 20. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.05.ST01
[14] 袁全, 袁驷. 运动方程一阶方程组格式的线性时域有限元及其EEP超收敛计算[J]. 工程力学, 2021, 38(增刊): 14 − 20. doi: 10.6052/j.issn.1000-4750.2020.07.S001 Yuan Quan, Yuan Si. A linear finite element and its eep super-convergent solution for first order odes converted from motion equations [J]. Engineering Mechanics, 2021, 38(Suppl): 14 − 20. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.07.S001
[15] 袁驷, 袁全. 再谈从矩阵位移法看有限元位移精度的损失与恢复[J]. 力学与实践, 2020, 42(6): 689 − 694. Yuan Si, Yuan Quan. Revisiting the loss and recovery of displacement accuracy in FEM as seen from matrix displacement method [J]. Mechanics in Engineering, 2020, 42(6): 689 − 694. (in Chinese)
[16] 袁驷, 袁全. 固端法: 二维有限元先验定量误差估计与控制[J]. 工程力学, 2021, 38(1): 8 − 14. doi: 10.6052/j.issn.1000-4750.2020.07.ST05 Yuan Si, Yuan Quan. Fix-end method: A priori quantitative error estimate and control for two-dimensional FEM [J]. Engineering Mechanics, 2021, 38(1): 8 − 14. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.07.ST05
[17] 袁全, 袁驷, 李易, 闫维明, 邢沁妍. 线性元时程积分按最大模自适应步长公式的证明[J]. 工程力学, 2018, 35(8): 9 − 13. doi: 10.6052/j.issn.1000-4750.2018.03.0106 Yuan Quan, Yuan Si, Li Yi, Yan Weiming, Xing Qinyan. Proof of adaptive time-step size formula based on maximum norm in time integration of linear elements [J]. Engineering Mechanics, 2018, 35(8): 9 − 13. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.03.0106
[18] 袁驷, 邢沁妍, 袁全. 基于EEP技术的一维有限元结点位移误差计算[J]. 工程力学, 2020, 37(9): 1 − 7, 29. doi: 10.6052/j.issn.1000-4750.2020.07.0446 Yuan Si, Xing Qinyan, Yuan Quan. Calculation of errors of nodal displacements in one-dimensional finite element methods using element energy projection technique [J]. Engineering Mechanics, 2020, 37(9): 1 − 7, 29. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.07.0446




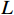
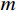
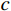
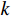
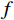
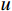
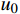
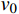
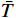
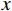
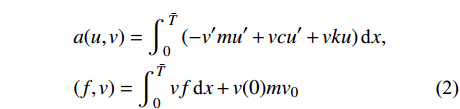
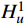
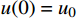
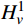
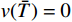
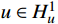
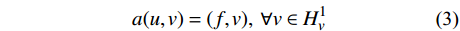
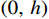
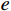
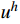
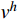
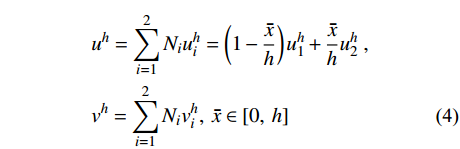
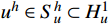
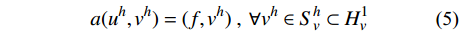
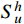
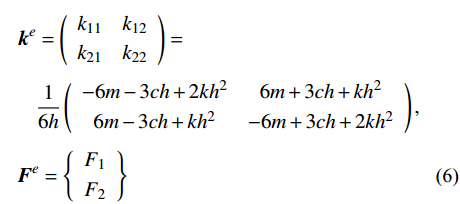
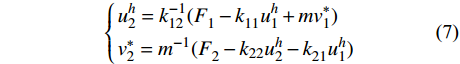
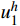
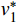
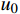
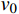
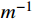
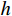
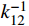
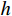
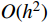
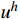
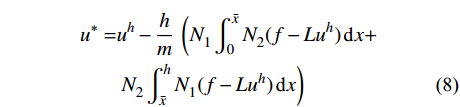

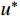
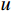
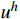
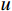
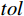
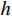
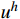
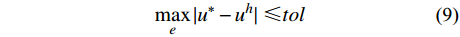
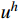
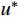
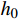
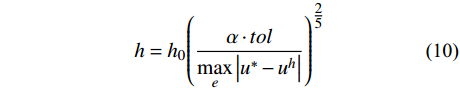

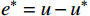
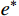
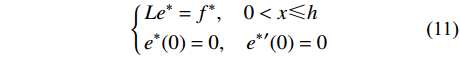
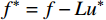
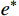
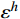
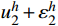
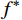
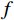
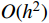
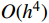
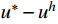
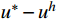
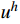
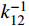
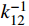
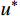
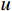
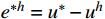
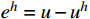
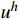
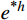
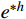
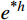
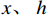
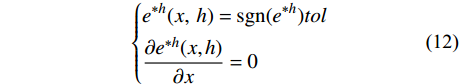
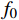
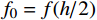
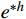
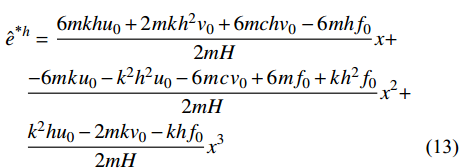
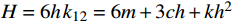
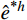
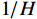
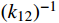
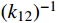
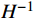
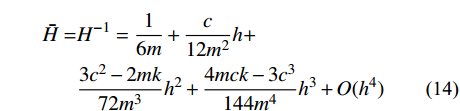
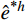
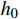
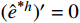
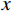
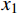
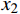
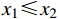
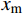
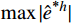
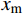
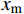
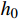
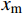
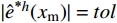
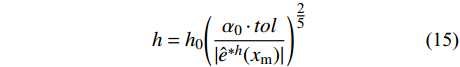
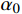
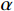
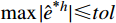
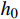
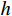
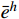
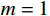
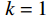
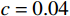
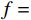
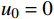
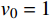
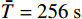
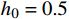
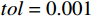
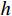
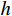
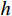
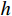
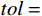
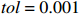
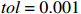
 下载:
下载: