对于混凝土重力坝，坝踵区基岩与混凝土的交界面是一个薄弱部位，明确界面断裂特性是评估断裂安全性的首要条件。目前，对准静态荷载条件下岩石-混凝土界面的断裂性能已开展了相关研究。主要集中于：1)岩石-混凝土界面断裂参数的影响因素，如界面粗糙度、界面两侧材料性能等^[1]；2)岩石-混凝土界面裂缝扩展判定以及裂缝扩展路径预测^[2-3]；3)混凝土重力坝界面的安全稳定性分析^[4]。考虑到某些重力坝处在高震区，如我国西南地区的白鹤滩大坝、溪洛渡大坝，强震将增大坝体动力响应，使得坝踵处的拉应力增加，导致该位置处易出现裂缝并产生扩展。同时考虑到大坝的蓄水工作状态，在地震期间库水更易渗入坝踵裂缝内产生局部高水压，作用在裂纹面的高水压产生的水力劈裂作用叠加水压在界面处产生的弯矩增加了界面的拉应力，更进一步驱动了坝踵裂缝的扩展，增大了坝体整体失稳的风险^[5-7]。此时，基于准静态条件下的断裂理论不能准确评价高应变率条件下岩石-混凝土界面的抗裂性能。因此，开展岩石-混凝土界面断裂性能的率相关性研究对重力坝抗震安全性评估具有重要意义。

目前，断裂性能的率相关性研究多针对混凝土材料，主要关注断裂韧度、断裂能、裂缝扩展速率等断裂参数。针对混凝土断裂韧度的率相关性，张秀芳等^[8]采用中央带裂缝的立方体试件开展了不同应变率下的劈拉试验，发现在10⁻⁵s⁻¹~10⁻²s⁻¹应变率范围内，起裂断裂韧度随应变率的提高而提高，而失稳断裂韧度随应变率的提高先提高后保持稳定。LAMBERT等^[9]采用分离式霍普金森压杆(SHPB)研究了混凝土在高应变率下的断裂韧度，研究表明，在应变率为2 s⁻¹~8 s⁻¹时，断裂韧度随应变率的提高而提高。针对断裂能的率相关性，BRARA等^[10]采用霍普金森杆进行混凝土动态拉伸断裂试验，发现高应变率下，混凝土的断裂能显著提高。CADONI等^[11]也得到了类似的结论，并发现断裂能与应变率的关系受骨料粒径影响。针对裂缝扩展速率的率相关性，PYO等^[12]研究了超高性能混凝土在大范围应变率下的裂缝扩展速率。结果表明：裂缝扩展速率随着应变率的增加而增加。以上研究表明：混凝土材料的断裂性能存在明显的率相关性，断裂韧度、断裂能、裂缝扩展率等随着应变率的提高而提高。而对于岩石-混凝土界面，由于两侧材料性能的差异性，界面裂缝尖端出现震荡应力奇异性并且裂缝面有嵌入的现象，这使得岩石-混凝土界面断裂性能的率相关问题更为复杂。对界面动态断裂问题，朱哲明等^[13-16]以混凝土细观中的砂浆-骨料界面为研究对象，开展了岩石-砂浆界面在冲击荷载作用下的动态断裂试验研究，结果表明：界面粗糙度和加载速率对界面裂缝扩展速度有显著影响^[14-15]，界面临界应力强度因子随着加载速率的增大而增大。KIM等^[17]以混凝土贴面堆石坝中的混凝土面层-岩石界面为研究对象，利用界面元模拟混凝土面板与岩石实体之间的摩擦行为，模拟结果与试验吻合良好。针对混凝土重力坝坝踵处岩石-混凝土界面处的动态断裂性能研究多集中于数值分析，如BAYRAKTAR等^[18]研究了基岩特性对重力坝动态响应的影响，对比分析了刚性地基、无质量地基和反褶积地基三种模型对结构动力响应的影响。刘钧玉等^[7]通过对重力坝-无限地基-库水系统进行频域分析，探讨了界面裂纹应力强度因子的时程变化规律。目前，有关岩石-混凝土界面动态断裂特性的试验研究开展较少，根据已有的报道，钟红等^[19]学者进行了花岗岩-混凝土界面动态轴拉试验，其研究侧重于比较复合材料与均质母材的断裂性能率效应差异。而开展岩石-混凝土界面动态张拉断裂性能测试，能够客观反映界面在不同率效应下的断裂性能，有助于评估大坝在地震作用下的抗裂性能及结构响应，也为数值计算结果提供试验验证。

基于此，本研究开展了不同应变率下岩石-混凝土界面轴向拉伸试验以及三点弯曲断裂试验，测定了不同应变率下的界面抗拉强度以及断裂参数，包括起裂韧度、临界裂缝扩展长度、失稳韧度、粘聚韧度、断裂能、断裂过程区长度、特征长度。分析了应变率对岩石-混凝土界面力学及断裂性能的影响。

1   试验概况

1.1   试件准备

本研究进行了岩石-混凝土复合试件的轴向拉伸试验与三点弯曲断裂试验，以测定界面抗拉强度与断裂参数。岩石选用大连岩石厂加工的花岗岩，混凝土选用强度等级为C30的普通混凝土。混凝土配合比(kg/m³)为水泥∶水∶砂子∶石子=314.5∶195∶568.5∶1322。其中，水泥为P.O.42.5普通硅酸盐水泥，砂子为河砂，石子为最大粒径为10 mm的瓜子石。

轴向拉伸试件的尺寸为，长×宽×高=200 mm × 100 mm × 100 mm，岩石与混凝土块长度各为100 mm，界面处不预制裂缝。三点弯曲断裂试件的尺寸为长×宽×高=500 mm × 100 mm × 100 mm，岩石与混凝土块长度各为250 mm，界面处预制裂缝。岩石的浇筑表面通过机械刻槽的方式进行粗糙处理，槽口与各边长呈45°，槽口深5 mm，宽2 mm。刻槽之后的岩石表面如图1(a)所示。对于三点弯曲断裂试件，界面处通过粘贴双层PVC薄板预制30 mm长的初始裂缝，裂缝预制方式如图1(b)所示。试件浇筑前，将岩石块置于清水中浸泡至饱和状态以避免浇筑养护过程中岩石吸收混凝土中的水分。浇筑过程中，试件在振动台振捣密实后抹平表面，并覆盖保鲜膜以防止水分散失。试件置于实验室环境养护48 h后，转移至温度为23 ℃的饱和石灰水中养护至90 d。岩石与混凝土的各项材料参数列于表1。

图  1  岩石表面处理方式

Figure  1.  Surface roughness characterization and pre-notch preparation

下载: 全尺寸图片 幻灯片

表  1  岩石与混凝土的材料参数

Table  1.  The material properties of concrete and rock

材料	密度/ (kg/m3)	弹性模量/ GPa	泊松比	抗压强度/ MPa	抗拉强度/ MPa
混凝土(28 d)	2400	26.00	0.238	38.73	3.42
混凝土(90 d)	2400	37.81	0.238	46.66	4.23
岩石	2668	43.00	0.170	142.72	8.21

下载: 导出CSV 

| 显示表格

1.2   轴拉试验

轴拉试验采用位移控制模式，以测定岩石-混凝土界面在不同应变率下的抗拉强度。地震应变率的范围为：10⁻⁴s⁻¹~10⁻¹s^−1[20]，本研究选取的应变率为10⁻⁵s⁻¹、10⁻⁴s⁻¹、10⁻³s⁻¹、10⁻²s⁻¹，对应的加载速率分别为2×10⁻³ mm/s、2×10⁻² mm/s、2×10⁻¹ mm/s、2 mm/s。每种工况准备3个试件，具体试验方案见表2。试验前，采用建筑结构胶于试件两端粘贴15 mm厚的等截面钢板。为避免偏心对抗拉强度的影响，钢板与试验平台通过球铰连接。轴拉试验在日本进口的岛津拉拔试验机上进行，该试验机最大加载速率可达1000 mm/min，最大采集频率可达1000 Hz，满足试验要求。

表  2  试验方案

Table  2.  Test plan

试件形式	长×宽×高/ (mm×mm×mm)	应变率/ s−1	加载速率/ (mm/s)	试件数量/ 个
轴拉试件	200×100×100	10−5	2×10−3	3
		10−4	2×10−2	3
		10−3	2×10−1	3
		10−2	2	3
三点弯曲断裂试件	500×100×100	10−5	10−3	3
		10−4	10−2	3
		10−3	10−1	3
		10−2	1	3

下载: 导出CSV 

| 显示表格

1.3   三点弯曲断裂试验

本研究通过三点弯曲断裂试验测定岩石-混凝土界面在不同应变率下的断裂参数，包括起裂韧度、临界裂缝扩展长度、失稳韧度以及断裂能。与轴拉试验相同，三点弯曲断裂试验的应变率为10⁻⁵ s⁻¹、10⁻⁴ s⁻¹、10⁻³ s⁻¹、10⁻² s⁻¹，对应的加载速率分别为10⁻³ mm/s、10⁻² mm/s、10⁻¹ mm/s、1 mm/s。每个工况准备3个试件，具体试验方案见表2。三点弯曲梁试件命名方式为：TPB-应变率-试件编号。该试验在250 kN电液伺服试验机(MTS)上进行，使用德国进口的高速采集系统(IMC)进行数据采集，最大加载速率为100 mm/s，最高采集频率为100 kHz，满足试验要求。

采用电阻应变片法监测裂缝的起裂。在试件两侧距离裂缝尖端5 mm位置处各粘贴2个标距为10 mm的电阻应变片，应变片布置方式如图2(a)所示。界面裂缝起裂前，缝尖应变随荷载的增大而增大，起裂将引起裂尖附近应变能的释放，这一现象在荷载-应变曲线上表现为应变发生明显的转折，由此可确定界面的起裂荷载(P_ini)，如图3(a)所示。采用两个夹式引伸计分别测量加载点位移(δ)和裂缝口张开位移(CMOD)，见图2(a)。此外，沿试件韧带方向从裂缝尖端到试件顶部等间距布置四个夹式引伸计以测量裂缝张开位移，如图2(b)所示。本研究采用以裂缝尖端张开位移(w)为判据的分析方法确定裂缝长度。通过试验标定起裂时刻对应的裂缝尖端张开位移(CTOD_ini)，当韧带上某一位置处的裂缝张开位移达到CTOD_ini时，该位置处于开裂状态。已有的研究表明^[21]，裂缝张开位移沿韧带方向呈线性分布。根据裂缝张开位移的拟合曲线，采用线性差值的方法可确定该时刻的裂尖位置，进而得到裂缝长度，该方法如图3(b)所示。此外，本研究采用高速DIC技术观测不同应变率下的裂缝扩展过程，该技术采用超高速摄像机进行图像采集，采集频率高达100 kHz，满足试验要求。试验前，试件表面采用黑白哑光漆间隔喷涂形成黑白相间的散斑图，如图4所示。图像分析时，选取覆盖韧带的计算区域，通过变形前后的图像对比分析每个像素点的应变、位移等信息。DIC三点弯曲梁试件命名方式为：TPB-DIC-应变率-试件编号。

图  2  三点弯曲断裂试验

Figure  2.  Three-point bending test setup

下载: 全尺寸图片 幻灯片

图  3  确定起裂荷载与裂缝扩展长度的方法

Figure  3.  Determination of crack initiation load and crack propagation length

下载: 全尺寸图片 幻灯片

图  4  DIC试验

Figure  4.  DIC test

下载: 全尺寸图片 幻灯片

2   试验结果分析

2.1   界面破坏形态

不同加载速率下的岩石-混凝土复合试件均沿界面发生破坏，裂缝沿界面扩展过程中，嵌入岩石槽口中的混凝土浆体被拔出或者拉断。以应变率10⁻⁵s⁻¹和10⁻³s⁻¹为例，三点弯曲断裂试验的界面破坏形态如图5所示。在低应变率下，较多水泥砂浆粘连在混凝土断面一侧，形成凸起的棱线，如图5(a)所示。而在较高应变率下，裂缝来不及沿着更为薄弱的砂浆界面扩展，而是直接贯穿开缝面，故断面比较平整，如图5(b)所示。

图  5  复合试件断面图

Figure  5.  Section view of composite specimen

下载: 全尺寸图片 幻灯片

2.2   抗拉强度

轴向拉伸试验中，界面抗拉强度f_t计算公式如下所示：

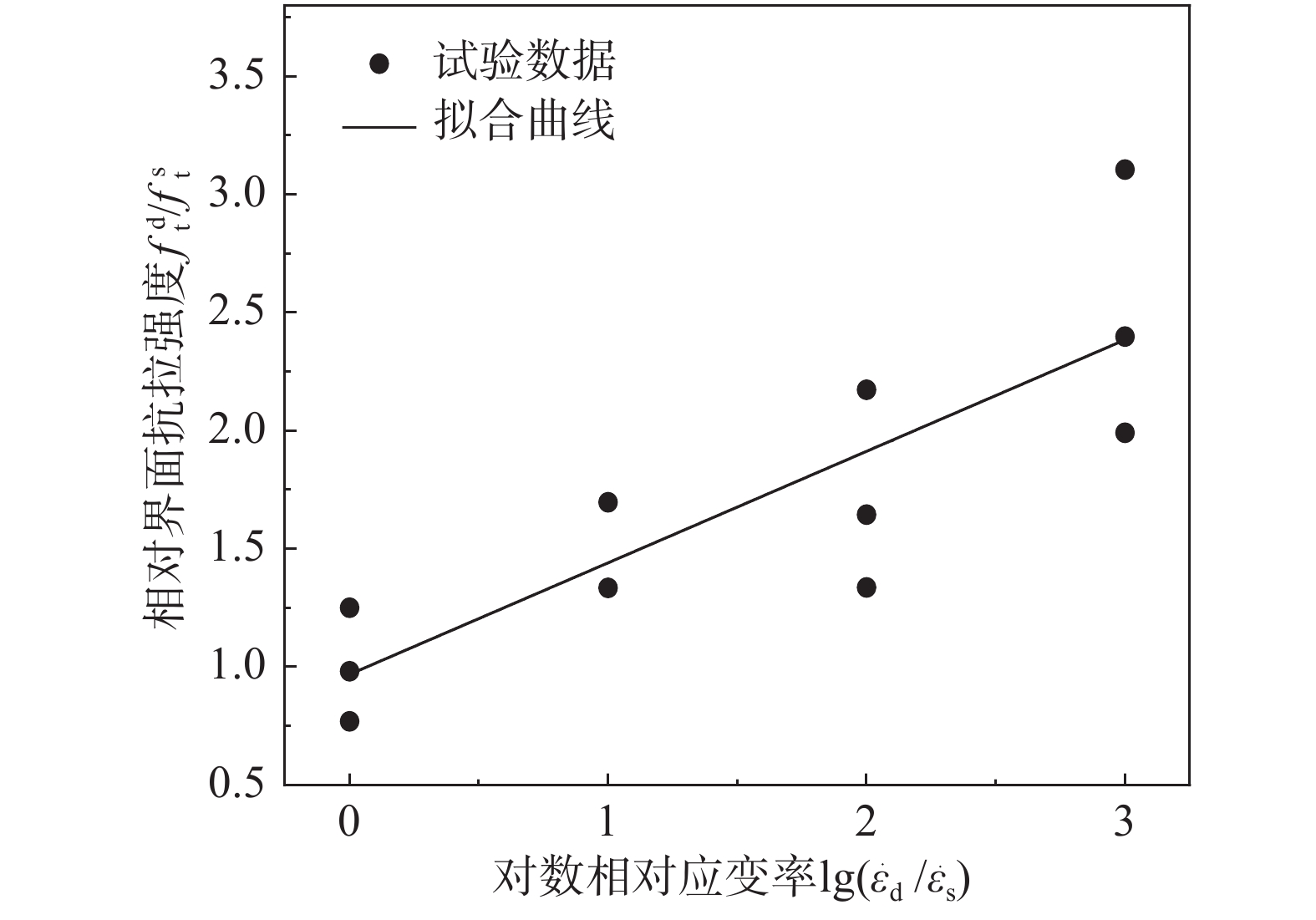
式中：T_max为最大荷载；A为岩石-混凝土界面面积。不同应变率下岩石-混凝土界面的抗拉强度见表3，界面抗拉强度与应变率对数的关系如图6所示。由图6可知，随着应变率的提高，界面抗拉强度逐渐提高。应变率对界面抗拉强度有显著影响。以10⁻⁵s⁻¹应变率为参照，10⁻⁴s⁻¹、10⁻³s⁻¹、10⁻²s⁻¹应变率下岩石-混凝土界面的抗拉强度分别提高了51.53%、71.79%、149.80%。需要特别指出的是，10⁻²s⁻¹应变率下抗拉强度提高量较大，这一现象可由不同应变率下试件的断面形态不同来解释。在低应变率下，试件断面如图5(c)所示，裂缝沿较为薄弱的砂浆界面扩展，所消耗的能量较低。而在10⁻²s⁻¹应变率下，裂缝沿最短路径扩展，即直接贯穿开缝面，断面平整，如图5(d)所示。此时，裂缝消耗的能量最高，故界面抗拉强度显著提升。以准静态条件下界面抗拉强度及应变率为基准，不同应变率下界面抗拉强度相对值与应变率相对值的对数近似呈线性关系，线性拟合曲线表达式如下：

式中： ${\dot \varepsilon _{\text{d}}}$ 为动态应变率； ${\dot \varepsilon _{\text{s}}}$ 为准静态应变率，本文为10⁻⁵s⁻¹； $f_{{\text{ t}}}^{\text{d}}$ 为不同应变率下的界面抗拉强度； $f_{{\text{ t}}}^{\text{s}}$ 为准静态应变率下的界面抗拉强度。

表  3  轴拉试验结果

Table  3.  The result of axial tensile test

应变率/s−1	界面抗拉强度ft/MPa
	试件1	试件2	试件3	平均值
10−5	0.963	1.228	0.755	0.982
10−4	1.310	1.666	−	1.488
10−3	1.615	1.312	2.134	1.687
10−2	1.955	2.355	3.049	2.453

下载: 导出CSV 

| 显示表格

图  6  界面抗拉强度与应变率的关系

Figure  6.  Relationship between interfacial tensile strength and strain rate

下载: 全尺寸图片 幻灯片

2.3   界面断裂能

不同应变率下的三点弯曲断裂试验均捕捉到完整的下降段，以荷载-加载点位移(P-δ)曲线为例，不同应变率下的P-δ曲线如图7所示。RILEM给出了根据P-δ曲线计算断裂能的方法，计算公式如下：

式中：W₀为P-δ曲线下的面积；mg为梁自重；δ₀为荷载为0时对应的加载点位移；D为试件高度；a₀为初始裂缝长度；t为试件厚度。不同应变率下的岩石-混凝土界面断裂能列于表4，断裂能与应变率对数的关系如图8所示。由图可知，随着应变率的提高，界面断裂能呈现线性提高的趋势，应变率对岩石-混凝土界面的断裂能有显著影响。以10⁻⁵s⁻¹应变率为参照，10⁻⁴s⁻¹、10⁻³s⁻¹、10⁻²s⁻¹应变率下岩石-混凝土界面的断裂能分别提高了10.34%、29.52%、54.79%。以准静态条件下界面断裂能及应变率为基准，不同应变率下界面断裂能相对值与应变率相对值的对数近似呈线性关系，线性拟合曲线表达式如下：

图  7  不同应变率下的P-δ曲线

Figure  7.  P-δ curves under different strain rates

下载: 全尺寸图片 幻灯片

式中： $G_{{\text{f}}}^{\text{d}}$ 为不同应变率下的断裂能； $G_{{\text{f}}}^{\text{s}}$ 为准静态应变率下的断裂能。

表  4  复合试件三点弯曲断裂试验结果

Table  4.  Three-point bending test result of composite spesimens

试件编号	起裂荷载/ kN	峰值荷载/ kN	起裂韧度 $K_{\rm{IC}}^{\rm{ini}}$/(MPa·m1/2)	临界裂缝扩展长度/ mm	失稳韧度 $K_{\rm{IC}}^{\rm{un}}$/(MPa·m1/2)	起裂荷载/ 峰值荷载	粘聚韧度 $K_{\rm{IC}}^{\rm{c}}$/(MPa·m1/2)	断裂能/ (N/m)
TPB-5-1	1.492	1.516	0.295	41.330	0.404	0.984	0.109	12.320
TPB-5-2	1.569	2.032	0.309	45.833	0.611	0.772	0.302	35.302
TPB-DIC-5-3	1.034	1.149	0.207	48.670	0.383	0.900	0.176	26.301
均值	1.365	1.566	0.270	45.000	0.466	0.885	0.196	24.641
TPB-4-1	1.399	1.766	0.277	52.540	0.656	0.792	0.379	19.873
TPB-4-2	1.515	1.851	0.299	47.346	0.584	0.818	0.285	30.518
TPB-DIC-4-3	1.846	1.963	0.362	49.050	0.651	0.940	0.289	31.174
均值	1.587	1.860	0.313	49.645	0.630	0.850	0.317	27.188
TPB-3-1	2.034	2.064	0.398	40.282	0.529	0.985	0.131	27.973
TPB-3-2	1.507	2.012	0.298	45.160	0.593	0.749	0.295	28.273
TPB-DIC-3-3	2.301	2.334	0.449	42.576	0.636	0.986	0.187	39.498
均值	1.947	2.137	0.382	42.673	0.586	0.907	0.204	31.915
TPB-2-1	1.951	2.218	0.382	39.256	0.552	0.880	0.170	32.268
TPB-2-2	1.774	2.185	0.349	39.580	0.549	0.812	0.200	33.049
TPB-DIC-2-3	2.340	2.423	0.456	37.438	0.573	0.966	0.117	49.108
均值	2.022	2.275	0.396	38.758	0.558	0.886	0.162	38.141

下载: 导出CSV 

| 显示表格

图  8  不同应变率下的断裂能

Figure  8.  Fracture energy under different strain rates

下载: 全尺寸图片 幻灯片

2.4   双K断裂参数

与混凝土材料类似，岩石-混凝土界面可视为典型的准脆性材料，界面的断裂过程分为裂缝起裂、稳定扩展和失稳扩展三个阶段。徐世烺等^{[3, 22]}以应力强度因子为参量提出了判定混凝土断裂过程的双K断裂模型。该模型中，起裂断裂韧度 $K_{\rm{IC}}^{\rm{ini}}$ 为起裂荷载P_ini和初始裂缝长度a₀对应的应力强度因子，表征材料抵抗开裂的能力；失稳断裂韧度 $K_{\rm{IC}}^{\rm{un}}$ 为最大荷载P_max和临界裂缝长度a_c对应的应力强度因子，表征结构抵抗失稳断裂破坏的能力^[23-25]。根据图3(a)可确定不同应变率下的起裂荷载，列于表4。临界裂缝长度是计算失稳韧度的重要参数，本研究采用两种方法测定岩石-混凝土界面的临界裂缝长度，即夹式引伸计法和DIC法。对于夹式引伸计法，通过提取峰值荷载时刻对应的裂缝张开位移，根据裂缝张开位移拟合曲线，采用线性差值可确定临界裂缝长度，如图3(b)所示。对于DIC法，通过吴智敏等^[26]采用的拉伸应变法确定裂尖点位置，进而确定临界裂缝长度。该方法认为当韧带上某一点应变达到材料的拉伸应变时，该点即处于开裂状态。对于岩石-混凝土界面而言，界面的临界开裂应变可由下式计算：

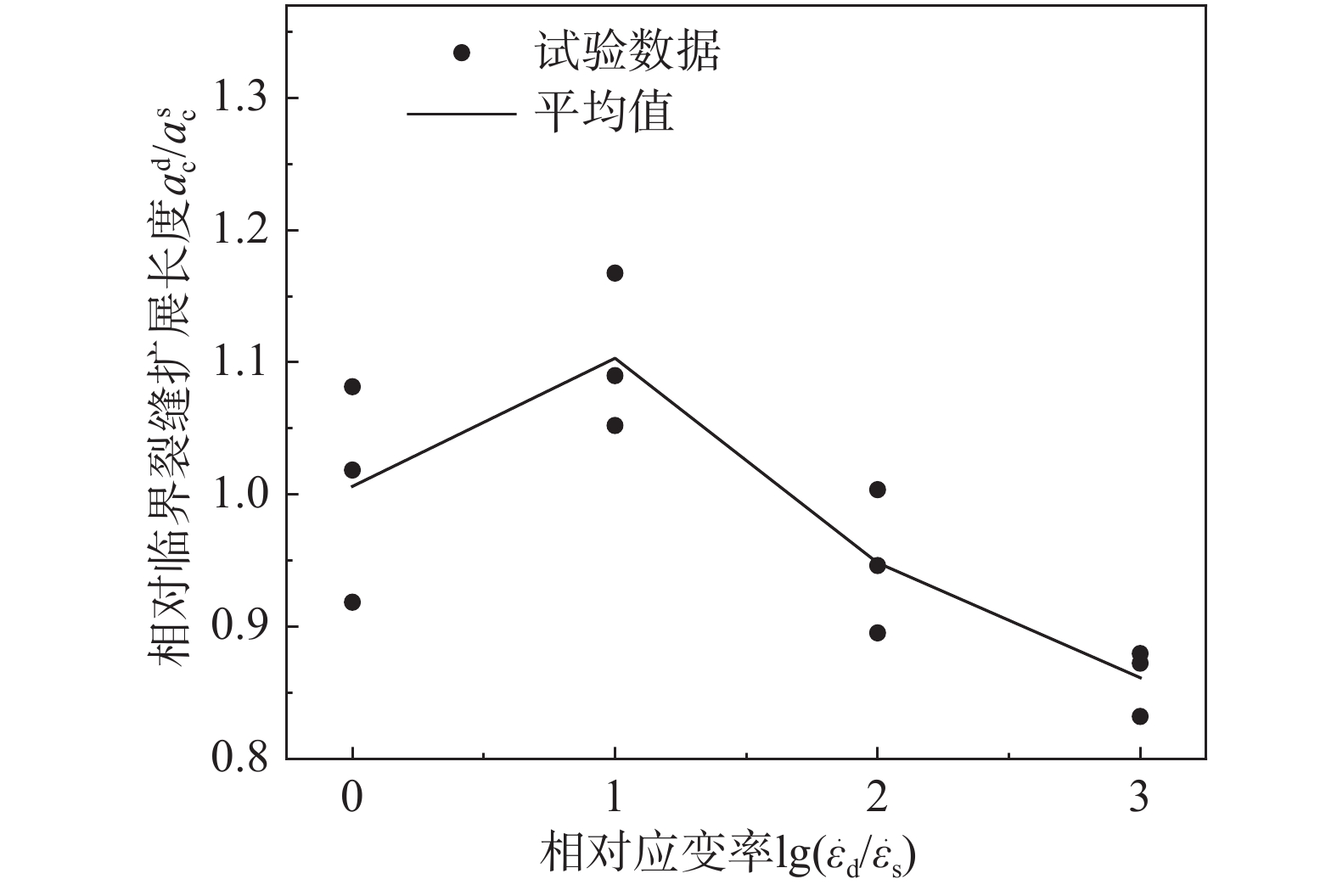
式中： ${\varepsilon _{\text{c}}}$ 为复合试件的拉伸应变；f_t为界面的抗拉强度；E_eff为等效弹性模量；可由式(6)计算^[27]，E₁为混凝土弹性模量；E₂为岩石弹性模量。根据已有研究^[28]，在10⁻⁵s⁻¹~10⁻²s⁻¹应变率范围内，弹性模量的率效应不明显。因此，本研究采用准静态下的弹性模量计算拉伸应变。以10⁻²s⁻¹应变率为例，采用DIC法确定的裂尖位置以及临界裂缝长度如图9所示。两种方法测得的不同应变率下界面的临界裂缝长度列于表4，临界裂缝长度相对值与应变率相对值的关系如图10所示。应变率对临界裂缝长度有显著影响，随着应变率的提高，临界裂缝长度呈现先提高后降低的趋势。

图  9  DIC法确定裂缝扩展长度

Figure  9.  DIC method is used to determine the crack propagation length

下载: 全尺寸图片 幻灯片

图  10  临界裂缝扩展长度与应变率的关系

Figure  10.  Relationship between critical crack propagation length and strain rate

下载: 全尺寸图片 幻灯片

本研究采用位移外推法计算界面应力强度因子。计算公式如下所示：

式中：

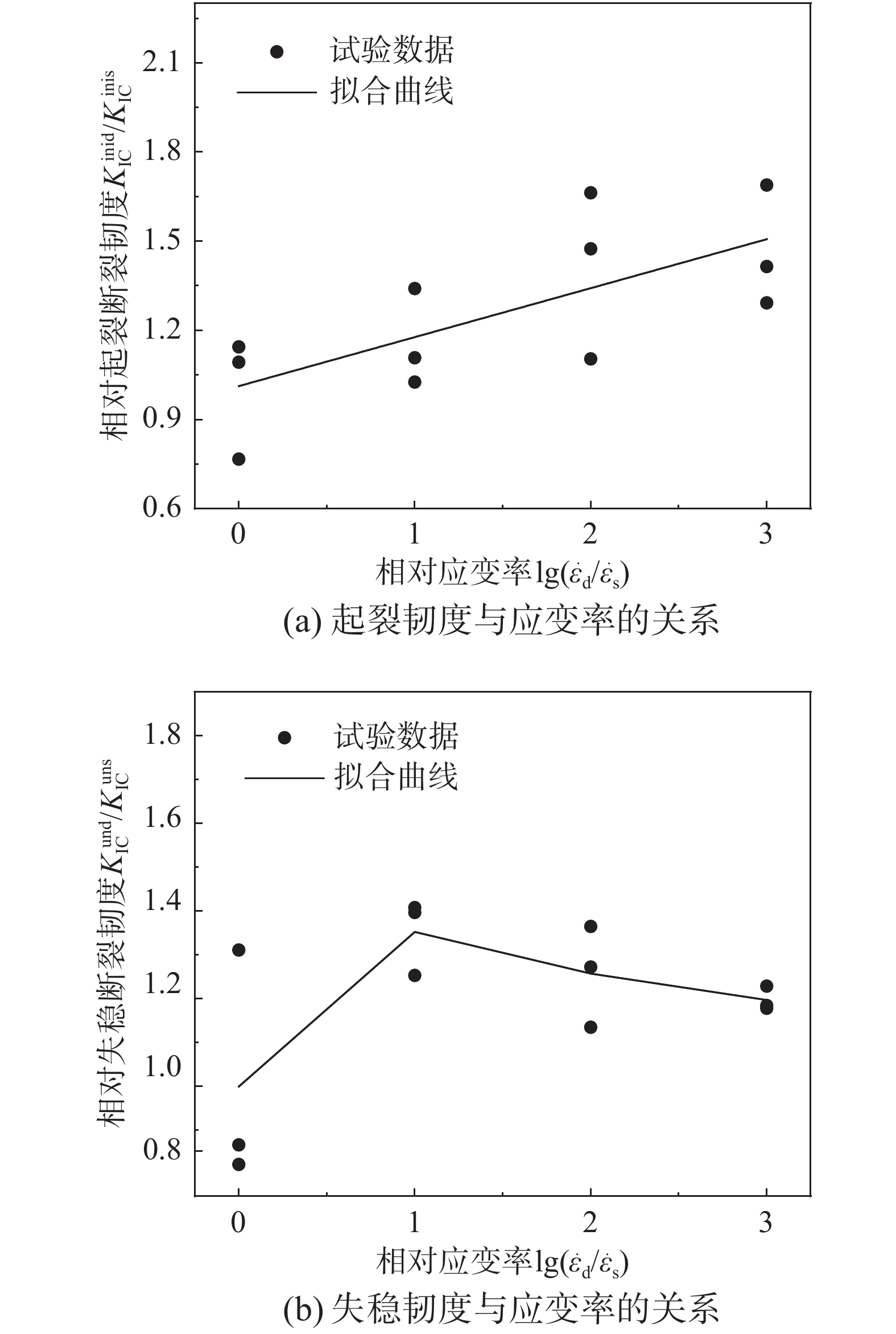
其中，E和ν分别为弹性模量和泊松比。根据位移外推法所确定的双K断裂参数列于表4，起裂断裂韧度相对值、失稳断裂韧度相对值与应变率相对值对数的关系分别如图11(a)、图11(b)所示。由图11(a)可知，随着应变率的提高，起裂断裂韧度逐渐提高，应变率对起裂韧度影响显著。以准静态条件下界面起裂韧度及应变率为基准，不同应变率下界面起裂断裂韧度相对值与应变率相对值的对数近似呈线性关系，线性拟合曲线表达式如下：

式中： $K_{{\text{IC}}}^{{\text{inid}}}$ 为不同应变率下的起裂韧度； $K_{{\text{IC}}}^{{\text{inis}}}$ 为准静态应变率下的起裂韧度。随着应变率从10⁻⁵s⁻¹升高到10⁻²s⁻¹，界面的起裂断裂韧度分别提升了15.93%、41.48%、46.67%。受裂缝扩展长度a_c的影响，失稳断裂韧度也呈现出先提高后降低的趋势。以10⁻⁵s⁻¹应变率为参照，10⁻⁴s⁻¹、10⁻³s⁻¹、10⁻²s⁻¹应变率下岩石-混凝土界面的失稳断裂韧度分别提高了35.19%、31.97%、19.74%，增量逐级递减。

定义粘聚韧度 $K_{\rm{IC}}^{\rm{c}}$ 为失稳断裂韧度 $K_{\rm{IC}}^{\rm{un}}$ 和起裂断裂韧度 $K_{\rm{IC}}^{\rm{ini}}$ 的差值^[22]。不同应变率下的粘聚韧度列于表4，平均值随应变率的变化见图12，由图可知，应变率从10⁻⁴s⁻¹~10⁻²s⁻¹，粘聚韧度分别减小了36%和49%。

图  11  双K断裂韧度与应变率的关系

Figure  11.  Relationship between double K fracture toughness and strain rate

下载: 全尺寸图片 幻灯片

图  12  不同应变率下的粘聚韧度

Figure  12.  Cohesive toughness at different strain rates

下载: 全尺寸图片 幻灯片

2.5   界面断裂过程区及特征长度

对于准脆性材料，在裂缝扩展过程中，裂纹尖端沿其扩展方向一定区域内形成微裂区。该区域内存在骨料桥联作用阻碍裂缝的张开与扩展，通常把该微裂区称为断裂过程区(FPZ)，其内部的裂缝阻力以与张开位移相关的粘聚应力形式进行数学表达^[29]。试件起裂之前，断裂过程区尚未形成，对应的断裂过程区长度为零。试件起裂后，断裂过程区开始形成并且向前扩展，当裂缝尖端张开位移CTOD小于w₀(粘聚力为零时所对应的裂缝宽度)时，裂缝扩展长度即为完整断裂过程区长度。试验结果表明，四种应变率下的试件均能形成完整的断裂过程区。在达到完整的断裂过程区之前，FPZ长度随裂缝扩展长度的增加而增加；形成完整的FPZ之后，FPZ长度随着裂缝扩展长度的增加而减小。10⁻⁵s⁻¹、10⁻⁴s⁻¹、10⁻³s⁻¹、10⁻²s⁻¹四种应变率对应的完整FPZ长度分别为：66.42 mm、63.05 mm、59.80 mm、55.59 mm，其与韧带长度的比值分别为0.98、0.93、0.90、0.84。完整FPZ长度随着应变率的升高而减小(见图13)。应变率越高，完整断裂过程区形成的越早。

图  13  不同应变率下的断裂过程区长度

Figure  13.  Length of fracture process zone at different strain rates

下载: 全尺寸图片 幻灯片

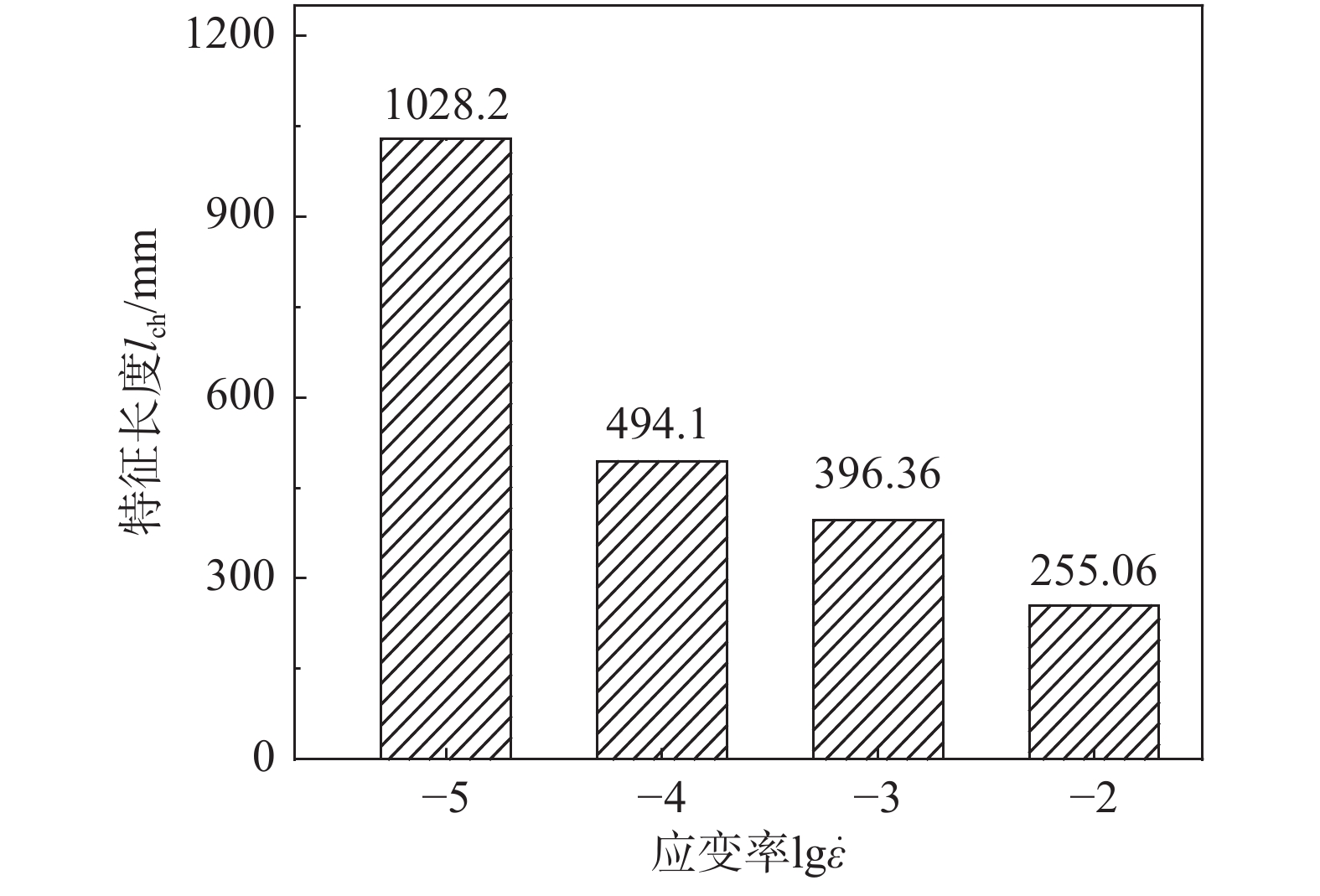
特征长度l_ch用来表征界面的脆性，特性长度越短，表明脆性越强。特征长度的计算公式如下所示：

不同速率下的特征长度见图14，由图可知，随着应变率的提高，特征长度降低，界面的脆性增强。以10⁻⁵s⁻¹应变率为参照，10⁻⁴s⁻¹、10⁻³s⁻¹、10⁻²s⁻¹应变率下岩石-混凝土界面的特征长度分别降低了52%、56%、75%。

图  14  不同应变率下的特征长度

Figure  14.  Characteristic lengths at different strain rates

下载: 全尺寸图片 幻灯片

2.6   率效应机理探讨

自ABRAMS在1917年发现了混凝土的抗压强度存在率敏感性以来，国内外学者对混凝土动态力学性能、动态断裂特性及破坏模式进行了广泛的研究^[30-33]。党发宁等^[34]从细观方面进行了混凝土强度率效应研究，得出在静力荷载作用下裂纹追随结构最弱方向发展，在动力荷载作用下裂纹追随能量释放最快路径发展。李庆斌等^[35]认为在中低应变率下，混凝土裂纹与孔隙中的自由水是影响混凝土抗拉强度的主要因素。对于更高应变率的情况，ROSSI等^[36]研究了应变率超过10 s⁻¹时混凝土强度的率效应，认为惯性力是导致动强度提高的主要原因。EIBL等^[37]也认为惯性效应导致了在高应变率下混凝土动强度提高。本文将从裂缝发展路径、水的黏性、惯性效应三方面来探讨界面强度率效应机理。

1) 通过对不同速率下的混凝土断面观察后发现^[28]，在准静态条件下，当裂缝的发展受到粗骨料的阻挡后，开始弯曲和分叉，形成狼牙状裂缝，断面比较粗糙，骨料破坏数量较少。随着应变速率的提高，裂纹产生和发展的时间越来越短，裂纹的发展在遇到粗骨料阻挡时来不及通过粗骨料与水泥砂浆结合部位的薄弱面，而直接穿过强度较高的区域(如骨料)，使破裂面趋于平整。本研究所采用的岩石-混凝土复合试件，在混凝土浇筑过程中，水泥砂浆及部分骨料会进入岩石槽口中。在10⁻⁵s⁻¹应变率下，槽口内的水泥浆体被拨出，断面处形成凸起的棱线。在较高应变率下，水泥浆体只有少量被拔出，多数是直接在界面处被拉断，故断面较为平整。裂缝发展在准静态的情况下遵循耗能最少原则，在较高应变率下遵循路径最快原则可以解释这一现象。

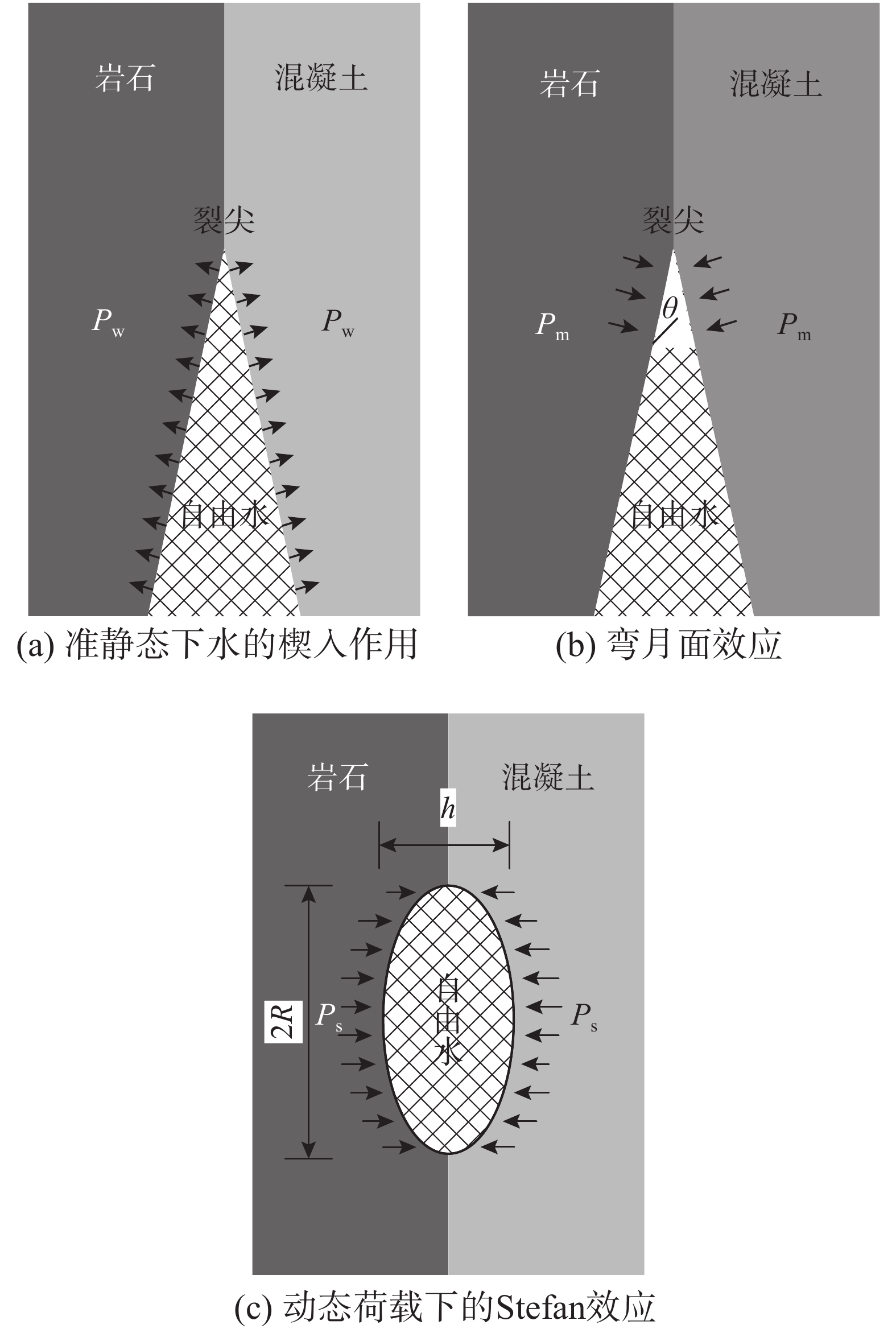
2) ROSSI等^[36]认为当应变率小于1 s⁻¹时，混凝土中自由水的粘性是导致混凝土强度随应变率提高而提高的主要原因。OŽBOLT等^[38]通过对前人工作的总结，也得出了相似的结论，认为从中低应变率到10 s⁻¹，抗力的增加主要是由粘弹性所控制。自由水粘性在不同应变率下表现出不同的作用形式，即准静态条件下的“楔入作用”^[39]和高应变率下“弯月面效应”^[40]、“Stefan效应”^[41]。

在准静态加载条件下，界面裂纹的开展速度较慢，自由水很容易到达裂尖，水的楔入作用促进了裂纹的扩展，此时自由水对裂纹的作用形式如图15(a)所示。当加载速率较高时，由于裂纹发展速度较快，自由水不易到达裂尖，其分布如图15(b)所示，弯月面上的表面力对裂纹面产生大小为2γcosθ/ρ的有益拉力，其阻碍了裂纹的扩展。此外，高加载速率下，物理学中的Stefan效应也可以作为材料峰值荷载提高的原因。Stefan效应指：两个相距h的半径为R的平行平板以相对速度 $\dot h$ 分离，若中间有黏性液体(粘度为η_w)存在，则会有一个P_s的力来阻止平板间的分离，可表示为： ${P_{\text{s}}} = 3{\eta _{\text{w}}}{R^2}\dot h/(2{h^3})$ 。图15(c)是Stefan效应物理模型。在准静态加载条件下，Stefan效应可忽略不计。而对于动态试验，加载速率越高，自由水的Stefan效应越明显，引起的粘聚力就越大，对裂纹的阻碍效果就越明显，使得在宏观上观察到试件的起裂荷载增加。

图  15  水的“双重作用”

Figure  15.  'two different effects' of water

下载: 全尺寸图片 幻灯片

3) ROSSI等^[36]认为当应变率超过10 s⁻¹时，惯性力是导致混凝土动强度提高的主要原因。闫东明^[28]通过研究混凝土的率敏感性也得出了相似的结论，即惯性的作用在应变率较高时会有一定影响，但是对较低应变率，惯性的影响并不明显。本文所研究的应变率范围是10⁻⁵s⁻¹~10⁻²s⁻¹，通过有限元软件ANSYS模拟了不同应变率下的三点弯曲试件加载过程，以加载点向下加载0.5 mm为例，不同应变率下计算所得的应力强度因子(单位：MPa·mm^1/2)分别为378.6826 91、378.6826 92、378.6827 04、378.6826 75。应力强度因子差值波动范围在2.64×10⁻⁹~3.17×10⁻⁸，可证明在地震应变率范围内惯性作用引起的率效应可忽略不计。

3   结论

本研究对岩石-混凝土复合试件进行了四种应变率(10⁻⁵s⁻¹、10⁻⁴s⁻¹、10⁻³s⁻¹、10⁻²s⁻¹)下的轴向拉伸试验和三点弯曲断裂试验。研究了应变率对复合试件断裂参数的影响，得到如下结论：

(1)复合试件的裂缝沿界面向上扩展，随着应变率的增加，断面凸横的饱满程度减弱，棱线趋于平整。裂缝发展在准静态条件下遵循耗能最少原则，在较高应变率下遵循路径最快原则。

(2)随应变率从10⁻⁵s⁻¹增加到10⁻²s⁻¹，起裂荷载，峰值荷载，界面抗拉强度，断裂能，起裂韧度线性增加。其中界面抗拉强度的率效应最为显著。

(3)应变率对临界裂缝长度有显著影响，随着应变率的提高，临界裂缝长度呈现先提高后降低的趋势。受裂缝扩展长度a_c的影响，失稳断裂韧度也呈现出先提高后降低的趋势。这与混凝土材料动态断裂性能的试验结果^[8]是相似的，但目前还缺乏对其机理的合理解释。

(4)在达到完整的断裂过程区(FPZ)之前，FPZ长度随着裂缝扩展长度的增加而增加；形成完整的FPZ之后，FPZ长度随着裂缝长度的增加而减小。完整FPZ长度随着应变率的增大而减小，其与韧带长度的比值分别为：0.98、0.93、0.90、0.84。特征长度随应变率的提高而降低，表明界面脆性随应变率的提高而增强。