IMPROVEMENT OF INTEGRAL RESPONSE DEFORMATION METHOD FOR UNDERGROUND STRUCTURES
-
摘要: 整体式反应位移法是目前常用的地下结构抗震实用分析方法，但在求解等效输入地震荷载的过程中，需对自由场土层模型中土-结构交界面所包围的所有土体单元施加自由场惯性力，处理过程相对复杂。该文基于有限元离散模型，从理论上证明了整体式反应位移法中由结构周边应力引起的等效地震荷载可通过仅由一层土体单元构成的子结构模型的一次静力分析获得，由此提出了一种基于土体内部子结构的地下结构整体式反应位移法，即改进方法一；进一步论证了改进方法一中内部土体子结构的惯性力对等效地震荷载的影响可以忽略，在此基础上提出地下结构整体式反应位移法的改进方法二，该方法避免了土层介质自由场惯性力的计算与施加，从而有效简化了整体式反应位移法的实施流程。通过与传统整体式反应位移法的对比分析，验证了该文改进方法具有良好的计算精度，可用于地铁车站、地下隧道等地下结构的地震反应分析与抗震性能研究。Abstract: The integral response deformation method is a commonly used seismic response analysis method for underground structures. However, in the process of solving the equivalent input seismic loads, it is necessary to apply the free-wave-field inertial force to all soil elements surrounded by the soil-structure interface in a free field model. The implementation processes are relatively complicated. Based on the discrete finite element model, the equivalent seismic loads caused by the surrounding stress of underground structures can be obtained through a static analysis of a substructure model consisting of only one layer of soil elements. On that basis, a modified integral response deformation method based on the substructure of soil layer is proposed, namely the first improved method. Furthermore, it is revealed that the influence of the inertial force of the soil layer on the equivalent seismic loads can be ignored. Then the second improved method of the integral response deformation method for underground structures is proposed. This method avoids the calculation and application of the free-wave-field inertial force of soil layers, thus effectively simplifying the implementation process of the integral response deformation method. The comparative analysis with the traditional integral response deformation method verifies that the proposed methods have good calculation accuracy, thus can be applied to the seismic response analysis and seismic performance research of underground structures such as subway stations and underground tunnels.
-
大型地下工程是重要的国家基础设施，由于财富集中度高，人员密集，其安全性至关重要。强震作用可能会使隧道、地铁车站等地下结构发生严重破坏及次生灾害[1-5]，因此，进行地下结构的抗震研究已成为一项紧迫的国家需求。
合理可靠的地下结构地震反应分析方法是开展地下结构抗震设计和地震灾害风险评估的基础。目前常用的地下结构地震反应分析方法主要包括动力时程法和简化的实用分析方法。其中基于动力有限元法的时程分析方法可有效模拟土-结构动力相互作用、截断边界处的波动辐射效应[6-10]以及不同类型和入射角度的地震波动输入问题[11-14]，是当前土-结构相互作用分析中最为全面、可信的数值模拟方法之一。但该方法涉及的计算模型通常较为复杂，实施难度较大，计算效率偏低。为解决实用性问题，研究人员在震害观测、模型试验、数值模拟和理论分析的基础上进行简化，提出了包括反应位移法[15-16]、反应加速度法[17]、地下结构Pushover分析方法[18-19]及不同方法的衍生方法[20-30]在内的多种地下结构地震反应实用分析方法。其中，反应位移法具有较为严密的理论基础和清晰明确的物理意义，在保证计算精度的前提下，计算效率优势突出，在实际工程问题中得到广泛应用。近年来，刘晶波等[31-32]在反应位移法的基础上，采用地下结构-岩土介质整体力学模型代替地基弹簧，提出了地下结构抗震分析的整体式反应位移法。该方法能够直接反映岩土介质与地下结构的相互作用，且不需考虑应力场在结构边界面上的分解与合成，适用于具有复杂横断面的地下结构的地震反应分析，其有效性与准确性已被大量相关研究验证[22, 33-35]，并已被我国《地下结构抗震设计标准》(GB/T 51336−2018)[36]采纳。
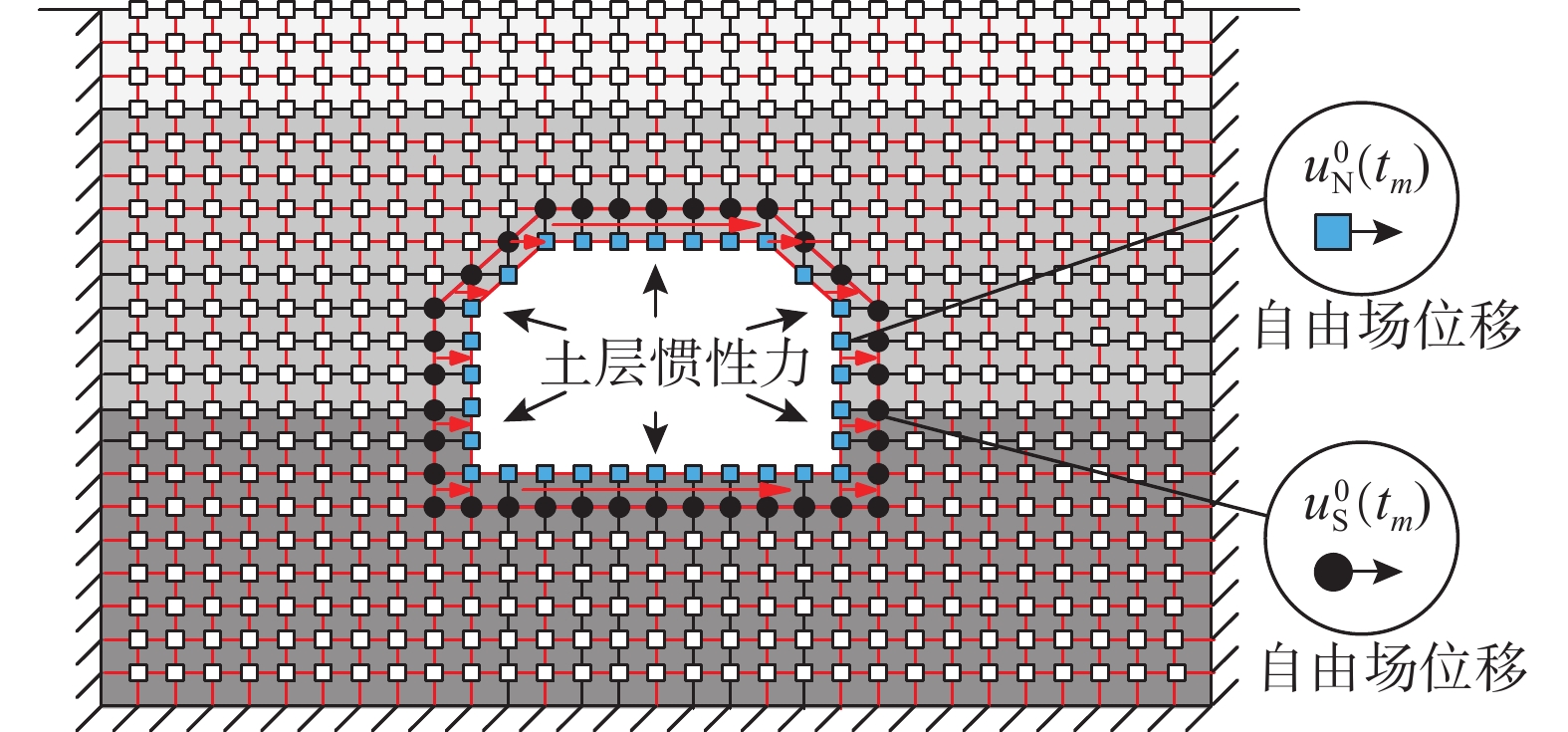
在采用整体式反应位移法求解等效输入地震荷载的过程中，需计算对应于结构位置处的土体介质自由场加速度，根据土层性质将其转化为惯性力，判断其作用方向，并逐一施加到土-结构交界面所包围的土体单元之上，处理过程相对复杂。本文基于有限元离散模型，从理论上证明了整体式反应位移法中由结构周边应力引起的等效地震荷载可通过仅由一层土体单元构成的子结构模型的一次静力分析获得，且此时土体惯性力对等效地震荷载的影响可以忽略。在此基础上提出地下结构整体式反应位移法的改进方法。改进方法在保证计算精度的前提下，避免了土层介质自由场惯性力的计算与施加，从而有效简化了整体式反应位移法的实施流程。
1 地下结构地震反应分析的整体式反应位移法
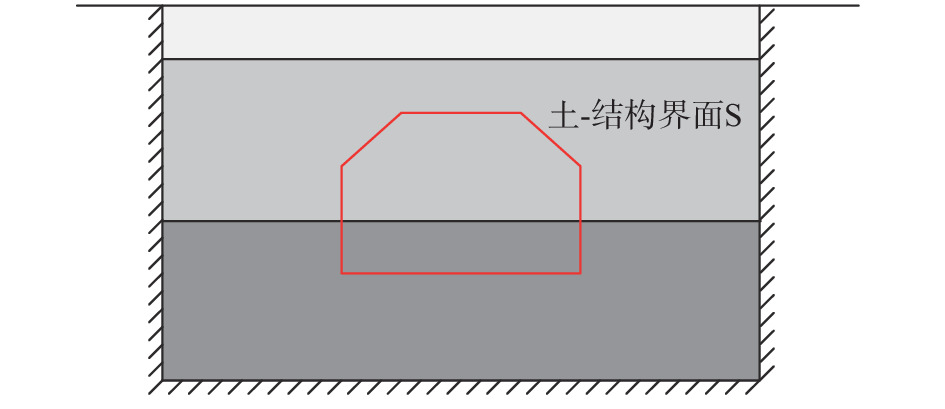
地下结构-岩土介质相互作用模型如图1所示，将土-结构交界面记为S。采用整体式反应位移法进行计算分析时，需建立如图2所示的辅助自由场模型，其中结构所在位置由自由场地基介质填充。
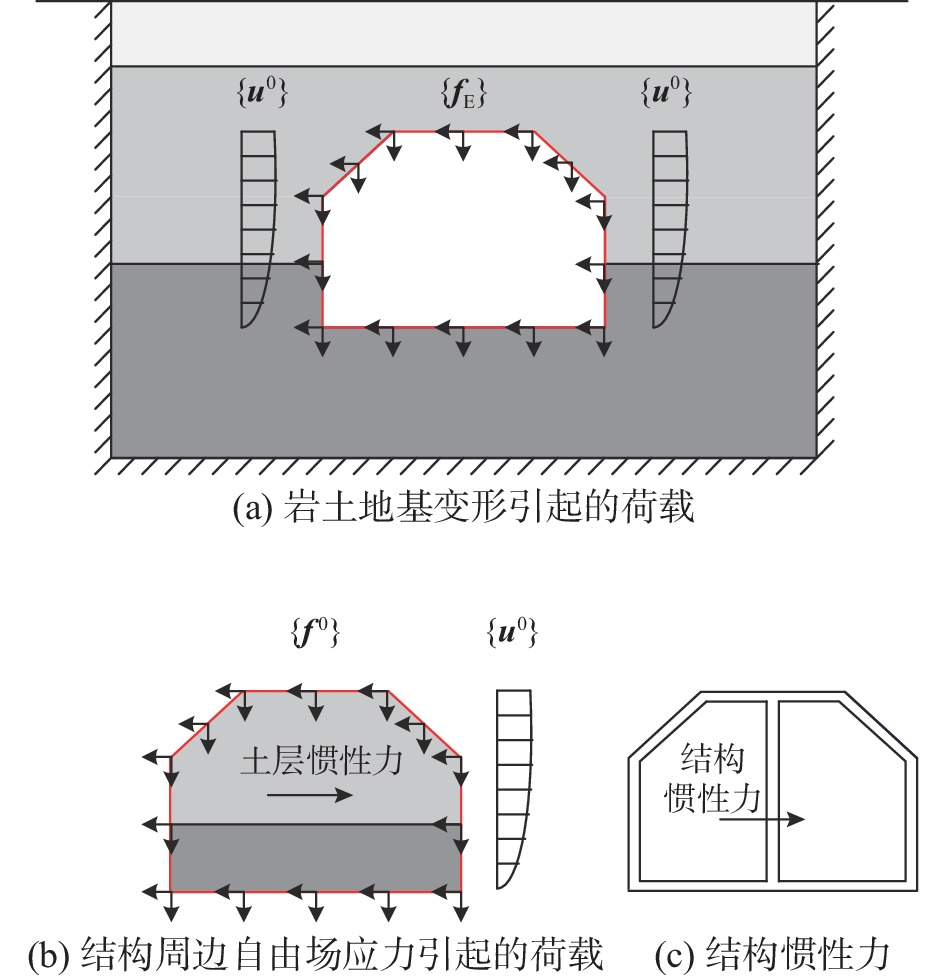
根据整体式反应位移法的基本理论[37]，地下结构所承受的地震作用由以下三部分构成：
1)岩土地基变形引起的荷载fE：等效于在去除结构的土层有限元模型中将土-结构界面拉至自由场变形位置处所需的荷载，如图3(a)所示；
![]()
图 3 整体式反应位移法中的等效地震荷载Figure 3. Equivalent seismic loads in the integral response deformation method2)由结构外侧的周边自由场应力产生的作用于结构之上的荷载
{{\boldsymbol{f}}}_{\text{S}}^0 ：在对应于结构位置处的自由场介质模型边界上施加自由场位移，并对内部自由场介质施加自由场惯性力，通过静力计算求解得到的界面S处的节点反力，如图3(b)所示。3)结构自身的惯性力，如图3(c)所示。
其中前两项之和称为等效输入地震荷载，记为FS。
在实际求解等效输入地震荷载的过程中，内部土体介质自由场惯性力的施加是一个相对复杂，且容易出错的过程，由于结构所在位置处每一层土体单元的土层性质和自由场加速度分布均不相同，因此，在实际计算时，首先，需提取最不利时刻的土层场地自由场加速度分布，判断其作用方向，然后，根据对应位置处的土层性质，逐一计算等效惯性力，并施加在每一土体单元上。鉴于此，本文重点研究整体式反应位移法中等效地震荷载的简化求解方法。
2 整体式反应位移法的改进
2.1 改进方法一
整体式反应位移法中由结构周边自由场应力引起的等效地震荷载
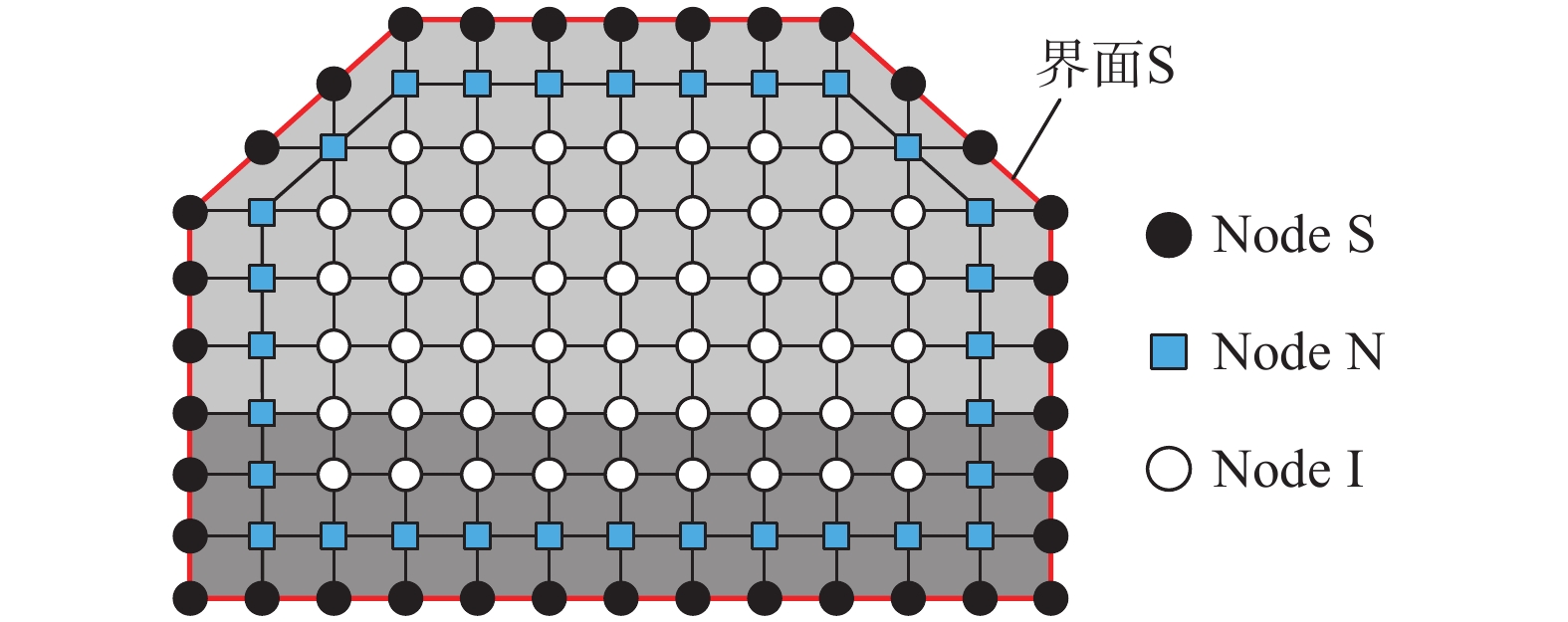
{{\boldsymbol{f}}}_{\text{S}}^0 本质上是自由场中土-结构界面对应位置处的土层应力。可建立如图4所示的对应于结构位置处的自由场岩土介质模型，并对其进行受力分析。按空间位置将模型节点分成三类，分别是土-结构界面节点S(用实心圆符号●表示)、与土-结构界面相邻的内部结点N(用实心方框表示■)和其余内部节点I(用空心圆符号○表示)。![]()
图 4 结构所在位置处的自由场岩土介质模型Figure 4. Free field model of soil medium corresponding to the structure location根据上述节点分类，可建立结构所在位置处的自由场岩土介质的运动方程：
\begin{split} &\left[ {\begin{matrix} {{{\boldsymbol M}_{{\text{SS}}}}}&{{{\boldsymbol M}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol M}_{{\text{NS}}}}}&{{{\boldsymbol M}_{{\text{NN}}}}}&{{{\boldsymbol M}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol M}_{{\text{IN}}}}}&{{{\boldsymbol M}_{{\text{II}}}}} \end{matrix}} \right]\left\{ {\begin{matrix} {{{{\ddot {\boldsymbol u}}}_{\text{S}}}(t)} \\ {{{{\ddot {\boldsymbol u}}}_{\text{N}}}(t)} \\ {{{{\ddot {\boldsymbol u}}}_{\text{I}}}(t)} \end{matrix}} \right\} + \\ &\quad\left[ {\begin{matrix} {{{\boldsymbol C}_{{\text{SS}}}}}&{{{\boldsymbol C}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol C}_{{\text{NS}}}}}&{{{\boldsymbol C}_{{\text{NN}}}}}&{{{\boldsymbol C}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol C}_{{\text{IN}}}}}&{{{\boldsymbol C}_{{\text{II}}}}} \end{matrix}} \right]\left\{ {\begin{matrix} {{{{\dot {\boldsymbol u}}}_{\text{S}}}(t)} \\ {{{{\dot {\boldsymbol u}}}_{\text{N}}}(t)} \\ {{{{\dot {\boldsymbol u}}}_{\text{I}}}(t)} \end{matrix}} \right\} + \\ &\quad\left[ {\begin{matrix} {{{\boldsymbol K}_{{\text{SS}}}}}&{{{\boldsymbol K}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol K}_{{\text{NS}}}}}&{{{\boldsymbol K}_{{\text{NN}}}}}&{{{\boldsymbol K}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol K}_{{\text{IN}}}}}&{{{\boldsymbol K}_{{\text{II}}}}} \end{matrix}} \right]\left\{ {\begin{matrix} {{{\boldsymbol u}_{\text{S}}}(t)} \\ {{{\boldsymbol u}_{\text{N}}}(t)} \\ {{{\boldsymbol u}_{\text{I}}}(t)} \end{matrix}} \right\} = \left\{ {\begin{matrix} {{{\boldsymbol f}_{\text{S}} }} \\ {{{\boldsymbol f}_{\text{N}}}} \\ {{{\boldsymbol f}_{\text{I}}}} \end{matrix}} \right\} \end{split} (1) 式中：M、C和K分别为质量矩阵、阻尼矩阵和刚度矩阵；
{\ddot {\boldsymbol{u}}} 、{\dot {\boldsymbol{u}}} 和u分别为加速度、速度和位移向量；f为节点力向量；下标S、N和I代表图4中的节点分类。根据隔离体理论，对于如图4所示的岩土介质模型，在土-结构界面S上施加荷载
{{\boldsymbol{f}}}_{\text{S}}^0 ，即可使模型内部的土体介质满足自由场运动状态：\begin{split} & \left[ {\begin{matrix} {{{\boldsymbol M}_{{\text{SS}}}}}&{{{\boldsymbol M}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol M}_{{\text{NS}}}}}&{{{\boldsymbol M}_{{\text{NN}}}}}&{{{\boldsymbol M}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol M}_{{\text{IN}}}}}&{{{\boldsymbol M}_{{\text{II}}}}} \end{matrix}} \right]\left\{ {\begin{aligned} {{\ddot {\boldsymbol u}}_{\text{S}}^0(t)} \\ {{\ddot {\boldsymbol u}}_{\text{N}}^0(t)} \\ {{\ddot {\boldsymbol u}}_{\text{I}}^0(t)} \end{aligned}} \right\} + \\ & \quad \left[ {\begin{matrix} {{{\boldsymbol C}_{{\text{SS}}}}}&{{{\boldsymbol C}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol C}_{{\text{NS}}}}}&{{{\boldsymbol C}_{{\text{NN}}}}}&{{{\boldsymbol C}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol C}_{{\text{IN}}}}}&{{{\boldsymbol C}_{{\text{II}}}}} \end{matrix}} \right]\left\{ {\begin{aligned} {{\dot {\boldsymbol u}}_{\text{S}}^0(t)} \\ {{\dot {\boldsymbol u}}_{\text{N}}^0(t)} \\ {{\dot {\boldsymbol u}}_{\text{I}}^0(t)} \end{aligned}} \right\} + \\ & \quad \left[ \begin{matrix} {{{\boldsymbol K}_{{\text{SS}}}}}&{{{\boldsymbol K}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol K}_{{\text{NS}}}}}&{{{\boldsymbol K}_{{\text{NN}}}}}&{{{\boldsymbol K}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol K}_{{\text{IN}}}}}&{{{\boldsymbol K}_{{\text{II}}}}} \end{matrix} \right]\left\{ {\begin{aligned} {{\boldsymbol u}_{\text{S}}^0(t)} \\ {{\boldsymbol u}_{\text{N}}^0(t)} \\ {{\boldsymbol u}_{\text{I}}^0(t)} \end{aligned}} \right\} = \left\{ {\begin{matrix} {{\boldsymbol f}_{\text{S}}^0} \\ 0 \\ 0 \end{matrix}} \right\} \end{split} (2) 式中，上标0代表自由场运动。
将对应于地下结构顶、底板位置处，自由场发生最大相对位移的时刻，即最不利时刻，记作tm，此时自由场运动方程表示为：
\begin{split} & \left[ {\begin{matrix} {{{\boldsymbol M}_{{\text{SS}}}}}&{{{\boldsymbol M}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol M}_{{\text{NS}}}}}&{{{\boldsymbol M}_{{\text{NN}}}}}&{{{\boldsymbol M}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol M}_{{\text{IN}}}}}&{{{\boldsymbol M}_{{\text{II}}}}} \end{matrix}} \right]\left\{ {\begin{aligned} {{\ddot {\boldsymbol u}}_{\text{S}}^0({t_{\text{m}}})} \\ {{\ddot {\boldsymbol u}}_{\text{N}}^0({t_{\text{m}}})} \\ {{\ddot {\boldsymbol u}}_{\text{I}}^0({t_{\text{m}}})} \end{aligned}} \right\} + \\ & \quad \left[ {{\begin{matrix} {{{\boldsymbol C}_{{\text{SS}}}}}&{{{\boldsymbol C}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol C}_{{\text{NS}}}}}&{{{\boldsymbol C}_{{\text{NN}}}}}&{{{\boldsymbol C}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol C}_{{\text{IN}}}}}&{{{\boldsymbol C}_{{\text{II}}}}} \end{matrix}}} \right]\left\{ {\begin{aligned} {{\dot {\boldsymbol u}}_{\text{S}}^0({t_{\text{m}}})} \\ {{\dot {\boldsymbol u}}_{\text{N}}^0({t_{\text{m}}})} \\ {{\dot {\boldsymbol u}}_{\text{I}}^0({t_{\text{m}}})} \end{aligned}} \right\} + \\ & \quad \left[ {\begin{matrix} {{{\boldsymbol K}_{{\text{SS}}}}}&{{{\boldsymbol K}_{{\text{SN}}}}}&{\mathbf{0}} \\ {{{\boldsymbol K}_{{\text{NS}}}}}&{{{\boldsymbol K}_{{\text{NN}}}}}&{{{\boldsymbol K}_{{\text{NI}}}}} \\ {\mathbf{0}}&{{{\boldsymbol K}_{{\text{IN}}}}}&{{{\boldsymbol K}_{{\text{II}}}}} \end{matrix}} \right]\left\{ {\begin{aligned} {{\boldsymbol u}_{\text{S}}^0({t_{\text{m}}})} \\ {{\boldsymbol u}_{\text{N}}^0({t_{\text{m}}})} \\ {{\boldsymbol u}_{\text{I}}^0({t_{\text{m}}})} \end{aligned}} \right\} = \left\{ {\begin{matrix} {{\boldsymbol f}_{\text{S}}^0({t_{\text{m}}})} \\ 0 \\ 0 \end{matrix}} \right\} \end{split} (3) 在传统的整体式反应位移法中，通过给出土-结构界面处的自由场位移
{\boldsymbol{u}}_{\text{S}}^0({t_{\text{m}}}) 和模型各节点的自由场加速度{\ddot {\boldsymbol u}}_{\text{S}}^0({t_{\text{m}}}) 、{\ddot {\boldsymbol u}}_{\text{N}}^0({t_{\text{m}}}) 、{\ddot {\boldsymbol u}}_{\text{I}}^0({t_{\text{m}}}) ，忽略影响较小的阻尼力，采用静力计算求解式(3)，得到由结构周边应力引起的等效地震作用{\boldsymbol{f}}_{\text{S}}^0 ：\begin{split} &{\boldsymbol{f}}_{\rm{S}}^0 = {{\boldsymbol K}_{{\rm{SS}}}}{\boldsymbol u}_{\rm{S}}^0({t_{\rm{m}}}) + {{\boldsymbol M}_{{\rm{SS}}}}{\ddot {\boldsymbol u}}_{\rm{S}}^0({t_{\rm{m}}}) + {{\boldsymbol M}_{{\rm{SN}}}}{\ddot {\boldsymbol u}}_{\rm{N}}^0({t_{\rm{m}}}) + \\ &\;\;\;\;\;\;\;{{\boldsymbol K}_{{\rm{SN}}}}{( {{{\boldsymbol K}_{{\rm{NN}}}} - {{\boldsymbol K}_{{\rm{NI}}}}{\boldsymbol K}_{{\rm{II}}}^{ - 1}{{\boldsymbol K}_{{\rm{IN}}}}} )^{ - 1}} \cdot \\ &\;\;\;\;\;\;\;[ {{{\boldsymbol K}_{{\rm{NI}}}}{\boldsymbol K}_{{\rm{II}}}^{ - 1}} ( {{{\boldsymbol M}_{{\rm{IN}}}}{\ddot {\boldsymbol u}}_{\rm{N}}^0({t_{\rm{m}}}) + } {{{\boldsymbol M}_{{\rm{II}}}}{\ddot {\boldsymbol u}}_{\rm{I}}^0({t_{\rm{m}}})} ) - \\ &\;\;\;\;\;\;\;( {{{\boldsymbol M}_{{\rm{NS}}}}{\ddot {\boldsymbol u}}_{\rm{S}}^0({t_{\rm{m}}}) + {{\boldsymbol M}_{{\rm{NN}}}}{\ddot {\boldsymbol u}}_{\rm{N}}^0({t_{\rm{m}}}) + {{\boldsymbol M}_{{\rm{NI}}}}{\ddot {\boldsymbol u}}_{\rm{I}}^0({t_{\rm{m}}})} ) - \\ &\;\;\;\;\;\;\; {{{\boldsymbol K}_{{\rm{NS}}}}{\boldsymbol u}_{\rm{S}}^0({t_{\rm{m}}})} ] \end{split} (4) 由式(4)可见，此时
{{\boldsymbol{f}}}_{\rm S}^0 的计算与{\boldsymbol u}_{\rm S}^0({t_{\text{m}}}) 有关，同时与{\ddot {\boldsymbol u}}_{\text{S}}^0({t_{\text{m}}}) 、{\ddot {\boldsymbol u}}_{\text{N}}^0({t_{\text{m}}}) 、{\ddot {\boldsymbol u}}_{\text{I}}^0({t_{\text{m}}}) 相对应的自由场惯性力均相关。若直接求解运动方程式(3)，并忽略阻尼力，可得：
{{\boldsymbol{f}}}_{\text{S}}^0 = {{\boldsymbol K}_{{\text{SS}}}}{\boldsymbol u}_{\text{S}}^0({t_{\text{m}}}) + {{\boldsymbol K}_{{\text{SN}}}}{\boldsymbol u}_{\text{N}}^0({t_{\text{m}}}) + {{\boldsymbol M}_{{\text{SS}}}}{\ddot {\boldsymbol u}}_{\text{S}}^0({t_{\text{m}}}) + {{\boldsymbol M}_{{\text{SN}}}}{\ddot {\boldsymbol u}}_{\text{N}}^0({t_{\text{m}}}) (5) 对比式(4)和式(5)可以得到：
\begin{split} &{\boldsymbol u}_{\rm{N}}^0({t_{\rm{m}}}) = {( {{{\boldsymbol K}_{{\rm{NN}}}} - {{\boldsymbol K}_{{\rm{NI}}}}{\boldsymbol K}_{{\rm{II}}}^{ - 1}{{\boldsymbol K}_{{\rm{IN}}}}} )^{ - 1}} \cdot \\ &\;\;\;\;\;[ {{{\boldsymbol K}_{{\rm{NI}}}}{\boldsymbol K}_{{\rm{II}}}^{ - 1}( {{{\boldsymbol M}_{{\rm{IN}}}}\ddot {\boldsymbol u}_{\rm{N}}^0({t_{\rm{m}}}) + {{\boldsymbol M}_{{\rm{II}}}}\ddot {\boldsymbol u}_{\rm{I}}^0({t_{\rm{m}}})} )} - \\ &\;\;\;\;\;( {{{\boldsymbol M}_{{\rm{NS}}}}\ddot {\boldsymbol u}_{\rm{S}}^0({t_{\rm{m}}}) + {{\boldsymbol M}_{{\rm{NN}}}}\ddot {\boldsymbol u}_{\rm{N}}^0({t_{\rm{m}}}) + {{\boldsymbol M}_{{\rm{NI}}}}\ddot {\boldsymbol u}_{\rm{I}}^0({t_{\rm{m}}})} ) - \\ & {\;\;\;\;\;{{\boldsymbol K}_{{\rm{NS}}}}{\boldsymbol u}_{\rm{S}}^0({t_{\rm{m}}})} ] \end{split} (6) 式(6)表明：截面S内部节点的惯性力仅用于产生节点位移
{\boldsymbol u}_{\text{N}}^0({t_{\text{m}}}) ，如果在计算模型中引入自由场位移{\boldsymbol u}_{\text{N}}^0({t_{\text{m}}}) ，则无需考虑内部节点惯性力的影响。由于通过直接求解式(5)得到的结构周边应力{{\boldsymbol{f}}}_{\text{S}}^0 仅与界面节点S及与其相邻的内部结点N有关，而与其余内部节点I无关。因此，可进一步建立仅由节点S、N包围的一层土体单元构成的自由场介质模型，将其定义为内部土层子结构模型，如图5所示。该内部土层子结构模型的运动方程可表示为：
\begin{split} & \left[ {\begin{aligned} &{{\boldsymbol M}_{{\text{SS}}}^{{\text{sub}}}}&{{\boldsymbol M}_{{\text{SN}}}^{{\text{sub}}}} \\ &{{\boldsymbol M}_{{\text{NS}}}^{{\text{sub}}}}&{{\boldsymbol M}_{{\text{NN}}}^{{\text{sub}}}} \end{aligned}} \right]\left\{ {\begin{aligned} &{{\ddot {\boldsymbol u}}_{\text{S}}^{{\text{sub}}}(t)} \\ &{{\ddot {\boldsymbol u}}_{\text{N}}^{{\text{sub}}}(t)} \end{aligned}} \right\} + \\ & \qquad \left[ {\begin{aligned} & {{\boldsymbol C}_{{\text{SS}}}^{{\text{sub}}}}&{{\boldsymbol C}_{{\text{SN}}}^{{\text{sub}}}} \\ & {{\boldsymbol C}_{{\text{NS}}}^{{\text{sub}}}}&{{\boldsymbol C}_{{\text{NN}}}^{{\text{sub}}}} \end{aligned}} \right]\left\{ {\begin{aligned} & {{\dot {\boldsymbol u}}_{\text{S}}^{{\text{sub}}}(t)} \\ & {{\dot {\boldsymbol u}}_{\text{N}}^{{\text{sub}}}(t)} \end{aligned}} \right\} + \\ & \qquad \left[ {\begin{aligned} & {{K}_{{\text{SS}}}^{{\text{sub}}}}&{{K}_{{\text{SN}}}^{{\text{sub}}}} \\ & {{K}_{{\text{NS}}}^{{\text{sub}}}}&{{K}_{{\text{NN}}}^{{\text{sub}}}} \end{aligned}} \right]\left\{ {\begin{aligned} & {{\boldsymbol u}_{\text{S}}^{{\text{sub}}}(t)} \\ & {{\boldsymbol u}_{\text{N}}^{{\text{sub}}}(t)} \end{aligned}} \right\} = \left\{ {\begin{aligned} & {{\boldsymbol{f}}_{\text{S}}^{{\text{sub}}}} \\ & {{\boldsymbol{f}}_{\text{N}}^{{\text{sub}}}} \end{aligned}} \right\} \end{split} (7) 式中，上标sub代表内部土层子结构。
分别对内部土层子结构模型中的节点S和节点N施加tm时刻的自由场位移
{\boldsymbol u}_{\text{S}}^0\left( {{t_m}} \right) 、{\boldsymbol u}_{\text{N}}^0\left( {{t_m}} \right) 和自由场加速度{\ddot {\boldsymbol u}}_{\text{S}}^0({t_{\text{m}}}) 、{\ddot {\boldsymbol u}}_{\text{N}}^0({t_{\text{m}}}) ，忽略惯性力影响，采用静力学方法可得到{\boldsymbol{f}}_{\text{S}}^{{\text{sub}}} 的解：\begin{split} & {{\boldsymbol{f}}}_{\text{S}}^{{\text{sub}}} = {\boldsymbol K}_{{\text{SS}}}^{{\text{sub}}}{\boldsymbol u}_{\text{S}}^0({t_{\text{m}}}) + {\boldsymbol K}_{{\text{SN}}}^{{\text{sub}}}{\boldsymbol u}_{\text{N}}^0({t_{\text{m}}})+\\ &\qquad\quad{\boldsymbol M}_{{\text{SS}}}^{{\text{sub}}}{\ddot {\boldsymbol u}}_{\text{S}}^0({t_{\text{m}}}) + {\boldsymbol M}_{{\text{SN}}}^{{\text{sub}}}{\ddot {\boldsymbol u}}_{\text{N}}^0({t_{\text{m}}}) \end{split} (8) 根据有限元法的基本原理可知，当图5中内部子结构模型的材料参数和单元划分与图4中的自由场土层模型完全一致时，以下方程成立：
{\boldsymbol K}_{\text{SS}}^{\text{sub}}={\boldsymbol K}_{\text{SS}},\;{\boldsymbol K}_{\text{SN}}^{\text{sub}}\text={\boldsymbol K}_{\text{SN}},\;{\boldsymbol M}_{\text{SS}}^{\text{sub}}\text={\boldsymbol M}_{\text{SS}},\;{\boldsymbol M}_{\text{SN}}^{\text{sub}}\text={\boldsymbol M}_{\text{SN}} (9) 将式(9)代入式(8)，并与式(5)对比，可以发现
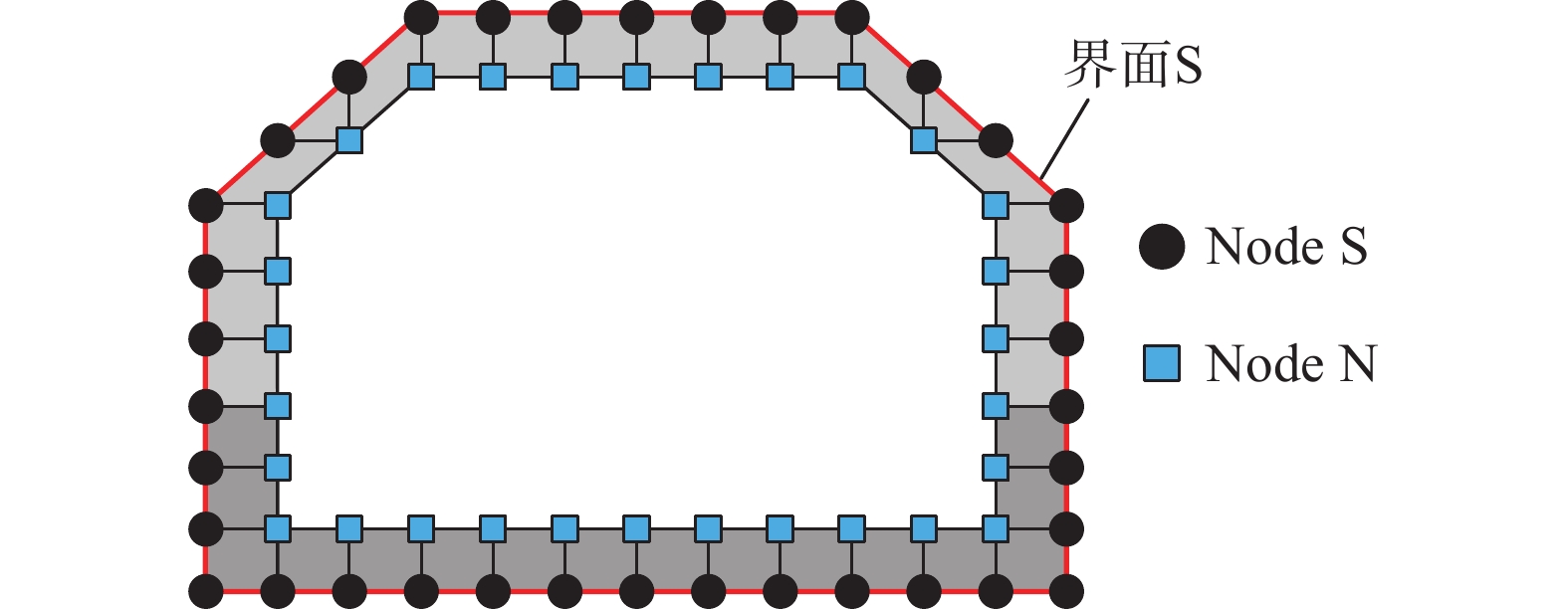
{{\boldsymbol{f}}}_{\text{S}}^{{\text{sub}}} = {{\boldsymbol{f}}}_{\text{S}}^0 ，即两者求解等效地震作用的计算公式完全相同，说明在整体式反应位移法中，由结构周边应力引起的地震荷载可通过建立如图5所示的仅由土-结构界面内侧一层土体单元构成的内部土层子结构模型计算得到。与传统的整体式反应位移法类似，由于该方法对内部土层子结构模型的土-结构界面节点施加了自由场变形，相应的位移边界条件与计算岩土地基变形引起的荷载fE时，挖除结构的自由场土层模型的土-结构界面边界条件一致，因此两者的计算可进行合并处理，即直接建立如图6所示的由结构周边土体及内部土层子结构构成的自由场土层有限元模型，并在全部土层子结构的节点上施加最不利时刻的自由场位移向量，同时对内部土层子结构单元施加自由场惯性力，忽略阻尼力的影响，采用静力学方法计算得到土-结构界面处的反力，即为进行地下结构拟静力分析的等效地震荷载，将该方法记为整体式反应位移法的改进方法一。
![]()
图 6 地下结构整体式反应位移法的改进方法一Figure 6. The first improved method of the integral response deformation method for underground structure2.2 改进方法二
由于改进方法一仍然需要在与土-结构界面相连的一层内部土体单元上施加惯性力，使得分析工作中仍需计算土层自由场惯性力，为此可以对改进方法一进行简化。
由式(8)可知，结构周边应力引起的地震荷载
{{\boldsymbol{f}}}_{\text{S}}^{{\text{sub}}} 由变形恢复力和惯性力构成。不同于传统整体式反应位移法中仅给定土-结构界面处的自由场位移，而依靠全部内部节点的自由场惯性力计算界面内的自由场变形，并进一步求解等效地震荷载的方法，采用内部土体子结构模型进行计算时，由于同时给出了土-结构界面节点和其内侧相邻节点的自由场位移，可提供式(8)中用于计算土-结构界面上变形恢复力的全部信息，而土层自由场加速度则仅用于计算与土-结构界面相连的一层土体单元的惯性力，其对等效地震荷载的贡献相比于传统整体式反应位移法将显著减小。因此可进一步忽略子结构单元层的惯性力，而仅在土-结构界面节点S及其内侧一层节点N上施加对应位置处的自由场变形，进行静力计算求解等效地震荷载，从而避免最不利时刻土层场地自由场惯性力的逐一计算和施加，使计算流程得以进一步简化。将这一方法记为整体式反应位移法的改进方法二，其具体实施步骤如下：1)求解自由场地震反应：采用等效线性化分析软件或自编程序，完成地震波竖直输入下的土层场地地震反应分析，可同时获得土层模型中相应于结构位置处最不利时刻的自由场位移和加速度；
2)求解等效输入地震荷载：建立仅包含结构周边土体及土-结构界面内侧一层土体单元的自由场土层有限元模型，在土-结构界面节点及内部节点位置处施加步骤1)中获得的土层变形，如图7(a)所示，计算土-结构交界面上的节点反力，即为等效输入地震荷载；
![]()
图 7 地下结构整体式反应位移法的改进方法二Figure 7. The second improved method of the integral response deformation method for underground structure3)求解结构惯性力：取步骤1)中得到的对应于结构位置处的最不利时刻自由场土层加速度，以惯性力的形式施加于结构自身；
4)完成整体模型的静力计算：建立土-结构相互作用模型，将外边界固定，施加等效输入地震荷载和结构自身惯性力，如图7(b)所示，通过静力计算得到地下结构的地震反应。
3 方法验证
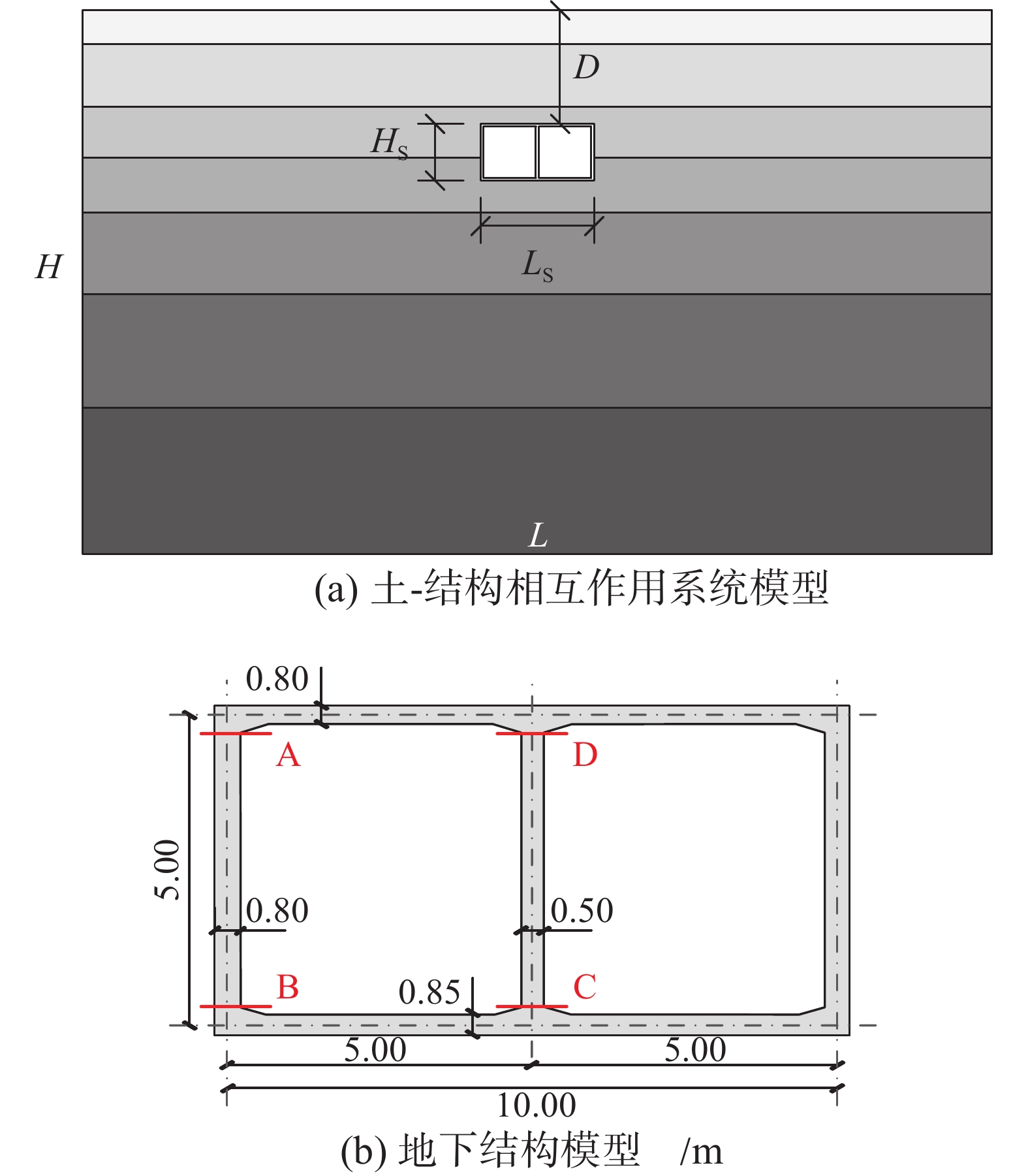
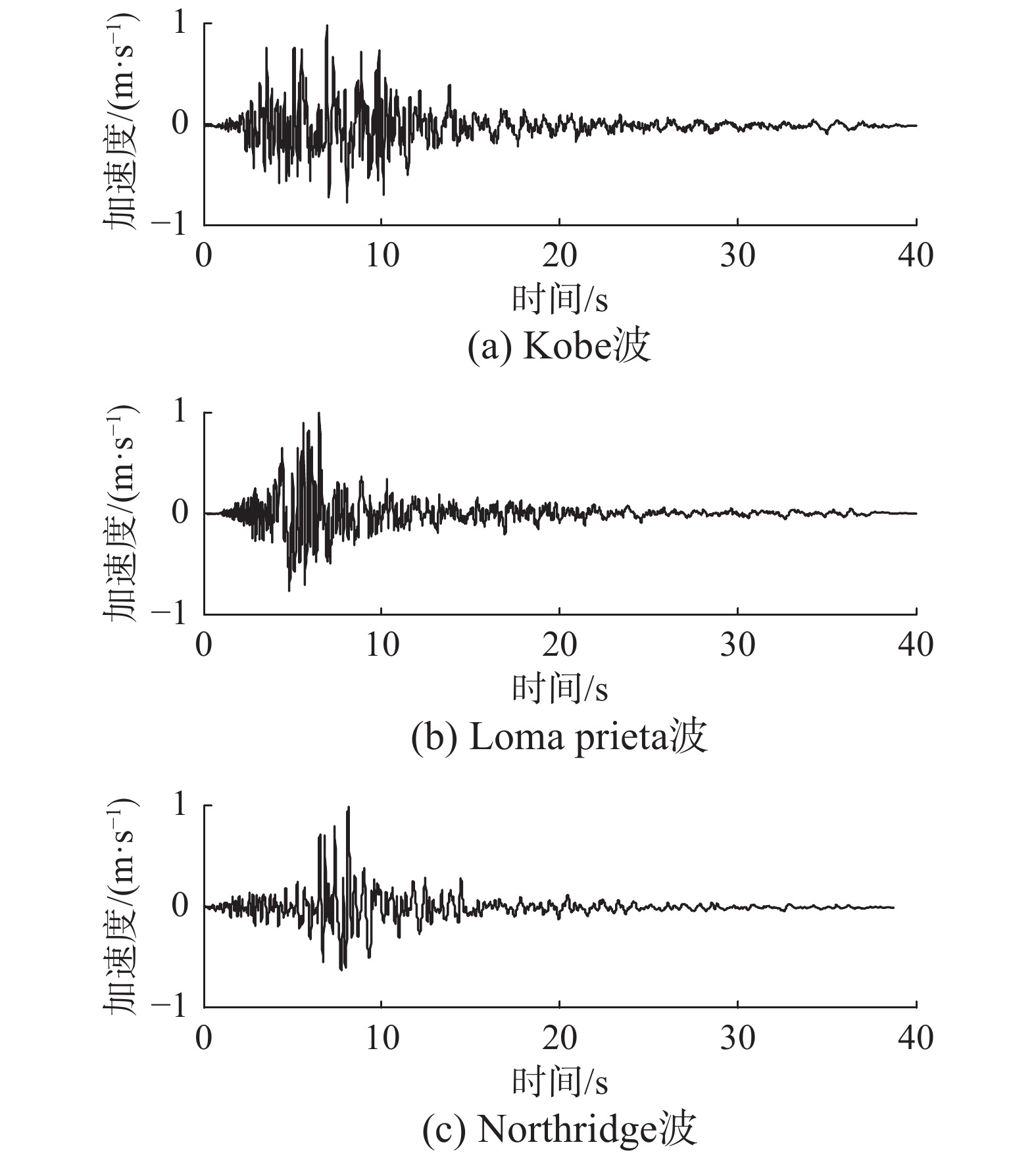
建立如图8(a)所示的单层双跨地下结构-土体相互作用模型。地下结构采用梁单元建模，其截面尺寸如图8(b)所示，结构跨度LS为10 m，高度HS为5 m，埋深D为10 m。结构材料采用C30混凝土，密度为2500 kg/m3，弹性模量为30 GPa，泊松比为0.15。土体采用四节点平面应变单元建模，单元尺寸为0.5 m×0.5 m，近场有限域的长度L取为80 m，土层厚度H为50 m。土体分为7层，各层土体参数由表1给出。选用图9所示的Kobe波、Loma Prieta波和Northridge波作为输入地震动，并将入射波的峰值加速度调幅为0.1 g。
![]()
图 8 地下结构及土-结构相互作用系统计算模型Figure 8. Calculation model of underground structure and soil-structure system表 1 土层物理性质Table 1. Physical properties of soil layers分层 土层 深度/m 密度/(kg·m−3) 剪切波速/(m·s−1) 泊松比 1 填土 0~1 1900 140 0.33 2 砂土 1~5 1900 140 0.32 3 砂土 5~8.5 1900 170 0.32 4 黏土 8.5~11.5 1900 190 0.40 5 黏土 11.5~17 1900 240 0.30 6 黏土 17~39 2000 330 0.26 7 基岩 >39 2100 500 0.30 3.1 不同输入地震动
采用传统的整体式反应位移法、改进方法一和改进方法二计算三条地震动作用下的等效地震荷载和结构地震反应。对比采用不同方法计算得到的地下结构侧墙与顶底面的平均等效地震荷载、典型截面A、B、C、D处的弯矩和以中柱顶底部位移差表示的结构变形。以传统整体式反应位移法的结果为基准，计算不同方法的相对误差，结果分别如表2和表3所示。
表 2 不同地震波作用下地下结构的等效地震荷载Table 2. Equivalent seismic loads of underground structure under different seismic waves地震波 计算方法 侧面平均压力/kPa 侧面平均剪力/kPa 顶面平均剪力/kPa 底面平均剪力/kPa Kobe波 传统方法 −58.03 39.01 −176.76 151.52 改进方法1 −57.97(−0.10%) 39.01(0.00%) −176.77(0.01%) 151.56(0.03%) 改进方法2 −58.60(0.98%) 39.01(0.00%) −177.77(0.57%) 151.26(−0.17%) Loma Prieta波 传统方法 58.47 −37.87 161.57 −153.75 改进方法1 57.69(−1.33%) −37.89(0.05%) 161.41(−0.10%) −153.99(0.16%) 改进方法2 58.93(0.79%) −37.89(0.05%) 163.32(1.08%) −153.52(−0.15%) Northridge波 传统方法 −71.63 48.05 −216.06 189.12 改进方法1 −71.69(0.08%) 48.04(−0.02%) −216.12(0.03%) 189.12(0.00%) 改进方法2 −72.64(1.41%) 48.04(−0.02%) −217.41(0.62%) 188.45(−0.35%) 表 3 不同地震波作用下地下结构的地震反应计算结果Table 3. Seismic responses of underground structure under different seismic waves地震波 计算方法 A截面弯矩/(kN·m) B截面弯矩/(kN·m) C截面弯矩/(kN·m) D截面弯矩/(kN·m) 结构变形/mm Kobe波 传统方法 353.26 366.34 219.19 219.59 −3.04 改进方法1 353.30(0.01%) 366.34(0.00%) 219.21(0.01%) 219.60(0.00%) −3.05(0.33%) 改进方法2 354.56(0.37%) 367.60(0.34%) 220.00(0.37%) 220.42(0.38%) −3.06(0.66%) Loma Prieta波 传统方法 −336.16 −356.39 −212.15 −209.42 2.92 改进方法1 −336.18(0.01%) −355.77(−0.17%) −211.99(0.08%) −209.21(−0.10%) 2.92(0.00%) 改进方法2 −338.64(0.73%) −358.30(0.54%) −213.55(0.66%) −210.83(0.67%) 2.94(0.68%) Northridge波 传统方法 434.61 452.21 270.49 270.21 −3.75 改进方法1 434.69(0.02%) 452.32(0.02%) 270.56(0.03%) 270.28(0.03%) −3.75(0.00%) 改进方法2 436.21(0.37%) 453.83(0.36%) 271.50(0.37%) 271.26(0.39%) −3.77(0.53%) 计算结果显示，采用考虑内部土层子结构惯性力影响的改进方法一计算得到的地下结构不同位置处的等效地震荷载与传统整体式反应位移法的计算结果极为接近，最大相对误差不超过1.33%，利用该地震荷载计算得到的截面弯矩和结构变形的最大误差分别为0.17%和0.33%，以上结果证明了第2.1节理论推导的正确性。当忽略内部土层子结构的惯性力时，改进方法二仍提供了良好的计算精度，在本文三条地震动作用下，该方法计算得到的结构侧面平均压力的相对误差不超过1.41%，侧面及顶底面的平均剪力误差最大不超过1.08%。另外，由于忽略了作用方向通常与自由场变形方向相同的内部土层子结构惯性力，改进方法二计算得到的等效地震荷载整体而言略大于传统整体式反应位移法的计算结果。由表3结果可见，将该等效地震荷载应用于地下结构的抗震计算时，典型截面弯矩和结构变形的最大相对误差分别为0.73%和0.68%，计算结果在保证精度的前提下略为保守。将该方法应用于抗震设计时，可使地下结构更为安全，从而验证了改进方法二的合理性和良好的适用性。
3.2 不同结构埋深
由于地下结构的地震反应与结构的埋深、土体的动力特性及结构的力学性能密切相关，为验证不同情况下本文改进方法的计算精度，以Loma Prieta波输入情况为例，将结构顶部埋深D分别取为2 m、5 m、10 m和15 m，保持其它模型与材料参数不变，采用传统的整体式反应位移法、本文改进方法一和改进方法二进行计算。对比不同方法计算得到的地下结构典型截面处的弯矩和结构变形，并以传统整体式反应位移法的结果为基准，计算不同方法的相对误差，结果由表4给出。
表 4 不同埋深情况下地下结构的地震反应计算结果Table 4. Seismic responses of the underground structure under different burial depths埋深/m 计算方法 A截面弯矩/(kN·m) B截面弯矩/(kN·m) C截面弯矩/(kN·m) D截面弯矩/(kN·m) 结构变形/mm 2 传统方法 −56.53 −61.77 −40.12 −38.77 0.60 改进方法1 −56.63(0.18%) −61.74(−0.05%) −40.17(0.12%) −38.81(0.10%) 0.60(0.00%) 改进方法2 −58.44(3.38%) −63.52(2.83%) −41.38(3.14%) −40.02(3.22%) 0.62(3.33%) 5 传统方法 329.16 356.20 222.16 219.55 −3.25 改进方法1 329.11(−0.02%) 356.40(0.06%) 222.17(0.00%) 219.59(0.02%) −3.25(0.00%) 改进方法2 332.57(1.04%) 359.91(1.04%) 224.45(1.03%) 221.92(1.08%) −3.28(0.92%) 10 传统方法 −336.16 −356.39 −212.15 −209.42 2.92 改进方法1 −336.18(0.01%) −355.77(−0.17%) −211.99(0.08%) −209.21(−0.10%) 2.92(0.00%) 改进方法2 −338.64(0.73%) −358.30(0.54%) −213.55(0.66%) −210.83(0.67%) 2.94(0.68%) 15 传统方法 321.36 324.13 183.35 184.45 −2.43 改进方法1 321.21(−0.05%) 324.00(−0.04%) 183.26(−0.05%) 184.35(−0.05%) −2.43(0.00%) 改进方法2 322.31(0.30%) 325.00(0.27%) 183.88(0.29%) 184.99(0.29%) −2.44(0.41%) 整体而言，随着结构埋深的增加，不同方法的计算误差均逐渐减小。其中，采用考虑内部土层子结构惯性力影响的改进方法一计算得到的地下结构地震反应与传统整体式反应位移法的计算结果最为接近，在不同埋深情况下截面弯矩的最大相对误差均不超过0.18%，结构变形的相对误差均为0。忽略内部土层子结构的惯性力影响时，本文改进方法二保持了良好的计算精度，当埋深为2 m时，结构地震反应的相对误差最大不超过3.4%，当埋深大于等于5 m时，相对误差最大不超过1.1%。
3.3 不同土层刚度
保持结构埋深为10 m，在表1给出的土层参数的基础上，分别将土体波速整体放缩为原始模型的0.5倍、1倍、1.5倍和2倍，即将土层刚度放缩为原始模型的0.25倍、1倍、2.25倍和4倍，采用Loma Prieta波作为输入地震动，对比不同方法计算得到的地下结构典型截面弯矩和结构变形，结果如表5所示。
表 5 不同土层波速情况下地下结构的地震反应计算结果Table 5. Seismic responses of the underground structure under different soil wave velocities波速缩放倍数 计算方法 A截面弯矩/(kN·m) B截面弯矩/(kN·m) C截面弯矩/(kN·m) D截面弯矩/(kN·m) 结构变形/mm 0.5 传统方法 −302.71 −320.23 −217.64 210.21 3.89 本文方法1 −302.65(−0.02%) −320.23(0.00%) −217.61(−0.01%) 210.90(−0.01%) 3.89(0.00%) 本文方法2 −304.88(0.72%) −322.45(0.69%) −219.15(0.69%) 211.77(0.74%) 3.92(0.71%) 1.0 传统方法 −336.16 −356.39 −212.15 −209.42 2.92 本文方法1 −336.18(0.01%) −355.77(−0.17%) −211.99(0.08%) −209.21(−0.10%) 2.92(0.00%) 本文方法2 −338.64(0.73%) −358.30(0.54%) −213.55(0.66%) −210.83(0.67%) 2.94(0.68%) 1.5 传统方法 −111.79 −121.81 −62.79 −60.97 0.83 本文方法1 −111.72(−0.06%) −121.68(−0.11%) −62.73(−0.01%) −60.90(−0.11%) 0.83(0.00%) 本文方法2 −112.44(0.58%) −122.41(0.49%) −63.12(0.53%) −61.32(0.57%) 0.84(1.20%) 2.0 传统方法 −79.38 −87.60 −39.88 −38.07 0.53 本文方法1 −79.36(−0.03%) −87.19(−0.47%) −39.77(−0.28%) −37.93(−0.37%) 0.53(0.00%) 本文方法2 −79.85(0.59%) −87.69(0.10%) −40.01(0.33%) −38.19(0.32%) 0.53(0.00%) 由计算结果可见，对于不同的土体刚度，本文两种改进方法仍能保持较高的计算精度。其中，考虑内部土体子结构的惯性力时，改进方法一计算得到的截面弯矩的最大相对误差不超过0.47%，结构变形的相对误差均为0；忽略内部土体子结构惯性力时，改进方法二在不同土体刚度条件下计算得到的截面弯矩和结构变形的相对误差最大分别不超过0.74%和1.20%。此外，对于不同的计算方法，随着土体刚度的增大，结构变形和内力均呈减小趋势，相对于传统整体式反应位移法的计算误差也逐渐减小。
3.4 不同结构刚度
保持其他模型与材料参数不变，分别将结构刚度放缩为原始模型的0.5倍、1倍、1.5倍和2倍，采用Loma Prieta波作为输入地震动，对比不同方法计算得到的地下结构典型截面弯矩和结构变形，结果如表6所示。
表 6 不同结构刚度情况下地下结构的地震反应计算结果Table 6. Seismic responses of the underground structure under different structure stiffness结构刚度缩放倍数 计算方法 A截面弯矩/(kN·m) B截面弯矩/(kN·m) C截面弯矩/(kN·m) D截面弯矩/(kN·m) 结构变形/mm 0.5 传统方法 −248.41 −266.12 −140.38 −138.74 3.76 本文方法1 −248.48(0.03%) −265.61(−0.19%) −140.27(−0.08%) −138.59(−0.11%) 3.76(0.00%) 本文方法2 −250.28(0.75%) −267.48(0.51%) −141.31(0.66%) −139.68(0.68%) 3.79(0.80%) 1.0 传统方法 −336.16 −356.39 −212.15 −209.42 2.92 本文方法1 −336.18(0.01%) −355.77(−0.17%) −211.99(0.08%) −209.21(−0.10%) 2.92(0.00%) 本文方法2 −338.64(0.73%) −358.30(0.54%) −213.55(0.66%) −210.83(0.67%) 2.94(0.68%) 1.5 传统方法 −387.20 −407.73 −256.07 −252.09 2.46 本文方法1 −387.18(−0.01%) −407.05(−0.17%) −255.87(−0.08%) −251.84(−0.10%) 2.45(−0.41%) 本文方法2 −390.03(0.73%) −409.97(0.55%) −257.76(0.66%) −253.78(0.67%) 2.47(0.41%) 2.0 传统方法 −420.87 −441.24 −285.65 −280.64 2.15 本文方法1 −420.83(−0.01%) −440.53(−0.16%) −285.42(−0.08%) −280.37(−0.10%) 2.15(0.00%) 本文方法2 −423.93(0.73%) −443.69(0.56%) −287.53(0.66%) −282.52 (0.67%) 2.16(0.47%) 由表6结果可见，在不同结构刚度的条件下，本文改进方法一和改进方法二在计算结构内力及变形时均具有良好的计算精度，与传统整体式反应位移法相比，最大计算误差分别不超过0.41%和0.80%。其中，改进方法二的计算结果在不同情况下均略大于整体式反应位移法，将其应用于地下结构的抗震设计时，可使结构偏于安全。此外，随着结构刚度的增大，各典型截面处的内力均逐渐增大，结构变形逐渐减小，不同方法的计算误差则基本不随结构刚度发生变化。
4 结论
本文基于整体式反应位移法的基本原理和有限元理论，提出了两种整体式反应位移法的改进方法。通过理论推导和算例分析，得到以下结论：
(1)基于有限元离散模型，从理论上证明了整体式反应位移法中由结构周边应力引起的等效地震荷载可通过仅由一层土体单元构成的内部子结构模型的一次静力分析获得，由此提出了一种基于土体内部子结构的地下结构整体式反应位移法，即改进方法一。
(2)进一步论证了改进方法一中内部土体子结构的惯性力对等效地震荷载的影响可以忽略，在此基础上提出地下结构整体式反应位移法的改进方法二。改进方法二在保证计算精度的前提下，避免了土层介质自由场惯性力的计算与施加，从而有效简化了整体式反应位移法的实施流程。
(3)通过与传统整体式反应位移法的数值对比分析，验证了本文两种改进方法计算得到的等效地震荷载和结构地震反应具有良好的计算精度。
(4)由于改进方法二的计算结果在保证精度的前提下偏于安全，且实施流程更为简单便捷，更适用于地铁车站、地下隧道等地下结构的地震反应分析与抗震性能研究。
-
![]()
图 3 整体式反应位移法中的等效地震荷载
Figure 3. Equivalent seismic loads in the integral response deformation method
![]()
图 4 结构所在位置处的自由场岩土介质模型
Figure 4. Free field model of soil medium corresponding to the structure location
![]()
图 6 地下结构整体式反应位移法的改进方法一
Figure 6. The first improved method of the integral response deformation method for underground structure
![]()
图 7 地下结构整体式反应位移法的改进方法二
Figure 7. The second improved method of the integral response deformation method for underground structure
![]()
图 8 地下结构及土-结构相互作用系统计算模型
Figure 8. Calculation model of underground structure and soil-structure system
表 1 土层物理性质
Table 1 Physical properties of soil layers
分层 土层 深度/m 密度/(kg·m−3) 剪切波速/(m·s−1) 泊松比 1 填土 0~1 1900 140 0.33 2 砂土 1~5 1900 140 0.32 3 砂土 5~8.5 1900 170 0.32 4 黏土 8.5~11.5 1900 190 0.40 5 黏土 11.5~17 1900 240 0.30 6 黏土 17~39 2000 330 0.26 7 基岩 >39 2100 500 0.30 
下载: 导出CSV
表 2 不同地震波作用下地下结构的等效地震荷载
Table 2 Equivalent seismic loads of underground structure under different seismic waves
地震波 计算方法 侧面平均压力/kPa 侧面平均剪力/kPa 顶面平均剪力/kPa 底面平均剪力/kPa Kobe波 传统方法 −58.03 39.01 −176.76 151.52 改进方法1 −57.97(−0.10%) 39.01(0.00%) −176.77(0.01%) 151.56(0.03%) 改进方法2 −58.60(0.98%) 39.01(0.00%) −177.77(0.57%) 151.26(−0.17%) Loma Prieta波 传统方法 58.47 −37.87 161.57 −153.75 改进方法1 57.69(−1.33%) −37.89(0.05%) 161.41(−0.10%) −153.99(0.16%) 改进方法2 58.93(0.79%) −37.89(0.05%) 163.32(1.08%) −153.52(−0.15%) Northridge波 传统方法 −71.63 48.05 −216.06 189.12 改进方法1 −71.69(0.08%) 48.04(−0.02%) −216.12(0.03%) 189.12(0.00%) 改进方法2 −72.64(1.41%) 48.04(−0.02%) −217.41(0.62%) 188.45(−0.35%)
下载: 导出CSV
表 3 不同地震波作用下地下结构的地震反应计算结果
Table 3 Seismic responses of underground structure under different seismic waves
地震波 计算方法 A截面弯矩/(kN·m) B截面弯矩/(kN·m) C截面弯矩/(kN·m) D截面弯矩/(kN·m) 结构变形/mm Kobe波 传统方法 353.26 366.34 219.19 219.59 −3.04 改进方法1 353.30(0.01%) 366.34(0.00%) 219.21(0.01%) 219.60(0.00%) −3.05(0.33%) 改进方法2 354.56(0.37%) 367.60(0.34%) 220.00(0.37%) 220.42(0.38%) −3.06(0.66%) Loma Prieta波 传统方法 −336.16 −356.39 −212.15 −209.42 2.92 改进方法1 −336.18(0.01%) −355.77(−0.17%) −211.99(0.08%) −209.21(−0.10%) 2.92(0.00%) 改进方法2 −338.64(0.73%) −358.30(0.54%) −213.55(0.66%) −210.83(0.67%) 2.94(0.68%) Northridge波 传统方法 434.61 452.21 270.49 270.21 −3.75 改进方法1 434.69(0.02%) 452.32(0.02%) 270.56(0.03%) 270.28(0.03%) −3.75(0.00%) 改进方法2 436.21(0.37%) 453.83(0.36%) 271.50(0.37%) 271.26(0.39%) −3.77(0.53%)
下载: 导出CSV
表 4 不同埋深情况下地下结构的地震反应计算结果
Table 4 Seismic responses of the underground structure under different burial depths
埋深/m 计算方法 A截面弯矩/(kN·m) B截面弯矩/(kN·m) C截面弯矩/(kN·m) D截面弯矩/(kN·m) 结构变形/mm 2 传统方法 −56.53 −61.77 −40.12 −38.77 0.60 改进方法1 −56.63(0.18%) −61.74(−0.05%) −40.17(0.12%) −38.81(0.10%) 0.60(0.00%) 改进方法2 −58.44(3.38%) −63.52(2.83%) −41.38(3.14%) −40.02(3.22%) 0.62(3.33%) 5 传统方法 329.16 356.20 222.16 219.55 −3.25 改进方法1 329.11(−0.02%) 356.40(0.06%) 222.17(0.00%) 219.59(0.02%) −3.25(0.00%) 改进方法2 332.57(1.04%) 359.91(1.04%) 224.45(1.03%) 221.92(1.08%) −3.28(0.92%) 10 传统方法 −336.16 −356.39 −212.15 −209.42 2.92 改进方法1 −336.18(0.01%) −355.77(−0.17%) −211.99(0.08%) −209.21(−0.10%) 2.92(0.00%) 改进方法2 −338.64(0.73%) −358.30(0.54%) −213.55(0.66%) −210.83(0.67%) 2.94(0.68%) 15 传统方法 321.36 324.13 183.35 184.45 −2.43 改进方法1 321.21(−0.05%) 324.00(−0.04%) 183.26(−0.05%) 184.35(−0.05%) −2.43(0.00%) 改进方法2 322.31(0.30%) 325.00(0.27%) 183.88(0.29%) 184.99(0.29%) −2.44(0.41%)
下载: 导出CSV
表 5 不同土层波速情况下地下结构的地震反应计算结果
Table 5 Seismic responses of the underground structure under different soil wave velocities
波速缩放倍数 计算方法 A截面弯矩/(kN·m) B截面弯矩/(kN·m) C截面弯矩/(kN·m) D截面弯矩/(kN·m) 结构变形/mm 0.5 传统方法 −302.71 −320.23 −217.64 210.21 3.89 本文方法1 −302.65(−0.02%) −320.23(0.00%) −217.61(−0.01%) 210.90(−0.01%) 3.89(0.00%) 本文方法2 −304.88(0.72%) −322.45(0.69%) −219.15(0.69%) 211.77(0.74%) 3.92(0.71%) 1.0 传统方法 −336.16 −356.39 −212.15 −209.42 2.92 本文方法1 −336.18(0.01%) −355.77(−0.17%) −211.99(0.08%) −209.21(−0.10%) 2.92(0.00%) 本文方法2 −338.64(0.73%) −358.30(0.54%) −213.55(0.66%) −210.83(0.67%) 2.94(0.68%) 1.5 传统方法 −111.79 −121.81 −62.79 −60.97 0.83 本文方法1 −111.72(−0.06%) −121.68(−0.11%) −62.73(−0.01%) −60.90(−0.11%) 0.83(0.00%) 本文方法2 −112.44(0.58%) −122.41(0.49%) −63.12(0.53%) −61.32(0.57%) 0.84(1.20%) 2.0 传统方法 −79.38 −87.60 −39.88 −38.07 0.53 本文方法1 −79.36(−0.03%) −87.19(−0.47%) −39.77(−0.28%) −37.93(−0.37%) 0.53(0.00%) 本文方法2 −79.85(0.59%) −87.69(0.10%) −40.01(0.33%) −38.19(0.32%) 0.53(0.00%)
下载: 导出CSV
表 6 不同结构刚度情况下地下结构的地震反应计算结果
Table 6 Seismic responses of the underground structure under different structure stiffness
结构刚度缩放倍数 计算方法 A截面弯矩/(kN·m) B截面弯矩/(kN·m) C截面弯矩/(kN·m) D截面弯矩/(kN·m) 结构变形/mm 0.5 传统方法 −248.41 −266.12 −140.38 −138.74 3.76 本文方法1 −248.48(0.03%) −265.61(−0.19%) −140.27(−0.08%) −138.59(−0.11%) 3.76(0.00%) 本文方法2 −250.28(0.75%) −267.48(0.51%) −141.31(0.66%) −139.68(0.68%) 3.79(0.80%) 1.0 传统方法 −336.16 −356.39 −212.15 −209.42 2.92 本文方法1 −336.18(0.01%) −355.77(−0.17%) −211.99(0.08%) −209.21(−0.10%) 2.92(0.00%) 本文方法2 −338.64(0.73%) −358.30(0.54%) −213.55(0.66%) −210.83(0.67%) 2.94(0.68%) 1.5 传统方法 −387.20 −407.73 −256.07 −252.09 2.46 本文方法1 −387.18(−0.01%) −407.05(−0.17%) −255.87(−0.08%) −251.84(−0.10%) 2.45(−0.41%) 本文方法2 −390.03(0.73%) −409.97(0.55%) −257.76(0.66%) −253.78(0.67%) 2.47(0.41%) 2.0 传统方法 −420.87 −441.24 −285.65 −280.64 2.15 本文方法1 −420.83(−0.01%) −440.53(−0.16%) −285.42(−0.08%) −280.37(−0.10%) 2.15(0.00%) 本文方法2 −423.93(0.73%) −443.69(0.56%) −287.53(0.66%) −282.52 (0.67%) 2.16(0.47%)
下载: 导出CSV
-
[1] IIDA H, HIROTO T, YOSHIDA N, et al. Damage to Daikai subway station [J]. Soils and Foundations, 1996, 36: 283 − 300. doi: 10.3208/sandf.36.Special_283
[2] 陈国兴, 陈苏, 杜修力, 等. 城市地下结构抗震研究进展[J]. 防灾减灾工程学报, 2016, 36(1): 1 − 23. CHEN Guoxing, CHEN Su, DU Xiuli, et al. Review of seismic damage, model test, available design and analysis methods of urban underground structures: retrospect and prospect [J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(1): 1 − 23. (in Chinese)
[3] DU X L, JIANG J W, NAGGAR M H E, et al. Interstory drift ratio associated with performance objectives for shallow-buried multistory and span subway stations in inhomogeneous soil profiles [J]. Earthquake Engineering and Structural Dynamics, 2021, 50: 655 − 672. doi: 10.1002/eqe.3351
[4] ZHUANG H Y, YANG J, CHEN S, et al. Statistical numerical method for determining seismic performance and fragility of shallow-buried underground structure [J]. Tunnelling and Underground Space Technology, 2021, 116: 104090. doi: 10.1016/j.tust.2021.104090
[5] 许民泽, 崔春义, 李静波, 等. 饱和砂土场地中地铁车站结构地震易损性分析[J]. 工程力学, 2021, 38(增刊 1): 251 − 258. doi: 10.6052/j.issn.1000-4750.2020.05.S044 XU Minze, CUI Chunyi, LI Jingbo, et al. Seismic vulnerability analysis of subway station embedded in saturated sand layers [J]. Engineering Mechanics, 2021, 38(Suppl 1): 251 − 258. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.S044
[6] LIAO Z P, WONG H L, YANG B P, et al. A transmitting boundary for transient wave analyses [J]. Science in China Series A, 1984, 27(10): 1063 − 1076.
[7] 刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6): 46 − 51. doi: 10.3969/j.issn.1000-4750.2005.06.008 LIU Jingbo, WANG Zhenyu, DU Xiuli, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems [J]. Engineering Mechanics, 2005, 22(6): 46 − 51. (in Chinese) doi: 10.3969/j.issn.1000-4750.2005.06.008
[8] 李述涛, 刘晶波, 宝鑫, 等. 采用粘弹性人工边界单元时显式算法稳定性分析[J]. 工程力学, 2020, 37(11): 10 − 20+55. doi: 10.6052/j.issn.1000-4750.2019.12.0755 LI Shutao, LIU Jingbo, BAO Xin, et al. Stability analysis of explicit algorithms with visco-elastic artificial boundary elements [J]. Engineering Mechanics, 2020, 37(11): 10 − 20+55. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.12.0755
[9] WU L H, ZHAO M, JENG D S, et al. A local time-domain absorbing boundary condition for scalar wave propagation in a multilayered medium [J]. Computers and Geotechnics, 2020, 128: 103809. doi: 10.1016/j.compgeo.2020.103809
[10] 赵密, 杜修力, 刘晶波. 一种高阶精度人工边界条件: 出平面外域波动问题[J]. 工程力学, 2012, 29(4): 7 − 14. ZHAO Mi, DU Xiuli, LIU Jingbo. A high-order accurate artificial boundary condition: out-of-plane exterior wave problem [J]. Engineering Mechanics, 2012, 29(4): 7 − 14. (in Chinese)
[11] 赵密, 孙文达, 高志懂, 等. 阶梯地形成层场地的斜入射地震动输入方法[J]. 工程力学, 2019, 36(12): 62 − 68. doi: 10.6052/j.issn.1000-4750.2018.10.0574 ZHAO Mi, SUN Wenda, GAO Zhidong, et al. Input method of obliquely incident earthquake for step-shaped layered site [J]. Engineering Mechanics, 2019, 36(12): 62 − 68. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.10.0574
[12] 赵密, 高志懂, 杜修力, 等. 地震作用下深厚土层-结构相互作用的高效分析方法[J]. 工程力学, 2019, 36(10): 58 − 65. doi: 10.6052/j.issn.1000-4750.2018.04.0245 ZHAO Mi, GAO Zhidong, DU Xiuli, et al. Efficient analysis scheme for seismic soil-structure interaction with deep soil layer [J]. Engineering Mechanics, 2019, 36(10): 58 − 65. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.04.0245
[13] 刘晶波, 宝鑫, 谭辉, 等. 土-结构动力相互作用分析中基于内部子结构的地震波动输入方法[J]. 土木工程学报, 2020, 53(8): 87 − 96. LIU Jingbo, BAO Xin, TAN Hui, et al. Seismic wave input method for soil-structure dynamic interaction analysis based on internal substructure [J]. China Civil Engineering Journal, 2020, 53(8): 87 − 96. (in Chinese)
[14] BAO X, LIU J B, LI S, et al. Seismic response analysis of the reef-seawater system under obliquely incident P and SV waves [J]. Ocean Engineering, 2020, 200: 107021. doi: 10.1016/j.oceaneng.2020.107021
[15] 川岛一彦. 地下构筑物の耐震设计[M]. 日本: 鹿岛出版会, l994. KAZUHIKO K. Seismic design of underground structures [M]. Japan: Kashima Publishing Company, 1994. (in Japanese)
[16] 禹海涛, 袁勇, 张中杰, 等. 反应位移法在复杂地下结构抗震中的应用[J]. 地下空间与工程学报, 2011, 7(5): 857 − 862. YU Haitao, YUAN Yong, ZHANG Zhongjie, et al. Application of response displacement method on seismic design of a complex underground structure [J]. Chinese Journal of Underground Space and Engineering, 2011, 7(5): 857 − 862. (in Chinese)
[17] 片山幾夫, 足立正信, 嶋田穰, 等. 地下埋設構造物の実用的な準動的解析手法「応答震度法」の提案[C]. 土木学会年次学術講演会講演概要集, 1985(40): 737 − 738. IKUO K, MASANOBU A, MINORU S, et al. Proposal of response seismic intensity method, a Practical semi-dynamic analysis method for underground structures [C]. Summary of JSCE Annual Academic Lecture, 1985(40): 737 − 738. (in Japanese)
[18] 刘晶波, 刘祥庆, 李彬. 地下结构抗震分析与设计的 Pushover 分析方法[J]. 土木工程学报, 2008, 41: 73 − 80. doi: 10.3321/j.issn:1000-131X.2008.04.011 LIU Jingbo, LIU Xiangqing, LI Bin. A pushover analysis method of seismic analysis and design of underground structures [J]. China Civil Engineering Journal, 2008, 41: 73 − 80. (in Chinese) doi: 10.3321/j.issn:1000-131X.2008.04.011
[19] LIU J B, ZHANG X B. Practical seismic analysis of large underground structures: Theory and application [J]. Science China, 2018, 61(9): 1417 − 1425. doi: 10.1007/s11431-018-9243-5
[20] 耿萍, 丰月华, 何川, 等. 盾构隧道横断面地震响应的广义反应位移法分析[J]. 铁道建筑, 2009, 6: 55 − 58. doi: 10.3969/j.issn.1003-1995.2009.08.017 GENG Ping, FENG Yuehua, HE Chuan, et al. Analysis of seismic response of shield tunnel cross-section using generalized response displacement method [J]. Railway Engineering, 2009, 6: 55 − 58. (in Chinese) doi: 10.3969/j.issn.1003-1995.2009.08.017
[21] 李亮, 杨晓慧, 杜修力. 地下结构地震反应计算的改进的反应位移法[J]. 岩土工程学报, 2014, 36(7): 1360 − 1364. doi: 10.11779/CJGE201407021 LI Liang, YANG Xiaohui, DU Xiuli. Improved response displacement method for evaluating seismic response of underground structures [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(7): 1360 − 1364. (in Chinese) doi: 10.11779/CJGE201407021
[22] 宾佳. 地下结构地震作用的简化分析方法研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2016. BIN Jia. Study on the simplified analysis methods of seismic effects of underground structures [D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2016. (in Chinese)
[23] 刘晶波, 王东洋, 谭辉, 等. 隧道纵向地震反应分析的整体式反应位移法[J]. 工程力学, 2018, 35(10): 20 − 29. doi: 10.6052/j.issn.1000-4750.2017.07.0526 LIU Jingbo, WANG Dongyang, TAN Hui, et al. Integral response displacement method for longitudinal seismic response analysis of tunnel structure [J]. Engineering Mechanics, 2018, 35(10): 20 − 29. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.07.0526
[24] 禹海涛, 张正伟, 李攀. 地下结构抗震设计的改进等效反应加速度法[J]. 岩土力学, 2020, 41(7): 2401 − 2410. YU Haitao, ZHANG Zhengwei, LI Pan. Improved equivalent response acceleration method for seismic design of underground structures [J]. Rock and Soil Mechanics, 2020, 41(7): 2401 − 2410. (in Chinese)
[25] 许紫刚, 杜修力, 许成顺, 等. 复杂断面地下结构地震反应分析的广义反应位移法研究[J]. 岩土力学, 2019, 40(8): 3247 − 3254. XU Zigang, DU Xiuli, XU Chengshun, et al. Research on generalized response displacement method for seismic analysis of underground structures with complex sections [J]. Rock and Soil Mechanics, 2019, 40(8): 3247 − 3254. (in Chinese)
[26] XU Z G, DU X L, XU C S, et al. Simplified equivalent static methods for seismic analysis of shallow buried rectangular underground structures [J]. Soil Dynamics and Earthquake Engineering, 2019, 121: 1 − 11. doi: 10.1016/j.soildyn.2019.02.022
[27] JIANG J W, XU C S, NAGGAR H M E, et al. Improved pushover method for seismic analysis of shallow buried underground rectangular frame structure [J]. Soil Dynamics and Earthquake Engineering, 2021, 140: 106363. doi: 10.1016/j.soildyn.2020.106363
[28] ZOU Y, ZHANG Y Q, LIU H Q, et al. Performance-based seismic assessment of shield tunnels by incorporating a nonlinear pseudostatic analysis approach for the soil-tunnel interaction [J]. Tunnelling and Underground Space Technology, 2021, 114: 103981. doi: 10.1016/j.tust.2021.103981
[29] 韩润波, 许成顺, 许紫刚, 等. 对称地下结构抗震分析的边界强制反应位移法[J]. 工程力学, 2021, 38(5): 50 − 60. doi: 10.6052/j.issn.1000-4750.2020.02.0075 HAN Runbo, XU Chengshun, XU Zigang, et al. A boundary forced response displacement method for seismic analysis of symmetrical underground structures [J]. Engineering Mechanics, 2021, 38(5): 50 − 60. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.02.0075
[30] 许紫刚, 杜修力, 徐长节, 等. 深埋地下结构地震反应分析的局部反应加速度法[J]. 工程力学, 2021, 38(6): 62 − 71. doi: 10.6052/j.issn.1000-4750.2020.06.0406 XU Zigang, DU Xiuli, XU Changjie, et al. Local response acceleration method for seismic analysis of deep buried underground structures [J]. Engineering Mechanics, 2021, 38(6): 62 − 71. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0406
[31] 刘晶波, 王文晖, 赵冬冬, 等. 地下结构抗震分析的整体式反应位移法[J]. 岩石力学与工程学报, 2013, 32(8): 1618 − 1624. LIU Jingbo, WANG Wenhui, ZHAO Dongdong, et al. Integral response deformation method for seismic analysis of underground structures [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(8): 1618 − 1624. (in Chinese)
[32] 刘晶波, 王文晖, 赵冬冬, 等. 复杂断面地下结构地震反应分析的整体式反应位移法[J]. 土木工程学报, 2014, 47(1): 134 − 142. LIU Jingbo, WANG Wenhui, ZHAO Dongdong, et al. Integral response deformation method in seismic analysis of complex section underground structures [J]. China Civil Engineering Journal, 2014, 47(1): 134 − 142. (in Chinese)
[33] 刘晶波, 谭辉, 张小波, 等. 不同规范中地下结构地震反应分析的反应位移法对比研究[J]. 土木工程学报, 2017, 50(2): 1 − 8. LIU Jingbo, TAN Hui, ZHANG Xiaobo, et al. Comparative study of response deformation methods for seismic analysis of underground structures in different design codes [J]. China Civil Engineering Journal, 2017, 50(2): 1 − 8. (in Chinese)
[34] 江志伟, 刘晶波, 许成顺. 振动台试验中地下结构地震响应预测方法[J]. 岩土工程学报, 2021, 43(7): 1220 − 1227. JIANG Zhiwei, LIU Jingbo, XU Chengshun. Prediction method for seismic response of underground structures in shaking table tests [J]. Chinese Journal of Geotechnical Engineering, 2021, 43(7): 1220 − 1227. (in Chinese)
[35] 江志伟, 刘晶波. 埋深对地下结构振动台模型试验结果的影响[J]. 工程力学, 2021, 38(增刊): 209 − 215. doi: 10.6052/j.issn.1000-4750.2020.06.S038 JIANG Zhiwei, LIU Jingbo. Influence of buried depth on the seismic response of underground structures in 1-g shaking table tests [J]. Engineering Mechanics, 2021, 38(Suppl): 209 − 215. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.S038
[36] GB/T 51336−2018, 地下结构抗震设计标准[S]. 北京: 中国建筑工业出版社, 2018. GB/T 51336−2018, Standard for seismic design of underground structures [S]. Beijing: China Architecture Industry Press, 2018. (in Chinese)
[37] 刘晶波, 王东洋, 谭辉, 等. 整体式反应位移法的理论推导及一致性证明[J]. 土木工程学报, 2019, 52(8): 18 − 23. LIU Jingbo, WANG Dongyang, TAN Hui, et al. Theoretical derivation and consistency proof of the integral response deformation method [J]. China Civil Engineering Journal, 2019, 52(8): 18 − 23. (in Chinese)
-
期刊类型引用(3)
1. 李宏男，张鸿志，李庆伟，付兴. FAST馈源舱结构气动力特性及耦联系统风振响应研究. 工程力学. 2025(06): 33-45 . 
本站查看
2. 翟露阳，韩佳颖，沈永利. 脉动风作用下船舶风载荷数值仿真. 天津理工大学学报. 2024(03): 17-23 . 百度学术
3. 李波，胡涛，田玉基，刘悦，卢啸，张范，宋晓峰，白凡. 北京2022年冬奥会内场主火炬抗风性能研究. 工程力学. 2024(10): 43-48 . 本站查看
其他类型引用(4)
计量
- 文章访问数: 387
- HTML全文浏览量: 90
- PDF下载量: 101
- 被引次数: 7
