随机多孔碳纤维纸的非线性面外压缩本构模型

石姗姗; 吕航宇; 吕超雨; 苏智博; 孙直

doi:10.6052/j.issn.1000-4750.2021.08.0607

随机多孔碳纤维纸的非线性面外压缩本构模型

石姗姗^1,,
吕航宇^1,,
吕超雨^1,,
苏智博^1,,
孙直^2, ,

1.
大连交通大学机车车辆工程学院，辽宁，大连 116028
2.
大连理工大学工业装备结构分析国家重点实验室，辽宁，大连 116023

基金项目: 国家自然科学基金面上项目(11872138)；国家自然科学基金青年基金项目(11702048)；辽宁省教育厅科学研究经费项目(JDL2020021)；大连市青年科技之星项目支持计划项目(2019RQ045，2019RQ069)；辽宁省高等学校创新团队支持计划项目(LT2016010)；大连市科技创新基金计划项目(2019J11CY017)

详细信息

作者简介:
石姗姗(1986−)，女，甘肃临夏人，副教授，博士，主要从事复合材料结构力学研究(E-mail: shishanshandjtu@foxmail.com)

吕航宇(1995−)，男(蒙古)，辽宁阜新人，博士生，主要从事复合材料结构力学研究(E-mail: hangyuemail@163.com)

吕超雨(1998−)，男，内蒙古乌兰察布人，硕士生，主要从事复合材料夹芯结构性能研究(E-mail: lvchaoyu98@163.com)

苏智博(1997−)，男，辽宁本溪人，硕士生，主要从事复合材料夹芯结构性能研究(E-mail: zhibo979@163.com)

通讯作者:
孙　直(1988−)，男，辽宁沈阳人，副教授，博士，博导，主要从事复合材料结构力学研究(E-mail: zhisun@dlut.edu.cn)

中图分类号: O343.5
计量
- 文章访问数: 335
- HTML全文浏览量: 153
- PDF下载量: 67
出版历程
- 收稿日期: 2021-08-05
- 修回日期: 2021-11-12
- 网络出版日期: 2021-11-17
- 刊出日期: 2022-12-31

THE NONLINEAR OUT-PLANE COMPRESSIVE CONSTITUTIVE MODEL FOR POROUS CARBON FIBER PAPER

1.
School of locomotive and rolling stock Engineering, Dalian Jiaotong University, Dalian, Liaoning 116028, China
2.
State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian, Liaoning 116023, China

摘要

摘要: 多孔碳纤维纸由随机分布的碳纤维构成，常用于燃料电池、发热材料等先进结构，其主要服役状态为面外压缩。碳纤维纸的压缩应变对其力学、热学、电学性能均有显著影响，因此迫切需要揭示其面外压缩本构关系。该文针对碳纤维纸微结构随机多孔的特点，提出了2种非线性面外压缩本构模型，分别是考虑赫兹接触影响的对数型模型和考虑孔隙率和单胞尺寸的幂函数型模型。基于3种商品化碳纤维纸的应力-应变实验数据，将该文提出的两种模型与传统的线性模型进行分析对比，并讨论了有、无额外有机物对碳纤维纸力学性能的影响。结果表明：碳纤维纸中的额外有机物对其应力-应变关系有比较明显的影响，全面考虑接触变形、弯曲变形与孔隙率变化的对数型本构模型具有较好的鲁棒性，适用范围较广；幂函数型本构模型能够较准确地预测有机物含量较低的碳纤维纸的应力-应变关系；传统的线性本构模型对各种碳纤维纸的预测均有较大的误差，该文提出的两种非线性本构模型对碳纤维纸具有较好的适用性，可以反映碳纤维纸的非线性应力-应变关系。
- 碳纤维纸 /
- 非线性 /
- 本构模型 /
- 多孔 /
- 压缩
Abstract: Porous carbon fiber papers, which are composed of randomly distributed carbon fibers, are now widely used in advanced structures such as fuel cells and heating materials. One of the most common working conditions for carbon fiber papers is out-plane compression. The compression deformation of carbon fiber papers has a significant impact on its mechanical, thermal and electrical properties. Therefore, understanding and revealing the out-plane constitutive relation of carbon fiber papers is essential for meeting the demand. Consequently, two nonlinear constitutive models are proposed for the porous carbon fiber papers. They are the logarithmic model considering the Hertz contact of fiber, and the power function model considering the variation of microstructure porosity and cell size. Based on the stress-strain experimental data of three commercial carbon fiber papers, the two nonlinear constitutive models proposed in the present study are compared with the traditional linear model, the mechanical properties of carbon fiber papers with/without additional organic matter are discussed. The study results indicate that: the extra resin in carbon fiber papers has an appreciable impact on the stress-strain curves, and the logarithmic-type constitutive model considering contact deformation, bending deformation and variation of structural porosity has good robustness and wide applicability; and the power-type constitutive model can accurately predict the stress-strain curves of carbon fiber papers with relatively small weight percentage resin. The determination of mechanical properties by conventional linear models for the commercial carbon fiber papers provided have relatively big errors. The comparisons indicate that the two nonlinear constitutive models proposed have good applicability in predicting the nonlinear stress-strain relation of carbon fiber papers.
- carbon fiber papers /
- nonlinear /
- constitutive model /
- porous /
- compression

HTML全文

碳纤维纸在先进能源以及先进环境材料领域中有广泛应用前景，如功能材料、电化学材料和新能源材料等^[1-6]，其主要服役状态为面外压缩。大量的实验和分析研究^[7-12]表明，碳纤维纸的面外压缩变形对其力学、热学、电学性能以及流体性能具有显著影响^[7-15]。碳纤维纸不同于分布规则的碳纤维编织结构^[16-18]，具有随机散乱的结构特征，其微观结构由杂乱的短切碳纤维形成低密度多孔结构，空间几何分布类似于无纺布。这种散乱的多孔结构与现有模型有很大差别，其性能随微孔半径大小而改变^[19]，导致碳纤维纸的应力-应变关系不同于常见的均匀材料或连续材料，并呈现出明显的非线性特征。

目前，针对碳纤维纸的研究主要集中于化学处理和微纳观改性领域^[20-24]，相关的力学研究较少。对于碳纤维纸的力学性能与耦合性能，多采用实验测量，并根据实验结果进行初步的数值分析。高源等^[25]使用随机重构技术建立三维微孔隙结构模型，通过改变孔隙率、纤维直径和燃料电池的气体扩散层厚度等参数观测碳纤维纸的渗透率的变化趋势。GARCÍA-SALABERRI等^[26]充分考虑了碳纤维纸的非线性特点，通过大量的实验数据，拟合了碳纤维纸的非线性应力-应变关系。该模型高度依赖于实验数据的数量和有效性，不利于实际使用，尤其是碳纤维纸型号改变的时候，其应力-应变关系会随着孔隙率、有机质含量、单胞尺寸等参数剧烈变化。BAHRAMI等^[6]基于梁理论，预测压缩载荷作用下碳纤维纸变形的力学解析模型。BAHRAMI模型考虑了碳纤维纸的微观纤维分布与纤维弯曲变形，但该模型是线性的，只能在很小的范围内与实验数据吻合。ZHANG等^[27]建立了碳纤维纸的随机微观结构，研究发现接触对和孔隙率是决定压缩非线性的2个关键因素。实际上，碳纤维纸在压缩载荷下，内部孔隙会不断减小，导致结构孔隙率下降，实体率上升，微观结构逐渐密实，从而引发碳纤维纸的弹性模量随压缩应变的增加而快速增加。针对碳纤维纸的非线性应力-应变关系，只有建立一种可以反映其特征的非线性本构模型，才能准确预测碳纤维纸的性能，进而更准确地分析碳纤维纸的力-电性能、力-热性能、力-渗透性能等多场耦合性能。然而，目前尚缺少有效的非线性碳纤维纸本构模型。

为建立有效的非线性本构模型，本文针对碳纤维纸微结构的随机多孔特点，提出了两种本构模型，分别是全面考虑微结构孔隙率、单胞尺寸变化及微结构弯曲与接触变形的对数型模型，以及忽略赫兹接触变形的幂函数型简化模型。首先选取典型六面体微结构作为碳纤维纸的代表性单胞结构，将碳纤维纸的压缩变形分解为接触变形和弯曲变形两部分。分别使用赫兹接触理论和弯曲梁理论分析典型纤维的接触变形和弯曲变形，并考虑压缩变形过程中，结构的孔隙率变化，及其对纤维直径、单胞长度、微结构单元面积等相关几何参数的影响，得到碳纤维纸的非线性本构关系。基于三种商品化的碳纤维纸的应力-应变实验数据，分析对比本文提出的两种本构模型的适用范围。

1 非线性面外压缩模型

1.1 碳纤维纸的代表性六面体单胞

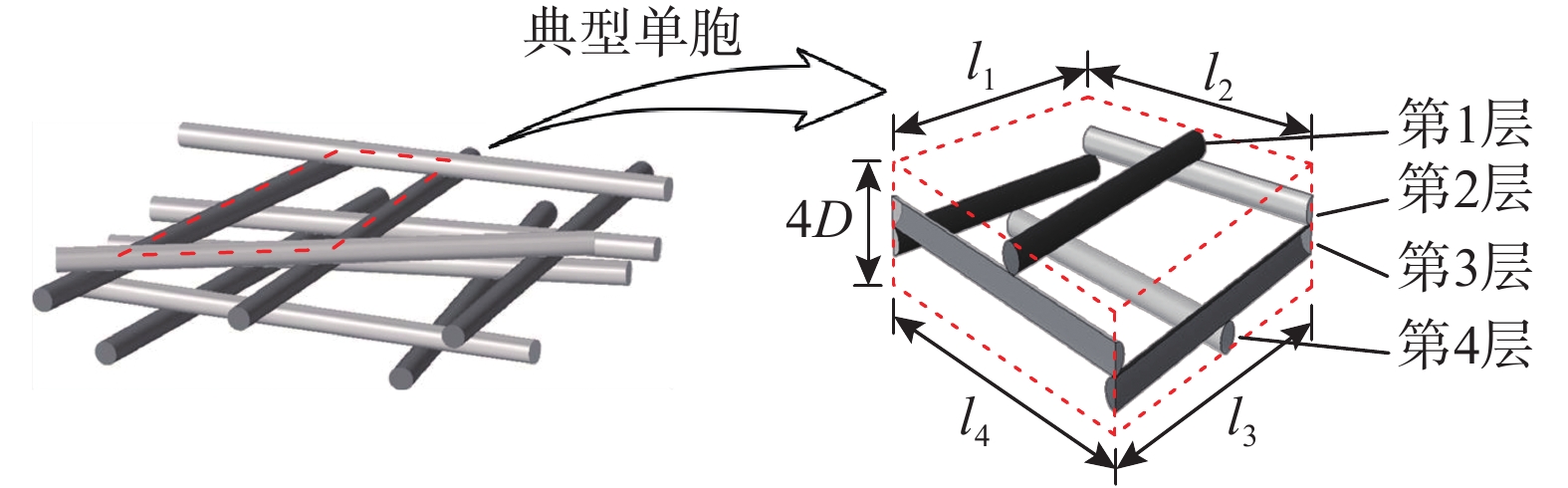
碳纤维纸的多孔结构由杂乱且低密度的短切碳纤维组成，如图1所示。观察俯视视角和横截面视角的扫描电镜图片，可以发现碳纤维在平面内的分布表现为随机长度和随机角度的四边形(图1(a))；在厚度方向的分布表现为较为规则的堆叠(图1(b))。根据碳纤维纸中碳纤维的实际分布规律，本文选用六面体作为碳纤维纸的代表性单胞，如图2中虚线所示。六面体单胞四周为4个矩形，高度是碳纤维直径的4倍；上、下表面为随机四边形，边长、单胞面积等参数的统计值详见表1。每个代表性六面体单胞包含2根横向纤维和2根纵向纤维(第1层含1根完整的横向碳纤维，第3层含有2个半根的横向碳纤维。同理，第2层、4层各含有1根纵向碳纤维)。

图 1 碳纤维纸扫描电镜图片

Figure 1. SEM images of commercial carbon fiber papers^[8]

下载: 全尺寸图片幻灯片

图 2 碳纤维纸的代表性六面体单胞示意图

Figure 2. Schematics of the proposed typical hexahedral unit cell model for the carbon fiber papers

下载: 全尺寸图片幻灯片

1.2 接触变形

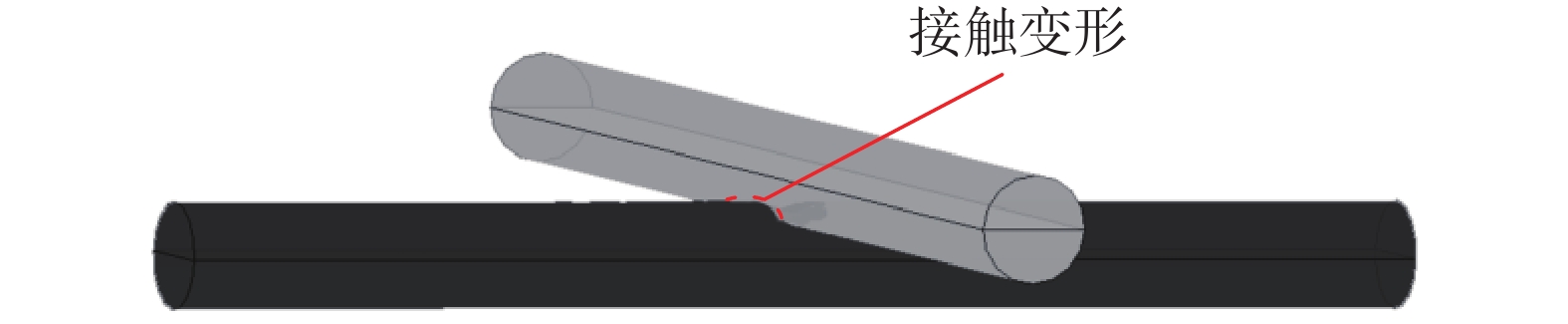
碳纤维纸最重要的力学行为是厚度方向上的压缩变形。当六面体单胞承受压缩应力时，水平方向纤维与相邻的垂直纤维发生紧密接触而产生非线性接触变形，如图3所示。它是碳纤维纸的主要变形方式之一，也是碳纤维纸发生非线性力学响应的重要原因。

表1给出了几种商用碳纤维纸的力学性能和几何参数。根据这些数据，可以发现碳纤维纸六面体单胞的平均长度(119 μm~136 μm)远大于平均纤维直径(6.95 μm)。因此，六面体单胞内纤维可以近似认为无限长圆柱体，碳纤维间的接触为无限长圆柱的正交(垂直)赫兹接触。

表 1 商用碳纤维纸的力学性能和几何参数

Table 1. Mechanical properties and geometric parameters of commercial carbon fiber papers

型号	厚度/ μm	面密度/ (g/m²)	孔隙率 μ/(%)	弹性模量 E/GPa	单胞平均长度l/μm	单胞投影面积A_pore/μm²	纤维平均直径D/μm	单胞边长 ${C}_{\rm l}$	变异系数 ${C}_{\rm D}$	树脂种类
SGL 24 AA ^[7,9,28]	190	51	88	225	130	9091	6.95	0.414	0.081	聚四氟乙烯
SGL 25 AA ^[7,9,28]	190	38	92	225	136	11284	6.95	0.433	0.081	聚四氟乙烯
SGL 10 BA ^[7,29]	400	85	88	225	119	8949	6.95	0.376	0.081	聚四氟乙烯

下载: 导出CSV

| 显示表格

图 3 碳纤维纸接触变形模式示意图

Figure 3. Schematics of contact deformation with use of Hertz's contact model

下载: 全尺寸图片幻灯片

根据正交赫兹接触^[30]圆柱的载荷-位移关系，得到：

$P = \frac{{\sqrt 2 }}{3}\frac{{E{D^{\tfrac{1}{2}}}}}{{1 - {\nu ^2}}}{u^{\tfrac{3}{2}}}$

(1)

式中：P和u分别为单胞所承受的压缩载荷和压缩位移；E、D和ν分别代表碳纤维的弹性模量、单根纤维的直径和碳纤维单丝的泊松比。由式(1)可以分别得到单胞平均压缩应力和赫兹接触变形引起的平均压缩应变：

$\begin{split} \;\\[-10pt] \sigma = \frac{P}{{{A_{\rm pore}}}} \end{split}$

(2)

${\varepsilon _{\rm c}} = u/4D$

(3)

式中： $\sigma$ 为碳纤维纸代表性单胞平均压缩应力； ${\varepsilon }_{\rm c}$ 为平均接触压缩应变； ${A}_{\rm pore}$ 为单胞在平面上的投影面积。因此，代表性单胞的压缩应力与接触压缩应变之间的关系可以表示为：

$\sigma = {E_{\rm c}}{( {{\varepsilon _{\rm c}}} )^{\tfrac{3}{2}}}$

(4)

其中， ${E_{\rm c}} = \dfrac{{8\sqrt 2 }}{3}\dfrac{{E{D^2}}}{{\left( {1 - {\nu ^2}} \right){A_{\rm pore}}}}$ 为碳纤维纸接触变形导致压缩应变的等效模量。以压缩应力作为自变量，可以得到压缩应力与接触压缩应变之间的微分关系如下所示：

${\text{d}}{\varepsilon _{\rm c}} = \frac{2}{3}E_{\rm c}^{ - \tfrac{2}{3}}{\sigma ^{-\tfrac{1}{3}}}{\text{d}}\sigma$

(5)

1.3 弯曲变形

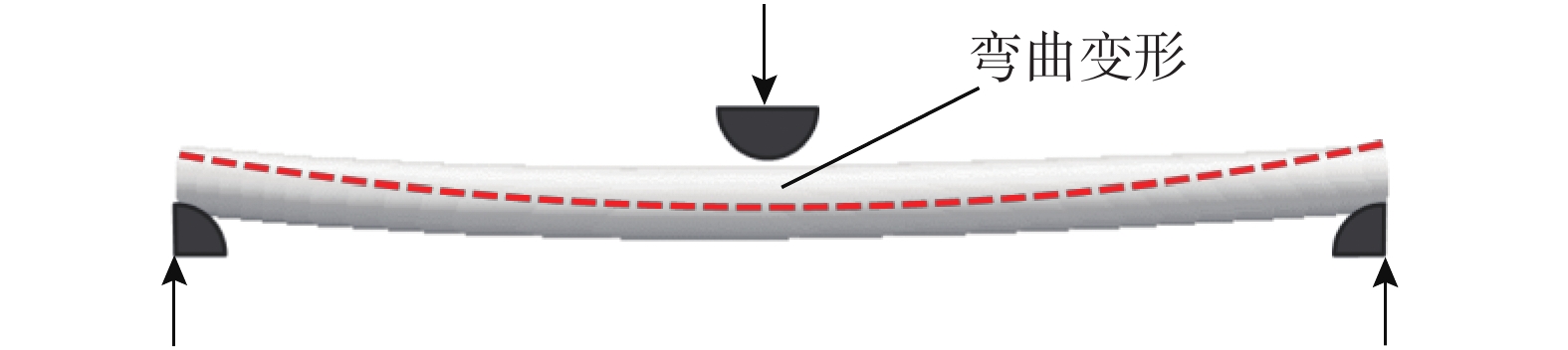
如图4所示，碳纤维纸代表性单胞在受到压缩载荷时，具有一定长度的纤维与纤维接触点会构成三点弯曲。因此，单胞内除了会产生接触变形外，还会产生弯曲变形。弯曲变形是碳纤维纸的另一种主要变形方式。

图 4 碳纤维纸弯曲变形模式示意图

Figure 4. Schematics of bending deformation with use of beam bending model

下载: 全尺寸图片幻灯片

对碳纤维纸结构的弯曲变形，BAHRAMI等^[6]利用欧拉-伯努利梁理论成功地建立了碳纤维纸六面体单胞的弹性本构模型。由于弯曲纤维所受弯矩和变形与纤维间的夹角无关，欧拉-伯努利梁理论同样适用于六面体单胞中的交叉纤维。因此，压缩载荷下六面体单胞的纤维弯曲变形引起的压缩应变^[6]可以表示为：

$\sigma = \frac{{105{\text{π }}E\mu {D^5}( {1 + 6C_l^2} )( {1 + 6C_{\rm D}^2} )}}{{16{l^3}{A_{\rm pore}}}}{\varepsilon _{\rm b}}$

(6)

式中： ${\varepsilon }_{\rm b}$ 为弯曲应变； $l$ 为单胞平均边长； $\mu$ 为材料孔隙率； ${C}_{\rm l}$ 和 ${C}_{\rm D}$ 分别为单胞边长和单根纤维直径的变异系数。设 ${E_{\rm b}} = \dfrac{{105{\text{π }}E\mu {D^5}( {1 + 6C_{\rm l}^2} )( {1 + 6C_{\rm D}^2} )}}{{16{l^3}{A_{\rm pore}}}}$ ，为碳纤维纸弯曲变形引起压缩应变的等效模量。式(6)的应力-应变关系可以简写为：

$\sigma = {E_{\rm b}}{\varepsilon _{\rm b}}$

(7)

以压缩应力作为自变量，可以得到压缩应力与弯曲应变之间的微分关系：

${\text{d}}{\varepsilon _{\rm b}} = E_{\rm b}^{ - 1}{\text{d}}\sigma$

(8)

1.4 考虑赫兹接触影响的对数型模型

碳纤维纸代表性单胞在受到压缩载荷时，主要发生2种变形，即接触变形和弯曲变形。其中，接触变形主要发生在纤维之间的接触点，如图3所示；弯曲变形主要体现为纤维轴线在厚度方向上发生挠度，如图4所示。在模型中，两种变形同时发生，单胞的压缩位移等于两种变形位移之和。根据式(5)和式(8)，可以得到 $\mathrm{d}\varepsilon$ 和 $\mathrm{d}\sigma$ 之间的微分关系如下：

${\text{d}}\varepsilon = {\text{d}}{\varepsilon _{\rm c}} + {\text{d}}{\varepsilon _{\rm b}} = \left( {\frac{2}{3}E_{\rm c}^{ - \tfrac{2}{3}}{\sigma ^{ - \tfrac{1}{3}}} + E_{\rm b}^{ - 1}} \right){\text{d}}\sigma$

(9)

对于六面体单胞，在投影平面上的孔洞面积比为 $\dfrac{{A}_{\rm pore}}{{l}^{2}}$ ，碳纤维面积占比 $1-\dfrac{{A}_{\rm pore}}{{l}^{2}}$ 。考虑到单胞四层结构中，每层的4条边仅有2条含有碳纤维，即单胞内理论碳纤维占比 ${\mu }_{u}$ 仅有其面积占比的1/2：

${\mu _{\rm u}} = \frac{1}{2}\left( {1 - \frac{{{A_{\rm pore}}}}{{{l^2}}}} \right)$

(10)

由式(10)计算得到的碳纤维占比均大于碳纤维纸的实测实体率，这说明碳纤维纸内含有大量空隙。考虑纤维分布的随机性，假设空隙均匀分布，可以得到单胞的充盈率 $\eta$ 。若 $\eta$ =1，则说明碳纤维纸被六面体单胞充满；若 $\eta$ ＜0，则碳纤维纸内含有 $\eta$ 的六面体单胞与1− $\eta$ 的空隙。单胞的充盈率 $\eta$ 可由碳纤维纸的实测孔隙率与单胞理论孔隙率之比得到：

$\eta = \frac{{1 - \mu }}{{1 - {\mu _{\rm u}}}}$

(11)

随着压缩位移与应变的增加，碳纤维纸会变得越来越密实(碳纤维的体积不变，碳纤维纸的体积减小)，即碳纤维纸的单胞充盈率会随着压缩应变增加而增加。忽略泊松效应对碳纤维纸单胞几何尺寸的影响，单胞名义充盈率 ${\eta }^{\mathrm{*}}$ 可表示为：

${\eta ^ * } = \frac{1}{{1 + \varepsilon }}\eta = \left( {\frac{1}{{1 + \varepsilon }}} \right) \cdot \left( {\frac{{1 - \mu }}{{1 - {\mu _u}}}} \right)$

(12)

式(12)显示，在压缩载荷下，随着名义应变( $\varepsilon$ ＜0)的减少，单胞名义充盈率η^*可能会大于1，这表示厚度方向上原本未接触的碳纤维发生了更多的接触，导致单胞尺寸变小、数量增加。本文近似地认为其对弹性模量的影响是线性的。

将式(12)代入式(9)，得：

${\text{d}}\varepsilon = \left( {\frac{2}{3}E_{\rm c}^{ - \tfrac{2}{3}}{\sigma ^{ - \tfrac{1}{3}}} + E_{\rm b}^{ - 1}} \right)\frac{{1 + \varepsilon }}{\eta }{\text{d}}\sigma$

(13)

通过对式(13)进行两边积分，可得到碳纤维纸的对数型本构关系：

$\eta \ln \left( {1 + \varepsilon } \right) = E_{\rm c}^{ - \tfrac{2}{3}}{\sigma ^{\tfrac{2}{3}}} + E_{\rm b}^{ - 1}\sigma$

(14)

1.5 同时考虑孔隙率和单胞尺寸的幂函数型模型

若进一步考虑压缩变形时，结构堆叠将对单胞尺寸产生影响。随着名义应变 $\varepsilon$ 的变化，例如，当名义应变达到−0.5时，单胞尺寸缩小为 $l$ · (1−0.5)，则单胞长度 $l$ 可写为：

$l = {l_0}\left( {1 + \varepsilon } \right)$

(15)

式中， ${l}_{0}$ 为压缩变形发生前单胞长度。

由于接触等效模量E_c和弯曲等效模量E_b与单胞尺寸的关系不一样，若同时考虑两种等效模量随单胞尺寸的变化，微分方程将无法分离变量，会给求解带来不便。而且随着压缩变形持续增加，接触变形的影响会变小，压缩变形导致的单胞尺寸变化对碳纤维纸应力-应变关系的作用变得明显。因此，本节只分析弯曲等效模量随单胞尺寸的变化，并建立相应的应力-应变关系。

对弯曲等效模量，根据BAHRAMI等^[6]模型，可得：

${E_{\rm b}} \propto \frac{{\text{1}}}{{{l^3}}}$

(16)

同时考虑孔隙率的变化，由式(12)、式(15)和式(16)，可以得到：

$E_{\rm b}^{^ * } = {E_{\rm b}}\frac{\eta }{{{{\left( {1 + \varepsilon } \right)}^4}}}$

(17)

即：

${\text{d}}\sigma = {E_{\rm b}}\frac{\eta }{{{{\left( {1 + \varepsilon } \right)}^4}}}{\text{d}}\varepsilon$

(18)

通过对式(18)进行两边积分，可得到碳纤维纸的幂函数型本构关系：

$\sigma = \frac{{{E_{\rm b}}\eta }}{3}\left( {1 - \frac{1}{{{{\left( {1 + \varepsilon } \right)}^3}}}} \right)$

(19)

2 结果与讨论

本节中，采用表1给出的SGL24AA、SGL25AA和SGL10BA三种商用碳纤维纸的力学性能和几何参数，将1.4节和1.5节中提出的全面考虑微结构孔隙率、单胞尺寸变化及微结构弯曲与接触变形的对数型模型和忽略赫兹接触变形的幂函数型简化模型，与这三种商用碳纤维纸实验所测应力-应变关系曲线进行对比分析。由于SGL10BA这类碳纤维纸中含有聚四氟乙烯或热塑性树脂等有机物，这将对其力学本构关系产生影响，因此本节将分别讨论有、无额外有机物的碳纤维纸。

2.1 无有机物碳纤维纸的本构模型验证

如图5所示，三角曲线分别代表了SGL 24AA和 SGL 25AA商业碳纤维纸应力-应变曲线的实验测试值；圆点曲线代表对数型本构模型；方形曲线代表幂函数型本构模型；直线代表线性本构模型^[6]。可以看出，针对SGL 24AA和 SGL 25AA这两类碳纤维纸，幂函数型本构模型与实验测量值呈现出高度吻合，幂函数型模型具有良好的非线性特征。对数型本构模型与实验数据具有相似的模量强化趋势，线性本构模型与实验结果相差最远。

图 5 对数型本构模型、幂函数型本构模型与线性本构模型和实验应力-应变曲线的对比图

Figure 5. Comparison of experimental stress-strain curves with the logarithmic-type model，the power-function-type model and the linear bending model

下载: 全尺寸图片幻灯片

考虑到碳纤维纸最优夹紧力为0.77 MPa^[31]，为了有一个更全的覆盖面，本文将讨论的压缩应力区间设定在0.4 MPa~1.2 MPa。如图6所示，对于SGL 24AA碳纤维纸，在其压缩应力为0.4 MPa~1.2 MPa时，线性本构模型分析得到的应变值与实验测得的应变平均值绝对误差值区间为41.8%~76.6%，对数型本构模型分析得到的应变值与实验测得的应变平均值绝对误差值区间为2.0%~41.8%，而幂函数型本构模型分析得到的应变值与实验测得的应变平均值绝对误差值区间为0.1%~35.0%。对于SGL 25AA 碳纤维纸，对数型本构模型分析得到的应变值与实验测得的应变平均值绝对误差值区间降为0.1%~37.5%；幂函数型本构模型与实验测得的应变平均值吻合度最高，最大绝对误差值为1.3%~33.1%；与SGL 24AA 碳纤维纸相比，线性本构模型分析得到的应变值与实验测得的应变平均值之间误差更大，绝对误差值区间为41.5%~79.8%。

图 6 对数型本构模型、幂函数型本构模型与线性本构模型和实验应力-应变曲线误差绝对值对比图

Figure 6. Comparison of absolute error values with experimental stress-strain curves between the logarithmic-type model，the power-function-type model and the linear bending model

下载: 全尺寸图片幻灯片

对比SGL24AA和SGL25AA碳纤维纸的应力-应变实验数据与线性、对数型本构及幂函数性本构预测结果，可以发现：首先，本文提出的两种本构模型的相对误差均远小于线性本构模型^[6]，其主要原因为线性本构未考虑压缩过程中纤维因接触点增加而发生的应变强化。其次，当碳纤维纸孔隙率增加时(SGL25AA的孔隙率大于SGL24AA)，本文提出的两种非线性本构模型的相对误差也会增加。这可能是因为孔隙率较大时，微观结构随机性更大，造成预测误差的增加。最后，对比本文提出的两种本构模型，可以发现在较高应变下，考虑接触变形的对数型本构模型和幂函数本构模型模拟结果相差较大，这主要是碳纤维纸孔隙率和弹性模量随应变改变造成的。在压缩应变较低时，弯曲变形明显大于接触变形，忽略接触变形的幂函数型简化模型具有形式更简单的优点，且在压缩应变较低时与对数型本构模型相差不大。随着压缩应变的增加，碳纤维纸的孔隙率减少、弹性模量成倍增加。此时，忽略接触变形与接触刚度的影响随着弹性模量的增加而增加，进而导致对数型本构模型和幂函数本构模型模拟结果相差较大。总体而言，幂函数型模型的参数较少，在准确性和便利性上更适合工程应用。

2.2 含有有机物的碳纤维纸本构模型验证

SGL10BA等碳纤维纸中含有较大比例的聚四氟乙烯或其他热塑性树脂，这将对其力学本构关系产生影响，本节将讨论本文提出的本构模型对这类碳纤维纸的适用性。考虑到聚四氟乙烯或热塑性树脂的影响，需要在现有的对数型本构模型和幂函数型本构模型中引入修正因子 $\gamma$ ，其中 $\gamma$ 代表碳纤维纸中碳纤维含量比值。由于有机物的弹性模量均小于碳纤维模量，因此可认为有机物对碳纤维纸模量贡献较小，碳纤维纸的弹性模量主要由其碳纤维在实体材料的比例 $\gamma$ 决定，式(14)和式(19)可以分别修正为：

$\eta \gamma \ln \left( {1 + \varepsilon } \right) = E_{\rm c}^{{ - \tfrac{2}{3}}}{\sigma ^{\tfrac{2}{3}}} + E_{\rm b}^{ - 1}\sigma$

(20)

$\sigma = \frac{{{E_{\rm b}}\gamma \eta }}{3}\left( {1 - \frac{1}{{{{\left( {1 + \varepsilon } \right)}^3}}}} \right) \;\;\;\;\;\;$

(21)

图7(a)为SGL10BA碳纤维纸的应力-应变曲线。其中黑色三角为实验测试值^[29]；圆点曲线代表对数型本构模型；方形曲线代表幂函数型本构模型；黑色直线代表线性本构模型^[6]。

图 7 SGL 10BA碳纤维纸

Figure 7. SGL 10BA carbon fiber paper

下载: 全尺寸图片幻灯片

对于SGL10BA型碳纤维纸，纸的一侧存在5%的聚四氟乙烯薄膜，因此碳纤维的实际含量需要相应减少5%，修正因子γ为0.95。观察图7(b)所示的应力-应变曲线可以发现，本文所提出的对数型本构模型与幂函数型本构模型依旧具有一定的准确性，两种模型的准确性均优于传统的线性本构模型。

基于以上结果对比，可以发现碳纤维纸中的额外树脂对其应力-应变关系有比较明显的影响。对比三种本构模型的预测结果，全面考虑接触变形、弯曲变形与孔隙率变化的对数型本构模型具有较好的鲁棒性，适用范围较广；简化后的幂函数型本构模型能够较准确的预测树脂含量较低的碳纤维纸的应力-应变关系；传统的线性本构模型^[6]对各种碳纤维纸的预测均有较大的误差。本文提出的两种本构模型的相对误差均远小于线性本构模型，其主要原因为线性本构未考虑压缩过程中纤维因接触点增加而发生的应变强化。对比本文提出的两种本构模型，可以发现对数型模型的误差最小，更适合含有机物碳纤维纸的理论与数值分析。

不过，在有额外有机物的条件下，三种本构模型与实验结果的相对误差均高于无有机物碳纤维纸，说明虽然有机物在碳纤维纸中含量较低，仍对其微观变形机制和压缩本构关系有较大影响。有必要根据碳纤维纸内的有机物分布，进行更深入的研究。

3 结论

本文针对碳纤维纸微结构随机多孔的特点，提出了两种非线性面外压缩本构模型，分别是全面考虑微结构孔隙率、单胞尺寸变化及微结构弯曲与接触变形的对数型模型，以及忽略赫兹接触变形的幂函数型简化模型。基于三种商品化碳纤维纸的应力-应变实验数据，将本文提出的两种本构模型与传统的线性本构模型进行分析对比，得到以下结论：

(1) 对于本文涉及的多种典型碳纤维纸，作者提出的幂函数型本构模型与对数型本构模型均能够描述材料的非线性应力-应变关系。两种本构模型与实验数据的相对误差均明显小于传统的线性本构模型，可以为相关结构的仿真分析提供有效的本构模型基础。

(2) 对于含树脂等有机物较少的碳纤维纸，幂函数型本构模型与实验数据的相对误差最小，在最优加紧应力附近的相对误差可低至0.1%。同时，由于幂函数型本构模型具有参数少的特点，仅通过一对应力-应变数据即可建立幂函数型本构，比较便于通过实验测试得到。

(3) 对于含树脂等有机物较多的碳纤维，由于这些随机分布有机物的模量较低，降低了碳纤维纸的等效模量。本文引入了体积分数修正因子 $\gamma$ ，以考虑有机物杂质对碳纤维纸本构模型的影响。与实验数据的对比显示，修正后的两种本构模型与实验数据的相对误差仍明显小于传统的线性本构模型，但其相对误差的离散性较大，仍有待于进一步修正。

图 1 碳纤维纸扫描电镜图片

Figure 1. SEM images of commercial carbon fiber papers^[8]

下载: 全尺寸图片幻灯片

图 2 碳纤维纸的代表性六面体单胞示意图

Figure 2. Schematics of the proposed typical hexahedral unit cell model for the carbon fiber papers

下载: 全尺寸图片幻灯片

图 3 碳纤维纸接触变形模式示意图

Figure 3. Schematics of contact deformation with use of Hertz's contact model

下载: 全尺寸图片幻灯片

图 4 碳纤维纸弯曲变形模式示意图

Figure 4. Schematics of bending deformation with use of beam bending model

下载: 全尺寸图片幻灯片

图 5 对数型本构模型、幂函数型本构模型与线性本构模型和实验应力-应变曲线的对比图

Figure 5. Comparison of experimental stress-strain curves with the logarithmic-type model，the power-function-type model and the linear bending model

下载: 全尺寸图片幻灯片

图 6 对数型本构模型、幂函数型本构模型与线性本构模型和实验应力-应变曲线误差绝对值对比图

Figure 6. Comparison of absolute error values with experimental stress-strain curves between the logarithmic-type model，the power-function-type model and the linear bending model

下载: 全尺寸图片幻灯片

图 7 SGL 10BA碳纤维纸

Figure 7. SGL 10BA carbon fiber paper

下载: 全尺寸图片幻灯片

表 1 商用碳纤维纸的力学性能和几何参数

Table 1 Mechanical properties and geometric parameters of commercial carbon fiber papers

型号	厚度/ μm	面密度/ (g/m²)	孔隙率 μ/(%)	弹性模量 E/GPa	单胞平均长度l/μm	单胞投影面积A_pore/μm²	纤维平均直径D/μm	单胞边长 ${C}_{\rm l}$	变异系数 ${C}_{\rm D}$	树脂种类
SGL 24 AA ^[7,9,28]	190	51	88	225	130	9091	6.95	0.414	0.081	聚四氟乙烯
SGL 25 AA ^[7,9,28]	190	38	92	225	136	11284	6.95	0.433	0.081	聚四氟乙烯
SGL 10 BA ^[7,29]	400	85	88	225	119	8949	6.95	0.376	0.081	聚四氟乙烯

下载: 导出CSV

参考文献(31)

[1]	CHOI B K, LEE H J, CHOI W K, et al. Effect of carbon fiber content on thermal and electrical conductivity, EMI shielding efficiency, and radiation energy of CMC/PVA composite papers with carbon fibers [J]. Synthetic Metals, 2021, 273: 116708. doi: 10.1016/j.synthmet.2021.116708
[2]	QI Y, CHEN X, LIU S, et al. Electrochemical sensor for Cd²⁺ detection based on carbon fiber paper sequentially modified with CoMOF, AuNPs, and Glutathione [J]. Journal of The Electrochemical Society, 2021, 168(6): 067526. doi: 10.1149/1945-7111/ac0c36
[3]	MATHEW A T, AKSHAYA K B, SIRIMAHACHAI U, et al. TEMPO mediated electrochemical oxidation of 4-pyridinemethanol using PD and PT Co-deposited polyaniline modified carbon fiber paper [J]. Synthetic Metals, 2021, 279: 116858. doi: 10.1016/j.synthmet.2021.116858
[4]	周远鹏, 汪称意, 陶正旺, 等. 一类低溶胀率磺化聚芳醚砜质子交换膜材料的制备及性能[J]. 高分子材料科学与工程, 2019, 35(12): 22 − 29. ZHOU Yuanpeng, WANG Chenyi, TAO Zhengwang, et al. Preparation and properties of sulfonated poly (aryl sulfone)s with low swelling ratio for proton exchange membrane [J]. Polymer Materials Science & Engineering, 2019, 35(12): 22 − 29. (in Chinese)
[5]	XU Z, PENG L, YI P, et al. An investigation on the formability of sheet metals in the micro/meso scale hydroforming process [J]. International Journal of Mechanical Sciences, 2018, 150: 265 − 276.
[6]	NOROUZIFARD V, BAHRAMI M. Deformation of PEM fuel cell gas diffusion layers under compressive loading: An analytical approach [J]. Journal of Power Sources, 2014, 264: 92 − 99.
[7]	SHI S, GUO X, CHEN B, et al. A logarithmic-type constitutive model for carbon fiber papers considering Hertz contact effect [J]. Journal of Engineered Fibers and Fabrics, 2019, 14: 1 − 10.
[8]	SIMAAFROOKHTEH S, SHAKERI M, BANIASSADI M, et al. Microstructure reconstruction and characterization of the porous GDLs for PEMFC based on fibers orientation distribution [J]. Fuel Cells, 2018, 18(2): 160 − 172.
[9]	SADEGHIFAR H, BAHRAMI M, DJILALI N. A statistically-based thermal conductivity model for fuel cell gas diffusion layers [J]. Journal of Power Sources, 2013, 233: 369 − 379. doi: 10.1016/j.jpowsour.2013.01.086
[10]	HEO Y J, PARK M, KANG W S, et al. Preparation and characterization of carbon black/pitch-based carbon fiber paper composites for gas diffusion layers [J]. Composites, 2019, 159: 362 − 368. doi: 10.1016/j.compositesb.2018.09.108
[11]	WANG J, YUAN J, YU J, et al. Investigation of effects of non-homogenous deformation of gas diffusion layer in a PEM fuel cell [J]. International Journal of Energy Research, 2017, 41(14): 2121 − 2137.
[12]	REZAEI NIYA S M, PHILLIPS R K, HOORFAR M. Improvement of the ohmic loss process model of the proton exchange membrane fuel cell [J]. Fuel Cells, 2016, 16(5): 538 − 546. doi: 10.1002/fuce.201500189
[13]	HE X, OHSAWA I, TAKAHASHI J. Influence of marine and harsh environments on performance of carbon fiber paper reinforced polyamide 6 [J]. Fibers and Polymers, 2021: 1 − 12.
[14]	DEY T, SINGDEO D, BOSE M, et al. Study of contact resistance at the electrode-interconnect interfaces in planar type solid oxide fuel cells [J]. Journal of Power Sources, 2013, 233: 290 − 298.
[15]	MOLAEIMANESH G R, NAZEMIAN M. Investigation of GDL compression effects on the performance of a PEM fuel cell cathode by lattice Boltzmann method [J]. Journal of Power Sources, 2017, 359: 494 − 506.
[16]	万军. 碳纤维布加固砌体填充墙抗近距离小当量炸药爆炸数值模拟研究[J]. 工程力学, 2020, 37(增刊 1): 82 − 90. doi: 10.6052/j.issn.1000-4750.2019.04.S012 WAN Jun. Numerical simulation of CFRP reinforced concrete masonry wall against small stand-off distance explosive charge [J]. Engineering Mechanics, 2020, 37(Suppl 1): 82 − 90. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S012
[17]	曹亮, 张海燕, 吴波. 纤维编织网增强地聚物砂浆加固钢筋混凝土梁受剪性能研究[J]. 工程力学, 2019, 36(1): 207 − 215. doi: 10.6052/j.issn.1000-4750.2017.11.0881 CAO Liang, ZHANG Haiyan, WU Bo. Shear behavior of RC beams strengthened with textile reinforced geopolymer mortar [J]. Engineering Mechanics, 2019, 36(1): 207 − 215. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.11.0881
[18]	田志强, 李彦斌, 张培伟, 等. 复合材料层合板多尺度交互渐进损伤分析[J]. 工程力学, 2019, 36(12): 247 − 256. doi: 10.6052/j.issn.1000-4750.2019.01.0006 TIAN Zhiqiang, LI Yanbin, ZHANG Peiwei, et al. Multi-scale interactive progressive damage analysis of composite laminates [J]. Engineering Mechanics, 2019, 36(12): 247 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.01.0006
[19]	WANG M L, BIAN W F. The relationship between the mechanical properties and microstructures of carbon fibers [J]. New Carbon Materials, 2020, 35(1): 42 − 49. doi: 10.1016/S1872-5805(20)60474-7
[20]	MOHAN J M, AMREEN K, JAVED A, et al. Highly selective electrochemical sensing of dopamine, xanthine, ascorbic acid and uric acid using a carbon fiber paper [J]. IEEE Sensors Journal, 2020, 20(19): 11707 − 11712.
[21]	JONG H, CHOI, DEOK G, et al. Highly active oxygen evolution on carbon fiber paper coated with atomic-layer-deposited cobalt oxide [J]. ACS Applied Materials & Interfaces, 2019, 11: 10608 − 10615.
[22]	MATHEW A T, HEGDE S, AKSHAYA K B, et al. MnO₂-Pi on biomass derived porous carbon for electro-catalytic oxidation of pyridyl carbinol [J]. Journal of The Electrochemical Society, 2020, 167(15): 155513. doi: 10.1149/1945-7111/abb8f7
[23]	汤龙其, 令旭霞, 王士华, 等. 聚吡咯/碳纤维纸电热复合材料的制备及性能[J]. 复合材料学报, 2020, 37(6): 1426 − 1433. TANG Longqi, LING Xuxia, WAN Shihua, et al. Preparation and properties of polypyrrole/carbon fiber paper electrothermal composites [J]. Acta Materiae Compositae Sinica, 2020, 37(6): 1426 − 1433. (in Chinese)
[24]	包永洁, 黄成建, 陈玉和, 等. 碳纤维纸木质电热复合材料面层电热效果的纵向尺寸效应[J]. 复合材料学报, 2020, 37(12): 3214 − 3219. BAO Yongjie, HUANG Chengjian, CHEN Yuhe, et al. Longitudinal scale effect of electro-thermal effectiveness of front panel of the integrated wooden electric heating composite based on carbon fiber paper [J]. Acta Materiae Compositae Sinica, 2020, 37(12): 3214 − 3219. (in Chinese)
[25]	高源, 吴晓燕, 孙严博. 新型随机重构微孔隙介质模型与扩散特性[J]. 同济大学学报(自然科学版), 2017, 45(1): 109 − 118. GAO Yuan, WU Xiaoyan, SUN Yanbo. Characterization and diffusion in reconstructed gas diffusion layer based on stochastic method [J]. Journal of Tongji University (Natural Science), 2017, 45(1): 109 − 118. (in Chinese)
[26]	GARCÍA-SALABERRI P A, VERA M, ZAERA R. Nonlinear orthotropic model of the inhomogeneous assembly compression of PEM fuel cell gas diffusion layers [J]. International Journal of Hydrogen Energy, 2011, 36(18): 11856 − 11870. doi: 10.1016/j.ijhydene.2011.05.152
[27]	ZHANG Z, HE P, DAI Y J, et al. Study of the mechanical behavior of paper-type GDL in PEMFC based on microstructure morphology [J]. International Journal of Hydrogen Energy, 2020, 45(53): 1 − 16.
[28]	KITAHARA T, KONOMI T, NAKAJIMA H, et al. Best combination of gas diffusion layers for polymer electrolyte fuel cell under cathode condition of very low humidity [J]. Ecs Transactions, 2008, 16(2): 1603 − 1613.
[29]	NITTA I, HOTTINEN T, HIMANEN O, et al. Inhomogeneous compression of PEMFC gas diffusion layer: Part I [J]. Journal of Power Sources, 2007, 171(171): 26 − 36.
[30]	ADAMS G G, NOSONOVSKY M. Contact modeling—forces [J]. Tribology International, 2000, 33(5/6): 431 − 442. doi: 10.1016/S0301-679X(00)00063-3
[31]	XING X Q, LUM K W, POH H J, et al. Optimization of assembly clamping pressure on performance of proton-exchange membrane fuel cells [J]. Journal of Power Sources, 2010, 195(1): 62 − 68. doi: 10.1016/j.jpowsour.2009.06.107