CONTINUUM EQUIVALENCE AND BEARING CHARACTERISTICS OF A TRI-PRISM STRAIGHT TRUSS
-
摘要: 随着大型装备制造及航天工程的发展,桁架在结构轻量化设计中的作用越来越显著。针对桁架结构各方向上不同的承载需求,利用连续体等效方法研究了三棱直线桁架的承载特性。考虑桁架截面特征,基于能量等效原则将离散桁架等效为连续介质梁模型,获得连续介质梁模型的等效刚度和等效质量,对比验证了桁架结构的数值计算频率和等效梁模型的理论推导结果,研究了在改变桁架横截面边长比例时其横向弯曲刚度和频率的变化趋势,分析了单胞形式对桁架横向弯曲刚度及频率的影响。研究结论对桁架结构在工程中的应用有一定的指导意义。Abstract: With the development of large equipment manufacturing and aerospace engineering, trusses play more and more significant roles in structural lightweight design. For different bearing requirements in each direction of truss structures, bearing characteristics of a tri-prism straight truss are studied with the continuum equivalent method. Based on the principle of energy equivalence, the configuration of the cross section is considered, the discrete truss is equivalent to a beam of a continuum model, the equivalent stiffness and mass of the beam model are obtained, and the numerical frequencies are compared with the theoretical results to verify the equivalent calculations. The changes of transverse bending stiffness and frequency are investigated with different side ratios in the cross section of a tri-prism truss. The influence on transverse bending stiffness and frequency of the tri-prism truss is studied by changing the configuration of the truss units. The research has certain guidance significance for applying truss structure in engineering fields.
-
Keywords:
- tri-prism straight truss /
- equivalence /
- continuum /
- frequency /
- bearing characteristics
-
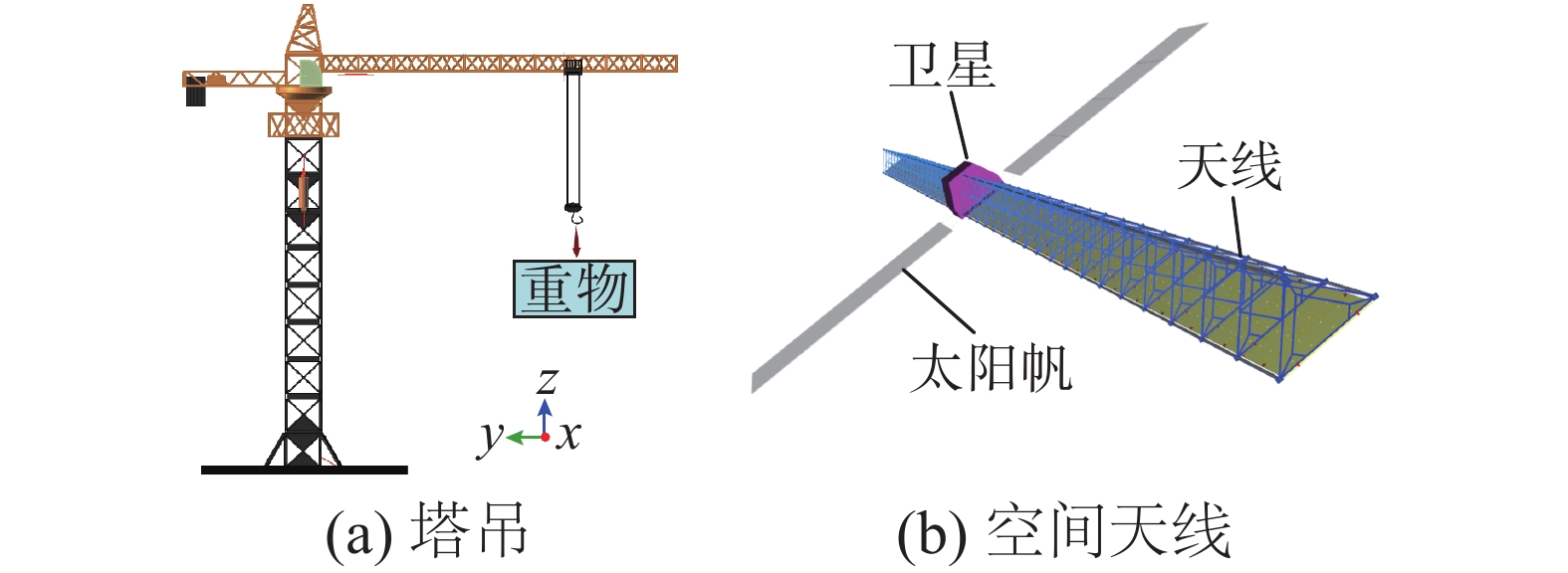
桁架常被用作设计轻量化结构[1]。在结构设计分析中,有限元方法应用广泛[2]。但桁架结构的元件众多、质量和刚度分布不均匀,利用等效动力学模型分析其本质动力学特性比利用有限元法更具优势[3]。国内外许多学者对其连续体等效建模与固有特性分析进行了研究[4-5]。直接用有限元法可以获取桁架的等效刚度等参数[6],利用谱元法和均匀化方法也可以构建周期性桁架的等效模型[7-8]。NOOR等[9-10]提出了基于能量互等原理的连续体建模方法,并对多种等效方法进行对比。STEPHEN和GHOSH[11]建立了铰接非对称周期桁架结构的等效梁模型,并对拉伸-扭转耦合振动问题进行了分析。SALEHIAN和INMAN[12]建立了铰接平面桁架结构的等效梁模型,利用哈密顿原理推导出等效梁模型的动力学偏微分方程,并通过实验验证了理论结果。蔡坤和史姣[13]将具有周期性微结构的平面网格结构比拟成均匀的连续体。李东旭等[14]研究了空间智能桁架的振动控制问题。关富玲和戴璐[15]对比了单环桁架与双环桁架的结构刚度,并研究了桁架口径尺寸对其动力学特性的影响。刘福寿和金栋平[16]将平面周期单胞等效为空间梁模型,并对比了原模型与等效模型的振动特性。GUO等[17]将双层铰接环形桁架结构等效为连续体模型,结合实验与有限元结果验证了等效方法的准确性。柳剑波等[18]建立双胞元平面桁架结构的等效梁模型后,分析了单胞数量及弹性模量对固有特性的影响。张伟等[19]将含间隙运动副的环形桁架结构等效为环形薄壁模型。GUZMAN等[20]研究了竖直放置的三棱柱塔架结构,将其等效为直梁模型并分析了其频率和屈曲特性。刘梅等[21]利用能量等效法研究了直线式正三棱柱桁架结构,基于数值结果对比分析了等效模型的振型。桁架用作承载结构时,其各方向的承载要求通常不同,如图1所示,桁架式吊臂主要是在垂向上克服重力,空间直线式天线的反射面板只安装于其支撑桁架的一侧,主要载荷发生在导致横向弯曲的一个侧面上。为了满足承载要求,同时实现轻量化或低成本设计等目标,对于静态承载,需要在结构不同方向上进行刚度设计,而对于动态载荷,应该考虑不同方向上的频率设计。许多学者研究了桁架的连续体等效问题,但针对桁架在各方向上不同的承载需求而开展的研究较少。
三棱直线桁架是具有代表性的空间梁式承载结构,通常是在某一个方向上有较高的承载要求。针对桁架结构各向承载异性问题,本文以三棱直线桁架为例,考虑非正三角形截面特征,利用能量等效方法推导桁架的等效参数的解析表达式,给定参数并利用有限元方法对理论推导进行验证,最后基于理论推导结果分析截面特征和单胞形式对三棱直线桁架承载特性的影响。
1 等效参数
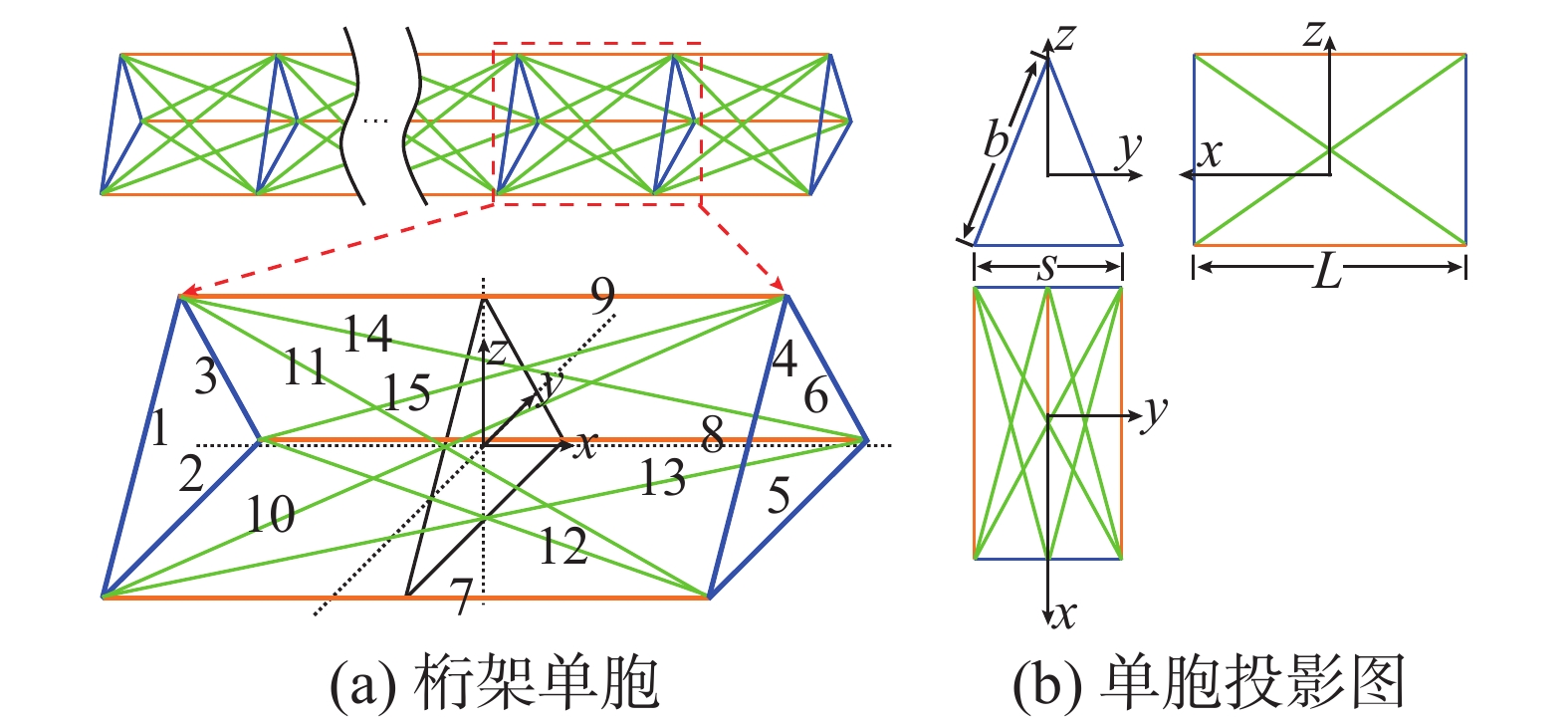
如图2所示,三棱直线桁架是由多个桁架单胞沿直线排列而成的周期结构,桁架单胞由多个杆件组成。其中:竖杆长
b ,底杆长s ,横杆长L 。直线桁架的连续体等效实质是将节点较多的桁架单胞简化为节点较少的梁单元,使得原结构与等效模型处于同样位移场和速度场时具有相等的应变能和动能。如图2(a)所示,在桁架结构中截取桁架单胞,设定坐标原点并建立坐标系,将单胞中任意点的位移表示成
x 轴线上变量,有:{{\boldsymbol{r}}}(x, y, {\textit{z}})=\left.\boldsymbol{r}\right|_{{{y}}=0} ^{{\textit{z}}=0}+\left.\frac{\partial \boldsymbol{r}}{\partial y}\right|_{\substack{{\textit{z}}=0 \\ {{y}}=0}} y+\left.\frac{\partial \boldsymbol{r}}{\partial {\textit{z}}}\right|_{\substack{{\textit{z}}=0 \\ {{y}}=0}} {\textit{z}} = \begin{split} & {[ {{u^0},{v^0},{w^0}} ]^{\rm{T}}} + {\left[ { - {\phi _{\textit{z}}},\varepsilon _{{y}}^0,{\phi _{{x}}} + \frac{1}{2}\gamma _{{y{\textit{z}}}}^0} \right]^{\rm{T}}}y +\\& {\left[ {{\phi _{{y}}}, - {\phi _{{x}}} + \frac{1}{2}\gamma _{{y{\textit{z}}}}^0,\varepsilon _{\textit{z}}^0} \right]^{\rm{T}}}{\textit{z}} \end{split} (1) 式中,
{u^0}、{v^0}、{w^0}、{\phi _x}、{\phi _y}、{\phi _{\textit{z}}}、\varepsilon _y^0、\varepsilon _{\textit{z}}^0、\gamma _{{y{\textit{z}}}}^0 都是x 的函数。基于小变形假设,将式(1)在坐标原点处对
x 进行一阶泰勒展开,有:\begin{split} \boldsymbol{r}(x, y, {\textit{z}})= &\left.\left[\left.\boldsymbol{r}\right|_{{{x}}=0}+\left.\dfrac{\partial \boldsymbol{r}}{\partial x}\right|_{{{x}}=0} x\right]\right|_{\substack{{\textit{z}}=0 \\ {{y}}=0}} + \\& \left.y\left[\left.\dfrac{\partial \boldsymbol{r}}{\partial y}\right|_{{{x}}=0}+\left.\dfrac{\partial^{2} \boldsymbol{r}}{\partial x \partial y}\right|_{{{x}}=0} x\right]\right|_{\substack{{\textit{z}}=0 \\ {{y}}=0}} + \\& \left.{\textit{z}}\left[\left.\frac{\partial \boldsymbol{r}}{\partial {\textit{z}}}\right|_{{{x}}=0}+\left.\frac{\partial^{2} \boldsymbol{r}}{\partial x \partial {\textit{z}}}\right|_{{{x}}=0} x\right]\right|_{\substack{{\textit{z}}=0 \\ {{y}}=0}} \end{split} (2) 单胞中各杆件的轴向正应变为:
\begin{split} {\varepsilon ^{( k )}} = &\varepsilon _{{x}}^{( k )}{l^{( k )}}^{^2} + \varepsilon _{{y}}^{( k )}{m^{( k )}}^{^2} + \varepsilon _{\textit{z}}^{( k )}{n^{( k )}}^{^2}{\text{ + }}\gamma _{{y{\textit{z}}}}^{( k )}{m^{( k )}}{n^{{( k )}}} + \\& \gamma _{{x{\textit{z}}}}^{( k )}{l^{( k )}}{n^{( k )}} + \gamma _{{xy}}^{( k )}{l^{( k )}}{m^{( k )}} \text{,} \end{split} (3) 式中:
{\varepsilon _{{x}}} = \dfrac{{\partial u}}{{\partial x}} ;{\varepsilon _{{y}}} = \dfrac{{\partial v}}{{\partial y}} ;{\varepsilon _{\textit{z}}} = \dfrac{{\partial w}}{{\partial {\textit{z}}}} ;{\gamma _{{xy}}} = \dfrac{{\partial v}}{{\partial x}} + \dfrac{{\partial u}}{{\partial y}} ;{\gamma _{{x{\textit{z}}}}} = \dfrac{{\partial w}}{{\partial x}} + \dfrac{{\partial u}}{{\partial {\textit{z}}}} ;{\gamma _{{y{\textit{z}}}}} = \dfrac{{\partial w}}{{\partial y}} + \dfrac{{\partial v}}{{\partial {\textit{z}}}} ;上标\left( k \right) 表示单胞中第k 个杆件;l 、m 和n 分别表示杆件轴线与单胞坐标系各轴的夹角的余弦。假定单胞中各杆件相互铰接,只考虑杆件的轴向正应变,第
k 个杆件的应变能计为:{U^{(k)}} = {E^{( {{k}} )}}{A^{( {{k}} )}}{L^{( {{k}} )}}{\varepsilon ^{{{( {{k}} )}^2}}}/2 (4) 不考虑杆件局部变形,其动能计为:
\begin{split} {T^{( {{k}} )}} = &\frac{1}{6}{\rho ^{( {{k}} )}}{A^{( {{k}} )}}{L^{( {{k}} )}}( {u_{{L}}^{{{( {{k}} )}^2}} + v_{{L}}^{{{( {{k}} )}^2}} + w_{{L}}^{{{( {{k}} )}^2}} + u_{{R}}^{{{( {{k}} )}^2}} + v_{{R}}^{{{( {{k}} )}^2}}} +\\& { w_{{R}}^{{{( {{k}} )}^2}} + u_{{L}}^{( {{k}} )}u_{{R}}^{( {{k}} )} + v_{{L}}^{( {{k}} )}v_{{R}}^{( {{k}} )} + w_{{L}}^{( {{k}} )}w_{{R}}^{( {{k}} )}} ) \end{split} (5) 式中,下标
{L} 和{R} 表示第k 个杆件的首尾端点。利用式(2)~式(5)可将桁架单胞的应变能和动能表示为:
\tag{6a} \begin{split} {U_e} = &\sum {{U^{({{k}})}}} = ( {{C_1}\varepsilon _{{{x}}0}^2 + {C_2}\gamma _{{{xy}}0}^2 + {C_3}\gamma _{x{\textit{z}}0}^2} )/2 + \\& {\text{ }}( {{C_4}\kappa _{{{x}}0}^2 + {C_5}\kappa _{{{y}}0}^2 + {C_6}\kappa _{{\textit{z}}0}^2} )/2 \end{split} (6a) \tag{6b} \begin{split} {T_e} =& \sum {{T^{(k)}}} = ( {{B_1}\dot u_0^2 + {B_2}\dot v_0^2 + {B_3}\dot w_0^2} )/2 + \\& {\text{ }}( {{B_4}\dot \phi _{{{x}}0}^2 + {B_5}\dot \phi _{{{y}}0}^2 + {B_6}\dot \phi _{{\textit{z}}0}^2} )/2 \end{split} (6b) 式中:
{u_0} = {u^0}\left( 0 \right) ;{v_0} = {v^0}\left( 0 \right) ;{w_0} = {w^0}\left( 0 \right) ;{\phi _{x0}} = {\phi _x}( 0 ) ;{\phi _{{{y}}0}} = {\phi _{{y}}}\left( 0 \right) ;{\phi _{{\textit{z}}0}} = {\phi _{\textit{z}}}\left( 0 \right) ;{\kappa _{{{x}}0}} = {\left. {\dfrac{{\partial {\phi _{{x}}}}}{{\partial x}}} \right|_{{{x}} = 0}} ;{\kappa _{{{y}}0}} = {\left. {\dfrac{{\partial {\phi _{\textit{z}}}}}{{\partial x}}} \right|_{{{x}} = 0}} ;{\kappa _{{\textit{z}}0}} = {\left. {\dfrac{{\partial {\phi _{{y}}}}}{{\partial x}}} \right|_{{{x}} = 0}} ;{\varepsilon _{{{x}}0}} = {\left. {\dfrac{{\partial {u^0}}}{{\partial x}}} \right|_{{{x}} = 0}} ;{\gamma _{{{xy}}0}} = {\left. {\left( {\dfrac{{\partial {v^0}}}{{\partial x}} - {\phi _{\textit{z}}}} \right)} \right|_{{{x}} = 0}} ;{\gamma _{x{\textit{z}}0}} = {\left. {\left( {\dfrac{{\partial {w^0}}}{{\partial x}} + {\phi _{{y}}}} \right)} \right|_{{{x}} = 0}} ;系数{B_i} 和{C_i} 详见附录。基于能量等效原则,将桁架单胞应变能和动能与等效连续体梁模型的应变能和动能分别相等,可得等效梁模型的拉伸刚度
E'A' 、弯曲刚度E'I_{{y}}^\prime 和E'{I_{\textit{z}}^\prime} 、剪切刚度G'{A_{{y}}^\prime} 和G^\prime {A_{\textit{z}}^\prime} 、扭转刚度G'J' 、单位长度质量{m_{\rm{c}}^\prime} 、扭转惯性参数{J_{{x}}^\prime} 和弯曲惯性参数{J_{{y}}^\prime} 和{J_{\textit{z}}^\prime} ,如下式所示:\begin{split} & E'A' = {C_1}, E'{I_{{y}}^\prime} = {C_5}, E'{I_{\textit{z}}^\prime} = {C_6}, \\& G'{A_{{y}}^\prime} = {C_2}, G^\prime {A_{\textit{z}}^\prime} = {C_3} , G'J' = {C_4}, \\& {m_{\rm{c}}^\prime} = {B_1} , {J_{{x}}^\prime} = {B_4} , {J_{{y}}^\prime} = {B_5} , {J_{\textit{z}}^\prime} = {B_6} \end{split} (7) 2 等效验证
某三棱直线桁架由10个如图2所示桁架单胞构成,单胞中各杆件的弹性模量为72 GPa,密度为2768 kg/m3,泊松比取0.33,几何参数如表1所示。
表 1 杆件参数Table 1. Parameters of bars竖杆
长度b/m底杆
长度s/m横杆
长度L/m竖杆和底杆
截面积Ab/m2横杆截
面积Al/m2底面斜杆和侧面
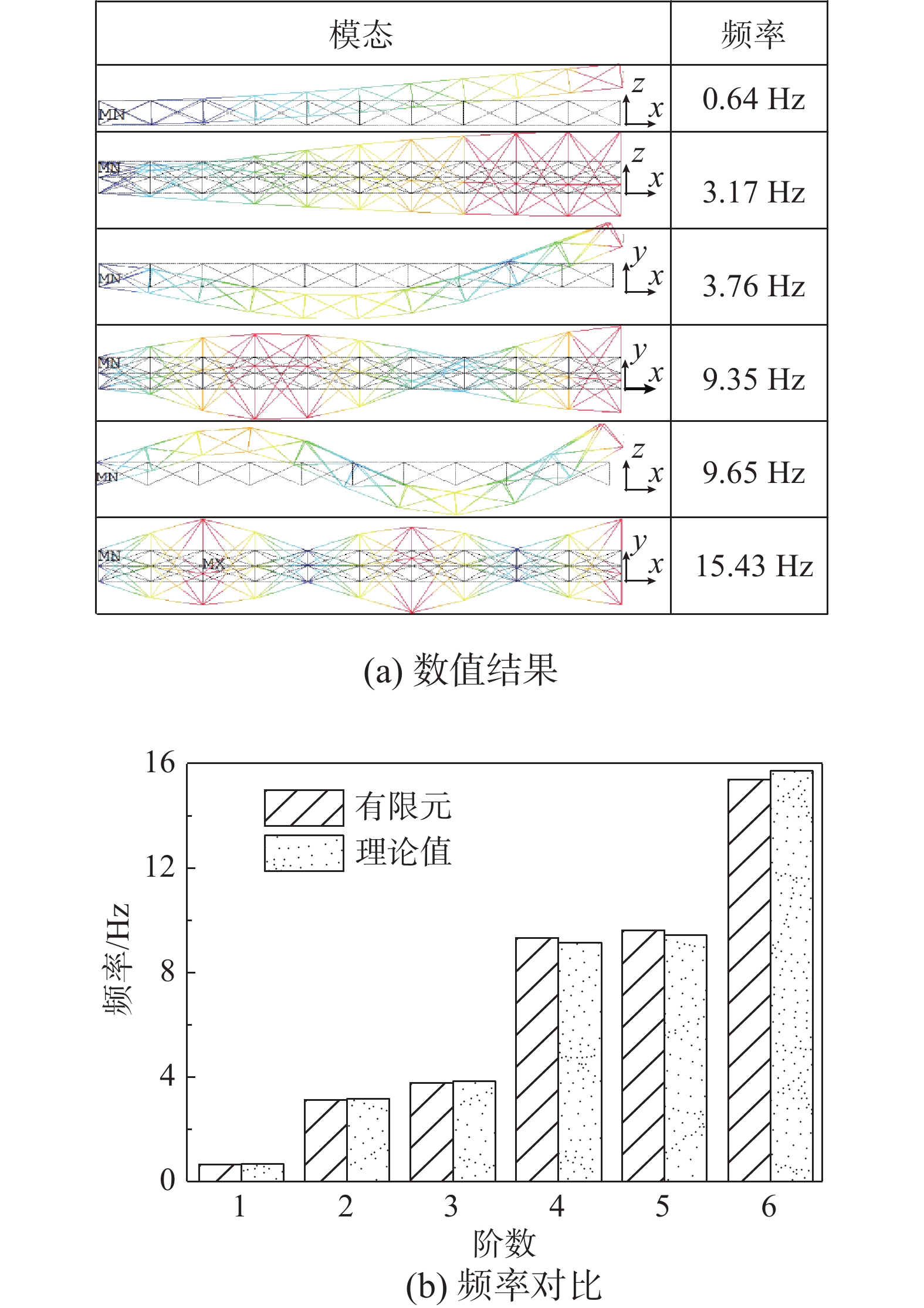
斜杆的截面积Ad/m25 5 7.5 6×10−5 8×10−5 4×10−5 令桁架一端固定一端自由,利用ANSYS计算出前几阶频率,如图3(a)所示。基于式(7)计算出悬臂梁的前三阶弯曲和扭转频率,将所得结果与有限元计算频率进行对比,如图3(b)所示。可以看出,仿真计算出的频率与等效参数所得结果基本一致。
3 单胞结构对桁架承载特性的影响
关于三棱直线桁架力学特性的文献通常将截面设定为正三角形,这意味着结构刚度或频率在三个侧向上都相等。但实际工程中,桁架通常是在某个侧向的承载要求高于其它方向。本节基于前两节推导和验证的等效参数研究单胞结构特征对桁架承载特性的影响。
3.1 底边与侧边的长度比
\eta 的影响为了满足桁架在不同方向的承载需求,同时实现轻量化设计,如式(8)所示,本文假定桁架截面的周长不变,研究底边与侧边的长度比
\eta 对三棱直线桁架的刚度和频率的影响。2b + s = \left( {2 + \eta } \right)b = Const (8) 在第2节给出的三棱直线桁架中,令其他条件不变,仅改变
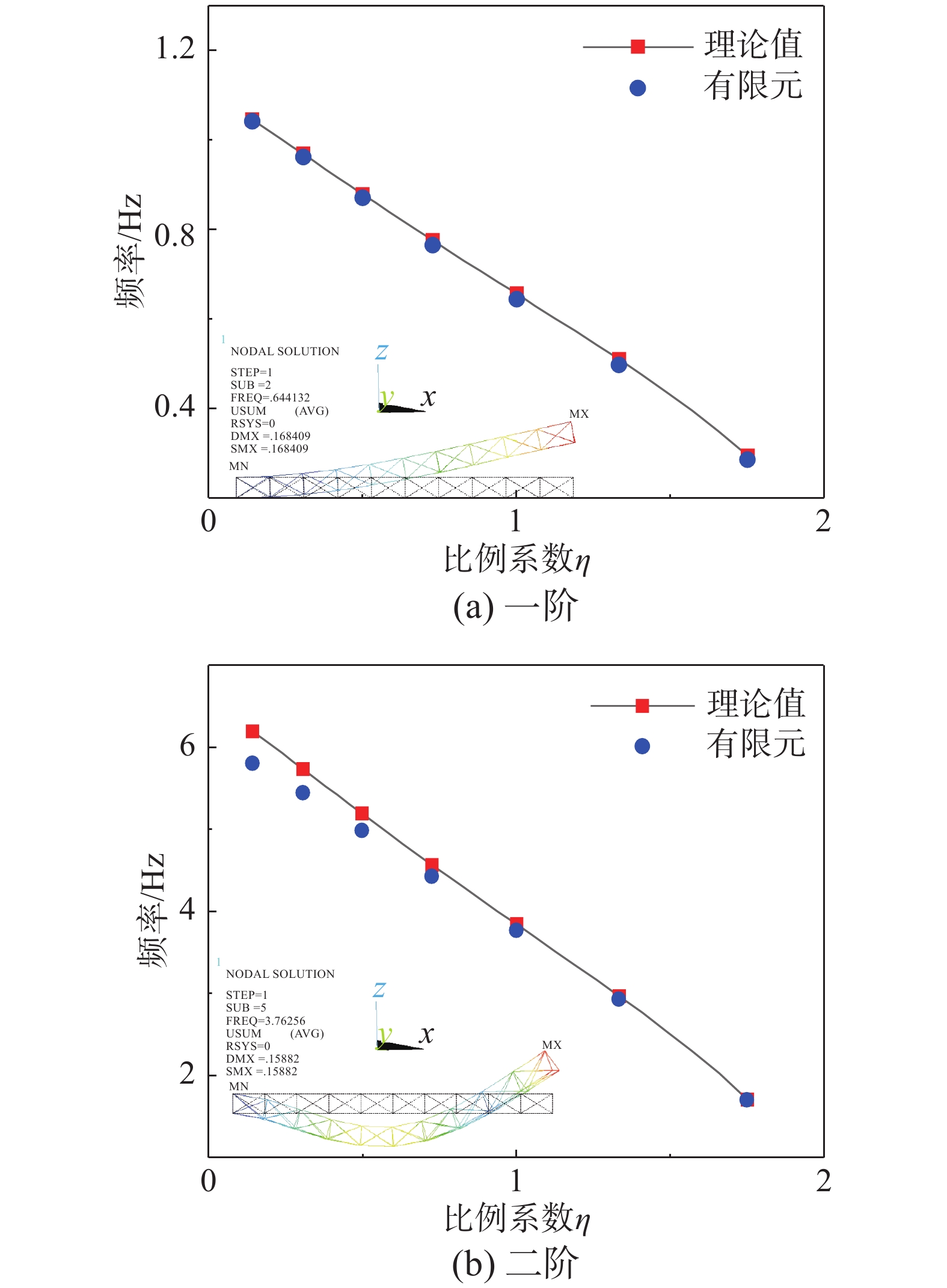
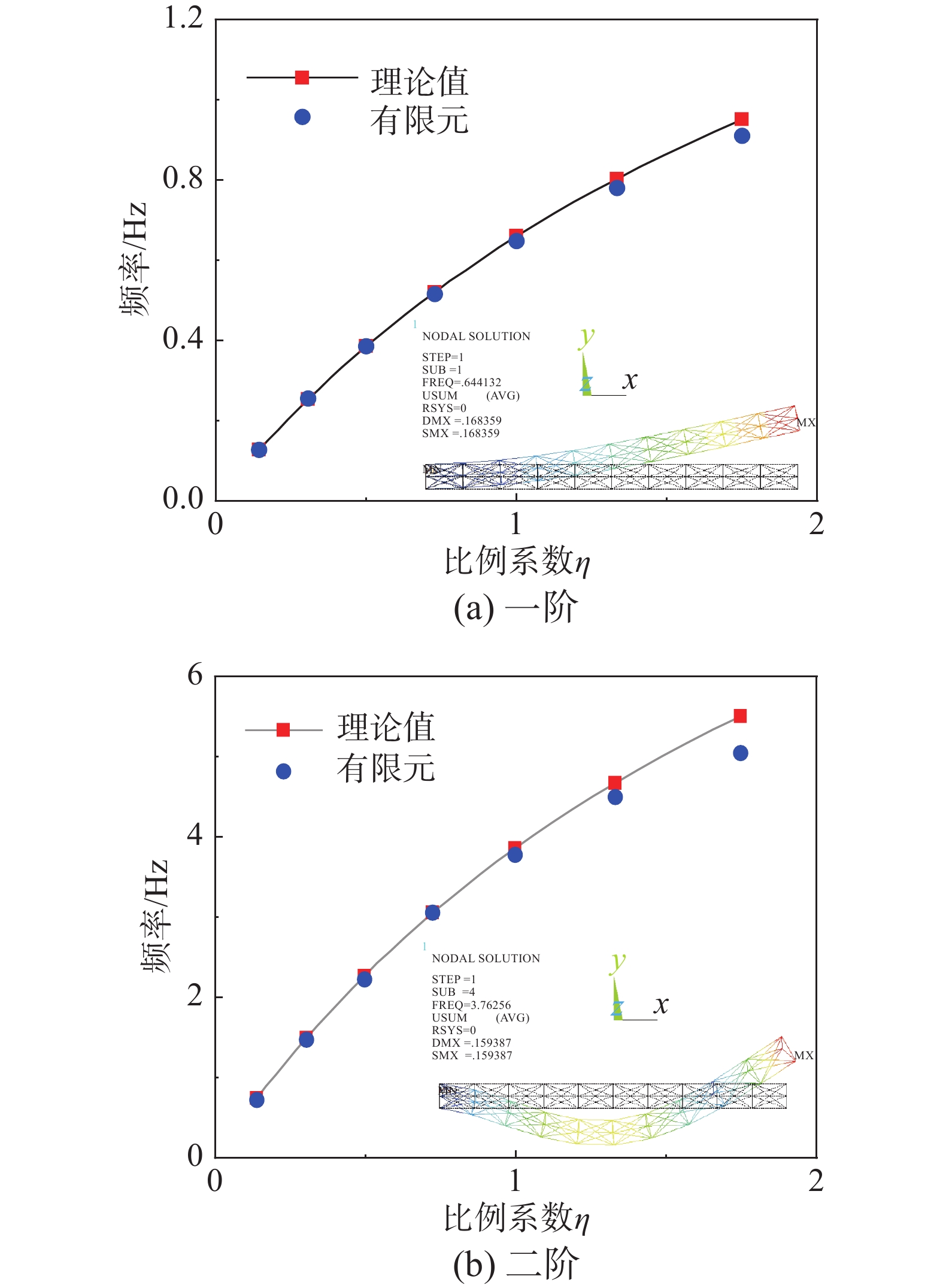
\eta ,计算三棱直线桁架的固有频率。三棱直线桁架侧向的前两阶弯曲频率与\eta 的关系如图4和图5所示。可以看出,随着\eta 增大,三棱直线桁架在z向上的前两阶弯曲频率都是减小,在y向上的前两阶弯曲频率都是增大。三棱直线桁架前两阶弯曲频率在两个侧向上的变化趋势相反,但是振型类似,表现为悬臂梁的前两阶弯曲振型。图6同时给出了两个侧向的弯曲频率,可以看出,当
\eta =1时,频率曲线有一个交点,表明截面为正三边形时,三棱直线桁架的两个侧向弯曲频率几乎相等。图6中,频率曲线将所在平面分割成多个区域,这表明可以利用\eta 的调整来指导桁架结构设计和承载设计,从而避免结构产生共振或者内共振。对于静态载荷,主要考虑承载方向的刚度。因此,图7给出了
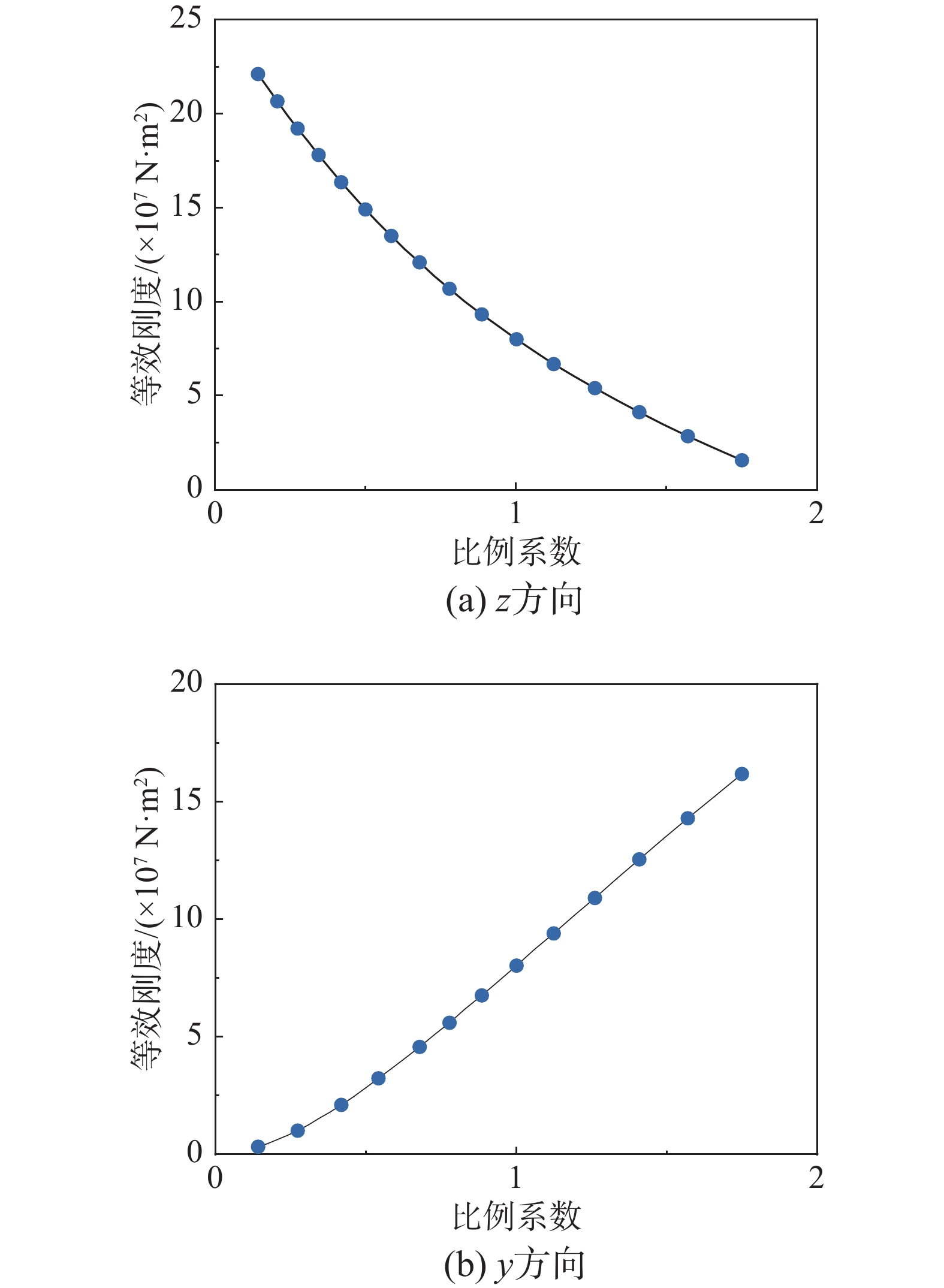
\eta 与三棱直线桁架侧向等效弯曲刚度的关系。可以看出,随着\eta 增大,三棱直线桁架在z向的刚度逐渐减小,在y向的刚度逐渐增大。3.2 单胞形式的影响
工程中常有不同单胞形式的三棱直线桁架[22],以适应不同的承载要求。单胞形式的改变必然导致桁架的频率和刚度等特性发生变化。为此,在图3所示桁架的基础上进行调整,得到如图8所示两种桁架。图8(a)所示三棱桁架Ⅱ中,截面的中线表示各截面上沿着z向加入一个直径为
{\text{6}} \times {10^{ - 5}}\,{{\text{m}}^{\text{2}}} 的杆件,成为底边的高。图8(b)所示三棱桁架Ⅲ中,桁架单胞斜向腹杆数减少一半,其他条件保持不变。利用第1节的等效方法得出图8中桁架的等效刚度和等效质量。设z向为主承载方向,计算出其弯曲频率及刚度,并与桁架Ⅰ进行对比,如表2所示。可以看出,桁架Ⅱ的z向前两阶弯曲频率降低,而等效弯曲刚度
E'{I_{\textit{z}}^\prime} 和等效质量{m_ {\rm{c}}^\prime} 有所增大。桁架Ⅲ中以上各量的变化与桁架Ⅱ刚好相反。桁架Ⅱ中等效质量相对增加率大于等效刚度相对增加率,桁架Ⅲ中等效质量相对减小率大于等效刚度相对减小率。因此,单胞形式改变后,桁架频率增减取决于等效刚度和等效质量的相对变化。表 2 单胞改变前后桁架特性Table 2. Features of trusses before and after changing units桁架类型 一阶频率f1/Hz 二阶频率f2/Hz 等效弯曲刚度E'{I_{\textit{z}}^\prime} /(MN·m2) 等效质量{m_{\rm{c}}^\prime }/(kg·m−1) Truss Ⅰ 0.6560 3.8450 80.1100 1.7949 Truss Ⅱ 0.6420 3.7590 80.6400 1.8908 Truss Ⅲ 0.7170 3.8860 76.3400 1.3957 以上分析表明单胞结构对三棱直线桁架的频率和刚度都有一定影响。针对桁架结构各方向上不同的承载需求,合理选择或设计单胞结构对三棱直线桁架的动静态承载性能有重要作用。
4 结论
针对桁架各向不同承载需求,以三棱直线桁架为例考虑其截面特征,利用等效方法推导了等腰三棱直线桁架的等效刚度与等效质量,通过算例对比理论推导结果与数值计算频率,验证了等效计算的正确性,分析了截面底边与侧边的长度比
\eta 以及单胞形式对三棱直线桁架的刚度和频率的影响。研究表明:(1)随着
\eta 增大,三棱直线桁架前两阶弯曲频率及刚度在两个侧向上的变化趋势相反,但振型相似;(2)改变单胞形式,三棱直线桁架的z向弯曲频率、等效弯曲刚度
E'{I_{\textit{z}}^\prime} 和等效质量{m_\mathrm c^\prime} 随之改变,桁架频率增减取决于等效刚度和等效质量的相对变化;(3)单胞结构特征对三棱直线桁架的动静态承载性能有重要影响,例如进行频率设计可以避免结构动态承载时产生共振或者内共振,而刚度设计则可以在满足静态承载需求的同时实现结构轻量化。
附录:
式(7)中的系数
{B_i} 和{C_i} 如下:{C_1} = \frac{{3{A_{{l}}}{E_{{l}}}{A_{{b}}^2}{E_{{b}}^2}{d^3}{d_{{s}}^3} + p + q + 4r}}{{( {2{A_{{d}}}{E_{{d}}}{b^3} + {A_{{b}}}{E_{{b}}}{d^3}} )( {{A_{{b}}}{E_{{b}}}{d_{{s}}^3} + 2{A_{{d}}}{E_{{d}}}{s^3}} )}} , {C_2} = {A_{{d}}}{E_{{d}}}L{s^2}( {2{d^3} + d_{{s}}^3} )/{d^3}d_{{s}}^3 , {C_3} = {A_{{d}}}{E_{{d}}}L( {4{b^2} - {s^2}} )/{d^3} , {C_4} = {A_{{d}}}{E_{{d}}}L{s^2}( {4{b^2} - {s^2}} )( {{d^3} + 2d_{{s}}^3} )/18{d^3}d_{{s}}^3 , {C_5} = \frac{{{s^2}( {{A_{{b}}}{A_{{d}}}{E_{{b}}}{E_{{d}}}{L^3} + 4{A_{{d}}}{A_{{l}}}{E_{{d}}}{E_{{l}}}{b^3} + 2{A_{{b}}}{A_{{l}}}{E_{{b}}}{E_{{l}}}{d^3}} )}}{{8{A_{{d}}}{E_{{d}}}{b^3} + 4{A_{{b}}}{E_{{b}}}{d^3}}} , {C_6} = \frac{{( {4{b^2} - {s^2}} )( {6{A_{{l}}}{E_{{l}}}{A_{{b}}^2}{E_{{b}}^2}{d^3}{d_{{s}}^3} + 2p + q{\text{ + }}r} )}}{{36( {2{A_{{d}}}{E_{{d}}}{b^3} + {A_{{b}}}{E_{{b}}}{d^3}} )( {{A_{{b}}}{E_{{b}}}{d_{{s}}^3} + 2{A_{{d}}}{E_{{d}}}{s^3}} )}} , {B_1} = {B_2} = {B_3} = [ {{\text{3}}{\rho _{{l}}}{{ A}_{{l}}}L + {\text{3}}{\rho _{{b}}}{{ A}_{{b}}}b + {\rho _{{d}}}{{ A}_{{d}}}( {2d + {d_{{s}}}} )} ]/L ,\;\quad\qquad {B_4} = \frac{{2{b^2} + {s^2}}}{{18L}}[ {6{\rho _{{l}}}{{ A}_{{l}}}L + {\text{3}}{\rho _{{b}}}{{ A}_{{b}}}b + {\rho _{{d}}}{{ A}_{{d}}}( {2d + {d_{{s}}}} )} ] , {B_5} = \frac{{4{b^2} - {s^2}}}{{36L}}[ {6{\rho _{{l}}}{{ A}_{{l}}}L + {\text{3}}{\rho _{{b}}}{{ A}_{{b}}}b + {\rho _{{d}}}{{ A}_{{d}}}( {2d + {d_{{s}}}} )} ] , \tag{A1} {B_6} = \frac{{{s^2}}}{{12L}}[ {6{\rho _{{l}}}{{ A}_{{l}}}L + {\text{3}}{\rho _{{b}}}{{ A}_{{b}}}b + {\rho _{{d}}}{{ A}_{{d}}}( {2d + {d_{{s}}}} )} ] 式中:
{{ A}_{{b}}} 为竖杆和底杆截面积;{{ A}_{{l}}} 为横杆截面积;{{ A}_{{d}}} 为底面斜杆和侧面斜杆的截面积;{E}_{b}、{E}_{d}、{E}_{l} 为弹性模量;{\rho }_{b}、{\rho }_{d}、{\rho }_{l} 为密度。竖杆和底杆的弹性模量及密度相同,底面斜杆和侧面斜杆的弹性模量及密度相同。侧面斜杆长度d = \sqrt {{b^2} + {l^2}} ,底面斜杆长度{d_{\rm{s}}} = \sqrt {{s^2} + {l^2}} 。p,{\text{ }}q,{\text{ }}r 是为了简化公式引入的函数,表达式如下:p = 6{A_{{l}}}{E_{{l}}}[ {{A_{{b}}}{A_{{d}}}{E_{{b}}}{E_{{d}}}( {{b^3}{d_{{s}}^3} + {d^3}{s^3}} ) + 2{A_{{d}}^2}{E_{{d}}^2}{b^3}{s^3}} ]\;, q = 2{A_{{b}}^2}{A_{{d}}}{E_{{b}}^2}{E_{{d}}}{L^3}{d^3} + 4{A_{{b}}}{A_{{d}}^2}{E_{{b}}}{E_{{d}}^2}{L^3}{b^3}\;, \tag{A2} r = {A_{{b}}^2}{A_{{d}}}{E_{{b}}^2}{E_{{d}}}{L^3}{d_{{s}}^3} + 2{A_{{b}}}{A_{{d}}^2}{E_{{b}}}{E_{{d}}^2}{L^3}{s^3} -
表 1 杆件参数
Table 1 Parameters of bars
竖杆
长度b/m底杆
长度s/m横杆
长度L/m竖杆和底杆
截面积Ab/m2横杆截
面积Al/m2底面斜杆和侧面
斜杆的截面积Ad/m25 5 7.5 6×10−5 8×10−5 4×10−5 表 2 单胞改变前后桁架特性
Table 2 Features of trusses before and after changing units
桁架类型 一阶频率f1/Hz 二阶频率f2/Hz 等效弯曲刚度E'{I_{\textit{z}}^\prime} /(MN·m2) 等效质量{m_{\rm{c}}^\prime }/(kg·m−1) Truss Ⅰ 0.6560 3.8450 80.1100 1.7949 Truss Ⅱ 0.6420 3.7590 80.6400 1.8908 Truss Ⅲ 0.7170 3.8860 76.3400 1.3957 -
[1] PICCARDO G, TUBINO F, LUONGO A. Equivalent timoshenko linear beam model for the static and dynamic analysis of tower buildings [J]. Applied Mathematical Modelling, 2019, 71: 77 − 95. doi: 10.1016/j.apm.2019.02.005
[2] 叶康生, 邱廷柱. 二阶非线性常微分方程边值问题有限元p型超收敛计算[J]. 工程力学, 2019, 36(12): 7 − 14. doi: 10.6052/j.issn.1000-4750.2019.01.0005 YE Kangsheng, QIU Tingzhu. A p-type superconvergent recovery method for fe analysis on boundary value problems of second-order nonlinear ordinary differential equations [J]. Engineering Mechanics, 2019, 36(12): 7 − 14. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.01.0005
[3] 胡海岩, 田强, 张伟, 等. 大型网架式可展开空间结构的非线性动力学与控制[J]. 力学进展, 2013, 43(4): 390 − 414. doi: 10.6052/1000-0992-13-045 HU Haiyan, TIAN Qiang, ZHANG Wei, et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes [J]. Advances in Mechanics, 2013, 43(4): 390 − 414. (in Chinese) doi: 10.6052/1000-0992-13-045
[4] 曹登庆, 刘梅, 朱东方, 等. 空间可展桁架结构等效动力学模型研究进展与展望[J]. 飞控与探测, 2020, 3(1): 8 − 17. CAO Dengqing, LIU Mei, ZHU Dongfang, et al. Research progress and prospect of equivalent dynamics model of space deployable truss structures [J]. Flight Control & Detection, 2020, 3(1): 8 − 17. (in Chinese)
[5] 朱博莉, 郭彦林. 梭形空间桁架约束型防屈曲支撑的性能研究[J]. 工程力学, 2020, 37(7): 35 − 46. doi: 10.6052/j.issn.1000-4750.2019.07.0424 ZHU Boli, GUO Junlin. Investigation on the performance of spatial-truss confined BRBs with shuttle shape longitudinally [J]. Engineering Mechanics, 2020, 37(7): 35 − 46. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.07.0424
[6] GANTES C, CONNOR J J, LOGCHER R D. Equivalent continuum model for deployable flat lattice structures [J]. Journal of Aerospace Engineering, 1994, 7(1): 72 − 91. doi: 10.1061/(ASCE)0893-1321(1994)7:1(72)
[7] LEE U. Equivalent continuum representation of lattice beams: Spectral element approach [J]. Engineering Structures, 1998, 20(7): 587 − 592. doi: 10.1016/S0141-0296(97)00063-1
[8] GLAESENER R N, LESTRINGANT C, TELGEN B, et al. Continuum models for stretching-and bending-dominated periodic trusses undergoing finite deformations [J]. International Journal of Solids and Structures, 2019, 171: 117 − 134. doi: 10.1016/j.ijsolstr.2019.04.022
[9] NOOR A K, NEMETH M P. Analysis of spatial beamlike lattices with rigid joints [J]. Computer Methods in Applied Mechanics and Engineering, 1980, 24(1): 35 − 59. doi: 10.1016/0045-7825(80)90039-0
[10] NOOR A K. Continuum modeling for repetitive lattice structures [J]. Applied Mechanics Reviews, 1988, 41(7): 285 − 296. doi: 10.1115/1.3151907
[11] STEPHEN N G, GHOSH S. Eigenanalysis and continuum modelling of a curved repetitive beam-like structure [J]. International Journal of Mechanical Sciences, 2005, 47(12): 1854 − 1873. doi: 10.1016/j.ijmecsci.2005.07.001
[12] SALEHIAN A, INMAN D J. Dynamic analysis of a lattice structure by homogenization: experimental validation [J]. Journal of Sound and Vibration, 2008, 316(1-5): 180 − 197. doi: 10.1016/j.jsv.2008.02.031
[13] 蔡坤, 史姣. 含周期性索-杆胞元的二维网格结构拟膜分析[J]. 工程力学, 2011, 28(10): 27 − 33. CAI Kun, SHI Jiao. Pseudo-membrane method for two-dimensional lattice structure with periodic cable-link cells [J]. Engineering Mechanics, 2011, 28(10): 27 − 33. (in Chinese)
[14] 李东旭, 刘望, 蒋建平, 等. 空间智能桁架的传感器作动器位置优化和分散化自适应模糊振动控制[J]. 中国科学:技术科学, 2011, 41(5): 602 − 610. LI Dongxu, LIU Wang, JIANG Jianping, et al. Placement optimization of actuator and sensor and decentralized adaptive fuzzy vibration control for large space intelligent truss structure [J]. Science China Technology Sciences, 2011, 41(5): 602 − 610. (in Chinese)
[15] 关富玲, 戴璐. 双环可展桁架结构动力学分析与试验研究[J]. 浙江大学学报(工学版), 2012, 46(9): 1605 − 1610, 1646. doi: 10.3785/j.issn.1008-973X.2012.09.009 GUAN Fuling, DAI Lu. Dynamic analysis and test research of double-ring deployable truss structure [J]. Journal of Zhejiang University (Engineering Science), 2012, 46(9): 1605 − 1610, 1646. (in Chinese) doi: 10.3785/j.issn.1008-973X.2012.09.009
[16] 刘福寿, 金栋平. 环形桁架结构径向振动的等效圆环模型[J]. 力学学报, 2016, 48(5): 1184 − 1191. doi: 10.6052/0459-1879-16-076 LIU Fushou, JIN Dongping. Equivalent circular ring model for the radial vibration analysis of hoop truss structures [J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(5): 1184 − 1191. (in Chinese) doi: 10.6052/0459-1879-16-076
[17] GUO H W, SHI C, LI M, et al. Design and dynamic equivalent modeling of double-layer hoop deployable antenna [J]. International Journal of Aerospace Engineering, 2018: 2941981.
[18] 柳剑波, 王立峰, 金栋平. 周期胞元平面桁架结构等效动力学分析[J]. 振动工程学报, 2018, 31(1): 67 − 73. LIU Jianbo, WANG Lifeng, JIN Dongping. Equivalent continuum modeling of a kind of planar lattice truss [J]. Journal of Vibration Engineering, 2018, 31(1): 67 − 73. (in Chinese)
[19] 张伟, 刘宏利, 郭翔鹰. 考虑间隙运动副的桁架单胞等效建模与分析[J]. 动力学与控制学报, 2018, 16(2): 136 − 143. doi: 10.6052/1672-6553-2018-080 ZHANG Wei, LIU Hongli, GUO Xiangying. Equivalent modeling and analysis of truss antenna unit cell with clearance joints [J]. Journal of Dynamics and Control, 2018, 16(2): 136 − 143. (in Chinese) doi: 10.6052/1672-6553-2018-080
[20] GUZMAN A M, ROSALES M B, FILIPICH C P. Continuous one-dimensional model of a spatial lattice. Deformation, vibration and buckling problems [J]. Engineering Structures, 2019, 182: 290 − 300. doi: 10.1016/j.engstruct.2018.12.074
[21] LIU M, CAO D Q, ZHU D F. Coupled vibration analysis for equivalent dynamic model of the space antenna truss [J]. Applied Mathematical Modelling, 2021, 89: 285 − 295. doi: 10.1016/j.apm.2020.07.013
[22] 朱东方, 刘付成, 黄静, 等. 一种柔性可展桁架结构的主动振动抑制技术[J]. 飞控与探测, 2019, 2(5): 33 − 40. ZHU Dongfang, LIU Fucheng, HUANG Jing, et al. Active vibration suppression technology of flexible deployable truss structure [J]. Flight Control & Detection, 2019, 2(5): 33 − 40. (in Chinese)
-
期刊类型引用(2)
1. 陈培见, 彭娟, 赵慧明, 沈晓明, 张桂民. 趣味“桁架”教学资源的探索和分析. 力学与实践. 2025(03)  百度学术
百度学术
2. 刘洋,付玲,刘延斌,尹莉. 细长桁架臂卸载反弹动应力分布规律及试验. 振动与冲击. 2024(15): 251-260 .  百度学术
百度学术
其他类型引用(3)



 下载:
下载: