新型建筑工业化需要装配式钢结构建筑。装配式钢结构可改变建造方式，实现精益化施工，促进建筑行业转型升级^[1-2]，如图1所示。同时，为了提高建筑的抗震减灾能力、构建可持续发展的城市和社区，结构需在塑性变形能力、耗能性能、可修复性能等方面得到提升。

图  1  装配式钢结构

Figure  1.  Prefabricated steel structure

下载: 全尺寸图片 幻灯片

装配式钢板剪力墙具有较高的抗侧性能，重量较、强度高的特点，同时可实现高效施工，被广泛应用到建筑当中^[3]。

各国学者针对钢板剪力墙抗震性能进行了研究。HITAKA等^[4]提出了带缝钢板剪力墙，并对该构造的钢板剪力墙抗震性能进行了详细的研究，表明带缝钢板剪力墙抗震性能良好。另外，CORTES等^[5]、蒋路等^[6]、张艳霞等^[7]对多层带缝钢板剪力墙及框架进行抗震性能研究，表明多层带缝钢板剪力墙抗震性良好。为了满足建筑开孔使用的功能，同时改善钢板剪力墙抗震性能，ROBERT等^[8]、ALAVI等^[9]、MATTEIS等^[10]、PHILLIPS等^[11]对开圆孔钢板剪力墙进行了抗震性能研究，得到开孔的钢板剪力墙可有效改善抗震性能的结果。YU等^[12]对螺栓连接密肋装配式钢板剪力墙进行有限元分析和试验研究，结果表明该无焊接装配式钢板剪力墙的面外屈曲得到有效约束，剪力墙的层间位移角和平面外变形分别降低了14.7%和57%。聂建国等^[13]、马尤苏夫等^[14]、牟在根等^[15]分别对竖向加劲、井字加劲、对角加劲钢板剪力墙框架结构进行了抗震性能研究，结果表明加劲可以有效防止墙板在荷载作用下发生屈曲。CHEN等^[16]、ZIRAKIAN等^[17]对屈服点为100 MPa的钢板剪力墙进行了抗震性能研究，得出低屈服点钢板剪力墙的变形能力和耗能性能良好的结果。

为了进一步增加装配式剪力墙的耗能性能，JIN等^[18]将屈曲约束钢板剪力墙的内板开斜槽形成一种新型装配式屈曲约束钢板剪力墙。该装配式屈曲约束钢板剪力墙相当于多个斜向平行放置的屈曲约束支撑，具有良好的耗能性能。范重等^[19]对屈曲约束钢板剪力墙边框刚度影响进行了研究，得出现行技术标准中对非加劲钢板剪力墙边框刚度的规定，不能很好地适用于屈曲约束钢板剪力墙的结论。LIU等^[20]、张爱林等^[21]提出部分连接装配式钢板剪力墙，并对剪力墙进行了抗震性能试验研究，结果表明部分连接装配式钢板剪力墙抗震性能良好。VALIZADEH等^[22]提出一种装配式蝶形连杆钢板剪力墙，并对该钢板剪力墙进行了抗震性能研究，结果表明该构造的装配式钢板剪力墙有效降低了平面外屈曲，滞回曲线的捏缩得改改善，耗能能力提高。

通过开缝、开孔、加劲、使用低屈服点钢、屈曲约束、部分连接等形式不同程度地改善装配式钢板剪力墙滞回性能，但在不损失承载力的情况下，不能根本上改善剪力墙的平面外屈曲、滞回曲线捏缩。

本文提出了一种带环形阻尼器的装配式高强钢板剪力墙。该装配式钢板剪力墙采用Q460C高强钢材，同时具有自重轻、运输便捷、施工高效的特点。针对该装配式高强钢板剪力墙进行了抗震性能有限元研究，分析了钢材牌号Q355B与Q460C、剪力墙内嵌板高厚比对其滞回性能影响，并提出了抗剪承载力设计方法。

1   带环形阻尼器的装配式高强钢板剪力墙构造

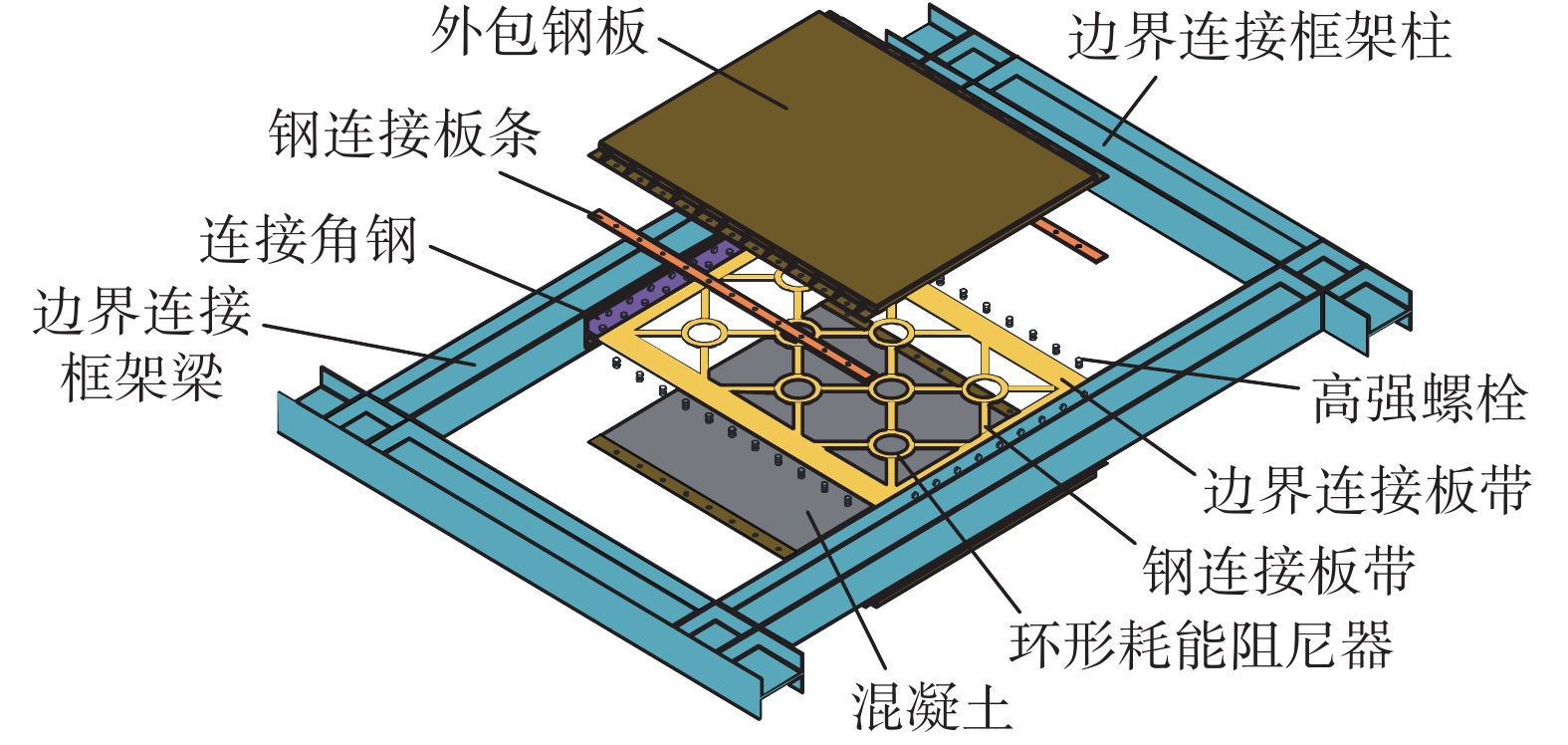
带环形阻尼器的装配式高强钢板剪力墙，由内嵌板和钢混凝土面外约束组合板组成，如图2所示。在钢混凝土面外约束组合板的有效约束作用下，带环形金属阻尼器的内嵌板为结构提供抗侧力、实现变形耗能。

图  2  带环形阻尼器的装配式高强钢板剪力墙构造示意图

Figure  2.  Configuration of prefabricated high-strength steel plate shear wall with annular dampers

下载: 全尺寸图片 幻灯片

内嵌板由环形金属阻尼器、钢连接板带、边界连接板带组成。环形金属阻尼器与钢连接板带交替布置，并与水平方向呈45°角，然后通过边界连接板带连接形成内嵌板。边界连接板带形成的外围边框可以承受竖向荷载，环形耗能阻尼器的数量可根据抗剪承载力的需求布置。

钢混凝土面外约束组合板由外包钢板和内填混凝土组成。外包钢板呈帽形，在帽形内凹处填充混凝土，混凝土外包钢板帽形内凹处填平，形成面外约束组合板。如此构造可不用考虑混凝土配筋，减小了面外约束组合板的厚度，便于运输和安装。该面外约束组合板的钢板外置，含混凝土面则与内嵌板接触，可有效防止混凝土受力破坏。在平行于柱方向上，将两块分别放置在内嵌板两侧的面外约束组合板采用高强螺栓进行对穿连接，同时在两面外约束组合板螺栓孔处内夹与内嵌板相同厚度的钢连接板条。这便于安装和拆卸，可实现重复利用，达到震后仅快速更换破坏耗能的内嵌板即可完成修复使用的目的。

2   有限元模型建立

2.1   模型设计

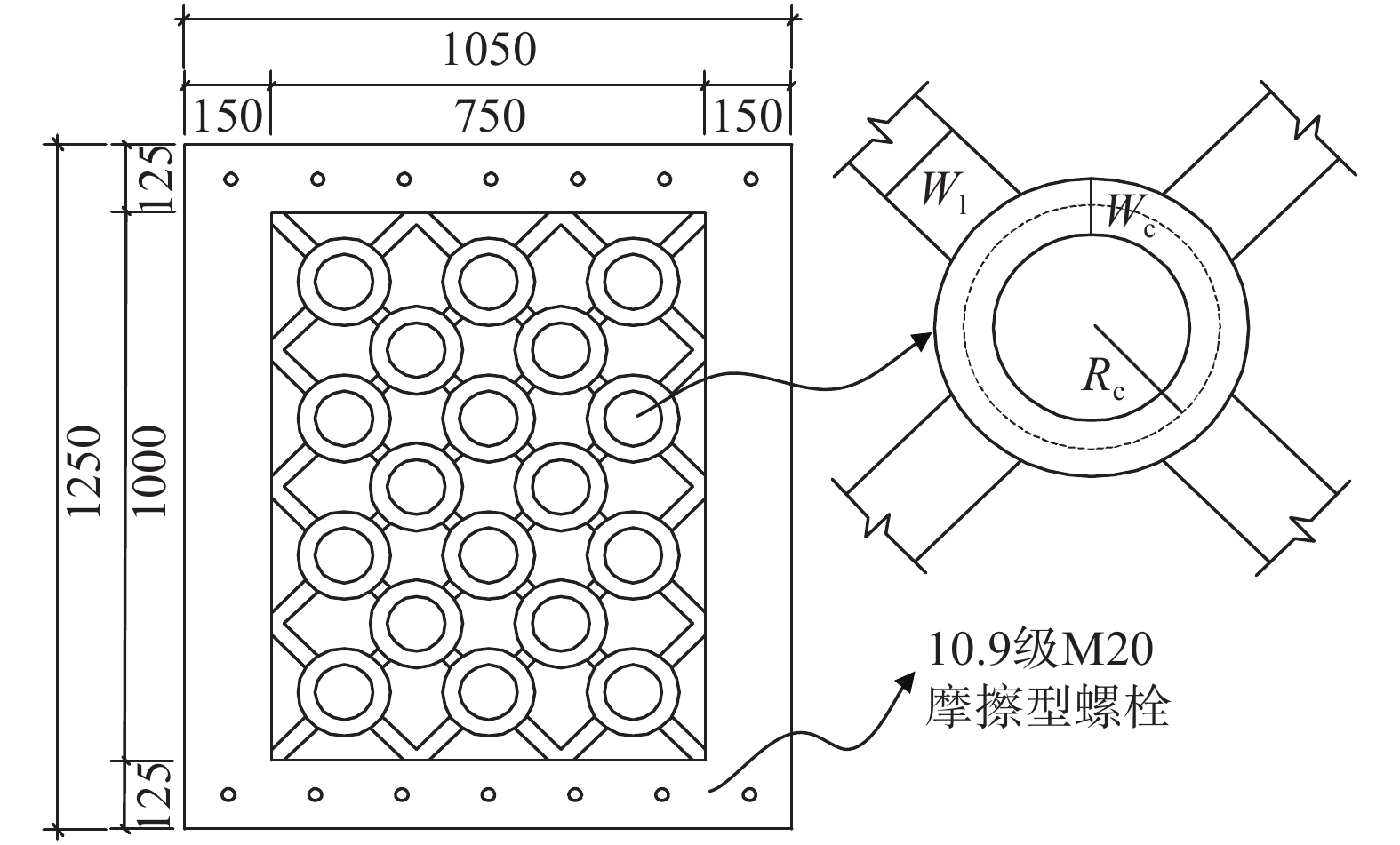
有限元模型与实际结构缩尺比例约为1∶3，具体尺寸如图3所示。有限元模型内嵌板尺寸为1250 mm×1050 mm(长×宽)，厚度分别为6 mm、8 mm和10 mm。钢连接板带宽w_l为50 mm，环形阻尼器宽w_c为30 mm，半径R_c为65 mm。外包钢板尺寸为1000 mm×1300 mm×40 mm×5 mm(长×宽×高×厚)，其中包混凝土，内填混凝土尺寸为990 mm×1200 mm×35 mm(长×宽×高)。

图  3  模型尺寸

Figure  3.  Model dimensions

下载: 全尺寸图片 幻灯片

剪力墙与钢梁采用角钢和螺栓连接，连接角钢尺寸为100 mm×10 mm(边宽×边厚)，高强螺栓采用10.9级M20摩擦型。

2.2   模型建立及加载制度

带环形阻尼器的装配式高强钢板剪力墙有限元模型如图4所示。内嵌钢板、外约束钢板、连接角钢及工字钢梁采用Q355B或Q460C钢材，混凝土强度指标为C30。依据《钢结构设计标准》(GB50017)，Q355B或Q460C钢材本构关系采用双折线理论模型，C30混凝土本构关系依据《混凝土设计规范》(GB50010)采用理论模型，同时考虑混凝土塑性损伤。

内嵌板、连接角钢、工字钢梁、外约束组合板以及高强螺栓采用8节点的C3D8R单元。高强螺栓与连接角钢、高强螺栓与内嵌板、连接角钢与内嵌板、内嵌板与外约束板、外约束板与高强螺栓、外约束板与钢连接板条、钢连接板条与高强螺栓之间为摩擦接触，接触滑移系数选取0.35。连接角钢与工字钢梁采用绑定接触。

图  4  有限元模型

Figure  4.  Finite element model

下载: 全尺寸图片 幻灯片

经过有限元参数模拟，选取关键影响参数进行抗震性能研究，具体参数变化如表1所示。

表  1  参数变化

Table  1.  Parameters

模型编号	钢材牌号	内嵌板高厚比
SPSW-RD-1	Q460C	208
SPSW-RD-2	Q460C	156
SPSW-RD-3	Q460C	125
SPSW-RD-4	Q355B	208
SPSW-RD-5	Q355B	156
SPSW-RD-6	Q355B	125

下载: 导出CSV 

| 显示表格

有限元模型在底梁采用固定约束，顶梁约束平面外平动和转动。有限元模型的水平低周往复循环加载以位移控制，加载制度如图5所示。

图  5  模型加载制度

Figure  5.  Loading protocol of FE model

下载: 全尺寸图片 幻灯片

3   有限元模拟

3.1   破坏模式

带环形阻尼器的装配式高强钢板剪力墙破坏模式如图6所示。从图中可以看出，在水平低周往复荷载作用下，该装配式高强钢板剪力墙内嵌板环形阻尼器屈服破坏，形成塑性铰，边界连接板带四角屈服破坏。面外约束组合板、高强螺栓、连接角钢、工字钢梁没有发生破坏。

图  6  破坏模式

Figure  6.  Failure mode

下载: 全尺寸图片 幻灯片

3.2   滞回曲线

带环形阻尼器的装配式高强钢板剪力墙滞回曲线如图7所示。从图中可以看出，只有模型SPSW-RD-3滞回曲线出现捏缩现象，在0.04层间位移角出现承载力下降。其他模型滞回曲线饱满，承载力没有下降。

图  7  模型滞回曲线

Figure  7.  Hysteretic curves of models

下载: 全尺寸图片 幻灯片

3.3   骨架曲线

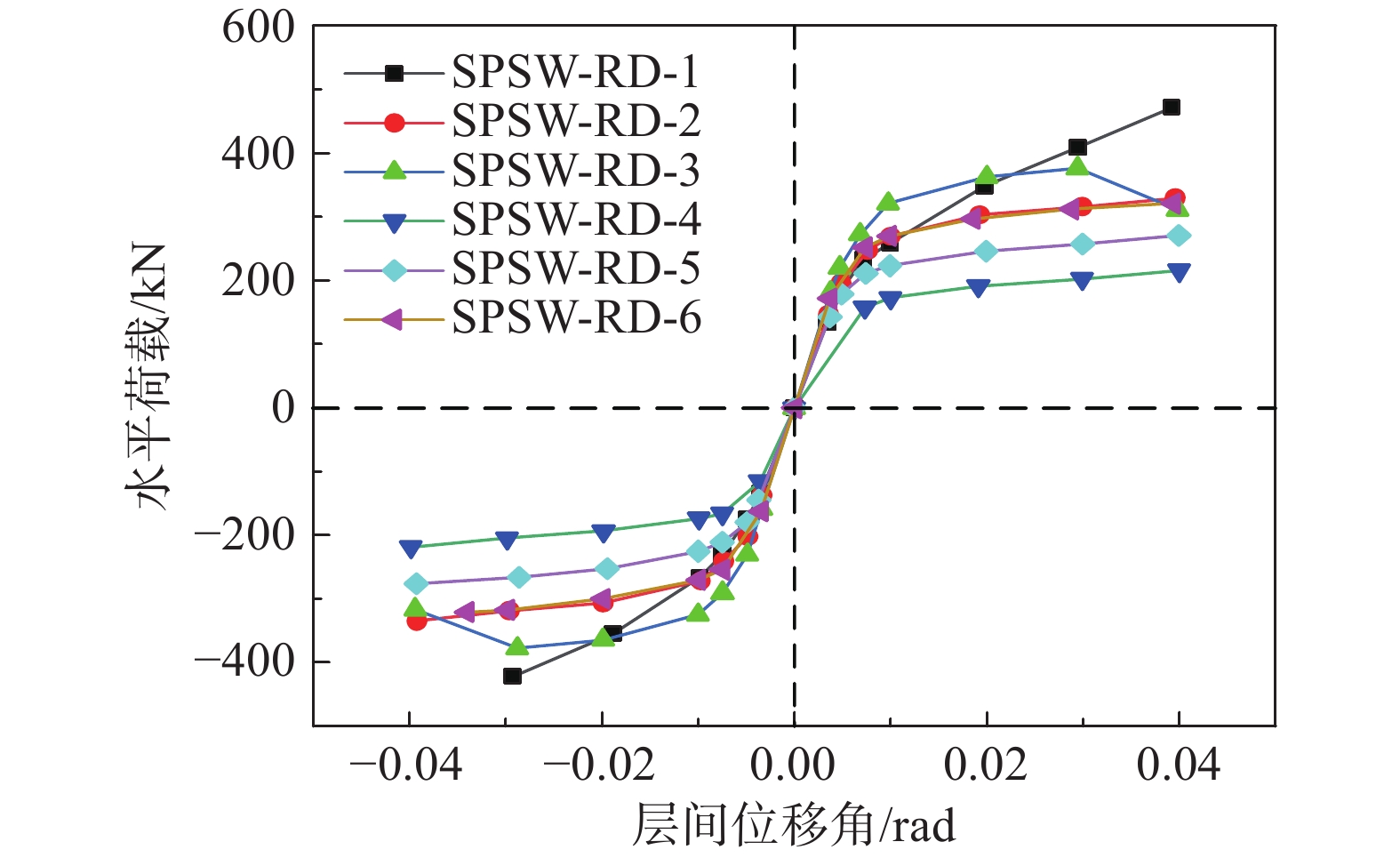
带环形阻尼器的装配式高强钢板剪力墙骨架曲线如图8所示，其特征值见表2。除了SPSW-RD-3模型在层间位移角加载到0.03时抗剪承载力出现了极值点和下降段，其他模型直至层间位移角加载到0.04时抗剪承载力都在上升。因此，定义模型极限荷载为骨架曲线极值点荷载，或模型没有出现极值荷载点时层间位移角加载到0.04时对应的荷载。定义模型破坏荷载为承载力下降到极限荷载的85%时的荷载，或模型没有出现承载力下降到极限荷载的85%的荷载时，选取层间位移角加载到0.04的荷载。

图  8  骨架曲线

Figure  8.  Skeleton curves

下载: 全尺寸图片 幻灯片

表  2  特征值

Table  2.  Characteristic values

模型编号	屈服荷载/kN	极限荷载/kN	破坏荷载/kN
SPSW-RD-1	167.0	471.9	471.9
SPSW-RD-2	193.1	330.0	330.0
SPSW-RD-3	273.4	376.7	320.2
SPSW-RD-4	132.5	215.9	215.9
SPSW-RD-5	178.6	271.0	271.0
SPSW-RD-6	213.8	321.0	321.0

下载: 导出CSV 

| 显示表格

对比屈服荷载。模型SPSW-RD-3的屈服荷载是SPSW-RD-1的1.64倍，模型SPSW-RD-4的屈服荷载是SPSW-RD-6的1.61倍，表明内嵌板高厚比从208降低到125时，该装配式高强钢板剪力墙屈服荷载增大，且增大幅度较大。模型SPSW-RD-1较模型SPSW-RD-4、模型SPSW-RD-2较模型SPSW-RD-5、模型SPSW-RD-3较模型SPSW-RD-6的屈服荷载分别大26.0%、8.1%、27.9%，表明随着剪力墙钢材牌号从Q355B提高到Q460C时，该装配式高强钢板剪力墙屈服荷载增大，且增大幅度较大。

对比极限荷载。模型SPSW-RD-2比模型SPSW-RD-1的极限荷载小43.0%，模型SPSW-RD-3比模型SPSW-RD-2的极限荷载大14.2%。表明，随着内嵌板高厚比从208降低到125时，采用Q460C钢材的带环形阻尼器的装配式高强钢板剪力墙极限荷载先减小后增大，这是由模型内嵌板中环形耗能阻尼器参与受力数量的多少所决定。模型SPSW-RD-1的内嵌板中环形耗能阻尼器都发生屈服破坏，承载力最高，而模型SPSW-RD-3和SPSW-RD-2的环形耗能阻尼器不能全部参与受力，且模型SPSW-RD-3屈服破坏的环形耗能阻尼器比SPSW-RD-2的更多，因此，模型SPSW-RD-1的极限承载力最大，模型SPSW-RD-2的最小。

模型SPSW-RD-6的极限荷载是模型SPSW-RD-4的极限荷载1.49倍，表明随着内嵌板高厚比从208降低到125时，采用Q355B钢材的带环形阻尼器的装配式钢板剪力墙极限荷载增大。模型SPSW-RD-1较模型SPSW-RD-4、模型SPSW-RD-2较模型SPSW-RD-5、模型SPSW-RD-3较模型SPSW-RD-6的极限荷载分别增大118.6%、21.8%、17.4%。表明随着剪力墙钢材牌号从Q355B提高到Q460C时，该装配式高强钢板剪力墙极限荷载增大。

对比破坏模型。模型SPSW-RD-3的破坏荷载较SPSW-RD-1的小32.2%，表明随着内嵌板高厚比从208降低到125时，采用Q460C钢材的带环形阻尼器的装配式高强钢板剪力墙破坏荷载减小，且减小幅度较大。模型SPSW-RD-6的破坏荷载较SPSW-RD-4的大48.7%，表明随着内嵌板高厚比从208降低到125时，采用Q355B钢材的带环形阻尼器的装配式高强钢板剪力墙破坏荷载增大，且增大幅度较大。模型SPSW-RD-1、模型SPSW-RD-2、模型SPSW-RD-3的破坏荷载分别是模型SPSW-RD-4、模型SPSW-RD-5、模型SPSW-RD-6的2.19倍、1.22倍、1.0倍，表明钢材牌号从Q355B提高到Q460C时，装配式高强钢板剪力墙破坏荷载增大，且内嵌板厚度越大的增大越多。

3.4   刚度退化

带环形阻尼器的装配式高强钢板剪力墙刚度退化可用等效刚度退化系数λ表示^[18]，如图9所示。等效刚度为每级加载点与原点连线的斜率，等效刚度退化系数λ为每个加载级的等效刚度与初始刚度的比值。

图  9  刚度退化

Figure  9.  Stiffness degenerations

下载: 全尺寸图片 幻灯片

从图9可以看出，较SPSW-RD-2和SPSW-RD-3，模型SPSW-RD-1的等效刚度在屈服后退化较慢；较SPSW-RD-5和SPSW-RD-6，模型SPSW-RD-4的等效刚度在正向加载时退化较慢。表明随着内嵌板高厚比从208降低到125时，该装配式高强钢板剪力墙等效刚度屈服后退化缓慢。

同时，随着钢材牌号从Q355B提高到Q460C时，该装配式高强钢板剪力墙等效刚度退化变缓。

3.5   耗能性能

带环形阻尼器的装配式高强钢板剪力墙耗能性能采用每级加载位移下的滞回耗能E和等效粘性阻尼系数ζ表示，如图10所示。从图10中可以看出，模型SPSW-RD-1的滞回耗能E明显大于其他模型的滞回耗能，且进入屈服阶段耗能增加更快。模型SPSW-RD-3的滞回耗能E在加载位移达到层间位移角0.03后，耗能增加减缓。其他模型的滞回耗能随着层间位移角的增加基本呈线性增加。

图  10  耗能性能

Figure  10.  Dissipation capacity

下载: 全尺寸图片 幻灯片

如图10(b)所示，随着内嵌板高厚比从208降低到125时，模型等效粘性阻尼系数减小。除模型SPSW-RD-3外，等效粘性阻尼系数最高值在0.27~0.51，较密肋屈曲约束钢板剪力墙^[18]等效粘性阻尼系数0.24和多层带缝钢板剪力墙^[5]等效粘性阻尼系数0.31更大。

整体上，随着内嵌板高厚比从208降低到125时，采用Q460C高强钢材的带环形阻尼器的装配式高强钢板剪力墙耗能减小，采用Q355B钢材的带环形阻尼器的装配式高强钢板剪力墙耗能增大。采用Q460C高强钢材的带环形阻尼器的装配式高强钢板剪力墙耗能大于采用Q355B钢材的剪力墙。

3.6   位移延性

各模型在水平加载位移达到0.04层间位移角时承载力都没有下降或下降不到极限荷载的85% (没有出现破坏荷载)，因此模型的位移延性系数为模型最终加载位移与屈服位移之比，如表3所示。各模型的位移延性系数在5.7~8.7，较密肋屈曲约束钢板剪力墙^[23]位移延性系数5.70~5.97和多层带缝钢板剪力墙^[7]位移延性系数2.96~4.00更大，表明带环形阻尼器的装配式高强钢板剪力墙延性较好。

表  3  位移延性

Table  3.  Displacement ductility

模型编号	屈服位移/mm	极限位移/mm	位移延性系数μ
SPSW-RD-1	7.0	60.0	8.6
SPSW-RD-2	7.4	59.4	8.0
SPSW-RD-3	10.2	57.7	5.7
SPSW-RD-4	6.9	60.0	8.7
SPSW-RD-5	7.4	60.0	8.1
SPSW-RD-6	7.4	60.0	8.1

下载: 导出CSV 

| 显示表格

模型SPSW-RD-3的位移延性系数较模型SPSW-RD-1降低34.2%，模型SPSW-RD-6的位移延性系数较模型SPSW-RD-4降低6.9%，表明随着内嵌板高厚比从208降低到125时，该装配式高强钢板剪力墙的位移延性系数降低，尤其是采用Q460C高强钢材的钢板剪力墙降低程度更大。整体上，采用Q460C高强钢材剪力墙的位移延性系数小于采用Q355B钢材的钢板剪力墙。

4   抗剪承载力

4.1   计算公式

由于外包钢板与混凝土组成的约束组合板不与边界框架连接，仅起到约束内嵌板不发生面外屈曲的作用，因此带环形阻尼器的装配式高强钢板剪力墙的抗剪承载力由内嵌板提供。则其抗剪承载力$V$由环形阻尼器的抗剪承载力${V}_{\text{s}}$和边界连接板带的抗剪承载力${V}_{\text{f}}$组成，计算公式如下：

环形阻尼器的抗剪承载力${V_{\text{s}}}$计算公式如下：

其中，${M_{\text{p}}}$为：

式中：$n$为环形阻尼器的列数；$R$、${w_{\text{r}}}$、${t}_{\text{r}}$分别为环形阻尼器半径、环形阻尼器宽度和内嵌板厚度，${w}_{{\rm{l}}}$为钢连接板带宽度，如图3所示。

边界连接板带的抗剪承载力${V}_{\text{f}}$计算公式如下：

式中：${M_{\text{t}}}$、${M}_{\text{b}}$分别为边界连接板带上部和下部抗弯承载力；${h_{\text{r}}}$为上、下边界连接板带净高。

4.2   公式验证

各模型抗剪承载力公式计算理论值与有限元计算模拟值如表4所示。从表4可以看出，带环形阻尼器的装配式高强钢板剪力墙抗剪承载力理论计算值与模拟值在比值在1.01~1.11，吻合程度较好，表明理论计算公式正确。

表  4  抗剪承载力对比

Table  4.  Comparison of shear capacities

模型	理论值/kN	模拟值/kN	理论值/模拟值
SPSW-RD-1	185.0	178.7	1.03
SPSW-RD-2	246.7	244.3	1.01
SPSW-RD-3	308.4	281.5	1.10
SPSW-RD-4	142.8	136.5	1.05
SPSW-RD-5	190.4	179.2	1.06
SPSW-RD-6	238.0	216.0	1.11

下载: 导出CSV 

| 显示表格

4.3   试验验证

选取理论值与模拟值误差较大的内嵌板10 mm厚的带环形阻尼器装配式钢板剪力墙进行试验验证。考虑到钢材采购的便利性，试件选取Q355B钢材，同时选取C30混凝土填充面外约束组合板。钢材和混凝土材料性能如表5所示，其中混凝土的强度指标是在与试件相同条件下养护28 d测试的。试验得到的滞回曲线和有限元模拟得到的滞回曲线及对比见图11，试件的破坏情况见图12。

表  5  试验材料性能

Table  5.  Test materials

10 mm内嵌板	屈服强度fy/MPa	极限强度fu/MPa	弹性模量Es/MPa	断裂伸长率/(%)
	381.9	510.2	2.06×105	23.4
C30混凝土	立方体抗压强度fcu/MPa	轴心抗压强度fc/MPa	轴心抗拉强度ft/MPa	弹性模量Ec/MPa
	42.18	28.21	2.42	3.31×104

下载: 导出CSV 

| 显示表格

图  11  有限元与试验滞回曲线验证

Figure  11.  Comparison of hysteretic curves between finite element analysis and test

下载: 全尺寸图片 幻灯片

图  12  有限元与试验破坏对比

Figure  12.  Comparison of failure between finite element analysis and test

下载: 全尺寸图片 幻灯片

从图11中看出，试验和有限元模型计算滞回曲线吻合良好。试验的滞回环稍小于有限元计算滞回环，这是因为试验试件加工制作时存在误差，外约束组合板与内嵌板不能完全贴合，滞回环没有有限元模型计算时饱满。

从图12中看出，有限元模型计算的破坏模式与试验的破坏模式一致。在水平力作用下，内嵌板环形阻尼器发生屈服破坏，平面外约束组合板和內填混凝土在整个加载过程中没有发生破坏。

10 mm厚内嵌板剪力墙的抗剪承载力公式计算理论值、有限元计算模拟值和试验值如表6所示。从表6可以看出，理论值和试验值与有限元模拟值相比分别为1.16和1.15，误差相对较大。但是带环形阻尼器的装配式高强钢板剪力墙抗剪承载力理论计算值与试验值相比为1.01，误差很小，这进一步说明理论公式正确且计算精确度高。

表  6  试验与有限元抗剪承载力对比

Table  6.  Comparison of shear capacities between test and finite element analysis

模型参数	理论值/kN	试验值/kN	模拟值/kN
10 mm/Q355B	256	253	221
比值	理论/试验	理论/模拟	试验/模拟
	1.01	1.16	1.15

下载: 导出CSV 

| 显示表格

5   结论

针对带环形阻尼器的装配式高强钢板剪力墙进行抗震性能研究，得出以下结论：

(1)带环形阻尼器的装配式高强钢板剪力墙抗震性能良好。该装配式高强钢板剪力墙滞回环饱满，等效粘性阻尼系数最高值在0.27~0.51，位移延性系数在5.7~8.7，耗能性能和延性良好。

(2)带环形阻尼器的装配式高强钢板剪力墙在水平荷载作用下，内嵌板的环形阻尼器和边界连接板带屈服破坏，面外约束组合板、高强螺栓、工字钢梁没有破坏，在震后可快速更换内嵌板实现快速修复使用的目的。

(3)随着内嵌板高厚比从208降低到125、钢材牌号从Q355B提高到Q460C，剪力墙等效刚度退化变缓；随着剪力墙内嵌板高厚比从208降低到125，位移延性系数降低。采用高强钢材Q460C的剪力墙耗能性能优于普通钢材Q355B的，内嵌板高厚比为208时钢板剪力墙耗能性能最好。

(4)剪力墙内嵌板高厚比从208降低到125，屈服荷载增大，采用Q460C钢材的剪力墙极限荷载先减小后增大，破坏荷载减小，采用Q355B钢材的剪力墙极限荷载和破坏荷载增大；钢材牌号从Q355B提高到Q460C，屈服荷载、极限承载力和破坏荷载增大。

(5)提出了带环形阻尼器的装配式高强钢板剪力墙的抗剪承载力的计算公式。该公式简单、概念明确，公式的计算结果与有限元模拟以及试验结果的吻合良好。