大量研究表明，局部场地条件对地震动有显著影响，通常体现为软硬程度不同的场地对地震动产生显著差别的与频率相关的放大效应^[1-6]。国内外抗震设计规范中均引入了场地分类的概念，并制定相应的划分标准，工程师需要根据场地类别确定设计地震动参数，从而进行抗震设计。因此合理的场地类别划分标准至关重要，通常采用能够表征场地效应的特征参数作为划分指标。各国规范采用的场地特征参数有所不同，具有代表性的是美国、日本和中国的场地分类标准，美国NEHRP规范^[7]中以地表30 m以内平均剪切波速V_S30作为划分指标；日本主要以场地自振周期T_S作为划分指标^[8]；中国《建筑抗震设计规范》(GB 50011−2010) ^[9]中采用双参数进行分类，综合考虑了20 m内等效剪切波速V_SE和覆盖层厚度的影响。

使用何种场地特征参数划分场地类别，一直存在争议^[10-12]。一些研究者认为V_S30是相对较为合适的参数，为反应谱在基岩场地与软土场地之间提供了平滑的过渡^[13-14]，也有一些研究者认为V_S30作为场地特征参数存在一定局限性，仅以浅层30 m的剪切波速很难体现复杂的场地效应^[15-19]；ZHAO^[20]则认为，从理论和实际两个方面，T_S都是合适的场地参数。齐文浩等^[21]认为中国规范采用V_SE和覆盖层厚度双指标的分类方案虽然经济合理，但仅适用于剪切波速随深度递增的场地，并提出使用场地基本周期估算V_SE代替原有计算公式的建议。陈国兴等^[22]提出在中国规范中加入场地基本周期指标，并将等效剪切波速的计算深度提高至30 m，基于30 m等效剪切波速、覆盖层厚度和场地基本周期三个指标进行场地分类。

然而，上述标准无论使用何种指标，都应具备体现场地放大差异性和集中性的定义功能，也就是确保不同场地类别间表现的地震动放大有所差异，同一场地类别内表现的地震动放大变异性较小。目前，关于中、日、美场地分类标准的对比研究已开展较多，例如，薄景山等^[23]对国内外抗震规范中场地分类研究历程进行了梳理和总结，定性地讨论了中、日、美抗震规范中场地分类标准的差异；周健等^[24]通过建立中美抗震规范中场地类别的对应关系讨论了中美场地分类标准的差异。但基于实际观测记录的检验与评价却鲜有开展。日本KiK-net台网台站密集，记录了大量高质量强震动数据，且提供了详实的台站场地资料，为计算不同的场地特征参数(如T_S、V_S30等)以及求解实际地震动放大因子提供了便利。

本文依据KiK-net台网提供的场地资料，将其台站所在场地分别以V_SE及覆盖层厚度、T_S、V_S30为场地分类指标，即按照中国《建筑抗震设计规范》(GB 50011−2010)、美国NEHRP规范和日本道路协会规范进行场地分类。基于地震动预测模型的残差分析方法计算真实的场地放大因子，分析同一类别下场地放大因子的离散程度以及其在不同场地类别间的差异程度，评价三个标准分类方案的实用性，为规范的完善和地震动预测模型的优化提供科学依据。

1   场地放大因子计算方法

利用强震动观测记录可计算得到场地真实的放大因子。地震动预测模型(GMM)通常综合考虑了震源、路径和场地效应对地震动的影响，给出较为可靠的地震动中位预测值。利用适用于目标场址的GMM，通过对实际强震动观测数据进行残差分析可分离震源、路径和场地的影响，对场地放大因子进行近似估计。本文研究选择适用于日本地区的ZHAO2006地震动预测模型^[20]计算预测值：

式中：Y_i,j为第i个地震事件中在第j个台站记录到的地震动强度指标观测值(如PGA、PGV、不同周期的反应谱值等)；f(M_wi, x_i,j, site)为地震动强度指标的中位预测值，M_w为矩震级，x为震源距；h为震源深度；h_c为深度常数，通常取15 km；当h≥h_c时δ_h=1，当h<h_c时δ_h=0；F_R为逆断层补偿项；S_I为俯冲带板间地震补偿项；S_S为俯冲带板内地震补偿项；S_SL为俯冲带板内地震的距离补偿项系数；C_site为场地项；$\phi$为事件内残差；η为事件间残差；a、b、c、d、e为回归系数。

将ln(Y_i,j)校正至基岩场地(HR)条件下，计算事件内残差：

式中：$\phi$(HR)_i,j代表第i个地震事件中第j个台站记录校正至基岩场地条件下的事件内残差；f(M_wi, x_i,j, HR)为硬基岩场地条件下地震动强度指标的中位预测值；η_i为第i个地震事件的事件间残差。

通过计算每个场地所有记录校正到基岩的事件内残差的均值，可获得不同的地震动强度指标近似的场地放大因子：

式中：A_j为第j个台站的近似平均场地放大函数；N为第j个台站收集到的强震动记录总数。

2   强震动数据集

选取日本KiK-net台网提供的2012年−2018年观测到的强震动记录，按照以下条件对记录进行挑选：

1) 所选记录的地震事件能够在Global CMT上查询到震源机制解，共有265个；

2) 震源距300 km以内的台站观测记录；

3) 能够确定场地类别的台站观测记录；

4) 所选台站至少在5次地震中获得了记录，以获得可靠的台站场地放大因子。

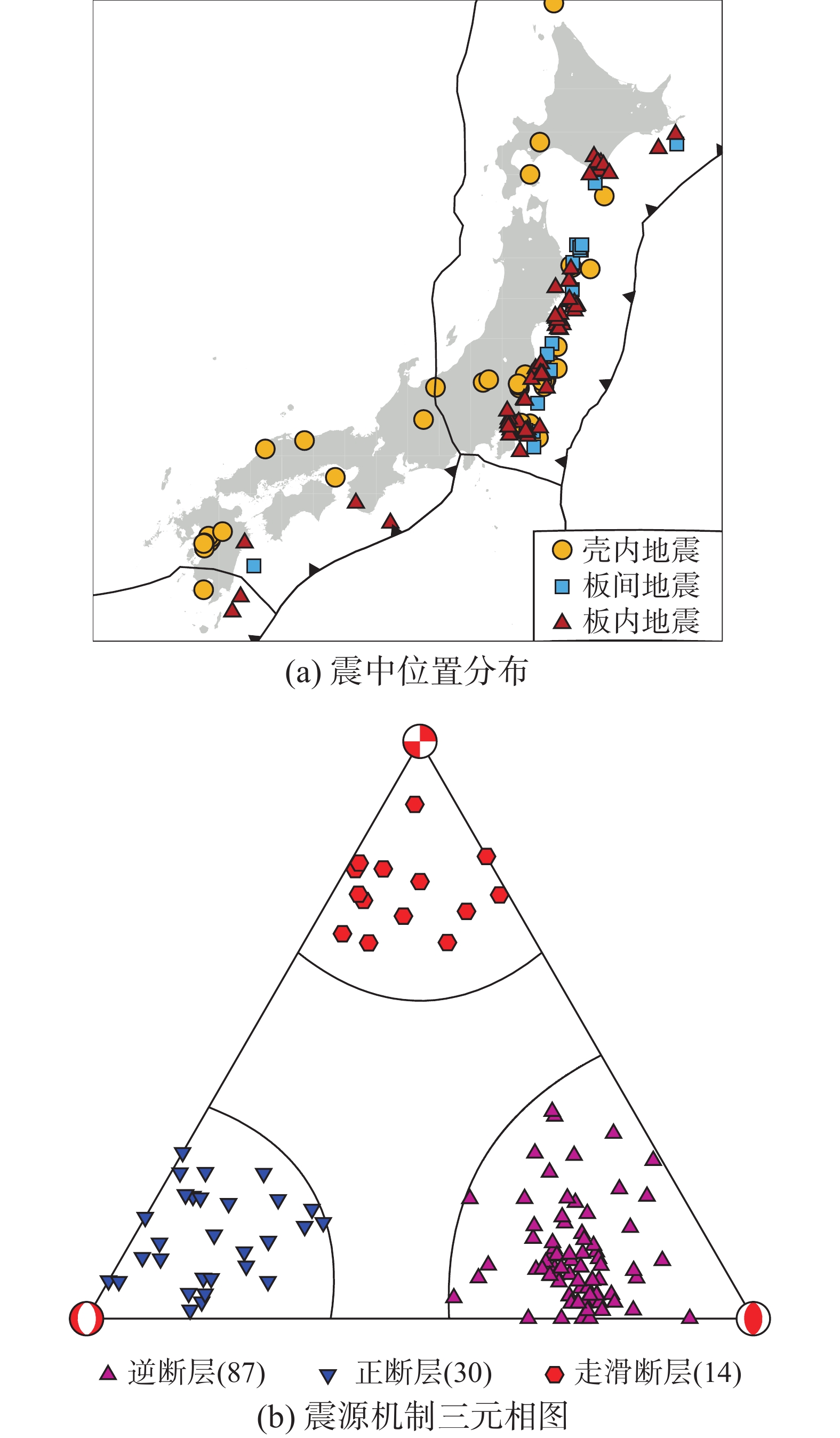
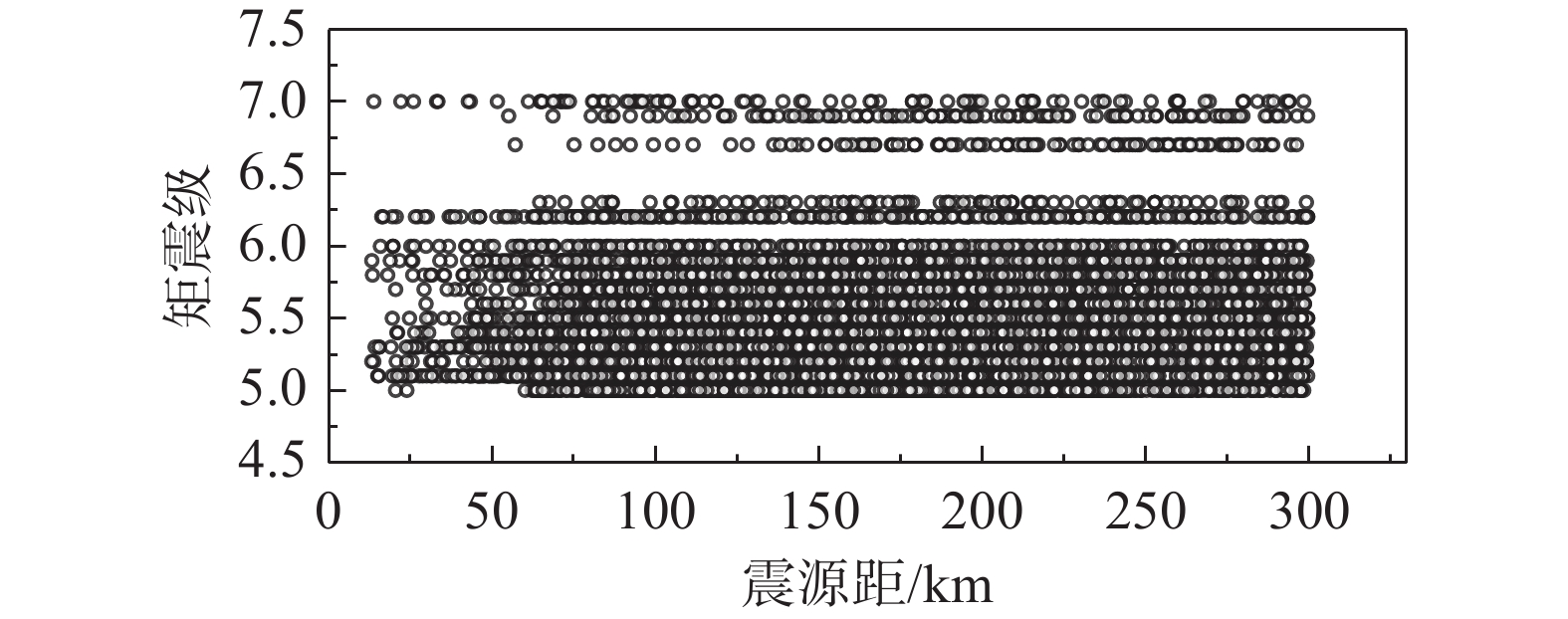
条件1)和2)是考虑本文采用的ZHAO2006地震动预测模型需要输入地震事件的震源机制类型，以及该模型仅适用于震源距300 km以内的地震动参数预测。由于部分KiK-net台站是无法确定确切的覆盖层厚度的，进而无法给出中国规范定义的场地类别，因此这类台站无法用于本文研究分析，应按条件3)进行排除。按照上述条件，选取了424个台站在131个地震中获取的10 731组地表观测记录用于研究分析。图1给出了这些记录的矩震级与震源距的对应分布关系，矩震级范围为5.0~7.0。

图  1  本文所选强震动数据集的震源距与矩震级对应分布

Figure  1.  Magnitude-source distance distribution of strong motion data set selected

下载: 全尺寸图片 幻灯片

应用FROHLICH^[25]提出的三元相图方法将震源机制进行分类。对震源机制进行分类的常规做法是根据断层面滑移方向分类，当断层面滑移方向是以水平分量居多时，划分为走滑断层；当断层面滑移方向以垂直分量居多时，划分为正断层或逆断层。但由于矩张量的对称性，存在断层面与辅助面难以识别的问题，因此造成了在断层类型分类时的不确切性。FROHLICH^[25]三元相图方法则克服了这一问题，根据判断震源机制中P、B、T轴中最大倾角的轴，判断断层属于哪种错动方式。当最大倾角轴为P轴时，表示在水平方向主要受到T轴，也就是张应力的作用，划分为正断层；当最大倾角轴为T轴时，表示在水平方向主要受到P轴，也就是压应力作用，划分为逆断层；当最大倾角轴为B轴时，表示在水平方向同时受P、T轴，也就是张应力和压应力共同作用，划分为走滑断层。根据FROHLICH^[25]的研究，T轴倾角δ_T>50°划分为逆断层、B轴倾角δ_B>60°时划分为走滑断层、P轴倾角δ_P>60°划分为正断层。根据应力轴倾角的性质，应力轴倾角的正弦值满足以下条件：

因此地震事件的P、T、B轴倾角数据可以以几何方式在三元相图上标识(如图2(b)所示)，清楚地将断层的错动方式划分为正断层地震、逆断层地震、走滑断层地震。本次研究131个地震事件按震源机制划分为：逆断层地震87个、正断层地震30个、走滑断层地震14个。

图  2  本文所选地震事件震中位置和震源机制三元相图

Figure  2.  The epicenter locations and triangle diagram displaying focal mechanism of selected earthquake events

下载: 全尺寸图片 幻灯片

由于ZHAO2006模型中考虑的地震构造类别对地震动参数估计的影响，在本文中使用ZHAO等^[26]提出的地震构造类别划分方法，依据震源位置与俯冲带界面的相对位置关系以及震源机制确定地震的构造类别，俯冲带界面位置参照Slab1.0模型^[27]。最终确认浅层壳内地震47个、俯冲带板间地震21个、俯冲带板内地震63个，震中位置分布如图2(a)所示。

由于数据量较多，考虑节约时间成本并未对强震动记录进行逐条人工处理，而是选用统一的频带0.1 Hz~50 Hz进行Butterworth非因果滤波。滤波完成后采用几何平均的方式计算了各记录水平向的PGA及不同周期的加速度反应谱值。

3   依据中、日、美三国规范的场地分类

中、日、美三国规范对场地类别的定义以及所采用的分类指标是不同的。中国《建筑抗震设计规范》(GB 50011−2010)采用覆盖层厚度和等效剪切波速两个指标将场地定义为I₀、I₁、II、III和IV这5类；日本道路协会规范依据场地自振周期T_S将场地定义SCI、SCII、SCIII和SCIV 4类，分别代表基岩、坚硬土、中硬土和软土；美国NEHRP规范根据V_S30将场地定义为A、B、C、D和E 5类。为了方便表述，下文分别使用中国分类标准、美国分类标准和日本分类标准代表以不同场地特征参数为依据的场地划分标准。

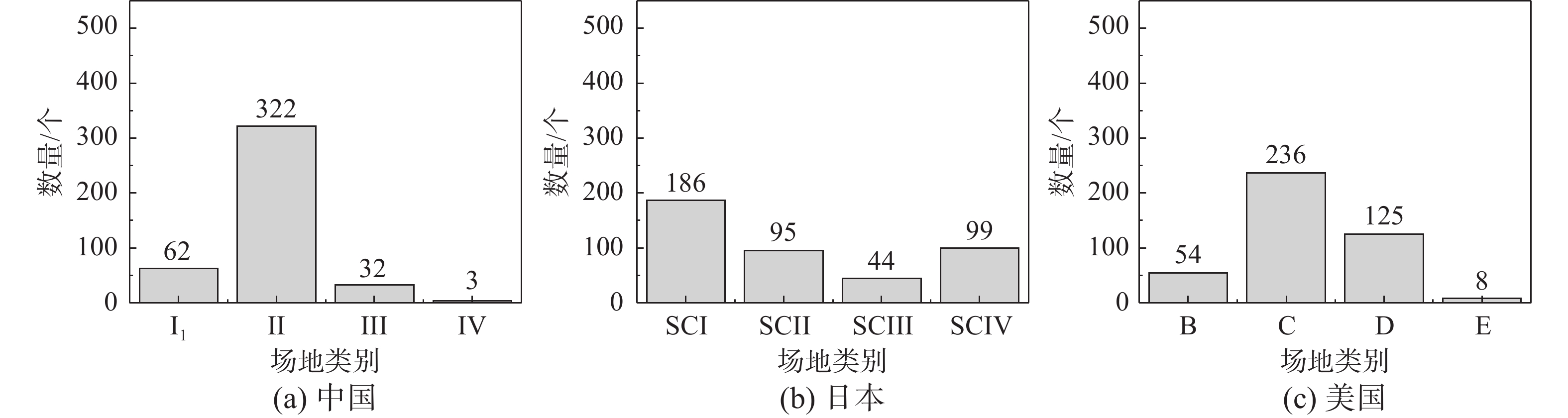
如图3(a)所示采用中国场地分类标准对本文所选424个台站进行场地分类，得到以下结果：62个台站被划分为I₁类场地，322个台站被划分为II类场地，32个台站被划分为III类场地，仅3个台站被划分为IV类场地。其中位于II类场地的台站数量最多，占总数的75.94%，超过了位于其他四个类别场地的台站数量总和。如图3(b)所示根据日本场地分类标准对这些台站划分场地类别，分别有186个、95个、44个和99个台站被划分为SC I、SC II、SC III和SC IV类场地。四个场地类别对应的台站数量分布相对较为均匀，位于SC I类场地的台站最多，位于SC III类场地的台站最少。如图3(c)所示根据美国分类标准对这些台站进行场地分类，分别有54个、236个、125个和8个台站被划分为B、C、D、E类场地。其中，C类场地数量最多，占总数的55.66%，D类次之，E类最少。按照这三国标准划分完的场地类别对应台站空间分布如图4所示。这里需要说明的是，由于中国分类标准的I₀类和美国分类标准的A类场地较为坚硬，相当于硬基岩，规范中不考虑场地放大影响，因此这里不作分析研究，上述分类结果中未包含这两类场地。

图  3  按照中国、日本、美国规范定义划分的场地类别对应台站数量(Kik-net台站)

Figure  3.  The number of station associated with different site classes defined by seismic codes of China, Japan and U.S.A (KiK-net stations)

下载: 全尺寸图片 幻灯片

图  4  按照中国、日本、美国规范定义划分的场地类别对应台站空间分布

Figure  4.  Spatial distribution of stations classified according to seismic codes of China, Japan and U.S.A

下载: 全尺寸图片 幻灯片

4   残差分析

ABRAHAMSON和YOUNGS^[28]随机效应模型将观测值与预测值之间的总残差分为两部分：事件内残差$\phi$和事件间残差η。事件内残差$\phi$代表了场地效应和地震波传播路径的不确定性，以及其他未被模拟的参数带来的随机误差；事件间残差η代表了震源效应的不确定性，具体定义如下：

式中：f(M_wi, x_i,j, site)为地震动强度指标的中位预测值；σ表示观测值与预测值之间的残差。研究表明地震动在震源距80 km以内时的中位值较为相近，受非弹性衰减的差异性影响较小^[29-30]；因此可将震源距80 km以内台站的总残差平均值近似代表事件间残差^[31-32]，再由式(7)可计算事件内残差。为了检验ZHAO2006模型给出的预测值与实际观测值的偏差情况，验证模型的可靠性和数据集的合理性，图5给出了预测PGA和SA(T=0.1 s、0.3 s、0.5 s、1 s、3 s)的事件内残差相对于震源距的变化情况。

图  5  基于ZHAO^[20]预测模型计算的PGA和SA事件内残差随震源距变化情况 (带有误差棒的圆点代表不同距离段的事件内残差均值及一倍标准差；实线代表路径修正函数)

Figure  5.  PGA and SA within-event residuals against hypo-central distance calculated based on ZHAO2^[20] ground motion model (circles with bar indicate the mean within one standard deviation of distance-binned within-event residuals; Solid lines indicate the path-corrected function)

下载: 全尺寸图片 幻灯片

从图5中可见，PGA和SA(T=0.1 s、0.3 s、0.5 s)的事件内残差值随震源距增大而增大，表明事件内残差受路径效应的影响较为显著。由此可见，由式(5)计算得到的场地平均放大因子还包含有路径效应的影响。图中可见，对于SA(T=1 s、3 s)的事件内残差随震源距的变化较小，均值基本处于0附近；PGA和SA(T=0.1 s、0.3 s、0.5 s)的事件内残差均值在震源距小于80 km时，也几乎接近于0；当震源距大于80 km时才出现随震源增大的趋势，这验证了前文提及的在震源距大于80 km里时，地震动才会受区域非弹性衰减差异的显著影响。由于本文使用的数据集与ZHAO2006模型使用的数据集并不完全一致，震中和台站分布的区域是有差别的，震源至场地的传播路径整体上存在区域性差异，因而非弹性衰减的区域性差异将会对模型的预测产生一定的影响。

为了消除由路径效应引起的非弹性衰减造成的偏差，参考BOORE等^[30]的研究，在本文中使用距离修正项描述这种偏差：

式中：R为震源距；Δc₃、Δ$\phi$为回归系数；$\phi$ _path为路径修正函数。图5中实线为拟合得到的路径修正函数， 带有误差棒的圆点代表不同距离段的事件内残差均值及一倍标准差 。从图中可以看到，事件内残差均值与路径修正函数吻合程度良好。经过路径修正后的近似场地放大因子可表示为：

5   结果与讨论

按照式(9)计算了每个台站的近似场地放大因子，针对图4给出的不同标准定义的台站场地类别，统计分析同一类别下场地放大因子的均值和标准差，结果如图6所示。

图  6  PGA和SA(T=0.1 s、0.3 s、0.5 s、1 s、3 s)在中国、日本、美国场地分类标准下不同场地类别上的场地放大因子均值与标准差

Figure  6.  The mean and standard deviation of site amplification factors for PGA and SA (T=0.1 s, 0.3 s, 0.5 s, 1 s and 3 s), in each site class defined by seismic codes of China, Japan and U.S.A respectively

下载: 全尺寸图片 幻灯片

图6中箱线图代表了中、日、美三国标准下不同场地类别的场地放大因子在自然对数下的均值、标准差、最大值和最小值，箱线图右侧的直方图代表场地放大因子自然对数下的分布情况。从图中可见，除按中国的IV类场地和美国的E类场地外同一类场地的放大因子全部呈正态分布。由前文可知，这两个类别的台站数量过少，这里的分析结果仅具有参考价值，尤其是关于场地放大因子的标准差并不能完全体现该场地类别下场地放大的不确定性。从图6可见，按日本场地分类标准进行分类时，对于短周期地震动(PGA和SA(T=0.1 s))，不同类别间的场地放大因子差异不明显；对于其他周期段的SA(中长周期)，各类别的场地放大因子体现出了一定程度的差异性。因此，可以说明日本的场地分类标准难以体现对短周期地震动的场地放大差异性。主要原因是，采用T_S进行场地类别划分时，类别SC II、SC III、SC IV将分别集中体现谱周期在0.2 s~0.4 s、0.4 s~0.6 s和>0.6 s范围内SA的场地放大程度，潜在的对PGA和SA(T=0.1 s)的场地放大不考虑表征，场地放大因子不仅没有差异性，其幅值也都较小(图6可见都小于1)。

按中国和美国的分类标准划分场地时，对于PGA和各个周期段的SA，不同的场地类别对场地放大的差异性实现了较好的体现，并且场地放大因子随场地变软逐渐增大。中国的I₁、II和III类的场地放大因子均值分别与日本的SC I、SC II和SC III类及美国的B、C和D类较为接近；对于SA(T=3 s)，IV场地的场地放大因子自然对数下的均值接近2.0，要高于SC IV和E类。我国规范采用双指标定义场地类别，要求IV场地的覆盖层厚度须大于80 m。根据实际工程经验，这类场地基本位于滨海、河湖沿岸，覆盖土层较为软弱，对长周期地震动的放大影响较为突出。

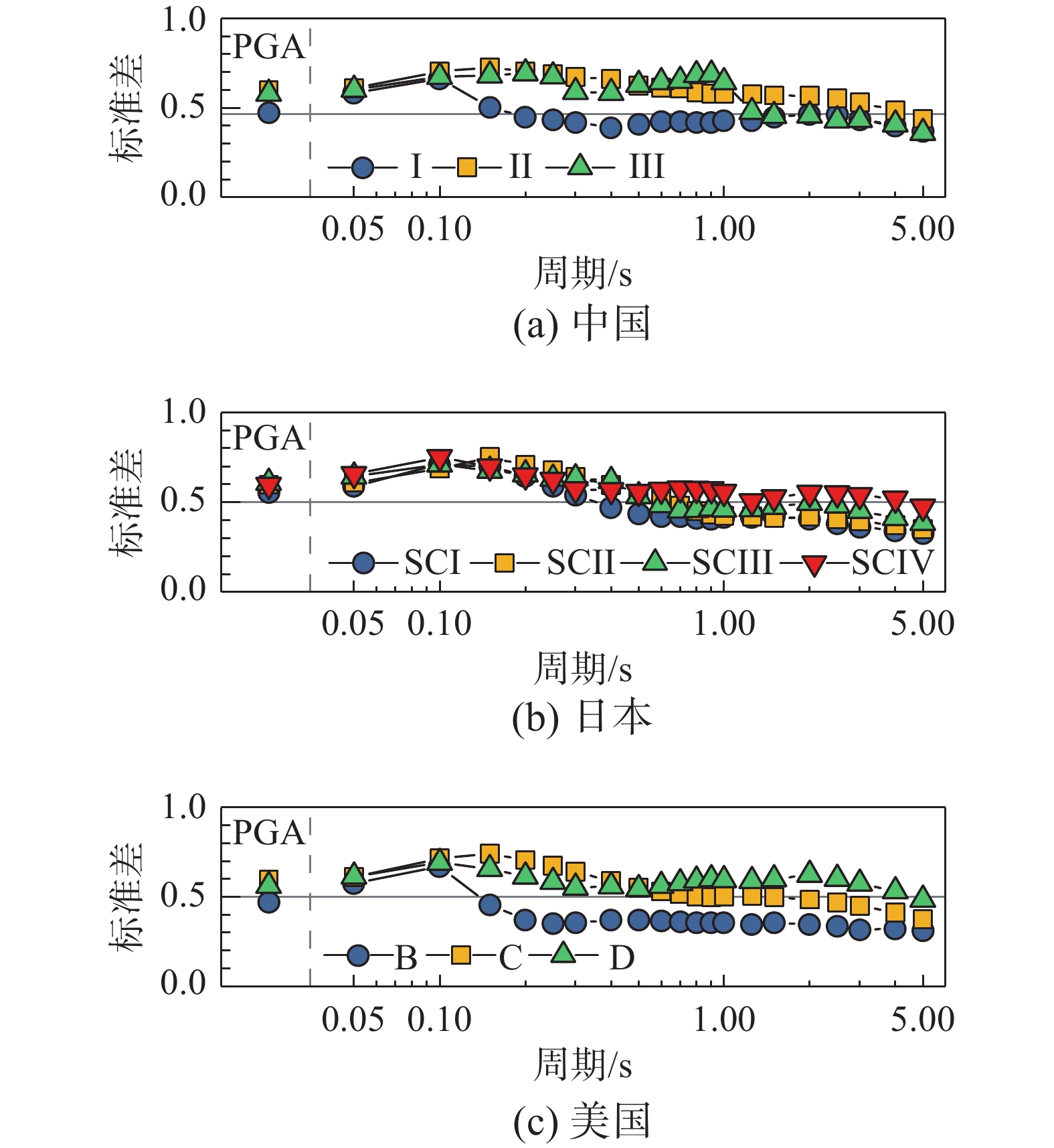
上文调查了各场地类别对地震动放大的差异性表现，接下来调查其集中性表现。图7展示了PGA和0.05 s~5 s内的SA在不同分类标准下不同场地类别的场地放大因子标准差，反映了相同场地类别内平均场地放大因子的离散程度。标准差越小，说明这一类别中场地的放大效应越集中，根据场地类别确定设计地震动时的不确定性越小。反之，标准差如果较大，说明各场地类别表征的场地放大影响存在互相重叠，该分类标准并不优越。同时，合理的分类标准还要尽可能地体现不同场地类别的标准差值相接近。需要说明的是，由于IV类和E类场地的台站数量较少，计算得到的标准差并不能体现该类别下场地放大因子真实的离散程度，这里不开展分析。

图  7  在不同场地分类标准下PGA和不同周期的SA在不同场地类别下的场地放大因子标准差

Figure  7.  Standard deviation of site amplification factors in each site class defined by seismic codes of China, Japan and U.S.A respectively for PGA and different spectral period SA

下载: 全尺寸图片 幻灯片

从图7中可见，按中国分类标准进行分类时，I、II和III类场地对于PGA和SA(≤0.1 s和≥1.25 s)的场地放大因子离散程度较为相近；对于SA(0.15 s~1 s)，标准差差异明显，III类场地离散程度最大，II类次之，I类最小。按日本标准进行分类时，PGA和SA(0.05 s~0.3 s)在不同场地类别下的场地放大因子标准差尽管都大于0.5，但都基本接近；当周期范围为0.4 s~5 s时，不同场地类别下的标准差存在显著差异，尤其是SC IV类在T>0.6 s时明显大于其他三类。这是由于SC IV类被定义为T_S>0.6 s的场地，较其他三类，T_S的范围较为宽广，所涵盖场地的放大因子也会较为离散。图中还可见，SC I类的标准差在任何谱周期点都是最小的，中国分类标准下的I₁类和美国分类标准下的B类也有类似现象，主要原因是这三个类别的场地较为坚硬，场地放大不明显，幅值相对较小(图6中)，因而离散性也较小。

按美国标准进行分类时，B类场地只有在T=0.05 s和0.1 s时标准差是大于0.5的；当T≥0.2 s时所有周期点的标准差都在0.3~0.4范围内，较中国分类标准下的I₁类和日本分类标准下的SC I类要小。原因是B类定义为V_S30>760 m/s，较I₁类(500 m/s<V_SE≤800 m/s)和日本分类标准下的SC I类(T_S<0.2 s)场地更为坚硬，场地放大效应相对较弱。在T<0.5 s的短周期段，D类场地的离散程度优于C类场地，而当T>0.5 s时，则相反。

从整体上，三种分类标准的各场地类别在SA(T<0.1 s)时标准差值相近，都有随周期增大的趋势，在SA(T=0.1 s)标准差达到最大，在SA(T>0.1 s)后标准差随周期增大而减小。日本标准定义的各类别间场地放大因子的标准差差异最小，美国的最大，中国则介于两者之间；除了美国标准定义的B类场地和和中国标准定义的I类场地外，日本标准定义的各类别场地在PGA和SA的中短周期段(T<2 s)的标准差都是最小的。说明整体上日本规范以T_S作为场地分类指标可以较好地对场地类别进行区分，能够相对较好地实现相同类别内场地放大的集中性。不过，由图7可见，中国的分类标准对于同类别内长周期(T>2 s)地震动的场地放大效应集中性表征是最优越的，无论是标准差值还是各类别间的标准差差异，相较于日本和美国标准都是较小的。

值得注意的是，中国III类场地对于SA(0.6 s~1.0 s)场地放大因子标准差明显大于其他三类，在T=0.9 s时差异最大。图8(a)给出了III类场地台站针对SA(在T=0.9 s时)的场地放大因子分布，图中可见，其分布离散性较大，主要因为KYTH05、FKIH05、AOMH16、AICH09和KSRH03这5个台站场地的放大因子出现较大或较小，与III类场的均值相差超过1倍标准差。图8(b)针对这5个台站绘制了场地放大因子随周期变化曲线，可见KYTH05、FKIH05、AOMH16和AICH09台站场地放大因子在任意周期点均大于III类场地的平均值，尤其在0.6 s~1.25 s中长周期段，放大因子远大于III类场地的均值；同时，KSRH03台站在此周期段内是远小于均值的。

图  8  III类场地放大因子分布

Figure  8.  Site amplification factors of site class III

下载: 全尺寸图片 幻灯片

为合理解释上述现象，本文针对场地放大非常显著的KYTH05和FKIH05台站，以及放大不明显的KSRH03台站，计算其理论传递函数，如图9所示。图中还给出了这三个台站所在场地钻孔剪切波速剖面，可见KYTH05和FKIH05台站浅层介质波速较小、至深层时都存在阶跃式变化，上、下两层介质存在较大阻抗比；理论上，这种介质波速分布将会引起场地在基本周期附近产生较大的放大效应；相对应地，由图8(b)可见KYTH05和FKIH05台站在0.7 s~1.0 s范围内场地放大十分显著。图9(b)显示的这两个台站的理论传递函数可判断场地卓越周期都在0.9 s附近，且放大幅值较大；理论放大与本文计算的实际观测场地放大较为一致。KSRH03台站场地存在波速大于600 m/s的岩石夹层，理论传递函数也与实际观测场地放大基本一致；场地放大主要集中在短周期段，对于中长周期几乎没有体现放大。值得注意的是，三个台站的实际观测场地放大仅在短周期段与理论传递函数相一致，而在长周期段要显著偏大。这是由于长周期段的场地放大主要体现深层介质的地震动力反应，本文在计算理论传递函数时只是针对浅层介质(即100 m以内，图9(a)所示)，其控制的是短周期段的场地地震反应。

图  9  典型台站的场地特征

Figure  9.  Site characteristic of typical stations

下载: 全尺寸图片 幻灯片

6   结论

针对中、日、美三国抗震规范不同的场地分类标准，利用日本KiK-net台网的10731组强震动记录，基于地震动预测残差分析方法计算台站的真实场地放大因子，评价不同分类标准是否可以合理体现同类别内场地放大的集中性以及不同类别间场地放大的差异性。主要结论如下：

(1) 在PGA和SA的短周期段(T<0.1 s)，以T_S作为分类指标的日本规范，不同类别场地间放大因子差异不明显，没有很好体现不同类别间场地放大效应的差异性。以V_SE及覆盖层厚度双指标的中国规范和以V_S30为指标的美国规范则表现较为良好。

(2) 以场地放大的均值衡量，中国的I₁、II和III类分别与日本的SC I、SC II和SC III类及美国的B、C和D类相对应；中国的IV场地对于长周期地震动(如，T=3.0 s)的放大效应要高于日本的SC IV和美国的E类。

(3) 日本规范在整体上体现相同场地类别内场地放大的集中性方面表现最好；对于长周期(T>2 s)地震动，无论是相同场地类别内场地放大的集中性，还是不同场地类别间放大的差异性，我国规范表现最优越。中国III类场地对中长周期地震动的放大体现出较大离散性，分类标准合理性还需要进一步检验分析。