在铁路道岔设计过程中，首先需要确定道岔的平面线形，而在设计中通常对于道岔尖轨在密贴状态下的线形会进行精确设计，但对于尖轨在斥离状态下的线形往往进行较为简化的处理。目前普遍采用的方法是：在设计确定尖轨在密贴状态下的线形后，将密贴状态下尖轨的可动段以尖轨跟端固定端为圆心进行旋转，旋转至尖轨在第一牵引点位置的位移与设计动程一致，旋转后的线形即作为尖轨在斥离状态下的线形^[1-5]。采用这种方法得到的尖轨在斥离状态下的线形往往与实际情况存在较大偏差。

然而，尖轨在斥离状态下的线形较为重要。对于采用内锁闭方式的道岔而言，需要根据尖轨在斥离状态下的线形来计算确定拉、连杆的长度，对于提速及高速道岔而言，需要根据尖轨在斥离状态下的线形来确定防跳卡铁等零部件的位置。另外，斥离状态的线形决定了尖轨与基本轨间最小轮缘槽宽度，进而会对牵引动程的合理设计产生直接影响。因此，在设计过程中有必要尽可能准确地确定尖轨在斥离状态下的线形。目前所采用的这种简化处理方法存在较大弊端，会造成相关零部件的设计以及牵引动程的设计出现相当的偏差，对道岔的制造、铺设和使用造成显著的不利影响。

目前中国国有铁路铺设60 kg/m钢轨12号道岔约6.7万组，铺设量巨大，主要产品图号为SC330和专线4249，设计年代分别为2001年和1999年，SC330适用于时速≤120 km/h的铁路线路，专线4249适用于时速≤160 km/h的铁路线路，侧向通过速度均为50 km/h^[6-9]。基于现场的使用反馈统计，目前60 kg/m钢轨12号道岔主要用于客货共线I级铁路正线、到发线道岔，重载铁路到发线道岔及其他站线道岔，使用过程中暴露出的问题较为突出，主要表现在道岔几何尺寸保持能力差、部件使用寿命短、养护维修工作量大等方面^[10-14]。提高60 kg/m钢轨12号道岔使用性能成为了铁路工务部门的迫切需求。基于此，国铁集团组织铁科院针对主型60 kg/m钢轨12号道岔进行改进设计^[15-17]。

基于60 kg/m钢轨12号单开道岔的优化需求，考虑既有道岔转换设计方法的不足，本文拟对60 kg/m钢轨12号单开道岔的转换设计进行优化研究，提出道岔尖轨斥离线形的仿真计算方法，并对牵引点动程、防跳卡铁位置等关键设计参数进行优化设计，最后通过实际转换试验对设计方法和参数方案的合理性进行验证。

1   道岔尖轨斥离状态线形计算方法

新型60 kg/m钢轨12号单开道岔沿用专线4249道岔平面尺寸，全长37 800 mm、前长16 592 mm、后长21 208 mm。考虑简化道岔侧股轨距变化，导曲线采取R350 m单圆曲线，道岔Q值为1975 mm，在尖轨尖端轨距加宽为1440 mm，直股部分，在直尖轨轨头刨切起点处，结束由曲基本轨偏斜带来的构造轨距加宽，其后轨距均为1435 mm，侧股轨距保持1440 mm设计，在道岔护轨前过渡回1435 mm。导曲线相离值按照36 mm设计，曲线尖轨前部直线段为5049 mm，半切点宽度为70.6 mm。

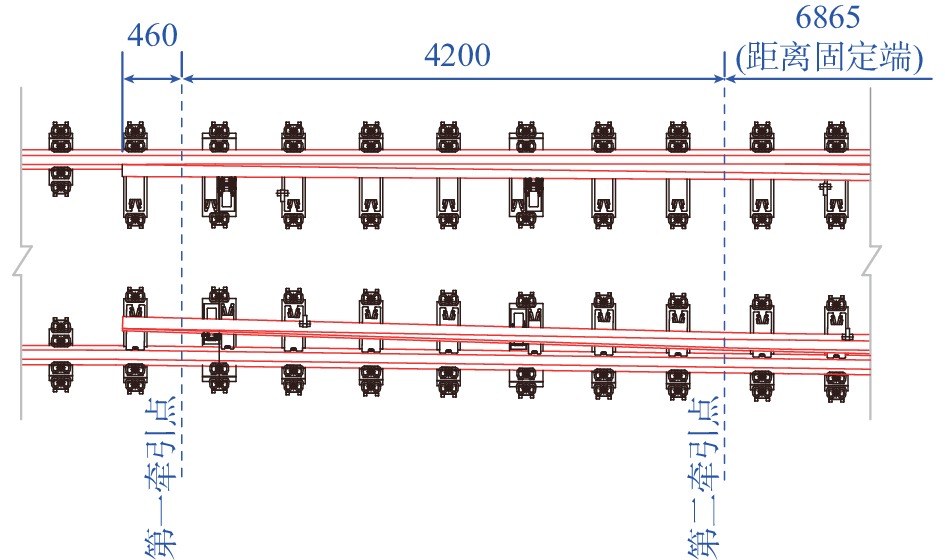
道岔转换采用联动内锁闭和分动外锁闭两种方式设计，转辙器设置2个牵引点，第一牵引点距离尖轨尖轨尖端460 mm，第二牵引点距离第一牵引点4200 mm，第二牵引点距离尖轨固定端6865 mm，如图1所示。

图  1  外锁闭设计方案　/mm

Figure  1.  Design scheme for separate external locking

下载: 全尺寸图片 幻灯片

相对于既有的12号道岔而言，由于对尖轨长度、牵引点位置等均进行了优化，既有的牵引点动程设计已不适应。为了确保最小轮缘槽宽度满足要求，并最大程度地降低转换力，需要对牵引点动程进行优化设计。另外，防跳卡铁位置也需要进行匹配设计。

首先，基于有限元理论建立道岔转换计算模型，得到尖轨斥离状态下的线形，为以上参数的科学设计提供准确依据和手段。

采用实体单元对尖轨进行模拟，材料密度取为7850 kg/m³，弹性模量取为2.1×10¹¹ Pa，泊松比取为0.3^[18-20]。充分考虑尖轨变截面的影响，自尖轨尖端至尖轨全断面分别导入尖轨的各个特征截面，分别为尖轨顶宽0 mm断面、5 mm断面、20 mm断面、50 mm断面、全断面，各特征截面之间采用线性插值过渡，如图2所示。

图  2  特征截面过渡

Figure  2.  Transition between characteristic sections

下载: 全尺寸图片 幻灯片

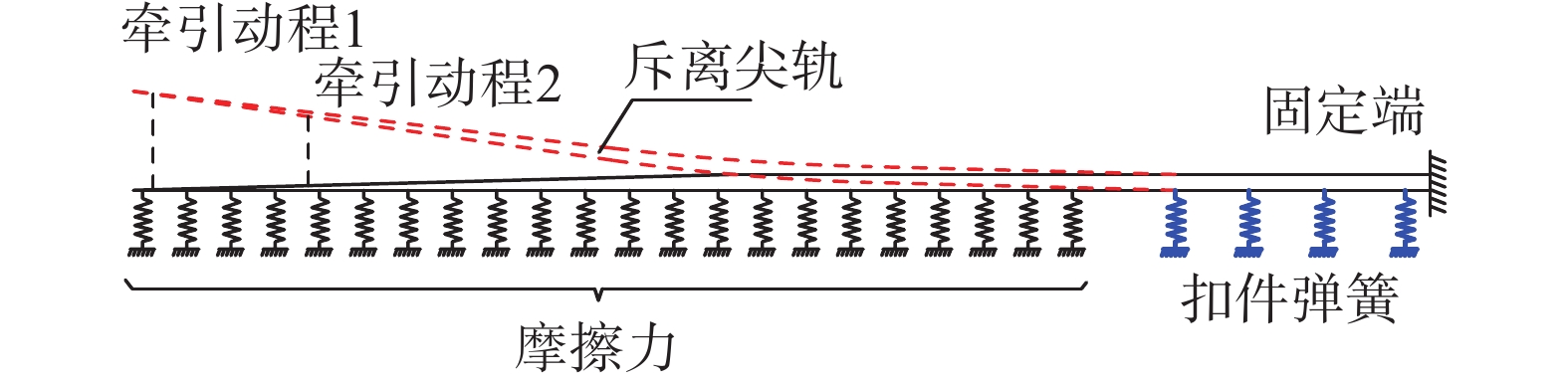
划分网格过程中，为了方便约束条件及荷载的施加，采用扫略网格划分方法沿纵向均匀划分，并在牵引点断面、扣件位置断面设置断面节点。对跟端断面节点施加固定约束。采用弹簧单元对尖轨后端扣件系统及尖轨转换过程中所受的摩擦力进行模拟。扣件系统横向刚度取值如图3所示，在扣件系统位置断面的轨底节点上施加均布弹簧，节点弹簧刚度根据该断面位置轨底节点数量换算得到。摩擦力施加均布荷载，尖轨重量取为70 kg/m，摩擦系数取为0.25，则施加摩擦力为175 N/m，通过在尖轨轨底节点施加均布常阻力弹簧实现，弹簧阻力大小根据节点数量换算得到。

尖轨斥离状态时，在各个牵引点位置断面的尖轨工作边侧轨腰节点上施加与预设动程相同的横向位移荷载，道岔转换力学模型如图4所示。

图  3  扣件系统横向刚度

Figure  3.  Transverse stiffness of the fastener system

下载: 全尺寸图片 幻灯片

图  4  道岔转换力学模型

Figure  4.  Mechanical model for turnout switching

下载: 全尺寸图片 幻灯片

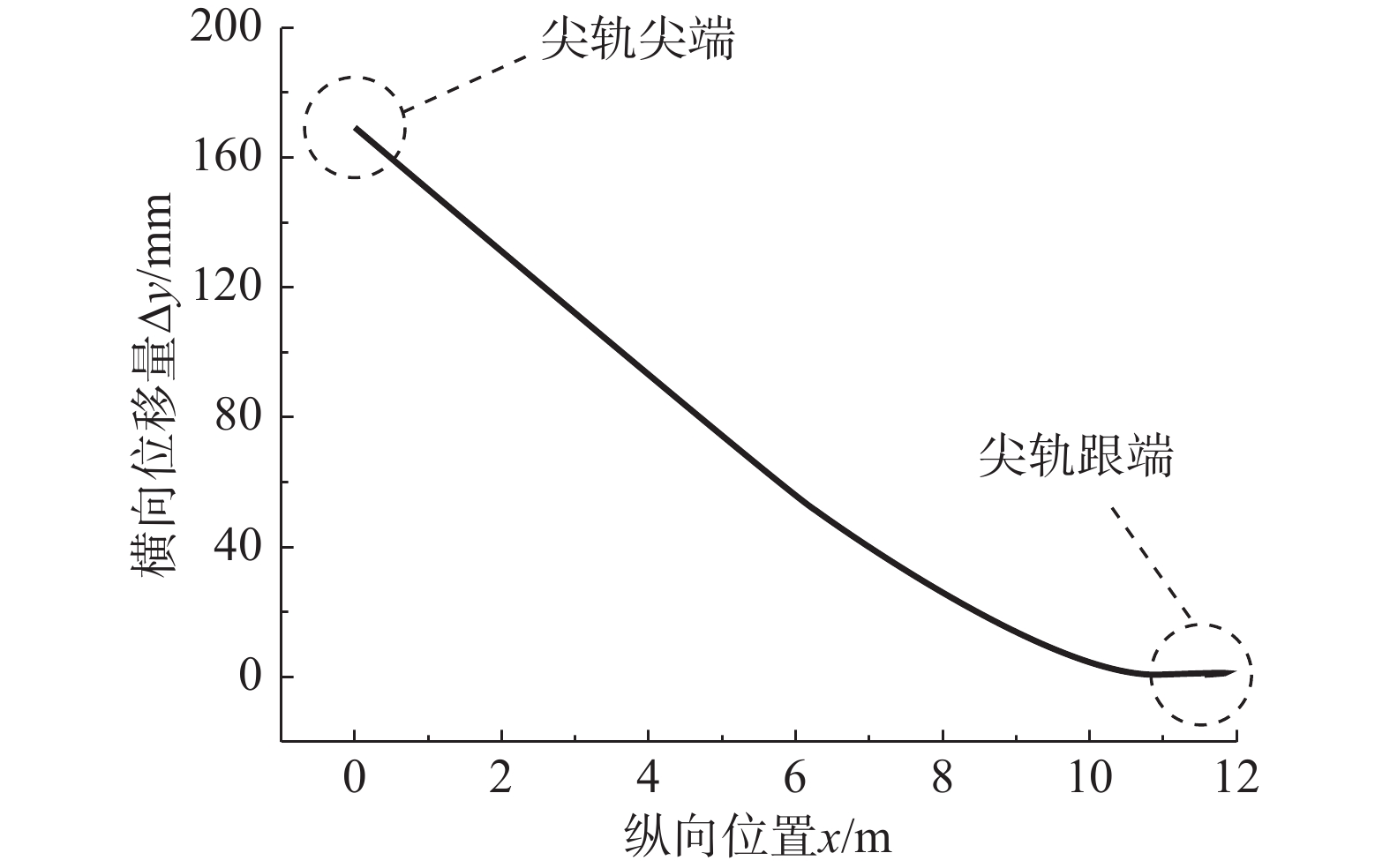
通过以上计算，可得到尖轨斥离状态下的横向位移分布曲线Δy(x)，如图5所示。其中x为沿尖轨纵向位置坐标，Δy为不同位置尖轨的横向位移量。为了便于后续分析，将其进行离散化处理。将尖轨沿纵向等分为n段，则共有n+1个节点，各节点位置坐标分别为x₁、 x₂、 x₃、···、x_n+1，则各节点对应的横向位移量分别为Δy(x₁)、Δy(x₂)、Δy(x₃)、···、Δy(x_n+1)。

图  5  尖轨斥离状态横向位移分布曲线

Figure  5.  Transverse displacement distribution curve of the switch rail separated from the stock rail

下载: 全尺寸图片 幻灯片

基于设计方案可知尖轨在密贴状态下的线形，采用同样的方法将尖轨进行离散化处理，可得尖轨在密贴状态下各个节点的纵向位置坐标x₁、x₂、x₃、···、x_n+1，以及对应横向位置坐标y_m(x₁)、y_m(x₂)、y_m(x₃)、···、y_m(x_n+1)。分别对各个离散节点P_i(i=1, 2, 3, ···, n+1)，基于尖轨密贴状态下的横向位置坐标y_m(x_i)以及斥离后的位移变化量Δy(x_i)通过叠加计算得到尖轨斥离状态下的横向位置坐标y_c(x_i)。

基于尖轨斥离状态下各个离散节点的位置坐标(x_i, y_c(x_i))，通过样条曲线拟合可得尖轨在斥离状态下的线形y_c(x)。

预设第一牵引点动程160 mm，第二牵引点动程75 mm，在此条件下，基于本文方法所得到的尖轨斥离状态线形与传统方法的差异如图6所示。可以看出，传统方法得到的尖轨斥离状态横向位移总体偏大，仅在第一牵引点之前的横向位移偏小，最大偏差量达29.46 mm，如此大的偏差量足以影响尖轨转换相关参数设计的准确性和合理性。另外，由于传统方法所得到的尖轨斥离状态横向位移比实际情况偏大，因此基于传统方法按照最小轮缘槽宽度65 mm进行设计时，实际组装后最小轮缘槽宽度是小于65 mm的，这会对列车通过道岔的安全性产生不利影响。本文提供的方法基于尖轨斥离状态的实际受力确定斥离线形，与实际情况更为相符，也更偏于安全。

图  6  尖轨斥离状态横向位移曲线的差异

Figure  6.  Difference in transverse displacement curves of the switch rail under the separated state

下载: 全尺寸图片 幻灯片

2   牵引点动程优化设计

基于所建立的道岔转换计算模型，针对新型60 kg/m钢轨12号单开道岔的牵引点动程进行优化设计。

首先，根据铁路道岔通用设计原则，第一牵引点动程固定设计为160 mm^[21-22]。新型60 kg/m钢轨12号单开道岔共设置2个牵引点，故需对第二牵引点动程进行优化设计。牵引点动程的设计首先必须满足最小轮缘槽的要求，即在尖轨斥离状态下，尖轨非工作边与基本轨工作边的距离应大于等于65 mm^[23-24]。由于新型60 kg/m钢轨12号单开道岔采用刨切基本轨加厚尖轨技术来提高曲线尖轨的抗磨耗性能，直基本轨工作边侧刨切了5 mm，故最小轮缘槽宽度应大于等于70 mm。

基于此，设计数值试验工况见表1。

表  1  数值试验工况

Table  1.  Numerical test conditions /mm

试验工况	第一牵引点动程	第二牵引点动程	说明
1	160	75	专线4249道岔设计值
2	160	80
3	160	85
4	160	90
5	160	95

下载: 导出CSV 

| 显示表格

不同计算工况下，尖轨斥离状态的横向位移曲线如图7所示，最小轮缘槽计算结果见表2。

下载: 全尺寸图片 幻灯片

  7  不同牵引点动程条件下尖轨斥离状态横向位移曲线

  7.  Transverse displacement curves of switch rail under the separated state and different traction point stroke conditions

下载: 全尺寸图片 幻灯片

表  2  不同牵引点动程条件下最小轮缘槽宽度

Table  2.  Minimum flangeway width for different traction point stroke conditions

实验工况	1	2	3	4	5
最小轮缘槽宽度/mm	63.5	68.1	71.9	75.7	79.2

下载: 导出CSV 

| 显示表格

由计算结果可知，采用既有60 kg/m钢轨12号单开道岔设计牵引动程时，最小轮缘槽宽度为63.5 mm，不能满足要求，影响列车安全通过道岔。随着第二牵引点动程的增大，最小轮缘槽逐渐增大。当第二牵引点动程达到85 mm时，最小轮缘槽宽度为71.9 mm，可满足要求，但安全裕量较小，考虑到制造公差的影响，不能满足要求。当第二牵引点动程达到90 mm和95 mm时，最小轮缘槽宽度分别为75.7 mm和79.2 mm，有较充分的安全裕量。

牵引点动程的设计在满足最小轮缘槽的基础上，应尽量减小第一牵引点和第二牵引点的牵引力，降低转辙机工作功率。另外，需要尽量使尖轨的变形协调，避免尖轨的不均匀变形。基于此，补充设置数值试验工况，见表3。

表  3  数值试验工况

Table  3.  Numerical test conditions

试验工况	第一牵引点动程	第二牵引点动程/mm
6	不控制	90
7	不控制	95

下载: 导出CSV 

| 显示表格

不同第二牵引点动程条件下，尖轨斥离状态的横向位移曲线如图8所示，第一牵引点位置的自由动程计算结果见表4。

图  8  不同第二牵引点动程条件下尖轨斥离状态横向位移曲线

Figure  8.  Transverse displacement curves of the switch rail separated from the stock rail under different stroke conditions at the second traction point

下载: 全尺寸图片 幻灯片

表  4  不同第二牵引点动程条件下第一牵引点自由动程

Table  4.  Free stroke for the first traction point under different stroke conditions at the second traction point

实验工况	6	7
第一牵引点自由动程/mm	171	182

下载: 导出CSV 

| 显示表格

由计算结果可知，当放开第一牵引点，第二牵引点动程为90 mm时，第一牵引点位置的自由动程为171 mm，因此，在第一牵引点施加160 mm动程时，尖轨变形虽存在一定的反弯变形，但总体来看较为协调，第一牵引点与第二牵引点动程较为匹配。而如果放开第一牵引点，第二牵引点动程增加到95 mm时，第二牵引点的牵引力将增大，且第一牵引点的自由动程将达到182 mm，此时如果在第一牵引点施加160 mm的动程，尖轨反弯变形显著增大，将变得不协调，第一牵引点将产生显著的反向阻碍作用，会导致第二牵引点的牵引力进一步增大。

综上所述，基于仿真计算可知，第二牵引点牵引动程设置为90 mm时，能够满足最小轮缘槽的要求，而且留有一定的安全裕量，同时，尖轨的变形总体来看较为协调，第一牵引点、第二牵引点的动程较为匹配。因此，对于新型60 kg/m钢轨12号单开道岔，设计第一牵引点动程为160 mm，第二牵引点动程为90 mm。

3   转换试验验证

基于所提出的设计方案进行了新型60 kg/m钢轨12号单开道岔的试制和试铺，如图9所示。

图  9  新型60 kg/m钢轨12号单开道岔厂内试铺

Figure  9.  Laying of the new No. 12 single turnout of 60 kg/m rail on the manufacturing site

下载: 全尺寸图片 幻灯片

在两个牵引点安装S700K型电动转辙机及配套锁闭装置，并进行调试，验收合格后进行尖轨转换试验。首先进行多个周期的预转换，然后测量并读取数据。

采用销轴式称重传感器对转换力进行测量，如图10所示，测量信号经动态信号测试分析仪进行数据转化，转化后的转换力数据使用DHDAS软件进行分析和存储。转换力测量完成后，采用卷尺对最小轮缘槽进行测量，如图11所示。

图  10  转换力测试

Figure  10.  Switching force test

下载: 全尺寸图片 幻灯片

图  11  最小轮缘槽测量

Figure  11.  Minimum flangeway measurement

下载: 全尺寸图片 幻灯片

预转换完成后，进行3次往返扳动。每次扳动过程中不同牵引点的转换力及扳动完成后对应的最小轮缘槽测试结果见表5、表6。

表  5  道岔转换力

Table  5.  Turnout switching force /N

扳动次数	第一次	第二次	第三次	平均值
第一牵引点	2360	2450	2310	2373
第二牵引点	3430	3230	3170	3277

下载: 导出CSV 

| 显示表格

表  6  最小轮缘槽

Table  6.  Minimum flangeway /mm

往返扳动次数	第一次	第二次	第三次	平均值
直尖轨斥离状态	74.0	74.1	74.0	74.0
曲尖轨斥离状态	73.7	73.9	73.5	73.7

下载: 导出CSV 

| 显示表格

从测试结果可以看出，第一牵引点的平均转换力为2373 N，第二牵引点的平均转换力为3277 N。直尖轨斥离状态下最小轮缘槽平均值为74.0 mm(因侧股轨距加宽5 mm，因此须大于等于70 mm)，有4.0 mm安全裕量；曲尖轨斥离状态下最小轮缘槽平均值为73.7 mm(因直基本轨刨切5 mm，因此须大于等于70 mm)，有3.7 mm安全裕量。

基于现场测试数据，既有60 kg/m钢轨12号主型道岔的转换力为3000 N~4000 N。总体来看，新型60 kg/m钢轨12号单开道岔的转换力较小，优于既有的12号主型道岔，最小轮缘槽宽度满足要求且具有一定的安全裕量。试验数据证明了本文所提出的转换设计方法的合理性和有效性。

4   结论

本文基于60 kg/m钢轨12号单开道岔的优化需求，考虑既有道岔转换设计方法的不足，对60 kg/m钢轨12号单开道岔的转换设计进行了优化研究。基于有限元理论建立了道岔转换仿真计算方法，可基于尖轨斥离状态的实际受力确定斥离线形，与实际情况更为相符，也更偏于安全。在此基础上，对牵引点动程的合理取值进行了深入研究，通过数值仿真试验系统分析了不同牵引点动程条件下的最小轮缘槽宽度及第一、第二牵引点动程匹配关系的变化规律，提出了第一牵引点动程160 mm、第二牵引点动程90 mm的优化方案。

进行了新型60 kg/m钢轨12号单开道岔的试制和试铺，并开展了尖轨转换试验。测试结果表明，新型12号道岔第一牵引点转换力为2400 N左右，第二牵引点转换力为3300 N左右，优于既有60 kg/m钢轨12号主型道岔。最小轮缘槽宽度满足要求，且有3 mm~4 mm的安全裕量。试验结果证明了本文所提出的转换设计方法和参数优化方案的合理性和有效性。

进一步工作中，拟将试制的新型60 kg/m钢轨12号单开道岔铺设到实际运营线路中，对道岔使用状态及转换状态进行长期跟踪测试，对设计方法和方案进行进一步的验证。另外，将在本文基础上开展以下几方面研究：① 系统进行道岔转换性能的理论试验研究，分析牵引点动作时差、滑床台摩擦系数、夹异物等各种影响因素对道岔转换的影响规律；② 道岔转换状态随时间的变化规律研究；③ 锁闭装置力学特性及对道岔转换的影响研究；④ 道岔转换计算模型的参数敏感性分析；⑤ 通过三维扫描复现道岔尖轨斥离状态的实际线形，与理论计算的线形进行更为精准的对比验证。