混凝土材料具有显著的非均质性。从细观尺度出发，通常将混凝土视为由砂浆、界面及骨料组成的三相复合材料^[1]。作者根据普通强度混凝土材料发生I-型开裂后的形态学特征，基于细观力学和断裂力学基本理论框架，建立了可定量分析混凝土细观断裂行为和宏观断裂参数的基于绕晶失效模式的三维细观断裂理论分析模型^[2]。为简化理论推导，不可避免地引入了若干强假定，如：骨料“绝对均匀”分布假定、仅考虑断裂破坏行为假定以及唯一裂缝面假定等，上述假定使得理论预测结果与实际情况存在差距。

物理试验是修正理论模型及验证其合理性最直接的研究手段，但容易受到试验条件、人为误差等因素的影响。此外，试验过程中混凝土各细观组分的力学性能难以得到把控，为从细观尺度修正理论模型带来了难度。数值分析是规避试验短板、实现理论预期的重要研究手段^[3]。随着计算机技术与数值计算理论的发展，数值试验已经逐渐成为替代物理试验研究混凝土物理及力学行为的一种有效途径^[4]。自“数值混凝土^[5]”概念提出以来，国内外学者已构建了多种体现混凝土材料非均质特性的数值分析模型用以研究混凝土宏观力学性能，典型的有格构模型^[6-7]、随机力学特性模型^[8-9]、随机粒子模型^[10]、刚体弹簧元模型^[11]和随机骨料模型^[12-13]等。基于成熟的数值模拟技术，通过开展细观尺度数值试验，模拟混凝土宏观力学性能随细观组成材料力学特性和结构特性的变化规律，不仅能够直接观察混凝土材料受力失效破坏的全过程，还能够根据需要针对不同骨料含量条件、不同骨料级配条件、不同骨料分布条件、不同界面力学性能条件等对混凝土宏观力学性能的影响规律开展研究^[14]。

本文基于骨料颗粒在混凝土材料内部空间的随机分布特征，编写三维数值混凝土骨料投放程序，构建不同级配混凝土标准立方体试件，对其在劈裂拉伸加载条件下的失效行为和力学特性开展细观尺度数值试验，讨论不同界面强度条件和不同骨料含量条件下混凝土宏观力学性能的变化规律，最终基于数值试验结果修正理论分析模型，并建立用于不同级配混凝土劈拉强度预测的半理论-半经验修正计算公式。

1   细观数值分析模型

1.1   模型建立

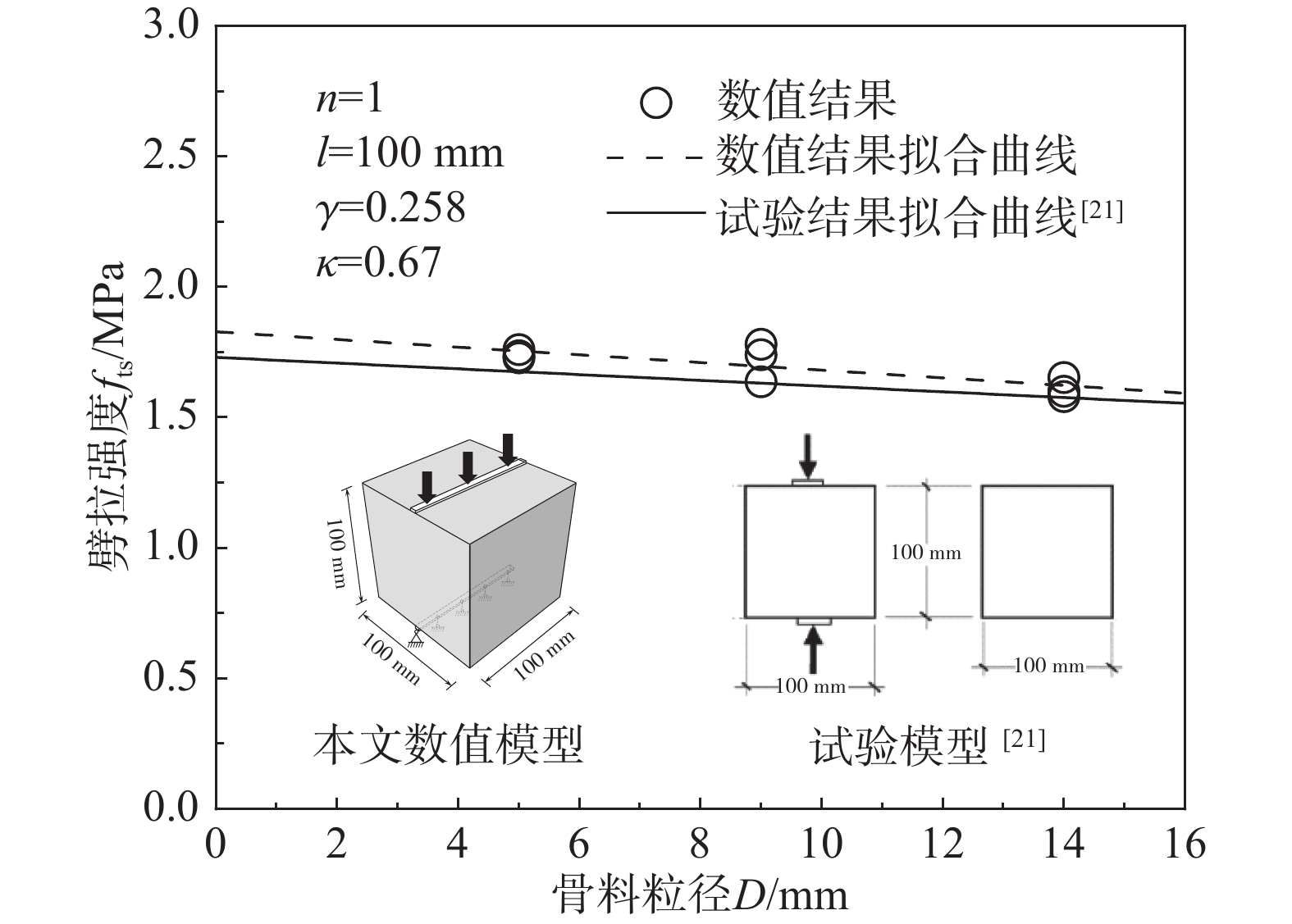
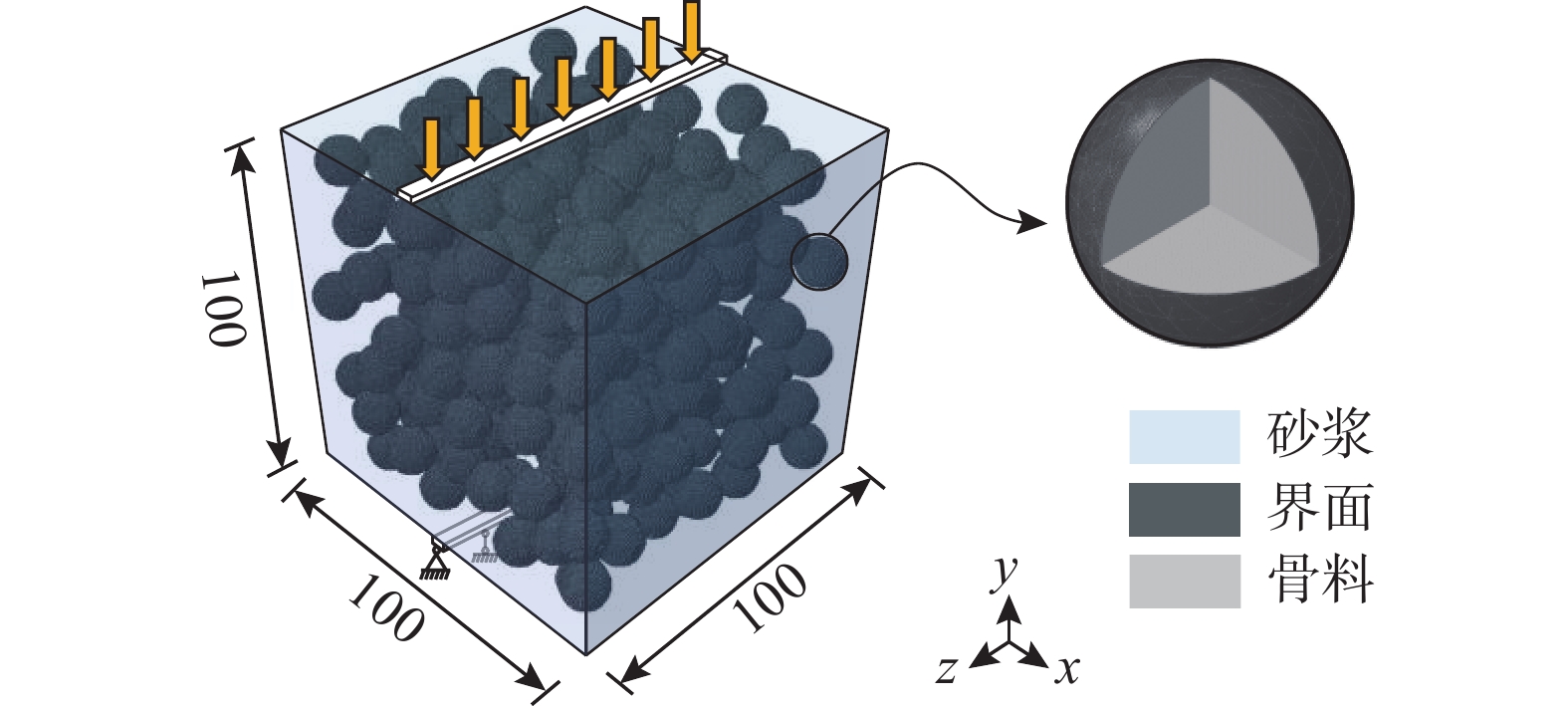
以典型一级配混凝土为例，图1给出了建立的混凝土三维细观数值分析模型示意图。模型为边长l = 100 mm的标准立方体试件，由砂浆、界面和骨料构成。骨料为等效粒径D₁ = 12 mm的标准球体，界面为位于球形骨料和基体砂浆之间的过渡区^[15-16]。为模拟还原真实状态下混凝土标准立方体试件的调试制备过程，基于FORTRAN语言编写骨料投放程序，采用“投-放”方法生成3组具有不同骨料颗粒空间分布状态的数值混凝土标准立方体试件。采用六面体三维实体单元进行网格划分，综合考虑计算精度和计算效率，经试算后确定本文模型采用的平均网格尺寸为2 mm^[17]。模型顶部放置垫条并承受纵向力，采用速度控制进行准静态加载，荷载应变率为10⁻⁵ s^−1[18]。混凝土劈拉强度f_ts采用我国《混凝土物理力学性能试验方法标准》(GB/T 50081−2019)^[19]建议的计算公式：

式中：F_max为试件破坏荷载；A为试件劈裂面面积，即A = l²。

图  1  典型一级配混凝土三维细观数值分析模型　/mm

Figure  1.  3D mesoscale numerical analysis model for typical 1-grade concrete

下载: 全尺寸图片 幻灯片

1.2   模拟工况

我国《水工混凝土配合比设计规程》(DL/T 5330−2015)^[20]建议的不同级配混凝土骨料组合比见表1。表2给出了本文数值试验模拟工况及依据表1计算得到的各数值混凝土模型中骨料颗粒的数量。

表  1  不同级配混凝土骨料组合比a_j^[20]

Table  1.  Aggregate ratio a_j of different graded concrete^[20]

粒径范围/mm		5~20	20~40	40~80	80~150
等效粒径/mm		12	30	60	120
组合比aj		a1	a2	a3	a4
骨料级配n	1	1.0	−	−	−
	2	0.4	0.6	−	−
	3	0.3	0.3	0.4	−
	4	0.2	0.2	0.3	0.3

下载: 导出CSV 

| 显示表格

表  2  数值试验模拟工况

Table  2.  Case design of numerical tests

骨料粒径/ mm		5	9	14	12	30	60	120
工况1 用于验证数值分析模型合理性[21-23]	n=1 l=100 mm γ=0.258	3942	−	−	−	−	−	−
	n=1 l=100 mm γ=0.258	−	676	−	−	−	−	−
	n=1 l=100 mm γ=0.258	−	−	180	−	−	−	−
工况2 用于修正理论分析模型	n=1 l=100 mm γ=0.25	−	−	−	276	−	−	−
	n=2 l=150 mm γ=0.25	−	−	−	373	36	−	−
	n=3 l=300 mm γ=0.25	−	−	−	2238	143	24	−
	n=4 l=450 mm γ=0.25	−	−	−	5036	322	60	8
工况3 用于验证修正后的理论分析模型	n=4 l=450 mm γ=0.10	−	−	−	2014	129	24	3
	n=4 l=450 mm γ=0.15	−	−	−	3021	193	36	5
	n=4 l=450 mm γ=0.20	−	−	−	4029	258	48	6
	n=4 l=450 mm γ=0.25	−	−	−	5036	322	60	8
	n=4 l=450 mm γ=0.30	−	−	−	6043	387	73	9
	n=4 l=450 mm γ=0.35	−	−	−	7050	451	85	11
	n=4 l=450 mm γ=0.40	−	−	−	8057	516	97	12

下载: 导出CSV 

| 显示表格

工况1：基于文献[21-23]中骨料含量γ = 0.258、骨料粒径分别为3 mm(考虑数值模型计算量，实际工况1中采用5 mm骨料粒径)、9 mm和14 mm的边长l = 100 mm的一级配混凝土立方体试件劈裂拉伸试验结果，对数值分析模型中采用的各项力学参数进行标定，进而验证数值模型的合理性。

工况2：设定骨料含量γ = 0.25，建立边长分别为100 mm、150 mm、300 mm和450 mm的一级配至四级配混凝土标准立方体试件，开展不同界面强度条件下混凝土标准立方体试件的劈裂拉伸数值试验，进而根据数值试验结果分别对一级配至四级配混凝土宏观力学参数的解析解进行修正。

工况3：以四级配混凝土为研究对象，开展不同骨料含量、不同界面强度条件下标准立方体试件的劈裂拉伸数值试验，通过对比数值试验结果与修正后的解析解初步验证理论分析模型的合理性。

1.3   模型验证及参数标定

数值试验模拟工况1：对设定的骨料含量γ = 0.258、骨料粒径分别为5 mm、9 mm和14 mm的边长l = 100 mm的一级配数值混凝土立方体试件开展劈裂拉伸试验。为模拟普通强度混凝土材料的受力失效行为，混凝土数值模型中砂浆和界面的力学性能采用塑性损伤本构模型^[24-26]来表征，骨料则设为弹性体。各细观组分力学参数见表3，其中砂浆力学参数取自文献[21-23]给出的试验实测值；界面力学参数则基于砂浆力学参数采用折减系数κ进行调节^[2]，经反复试算后确定；骨料力学参数取自文献[27]。

表  3  细观组分力学参数

Table  3.  Mechanical parameters of the three meso components

细观结构	砂浆(i=mo)	界面(i=itz)	骨料(i=agg)
抗拉强度ft,i /MPa	*2.18	^2.18×κ	−
弹性模量Ei /GPa	*30	^30	#70
泊松比νi	*0.2	^0.2	#0.16
剪胀角ψi /(°)	18	15	−
偏心率ηi /(%)	0.1	0.1	−
应力比(fb0/fc0)i	1.16	1.16	−
Ki	0.667	0.667	−
注：“*”数据取自文献[21-23]；“#”数据取自文献[27]；“^”数据为反复试算值；其他力学数据为默认值。

下载: 导出CSV 

| 显示表格

如图2所示，当界面力学性能相对砂浆力学性能的折减系数κ = 0.67时，混凝土劈拉强度f_ts随骨料粒径D变化趋势与试验结果趋势基本一致。图3给出了不同骨料粒径条件下数值混凝土立方体试件的劈拉破坏模式。如图3(a)所示，宏观尺度上，劈裂拉伸加载条件下，试件失效主要集中在垫条下的截面，与理论分析模型的“唯一裂缝面假定”基本吻合；如图3(b)所示，细观尺度上，通过分析失效截面上细观结构的破坏形态可以发现：随骨料粒径D增大，骨料比表面积减小，亦即界面面积减小，则界面破坏导致的耗能减少，因而表现为劈拉强度f_ts随骨料粒径D增大而减小；如图3(c)所示，从试件内部损伤破坏形态可以看到，除主裂缝面外，在其附近还存在若干未贯通的损伤破坏区域，该区域形态主要受到混凝土材料非均质性和骨料分布随机性等影响，并与试件受荷形式相关，即不可避免存在一定的结构效应。上述分析结果表明：建立的混凝土三维细观数值分析模型及其力学参数确定方法是合理的。后续将基于验证的分析模型和标定的力学参数开展数值试验模拟工况2和数值试验模拟工况3。

图  2  混凝土劈拉强度f_ts随骨料粒径D变化趋势

Figure  2.  Variation of splitting tensile strength f_ts with aggregate size D

下载: 全尺寸图片 幻灯片

图  3  数值混凝土劈拉破坏模式

Figure  3.  Splitting tensile failure mode of numerical concrete

下载: 全尺寸图片 幻灯片

2   劈裂拉伸破坏形态

2.1   主裂缝面宏/细观结构破坏形态

图4给出了劈裂拉伸加载条件下数值试验模拟工况2中不同级配数值混凝土立方体试件主裂缝面的宏/细观结构破坏形态。可以看到，随界面力学性能降低(即κ减小)，破坏截面上损伤面积逐步增大。这是由于κ值越小，η值越大，根据界面裂缝指数η定义可知，单颗骨料周围破坏的界面面积越大^[2]，则失效截面上破坏的界面面积亦越大，因此拉伸破坏面更加曲折。

图5给出了劈裂拉伸加载条件下数值试验模拟工况3中κ = 0.7(即η = 0.255)时四级配数值混凝土立方体试件主裂缝面的宏/细观结构破坏形态。可以看到，随骨料含量增大(即γ增大)，破坏截面上损伤面积逐步增大。这是由于随骨料含量增大，界面总面积必然增大，失效截面上破坏的界面面积亦增大，因此拉伸破坏面更加曲折。

图  4  数值混凝土立方体试件宏/细观结构破坏形态

Figure  4.  Failure modes of macro/meso structures of numerical concrete cube specimens

下载: 全尺寸图片 幻灯片

图  5  四级配数值混凝土立方体试件宏/细观结构破坏形态

Figure  5.  Failure modes of macro/meso structures of 4-grade numerical concrete cube specimens

下载: 全尺寸图片 幻灯片

2.2   试件内部损伤破坏形态

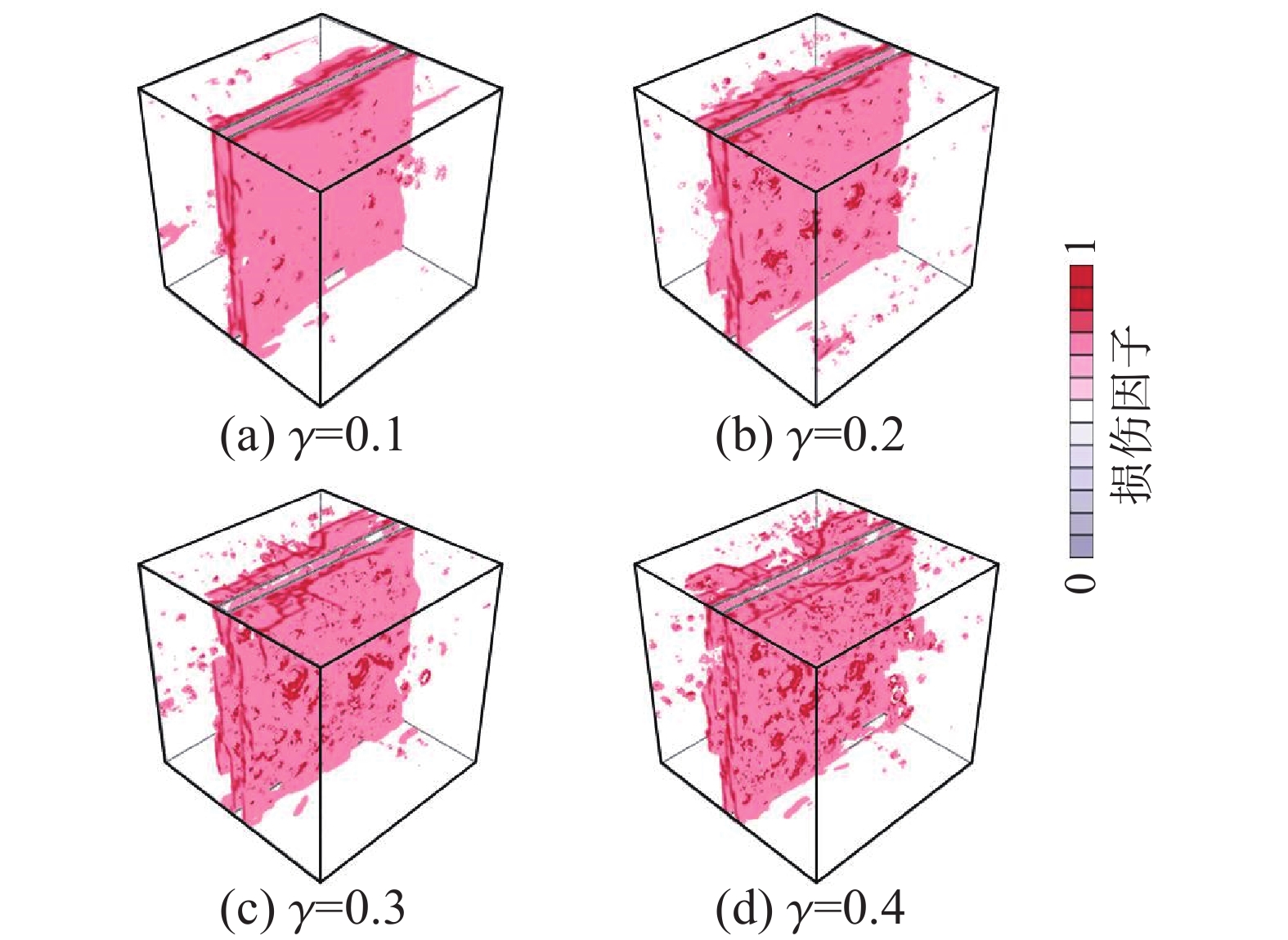
图6给出了劈裂拉伸加载条件下数值试验模拟工况2中不同级配数值混凝土立方体试件内部损伤破坏形态。可以看到，随界面力学性能降低(即κ减小)，混凝土内部损伤破坏区域逐步扩大。这是由于κ值越小，界面力学性能越弱，试件受荷过程中界面越容易出现损伤，则总体上表现为损伤破坏区域的扩大，结构效应更为显著。

图  6  数值混凝土立方体试件内部损伤破坏形态

Figure  6.  Internal damage failure modes of numerical concrete cube specimens

下载: 全尺寸图片 幻灯片

图7给出了劈裂拉伸加载条件下数值试验模拟工况3中κ = 0.7(即η = 0.255)时四级配数值混凝土立方体试件内部损伤破坏形态。可以看到，随骨料含量增大(即γ增大)，混凝土内部损伤破坏区域逐步扩大。这是由于随骨料含量增大，界面数量必然增多，试件受荷过程中出现损伤的界面也增多，总体上表现为损伤破坏区域的扩大，结构效应更为显著。

图  7  四级配数值混凝土立方体试件内部损伤破坏形态

Figure  7.  Internal damage failure modes of 4-grade numerical concrete cube specimens

下载: 全尺寸图片 幻灯片

上述分析表明：界面力学性能和骨料含量均能够显著影响劈裂拉伸加载条件下混凝土细观结构的破坏形态，进而影响混凝土失效破坏最终所耗散的能量，宏观上则表现为混凝土劈拉强度f_ts随界面裂缝指数η和骨料含量γ发生变化。

3   理论模型修正及劈拉强度预测

3.1   理论模型修正方法及修正系数物理意义

文献[2]建立的基于绕晶失效模式的混凝土三维细观断裂理论分析模型给出的混凝土断裂能G_f解析表达式为：

式中：G_f,mo为砂浆断裂能；λ为细观断裂面的曲折度指数；η为界面裂缝指数；n为骨料级配；γ为骨料含量；a_j为等效粒径为D_j的骨料颗粒占所有骨料颗粒的百分比；j为粒级；κ为界面力学性能相对砂浆力学性能的折减系数，显然，若0 ≤ κ ≤ 1，则有0 ≤ η ≤ 0.5。此外，基于推导得到的细观断裂面曲折度指数λ还可以给出I-型开裂模式下多级配混凝土试件细观断裂面积$A_{\text{f}}^{{\text{meso}}}$的定量表达式为：

文献[2]中的参数分析结果显示：界面力学性能(以界面裂缝指数η表征)显著影响混凝土宏观力学性能。此外，混凝土宏观力学性能随最大骨料粒径(以骨料级配n表征)和骨料体积分数γ的变化行为亦受到界面力学性能(即界面裂缝指数η)的影响。因此，本文以界面裂缝指数η为主要影响参数，开展不同界面强度条件下数值混凝土标准立方体试件的劈裂拉伸加载试验，进而基于数值试验结果对理论分析模型进行修正。为简化理论推导，假设混凝土和砂浆的宏观力学性能均可采用典型双线性弹性本构模型进行表征，则混凝土断裂能G_f和砂浆断裂能G_f,mo可由下式计算得到：

式中：ω为混凝土应变能密度；f_t为混凝土抗拉强度；ε_u为混凝土极限应变；ω_mo为砂浆应变能密度；f_t,mo为砂浆抗拉强度；ε_u,mo为砂浆极限应变，且根据混凝土材料I-型开裂形态学特征有ε_u = ε_u,mo^[28]；l_r为拉伸荷载方向上的参考尺寸^[28]。进一步，假设l_r = l，即用于测试混凝土和砂浆宏观力学性能的标准试件边长均取为l^[28]，则结合式(2)、式(3)、式(6)和式(7)可以推导得到混凝土抗拉强度f_t的理论预测公式为：

根据数值试验模拟工况2，将γ = 0.25、f_t,mo = 2.18 MPa以及a_j(表1)等初始条件代入式(8)，可以给出不同级配n情况下混凝土抗拉强度f_t随界面裂缝指数η变化的理论预测曲线，如图8中黑色虚线所示。表4给出了数值试验模拟工况2测试得到的取不同κ值时的混凝土劈拉强度f_ts(均值)。

此外，根据式(4)给出的η~κ转换关系，可以建立混凝土劈拉强度f_ts与界面裂缝指数η的对应关系。图8给出了不同级配n情况下f_ts~η对应关系散点图及其拟合曲线(黑色点线)。

图  8  f_ts随η变化关系

Figure  8.  Relations between f_ts and η

下载: 全尺寸图片 幻灯片

表  4  工况2数值试验结果

Table  4.  Numerical test results of case-2

折减系数 κ	界面裂缝 指数η	劈拉强度fts/MPa (均值)
		骨料级配 n = 1	骨料级配 n = 2	骨料级配 n = 3	骨料级配 n = 4
0.9	0.095	1.815	1.856	1.863	1.876
0.8	0.180	1.767	1.803	1.778	1.773
0.7	0.255	1.705	1.729	1.709	1.682
0.6	0.320	1.628	1.663	1.639	1.590
0.5	0.375	1.580	1.586	1.568	1.512
0.4	0.420	1.526	1.515	1.499	1.434
0.3	0.455	1.476	1.461	1.437	1.360

下载: 导出CSV 

| 显示表格

由图8中黑色虚线和黑色点线的对比可以看到，数值试验结果与基于式(8)的理论预测结果趋势一致，但仍存在一定偏差，主要原因分析如下：

1) 重叠效应影响。文献[2]指出：提出的用于多级配混凝土试件细观断裂面积$A_{\text{f}}^{{\text{meso}}}$的定量计算方法运用了叠加原理，并且这种初步的、基于线性叠加的定量计算方法未能考虑不同等效粒径骨料在空间上的重叠效应，将使理论模型预测结果失真。根据混凝土材料发生I-型开裂后的形态学特征及文献[2]建立的基于绕晶失效模式的混凝土三维细观断裂理论分析模型分析可知：

① 当η = 0时，由界面裂缝指数定义可知细观裂缝仅穿过砂浆，则极限状态下细观断裂面积最小值为$A_{\text{f}}^{{\text{meso}}} = {l^2}$，进而由式(5)可以计算得到细观断裂面曲折度指数可取得的最小值为λ = 0。

② 当η = 0.5时，首先，根据文献[2]中式(11)可以计算得到$A_{{\text{f,itz}}}^{( {{D_j}} )} = \pi D_j^2/2$，即等效粒径为D_j的骨料颗粒对应的“单独”界面断裂面积达到最大值；其次，根据文献[2]中式(16)可以计算得到，$A_{{\text{f,itz}}}^{( {{D_j}} )*} = \pi D_j^2/4 = A_{{\text{f,itz}}}^{( {{D_j}} )}/2$即任意等效粒径为D_j的骨料颗粒对应的“单独”界面断裂面积$A_{{\text{f,itz}}}^{( {{D_j}} )}$是其阴影面积$A_{{\text{f,itz}}}^{( {{D_j}} )*}$的2倍；最终，若考虑骨料颗粒占满整个细观断裂面(即曲折程度最大)的极限状态，设断裂面上存在任意N颗骨料，则有$A_{\text{f}}^{{\text{meso}}} = NA_{{\text{f,itz}}}^{( {{D_j}} )} = 2NA_{{\text{f,itz}}}^{( {{D_j}} )*} = 2{l^2}$，进而根据本文式(5)可以计算得到细观断裂面曲折度指数可取得的最大值为λ = 1。

基于上述分析可以看到：实际情况中细观断裂面曲折度指数λ应在0和1之间变化。此外，由式(2)亦可以看到，若λ > 1，则计算得到的混凝土断裂能G_f将为负值而失真。然而，如图9所示，以二级配(n = 2)和四级配(n = 4)混凝土为例，若根据式(3)计算不同界面裂缝指数η和不同骨料含量γ条件下的细观断裂面曲折度指数λ，可以发现随界面力学性能降低(即η增大)和骨料含量γ增大将得到λ > 1的结论，即是受到了不同等效粒径骨料在空间上的重叠效应影响。

图  9  细观断裂面曲折度指数λ失真分析

Figure  9.  Analysis of tortuosity index λ distortion of meso-fracture surface

下载: 全尺寸图片 幻灯片

鉴于此，应首先在计算方法上针对细观断裂面曲折度指数λ引入考虑骨料空间重叠效应的修正系数。由图6中黑色虚线和黑色点线对比及式(8)可知该系数主要影响理论曲线的弯曲程度，故假定为曲率修正系数a_n。

2) 结构效应影响。为了能够给出混凝土宏观断裂参数的定量计算方法，理论分析模型是建立在若干强假定基础之上的，并且摒弃了诸多随机性影响因素。对于混凝土材料的I-型开裂破坏，基于前文损伤破坏形态的分析可知，若以标准立方体试件作为基本分析单元，则必然存在一定的结构效应影响，即除了引起最终断裂的主裂缝面外，试件中还存在其他随机产生的塑性变形以及开裂但未产生贯通裂缝的区域，这些区域均会增加标准立方体试件破坏时的耗能。实际情况中通过物理试验测试材料基本力学性能时亦无法消除这种结构效应的影响。

由图8中黑色虚线和黑色点线的对比可以发现，劈裂拉伸加载条件下的结构效应缓解了理论上劈拉强度f_ts随界面裂缝指数η增大而降低的速率。此外，实际情况中η→0时的劈拉强度f_ts渐进值较理论值低，而η→0.5时的劈拉强度f_ts渐进值较理论值高，其主要原因即是受到了结构效应影响。若从试件破坏耗散能量角度分析，假设外力所做总功为W，则混凝土劈拉强度f_ts可由下式计算得到：

式(9)是在假定混凝土材料在劈裂拉伸加载条件下力-位移曲线为双线性情况下给出的(实际应为积分形式)，这里仅用于解释结构效应影响机理。进一步，若考虑劈裂拉伸加载条件下的结构效应影响，则有：

式中，W_f为劈裂拉伸加载条件下混凝土断裂主裂缝面所耗散的能量，W_ts为劈裂拉伸加载条件下其他随机产生的塑性变形以及开裂但未产生贯通裂缝的区域所耗散的能量。将式(10)代入式(9)，得到：

由图6所示劈裂拉伸加载条件下的试件内部损伤形态可以发现，随折减系数κ减小(即界面裂缝指数η增大)，主裂缝外随机产生的塑性变形以及开裂但未产生贯通裂缝区域的面积逐渐增大。由此表明，界面性能越弱，W_ts在W中的比重将越大。基于此，结构效应影响机理分析如下：

① 当界面裂缝指数η较小并趋近于0时，界面性能相对较强，W_ts在W中的比重则较小，因此不作为主要影响因素。此外，根据界面裂缝指数定义可知裂缝绕行骨料(即穿过力学性能相对较弱的界面)应较少。然而，实际情况中骨料在试件内部的随机分布将导致裂缝不得不仍旧绕行骨料，进而产生大量界面裂缝，实际耗能较理论模型预测减小。因此，主要影响因素W_f较理论值所有降低，故根据式(11)计算得到的劈拉强度f_ts较理论值亦有所降低。

② 当界面裂缝指数η较大并趋近于0.5时，界面性能相对较弱，W_ts在W中的比重则较大，且η值越大，W_ts比重越大，影响越显著，则根据式(11)计算得到的劈拉强度f_ts较理论值亦有所升高。

上述提出的曲率修正系数a_n主要针对重叠效应影响进行修正，图8中黑色点线在坐标轴两端的截距值可以用来针对结构效应影响进行修正。鉴于此，在式(8)中括号项内引入考虑上述结构效应的修正系数，假定为截距修正系数b_n。

3.2   混凝土劈拉强度半理论-半经验修正计算公式

基于上述分析可知，未修正的理论预测结果虽然符合一般规律，且理论公式中各项参数均存在实际物理意义，但仍需根据实际情况进行修正。因此，可以将式(8)作为基本计算公式，根据不同加载条件下混凝土材料发生I-型开裂的破坏特征及其宏观力学性能的演化规律，通过引入相应的拟合参数建立半理论-半经验的修正计算公式。

本文以图8中数值试验结果为基准，结合提出的曲率修正系数a_n和截距修正系数b_n建立如下基于式(8)的用于混凝土劈拉强度f_ts预测的半理论-半经验修正计算公式：

式(12)中，a_n和b_n需要基于图8中不同级配n情况下f_ts~η拟合曲线加以确定。结合数值试验结果拟合曲线确定的η = 0和η = 0.5两端点劈拉强度f_ts值，令：

根据式(13)~式(16)计算结果，表5给出了基于本文数值试验结果的不同级配混凝土劈拉强度半理论-半经验修正计算公式中曲率修正系数a_n和截距修正系数b_n的取值。

表  5  不同级配混凝土修正系数取值

Table  5.  Correction coefficient values for different graded concrete

修正系数	骨料级配
	n = 1	n = 2	n = 3	n = 4
an	0.425	0.387	0.362	0.406
bn	−0.147	−0.134	−0.122	−0.103

下载: 导出CSV 

| 显示表格

最终，根据表5，式(17)给出了不同级配混凝土劈拉强度半理论-半经验修正计算公式。同样，将γ = 0.25、f_t,mo = 2.18 MPa以及a_j(表1)等初始条件代入式(17)，可以给出不同级配n情况下混凝土劈拉强度f_ts随界面裂缝指数η变化的理论预测曲线，如图8中黑色实线所示。可以看到，数值试验结果与基于式(17)的理论预测结果基本一致，可决系数R²值均较高。

讨论：由图8可以看到，可决系数R²有随骨料级配增大而降低的趋势，表明拟合效果随最大骨料粒径增大而减弱。产生这一现象的主要原因包括：

1) 每组工况中的每个独立加载试验数据均是基于3组具有不同骨料空间分布状态的立方体试件得到的，试验本身的离散性不可忽略。

2) 由表2中工况2可以看到，一级配和二级配混凝土中最大骨料粒径较小，不同粒径骨料数量均相对较多，因此在生成具有不同骨料空间分布状态的混凝土立方体试件时可以得到骨料分布相对较为均匀、离散性相对较小的试件；三级配和四级配混凝土中最大骨料粒径较大，不同粒径骨料数量相差较为悬殊(例如：四级配中最小粒径骨料有5036个，最大粒径骨料仅有8个)，则容易产生大粒径骨料在试件内部分布不均匀的情况；由于大粒径骨料对混凝土材料的裂缝扩展路径及宏观力学性能影响较为显著，其空间分布状态的不均匀更容易引起试验结果的离散性加剧。

4   模型验证

4.1   基于本文数值试验结果的修正模型初步验证

表6给出了数值试验模拟工况3测试得到的κ = 0.9、0.7、0.5、0.3(即η = 0.095、0.255、0.375、0.455)时不同骨料含量条件下四级配数值混凝土立方体试件劈拉强度f_ts(均值)。

表  6  工况3数值试验结果

Table  6.  Numerical test results of working condition 3

骨料 含量γ	劈拉强度fts /MPa(均值)
	折减系数 κ = 0.9	折减系数 κ = 0.7	折减系数 κ = 0.5	折减系数 κ = 0.3
0.10	1.858	1.817	1.761	1.710
0.15	1.862	1.796	1.702	1.618
0.20	1.894	1.769	1.667	1.527
0.25	1.876	1.682	1.512	1.360
0.30	1.925	1.710	1.510	1.292
0.35	1.928	1.703	1.480	1.217
0.40	1.909	1.659	1.387	1.106

下载: 导出CSV 

| 显示表格

图10给出了f_ts~γ对应关系散点图。此外，将η = 0.095、0.255、0.375、0.455，f_t,mo = 2.18 MPa以及a_j(表1)等初始条件代入式(17)，可以给出修正后的四级配混凝土劈拉强度f_ts随骨料含量γ变化的理论预测曲线，如图10中黑色实线所示。可以看到，理论预测结果与数值试验结果吻合较好。

图  10  劈拉强度f_ts随骨料含量γ变化关系

Figure  10.  Relations between f_ts and γ

下载: 全尺寸图片 幻灯片

4.2   基于文献中试验结果的修正模型初步验证

表7归纳了文献[21, 29-32]中测试得到的混凝土抗拉强度值。考虑不同试验在不同配合比条件下测试得到的参数值离散性较大，故将混凝土抗拉强度作归一化处理。图11给出了基于文献[21, 29-32]中试验结果的修正模型验证，可以看到，归一化强度(f_ts/f_t,mo)随骨料含量γ或界面裂缝指数η(即界面力学性能)变化的理论预测结果与文献中的试验结果较为吻合，初步验证了修正模型的合理性。

表  7  文献[21, 29-32]中试验结果

Table  7.  Test results in refs. [21, 29-32]

试验 结果	骨料 级配n	水灰比 w/c	折减 系数κ	界面 裂缝 指数η	骨料 含量 γ	砂浆 强度 ft,mo/MPa	混凝土劈拉 强度fts/MPa
文献 [21]	1	0.45	0.65	0.289	0.258	3.26	2.62
		0.70	0.90	0.095	0.258	2.18	1.70	1.78
文献 [29]	1	0.35	0.55	0.349	0.45*	3.81^	2.80	2.58	2.55	2.78
		0.45	0.65	0.289	0.45*	3.22^	2.50	2.35	2.48
		0.55	0.75	0.219	0.45*	2.52^	2.16	1.93	2.23
文献 [30]	2	0.30	0.50	0.375	0.40	5.45^	3.78	3.69	3.83
	3	0.55	0.75	0.219	0.40	2.68^	2.15	2.34	2.07	2.02	2.04	1.91
文献 [31]	1	0.45	0.65	0.289	0.33	3.21^	2.57	2.37	2.31	2.61	2.56	2.45
文献 [32]	1	0.36	0.56	0.343	0.49	4.58^	3.45
		0.36	0.56	0.343	0.49	5.42^	4.03
注：*为一般值；^为等效替代值(试验实测)；其余均为试验实测值。

下载: 导出CSV 

| 显示表格

图  11  基于文献中试验结果的修正模型验证

Figure  11.  Validation of the revised model based on experimental results in the literature

下载: 全尺寸图片 幻灯片

5   结论

本文采用自编骨料投放程序，建立了以砂浆、界面和骨料为主要非均质特征的混凝土三维细观数值分析模型。通过开展不同界面强度条件下混凝土标准立方体试件劈裂拉伸加载数值试验，对建立的基于绕晶失效模式的混凝土三维细观断裂理论分析模型进行了修正，并提出了用于不同级配混凝土劈拉强度预测的半理论-半经验修正计算公式。通过与不同骨料含量、不同界面强度条件下混凝土标准立方体试件劈裂拉伸加载数值试验结果以及文献中物理试验结果的对比，验证了修正模型能够有效表征混凝土宏观力学性能随细观组成材料力学特性和结构特性的变化规律。

需要说明的是，本文给出的拟合修正系数实际上主要体现了标准立方体试件在劈裂拉伸加载条件下的结构效应。直接拉伸或三点弯曲等其他加载条件下混凝土材料产生的I-型开裂破坏，其测试得到的材料抗拉强度将随试件不同破坏形态下的耗能不同(即主要受到结构效应的影响)而发生变化，因此亦需根据不同加载条件给出考虑不同结构效应影响的拟合参数，进而建立相应半理论-半经验修正计算公式。