RC框架结构基本自振周期个体间不确定性量化

项梦洁; 陈隽

doi:10.6052/j.issn.1000-4750.2022.05.0404

RC框架结构基本自振周期个体间不确定性量化

项梦洁^1,,
陈隽^{1, 2, ,}

1.
同济大学土木工程学院，上海 200092
2.
土木工程防灾减灾全国重点实验室，上海 200092

基金项目: 国家自然科学基金重点项目(52178151)；土木工程防灾国家重点实验室项目(SLDRCE19-B-22)

详细信息

作者简介:
项梦洁(1994−)，女，湖北人，博士生，从事区域建筑地震风险及可靠性评估研究 (E-mail: xmengjie0930@163.com)

通讯作者:
陈　隽(1972−)，男，河南人，教授，博士，博导，主要从事工程结构防灾、土木工程大数据方面的研究 (E-mail: cejchen@tongji.edu.cn)

中图分类号: P315.9
计量
- 文章访问数: 261
- HTML全文浏览量: 78
- PDF下载量: 56
出版历程
- 收稿日期: 2022-05-03
- 修回日期: 2022-09-02
- 网络出版日期: 2022-09-15
- 刊出日期: 2024-05-24

QUANTIFICATION OF INTER-BUILDING VARIABILITY OF NATURAL VIBRATION PERIOD OF RC FRAME BUILDINGS

XIANG Meng-jie^1,,
CHEN Jun^{1, 2, ,}

1.
College of Civil Engineering, Tongji University, Shanghai 200092, China
2.
State Key Laboratory of Disaster Reduction in Civil Engineering, Shanghai 200092, China

摘要

摘要:
钢筋混凝土(RC)框架结构是城市区域地震风险评估重要对象，其基本自振周期存在明显个体间变异性，如相同高度周期不同。通常采用的确定性结构高度-周期经验公式主要面向新结构设计，未能考虑既有RC建筑物周期的个体间变异性，影响区域地震风险评估的准确性，因此需要合理量化。该研究通过大量文献检索，收集了不同地区的641栋RC框架结构实测长轴、短轴方向基本周期以及高度、结构形式等信息，开展了严格的数据库清洗，并采用物理准则-数据驱动相结合的方式，建立了高度相依基本周期随机函数模型描述个体间变异性。与经典统计回归基本周期随机模型相比，新模型可以更好地反映结构间基本周期的物理机制差异以及观测数据的联合概率特性，便于在区域地震风险评估中应用。
- RC框架结构 /
- 基本自振周期 /
- 个体间变异性 /
- 随机函数模型 /
- 区域地震风险评估
Abstract:
Reinforced concrete (RC) frame structures are important targets in urban seismic risk assessment with their natural vibration periods exhibiting significant inter-building variability, i.e. different periods for the same height. This is neglected in seismic design stage by using a deterministic building height-period formula, as a result, the seismic performance of existing buildings may be incorrectly estimated, and thus the natural vibration period needs to be reasonably quantified in regional seismic risk assessment. In this study, a database containing measured building heights and natural periods in the longitudinal and transverse directions of 641 RC frame buildings is constructed through literature searching, and a height-dependent random period function model is proposed based on stringent data filtering and a physics-guided data-driven methodology to consider the interbuilding variability. The comparison with the classical statistical regression random period model shows that the proposed model can better represent the difference in physical mechanisms of interbuilding natural periods and meanwhile well capture the joint probability characteristics of observed data, therefore could be applicable in regional seismic risk assessment.
- reinforce concrete frame building /
- natural vibration period /
- inter-building variability /
- random function model /
- regional seismic risk assessment

HTML全文

正确评估区域地震风险是韧性城市建设的先决条件^[1-2]，要求合理考虑地震激励和区域建筑力学特性的不确定性，量化区域建筑可能遭受的概率地震损失。钢筋混凝土(reinforced concrete, RC)框架结构是最主要的城市区域建筑形式，其基本自振周期(后文简称基本周期)是区域震损估计的基础参数，综合反映了结构的质量和刚度特性，决定了区域既有结构力学模型、抗震能力和震损估计的准确与否^[3-4]，进而显著影响区域地震风险估计的正确性。因此，对RC框架结构基本周期的研究对于城市区域地震风险评估和预防具有重要意义。

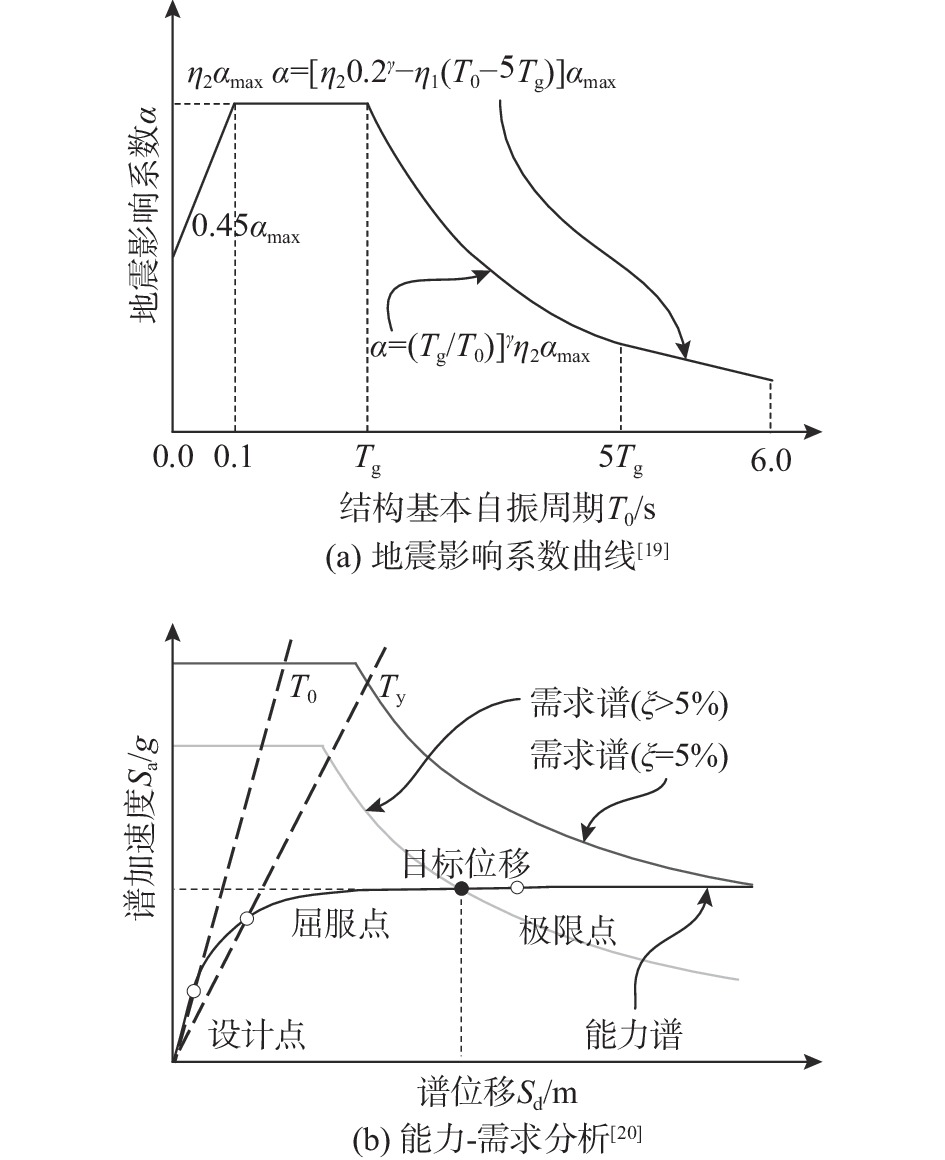
针对RC框架结构基本周期的研究方法通常包括理论分析^[5]和实测回归两类，后者指利用地震激励、强迫振动或环境脉动等手段，测试大量既有RC框架结构基本周期数据，并通过回归分析确定基本周期关于结构参数(如结构高度、层数、结构平面尺寸)的经验公式。实测回归研究方式可靠性高和便利性强，因而被世界各国学者广泛应用并积累了大批实测数据^[6-17]，也据此提出了几类经典(如高度-周期、层数-周期)经验公式^[18]。相关成果也逐步纳入世界各国抗震设计规范，如用于底部剪力法(如图1(a)所示)中估算拟建RC框架结构承受的地震作用^[19]。同时，在区域地震风险评估中，这些经验公式也被用来确定既有RC框架结构的能力曲线，完成结构地震损伤的估计^[20] (如图1(b)所示)。综上，RC框架结构基本周期实测回归研究是城市区域建筑抗震设计及性能评估决策的关键环节。

图 1 基本周期在区域抗震设计和性能评估中的应用

Figure 1. Applications of natural period in regional seismic design and performance evaluation

下载: 全尺寸图片幻灯片

事实上，RC框架结构基本周期存在个体间变异性(即同类型相同高度结构具有不同周期值)，并随实测数据不断积累而显著。已有学者观测并发现，其主要源自不同个体结构设计建造、功能及服役年限、激励和测试手段等因素的差异，同时由其引发的统计误差不可忽略^{[6, 21-22]}。现有面向设计决策的基本周期实测回归研究，主要通过细化结构分类、引入如填充墙布置修正系数^[18]等更多结构参数(通常难以直接获得)以减少估计相对误差，或者采用均值减1倍标准差形式的保守估计公式^[15]。遗憾的是，以上做法本质上仍仅给出确定性周期估计，不仅无法合理描述RC框架结构基本周期固有个体间变异性，而且通常导致预测公式复杂程度增加从而大大降低使用便利性。尤其是，在区域地震风险评估中使用这类确定性周期公式，会导致区域RC框架结构基本周期的不合理估计，进而错估区域建筑抗震性能以及地震风险。鉴于基本周期参数对既有结构抗震性能评估的重要性，而结构间参数变异性是区域地震风险的重要不确定性来源之一^[23-24]，发展应用便捷且能合理反映区域RC框架结构基本周期实际分布的随机函数模型，对于合理量化城市区域地震风险，增强城市对地震灾害的抗御、适应和快速恢复能力具有重要价值。

针对上述问题，本文系统性收集了大样本已有文献中不同地区的既有RC框架结构基本周期实测值，通过严格的数据清洗确定了基本周期个体间变异性的分布区间，并根据物理指导-数据驱动的建模方式建立了高度相依基本周期随机函数模型。并与考虑个体间变异性的经典统计回归模型的对比分析，阐述了所提模型的优越性。所提模型结合区域建筑群时程分析震害模拟方法和概率密度演化方法，即可进行区域建筑群概率地震损伤分析和地震风险评估。

1 RC框架结构基本周期实测数据库

1.1 数据收集标准

RC框架结构基本周期的影响因素众多，如结构高度、高宽比、建筑材料、非结构构件、场地条件以及土-结相互作用等，考虑上述全部因素建立实测周期数据库会造成数据收集困难和数据库稀疏等问题。由于增大数据样本对合理反映基本周期变异区间的必要性，因此需要筛选关键参数并明确数据收集标准。鉴于：① 基于结构高度或层数的RC框架结构基本周期实测回归研究积累了大量成果；② 结构高度和层数信息易于获得、使用且相互转换；③ 既有研究表明，对于主要建筑材料和抗侧力体系一致的同类型建筑，结构高度和层数是结构基本周期的主要影响因素^[25]。因此，本研究检索和查阅大量相关已发表文献，以结构高度(从地面计算)、层数(不含地下室)、长轴和短轴两个正交方向(后文简称正交方向)基本周期为必要参数，收集高度60 m以下RC框架结构实测数据，以及原文献中涉及如激励方法和测试地区等数据，以建立大样本RC框架结构实测周期数据库。需指出，以往研究表明^[26]，众多因素中建筑所在地区对周期影响弱，因此本研究忽略地区因素影响以扩大样本量。

1.2 数据库概况

数据库共包含641栋不同国家和地区的高度60 m以下RC框架结构正交方向1212条基本周期实测值(理论存为1282条，此处差值为正交方向缺失样本)。其中，所收录建筑主要为住宅、办公楼、商店、酒店等民用建筑(不包含露天框架、工业厂房等工业建筑)；结构体系主要包含混合砖墙RC框架结构(MRCF)和RC框架结构(RCF)(部分文献亦称为RC抗弯框架结构)；结构高度最低3 m，最高59.98 m；建筑层数最低1层，最高20层。数据库文献来源、数据测试方法等信息如表1所示。其中，数据涉及13个文献来源(年代跨度30年)和9个国家，相应测试建筑数量分布并不均匀，以文献[11](218栋)和中国地区(331栋)占比最多，分别为34%和52%。同时，数据近九成来自脉动测试，地震激励建筑数量(共66栋)仅占总比10%；而原文声明的受损建筑数量(共22栋)占比更不足4%，说明地震观测数据和受损建筑实测数据的稀缺性。

表 1 数据库信息

Table 1. Information of database

年份	学者	结构形式	激励方法	测试地区	建筑数量	周期数据数量
1988	王广军等^[5]	MRCF	脉动测试	中国北京、上海等	28	48
1988	王广军等^[5]	RCF		中国北京、上海等	55	110
1995	DAVID等*^[6]	RCF		墨西哥	32	63
2008	GULER等^[7]	RCF		土耳其	6	12
2010	GALLIPOLI等^[8]	RCF		意大利、马其顿共和国	113	176
2010	OLIVEIRA等^[9]	RCF		葡萄牙	74	147
2011	刘红彪等^[10]	RCF		中国四川	6	12
2013	施卫星等^[11]	MRCF		中国上海	62	124
2013	施卫星等^[11]	RCF		中国上海	156	312
2013	杨东晖*^[12]	RCF		中国青海	6	12
2014	AL-NIMRY等^[13]	RCF		约旦	23	46
2016	ALGUHANE等^[14]	RCF		麦地那	14	21
1997	GOEL等*^[15]	RCF	地震激励	美国加利福利亚	28	54
2000	HONG等^[16]	RCF		中国台湾	18	35
2018	GATTI^[17]	RCF		意大利	20	40
注：1) DAVID等数据中8栋位于硬土地基，其余24栋位于软土地基；2) GATTI数据来自2012年Emilia地震事件，M5.9级，峰值加速度0.264 g；3) GOEL等数据来自1971年San Fernando地震及后续地震事件，其中12栋建筑地震事件峰值加速度超过0.15 g；4) HONG等数据来自1993年−1996年中国台湾地区四次非强震事件，原文称结构均处于线弹性状态故无需考虑峰值加速度影响；5) *代指包含受损结构，包括VILA等数据中4栋受损建筑(均位于软土地基上)+杨东晖数据中6栋玉树地震中损伤建筑+GOEL等数据中12栋建筑(原文以峰值加速度是否超过0.15 g区分结构是否发生损伤)。

下载: 导出CSV

| 显示表格

1.3 数据分析和清洗

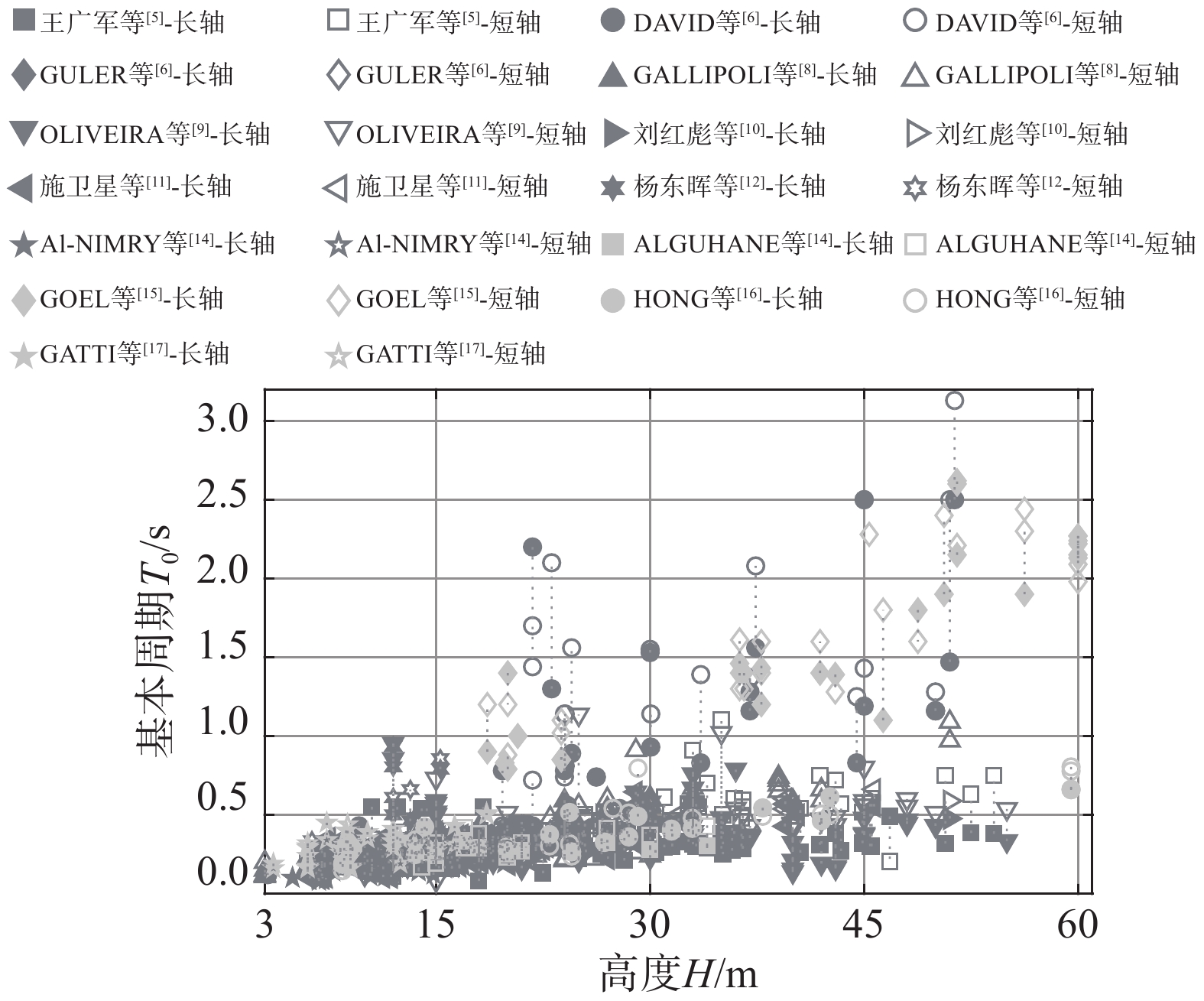
图2展示了结构高度-基本周期散点图，其中不同颜色区分不同文献来源，方形和菱形区分脉动测试和地震激励结果，实心点和空心点区分结构长轴和短轴周期，相同结构的长短轴数据以虚线相连。可以发现，RC框架结构基本周期因多源数据集成方式呈现显著离散性，主要分为由结构平面构型导致的长短轴周期差异(个体内变异性)、同一激励方式和因激励方式不同引发的个体间差异。此外，结构基本周期离散性随结构高度增大而增大，因此呈现显著的高度相依性。

图 2 结构高度-基本周期散点图

Figure 2. Building height – natural period scatterplot

下载: 全尺寸图片幻灯片

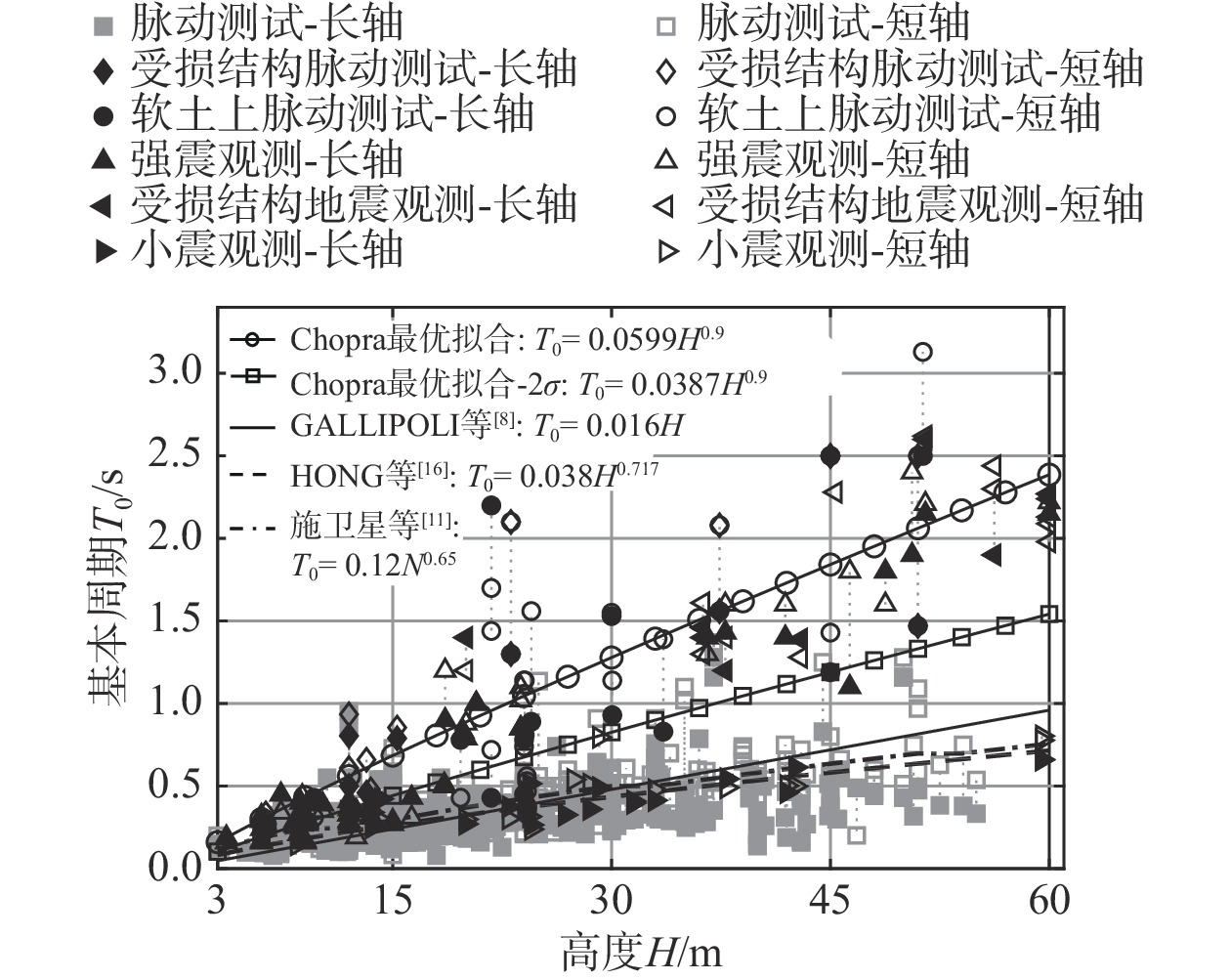
为界定RC框架结构基本周期个体间变异性的合理分布区间，图3进一步区分了显著增大实测数据离散性的数据源(如彩色数据所示)，绘制了代表性学者的经验周期公式，其中缺失高度信息采用层数乘以假设层高3.5 m填充。总结以下重要特征：① Chopra最优拟合减2倍标准差曲线^[15]恰当地将实测数据分为两类，曲线上方为绝大部分强震观测数据和受损及软弱地基结构脉动观测数据(下称I类数据)，曲线下方包含绝大部分环境脉动测试数据和Hong小震观测数据(下称II类数据)；② II类数据量占总比超过90%，其中不同数据源样本分布区间较为一致，基于相关数据的代表性周期曲线(均值意义)也十分接近，验证了不同数据源融合分析的可行性，此时II类数据界定了结构线弹性阶段基本周期的个体间变异性；③ I类数据量稀少占总比不足10%，受损结构和未受损结构样本均分布于Chopra最优拟合曲线上、下，结构是否损伤难以有效界定。同时，I类数据数值偏高且变异性更大，说明强震激励和由此造成的结构损伤，以及软弱地基因素会显著延长结构基本周期并增大个体间变异性。因此，I类数据涵盖了考虑强震、结构损伤和软弱地基影响的基本周期个体间变异性。

图 3 实测数据散点图和经验周期公式

Figure 3. Scatterplot of measured data and empirical formulas

下载: 全尺寸图片幻灯片

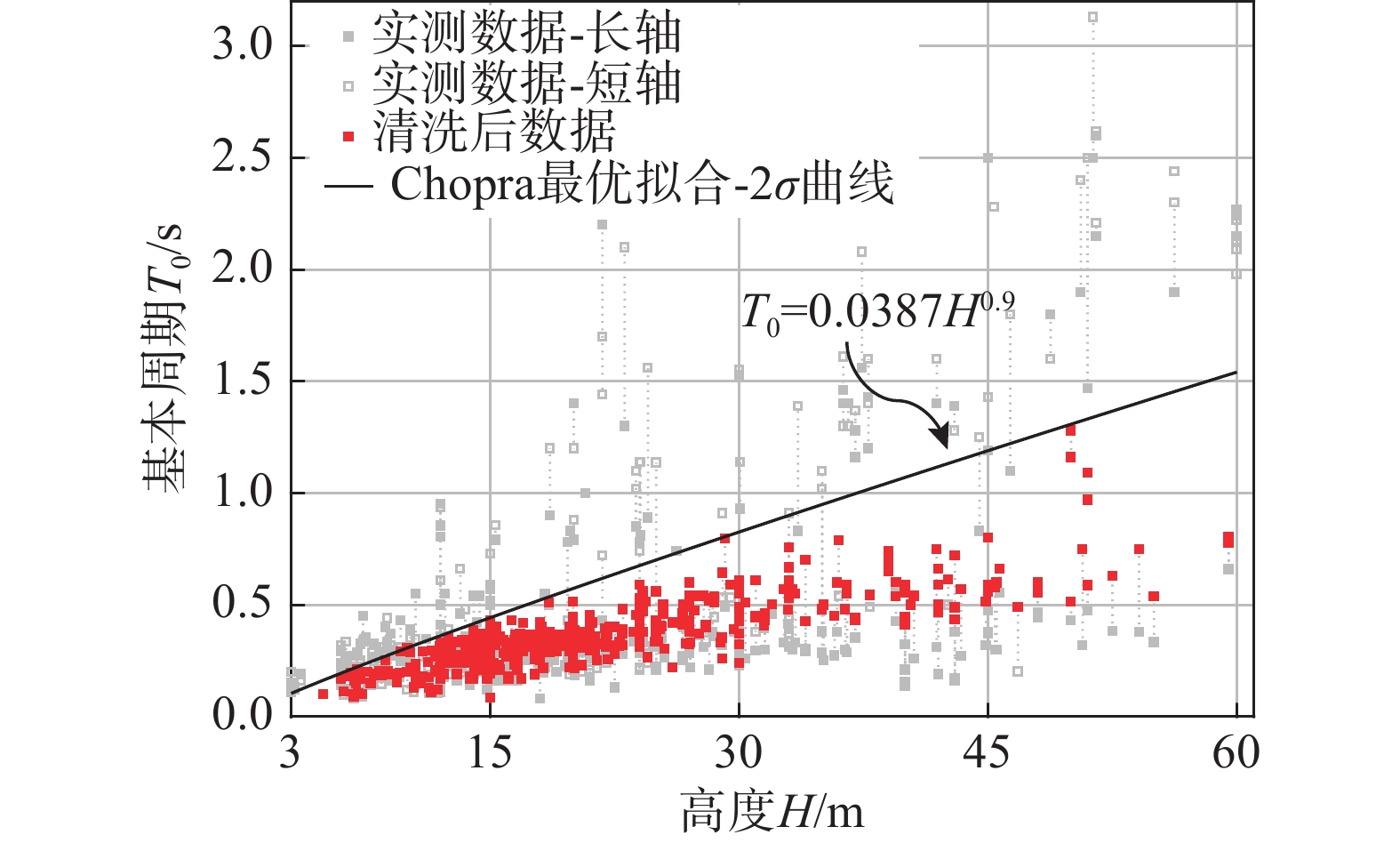
鉴于I类数据样本过小却显著增大数据离散性，其数据质量难以保证，而II类数据质量高且样本充足，本研究将重点关注II类数据，发展考虑RC框架结构线弹性阶段个体间变异性的高度相依基本周期随机函数模型。基于以下步骤对数据库进行清洗：1) 略去数据库中超过Chopra最优拟合减两倍标准差曲线的基本周期实测值；2) 取相同结构长短轴方向基本周期较大值作为该个体结构代表值，消除基本周期个体内变异性。需指出，步骤2)意味着对RC框架结构正交方向抗震性能的保守估计。清洗后的数据如图4所示。

图 4 数据清洗

Figure 4. Data cleaning

下载: 全尺寸图片幻灯片

2 高度相依基本周期随机函数模型

2.1 相依随机变量的随机函数模型

为描述基本周期T₀和高度H之间呈现出的相依随机性，本研究引入由陈等提出的随机函数模型^[27]进行不确定性量化。对于二维非独立随机变量T₀和H，存在以下函数关系：

${T_0} = {{{g}}_1}\left( H \right) + \zeta {{{g}}_2}\left( H \right)$

(1)

式中：ζ为与H无关的标准化随机变量，满足E[ζ]=0、E[ζ²]=1、E[·]为数学期望算子；g₁(H)为T₀关于H的条件期望函数，而g₂(H)为条件标准差函数，分别满足式(2)和式(3)：

${{\rm E}}[ {{T_0}\mid H} ] = {{{g}}_1}( H )$

(2)

${{\rm E}}[ {{{( {{T_0} - {{\rm E}}[ {{T_0}\mid H} ]} )}^2}\mid H} ] = {{g}}_2^2( H )$

(3)

可以发现，相依随机向量(T₀, H)可以通过函数g₁(·)和g₂(·)转化为彼此独立的随机向量(T₀, ζ)，其中，g₁(·)刻画了T₀和H的主要趋势，而g₂(·)描述了T₀关于H的不确定性。g₁(·)和g₂(·)均应为线性或弱非线性，从而避免较大的分析误差，一般可以通过内嵌物理机制或基于样本观测数据的统计回归来确定。在统计回归中，g₁(·)和g₂(·)均应满足均方估计误差最小的最优函数。相应地，随机变量ζ的概率分布亦可根据以上方法决定。一般采用统计推断确定ζ时，ζ第i个样本值为：

${\zeta _i} = {{( {{T_{0,}}_i - {{{g}}_1}( {{H_i}} )} )} / {{{{g}}_2}( {{H_i}} )}}$

(4)

2.2 物理准则-数据驱动建模

多自由度剪切型结构基本周期可由瑞雷法^[28]表示为：

${T_{\text{0}}} = {\text{2}}\pi \sqrt {{{\sum\limits_{j = {\text{1}}}^N {{m_j}\varPsi _j^{\text{2}}} } \Bigg/ {\sum\limits_{j = {\text{1}}}^N {{k_j}{{\left( { {\varPsi _j} - {\varPsi _{j - {\text{1}}}}} \right)}^{\text{2}}}} }}}$

(5)

式中：m_j和k_j分别为结构第j层集中质量和横向剪切刚度；Ψ_j为结构第j层横向变形。若假设结构质量沿高度均匀分布(即m_j=m, j=1, 2, ···, N)以及横向荷载作用下结构横向变形沿楼层线性变化(Ψ_j=j/N)，式(5)可简化为：

$\begin{split} {T_{\text{0}}} =& {\text{2}}\pi \sqrt {{{\frac{m}{N}\sum\limits_{j = {\text{1}}}^N {{j^{\text{2}}}} } \Bigg/ {\sum\limits_{j = {\text{1}}}^N {{k_j}{{\left( {\frac{j}{N} - \frac{{j - {\text{1}}}}{N}} \right)}^{\text{2}}}} }}} =\\& {\text{2}}\pi \sqrt {{{m\left( {N + {\text{1}}} \right)\left( {{\text{2}}N + {\text{1}}} \right)} \Bigg/ {\sum\limits_{j = {\text{1}}}^N {{k_j}} }}} \end{split}$

(6)

式(6)表明，结构基本周期依赖于结构质量、刚度以及结构高度信息。如假设结构刚度沿高度均匀分布(也即k_j=k, j=1,2,···,N)或沿高度线性递减(即k_j=k(N–j+1))时，可导出式(7)、式(8)：

$\begin{split} {T_{\text{0}}} = &{\text{2}}\pi \sqrt {{{m\left( {{\text{2}}{N^2} + {\text{3}}N + {\text{1}}} \right)} /{{\text{6}}k}}} = \\& {c_{\text{1}}}N = {{\bar c}_{\text{1}}}H{\text{, }}N > {\text{6}} \end{split}$

(7)

$\begin{split} {T_{\text{0}}} = &{\text{2}}\pi \sqrt {{{m\left( {{\text{2}}N + {\text{1}}} \right)} / {{\text{3}}{k_N}}}} =\\& {c_{\text{2}}}\sqrt N = {{\bar c}_{\text{2}}}\sqrt H {\text{, }}N > {\text{3}} \end{split}$

(8)

以上两特例中，T₀分别为H和H^1/2的线性函数。更一般地，由上两式归纳出一类应用最为广泛的高度-周期回归公式形式：

${T_{\text{0}}} = \alpha {H^\beta }$

(9)

式(9)表明，多自由度剪切型结构基本周期T₀与幂次高度系数H^β呈线性关系，其比值α取决于结构质量和刚度比值，而幂系数β则取决于结构刚度沿高度的分布情况。根据相关实测统计研究^{[6-9, 13-14, 16]}，β通常为趋近于1的实数，因此式(9)表现为基本周期与结构高度的线性或弱非线性关系。基于此，采用式(10)的线性函数形式建立条件均值函数g₁(H)，此时假设结构刚度沿高度近似均匀分布，基本周期随高度增大而线性增大。

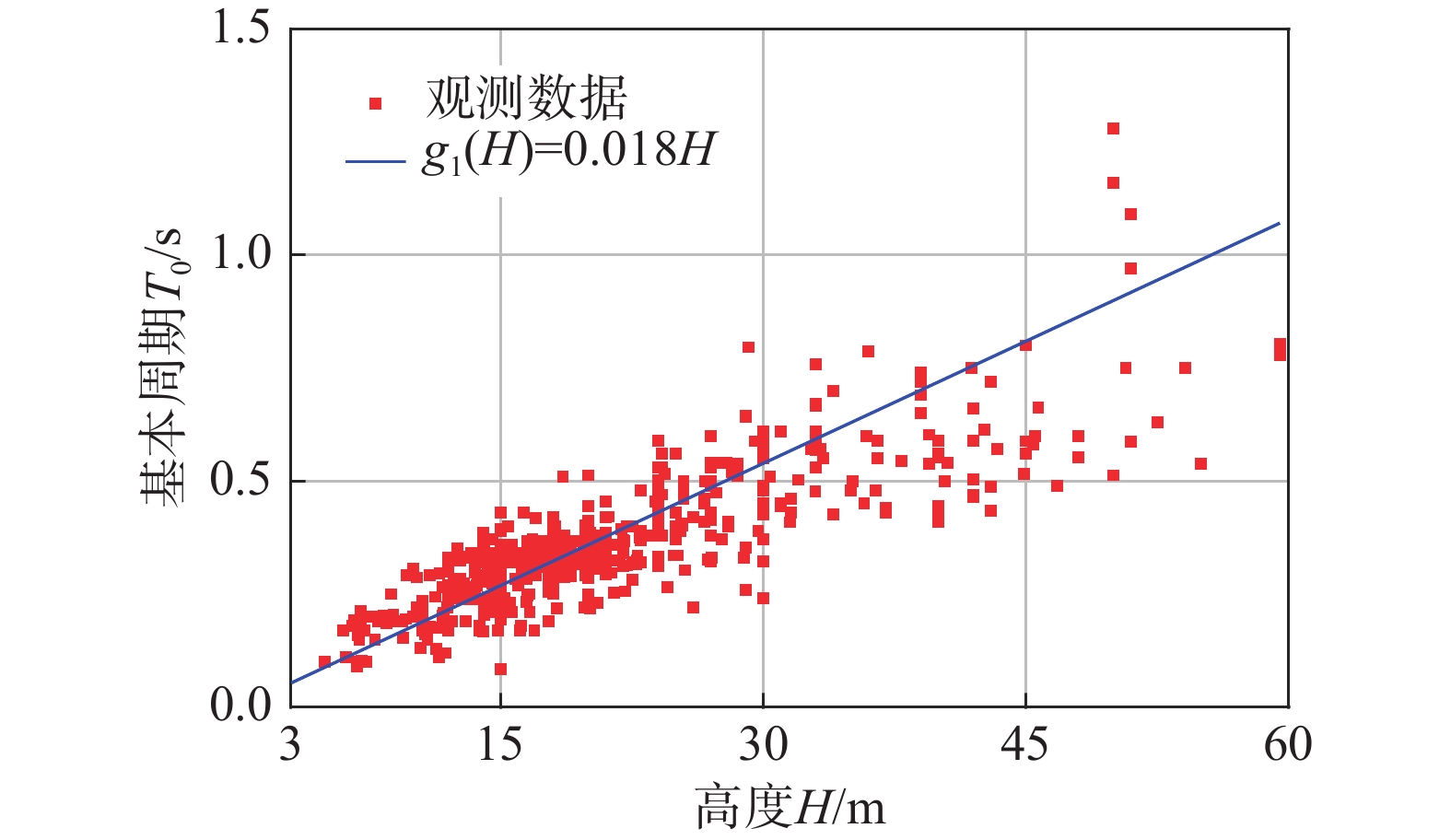
${g_{\text{1}}}\left( H \right) = {C_{\text{1}}}H$

(10)

式中，C₁为待识别参数。根据得到的观测数据样本，采用最小二乘法识别参数C₁，回归结果如图5所示。

图 5 条件均值函数

Figure 5. Conditional mean function

下载: 全尺寸图片幻灯片

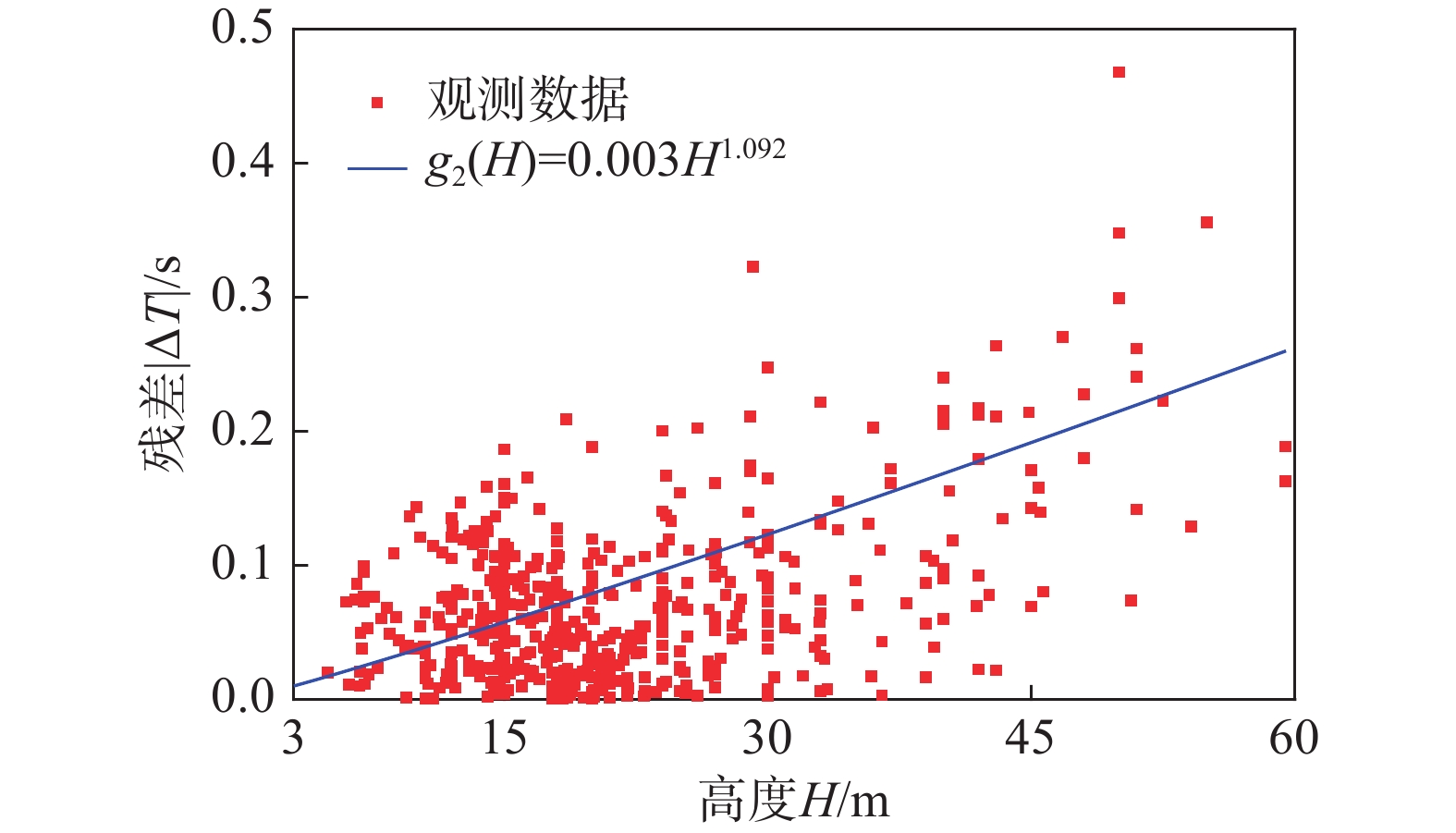
条件标准差函数g₂(H)需要根据观测数据与条件均值函数的残差|ΔT|=|T₀–g₁(H)|确定(如图6所示)。注意，由于式(9)本身的弱非线性形式，因此g₂(H)应为H的弱非线性函数。因此，采用式(11)所示的函数形式建立：

${g_{\text{2}}}\left( H \right) = {C_{\text{2}}}{H^{{C_{\text{3}}}}}$

(11)

图 6 条件标准差函数

Figure 6. Conditional standard deviation function

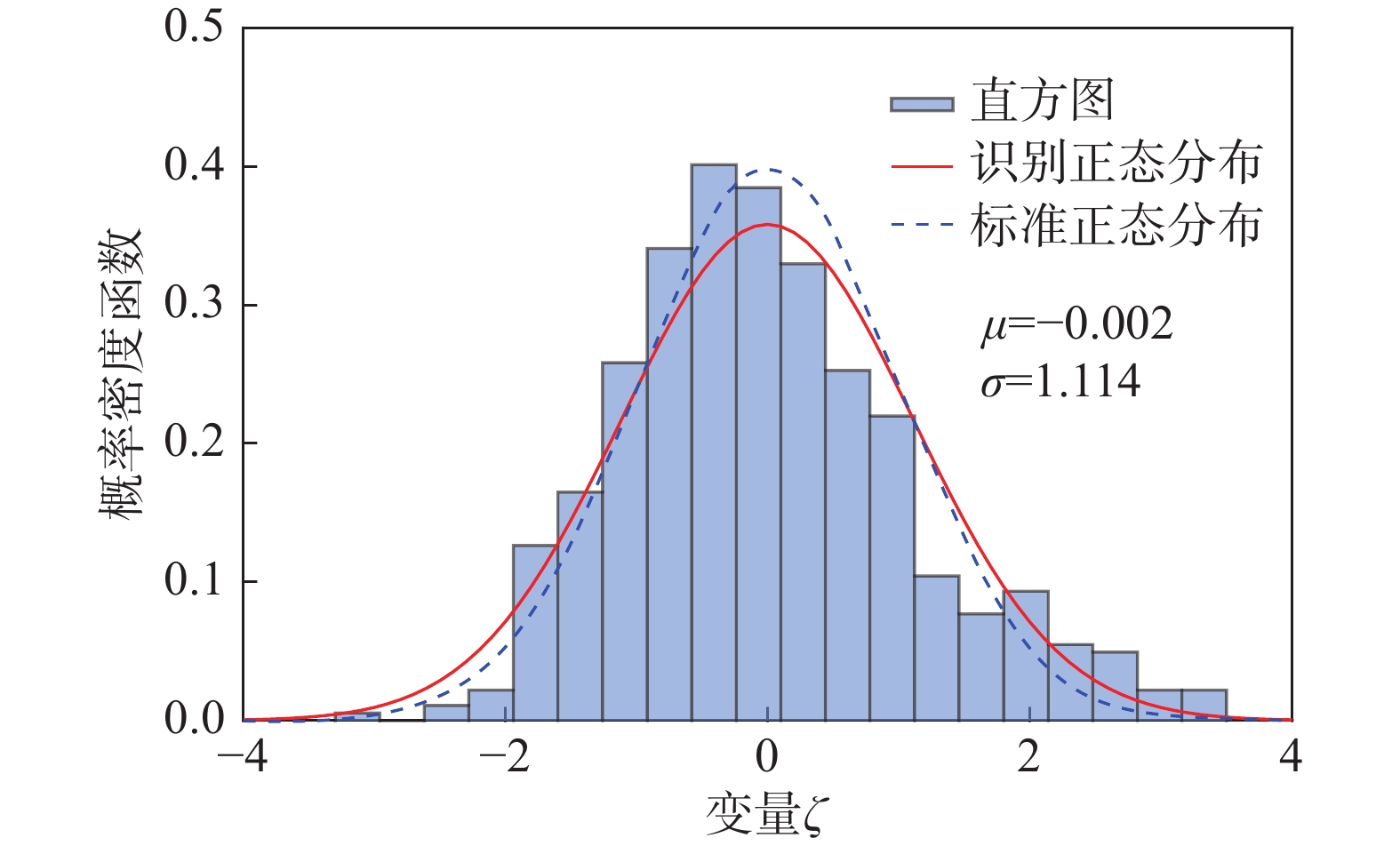
下载: 全尺寸图片幻灯片

基于最小二乘方法对参数C₂和C₃进行识别，g₂(H)的回归结果见图6。接着，根据式(4)得到随机变量ζ的观测数据集，进而确定ζ的分布。ζ的统计直方图和识别边缘概率密度函数(PDF)如图7所示，通过K-S检验，ζ服从接近标准分布的正态分布，其中的偏差可能由于统计误差导致但是可以忽略^[29]，同时可以根据识别分布前二阶矩转换为标准正态分布。至此，RC框架结构高度相依基本周期随机函数模型所有参数识别完毕，模型如式(12)所示：

${T_{\text{0}}} = {C_{\text{1}}}H + \left( {\zeta \sigma + \mu } \right){C_{\text{2}}}{H^{{C_{\text{3}}}}}$

(12)

图 7 随机变量ζ直方图和分布识别

Figure 7. Histogram of variable ζ and distribution identification

下载: 全尺寸图片幻灯片

模型参数取值如表2所示。注意到，当不考虑随机变量ζ并考虑C₃为整数时，式(12)同样可理解为式(9)的泰勒展开式。

表 2 高度相依基本周期随机函数模型参数取值

Table 2. Values of Parameters in height-dependent natural period random function model

参数	取值	参数	取值
C₁	0.018	μ	−0.002
C₂	0.003	σ	1.114
C₃	1.092	−	−

下载: 导出CSV

| 显示表格

2.3 模型验证

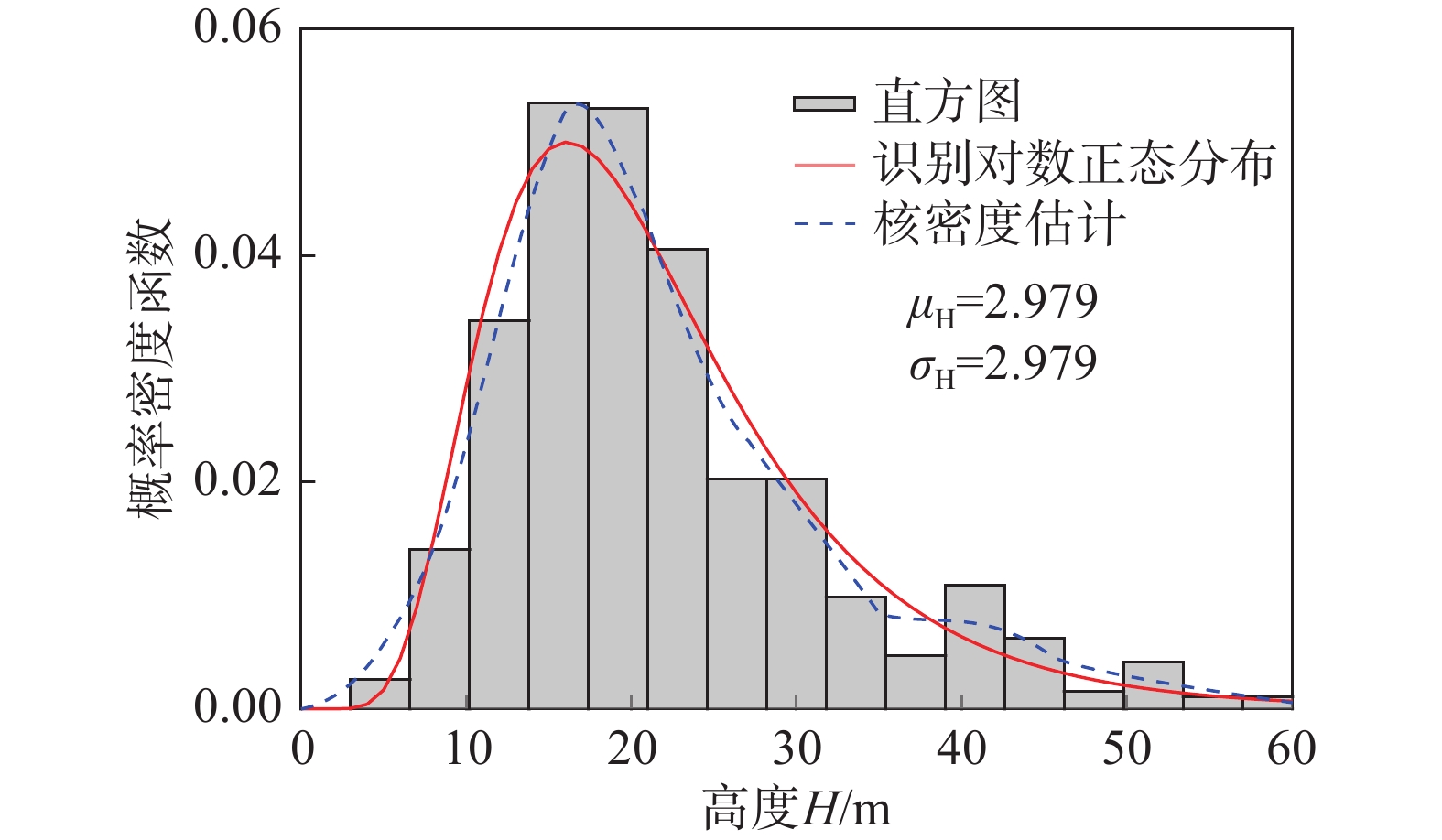
本研究建立的基本周期随机函数模型与观测数据对比如图8所示。注意到g₁(H)±g₂(H)曲线包络绝大部分观测数据，说明本研究模型可以较好捕捉基本周期个体间变异性的上、下边界，同时可以合理反映基本周期变异性随结构高度增大而增大的高度相依性。需指出，本模型可以用于模拟相同高度(此时H为常数)以及高度各异(此时H为变量)时RC框架建筑群基本周期个体间不确定性，尤其当区域内RC框架结构样本充足，此时结构高度H存在统计规律性从而可识别为随机变量。因此，统计识别了数据库中结构高度的概率分布(如图9所示)，结果表明H~LN(2.979,0.488²)。

图 8 高度相依基本周期随机函数模型

Figure 8. Height-dependent natural period random function model

下载: 全尺寸图片幻灯片

图 9 数据库结构高度H直方图和分布识别

Figure 9. Histogram of H and distribution identification

下载: 全尺寸图片幻灯片

2.4 模型应用

基于所提模型，利用变量ζ和H概率信息并结合随机抽样方法，即可生成基本周期随机样本，用于区域建筑地震风险评估。样本量为200和1000的随机样本与观测数据对比如图10(a)、图10(b)所示，随机模拟样本与观测数据吻合良好，并可以对实测数据相对缺少的区间进行可靠的数据填充。

图 10 随机样本生成

Figure 10. Histogram of H and distribution identification

下载: 全尺寸图片幻灯片

需指出，由于工程实践和潜在物理机制，如规范基于安全性考虑对RC框架建筑结构高度的限制，以及基本周期应为大于0的实数，则H和ζ应服从有界分布，否则随模拟样本采样数量的增大，可能会产生少量异常数据。当所需模拟样本较大时，建议RC框架建筑结构高度不超过60 m，同时建议采用g₁(H)–g₂(H)曲线作为基本周期随机样本的下界，此时ζ应服从[−2, ∞)内的截尾正态分布。

3 与经典统计回归随机周期模型对比

3.1 基于高度幂系数的统计回归随机周期模型

针对式(9)的物理机制，一种经典回归分析方法为使用对数变换式lgT₀=lgA+BlgH线性拟合对数坐标下的观测数据，以识别A和B，并计算统计标准差s_e：

${s_{\rm e}} = \sqrt {{{\sum\limits_{i = {\text{1}}}^n {{{\left[ {{\text{lg}}{T_{{\text{0,}}i}} - \left( {A + B{\text{lg}}{H_i}} \right)} \right]}^{\text{2}}}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = {\text{1}}}^n {{{\left[ {{\text{log}}{T_{{\text{0,}}i}} - \left( {A + B{\text{log}}{H_i}} \right)} \right]}^{\text{2}}}} } {\left( {n - {\text{2}}} \right)}}} \right. } {\left( {n - {\text{2}}} \right)}}}$

(13)

式中，n为观测样本数量。

事实上，由式(12)可知，如果引入与统计标准差相关的标准正态变量ξ表征个体间变异性，即可获得基于高度幂系数的统计回归随机周期模型：

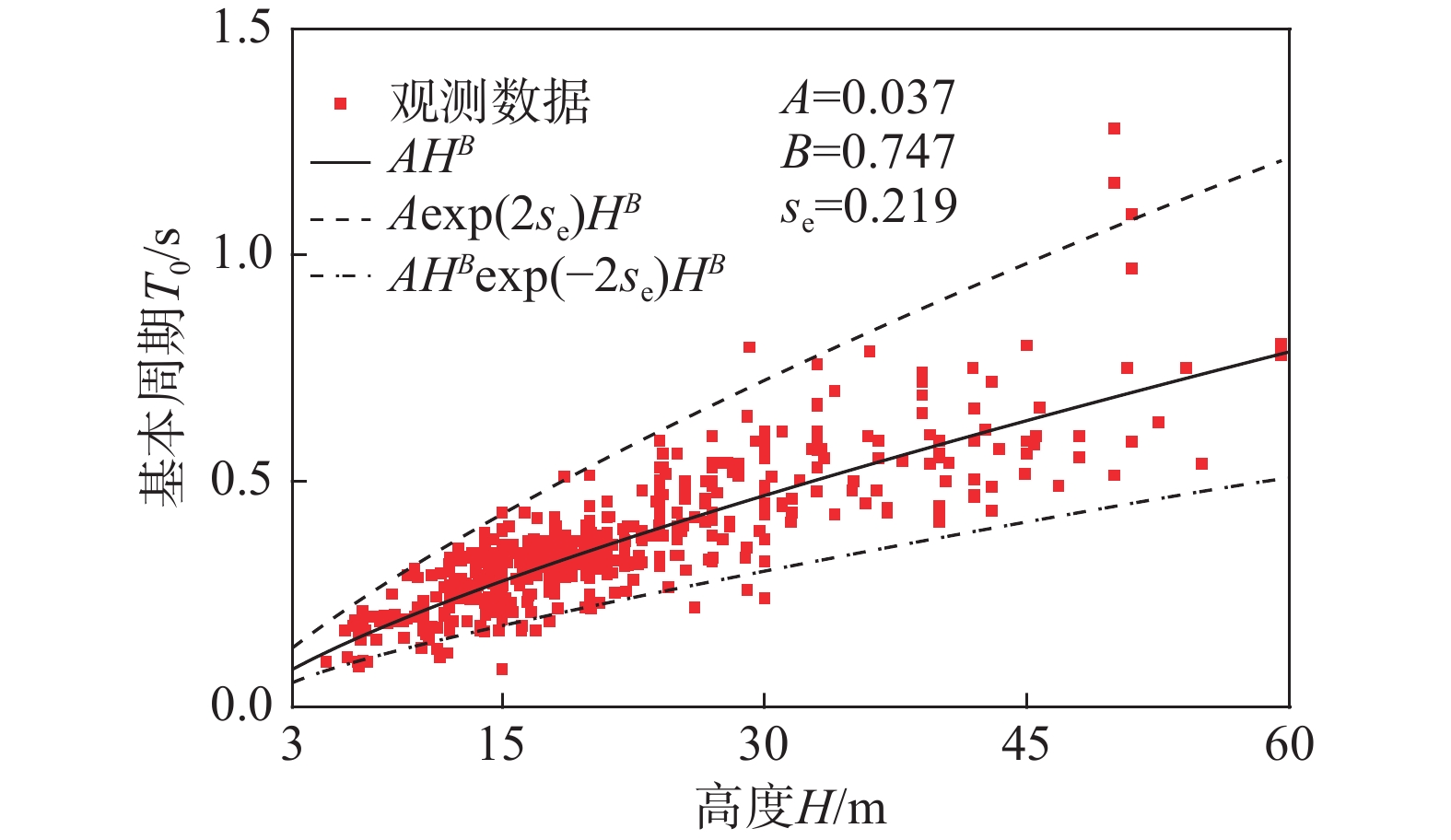
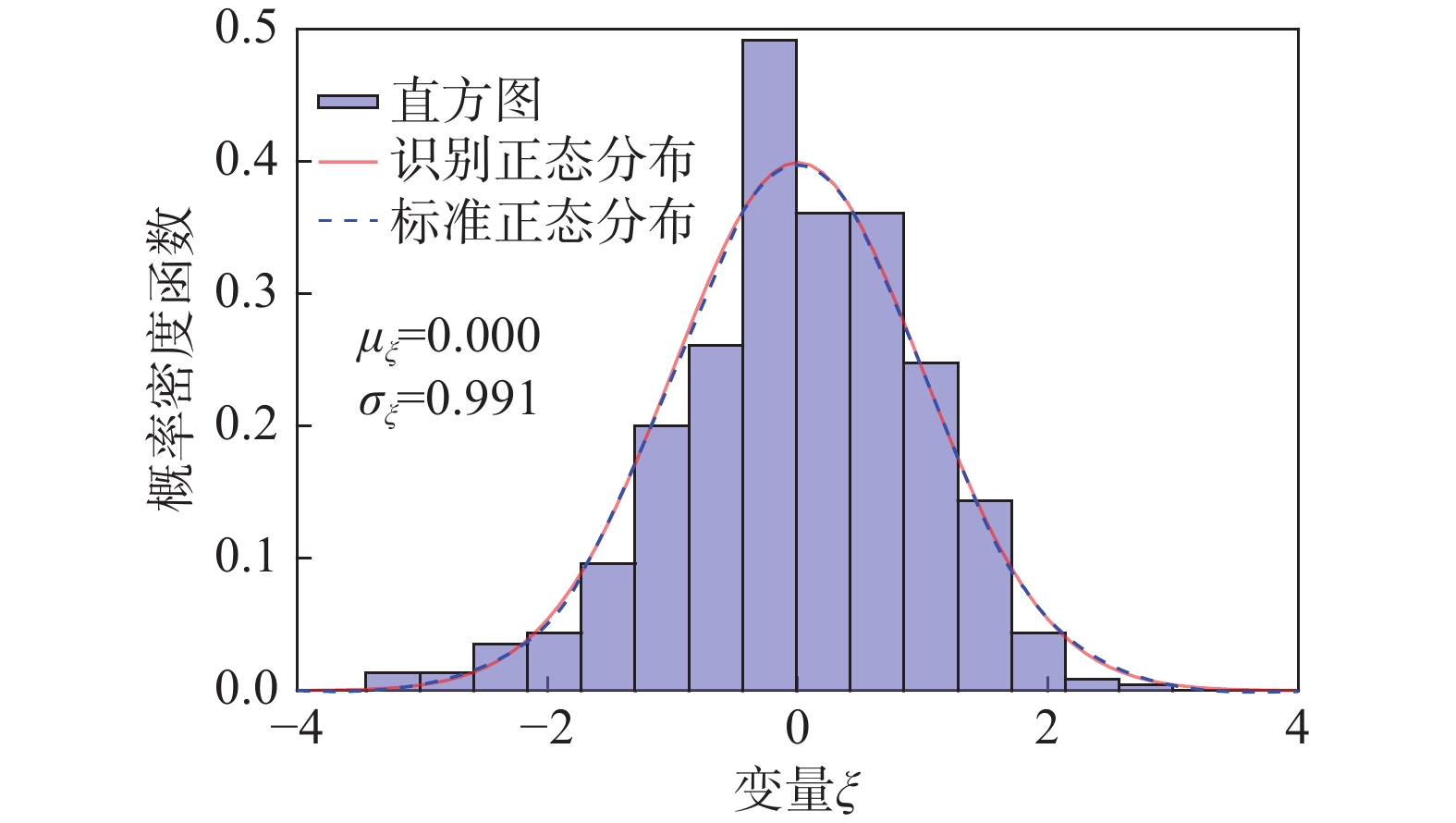
$\begin{split} {\text{lg}}{T_{\text{0}}} =& \left( {{\text{lg}}A + \xi {s_{\rm e}}} \right) + B{\text{lg}}H \Rightarrow\\& {T_{\text{0}}} = A{\text{exp}}\left( {\xi {s_{\rm e}}} \right){H^B} \end{split}$

(14)

根据式(14)，同样可通过生成ξ和H的随机样本获得基本周期随机样本。虽然此前文献中并未明确给出式(14)，由于是从经典方法(式(9))中推演而来，这里仍称为经典模型。为对比经典模型和本研究模型(式(12))，首先根据式(14)拟合观测数据得到模型参数，相应结果如图11所示，并基于观测数据和K-S检验验证了ξ标准正态分布假设的合理性(如图12所示)。

图 11 基于高度幂系数的统计回归随机周期模型

Figure 11. Statistical regression-based random period model

下载: 全尺寸图片幻灯片

图 12 随机变量ξ直方图和分布识别

Figure 12. Histogram of variable ξ and distribution identification

下载: 全尺寸图片幻灯片

3.2 模型对比

表3整理了两类随机模型的函数形式、基本随机变量和联合概率分布。以下将从模型物理机制和概率信息表达两方面对比以说明本研究模型的优越性。

1) 模型物理机制。如前所述，RC框架结构基本周期与结构高度的物理关系T₀=αH^β表明，α和β反映了不同结构几何尺寸、整体质量和刚度物理特性的差异。尤其考虑个体间变异性时，α和β不仅应为H的函数，而且在结构高度相同时也会存在变异性。对比两模型发现，经典模型基本变量的随机取值仅能影响α的大小，β始终为常数，这说明对结构间物理特性的差异反映不足。而本研究模型由于采用类似泰勒展开式的函数形式来表征T₀=αH^β，其基本变量的变化使得α和β因个体结构不同而取值改变，因此可以更合理地在物理机制上反映结构的个体间差异。

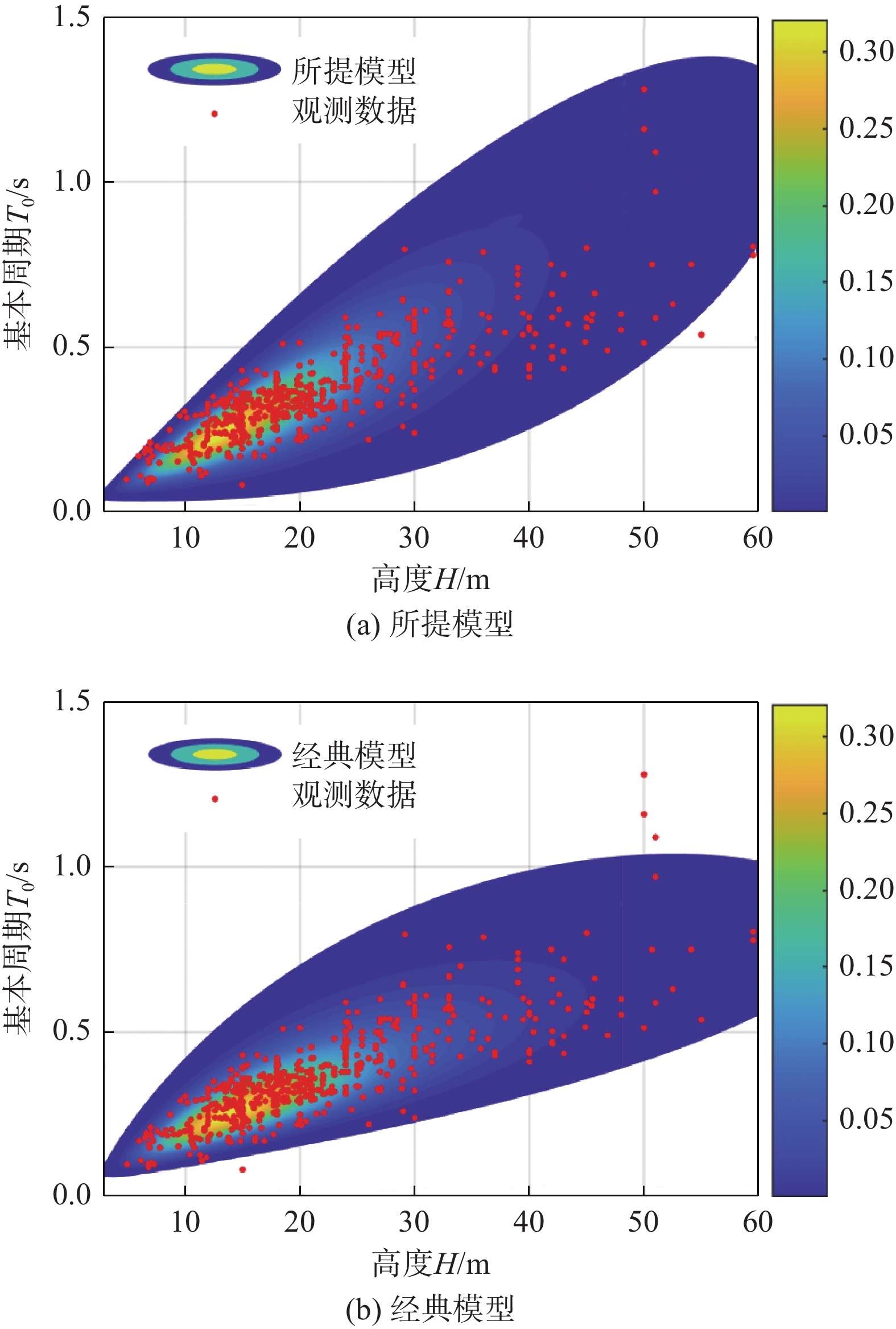
2) 概率信息表达。基于表3给出的两类模型基本周期-结构高度联合概率密度函数理论解，图13绘制了两种模型的联合PDF数值计算结果。从图中可见，两种模型都能较好地反映周期变量关于高度变量的相依性，经典模型更好模拟了数据下限，而所提模型则更吻合数据上限。同时，所提模型更好地覆盖了实测数据，对周期大于1 s的实测点的概率描述更为合理，亦可以对实测数据较少的区域(高于30 m且周期大于1 s)进行有效的数据填充。而经典模型则无法覆盖上述区域，尽管概率意义上同样可以模拟周期大于1 s的实测样本，但显然其概率较低。

表 3 两种随机周期模型对比

Table 3. Comparison of two period models

模型名称	所提模型	经典模型
模型名称	基本周期随机函数模型	统计回归基本周期随机模型
函数形式	${T_{\text{0}}} = {C_{\text{1}}}H + \left( {\zeta \sigma + \mu } \right){C_{\text{2}}}{H^{{C_{\text{3}}}}}$	${T_{\text{0} } } = A{\text{exp} }\left( {\xi {s_{\rm e}} } \right){H^B}$
基本随机变量及其边缘概率	$\zeta {\text{:}}{p_\zeta }\left( \zeta \right) = \dfrac{{\text{1}}}{{\sqrt {{\text{2}}\pi } }}{\text{exp}}\left( { - \dfrac{{{\zeta ^{\text{2}}}}}{{\text{2}}}} \right)$ $H{\text{:}}{p_H}\left( h \right) = \dfrac{{\text{1}}}{{h{\sigma _H}\sqrt {{\text{2}}\pi } }}{\text{exp}}\left( {-\dfrac{{{{\left[ {{\text{ln}}\left( h \right)-{\mu _H}} \right]}^{\text{2}}}}}{{{\text{2}}\sigma _H^2}}} \right)$	$\xi {\text{:}}{p_\xi }\left( \xi \right) = \dfrac{{\text{1}}}{{\sqrt {{\text{2}}\pi } }}{\text{exp}}\left( { - \dfrac{{{\xi ^{\text{2}}}}}{{\text{2}}}} \right)$ $H{\text{:}}{p_H}\left( h \right) = \dfrac{{\text{1}}}{{h{\sigma _H}\sqrt {{\text{2}}\pi } }}{\text{exp}}\left( {-\dfrac{{{{\left[ {{\text{ln}}\left( h \right)-{\mu _H}} \right]}^{\text{2}}}}}{{{\text{2}}\sigma _H^2}}} \right)$
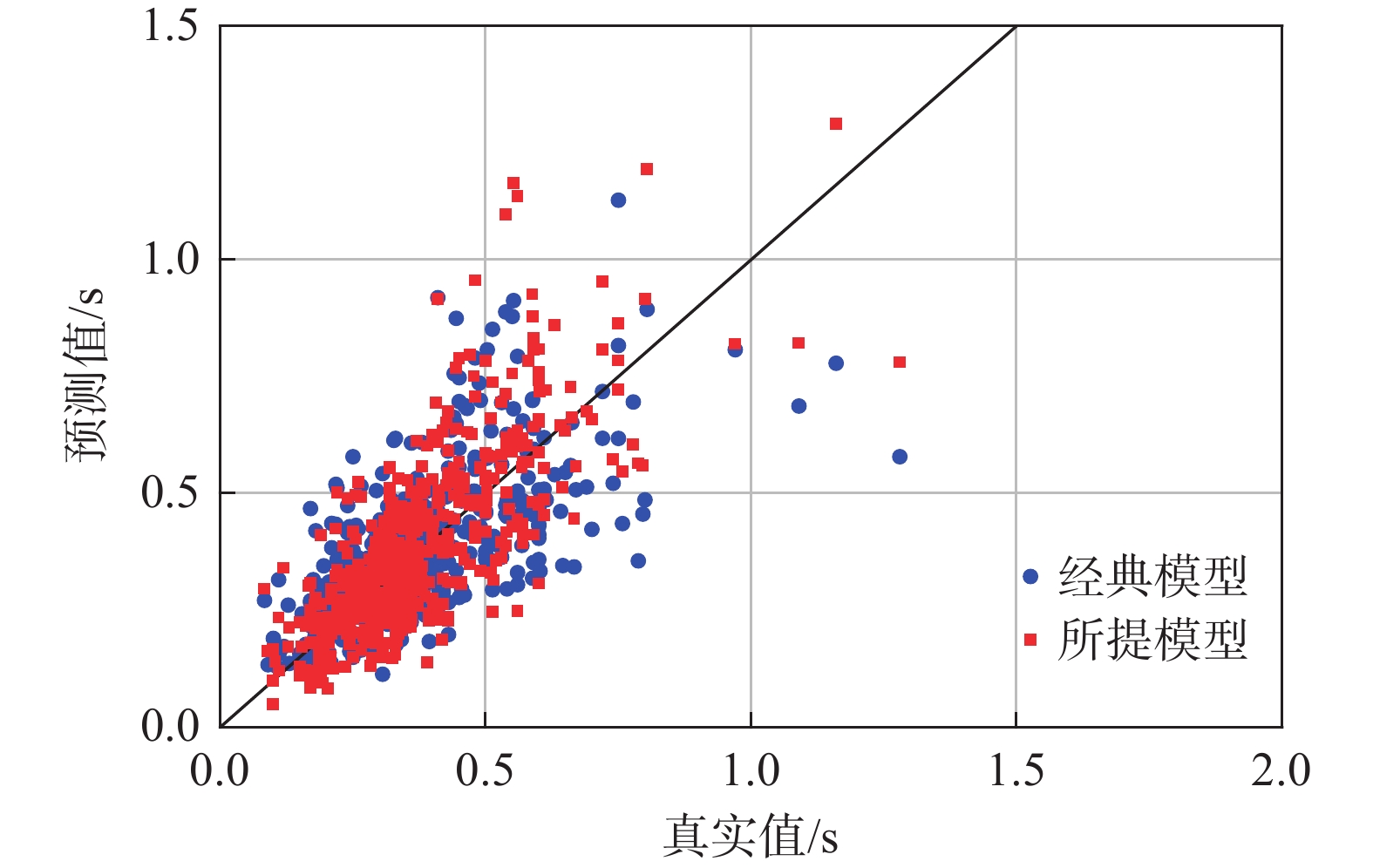
联合概率密度函数	${p_{H{T_0}}}\left( {h{\text{,}}t} \right) = \dfrac{{\text{1}}}{{{C_{\text{2}}}{h^{{C_{\text{3}}}}}}}{p_H}\left( h \right){p_\zeta }\left( {\zeta = \dfrac{{t-{C_{\text{1}}}h}}{{{C_{\text{2}}}{h^{{C_{\text{3}}}}}}}} \right)$	${p_{H{T_0}}}\left( {h{\text{,}}t} \right) = \dfrac{{\text{1}}}{{{s_e}t}}{p_H}\left( h \right){p_\xi }\left( {\xi = \dfrac{{\text{1}}}{{{s_e}}}{\text{ln}}\left( {\dfrac{t}{{A{h^B}}}} \right)} \right)$

下载: 导出CSV

| 显示表格

图 13 基本周期-结构高度联合概率分布对比

Figure 13. Comparison of joint PDFs of T - H

下载: 全尺寸图片幻灯片

图14进一步对比了两种模型生成的随机样本。可以发现，两种模型整体预测能力相当，但对于周期长于1 s的数据，所提模型预测值更接近真实值，经典模型预测值明显偏低。同时，选择3种典型误差指标评估两种模型预测能力，为避免一次随机抽样偶然性，进行1000次重复抽样后取指标均值，结果如表4所示。本研究模型三个指标均低于经典模型，说明本模型预测样本与实测数据的吻合性略优于经典模型。

图 14 随机样本对比

Figure 14. Comparison of randomly generated samples

下载: 全尺寸图片幻灯片

表 4 预测样本误差对比

Table 4. Error comparison of random samples

误差指标	计算公式	所提模型	经典模型
RMSE	$\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }$	0.124 9	0.126 9
MAE	$\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\left\| {{y_i} - \left. {{{\hat y}_i}} \right\|} \right.}$	0.091 4	0.093 4
MAPE/(%)	$\dfrac{{100\text{%} }}{n}\displaystyle\sum\limits_{i = 1}^n {\left\| {\left. {\dfrac{{{y_i} - {{\hat y}_i}}}{{{y_i}}}} \right\|} \right.}$	26.020 0	26.590 0
注：计算公式中n指样本数量； ${y_i}$ 为真实值； ${\hat y_i}$ 为预测值。

下载: 导出CSV

| 显示表格

4 结论

针对既有RC框架结构基本自振周期个体间变异性缺乏合理量化模型的问题，基于大样本实测数据和物理指导-数据驱动的建模方式，建立了高度相依基本周期随机函数模型，与引入个体间变异性的经典统计回归模型的对比验证了所提模型的优越性。主要结论如下：

(1) 本研究所提出的基本周期随机函数模型物理机制明确，函数形式简洁，可以合理反映RC框架结构线弹性阶段基本周期的个体间变异性和变异性的高度相依性。

(2) 与基于高度幂系数的统计回归随机模型对比表明，本研究模型可以更好地反映结构基本周期的物理特性差异以及模拟观测数据的实际分布。而本研究模型在区域地震风险评估中的应用，两种模型生成样本对区域概率地震损伤的影响及其差异，还需进一步探究。

(3) RC框架结构基本周期实测数据表明，相较脉动测试结果，强震激励和由此造成的结构损伤，以及软弱地基因素会显著延长结构基本周期并增大个体间变异性。但此类数据相对稀缺，还需进一步积累以开展有益研究。

图 1 基本周期在区域抗震设计和性能评估中的应用

Figure 1. Applications of natural period in regional seismic design and performance evaluation

下载: 全尺寸图片幻灯片

图 2 结构高度-基本周期散点图

Figure 2. Building height – natural period scatterplot

下载: 全尺寸图片幻灯片

图 3 实测数据散点图和经验周期公式

Figure 3. Scatterplot of measured data and empirical formulas

下载: 全尺寸图片幻灯片

图 4 数据清洗

Figure 4. Data cleaning

下载: 全尺寸图片幻灯片

图 5 条件均值函数

Figure 5. Conditional mean function

下载: 全尺寸图片幻灯片

图 6 条件标准差函数

Figure 6. Conditional standard deviation function

下载: 全尺寸图片幻灯片

图 7 随机变量ζ直方图和分布识别

Figure 7. Histogram of variable ζ and distribution identification

下载: 全尺寸图片幻灯片

图 8 高度相依基本周期随机函数模型

Figure 8. Height-dependent natural period random function model

下载: 全尺寸图片幻灯片

图 9 数据库结构高度H直方图和分布识别

Figure 9. Histogram of H and distribution identification

下载: 全尺寸图片幻灯片

图 10 随机样本生成

Figure 10. Histogram of H and distribution identification

下载: 全尺寸图片幻灯片

图 11 基于高度幂系数的统计回归随机周期模型

Figure 11. Statistical regression-based random period model

下载: 全尺寸图片幻灯片

图 12 随机变量ξ直方图和分布识别

Figure 12. Histogram of variable ξ and distribution identification

下载: 全尺寸图片幻灯片

图 13 基本周期-结构高度联合概率分布对比

Figure 13. Comparison of joint PDFs of T - H

下载: 全尺寸图片幻灯片

图 14 随机样本对比

Figure 14. Comparison of randomly generated samples

下载: 全尺寸图片幻灯片

表 1 数据库信息

Table 1 Information of database

年份	学者	结构形式	激励方法	测试地区	建筑数量	周期数据数量
1988	王广军等^[5]	MRCF	脉动测试	中国北京、上海等	28	48
1988	王广军等^[5]	RCF		中国北京、上海等	55	110
1995	DAVID等*^[6]	RCF		墨西哥	32	63
2008	GULER等^[7]	RCF		土耳其	6	12
2010	GALLIPOLI等^[8]	RCF		意大利、马其顿共和国	113	176
2010	OLIVEIRA等^[9]	RCF		葡萄牙	74	147
2011	刘红彪等^[10]	RCF		中国四川	6	12
2013	施卫星等^[11]	MRCF		中国上海	62	124
2013	施卫星等^[11]	RCF		中国上海	156	312
2013	杨东晖*^[12]	RCF		中国青海	6	12
2014	AL-NIMRY等^[13]	RCF		约旦	23	46
2016	ALGUHANE等^[14]	RCF		麦地那	14	21
1997	GOEL等*^[15]	RCF	地震激励	美国加利福利亚	28	54
2000	HONG等^[16]	RCF		中国台湾	18	35
2018	GATTI^[17]	RCF		意大利	20	40
注：1) DAVID等数据中8栋位于硬土地基，其余24栋位于软土地基；2) GATTI数据来自2012年Emilia地震事件，M5.9级，峰值加速度0.264 g；3) GOEL等数据来自1971年San Fernando地震及后续地震事件，其中12栋建筑地震事件峰值加速度超过0.15 g；4) HONG等数据来自1993年−1996年中国台湾地区四次非强震事件，原文称结构均处于线弹性状态故无需考虑峰值加速度影响；5) *代指包含受损结构，包括VILA等数据中4栋受损建筑(均位于软土地基上)+杨东晖数据中6栋玉树地震中损伤建筑+GOEL等数据中12栋建筑(原文以峰值加速度是否超过0.15 g区分结构是否发生损伤)。

下载: 导出CSV

表 2 高度相依基本周期随机函数模型参数取值

Table 2 Values of Parameters in height-dependent natural period random function model

参数	取值	参数	取值
C₁	0.018	μ	−0.002
C₂	0.003	σ	1.114
C₃	1.092	−	−

下载: 导出CSV

表 3 两种随机周期模型对比

Table 3 Comparison of two period models

模型名称	所提模型	经典模型
模型名称	基本周期随机函数模型	统计回归基本周期随机模型
函数形式	${T_{\text{0}}} = {C_{\text{1}}}H + \left( {\zeta \sigma + \mu } \right){C_{\text{2}}}{H^{{C_{\text{3}}}}}$	${T_{\text{0} } } = A{\text{exp} }\left( {\xi {s_{\rm e}} } \right){H^B}$
基本随机变量及其边缘概率	$\zeta {\text{:}}{p_\zeta }\left( \zeta \right) = \dfrac{{\text{1}}}{{\sqrt {{\text{2}}\pi } }}{\text{exp}}\left( { - \dfrac{{{\zeta ^{\text{2}}}}}{{\text{2}}}} \right)$ $H{\text{:}}{p_H}\left( h \right) = \dfrac{{\text{1}}}{{h{\sigma _H}\sqrt {{\text{2}}\pi } }}{\text{exp}}\left( {-\dfrac{{{{\left[ {{\text{ln}}\left( h \right)-{\mu _H}} \right]}^{\text{2}}}}}{{{\text{2}}\sigma _H^2}}} \right)$	$\xi {\text{:}}{p_\xi }\left( \xi \right) = \dfrac{{\text{1}}}{{\sqrt {{\text{2}}\pi } }}{\text{exp}}\left( { - \dfrac{{{\xi ^{\text{2}}}}}{{\text{2}}}} \right)$ $H{\text{:}}{p_H}\left( h \right) = \dfrac{{\text{1}}}{{h{\sigma _H}\sqrt {{\text{2}}\pi } }}{\text{exp}}\left( {-\dfrac{{{{\left[ {{\text{ln}}\left( h \right)-{\mu _H}} \right]}^{\text{2}}}}}{{{\text{2}}\sigma _H^2}}} \right)$
联合概率密度函数	${p_{H{T_0}}}\left( {h{\text{,}}t} \right) = \dfrac{{\text{1}}}{{{C_{\text{2}}}{h^{{C_{\text{3}}}}}}}{p_H}\left( h \right){p_\zeta }\left( {\zeta = \dfrac{{t-{C_{\text{1}}}h}}{{{C_{\text{2}}}{h^{{C_{\text{3}}}}}}}} \right)$	${p_{H{T_0}}}\left( {h{\text{,}}t} \right) = \dfrac{{\text{1}}}{{{s_e}t}}{p_H}\left( h \right){p_\xi }\left( {\xi = \dfrac{{\text{1}}}{{{s_e}}}{\text{ln}}\left( {\dfrac{t}{{A{h^B}}}} \right)} \right)$

下载: 导出CSV

表 4 预测样本误差对比

Table 4 Error comparison of random samples

误差指标	计算公式	所提模型	经典模型
RMSE	$\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }$	0.124 9	0.126 9
MAE	$\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\left\| {{y_i} - \left. {{{\hat y}_i}} \right\|} \right.}$	0.091 4	0.093 4
MAPE/(%)	$\dfrac{{100\text{%} }}{n}\displaystyle\sum\limits_{i = 1}^n {\left\| {\left. {\dfrac{{{y_i} - {{\hat y}_i}}}{{{y_i}}}} \right\|} \right.}$	26.020 0	26.590 0
注：计算公式中n指样本数量； ${y_i}$ 为真实值； ${\hat y_i}$ 为预测值。

下载: 导出CSV

参考文献(29)

[1]	闫佳琦, 陈相兆, 孙柏涛. 地震人员伤亡评估方法及损失评估系统综述[J]. 工程力学, 2021, 38(12): 1 − 16. doi: 10.6052/j.issn.1000-4750.2020.11.0861 YAN Jiaqi, CHEN Xiangzhao, SUN Baitao. Review of estimation methods and systems used to predict earthquake casualties [J]. Engineering Mechanics, 2021, 38(12): 1 − 16. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.11.0861
[2]	KANG C, KWON O S, SONG J H. Evaluation of correlation between engineering demand parameters of structures for seismic system reliability analysis [J]. Structural Safety, 2021, 93: 102133. doi: 10.1016/j.strusafe.2021.102133
[3]	王东明, 高永武. 城市建筑群概率地震灾害风险评估研究[J]. 工程力学, 2019, 36(7): 165 − 173. doi: 10.6052/j.issn.1000-4750.2018.06.0331 WANG Dongming, GAO Yongwu. Study on the probabilistic seismic disaster risk assessment of urban building complex [J]. Engineering Mechanics, 2019, 36(7): 165 − 173. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.06.0331
[4]	陈隽, 宋颖豪, 王泽涛. 建筑基本周期多因素机器学习预测模型[J]. 工程力学, 2024, 41(2): 171 − 179. doi: 10.6052/j.issn.1000-4750.2022.03.0274 CHEN Jun, SONG Yinghao, WANG Zetao. Multi-factor machine learning prediction model for the natural period of buildings [J]. Engineering Mechanics, 2024, 41(2): 171 − 179. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.03.0274
[5]	王广军, 樊水荣. 建筑自振周期计算方法和实测资料手册 [M]. 北京: 中国建筑科学研究院, 1988. WANG Guangjun, FAN Shuirong. Manual of calculation method and measured data for building natural vibration period [M]. Beijing: China Academy of Building Research, 1988. (in Chinese)
[6]	DAVID M V, RICARDO G A. Propiedades dinámicas de edificios de la ciudad de México [J]. Revista de Ingeniería Sismica, 1995(51): 25 − 45.
[7]	GULER K, YUKSEL E, KOCAK A. Estimation of the fundamental vibration period of existing RC buildings in Turkey utilizing ambient vibration records [J]. Journal of Earthquake Engineering, 2008, 12(Suppl 2): 140 − 150.
[8]	GALLIPOLI M R, MUCCIARELLI M, ŠKET-MOTNIKAR B, et al. Empirical estimates of dynamic parameters on a large set of European buildings [J]. Bulletin of Earthquake Engineering, 2010, 8(3): 593 − 607. doi: 10.1007/s10518-009-9133-6
[9]	OLIVEIRA C S, NAVARRO M. Fundamental periods of vibration of RC buildings in Portugal from in-situ experimental and numerical techniques [J]. Bulletin of Earthquake Engineering, 2010, 8(3): 609 − 642. doi: 10.1007/s10518-009-9162-1
[10]	刘红彪, 郭迅, 梁永朵, 等. 9度设防区房屋结构自振周期测试[J]. 建筑结构, 2011, 41(5): 60 − 62,77. doi: 10.19701/j.jzjg.2011.05.014 LIU Hongbiao, GUO Xun, LIANG Yongduo, et al. Structural natural period measurement in seismic fortification intensity 9 [J]. Building Structure, 2011, 41(5): 60 − 62,77. (in Chinese) doi: 10.19701/j.jzjg.2011.05.014
[11]	施卫星, 陈希, 曹加良. 多因素型结构基本自振周期预测模型的研究[J]. 工程力学, 2013, 30(3): 146 − 151. doi: 10.6052/j.issn.1000-4750.2011.09.0617 SHI Weixing, CHEN Xi, CAO Jialiang. Multi-factor predictive models of structural fundamental natural period [J]. Engineering Mechanics, 2013, 30(3): 146 − 151. (in Chinese) doi: 10.6052/j.issn.1000-4750.2011.09.0617
[12]	杨东晖. 地震受损房屋结构自振特性测试[J]. 世界地震工程, 2013, 29(1): 92 − 97. doi: 10.3969/j.issn.1007-6069.2013.01.014 YANG Donghui. Field test to natural characteristics of earthquake damaged building structures [J]. World Earthquake Engineering, 2013, 29(1): 92 − 97. (in Chinese) doi: 10.3969/j.issn.1007-6069.2013.01.014
[13]	AL-NIMRY H, RESHEIDAT M, AL-JAMAL M. Ambient vibration testing of low and medium rise infilled RC frame buildings in Jordan [J]. Soil Dynamics and Earthquake Engineering, 2014, 59: 21 − 29. doi: 10.1016/j.soildyn.2014.01.002
[14]	ALGUHANE T M, FAYED M N, HUSSIN A, et al. Simplified equations for estimating the period of vibration of Ksa existing building Using Ambient vibration testing [J]. Journal of Multidisciplinary Engineering Science and Technology, 2016, 3(3): 4335 − 4343.
[15]	GOEL R K, CHOPRA A K. Period formulas for moment-resisting frame buildings [J]. Journal of Structural Engineering, 1997, 123(11): 1454 − 1461. doi: 10.1061/(ASCE)0733-9445(1997)123:11(1454)
[16]	HONG L L, HWANG W L. Empirical formula for fundamental vibration periods of reinforced concrete buildings in Taiwan [J]. Earthquake Engineering & Structural Dynamics, 2000, 29(3): 327 − 337.
[17]	GATTI M. Elastic period of vibration calculated experimentally in buildings hosting permanent GPS stations [J]. Earthquake Engineering and Engineering Vibration, 2018, 17(3): 607 − 625. doi: 10.1007/s11803-018-0466-5
[18]	阎红霞, 杨庆山, 秦敬伟, 等. 各国规范中RC框架自振周期的对比和探讨[J]. 振动与冲击, 2012, 31(11): 108 − 113. doi: 10.3969/j.issn.1000-3835.2012.11.023 YAN Hongxia, YANG Qingshan, QIN Jingwei, et al. Comparison and comment for computing natural vibration period of RC frames in codes of some countries [J]. Journal of Vibration and Shock, 2012, 31(11): 108 − 113. (in Chinese) doi: 10.3969/j.issn.1000-3835.2012.11.023
[19]	GB 50011−2010, 建筑抗震设计规范 [S]. 北京: 中国建筑工业出版社, 2010. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[20]	FEMA. Multi-Hazard loss estimation methodology-earthquake model technical manual (HAZUS^®-MH 2.1) [R]. Washington, DC: Federal Emergency Management Agency, 2012.
[21]	王广军, 樊水荣. 建筑自振周期经验公式的述评(下)[J]. 世界地震工程, 1989, 5(4): 35 − 43. WANG Guangjun, FAN Shuirong. A review of empirical formulas for the natural vibration period of buildings (below) [J]. World Earthquake Engineering, 1989, 5(4): 35 − 43. (in Chinese)
[22]	FRITZ W P, JONES N P, IGUSA T. Predictive models for the median and variability of building period and damping [J]. Journal of Structural Engineering, 2009, 135(5): 576 − 586. doi: 10.1061/(ASCE)0733-9445(2009)135:5(576)
[23]	CROWLEY H, PINHO R, BOMMER J J. A probabilistic displacement-based vulnerability assessment procedure for earthquake loss estimation [J]. Bulletin of Earthquake Engineering, 2004, 2(2): 173 − 219. doi: 10.1007/s10518-004-2290-8
[24]	ROMÃO X, CASTRO J M, PEREIRA N, et al. European physical vulnerability models (SERA Deliverable) [R]. Portugal: University of Porto, 2019.
[25]	WANG Z T, CHEN J, SHEN J X. Multi-factor and multi-level predictive models of building natural period [J]. Engineering Structures, 2021, 242: 112622. doi: 10.1016/j.engstruct.2021.112622
[26]	FRITZ W P. Period and damping selection for the design and analysis of building structures [D]. Baltimore: The Johns Hopkins University, 2004.
[27]	陈建兵, 万志强, 宋鹏彦. 相依随机变量的随机函数模型[J]. 中国科学: 物理学力学天文学, 2018, 48(1): 103 − 112. CHEN Jianbing, WAN Zhiqiang, SONG Pengyan. Random function model for dependent random variables [J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2018, 48(1): 103 − 112. (in Chinese)
[28]	GOEL R K, CHOPRA A K. Vibration properties of buildings determined from recorded earthquake motions [R]. Berkeley: University of California, 1997.
[29]	WAN Z Q, CHEN J B, LI J. Probability density evolution analysis of stochastic seismic response of structures with dependent random parameters [J]. Probabilistic Engineering Mechanics, 2020, 59: 103032. doi: 10.1016/j.probengmech.2020.103032

施引文献(1)

期刊类型引用(1)

陈楠, 项梦洁, 庞云升, 许泽坤, 陈隽. 城市区域建筑群震灾分析的统一参数化建模方法. 建筑结构学报. 2025(07)

百度学术

其他类型引用(0)

资源附件(0)

图(14) / 表(4)

计量

文章访问数: 261
HTML全文浏览量: 78
PDF下载量: 56
被引次数: 1

1 RC框架结构基本周期实测数据库
1.1 数据收集标准
1.2 数据库概况
1.3 数据分析和清洗
2 高度相依基本周期随机函数模型
2.1 相依随机变量的随机函数模型
2.2 物理准则-数据驱动建模
2.3 模型验证
2.4 模型应用
3 与经典统计回归随机周期模型对比
3.1 基于高度幂系数的统计回归随机周期模型
3.2 模型对比
4 结论

1 RC框架结构基本周期实测数据库
1.1 数据收集标准
1.2 数据库概况
1.3 数据分析和清洗
2 高度相依基本周期随机函数模型
2.1 相依随机变量的随机函数模型
2.2 物理准则-数据驱动建模
2.3 模型验证
2.4 模型应用
3 与经典统计回归随机周期模型对比
3.1 基于高度幂系数的统计回归随机周期模型
3.2 模型对比
4 结论

参考文献(29)

施引文献(1)

资源附件(0)

RC框架结构基本自振周期个体间不确定性量化

作者简介: 项梦洁(1994−)，女，湖北人，博士生，从事区域建筑地震风险及可靠性评估研究 (E-mail: xmengjie0930@163.com)

通讯作者: 陈 隽(1972−)，男，河南人，教授，博士，博导，主要从事工程结构防灾、土木工程大数据方面的研究 (E-mail: cejchen@tongji.edu.cn)

计量

出版历程

QUANTIFICATION OF INTER-BUILDING VARIABILITY OF NATURAL VIBRATION PERIOD OF RC FRAME BUILDINGS

1 RC框架结构基本周期实测数据库

1.1 数据收集标准

1.2 数据库概况

1.3 数据分析和清洗

2 高度相依基本周期随机函数模型

2.1 相依随机变量的随机函数模型

2.2 物理准则-数据驱动建模

2.3 模型验证

2.4 模型应用

3 与经典统计回归随机周期模型对比

3.1 基于高度幂系数的统计回归随机周期模型

3.2 模型对比

4 结论

期刊类型引用(1)

其他类型引用(0)

计量

出版历程

目录

1 RC框架结构基本周期实测数据库

1.1 数据收集标准

1.2 数据库概况

1.3 数据分析和清洗

2 高度相依基本周期随机函数模型

2.1 相依随机变量的随机函数模型

2.2 物理准则-数据驱动建模

2.3 模型验证

2.4 模型应用

3 与经典统计回归随机周期模型对比

3.1 基于高度幂系数的统计回归随机周期模型

3.2 模型对比

4 结论

作者简介:
项梦洁(1994−)，女，湖北人，博士生，从事区域建筑地震风险及可靠性评估研究 (E-mail: xmengjie0930@163.com)

通讯作者:
陈　隽(1972−)，男，河南人，教授，博士，博导，主要从事工程结构防灾、土木工程大数据方面的研究 (E-mail: cejchen@tongji.edu.cn)