中国木结构古建筑具有独特的结构形式，其最主要的特点就是梁与柱组成的柱架系统及榫卯连接方法。据相关研究得出，榫卯连接的木结构节点表现出一定的转动能力，并具有良好的耗能能力^[1]。因此，研究榫卯节点在水平往复荷载作用下的力学性能具有较高的科研价值与社会意义。

目前，学者对木结构古建筑的研究主要集中在榫卯连接的力学性能及柱体摇摆对结构的影响等方面。关于榫卯节点，郭婷等^[2]通过试验研究与有限元分析得出，榫卯节点具有较好的转动能力但其节点处抗弯承载力较弱；谢启芳等^[3]基于理论分析推导出燕尾榫节点弯矩-转角理论计算公式，为木结构受力分析提供依据；XUE等^[4]、LI等^[5]和苏海红等^[6]对透榫节点的试验研究表明，连接紧密的榫卯节点极限承载能力、初始刚度均得到提升，但其榫卯节点的延性降低；谢启芳等^[7]和潘毅等^[8]基于理论分析提出了榫卯节点M-θ三折线模型来预测节点的力学性能；王展光等^[9]和石昂等^[10]对西南地区榫卯节点进行弯曲单调加载试验及ABAQUS数值模拟，对比分析了透榫和直榫节点的抗弯性能，推导出了节点的弯矩理论公式。

关于柱体摇摆效应，王娟等^[11]发现木构架屈服后柱体摇摆使结构发生整体的抬升摆动，具有较好的整体性能，提高了木构架的耗能能力；潘毅等^[12]和HE等^[13]研究了考虑柱体摇摆作用下木结构柱脚节点的力学性能，建立了柱脚节点的弯矩-转角(M-θ)力学模型；贺俊筱等^[14]和谢启芳等^[15]通过试验研究发现木柱初始的抗侧刚度最大，滞回曲线具有一定的“捏拢”效应；张锡成等^[16]在研究榫卯柱架抗侧行为时考虑了榫卯节点的半刚性及木柱的摇摆特性等因素，提出了能准确计算柱架在弹性阶段内的抗侧刚度计算公式。

综上所述，相关学者对于半刚性榫卯节点及柱体的“摇摆效应”做了大量的研究，发现柱体的摇摆可以提高结构的抗侧刚度，考虑柱体摇摆的柱架抗侧刚度计算值与试验值的度误差较小。学者在对木结构古建筑非线性动力分析时考虑了半刚性榫卯节点及斗栱的影响等因素，但未能考虑柱体的“摇摆效应”。因此，对于木结构非线性地震分析还需深入研究。为此，本文对考虑榫卯连接的柱架体系的动力性能进行研究，并考虑柱体摇摆、榫卯节点及斗栱节点非线性结构特性的影响，提出殿堂式木结构古建筑的动力简化分析模型，在此基础上模拟结构在地震作用下的动力响应，并通过振动台试验结果验证了上述模型的准确性，最后基于简化模型进一步研究了各结构参数变化对地震位移响应的影响规律。

1   柱体的摇摆效应

1.1   木结构中柱体的摇摆

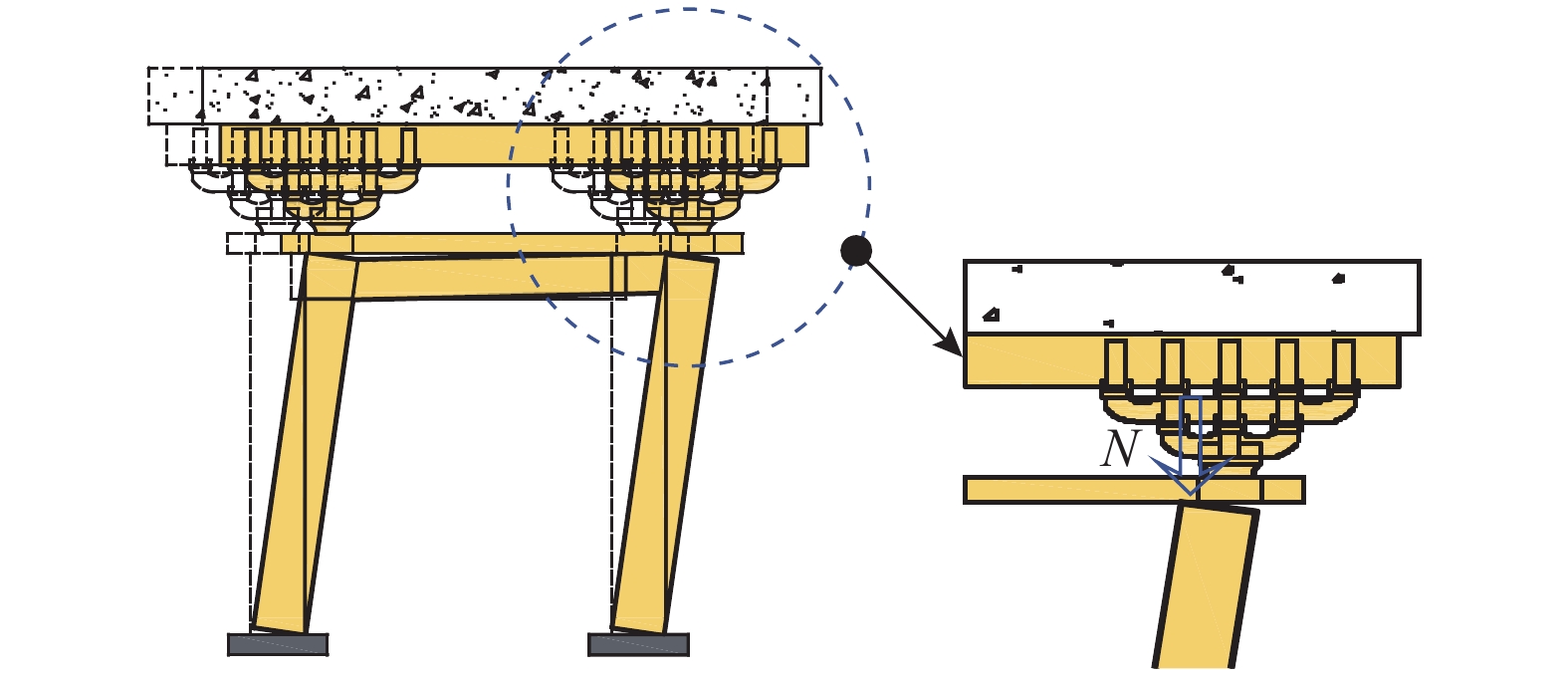
在古建筑中，木柱通常浮搁在础石之上，如图1所示，础石的横截面积要比柱脚的横截面积大一倍左右。

图  1  平摆浮搁

Figure  1.  Floating column foot

下载: 全尺寸图片 幻灯片

柱架在水平反复荷载的作用下，柱子以柱脚边缘为支撑发生反复的抬升与复位，称为“摇摆效应”^[17]，如图2所示。在摇摆过程中，殿堂式木结构的抗侧刚度由三部分组成：一是榫卯节点的嵌固和摩擦；二是柱体的摇摆；三是斗栱节点的摩擦。由图2可知，在单层柱架摇摆过程中上部荷载的作用点会由柱径的中心位置偏移到柱的外侧边缘。本文以单层殿堂式木结构作为研究对象。

1.2   摇摆柱体的恢复力模型

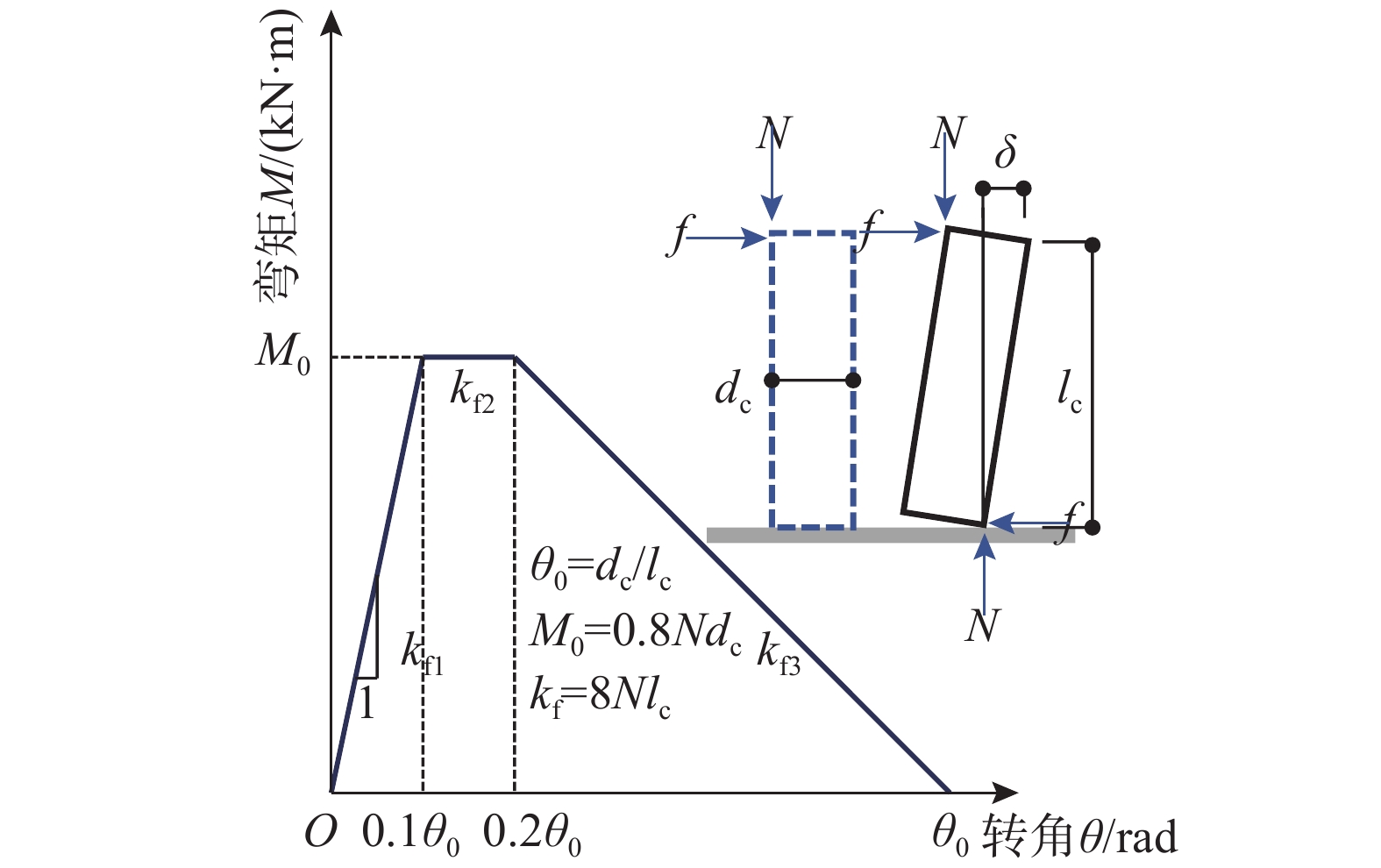
日本学者通过大量的试验及数值模拟研究，提出了木结构摇摆柱体的恢复力模型^[18-20]，如图3所示，其中：柱体摇摆可以分为4个阶段，弹性阶段(δ≤0.1d_c)、塑性阶段(0.1d_c<δ≤0.2d_c)、破坏阶段(0.2d_c<δ≤d_c)、倒塌阶段(当δ>d_c)。其中，阶段1和阶段2为柱架抗侧刚度的计算提供依据。

图  2  柱架的摇摆效应

Figure  2.  Rocking effect of column frame

下载: 全尺寸图片 幻灯片

图  3  摇摆柱恢复力模型

Figure  3.  Restoring force model of rocking column

下载: 全尺寸图片 幻灯片

由图3中的摇摆柱恢复力模型可以得到柱体摇摆时柱脚节点的弹塑性恢复力模型，如图4所示，其中每个阶段的直线斜率为此阶段柱脚弹簧的转动刚度。其中：图示d_c为木柱直径；l_c为木柱高度；δ为木柱侧移变形。

图  4  柱脚旋转弹簧恢复力模型

Figure  4.  Restoring force model of rotating spring representing column base

下载: 全尺寸图片 幻灯片

2   殿堂式木结构古建筑的简化力学模型

2.1   计算假定

殿堂式结构是一种典型的中国木结构古建筑，其结构的受力性能比较复杂。为了建立较为准确的力学模型，本文采用了一些假设以建立单层单自由度殿堂式木结构的简化模型，假设都是源自结构本身的特点。殿堂式木结构的受力特性表现为：柱与梁、柱与普拍枋及斗栱与其顶部梁的连接方式都是榫卯连接，这种连接方式既能使榫卯节点发生一定的转动又能传递弯矩，表现出半刚性的特征。因此，建立殿堂式木结构古建筑的简化模型时要考虑构件之间的连接方式及其变形特征。其中，殿堂式木结构的计算假定归纳为以下几个方面：

1)由于振动台试验模型的结构布置较为均匀、平面形状较为对称，故其刚度、质量、几何中心重合，因此假设试验模型不发生扭转变形，不考虑空间扭转耦合作用；

2)榫卯节点的各卯口紧密连接、做工相同，故不考虑榫卯连接的差异性；

3)水平荷载作用下，斗栱可以发生整体的层间剪切变形，这就使得其具有耗能能力及抗侧性能；

4)殿堂式木结构古建筑的尺寸较小，因此不考虑地震波的行波效应。

2.2   殿堂式木结构计算简图

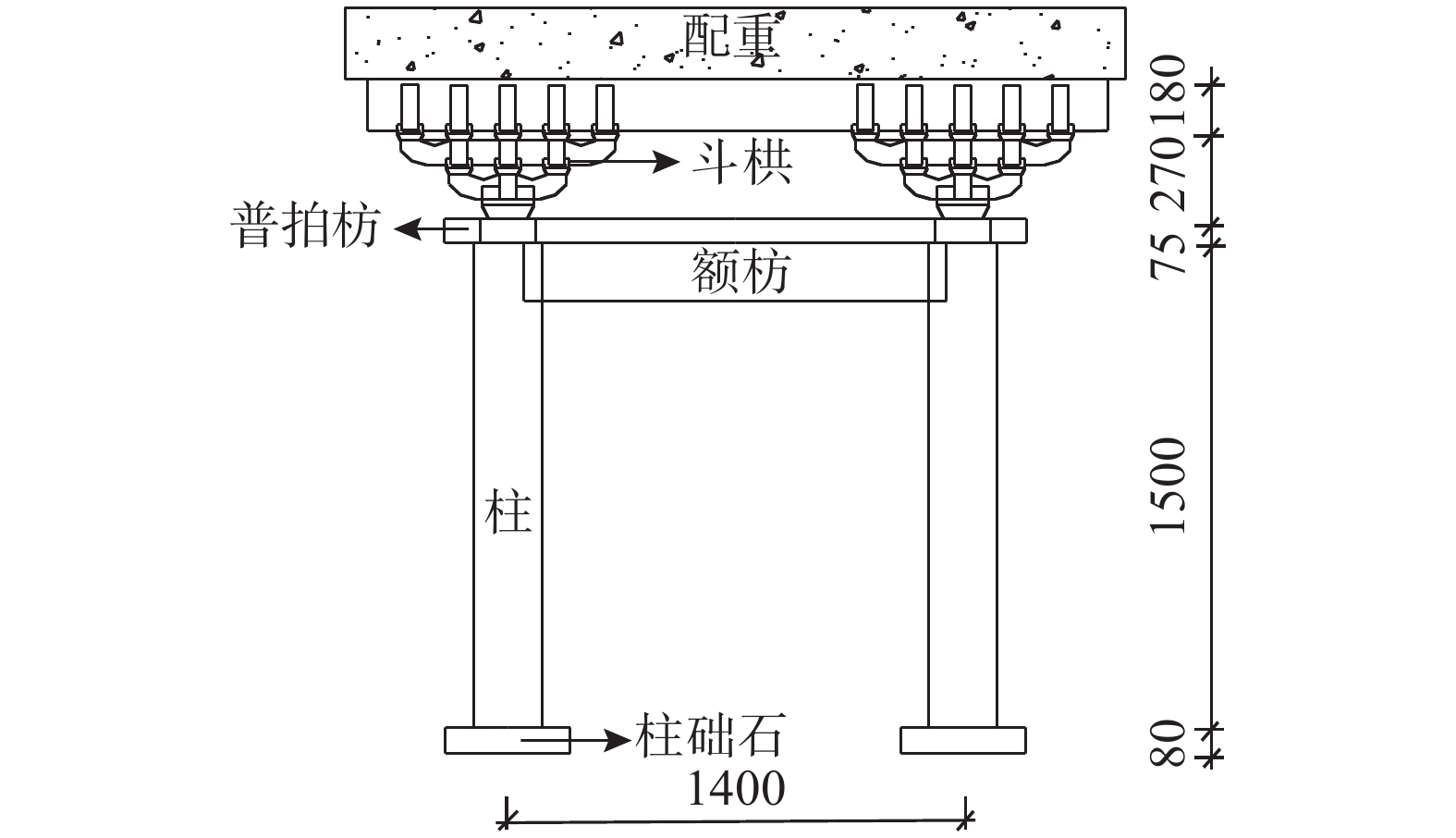
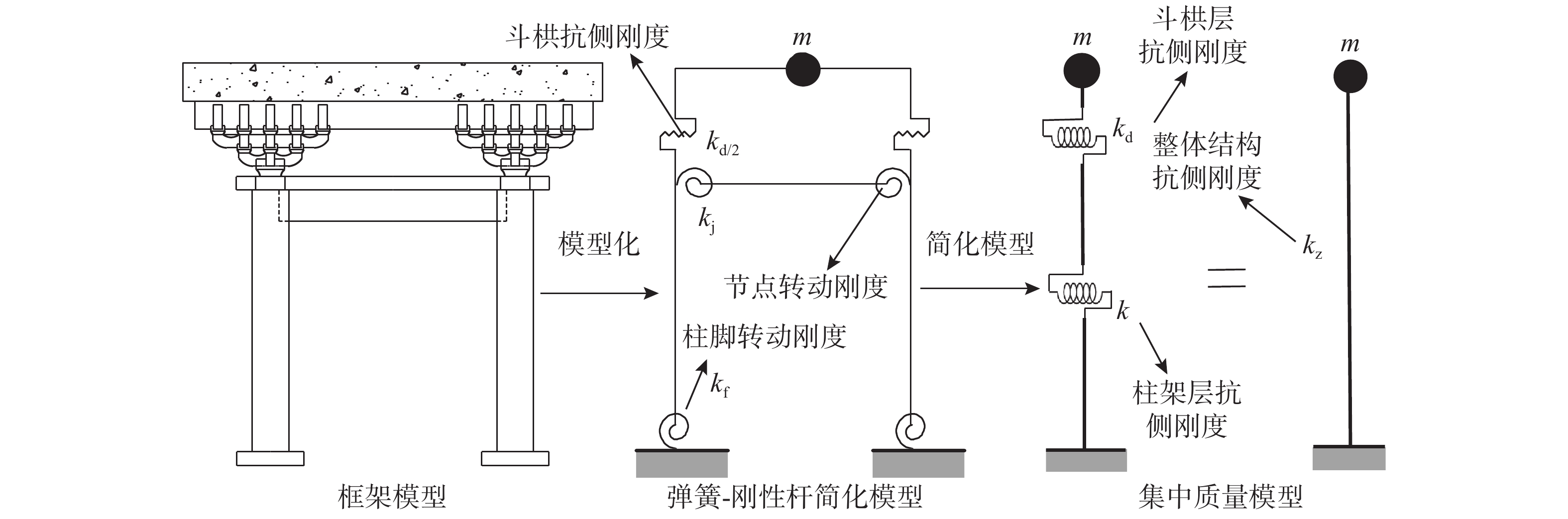
文献[21]按照营造法式以1∶3.52的比例缩尺，建造了一间由燕尾榫连接的单层单跨的殿堂式建筑，在忽略建筑物的空间效应的前提下，选取殿堂式木结构古建筑的一榀柱架作为研究对象，如图5所示。

图  5  试验模型

Figure  5.  Test model

下载: 全尺寸图片 幻灯片

殿堂式木结构古建筑可以分为柱架层以及斗栱层两部分。首先，对斗栱层的简化，假设斗栱在水平荷载作用下仅提供水平的抗侧刚度，因此两斗栱可视为水平抗侧单元，其刚度的大小与斗栱的相对侧移量有关。单元计算简图如图6所示，其中k_d为斗栱层的抗侧刚度。

图  6  斗栱层简化模型

Figure  6.  Simplified model of bracket sets layer

下载: 全尺寸图片 幻灯片

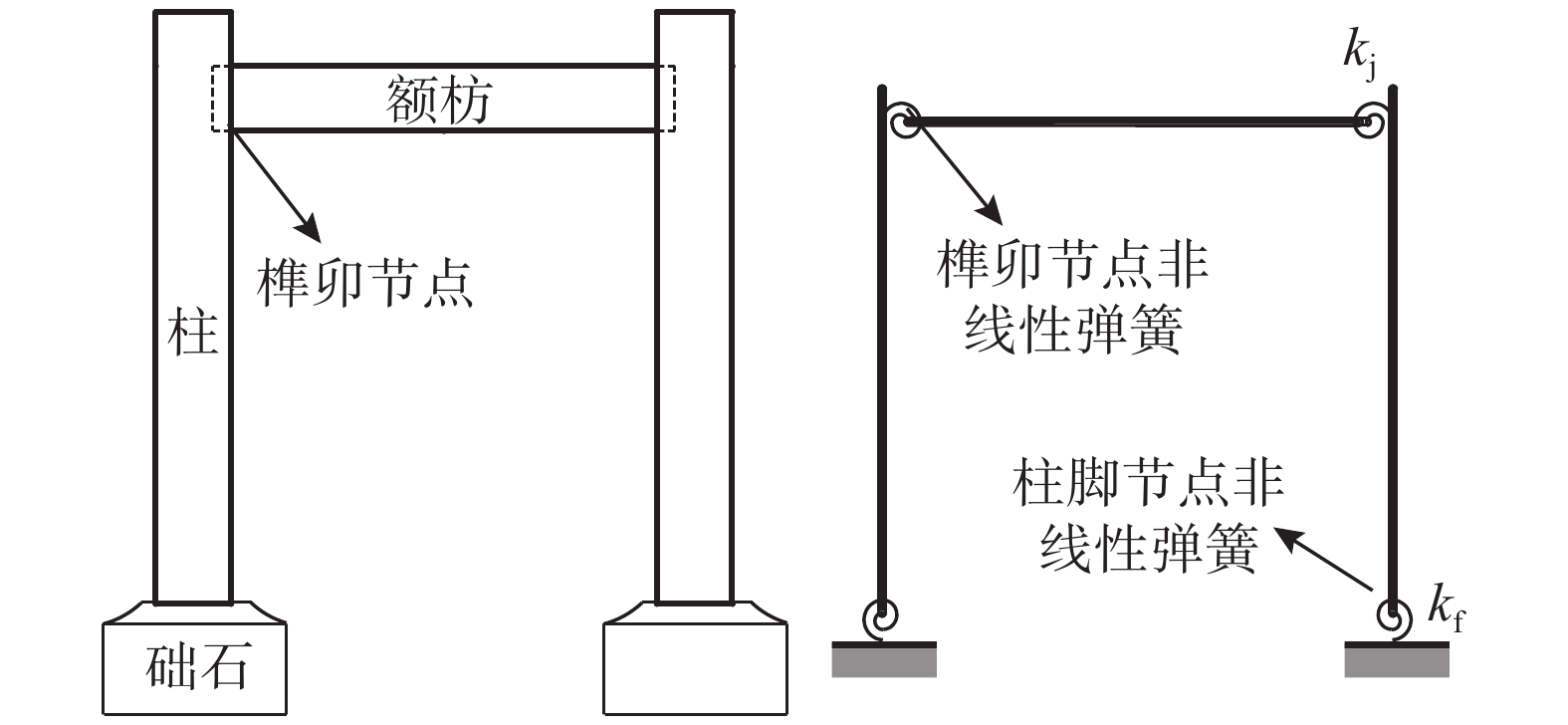
其次，对柱架层的简化，当木构架柱径D>200 mm时，就要考虑在水平荷载作用下导致柱体的“摇摆效应”^[20]。柱脚可引入转动刚度为k_f的非线性弹簧来模拟摇摆柱体柱脚的恢复力，榫卯连接简化为带有一定转动刚度的非线性弹簧，设为k_j。柱脚节点与榫卯节点的非线性转动弹簧的刚度会随研究阶段的不同而发生改变。其中，柱架层的弹簧-刚性杆单元模型如图7所示。

柱架抗侧刚度可参考弹簧-刚性杆单元，文献[16]已推导出考虑柱体“摇摆效应”和半刚性榫卯柱架的抗侧刚度简化计算公式。值得注意，榫卯节点及柱脚转动刚度的变化对结构整体抗侧刚度的影响可以通过改变k_f和k_j的数值来实现。

2.3   柱架抗侧刚度计算

假设梁柱和额枋的轴向变形、质点转动惯性的影响及榫卯节点的差异性可忽略不计，且质量与刚度中心重合。在上述假设的前提下，柱架模型的杆件可假设为刚性杆，并将试验柱架模型中的分布质量集中于梁的中部，其弹簧-刚性杆简化模型如图8(中)所示。对于考虑“摇摆效应”的木结构古建筑而言，整体结构抗侧刚度k_z主要由榫卯节点的转动刚度k_j、柱脚节点的转动刚度k_f及斗栱层的抗侧刚度k_d三部分组成。假设整体结构抗侧刚度为k_z，则弹簧-刚性杆简化模型可进一步简化为集中质量模型，如图8(右)所示。

图  7  柱架层简化模型

Figure  7.  Simplified model of column frame layer

下载: 全尺寸图片 幻灯片

图  8  柱架计算简图

Figure  8.  Calculation diagram of column frame

下载: 全尺寸图片 幻灯片

斗栱在地震作用下发生平动，斗栱层与柱架层的抗侧刚度为串联关系，因此整体结构抗侧刚度的计算公式为：

其中，柱架抗侧刚度k如式(2)所示：

通过式(1)和式(2)可得到斗栱节点、榫卯节点及柱脚节点与整体结构之间的刚度关系，采用MATLAB编程可调用各阶段各节点的刚度值并计算得到整体结构抗侧刚度k_z。注意：柱架抗侧刚度k考虑了榫卯节点的转动刚度及柱脚节点的转动刚度；整体结构抗侧刚度k_z进一步考虑了斗栱的抗侧刚度对结构的影响。

2.4   恢复力特性及特征参数取值

2.4.1   恢复力特性

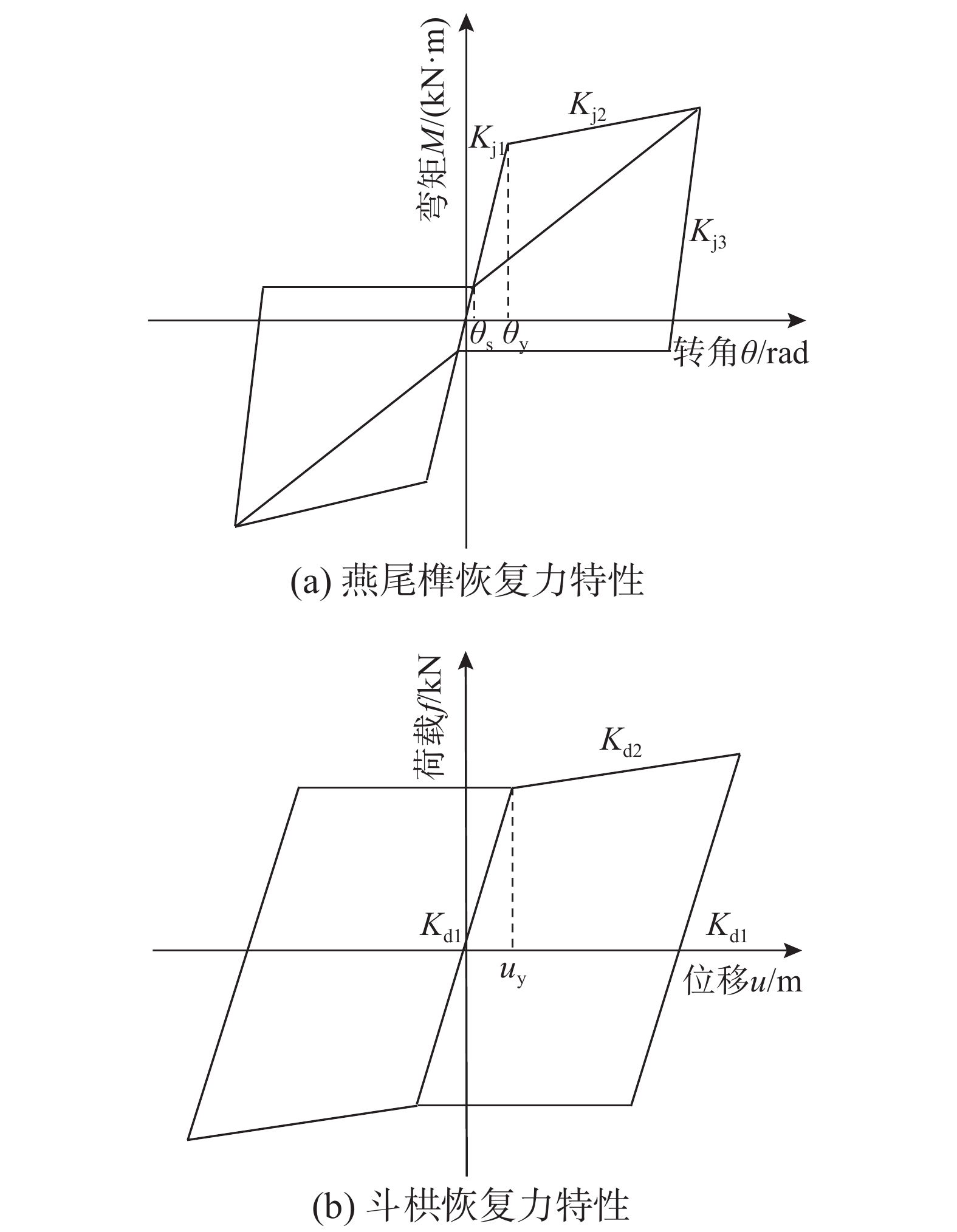
木结构古建筑在地震作用下，榫卯节点和斗栱节点通常表现出明显的非线性行为。在保证准确性的前提下，工程分析中通常采用分段线性的滞回模型来简化分析。根据单层单跨燕尾榫连接的柱架在水平荷载作用下的拟静力试验^[22]表明，燕尾榫节点的恢复力特性如图9(a)所示；斗栱节点的恢复力特性如图9(b)所示；柱脚节点的恢复力特性如图4所示。其中，各个节点的刚度及节点信息如表1所示。柱脚的转动刚度计算表达式如式(3)所示。

图  9  恢复力特性

Figure  9.  Restoring force behavior

下载: 全尺寸图片 幻灯片

表  1  各节点的恢复力特征参数取值

Table  1.  The value of the restoring force parameter of each node

试件名称	特征参数	取值
燕尾榫	Kj1/(kN·m/rad)	17.14
	Kj2/(kN·m/rad)	2.92
	Kj3/(kN·m/rad)	111.66
	$\theta$s/rad	0.01
	θy/rad	0.06
斗栱	Kd1/(kN/m)	1460
	Kd2/(kN/m)	140
	Kd1/(kN/m)	1460
	uy/m	0.04
柱脚	Kf1/(kN·m/rad)	640
	Kf2/(kN·m/rad)	10−10
	Kf3/(kN·m/rad)	−80
	θs/rad	0.015
	θy/rad	0.030

下载: 导出CSV 

| 显示表格

式中：N为柱头竖向荷载，模型梁上嵌固的钢筋土板的配重为14 kN/m²，因此单柱承担的竖向荷载为19 kN；l_c为柱高度，由图5可知柱高为1.5 m。

3   非线性时程分析编程

3.1   状态及特征点的判断

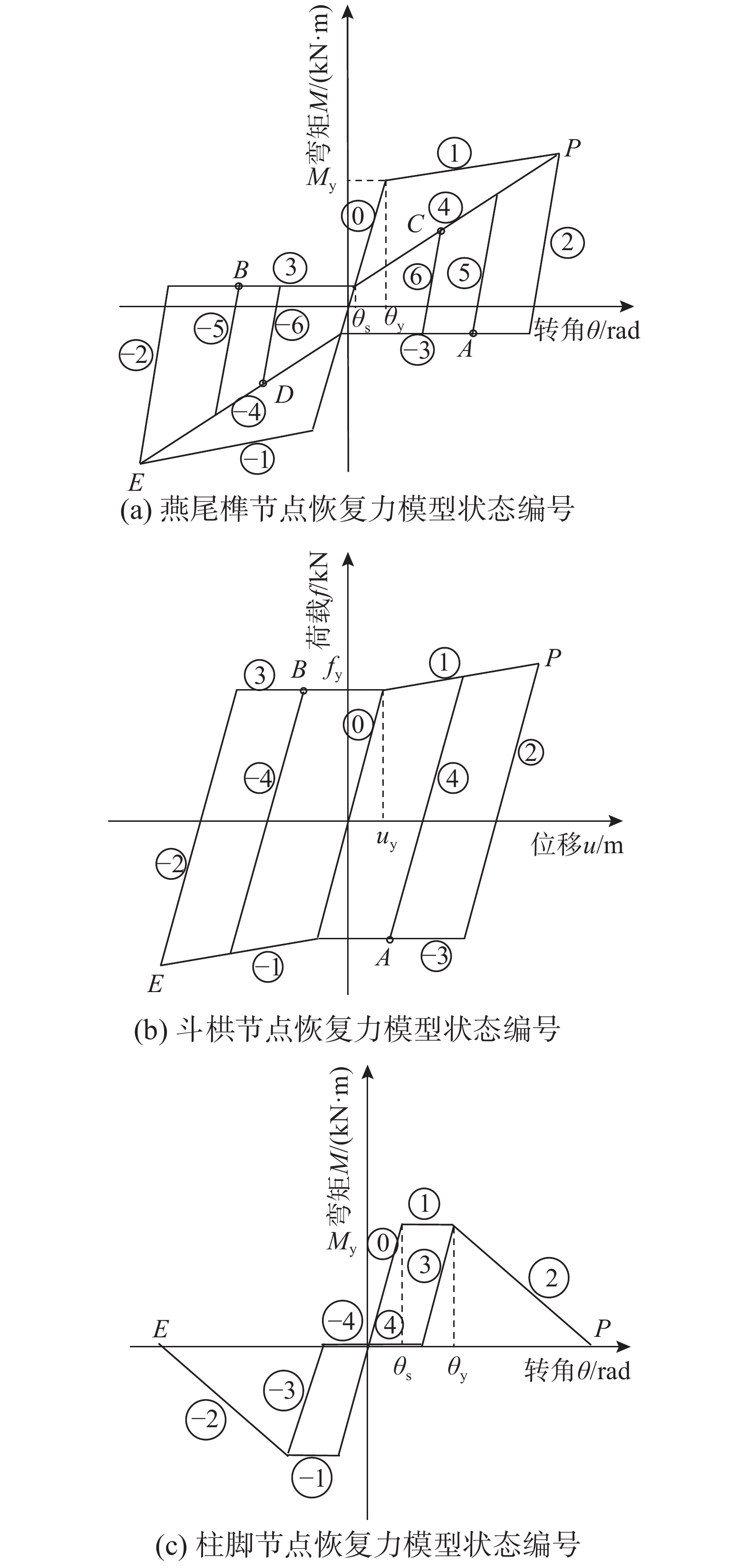
综合考虑柱架榫卯节点、斗栱节点及柱脚节点的恢复力特性，采用MATLAB编写殿堂式木结构的恢复力曲线，可准确地描述结构在各个阶段的刚度值，使结构的位移曲线更加符合实际。将上述恢复力特性曲线中的各类直线进行状态编号，根据燕尾榫节点的恢复力特性(图9(a))，燕尾榫节点的恢复力特性曲线设置了13个状态及6个特征点，如图10(a)所示，其中P点代表柱架的正向最大位移，E点代表柱架的负向最大位移，A、B、C、D分别代表着状态5、−5、6、−6的起始点。根据斗栱节点的恢复力特性(图9(b))，斗栱节点的恢复力特性曲线设置了9个状态及4个特征点，如图10(b)所示，其中P点与E点分别代表斗栱层的正向及负向的最大位移。根据柱脚节点的恢复力特性(图4)，柱脚节点的恢复力特性曲线设置了9个状态及2个特征点，如图10(c)所示，其中P点与E点分别代柱架的正向及负向的最大位移。

图  10  状态编号的规定

Figure  10.  Regulation of status numbers

下载: 全尺寸图片 幻灯片

3.2   拐点处理

拐点在恢复力模型中表现为两条恢复力直线的交点，由此可知，拐点两侧直线的刚度发生了改变。当不考虑拐点的影响时，结构时程曲线的计算将产生较大的误差。目前具有较多的方法处理恢复力拐点^[23]，引入线性内插比例因子p的是较常用方法，该方法是在拐点处将原始积分步长Δt分开，然后将积分步长缩小Δt′=pΔt，使得Δt′的末端正好是恢复力曲线的拐点，最后在(t+Δt′，t+Δt)范围内进行积分。

3.3   动力方程表达式

采用MATLAB分别编制了考虑柱体摇摆与不考虑柱体摇摆的分析模型，两者的区别在于：当模型考虑了摇摆效应时，程序同时调用燕尾榫节点、斗栱节点及柱脚节点的刚度并通过式(1)计算出整体结构抗侧刚度k_z；当模型不考虑摇摆效应时，程序将不会提取柱脚节点的转动刚度。因此，在两种工况下的动力方程为：

模型假设为单层单自由度柱架体系，因此质量m及阻尼系数c为常数，加速度矩阵$\ddot u$、速度矩阵$\dot u$、位移矩阵$u$、刚度矩阵k_z是关于时间t的函数。

对于殿堂式木结构的阻尼系数c选用Rayleigh阻尼，则阻尼系数的表达式如式(5)所示：

对于体系的自振频率可通过式(6)计算得出：

根据式(6)可以求出结构所对应的固有频率，而木结构古建筑体系的阻尼比ξ取0.05^[24]。

3.4   非线性时程分析流程图

动力非线性分析程序流程图如图11所示，本文按照此序流程图利用MATLAB软件建立了单层单自由度柱架体非线性时程分析的计算程序。

图  11  动力非线性分析程序流程图

Figure  11.  Flow chart of dynamic nonlinear analysis program

下载: 全尺寸图片 幻灯片

4   试验验证

4.1   地震波的选用

为了验证考虑斗栱节点、半刚性榫卯节点及柱体“摇摆效应”的单层单自由度柱架体系模型的准确性，本文将选用与试验相同的地震波TFT-300及LZ-300。

4.2   理论计算与试验结果对比

根据殿堂式木结构的刚度、层高、各节点恢复力模型及试验采用的地震加速度等信息，以Wilson-θ法为动力学计算方法，采用MATLAB编程模拟结构的受力过程，以柱体是否摇摆为影响因素，研究整体结构的地震位移响应。计算得到榫卯连接殿堂式木结构古建筑的非线性时程分析曲线并与试验结果相对比，如图12所示，并将各工况下的峰值位移汇总于表2。

由图12及表2可知，考虑柱体摇摆的非线性时程分析计算值曲线与试验值曲线更加接近。其中，与不考虑柱体摇摆时的结构非线性动力分析相比发现考虑柱体摇摆非线性时程分析的计算峰值与试验峰值的误差较小。因此，考虑柱体“摇摆效应”可以明显降低结构的位移幅度，使得计算值更加准确。

图  12  非线性时程分析对比图

Figure  12.  Comparison diagram of nonlinear time history analysis

下载: 全尺寸图片 幻灯片

表  2  各工况下的位移峰值

Table  2.  Peak displacement under each operating condition

工况	计算值 /mm	试验值 /mm	是否考虑 柱体摇摆	误差/(%)
TFT-300	−29.66	−30.52	是	−2.8
	−35.00	−30.52	否	17.1
	+28.56	22.56	是	26.6
	+40.29	22.56	否	78.6
LZ-300	−35.29	−45.87	是	−23.1
	−60.72	−45.87	否	32.4
	40.27	41.37	是	−2.7
	70.70	41.37	否	70.9

下载: 导出CSV 

| 显示表格

5   参数分析

为了深入研究各物理参数对殿堂式木结构古建筑非线性地震反应的影响规律，本文研究仍以图5的实验模型为原型，以式(4)为计算公式，并考虑柱体的“摇摆效应”，选取竖向荷载N、斗栱个数X、榫卯刚度k_j、柱高l_c为研究对象，基于MATLAB建立的单层单自由度柱架体系的程序来研究各结构各参数的变化对地震位移响应的影响。值得注意：各参数的选取均以既有木结构古建筑为指导，取值都在合理的范围之内。

5.1   竖向荷载N的影响

假设初始结构的竖向荷载为N₀，模型中竖向荷载的值为N。因此，在数值模型中调整原结构的竖向荷载可以模拟出屋面荷载对结构地震位移响应的影响，其结果如图13所示。

图  13  不同竖向荷载下殿堂式木结构的非线性时程分析曲线

Figure  13.  Nonlinear time-history analysis curves of palace-style timber structure under different vertical loads

下载: 全尺寸图片 幻灯片

由图13可知，随着竖向荷载的增大殿堂式木结构的地震位移响应显著降低。由式(1)、式(2)、式(3)可知随着屋面荷载N的增大，柱脚的转动刚度k_f也随之增大，因此整体结构的抗侧刚度k_z明显提高，从而降低了木结构的侧向位移。表3列出了竖向荷载不同时，计算得到的殿堂式木结构非线性时程分析的位移峰值。

由表3可知，当竖向荷载在初始值的基础上上下浮动20%时，结构地震位移响应峰值的变化量在初始值的−34.7%~53.0%之间变动，这也说明了竖向荷载N对结构地震位移响应的影响较大。因此，木结构古建筑大屋盖存在具有重要意义。

表  3  不同竖向荷载下的位移峰值

Table  3.  Peak displacements under different vertical loads

工况	荷载N	峰值位移/mm
TFT-300	0.8 N0	−32.95	+34.66
	N0	−27.81	+26.64
	1.2 N0	−30.52	+22.56
LZ-300	0.8 N0	−59.10	+63.31
	N0	−45.87	+41.37
	1.2 N0	−29.92	+30.46

下载: 导出CSV 

| 显示表格

5.2   斗栱数量X的影响

假设初始结构的斗栱数量为X₀，模型中斗栱数量为X。因此，在数值模型中调整原结构斗栱的数量可以模拟出不同斗栱个数对结构地震位移响应的影响，其结果如图14所示。

图  14  不同的斗栱数量下殿堂式木结构的非线性时程分析曲线

Figure  14.  Nonlinear time history analysis curves of palace-style timber structure under different numbers of buckets

下载: 全尺寸图片 幻灯片

由图14可知，随着斗栱的数量的增加殿堂式木结构的地震位移响应有所降低。斗栱数量X的增加，斗栱层抗侧刚度k_d也随之增大，由式(1)可知，整体结构抗侧刚度k_z有所提高，从而降低了木结构的侧向位移。表4列出了斗栱数量不同时，计算得到的殿堂式木结构非线性时程分析的位移峰值。

表  4  不同斗栱数量下的位移峰值

Table  4.  Peak displacements under different numbers of bracket sets

工况	斗栱数量X	峰值位移/mm
TFT-300	0.5 X0	−30.58	+28.96
	X0	−30.51	+22.56
	2.0 X0	−28.51	+26.77
LZ-300	0.5 X0	−40.24	+44.90
	X0	−45.87	+41.37
	2.0 X0	−30.94	+32.34

下载: 导出CSV 

| 显示表格

由表4可知，当斗栱数量在初始值的基础上上下浮动50%时，结构地震位移响应峰值的变化量在初始值的−32.5%~28.4%之间变动，这也说明了斗栱数量X对结构地震位移响应的影响较大。因此，合理的增加斗栱的数量可以降低木结构的地震位移响应。

5.3   榫卯刚度k_j的影响

假设初始结构的榫卯刚度k_j0，模型中榫卯刚度为k_j。因此，在数值模型中调整原结构梁柱间的榫卯刚度可以模拟出不同的连接方式对结构地震位移响应的影响，其结果如图15所示。

图  15  不同的连接方式下殿堂式木结构的非线性时程分析曲线

Figure  15.  Nonlinear time history analysis curves of palace-style timber structure under different connection methods

下载: 全尺寸图片 幻灯片

由图15可知，随着榫卯刚度k_j的增大殿堂式木结构的地震位移响应显著降低。由式(1)、式(2)可知整体结构抗侧刚度k_z随着榫卯刚度k_j的增加而增大。表5列出了连接方式不同时，计算得到的殿堂式木结构非线性时程分析的位移峰值。

表  5  不同连接方式下的位移峰值

Table  5.  Peak displacements under different connection methods

工况	榫卯刚度kj	峰值位移/mm
TFT-300	0.1 kj0	−57.46	+52.32
	kj0	−30.52	+22.56
	10.0 kj0	−23.89	+21.18
LZ-300	0.1 kj0	−65.81	+64.98
	kj0	−45.87	+41.37
	10.0 kj0	−11.75	+15.97

下载: 导出CSV 

| 显示表格

由表5可知，当榫卯刚度在初始值的基础上上下浮动90%时，结构地震位移响应峰值的变化量在初始值的−74.4%~131.9%之间变动，这也说明了连接方式对结构地震位移响应的影响较大。因此，合理的选择榫卯连接方式可以大幅降低木结构的地震位移响应。

5.4   层高l_c的影响

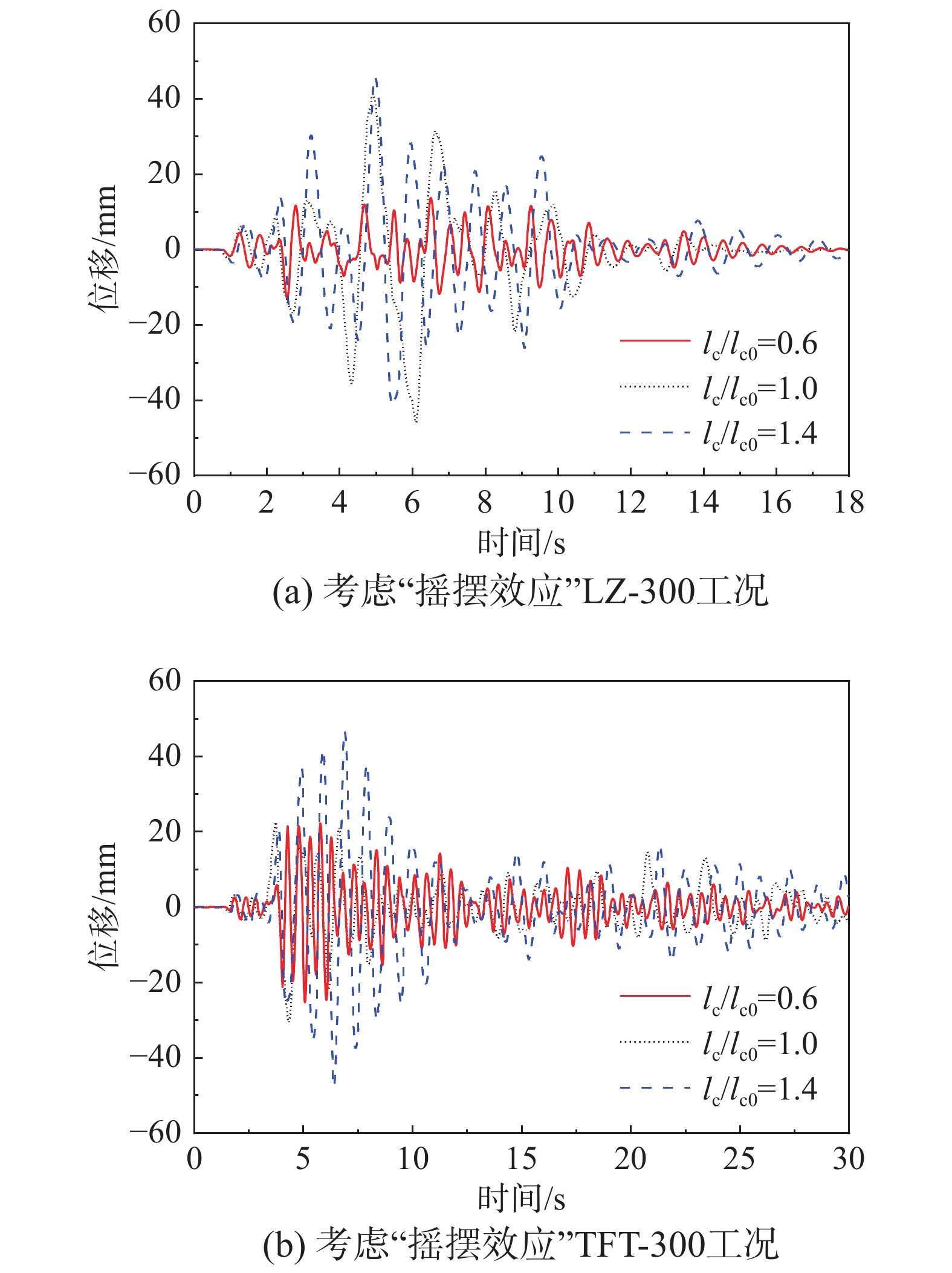
假设结构的初始层高为l_c0，模型中的层高为l_c。因此，在数值模型中调整原结构的层高可以模拟出不同高度的殿堂式木结构古建筑的位移响应，其结果如图16所示。

图  16  不同层高下殿堂式木结构的非线性时程分析曲线

Figure  16.  Nonlinear time history analysis curves of palace-style timber structure under different storey levels

下载: 全尺寸图片 幻灯片

由图16可知，随着层高l_c的增加殿堂式木结构的地震位移响应显著增大。由式(2)可知增大殿堂式木结构的层高l_c使柱架抗侧刚度k显著降低，而由式(1)可以推出整体结构抗侧刚度k_z也随之降低。表6列出了层高不同时，计算得到的殿堂式木结构非线性时程分析的位移峰值。

由表6可知，当层高在初始值的基础上上下浮动40%时，结构地震位移响应峰值的变化量在初始值的−71.9%~106.7%之间变动，这也说明了柱高对结构地震位移响应的影响较大。因此，合理的降低层高l_c可以大幅降低木结构的地震位移响应。

表  6  不同层高下的位移峰值

Table  6.  Peak displacements under different storey heights

工况	层高lc	峰值位移/mm
TFT-300	0.6 lc0	−25.38	+22.27
	lc0	−30.52	+22.56
	1.4 lc0	−47.71	+46.63
LZ-300	0.6 lc0	−12.91	+13.83
	lc0	−45.87	+41.37
	1.4 lc0	−40.85	+45.83

下载: 导出CSV 

| 显示表格

6   结论

本文采用非线性转动弹簧以模拟柱体在地震作用下摇摆行为，基于柱体、榫卯节点及斗栱的非线性恢复力模型，提出了单层殿堂式木结构地震分析的集中质量简化分析模型，进行了地震作用下的结构动力响应时程分析。

(1)考虑柱体“摇摆效应”，斗栱节点及半刚性榫卯节点的抗侧刚度，使殿堂式木结构的地震位移响应峰值的计算值与试验值的误差较小，且峰值出现的时间基本相同；

(2)竖向荷载可以显著降低殿堂式木结构的地震位移响应；柱高越大，结构的地震位移响应越大；结构的地震位移响应随着榫卯节点抗转动刚度的增大而逐渐降低；斗栱数量的增加提高了柱架抗侧刚度，从而降低了结构的地震位移响应。