SIMPLIFIED ANALYSIS METHOD FOR VERTICALLY LOADED ENERGY PILE CONSIDERING LONGITUDINAL AND RADIAL THERMAL STRAIN
-
摘要:
为探究温度对能量桩荷载传递机理及相关力学响应的影响,引入平面瞬态温度场方程,将温度场与应力场解耦。基于平面应力模型,将能量桩与桩周土考虑为具有协调变形的整体,计算了径向热应力。在此基础上,将其与双曲线荷载传递模型结合,对桩土界面处的极限摩阻力进行修正。将纵向热应变考虑在竖向荷载传递方程中,得到可同时衡量纵向和径向热效应的竖向受荷能量桩承载特性分析方法。利用增量法对能量桩荷载传递控制方程进行求解,得到桩身轴力、桩侧阻力、桩身位移等相关力学响应。通过与既有文献进行对比,验证了该模型的合理性。通过参数分析,研究了温度和竖向力作用下能量桩的荷载传递特性。结果表明:温度会改变能量桩的荷载传递特性,提高能量桩的运行温度可小幅增加其承载力。该文方法的计算流程清晰,可为能量桩的设计提供参考。
Abstract:To explore the effect of temperature on the load transfer mechanism and related mechanical responses of energy piles, a plane transient temperature field equation was introduced to decouple the temperature field from the stress field. Based on the plane stress model, the energy pile and the surrounding soil of the pile are considered as a whole with coordinated deformation, and the radial thermal stress is calculated. It is then further combined with the hyperbolic load transfer model to modify the ultimate frictional resistance at the pile-soil interface. Considering the longitudinal thermal strain in the vertical load transfer equation, a method for analyzing the bearing characteristics of vertically loaded energy piles that can simultaneously consider the longitudinal and radial thermal effects is obtained. The incremental method is used to solve the governing equation of energy pile load transfer. The relevant mechanical responses such as the axial force of pile, shaft resistance, and pile displacement are obtained. Through a comparison with the existing literature, the rationality of the model is verified. Through parametric analysis, the load transfer characteristics of energy piles under the action of temperature and vertical force are studied. The results show that the temperature will change the load transfer characteristics of the energy pile, and increasing the operating temperature of the energy pile can slightly increase its bearing capacity. The calculation process of the method in this paper is clear, which can provide a reference for the design of energy piles.
-
桩基础具有优良的承载特性[1],广泛地存在于桥梁、高层建筑和海上风电[2]等领域。近年来,基于传统地源热泵发展而来的能量桩技术已有一定的实际应用[3],如宁波市某办公楼项目[4]、信阳市高铁站项目[5]、某学生宿舍楼项目[6]。其作为利用浅层低品位地热能的代表构件,具有承受上部建筑荷载和与上部建筑换热的双重功能[7-8]。国内外学者对能量桩的承载特性进行了大量研究[9-11]。由于对桩-土热应力耦合行为认识不足,给能量桩的合理设计带来了诸多困难。为了更加合理的评估能量桩的安全性,现有的桩基计算理论亟待完善。
研究能量桩承载性能的研究方法主要有现场测试、数值模拟和理论分析。路宏伟等[12]对能量桩进行了现场足尺试验。结果表明,温度变化会引起桩体热胀冷缩,从而影响桩-土间的相对位移,这导致能量桩的轴力、侧阻力等力学效应与常规桩之间存在明显差异。NG等[13]采用离心机试验比较了不同温度增量下能量桩的承载和变形特性。陆浩杰等[14]、王成龙[15]等通过室内缩尺试验发现在桩身温度降低时,土体会产生塑性应变,能量桩出现下沉现象。为深入研究复杂工况下的能量桩承载变形特性,蒋刚等[16]建立了能量桩热-力耦合数值模型,认为桩体运行温度的升高与降低会产生附加热应力,其大小与分布受桩身温度和桩端约束共同影响。LORIA等[17]对不同温度、力学荷载作用下的能量桩进行了热-水-力有限元耦合分析,研究了桩身的轴力分布。认为对桩顶自由的摩擦型桩,升温时桩体膨胀,桩顶和桩端围绕桩身某点分别向上、下产生位移,该点称为温度位移零点。以上成果充分表明,在能量桩服役期间温度变化会产生附加应力从而影响其荷载传递和位移分布,在进行能量桩设计计算过程中需要合理确定温度对桩身应力和变形的影响。
在能量桩计算理论的研究方面,已有诸多学者做出了贡献。KNELLWOLF等[18]将荷载传递法引入到能量桩的计算中,利用摩阻力中性点的静力平衡条件,构造了荷载-温度耦合荷载传递方程,采用折线型荷载传递模型计算能量桩相关力学响应,但该方法需要预先假定摩擦力中性点的位置,再迭代求解准确位置,并且折线型荷载传递模型无法真实的反映土体应变趋势的渐进性。基于此,费康等[19]基于传统的荷载传递法,建立了热力耦合作用下能量桩单桩工作特性的简化分析方法,无须假设摩擦力中性点。随后,董龙龙等[20]基于指数型荷载传递模型,对循环荷载作用下能量桩长期响应进行了研究。上述文献主要将温度引起的应变体现在桩段单元压缩量的计算之中,忽略了径向热应力对荷载传递函数的影响。为此,骆湘勤等[21]考虑了径向温度效应,在计算时对极限土抗力进行了修正,通过假设热响应半径计算稳态温度场中桩土界面径向热应力,但却忽略了纵向热应变,并且在能量桩服役期间,热响应半径[22]会随运行温度和时间变化,故应该考虑温度扩散的影响。综合上述文献可知,在温度扩散作用下,能量桩荷载工作特性力学机理的理论研究相对不够完善。
本文基于前人的成果,引入简化的平面温度场方程,将桩体及土体简化为平面应力模型,得到考虑温度扩散的桩周土体径向热应力表达式。将其与传统的荷载传递法结合,进而得到可以同时考虑径向和纵向热应变的能量桩竖向承载特性分析方法,并结合已有文献对所提方法的合理性和可靠性进行了验证,分析了温度荷载影响下能量桩的力学响应,以及径向热应力变化规律和影响因素。
1 能量桩承载力计算模型
1.1 基本假设
为建立能量桩承载力计算模型,需做以下基本假设:
1)能量桩及桩周土为线性各向同性的热弹性体;能量桩及桩周土的热应变为小变形;
2)当温度变化时,不考虑土中水的相变;
3)桩体及桩周土体的弹性模量、热膨胀系数等材料性质不随温度变化;忽略桩身自重,取压应力为正,位移向下为正。
1.2 考虑温度影响的荷载传递模型
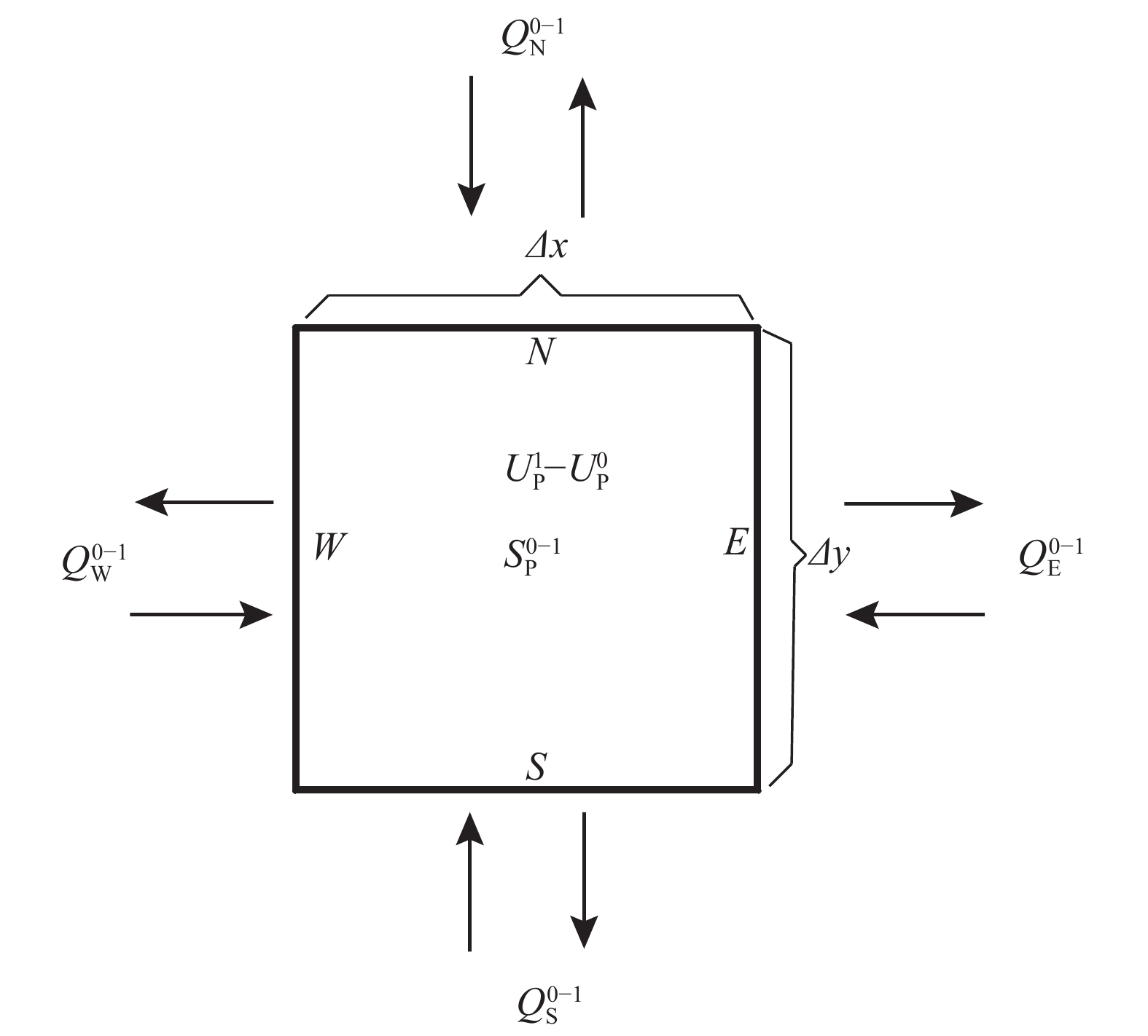
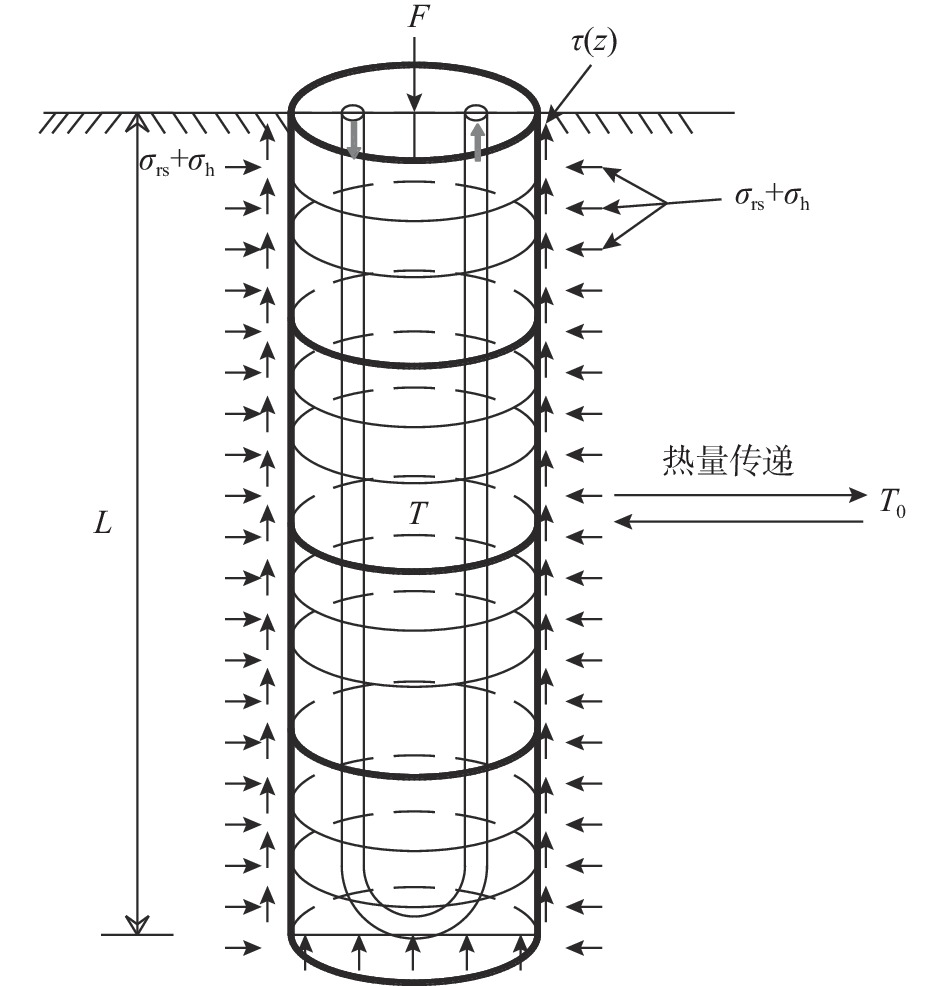
在一般分析中,学者往往关注桩基自身的热应力和热应变。其实,在能量桩服役期间,其周围土体也同样会因温度变化而产生形变,最终在桩土界面处产生附加的热应力[21],具体细节如图1所示。其中,径向正应力由σrs和σh组成,侧摩阻力τ计算方法如式(1)所示。
双曲线模型可同时考虑径向土压力和桩土接触面的非线性滑移行为,且参数意义明确。基于此,本文荷载传递函数采用双曲线模型,则有:
τ=Sas+bs|S| (1) 式中:τ为桩侧摩阻力;S为桩土相对位移;as、bs为与桩侧土体有关的参数:
1bs=Cs+ζ(σh+σrs) (2) 式中:Cs为土体粘聚力;ζ为界面摩擦系数;σh为静止土压力;σrs为土体对桩体的径向热应力,后文将详细讨论:
as=R0ln(RR0)G0 (3) 式中:R0为桩身半径;R为竖向力作用下桩侧土变形的半径;G0为土体剪切模量。
特别地,对于桩端土体有:
σb=Sbab+bbSb (4) 式中:σb为桩端土反力;Sb为桩端位移;ab、bb为桩端土的荷载传递参数。
根据RANDOLPH等[23]的建议:
ab=πD(1−μs)8Gs (5) bb=1pf=RbfPu (6) 式中:Gs为桩端土体剪切模量;μs为桩土土体泊松比;Rbf为桩端土破坏比,本文中取为1.0;Pf为桩端阻力极限值;Pu为桩端阻力破坏值。
1.3 温度场描述
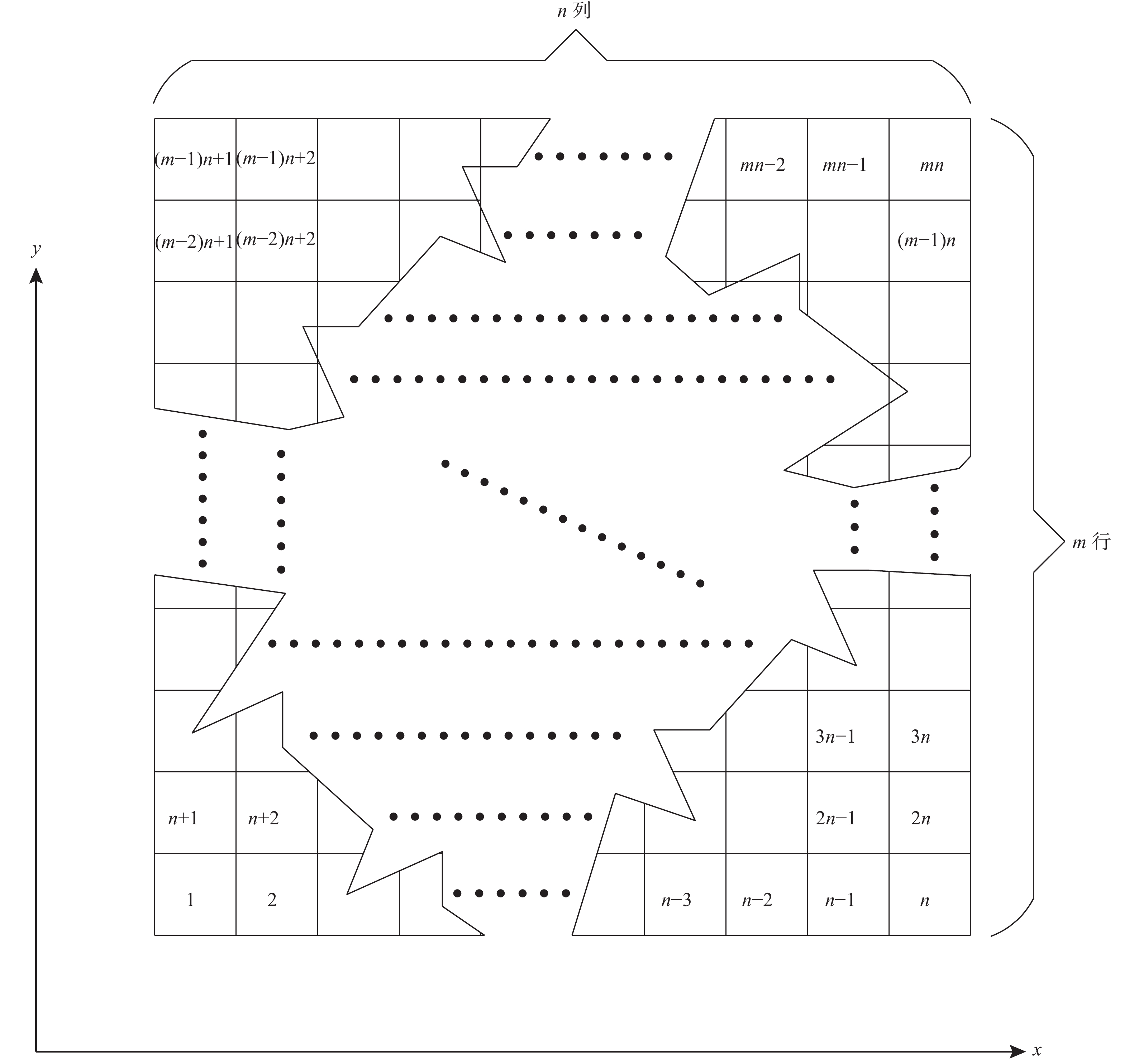
在确定双曲线模型的参数bs时,需要考虑温差引起的径向热应力σrs,然而能量桩服役期间温度场会随时间扩散[24],这将导致σrs随之变化,故首先应对考虑时间效应的能量桩温度场进行描述。基于传热学基本理论,本文采用有限差分法对温度场进行描述。如图2所示,根据能量守恒定律,可得:
U1P−U0P=Q0−1W+Q0−1E+Q0−1S+Q0−1N + S0−1P (7) UP=ρcTΔxΔy (8) S0−1P=sΔxΔyΔt (9) 式中:UP为单元的内能密度;U1P、U0P分别为单个时间步长内单元最后时刻和初始时刻的内能密度;Q0−1W、Q0−1E、Q0−1S、Q0−1N为单个时间步长内由单元四面流入流出的热量;S0−1P为内热源所产生的热量;s为加热功率;ρ为密度;c为比热容;T为传热微元的温度;Δx、Δy、Δt为距离和时间增量。
考虑单元径向温度不均匀,用单元温度的平均值代替整个微元体的温度:
UP=¯(ρcT)PΔxΔy (10) 根据傅里叶定律,可知通过W面的热量:
Q0−1W=−k∂T∂xΔyΔt (11) 式中,k为导热系数。
用W面热流密度的平均值代替W面的热流密度:
Q0−1W=−k∂T∂xΔyΔt (12) 同理,用微元体中心的热源强度代替整个微元体的热源强度,则有:
S0−1P=ˉs0−1ΔxΔyΔt (13) 综合式(7)~式(13)可以得到平面导热问题的能量守恒方程离散格式:
[(¯ρcT)1P−(¯ρcT)0P]ΔxΔy=[(¯k∂T∂x)0−1E−(¯k∂T∂y)0−1W]ΔyΔt+[(¯k∂T∂x)0−1N−(¯k∂T∂y)0−1W]ΔxΔt+¯s0−1ΔxΔyΔt (14) 假设比热容c、密度ρ、导热系数k都是均匀且不随时间变化,可继续简化:
首先,用单元土体中心温度代替单元土体平均温度,即:
T1P∼¯T1P、T0P∼¯T0P 则有:
ρc(¯T1P−¯T0P)ΔxΔy=k[(¯∂T∂x)0−1E−(¯∂T∂y)0−1W]ΔyΔt+k[(¯∂T∂x)0−1N−(¯∂T∂y)0−1W]ΔxΔt+¯s0−1ΔxΔyΔt (15) 其次,用相邻土体中心温度的差分代替温度在土体表面的偏微分,即:
TE−TPδxE∼(∂T∂x)E,TP−TWδxW∼(∂T∂x)W, TN−TPδyN∼(∂T∂y)N,TP−TSδyS∼(∂T∂y)S。 最后,用最后时刻的温度值代替整个时间步内的温度的平均值,即:
T1E−T1PδxE∼(¯TE−TPδxE)0−1,T1P−T1WδxW∼(¯TP−TWδxW)0−1, T1N−T1PδyN∼(¯TN−TPδyN)0−1,T1P−T1SδyS∼(¯TP−TSδyS)0−1。 可得以下离散格式:
ρcΔxΔy(T1P−T0P)=k(T1E−T1PδxE−T1p−T1WδxW)ΔyΔt+k(T1N−T1PδyN−T1p−T1SδyS)ΔxΔt+sΔxΔyΔt (16) 整理可得:
ρcΔxΔyΔt(T1P−T0P)=kΔy(T1E−T1PδxE−T1p−T1WδxW)+kΔx(T1N−T1PδyN−T1p−T1SδyS)+sΔxΔy (17) (ρcΔxΔyΔt+kΔyδxE+kΔyδxW+kΔxδyN+kΔxδyS)T1P=kΔyδxET1E+kΔyδxWT1W+kΔxδyNT1N+kΔxδyST1S+ρcΔxΔyΔtT0P+sΔxΔy (18) 化简为:
a1PT1P=a1ET1E+a1WT1W+a1NT1N+a1ST1S+a0PT0P+bp (19) 其中:
a1P=(ρcΔxΔyΔt+kΔyδxE+kΔyδxW+kΔxδyN+kΔxδyS);a1E=kΔyδxE;a1W=kΔyδxW;a1N=kΔxδyN;a1S=kΔxδyS;a0P=ρcΔxΔyΔt;bP=sΔxΔy。
在划分网格时,对单元连续编号,如图3所示,可得二维热传导的时间隐式的有限差分格式,如式(20)所示。求解式(20)即可得到能量桩径向温度场的逐时变化情况。
a1P,1T1P,1−a1E,1T1E,1−a1W,1T1W,1−a1N,1T1N,1−a1S,1T1S,1=a0P,1T0P,1+bP,1a1P,2T1P,2−a1E,2T1E,2−a1W,2T1W,2−a1N,2T1N,2−a1S,2T1S,2=a0P,2T0P,2+bP,2⋮⋮⋮⋮⋮⋮a1P,nT1P,n−a1E,nT1E,n−a1W,nT1W,n−a1N,nT1N,n−a1S,nT1S,n=a0P,nT0P,n+bP,na1P,n+1T1P,n+1−a1E,n+1T1E,n+1−a1W,n+1T1W,n+1−a1N,n+1T1N,n+1−a1S,n+1T1S,n+1=a0P,n+1T0P,n+1+bP,n+1⋮⋮⋮⋮⋮⋮a1P,mnT1P,mn−a1E,mnT1E,mn−a1W,mnT1W,mn−a1N,mnT1N,mn−a1S,mnT1S,mn=a0P,mnT0P,mn+bP,mn (20) 1.4 径向热应力计算
当不计体力时,空间轴对称弹性力学问题的平衡微分方程[25]为:
∂σr∂r+∂τzr∂z+σr−σφr=0 (21) ∂σz∂z+∂τrz∂r+τrzr=0 (22) 考虑轴对称性,则此几何方程为
{εr=∂ur∂r, εr=ur, εz=∂w∂rγzr=∂w∂r+∂u∂r (23) 基于线性热应力理论,对于各向同性材料,应力、应变和温差的函数可表达为:
{σr=E(1−2μ)(1+μ)[(1−μ)εr+μ(εφ+εz)]−αEΔT1−2μσφ=E(1−2μ)(1+μ)[(1−μ)εφ+μ(εz+εr)]−αEΔT1−2μσz=E(1−2μ)(1+μ)[(1−μ)εz+μ(εr+εφ)]−αEΔT1−2μτzr=E2(1+μ)γzr (24) 将式(23)代入式(24)可得位移和温度表示的应力表达式:
σr=E1+μ[1−μ1−2μ∂μr∂r+μ1−2μ(urr+∂uz∂z)]−αEΔT1−2μ (25) σφ=E1+μ[1−μ1−2μμrr+μ1−2μ(∂uz∂z+∂ur∂r)]−αEΔT1−2μ (26) σz=E1+μ[1−μ1−2μ∂μz∂z+μ1−2μ(∂ur∂r+urr)]−αEΔT1−2μ (27) τzr=E2(1+μ)(∂ur∂r+∂uz∂z) (28) 式中:σr、σφ、σz为三个方向的正应力;τzr、τrφ、τzφ为三个方向的切应力;εr、εφ、εz为三个方向的正应变;γzr、γrφ、γφz为三个方向的切应变;r为径向距离;ur、uz为径向和轴向位移;μ为泊松比。
考虑单根能量桩温度场为轴对称分布,则有:
ΔT=ΔT(r,t),τrz=0 故式(21),可简化为:
∂σr∂r+σr−σφr=0 (29) 考虑桩体单元较薄,将其视为平面应力[26]问题,则有σz=0,则由式(27)可得:
∂uz∂z=1+μ1−μαΔT−μ1−μ(durdr+urr) (30) 将式(30)代入式(25)、式(26),整理得:
σr=E(1+μ)(1−μ)durdr+μE(1+μ)(1−μ)urr−αEΔT1−μ (31) σφ=E(1+μ)(1−μ)urr+μE(1+μ)(1−μ)dudr−αEΔT1−μ (32) 将式(31)和式(32)代入式(29),整理得:
d2urdr2+1rdudr−ur2=(1+μ)α∂(ΔT)∂r (33) 求解式(33)可得:
ur=(1+μ)αr∫r2riΔTrdr+C1r+C2r (34) 式中:r1为圆盘内径;r2为圆盘外径。
对式(34)求解微分,将ur及dur/dr代入式(31),可得土体的径向热应力:
σrs=EsC11−μs−EsC21+μ1r2−αsr2∫r∞rpTsrdr (35) 式中:Ts为土体径向温度增量,是时间和径向距离的函数;αs为土体的线膨胀系数;r∞为热响应半径;rp为桩体半径;Es为土体弹性模量;μs为土体泊松比。
同理,对于桩体单元,可视为内径r1=0;外径r2=rp的圆盘,则其径向应力表达式为:
σrp=EPC31−μp−EpC41+μp1r2−αpEpr2∫rp0Tprdr (36) 式中:Tp为桩体的温度增量;αp为桩体的热膨胀系数;μp为桩体泊松比;C3、C4为积分常数。
积分常数C1、C2、C3、C4是依赖于温度扩散的相互耦合的系数,可联立式(37)~式(40)确定:
边界条件:
urp|r=0=0 (37) urs|r=r∞=0 (38) 应力连续条件:
σrp|r=rp=σrs|r=rp (39) 位移连续条件:
urp|r=rp=urs|r=rp (40) 通过MATLAB编程,将式(20)计算出的温度场代入式(35)可得考虑瞬态温度影响的土体径向热应力σrs。
1.5 考虑温度影响的荷载传递法
将桩长为L的能量桩离散为N个单元。由单元i的力学平衡条件有:
ΔPi=ΔPi+1+Δfi (41) 式中:ΔPi和ΔPi + 1分别为单元上界面的受力增量;Δfi为桩侧摩阻力增量,可由下式计算:
Δfi=ksiπD⋅ΔLiΔui+Δui+12 (42) 式中:ksi为单元i中心点处桩侧土的剪切刚度;ΔLi为单元长度;D为能量桩的直径;Δui及Δui+1分别为单元上下截面的位移增量。
由单元i的位移协调条件可得:
Δui=Δui+1+Δsi (43) 式中:Δsi为单元压缩量,考虑热力耦合作用,有:
Δsi=ΔPi+ΔPi+12EpApΔLi−αp⋅ΔT⋅ΔLi (44) 式中:Ep为能量桩的弹性模量,Ap为横截面积,αp为桩身材料的热膨胀系数,ΔT为温度增量。
由式(41)~式(44)有:
ΔPi=Ai⋅Δui−Bi⋅Δui+1+C⋅ΔT (45) ΔPi+1=Bi⋅Δui−Ai⋅Δui+1+C⋅ΔT (46) 其中:
{Ai=EAΔLi+πDksi⋅ΔLi4Bi=EAΔLi−πDksi⋅ΔLi4C=EpApαp (47) 对于式(45),当i=i+1时,有:
ΔPi+1=Ai+1⋅Δui+1−Bi+1⋅Δui+2+C⋅ΔT (48) 结合式(46)与式(48)可得:
BiΔui−(Ai+Ai+1)⋅Δui+1+Bi+1⋅Δui+2=0 (49) 1.6 定解条件
假设桩顶可自由变形,则第一个节点处的轴力增量ΔP1即为桩顶外荷载F,代入式(45)得:
{A_1} \cdot \varDelta {u_1} - {B_1} \cdot \varDelta {u_2} = F - C \cdot \varDelta T (50) 同理,对于桩底处有:
\varDelta {P_{N + 1}}{\text{ = }}{k_{\rm{b}}}{A_{\rm{p}}} \cdot \varDelta {u_{N + 1}} (51) 式中:{k_{\rm{b}}}为桩端土体的刚度系数,将式(51)代入式(46)后,有:
{B_N} \cdot \varDelta {u_N} - \left( {{A_{N + 1}} + {k_{\rm{b}}}{A_{\rm{p}}}} \right)\varDelta {u_{N + 1}} = - C \cdot \varDelta T (52) 将式(49)~式(51)整理可得单调温度作用下能量桩受力特性控制方程组:
\boldsymbol{K} \boldsymbol{\varDelta} \boldsymbol{u}=\boldsymbol{\varDelta} \boldsymbol{F} (53) 式中:\boldsymbol{\varDelta} \boldsymbol{u}=\left\{\varDelta u_{1}, \varDelta u_{2}, \cdots, \varDelta u_{N}, \varDelta u_{N+1}\right\}^{\mathrm{T}}为节点位移向量;\boldsymbol{\varDelta} \boldsymbol{F}= {\left\{ {F - C \cdot \varDelta T,0, \cdots ,0, - C \cdot \varDelta T} \right\}^{\text{T}}} 为节点荷载向量;\boldsymbol{K}_{(N+1) \times(N+1)}为刚度矩阵,其非零元素为:
\left\{ \begin{aligned} & {\boldsymbol{K}_{1,1}} = {A_1},{\boldsymbol{K}_{1,2}} = - {B_1},i = 1 \\& {\boldsymbol{K}_{i,i - 1}} = {B_{i - 1}},{\boldsymbol{K}_{i,i}} = - \left( {{A_{i - 1}} + {A_i}} \right) \\& {\boldsymbol{K}_{i,i + 1}} = {B_i},i = 2,3, \cdots N \\& {\boldsymbol{K}_{N + 1,N}} = {B_N},{\boldsymbol{K}_{N + 1,N + 1}} = \\&\qquad - \left( {{A_N} + {\boldsymbol{K}_{\rm{b}}}A} \right),i = N + 1 \end{aligned} \right. (54) 求解式(53)可得能量桩节点位移,进而得到桩侧阻力和轴力分布。
1.7 求解流程
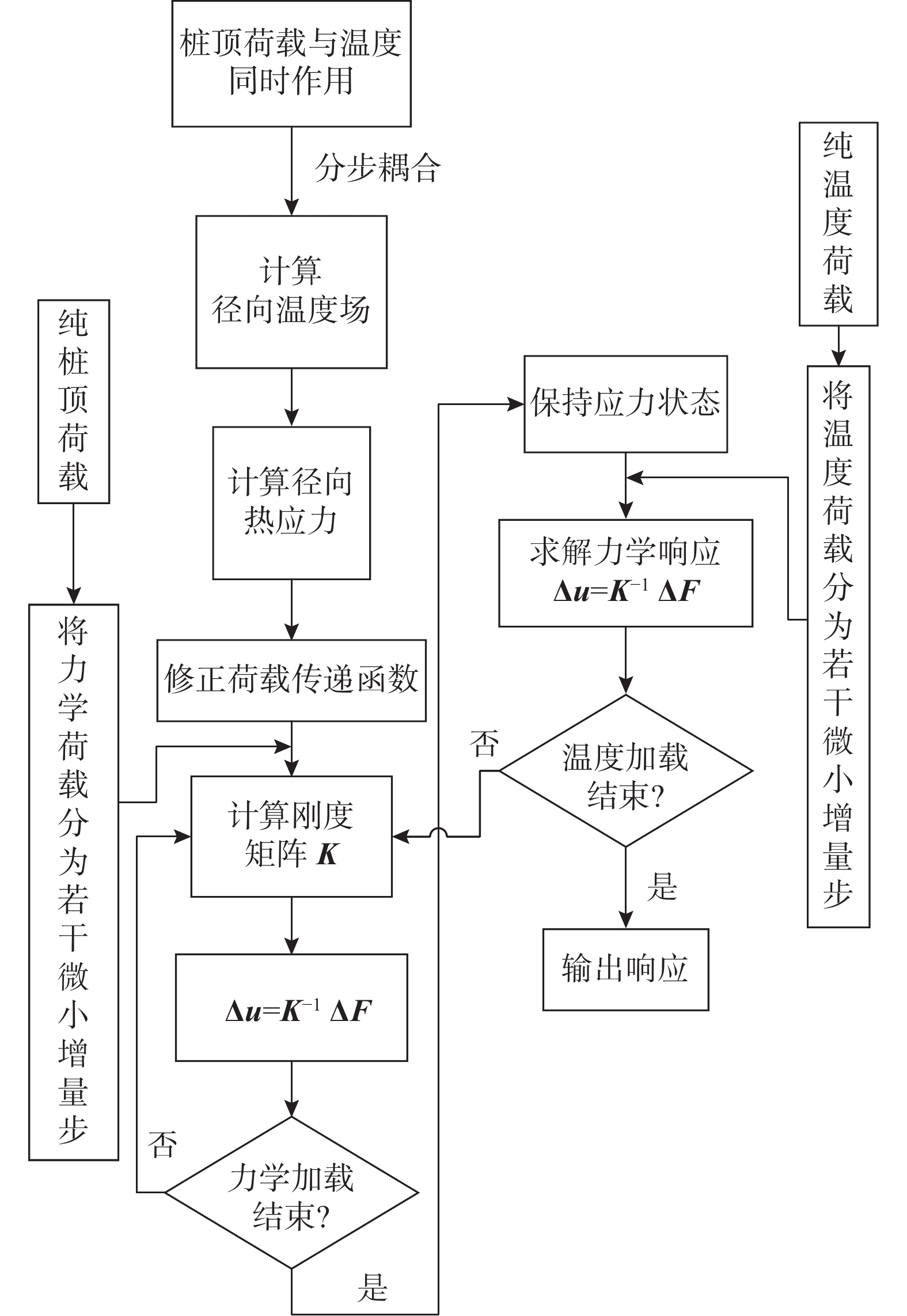
如图4所示,针对能量桩不同的受力情况,有不同的求解思路。当无温度荷载时,计算模型退化为传统桩基计算模型。当温度与桩顶荷载同时作用时,假设温度荷载与桩顶荷载分步耦合,先由式(20)计算逐时的径向温度分布;再由式(35)计算土体径向热应力;从而修正荷载传递函数以求得初始刚度矩阵,然后由增量法求得桩顶荷载下的力学响应状态,温度加载将以力学响应的最终状态为初始状态继续使用增量法求解。当只有温度荷载时,则从初始刚度矩阵开始计算。
2 模型验证
2.1 径向热应力验证
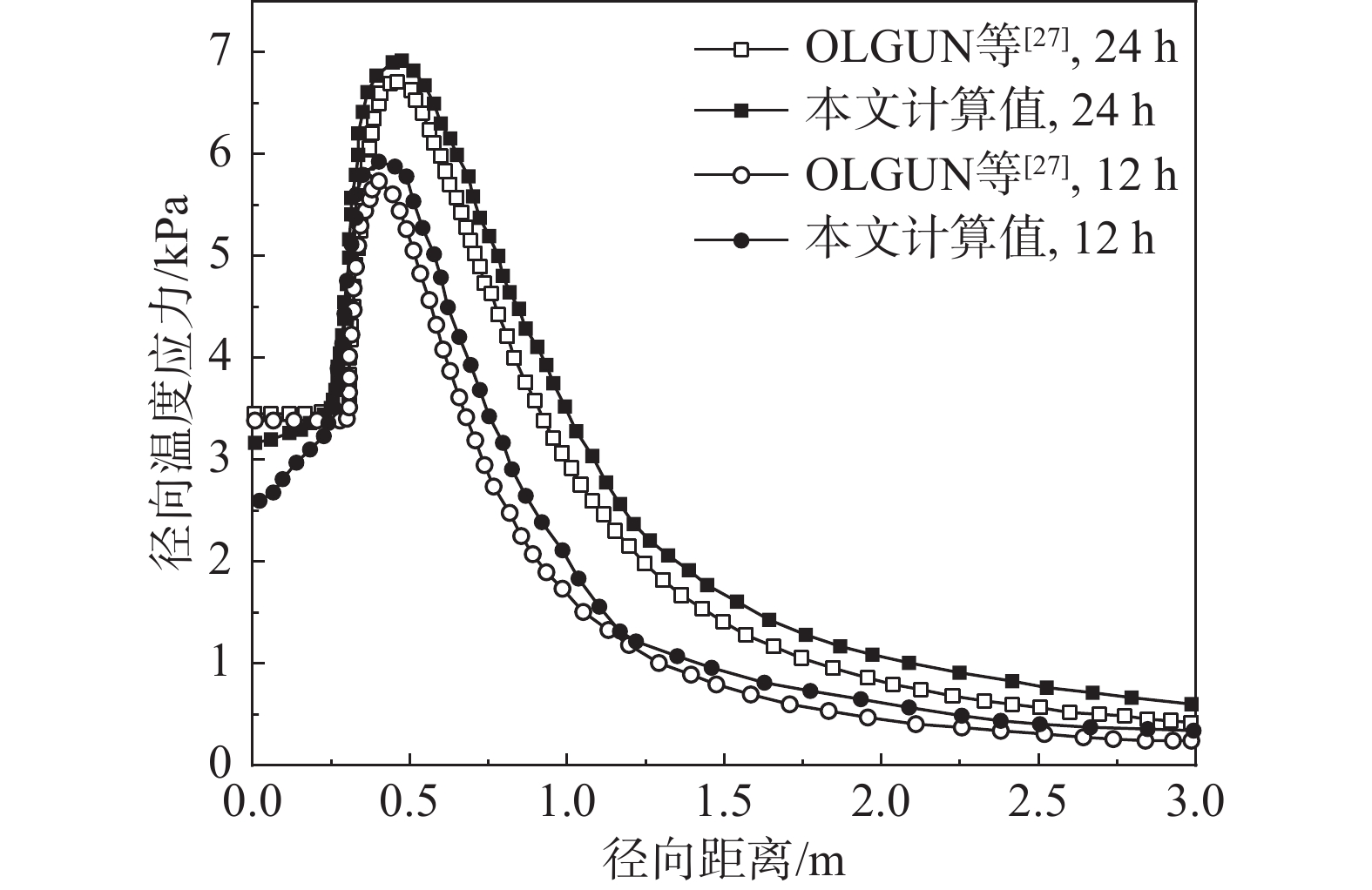
OLGUN等[27]采用平面有限元模型对能量桩径向热应力变化规律进行了探究。其计算了运行温度为25 ℃,运行时间为12 h、24 h的径向热应力分布情况。本文参数取值与其相同,详见表1。与文献[21]相同,取\varDelta T恰好为零处为积分边界。通过式(20)可计算出逐时温度场,将其代入式(35)可得土体径向热应力{\sigma _{r{\rm{s}}}}。将所计算出的径向热应力汇总如图5所示。
由图可知,在桩土界面处由于材料性质差异,温度升高时,桩土之间产生了挤压应力,{\sigma _r}沿径向在数值上呈先急剧增加后缓慢减小的趋势。值得注意的是,径向热应力最大值产生于土体内部而不是桩土接触面。并且随着运行时间的增加,由于温度扩散作用,径向热应力有增大的趋势,这与OLGUN等[27]的规律基本一致。
表 1 径向热应力计算参数Table 1. Radial thermal stress calculation parameters参数 值 土体密度{\rho _{\rm{s}}}/(kg·m−3) 1500 土体热容量{c_{\rm{s}}}/(J·kg−1·℃−1) 1500 土体热导率{k_{\rm{s}}}/(W·m−1·℃−1) 2.0 土体泊松比 {\mu _{\rm{s} }} 0.495 土体弹性模量{E_{\rm{s}}}/MPa 50 土体热膨胀系数{\alpha }_{{\rm{s}}}/(με·℃−1) 30 桩体密度{\rho _{\rm{p}}}/(kg·m−3) 2500 桩体热容量{c_{\rm{p}}}/(J·kg−1·℃−1) 1200 桩体热导率{k_{\rm{p}}}/(W·m−1·℃−1) 1.5 桩体泊松比 {\mu _{\rm{p} }} 0.15 桩体弹性模量{E_{\rm{p}}}/GPa 30 桩体热膨胀系数{\alpha _{\rm{p}}}/(με·℃−1) 10 桩径D/m 0.6 2.2 纯温度荷载作用下桩身轴力验证
NG等[13]对温度作用下能量桩的轴力分布进行了40倍重力的离心机试验,研究了在桩顶自由,温差为15 ℃和30 ℃时的桩身轴力分布情况。根据温差及表2所提供的数据[19],可分别计算出径向热应力约为0.8 kPa和1.5 kPa,进而求出桩侧土体以及桩端土体的所对应的荷载传递参数。其中,{a_{\rm{b}}}约为6.03×10−5 m3/kN,{b_{\rm{b}}}约为1.6×10−4 m2/kN[19]。
图6为本文计算方法与NG等[13],费康等[19]的结果对比,从图中可以看出桩身轴力沿桩长呈现先增大后减小的规律并且温度位移零点低于桩体几何中点。这是因为桩顶自由,桩底相对刚度较大,能量桩向下膨胀量较小。另外,对比可以看出,由于本文考虑了径向热应力从而对极限土抗力进行了修正,故本文所计算的轴力比费康等[19]的结果稍大。这是因为当能量桩温度升高时,桩土界面会产生挤压,导致能量桩整体的刚度变大,从而影响了能量桩桩身轴力分布。
表 2 模型参数Table 2. Model parameters定义 值 桩长/m 19.6 直径/m 0.88 桩体弹性模量/GPa 27.8 桩体热膨胀系数/(m \cdot ℃−1) 2.22×10−5 土体弹性模量/MPa 11 摩擦角/(°) 31 土体热导率/( W \cdot (m \cdot ℃)−1) 2.3 桩体导热系数/(W/ (m \cdot ℃)) 2.3 土体有效重度/(kN \cdot m−3) 15.4 土体热膨胀系数/(m \cdot ℃−1) 5×10−6 2.3 竖向力及温度荷载作用下桩身轴力验证
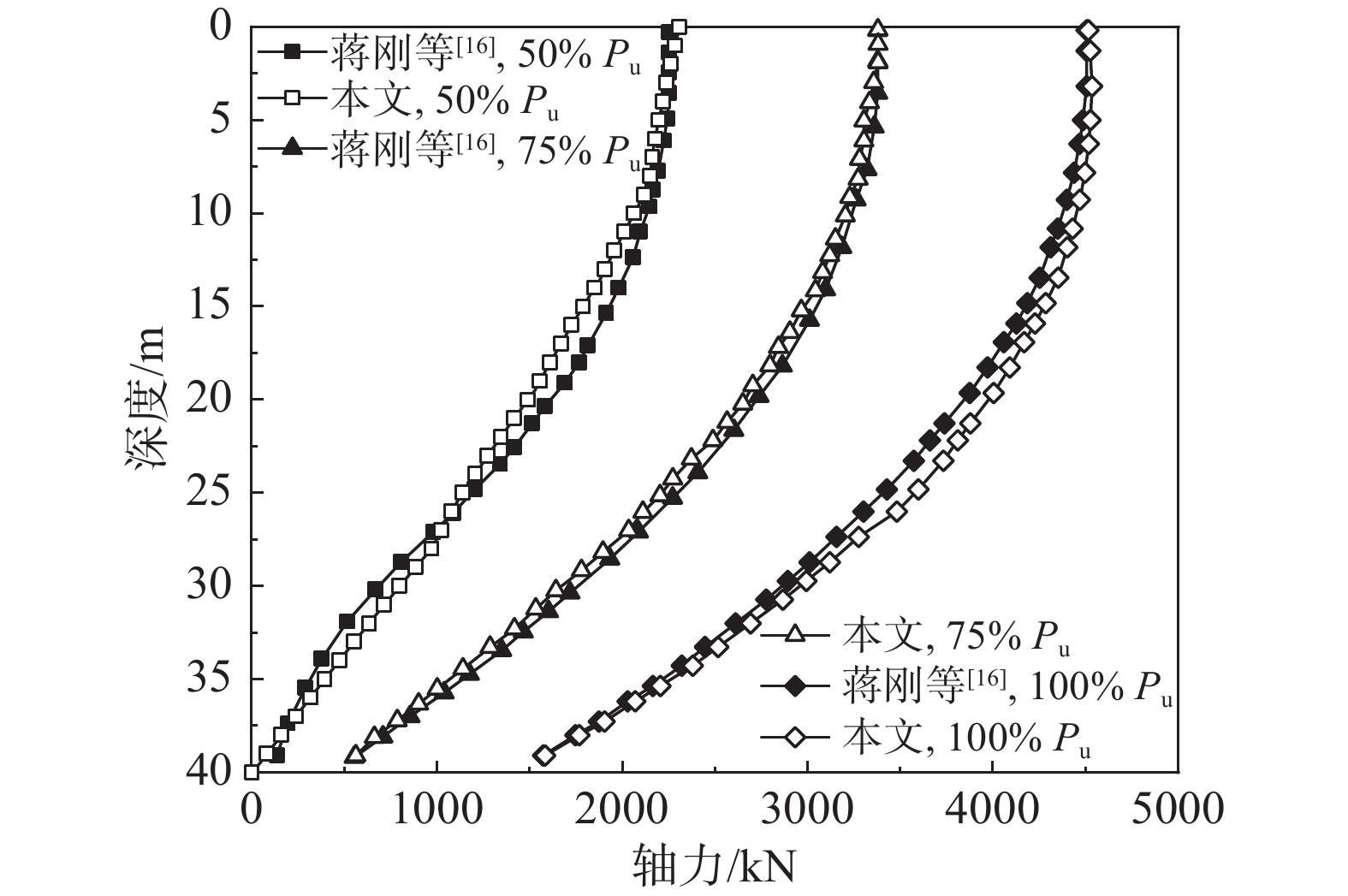
蒋刚等[16]基于现场实测数据,利用简化热力耦合方法建立了40 m摩擦型能量桩的数值模型,并分别计算了不同桩顶荷载作用下所对应的桩身轴力沿深度的分布曲线。本文分别采用文献[16]中的50% Pu、75% Pu、100% Pu、\varDelta T= −15 ℃,所对应的轴力分布曲线进行验证。文献[16]给出了工程场地的土层分布以及详细的热学、力学参数,如表3所示。据此可计算径向温度分布,从而得到径向热应力{\sigma _{r{\rm{s}}}},进而逐层计算\tau {{ - {\rm{s}}}}曲线的参数{a_{\rm{s}}}、{b_{\rm{s}}},取每个桩体单元为0.5 m。
对比结果如图7所示,对于竖向受荷的摩擦型能量桩,侧摩阻力作为其承载力的来源,在桩顶荷载作用下,侧摩阻力逐层发挥,呈现典型的非线性衰减。从图中可以看出,当桩顶荷载为50%Pu,此时荷载主要由上层土体承担,当桩顶荷载达到100%Pu时,荷载已贯穿整个桩体,此时上部能量桩桩土接触面已发生较大滑移。
表 3 桩土热学力学参数Table 3. Thermal mechanical parameters of pile and soil土层 厚度/m 密度ρs/(kg·m−3) 粘聚力Cs/kPa 内摩擦角 \varphi /(°) 泊松比{\mu _{\rm{s}}} 弹性模量Es/MPa 桩土摩擦系数 素填土 3.0 1800 9 11.6 0.35 28 0.2 表土 2.0 1800 9 11.6 0.35 28 0.2 粉质黏土 1.5 1830 22 12.8 0.35 25 0.2 淤泥质粉质黏土 2.0 1830 13 10.0 0.40 15 0.2 粉质黏土 5.0 1940 42 15.0 0.35 80 0.2 粉土夹粉砂 6.0 1840 8 25.1 0.30 100 0.3 粉砂夹粉土 6.0 1860 6 27.1 0.30 140 0.3 粉土 2.5 1810 9 22.1 0.30 120 0.3 粉土 12.0 1840 8 25.2 0.30 200 0.3 桩体导热系数/(W \cdot (m \cdot ℃)−1) 桩体密度/(kg \cdot m−3) 桩体泊松比 桩体比热容/(J \cdot (kg \cdot ℃)−1) 2.3 2500 0.2 960 桩体热膨胀系数/(m \cdot ℃−1) 土体导热系数/( W \cdot (m \cdot ℃)−1) 土体比热容/(J \cdot (kg \cdot ℃)−1) 土体热膨胀系数/(m \cdot ℃−1) 1.0×10−5 1.8 1500 5×10−6 3 参数分析
3.1 温度对荷载沉降曲线的影响
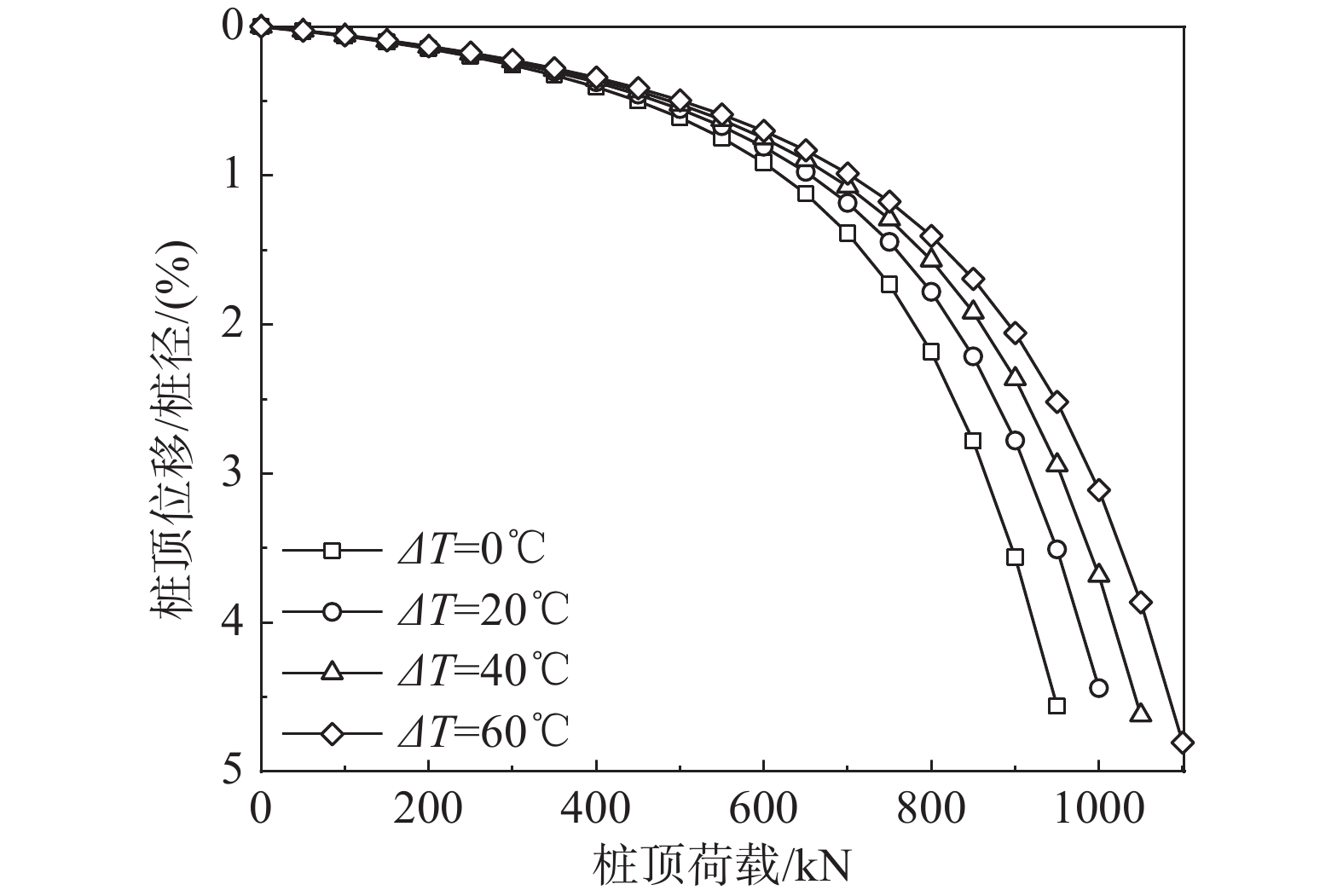
为分析不同运行温度下能量桩热力耦合的承载性能,假设能量桩运行时间为24 h,运行温度分别为20 ℃、40 ℃、60 ℃。土体热学、力学参数如表4所示。取桩长为15 m,桩径为0.6 m的能量桩进行分析。其中,{a_{\rm{b}}}取为6.03×10−5 m3/kN,{b_{\rm{b}}}取为1.6×10−4 m2/kN,静止土压力系数取为0.5,桩土界面摩擦系数取为0.5。
表 4 计算参数Table 4. Calculation parameters参数 值 土体密度{\rho _{\rm{s}}}/(kg·m−3) 1500[27] 土体热容量{c_{\rm{s}}}/(J·kg−1·℃−1) 1500[27] 土体热导率{k_{\rm{s}}}/(W·m−1·℃−1) 2.0[27] 土体泊松比{\mu _{\rm{s}}} 0.495[27] 土体弹性模量{E_{\rm{s}}}/MPa 40 土体热膨胀系数{\alpha _{\rm{s}}}/(με·℃−1) 30[28] 桩体密度{\rho _{\rm{p}}}/(kg·m−3) 2500[27] 桩体热容量{c_{\rm{p}}}/(J·kg−1·℃−1) 1200[27] 桩体热导率{k_{\rm{p}}}/(W·m−1·℃−1) 1.5[27] 桩体泊松比{\mu _{\rm{p}}} 0.15[27] 桩体弹性模量{E_{\rm{p}}}/GPa 30[27] 桩体热膨胀系数{\alpha _{\rm{p}}}/(με·℃−1) 10[28] 桩径D/m 0.6 图8为不同运行温度下的能量桩荷载沉降曲线。本文采用桩顶位移与桩径的百分率比值来衡量桩顶位移量。从图8中可以看出,当桩顶荷载较小时,不同工况下的沉降曲线比较重合,部分原因是本文未能考虑运行温度对桩土接触面的初始剪切刚度的影响。当桩顶荷载达到一定程度时,温度效应才开始呈现。当无运行温度作用时,算例的极限承载力约为975 kN;运行温度为20 ℃时,能量桩极限承载力变为1025 kN,涨幅约5%,略低于MCCARTNEY等[29]所测涨幅(7%)。
3.2 温度对桩身力学性质的影响
图9(a)和图9(b)分别是桩顶荷载500 kN和900 kN时,不同运行温度所对应的桩身位移曲线。由图9(a)可知,当桩顶荷载为500 kN时,由于塑性区未发展至桩体下部,桩身位移曲线存在明显的曲度。当温度增加时,土体侧摩阻力得到增强,桩身位移随之减小;运行温度从0 ℃增加至60 ℃时,桩顶位移从3.6 mm减少至2.9 mm,平均变化率约为0.01 mm/℃。当桩顶荷载为900 kN时,此时塑性区已发展至桩体下部,所以桩身位移呈近似直线分布;运行温度从0 ℃增加至60 ℃时,桩顶位移从21 mm减少至12 mm,平均变化率约为0.15 mm/℃。
使用\tau /{\tau _{\rm{u}}}衡量桩侧土体的塑性发展程度。图10(a)和图10(b)分别是桩顶荷载为500 kN和900 kN时,不同运行温度所对应的塑性发展曲线。从图中可以看出,上侧土体的塑性发展程度更大,随着运行温度的升高,桩侧土体的塑性发展程度在逐渐减弱。假设\tau /{\tau _{\rm{u}}} > 0.75时桩侧土体开始进入塑性状态。如图10(a)所示,当桩顶荷载为500 kN,运行温度为0 ℃时,桩侧土的塑性深度约为0.24倍桩长,当 \varDelta T 为40 ℃时,桩侧土的塑性深度约为0.14倍桩长。如图10(b)所示,当桩顶荷载900 kN,运行温度为0 ℃时,桩侧土的塑性深度已贯穿整个桩体,当 \varDelta T 为40 ℃时,桩侧土的塑性深度约为0.72倍桩长。
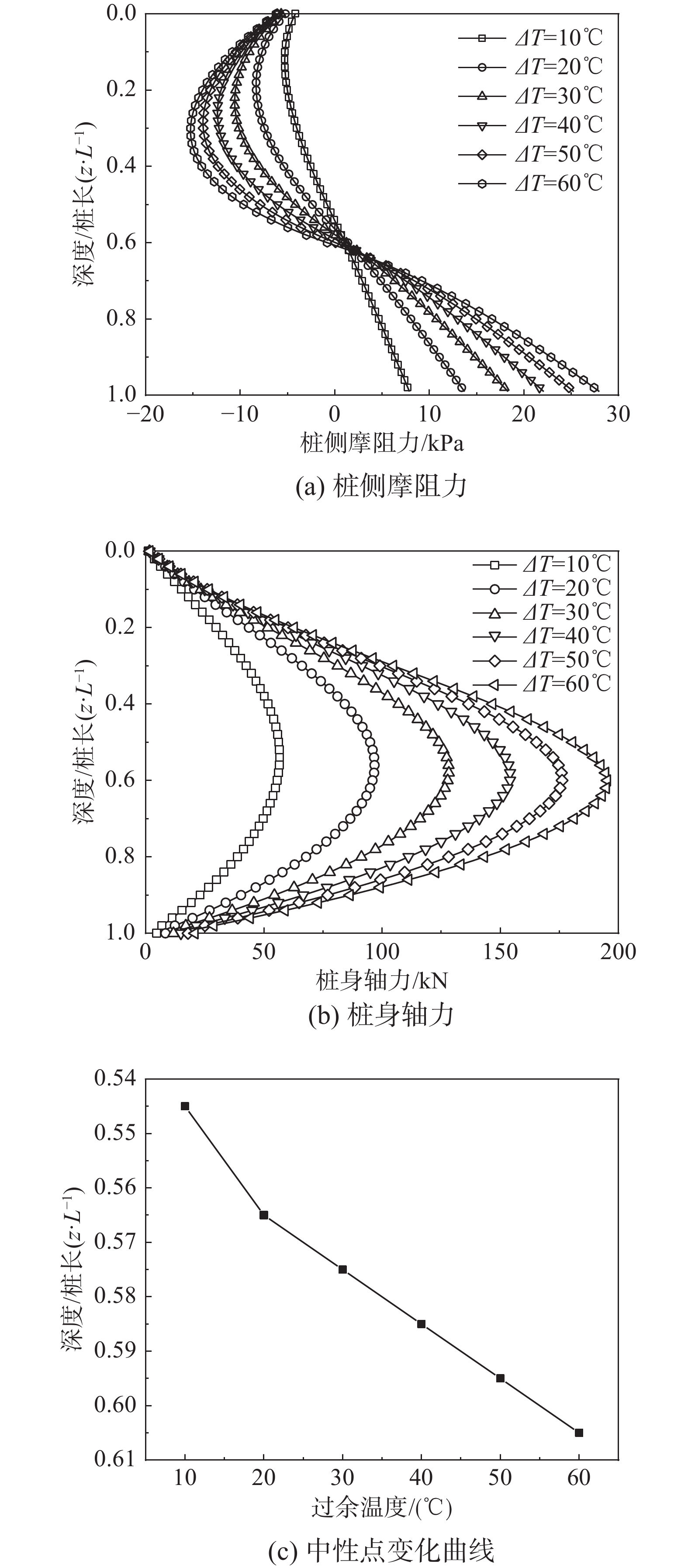
图11(a)所示为桩顶自由时的不同温度所对应的桩侧摩阻力分布曲线,由图可知,能量桩温度升高时,桩体将沿中性点产生纵向位移。以中性点为界,上侧桩体受负摩阻力作用,下侧桩体受正摩阻力作用。从图中可以看出,桩侧摩阻力数值上沿深度先增大后减小,然后反向增大。对桩侧摩阻力求和可得到如图11(b)所示的桩身轴力分布。从图11(b)看出纯温度荷载作用下,能量桩桩身轴力呈先增大后减小趋势。轴力最大值位于桩身中下部分。能量桩运行温度从10 ℃增加至60 ℃时,最大桩身轴力从55 kN增长至195 kN,平均变化幅度约为2.8 kN/℃。图11(c)为中性点[13]随温度的变化曲线,由图可知,当能量桩温度升高10 ℃时,中性点位于约0.55倍桩长处,当能量桩温度升至60 ℃时,中性点下移至约0.61倍桩长处。即桩顶自由时,提高能量桩温度将引起中性点下移。这与文献[13]规律基本一致。
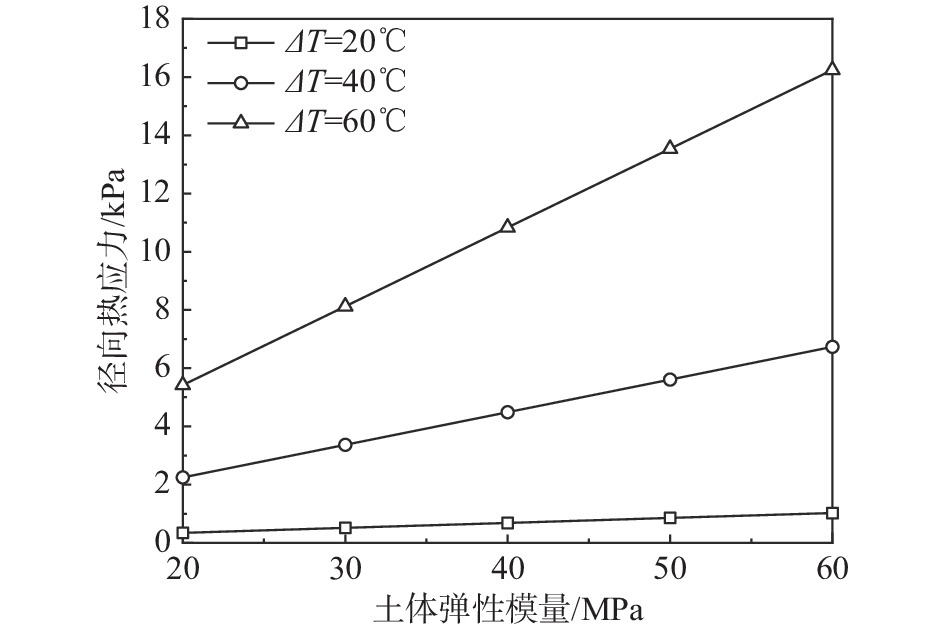
3.3 {E_{\rm{s}}}和{\alpha _{\rm{s}}}对径向热应力的影响
土体弹性模量的一定程度上反映了桩侧土体对能量桩径向膨胀的限制能力,从而影响径向热应力。图12展示了不同运行温度下,土体弹性模量对桩土界面处径向热应力的影响,其中运行时间为24 h,桩-土热学力学参数见表4。由图12可知,当 \varDelta T 为20 ℃时,即运行温度较低时,径向热应力基本不随土体弹性模量变化,始终处于较低水平。当土体弹性模量为60 MPa, \varDelta T 从20 ℃增加至60 ℃,径向热应力从1 kPa增加至16 kPa,平均增长率约为0.4 kPa/℃,略低于FAIZAL等[6]的计算值0.54 kPa/℃。
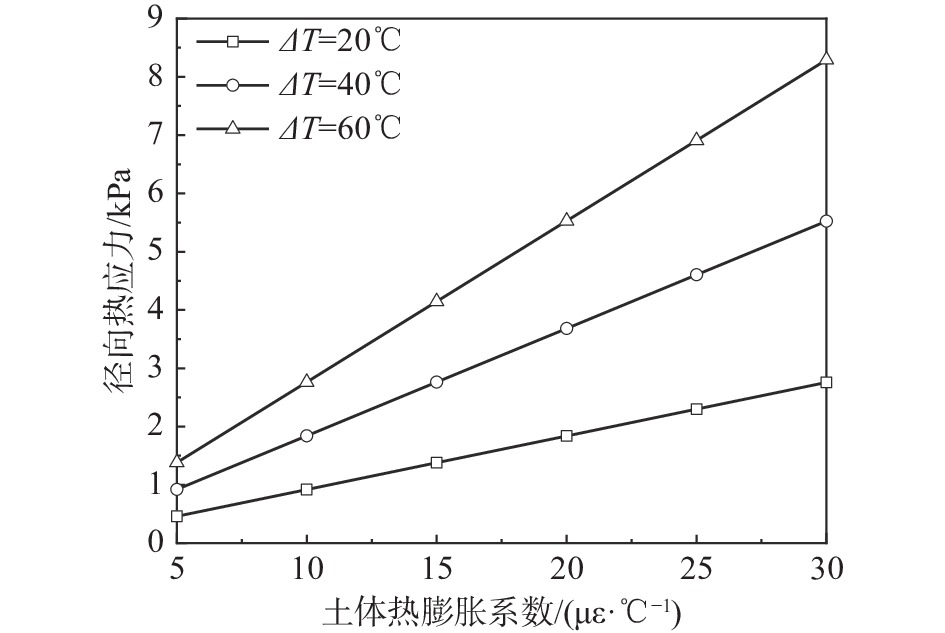
图13展示了不同运行温度下,土体热膨胀系数对桩土界面处径向热应力的影响。运行时间为24 h,{\alpha _{\rm{s}}}从5 με/℃变化至30 με/℃[28, 30-31],其余桩-土热学力学参数见表4。从图中可以看出,随着土体热膨胀系数的增大,桩土界面的径向热应力有增长趋势。当过余温度为20 ℃时,{\alpha _{\rm{s}}}从5 με/℃增加至30 με/℃,径向热应力从0.5 kPa增加至2.8 kPa;当运行过余温度为60℃时,径向热应力从1.4 kPa增加至8.3 kPa。综合图12与图13可以发现,{E_{\rm{s}}}、{\alpha _{\rm{s}}}、 \varDelta T 对桩土界面处的径向热应力的影响具有叠加效应。
4 结论
本文在计算能量桩竖向承载力时考虑了温度引起的径向热应力,对桩侧土体的极限侧摩阻力进行了修正。基于温度场和应力场的顺序耦合,将桩与土考虑为具有协调变形的整体,计算了温度荷载作用下能量桩的承载特性,改进了已有的竖向受荷能量桩分析方法。主要得到以下结论:
(1) 温度作用会影响能量桩的荷载传递,导致其轴力重分布。提高能量桩的运行温度可小幅增加其承载力,缓解塑性区向下发展。本文工况中,能量桩运行温度增加20 ℃,极限承载力提升约5%。
(2) 当能量桩的桩顶自由时,温度效应将使能量桩关于中性点发生位移,增大运行温度将引起中性点下移;桩侧摩阻力呈现先增大后减小,然后反向增大的变化趋势。
(3)当运行温度不变时,随着运行时间的增加,由于温度扩散作用,径向热应力有增大趋势。热应力沿径向呈先剧烈增大后缓慢减小的趋势。当运行时间一定时,{E_{\rm{s}}}、{\alpha _{\rm{s}}}、 \varDelta T 对桩土界面处的径向热应力的影响具有叠加效应。
(4) 本文方法具有一定的假设前提,主要基于热弹性理论,且未能考虑温度变化对桩土接触面初始剪切刚度的影响。对力学性质随温度有明显变化的黏性土,该方法的适用性需要进一步的探究。
-
表 1 径向热应力计算参数
Table 1 Radial thermal stress calculation parameters
参数 值 土体密度{\rho _{\rm{s}}}/(kg·m−3) 1500 土体热容量{c_{\rm{s}}}/(J·kg−1·℃−1) 1500 土体热导率{k_{\rm{s}}}/(W·m−1·℃−1) 2.0 土体泊松比 {\mu _{\rm{s} }} 0.495 土体弹性模量{E_{\rm{s}}}/MPa 50 土体热膨胀系数{\alpha }_{{\rm{s}}}/(με·℃−1) 30 桩体密度{\rho _{\rm{p}}}/(kg·m−3) 2500 桩体热容量{c_{\rm{p}}}/(J·kg−1·℃−1) 1200 桩体热导率{k_{\rm{p}}}/(W·m−1·℃−1) 1.5 桩体泊松比 {\mu _{\rm{p} }} 0.15 桩体弹性模量{E_{\rm{p}}}/GPa 30 桩体热膨胀系数{\alpha _{\rm{p}}}/(με·℃−1) 10 桩径D/m 0.6 表 2 模型参数
Table 2 Model parameters
定义 值 桩长/m 19.6 直径/m 0.88 桩体弹性模量/GPa 27.8 桩体热膨胀系数/(m \cdot ℃−1) 2.22×10−5 土体弹性模量/MPa 11 摩擦角/(°) 31 土体热导率/( W \cdot (m \cdot ℃)−1) 2.3 桩体导热系数/(W/ (m \cdot ℃)) 2.3 土体有效重度/(kN \cdot m−3) 15.4 土体热膨胀系数/(m \cdot ℃−1) 5×10−6 表 3 桩土热学力学参数
Table 3 Thermal mechanical parameters of pile and soil
土层 厚度/m 密度ρs/(kg·m−3) 粘聚力Cs/kPa 内摩擦角 \varphi /(°) 泊松比{\mu _{\rm{s}}} 弹性模量Es/MPa 桩土摩擦系数 素填土 3.0 1800 9 11.6 0.35 28 0.2 表土 2.0 1800 9 11.6 0.35 28 0.2 粉质黏土 1.5 1830 22 12.8 0.35 25 0.2 淤泥质粉质黏土 2.0 1830 13 10.0 0.40 15 0.2 粉质黏土 5.0 1940 42 15.0 0.35 80 0.2 粉土夹粉砂 6.0 1840 8 25.1 0.30 100 0.3 粉砂夹粉土 6.0 1860 6 27.1 0.30 140 0.3 粉土 2.5 1810 9 22.1 0.30 120 0.3 粉土 12.0 1840 8 25.2 0.30 200 0.3 桩体导热系数/(W \cdot (m \cdot ℃)−1) 桩体密度/(kg \cdot m−3) 桩体泊松比 桩体比热容/(J \cdot (kg \cdot ℃)−1) 2.3 2500 0.2 960 桩体热膨胀系数/(m \cdot ℃−1) 土体导热系数/( W \cdot (m \cdot ℃)−1) 土体比热容/(J \cdot (kg \cdot ℃)−1) 土体热膨胀系数/(m \cdot ℃−1) 1.0×10−5 1.8 1500 5×10−6 表 4 计算参数
Table 4 Calculation parameters
参数 值 土体密度{\rho _{\rm{s}}}/(kg·m−3) 1500[27] 土体热容量{c_{\rm{s}}}/(J·kg−1·℃−1) 1500[27] 土体热导率{k_{\rm{s}}}/(W·m−1·℃−1) 2.0[27] 土体泊松比{\mu _{\rm{s}}} 0.495[27] 土体弹性模量{E_{\rm{s}}}/MPa 40 土体热膨胀系数{\alpha _{\rm{s}}}/(με·℃−1) 30[28] 桩体密度{\rho _{\rm{p}}}/(kg·m−3) 2500[27] 桩体热容量{c_{\rm{p}}}/(J·kg−1·℃−1) 1200[27] 桩体热导率{k_{\rm{p}}}/(W·m−1·℃−1) 1.5[27] 桩体泊松比{\mu _{\rm{p}}} 0.15[27] 桩体弹性模量{E_{\rm{p}}}/GPa 30[27] 桩体热膨胀系数{\alpha _{\rm{p}}}/(με·℃−1) 10[28] 桩径D/m 0.6 -
[1] 江杰, 付臣志, 王顺苇, 等. 考虑实际分布形式的水平受荷桩桩周土抗力分析方法[J]. 工程力学, 2021, 38(11): 199 − 211. doi: 10.6052/j.issn.1000-4750.2020.11.0842 JIANG Jie, FU Chenzhi, WANG Shunwei, et al. Analytical method of soil resistance around laterally loaded piles considering its actual distribution [J]. Engineering Mechanics, 2021, 38(11): 199 − 211. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.11.0842
[2] 孙毅龙, 许成顺, 杜修力, 等. 海上风电大直径单桩的修正p-y曲线模型[J]. 工程力学, 2021, 38(4): 44 − 53. doi: 10.6052/j.issn.1000-4750.2020.01.0051 SUN Yilong, XU Chengshun, DU Xiuli, et al. A modified p-y curve model of large-monopiles of offshore wind power plants [J]. Engineering Mechanics, 2021, 38(4): 44 − 53. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.01.0051
[3] PARK S, LEE S, SUNG C, et al. Applicability evaluation of cast-in-place energy piles based on two-year heating and cooling operation [J]. Renewable and Sustainable Energy Reviews, 2021, 143: 110906. doi: 10.1016/j.rser.2021.110906
[4] 方鹏飞, 高翔, 娄扬, 等. 夏季工况下正常服役地热能源桩承载性能原位试验研究[J]. 岩石力学与工程学报, 2021, 40(5): 1032 − 1042. FANG Pengfei, GAO Xiang, LOU Yang, et al. Field test on the bearing behaviors of geothermal energy piles in natural service under the summer condition [J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(5): 1032 − 1042. (in Chinese)
[5] 桂树强, 程晓辉. 能源桩换热过程中结构响应原位试验研究[J]. 岩土工程学报, 2014, 36(6): 1087 − 1094. GUI Shuqiang, CHENG Xiaohui. In-situ tests on structural responses of energy piles during heat exchanging process [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1087 − 1094. (in Chinese)
[6] FAIZAL M, BOUAZZA A, HABERFIELD C, et al. Axial and radial thermal responses of a field-scale energy pile under monotonic and cyclic temperature changes [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2018, 144(10): 04018072. doi: 10.1061/(ASCE)GT.1943-5606.0001952
[7] SANI A K, SINGH R M, AMIS T, et al. A review on the performance of geothermal energy pile foundation, its design process and applications [J]. Renewable and Sustainable Energy Reviews, 2019, 106: 54 − 78. doi: 10.1016/j.rser.2019.02.008
[8] 陈忠购, 赵石娆, 张正威. 内置并联U形埋管能量桩的换热性能研究[J]. 工程力学, 2013, 30(5): 238 − 243. doi: 10.6052/j.issn.1000-4750.2012.07.0538 CHEN Zhonggou, ZHAO Shirao, ZHANG Zhengwei. Heat transfer analysis of energy piles with parallel connected U-tubes [J]. Engineering Mechanics, 2013, 30(5): 238 − 243. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.07.0538
[9] BATINI N, LORIA A F R, CONTI P, et al. Energy and geotechnical behaviour of energy piles for different design solutions [J]. Applied Thermal Engineering, 2015, 86: 199 − 213. doi: 10.1016/j.applthermaleng.2015.04.050
[10] NG C W W, FARIVAR A, GOMAA S M M H, et al. Centrifuge modeling of cyclic nonsymmetrical thermally loaded energy pile groups in clay [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2021, 147(12): 04021146. doi: 10.1061/(ASCE)GT.1943-5606.0002689
[11] MORADSHAHI A, FAIZAL M, BOUAZZA A, et al. Effect of nearby piles and soil properties on thermal behaviour of a field-scale energy pile [J]. Canadian Geotechnical Journal, 2021, 58(9): 1351 − 1364. doi: 10.1139/cgj-2020-0353
[12] 路宏伟, 蒋刚, 王昊, 等. 摩擦型能源桩荷载-温度现场联合测试与承载性状分析[J]. 岩土工程学报, 2017, 39(2): 334 − 342. LU Hongwei, JIANG Gang, WANG Hao, et al. In-situ tests and thermo-mechanical bearing characteristics of friction geothermal energy piles [J]. Chinese Journal of Geotechnical Engineering, 2017, 39(2): 334 − 342. (in Chinese)
[13] NG C W W, SHI C, GUNAWAN A, et al. Centrifuge modelling of heating effects on energy pile performance in saturated sand [J]. Canadian Geotechnical Journal, 2015, 52(8): 1045 − 1057. doi: 10.1139/cgj-2014-0301
[14] 陆浩杰, 吴迪, 孔纲强, 等. 循环温度作用下饱和黏土中摩擦型桩变形特性研究[J]. 工程力学, 2020, 37(5): 156 − 165. doi: 10.6052/j.issn.1000-4750.2019.07.0353 LU Haojie, WU Di, KONG Gangqiang, et al. Displacement characteristics of friction piles embedded in saturated clay subjected to thermal cycles [J]. Engineering Mechanics, 2020, 37(5): 156 − 165. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.07.0353
[15] 王成龙, 刘汉龙, 孔纲强, 等. 不同埋管形式下能量桩热力学特性模型试验研究[J]. 工程力学, 2017, 34(1): 85 − 91. doi: 10.6052/j.issn.1000-4750.2015.05.0455 WANG Chenglong, LIU Hanlong, KONG Gangqiang, et al. Model tests on thermal mechanical behavior of energy piles influenced with heat exchangers types [J]. Engineering Mechanics, 2017, 34(1): 85 − 91. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.05.0455
[16] 蒋刚, 李仁飞, 王昊, 等. 摩擦型能源桩热–力耦合全过程承载性能分析[J]. 岩石力学与工程学报, 2019, 38(12): 2525 − 2534. JIANG Gang, LI Renfei, WANG Hao, et al. Numerical analysis of the bearing capacity of floating energy piles during the full process of thermal-mechanical coupling [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(12): 2525 − 2534. (in Chinese)
[17] LORIA A F R, GUNAWAN A, SHI C, et al. Numerical modelling of energy piles in saturated sand subjected to thermo-mechanical loads [J]. Geomechanics for Energy and the Environment, 2015, 1: 1 − 15. doi: 10.1016/j.gete.2015.03.002
[18] KNELLWOLF C, PERON H, LALOUI L. Geotechnical analysis of heat exchanger Piles [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(10): 890 − 902. doi: 10.1061/(ASCE)GT.1943-5606.0000513
[19] 费康, 戴迪, 洪伟. 能量桩单桩工作特性简化分析方法[J]. 岩土力学, 2019, 40(1): 70 − 80, 90. FEI Kang, DAI Di, HONG Wei, et al. A simplified method for working performance analysis of single energy piles [J]. Rock and Soil Mechanics, 2019, 40(1): 70 − 80, 90. (in Chinese)
[20] 董龙龙, 吴文兵, 梁荣柱, 等. 基于指数模型的能源桩长期响应研究[J]. 岩石力学与工程学报, 2021, 40(3): 629 − 639. DONG Longlong, WU Wenbing, LIANG Rongzhu, et al. Long-term responses of energy piles based on exponential model [J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 629 − 639. (in Chinese)
[21] 骆湘勤, 刘干斌, 郑言东, 等. 考虑温度影响的能源桩桩-土界面荷载传递模型[J]. 岩石力学与工程学报, 2019, 38(1): 171 − 179. LUO Xiangqin, LIU Ganbin, ZHENG Yandong, et al. A load transfer model of energy pile-soil interfaces under temperature variation [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(1): 171 − 179. (in Chinese)
[22] 王哲, 刘耶军, 张正威, 等. 能源桩全生命周期热响应半径简化计算方法[J]. 中南大学学报(自然科学版), 2020, 51(2): 514 − 522. WANG Zhe, LIU Yejun, ZHANG Zhengwei, et al. Simplified calculation method of thermal response radius of energy pile in its whole life cycle [J]. Journal of Central South University (Science and Technology), 2020, 51(2): 514 − 522. (in Chinese)
[23] RANDOLPH M F, WROTH C P. An analysis of the vertical deformation of pile groups [J]. Géotechnique, 1979, 29(4): 423 − 439.
[24] MIMOUNI T, LALOUI L. Behaviour of a group of energy piles [J]. Canadian Geotechnical Journal, 2015, 52(12): 1913 − 1929. doi: 10.1139/cgj-2014-0403
[25] 李维特, 黄保海, 毕仲波. 热应力理论分析及应用[M]. 北京: 中国电力出版社, 2004: 94 − 95. LI Weite, HUANG Baohai, BI Zhongbo. Theoretical analysis and application of thermal stress [M]. Beijing: China Electric Power Press, 2004: 94 − 95. (in Chinese)
[26] 赵海丰, 桂树强, 唐荣彬, 等. 螺旋型埋管能源桩传热模型的适用性及其试验验证[J]. 长江科学院院报, 2017, 34(4): 111 − 116. ZHAO Haifeng, GUI Shuqiang, TANG Rongbin, et al. Applicability of heat transfer model of energy pile with buried spiral pipe and its experimental verification [J]. Journal of Yangtze River Scientific Research Institute, 2017, 34(4): 111 − 116. (in Chinese)
[27] OLGUN C G, ARSON C F, OZUDOGRU T Y. Thermo-mechanical radial expansion of heat exchanger piles and possible effects on contact pressures at pile–soil interface [J]. Géotechnique Letters, 2014, 4(3): 170 − 178.
[28] SALCIARINI D, RONCHI F, CATTONI E, et al. Thermomechanical effects induced by energy piles operation in a small piled raft [J]. International journal of Geomechanics, 2015, 15(2): 04014042. doi: 10.1061/(ASCE)GM.1943-5622.0000375
[29] MCCARTNEY J S, ROSENBERG J E. Impact of heat exchange on side shear in thermo-active foundations [C]// Geo-Frontiers Congress 2011. Dallas, Texas, ASCE, 2011: 488 − 498.
[30] SURYATRIYASTUTI M E, MROUEH H, BURLON S. A load transfer approach for studying the cyclic behavior of thermo-active piles [J]. Computers and Geotechnics, 2014, 55: 378 − 391. doi: 10.1016/j.compgeo.2013.09.021
[31] KONG G Q, CAO T, HAO Y H, et al. Thermomechanical properties of an energy micro pile-raft foundation in silty clay [J]. Underground Space, 2021, 6(1): 76 − 84. doi: 10.1016/j.undsp.2019.09.005
-
期刊类型引用(1)
1. 《中国公路学报》编辑部. 中国桥梁工程学术研究综述·2024. 中国公路学报. 2024(12)  百度学术
百度学术
其他类型引用(0)



 下载:
下载: