深部工程岩体温度与渗流耦合作用下复杂应力场反演方法

周家兴; 王金安; 李飞

doi:10.6052/j.issn.1000-4750.2022.05.0495

深部工程岩体温度与渗流耦合作用下复杂应力场反演方法

周家兴^{1, 2,},
王金安^2,,
李飞^2, ,

1.
清华大学水利水电工程系，北京 100084
2.
北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083

基金项目: 国家重点研发计划项目(2017YFC1503104)

详细信息

作者简介:
周家兴(1993−)，男，山东乳山人，博士，主要从事地应力场反演与计算方面的研究(E-mail: zhoujx1993@tsinghua.edu.cn)

王金安(1958−)，男，河北昌黎人，教授，博士，博导，主要从事岩石力学与工程方面的研究(E-mail: wja@ustb.edu.cn)

通讯作者:
李　飞(1985−)，女，山西运城人，副教授，博士，主要从事岩石力学与工程方面的研究(E-mail: lifei3522883@163.com)

中图分类号: TD311
计量
- 文章访问数: 273
- HTML全文浏览量: 94
- PDF下载量: 68
出版历程
- 收稿日期: 2022-05-29
- 修回日期: 2022-11-24
- 网络出版日期: 2023-02-21
- 刊出日期: 2024-06-24

INVERSION METHOD FOR COMPLEX STRESS FIELD UNDER COUPLING EFFECT OF TEMPERATURE AND SEEPAGE IN DEEP ENGINEERING ROCK MASS

ZHOU Jia-xing^{1, 2,},
WANG Jin-an^2,,
LI Fei^2, ,

1.
Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, China
2.
State Key Lab of Education Ministry for High Efficient Mining and Safety of Metal Mines, University of Science and Technology Beijing, Beijing 100083, China

摘要

摘要:
深部地质体应力场的复杂性可归因于高地温和高岩溶水压覆存环境中的岩体非线性特征和局部构造应力场重构。该文结合岩体在流-固-热多场耦合作用下的力学响应机制，建立了能够解析深部各应力测点构造信息特征的非线性反演与优化方法。系统地分析了深部地质体温度场—渗流场—地应力场的耦合作用，以及温度场和渗流场对地应力场的影响机理，开展了三山岛金矿区深部岩体在不同围压及孔隙水压力作用下的三轴压缩试验，探究了深部岩体物理力学参数随不同孔隙水压及围压的非线性变化规律。提出了一种非线性特征延扩迭代算法(NCEI算法)，该算法能够对各区域实测地应力数据中“弱”非线性与连续性部分的特征信息进行整体优化拟合，以及对局部构造区地应力中“强”非线性和非连续部分的特征信息进行强化解析。基于ABAQUS软件的二次开发接口，编写出多耦合计算子程序，实现了岩体地应力场—温度场—渗流场的耦合迭代计算，并对三山岛矿区深部地应力场进行了反演计算和分析。反演结果表明，考虑岩体多场耦合作用下的NCEI算法的各测点应力分量的平均反演精度为85.62%，高于BP神经网络算法与不考虑岩体耦合作用下NCEI算法的反演计算结果。因此，该研究方法可充分考虑深部地质环境的特征，为深部岩体复杂地应力场的反演与构建提供新的思路。
- 深部岩体 /
- 地应力 /
- 温度场 /
- 渗流场 /
- 耦合作用
Abstract:
The complexity of the stress field of deep geologic body can be attributed to the nonlinear characteristics of the rock mass in highland and high karst water pressure overburden environments, as well as the reconstruction of local tectonic stress field. A nonlinear inversion and optimization method that can analyze the characteristics of the tectonic information at deep stress measurement points is established considering the mechanical response mechanism of multi-field coupling for rock bodies. The coupling effect of temperature-percolation-ground stress field in deep geological body and the mechanism of temperature & percolation fields affecting the ground stress field are systematically analyzed. And the triaxial compression test of the deep rock body in Sanshan Island gold mining area under different surrounding pressures and pore water pressures is carried out to explore the non-linear variation law of physical and mechanical parameters in deep rock body with different pore water pressure and surrounding pressure. The nonlinear feature extended iteration algorithm (NCEI algorithm) is proposed to optimize the overall fitting of the feature information for weakly nonlinear and continuous parts of the measured in-situ stress in each region, and to enhance the resolution of the feature information for strongly nonlinear and discontinuous parts of the in-situ stress. Based on the secondary development interface of ABAQUS software, a muti-coupling calculation subroutine is written to realize the coupled iterative calculation of in-situ stress field-temperature field-percolation field. Then, the deep in-situ stress field in Sanshan Island mining area is inversely calculated and analyzed. The inversion results show that the average inversion accuracy of the in-situ stress components at each measurement point using the NCEI algorithm and considering the multi-field coupling effect of rock mass is 85.62%, which is higher than that of the BP neural network algorithm and the NCEI algorithm without considering the coupling effect of rock mass. Therefore, the algorithm proposed in the paper can fully consider the characteristics of the deep geological environment, and provide a new idea for the inversion and construction of deep complex in-situ stress field.
- deep rock mass /
- in-situ stress field /
- temperature field /
- seepage field /
- coupling effect

HTML全文

浅部资源日益匮乏，常态化的深部开采已成为我国“深地”领域创新的发展方向^[1-3]。在深部开采过程中，“三高”的赋存环境和复杂的地质特征对地应力场分布的反演与构建方面的研究带来严峻挑战^[4-5]。地应力场作为诱发灾害的主要因素，掌握精确的地应力场分布，可为改善岩体工程性质、提高资源开采效率、节省工程建设投资以及增强防灾减灾能力等方面发挥重要的作用^[6-7]。

深部测量岩体应力场工程无法进行大规模与广泛化，且稀少的局部小范围测点地应力值受地质构造、岩性与赋存环境等方面影响，仅能够反映局部地应力场分布特征，有效地解析大区域地应力场分布的规律存在巨大挑战，因此，非常有必要对区域地应力场进行反演分析。近几年，学者们进行了大量的地应力场反演与重构方面的研究工作。蒙伟等^[8-9]针对地质体回归计算结果存在过大的模型边界面载荷及拉应力形式的边界面载荷等，与实际构造地质类型不符的问题，采用了数理统计的相关理论与方法，优化了回归模型和回归系数，计算出满足实际构造特征的模型边界载荷条件，获得了高精度的地应力场反演结果。李飞等^[10]在考虑岩土体孔隙水对物理力学参数的影响的条件下，采用多元选择性回归方法，基于模型边界载荷的贡献度进行合理筛选，反演获得了温度异常区域的深部岩体的应力场分布。刘泉声等^[11]采用了SVR优化地应力场反演算法，解决了煤矿深部地层应力实测值误差较大的问题，其反演地应力场具有较高的反演精度。上述学者们的研究十分具有借鉴性，相关的反演方法使得越来越多的复杂地应力场被解析。然而，在深部“三高”的复杂性环境地质条件和测点应力数据噪声的不确定性与局部性等方面的影响，深部复杂地应力场仅在边界载荷条件进行优化往往是无法满足精度要求的。因此，建立一套能够考虑深部复杂地质属性的多因素耦合作用条件下的地应力场反演方法显得尤为重要。

有鉴于此，本研究系统分析了深部工程岩体的多场耦合作用机制，建立了岩体温度—应力—渗流相互耦合迭代计算方法。并基于机器学习理论与统计优化分析理论，提出了适用于深部复杂地应力数据的非线性特征延扩迭代算法(NCEI算法)，该算法能够对地应力数据中弱非线性与连续性部分的特征信息进行整体优化拟合，也能对局部构造区地应力中强非线性和非连续部分的特征信息进行强化解析。最后，以三山岛矿区为研究对象，对矿区深部复杂地应力场进行了精确地反演与解析，其研究方法可为深部工程区域的复杂应力场的反演与构建工作提供参考。

1 深部地质体多场耦合机制

岩体的多场耦合是指温度场、渗流场及应力场间的相互作用和影响，受深部复杂地质条件及赋存环境的影响，三场间的耦合效应十分明显^[12-13]。

1.1 地温场与地应力场的耦合作用

地温场对地应力场的影响可分为直接及间接两方面，直接影响为岩体在地温差异和相互约束作用下产生的温度应力^[14-15]；间接影响是在温度变化的作用下，岩体力学性质所发生的非线性变化响应，岩土介质的力学参数变化量是以温度等为自变量的非线性函数。另外，地应力场的改变也会引起温度场的变化：其一，岩体因受高应力作用而产生变形与屈服，部分应变势能转换为热能，直接改变地温场分布变化^[16-17]；其二，岩体应力场的变化引起其热力学参数变化，间接影响温度场分布。

1.1.1 温度应力场的分布规律

温度应力场是岩体在围压约束作用下因温度变化而产生的应力场，岩体温度应变及应力计算如式(1)~式(2)：

${e_{\rm T}} = \int_0^T {\alpha (T){\rm d}t}$

(1)

${\sigma _{\rm T}} = r{e_{\rm T}} = rE({T})\int_0^T {\alpha (T){\rm d}t}$

(2)

式中： ${\sigma _{\rm T}}$ 、 ${e_{\rm T}}$ 分别是温度应力和温度应变； $\alpha (T)$ 、 $E(T)$ 分别是线膨胀系数及弹性模量，它们可视为温度的函数； $r$ 为热应变约束系数， $r \in [0,1]$ ，深部工程岩体的约束系数较大，温度应力相对较大。

$\left\{ \begin{aligned} & {r_{\rm v}}E(T)\int_0^T {\alpha (T){\rm d}t} = g\int_0^h {\rho (h){\rm d}h} \\& {r_{\rm H}}E(T)\int_0^T {\alpha (T){\rm d}t} = {\lambda _{\rm H}}g\int_0^h {\rho (h){\rm d}h} \\& {r_{\rm h}}E(T)\int_0^T {\alpha (T){\rm d}t} = {\lambda _{\rm h}}g\int_0^h {\rho (h){\rm d}h} \end{aligned} \right.$

(3)

式中， ${r_{\rm v}}$ 、 ${r_{\rm H}}$ 、 ${r_{\rm h}}$ 分别为竖直、最大水平及最小水平主应力方向上的岩体热应变约束系数，各约束系数随着深度的增加逐渐趋近1。

1.1.2 温度对深部岩体力学参数的影响

深部岩土工程涉及的地温场隶属于增温带区域，地温梯度约为0.03 ℃/m~0.09 ℃/m，同深度水平的岩体温度也存在差异性^{[10, 18]}。诸如断层等非连续性地质构造的区域，由于受到填充的岩土介质热力学性质优良、流体介质的流动性强烈等因素的影响，岩体的温度值往往相对于同埋深水平较高。深部岩体在高温度及水平温度差的影响下，在微细观层面上会产生大量的裂隙、裂纹，从而使得岩体的宏观力学性质损伤劣化^[19]。

岩体弹性模量随着温度升高而减小，岩浆岩的弹性模量随温度的变化关系如式(4)所示：

$E(T) = {\alpha _1}{E_0}\exp ( - {\alpha _2}T)$

(4)

式中： ${\alpha _1}$ 、 ${\alpha _2}$ 为待拟合系数； ${E_0}$ 为常温条件下的岩体弹性模量。

另外，在0 ℃~300 ℃范围内，随着温度的升高，岩浆岩内部裂隙发育程度增加，泊松比随着温度升高而呈现小幅度增加，可近似将泊松比视为常数。

1.2 渗流场与地应力场的耦合作用

渗流场与地应力场的耦合特征主要体现在两个方面：当渗流场改变时，孔隙及裂隙中流体渗流压力的变化会直接影响到岩体骨架上的有效应力分布，从而使得深部地质体的应力场分布与孔隙水流动规律发生变化；另外，岩体作为典型的多孔介质，渗透压力的变化无疑将会使孔隙体积和裂隙空间展布特征与规律改变，进而导致岩体的力学特性变化和地应力场变化^[20-21]。

当岩体应力场变化时，岩体孔隙体积变化将直接使得渗流场变化，且岩体孔隙及裂隙的张开与闭合会影响其渗流性，并间接引起渗流场的改变。

1.2.1 渗流场对地应力场影响

渗流压力为自由水面以下的岩体因渗流作用会产生各向同性的拉应力，可通过钻柱测试、重复地层测试、模块动态测试及泥浆重量测试等方式得到。渗透压力对地应力的影响如式(5)所示^{[14, 22]}：

$\left\{ \begin{gathered} {\sigma _{\rm v}^\prime} = {\sigma _{\rm v}} - 2\left[\frac{{{C_{\rm a}}E}}{{2(1 - 2\mu )}} - 1\right]{\gamma _{\rm w}}(H - {H_0}) \\ {\sigma _{\rm H}^\prime} = {\sigma _{\rm H}} - 2\left[\frac{{{C_{\rm a}}E}}{{2(1 - 2\mu )}} - 1\right]{\gamma _{\rm w}}(H - {H_0}) \\ {\sigma _{\rm h}^\prime} = {\sigma _{\rm h}} - 2\left[\frac{{{C_{\rm a}}E}}{{2(1 - 2\mu )}} - 1\right]{\gamma _{\rm w}}(H - {H_0}) \\ \end{gathered} \right.$

(5)

式中： ${\sigma _{\rm v}^\prime}$ 和 ${\sigma _{\rm v}}$ 为竖直方向上的有效应力和总应力；H和H′为最大水平主应力方向上的有效应力和主应力；h和h′为最小水平主应力方向上的有效应力和主应力； ${\gamma _{\rm w}}$ 为流体介质的重度； $H$ 、 ${H_0}$ 分别表征岩体埋深及水位深度； ${C_{\rm a}}$ 为岩石颗粒骨架的压缩系数； $E$ 、 $\mu$ 为弹性参数。

深部隔水层的局部区域因渗流作用的差异性而导致负渗透压力^[23]，其对地应力场的直接影响作用可如式(6)所示：

$\left\{ \begin{gathered} {\sigma _{\rm v}^\prime} = {\sigma _{\rm v}} + \frac{{{\gamma _{\rm w}}}}{2}\left[\frac{{{C_{\rm a}}E}}{{(1 - 2\mu )}} - 2\right]\frac{h}{{\cos \theta }} \\ {\sigma _{\rm H}^\prime} = {\sigma _{\rm H}} + \frac{{{\gamma _{\rm w}}}}{2}\left[\frac{{{C_{\rm a}}E}}{{(1 - 2\mu )}} - 2\right]\frac{h}{{\cos \theta }} \\ {\sigma _{\rm h}^\prime} = {\sigma _{\rm h}} + \frac{{{\gamma _{\rm w}}}}{2}\left[\frac{{{C_{\rm a}}E}}{{(1 - 2\mu )}} - 2\right]\frac{h}{{\cos \theta }} \\ \end{gathered} \right.$

(6)

式中： $h$ 为隔水层区域到下覆含水层竖直距离； $\theta$ 为水与毛细管壁侵润接触角度。

1.2.2 渗流场对深部岩体力学参数影响

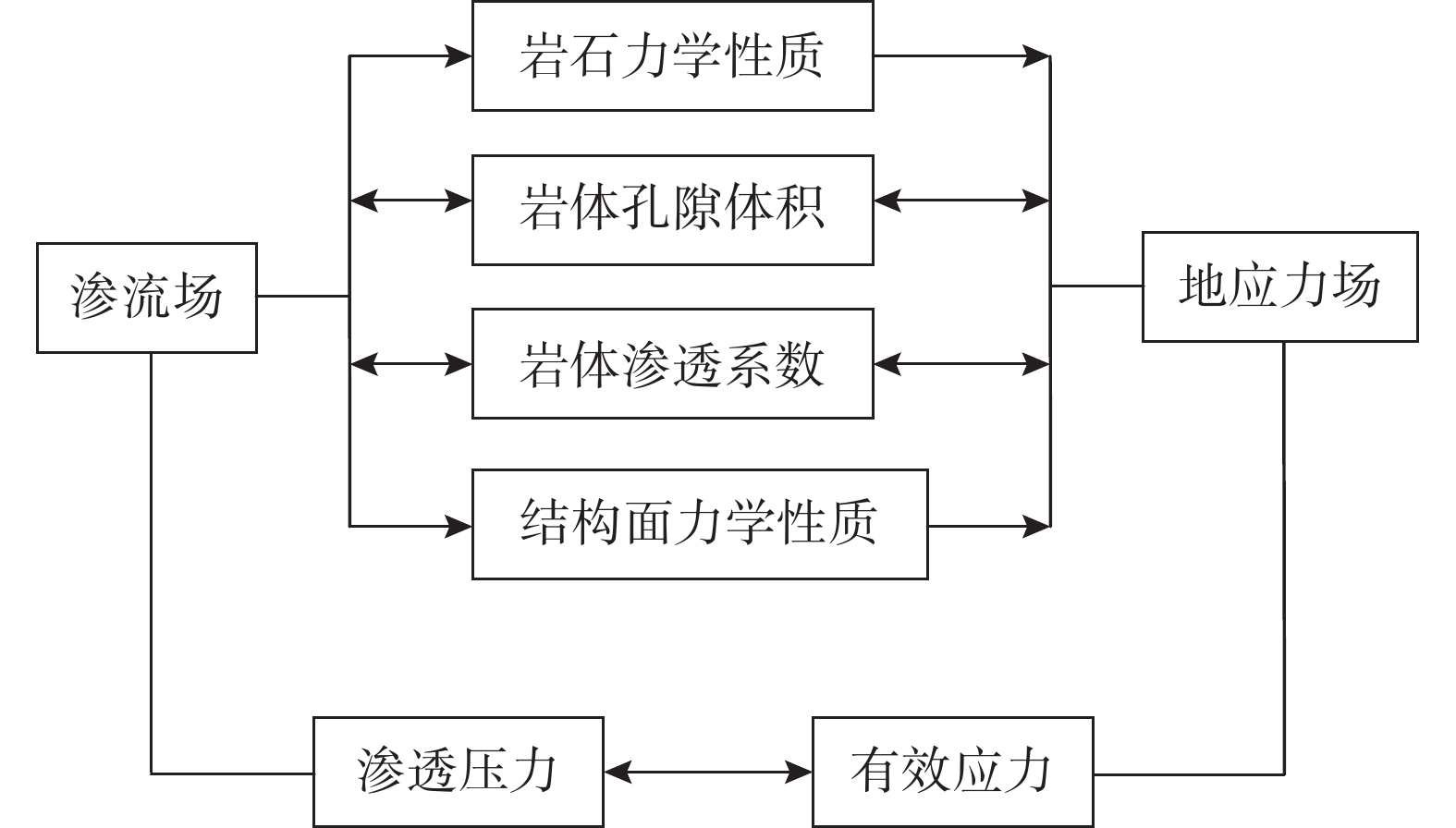
深部岩体在高压力水头的作用下，孔隙水、岩溶水在水平和竖直方向的渗流作用增强，使岩体力学参数和孔隙度发生变化。在深部高围压作用下，岩体孔隙度降低，渗流作用受到制约，渗透系数改变。深部岩体力学性质与渗流作用耦合作用明显，渗流场对岩体性质的影响机制如图1所示。

图 1 渗流场对地应力场的间接影响

Figure 1. Indirect influence of seepage field on in-situ stress field

下载: 全尺寸图片幻灯片

图1中的单向箭头是一方面影响作用强烈，另一方面作用较弱或无作用；双向箭头表征两方面作用均强烈。

岩体弹性模量与泊松比随渗透压力增加而降低，可用式(7)和式(8)进行定量化表征：

$E = {E_0}\sum\limits_{i = 1}^n {[{\beta _{i - 1}}{{({\sigma _{\rm v}} - {P_{\rm w}})}^{i - 1}}]}$

(7)

$\mu = {\mu _0}\sum\limits_{i = 1}^n {[{\chi _{i - 1}}{{({\sigma _{\rm v}} - {P_{\rm w}})}^{i - 1}}]}$

(8)

式中： ${\beta _{i - 1}}$ 、 ${\chi _{i - 1}}$ 为待拟合参数； ${E_0}$ 、 ${\mu _0}$ 为未考虑渗流作用下的岩体弹性模量及泊松比。

1.3 渗流场与温度场的耦合作用

在工程深部的涉及范围内，岩体渗流场与温度场的耦合效应较弱，即岩体中因孔隙水渗流而导致温度的变化量，以及岩体中因温度差而引起渗透压力的变化量均相对较小。

在岩体渗流场变化后，流体的流动加速了热量的迁移与传递，导致温度场变化。岩体内部生热由多方面因素所导致，温度变化量如式(9)，鉴于量值变化较小，可将式(9)进行泰勒展开(式(10))。

$\begin{split} \Delta T = & T(P + \Delta P,\sigma + \Delta \sigma ,\varepsilon + \Delta \varepsilon , \cdots ) - \\& T(P,\sigma ,\varepsilon , \cdots ) \end{split}$

(9)

$\begin{split} & \Delta T = {a_1}\Delta \sigma \Delta P\Delta \varepsilon + {b_1}\Delta P + {c_1}\Delta \varepsilon + {d_1}\Delta \sigma \\& {e_1}{(\Delta P)^2} + {f_1}{(\Delta \varepsilon )^2} + {g_1}{(\Delta \sigma )^2} + {h_1}\Delta \varepsilon \Delta \sigma + \\&\qquad {i_1}\Delta \varepsilon \Delta P + {k_1}\Delta \sigma \Delta P + o(\Delta P,\Delta \sigma ,\Delta \varepsilon ) \end{split}$

(10)

式中， ${a_1}\sim {k_1}$ 为待拟合参数。

在岩体温度场变化后，岩体内部孔隙流体与颗粒的性质会发生改变，从而影响孔隙水压的分布，其孔隙水压改变量如式(11)，泰勒展开如式(12)。

$\begin{split} & \Delta P = P(T + \Delta T,\sigma + \Delta \sigma ,\varepsilon + \Delta \varepsilon , \cdots ) - \\&\qquad P(T,\sigma ,\varepsilon , \cdots ) \end{split}$

(11)

$\begin{split} & \Delta P = {a_2}\Delta \sigma \Delta T\Delta \varepsilon + {b_2}\Delta T + {c_2}\Delta \varepsilon + {d_2}\Delta \sigma \\& {e_2}{(\Delta T)^2} + {f_2}{(\Delta \varepsilon )^2} + {g_2}{(\Delta \sigma )^2} + {h_2}\Delta \varepsilon \Delta T + \\&\qquad {i_2}\Delta \sigma \Delta T + {k_2}\Delta \varepsilon \Delta \sigma {\text{ + }}o(\Delta T,\Delta \sigma ,\Delta \varepsilon ) \end{split}$

(12)

式中， ${a_2}\sim {k_2}$ 为待拟合参数。

2 非线性特征延扩迭代算法

深部地应力场受多期构造旋回与多场耦合作用的影响而呈现非线性、非连续性和复杂性特征，测点数据信息难以解析。为了使反演地应力场与实际地应力场(实测应力场)相吻合，提出了非线性特征延扩迭代算法(NCEI算法)，该算法一方面解析了地应力场数据中的弱非线性与连续性特征信息，可将结果寻至全局最优区间；另一方面可对强非线性与非连续地应力场信息进行特征延扩解析，并通过迭代计算在最优区间内将结果收敛至最优解。

2.1 NCEI算法理论基础

NCEI算法是基于泛化风险最小原则与计算学习的VC维理论建立的，针对样本数据的复杂程度，寻找满足VC维的解析函数，并采用核函数计算进行合理延扩解析，从而保证了算法的泛化能力^[24]。该算法的解析控制方程如式(13)和式(14)所示。

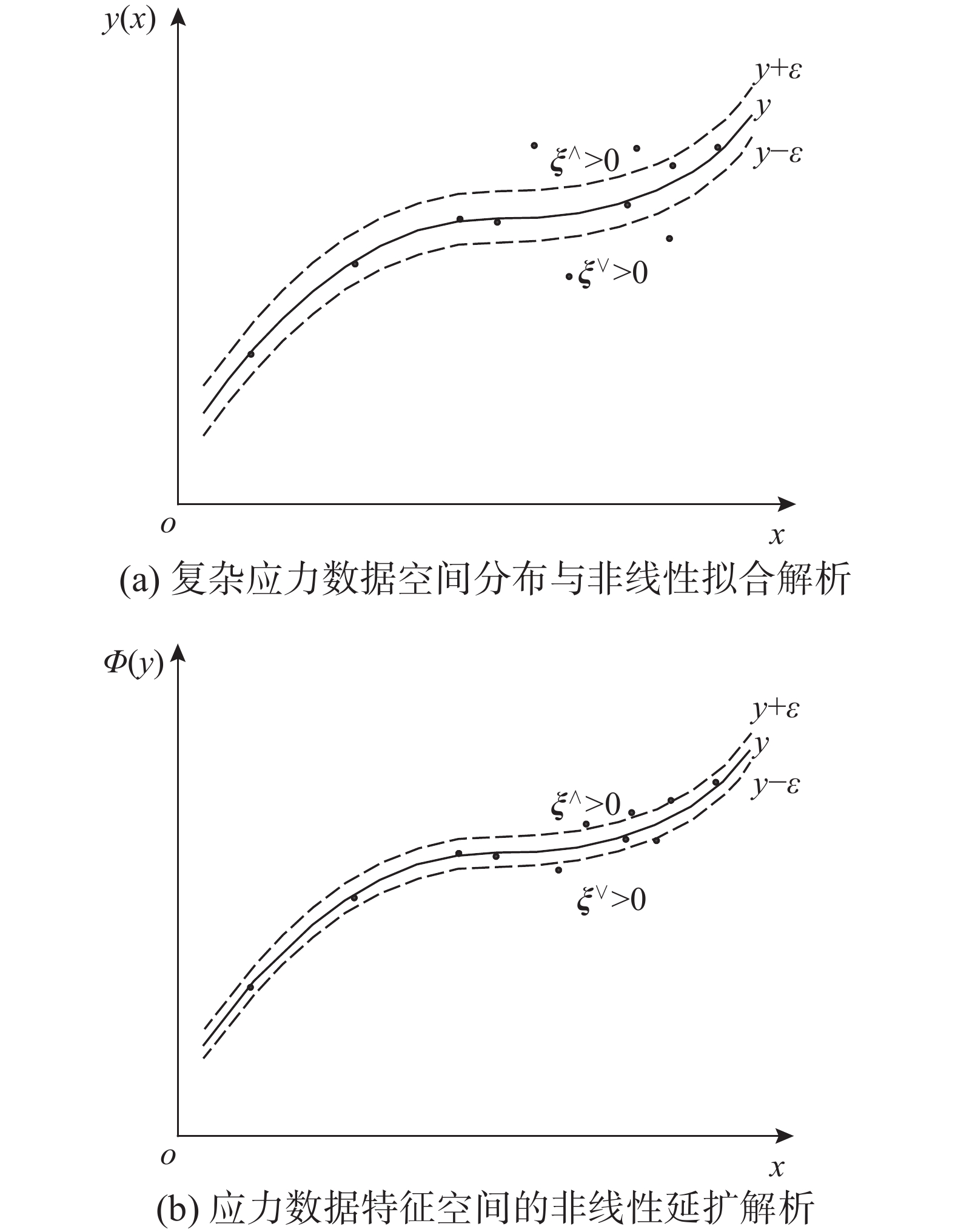
$\boldsymbol{\sigma} =\boldsymbol{k} \otimes \boldsymbol{\sigma _0} + \boldsymbol{e}$

(13)

$\boldsymbol{K} = \boldsymbol{w} ^{\rm T} \cdot \boldsymbol{\phi} ({\boldsymbol{\sigma} ^{(k')}}) + \boldsymbol{b}, \begin{array}{*{20}{c}} {}&{k' \in 1\sim N(N \geqslant n)} \end{array}$

(14)

式(13)为弱非线性应力场拟合解析方程，式中： $\boldsymbol{\sigma}$ 为实测地应力数据向量； $\boldsymbol{\sigma _0}$ 为弱非线性解析拟合计算地应力矩阵，如式(15)所示； $\otimes$ 为行向量与对应矩阵中对应列向量的数乘符号； $\boldsymbol k$ 为 $n$ 维地应力场的弱非线性解析向量； $\boldsymbol e$ 为实测点应力分量的误差向量，误差向量中各分量均满足高斯白噪声分布，分别如式(16)和式(17)所示。

式(14)为非线性延扩解析方程，式中： $K$ 为地应力场的优化解析向量； $\boldsymbol \phi ( \cdot )$ 为映射向量函数族，用于将低维数据映射到高维数据，即将原始空间()映射到特征空间()； ${\boldsymbol \sigma ^{(k')}}$ 为弱非线性解析应力场； $\boldsymbol w$ 和 $\boldsymbol b$ 分别表示拟合系数矩阵。

$\boldsymbol {\sigma} _0 = [\boldsymbol {\sigma} ^{(1)}, \cdots ,{\boldsymbol \sigma ^{(k)}}, \cdots ,{\boldsymbol \sigma ^{(n)}}],\;\;{k \in 1\sim n}$

(15)

$\boldsymbol e = {[{\boldsymbol{e} _1}, \cdots ,{\boldsymbol{e}_i}, \cdots ,{\boldsymbol{e}_n}]^{\rm T}}$

(16)

${\boldsymbol{e}_i}\sim {N_i}(0,\boldsymbol{\varphi} _i^2),\begin{array}{*{20}{c}} {}&{i \in 1\sim m×q} \end{array}$

(17)

式中： ${\boldsymbol{\varphi} _i}$ 为测点应力的第 $i$ 个分量的弱非线性解析误差的方差； $q$ 为实测点数量； $m$ 为应力分量个数。

图 2 NCEI算法对应力数据的延扩与解析

Figure 2. Extension and analysis of stress data based on NCEI algorithm

下载: 全尺寸图片幻灯片

算法的控制方程式(13)和式(14)转化为目标函数式(18)和对应的KKT条件(式(19))。

$\left\{ \begin{aligned} & \mathop {\min }\limits_{\boldsymbol k = {{[{\boldsymbol{k}_1}, \cdots ,{\boldsymbol{k}_2}, \cdots ,{\boldsymbol{k}_n}]}^{\rm T}}} {\left| {\boldsymbol \sigma - \sum\limits_{j = 1}^n {{\boldsymbol{k}_j}{{\boldsymbol \sigma }^{(j)}}} } \right|^2} \\& \mathop {\min }\limits_{\boldsymbol w ,\boldsymbol \varepsilon ,\boldsymbol \xi _i^ \vee ,\boldsymbol \xi _i^ \wedge } \frac{1}{2}\left\| {{{\boldsymbol w }^{\rm T}}} \right\|_0^2 + \boldsymbol C \odot \left[\sum\limits_{i = 1}^N (\boldsymbol \xi _i^ \vee + \boldsymbol \xi _i^ \wedge ) + \boldsymbol \varepsilon \right] \end{aligned} \right.$

(18)

式中： $\boldsymbol C$ 为 $n$ 维惩罚因子向量； $\boldsymbol \xi _i^ \vee$ 、 $\boldsymbol \xi _i^ \wedge$ 、 $\boldsymbol \varepsilon$ 分别为非线性拟合正负误差和泛化间隔，如所示，泛化界内间隔值为0； $\left\| \cdot \right\|$ 为对矩阵各行向量求Euclid范数值。

$\left\{ \begin{aligned} & {\boldsymbol k ^{(i)}} - {\boldsymbol w ^{\rm T}} \cdot \boldsymbol \phi ({\boldsymbol \sigma ^{(i)}}) - \boldsymbol b \geqslant - \boldsymbol {\varepsilon} + \boldsymbol \xi _i^ \vee \\& {\boldsymbol k ^{(i)}} - {\boldsymbol w ^{\rm{T}}} \cdot \boldsymbol \phi ({\boldsymbol \sigma ^{(i)}}) -\boldsymbol b \leqslant \boldsymbol {\varepsilon} + \boldsymbol \xi _i^ \wedge \\& \boldsymbol{\xi} _{ij}^ \wedge ,\boldsymbol{\xi} _{ij}^ \vee ,{\boldsymbol{\varepsilon} _j} \geqslant 0,\begin{array}{*{20}{c}} {}&{j \in 1\sim m×q + g} \end{array} \\& {\left| {\boldsymbol \sigma - {{\boldsymbol k }^{(i)}} \otimes {\boldsymbol{\sigma} _0}} \right|^2} \leqslant \delta \end{aligned} \right.$

(19)

式中： $g$ 为延扩维度； $\delta$ 为局部优解的偏置值，取值为0.2倍~0.4倍局部优值。

式(18)是一个凸规划问题，基于拉格朗日乘子法，可确定如式(20)所示的求解方程，而算法的解析方程可转化为式(21)。

$\begin{split} & \boldsymbol L (\boldsymbol w ,\boldsymbol b ,{\boldsymbol \xi ^ \vee },{\boldsymbol \xi ^ \wedge },\boldsymbol \varepsilon ,{\boldsymbol \beta ^ \vee },{\boldsymbol \beta ^ \wedge },{\boldsymbol \alpha ^ \vee },{\boldsymbol \alpha ^ \wedge },{\bf\textit{μ}} ) =\\&\;\;\;\; \frac{1}{2}{\left\| {{{\boldsymbol w }^{\rm T}}} \right\|^2} + \sum\limits_{i = 1}^N {\Bigg\{\boldsymbol C \odot [(\boldsymbol \xi _i^ \vee + \boldsymbol \xi _i^ \wedge ) + \boldsymbol \varepsilon } ] +\\&\;\;\;\; \boldsymbol D \odot \Bigg[{\Bigg| {\boldsymbol \sigma - {{\boldsymbol k }^{(i)}} \otimes \boldsymbol{\sigma} _0} \Bigg|^2} - \boldsymbol \delta \Bigg]\Bigg\} - {\bf\textit{μ}} \odot \boldsymbol \varepsilon + \\&\;\;\;\; \sum\limits_{i = 1}^N {\text{\{ }}\boldsymbol \beta _i^ \wedge \odot [{{\boldsymbol k }^{(i)}} -\boldsymbol w \cdot \boldsymbol \phi ({{\boldsymbol \sigma }^{(i)}}) - \boldsymbol b - \boldsymbol \varepsilon -\boldsymbol \xi _i^ \wedge ] - \\&\;\;\;\; \boldsymbol \beta _i^ \vee \odot [{{\boldsymbol k }^{(i)}} - \boldsymbol w \cdot \boldsymbol \phi ({{\boldsymbol \sigma }^{(i)}}) - \boldsymbol b + \boldsymbol \varepsilon - \boldsymbol \xi _i^ \vee ] -\\&\;\;\;\; \boldsymbol \alpha _i^ \wedge \odot \boldsymbol \xi _i^ \wedge - \boldsymbol \alpha _i^ \vee \odot \boldsymbol \xi _i^ \vee \} \end{split}$

(20)

式(20)中，各拉格朗日乘子满足的条件为： ${C_i}$ ， ${D_i}$ ， $\alpha _{ij}^ \wedge$ ， $\alpha _{ij}^ \vee$ ， ${\mu _j} {\geqslant} 0$ ， $0 {\leqslant} \beta _{ij}^ \wedge {\leqslant} {C_{\text{i}}}$ ， $0 {\leqslant} \beta _{ij}^ \vee {\leqslant} {C_{\text{i}}}$ 。

$\begin{split} \overrightarrow K =& \sum\limits_{i = 1}^N {(\overrightarrow \beta {}_i^ \wedge - \overrightarrow \beta {} _i^ \vee ){\varPhi _{i\sigma }}} + \frac{1}{N}\sum\limits_{j = 1}^N {{{\overrightarrow k }^{(j)}}} -\\&\qquad \frac{1}{N}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {(\overrightarrow \beta {}_i^ \wedge - \overrightarrow \beta {} _i^ \vee ){\varPhi _{ij}}} } \end{split}$

(21)

式(21)中，核函数 ${\varPhi _{ij}}$ 和 ${\varPhi _{i\sigma }}$ ，分布如式(22)和式(23)所示。

${\varPhi _{ij}} = \exp ( - \gamma {| {\boldsymbol{\phi} ({{\boldsymbol \sigma }^{(i)}}) - \boldsymbol{\phi} ({{\boldsymbol \sigma }^{(j)}})} |^2})$

(22)

${\varPhi _{i\sigma }} = \exp ( - \gamma {| {\boldsymbol{\phi} ({{\boldsymbol \sigma }^{(i)}}) - \boldsymbol{\phi} (\boldsymbol \sigma )} |^2}) \;\;$

(23)

令 $\boldsymbol \beta _i^ \wedge - \boldsymbol \beta _i^ \vee = {\boldsymbol \beta _i}$ ，式(20)解析方程的最小值是对偶问题(式(24))的最大值，约束条件如式(25)。

$\boldsymbol W (\boldsymbol \beta ) = \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{{\boldsymbol \beta }_i}} {{\boldsymbol \beta }_j}} {\varPhi _{ij}} - \sum\limits_{i = 1}^N {{{\boldsymbol \beta }_i}} {\boldsymbol k ^{(i)}}$

(24)

$\left\{ \begin{gathered} \sum\limits_{i = 1}^m {{\boldsymbol{\beta} _{ij}} = } 0 \\ - {\boldsymbol{C}_j} \leqslant {\boldsymbol{\beta} _{ij}} \leqslant {\boldsymbol{C}_j} \\ \end{gathered} \right.$

(25)

式(22)和式(23)中， $\gamma$ 为待求解参数。

基于SMO算法与交叉学习算法理论，将求(24)的多参数优化问题转化为两变量参数优化(式(26))。求解式(26)是该算法实现的关键，对其求解之后，可获得如式(27)所示的延扩解析式。

${\boldsymbol{W}_j}({\boldsymbol{\beta} _{ja}},{\boldsymbol{\beta} } _{jb}) = \frac{1}{2}{\boldsymbol{\beta} _{ja}}{\boldsymbol{\beta} _{ja}}{\varPhi _{aa}} + \frac{1}{2}{\boldsymbol{\beta} } _{jb}{\boldsymbol{\beta} } _{jb}{\varPhi _{bb}} + {\boldsymbol{\beta} _{ja}}{\boldsymbol{\beta} } _{jb}{\varPhi _{ab}} +$

${\boldsymbol{\beta} _{ja}}{\boldsymbol{v}_{ja}} + {\boldsymbol{\beta} } _{jb}{\boldsymbol{v}_{jb}} - ({\boldsymbol{\beta} _{ja}}\boldsymbol{k}_j^{(a)} + {\boldsymbol{\beta} } _{jb}\boldsymbol{k}_j^{(b)})$

(26)

${\boldsymbol{v}_{ij}} = {\boldsymbol{K}_i}({\boldsymbol \sigma ^{(j)}}) - \sum\limits_{i = 1}^N {\boldsymbol k _j^{(i)}} - \sum\limits_{i = 1}^N {\sum\limits_{k = 1}^N {{\boldsymbol{\beta} _{ij}}{\varPhi _{ik}}} }$

(27)

${\boldsymbol{\beta} _{ja}} + {\boldsymbol{\beta} } _{jb} = - \sum\limits_{k = 1(k \ne a,b)}^N {{\boldsymbol{\beta} _{jk}}} = r$

(28)

式(28)中： ${\boldsymbol{\beta} } _{jb}$ 为向量 ${\boldsymbol{\beta} _j}$ 的第 $b$ 分量； $\boldsymbol{k} _j^{(a)}$ 为行向量 ${\boldsymbol k _j}$ 的第 $a$ 分量； $r$ 为常数。

2.2 NCEI算法实现流程

算法的实现过程就是对式(26)进行迭代寻优，求出最优解 $\boldsymbol \beta _i^ \wedge$ 和 $\boldsymbol \beta _i^ \vee$ ，并代入非线性延扩解析式(式(27))。主要计算流程如下：

1) 输入 $m$ 组待解析地应力场的信息数据，分5组进行交互式学习与评价，平均评价值作为算法泛化性能指标，取初值 $j = 1$ 、 $kk = 1$ 。

2) ${\boldsymbol{C}^{kk}} = {\boldsymbol{A}_{kk}}$ 、 ${\boldsymbol{\gamma} ^{kk}} = {({\boldsymbol{A}_{kk}})^{\rm T}}$ ， ${\boldsymbol{A}_{kk}}$ 如式(29)。

${\boldsymbol{A}^{kk}} = {\left[\begin{array}{*{20}{c}} {{a_{11}}}& \cdots &{{a_{11}}} \\ \vdots &{{a_{k1}}}& \vdots \\ {{a_{m1}}}& \cdots &{{a_{m1}}} \end{array}\right]_{m \times m}}$

(29)

3) 取初值 $k = 0$ ，定义 $\boldsymbol{\beta} _{ji}^k = 0$ 和 $E_i^k = 0$ ， $i = 1\sim N$ ， $b_j^k = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N { \boldsymbol{k}_j^{(i)}}$ 。

4) 基于启发式学习原理^[25]，采用式(30)选取两工作集变量 ${\boldsymbol{\beta} _{ja}}$ 和 ${\boldsymbol{\beta} } _{jb}$ ， ${\boldsymbol{\beta} }_{ji} (i\ne a,b)$ 为非工作集，各值均为固定常数。

$\left\{ \begin{gathered} a = \mathop {\arg \max }\limits_{a \in \{ - {\boldsymbol {C}^{kk}} \leqslant {\boldsymbol{\beta}} _{ja} < {\boldsymbol {C}^{kk}}\} } \left[\boldsymbol{k} _j^{(a)} - \sum\limits_{i = 1}^N {{\boldsymbol{\beta}} _{ja}{\varPhi _{ai}}} \right] \\ b = \mathop {\arg \min }\limits_{b \in \{ - {\boldsymbol {C}^{kk}} < {\boldsymbol{\beta} } _{jb} \leqslant {\boldsymbol {C}^{kk}}\} } \left[\boldsymbol{k} _j^{(b)} - \sum\limits_{i = 1}^N {{\boldsymbol{\beta} } _{jb}{\varPhi _{bi}}} \right] \\ \end{gathered} \right.$

(30)

5) 选定两变量 $\boldsymbol{\beta} _{ja}^k$ 和 $\boldsymbol{\beta} _{jb}^k$ ，以式(31)求解 $\boldsymbol{\beta} _{jb}^{\rm new,unc}$ 。

${\boldsymbol{\beta} } _{jb}^{\rm new,unc} = {\boldsymbol{\beta} } _{jb}^k + \frac{{(E_a^k - E_b^k)}}{{({\varPhi _{aa}} + {\varPhi _{bb}} - 2{\varPhi _{ab}})}}$

(31)

6) 基于式(32)和式(33)，求出 $\boldsymbol{\beta} _{ja}^{k + 1}$ 与 $\boldsymbol{\beta} _{jb}^{k + 1}$ 。

${\boldsymbol{\beta} } _{jb}^{k + 1} = \left\{ \begin{aligned} & \min ({\boldsymbol {C}^{kk}},{\boldsymbol{\beta} } _{jb}^k + {\boldsymbol{\beta}} _{ja}^k),\;\\&\qquad{{\boldsymbol{\beta} } _{jb}^{\rm new,unc} > \min ({\boldsymbol {C}^{kk}},{\boldsymbol{\beta} } _{jb}^k + {\boldsymbol{\beta}} _{ja}^k)} \\& {\boldsymbol{\beta} } _{jb}^{\rm new,unc},\;\\&\qquad\max (0,{\boldsymbol{\beta} } _{jb}^k + {\boldsymbol{\beta}} _{ja}^k - {\boldsymbol {C}^{kk}}) \leqslant {\boldsymbol{\beta} } _{jb}^{\rm new,unc} < \\&\qquad \min ({\boldsymbol {C}^{kk}},{\boldsymbol{\beta} } _{jb}^k + {\boldsymbol{\beta}} _{ja}^k) \\& \max (0,{\boldsymbol{\beta} } _{jb}^k + {\boldsymbol{\beta}} _{ja}^k - {\boldsymbol {C}^{kk}}),\;\\&\qquad{{\boldsymbol{\beta} } _{jb}^{\rm new,unc} < \max (0,{\boldsymbol{\beta} } _{jb}^k + {\boldsymbol{\beta}} _{ja}^k - {\boldsymbol {C}^{kk}})} \end{aligned}\right.$

(32)

${\boldsymbol{\beta}} _{ja}^{k + 1} = {\boldsymbol{\beta}} _{ja}^k - ({\boldsymbol{\beta} } _{jb}^{k + 1} - {\boldsymbol{\beta} } _{jb}^k)$

(33)

7) 基于式(34)和式(35)，计算阈值 $b_j^{k + 1}$ 和误差值 $E_i^{k + 1}$ 。

$\begin{split} & b_j^{k + 1} = [2b_j^k - E_a^k - E_b^k - ({\boldsymbol{\beta}} _{ja}^{k + 1} - {\boldsymbol{\beta}} _{ja}^k){\varPhi _{aa}} - ({\boldsymbol{\beta} } _{jb}^{k + 1} -\\&\qquad {\boldsymbol{\beta} } _{jb}^k){\varPhi _{ab}} - ({\boldsymbol{\beta}} _{ja}^{k + 1} - {\boldsymbol{\beta}} _{ja}^k){\varPhi _{ab}} - ({\boldsymbol{\beta} } _{jb}^{k + 1} - {\boldsymbol{\beta} } _{jb}^k){\varPhi _{bb}}]/{2} \end{split}$

(34)

${E_i}^{k + 1} = \sum\limits_{h = 1}^N {{\boldsymbol{\beta}} _{jh}^{k + 1}{\varPhi _{hi}} + b_j^{k + 1} - } k_j^{(i)}\qquad$

(35)

8) 验证停机准则为 ${B_{\rm low}} \leqslant {B_{\rm up}} + 2e$ ，满足准则，计算结束并获得本轮最优解。否则， $k = k + 1$ ，返回步骤4，继续迭代优化。

$\left\{ \begin{gathered} {B_{\rm up}} = \min \left\{ k_j^{(i)} - \sum\limits_{h = 1}^N {{\boldsymbol{\beta}} _{jh}^{k + 1}{\varPhi _{hi}}} \right\} \\ {B_{\rm low}} = \max \left\{ k_j^{(i)} - \sum\limits_{h = 1}^N {{\boldsymbol{\beta}} _{jh}^{k + 1}{\varPhi _{hi}}} \right\} \\ \end{gathered} \right.$

(36)

式中， $i \in \{ - {\boldsymbol {C}^{kk}} < \boldsymbol{\beta} _{ji}^{k + 1} \leqslant {\boldsymbol {C}^{kk}}\}$ 。

9) 检验并评价模型精度，如式(37)。

$E{E_{j.kk}} = \sum\limits_{i = 1}^N {\left| {\sum\limits_{h = 1}^N {{\boldsymbol{\beta}} _{jh}^{k + 1}{\varPhi _{ih}} + b_j^{k + 1} - k_j^{(i)}} } \right|}$

(37)

10) 记录第 $kk$ 组的误差值。若 $j \leqslant n$ ，则令 $kk = 0$ ， $j = j + 1$ 进入步骤2；若 $j > n$ ，计算完成，获得算法控制方程的最优解参数。

3 工程应用

3.1 地质概况

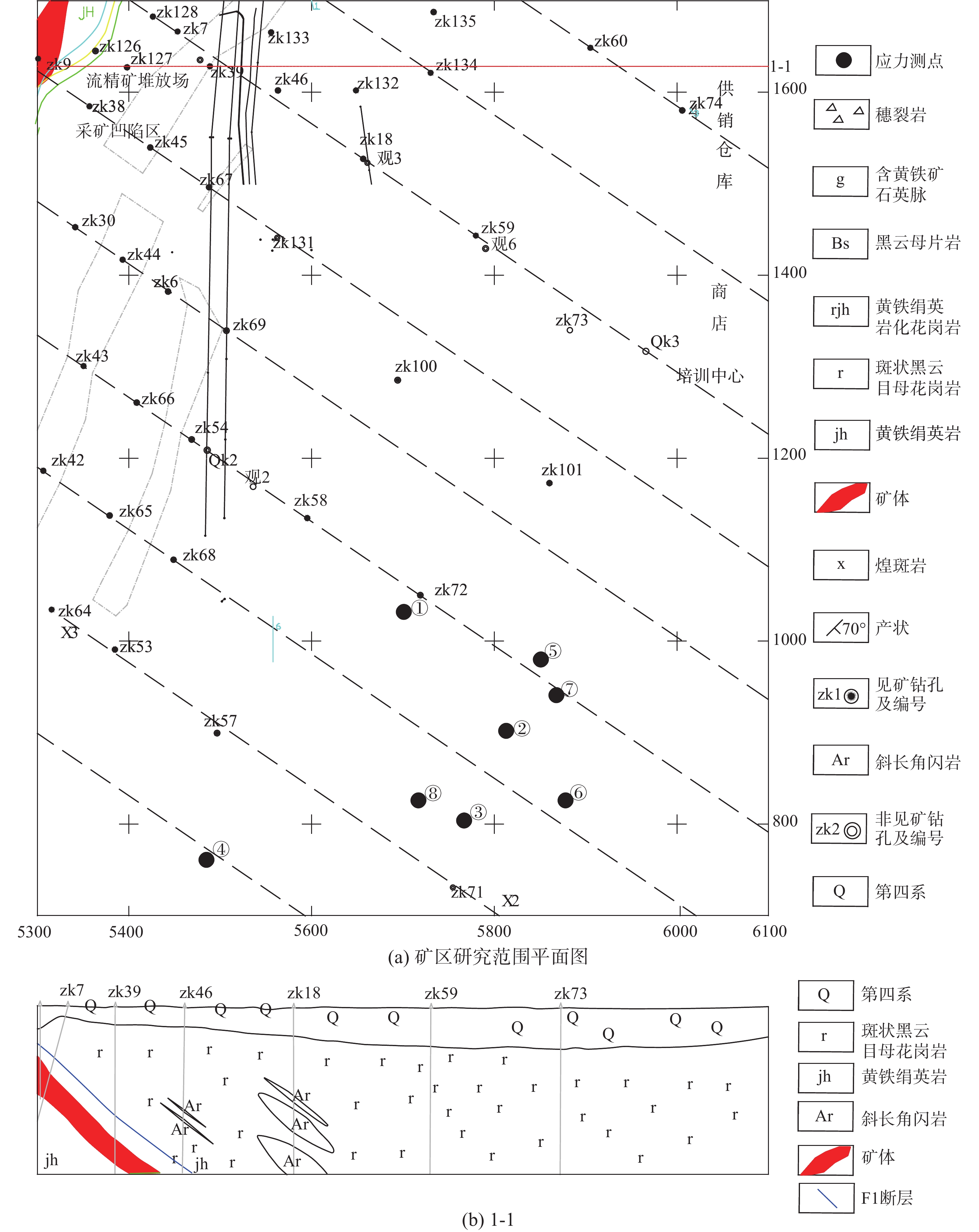
三山岛金矿区位于华北地台、胶辽台隆和胶北隆起西侧边缘，西邻沂沭断裂带，区内侵入岩广泛发育，如图3所示。矿区内赋存F1和F3断层，F1为胶结压扭断层，倾角约为40°，走向为SE40°，F3断层为近直立张扭性断层，走向为NE50°，角砾填充导水性较好^[26]。地层由浅至深为：第四系堆积物松散软弱岩组、软弱岩风化及构造蚀变岩组、坚硬岩块状岩组。矿区地质体受海水侵入影响、岩溶水压高，岩体温度梯度约为0.022 ℃/m~0.026 ℃/m^[27]。

图 3 三山岛矿区地质

Figure 3. Geology of Sanshan island mining area

下载: 全尺寸图片幻灯片

3.2 深部花岗岩流固耦合作用下的力学性质分析

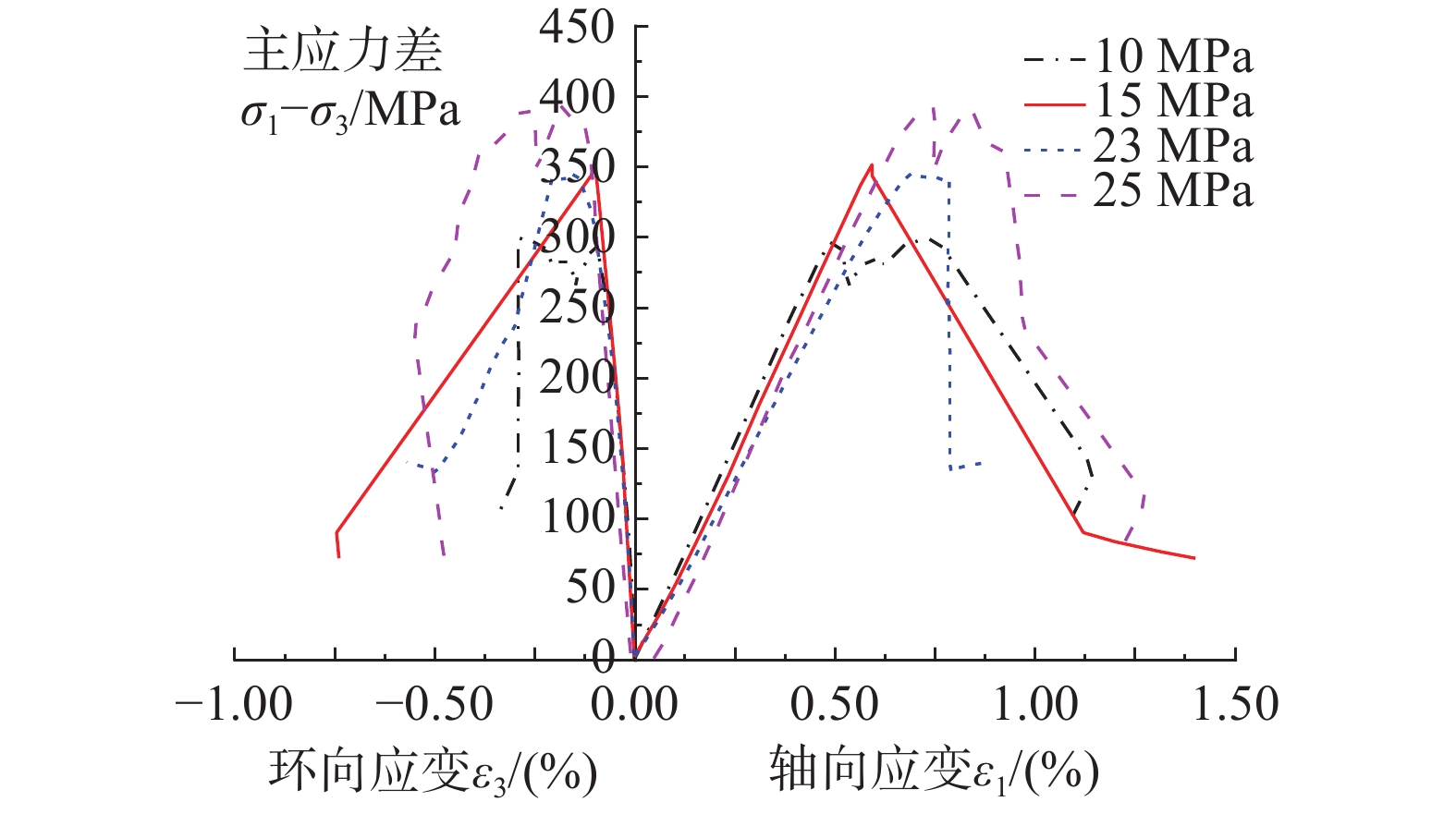
采矿区域埋深为600 m~800 m，根据岩样原位应力水平，围压保持为30 MPa，孔隙水压力分别施加0 MPa、15 MPa、20 MPa、23 MPa和25 MPa，绘制了花岗岩轴向压力差与轴向及径向应变变化曲线。

从图4可以看出，随着孔隙水压力的增加，岩石具有脆延转化的力学特征，转化区间约为15 MPa~23 MPa。岩石峰后塑性逐渐增强, 出现塑性流动特征，岩石抗压强度与孔隙水压力呈正相关变化趋势。

图 4 不同孔隙水压力作用下岩石全应力-应变曲线

Figure 4. Total stress-strain curves of rock under different pore water pressures

下载: 全尺寸图片幻灯片

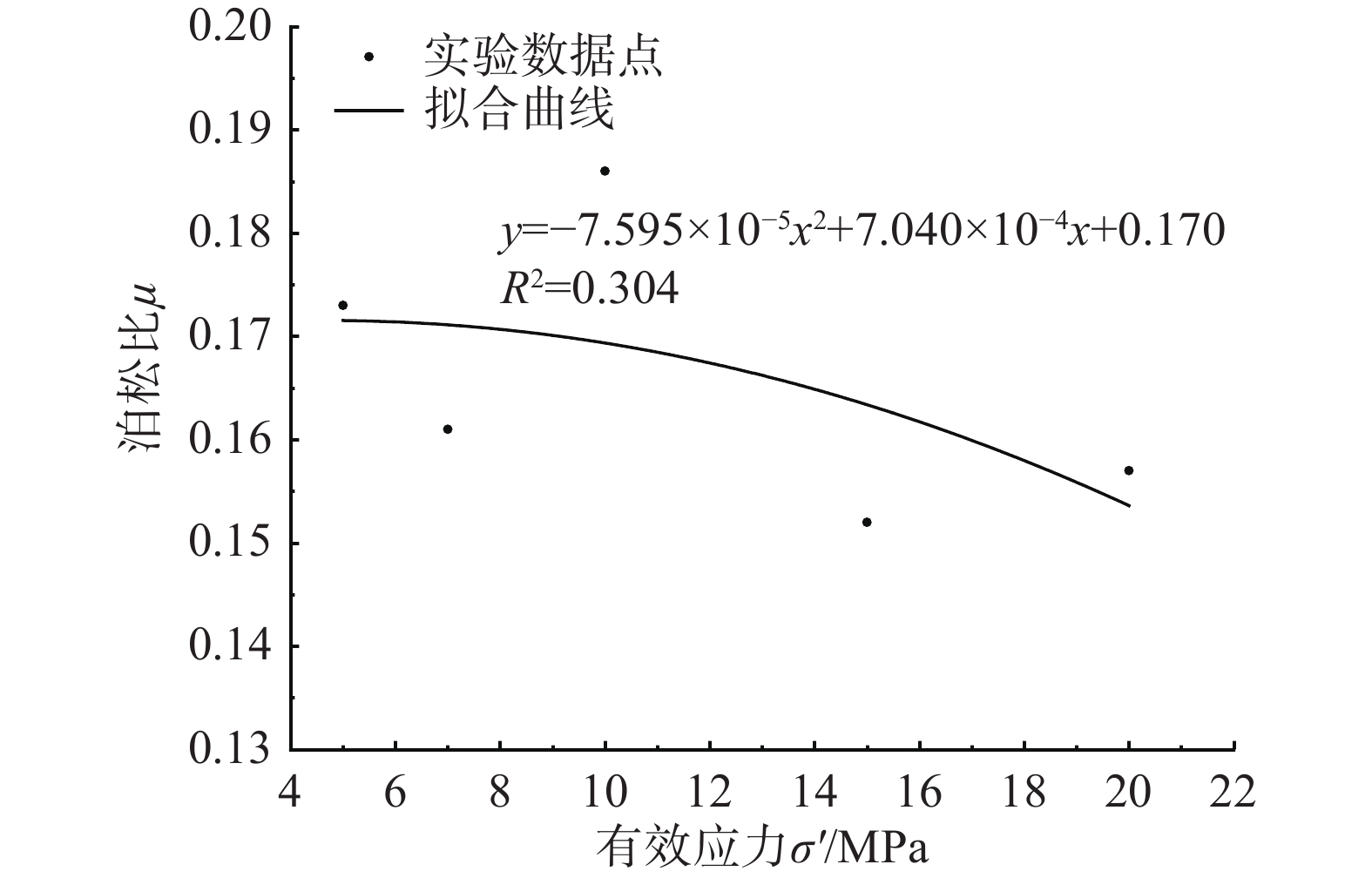
在不同孔隙压力作用下，岩石弹性模量、泊松比与有效应力变化规律曲线分别如图5和图6所示，拟合式分别为式(38)及式(39)。

$E = - 1.09 \times {10^{ - 3}}{\sigma '^2} + 0.410\sigma ' + 55.441$

(38)

图 5 花岗岩弹性模量与有效应力的变化关系

Figure 5. Relationship between elastic modulus and effective stress of granite

下载: 全尺寸图片幻灯片

图 6 花岗岩泊松比与有效应力的变化关系

Figure 6. Relationship between Poisson's ratio and effective stress of granite

下载: 全尺寸图片幻灯片

岩石弹性模量随着有效应力增加呈非线性增加趋势，原因是在高应力作用下岩体孔隙及裂隙体积减小而导致岩体致密且坚硬。

$\mu = - 7.595 \times {10^{ - 5}}{\sigma '^2} + 7.040 \times {10^{ - 4}}\sigma ' + 0.17$

(39)

岩体泊松比随有效应力增加呈非线性减小趋势，产生此类情况的原因是岩体本身的不连续构造及缺陷分布的各向异性。

为了探讨不同埋深花岗岩的渗透系数，分别对试件施加20 MPa、25 MPa、30 MPa的围压以此还原深部岩体的原位应力状态。受力稳定后开始施加渗透压力，得出在不同围压下的花岗岩渗透系数取值见图7，拟合表达式见式(40)。渗透系数与孔隙比的关系曲线见图8，拟合表达式见式(41)。

$k = - 1.700 \times {10^{ - 2}}{\sigma ^2} + 7.262$

(40)

$k = 319.174e - 9.069\qquad \;\;\;\;$

(41)

渗透系数与围压呈反比关系，与孔隙比呈正比关系。此现象的原因是围压增大，岩体体积减小，而岩块固体压缩量很小，由于内部孔隙压缩及孔隙比减小导致了岩体渗透系数减小。

图 7 花岗岩渗透系数与围压的关系

Figure 7. Relationship between permeability coefficient and confining pressure of granite

下载: 全尺寸图片幻灯片

图 8 花岗岩渗透系数与孔隙比的关系

Figure 8. Relationship between permeability coefficient and void ratio of granite

下载: 全尺寸图片幻灯片

3.3 地应力场反演计算

以图3所示的矿区区域为研究对象，建立如图9所示地质模型，采用四面体网格，边长为25 m，数量为455 961个，沿着约1000 m的埋深分为11个近水平产状岩层以及1个倾斜产状矿体，岩体及矿体初始力学参数见表1。根据试验结果，各层岩体弹性模量与泊松比在计算中随着有效应力、温度与渗透压力的变化关系如式(42)和式(43)。

$\begin{split} & {E_i} = E_i^0( - 1.966 \times {10^{ - 5}}{{\sigma '}^2} + 7.395 \times {10^{ - 3}}\sigma ' + 1) \cdot \\&\qquad \exp ( - 0.0054\Delta T)\exp ( - 7.930 \times {10^{ - 11}}\Delta P) \end{split}$

(42)

${\mu _i} = \mu _i^0( - 4.468 \times {10^{ - 4}}{\sigma '^2} + 4.141 \times {10^{ - 3}}\sigma ' + 1)$

(43)

图 9 三山岛矿区地质模型

Figure 9. Geological model of Sanshan island mining area

下载: 全尺寸图片幻灯片

表 1 各层岩体力学参数

Table 1. Mechanical parameters of rock mass in each layer

岩层	密度ρ_i/(g·cm⁻³)	弹性模量E_i/GPa	泊松比μ_i	岩层	密度ρ_i/(g·cm⁻³)	弹性模量E_i/GPa	泊松比μ_i
1层	2.882	10.58	0.247	7层	2.799	43.79	0.218
2层	2.882	21.16	0.247	8层	2.575	45.59	0.244
3层	2.575	30.32	0.178	9层	2.799	45.59	0.268
4层	2.729	33.08	0.213	10层	2.611	58.10	0.262
5层	2.729	37.88	0.178	11层	2.706	58.10	0.262
6层	2.597	41.39	0.268	矿体	2.663	31.70	0.275

下载: 导出CSV

| 显示表格

多场耦合地应力场计算是基于ABAQUS二次开发接口，通过编写umat等子程序实现的。在迭代计算步中，岩体的温度、渗流、应力不断耦合变化，直至达到平衡态。地质体温度梯度增量如式(44)，鉴于在工程深度范围内的岩体生热量较小，岩体生热增量可视为如式(10)所示的应力、渗流和应变增量的非线性函数。渗流场按静水压力场和承压孔隙水场两部分计算，静水压力场变化增量如式(45)，局部承压孔隙水压变化量函数的泰勒二阶展开式如式(12)。

$\Delta T = {a_3} + {b_3}{\textit{z}}$

(44)

$\Delta {P_{\rm w1}} = {10^4}{\textit{z}}\;\;\;$

(45)

地应力场反演计算流程为：首先，基于测点数据反映的边界载荷量与多场耦合条件系数的置信区间，随机生成10组边界载荷条件和多场耦合系数，并通过迭代计算，获得小样本训练数据；其次，将训练样本数据带入算法中学习、优化、泛化误差检验与应用，获得最优化边界条件(式(46))，而各区域岩体温度梯度如式(47)，岩体生热量中的系数较小，故将其忽略，这也表明工程深度的岩体本身生热量要比地幔热流密度传递热量小的多。渗流场变化式系数如表2，地质体上表面温度为14.3 ℃，下表面温度为55 ℃，侧表面温度梯度为1.96 ℃/100 m。最后，基于边界条件与多场耦合系数，进行迭代计算，获得反演应力场。

$\left\{ \begin{gathered} G = {\text{10}}{\text{.547}} \\ {P_{xx}} = 2.772{{\textit{z}}^2} - 29379.800{\textit{z}}{\text{ + }}6.898 \times {10^6} \\ {P_{xy}} = 1.397{{\textit{z}}^2} - 3306.400{\textit{z}} + 2.352 \times {10^6} \\ {P_{x{\textit{z}}}} = - 6.504{{\textit{z}}^2} - 1781.600{\textit{z}} + 1.521 \times {10^6} \\ {P_{yy}} = {\text{4}}{\text{.280}}{{\textit{z}}^2} - {\text{7842}}{\text{.418}}{\textit{z}} + {\text{11}}{\text{.602}} \times {10^6} \\ {P_{yx}} = {\text{7}}{\text{.003}}{{\textit{z}}^2} + {\text{2464}}{\text{.283}}{\textit{z}} + {\text{6}}{\text{.464}} \times {10^6} \\ {P_{x{\textit{z}}}} = - {\text{17}}{\text{.128}}{{\textit{z}}^2} - {\text{3780}}{\text{.663}}{\textit{z}} + {\text{4}}{\text{.379}} \times {10^6} \\ \end{gathered} \right.$

(46)

式中： $G$ /( ${\rm m} \cdot {{\rm s}^{ - 2}}$ )为重力加速度； ${P_{xx}}$ / ${\rm Pa}$ 、 ${P_{xy}}$ / ${\rm Pa}$ 、 ${P_{x{\textit{z}}}}$ / ${\rm Pa}$ 分别约模型 $x$ 轴东西向的挤压载荷、水平和竖直剪切载荷； ${P_{yy}}$ / ${\rm Pa}$ 、 ${P_{yx}}$ / ${\rm Pa}$ 、 ${P_{y{\textit{z}}}}$ / ${\rm Pa}$ 分别约模型 $y$ 轴那南北向的挤压载荷、水平和竖直剪切载荷； ${\textit{z}}$ 为埋深标高， $0 \;{\rm m}\sim 1000 \;{\rm m}$ 。

$\left\{ \begin{gathered} \Delta {T_1} = 27.239 - 0.020{\textit{z}} \\ \Delta {T_2} = 20.820 - 0.031{\textit{z}} \\ \Delta {T_3} = 19.499 - 0.025{\textit{z}} \\ \end{gathered} \right.$

(47)

式中， $\Delta {T_1}$ 、 $\Delta {T_2}$ 和 $\Delta {T_3}$ 分别为F3断层构造温度异常区、F1断层构造温度异常区和沉积地层的温度梯度增量。

表 2 承压层孔隙水压迭代增量参数值

Table 2. Iterative increment parameter values of pore water pressure in the pressure-bearing layer

系数	含水层	F1断层域	F3断层域	区域渗流场
a₅	8.467×10⁶	1.001×10⁷	1.078×10⁷	7.697×10⁶
b₅	9.203×10²	1.088×10³	1.171×10³	8.367×10²
c₅	1.299×10⁸	1.536×10⁸	1.653×10⁸	1.181×10⁸
d₅	6.573×10²	7.768×10²	8.366×10²	5.975×10²
e₅	6.517×10¹	7.702×10¹	8.294×10¹	5.924×10¹
f₅	2.114×10¹³	2.499×10¹³	2.691×10¹³	1.922×10¹³
g₅	2.331×10²	2.755×10²	2.967×10²	2.119×10²
h₅	4.472×10⁶	5.285×10⁶	5.691×10⁶	4.065×10⁶
i₅	2.374×10²	2.805×10²	3.021×10²	2.160×10²
k₅	1.345×10⁷	1.590×10⁷	1.712×10⁷	1.223×10⁷

下载: 导出CSV

| 显示表格

3.4 地应力场反演结果分析

1) 测点应力的反演精度与误差分析

选取研究区域中8个测点(图3(a))，应力解除法的测量数据与算法反演数据对比结果见表3。

2) 测点应力的反演精度与误差分析

考虑地质体多场耦合作用下的NCEI算法获得的测点应力分量反演精度达到85.62%，主应力空间展布方向的误差小于10°，该算法反演的地应力场与实际相吻合，可有效指导工程设计与施工。

表 3 各测点地应力实测值与反演值

Table 3. Measured and inversion values of ground stress at each measuring point

编号	深度/ m	最大主应力						中间主应力					最小主应力
编号	深度/ m	实测值/ MPa	反演值/ MPa	误差/ (%)	方向/ (°)	倾角/ (°)	误差/ (%)	实测值/ MPa	反演值/ MPa	误差/ (%)	方向/ (°)	倾角/ (°)	实测值/ MPa	反演值/ MPa	误差/ (%)	方向/ (°)	倾角/ (°)
1	512.5	24.64	22.73	7.74	−111	3	8.26	15.68	18.81	19.95	155	82	15.02	13.84	7.87	161	−10
2	647	29.57	27.09	8.39	112	−3	12.60	19.56	24.47	25.08	−177	−80	15.48	16.43	6.14	−156	−9
3	602.2	28.88	27.85	3.56	103	1	10.95	16.54	22.93	38.64	10	76	14.77	11.80	20.12	13	−8
4	603	30.17	28.93	4.12	110	−16	6.54	18.83	24.77	31.53	24	−11	16.94	12.37	26.97	236	−70
5	693	31.50	27.79	11.78	−80	2	16.16	19.08	24.30	27.37	230	−79	17.54	17.70	0.93	10	−10
6	693	29.77	27.18	8.69	−83	4	14.76	20.84	23.62	13.34	−8	−74	19.63	14.71	25.08	8	15
7	750	33.22	29.12	12.34	119	−10	4.64	19.93	25.13	26.11	−89	−82	17.10	16.99	0.67	208	−8
8	553	25.71	26.42	2.74	−45	−13	16.29	14.00	20.99	49.96	14	73	13.00	11.17	14.05	50	−20

下载: 导出CSV

| 显示表格

少数测点处应力分量反演误差较大，如3和8测点的中间主应力，原因是深部复杂地质特征条件下的测量精度、地质体模型概化及参数选取差异性等因素所致。有以下两点降低误差的方法：在钻孔测量过程中，采用滤波方法对测量数据优化，提高地应力的测量精度和降低地应力测量误差。且对现场测量数据处理时，可采用噪声处理等相关理论进行二次优化；另外，进行全面的地质调查，获得详尽的地质资料，建立与实际吻合度较高的地质模型。

3) 区域地应力场的分布规律

图10为研究区域岩体应力场、温度场与渗流场分布图。如图所示，区域的最大主应力量值位于2.02 MPa~52.69 MPa，在水平向呈现一定的分带特征。最大主应力场浅部以近水平方向为主，向深部逐渐过渡至与竖直向呈45°夹角，应力场量值在F1压扭断层处有所增加，这符合断层的形成机制；地质体温度场竖直分层特征明显，F1断层邻域内的岩体温度比同水平岩层与F3断层岩体温度高，这与胶结质破碎带内的岩体导热性高，以及在水平挤压运动作用下的断层岩体摩擦运动而生热等因素有关；渗流场整体上以静水压力场分布为主，但深部的含水层中孔隙水压力受上部与下部隔水层的影响，在地应力的挤压作用下有所增加。F1断层为隔水性断层，在高地应力下作用下，孔隙水压力增加，而F3断层为角砾岩填充的导水性断层，存在大量孔隙和裂隙，渗透压力也相对较高。通过对上述描述可知，反演应力场、温度场与渗流场均与实际地质条件和岩体赋存环境特征相吻合。

图 10 矿区岩体应力矢量场、温度场与渗流场分布

Figure 10. Distribution of stress vector field, temperature field and seepage field of rock mass in mining area

下载: 全尺寸图片幻灯片

选取临近矿体开采区域的东西向 $y = 1500 {\text{ m}}$ 剖面进行应力场、温度场与渗流场分布规律研究。

如图11所示，最大主应力随着深度的稳定增加，在F3直立断层处的竖直和水平应力有所降低， F1断层为压性断层，水平应力量值较大，自重应力变化较小。浅部应力场方向处于竖向偏转30°的范围内，而深部应力场方向以水平向为主。温度场在两条断层处的增幅量较大，比平均地温梯度约高1.5倍，且孔隙水压力也相对较大，这由于破碎带内孔隙和裂隙流体与高应力水平的复合作用，以及来自深部的热流体源源不断向上传递所致。F1断层处的温度梯度较F3断层处较高，但孔隙水压几乎同岩层静水压力场梯度相等，这由于F1断层为胶结质填充，导热性较好而隔水性较差，而温度场增加主要来源于岩体传热的作用。

图 11 y=1500 m剖面区域应力场、温度场与渗流场

Figure 11. Stress field, temperature field and seepage field in section at y=1500 m profile

下载: 全尺寸图片幻灯片

4 讨论

为了对地应力场反演精度与既有误差的存在原因与解析方式进一步的分析与研究，对考虑多场耦合与不考虑多场耦合因素下NCEI算法与BP神经网络算法在测点应力的反演结果进行统计分析。

对图12分析可知，NCEI算法在考虑多场耦合作用下的反演精度为85.62%，不考虑多场耦合作用下的NCEI算法解析地应力场精度为83.45%；而BP神经网络算法反演精度低于80%，表明NCEI算法对非线性和离散性大的数据有更好的解析能力。

图 12 不同反演方法的应力场误差对比

Figure 12. Comparison of stress field errors of different inversion methods

下载: 全尺寸图片幻灯片

采用NCEI算法进行地应力场反演时，岩体的温度、渗流、应力的耦合计算并未对测点平均反演精度产生明显提高，这不能说明深部岩体的多场耦合计算是可被忽略，而地应力场反演精度的定量化评价不能仅以测点应力为表征，基于地质条件对区域应力场进一步的评定是必不可少的研究工作。多场耦合作用下的反演地应力场能够将各类构造区域应力、温度及渗流水压分布状态进行有效表征，不考虑耦合作用下的地应力场反演仅是从边界条件上进行拼凑和折算，极易出现过大的挤压载荷与拉伸的载荷条件，这也地质体岩层沉积与构造运动机制不符。错误边界条件的出现，主要是因为忽略了太多的地应力场影响因素，而算法进行了过多的学习与优化，将优化的特征信息错误地归为载荷边界系数影响(“硬”回归)，使得反演地应力场陷入局部最优化，即仅仅在稀少的测点邻域内满足精度要求，其他大规模区域的应力场无法满足实际工程需要。

另外，NCEI算法在局部测点误差相对较大，从算法本身进行分析，样本数据的信息维度缺失存在，在希尔伯特空间上，由实测点数据信息形成的子集维度大于实测样本数据子集维度，该算法对于此类样本的解析与优化，只能在保障置信风险误差的基础上，最大程度地降低经验误差。因此，地应力场反演计算需进一步考虑地质因素与地应力场形成机制，根据构造回旋的周期性与差异性，建立沿深度的非连续性边界载荷，扩大地应力样本训练数据子集空间维度，从而进一步提高地应力反演精度。

5 结论

针对深部岩体温度场、渗流场和地应力场的复杂性，本研究提出了多场耦合条件下的NCEI反演算法，探究出岩体温度场、应力场、渗流场的耦合作用机制，并通过三山岛金矿算例，有效解析了深部非线性、非连续性地应力场、渗流场与温度场的分布特征，从而验证了反演方法的有效性。所得结论如下：

(1) 深部工程岩体温度场对地应力场的影响主要体现在温度应力的各项异性和岩体力学性质的变化性；岩体渗流场对地应力场的影响主要是改变岩体孔隙与空隙的分布，并影响岩体的力学性质。

(2) 深部各构造区域地应力场受温度场和渗流场影响显著，导致测点应力数据呈现出非连续、非线性等特征，提出的NCEI算法能够针对各测点应力数据所反映的构造地质与形成机制等进行充分的挖掘与解析，可有效提高地应力场反演精度。

(3) 三山岛金矿区深部花岗岩在低孔隙压作用下呈现脆性特征，高孔隙压作用下呈现延性特征，抗压强度与孔隙水压力呈正相关。岩石的弹性模量与泊松比同孔隙水压力和有效应力均呈二次函数形式的非线性变化关系、渗流系数与地应力水平也呈现二次函数形式的非线性变化关系。

(4) 基于ABAQUS子程序编程，实现了地质体温度、渗流、应力相互作用和影响的迭代计算，计算结果符合实际地质条件下的多场准静态的赋存状态，说明深部地应力场反演计算需从岩体实际赋存地质条件和应力形成机制等方面开展研究。

(5) 对比是否考虑岩体多场耦合条件下的NCEI算法和BP神经网络算法的反演结果，考虑岩体多场耦合作用下的NCEI算法的各测点应力分量反演精度为85.62%，不考虑多场耦合作用下的NCEI算法解析地应力场反演为83.45%，而BP神经网络算法的反演精度均低于80%，表明NCEI算法对于解析复杂地应力场具有更好优势。

(6) 地应力场反演精度的主要影响因素为：其一，合理概化模型，建立与实际地层吻合度高的地质模型；其二，采用能够对小样本数据进行信息挖掘的算法；其三，对研究区域岩体的构造历史与地质条件进行详尽分析，将尽可能多的因素引入算法或应力场计算中，从而提高样本数据子集维度，并助力于算法优化与学习。

图 1 渗流场对地应力场的间接影响

Figure 1. Indirect influence of seepage field on in-situ stress field

下载: 全尺寸图片幻灯片

图 2 NCEI算法对应力数据的延扩与解析

Figure 2. Extension and analysis of stress data based on NCEI algorithm

下载: 全尺寸图片幻灯片

图 3 三山岛矿区地质

Figure 3. Geology of Sanshan island mining area

下载: 全尺寸图片幻灯片

图 4 不同孔隙水压力作用下岩石全应力-应变曲线

Figure 4. Total stress-strain curves of rock under different pore water pressures

下载: 全尺寸图片幻灯片

图 5 花岗岩弹性模量与有效应力的变化关系

Figure 5. Relationship between elastic modulus and effective stress of granite

下载: 全尺寸图片幻灯片

图 6 花岗岩泊松比与有效应力的变化关系

Figure 6. Relationship between Poisson's ratio and effective stress of granite

下载: 全尺寸图片幻灯片

图 7 花岗岩渗透系数与围压的关系

Figure 7. Relationship between permeability coefficient and confining pressure of granite

下载: 全尺寸图片幻灯片

图 8 花岗岩渗透系数与孔隙比的关系

Figure 8. Relationship between permeability coefficient and void ratio of granite

下载: 全尺寸图片幻灯片

图 9 三山岛矿区地质模型

Figure 9. Geological model of Sanshan island mining area

下载: 全尺寸图片幻灯片

图 10 矿区岩体应力矢量场、温度场与渗流场分布

Figure 10. Distribution of stress vector field, temperature field and seepage field of rock mass in mining area

下载: 全尺寸图片幻灯片

图 11 y=1500 m剖面区域应力场、温度场与渗流场

Figure 11. Stress field, temperature field and seepage field in section at y=1500 m profile

下载: 全尺寸图片幻灯片

图 12 不同反演方法的应力场误差对比

Figure 12. Comparison of stress field errors of different inversion methods

下载: 全尺寸图片幻灯片

表 1 各层岩体力学参数

Table 1 Mechanical parameters of rock mass in each layer

岩层	密度ρ_i/(g·cm⁻³)	弹性模量E_i/GPa	泊松比μ_i	岩层	密度ρ_i/(g·cm⁻³)	弹性模量E_i/GPa	泊松比μ_i
1层	2.882	10.58	0.247	7层	2.799	43.79	0.218
2层	2.882	21.16	0.247	8层	2.575	45.59	0.244
3层	2.575	30.32	0.178	9层	2.799	45.59	0.268
4层	2.729	33.08	0.213	10层	2.611	58.10	0.262
5层	2.729	37.88	0.178	11层	2.706	58.10	0.262
6层	2.597	41.39	0.268	矿体	2.663	31.70	0.275

下载: 导出CSV

表 2 承压层孔隙水压迭代增量参数值

Table 2 Iterative increment parameter values of pore water pressure in the pressure-bearing layer

系数	含水层	F1断层域	F3断层域	区域渗流场
a₅	8.467×10⁶	1.001×10⁷	1.078×10⁷	7.697×10⁶
b₅	9.203×10²	1.088×10³	1.171×10³	8.367×10²
c₅	1.299×10⁸	1.536×10⁸	1.653×10⁸	1.181×10⁸
d₅	6.573×10²	7.768×10²	8.366×10²	5.975×10²
e₅	6.517×10¹	7.702×10¹	8.294×10¹	5.924×10¹
f₅	2.114×10¹³	2.499×10¹³	2.691×10¹³	1.922×10¹³
g₅	2.331×10²	2.755×10²	2.967×10²	2.119×10²
h₅	4.472×10⁶	5.285×10⁶	5.691×10⁶	4.065×10⁶
i₅	2.374×10²	2.805×10²	3.021×10²	2.160×10²
k₅	1.345×10⁷	1.590×10⁷	1.712×10⁷	1.223×10⁷

下载: 导出CSV

表 3 各测点地应力实测值与反演值

Table 3 Measured and inversion values of ground stress at each measuring point

编号	深度/ m	最大主应力						中间主应力					最小主应力
编号	深度/ m	实测值/ MPa	反演值/ MPa	误差/ (%)	方向/ (°)	倾角/ (°)	误差/ (%)	实测值/ MPa	反演值/ MPa	误差/ (%)	方向/ (°)	倾角/ (°)	实测值/ MPa	反演值/ MPa	误差/ (%)	方向/ (°)	倾角/ (°)
1	512.5	24.64	22.73	7.74	−111	3	8.26	15.68	18.81	19.95	155	82	15.02	13.84	7.87	161	−10
2	647	29.57	27.09	8.39	112	−3	12.60	19.56	24.47	25.08	−177	−80	15.48	16.43	6.14	−156	−9
3	602.2	28.88	27.85	3.56	103	1	10.95	16.54	22.93	38.64	10	76	14.77	11.80	20.12	13	−8
4	603	30.17	28.93	4.12	110	−16	6.54	18.83	24.77	31.53	24	−11	16.94	12.37	26.97	236	−70
5	693	31.50	27.79	11.78	−80	2	16.16	19.08	24.30	27.37	230	−79	17.54	17.70	0.93	10	−10
6	693	29.77	27.18	8.69	−83	4	14.76	20.84	23.62	13.34	−8	−74	19.63	14.71	25.08	8	15
7	750	33.22	29.12	12.34	119	−10	4.64	19.93	25.13	26.11	−89	−82	17.10	16.99	0.67	208	−8
8	553	25.71	26.42	2.74	−45	−13	16.29	14.00	20.99	49.96	14	73	13.00	11.17	14.05	50	−20

下载: 导出CSV

参考文献(27)

[1]	HU YB, LI W P, CHEN X M, et al. Temporal and spatial evolution characteristics of fracture distribution of floor strata in deep coal seam mining [J]. Engineering Failure Analysis, 2022, 132: 105931. doi: 10.1016/j.engfailanal.2021.105931
[2]	JIANG S Y, FAN G W, LI Q Z, et al. Effect of mining parameters on surface deformation and coal pillar stability under customized shortwall mining of deep extra-thick coal seams [J]. Energy Reports, 2021, 7: 2138 − 2154. doi: 10.1016/j.egyr.2021.04.008
[3]	LAVOIE T, EBERHARDT E, PIERCE M E. Numerical modelling of rock mass bulking and geometric dilation using a bonded block modelling approach to assist in support design for deep mining pillars [J]. International Journal of Rock Mechanics and Mining Sciences, 2022, 156: 105145. doi: 10.1016/j.ijrmms.2022.105145
[4]	赵志宏, 刘桂宏, 徐浩然. 深地能源工程热水力多场耦合效应高效模拟方法[J]. 工程力学, 2020, 37(6): 1 − 18. doi: 10.6052/j.issn.1000-4750.2019.05.ST09 ZHAO Zhihong, LIU Guihong, XU Haoran. A robust numerical modeling framework for coupled thermo-hydro-mechanical process in deep geo-energy engineering [J]. Engineering Mechanics, 2020, 37(6): 1 − 18. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.05.ST09
[5]	张进平, 王煜曦, 刘桂宏, 等. 通州区地热资源优化开采模式动态研究[J]. 工程力学, 2022, 39(6): 247 − 256. doi: 10.6052/j.issn.1000-4750.2021.01.0086 ZHANG Jinping, WANG Yuxi, LIU Guihong, et al. Dynamic study on optimal exploitation mode of geothermal resources in Beijing Tongzhou district [J]. Engineering Mechanics, 2022, 39(6): 247 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.01.0086
[6]	苗胜军, 杨鹏锦, 王辉, 等. 循环荷载作用下粉砂岩疲劳流变损伤模型研究[J]. 工程力学, 2022, 39(7): 70 − 80. doi: 10.6052/j.issn.1000-4750.2021.03.0235 MIAO Shengjun, YANG Pengjin, WANG Hui, et al. Study on fatigue rheological damage model of siltstone under cyclic loading [J]. Engineering Mechanics, 2022, 39(7): 70 − 80. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.03.0235
[7]	HUANG Y, ZOLFAGHARI N, OHANIAN O J, et al. Technical note: An inversion algorithm to estimate maximum and minimum horizontal stress based on field test data for sleeve fracturing [J]. Computers and Geotechnics, 2021, 137: 104274. doi: 10.1016/j.compgeo.2021.104274
[8]	蒙伟, 何川, 陈子全, 等. 岭回归在岩体初始地应力场反演中的应用[J]. 岩土力学, 2021, 42(4): 1156 − 1169. MENG Wei, HE Chuan, CHEN Ziquan, et al. Application of ridge regression in the inversion analysis of the initial geo-stress field of rock masses [J]. Rock and Soil Mechanics, 2021, 42(4): 1156 − 1169. (in Chinese)
[9]	蒙伟, 何川, 晏启祥, 等. p值法在岩体初始地应力场反演中的应用[J]. 中国铁道科学, 2021, 42(1): 71 − 79. MENG Wei, HE Chuan, YAN Qixiang, et al. Application of p-value approach in inversion of initial geo-stress field of rock masses [J]. China Railway Science, 2021, 42(1): 71 − 79. (in Chinese)
[10]	李飞, 周家兴, 王金安. 深部多场耦合作用的非线性地应力构建方法[J]. 煤炭学报, 2021, 46(增刊 1): 116 − 129. doi: 10.13225/j.cnki.jccs.2020.0857 LI Fei, ZHOU Jiaxing, WANG Jin’an. Method of nonlinear in-situ stress construction with deep multi-field coupling [J]. Journal of China Coal Society, 2021, 46(Suppl 1): 116 − 129. (in Chinese) doi: 10.13225/j.cnki.jccs.2020.0857
[11]	刘泉声, 王栋, 朱元广, 等. 支持向量回归算法在地应力场反演中的应用[J]. 岩土力学, 2020, 41(增刊 1): 319 − 328. doi: 10.16285/j.rsm.2019.0860 LIU Quansheng, WANG Dong, ZHU Yuan'guang, et al. Application of support vector regression algorithm in inversion of geostress field [J]. Rock and Soil Mechanics, 2020, 41(Suppl 1): 319 − 328. (in Chinese) doi: 10.16285/j.rsm.2019.0860
[12]	施斌. 论工程地质中的场及其多场耦合[J]. 工程地质学报, 2013, 21(5): 673 − 680. doi: 10.3969/j.issn.1004-9665.2013.05.001 SHI Bin. On fields and their coupling in engineering geology [J]. Journal of Engineering Geology, 2013, 21(5): 673 − 680. (in Chinese) doi: 10.3969/j.issn.1004-9665.2013.05.001
[13]	周创兵, 陈益峰, 姜清辉, 等. 论岩体多场广义耦合及其工程应用[J]. 岩石力学与工程学报, 2008, 27(7): 1329 − 1340. doi: 10.3321/j.issn:1000-6915.2008.07.005 ZHOU Chuangbing, CHEN Yifeng, JIANG Qinghui, et al. On generalized multi-field coupling for fractured rock masses and its applications to rock engineering [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(7): 1329 − 1340. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.07.005
[14]	安欧. 构造应力场 [M]. 北京: 地震出版社, 1992: 165−185 . AN Ou. Structural stress field [M]. Beijing: Seismological Press, 1992: 165−185 . (in Chinese)
[15]	李馨馨, 李典庆, 徐轶. 地热对井系统裂隙岩体三维渗流传热耦合的等效模拟方法[J]. 工程力学, 2019, 36(7): 238 − 247. doi: 10.6052/j.issn.1000-4750.2018.06.0340 LI Xinxin, LI Dianqing, XU Yi. Equivalent simulation method of three-dimensional seepage and heat transfer coupling in fractured rock mass of geothermal-borehole system [J]. Engineering Mechanics, 2019, 36(7): 238 − 247. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.06.0340
[16]	邓明德, 耿乃光, 崔承禹, 等. 岩石应力状态改变引起岩石热状态改变的研究[J]. 中国地震, 1997, 13(2): 179 − 185. DENG Mingde, GENG Naiguang, CUI Chengyu, et al. The study on the variation of thermal state of rocks caused by the variation of stress state of rocks [J]. Earthquake Research in China, 1997, 13(2): 179 − 185. (in Chinese)
[17]	ZHOU X P, DU E B, WANG Y T. Thermo-hydro-chemo-mechanical coupling peridynamic model of fractured rock mass and its application in geothermal extraction [J]. Computers and Geotechnics, 2022, 148: 104837. doi: 10.1016/j.compgeo.2022.104837
[18]	蒙伟, 何川, 张钧博, 等. 高地温高地应力下岩体初始地应力场反演分析[J]. 岩石力学与工程学报, 2020, 39(4): 749 − 760. doi: 10.13722/j.cnki.jrme.2019.0818 MENG Wei, HE Chuan, ZHANG Junbo, et al. Inverse analysis of the initial geostress field of rock masses under high geo-temperature and high geostress [J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(4): 749 − 760. (in Chinese) doi: 10.13722/j.cnki.jrme.2019.0818
[19]	郤保平, 吴阳春, 王帅, 等. 青海共和盆地花岗岩高温热损伤力学特性试验研究[J]. 岩石力学与工程学报, 2020, 39(1): 69 − 83. doi: 10.13722/j.cnki.jrme.2019.0182 XI Baoping, WU Yangchun, WANG Shuai, et al. Experimental study on mechanical properties of granite taken from Gonghe basin, Qinghai province after high temperature thermal damage [J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(1): 69 − 83. (in Chinese) doi: 10.13722/j.cnki.jrme.2019.0182
[20]	陈卫忠, 伍国军, 贾善坡. ABAQUS在隧道及地下工程中的应用 [M]. 北京: 中国水利水电出版社, 2013: 228 − 300. CHEN Weizhong, WU Guojun, JIA Shanpo. Application of ABAQUS in tunnel and underground engineering [M]. Beijing: China Water Power Press, 2013: 228 − 300. (in Chinese)
[21]	高彦芳, 陈勉, 林伯韬, 等. 多相非饱和多重孔隙介质的有效应力定律[J]. 工程力学, 2019, 36(1): 32 − 43. doi: 10.6052/j.issn.1000-4750.2017.11.0790 GAO Yanfang, CHEN Mian, LIN Botao, et al. Generalized effective stress law for multi-porosity media unsaturated with multiphase fluids [J]. Engineering Mechanics, 2019, 36(1): 32 − 43. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.11.0790
[22]	许永猛. 不同地质构造地应力特性研究 [D]. 北京: 中国石油大学, 2016: 6 − 33 . XU Yongmeng. Research of In-situ stress in different geological structure [D]. Beijing: China University of Petroleum, 2016: 6 − 33 . (in Chinese)
[23]	赵成刚, 白冰, 王运霞. 土力学原理 [M]. 北京: 清华大学出版社, 北京交通大学出版社, 2004: 122 − 130. ZHAO Chenggang, BAI Bing, WANG Yunxia. Fundamentals of soil mechanics [M]. Beijing: Tsinghua University Press, Beijing Jiaotong University Press, 2004: 122 − 130. (in Chinese)
[24]	周志华. 机器学习 [M]. 北京: 清华大学出版社, 2015: 121 − 145. ZHOU Zhihua, WABG Jue. MACHINE LEARNING [M]. Beijing: Tsinghua University Press, 2015: 121 − 145. (in Chinese)
[25]	周晓剑, 马义中. 两种求解非正定核Laplace-SVR的SMO算法[J]. 控制与决策, 2009, 24(11): 1657 − 1662, 1667. doi: 10.3321/j.issn:1001-0920.2009.11.011 ZHOU Xiaojian, MA Yizhong. Two types of SMO algorithms for solving Laplace-SVR with non-positive kernels [J]. Control and Decision, 2009, 24(11): 1657 − 1662, 1667. (in Chinese) doi: 10.3321/j.issn:1001-0920.2009.11.011
[26]	宋明春, 张军进, 张丕建, 等. 胶东三山岛北部海域超大型金矿床的发现及其构造-岩浆背景[J]. 地质学报, 2015, 89(2): 365 − 383. SONG Mingchun, ZHANG Junjin, ZHANG Pijian, et al. Discovery and tectonic-magmatic background of superlarge gold deposit in offshore of northern Sanshandao, Shandong peninsula, China [J]. Acta Geologica Sinica, 2015, 89(2): 365 − 383. (in Chinese)
[27]	沃杭帅. 三山岛金矿热害影响与控制方法研究 [D]. 沈阳: 东北大学, 2015: 11 − 36 . WO Hangshuai. Study on Thermal Damage Influence and Control Methods in Sanshandao Gold Mine [D]. Shenyang: Northeastern University, 2015: 11 − 36 . (in Chinese)

施引文献(5)

期刊类型引用(4)

1.	杨建，李俊杰，陈前，罗荣，郭永成. 温度效应在岩土工程中的表现兼论反应力应变岩石力学. 安徽建筑. 2025(04): 113-115 . 百度学术
2.	周家兴，王金安，李飞. 深部煤层非连续区地应力场反演方法. 清华大学学报(自然科学版). 2024(12): 2166-2176 . 百度学术
3.	周扬松，乔宇. 基于物理模型试验的隧道涌水量预测参数优化研究. 吉林水利. 2024(12): 24-27 . 百度学术
4.	齐宁，马腾飞，章泽辉，刘湘华，刘练. 石灰岩酸压裂缝蠕变闭合机理研究. 天然气工业. 2024(12): 73-82 . 百度学术

其他类型引用(1)

资源附件(0)

图(12) / 表(3)

计量

文章访问数: 273
HTML全文浏览量: 94
PDF下载量: 68
被引次数: 5

1 深部地质体多场耦合机制
1.1 地温场与地应力场的耦合作用
1.1.1 温度应力场的分布规律
1.1.2 温度对深部岩体力学参数的影响
1.2 渗流场与地应力场的耦合作用
1.2.1 渗流场对地应力场影响
1.2.2 渗流场对深部岩体力学参数影响
1.3 渗流场与温度场的耦合作用
2 非线性特征延扩迭代算法
2.1 NCEI算法理论基础
2.2 NCEI算法实现流程
3 工程应用
3.1 地质概况
3.2 深部花岗岩流固耦合作用下的力学性质分析
3.3 地应力场反演计算
3.4 地应力场反演结果分析
4 讨论
5 结论

1 深部地质体多场耦合机制
1.1 地温场与地应力场的耦合作用
1.1.1 温度应力场的分布规律
1.1.2 温度对深部岩体力学参数的影响
1.2 渗流场与地应力场的耦合作用
1.2.1 渗流场对地应力场影响
1.2.2 渗流场对深部岩体力学参数影响
1.3 渗流场与温度场的耦合作用
2 非线性特征延扩迭代算法
2.1 NCEI算法理论基础
2.2 NCEI算法实现流程
3 工程应用
3.1 地质概况
3.2 深部花岗岩流固耦合作用下的力学性质分析
3.3 地应力场反演计算
3.4 地应力场反演结果分析
4 讨论
5 结论

参考文献(27)

施引文献(5)

资源附件(0)

深部工程岩体温度与渗流耦合作用下复杂应力场反演方法

通讯作者: 李 飞(1985−)，女，山西运城人，副教授，博士，主要从事岩石力学与工程方面的研究(E-mail: lifei3522883@163.com)

计量

出版历程

INVERSION METHOD FOR COMPLEX STRESS FIELD UNDER COUPLING EFFECT OF TEMPERATURE AND SEEPAGE IN DEEP ENGINEERING ROCK MASS

1 深部地质体多场耦合机制

1.1 地温场与地应力场的耦合作用

1.1.1 温度应力场的分布规律

1.1.2 温度对深部岩体力学参数的影响

1.2 渗流场与地应力场的耦合作用

1.2.1 渗流场对地应力场影响

1.2.2 渗流场对深部岩体力学参数影响

1.3 渗流场与温度场的耦合作用

2 非线性特征延扩迭代算法

2.1 NCEI算法理论基础

2.2 NCEI算法实现流程

3 工程应用

3.1 地质概况

3.2 深部花岗岩流固耦合作用下的力学性质分析

3.3 地应力场反演计算

3.4 地应力场反演结果分析

4 讨论

5 结论

期刊类型引用(4)

其他类型引用(1)

计量

出版历程

目录

1 深部地质体多场耦合机制

1.1 地温场与地应力场的耦合作用

1.1.1 温度应力场的分布规律

1.1.2 温度对深部岩体力学参数的影响

1.2 渗流场与地应力场的耦合作用

1.2.1 渗流场对地应力场影响

1.2.2 渗流场对深部岩体力学参数影响

1.3 渗流场与温度场的耦合作用

2 非线性特征延扩迭代算法

2.1 NCEI算法理论基础

2.2 NCEI算法实现流程

3 工程应用

3.1 地质概况

3.2 深部花岗岩流固耦合作用下的力学性质分析

3.3 地应力场反演计算

3.4 地应力场反演结果分析

4 讨论

5 结论

通讯作者:
李　飞(1985−)，女，山西运城人，副教授，博士，主要从事岩石力学与工程方面的研究(E-mail: lifei3522883@163.com)