纵向非均匀温度下钢柱弹性屈曲荷载

王卫永; 杨竞杰

doi:10.6052/j.issn.1000-4750.2022.05.0497

纵向非均匀温度下钢柱弹性屈曲荷载

王卫永^{1, 2, ,},
杨竞杰^1,

1.
重庆大学土木工程学院，重庆 400045
2.
重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400045

基金项目: 国家自然科学基金面上项目(52178110)；重庆市自然科学基金杰出青年基金项目(cstc2021jcyj-jqX0021)

详细信息

作者简介:
杨竞杰(1993−)，男，重庆人，博士生，主要从事钢结构抗火研究(E-mail: jingjieyoung@foxmail.com)

通讯作者:
王卫永(1982−)，男，河南人，教授，博士，主要从事钢结构抗火研究(E-mail: wywang@cqu.edu.cn)

中图分类号: TU313.1
计量
- 文章访问数: 191
- HTML全文浏览量: 89
- PDF下载量: 58
出版历程
- 收稿日期: 2022-05-29
- 修回日期: 2022-08-27
- 网络出版日期: 2022-10-28
- 刊出日期: 2024-06-24

ELASTIC BUCKLING LOAD OF STEEL COLUMN UNDER LONGITUDINAL NON-UNIFORM TEMPERATURE

WANG Wei-yong^{1, 2, ,},
YANG Jing-jie^1,

1.
School of Civil Engineering, Chongqing University, Chongqing 400045, China
2.
Key Laboratory of New Technology for Construction of Cities in Mountain Area of China Ministry of Education, Chongqing University, Chongqing 400045, China

摘要

摘要:
在大空间建筑火灾中，由于热空气的上升，在纵向空间上的温度分布常常是不均匀的，上部的温度会远远高于下部的温度。该现象在火灾的轰燃发生后是十分显著的。在钢柱的抗火设计中考虑纵向温度的不均匀分布不仅符合实际情况，也更符合基于性能化的抗火设计理念。该文先以无端部约束钢柱为研究对象并假定其横截面上的温度均匀分布，基于能量法推导了其在一般场模型火灾条件下的弹性屈曲荷载；在简化的双区域火灾模型条件下，分别基于平衡微分方程以及能量法推导其弹性屈曲荷载，并采用数值分析对推导结果进行验证。发现基于平衡微分方程推导的精确解相较于数值模拟结果，误差均小于3%，而基于能量法推导的结果则在部分情况下显著偏大。此外，研究结果表明：如果忽略温度的纵向不均匀分布，对于受热长度与非受热长度等长的钢柱，其弹性临界荷载会被严重低估，甚至达到约37%。考虑柱端轴向约束的作用，该文给出了不均匀温度分布条件下约束柱的弹性屈曲荷载计算方法。
- 钢结构 /
- 弹性屈曲 /
- 能量法 /
- 抗火 /
- 轴向约束 /
- 非均匀温度
Abstract:
In large-scale building fires, due to the rising of hot air, the temperature distribution is usually non-uniform in the longitudinal space around a steel column, and the temperature in its upper zone is much higher than that in its lower zone. This phenomenon is very significant after the flashover condition. It is practical to consider the longitudinally non-uniform temperature for the fire resistance design of steel columns. Besides, advantage can be made of this in a performance-based approach to ascertain the stability of a steel column subjected to prescribed fire size. This paper takes the steel column that has no ending restraint as the research object and assumes that the temperature distribution on the cross-section is uniform. The elastic buckling load of the steel column under the field model fire is derived upon the energy method. Under the condition of the simplified two-zone fire model, the elastic buckling load is derived by the equilibrium differential equation and by the energy method, respectively. The derived results are verified by numerical analysis. It is found that: the error of the exact solution derived upon the equilibrium differential equation is less than 3% compared with the numerical simulation results, while the results derived based on the energy method are significantly larger in some cases. In addition, the results show that: if the longitudinally non-uniform temperature distribution is ignored, the elastic critical load will be seriously underestimated, even reaching about 37%, for a steel column with the same length as the unheated length. Considering the influence of the axial restraint, the calculation method of the buckling load of the steel column with longitudinally non-uniform temperature is proposed.
- steel structure /
- elastic buckling /
- energy method /
- fire resistance /
- axial restraint /
- non-uniform temperature

HTML全文

在实际的建筑火灾中，如果在纵向空间内将温度假定为均匀分布是不合理的。因为在热对流过程中，最热的一层空气会上升到顶部，而较冷的一层停留在底部。在均匀温度假设的基础上，工程师通常认为柱顶的最高温度在整个柱高都是相同的，但是在众多关于钢柱抗火性能的试验中^[1-4]，试件的纵向温度分布通常都是不均匀的，而且该温度差在试验过程中可能会达到100 ℃。因此将钢柱的温度简化为均匀分布，是不符合工程实际的，会导致计算钢柱的耐火极限偏于保守。

CULVER^[5]在1972年分析了宽翼缘钢柱在高温作用下的稳定性，通过有限差分法求解控制微分方程确定屈曲载荷，但是该研究并没有考虑柱端约束的影响。CAI等^[6]分析了横截面温度线性分布的约束柱的弹性临界荷载，发现横截面非均匀温度分布的钢柱弹性临界荷载相对于均匀温度下钢柱的弹性临界荷载可能被严重低估，但是该研究中只考虑了温度的横向不均匀分布，并未考虑温度的纵向不均匀分布。王培军和王晓^[7]试验研究了不同轴向约束刚度比以及横截面温度分布模式对钢柱抗火性能的影响，研究结果表明横截面温度的不均匀分布可能会导致钢柱产生扭转屈曲，此外横截面上温差越大，钢柱屈曲温度和破坏温度越高。YANG等^[4]试验研究了冷弯薄壁型钢柱在受到纵向不均匀火灾时抗火性能，并指出纵向不均匀温度分布不仅影响试件破坏区域，还会影响其临界温度，非均匀升温试件的临界温度会略高于均匀升温试件的临界温度。

XU和ZHUANG^[8]基于双区域火灾模型研究了纵向非均匀温度分布的无支撑钢框架的弹性稳定性，基于欧拉-伯努利梁理论推导了柱模型的横向刚度方程，通过数值算例验证了该方法的评估过程，并研究了暴露于非均匀高温分布的框架构件在不同情况下的框架稳定性。BECKER^[9]研究了纵向不均匀温度分布对耐火钢结构的影响，但该研究是通过试验或数值方法完成的，虽然有限元程序较为灵活，但是建立理论计算方法同样重要，因为它可以使工程师迅速确定柱屈曲载荷。也有学者^[10-17]对柱构件常温和高温下的屈曲荷载开展研究。

基于以上文献回顾可以看出，有较多的学者对横截面温度分布不均匀钢柱受力性能进行研究，而对于纵向温度不均分布结构受力性能的研究还不够充分。在常温环境下，钢柱的弹性屈曲荷载通常是通过经典欧拉方程获得，它表征了理想柱抗屈曲能力的上限，是指导钢柱承载力设计至关重要的参数。钢柱在实际受火时往往处于弹塑性状态，本文研究的基本假定是只考虑弹性状态下的整体屈曲。虽然弹性屈曲在工程中是很难发生，但是弹性临界荷载对于指导工程设计有极为重要的意义，例如在冷弯薄壁型钢柱设计中最常用的“直接强度法”^[18]，构件的承载能力是直接在弹性屈曲荷载基础上折减得到的。REN等^[19]在研究冷弯薄壁型钢柱受到纵向不均匀温度时的高温承载力，对构件的整体屈曲临界应力采用了“修正长细比”的简化计算方法，并代入直接强度法中计算极限承载能力，发现计算结果与数值模拟结果能较好地吻合。因此获取纵向不均匀温度分布钢柱的弹性临界荷载理论计算方法对于指导钢结构抗火设计同样有重要意义。本文的研究目的是建立钢柱在纵向不均匀温度分布下的弹性屈曲荷载计算方法，以便于工程应用。

1 常见的温度分布模型

在实际的建筑结构分析中，为对火灾温度分布及随时间的变化进行分析可采用基于一定假定的物理模型，并根据能量守恒定律计算空间温度分布。

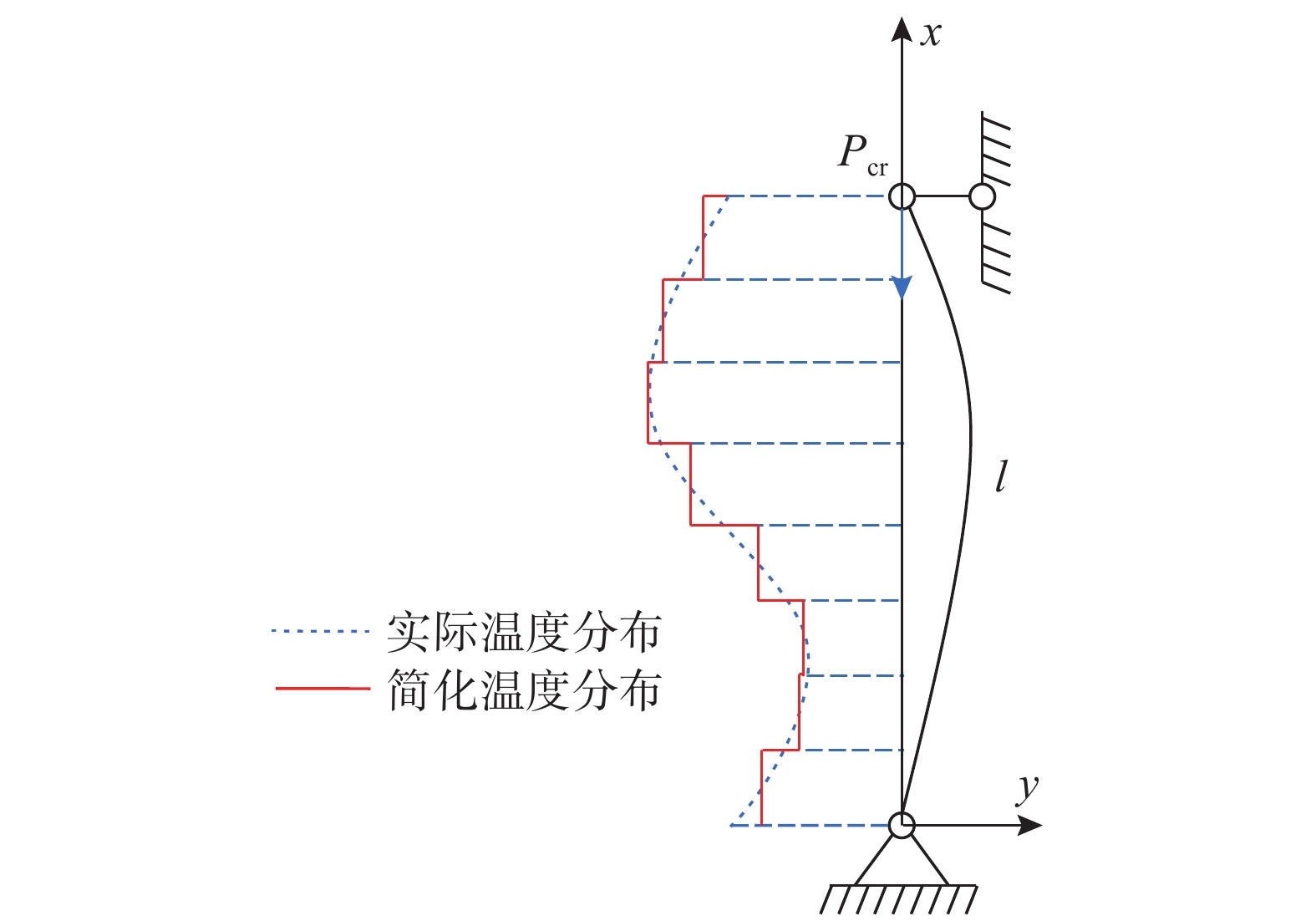
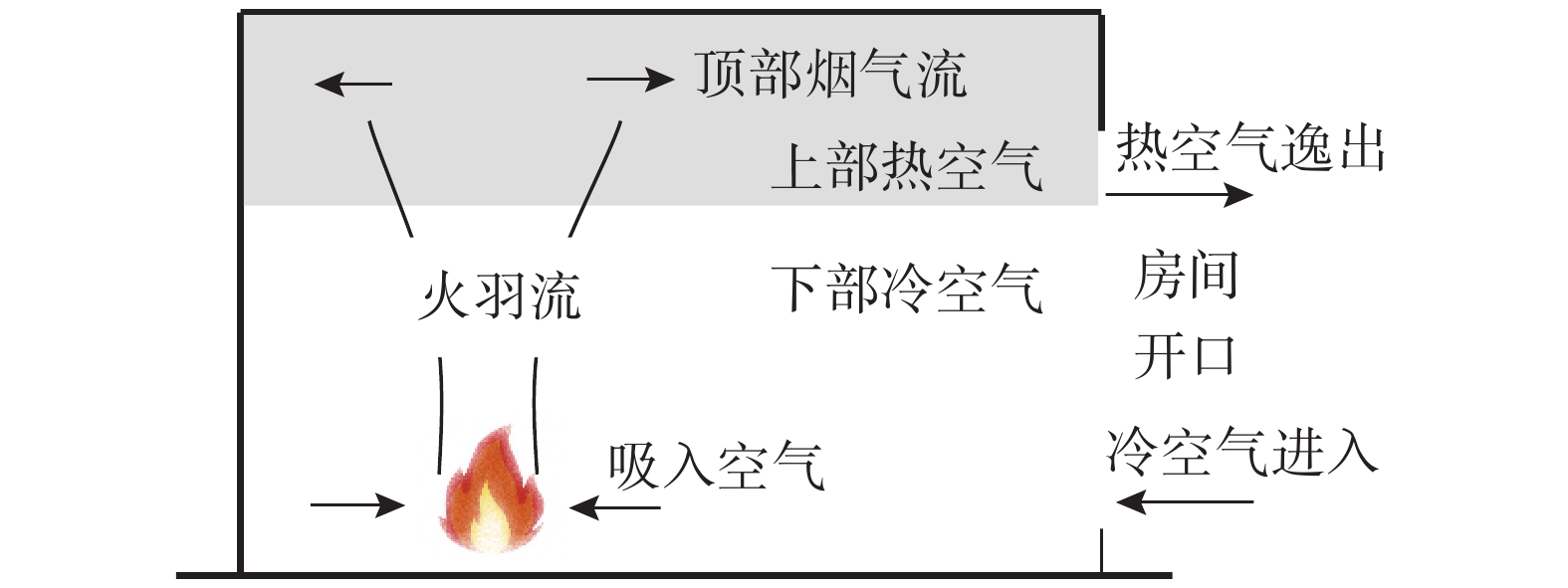
目前进行建筑室内火灾分析的模型主要包含场模型和双区域模型。场模型是基于质量守恒、动量守恒、能量守恒定律及化学反应通过对空间进行离散，用数值方法求解出火灾各时刻的状态参数(速度、温度以及组分浓度等)在空间的分布，场模型适用于分析任何类型的火灾，但是对于燃烧学和计算理论要求较高。而双区域模型是火灾状态下的一种理想模型，该模型通常将失火空间分为上下两个区域，即上部相对热的烟气和下部相对较冷的空气(图1)，并假定两层之间分界高度在各处一致，每个区域内的压力、温度、密度、烟气浓度等物理参数均匀一致。这种双层温度的假设与火灾发生轰燃前观察到的试验结果非常吻合^[20-21]。根据相关的研究表明，上下区域之间的温度差可能会超过450 ℃，这主要取决于空间尺寸以及火灾大小等因素。因此，本文首先考虑在场模型火灾中，建立求解钢柱弹性屈曲荷载的一般通解，然后，将该通解应用简化的双区域模型中，获取该工况下的理论计算方法。

图 1 双区域火灾模型示意图

Figure 1. Schematic diagram of two-zone fire model

下载: 全尺寸图片幻灯片

2 场模型火灾中杆件整体屈曲弹性屈曲荷载

在基于场模型的火灾工况下，温度在纵向空间内的分布相对复杂，对于不同的火灾场景，温度分布受到燃烧物密度，空间大小，开口高度等因素的影响。首先以普通的杆件作为分析对象，采用函数T(x)来表达沿钢柱高度(x方向)的温度分布，如图2(a)。当钢材处于不同的温度环境时，总会有唯一对应弹性模量，因此可以用函数E(x)来表达沿钢柱高度的弹性模量大小，如图2(b)。本研究假定钢柱在横截面上的温度是均匀分布的。

图 2 纵向不均匀温度分布钢柱计算模型

Figure 2. Calculation model of a steel column with longitudinally non-uniform temperature

下载: 全尺寸图片幻灯片

对于如图2的杆件在发生整体弯曲时，采用能量法对其弹性屈曲荷载近似求解，假定屈曲曲线方程为：

$y = {a_1}{f_1}(x) + {a_2}{f_2}(x) + \cdot \cdot \cdot {a_n}{f_n}(x) = \sum\limits_{i = 1}^n {{a_i}{f_i}(x)}$

(1)

式中：f_i(x)为满足杆端点条件的x的函数；a_i为确定各项幅度的常数。对于两端铰接的杆件，每一函数f_i(x)需要满足的端点条件为：

${f_i}(x) = {f_i}^{\prime \prime }(x) = 0 \;,\qquad 当x=0和x=l时$

(2)

值得注意的是钢柱受热的能量输入会转化为热膨胀的应变能以及在热膨胀方向荷载做功之和，三者之间是处于平衡状态，不会对钢柱的弹性临界荷载产生影响。另外，考虑到做功的顺序并不会改变最终的能量状态，因此可以将弹性临界荷载的求解过程看作是稳态的加载过程，也就是先升温到特定温度再进行加载，在升温过程中没有外荷载作用，在达到特定温度后施加的外荷载做功仅仅会转化为杆件的应变能。当杆件发生屈曲时外力所作的功及应变能的改变由以下表达式给出：

$\Delta T = \frac{P}{2}{\int_0^l {\left( {y'} \right)} ^2}{\rm{d}}x$

(3)

$\Delta U = \frac{{{P^2}}}{2}\int_0^l {\frac{{{y^2}}}{{E(x)I}}} {\rm{d}}x$

(4)

由能量守恒可知，ΔU=ΔT，可得：

$P = {{{\int_0^l \left( {y'} \right) ^2}{\rm{d}}x} \Bigg/ {\int_0^l {\frac{{{y^2}}}{{E(x)I}}} {\rm{d}}x}}$

(5)

要得到P_cr的值，须选择式(1)中的各项系数a_i使式(5)为最小。这就需要式(5)对每一项a_i的导数必须等于零，于是可得如下形式的方程：

$\begin{split} & \int_0^l {\frac{{{y^2}}}{{E(x)I}}} {\rm{d}}x\frac{\partial }{{\partial {a_i}}}\int_0^l {{{\left( {y'} \right)}^2}} {\rm{d}}x - \\&\qquad \int_0^l {{{\left( {y'} \right)}^2}} {\rm{d}}x\frac{\partial }{{\partial {a_i}}}\int_0^l {\frac{{{y^2}}}{{E(x)I}}} {\rm{d}}x = 0 \end{split}$

(6)

由式(1)可知屈曲曲线对各项系数的偏导为：

$\frac{{\partial y}}{{\partial {a_i}}} = {f_i}(x) \;, \qquad \frac{{\partial y'}}{{\partial {a_i}}} = {f'_i}(x)$

(7)

将式(7)代入式(6)可得：

$\int_0^l {y'{f'_i}} (x){\rm{d}}x - P\int_0^l {\frac{{y{f_i}(x)}}{{E(x)I}}} {\rm{d}}x = 0$

(8)

将式(1)代入式(6)进行积分，得到a_1,a₂, ···, a_i的齐次线性方程。式(8)的数目与a₁, a₂, ··· , a_i的数目相同。若要使杆件发生屈曲，a₁, a₂, ···, a_i不能全部等于零，仅当式(8)的行列式等于零才可能，因此令这行列式为零，即可计算得到P_cr。

由分部积分，可将式(8)的第一项转换为：

$\int_0^l {y'{f'_i}} (x){\rm{d}}x = \left[ {y'{f_i}(x)} \right]_0^l - \int_0^l {y''{f_i}(x)} {\rm{d}}x$

(9)

由于杆件两端均匀铰接，因此，在杆的两端f_i(x)等于零，式(9)右边第一项等于零，进而式(8)可转化为：

$\int_0^l {\left( {\frac{P}{{E(x)I}}y + y''} \right){f_i}(x)} {\rm{d}}x = 0$

(10)

因为，轴向受压杆件的挠曲线微分方程为：

$\frac{P}{{E(x)I}}y + y'' = 0$

(11)

y的精确表示必须满足式(11)，但是若要由式(1)得到y的近似解，须选择合适的系数a₁, a₂, ···, a_i使得式(10)的左边为零。将式(1)代入式(10)，可以得到决定a₁, a₂, ··· , a_i的线性方程：

$\begin{split} & {a_1}\int_0^l {\left( {{f_1^{\prime \prime }}(x) + \frac{{P{f_1}(x)}}{{E(x)I}}} \right){f_i}(x)} {\rm{d}}x + \\&\qquad {a_2}\int_0^l {\left( {{f_2^{\prime \prime }}(x) + \frac{{P{f_2}(x)}}{{E(x)I}}} \right){f_i}(x)} {\rm{d}}x + \cdot \cdot \cdot + \\&\qquad a_i \int_0^l\left(f_i^{\prime \prime}(x)+\frac{P f_i(x)}{E(x) I}\right) f_i(x) {\rm{d}} x = 0 \end{split}$

(12)

一般情况下，为提高计算精度可对式(1)的挠曲方程表达为三角级数并取i=2，令f₁(x)=sin(πx/l)，f₂(x)=sin(2πx/l)，可得：

$y = {a_1}\sin \frac{{\pi x}}{l} + {a_2}\sin \frac{{2\pi x}}{l}$

(13)

将式(13)代入式(12)可得式(14)和式(15)，其中系数A₁、A₂、B₁、B₂、C₁、C₂、D₁、D₂取值见表1：

${a_1}\left( {{A_1} + {B_1}P} \right) + {a_2}\left( {{C_1} + {D_1}P} \right) = 0$

(14)

${a_1}\left( {{A_2} + {B_2}P} \right) + {a_2}\left( {{C_2} + {D_2}P} \right) = 0$

(15)

式(14)~式(15)可进一步转换为矩阵形式：

$\left[ {\begin{array}{*{20}{c}} {{A_1} + {B_1}P}&{{C_1} + {D_1}P} \\ {{A_2} + {B_2}P}&{{C_2} + {D_2}P} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_1}} \\ {{a_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right]$

(16)

表 1 不均匀升温弹性屈曲荷载系数表达式

Table 1. Expression of elastic buckling load coefficient under non-uniform temperature

待定系数	系数表达式
A₁	${A_1} = - \displaystyle\int_0^l {\dfrac{ { {\pi ^2} } }{ { {l^2} } }\sin \dfrac{ {\pi x} }{l}\sin \dfrac{ {\pi x} }{l} } {\rm{d}}x = - \dfrac{ { {\pi ^2} } }{ {2l} }$
A₂	${A_2} = - \displaystyle\int_0^l {\dfrac{ { {\pi ^2} } }{ { {l^2} } }\sin \dfrac{ {\pi x} }{l}\sin \dfrac{ {2\pi x} }{l} } {\rm{d}}x = 0$
B₁	${B_1} = \displaystyle\int_0^l {\dfrac{ { { {\sin }^2}\dfrac{ {\pi x} }{l} } }{ {E(x)I} } } {\rm{d}}x$
B₂	${B_2} = \displaystyle\int_0^l {\dfrac{ {\sin \dfrac{ {\pi x} }{l}\sin \dfrac{ {2\pi x} }{l} } }{ {E(x)I} } } {\rm{d}}x$
C₁	${C_1} = - \displaystyle\int_0^l {\dfrac{ {4{\pi ^2} } }{ { {l^2} } }\sin \dfrac{ {2\pi x} }{l}\sin \dfrac{ {\pi x} }{l} } {\rm{d}}x = 0$
C₂	${C_2} = - \displaystyle\int_0^l {\dfrac{ {4{\pi ^2} } }{ { {l^2} } }\sin \dfrac{ {2\pi x} }{l}\sin \dfrac{ {2\pi x} }{l} } {\rm{d}}x = - \dfrac{ {2{\pi ^2} } }{l}$
D₁	${D_1} = \displaystyle\int_0^l {\dfrac{ {\sin \dfrac{ {2\pi x} }{l}\sin \dfrac{ {\pi x} }{l} } }{ {E(x)I} } } {\rm{d}}x = {B_2}$
D₂	${D_2} = \displaystyle\int_0^l {\dfrac{ { { {\sin }^2}\dfrac{ {2\pi x} }{l} } }{ {E(x)I} } } {\rm{d}}x$

下载: 导出CSV

| 显示表格

由于a₁~a₃不能全为零，因此得到行列式：

$\left| {\begin{array}{*{20}{c}} {{A_1} + {B_1}P}&{{C_1} + {D_1}P} \\ {{A_2} + {B_2}P}&{{C_2} + {D_2}P} \end{array}} \right| = 0$

(17)

进一步化简可得：

$( {{B_1}{D_2} - B_2^2} ){P^2} + ( {{A_1}{D_2} + {B_1}{C_2}} )P + {A_1}{C_2} = 0$

(18)

可得不均匀升温时屈曲荷载P_crg表达式，其中各系数的计算式以及取值见表1。

$\begin{split} & {P_{{\rm{crg}}}} = \\& \frac{{{A_1}{D_2} + {B_1}{C_2} \pm \sqrt {( {{A_1}{D_2} + {B_1}{C_2}} )^2 - 4( {{B_1}{D_2} - B_2^2} ){A_1}{C_2} } }}{{ - 2( {{B_1}{D_2} - B_2^2} )}} \end{split}$

(19)

由于在不均匀的纵向温度下，E(x)的表达式十分复杂，系数B₁、B₂、D₁、D₂通常难以求得数值解，进而需要对不均分布的温度进行简化。可以沿纵向将试件等分后，取每一段中点的温度作为均匀温度施加在这一段上，例如图3就给出了该等效温度的方法，若等分段数越多，等效的温度场越接近真实的不均匀温度分布场。在知道杆件纵向T(x)分布后，即可得到杆件沿长度的弹性模量E(x)分布，采用式(19)并结合式(23)~式(25)即可计算得到试件的弹性屈曲荷载近似值。

图 3 不均匀温度简化示意图

Figure 3. Simplified diagram of non-uniform temperature distribution

下载: 全尺寸图片幻灯片

在此情况下，可以对系数B₁、B₂、D₁和D₂进行分段积分：

$\begin{split} {B_1} = &\frac{1}{{E({l_1})I}}\int_{{l_0}}^{{l_1}} {{{\sin }^2}\frac{{\pi x}}{l}} {\rm{d}}x + \frac{1}{{E({l_2})I}}\int_{{l_1}}^{{l_2}} {{{\sin }^2}\frac{{\pi x}}{l}} {\rm{d}}x + \cdot \cdot \cdot +\\& \frac{1}{{E({l_n})I}}\int_{{l_{n - 1}}}^{{l_n}} {{{\sin }^2}\frac{{\pi x}}{l}} {\rm{d}}x \end{split}$

(20)

$\begin{split} & {B_2} = \frac{1}{{E({l_1})I}}\int_{{l_0}}^{{l_1}} {\sin \frac{{\pi x}}{l}\sin \frac{{2\pi x}}{l}} {\rm{d}}x +\frac{1}{{E({l_2})I}}\cdot\\& \int_{{l_1}}^{{l_2}} {\sin \frac{{\pi x}}{l}\sin \frac{{2\pi x}}{l}} {\rm{d}}x+\cdot \cdot \cdot + \frac{1}{{E({l_n})I}}\int_{{l_{n - 1}}}^{{l_n}} {\sin \frac{{\pi x}}{l}\sin \frac{{2\pi x}}{l}} {\rm{d}}x \end{split}$

(21)

$\begin{split} & {D_2} = \frac{1}{{E({l_1})I}}\int_{{l_0}}^{{l_1}} {{{\sin }^2}\frac{{2\pi x}}{l}} {\rm{d}}x+\\& \frac{1}{{E({l_2})I}}\int_{{l_1}}^{{l_2}} {{{\sin }^2}\frac{{2\pi x}}{l}} {\rm{d}}x+ \cdot \cdot \cdot + \frac{1}{{E({l_n})I}}\int_{{l_{n - 1}}}^{{l_n}} {{{\sin }^2}\frac{{2\pi x}}{l}} {\rm{d}}x \end{split}$

(22)

将各系数进一步化简并写成求和公式可得：

$\begin{split} {B_1} =& \sum\limits_{i = 1}^n {\frac{1}{{E({l_i})I}}\int_{{l_{i - 1}}}^{{l_i}} {{{\sin }^2}\frac{{\pi x}}{l}} {\rm{d}}x} =\\& \sum\limits_{i = 1}^n {\frac{1}{{E({l_i})I}}\left. {\left[ {\frac{x}{2} - \frac{l}{{4\pi }}\sin \left( {\frac{{2\pi }}{l}x} \right)} \right]} \right|_{{l_{i - 1}}}^{{l_i}}} \end{split}$

(23)

$\begin{split} {B_2} =& \sum\limits_{i = 1}^n {\frac{1}{{E({l_i})I}}\int_{{l_{i - 1}}}^{{l_i}} {\sin \frac{{\pi x}}{l}\sin \frac{{2\pi x}}{l}} {\rm{d}}x} =\\& \sum\limits_{i = 1}^n {\frac{1}{{E({l_i})I}}\left. {\left[ \frac{l}{{2\pi }}\sin \left( {\frac{\pi }{l}x} \right) - \frac{l}{{6\pi }}\sin \left( {\frac{{3\pi }}{l}x} \right) \right]} \right|_{{l_{i - 1}}}^{{l_i}}} \end{split}$

(24)

$\begin{split} {D_2} = &\sum\limits_{i = 1}^n {\frac{1}{{E({l_i})I}}\int_{{l_{i - 1}}}^{{l_i}} {{{\sin }^2}\frac{{2\pi x}}{l}} {\rm{d}}x} =\\& \sum\limits_{i = 1}^n {\frac{1}{{E({l_i})I}}\left. {\left[ {\frac{x}{2} - \frac{l}{{8\pi }}\sin \left( {\frac{{4\pi }}{l}x} \right)} \right]} \right|_{{l_{i - 1}}}^{{l_i}}} \end{split}$

(25)

3 双区域模型火灾中普通杆件整体屈曲弹性屈曲荷载

第2节推导了在任意温度分布情况下普通杆件的整体屈曲弹性屈曲荷载P_crg计算方法，该方法不仅可以指导计算复杂温度分布情况下的P_crg，同时，也可以用于计算简化的双区域火灾中的P_crg。因此，本小节首先基于平衡微分方程给出双区域火灾中的P_crg精确解，再基于第2节中的能量法计算公式给出双区域火灾中的P_crg的近似解，并研究能量法计算结果的相对误差，以便于为实际应用提供指导。

3.1 弹性屈曲荷载精确解

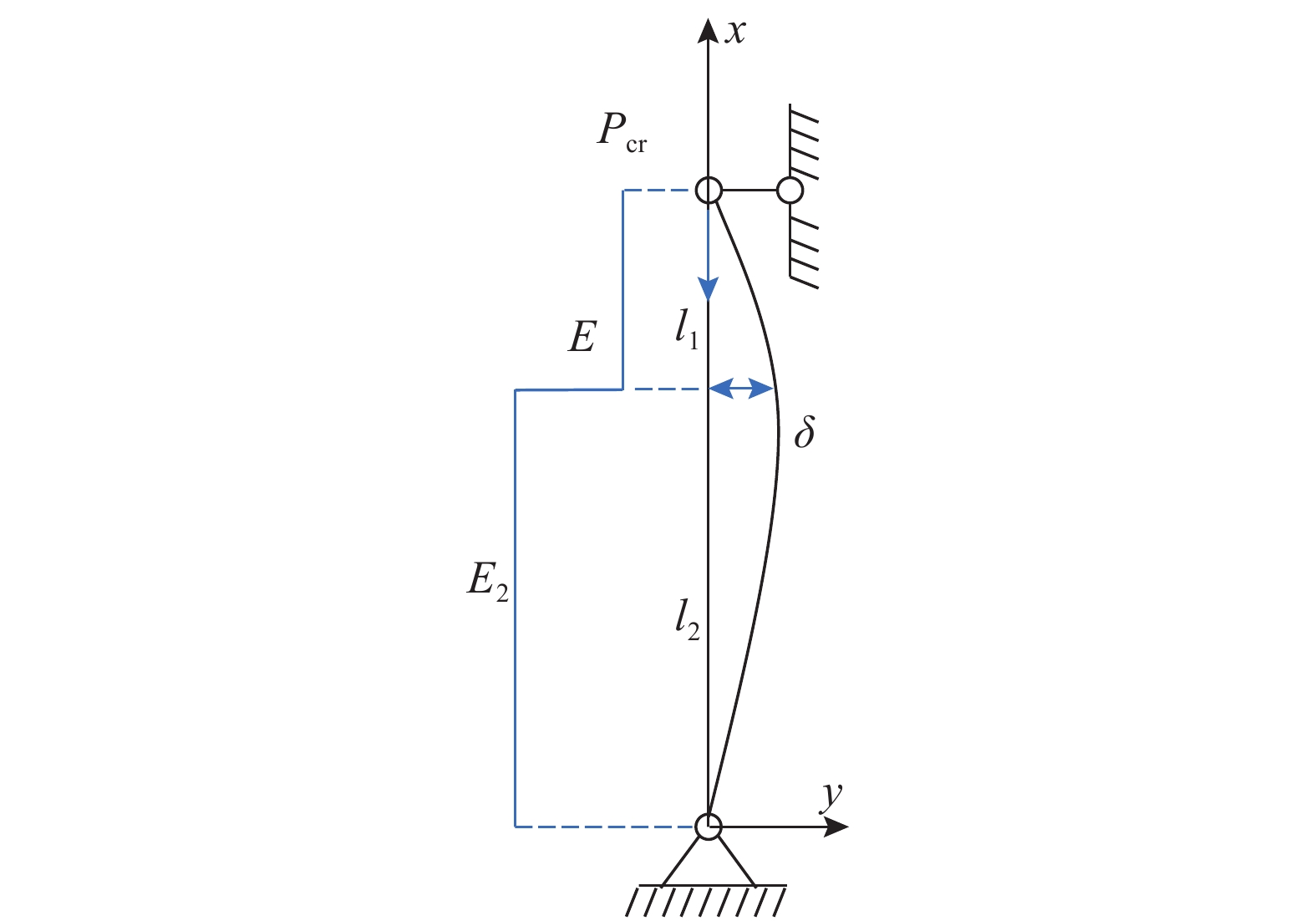
双区域模型火灾的力学模型相对于场模型更为简单，因此，可以从平衡微分方程的角度去寻求弹性屈曲荷载精确解，杆件的力学分析模型如图4。双区域模型上部温度为T₁，总长度为l₁，下部温度为T₂，总长度为l₂。相应的，假定温度T₁对应的钢材弹性模量为E₁，T₂对应的钢材弹性模量为E₂。此外，令上部杆件的挠度为y₁，下部杆件的挠度为y₂，在两区域交界处的挠度为δ。

图 4 双区域火灾模型整体屈曲示意图

Figure 4. Global buckling of steel column in two-zone fire model

下载: 全尺寸图片幻灯片

由于上下两部分杆件的弹性模量不一致，因此需要分别建立微分方程：

${E_1}I\frac{{{{\rm{d}}^2}{y_1}}}{{{\rm{d}}{x^2}}} = - P{y_1}$

(26)

${E_2}I\frac{{{{\rm{d}}^2}{y_2}}}{{{\rm{d}}{x^2}}} = - P{y_2}$

(27)

令 $k_1^2 = {P / {{E_1}I}}$ 以及 $k_2^2 = {P / {{E_2}I}}$ ，于是式(26)和式(27)的通解为：

${y_1} = {C_1}\sin {k_1}x + {C_2}\cos {k_1}x,\;\; {l_2} \leqslant x \leqslant l$

(28)

${y_2} = {C_3}\sin {k_2}x + {C_4}\cos {k_2}x ,\;\; 0 \leqslant x \leqslant {l_2}$

(29)

积分常数C_1、C_2、C₃和C₄取决于杆件的端部条件：

${\left( {{y_1}} \right)_{x = l}} = 0$

(30)

${\left( {{y_1}} \right)_{x = {l_2}}} = \delta$

(31)

${\left( {{y_2}} \right)_{x = {l_2}}} = \delta$

(32)

${\left( {{y_2}} \right)_{x = 0}} = 0$

(33)

将式(30)~式(33)代入式(28)~式(29)可得：

${C_1} = \frac{\delta }{{\cos ({k_1}{l_2})\left[ {\tan ({k_1}{l_2}) - \tan ({k_1}l)} \right]}}$

(34)

${C_2} = - {C_1}\tan \left( {{k_1}l} \right)$

(35)

${C_3} = \frac{\delta }{{\sin \left( {{k_2}{l_2}} \right)}}$

(36)

${C_4} = 0$

(37)

由杆件的连续条件可得：

${\left( {\frac{{{\rm{d}}{y_1}}}{{{\rm{d}}x}}} \right)_{x = {l_2}}} = {\left( {\frac{{{\rm{d}}{y_2}}}{{{\rm{d}}x}}} \right)_{x = {l_2}}}$

(38)

可得到计算屈曲荷载的方程：

$\frac{{{k_1} + {k_1}\tan \left( {{k_1}l} \right)\tan \left( {{k_1}{l_2}} \right)}}{{\tan \left( {{k_1}{l_2}} \right) - \tan \left( {{k_1}l} \right)}} = \frac{{{k_2}}}{{\tan \left( {{k_2}{l_2}} \right)}}$

(39)

式(39)为超越方程，无法得到解析解，只能通过试算法求解屈曲荷载P_crg，为了便于工程应用，考虑到上部火灾温度高于下部温度，因此引入上下层弹性模量比例系数α_E和下层受热长度系数β如式(40)和式(41)：

${E_1} = {\alpha _{\rm{E}}}{E_2} \;,\qquad\quad 0 < {\alpha _{\rm{E}}} \leqslant 1$

(40)

${l_2} = \beta l \;,\qquad\qquad\quad 0 < \beta \leqslant 1$

(41)

${P_{{\text{cr}}}} = \chi \frac{{{\pi ^2}{E_2}I}}{{{l^2}}}\;, \qquad 0 < \chi \leqslant 1$

(42)

因此，杆件的弹性屈曲荷载可以用式(42)表示，其中系数χ为杆件不均匀温度分布弹性屈曲荷载系数，当χ=1时，表征杆件上部和下部的温度相同(纵向温度分布均匀)；当χ越小，就表征上部的高温对于杆件的弹性屈曲荷载影响越严重。

将式(40)~式(42)代入式(39)，化简后可以得到弹性屈曲荷载系数χ关于α_E和β的计算公式：

$\dfrac{{1 + \tan \left( {\pi \beta \sqrt {\dfrac{\chi }{{{\alpha _{\rm{E}}}}}} } \right)\tan \left( {\pi \sqrt {\dfrac{\chi }{{{\alpha _{\rm{E}}}}}} } \right)}}{{\tan \left( {\pi \beta \sqrt {\dfrac{\chi }{{{\alpha _{\rm{E}}}}}} } \right) - \tan \left( {\pi \sqrt {\dfrac{\chi }{{{\alpha _{\rm{E}}}}}} } \right)}} = \dfrac{{\sqrt {{\alpha _{\rm{E}}}} }}{{\tan ( {\pi \beta \sqrt \chi } )}}$

(43)

借助试算法，可以得到弹性屈曲荷载系数χ在不同的α_E和β取值情况下的精确解，如表2。

在实际工程中，首先根据实际火灾工况计算出系数α_E和β后，再代入表中通过线性插值得到弹性屈曲荷载系数χ，最后将χ代入式(42)即可计算试件的整体弯曲弹性屈曲荷载。

表 2 χ在不同的α_E和β取值情况下的取值表(精确解)

Table 2. Value of the χ at different α_E and β (exact solution)

上下层弹性模量比例系数α_E	下层受热长度系数β
上下层弹性模量比例系数α_E	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
0.1	0.101	0.104	0.113	0.129	0.159	0.213	0.317	0.551	0.926	1.000
0.2	0.201	0.207	0.223	0.253	0.303	0.390	0.541	0.782	0.971	1.000
0.3	0.301	0.310	0.331	0.369	0.433	0.534	0.690	0.876	0.984	1.000
0.4	0.401	0.411	0.435	0.478	0.548	0.651	0.788	0.922	0.989	1.000
0.5	0.502	0.512	0.537	0.581	0.649	0.743	0.855	0.949	0.993	1.000
0.6	0.602	0.611	0.635	0.677	0.739	0.818	0.902	0.967	0.996	1.000
0.7	0.701	0.710	0.731	0.767	0.817	0.878	0.937	0.979	0.997	1.000
0.8	0.801	0.808	0.824	0.85	0.886	0.926	0.963	0.988	0.998	1.000
0.9	0.901	0.904	0.913	0.928	0.947	0.967	0.983	0.995	0.999	1.000
1.0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000

下载: 导出CSV

| 显示表格

3.2 弹性屈曲荷载近似解

在3.1节给出了双区域模型下求解弹性屈曲荷载精确解的方法，但是该方法的缺点是没有显式的计算公式，当系数α_E和β不是表中的取值时，只能通过插值法去寻找近似解，本小节将借助第2节中的能量法方程，给出双区域模型下求解弹性屈曲荷载的显式计算公式。同样对于图4中的杆件，并结合式(23)~式(25)可以解得参数B₁、B₂和D₂，如式(44)~式(46)：

${B_1} = \frac{l}{{{E_2}I}}{K_1}$

(44)

${B_2} = \frac{l}{{{E_2}I}}{K_2}$

(45)

${D_2} = \frac{l}{{{E_2}I}}{K_3}$

(46)

式中引入了参数K₁、K₂、和K₃以便于化简和计算：

${K}_{1}=\frac{2\pi ({\alpha }_{{\rm{E}}}\beta +1-\beta )+(1-{\alpha }_{{\rm{E}}})\mathrm{sin}(2\pi \beta )}{4{\alpha }_{{\rm{E}}}\pi }$

(47)

${K_2} = \frac{{\left( {{\alpha _{\rm{E}}} - 1} \right)\left[ {3\sin \left( {\beta \pi } \right) - \sin \left( {3\beta \pi } \right)} \right]}}{{6\pi {\alpha _{\rm{E}}}}}$

(48)

${K}_{3}=\frac{4\pi ({\alpha }_{{\rm{E}}}\beta +1-\beta )+(1-{\alpha }_{{\rm{E}}})\mathrm{sin}(4\pi \beta )}{8{\alpha }_{{\rm{E}}}\pi }$

(49)

将B₁、B₂和D₂代入式(19)可以得到弹性屈曲荷载近似解的表达式，同样将该表达式以式(42)的形式给出，则杆件不均匀温度分布弹性屈曲荷载系数χ的表达式为式(50)。为对比近似解与精确解与之间的相对误差，表3给出了χ在不同的α_E和β取值情况下的近似解：

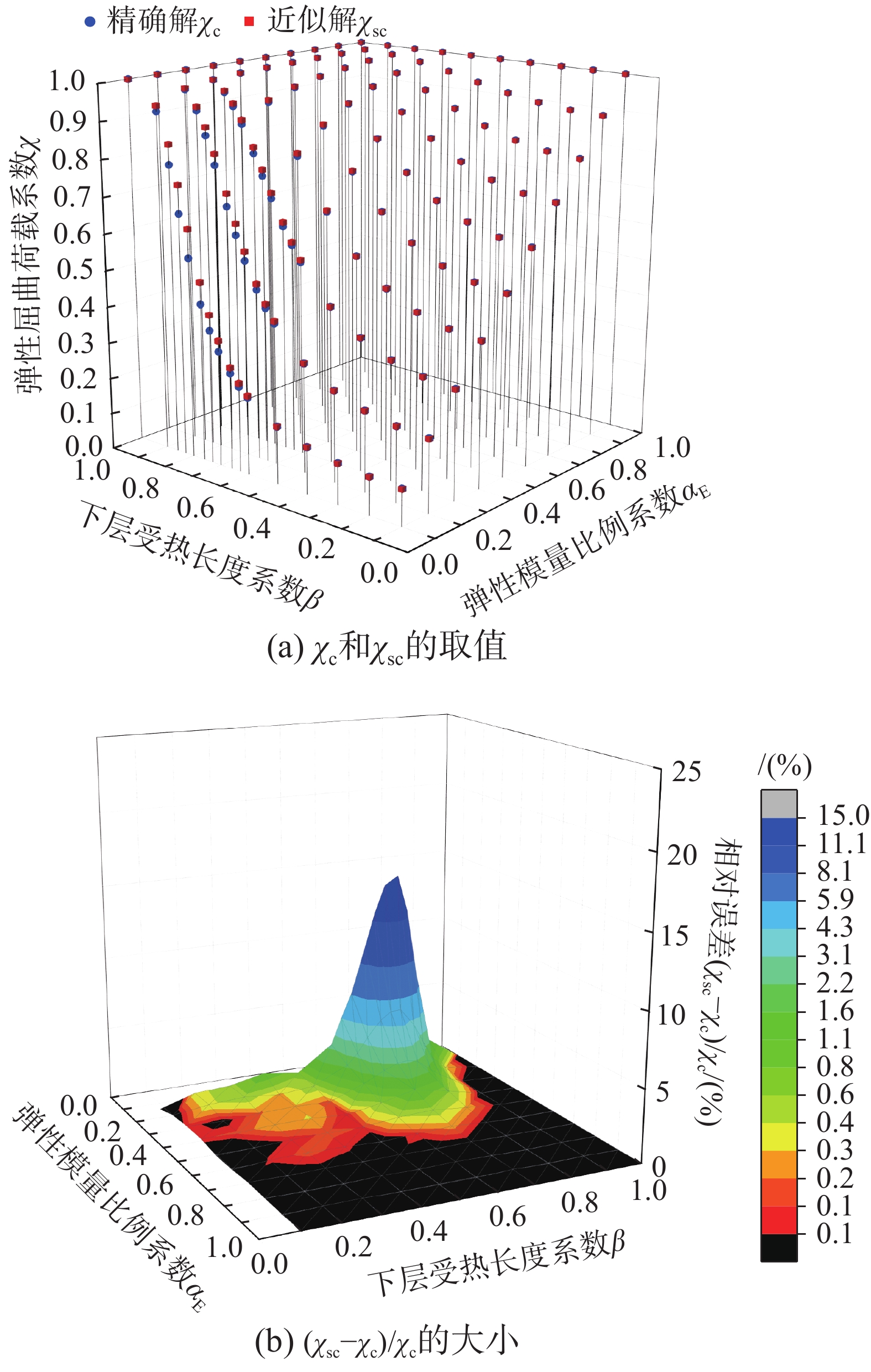
$\chi = \frac{{{K_3} + 4{K_1} - \sqrt {K_3^2 + 16K_1^2 - 8{K_1}{K_3} + 16K_2^2 } }}{{4{K_1}{K_3} - 4K_2^2}}$

(50)

将系数χ的精确解记为χ_c以及近似解记为χ_sc，图5(a)对比了在不同α_E和β取值情况下χ_c以及χ_sc的大小，可以看出在大多数情况下，χ_c与χ_sc十分接近，只有在0.1≤α_E≤0.2以及0.6≤β≤0.8时，近似解的误差相对较为明显，且χ_sc始终大于χ_c。为进一步分析近似解的误差范围，图5(b)绘制了近似解的相对误差(χ_sc−χ_c)/χ_c在与不同α_E和β取值情况下三维曲面图，由图中可知，精确解与近似解的相对误差在大多数情况下都小于1%，在α_E=0.1且同时0.6≤β≤0.8时，最大相对误差能达到14%，而在α_E=0.2且同时0.6≤β≤0.8时，最大相对误差能达到约5%。造成这种现象的原因是当上下部分弹性模量相差较大时，能量法假设的杆件扰度曲线会与实际情况有较大出入，因此计算结果偏差也较大。综上所述，本小节推导的近似解在绝大多数情况下都可以较为准确的计算杆件的弹性屈曲荷载，只有当系数0.1≤α_E≤0.2且同时0.6≤β≤0.8时，近似解的相对误差较大，此时建议按照式(43)通过试算法或者插值计算χ。

为了进一步验证本章节基于平衡微分方程以及能量法建立的不均匀温度下杆件整体屈曲弹性屈曲荷载计算方法准确性，基于ABAQUS建立了有限元模型，模型的采用梁单元建模，在单元端部采用铰接连接，为了便于计算，梁单元长度设计为1000 mm，梁单元截面形式为工字形；在定义材料属性时忽略了塑性，并且在梁单元的不同长度范围分别定义不同大小的弹性模量(可得到相应的β和α_E)，使用屈曲分析求解屈曲荷载，再将该屈曲荷载按照式(42)定义进行相应的计算即可得到χ。为验证数值模型准确性，对纵向温度均匀的杆件，即α_E=1，进行弹性屈曲应力求解，发现数值模拟得到的弹性临界应力与欧拉临界应力的相对误差不超过1‰，进而验证了本文数值模型在计算弹性临界应力时的准确性。

表 3 χ在不同的α_E和β取值情况下的取值表(近似解)

Table 3. Value of the χ at different α_E and β (approximate solution)

上下层弹性模量比例系数α_E	下层受热长度系数β
上下层弹性模量比例系数α_E	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
0.1	0.101	0.104	0.114	0.130	0.160	0.218	0.346	0.629	0.941	1.000
0.2	0.201	0.208	0.224	0.254	0.304	0.396	0.566	0.813	0.974	1.000
0.3	0.301	0.310	0.332	0.370	0.434	0.540	0.705	0.888	0.985	1.000
0.4	0.402	0.412	0.436	0.479	0.549	0.655	0.797	0.927	0.990	1.000
0.5	0.502	0.512	0.538	0.582	0.650	0.746	0.859	0.951	0.994	1.000
0.6	0.602	0.612	0.636	0.678	0.739	0.819	0.904	0.968	0.996	1.000
0.7	0.701	0.710	0.731	0.767	0.817	0.878	0.937	0.979	0.997	1.000
0.8	0.801	0.808	0.824	0.851	0.886	0.927	0.963	0.988	0.998	1.000
0.9	0.901	0.904	0.913	0.928	0.947	0.967	0.984	0.995	0.999	1.000
1.0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000

下载: 导出CSV

| 显示表格

图 5 系数χ的精确解与近似解对比

Figure 5. Comparison between exact solution and approximate solution of the coefficient χ

下载: 全尺寸图片幻灯片

图6分别给出了不同β和α_E时，计算得到的χ与模拟结果(χ_s)的相对误差，其中图6(a)为精确解计算结果(χ_c)，图6(b)为近似解计算结果(χ_sc)。从对比结果可以看出，精确解与模拟结果的相对误差较小，总体上不超过3%。而近似解的相对误差在β>0.6且α_E<0.3时较为显著，达到了10%左右，而在其他范围内二者的相对误差同样小于3%。

图 6 系数χ的精确解，近似解与有限元模拟对比

Figure 6. Comparison between exact solution, approximate solution and finite element simulation of the coefficient χ

下载: 全尺寸图片幻灯片

在工程设计中，如若忽略了温度的纵向不均匀分布，则假定全柱长范围内的温度均为T₁，其欧拉临界应力为：

${P_{{\text{cr-uni}}}} = \frac{{{\pi ^2}{E_1}I}}{{{l^2}}}$

(51)

该临界应力与非均匀温度工况下计算得到的临界应力，即式(52)，的比值为：

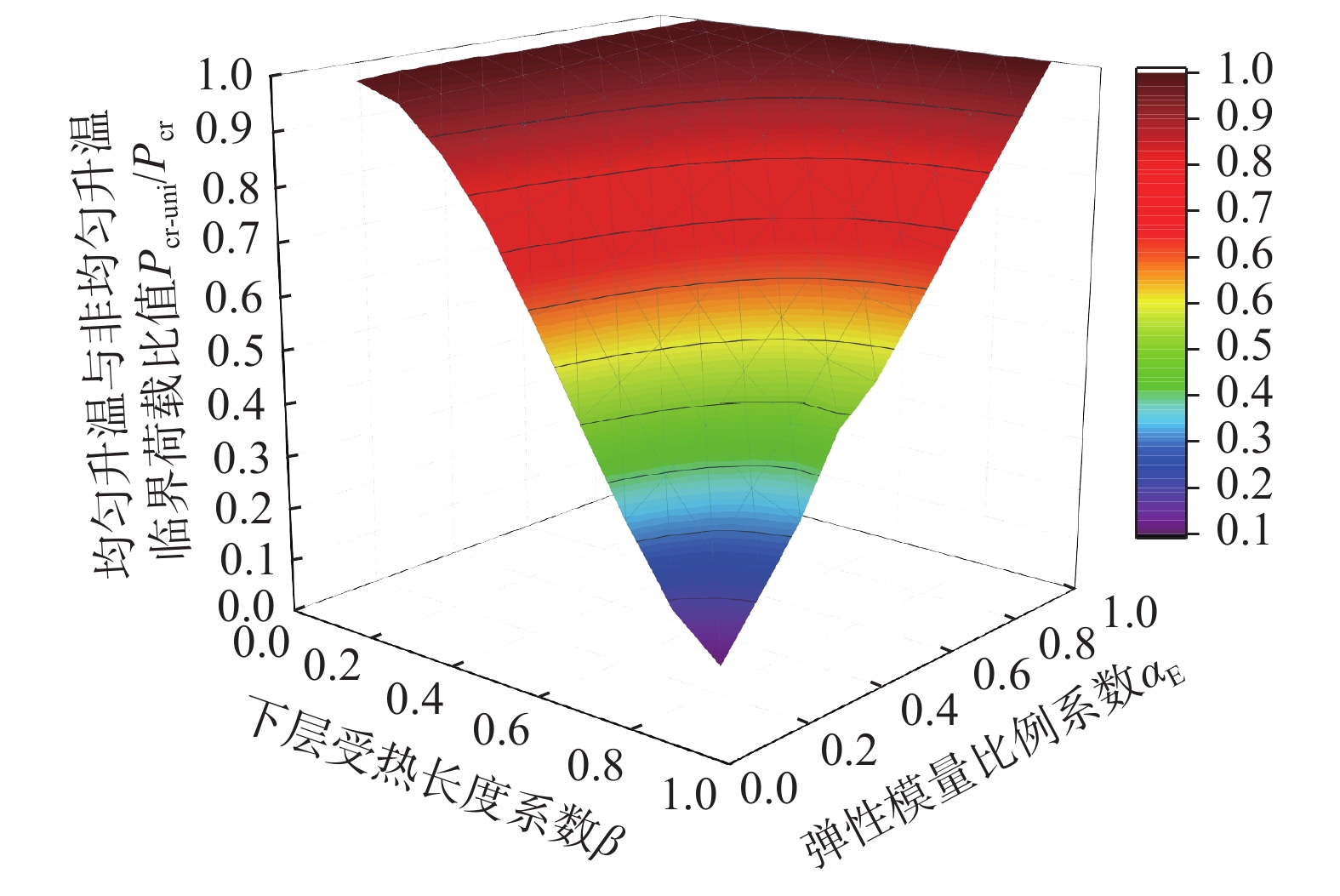
${{{P_{{\text{cr-uni}}}}} /{{P_{{\text{cr}}}}}} = \frac{{{\alpha _E}}}{\chi }$

(52)

图7绘制了P_cr-uni/P_cr在不同α_E和β下的计算结果，可以看出该比值随着β的增大或α_E的降低而显著降低。以工程中常见的β=0.5为例(即受火长度与未受火长度等长)，假定钢柱下部未受火部分的温度低于200 ℃，而上半部分温度逐渐升至800 ℃，参考欧洲规范EN 1993-1-2^[22]中普通碳钢的弹性模量高温折减系数，则α_E的变化范围约为0.1~1，相应计算可得P_cr-uni/P_cr比值的变化范围为0.63~1。由此可知，若忽略温度的不均匀分布，计算得到的试件弹性临界荷载(P_cr-uni)会相对偏于保守，在受火长度与未受火长度等长的情况下，最大的相对计算误差可达到37%。

图 7 P_cr-uni/P_cr在不同α_E和β下的取值

Figure 7. Value of the P_cr-uni/P_cr at different α_E and β

下载: 全尺寸图片幻灯片

4 轴向约束钢柱整体屈曲弹性屈曲荷载

当框架中的钢柱受火热膨胀时，由于受到柱顶的梁和板等构件的纵向约束作用，会抑制其轴向膨胀，并在构件内部产生热膨胀内力。热膨胀内力的大小能较为明显地影响钢柱的耐火性能，导致钢柱在火灾下提前屈曲破坏。而热膨胀内力受到温度，受热长度以及柱端约束大小等因素影响。在以往对于约束钢柱的内力和屈曲临界温度计算方法的研究中^[23-26]，主要是考虑受到纵向均匀温度分布的钢柱，仍缺少对于纵向温度不均匀分布的钢柱内力及屈曲临界温度计算方法。

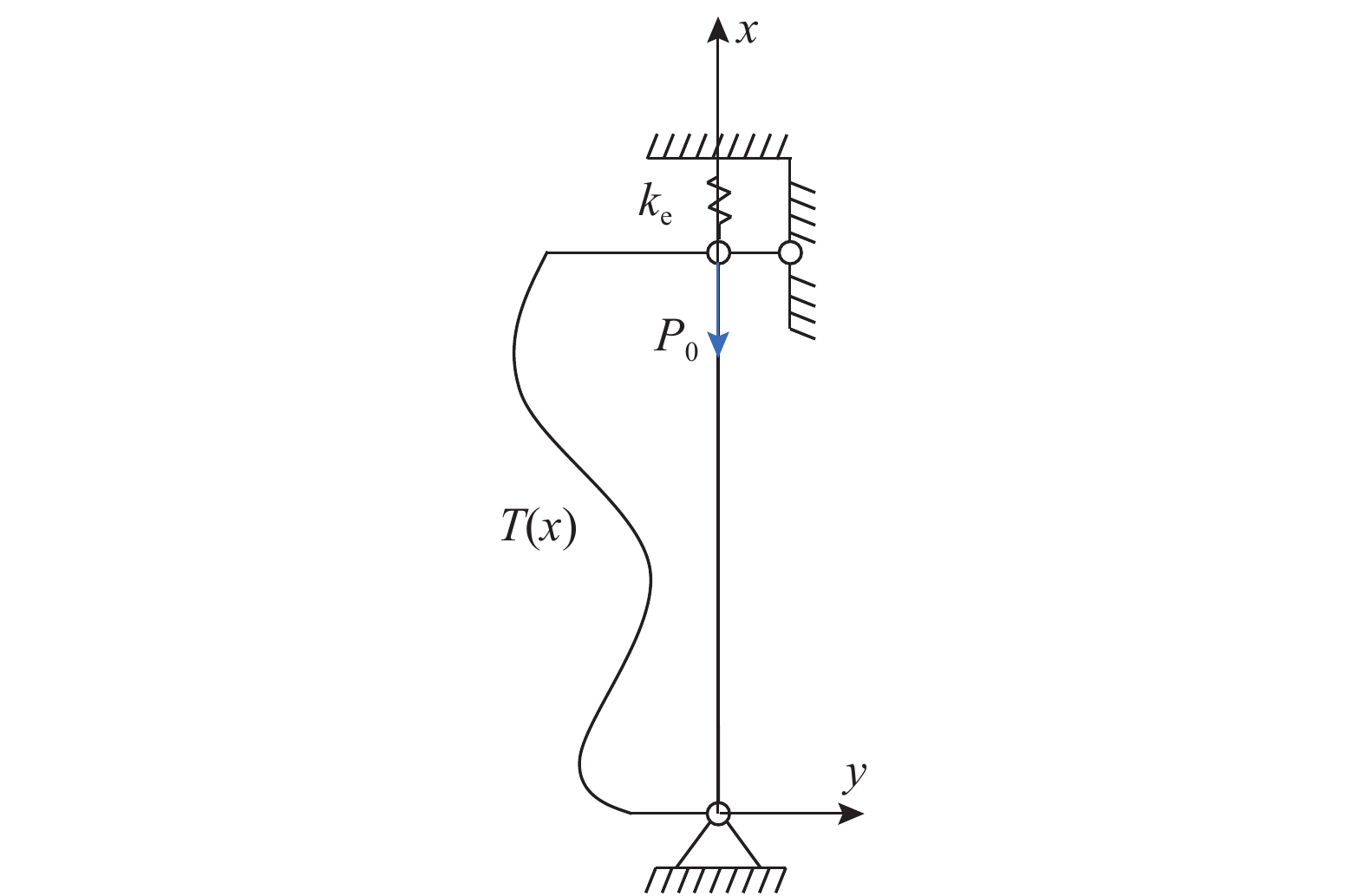
两端铰接的轴向约束柱在高温下的分析模型如图8，将试件所受到的轴向约束作用等效为一个作用在柱顶端的刚度为k_e的弹簧，P₀为试件施加的初始荷载，T(x)为沿试件长度方向的温度函数，由于钢材的弹性模量会随着温度的升高而折减，因此在试件各截面高度处的弹性模量可采用E(x)表示。忽略试件在发生屈曲破坏前的弯曲变形，因为该弯曲变形对于计算柱端在x方向上的位移影响较小^[27]。

图 8 轴向约束柱在高温下的分析模型

Figure 8. Analytical model of axially restrained column at elevated temperatures

下载: 全尺寸图片幻灯片

在任意温度T下，设钢柱的内力为P_T，弹簧的收缩量为Δ_T，截面面积为A，因此可以得到表达式：

${P_{\rm{T}}} = {P_0} + {k_{\rm{e}}}{\Delta _{\rm{T}}}$

(53)

高度x处截面的应变表达式为：

$\varepsilon (x) = {\varepsilon _{{\rm{th}}}}(x) - {\varepsilon _{\rm{e}}}(x)$

(54)

式中：ε为总应变；ε_e为应力引起的机械应变；ε_th为热膨胀应变。基于变形协调可知，试件在轴线方向的伸长等于弹簧的压缩变形，因此，可以得到以下表达式：

${\Delta _{\rm{T}}} = \int_0^L {{\varepsilon _{{\rm{th}}}}(x){\rm{d}}x} - \int_0^L {{\varepsilon _{\rm{e}}}} (x){\rm{d}}x$

(55)

假定室温为20 ℃，E₂₀为试件室温下的弹性模量，在温度为T时的附加机械应变为：

${\varepsilon _{\rm{e}}}(x) = \frac{{{P_{\rm{T}}}}}{{{E_{\rm{T}}}(x) \cdot A}} - \frac{{{P_0}}}{{{E_{20}} \cdot A}}$

(56)

若α_th为材料在温度为T时的热膨胀系数，试件的热膨胀应变为：

${\varepsilon _{{\rm{th}}}}(x) = {\alpha _{{\rm{th}}}} \cdot (T - 20)$

(57)

将式(54)~式(57)代入式(53)可以得到内力P在任意温度T时的表达式：

$\begin{split} {P_{\rm{T}}} = &{P_0} + {k_{\rm{e}}}\int_0^L {{\varepsilon _{{\rm{th}}}}{\rm{d}}x} - {k_{\rm{e}}}{P_{\rm{T}}} \cdot \\& \int_0^L {\frac{1}{{{E_{\rm{T}}}(x)A}}} {\rm{d}}x + {k_{\rm{e}}}{P_0}\int_0^L {\frac{1}{{{E_{20}}A}}} {\rm{d}}x \end{split}$

(58)

进一步化简可得：

${P_{\rm{T}}} = \dfrac{{\left( {1 + {k_{\rm{e}}}\displaystyle\int_0^L {\dfrac{1}{{{E_{20}}A}}{\rm{d}}x} } \right){P_0} + {k_{\rm{e}}}\displaystyle\int_0^L {{\varepsilon _{{\rm{th}}}}} {\rm{d}}x}}{{1 + {k_{\rm{e}}}\displaystyle\int_0^L {\dfrac{1}{{{E_{\rm{T}}}(x)A}}{\rm{d}}x} }}$

(59)

在场模型火灾下，只需要得到温度沿钢柱高度方向的分布函数T(x)，再按照式(59)进行积分，即可得到其温度内力。但是由于E_T(x)通常为分段函数，因此，在对场模型火灾下约束柱内力进行计算时同样可以采用图3所示的简化温度模型。

假定钢柱的温度为均匀分布，则该式可简化为：

${P_{\rm{T}}} = \dfrac{{\left( {1 + {k_{\rm{e}}}\dfrac{L}{{{E_{20}}A}}} \right){P_0} + {k_{\rm{e}}}{\alpha _{{\rm{th}}}}\left( {T - 20} \right)L}}{{1 + {k_{\rm{e}}}\dfrac{L}{{{E_{\rm{T}}}A}}}}$

(60)

当约束刚度k_e为0时可得：

${P_{\rm{T}}} = {P_0}$

(61)

此时试件为无约束柱，内力始终等于初始荷载，当约束刚度k_e无限大时，式(60)化简为：

${P_{\rm{T}}} = \frac{{{E_{\rm{T}}}}}{{{E_{20}}}}{P_0} + {\alpha _{\rm{T}}}T{E_{\rm{T}}}A$

(62)

假定试件的温度为双区域型非均匀分布，且上部温度为T_top，下部温度为T_bottom，下部不均匀受热长度系数为β，则试件在任意温度下的内力：

$\begin{split} & {P_{\rm{T}}} = \Bigg[ \left( {1 + {k_{\rm{e}}}\dfrac{L}{{{E_{20}}A}}} \right){P_0} + {k_{\rm{e}}}{\alpha _{{\rm{th}}}}( {{T_{{\rm{bottom}}}} - 20} )\beta L + \\& {k_{\rm{e}}}{\alpha _{{\rm{th}}}}( {{T_{{\rm{top}}}} - 20} )( {1 - \beta } )L \Bigg]\Bigg/\Bigg[{1 + {k_{\rm{e}}}\dfrac{{\beta L}}{{{E_{{T_{{\rm{bottom}}}}}}A}} + {k_{\rm{e}}}\dfrac{{( {1 - \beta } )L}}{{{E_{{T_{{\rm{top}}}}}}A}}} \Bigg] \end{split}$

(63)

随着温度的升高，钢柱的内力为P_T会逐渐增大，构件的无约束情况下的屈曲荷载P_cr则逐渐下降，当P_T等于P_cr时，试件就发生屈曲破坏，此时的内力P_T即为构件在有约束情况下的屈曲荷载，但是该屈曲荷载无解析解，只能通过试算法求解。

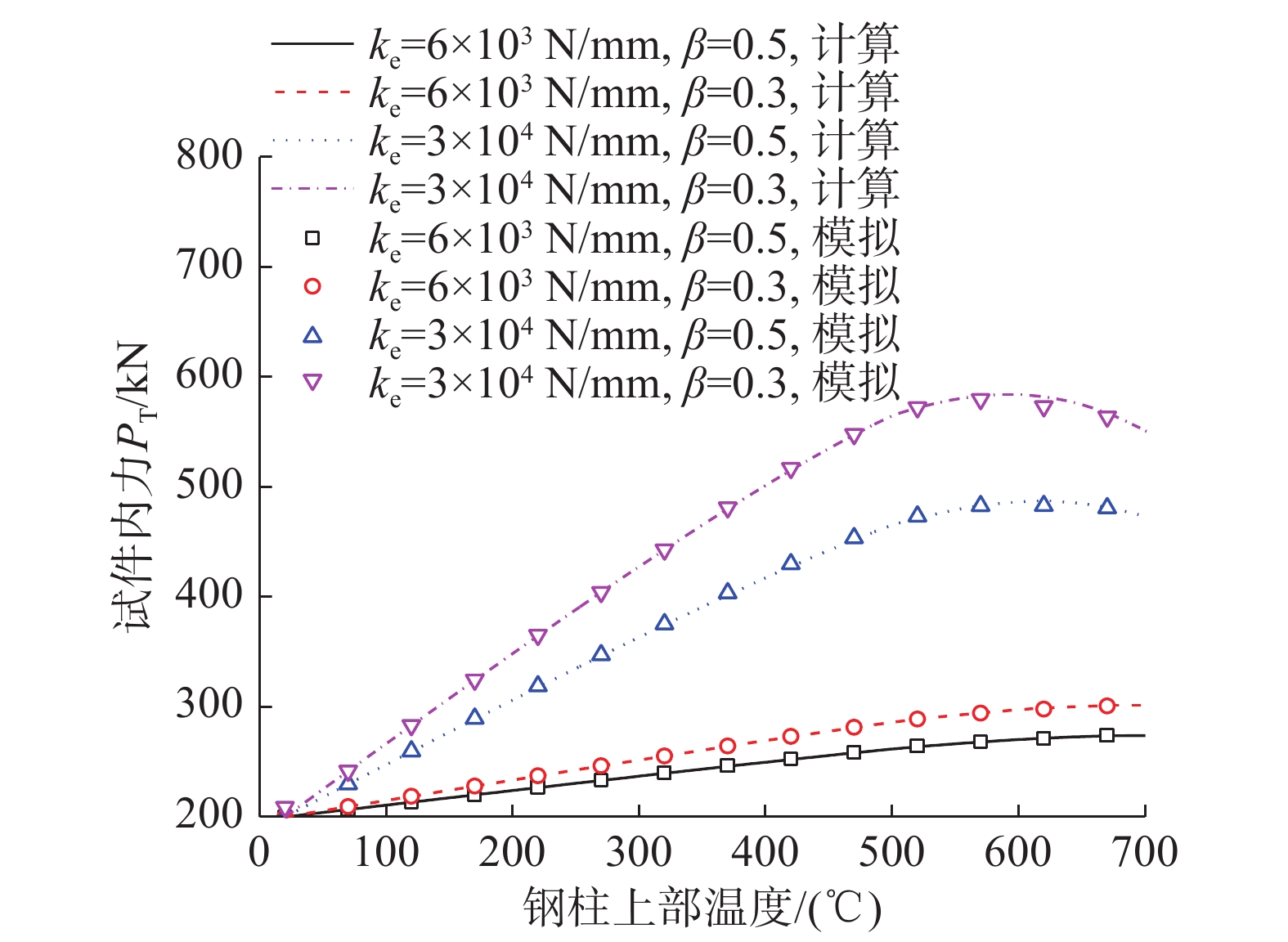
为了验证内力计算公式的准确性，本研究建立了4个数值分析模型，数值模型采用梁单元建模。钢柱的横截面为箱型截面，面积为3000 mm²，长度为3300 mm，柱端轴向约束刚度分别为k_e=6000 N/mm和30 000 N/mm，初始荷载大小为P₀=200 kN，假定其下层受热长度系数分别为β=0.5和β=0.3，且下层的温度始终为常温，上层的温度则由常温增大到700 ℃。材料在常温下弹性模量为210 GPa，高温下弹性模量折减系数取值参考欧洲规范EN 1993-1-2^[22]，热膨胀系数为1.4×10⁻⁵。图9对比了理论计算方法与数值模拟结果，可以看出本文建立的约束柱在不均匀温度下的内力计算公式是较为精确的。

图 9 内力温度曲线

Figure 9. Internal force versus temperature curves

下载: 全尺寸图片幻灯片

5 结论

本文研究了两端铰接钢柱在不均匀温度分布下的弹性屈曲荷载，首先，基于能量法推导了在一般场模型火灾工况下钢柱弹性屈曲荷载的通解，然后，将该通解应用于简化的双区域火灾模型中计算弹性屈曲荷载。通过对比能量法计算结果，平衡微分方程计算推导结果以及数值模拟结果，验证了本文能量法推导过程的正确性。研究结果表明纵向的不均匀温度分布对于试件的弹性屈曲荷载影响严重，若忽略该影响会导致计算构件高温下承载能力偏于保守，例如，在受火长度与未受火长度等长的情况下，如果忽略温度的纵向不均匀分布，当上下区域温差较大时，弹性临界荷载的相对计算误差甚至可达到37%。因此，在基于性能化的抗火设计中有必要考虑纵向不均匀温度分布的影响。

另外，通过对能量法计算结果的误差分析，发现在大多数情况下其计算误差均小于1%，只有当0.1≤α_E≤0.2以及0.6≤β≤0.8时，能量法计算结果误差最大达到了14%，因此，本研究通过列表的方式给出了在该区间时精确解，在实际使用时可以采用插值的方法确定屈曲荷载。最后，本文将不均匀温度分布与轴向约束作用相互耦合，提出约束柱的屈曲荷载计算方法，并且与数值模拟结果进行了对比，验证了内力计算过程的准确性。

图 1 双区域火灾模型示意图

Figure 1. Schematic diagram of two-zone fire model

下载: 全尺寸图片幻灯片

图 2 纵向不均匀温度分布钢柱计算模型

Figure 2. Calculation model of a steel column with longitudinally non-uniform temperature

下载: 全尺寸图片幻灯片

图 3 不均匀温度简化示意图

Figure 3. Simplified diagram of non-uniform temperature distribution

下载: 全尺寸图片幻灯片

图 4 双区域火灾模型整体屈曲示意图

Figure 4. Global buckling of steel column in two-zone fire model

下载: 全尺寸图片幻灯片

图 5 系数χ的精确解与近似解对比

Figure 5. Comparison between exact solution and approximate solution of the coefficient χ

下载: 全尺寸图片幻灯片

图 6 系数χ的精确解，近似解与有限元模拟对比

Figure 6. Comparison between exact solution, approximate solution and finite element simulation of the coefficient χ

下载: 全尺寸图片幻灯片

图 7 P_cr-uni/P_cr在不同α_E和β下的取值

Figure 7. Value of the P_cr-uni/P_cr at different α_E and β

下载: 全尺寸图片幻灯片

图 8 轴向约束柱在高温下的分析模型

Figure 8. Analytical model of axially restrained column at elevated temperatures

下载: 全尺寸图片幻灯片

图 9 内力温度曲线

Figure 9. Internal force versus temperature curves

下载: 全尺寸图片幻灯片

表 1 不均匀升温弹性屈曲荷载系数表达式

Table 1 Expression of elastic buckling load coefficient under non-uniform temperature

待定系数	系数表达式
A₁	${A_1} = - \displaystyle\int_0^l {\dfrac{ { {\pi ^2} } }{ { {l^2} } }\sin \dfrac{ {\pi x} }{l}\sin \dfrac{ {\pi x} }{l} } {\rm{d}}x = - \dfrac{ { {\pi ^2} } }{ {2l} }$
A₂	${A_2} = - \displaystyle\int_0^l {\dfrac{ { {\pi ^2} } }{ { {l^2} } }\sin \dfrac{ {\pi x} }{l}\sin \dfrac{ {2\pi x} }{l} } {\rm{d}}x = 0$
B₁	${B_1} = \displaystyle\int_0^l {\dfrac{ { { {\sin }^2}\dfrac{ {\pi x} }{l} } }{ {E(x)I} } } {\rm{d}}x$
B₂	${B_2} = \displaystyle\int_0^l {\dfrac{ {\sin \dfrac{ {\pi x} }{l}\sin \dfrac{ {2\pi x} }{l} } }{ {E(x)I} } } {\rm{d}}x$
C₁	${C_1} = - \displaystyle\int_0^l {\dfrac{ {4{\pi ^2} } }{ { {l^2} } }\sin \dfrac{ {2\pi x} }{l}\sin \dfrac{ {\pi x} }{l} } {\rm{d}}x = 0$
C₂	${C_2} = - \displaystyle\int_0^l {\dfrac{ {4{\pi ^2} } }{ { {l^2} } }\sin \dfrac{ {2\pi x} }{l}\sin \dfrac{ {2\pi x} }{l} } {\rm{d}}x = - \dfrac{ {2{\pi ^2} } }{l}$
D₁	${D_1} = \displaystyle\int_0^l {\dfrac{ {\sin \dfrac{ {2\pi x} }{l}\sin \dfrac{ {\pi x} }{l} } }{ {E(x)I} } } {\rm{d}}x = {B_2}$
D₂	${D_2} = \displaystyle\int_0^l {\dfrac{ { { {\sin }^2}\dfrac{ {2\pi x} }{l} } }{ {E(x)I} } } {\rm{d}}x$

下载: 导出CSV

表 2 χ在不同的α_E和β取值情况下的取值表(精确解)

Table 2 Value of the χ at different α_E and β (exact solution)

上下层弹性模量比例系数α_E	下层受热长度系数β
上下层弹性模量比例系数α_E	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
0.1	0.101	0.104	0.113	0.129	0.159	0.213	0.317	0.551	0.926	1.000
0.2	0.201	0.207	0.223	0.253	0.303	0.390	0.541	0.782	0.971	1.000
0.3	0.301	0.310	0.331	0.369	0.433	0.534	0.690	0.876	0.984	1.000
0.4	0.401	0.411	0.435	0.478	0.548	0.651	0.788	0.922	0.989	1.000
0.5	0.502	0.512	0.537	0.581	0.649	0.743	0.855	0.949	0.993	1.000
0.6	0.602	0.611	0.635	0.677	0.739	0.818	0.902	0.967	0.996	1.000
0.7	0.701	0.710	0.731	0.767	0.817	0.878	0.937	0.979	0.997	1.000
0.8	0.801	0.808	0.824	0.85	0.886	0.926	0.963	0.988	0.998	1.000
0.9	0.901	0.904	0.913	0.928	0.947	0.967	0.983	0.995	0.999	1.000
1.0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000

下载: 导出CSV

表 3 χ在不同的α_E和β取值情况下的取值表(近似解)

Table 3 Value of the χ at different α_E and β (approximate solution)

上下层弹性模量比例系数α_E	下层受热长度系数β
上下层弹性模量比例系数α_E	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
0.1	0.101	0.104	0.114	0.130	0.160	0.218	0.346	0.629	0.941	1.000
0.2	0.201	0.208	0.224	0.254	0.304	0.396	0.566	0.813	0.974	1.000
0.3	0.301	0.310	0.332	0.370	0.434	0.540	0.705	0.888	0.985	1.000
0.4	0.402	0.412	0.436	0.479	0.549	0.655	0.797	0.927	0.990	1.000
0.5	0.502	0.512	0.538	0.582	0.650	0.746	0.859	0.951	0.994	1.000
0.6	0.602	0.612	0.636	0.678	0.739	0.819	0.904	0.968	0.996	1.000
0.7	0.701	0.710	0.731	0.767	0.817	0.878	0.937	0.979	0.997	1.000
0.8	0.801	0.808	0.824	0.851	0.886	0.927	0.963	0.988	0.998	1.000
0.9	0.901	0.904	0.913	0.928	0.947	0.967	0.984	0.995	0.999	1.000
1.0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000

下载: 导出CSV

参考文献(27)

[1]	YANG J J, SHI Y, WANG W Y, et al. Experimental and numerical studies on axially restrained cold-formed steel built-up box columns at elevated temperatures [J]. Journal of Constructional Steel Research, 2020, 171: 106143. doi: 10.1016/j.jcsr.2020.106143
[2]	李翔, 王卫永, 于克强. 高温下轴心受压高强Q690钢柱的局部稳定[J]. 建筑钢结构进展, 2021, 23(3): 54 − 63. doi: 10.13969/j.cnki.cn31-1893.2021.03.006 LI Xiang, WANG Weiyong, YU Keqiang. Local bucking of Q690 high-strength steel columns subjected to axial compression at elevated temperature [J]. Progress in Steel Building Structures, 2021, 23(3): 54 − 63. (in Chinese) doi: 10.13969/j.cnki.cn31-1893.2021.03.006
[3]	YANG J J, XIA Y, WANG W Y, et al. Fire resistance of axially restrained Q690 H-shaped welded steel columns: Test, simulation and design [J]. Journal of Constructional Steel Research, 2021, 177: 106413-1 − 106413-15. doi: 10.1016/j.jcsr.2020.106413
[4]	YANG J J, WANG W Y, SHI Y, et al. Experimental study on fire resistance of cold-formed steel built-up box columns [J]. Thin-Walled Structures, 2020, 147: 106564-1 − 106564-17. doi: 10.1016/j.tws.2019.106564
[5]	CULVER C G. Steel column buckling under thermal gradients [J]. Journal of the Structural Division, 1972, 92(8): 1853 − 1865. doi: 10.1061/JSDEAG.0003307
[6]	CAI J G, FENG J, ZHAO Y Z, et al. Stability of axially restrained steel columns under temperature action [J]. Science China Technological Sciences, 2010, 53(12): 3349 − 3355. doi: 10.1007/s11431-010-4108-z
[7]	王培军, 王晓. 截面温度不均匀受约束钢柱抗火性能试验研究与有限元分析[J]. 建筑结构学报, 2013, 34(3): 28 − 34. doi: 10.14006/j.jzjgxb.2013.03.018 WANG Peijun, WANG Xiao. Experimental and numerical studies on restrained steel columns with non-uniform temperature distribution across section in fire [J]. Journal of Building Structures, 2013, 34(3): 28 − 34. (in Chinese) doi: 10.14006/j.jzjgxb.2013.03.018
[8]	XU L, ZHUANG Y. Storey stability of unbraced steel frames subjected to non-uniform elevated temperature distribution [J]. Engineering Structures, 2014, 62/63: 164 − 173. doi: 10.1016/j.engstruct.2014.01.039
[9]	BECKER R. Structural behavior of simple steel structures with non-uniform longitudinal temperature distributions under fire conditions [J]. Fire Safety Journal, 2002, 37(5): 495 − 515. doi: 10.1016/S0379-7112(02)00009-7
[10]	陈驹, 金伟良. 高强冷弯薄壁卷边槽钢柱在高温下的性能[J]. 工程力学, 2009, 26(12): 167 − 174. CHEN Ju, JIN Weiliang. Behaviour of high strength cold-formed steel columns under elevated temperatures [J]. Engineering Mechanics, 2009, 26(12): 167 − 174. (in Chinese)
[11]	YANG J J, XU L, SHI Y, et al. Experimental and analytical study of flexural buckling of cold-formed steel quadruple-limb built-up box columns [J]. Journal of Structural Engineering, 2022, 148(1): 04021228. doi: 10.1061/(ASCE)ST.1943-541X.0003193
[12]	黄丽华, 史婷伟, 徐嘉. 薄壁槽形截面压杆弹性整体屈曲数值计算研究[J]. 建筑钢结构进展, 2020, 22(2): 11 − 17. doi: 10.13969/j.cnki.cn31-1893.2020.02.002 HUANG Lihua, SHI Tingwei, XU Jia. Numerical study on the elastic overall buckling of thin-walled channel compressive members [J]. Progress in Steel Building Structures, 2020, 22(2): 11 − 17. (in Chinese) doi: 10.13969/j.cnki.cn31-1893.2020.02.002
[13]	杨竞杰, 王卫永. 高温蠕变对冷弯薄壁型钢柱抗火性能的影响[J]. 建筑钢结构进展, 2021, 23(7): 67 − 75. doi: 10.13969/j.cnki.cn31-1893.2021.07.008 YANG Jingjie, WANG Weiyong. The influence of high temperature creep on the fire resistance of cold-formed steel columns [J]. Progress in Steel Building Structures, 2021, 23(7): 67 − 75. (in Chinese) doi: 10.13969/j.cnki.cn31-1893.2021.07.008
[14]	罗霞, 韦建刚, 杨艳, 等. 高强钢管UHSC轴压柱整体稳定性能研究[J]. 工程力学, 2022, 39(1): 151 − 163. doi: 10.6052/j.issn.1000-4750.2020.12.0901 LUO Xia, WEI Jiangang, YANG Yan, et al. Study on the overall buckling of ultra-high strength concrete (UHSC) filled high strength steel tube columns under axial load [J]. Engineering Mechanics, 2022, 39(1): 151 − 163. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.12.0901
[15]	杜辉波, 程欣, 张超, 等. 薄柔H形截面双向压弯钢构件极限承载力研究[J]. 工程力学, 2022, 39(9): 191 − 203. doi: 10.6052/j.issn.1000-4750.2021.05.0390 DU Huibo, CHENG Xin, ZHANG Chao, et al. Study on ultimate bearing capacity of biaxial compression-bending steel members with thin and slender H-shaped section [J]. Engineering Mechanics, 2022, 39(9): 191 − 203. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.05.0390
[16]	范浩, 王新, 董卫国, 等. 基于屈曲模态的弹性压弯构件平面内二阶弯矩计算[J]. 工程力学, 2022, 39(2): 37 − 50. doi: 10.6052/j.issn.1000-4750.2020.12.0900 FAN Hao, WANG Xin, DONG Weiguo, et al. Calculation of second-order in-plane bending moment of elastic compression-bending members based on buckling modes [J]. Engineering Mechanics, 2022, 39(2): 37 − 50. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.12.0900
[17]	秦剑, 万建成, 夏拥军, 等. 轴心受压开口薄壁构件弹塑性屈曲荷载的统一计算方法[J]. 建筑结构学报, 2017, 38(5): 143 − 148. doi: 10.14006/j.jzjgxb.2017.05.018 QIN Jian, WAN Jiancheng, XIA Yongjun, et al. Integrated calculation method for elasto-plastic buckling load of thin-walled axial compression member with open cross-section [J]. Journal of Building Structures, 2017, 38(5): 143 − 148. (in Chinese) doi: 10.14006/j.jzjgxb.2017.05.018
[18]	AISI S100-07, North American specification for the design of cold-formed steel structural members [S]. Washington DC: American Iron and Steel Institute, 2007.
[19]	REN C, ZHANG P, YAN S, et al. Analysis and design of cold-formed steel storage rack uprights under localised fires [J]. Structures, 2020, 27: 2082 − 2095. doi: 10.1016/j.istruc.2020.08.022
[20]	DEMBSEY N A, PAGNI P J, WILLIAMSON R B. Compartment fire near-field entrainment measurements [J]. Fire Safety Journal, 1995, 24(4): 383 − 419. doi: 10.1016/0379-7112(95)00030-5
[21]	REMESH K, TAN K H. Field model analysis and experimental assessment of fire severity and smoke movement in a partitioned and a non-partitioned dwelling unit [J]. Journal of Fire Sciences, 2006, 24(5): 365 − 391. doi: 10.1177/0734904106061524
[22]	EN 1993-1-2, Eurocode 3: Design of steel structures- Part 1-2: General rules-structural fire design [S]. Brussels: European Committee for Standardization, 2005.
[23]	AL-AZZANI H, YANG J J, SHARHAN A, et al. A practical approach for fire resistance design of restrained high-strength Q690 steel beam considering creep effect [J]. Fire Technology, 2021, 57(4): 1683 − 1706. doi: 10.1007/s10694-020-01078-7
[24]	SIMÃO P D, RODRIGUES J P C, OLIVEIRA R L G. Simple analytical models for restrained steel columns in fire [J]. Engineering Structures, 2021, 236: 112119. doi: 10.1016/j.engstruct.2021.112119
[25]	DING R M, FAN S G, CHEN G Q, et al. Fire resistance design method for restrained stainless steel H-section columns under axial compression [J]. Fire Safety Journal, 2019, 108: 102837. doi: 10.1016/j.firesaf.2019.102837
[26]	POURNAGHSHBAND A, AFSHAN S, FOSTER A S J. Structural fire performance of axially and rotationally restrained stainless steel columns [J]. Thin-Walled Structures, 2019, 137: 561 − 572. doi: 10.1016/j.tws.2019.01.010
[27]	TIMOSHENKO S P, GERE J M. Theory of elastic stability [M]. New York: McGraw-Hill, 1961: 138.

施引文献(10)

期刊类型引用(4)

1.	于红, 任行, 雷迪豪. 基于灰色关联和神经网络的剩余电流预测模型. 机电工程技术. 2025(11) 百度学术
2.	孙祥涛，俞承序，杨霞，马彬，孔庆钊. 基于同步挤压小波变换和超声导波的锈蚀钢筋直径评估方法研究. 应用基础与工程科学学报. 2025(01): 50-59 . 百度学术
3.	孔祥清，张明亮，康然，赵元浩. 机器学习用于预测混凝土性能的研究进展. 科学技术与工程. 2025(05): 1764-1773 . 百度学术
4.	范明辉，杨普新，李薇，任文渊，马驰骋. 高性能混凝土的早期抗压强度预测和极值寻优. 硅酸盐通报. 2024(12): 4339-4349 . 百度学术

其他类型引用(6)

资源附件(0)

图(9) / 表(3)

计量

文章访问数: 191
HTML全文浏览量: 89
PDF下载量: 58
被引次数: 10

1 常见的温度分布模型
2 场模型火灾中杆件整体屈曲弹性屈曲荷载
3 双区域模型火灾中普通杆件整体屈曲弹性屈曲荷载
3.1 弹性屈曲荷载精确解
3.2 弹性屈曲荷载近似解
4 轴向约束钢柱整体屈曲弹性屈曲荷载
5 结论

纵向非均匀温度下钢柱弹性屈曲荷载

作者简介: 杨竞杰(1993−)，男，重庆人，博士生，主要从事钢结构抗火研究(E-mail: jingjieyoung@foxmail.com)

通讯作者: 王卫永(1982−)，男，河南人，教授，博士，主要从事钢结构抗火研究(E-mail: wywang@cqu.edu.cn)

计量

出版历程

ELASTIC BUCKLING LOAD OF STEEL COLUMN UNDER LONGITUDINAL NON-UNIFORM TEMPERATURE

1 常见的温度分布模型

2 场模型火灾中杆件整体屈曲弹性屈曲荷载

3 双区域模型火灾中普通杆件整体屈曲弹性屈曲荷载

3.1 弹性屈曲荷载精确解

3.2 弹性屈曲荷载近似解

4 轴向约束钢柱整体屈曲弹性屈曲荷载

5 结论

期刊类型引用(4)

其他类型引用(6)

计量

出版历程

目录

1 常见的温度分布模型

2 场模型火灾中杆件整体屈曲弹性屈曲荷载

3 双区域模型火灾中普通杆件整体屈曲弹性屈曲荷载

3.1 弹性屈曲荷载精确解

3.2 弹性屈曲荷载近似解

4 轴向约束钢柱整体屈曲弹性屈曲荷载

5 结论

作者简介:
杨竞杰(1993−)，男，重庆人，博士生，主要从事钢结构抗火研究(E-mail: jingjieyoung@foxmail.com)

通讯作者:
王卫永(1982−)，男，河南人，教授，博士，主要从事钢结构抗火研究(E-mail: wywang@cqu.edu.cn)