ANALYSIS OF THE TEMPERATURE FIELD BASED ON RANDOM AGGREGATE FOR CRTS-II SLAB TRACK
-
摘要: 无砟轨道因温度作用产生的损伤会影响高速铁路运营的安全性，所以对其温度场的精确求解是重要的。该文为了获得细观尺度下无砟轨道温度场，基于混凝土随机骨料分布算法以及传热学原理建立细观尺度CRTSⅡ型轨道二维传热有限元模型。通过实测数据验证模型可靠性后，分析细观尺度轨道内部温度场时变规律和空间分布规律，并研究轨道板粗骨料最大粒径和粗骨料分布不均两个因素对轨道板温度场的影响。研究结果表明：不同时刻细观尺度轨道结构温度场随深度非线性变化；在轨道结构中心位置处等温线基本平行于地面，但在局部发生起伏；砂浆内热流方向多指向骨料所在位置，且优先通过粗骨料组成的通道进行传递；粗骨料最大粒径和不均匀分布两因素对轨道板中线不同深度的温度影响几乎可不计。Abstract: The slab track damage caused by thermal action will affect the high-speed railway operation safety, therefore, the exact solution about its temperature field is crucial. Based on the concrete random aggregate distribution algorithm and the heat transfer theory, develops a two-dimensional thermal transfer finite element model of the CRTSⅡ track at mesoscale to investigate the mesoscale temperature field. After the model’s reliability is confirmed by comparing the field measurements, the model is analyzed to determine the time-varying rule and spatial distribution rule of the internal temperature characteristics to the track at the mesoscale, and the two influence factors are the coarse aggregate maximum diameter and uneven distribution. The results show that the temperature field changes nonlinearly with depth at different time. The isotherm is generally parallel to the ground at the center of the track but fluctuates locally. The heat flux is preferentially transferred through the coarse aggregate passage, and its direction in the mortar points to the aggregates. The influence of the coarse aggregate maximum diameter and uneven distribution on the precast slab centerline temperature is almost negligible at different depths.
-
Keywords:
- slab track /
- random aggregate /
- heat transfer theory /
- finite element method /
- temperature field
-
CRTSⅡ型板式无砟轨道被我国广泛应用于京津、京沪、武广等高铁线路，与传统有砟轨道相比，其整体性和稳定性更好，但由于其独特的“连续体”结构所以受温度影响更加敏感[1]。无砟轨道在吸收太阳辐射和大气温度后产生整体温升和温度梯度并伴随翘曲变形进而导致不同结构层之间的离缝和连接区的其他损伤[2-3]。因此，研究自然环境下无砟轨道温度场有助于明确无砟轨道损伤机理并为铁路部门运营维护提供建议。
目前，国内外学者对无砟轨道结构的温度场研究多采用统计分析和理论分析两种方法。统计分析法基于现场实测数据，采用统计方法估算温度场[4-5]。理论分析法则大多采用传热学原理建立控制方程并以有限单元法求解温度场[6-7]。相对于统计分析法，理论分析法的结果更加丰富，能全面的反映无砟轨道在空间和时间上温度场变化。传统的宏观尺度传热有限元已被大量用于无砟轨道温度场模拟，但构成无砟轨道的材料混凝土本质上是一种多相非均质复合材料，其各项成分的传热学参数并不相同，采用宏观均质体来模拟会造成不可避免的误差。
最近迅速发展的基于“随机骨料算法”的细观尺度数值混凝土模型[8-9]则可以较好的解决这一问题。其首先生成混凝土细观几何结构随后分别定义不同成分的物理参数，以此合理的模拟多相材料的传热性能，进而对混凝土结构的温度场进行精确模拟[10]。
本文先采用传热学原理建立基于随机骨料算法的二维细观有限元传热模型，并通过实测数据验证模型的准确性。在分析完细观尺度温度场后，基于此模型以轨道板粗骨料最大粒径和骨料不均匀分布程度为影响因素，分析两种细观尺度因素对无砟轨道温度场的影响。
1 随机骨料模拟
CRTSⅡ型轨道采用的混凝土材料为典型的多相非均质结构，其中骨料形状、大小、含量等参数均影响混凝土的传热特性[11]。本文则采用随机骨料算法来计算其细观几何结构，该算法由多个随机数控制编写并根据既有文献[12-14]中的“生成区域网格划分”、“区域剔除”、“圆内接多边形骨料”、“圆心距离控制准则”等方法进行多边形骨料的生成与投放。随机骨料分布如图1所示，轨道板粗骨料最小粒径为5 mm，最大粒径为20 mm，支撑层粗骨料最小粒径为5 mm，最大粒径为31.5 mm。算法先通过随机数在目标区域内生成多边形粗骨料的中心坐标，以及服从富勒级配的粒径，再根据式(1)生成多边形骨料顶点角度，并以角度和粒径为基础计算对应顶点坐标。之后，对生成区域划分网格，并标记与多边形相交或重合的网格单元，以圆心距离公式判断多边形是否重合，不重合的多边形内网格单元被剔除，最终以多边形骨料累加面积是否超过实际骨料面积作为程序终止准则。
ai=360/n⋅(i−1)+360/n⋅[0.2+(0.8+0.2)⋅rand] (1) 式中：αi为圆心角；i为多边形角点顺时针序号；n为5~9的随机数(代表边数)；rand为0~1随机数。
2 传热学模型
2.1 轨道传热原理
无砟轨道结构在自然环境下的主要热源是太阳辐射，本文采用ASHRAE晴空模型[15]计算太阳辐射强度，太阳辐射总量Gt由三部分组成：垂直直射辐射GND、天空散射辐射Gdθ和环境反射辐射GR，可表示为式(2)：
Gt=GND+Gdθ+GR (2) 晴天表面太阳直射辐射强度为式(3)：
GND=Aexp(B/sinβ)CN (3) 式中：GND/(W/m2)为太阳直射辐射强度；A为太阳常数，取值1353 W/m2；B为大气消光系数；β为太阳高度角(与纬度相关)；CN为大气清洁度。晴天表面太阳散射辐射强度为Gdθ=CGND，C为平面上散射辐射与垂直入射辐射的比值。晴天表面太阳反射辐射强度为GR=GtH ρg，GR/(W/m2)为反射到表面上的辐射量，GtH/(W/m2)为地面总辐射量(直射加散射)，ρg为地面的辐射反射率。
根据统计规律发现晴天大气温度具有一定的规律性可通过经验公式进行拟合，本文采用文献[16]中使用的双正弦组合函数来模拟大气温度Ta变化，表示见式(4)：
Ta=˜Ta+¯Ta[0.96sinw(t−9)+0.146sin2w(t−9)] (4) 式中：
˜Ta=(Ta-max+Ta-min)/2 为日平均气温；¯Tα=(Ta-max−Ta-min)/2 为日气温差之半，Ta-max为日最高气温，Ta-min为日最低气温；t/h为时间；w为频率取2π/24。轨道结构暴露于大气环境中，外表面根据牛顿冷却公式与空气进行对流热交换，对流传热系数h采用文献[17]中经验式(5)：h={4.0v+5.6,v⩽ (5) 式中，v/(m/s)为日均风速。综上所述，轨道结构的表面热流包含直接短波太阳辐射、其他表面反射的短波太阳辐射、大气层长波辐射、表面自身向外的长波辐射以及与周围大气的对流换热，具体的热流边界条件见式(6)：
- {k_i}{\left. {\frac{{\partial T}}{{\partial {\boldsymbol{n}}}}} \right|_s} = {a_{\rm{s}}}( {{F_{\rm{a}}}{G_{\rm{t}}} + {F_{{\rm{b,c}}}}{G_{\rm{b}}}} ) + \varepsilon \sigma ( {T_{{\rm{sky}}}^4 - T_{\rm{s}}^4} ) + h({T_{\rm{s}}} - {T_{\rm{a}}}) (6) 式中：T/K为混凝土温度；ki/(W/m·K)为第i层导热系数；as为表面太阳辐射吸收率；Fa为表面对直接太阳辐射的角系数；Gb为各表面间反射的短波太阳辐射；Fb,c为各表面间辐射的角系数；ε为表面长波辐射发射率；σ为斯蒂芬-玻尔兹曼常数5.67×10−8 W/(m2·K4)；Tsky为大气层有效天空温度，其值为Ta−6；Ts为轨道结构表面温度。在计算轨道表面各面之间的相互反射辐射时，表面A1对表面A2的角系数F1,2，见式(7)：
{F_{1,2}} = \frac{1}{{{A_1}}}\iint\limits_{{A_1}{A_2}} {\frac{{\cos {\theta _1}\cos {\theta _2}}}{{\pi {r^2}}}{{\rm{d}}} {A_1}{{\rm{d}}} {A_2}} (7) 式中：A1、A2分别为两面的表面积；θ1和θ2分别为两面的法线与连线间的夹角；r为两面间的距离。在轨道结构内部，温度满足二维无内热源热传导瞬态方程式(8)：
\frac{{\partial {T_i}}}{{\partial t}} = \frac{{{k_i}}}{{{\rho _i}{c_i}}}\left( {\frac{{{\partial ^2}{T_i}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{T_i}}}{{\partial {y^2}}}} \right){\text{ }},\; {i{\text{ = 1,2,3,4}}} (8) 式中：ρi/(kg/m3)为第i层密度；ci/(J/(kg·K))为第i层比热容。
2.2 有限元模型及验证
CRTSⅡ型无砟轨道是纵向连续结构，可认为其沿长度方向温度无变化，故将其简化为二维平面传热问题。建立的细观尺度传热有限元模型如图2所示，包括预制轨道板、CA砂浆、支撑层、基床表层，随机骨料算法则应用于轨道板和支撑层。模型所有与空气接触的外表面都考虑对流换热和吸收热辐射，基床表层底面采用绝热边界，且忽略各层之间的接触热阻。模型的混凝土材料中粗骨料和砂浆分别赋予不同的物理属性，所有的几何及传热学参数[1-2, 10]见表1。模型中的太阳辐射方向垂直于地面，计算时长为48 h。模型初始温度场通过迭代计算获得，即首先假定上午0:00时轨道初始温度场为室温300 K，将计算得到的48 h后温度场结果再次设定为初始温度场，经多次迭代后模型结果稳定，最终将稳定后48 h的温度场结果作为最终的初始温度场使用，且计算其之后的48 h轨道温度场并以此为研究对象。
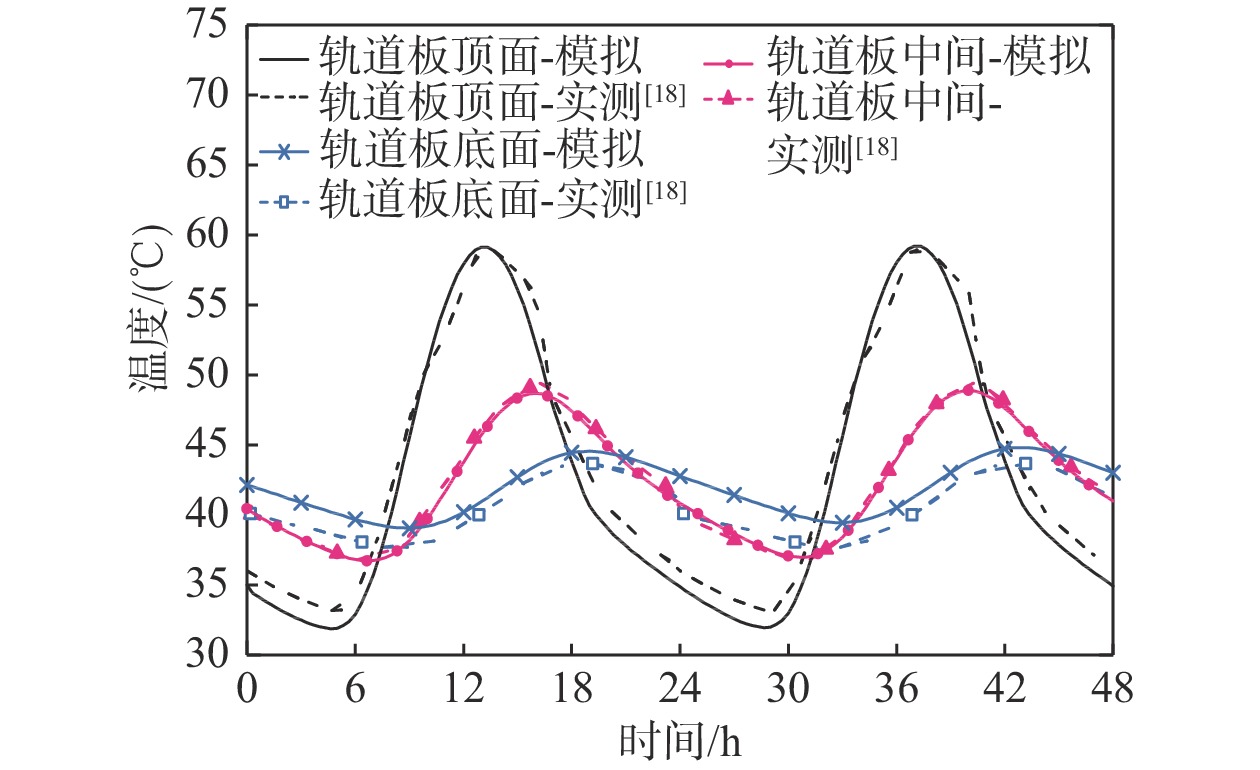
表 1 模型几何及材料参数Table 1. Model geometry and material parameters结构名称 几何参数/m 密度/(kg/m3) 比热容/(J/(kg·K)) 导热系数/(W/(m·K)) 太阳辐射吸收率 长波辐射吸收率 高度 上顶面宽度 下顶面宽度 轨道板 0.20 2.55 2.55 − − − − − 支撑层 0.30 2.95 3.25 − − − − − 轨道板骨料 − − − 2680 800 2.0 − − 支撑层骨料 − − − 2680 830 2.0 − − 水泥砂浆 − − − 1860 750 0.6 0.57 0.88 CA砂浆 0.03 2.55 2.55 2300 850 0.7 0.57 0.88 基床表层 0.40 8.60 9.40 2050 1200 1.0 0.50 0.88 为了与文献[18]实测数据对比验证模型的正确性，轨道结构采用的气象数据地点为上海市(北纬31°29')，具体时间为2017年7月21日。当日最高气温为40 ℃，最低气温为30 ℃，大气消光系数为0.46，散射辐射与入射辐射比值为0.11，地面辐射反射率为0.08。在图3中绘制细观尺度轨道结构模型的温度场随时间变化数据和文献[18]实测数据。
![]()
图 3 轨道板中线不同深度处温度Figure 3. The precast slab centerline temperature at different depths从图3中可以看出细观尺度轨道模型与文献[18]的数据变化趋势相同、数值接近，误差在容许范围内。
3 混凝土细观参数影响分析
基于细观尺度无砟轨道传热有限元模型进行48 h的温度场分析，发现如下规律。从图3中可知，轨道板中线表面温度从上午6:00时开始增长，到下午14:00时温度达到峰值58 ℃，次日凌晨4:00时温度达到最低值33 ℃，且随着深度的增加温度变化出现峰值的减小与峰值对应时间的延迟。图4则表明随机骨料轨道模型温度沿纵向分布是非线性的，在轨道板顶面0.6 m以下温度基本无变化，说明在本文气象温度环境下，轨道结构内的热量大多数无法传递到基床表层。
将轨道板、CA砂浆和支撑层下午14:00时右半侧平面温度数据绘制于图5。从中可知，此时轨道结构的温度整体上外热内冷，在轨道结构的中心位置等温线基本平行于地面，取轨道板中间10 cm×5 cm的长方形区域放大发现随机骨料模型的等温线在局部会发生细小的起伏，原因是随机骨料模型中粗骨料与水泥砂浆的导热性能不同，且粗骨料分布位置与形状随机，进而影响温度分布。
具体分布上，轨道板及支撑层外露上表面温度最高，其次为轨道板、CA砂浆和支撑层侧面。原因是轨道板上表面与支撑层外露上表面的外法线方向与太阳辐射方向平行，直接接受太阳辐射，且其对太阳辐射的角系数接近1，而轨道板、CA砂浆和支撑层侧面的外法线方向与太阳辐射方向存在90º、90º、约60º的夹角，所以轨道板及CA砂浆侧面对太阳辐射的角系数为0，其则主要接收轨道结构其他表面的反射太阳辐射，故温度最低。相比之下，支撑层侧面能够接收直接太阳辐射，但其对太阳辐射的角系数小于1，故温度居中。
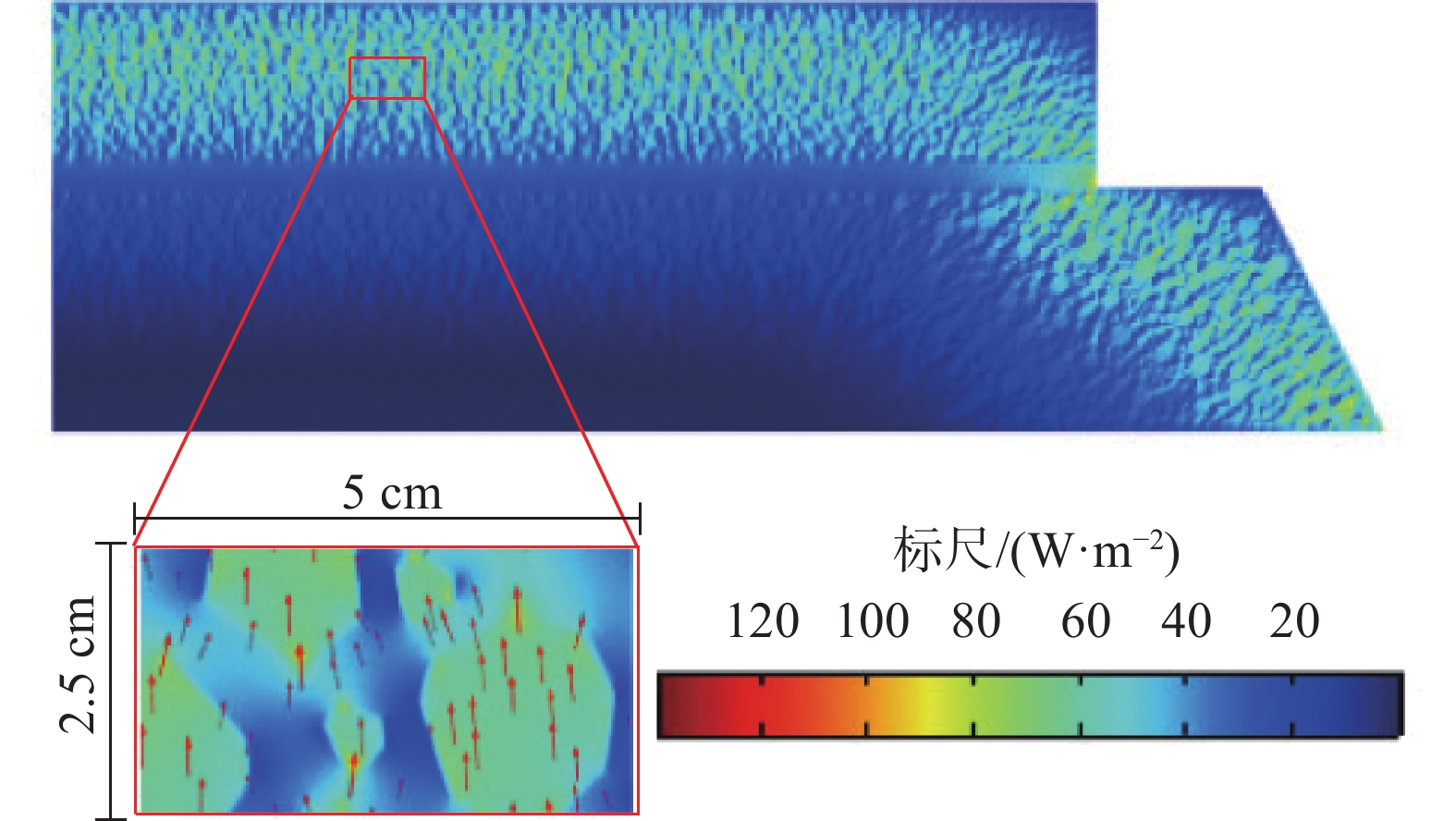
上午6:00时轨道结构右半侧热流平面分布见图6，从图6中可以看出细观尺度轨道模型的热流大小在局部分布不均，且方向不统一。取轨道板中间5 cm×2.5 cm的长方形区域放大发现热流向量出现较多的水平分量，方向偏向粗骨料，且热流数值在粗骨料处明显大于水泥砂浆处。这种现象的原因是粗骨料的导热系数大于水泥砂浆导，故而热流优先通过粗骨料组成的通道进行传递。
3.1 粗骨料最大粒径
保持轨道板配合比(水泥：480 kg，砂：680 kg，石子：1080 kg，水：140 kg)和骨料粒径服从富勒级配曲线两个条件不变，以粗骨料最大粒径为影响因素，研究其对轨道板温度和热流的影响，其中最大粒径取值范围为15 mm、20 mm、25 mm。
从图7中可知，粗骨料最大粒径的改变对轨道板中心线处不同深度的温度时程曲线影响几乎可不计。原因是在式(8)热传导方程中温度变量T是低阶变量，相对于式(9)中温度梯度
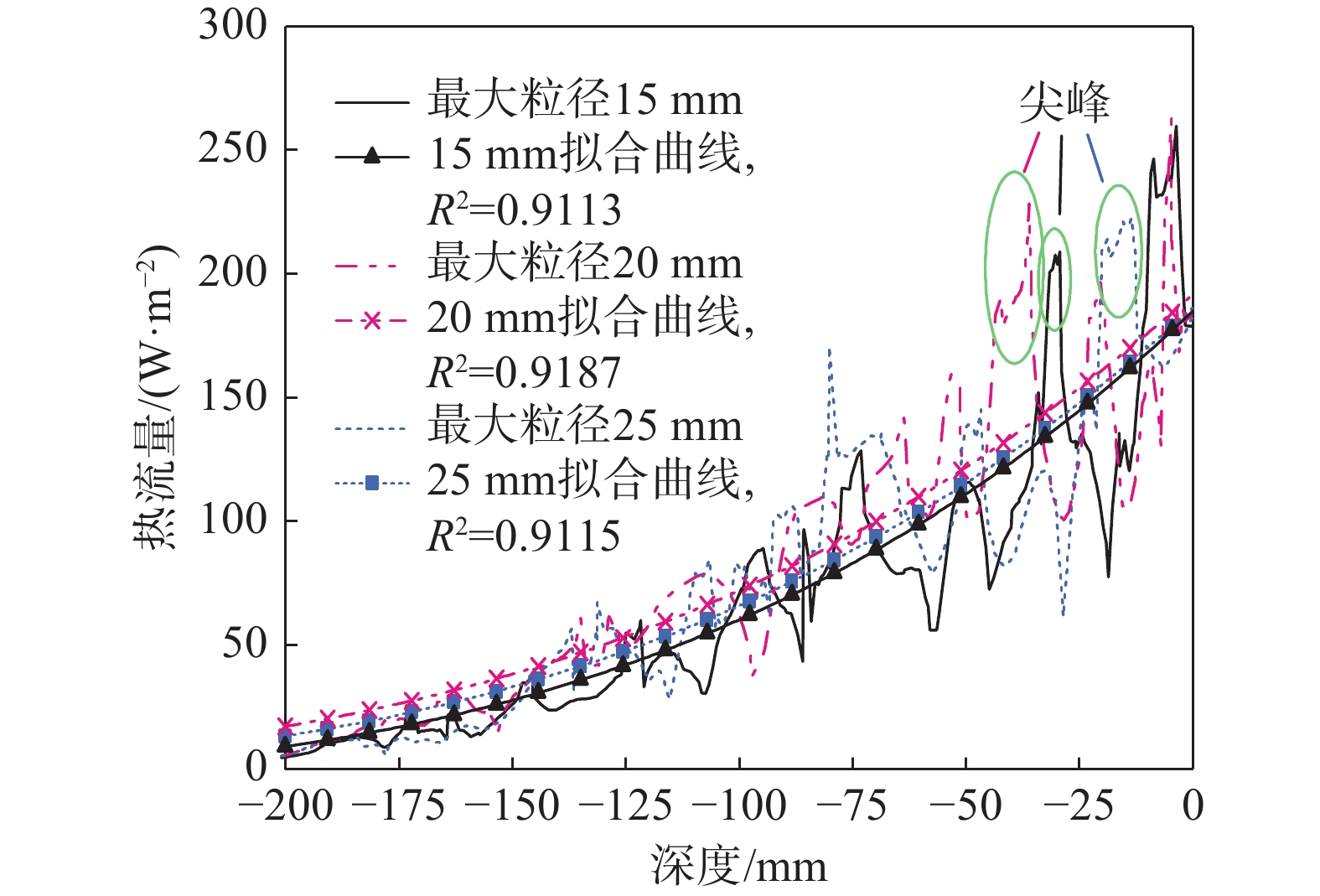
{{\partial {T_i}} \mathord{\left/ {\vphantom {{\partial {T_i}} {\partial x}}} \right. } {\partial x}} 和热流qi等高阶变量其对导热系数ki的改变并不特别敏感，而且改变粗骨料最大粒径并不显著改变粗骨料占混凝土中的整体体积。{q_i} = - {k_i}\frac{{\partial {T_i}}}{{\partial x}}{\text{ }} ,\;{i{\text{ = 1,2,3,4}}} (9) ![]()
图 7 粗骨料最大粒径对轨道板中线温度的影响Figure 7. The influence of the coarse aggregate maximum diameter on the precast slab centerline temperature选取不同粗骨料最大粒径对应的轨道板中线上午12:00时热流量数据绘制于图8。从图8中可知，粗骨料最大粒径的改变对轨道板中心线处热流量的影响明显。因为粗骨料是随机均匀分布的，所以热流量曲线的起伏也是随机的，但随着粗骨料最大粒径的增大，热流量曲线中尖峰的宽度变宽。同时，对不同最大粒径对应的热流量曲线进行数据拟合并计算相应的决定系数R2，发现所有的拟合曲线趋势基本相同，说明粗骨料最大粒径对轨道板热流量的影响主要集中在局部但并不改变其整体趋势。
![]()
图 8 粗骨料最大粒径对轨道板中线12:00时热流量的影响Figure 8. The influence of the coarse aggregate maximum diameter on the precast slab centerline heat flux at 12:00 am3.2 粗骨料分布不均
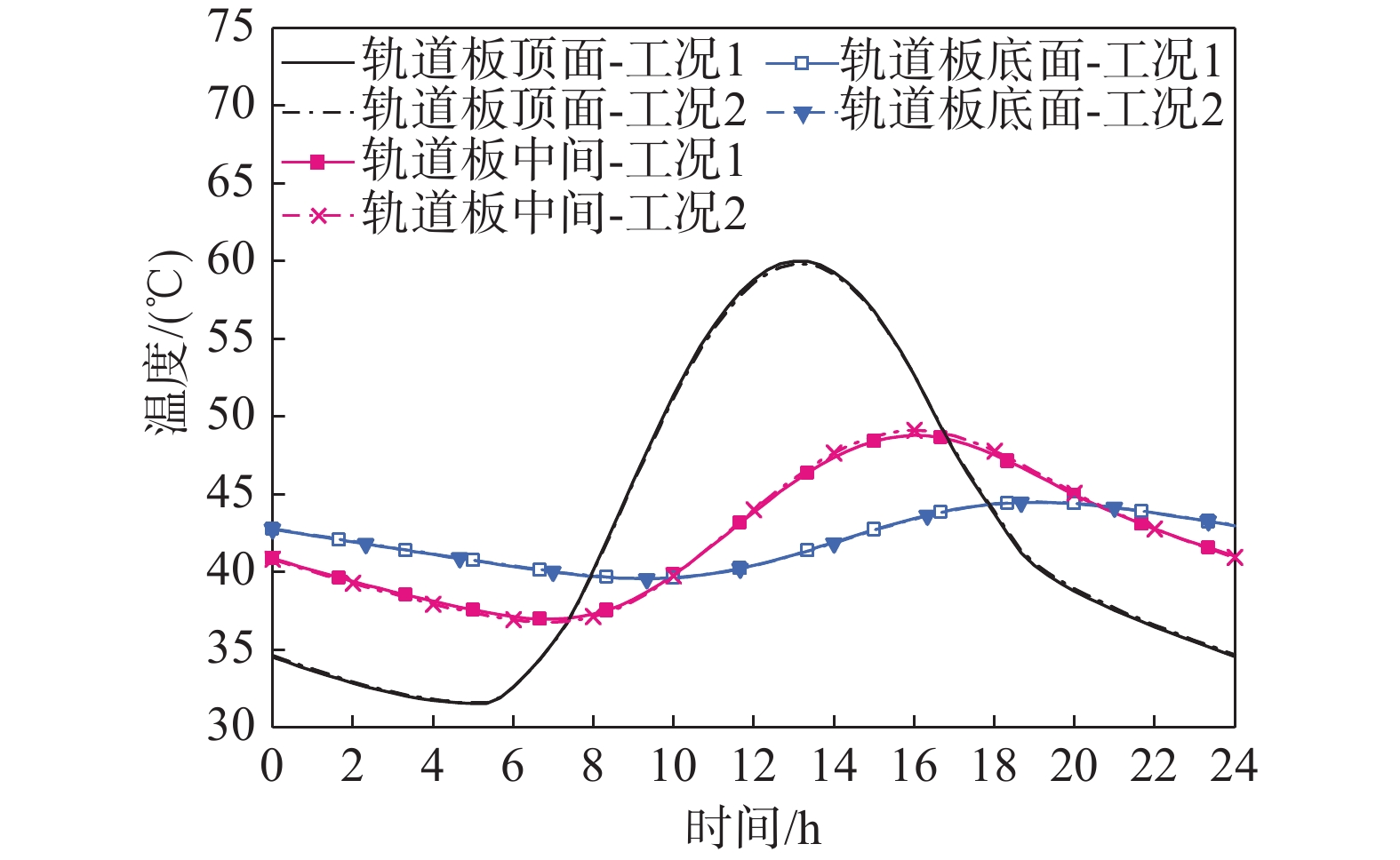
在轨道结构施工中混凝土振捣不充分而导致的骨料分布不均是存在的。本文设计两种工况来模拟轨道板内粗骨料的不均匀分布：第一种工况是轨道板上半部分粗骨料最大粒径为15 mm，下半部分粗骨料最大粒径为20 mm；第二种工况是轨道板上半部分粗骨料最大粒径为20 mm，下半部分粗骨料最大粒径为15 mm。两种工况的所有粗骨料级配皆满足富勒曲线。将不同工况下轨道板中线不同深度的温度数据绘制于图9。
![]()
图 9 骨料不均匀分布对轨道板中线温度的影响Figure 9. The influence of the aggregate unevenness distribution on the precast slab centerline temperature从图9中可知，粗骨料不均匀分布对轨道板中心线处不同深度的温度时程曲线影响几乎可不计，其原因同3.1节中粗骨料最大粒径对温度的影响相同。
将不同工况对应的轨道板中线上午12:00时热流量数据绘制于图10。从图10中可知不均匀的粗骨料分布依旧不改变轨道板内热流量的整体分布趋势，但对局部位置的起伏影响较大，随着指定区域内粗骨料最大粒径的变小热流量曲线尖峰宽度变窄，反之则变宽。
![]()
图 10 骨料不均匀分布对轨道板中线热流量的影响Figure 10. The influence of the aggregate unevenness distribution on the precast slab centerline heat flux4 结论
本文通过细观尺度CRTSⅡ型轨道传热模型研究了轨道板及支撑层材料非均质对温度场的影响，模型验证证明其能较真实的反映轨道结构夏季服役状态下的温度特性，得到的主要结论如下：
(1)轨道结构内粗骨料与水泥砂浆导热特性的不同对其内部的温度场有明显的影响，主要表现为等温线在局部出现波动以及热流方向的非一致性。
(2)轨道结构温度沿纵向分布是非线性的，轨道结构中心位置处等温线基本平行于地面，但在局部会发生细小的起伏。
(3)轨道结构表面的角系数不同对太阳辐射吸收有重要影响，进而影响温度场分布，说明CRTSⅡ型轨道的几何形状对温度场的影响明显。
(4)轨道中热流方向是非一致的，较多指向骨料所在位置，且优先通过粗骨料组成的通道进行传递。
(5)粗骨料最大粒径和本文设计的粗骨料不均匀分布工况对轨道板中线不同深度的温度影响几乎可不计，但对热流量的影响明显。
-
![]()
图 3 轨道板中线不同深度处温度
Figure 3. The precast slab centerline temperature at different depths
![]()
图 7 粗骨料最大粒径对轨道板中线温度的影响
Figure 7. The influence of the coarse aggregate maximum diameter on the precast slab centerline temperature
![]()
图 8 粗骨料最大粒径对轨道板中线12:00时热流量的影响
Figure 8. The influence of the coarse aggregate maximum diameter on the precast slab centerline heat flux at 12:00 am
![]()
图 9 骨料不均匀分布对轨道板中线温度的影响
Figure 9. The influence of the aggregate unevenness distribution on the precast slab centerline temperature
![]()
图 10 骨料不均匀分布对轨道板中线热流量的影响
Figure 10. The influence of the aggregate unevenness distribution on the precast slab centerline heat flux
表 1 模型几何及材料参数
Table 1 Model geometry and material parameters
结构名称 几何参数/m 密度/(kg/m3) 比热容/(J/(kg·K)) 导热系数/(W/(m·K)) 太阳辐射吸收率 长波辐射吸收率 高度 上顶面宽度 下顶面宽度 轨道板 0.20 2.55 2.55 − − − − − 支撑层 0.30 2.95 3.25 − − − − − 轨道板骨料 − − − 2680 800 2.0 − − 支撑层骨料 − − − 2680 830 2.0 − − 水泥砂浆 − − − 1860 750 0.6 0.57 0.88 CA砂浆 0.03 2.55 2.55 2300 850 0.7 0.57 0.88 基床表层 0.40 8.60 9.40 2050 1200 1.0 0.50 0.88 
下载: 导出CSV
-
[1] SONG L, LIU H B, CUI C X, et al. Thermal deformation and interfacial separation of a CRTS II slab ballastless track multilayer structure used in high-speed railways based on meteorological data [J]. Construction and Building Materials, 2020, 237: 117528. doi: 10.1016/j.conbuildmat.2019.117528
[2] 钟阳龙, 高亮, 王璞, 等. 温度荷载下CRTS II型轨道板与CA砂浆界面剪切破坏机理[J]. 工程力学, 2018, 35(2): 230 − 238. doi: 10.6052/j.issn.1000-4750.2016.09.0753 ZHONG Yanglong, GAO Liang, WANG Pu, et al. Mechanism of interfacial shear failure between CRTSⅡ slab and ca mortar under temperature loading [J]. Engineering Mechanics, 2018, 35(2): 230 − 238. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.09.0753
[3] HUANG Y C, GAO L, ZHONG Y L, et al. Study on the damage evolution of the joint and the arching deformation of CRTS-II ballastless slab track under complex temperature loading [J]. Construction and Building Materials, 2021, 309: 125083. doi: 10.1016/j.conbuildmat.2021.125083
[4] 戴公连, 苏海霆, 闫斌, 等. 春季纵连板式无砟轨道非线性温度分布[J]. 华南理工大学学报(自然科学版), 2016, 44(2): 20 − 25, 32. DAI Gonglian, SU Haiting, YAN Bin, et al. Nonlinear temperature distribution of longitudinal plate-type Ballastless track in spring [J]. Journal of South China University of Technology (Natural Science Edition), 2016, 44(2): 20 − 25, 32. (in Chinese)
[5] 戴公连, 杨凌皓, 朱俊樸, 等. 桥上CRTS Ⅱ型板式无砟轨道均匀温度研究[J]. 湖南大学学报(自然科学版), 2017, 44(7): 136 − 142. DAI Gonglian, YANG Linghao, ZHU Junpu, et al. Research on uniform temperature of CRTS Ⅱ Slab-type ballastless track on bridge [J]. Journal of Hunan University (Natural Sciences), 2017, 44(7): 136 − 142. (in Chinese)
[6] LIU S, CHEN X H, YANG J, et al. Numerical study and in-situ measurement of temperature features of asphalt supporting layer in slab track system [J]. Construction and Building Materials, 2020, 233: 117343. doi: 10.1016/j.conbuildmat.2019.117343
[7] 陈先华, 马丽莉, 蔡德钩. 含薄层沥青混凝土的CRTS Ⅲ型轨道结构温度场特性研究[J]. 铁道学报, 2019, 41(12): 89 − 95. doi: 10.3969/j.issn.1001-8360.2019.12.012 CHEN Xianhua, MA Lili, CAI Degou. Temperature field characteristics of CRTS Ⅲ ballastless track system inserted with thin asphalt concrete layer [J]. Journal of the China Railway Society, 2019, 41(12): 89 − 95. (in Chinese) doi: 10.3969/j.issn.1001-8360.2019.12.012
[8] JIN L, ZHANG R B, DU X L. Characterisation of temperature-dependent heat conduction in heterogeneous concrete [J]. Magazine of Concrete Research, 2018, 70(7): 325 − 339. doi: 10.1680/jmacr.17.00174
[9] WU Z Y, ZHANG J H, FANG Q, et al. Mesoscopic modelling of concrete material under static and dynamic loadings: A review [J]. Construction and Building Materials, 2021, 278: 122419. doi: 10.1016/j.conbuildmat.2021.122419
[10] ZHANG P J, WEI W, SHAO Z S. Multifield coupling study on random aggregate concrete under microwave irradiation [J]. Construction and Building Materials, 2022, 318: 126025. doi: 10.1016/j.conbuildmat.2021.126025
[11] DAUTI D, DAL PONT S, BRIFFAUT M, et al. Modeling of 3D moisture distribution in heated concrete: From continuum towards mesoscopic approach [J]. International Journal of Heat and Mass Transfer, 2019, 134: 1137 − 1152. doi: 10.1016/j.ijheatmasstransfer.2019.02.017
[12] 宋来忠, 沈涛, 余波. 混凝土二维参数化骨料模型的创建方法[J]. 工程力学, 2013, 30(10): 5 − 13. doi: 10.6052/j.issn.1000-4750.2012.05.0390 SONG Laizhong, SHEN Tao, YU Bo. The approach to establishing a two-dimensional parameterized aggregate model for concrere simulation [J]. Engineering Mechanics, 2013, 30(10): 5 − 13. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.05.0390
[13] 陈恒, 肖映雄, 郭瑞奇. 基于p型自适应有限元法的混凝土骨料模型数值模拟[J]. 工程力学, 2019, 36(增刊 1): 158 − 164. doi: 10.6052/j.issn.1000-4750.2018.05.S030 CHEN Heng, XIAO Yingxiong, GUO Ruiqi. Numerical simulation for concrete aggregate models based on the p-version adaptive fem method [J]. Engineering Mechanics, 2019, 36(Suppl 1): 158 − 164. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.S030
[14] SUN Y R, WEI X, GONG H R, et al. A two-dimensional random aggregate structure generation method: Determining effective thermo-mechanical properties of asphalt concrete [J]. Mechanics of Materials, 2020, 148: 103510. doi: 10.1016/j.mechmat.2020.103510
[15] AHMAD M J, TIWARI G N. Solar radiation models—A review [J]. International Journal of Energy Research, 2011, 35(4): 271 − 290. doi: 10.1002/er.1690
[16] ZHU S Y, CAI C B. Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads [J]. International Journal of Non-Linear Mechanics, 2014, 58: 222 − 232. doi: 10.1016/j.ijnonlinmec.2013.10.004
[17] 闫斌, 刘施, 戴公连, 等. 我国典型地区无砟轨道非线性温度梯度及温度荷载模式[J]. 铁道学报, 2016, 38(8): 81 − 86. doi: 10.3969/j.issn.1001-8360.2016.08.012 YAN Bin, LIU Shi, DAI Gonglian, et al. Vertical nonlinear temperature distribution and temperature mode of unballasted track in typical areas of China [J]. Journal of the China Railway Society, 2016, 38(8): 81 − 86. (in Chinese) doi: 10.3969/j.issn.1001-8360.2016.08.012
[18] 孙泽江, 王泽萍, 汪杰, 等. 极端高温天气下CRTS Ⅱ型板式无砟轨道温度分析[J]. 铁道标准设计, 2018, 62(11): 64 − 68. SUN Zejiang, WANG Zeping, WANG Jie, et al. Temperature analysis of CRTS II slab ballastless track in extremely hot weather [J]. Railway Standard Design, 2018, 62(11): 64 − 68. (in Chinese)
-
期刊类型引用(1)
1. 李景哲，高鹏，詹炳根，胡焱博，沙慧玲，余其俊. 基于球面DOG小波框架的骨料形状重构研究. 工程力学. 2025(06): 195-202 . 
本站查看
其他类型引用(1)
计量
- 文章访问数: 122
- HTML全文浏览量: 39
- PDF下载量: 24
- 被引次数: 2
