SEISMIC PERFORMANCE EVALUATION AND DAMAGE EVOLUTION ANALYSIS OF SELF-CENTERING BRACED STEEL FRAME
-
摘要:
为研究自复位耗能(SCED)支撑失效前后支撑钢框架结构的抗震韧性及损伤演化规律，设计了一单榀三层自复位支撑钢框架(SCBSF)并对其进行精细化有限元模拟，探究了支撑第二刚度和摩擦力在考虑支撑失效时对结构宏观响应和关键构件损伤状态的影响规律。结果表明，在地震作用下，SCED支撑作为SCBSF第一道抗震防线，激活工作后为结构提供了稳定的耗能与卓越的复位能力，相比屈曲约束支撑(BRB)框架残余变形角最大减小了84.9%，显著降低结构震后修复成本；支撑达到最大行程破坏失效后，结构层间变形加剧，框架梁和柱塑性耗能占比增加了92.33%，主体结构损伤值增加了48.45%，结构的抗震性能与韧性水平明显降低。参数分析结果表明，提升支撑的第二刚度和摩擦力能有效降低结构响应，但具有较大第二刚度和摩擦力的支撑框架仍抵抗不了强震作用时，可能导致更多的支撑失效破坏，结构损伤加剧。因此，设计SCED支撑时，需要适当提高支撑第二刚度和摩擦力，建议第二刚度取值为第一刚度的7/50~4/25，支撑摩擦力与预压力比值取为1~1.2；提升支撑第二刚度相比提升摩擦力对结构损伤值控制效果更好，随着地震动强度增大，摩擦力与第二刚度对结构抗震性能的影响逐渐减小。
Abstract:To study the seismic resilience and damage evolution law of braced steel frames before and after the failure of self-centering energy dissipation braces (SCED), a single-span three-storey self-centering braced steel frame (SCBSF) was designed. The refined finite element model was established to investigate the influence of the second stiffness and friction force of braces on macroscopic responses of structures and the damage state of key components, considering the failure of braces. The results indicate that the SCED brace as the first seismic line of SCBSF provides stable energy dissipation and excellent self-centering behavior after activation. Compared with the buckling restrained braced (BRB) frame, the residual interstorey drift ratio of the SCBSF is reduced by 84.9%, significantly reducing the repair costs of structures after earthquakes. When the brace begins to fail after reaching its maximum stroke, the interstorey drift of the frame aggravates, and the plastic energy dissipation ratio of frame beam to column increases by 92.33%; the damage value of the main frame increases by 48.45%; and the seismic performance and resilience level of the structure decrease obviously. The results of parameter analysis show that increasing the stiffness and the friction force of the brace can effectively reduce the structural response. However, when the braced frame with large second stiffness and friction force is still unable to resist strong earthquakes, the number of brace failure may increase, causing structural damage aggravation. Thus, it is necessary to appropriately improve the second stiffness and friction force when designing SCED braces. It is suggested that: the second stiffness should be 7/50-4/25 of the first stiffness; the ratio of friction to pre-pressed force should be 1-1.2. The damage control effect of increasing the second stiffness of the brace is better than that of increasing the friction force. With the increase of ground motion intensity, the influence of friction force and the second stiffness on the seismic performance of braced frames decreases gradually.
-
我国是世界上地震灾害最为严重国家之一。地震会带来大量的人员伤亡和严重的经济损失，并且建筑结构震后过大的残余变形也会导致高昂的修复成本。因此，人们对结构的安全性提出了更高的要求，提升结构的抗震韧性也成为目前研究热点。在结构工程中，韧性主要是用于度量和评判建筑物灾后的功能恢复能力[1]。现有的功能可恢复结构主要通过降低地震发生时的功能损失，提高震后修复速度来提升抗震韧性。
自复位耗能(Self-centering Energy Dissipation, SCED)支撑作为一种韧性构件，兼具耗能和复位功能，能够实现结构震后的快速恢复，得到了广泛关注。LIU等[2]分别对SCED支撑和屈曲约束支撑(Buckling Restrained Brace, BRB)钢框架结构进行非线性地震响应模拟分析，结果证明SCED支撑对结构层间位移和震后残余变形响应均起到了较好的控制作用。EATHERTON等[3]设计了15种具有不同结构形式、不同SCED支撑设计参数的框架结构，分析其在不同地震作用下的结构响应，结果表明支撑结构残余变形很小，SCED支撑的承载力和耗能能力并无明显退化现象，通过限制支撑最大出力能够减少其对周围梁柱的需求。徐龙河等[4-6]则对采用不同连接方式的SCED支撑-框架子结构进行了精细化建模分析，研究了刚接和铰接两种支撑连接方式下SCED支撑、节点板、框架梁和柱的受力特性，并针对结构中SCED支撑设计参数及布置位置提出了一种基于智能算法的优化设计方法[7]。
本文设计了一单榀三层自复位支撑钢框架(Self-centering Braced Steel Frame, SCBSF)并进行精细化有限元模拟，分析SCED支撑处于不同工作状态时结构的抗震性能及损伤演化过程，揭示SCED支撑第二刚度和摩擦力在考虑支撑失效时对结构宏观响应和关键构件损伤状态的影响规律。
1 自复位支撑钢框架结构
1.1 结构信息
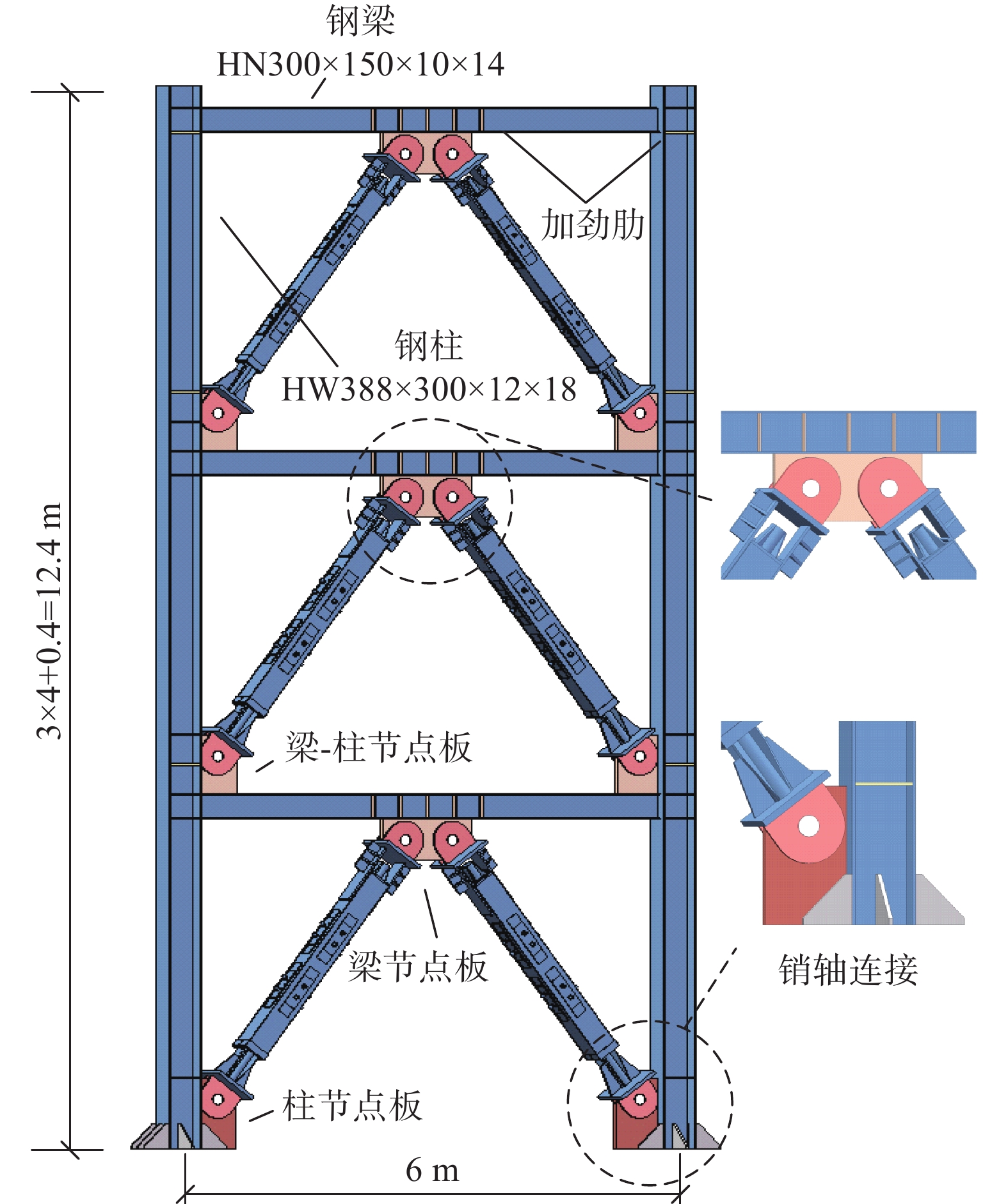
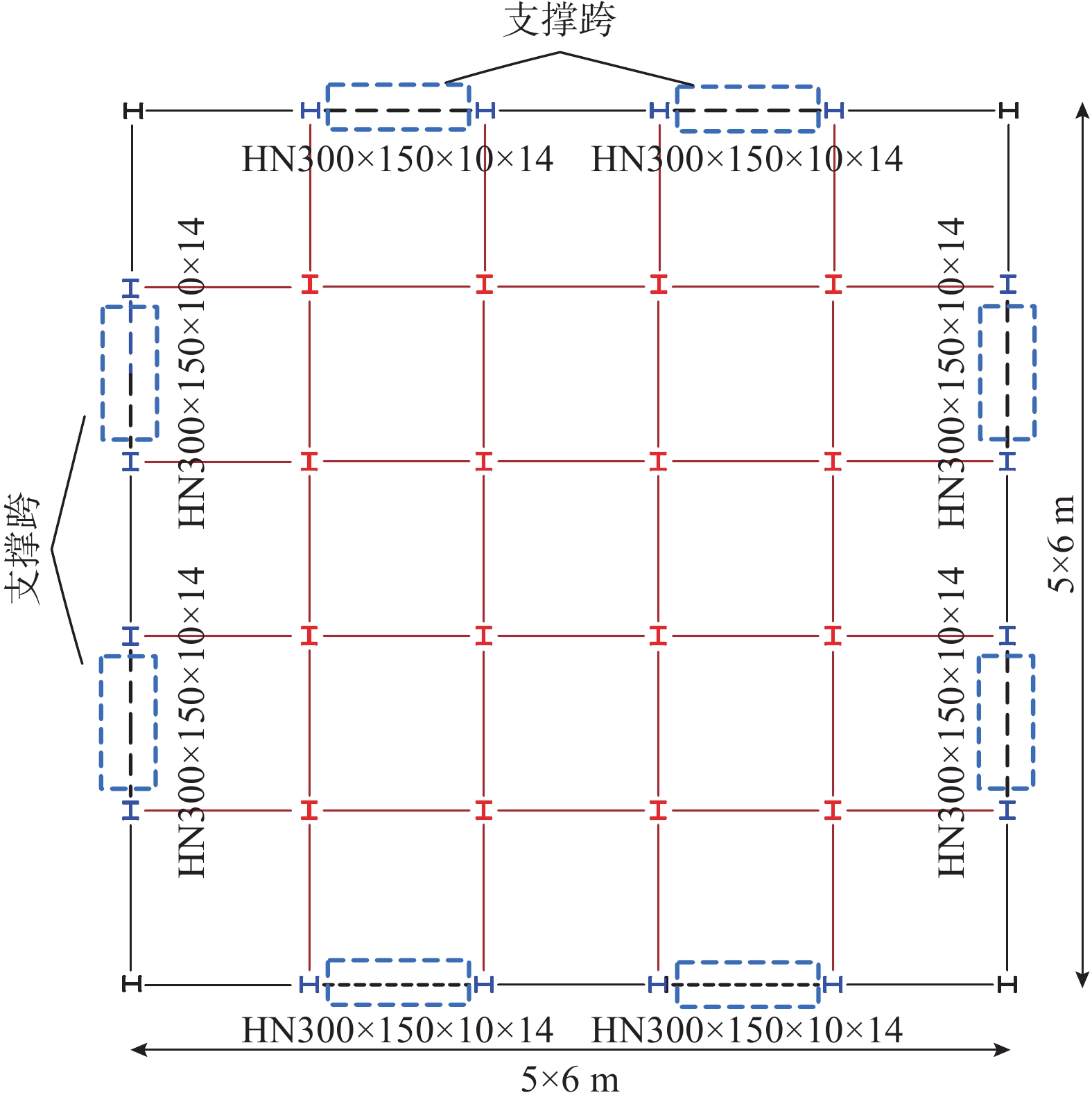
参考中国《建筑抗震设计规范》(GB50011−2010)[8]和《钢结构设计规范》(GB50017−2017)[9]设计了3层自复位支撑钢框架原型结构，如图1所示，结构平面尺寸为30 m×30 m，5榀5跨，跨度均为6 m，各层层高为4 m，楼面恒荷载为5.0 kN/m2，活荷载为2.0 kN/m2。支撑构件按人字型布置，与钢框架之间采用销轴连接，保证支撑处于轴向受力状态。梁柱刚接，除与支撑相连的柱外，其余柱均为重力柱。并在同等条件下建立BRB框架结构用以对比分析。结构场地类别为二类，抗震分组为第一组，设防烈度8度，设计基本地震加速度为0.2 g，按四水准进行抗震设防[10]。由于平面布置对称规则，为对结构进行精细化模拟，故仅选取支撑跨作为分析单元，单榀框架立面图如图2所示，梁柱均采用Q345钢材，框架梁柱截面尺寸如表1所示。
表 1 梁柱截面尺寸Table 1. Sections of beams and columns结构构件 截面 面积/cm2 惯性矩 Ix/cm4 Iy/cm4 梁 HN300×150×10×14 69.20 123 400 2218 柱 HW388×300×12×18 150.24 41 350 17 230 按照SCED支撑与BRB具有同等初始刚度，SCED支撑激活力与BRB屈服力相同以及两种支撑在支撑最大设计行程即结构层间位移角达到2%时具备相同轴向恢复力的原则，对SCED支撑的参数进行设计，表2为结构中SCED支撑设计参数。P0为施加在碟簧上的预压力；F0为摩擦装置提供的摩擦力；δ0为支撑激活位移；δu为支撑最大设计行程。
表 2 SCED支撑设计参数Table 2. Design parameters of SCED braces楼层 第一刚度
K1
/(kN·mm−1)第二刚度
K2
/(kN·mm−1)摩擦力
F0
/kN预压力
P0
/kN支撑激活位移
δ0
/mm支撑最大
设计行程
δu
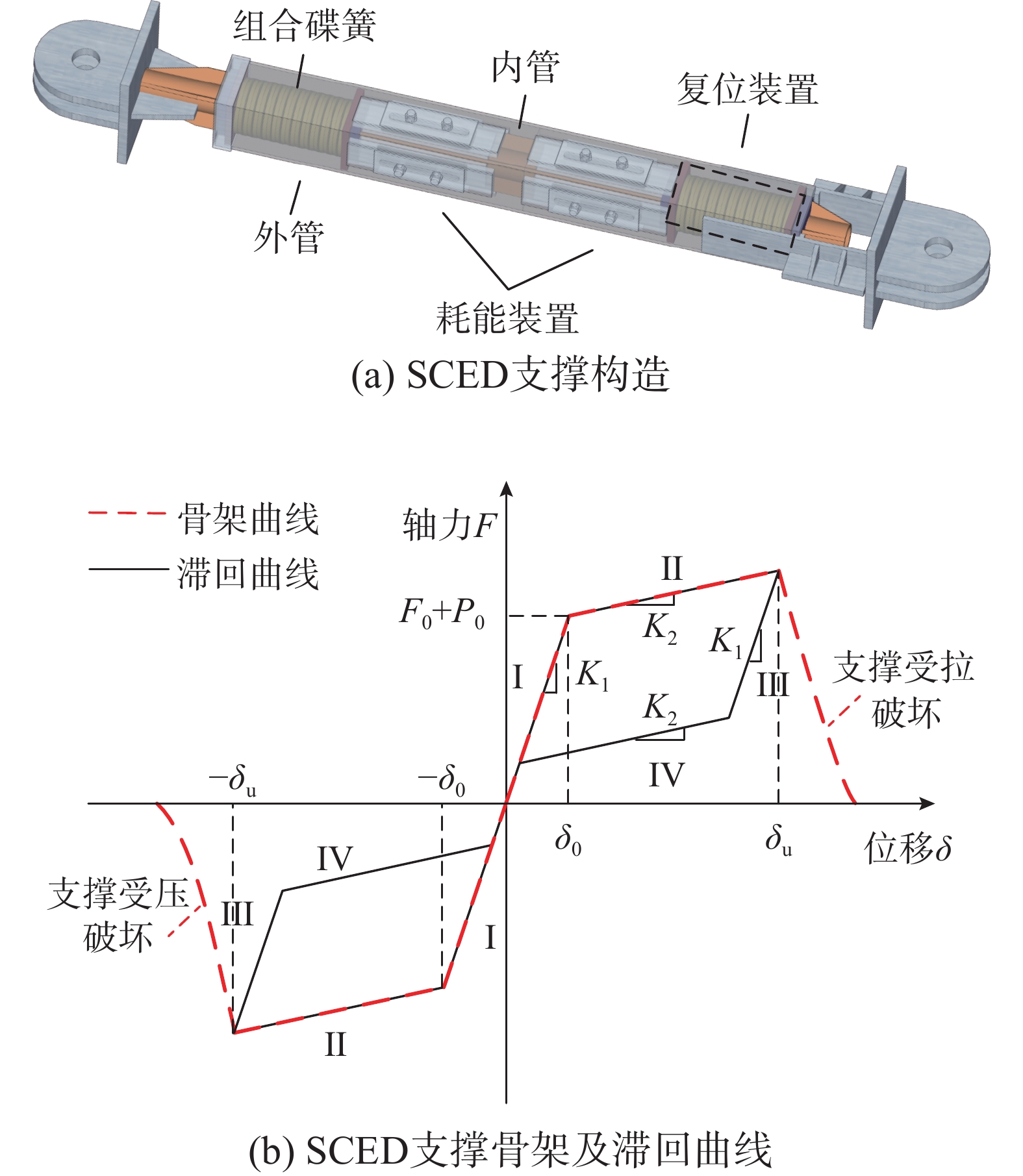
/mm1 230 23 280 280 2.0 48 2 230 23 230 230 2.4 48 3 80 8 135 135 3.4 48 图3为SCED支撑构造及滞回响应[11]，可以看出，支撑在低周往复荷载作用下的滞回曲线具有拉压对称性。加载位移达到支撑最大设计行程前，支撑正常工作，其力学性能可分为四个阶段：第一阶段即开始加载至支撑内外管即将发生相对运动，第一刚度K1由内外管及碟簧共同提供；第二阶段支撑内外管发生相对变形并逐渐达到支撑最大位移，碟簧装置激活，摩擦装置耗能工作，支撑的第二刚度K2主要由碟簧复位系统决定；第三阶段支撑开始卸载，摩擦力反向阻碍内外管发生相对变形，支撑刚度等于K1；第四阶段内外管重新开始相对滑动，碟簧推动支撑复位，直至恢复到初始状态，支撑刚度等于K2。当支撑变形超过最大设计行程时，内外管开始进入塑性；支撑变形继续增加，内外管塑性发展程度加深直至断裂，支撑破坏失效。
1.2 数值模拟
基于有限元软件ABAQUS建立上述支撑钢框架数值模型，如图4所示。结构梁、柱构件及加劲肋由壳单元S4R模拟，节点板采用实体单元C3D8R模拟，钢材本构选用双线性等向强化模型，屈服强度345 MPa[12]。BRB采用弹塑性连接器模拟，SCED支撑采用双折线连接器与弹塑性连接器叠加组成的简化模型进行模拟[13]。模拟SCED支撑失效时，为避免数值不稳定性，在支撑达到最大设计行程后，使支撑轴力在接下来的每个时间步逐渐减少，约25个加载步后支撑轴力基本为0，即支撑达到最大行程后将在0.5 s内从分析模型中有效移除[14]。为考虑支撑框架的实际水平惯性力，在每层柱顶施加68.9 t的附加质量，该附加质量不提供重力，梁柱考虑材料和几何非线性，每层柱顶施加85.2 kN的竖向集中力。结构阻尼比取为5%，因假定SCED支撑的第一刚度与BRB的初始弹性刚度相同，故BRB框架和SCED支撑框架的结构自振周期相同，前三阶自振周期为0.511 s、0.208 s和0.108 s。
1.3 地震波的选取
根据结构的场地及抗震分组等设计信息，按照《建筑抗震设计规范》(GB 50011−2010)[8]得到的目标反应谱，在美国太平洋地震工程研究中心数据库中选取了7条地震动记录，详细信息见表3。所选7条地震动记录的均值谱和目标反应谱的对比如图5所示，可见二者吻合较好。
表 3 所选地震动信息Table 3. Information of selected earthquake ground motions序号 事件 年份 站台 震级 GM-1 Imperial Valley-02 1940 El Centro Array #9 6.95 GM-2 Parkfield 1966 Cholame – Shandon Array #8 6.19 GM-3 Westmorland 1981 Parachute Test Site 5.90 GM-4 Loma Prieta 1989 Agnews State Hospital 6.93 GM-5 Chi-Chi-04 1999 CHY101 6.20 GM-6 Cape Mendocino 1992 Loleta Fire Station 7.01 GM-7 Iwate 2008 MYG004 6.90 为研究SCBSF在支撑失效前后的抗震性能，针对不同水准，将所选7条地震波的峰值地面加速度(Peak Ground Acceleration, PGA)调幅至0.7 m/s2、1.96 m/s2、4 m/s2、5.88 m/s2、7 m/s2、8 m/s2、9 m/s2、10 m/s2。为了获取结构的残余变形响应，在每条地震记录后面增加了10 s的空白波，使结构在地震作用后可以自由振动，以便分析结构的复位性能。
2 抗震性能分析
3层单榀SCBSF层间位移角均值分布如图6所示。PGA小于8 m/s2时，结构层间位移角均值最大为1.38%，小于2%，此时支撑处于正常使用状态。PGA增大至8 m/s2、9 m/s2和10 m/s2时，结构层间位移角最大值分别为2.01%、2.16%和2.45%。图7(a)为不同地震波下结构的最大层间位移角，可以看出PGA达到8 m/s2以后，在部分所选地震波作用下，结构最大层间位移角超过2%；图7(b)给出了地震波GM-3作用对应层间位移角下支撑的滞回曲线，此时三层SCED支撑达到最大设计行程开始失效，导致该层刚度急剧降低，层间变形集中，形成薄弱层，结构抗震能力大幅减弱。因此，以PGA为8 m/s2为界限分析SCED支撑失效前后支撑钢框架结构的抗震性能。
![]()
图 7 PGA为8 m/s2时结构最大层间位移角与支撑滞回曲线Figure 7. Maximum interstory drift ratios of structures and hysteretic curves of braces under earthquake with PGA of 8 m/s22.1 支撑正常工作时的性能评价
2.1.1 结构位移响应与残余变形
图8(a)为SCED支撑框架和BRB框架在不同PGA地震波作用下层间位移角与残余变形角均值。可以看出，SCED支撑和BRB均能有效控制结构层间位移角响应，保护主体结构。PGA为0.7 m/s2、1.96 m/s2、4 m/s2、5.88 m/s2、7 m/s2时，相比SCED支撑框架，BRB框架的层间位移角分别减小了4.59%、22.78%、32.31%、27.42%、10.83%。图8(b)给出了PGA为7 m/s2时，地震波GM-3作用下两类支撑的滞回曲线，可以看出在相同轴向变形下，BRB的平行四边形滞回曲线相较于SCED支撑的旗形滞回曲线更加饱满，耗散的能量更多，降低了结构响应。但随着PGA的逐渐增加，两种支撑框架结构的层间位移角差值减小，表明在强地震作用下SCED支撑可具备与BRB同等的控制效果。
![]()
图 8 两类支撑框架的层间位移响应与支撑滞回曲线Figure 8. Interstory drift response and hysteretic curves of two braced framesSCED支撑框架震后残余变形角均明显小于BRB框架，PGA为0.7 m/s2、1.96 m/s2、4 m/s2、5.88 m/s2、7 m/s2时，相比BRB框架，SCED支撑框架残余变形角分别减小了59.72%、84.89%、76.91%、82.73%、83.88%。这表明SCED支撑正常工作时，能更加有效地控制结构残余变形，降低结构震后修复成本，缩短修复时间。
2.2 支撑失效后的性能评价
2.2.1 结构耗能分配
支撑框架结构主要通过支撑激活耗能、梁柱构件的塑性变形及结构固有阻尼来耗散地震输入能量。图9为框架各部分耗能随PGA增加的变化情况。不考虑支撑失效时，在PGA达到8 m/s2、9 m/s2和10 m/s2的地震作用下，SCED支撑耗能占比最大达到59.44%，梁柱构件的塑性耗能占比最大为10.56%，说明SCED支撑激活工作后耗散绝大部分输入的能量，结构整体塑性发展程度相对较低，有效保护了主体结构。考虑支撑失效时，随着PGA增大，SCED支撑作为结构第一道抗震防线在达到最大行程后逐步失效退出工作，导致其耗能占比减小，最大减小了26.42%，而梁柱构件塑性变形耗能则迅速增加，最大增加了92.33%，主体结构损伤程度加深。
![]()
图 9 在不同PGA地震波作用下结构耗能占比均值Figure 9. Average value of energy dissipation proportion of the structure under seismic records with different PGAs2.2.2 结构累积塑性应变
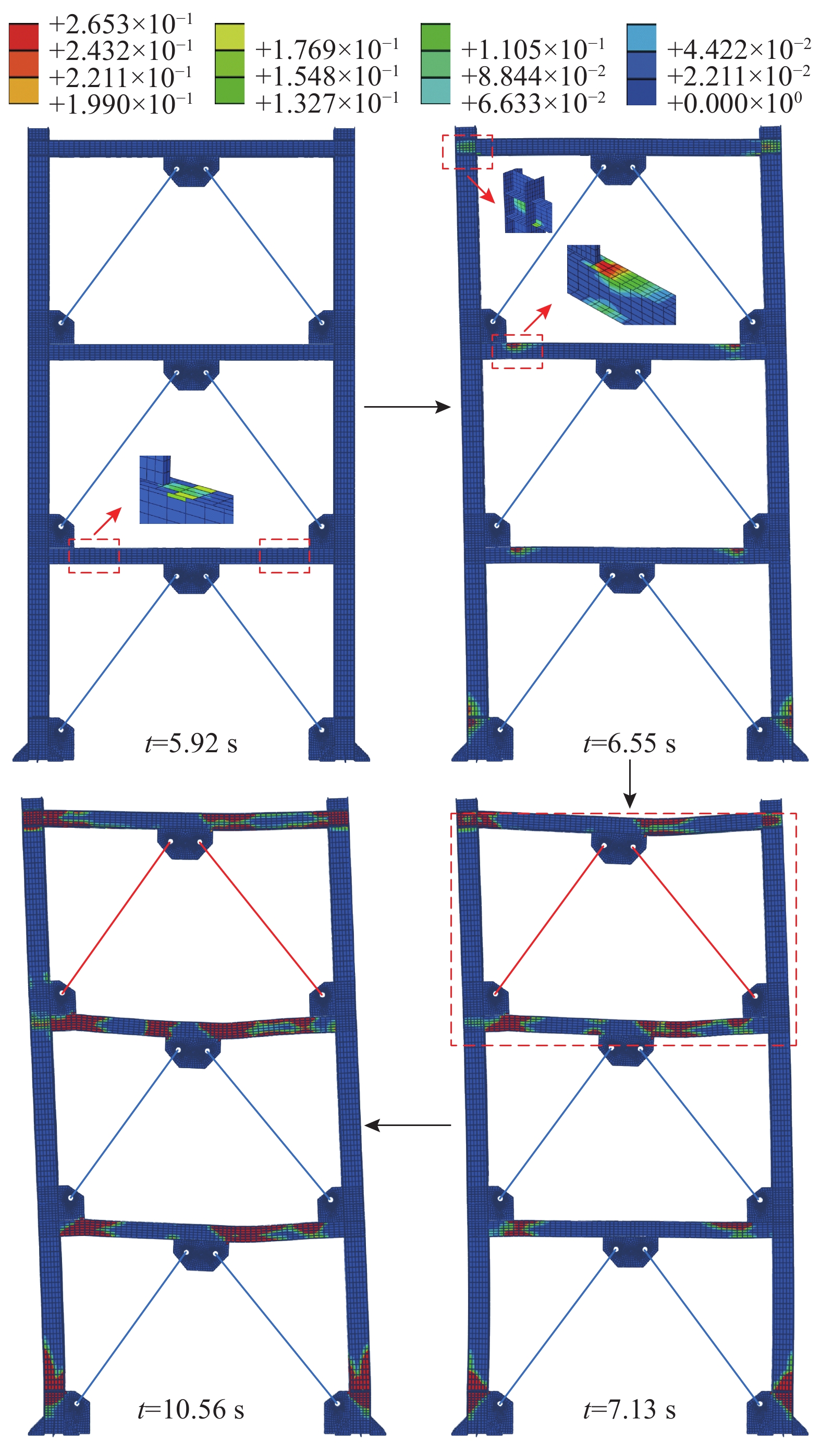
图10给出了在GM-3地震波PGA为8 m/s2作用下考虑支撑失效时SCBSF累积塑性应变在不同时刻的分布情况。可以看出，在地震波加载到5.92 s之前，结构累积塑性应变基本为0，说明此时结构主体基本完好；地震波加载至第5.92 s时，框架一层梁端翼缘最先出现塑性损伤，此时地震波已经超过峰值，柱脚即将形成塑性铰，损伤开始不断累积；地震波加载至6.13 s时，框架一层柱脚开始形成塑性铰，一层梁端塑性铰继续发展；地震波加载至6.55 s时，二层梁端与三层梁柱节点也相继进入塑性阶段，此时结构整体塑性程度仍然较低；地震波加载至7.13 s时，框架三层层间位移角达到2.27%，三层SCED支撑因达到最大行程开始失效退出工作，该层变形急剧增加，损伤随着塑性变形的增加而不断增大，地震波加载至10.56 s时框架发生严重破坏。说明SCED支撑发生破坏后，框架梁柱构件更易损坏，结构的塑性应变水平迅速提高，结构抗震能力明显减弱。
![]()
图 10 在地震波GM-3作用下框架累积塑性应变发展过程Figure 10. Development of cumulative plastic strain of frame under seismic record GM-32.2.3 结构损伤指数
双参数损伤模型能同时反映最大响应及累积损伤效应对结构破坏的影响，因此基于变形和能量双参数组合的损伤指标受到普遍认可[15]，本文采用KUNNATH等[16]考虑扣除弹性变形所提出的改进的Park-Ang双参数损伤指标来评价主体梁柱构件的破坏程度，表达式如下：
DIPA=θm−θrθu−θr+βPA∫dEMyθu = θpθu−θy+βPA∫dEMyθu (1) 式中：θr为构件卸载时可恢复的截面转角，可按截面屈服转角θy[17]计算；θm为构件截面转角的最大值；θu为单调荷载下截面转角的极限值；θp为截面塑性转角的最大值；My为截面屈服弯矩；βPA为构件耗能因子，对钢结构按0.025取值[18]。
通过对各个构件的损伤指数加权平均，得到该层的地震损伤指数，计算公式如下：
DIL=∑λPA,iDIPA,i (2) 式中：DIL为结构层的损伤指标；DIPA,i为第i个构件损伤指标；λPA,i为第i个构件的加权系数，按其耗能占各构件耗能之和的比值计算[19]。
为了得到框架梁柱的整体损伤程度，进一步对每层地震损伤指数进行加权平均，结构整体损伤指数可表示为：
DIT=∑λL,iDIL,i (3) 式中：DIT为结构整体的损伤指标；DIL,i为结构第i层的损伤指标；λL,i为结构层的权重系数。计算时，按照吴波和欧进萍[20]给出的建议，同时考虑构件损伤程度及其所处楼层位置对整体损伤的影响，其权值系数为：
λL,i=(n+1−i)DL,in∑i=1(n+1−i)DL,i (4) 式中，n为结构层数。
图11给出了考虑支撑失效和不考虑支撑失效两种工况下，SCBSF损伤发展曲线。结果表明，框架梁柱损伤值随PGA的增大而增大，PGA为8 m/s2是损伤指标的转折点，定义PGA为8 m/s2时的地震响应为结构失效界限。PGA小于8 m/s2时，支撑完好并正常工作，结构损伤累积值较小，最大仅为0.26；PGA≥8 m/s2后，支撑接连失效退出工作，相比不考虑支撑失效情况，结构的损伤程度迅速增加，损伤值达到0.82，直至严重破坏和倒塌。可以看出，SCED支撑失效前后框架梁柱的损伤值相差较大，说明支撑作为结构第一道抗震防线失效后对结构的抗震性能和韧性水平有重大影响。
![]()
图 11 在不同PGA地震作用下支撑框架损伤值Figure 11. Damage values of braced frames under seismic records with different PGAs3 支撑设计参数对结构抗震性能影响
3.1 支撑参数设计
为探究SCED支撑设计参数对考虑支撑失效的SCBSF结构抗震性能的影响规律，采用控制变量法设计具有不同第二刚度K2及摩擦力F0的参数分析工况，如表4所示。将SCED支撑初始设计值记作工况0用以对比，Δ(*)表示各参数基于工况0的变化率。在PGA为8 m/s2、9 m/s2时，选取最不利的地震波GM-3对单榀三层SCBSF结构进行地震时程分析，且不改变每个工况中框架梁柱截面尺寸、支撑激活力Fy以及第一刚度K1。
表 4 SCBSF中SCED支撑的设计参数Table 4. Design parameters of the SCED braces in the SCBSF工况 第二刚度变化率
ΔK2 /(%)刚度比α 摩擦力变化率
ΔF0 /(%)摩擦力/预压力
F0/P00 +0 0.10 +0 1.0 1 −20 0.08 +0 1.0 2 +20 0.12 3 +40 0.14 4 +60 0.16 5 +0 0.10 −20 0.6 6 −10 0.8 7 +10 1.2 8 +20 1.5 3.2 结果分析
3.2.1 第二刚度K2的影响
图12给出了不同K2取值下结构的最大层间位移角和残余变形角。PGA为8 m/s2时，工况1、工况2、工况3、工况4的最大层间位移角相较工况0的增量分别为24.81%、0.44%、−12.39%、−14.61%；PGA为9 m/s2时，增量分别为84.26%、26.59%、−2.24%、−0.04%。PGA为8 m/s2时，工况1、工况2、工况3、工况4的残余变形角相较工况0的增量分别为198.35%、3.13%、−92.94%、−95.42%；PGA为9 m/s2时，增量分别为213.88%、122.23%、−36.11%、−33.33%。工况3、工况4下即K2提升40%~60%时控制效果最优，说明适当增大K2取值，可以减小结构层间位移角和残余变形角。但随着PGA增大，提升K2对层间位移角和残余变形角的控制效果减弱。这主要是由于具有较大第二刚度的SCED支撑可为结构提供更大的抗侧刚度，会影响支撑失效的数量与位置。
![]()
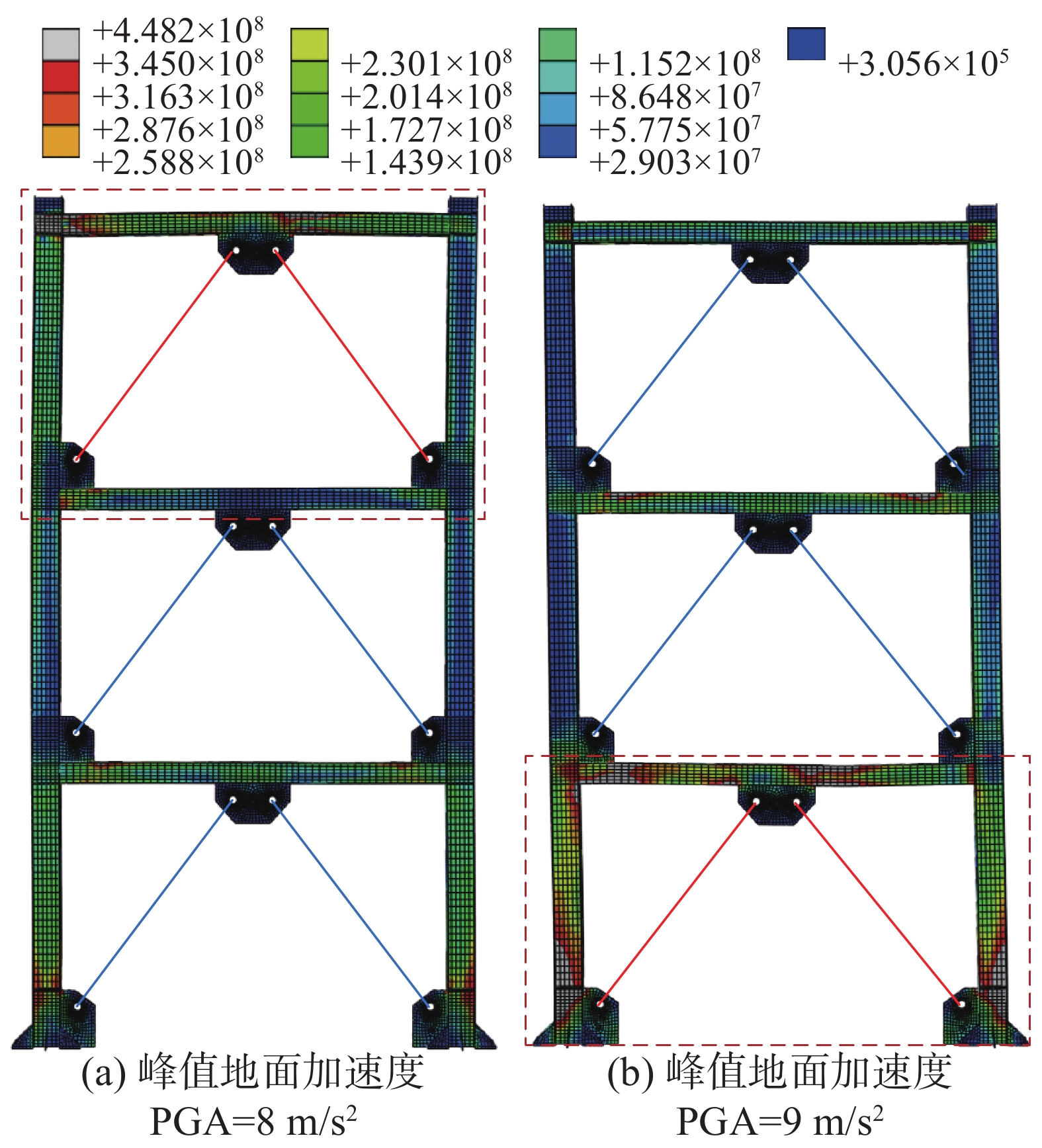
图 12 不同K2下结构的最大层间位移角和残余变形角Figure 12. Maximum interstory drift ratios and residual interstory drift ratios of structure with different K2图13给出了结构最大层间位移角处工况0的应力云图。图14给出了不同工况下模型中各构件的最大塑性应变。如图13(a)和图14所示，PGA为8 m/s2时，工况0与工况2均为三层支撑失效，三层钢梁塑性发展程度较深。工况2提高K2后支撑在相同位移角下能提供更大的复位力，而支撑失效退出工作后，分担的水平力会传递给框架柱，因此造成框架损伤更严重。工况3、工况4进一步提高K2，继续提升SCBSF的抗震性能，SCED支撑不发生失效，降低了层间位移角响应，框架整体塑性发展得到有效控制。工况1减小了K2，支撑所能提供的复位力减小，结构层间位移角响应增大，导致二层、三层支撑接连失效，二层、三层钢梁塑性应变水平迅速提高。
如图13(b)和图14所示，PGA增大至9 m/s2时，结构一层支撑失效，应力主要集中于一层柱脚及一层梁节点板处翼缘。工况2提高K2，各层支撑提供更强的复位力，降低结构响应，一层支撑不失效；但对结构二层、三层来说，提升K2层间位移角响应仍超过2%，支撑破坏失效，支撑失效数量增多，结构整体发展塑性程度大于仅一层支撑失效的情况。工况3、工况4进一步提高K2，三层支撑失效，薄弱层变为三层，三层钢梁塑性应变水平明显提升，但结构层间位移角响应降低，说明支撑失效数量不变时，底层支撑失效对结构影响更大。工况1减小了K2，导致所有支撑均失效，结构各构件塑性应变水平迅速增加，结构变形加剧，层间位移角变化明显。
![]()
图 13 最大层间位移角处SCBSF结构应力云图Figure 13. Stress distribution of SCBSF at maximum interstory drift ratios![]()
图 14 不同工况下SCBSF结构各构件的累积塑性应变Figure 14. Cumulative plastic strain of each member of SCBSF under different cases可见，提升SCED支撑的第二刚度使支撑提供更大的复位力，增强了结构的抗震能力，降低结构响应，可以使支撑不发生破坏或改变支撑失效位置来保护主体结构。但当具有较大第二刚度的SCED支撑在强震作用下发生失效后，框架柱承担全部的层间剪力，支撑失效数目可能增多，结构损伤加剧。因此，在设计SCED支撑时，应适当增大其第二刚度，使支撑在强地震作用下仍能正常工作，尽量避免支撑破坏对结构抗震性能的影响，第一刚度不变的前提下，建议取值为第一刚度的7/50~4/25，即第二刚度在初始设计值基础上提升40%~60%。
3.2.2 摩擦力F0的影响
图15给出了不同F0取值下结构的最大层间位移角和残余变形角。PGA为8 m/s2时，工况5、工况6、工况0、工况7、工况8的最大层间位移角分别为2.43%、2.35%、2.27%、2.21%、2.19%；残余变形角分别为0.24%、0.22%、0.21%、0.19%、0.17%。结构层间位移与残余变形呈现正相关，结构层间位移角与残余变形角均随着F0增大而减小。改变支撑的F0主要是通过提高支撑耗能来降低结构的塑性变形从而确保框架梁和柱的损伤程度维持在较低水平。图16为不同工况下结构耗能占比，PGA为8 m/s2时，支撑耗能随F0增大而增大，结构塑性耗能占比不断减小，最小为15.9%，有效控制结构层间变形。
![]()
图 15 不同F0下结构的最大层间位移角和残余变形角Figure 15. Maximum interstory drift ratios and residual interstory drift ratios of structure with different F0如图15所示，PGA为9 m/s2时，工况5、工况6、工况0、工况7、工况8的最大层间位移角分别为2.95%、2.92%、2.68%、2.54%、3.99%；残余变形角分别为0.52%、0.42%、0.36%、0.31%、0.69%。结构层间位移角与残余变形角随着F0增大呈先减小后增大趋势，工况7下即F0提升10%时控制效果最优。由图16可以看出，PGA达到9 m/s2时，工况5~工况7，支撑始终为一层失效，F0增大支撑消耗更多的能量，减小结构塑性变形，控制层间位移。工况8进一步提高F0，此时耗能能力的提升对结构响应的影响不如增大PGA的影响明显，一层支撑不发生失效，损伤集中于二层、三层，二层、三层支撑达到最大行程破坏，支撑耗能占比急剧减小为28.2%，结构塑性耗能占比增加到30.2%，损伤程度加剧。
![]()
图 16 不同工况下结构耗能占比Figure 16. Energy dissipation proportion of the structure under different cases提升支撑摩擦力增大了SCED支撑耗能能力，从一定程度上降低了结构响应。在强地震作用下，SCED支撑一定会发生破坏失效时，具有较大支撑摩擦力的SCBSF结构中的支撑失效数目增多，结构塑性程度加深。因此，为了实现最优的抗震性能和结构复位性能，减小支撑失效带来的影响，激活力不变时，支撑摩擦力与预压力的取值需相互协调，建议摩擦力与预压力比值取为1~1.2，即支撑摩擦力在初始设计值的基础上提升0~10%。
3.2.3 结构损伤
不同工况下结构的损伤值如图17所示。PGA为8 m/s2时，工况4和工况8损伤值最小，分别为0.32和0.52，相比工况0分别减小43.41%和9.25%；PGA为9 m/s2时，工况3和工况7损伤值最小，分别为0.63和0.67，相比工况0分别减小10.71%和5.53%。可以看出，考虑支撑失效时，适当增大K2和F0均能减小结构损伤，但改变K2从而改变结构抗侧刚度，对损伤值的影响更明显，而增大F0所增加的耗能在强地震动下作用很小，对损伤值控制效果不显著。随着PGA增大，结构响应增大，因更多的SCED支撑失效，结构损伤逐渐加剧，改变K2和F0对结构损伤的控制效果逐渐减小。
4 结论
本文分析了SCED支撑失效前后自复位支撑钢框架结构的抗震性能与韧性水平，探究了SCED支撑设计参数对结构宏观响应和关键构件损伤状态的影响规律，所得结论如下：
(1) SCED支撑作为SCBSF第一道抗震防线，在地震作用下激活工作后为结构提供了稳定的耗能与卓越的复位能力，从而有效减小了结构的残余变形并起到了保护主体结构的作用。支撑达到最大行程破坏失效后，结构层间变形加剧，框架梁和柱塑性耗能占比增加了92.33%，主体结构损伤值增加了48.45%，结构的抗震性能与韧性水平明显降低。
(2) 参数分析结果表明，提升SCED支撑的第二刚度增强了结构的抗震能力，可以使支撑不发生破坏或改变支撑失效位置来保护主体结构，层间位移角最大减小了14.61%，结构损伤值降低了43.41%。具有较大第二刚度的SCED支撑在强震作用下发生失效后，框架柱承担全部的层间剪力，结构损伤最大增加了44.83%。因此，设计支撑时，应适当增大第二刚度，使支撑在强地震作用下仍能正常工作，尽量避免支撑破坏对结构抗震性能的影响，建议取值为第一刚度的7/50~4/25。
(3) 改变支撑摩擦力，SCBSF中SCED支撑仍然会破坏失效，但提升摩擦力，提高了支撑耗能能力，从而降低结构的塑性变形，结构损伤值最大降低了9.25%。在强地震作用下，SCED支撑一定会发破坏失效时，具有较大支撑摩擦力的SCBSF结构中的支撑失效数目增多，结构塑性程度加深，结构损伤值最大增加20.02%。因此，为了实现最优的抗震性能和结构复位性能，减小支撑失效带来的影响，支撑摩擦力与预压力的取值需相互协调，建议支撑摩擦力与预压力比值取为1~1.2。
(4)相比增大支撑摩擦力，增大第二刚度对结构损伤控制效果更显著。随着PGA增大，结构宏观响应增大，因更多的SCED支撑失效，结构损伤逐渐加深，改变支撑第二刚度和摩擦力对结构抗震性能的影响逐渐减小。
-
![]()
图 7 PGA为8 m/s2时结构最大层间位移角与支撑滞回曲线
Figure 7. Maximum interstory drift ratios of structures and hysteretic curves of braces under earthquake with PGA of 8 m/s2
![]()
图 8 两类支撑框架的层间位移响应与支撑滞回曲线
Figure 8. Interstory drift response and hysteretic curves of two braced frames
![]()
图 9 在不同PGA地震波作用下结构耗能占比均值
Figure 9. Average value of energy dissipation proportion of the structure under seismic records with different PGAs
![]()
图 10 在地震波GM-3作用下框架累积塑性应变发展过程
Figure 10. Development of cumulative plastic strain of frame under seismic record GM-3
![]()
图 11 在不同PGA地震作用下支撑框架损伤值
Figure 11. Damage values of braced frames under seismic records with different PGAs
![]()
图 12 不同K2下结构的最大层间位移角和残余变形角
Figure 12. Maximum interstory drift ratios and residual interstory drift ratios of structure with different K2
![]()
图 13 最大层间位移角处SCBSF结构应力云图
Figure 13. Stress distribution of SCBSF at maximum interstory drift ratios
![]()
图 14 不同工况下SCBSF结构各构件的累积塑性应变
Figure 14. Cumulative plastic strain of each member of SCBSF under different cases
![]()
图 15 不同F0下结构的最大层间位移角和残余变形角
Figure 15. Maximum interstory drift ratios and residual interstory drift ratios of structure with different F0
![]()
图 16 不同工况下结构耗能占比
Figure 16. Energy dissipation proportion of the structure under different cases
表 1 梁柱截面尺寸
Table 1 Sections of beams and columns
结构构件 截面 面积/cm2 惯性矩 Ix/cm4 Iy/cm4 梁 HN300×150×10×14 69.20 123 400 2218 柱 HW388×300×12×18 150.24 41 350 17 230 
下载: 导出CSV
表 2 SCED支撑设计参数
Table 2 Design parameters of SCED braces
楼层 第一刚度
K1
/(kN·mm−1)第二刚度
K2
/(kN·mm−1)摩擦力
F0
/kN预压力
P0
/kN支撑激活位移
δ0
/mm支撑最大
设计行程
δu
/mm1 230 23 280 280 2.0 48 2 230 23 230 230 2.4 48 3 80 8 135 135 3.4 48
下载: 导出CSV
表 3 所选地震动信息
Table 3 Information of selected earthquake ground motions
序号 事件 年份 站台 震级 GM-1 Imperial Valley-02 1940 El Centro Array #9 6.95 GM-2 Parkfield 1966 Cholame – Shandon Array #8 6.19 GM-3 Westmorland 1981 Parachute Test Site 5.90 GM-4 Loma Prieta 1989 Agnews State Hospital 6.93 GM-5 Chi-Chi-04 1999 CHY101 6.20 GM-6 Cape Mendocino 1992 Loleta Fire Station 7.01 GM-7 Iwate 2008 MYG004 6.90
下载: 导出CSV
表 4 SCBSF中SCED支撑的设计参数
Table 4 Design parameters of the SCED braces in the SCBSF
工况 第二刚度变化率
ΔK2 /(%)刚度比α 摩擦力变化率
ΔF0 /(%)摩擦力/预压力
F0/P00 +0 0.10 +0 1.0 1 −20 0.08 +0 1.0 2 +20 0.12 3 +40 0.14 4 +60 0.16 5 +0 0.10 −20 0.6 6 −10 0.8 7 +10 1.2 8 +20 1.5
下载: 导出CSV
-
[1] EROCHKO J, CHRISTOPOULOS C, TREMBLAY R, et al. Residual drift response of SMRFs and BRB frames in steel buildings designed according to ASCE 7-05 [J]. Journal of Structural Engineering, 2011, 137(5): 589 − 599. doi: 10.1061/(ASCE)ST.1943-541X.0000296
[2] LIU L, ZHAO J, LI S. Nonlinear displacement ratio for seismic design of self-centering buckling-restrained braced steel frame considering trilinear hysteresis behavior [J]. Engineering Structures, 2018, 158: 199 − 222. doi: 10.1016/j.engstruct.2017.12.026
[3] EATHERTON M R, FAHNESTOCK L A, MILLER D J. Self-centering buckling restrained brace development and application for seismic response mitigation [C]// Proceedings of 10th U. S. National Conference on Earthquake Engineering: Frontiers of Earthquake Engineering. Anchorage: NCEE, 2014: 1−11.
[4] 徐龙河, 樊晓伟, 代长顺, 等. 预压弹簧自恢复耗能支撑受力性能分析与试验研究[J]. 建筑结构学报, 2016, 37(9): 142 − 148. doi: 10.14006/j.jzjgxb.2016.09.018 XU Longhe, FAN Xiaowei, DAI Changshun, et al. Mechanical behavior analysis and experimental study on pre-pressed spring self-centering energy dissipation brace [J]. Journal of Building Structures, 2016, 37(9): 142 − 148. (in Chinese) doi: 10.14006/j.jzjgxb.2016.09.018
[5] 樊晓伟. 新型预压弹簧自恢复耗能支撑结构抗震性能设计理论与试验研究[D]. 北京: 北京交通大学, 2019. FAN Xiaowei. Theoretical and experimental research on seismic performance design of buildings with pre-pressed spring self-centering energy dissipation braces [D]. Beijing: Beijing Jiaotong University, 2019. (in Chinese)
[6] 徐龙河, 张格, 颜欣桐. 设置自复位支撑的钢筋混凝土框架结构抗震性能研究[J]. 工程力学, 2020, 37(2): 90 − 97. doi: 10.6052/j.issn.1000-4750.2019.01.0100 XU Longhe, ZHANG Ge, YAN Xintong. Seismic performance study of reinforced concrete frame with self-centering braces [J]. Engineering Mechanics, 2020, 37(2): 90 − 97. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.01.0100
[7] 颜欣桐, 徐龙河. 基于遗传算法的钢筋混凝土框架-剪力墙结构失效模式多目标优化[J]. 工程力学, 2018, 35(4): 69 − 77. doi: 10.6052/j.issn.1000-4750.2016.12.0981 YAN Xintong, XU Longhe. Multi-objective optimization of genetic algorithm-based failure mode for reinforced concrete frame-shear wall structures [J]. Engineering Mechanics, 2018, 35(4): 69 − 77. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.12.0981
[8] GB 50011−2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[9] GB 50017−2017, 钢结构设计标准[S]. 北京: 中国建筑工业出版社, 2017. GB 50017−2017, Code for design of steel structures [S]. Beijing: China Architecture & Building Press, 2017. (in Chinese)
[10] XU L H, XIE X S, LI Z X. Seismic behavior and design approach of variable-damping self-centering braced frame [J]. Journal of Structural Engineering, 2021, 147(6): 05021001. doi: 10.1061/(ASCE)ST.1943-541X.0003031
[11] 徐龙河, 樊晓伟, 逯登成, 等. 预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究[J]. 工程力学, 2016, 33(10): 116 − 122. doi: 10.6052/j.issn.1000-4750.2015.03.0216 XU Longhe, FAN Xiaowei, LU Dengcheng, et al. Study on restoring force model and hysteretic behaviors of pre-pressed spring self-centering energy dissipation brace [J]. Engineering Mechanics, 2016, 33(10): 116 − 122. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.03.0216
[12] 李然. SMA自复位耗能装置的研发及其在钢框架-支撑结构中抗震性能的应用研究[D]. 南京: 东南大学, 2019. LI Ran. Development of self-centering-energy-dissipation device based on shape memory alloys and application research on seismic performance of steel frame-bracing structures [D]. Nanjing: Southeast University, 2019. (in Chinese)
[13] 刘嘉琳, 徐龙河. 带自复位耗能支撑钢板剪力墙墙板受力性能研究[J]. 工程力学, 2019, 36(7): 156 − 164. doi: 10.6052/j.issn.1000-4750.2018.06.0316 LIU Jialin, XU Longhe. Study on the mechanical behavior of wall plate of steel plate shear wall with self-centering energy dissipation braces [J]. Engineering Mechanics, 2019, 36(7): 156 − 164. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.06.0316
[14] 崔瑶, 许肖卓, 林迟. 考虑支撑断裂及节点板作用的中心支撑框架抗震性能研究[J]. 工程力学, 2020, 37(10): 85 − 92. doi: 10.6052/j.issn.1000-4750.2019.11.0648 CUI Yao, XU Xiaozhuo, LIN Chi. Seismic performance of concentrically braced frames considering the brace fracture and gusset plate effect [J]. Engineering Mechanics, 2020, 37(10): 85 − 92. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.11.0648
[15] 门进杰, 张谦, 徐超, 等. 基于改进Park-Ang双参数模型的RCS混合框架结构地震损伤评估[J]. 工程力学, 2020, 37(9): 133 − 143. doi: 10.6052/j.issn.1000-4750.2019.10.0604 MEN Jinjie, ZHANG Qian, XU Chao, et al. Seismic damage assessment of composite frame with reinforced concrete columns and steel beams based on improved Park-Ang double parameter model [J]. Engineering Mechanics, 2020, 37(9): 133 − 143. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.10.0604
[16] KUNNATH S K, REINHORN A M, PARK Y J. Analytical modeling of inelastic seismic response of R/C structures [J]. Journal of Structural Engineering, 1990, 116(4): 996 − 1017. doi: 10.1061/(ASCE)0733-9445(1990)116:4(996)
[17] PARK Y J, ANG A H S. Mechanistic seismic damage model for reinforced concrete [J]. Journal of Structural Engineering, 1985, 111(4): 722 − 739. doi: 10.1061/(ASCE)0733-9445(1985)111:4(722)
[18] FEMA 356, Prestandard and commentary for the seismic rehabilitation of buildings [S]. Washington: Federal Emergency Management Agency, 2000.
[19] PARK Y J, ANG A H S, WEN Y K. Damage-limiting aseismic design of buildings [J]. Earthquake Spectra, 1987, 3(1): 1 − 26. doi: 10.1193/1.1585416
[20] 吴波, 欧进萍. 钢筋砼结构在主余震作用下的反应与损伤分析[J]. 建筑结构学报, 1993, 14(5): 45 − 53. doi: 10.14006/j.jzjgxb.1993.05.006 WU Bo, OU Jinping. Response and damage analysis of reinforced concrete structures under main shock and aftershocks [J]. Journal of Building Structures, 1993, 14(5): 45 − 53. (in Chinese) doi: 10.14006/j.jzjgxb.1993.05.006
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 267
- HTML全文浏览量: 90
- PDF下载量: 73
- 被引次数: 1
