ANALYSIS OF THE INFLUENCE OF MASS MATRIX ON THE PRECISION OF DYNAMIC CALCULATION
-
摘要: 通过一致质量矩阵和集中质量矩阵的显式表达，对比分析了质量矩阵对Euler-Bernoulli梁理论和两结点双线性插值梁理论动力计算精度的影响。并通过Python有限元程序的数值模拟，揭示了两结点双线性插值梁的优越性。理论推导和数值分析结果表明：梁单元动力计算前必须进行网格剖分；网格密度的增大并不能提高Euler-Bernoulli梁集中质量矩阵的动力精度，而一致质量矩阵的收敛性显著高于集中质量矩阵。
-
关键词:
- 有限元 /
- 质量矩阵 /
- 两结点双线性插值梁 /
- Euler-Bernoulli /
- 转动质量
Abstract: The influence of mass matrix on dynamic calculation accuracy of Euler-Bernoulli beam theory and two-node bilinear interpolation beam theory is compared and analyzed by displaying uniform mass matrix and concentrated mass matrix. The superiority of two-node bilinear interpolation beam is revealed by numerical simulation using the finite element program Python. The results of theoretical derivation and numerical analysis show that the grid must be divided before the dynamic calculation of beam element. The increase of mesh density does not improve the dynamic accuracy of Euler-Bernoulli beam using concentrated mass matrix, while the convergence of uniform mass matrix is significantly higher than that of concentrated mass matrix. -
梁作为工程中的基础构件，广泛应用于桥梁、房屋、高速铁路、机械制造等领域。在有限单元法中，对于梁动力计算的精度控制，一直是数学家、力学家、数值分析学家研究的核心内容。
在有限元动力学中，由于引入了“惯性”的概念，动力计算与静力计算存在着本质的区别。通过研究发现，合理的构造、使用梁的质量矩阵，能有效提高梁动力响应和动力特性的计算精度[1-13]，对工程实践具有指导价值。目前梁的质量矩阵一般分为两种：一致质量矩阵(也叫协调质量矩阵)、集中质量矩阵(也叫堆聚质量矩阵、集总质量矩阵、团聚质量矩阵)。
一致质量矩阵的计算公式，可结合伽辽金法，通过有限元的弱势积分导出。虽然一致质量矩阵有定理的保证，但在有限元高次单元中存在一定的缺陷。例如：8结点矩形单元的一致质量矩阵，主对角元素存在小于零的情况[14]。因此，一致质量矩阵在高次单元中，一般不提倡使用。
集中质量矩阵，可通过以下四种方法得到：行(列)相加法[8-9, 14]、对角项系数法(HRZ)[10, 14]、虚功原理法(RC)[12]、数值流行法(NMM)[13]得到：
1)行(列)相加法[8-9, 14]：将一致质量矩阵中每一行的元素集中于主对角，并将非主对角元素置零。
2)对角项系数法(HRZ)[10, 14]：将一致质量矩阵中主对角元素进行放缩，非主对角元素置零。
3)虚功原理法(RC)[12]：利用刚体虚功原理，比较分布质量梁、集中质量梁的转动惯量，引入修正系数对转动质量进行修正。
4)数值流行法(NMM)[13]：将梁拓扑为无数的物理片，以形函数作为相应物理片的权函数，将两物理片的公共部分(流形单元)进行组装得到质量矩阵。
由于上述四种方法仅NMM法有数学定理的保证，以集中质量矩阵替代一致质量矩阵合理性备受争议。这些争议主要体现在以下三个方面：
1)在集中质量矩阵的转动质量方面，不同的方法会得到不同的结果。行(列)相加法得到的转动质量为零。HITION等[10]于1976年，通过HRZ方法给出梁单元的转动质量为ρAl3/78。PARK和JENSEN[11]通过傅里叶分析，认为梁单元的转动质量为ρAl3/105。ARCHER和WHALEN[12]通过RC方法，计算出梁单元的转动质量为−ρAl3/12；并将RC和HRZ的计算结果平均化，得到−11ρAl3/156。左占宣[7]对比研究了RC法与解析解的固有频率，得到不同边界条件、不同网格密度下，梁单元转动质量的最优解。
2)在集中质量矩阵的合理性方面，普遍认为集中质量矩阵忽略了自由度之间的耦合关系。郑艳和车树汶等[1-2]认为梁的转动惯性力影响很小，可以忽略不计，集中质量矩阵不能反映结构在空间的真实分布模态。汪梦甫和王朝晖[5]认为一致质量矩阵考虑了移动惯性和弯曲惯性，集中质量矩阵忽略了弯曲惯性。杨亚平和沈海宁[6]认为当网格较密时，由于相邻结点运行的连续性，可以近似认为惯性项之间互不耦合，但高阶单元不宜采用集中质量矩阵。高岱恒等[13]认为转动质量为零会牺牲很多数值特性，而HRZ法没有数学基础，并提出具备数学基础的NMM法，但没有验证高阶振型的角频率精度。左占宣[7]认为一般的集中质量(转动质量为零)矩阵会丢失单元信息，影响计算结果的精度。
3)在动力响应的计算精度方面，两种质量矩阵的计算结果也存在一定的差异。王勖成[14]认为一般情况下，两种矩阵的计算精度差异不大。郑艳等[1]、车树汶等[2]、汪梦甫和王朝晖[5]认为发现两种质量矩阵的角频率在高阶振型中差异较大。刘瑞岩[4]认为全耦合单元的一致质量矩阵为固有频率准确值的上限，当研究纵向振动或扭转振动时，弯曲分量不可忽略。车树汶等[2]认为桥梁跨度、宽度会影响低阶频率的精度。
基于上述学者的研究，可以发现两种质量矩阵之间存在一定的联系，即集中质量矩阵是一致质量矩阵解耦后的结果。因为集中质量矩阵存在转动质量不确定性的缺陷，以及一致质量矩阵在高次单元中的异常，使得笔者怀疑一致质量矩阵的正确性。认为上述质量矩阵的缺陷，是由单元位移模式的缺陷造成[3]，并最终指向Euler-Bernoulli梁理论的缺陷[15]。为了解决梁理论的缺陷，本文基于自编的Python有限元程序，以网格密度对动力计算精度的影响作为收敛性衡量指标，采用全耦合梁单元“两结点双线性插值梁单元[15]”(后文简称插值梁)进行数值模拟，探索两种质量矩阵的精度，并校核“两结点双线性插值梁单元”理论的正确性。
1 理论推导与分析
基于文献[15]的二维面积分，以b×h实腹矩形为梁的截面形状，L为梁的长度，分别给出插值梁、Euler-Bernoulli梁的形函数矩阵N式(1)、式(2)：
{{\boldsymbol{N}}_{\rm{Z}}} = \left[\begin{matrix} {\dfrac{{L - x}}{L}}&{\dfrac{{ - y}}{L}}&{\dfrac{{ - 2Ly + 2xy}}{L}}&{\dfrac{x}{L}}&{\dfrac{y}{L}}&{\dfrac{{ - 2xy}}{L}} \\ 0&{\dfrac{{L - x}}{L}}&0&0&{\dfrac{x}{L}}&0 \\ 0&0&{\dfrac{{L - x}}{L}}&0&0&{\dfrac{x}{L}} \end{matrix} \right] (1) {{\boldsymbol{N}}_{\rm{B}}} = \left[ {\begin{matrix} {\dfrac{{L - x}}{L}}&{\dfrac{{6Lxy - {\text{6}}{x^2}y}}{{{L^3}}}}&{\dfrac{{ - {L^2}y + 4Lxy - 3{x^2}y}}{{{L^2}}}}&{\dfrac{x}{L}}&{\dfrac{{ - 6Lxy + {\text{6}}{x^2}y}}{{{L^3}}}}&{\dfrac{{2Lxy - 3{x^2}y}}{{{L^2}}}} \\ 0&{\dfrac{{{L^3} - 3L{x^2}{\text{ + }}2{x^3}}}{{{L^3}}}}&{\dfrac{{{L^2}x - 2L{x^2}{\text{ + }}{x^3}}}{{{L^2}}}}&0&{\dfrac{{3L{x^2} - 2{x^3}}}{{{L^3}}}}&{\dfrac{{ - L{x^2}{\text{ + }}{x^3}}}{{{L^2}}}} \\ 0&0&0&0&0&0 \end{matrix}} \right] (2) 式(2)是严格按照《弹性力学》几何关系(二维面积分)、梁单元的位移模式推导获得，因此式(2)考虑了梁结点的横向位移和转角位移，相较于传统的形函数矩阵(1×6的矩阵[14])，由式(2)所表征的Euler-Bernoulli梁更为合理。现将式(1)和式(2)代入几何关系，得到两种梁单元的几何矩阵B：
{{\boldsymbol{B}}_{\rm{Z}}} = \left[ {\begin{matrix} {\dfrac{{ - 1}}{L}}&0&{\dfrac{{2y}}{L}}&{\dfrac{1}{L}}&0&{\dfrac{{ - 2y}}{L}} \\ 0&0&0&0&0&0 \\ 0&{\dfrac{{ - 2}}{L}}&{\dfrac{{ - 2L + 2x}}{L}}&0&{\dfrac{2}{L}}&{\dfrac{{ - 2x}}{L}} \end{matrix}} \right] (3) {{\boldsymbol{B}}_{\rm{B}}} = \left[ {\begin{matrix} {\dfrac{{ - 1}}{L}}&{\dfrac{{6Ly - 12xy}}{{{L^3}}}}&{\dfrac{{4Ly - 6xy}}{{{L^2}}}}&{\dfrac{1}{L}}&{\dfrac{{ - 6Ly + 12xy}}{{{L^3}}}}&{\dfrac{{2Ly - 6xy}}{{{L^2}}}} \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \end{matrix}} \right] (4) 通过有限元弱式积分，得到两种梁单元的一致质量矩阵Mc：
{{\boldsymbol{M}}_{{\rm{Zc}}}} = \rho bhL\left[ {\begin{matrix} {\dfrac{1}{3}}&0&0&{\dfrac{1}{6}}&0&0 \\ 0&{\dfrac{1}{3} + \dfrac{{{h^2}}}{{12{L^2}}}}&{\dfrac{{{h^2}}}{{12L}}}&0&{\dfrac{1}{6} - \dfrac{{{h^2}}}{{12{L^2}}}}&{\dfrac{{{h^2}}}{{12L}}} \\ 0&{\dfrac{{{h^2}}}{{12L}}}&{\dfrac{1}{3} + \dfrac{{{h^2}}}{9}}&0&{\dfrac{{ - {h^2}}}{{12L}}}&{\dfrac{1}{6} + \dfrac{{{h^2}}}{{18}}} \\ {\dfrac{1}{6}}&0&0&{\dfrac{1}{3}}&0&0 \\ 0&{\dfrac{1}{6} - \dfrac{{{h^2}}}{{12{L^2}}}}&{\dfrac{{ - {h^2}}}{{12L}}}&0&{\dfrac{1}{3} + \dfrac{{{h^2}}}{{12{L^2}}}}&{\dfrac{{ - {h^2}}}{{12L}}} \\ 0&{\dfrac{{{h^2}}}{{12L}}}&{\dfrac{1}{6} + \dfrac{{{h^2}}}{{18}}}&0&{\dfrac{{ - {h^2}}}{{12L}}}&{\dfrac{1}{3} + \dfrac{{{h^2}}}{9}} \end{matrix}} \right] (5) {{\boldsymbol{M}}_{{\rm{Bc}}}} = \rho bhL\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{3}}&0&0&{\dfrac{1}{6}}&0&0 \\ 0&{\dfrac{{13}}{{35}} + \dfrac{{{h^2}}}{{10{L^2}}}}&{\dfrac{{11L}}{{210}} + \dfrac{{{h^2}}}{{120{L^2}}}}&0&{\dfrac{9}{{70}} - \dfrac{{{h^2}}}{{10{L^2}}}}&{\dfrac{{ - 13L}}{{420}} + \dfrac{{{h^2}}}{{120{L^2}}}} \\ 0&{\dfrac{{11L}}{{210}} + \dfrac{{{h^2}}}{{120{L^2}}}}&{\dfrac{{{L^2}}}{{105}} + \dfrac{{{h^2}}}{{90}}}&0&{\dfrac{{13L}}{{420}} - \dfrac{{{h^2}}}{{120{L^2}}}}&{\dfrac{{ - {L^2}}}{{315}} - \dfrac{{{h^2}}}{{360}}} \\ {\dfrac{1}{6}}&0&0&{\dfrac{1}{3}}&0&0 \\ 0&{\dfrac{9}{{70}} - \dfrac{{{h^2}}}{{10{L^2}}}}&{\dfrac{{13L}}{{420}} - \dfrac{{{h^2}}}{{120{L^2}}}}&0&{\dfrac{{13}}{{35}} + \dfrac{{{h^2}}}{{10{L^2}}}}&{\dfrac{{ - 11L}}{{210}} - \dfrac{{{h^2}}}{{120{L^2}}}} \\ 0&{\dfrac{{ - 13L}}{{420}} + \dfrac{{{h^2}}}{{120{L^2}}}}&{\dfrac{{ - {L^2}}}{{140}} - \dfrac{{{h^2}}}{{360}}}&0&{\dfrac{{ - 11L}}{{210}} - \dfrac{{{h^2}}}{{120{L^2}}}}&{\dfrac{{{L^2}}}{{105}} + \dfrac{{{h^2}}}{{90}}} \end{array}} \right] (6) 式(5)和式(6)分别通过行相加法，得到两种梁单元的集中质量矩阵Mf：
{{\boldsymbol{M}}_{{\rm{Zf}}}} = \rho bhL\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{2}}&0&0&0&0&0 \\ 0&{\dfrac{1}{2} + \dfrac{{{h^2}}}{{6L}}}&0&0&0&0 \\ 0&0&{\dfrac{1}{2} + \dfrac{{{h^2}}}{6}}&0&0&0 \\ 0&0&0&{\dfrac{1}{2}}&0&0 \\ 0&0&0&0&{\dfrac{1}{2} - \dfrac{{{h^2}}}{{6L}}}&0 \\ 0&0&0&0&0&{\dfrac{1}{2} + \dfrac{{{h^2}}}{6}} \end{array}} \right] (7) {{\boldsymbol{M}}_{{\rm{Bf}}}} = \rho bhL\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{2}}&0&0&0&0&0 \\ 0&{\dfrac{1}{2} + \dfrac{{3L}}{{140}} + \dfrac{{{h^2}}}{{60{L^2}}}}&0&0&0&0 \\ 0&0&{\dfrac{L}{{12}} + \dfrac{{2{L^2}}}{{315}} + \dfrac{{{h^2}}}{{120}}}&0&0&0 \\ 0&0&0&{\dfrac{1}{2}}&0&0 \\ 0&0&0&0&{\dfrac{1}{2} - \dfrac{{3L}}{{210}} - \dfrac{{{h^2}}}{{60{L^2}}}}&0 \\ 0&0&0&0&0&{\dfrac{{ - L}}{{12}} - \dfrac{{{L^2}}}{{420}} + \dfrac{{{h^2}}}{{120}}} \end{array}} \right] (8) 现从以下几个方面，考察两种梁理论的一致质量矩阵和集中质量矩阵：
1)矩阵的轮换性：MBf (Euler-Bernoulli梁)并不具备轮换性，即当梁单元结点进行轮换后，动力计算的结果与轮换前存在差异，这显然与实际情况矛盾。但在商业软件中(例如Abaqus、Ansys等)，由于Euler-Bernoulli梁的形函数矩阵的维度为1×6(一维线积分[14])，单元无法显示这种轮换性的缺陷。若进一步考虑梁单元变截面的情况，则会发现MZf具备MBf无法比拟的轮换性优势。(由于变截面显示公式的复杂性和冗长性，本文不再给出赘述，仅在附录1中给出“空心变截面梁单元”的推导结果)。
2)自由度的耦合项：虽然两种梁单元的一致质量矩阵，均具备考虑剪切变形的耦合项hi/Lj(i、j为自然数)，但MBc存在异常的耦合项Lj。异常的耦合项同时也是破坏矩阵轮换性的主要因素，并最终影响动力计算的精度。因此，当采用行相加法计算集中质量时，应将所有的耦合项置零。
3)转动惯性的影响：置零后的MBf转动质量为零，说明Euler-Bernoulli梁的集中质量矩阵实际上已经考虑了转动惯性的影响，但由于单元本身存在一定的缺陷，计算得到的转动质量为零。而插值梁的转动质量与平动质量相同。
4)梁尺寸的影响：由MZf和MBf可以得出，结构在进行动力分析时，一致质量矩阵各个自由度分配到的质量与梁长L、截面高度h有关。控制L不变，随着高跨比的减小(梁越细长)，MZc和MBc矩阵转动质量将逐渐减小，转动惯性对动力计算结果的影响将逐渐减小；当梁的高跨比趋于零时，插值梁转动质量系数趋于0.5，Euler-Bernoulli梁则没有此特性。
5)网格密度的影响：从几何矩阵BB、BZ中可以看出，插值梁兼具“细长梁”和“深梁”的计算要求。梁单元的网格剖分本质是改变梁单元的高跨比。由于Euler-Bernoulli梁仅适用于“细长梁”，在“深梁”中存在剪切闭锁效应，网格密度的增加并不能提高Euler–Bernoulli梁单元的计算精度。
2 数值模拟及动力计算
2.1 程序可靠性分析
为了说明本文自编的Python有限元程序计算结果的可靠性，对文献[16]中动力特性算例5.5和动力响应算例2.2进行分析。Python程序的动力特性、动力响应分别采用了系统模块numpy、自编的NewMark-β无条件收敛模块进行计算。图1和图2的计算结果与文献[16]基本一致，证明了本文Python程序动力特性和动力响应计算结果的可靠性。
![]()
图 2 算例2.2跨中结点竖向位移时程曲线图Figure 2. Time history curve of vertical displacement across middle nodes of Example 2.22.2 建立有限元模型
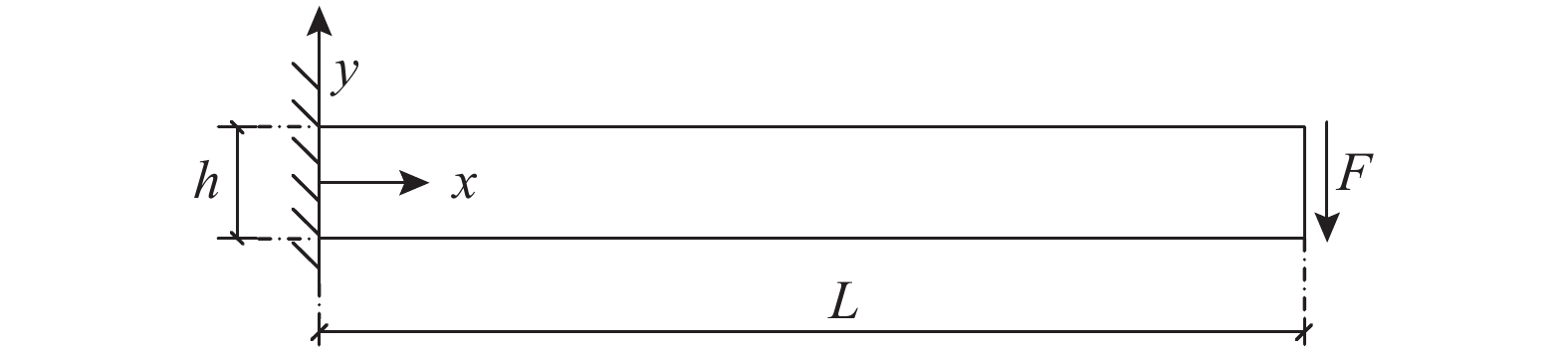
为了便于对比分析、模型复现，并降低程序的截断误差或舍入误差，采用图3所示平面悬臂梁结构，并定义程序的录入参数(国际单位制SI)：悬臂梁为无阻尼理想弹性材料，加速度为北京地区的重力加速度9.798 m/s2，密度ρ=1 kg/m3，梁长L=1 m，实腹矩形等截面0.03 m×0.04 m(宽×高)，悬臂端集中荷载F=1 N(常数)，弹性模量E=1 kPa，泊松比µ=0，初始时间步长为0.001 s(等步长)，迭代总时间为1 s。分别采用Euler-Bernoulli梁单元(二维面积分单元)、插值梁单元(二维面积分单元)进行分析。
2.3 数值模拟
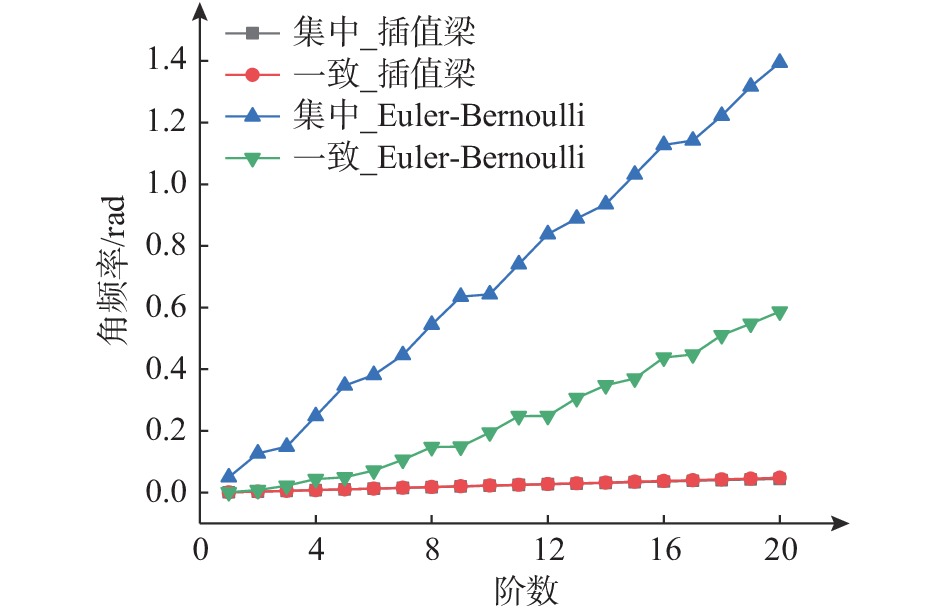
将梁单元进行等长度网格剖分，设置一些列单元数目梯度：1, 2, 4, …, 64。附录2为Python程序的结果文件。图4为剖分成64个单元的时程曲线图。图5为剖分成64个单元的前20阶角频率曲线图。图6为两种梁单元的收敛性分析图。
![]()
图 4 悬臂端竖向位移时程曲线图Figure 4. Time history curve of vertical displacement of cantilever beam从图5可以发现：两种质量矩阵的插值梁角频率差异微小，相对误差最大为−7.33% (第20阶)；而Euler-Bernoulli梁的角频率差异较大，且随着振型阶数的增大，两种质量矩阵计算的角频率差异也逐渐增大，相对误差最大为+3770.11% (第1阶)。插值梁的低阶角频率与Euler-Bernoulli梁差异较小，两者高阶角频率差异较大。
![]()
图 6 悬臂端竖向位移与网格密度的曲线图Figure 6. Vertical displacement of cantilever beam and mesh density curve从图4中可以发现，当梁理论相同时，一致质量的位移计算值小于集中质量；插值梁的两种质量矩阵的竖向位移差异较小，相对误差为−8.50%；而Euler-Bernoulli梁的竖向位移差异较大，两种质量矩阵计算值的相对误差为+66.61%。相较于一致质量矩阵，集中质量矩阵的动力响应受到高阶振型的影响较大，梁端转角与竖向位移的相位存在明显的差异。
基于有限元的基础定理：随着网格的不断加密(无异常网格)，有限元的计算结果应收敛于力学模型的理论解，当简化的力学模型能够最大程度地模拟真实结构时，数值解将趋于结构的真实解。
在图6中，随着网格的加密，两种梁单元一致质量矩阵计算得到的竖向位移逐渐收敛，随着单元数目的增大，存在较小的波动；而Euler-Bernoulli梁的集中质量矩阵则出现异常，曲线图在单元数目为32时，出现明显的“非平滑点”，验证了第1节中，“网格加密并不能提高Euler-Bernoulli动力响应的计算精度”的结论。因此，Euler-Bernoulli梁两种质量矩阵的差异性，证明了该梁单元的计算结果不可靠。而插值梁的集中质量矩阵和一致质量矩阵的计算误差、收敛趋势、特征点的单元数目基本一致，证明了插值梁在动力计算的优越性。
3 结论与展望
基于两结点双线性插值梁理论和Euler-Bernoulli梁理论，通过自编的Python有限元程序，对一致质量矩阵和集中质量矩阵的动力响应和动力特性进行分析，得到如下结论：
(1)梁单元的动力响应计算，必须进行网格剖分，较低的网格密度无法得到收敛的响应结果。
(2) Euler-Bernoulli梁单元的动力响应计算，应优先采用一致质量矩阵。当采用集中质量矩阵时，较高或较低密度的网格尺寸，会降低动力响应的计算精度。
(3)“两结点双线性插值梁单元”集中质量矩阵的转动质量与网格密度、单元尺寸有关；Euler-Bernoulli梁的集中质量矩阵实际上已经考虑了转动惯性的影响，但由于单元本身存在一定的缺陷，计算得到的转动质量为零。
虽然“两结点双线性插值梁单元”由于位移模式的完备性，解决了集中质量矩阵中转动质量“不确定”的缺陷，且动力计算结果证明了插值梁理论的正确性、单元构造方法的有效性。但从应用角度出发，单元的计算值与经典理论存在较大的差异。从文献[15]单元刚度的轴向拉压刚度可以看出，分离弹性模量E中的“截面泊松效应”，并进行足尺实验，是作者下一步的主要工作。
附录1：变截面和空心情况的一致质量矩阵(平面局部坐标系)
符号说明：
h_1、b_1：外部矩形截面的高度、宽度
h_2、b_2：内部矩形截面的高度、宽度
r_1、r_2：外部圆形截面的半径、内部圆形截面的半径
ration_1：1结点外部截面尺寸与2结点外部截面尺寸的比值(默认外部1、2结点处截面形心重合)
ration_2：1结点内部截面尺寸与2结点内部截面尺寸的比值(默认内部空心1、2结点处截面形心重合)
pi：圆周率π
Density，L：梁单元的密度，长度
Python公式推导程序运行结果：
![]()
1 一致质量矩阵(两结点双线性插值梁)1. Uniform mass matrix (Bilinear interpolation beam with two nodes)附录2：Python程序计算结果
说明：Python程序具备GUI界面，用Excel(*.xlsx)文件进行数据读取和结果存储。
-
![]()
图 2 算例2.2跨中结点竖向位移时程曲线图
Figure 2. Time history curve of vertical displacement across middle nodes of Example 2.2
![]()
图 4 悬臂端竖向位移时程曲线图
Figure 4. Time history curve of vertical displacement of cantilever beam
![]()
图 6 悬臂端竖向位移与网格密度的曲线图
Figure 6. Vertical displacement of cantilever beam and mesh density curve
![]()
1 一致质量矩阵(两结点双线性插值梁)
1. Uniform mass matrix (Bilinear interpolation beam with two nodes)
-
[1] 郑艳, 车树汶. 不同质量矩阵对桥梁自振特性的影响分析[J]. 哈尔滨商业大学学报(自然科学版), 2007, 23(2): 241 − 244. doi: 10.19492/j.cnki.1672-0946.2007.02.028 ZHENG Yan, CHE Shuwen. Influence of different quality matrix on natural vibration characteristic of bridges [J]. Journal of Harbin University of Commerce (Natural Sciences Edition), 2007, 23(2): 241 − 244. (in Chinese) doi: 10.19492/j.cnki.1672-0946.2007.02.028
[2] 车树汶, 陈权, 楼松庆. 质量矩阵模式对桥梁自振频率的影响[J]. 兰州铁道学院学报(自然科学版), 2003, 22(6): 80 − 83, 98. CHE Shuwen, CHEN Quan, LOU Songqing. Influence of mass matrix model on natural vibration frequency of bridges [J]. Journal of Lanzhou Railway University (Natural Sciences), 2003, 22(6): 80 − 83, 98. (in Chinese)
[3] 钱伟长. 具有对角线化的一致质量矩阵的动力有限元和弹塑性撞击计算[J]. 应用数学和力学, 1982, 3(3): 281 − 296. QIAN Weichang. Dynamic finite element with diagonalized consistent mass matrix and elastic-plastic impact calculation [J]. Applied Mathematics and Mechanics, 1982, 3(3): 281 − 296. (in Chinese)
[4] 刘瑞岩. 全耦合梁单元的一致质量矩阵[J]. 国防科技大学学报, 1984(1): 101 − 108. LIU Ruiyan. Consistent mass matrix for complete coupled beam elements [J]. Journal of National University of Defense Technology, 1984(1): 101 − 108. (in Chinese)
[5] 汪梦甫, 王朝晖. 两种质量矩阵在梁模态分析中差异的比较[J]. 地震工程与工程振动, 2006, 26(6): 83 − 86. doi: 10.13197/j.eeev.2006.06.014 WANG Mengfu, WANG Zhaohui. Analysis of differences between two types of mass matrixes in beam modal analysis [J]. Earthquake Engineering and Engineering Vibration, 2006, 26(6): 83 − 86. (in Chinese) doi: 10.13197/j.eeev.2006.06.014
[6] 杨亚平, 沈海宁. 集中质量矩阵替代一致质量矩阵的合理性与局限性[J]. 青海大学学报(自然科学版), 2010, 28(1): 35 − 39. doi: 10.13901/j.cnki.qhwxxbzk.2010.01.011 YANG Yaping, SHEN Haining. The rationality and limitation on the substitution of the concentrated mass matrix for the consistent mass matrix [J]. Journal of Qinghai University (Nature Science), 2010, 28(1): 35 − 39. (in Chinese) doi: 10.13901/j.cnki.qhwxxbzk.2010.01.011
[7] 左占宣. 基于力的梁—柱单元一致质量矩阵和集中质量矩阵[D]. 哈尔滨: 哈尔滨工业大学, 2010. ZHUO Zhanxuan. Consistent and lumped mass matrixes for force-based beam-column element [D]. Harbin: Harbin Institute of Technology, 2010. (in Chinese)
[8] WU S R. Lumped mass matrix in explicit finite element method for transient dynamics of elasticity [J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(44/45/46/47): 5983 − 5994.
[9] WU S R, QIU W F. Nonlinear transient dynamic analysis by explicit finite element with iterative consistent mass matrix [J]. Communications in Numerical Methods in Engineering, 2009, 25(3): 201 − 217. doi: 10.1002/cnm.1110
[10] HINTON E, ROCK T, ZIENKIEWICZ O C. A note on mass lumping and related processes in the finite element method [J]. Earthquake Engineering & Structural Dynamics, 1976, 4(3): 245 − 249.
[11] PARK K C, JENSEN D D. A systematic determination of lumped and improved consistent mass matrices for vibration analysis [C]// Proceedings of the 30th Structures, Structural Dynamics and Materials Conference. Mobile: AIAA, 1989: 1532 − 1540.
[12] ARCHER G C, WHALEN T M. Development of rotationally consistent diagonal mass matrices for plate and beam elements [J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(6/7/8): 675 − 689.
[13] 高岱恒, 郭宏伟, 郑宏. 梁动力分析的集中质量矩阵严格生成方法[J]. 长江科学院院报, 2019, 36(4): 118 − 122, 139. GAO Daiheng, GUO Hongwei, ZHENG Hong. A rigorous mass lumping scheme for vibration of beams [J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(4): 118 − 122, 139. (in Chinese)
[14] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003. WANG Xucheng. Finite element method [M]. Beijing: Tsinghua University Press, 2003. (in Chinese)
[15] 张尧, 董军, 李国华, 等. 两结点双线性插值梁单元[C]. 广州: 第30届全国结构工程学术会议论文集(第Ⅱ册), 2021: 131 − 138. ZHANG Yao, DONG Jun, LI Guohua, et al. Two-node bilinear interpolation beam element [C]. Guangzhou: Proceedings of the 30th National Conference on Structural Engineering (No. II), 2021: 131 − 138. (in Chinese)
[16] 徐斌, 高跃飞, 余龙. MATLAB有限元结构动力学分析与工程应用[M]. 北京: 清华大学出版社, 2009. XU Bin, GAO Yuefei, YU Long. MATLAB finite element structural mechanics analysis and engineering application [M]. Beijing: Tsinghua University Press, 2009. (in Chinese)
下载:
计量
- 文章访问数: 337
- HTML全文浏览量: 79
- PDF下载量: 69
