HORIZONTAL LOAD TRANSFER MECHANISM OF COMPOSITE CABLE TOWER ANCHORAGE ZONE WITH EXPOSED STEEL ANCHOR BOX
-
摘要:
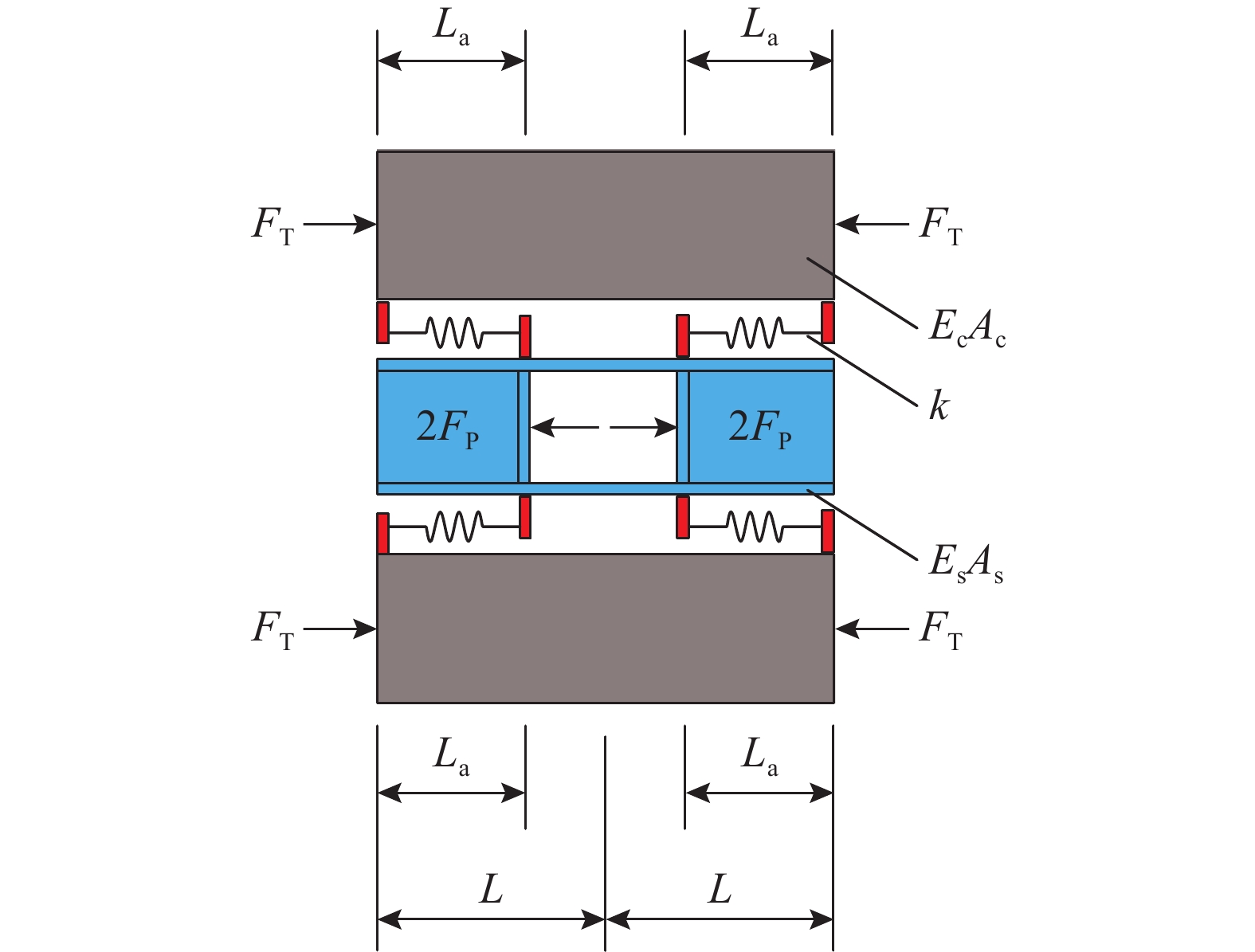
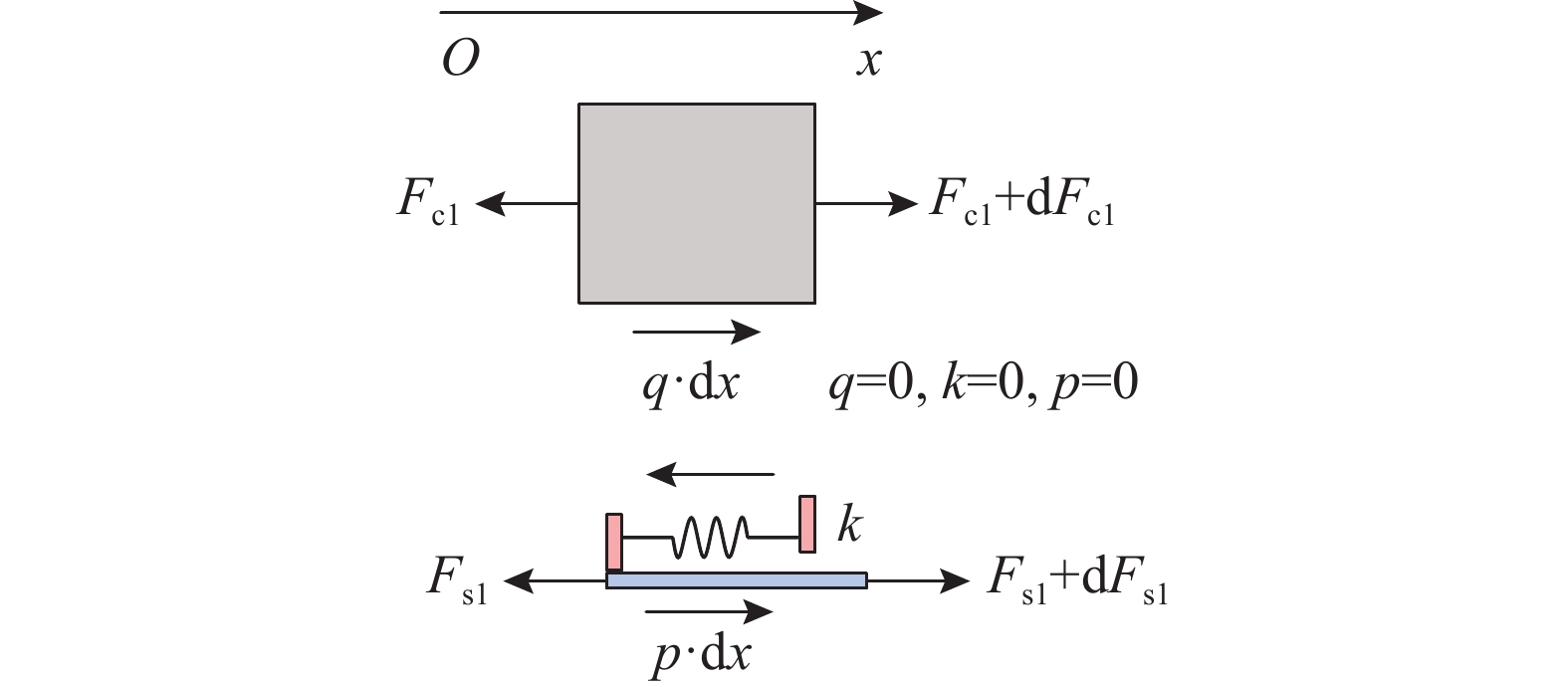
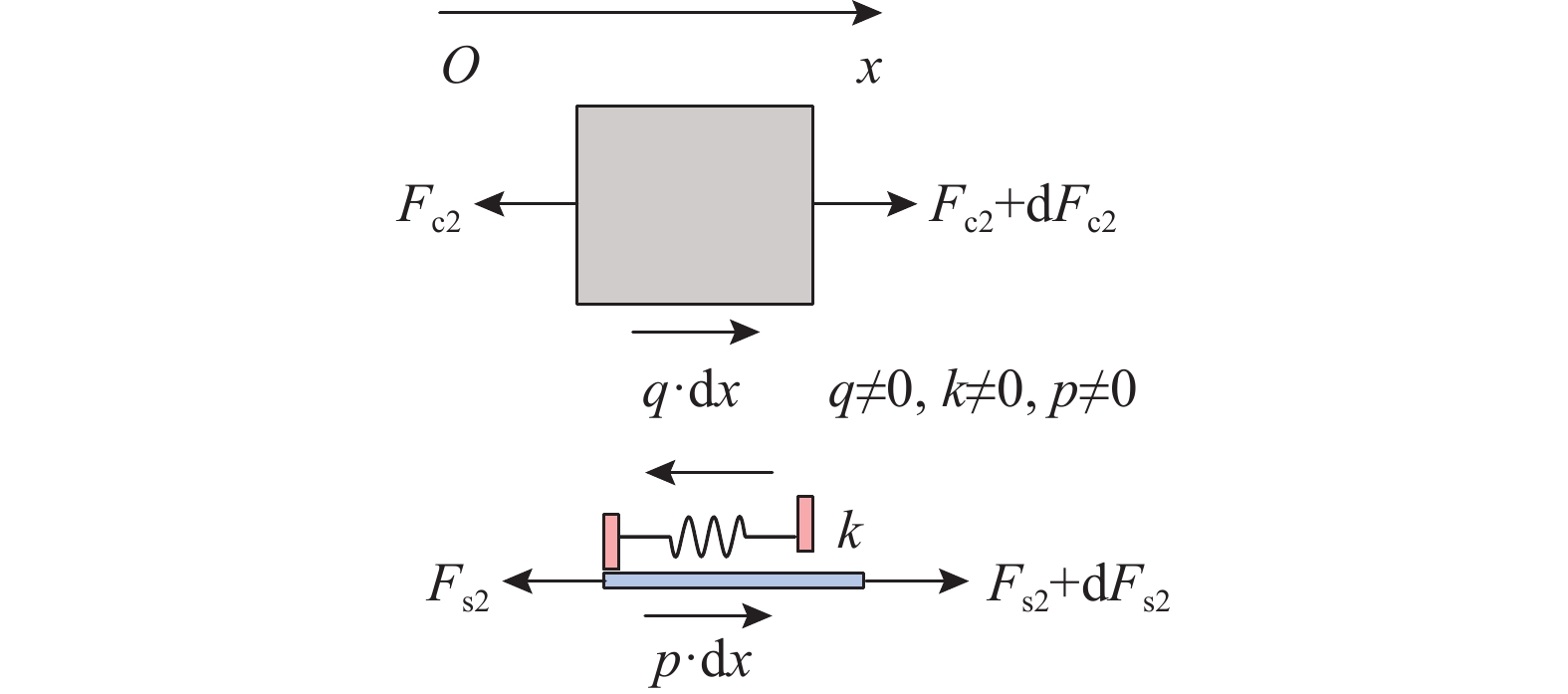
为揭示外露型钢锚箱组合索塔锚固区水平传力机理,基于弹性介质层法推导钢锚箱壁板-混凝土塔壁结合面滑移的理论计算式,进而得到连接件剪力流、钢与混凝土构件轴力的计算方法。通过平截面假定、理论计算式与锚固区节段模型试验结果的比较,验证理论计算式合理性并进行参数化影响分析。研究结果表明:顺桥向预应力和水平索力同时作用时,钢混结合面最大相对滑移0.055 mm,焊钉连接件最大剪力15.99 kN,钢锚箱侧壁板受拉应力6.55 MPa,混凝土塔壁受压应力−1.07 MPa;钢锚箱侧壁板、混凝土塔壁承担顺桥向预应力的比例为10%和90%,水平索力的比例为26%和74%;锚固区水平传力机理受钢锚箱侧壁板厚度、混凝土塔壁厚度、结合面传力长度、连接件抗剪刚度与顺桥向预应力作用的影响很大。
Abstract:In order to reveal the horizontal load transfer mechanism in the composite cable tower anchorage zone with exposed steel anchor box, a theoretical calculation formula for the relative slip between steel anchor box side plate and concrete tower wall is derived upon the elastic medium layer method, and then the calculation methods of shear flow of connectors and axial forces of steel and concrete members are obtained. Through the comparison of plane section assumptions, theoretical calculation formulae and segment model test results of anchorage zone, the rationality of theoretical calculation formulae proposed is verified, and parametric influence analysis is carried out. The results show that: the maximum relative slip of the steel-concrete interface is 0.055 mm, the maximum shear force of the stud connectors is 15.99 kN, the tensile stress of the steel anchor box side plate is 6.55 MPa, and the compressive stress of the concrete tower wall is −1.07 MPa. The proportion of prestress along the bridge direction between steel anchor box side plate and concrete tower wall is 10% and 90%, and the proportion of horizontal cable force is 26% and 74%. The horizontal force transfer mechanism of anchorage zone is greatly influenced by the thickness of steel anchor box side plate, by the thickness of concrete tower wall, by the force transfer length of steel-concrete interface, by the shear stiffness of connectors and, by the prestress along the bridge direction.
-
藏式古建筑木结构是西藏人民的伟大创造,是雪域高原物质文明和精神文明的结晶,也是藏汉团结和文化交流的见证(见图1(a))。遗憾的是,环境因素和人为因素使得藏式古建筑木结构出现各种形式的损伤。北京交通大学古建筑结构研究所人员经过实地考察发现,藏式古建筑木结构中出现木材的腐朽、虫蛀和裂缝,梁构件的下挠、外闪和扭曲,柱构件的倾斜和弯曲,见图1(b),这些损伤极大地威胁着藏式古建筑木结构的健康状态。
预防性保护[1]观念的普及,使得目前藏式古建筑木结构中已经布设了完整的健康监测系统[2]。在健康监测系统中,光纤光栅传感器最为普遍,用于获取构件的应变监测数据,以反映结构的健康状态。
对于结构健康监测数据的挖掘,能够获得更多的结构健康状态信息,有利于结构的保护。例如:1)挖掘结构健康监测数据,解释桥梁和建筑结构在荷载作用和环境作用下的动力行为、静力行为、力学机理、演化过程等,为结构保护工作奠定基础[3-4];2)使用结构健康监测数据挖掘结果,进行荷载作用、环境作用、结构响应、结构性能等统计模型建立,明确结构保护方向[5];3)通过结构健康监测数据挖掘,获取预警值,并评估其寿命,为结构保护建立可靠阈值[6];4)基于健康监测数据的挖掘结果,校验结构全寿命设计理论、可靠度预测理论、安全风险评估理论以及新型建筑结构和桥梁结构的设计理论、假定等[7]。
对于现代建筑结构和桥梁结构,挖掘结构健康监测数据获取结构健康状态信息的方法较为成熟。对于藏式古建筑木结构中光纤光栅传感器提供的应变监测数据的挖掘却十分少见,这已经阻碍了藏式古建筑木结构的保护工作。究其原因,藏式古建筑木结构结构监测系统初立,且其材料类别、构件连接、结构形式、激励种类、响应类别均十分特殊,这使得藏式古建筑木结构监测物理量、监测方法、监测仪器、监测要求均有别于现代建筑结构和桥梁结构,致使目前已有的数据挖掘方法存在适用性问题。更值得注意的是,现代建筑结构和桥梁结构依照明确的规范进行设计和建造,结构的用材、尺寸、荷载、损伤、维修加固、边界条件均清晰。故此,在监测物理量到达阈值时,结构往往存在一定的延性,目前在线监测数据的时时分析可以满足结构安全性要求[8]。而藏式古建筑木结构建造年代久远,结构建造过程往往凭借经验,结构相关的一切条件均存在较大的不确定性,在监测物理量到达阈值时,这些不确定性可能会导致脆性破坏的发生,结构安全冗余度差,无法到达预防性保护的效果。矛盾的是,盲目降低阈值会极大的增加维修费用,与最小干预的保护准则相悖,严重影响藏式古建筑木结构的价值。故此,本文将对藏式古建筑木结构应变监测数据进行短期预测,通过预测数据与阈值的比对,能够提前悉知结构的异常,采用合适的手段合理增加结构安全冗余度。这样既能做到藏式古建筑木结构的预防性保护,又能满足保护过程中的最小扰动原则,避免盲目修缮带来的损伤和浪费。避免盲目维修带来的损失。本文研究框架见图2。
1 研究对象介绍
1.1 监测主体
监测主体为某藏式古建筑建筑群(建筑群位于中国西藏自治区首府拉萨市区西北的玛布日山上,属于西藏政教合一的统治中心,见图3(a))中的一个三层回廊结构,该结构目前对游客开放,见图3(b)。以此结构作为本文分析对象是因为:该结构的结构形式、构件形式、连接形式、材料形式能够代表藏式古建筑木结构;该结构处于整个建筑群的枢纽位置,连接建筑群中最为重要的两个宫殿;该结构所受激励(如光照、游客)和存在的损伤形式同样具有代表性。
为方便后续分析,本节将对监测主体进行简要介绍,监测主体主要依靠内部的木框架承担荷载,外部石墙作为监测主体的围护结构。木框架中的柱和梁依靠雀替(弓木和垫木)进行荷载的均匀分布,梁、柱、弓木、垫木、坐斗之间使用暗销连接。梁与梁间采用类似“燕尾榫”的方式连接,共同组成较长的“通梁”,边跨梁嵌入到石墙中,故中间跨的梁端为“半刚性”连接,而边跨梁端为固定端连接。梁上浮搁厚重的楼板,楼板由椽子、阿嘎土、鹅卵石等组成,具体结构形式见图4[2, 9]。
1.2 监测系统
由于回廊结构受人为因素和环境因素的双重影响,2012年11月1日北京交通大学古建筑结构研究所在回廊结构中布设光纤光栅应变传感器,梁传感器布设于梁底部跨中位置(见图5(a)),柱传感器布设于柱半高处(见图5(b)),回廊为三层结构,回廊结构中2层楼面和3层楼面承受人群荷载,因此应变传感器布设于一层柱和其顶面的梁上,二层柱和其顶面的梁上,用于监测人群和温度引起的应变。回廊结构三层柱和其顶面的梁同样布设应变传感器,仅用于监测温度引起的应变,回廊结构各层位置见图3(b),各层监测点位详图,见图5(c)~图5(e),图中标记了游客游览路径和阳光入射位置,以方便述清应变与温度和人群的相关性。传感器获取的所有数据通过北京基康科技股份有限公司的BGK-FBG-8600型16通道的数据采集仪采集和传输。从2012年11月1日起,监测系统中的每个传感器每小时采集一次构件的应变监测数据和其对应的温度监测数据。
1.3 数据特征
监测主体中监测数据具有如下特征:
1)由于监测主体具有千百年的历史,故光纤光栅传感器记录的监测数据仅为相对值[10]。初始变形,尤其是结构自重带来的初始应变的影响不会表现在监测数据中。
2)温度监测数据具有日周期(即一日之内中午温度到达最大值,夜晚温度到达最小值)和年周期(即一年之内夏季温度到达最大值,冬季温度到达最小值)。
3)应变监测数据是多种影响因素共同叠加的结果,对于监测主体(回廊结构)来说,应变的主要影响因素是环境温度和人群荷载,这一点在文献[9]和文献[10]中进行了详细的描述。
4)回廊结构中应变监测数据与温度监测数据存在明显的相关性,温度是应变监测数据变化的主要诱因,后续章节将通过时域和频域两种方法证明这一点。
5)西藏地区相对湿度低,且湿度变化量小,阳光的直射会使回廊结构昼夜温差较大,导致监测主体虽是木结构,但是湿度对其应变监测数据的影响较小,可以忽略。
6)回廊结构对游客开放,且在旅游旺季时,每天游客数量巨大(日接待游客量最高可达6000人次),人群荷载已经成为应变监测数据中不可忽视的影响因素。另外,结构本身具有宗教、文化价值,游客会保持缓慢有序的游览,未有跑跳现象,且回廊结构中楼板厚度可达750 mm~1000 mm,故人群荷载引起的应变是静态、缓慢的,这与大跨结构、人行天桥,长悬臂结构、看台上人群荷载引起的应变不同,不需考虑人群荷载动力特征[11-12]。
图6中将展示光纤光栅传感器记录的温度监测数据和应变监测数据,数据区间为2012年11月1日−2020年11月1日,共8年数据,所展示数据为原始数据,故存在失真现象。
2 失真应变监测数据处理
2.1 数据失真的概念与分类
在监测主体实际监测过程中,传感器自身误差、现场环境噪声、传感器性能衰退、设备断电及数据采集与传输故障等原因会导致失真应变监测数据的出现。失真应变监测数据中不但不包含监测主体结构状态改变的有效信息,且会干扰监测主体结构异常的判断,因此在使用应变监测数据对监测主体结构异常进行判断前,需对失真应变监测数据进行识别和剔除。
结合本文监测主体历年应变监测数据的实际情况可知,光栅光纤传感器正常工作时间占多数,失真数据占比较少,监测主体采集的应变监测数据中常见数据失真模式有数据缺失、数据重复、离群值[2]。
数据缺失主要表现形式为单个或多个数据在时间轴上的缺失。数据重复主要表现形式为多个数据不随时间的增长而变化,即变化率为0。离群值主要表现形式为单个或多个数据与两侧数据不连续,变化率较大,且其变化率异常值超出正常变化范围,除去异常数据后,两侧数据回归连续变化。上述失真模式的图示如表1所示。
表 1 应变监测数据失真模式Table 1. Distortion modes of strain monitoring data编号 异常模式 现象 图例 1 数据缺失 曲线不连续,缺失部分显示为空白 
2 数据重复 曲线存在不随时间改变的直线 
3 离群值 曲线中存在不合常理的跳点 
2.2 基于Sobel+CNN的失真监测数据处理方法
目前现代建筑结构和桥梁结构健康监测领域中提出多种失真监测数据的处理办法,大多数依赖于基于距离、密度和聚类等诊断方法,但是目前的方法侧重于单一模式失真监测数据的处理,多模式失真监测数据处理则存在误检问题[13]。
为适应监测主体中失真应变监测数据的特征,本节将失真应变监测数据处理过程分解,即使用计算机视觉代替人眼的数据获取过程,使用深度学习代替大脑的数据决策过程,故提出一种Sobel算子和卷积神经网络(Convolutional neural net,CNN)结合的失真应变监测数据处理方法,方法具体实现过程如下:
步骤1(基于Sobel算子的数据可视化):查看2012年11月1日−2020年11月1日内所有光纤光栅传感器提供的应变和温度监测数据,以7日为一段,采用无重叠的加窗方式将原始数据分割成多段。该分段能够清晰地展示表1中给出的3种应变监测数据失真模式。将分割好的数据进行图像化处理,为了简化运算,使用灰度化的处理方式将图片转为灰度图片,使得每个像素点能够使用0~255的灰度值表达。其后,将每段图片分辨率设为100×100像素,以平衡图像的清晰度和经济的数据存储需求。因为后续深度学习过程需要以图片的像素值和像素值变化为指标,故增强背景和数据线上像素点的灰度值差异将有利于提高后续深度学习算法的精度,因此本节引入Sobel算子对图像进行处理。Sobel算子常被用于边缘检测,即使用3×3矩阵和其转置矩阵对图像进行卷积,用来计算图像灰度的近似梯度,梯度大的地方则为图像边缘。对于应变监测数据生成的图像来说,数据本身即是边界,故使用Sobel算子能够增强背景和数据线上像素点的灰度值差异,具体结果见图7。
步骤2(基于CNN的数据深度学习):深度学习是目前人工智能技术的核心领域,与机器学习相比,深度学习能够获得研究对象间的非线性关系,卷积神经网络是深度学习的重要组成部分之一。卷积神经网络(CNN)是一种包含卷积算法的前馈式深度学习方法,其基本结构包括输入层(Input layer)、卷积层(Convolutional layer)、池化层(Pooling layer)、全连接层(Fully connected layer)、输出层(Output layer)五部分,如图8所示。
过程中最为关键的是卷积层,卷积层由卷积核对输入图片的特征进行提取、位置进行编码,其中卷积层的计算式如下:
yli=f(n∑i=1xl−1i⋅ωl−1ij+blj),j∈[1,J] (1) 式中:
yli 为第l层第i个神经元输出值;xl−1i 为第l−1 层中第i 个神经元的输入值;ωl−1ij 为第l−1 层中第i 个神经元与第j 个神经元的连接权值;blj 为第l层第j 个神经元的偏置值;f(⋅) 为激活函数,此模型在卷积层与池化层之间取ReLU函数作为激活函数,可以很好地解决卷积神经网络的梯度消失问题。对监测主体提供的应变监测数据进行浏览,获取先验知识集。对随机选取的应变监测数据进行可视化处理,获取正常样本个数为27 230个、异常样本中数据缺失样本个数为5975个、数据重复样本个数为3000个、离群值样本个数为15 040个,总样本数共计51 245个。值得注意的是,上述数据属于先验知识集数据,而非完整的原始监测数据。上述数据比例与使用者对于模型的需求有关,也与不同数据异常间的比例有关,同时为了降低误识别率,先验知识集中保留了大量的正常数据样本。对先验知识集中的数据打标签,正常样本标签为“normal”,数据缺失样本标签为“missing”,数据重复样本标签为“duplication”,离群值样本标签为“outlier”。将先验知识集以6:2:2的比例分离为训练集、验证集和测试集。
使用训练集训练模型,训练该模型时长为216 min,其精度可达到95.24%,训练过程如图9所示。验证集通常被用来调参,以增加训练模型的泛化能力,过程与使用训练集训练过程一致。
步骤3(模型精度评价):训练完成后保存模型,使用测试集评价该模型的精度,评价指标为混淆矩阵。混淆矩阵以矩阵的形式可视化呈现分类结果的好坏,评价结果见图10。图10中混淆矩阵将数据分为4类,第一行(列)代表数据重复的预测结果(真实结果),第二行(列)代表数据缺失的预测结果(真实结果),第三行(列)代表正常数据的预测结果(真实结果),第四行(列)代表离群值的预测结果(真实结果)。混淆矩阵非主对角线元素为误分类数量和占比,主对角线元素为正确分类数量和占比,混淆矩阵主对角线上元素越接近100%,证明CNN训练模型精度越高。
使用Sobel+CNN方法能够精确地识别监测主体应变监测数据中的失真数据,准确度高达96.1%。利用Python中的Numpy和Scipy将识别到的失真数据进行填充和替换,填充和替换的数值根据两侧数据的插值选取。使用Sobel+CNN方法对监测主体中的应变监测数据进行批量处理,处理后的数据用于后续章节的分析。
3 应变监测数据解耦
应变监测数据是判断结构健康状态的常用量,本节将使用经过2.2节方法处理后的数据,即可认为该数据中不包含传感器原因导致的数据异常,数据中的异常可以视为结构健康状态异常的表达。本节将应变监测数据按照激励方式进行解耦,以方便后续对结构健康状态的评估。
值得注意的是,由于藏式古建筑木结构构件间的连接形式为“半刚接”,温度引起的热胀冷缩会产生温度应力,而这种循环往复的温度应力会导致藏式古建筑木结构的累计损伤,故此回廊的应变监测数据解耦后获取的温度应变与结构异常相关,该温度应变解耦后应该被保留,并对其进行预测,作为结构健康状态评估的依据。上述论述与现代建筑结构和桥梁结构不同,因为温度伸缩缝的存在,导致这些结构不会因为温度产生温度应力,故此现代建筑结构和桥梁结构应变监测数据中温度应变与结构损伤无关,这种结构正常的“呼吸”会掩盖结构的真实损伤,往往需要解耦后剔除[14]。
3.1 应变监测数据激励方式分类
监测主体获取的应变监测数据可以分为温度应变(由环境温度导致)和人群应变(由游客导致):
ε=εT+εC (2) 式中:ε为监测获取的总应变;εT为温度应变;εC为人群应变。温度激励产生的应变是周期性的、缓变的,而人群激励产生的应变是随机的、突变的,这两种激励方式引起的应变特征不同,故需解耦后分别预测。本节分别通过多项式回归和功率谱密度两种方式证明应变监测数据与温度具有极高的相关性,即温度应变占应变监测数据比重较大。
1)多项式回归:多项式回归是一种能够直观呈现两变量相关关系的方法,如式(3)所示:
F(x)=anxn+an−1xn−1+⋯+a1x+a0 (3) 式中:
F(x) 为响应变量;x 为其自变量;an 为各项回归系数。两个变量间的相关关系可通过决定系数
R2 衡量,R2 计算公式如式(4)所示:R2=n∑i=1(ˆxi−ˉx)2n∑i=1(xi−ˉx)2 (4) 式中:
xi 为待拟合数值,数据均值为ˉx ,每一点的拟合值为ˆxi ,R2 取值越接近于1,可认为多项式回归结果越好。本节选择回廊结构中任意光纤光栅传感器,获取其温度和应变监测数据,随机选取该传感器2019年全年数据,如图11所示。将温度监测数据和应变监测数据放置于同一张图中,按照月份进行分段拟合,拟合函数选取一元二次多项式,以描述“半刚性”连接导致的非线性,各月份的决定系数R2见表2。
表 2 各月份决定系数R2Table 2. Coefficient of determination R2 of each month月份 1 2 3 4 5 6 R2 0.85 0.87 0.86 0.87 0.89 0.84 月份 7 8 9 10 11 12 R2 0.76 0.75 0.77 0.87 0.88 0.89 通过表2中数据可以看出,大部分月份中温度监测数据与应变监测数据具有极高相关性,R2大于0.8,这可说明温度应变占总监测应变的比例较大,仅有7月、8月、9月份相关性略低,是因为上述月份为藏式古建筑木结构旅游旺季,人群应变占比变高。
2)功率谱密度:功率谱密度(Power spectral density,PSD)是表征信号功率能量与频率间关系的物理量,当两个变量主频一致,即两个变量在频域中同时达到极值时,可以认为两个变量具有极高的相关性,温度监测数据和应变监测数据的PSD分析结果见图12,两者主频一致,具有极高的相关性。
将回廊结构获取的应变监测数据中的温度应变解耦后,剩余部分可以认为由游客引起,即可以认为是人群应变,文献[2]和文献[9]通过试验和计算方法充分地证明了上述论述,在此不再赘述。
3.2 基于激励方式的应变监测数据解耦
将总监测应变分解为具有周期性的温度应变和非周期的人群应变,其本质是将信号分解为不同频率的子信号。小波变换、滑动窗口平均法、主成分分析、经验模式分解、希尔伯特振动分解等方法均有上述功能。变分模态分解法(Variational mode decomposition,VMD)[15]在上述算法基础上发展而来,该方法将分类的获取过程转移到变分框架内,采用一种非递归的处理策略,通过构造并求解约束变分问题实现原始信号的分解,以有效避免已有方法的模态混叠、过包络、欠包络、边界效应等问题,具有较好的复杂数据分解能力,VMD方法的核心公式如下:
{min (5) 式中:
{u_k} 为分解获得的k个模态分量;{\omega _k} 为每个模态分量的中心频率;f(t) 为原始信号,同样是约束条件,确保所有的子信号分量之和为原始输入信号。同样随机选取监测主体中某一光栅光纤传感器获取的应变监测数据,使用VMD方法对应变进行解耦得到温度应变(图13(a))和人群应变(图13(b))。数据范围为2012年11月1日−2020年11月1日。通过温度应变图可以看出:1)每年11月~12月,由于环境温度的降低,构件比初始状态收缩,温度应变转为负值;2)每年1月~3月是拉萨一年中最冷的时间,温度引起的应变达到一年中的最小值;3)环境温度升高后,构件由收缩变为膨胀。从每年的6月~7月,构件相对于初始状态膨胀,因此温度引起的应变转为正值;4)每年8月~10月是拉萨市一年中最热的时间,温度引起的应变达到全年最大值。图13(a)可以证明基于VMD方法获取的温度应变的正确性。
从2012年11月−2013年3月,人群应变较大。从2013年5月起,西藏政府限制游客数量,以保护监测主体。在西藏旅游淡季,监测主体每天最多可接待游客3000人;在西藏旅游旺季,监测主体每天的最大游客人数可达6000人。从图13(b)可清晰地看出,在游客人数限制之后,人群应变明显下降。西藏旅游的旺季为每年6月~10月,该时间段的人群应变比其他月份要大得多,在此期间,人群应变峰值屡屡出现。同时,在藏历新年当天,监测主体不限制游客数量,故藏历新年当天的人群应变往往高于西藏旅游淡季(1月~5月、11月和12月)的其他时间。另外,对上述分解的数据进行局部检查,随机抽取几天(仅展示2天)的总应变数据、温度应变数据和人群应变数据,如图13(c)~图13(f)所示。经过对数据的细致检查发现,人群应变在晚间往往降为零,仅有部分噪声干扰,即晚间没有游客时,总应变基本为温度应变。上述可证明,温度和人群是监测应变变化的主导因素,亦是结构损伤的主导诱因,也可证明基于VMD方法获取的温度应变和人群应变数值的正确性。
4 应变预测
4.1 基于Prophet算法的温度应变预测
通过积累八年的历史数据可知,温度应变是占总监测应变比例较大,“半刚性”连接使得温度应力会不间断循环作用于监测主体,从而造成累计损伤。因此,对温度应变进行预测,并获取其中峰值,可作为结构健康状态评估的依据。
通过解耦后的结果(图13(a))可以看出,温度应变每年的变化趋势平稳,其中异常值(人群应变)已经被分离。本节采用Prophet算法对温度应变进行预测。Prophet算法是2017年TAYLOR和LETHAM[16]基于Python平台开发的开源算法。模型核心公式如下:
{y_t} = S(t) + T(t) + H(t) + {\varepsilon _t} (6) 式中:
S(t) 为周期项,该项使用正弦和余弦函数描述和预测温度应变的周期性;T(t) 为趋势项,该项使用逻辑回归的方法描述和预测温度应变带来的累计损伤;H(t) 为突变项,用于定义环境温度骤然升降带来的温度应变的突变;剩余项为{\varepsilon _t} ,用于描述拟合后的误差,假设其为服从一维高斯分布的噪声因子。该模型预测精度通过准确率指标(Accuracy,ACC)表示,该指标为机器学习中常用的检验算法预测精度的指标,其公式如式(7)所示,当ACC取值越接近1,则表示预测精度越好:
{\text{ACC}} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {|{y_i}} - {{\hat y}_i}|}}{{\displaystyle\sum\limits_{i = 1}^n {{y_i}} }} (7) 式中:
{y_i} 为真实值;{\hat y_i} 为预测值。选择图13(a)的中监测主体某构件的温度应变数据,选择2012年11月1日—2016年11月1日时间段内的温度应变数据作为Prophet模型的训练集,以图14(a)中的黑色离散点表示;2016年11月2日—2018年11月1日时间段内的温度应变数据作为Prophet模型的验证集,以增加参数的泛化能力,同样用图14(a)中的黑色离散点表示;2018年11月2日—2020年11月1日时间段内的温度应变数据作为Prophet模型的测试集,测试集的预测结果用曲线表示,测试集中预测值和真实值的对比结果见图14(b),ACC计算结果为0.901,能够说明训练后的模型的准确性,Prophet模型能够较为准确地预测未来趋势;使用该模型预测2020年11月2日—2022年11月1日温度应变数据,以获取温度应变峰值点(根据结构受力形式、构件初始状态以及光纤光栅传感器安装位置,梁构件选择温度应变波峰值,柱构件选择温度应变波谷值),对监测主体的健康状态进行评估。预测集曲线后的阴影表示该模型95%置信区域,由图14(a)可知,随着预测年份的增长,置信区间面积也随之增大,由此可以推断随着预测时期的增长,预测精度是不断下降的,这符合预测模型的特征。故,基于ACC的计算结果,本文将目标拟定为短期(两年)预测。
4.2 基于Gumbel极值理论的人群应变预测
极值分析专门研究很少发生,然而一旦发生却产生极大影响的随机事件,其广泛运用于气象预测、地震预测、海洋工程、水文观测、环境工程、灾害性干旱,金融等领域。近年来,因土木工程事故频发,极值理论也逐渐被应用于土木工程领域[17]。监测主体中的人群应变数据具备极值分析的特征,某一构件提取的人群应变与游客数量、游客集中情况、游客行走状态均有关系,人群应变的极值具有较大的随机性,若人群应变的极值与温度应变峰值点相遇,则容易引起极端事件的发生。因此,对监测主体人群应变数据进行极值分析,获取其极值分布情况,并引入重现期的概念对极值进行预测,则能够实现结构健康状态评估。
Gumbel极值理论是极值分析中常用的理论,Gumbel极值理论的累计概率函数见式(8):
F(x) = \exp \left[ {{{ - }}\exp \left( {{{ - }}\frac{{x - l}}{k}} \right)} \right] (8) 式中:x代表最大人群应变的随机变量值;l为位置参数;k为尺寸参数。
位置参数l和尺寸参数k的求解是极值分布过程的关键,本节采用Gumbel法对上述参数进行估计。参数估计过程中,首先将监测主体中某一构件提供的人群应变数据(图13(b))分成若干单元,本节将按月份切割,每月为一个单元(旅游淡旺季会导致每月参观游客数量不同),每个传感器提供的数据可以分成96个单元,每个单元中包含720个人群应变数据。获取每个单元内最大的人群应变值,共可获得96个最大人群应变值。对上述最大人群应变数据进行编号,1号为最小值,96号为最大值,通过顺序排列获取如下累计概率函数:
F({x_i}) = \frac{i}{{N + 1}} (9) 式中:i代表第i个最大人群应变的随机变量对应序号,i = 1, 2,
\cdots , N,本节N = 96。利用Gumbel法进行参数估计,是将统计样本直接与经验频率相结合,即使用式(9)中顺序排列的累计概率函数代替式(8)中的极值分布累计概率函数进行参数估计。将式(8)对数化可得:
{{ - \ln( - }}\ln (F(x))) = \frac{{x - l}}{k} (10) 将式(10)转为线性关系是:
y{\text{ = }}Ax + B (11) 式中:
y{=-\ln(-}\mathrm{ln}(F(x)));A=\dfrac{1}{k};B=-\dfrac{l}{k} 。利用式(9)和式(10)获取式(11)中的y值,将x和其对应的y值绘制在同一图中,其呈现明显的线性关系,可证明本节中关注的人群应变满足Gumbel极值理论的分布形式,见图15。通过最小二乘法获取式(11)中的A = 0.124、B = −0.8881,R2 = 0.9788,而式(8)中的位置参数l = −B/A = 7.162,尺寸参数k = 1/A = 8.064。
将位置参数l = 7.162,尺寸参数k = 8.064代入式(8),能够获取描述最大人群应变的Gumbel分布的累计概率函数。引入地震和台风领域重现期[18]的概念对人群荷载进行预测,为提高藏式古建筑木结构监测信息的决定性,本节选取了罕遇事件(超越概率p1=2%)重现期,多遇事件(p2=超越概率63%)重现期。重现期为超越概率倒数,因此罕遇事件的重现期为50个月,而多遇事件的重现期近似2个月。根据超越概率和累计概率关系,可将式(10)转为下式:
\left\{ \begin{gathered} {x_1}{{ = }}l{{ - }}k{{\ln( - }}\ln (1{{ - }}{p_1})) \\ {x_2}{{ = }}l{{ - }}k{{\ln( - }}\ln (1{{ - }}{p_2})) \\ \end{gathered} \right. (12) 式中:x1为罕遇事件重现期对应的最大人群应变;x2为多遇事件重现期对应的最大人群应变。由计算结果可知x1= 38.62 με,x2= 7.21 με。
5 算例分析
通过《古建筑木结构维护与加固技术标准》(GB/T 50165−2020)[19]可知,在基于应变监测数据鉴定梁构件、柱构件安全状态时,工程人员关注柱的弯曲矢高,即柱身弯曲时,安装在柱上的光纤光栅传感器采集的应变监测数据能够描述柱构件相对于安装时刻的弯曲程度。通过现场调研发现,监测主体中并没有已经发生弯曲的柱构件,所有柱构件均处于受压状态,而在常规荷载状态下,柱构件很难发生压溃,因此本节并不分析柱身安装的光纤光栅传感器提供的应变监测数据。对于梁构件,工程人员关注梁构件跨中位置的竖向挠度,该物理量与梁构件底部跨中位置安装的光纤光栅传感器采集的应变监测数据相关。在评估梁构件的健康状态时,上述规范给出了相应阈值,即梁构件跨中位置竖向挠度大于该阈值时,梁构件需要进行修缮、加固。该阈值能够通过简单的几何关系转为梁构件底部跨中位置处的应变,具体阈值见表3。本节选择监测主体结构中最底层的4个置于梁底部跨中位置的光纤光栅传感器采集的数据进行分析,具体位置见图16,即图中B10、B11、B22、B23位置。
表 3 预测结果与阈值对比Table 3. Comparison between prediction results and threshold位置 温度应变
预测峰值/με人群应变
预测值/με初始应
变/με叠加应
变/με规范阈
值/μεB10 56.35 罕遇:31.76 2.25 90.36 171.81 多遇:6.99 65.59 B11 50.23 罕遇:33.53 0.33 84.09 171.81 多遇:7.19 57.75 B23 61.35 罕遇:38.62 7.36 107.33 171.81 多遇:7.21 75.92 B24 67.66 罕遇:35.11 2.71 105.48 171.81 多遇:8.13 78.51 1)提取上述4个传感器采集的2012年11月2日—2020年11月1日的应变原始监测数据和温度原始监测数据,后续对其分别处理;
2)利用Sobel+CNN的方法对原始数据进行处理,去除原始数据中缺失、重复和离群问题,进而消除因传感器自身带来的数据异常,得到可以描述结构异常的数据;
3)使用VMD方法将步骤2中处理好的应变监测数据解耦为温度应变数据和人群应变数据;
4)使用Prophet方法对带有周期性的温度应变数据进行预测,预测2020年11月2日—2022年11月1日两年的温度应变数据,提取两年中的峰值温度应变,用于后续预测;
5)使用Gumbel极值理论获取人群应变的极值分布,引入重现期概念,获取罕遇事件重现期对应的最大人群应变和多遇事件重现期对应的最大人群应变;
6)通过《古建筑木结构维护与加固技术标准》(GB/T 50165−2020)[19]获取梁构件竖向挠度阈值,该规范为目前古建木构领域中最为常见的规范,具有普适性。竖向挠度阈值的选取与古建木构梁的高跨比有关。在竖向挠度、梁原始长度已知的情况下,可通过几何关系,将梁的竖向挠度阈值转为梁底部跨中应变阈值。将步骤4和步骤5中获取的应变预测值叠加,并叠加初始安装时刻记录的原始应变,此初始应变由北京交通大学古建筑结构研究团队、北京交通大学布达拉宫监测中心、北京基康科技有限公司共同记录。值得注意的是,初始应变中包含结构自重引起的应变,但该数值较小,首先是因为藏式古建木构梁的跨度普遍偏小,且下部有弓木和垫木的支撑。其次,回廊结构中梁的上部仅有楼板,并无其他沉重物体;
7)通过叠加结果和阈值的对比,可以对梁构件的健康状态进行评估,基于监测数据判断梁是否需要修缮和加固。值得注意的是,为了增加应变监测数据的可决性,避免盲目修缮带来的损害和浪费,本文给出了罕遇条件下的预测结果和多遇条件下的预测结果,工程人员首先对比罕遇条件下的预测结果和阈值,一旦预测结果超出阈值则证明该梁构件有破坏的可能,相关单位可以通过改变游客路径或增加临时支撑等办法对该梁进行维护,后续进行针对性监测。其次,对比多遇条件下的预测结果和阈值,一旦预测结果超出阈值则证明该梁构件有修缮加固的需求,需要尽快拟定方案进行修缮加固。
使用上述7个步骤,对选定的应变监测数据进行处理,结果见表3。
通过观察可知,在罕遇人群应变条件下,B23传感器对应的梁构件底部应变达到极限阈值的62%,B23传感器对应的梁构件底部应变达到极限阈值的61%,应予以重视,但在多遇人群应变条件下,上述梁构件底部应变仅为44%和45%,故此无须修缮。另外,B10和B11传感器对应的梁构件健康状况优于B23和B24传感器对应的梁构件健康状况,无须进行针对性监测,仅需持续监测。
6 结论
本文使用应变监测数据预测值对结构短期内的健康状态进行评估,结论如下:
(1)本文提出了能够同时处理多种数据失真问题的Sobel+CNN方法,以消除传感器造成的数据异常。确保后续数据的异常能够表达结构异常。利用多项式回归方法和功率谱密度方法确定上述数据组分,并引入VMD方法将应变数据解耦为温度应变数据和人群应变数据,为短期预测提供条件。
(2)引入Prophet算法对温度应变数据进行短期预测,并以ACC为指标衡量模型的准确性。引入Gumbel极值理论获取罕遇条件对应的人群应变,以及多遇条件对应的人群应变。
(3)以回廊结构中4个梁应变监测数据为例,将初始应变、温度应变预测峰值和罕遇条件下的人群应变预测值叠加,以确定短期内需要关注的结构位置,将初始应变、温度应变预测峰值和多遇条件下的人群应变预测值叠加,以确定短期内需要及时修缮加固的结构位置。
-
表 1 试验与计算结果比较
Table 1 Comparison of tested and calculated results
工况 横桥向
预应力/kN顺桥向
预应力/kN竖向
索力/kN水平
索力/kN钢侧板正应力 混凝土塔壁正应力 试验值/
MPa平截面/
MPa计算式/
MPa(平截面/
试验值)/(%)(计算式/
试验值)/(%)试验值/
MPa平截面/
MPa计算式/
MPa(平截面/
试验值)/(%)(计算式/
试验值)/(%)1 120 378 0 0 −19.8 −12.20 −10.80 62 55 −1.89 −2.23 −2.26 118 120 2 120 378 1010 1442 21.6 −4.46 6.55 −21 30 −1.26 −0.81 −1.07 64 85 3 120 0 1010 1442 35.0 7.78 17.40 22 50 0.83 1.42 1.18 171 142 -
[1] 张喜刚, 刘玉擎. 组合索塔锚固结构[M]. 北京: 人民交通出版社, 2010: 5 − 8. ZHANG Xigang, LIU Yuqing. Cable-tower composite anchorage [M]. Beijing: China Communications Press, 2010: 5 − 8. (in Chinese)
[2] HUANG W, PEI M S, LIU X D, et al. Design and construction of super-long span bridges in China: Review and future perspectives [J]. Frontiers of Structural and Civil Engineering, 2020, 14(4): 803 − 838. doi: 10.1007/s11709-020-0644-1
[3] 向雅娟. 比利时Ben-Ahin桥的施工[J]. 国外公路, 1994, 14(6): 33 − 36. XIANG Yajuan. Construction of Ben-Ahin bridge in Belgium [J]. Foreign Highway, 1994, 14(6): 33 − 36. (in Chinese)
[4] VIRLOGEUX M. The Normandie Bridge, France: A new record for cable-stayed bridges [J]. Structural Engineering International, 1994, 4(4): 208 − 213. doi: 10.2749/101686694780601629
[5] 张奇志, 李明俊. 斜拉桥钢-混组合索塔锚固区节段模型试验研究[J]. 桥梁建设, 2006(3): 16 − 19. doi: 10.3969/j.issn.1003-4722.2006.03.005 ZHANG Qizhi, LI Mingjun. Segmental model test study of steel and concrete composite anchor zone on pylon of cable-stayed bridge [J]. Bridge Construction, 2006(3): 16 − 19. (in Chinese) doi: 10.3969/j.issn.1003-4722.2006.03.005
[6] 陈开利. 钢锚箱索塔锚固区受力机理[J]. 中国铁道科学, 2008, 29(4): 58 − 64. CHEN Kaili. Mechanical mechanism of the steel anchor housing in the anchorage zones of the cable pylons [J]. China Railway Science, 2008, 29(4): 58 − 64. (in Chinese)
[7] 杨允表, 吕忠达. 大跨度斜拉桥索塔锚固区钢-混凝土结构竖向受力机理的有限元法[J]. 工程力学, 2008, 25(12): 153 − 161. YANG Yunbiao, LYU Zhongda. A finite element method for vertical mechanics analysis of steel-concrete composite structure in pylon cable anchor zone of long span cable-stayed bridge [J]. Engineering Mechanics, 2008, 25(12): 153 − 161. (in Chinese)
[8] 苏庆田, 秦飞. 斜拉桥钢锚箱组合索塔水平受力性能简化分析模型[J]. 工程力学, 2011, 28(增刊 1): 172 − 177. SU Qingtian, QIN Fei. Simplified analytical model for horizontal mechanical behavior of composite cable-pylon with steel-anchor-box in cable-stayed bridges [J]. Engineering Mechanics, 2011, 28(Suppl 1): 172 − 177. (in Chinese)
[9] 徐海军, 刘玉擎, 李炀, 等. 外露型钢锚箱索塔锚固结构受力机理试验[J]. 同济大学学报(自然科学版), 2014, 42(5): 672 − 676. doi: 10.3969/j.issn.0253-374x.2014.05.002 XU Haijun, LIU Yuqing, LI Yang, et al. Experimental study on stress mechanism of exposed steel anchor box cable-tower Achorage [J]. Journal of Tongji University (Natural Science), 2014, 42(5): 672 − 676. (in Chinese) doi: 10.3969/j.issn.0253-374x.2014.05.002
[10] 郑双杰, 刘玉擎, 徐海军. 组合索塔锚固区钢牛腿-塔壁作用机理分析[J]. 工程力学, 2014, 31(5): 197 − 202. doi: 10.6052/j.issn.1000-4750.2012.12.0954 ZHENG Shuangjie, LIU Yuqing, XU Haijun. Structural analysis of steel bracket-concrete walls in cable-tower composite anchorage [J]. Engineering Mechanics, 2014, 31(5): 197 − 202. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.12.0954
[11] 刘玉擎, 陈聪, 郑双杰. 钢锚箱嵌固型索塔锚固结构受力机理分析[J]. 桥梁建设, 2015, 45(1): 33 − 38. LIU Yuqing, CHEN Cong, ZHENG Shuangjie. Analysis of force mechanism of pylon anchorage structure of fixed-end steel anchor box type [J]. Bridge Construction, 2015, 45(1): 33 − 38. (in Chinese)
[12] 武芳文, 冯彦鹏, 戴君, 等. 钢-UHPC组合结构中栓钉剪力键力学性能研究[J]. 工程力学, 2022, 39(2): 222 − 234, 243. doi: 10.6052/j.issn.1000-4750.2021.05.0389 WU Fangwen, FENG Yanpeng, DAI Jun, et al. Study on mechanical properties of stud shear connectors in steel-UHPC composite structures [J]. Engineering Mechanics, 2022, 39(2): 222 − 234, 243. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.05.0389
[13] 张凡, 陈炳聪, 刘爱荣, 等. 装配式钢-混凝土组合梁高强螺栓剪力连接件力学模型[J]. 工程力学, 2022, 39(增刊 1): 173 − 179. doi: 10.6052/j.issn.1000-4750.2021.05.S033 ZHANG Fan, CHEN Bingcong, LIU Airong, et al. Mechanical model of high strength bolt shear connector of fabricated steel-concrete composite beam [J]. Engineering Mechanics, 2022, 39(Suppl 1): 173 − 179. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.05.S033




 下载:
下载: