基于场址复杂入射波场的非一致波动输入模型

何卫平; 杜修力; 陈平; 刘聪宇; 王峰

doi:10.6052/j.issn.1000-4750.2022.08.0688

基于场址复杂入射波场的非一致波动输入模型

何卫平^{1, 2, ,},
杜修力^2,,
陈平^3,,
刘聪宇^1,,
王峰^1,

1.
三峡大学湖北省水电工程施工与管理重点实验室，湖北，宜昌 443002
2.
北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124
3.
中国电建集团中南勘测设计研究院有限公司，湖南，长沙 410014

基金项目: 国家自然科学基金青年项目(51809152)；北京市博士后基金项目(Q6004014202002)；湖北省重点实验室开放基金项目(2020KSD16)

详细信息

作者简介:
杜修力(1962−)，男，四川人，教授，博士，院士，主要从事土木、水利工程结构抗震防灾研究(E-mail: duxiuli@bjut.edu.cn)

陈　平(1987−)，男，湖南人，高工，硕士，主要从事水工结构设计研究(E-mail: 362437373@qq.com)

刘聪宇(1998−)，男，湖北人，硕士生，主要从事水工结构抗震研究(E-mail: 2017101230@ctgu.edu.cn)

王　峰(1987−)，男，山东人，副教授，博士，主要从事水工结构研究(E-mail: wangfengctgu@ctgu.edu.cn)

通讯作者:
何卫平(1987−)，男，河南人，副教授，博士，主要从事地震动输入模型研究(E-mail: heweiping_hwp@126.com)

中图分类号: TV312；O347.4
计量
- 文章访问数: 182
- HTML全文浏览量: 63
- PDF下载量: 55
出版历程
- 收稿日期: 2022-08-06
- 修回日期: 2023-01-09
- 网络出版日期: 2023-03-06
- 刊出日期: 2024-12-24

A NON-UNIFORM WAVE INPUT MODEL BASED ON COMPLEX INCIDENT SITE WAVES

HE Wei-ping^{1, 2, ,},
DU Xiu-li^2,,
CHEN Ping^3,,
LIU Cong-yu^1,,
WANG Feng^1,

1.
Hubei Key Laboratory of Construction and Management in Hydropower Engineering, China Three Gorges University, Yichang, Hubei 443002, China
2.
Key Laboratory of Urban Security and Disaster Engineering of the Ministry of Education, Beijing University of Technology, Beijing 100124, China
3.
Powerchina Zhongnan Engineering Corporation Limited, Changsha, Hu’nan 410014, China

摘要

摘要:
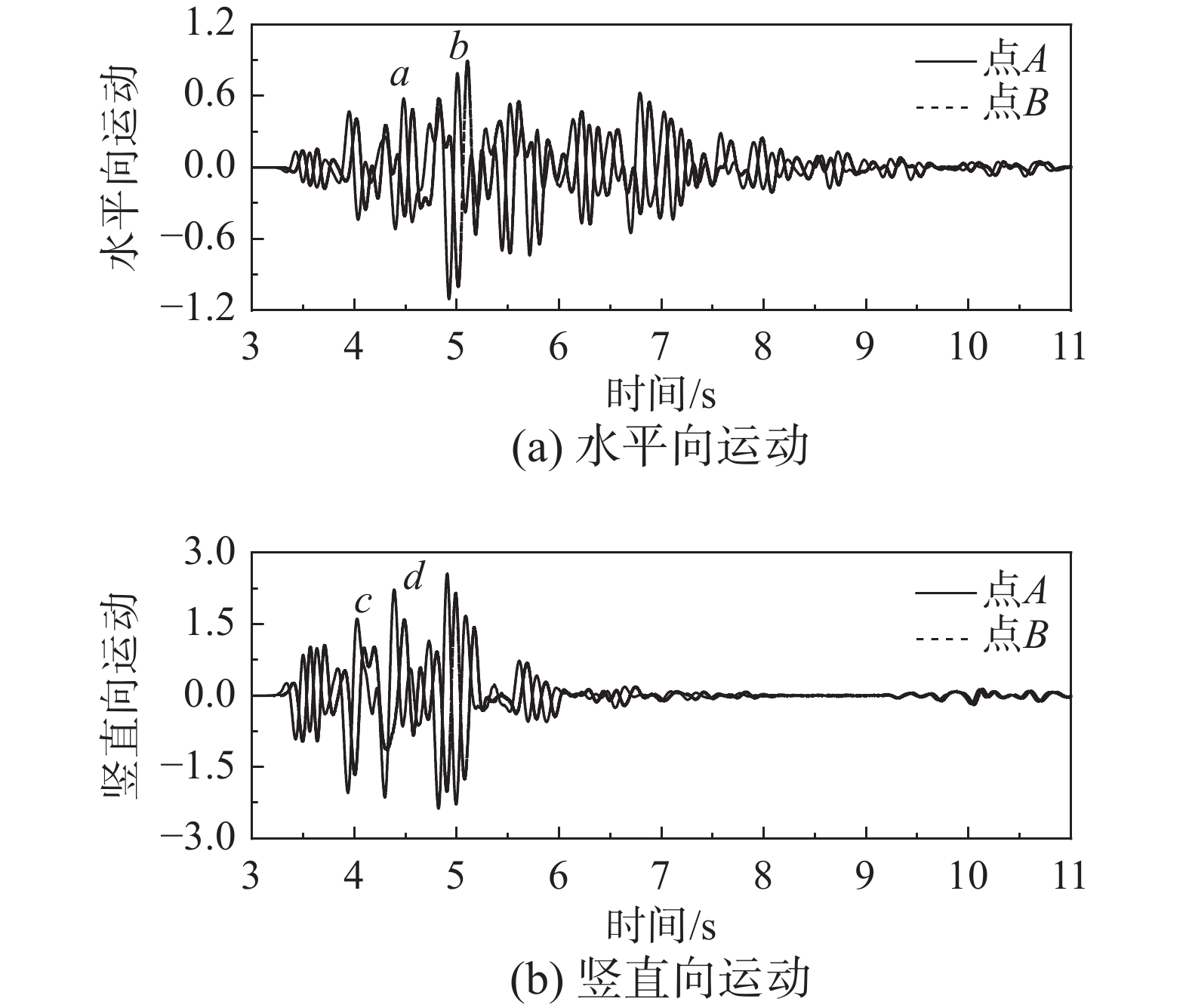
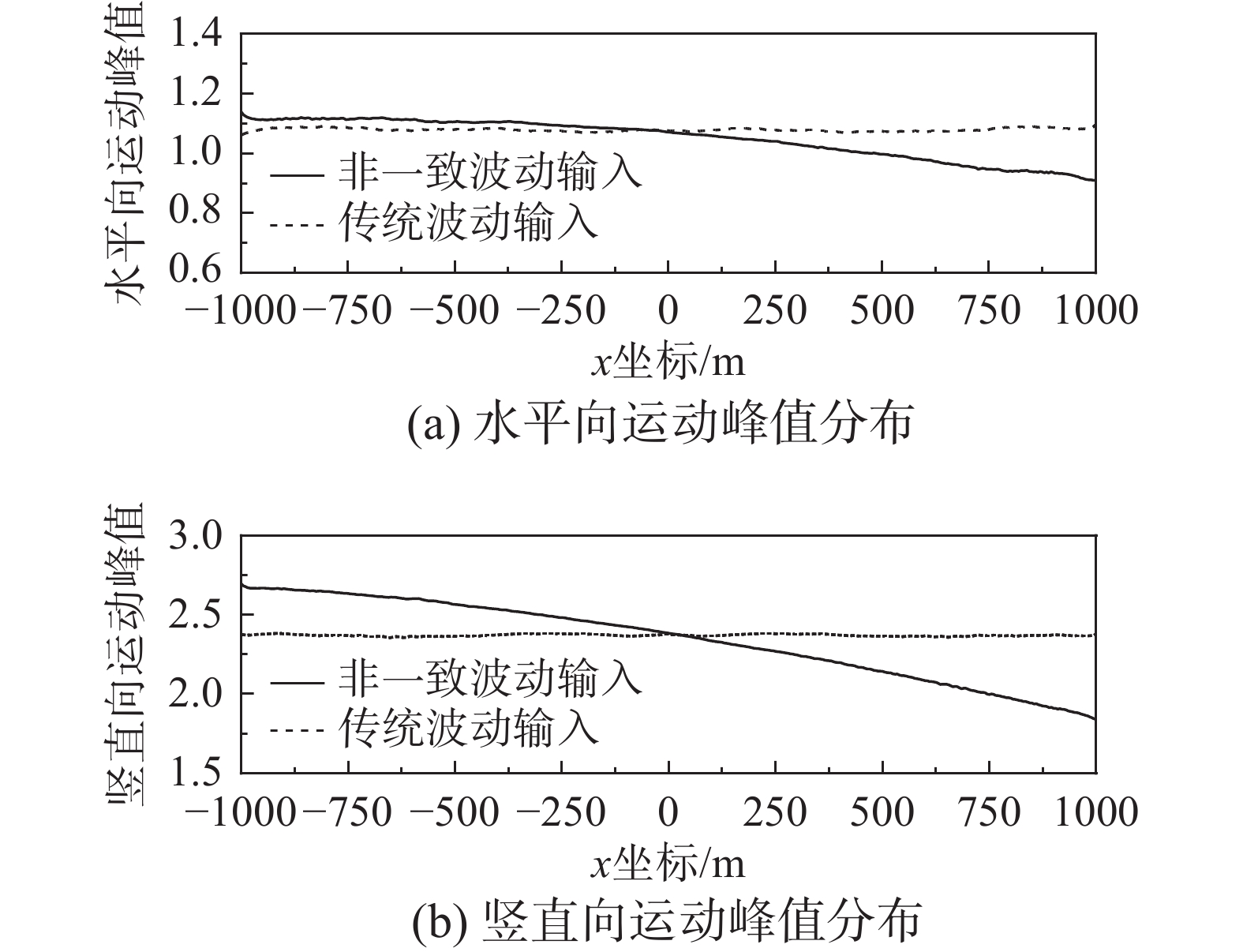
波动输入模型在表达地面运动非一致特征方面存在局限。为解决该问题，首先通过地震波空间演化分析证实场址入射地震波为复杂波场，进而提出拓展入射波假定至复杂波场的方法发展非一致波动输入模型。该文以确定性波场和粘弹性边界实现非一致波动输入模型，通过数值模拟地面运动与解析解对比验证其可行性。研究结果显示，非一致波动输入模型继承了波动输入模型在模拟地震波传播效应和地基辐射阻尼效应方面的优势，可有效实现场址复杂入射波场的输入。与传统波动输入模型相比，非一致波动输入模型可全面表达地面运动的时间滞后、峰值变化和时程形状差异等非一致特征。
- 近场波动 /
- 非一致波动输入模型 /
- 复杂入射波场 /
- 地震波空间演化 /
- 时程形状差异
Abstract:
The wave input model (WIM) cannot express the non-uniform characteristics of ground motions completely. By analyzing the spatial evolution of seismic waves from the source to the site, the incident site waves are proved to be complex waves. A strategy for improving the WIM by expanding incident waves to complex waves is proposed. The new model is named the non-uniform wave input model (NUWIM). The NUWIM is accomplished by the deterministic incident site waves and the visco-elastic boundary and is verified by the analytical ground motion. The result shows that the advantages of WIM in simulating the wave propagation effect and the radiation damping effect are inherited in the NUWIM, which can effectively achieve the input of complex incident site waves. Compared with the WIM, the non-uniform characteristics of ground motions, such as time delays, peak variations, and time history shape differences, can be synthetically simulated by the NUWIM.
- near-field wave /
- non-uniform wave input model /
- complex incident site waves /
- spatial evolution of seismic wave /
- time history shape difference

HTML全文

图 1 震源地震波与场址入射地震波波形

Figure 1. Waveforms of source wave and incident site wave

下载: 全尺寸图片幻灯片

图 2 场址地面运动形成机制

Figure 2. Motion formation mechanism at the site

下载: 全尺寸图片幻灯片

图 3 复杂入射波场场址地面运动与数值解对比

Figure 3. Motions at the site by complex incident waves and numerical simulation

下载: 全尺寸图片幻灯片

图 4 算例模型

Figure 4. Example model

下载: 全尺寸图片幻灯片

图 5 非一致波动输入模型得到的参考点运动与解析解对比(A=0.8，B=1.1)

Figure 5. Motion at point R from NUWIM and analytical result (A=0.8, B=1.1)

下载: 全尺寸图片幻灯片

图 6 不同时刻波场快照和波前示意图

Figure 6. Wavefield snapshot at different times and wavefronts

下载: 全尺寸图片幻灯片

图 7 点A和点B的运动差异

Figure 7. Motion shape difference at Points A and B

下载: 全尺寸图片幻灯片

图 8 自由面运动峰值分布

Figure 8. Peak motion distribution at the free surface

下载: 全尺寸图片幻灯片

表 1 传播介质参数

Table 1 Propagation medium parameters

介质	波速/(m/s)		密度/(kg/m³)	厚度/m	品质因子
介质	P波	SV波	密度/(kg/m³)	厚度/m	Q_P	Q_S
地层1	2500	1070	2110	1000	80	100
地层2	4600	2590	2460	1500	100	150
地层3	6100	3530	2740	10 780	200	300
地层4	6500	3710	2830	12 120	200	300
地层5	6900	3930	2920	10 780	200	300
上地幔	7960	4430	3280	−	−	−

下载: 导出CSV

表 2 场址复杂入射地震波信息

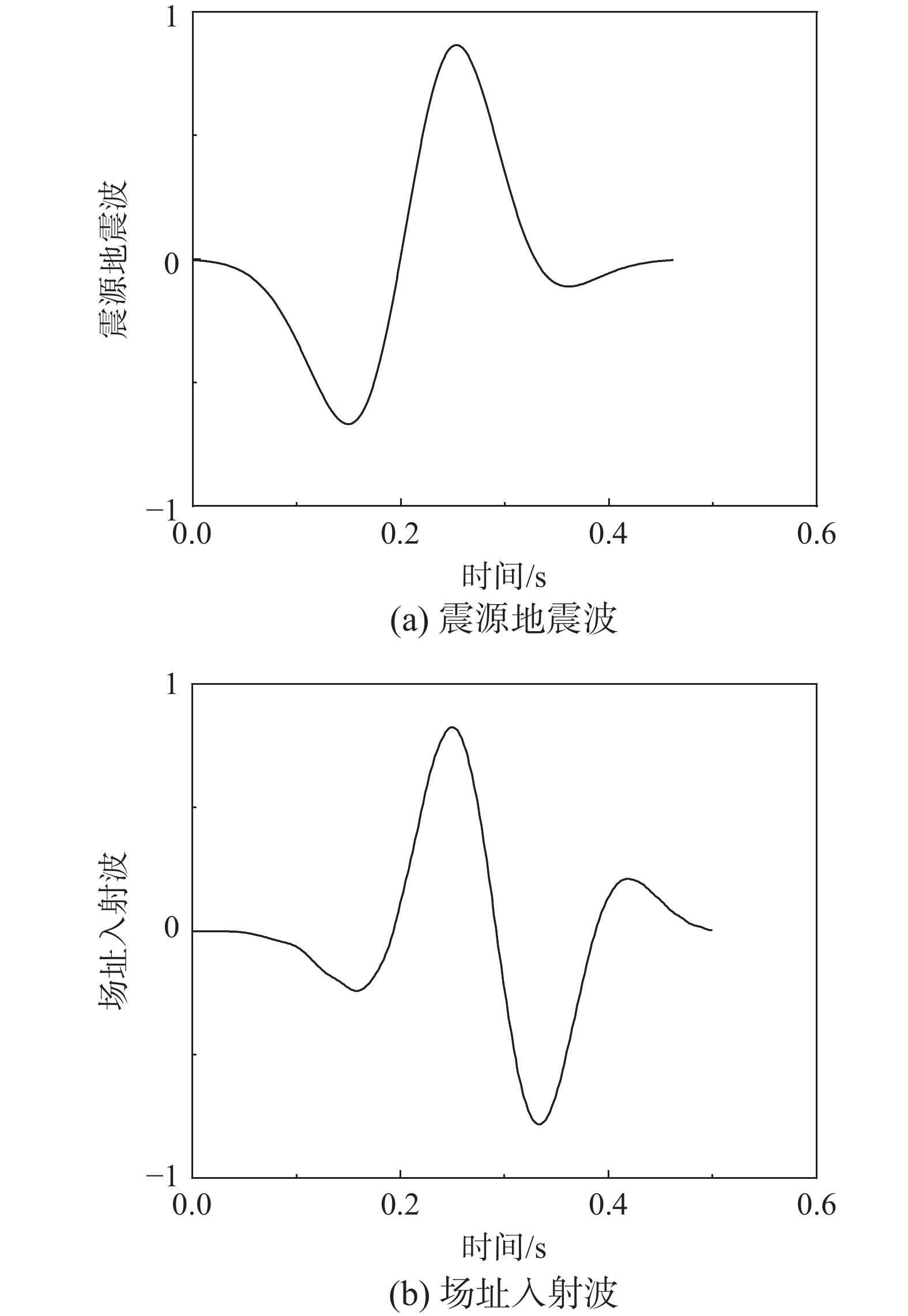
Table 2 Information of incident site waves

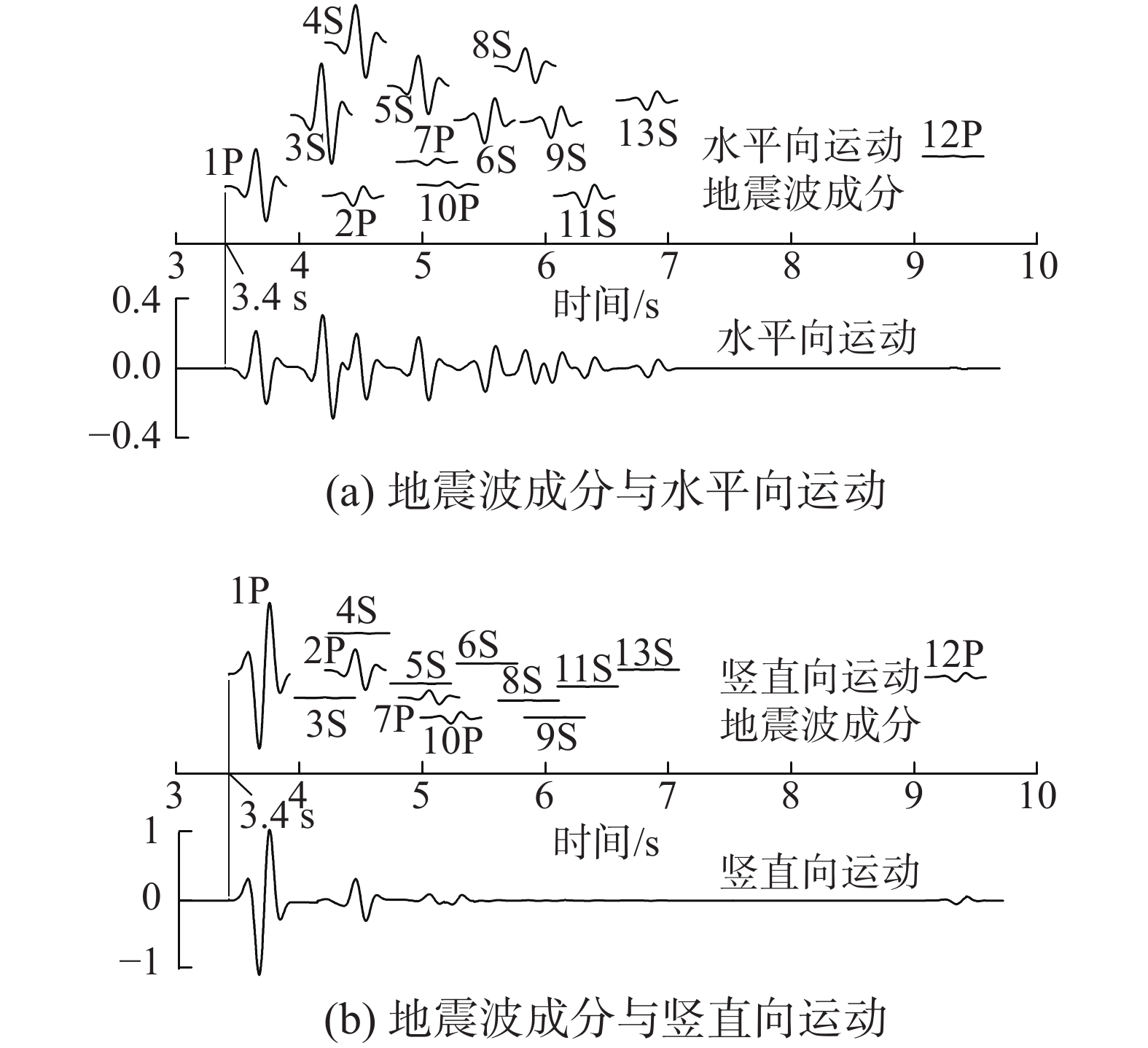
编号	入射波性质	幅值	入射角/(°)	到时/s
1	P	0.679	13.0	3.40
2	P	−0.189	12.6	4.18
3	S	0.185	5.6	3.94
4	S	0.134	5.7	4.21
5	S	0.107	5.4	4.72
6	S	−0.083	5.5	5.26
7	P	−0.064	11.5	4.79
8	S	0.064	5.0	5.59
9	S	−0.058	5.5	5.80
10	P	0.053	12.2	4.96
11	S	−0.041	5.6	6.07
12	P	0.038	3.9	9.07
13	S	−0.034	5.3	6.58

下载: 导出CSV

表 3 非一致波动输入模型参考点运动误差

Table 3 Motion errors at point R from NUWIM

文献推荐参数	算例	运动分量	运动峰值		误差/(%)
文献推荐参数	算例	运动分量	NUWIM	解析解	误差/(%)
A=0.8, B=1.1^[23]	1	水平向	−0.3245	−0.3211	1.06
	1	竖直向	1.1387	1.1370	0.14
	2	水平向	−1.0718	−1.0833	1.07
	2	竖直向	2.3834	2.3744	0.38
A=1.0, B=1.0^[24]	1	水平向	−0.3246	−0.3211	1.08
	1	竖直向	1.1387	1.1370	0.15
	2	水平向	−1.0721	−1.0833	1.04
	2	竖直向	2.3837	2.3744	0.39

下载: 导出CSV

参考文献(40)

[1]	JOYNER W B, CHEN A T F. Calculation of nonlinear ground response in earthquakes [J]. Bulletin of the Seismological Society of America, 1975, 65(5): 1315 − 1336.
[2]	廖振鹏. 工程波动理论导论 [M]. 2版. 北京: 科学出版社, 2002: 136 − 285. LIAO Zhenpeng. Introduction to wave motion theories in engineering [M]. 2nd ed. Beijing: Science Press, 2002: 136 − 285. (in Chinese)
[3]	刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报, 1998, 31(3): 55 − 64. LIU Jingbo, LYU Yandong. A direct method for analysis of dynamic soil-structure interaction [J]. China Civil Engineering Journal, 1998, 31(3): 55 − 64. (in Chinese)
[4]	杜修力. 工程波动理论与方法 [M]. 北京: 科学出版社, 2009: 367 − 431. DU Xiuli. Theories and methods of wave motion for engineering [M]. Beijing: Science Press, 2009: 367 − 431. (in Chinese)
[5]	赵密. 近场波动有限元模拟的应力型时域人工边界条件及其应用[D]. 北京: 北京工业大学, 2009. ZHAO Mi. Stress-type time-domain artificial boundary condition for finite-element simulation of near-field wave motion and its engineering application [D]. Beijing: Beijing University of Technology, 2009. (in Chinese)
[6]	孔宪京, 屈永倩, 邹德高, 等. 强震作用下面板堆石坝跨尺度面板开裂演化分析[J]. 岩土工程学报, 2020, 42(6): 989 − 996. KONG Xianjing, QU Yongqian, ZOU Degao, et al. Cross-scale crack evolution analysis for face slab in concrete faced rockfill dams under strong earthquake [J]. Chinese Journal of Geotechnical Engineering, 2020, 42(6): 989 − 996. (in Chinese)
[7]	梁建文, 梁佳利, 张季, 等. 深厚软土场地中三维凹陷地形非线性地震响应分析[J]. 岩土工程学报, 2017, 39(7): 1196 − 1205. doi: 10.11779/CJGE201707005 LIANG Jianwen, LIANG Jiali, ZHANG Ji, et al. Nonlinear seismic response of 3D canyon in deep soft soils [J]. Chinese Journal of Geotechnical Engineering, 2017, 39(7): 1196 − 1205. (in Chinese) doi: 10.11779/CJGE201707005
[8]	李明超, 张佳文, 张梦溪, 等. 地震波斜入射下混凝土重力坝的塑性损伤响应分析[J]. 水利学报, 2019, 50(11): 1326 − 1338, 1349. doi: 10.13243/j.cnki.slxb.20190538 LI Mingchao, ZHANG Jiawen, ZHANG Mengxi, et al. Plastic damage response analysis of concrete gravity dam due to obliquely incident seismic waves [J]. Journal of Hydraulic Engineering, 2019, 50(11): 1326 − 1338, 1349. (in Chinese) doi: 10.13243/j.cnki.slxb.20190538
[9]	HUANG J Q, ZHAO M, DU X L. Non-linear seismic responses of tunnels within normal fault ground under obliquely incident P waves [J]. Tunnelling and Underground Space Technology, 2017, 61: 26 − 39. doi: 10.1016/j.tust.2016.09.006
[10]	岑威钧, 袁丽娜, 袁翠平, 等. 地震波斜入射对高面板坝地震反应的影响[J]. 地震工程学报, 2015, 37(4): 926 − 932. doi: 10.3969/j.issn.1000-0844.2015.04.0926 CEN Weijun, YUAN Li’na, YUAN Cuiping, et al. Influence on seismic response of high concrete face rockfill dams due to obliquely incident seismic waves [J]. China Earthquake Engineering Journal, 2015, 37(4): 926 − 932. (in Chinese) doi: 10.3969/j.issn.1000-0844.2015.04.0926
[11]	马怀发, 杨茹. 三维饱和地基人工黏弹性边界[J]. 中国水利水电科学研究院学报, 2015, 13(2): 128 − 135. MA Huaifa, YANG Ru. 3D viscous-spring artificial boundaries of infinite saturated foundation [J]. Journal of China Institute of Water Resources and Hydropower Research, 2015, 13(2): 128 − 135. (in Chinese)
[12]	郭胜山, 陈厚群, 李德玉, 等. 重力坝与坝基体系地震损伤破坏分析[J]. 水利学报, 2013, 44(11): 1352 − 1358. doi: 10.13243/j.cnki.slxb.2013.11.016 GUO Shengshan, CHEN Houqun, LI Deyu, et al. Seismic damage and failure analysis of gravity dam and foundation system [J]. Journal of Hydraulic Engineering, 2013, 44(11): 1352 − 1358. (in Chinese) doi: 10.13243/j.cnki.slxb.2013.11.016
[13]	WANG F, SONG Z Q, LIU Y H, et al. Seismic wave input method for high earth dams considering the transmission amplification effect of the bedrock–overburden interface [J]. Computers and Geotechnics, 2021, 130: 103927. doi: 10.1016/j.compgeo.2020.103927
[14]	李亮, 李果, 杜修力, 等. 饱和两相介质近场波动问题的一种时域全显式数值计算方法[J]. 工程力学, 2020, 37(8): 20 − 31. doi: 10.6052/j.issn.1000-4750.2019.08.0479 LI Liang, LI Guo, DU Xiuli, et al. A full explicit numerical algorithm for near-field wave motion of fluid-saturated porous media in time domain [J]. Engineering Mechanics, 2020, 37(8): 20 − 31. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.08.0479
[15]	宝鑫, 刘晶波, 李述涛, 等. 土-结构相互作用对储液结构动力反应的影响研究[J]. 工程力学, 2021, 38(增刊 1): 125 − 132. doi: 10.6052/j.issn.1000-4750.2020.06.S022 BAO Xin, LIU Jingbo, LI Shutao, et al. Influence analysis of soil-structure interaction on the dynamic response of storage tanks [J]. Engineering Mechanics, 2021, 38(Suppl 1): 125 − 132. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.S022
[16]	章旭斌, 谢志南. 波动谱元模拟中透射边界稳定性分析[J]. 工程力学, 2022, 39(10): 26 − 35. doi: 10.6052/j.issn.1000-4750.2021.06.0428 ZHANG Xubin, XIE Zhinan. Stability analysis of transmitting boundary in wave spectral element simulation [J]. Engineering Mechanics, 2022, 39(10): 26 − 35. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.06.0428
[17]	李会芳, 赵密, 杜修力. 竖向成层介质中标量波传播问题的高精度人工边界条件[J]. 工程力学, 2022, 39(5): 55 − 64. doi: 10.6052/j.issn.1000-4750.2021.02.0112 LI Huifang, ZHAO Mi, DU Xiuli. High-precision artificial boundary condition for scalar wave propagation in vertical stratified media [J]. Engineering Mechanics, 2022, 39(5): 55 − 64. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.02.0112
[18]	BAO X, LIU J B, LI S T, et al. A new viscoelastic artificial boundary with improved numerical stability in explicit calculation of wave propagation problems in infinite domains [J]. Computers and Geotechnics, 2022, 145: 104698. doi: 10.1016/j.compgeo.2022.104698
[19]	WANG F M, TULAMAITI Y, FANG H Y, et al. Seismic response characteristics of polymer anti-seepage wall in earth dam based on earthquake wave motion input method [J]. Structures, 2023, 47: 358 − 373. doi: 10.1016/j.istruc.2022.11.060
[20]	LYSMER J, Kuhlemeyer R L. Finite dynamic model for infinite media [J]. Journal of the Engineering Mechanics Division, 1969, 95(4): 859 − 877. doi: 10.1061/JMCEA3.0001144
[21]	LIAO Z P, Wong H L. A transmitting boundary for the numerical simulation of elastic wave propagation [J]. International Journal of Soil Dynamics and Earthquake Engineering, 1984, 3(4): 174 − 183. doi: 10.1016/0261-7277(84)90033-0
[22]	DEEKS A J, RANDOLPH M F. Axisymmetric time-domain transmitting boundaries [J]. Journal of Engineering Mechanics, 1994, 120(1): 25 − 42. doi: 10.1061/(ASCE)0733-9399(1994)120:1(25)
[23]	杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49 − 56. doi: 10.3321/j.issn:0459-1879.2006.01.007 DU Xiuli, ZHAO Mi, WANG Jinting. A stress artificial boundary in FEA for near-field wave problem [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 49 − 56. (in Chinese) doi: 10.3321/j.issn:0459-1879.2006.01.007
[24]	刘晶波, 杜义欣, 闫秋实. 粘弹性人工边界及地震动输入在通用有限元软件中的实现[J]. 防灾减灾工程学报, 2007, 27(增刊 1): 37 − 42. LIU Jingbo, DU Yixin, YAN Qiushi. A stress artificial boundary in FEA for near-field wave problem [J]. Journal of Disaster Prevention and Mitigation Engineering, 2007, 27(Suppl 1): 37 − 42. (in Chinese)
[25]	ZERVA A. Spatial variation of seismic ground motions: Modeling and engineering applications [M]. Boca Raton: CRC Press, 2009: 1 − 64.
[26]	何卫平, 熊堃, 卢晓春. 确定性地震动空间差异对重力坝地震响应影响研究[J]. 水利学报, 2019, 50(8): 913 − 924. HE Weiping, XIONG Kun, LU Xiaochun. Influence of deterministic spatial variation of motions on seismic response of gravity dam [J]. Journal of Hydraulic Engineering, 2019, 50(8): 913 − 924. (in Chinese)
[27]	KOMADA H, HAYASHI M, KITAHARA Y, et al. Three-dimensional dynamic analysis of a rockfill dam for inclined incident traveling seismic wave [C]// Proceedings of the Japan Society of Civil Engineers. Japan Society of Civil Engineers, 1977, 1977(261): 77 − 92.
[28]	苑举卫, 杜成斌, 刘志明. 基于设计地震动的地震波斜入射波动输入研究[J]. 四川大学学报(工程科学版), 2010, 42(5): 250 − 255. YUAN Juwei, DU Chengbin, LIU Zhiming. Study on oblique wave input based on design seismic component [J]. Journal of Sichuan University (Engineering Science Edition), 2010, 42(5): 250 − 255. (in Chinese)
[29]	何卫平, 何蕴龙. 基于两向设计地震动的二维自由场构建[J]. 工程力学, 2015, 32(2): 31 − 36, 44. HE Weiping, HE Yunlong. Free field wave motions based on two components of design earthquake ground motion [J]. Engineering Mechanics, 2015, 32(2): 31 − 36, 44. (in Chinese)
[30]	韩鲁, 宋志强, 王飞, 等. 基于设计地震动的覆盖层场地空间自由场构建[J]. 工程力学, 2022, 39(7): 137 − 146. doi: 10.6052/j.issn.1000-4750.2021.04.0255 HAN Lu, SONG Zhiqiang, WANG Fei, et al. Construction of free fields in bedrock-overburden site spaces based on designed ground motions [J]. Engineering Mechanics, 2022, 39(7): 137 − 146. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.04.0255
[31]	李闯, 宋志强, 王飞, 等. 地震动空间差异对沥青混凝土心墙土石坝-覆盖层地基系统响应影响研究[J]. 振动与冲击, 2022, 41(19): 37 − 47. LI Chuang, SONG Zhiqiang, WANG Fei, et al. Effects of spatial difference of ground motion on seismic response of asphalt concrete core wall rockfill dam-overburden foundation system [J]. Journal of Vibration and Shock, 2022, 41(19): 37 − 47. (in Chinese)
[32]	何卫平. 重大工程场址复杂入射波场信息的确定性评估方法 [R]. 北京: 北京工业大学, 2021: 5 − 26. HE Weiping. Deterministic assessment of site wave field in major project site [R]. Beijing: Beijing University of Technology, 2021: 5 − 26. (in Chinese)
[33]	陈运泰. 多层弹性半空间中的地震波(一)[J]. 地球物理学报, 1974, 17(1): 20 − 43. CHEN Yuntai. Seismic waves in multilayered elastic half-space (I) [J]. Acta Geophysic Sinica, 1974, 17(1): 20 − 43. (in Chinese)
[34]	布列霍夫斯基赫. 分层介质中的波 [M]. 杨训仁, 译. 2版. 北京: 科学出版社, 1985: 1 − 81. BREKHOVSKIKH L M. Waves in layered media [M]. YANG Xunren, trans. 2nd ed. Beijing: Sicence Press, 1985: 1 − 81. (in Chinsese)
[35]	高永新, 胡恒山. 水平分层孔隙介质中点源激发的震电波场数值模拟及分析[J]. 地球物理学报, 2009, 52(8): 2093 − 2104. doi: 10.3969/j.issn.0001-5733.2009.08.018 GAO Yongxin, HU Hengshan. Numerical simulation and analysis of seismoelectromagnetic wave fields excited by a point source in layered porous media [J]. Chinese Journal of Geophysics, 2009, 52(8): 2093 − 2104. (in Chinese) doi: 10.3969/j.issn.0001-5733.2009.08.018
[36]	何耀锋, 陈蔚天, 陈晓非. 利用广义反射-透射系数方法求解含低速层水平层状介质模型中面波频散曲线问题[J]. 地球物理学报, 2006, 49(4): 1074 − 1081. doi: 10.3321/j.issn:0001-5733.2006.04.020 HE Yaofeng, CHEN Weitian, CHEN Xiaofei. Normal mode computation by the generalized reflection-transmission coefficient method in planar layered half space [J]. Chinese Journal of Geophysics, 2006, 49(4): 1074 − 1081. (in Chinese) doi: 10.3321/j.issn:0001-5733.2006.04.020
[37]	LASKE G, MASTERS G, MA Z, et al. Update on CRUST1. 0—A 1-degree global model of Earth’s crust [C]// Geophysical Research Abstracts. Vienna, Austria: EGU General Assembly 2013, 2013, 15(15): 2658.
[38]	BARTON N. Rock quality, seismic velocity, attenuation and anisotropy [M]. London: Taylor & Francis, 2006: 181 − 294.
[39]	AKI K, RICHARDS P G. Quantitative seismology [M]. 2nd ed. Sausalito: University Science Books, 2002: 119 − 188.
[40]	万永革. 地震学导论[M]. 北京: 科学出版社, 2016: 83 − 113. WAN Yongge. Introduction to seismology [M]. Beijing: Science Press, 2016: 83 − 113. (in Chinese)

施引文献(63)

期刊类型引用(28)

1.	王朋，尤学辉，史庆轩，陶毅，戎翀，黄杰. UHPC免拆模板钢筋混凝土柱抗震性能参数分析及承载力计算. 建筑科学与工程学报. 2025(01): 41-50 . 百度学术
2.	王彦朋，张恒，聂晓梅，张芳芳. GFRP筋超高性能混凝土梁受弯性能有限元分析. 混凝土与水泥制品. 2025(02): 63-69 . 百度学术
3.	王朋，尤学辉，黄杰，史庆轩，陶毅，王秋维. 拼接成型UHPC免拆模板钢筋混凝土柱的抗震性能. 哈尔滨工业大学学报. 2024(01): 103-116 . 百度学术
4.	姜立春，李金柱. 倾斜矿体采空区非对称顶板-矿柱结构体协同承载机理. 中国有色金属学报. 2024(01): 329-343 . 百度学术
5.	秦朝刚，吴涛，刘伯权，王博，李寓. 预制UHPC-RAC组合梁受弯性能试验与理论计算. 复合材料学报. 2024(03): 1420-1435 . 百度学术
6.	王佳玮，孟醒. UHPC梁极限承载力计算方法研究. 城市建设理论研究(电子版). 2024(11): 78-80 . 百度学术
7.	卜良桃，刘港平. RPC应力-应变曲线系数与塑性损伤因子无量纲化计算模型研究. 工程力学. 2024(05): 120-133 . 本站查看
8.	秦朝刚，杜锦霖，吴涛，刘伯权. U型UHPC与再生混凝土组合梁受弯性能分析. 建筑科学. 2024(03): 110-120 . 百度学术
9.	许有胜，杨纪豪，夏樟华，孙康平. UHPC预制拼装综合管廊的抗弯性能试验. 福州大学学报(自然科学版). 2024(03): 353-361 . 百度学术
10.	常亚峰，尹文哲，侯亚鹏，曹小杉，师俊平，梁兴文. 超高性能混凝土预制板-叠合剪力墙抗震性能研究. 地震工程与工程振动. 2024(03): 96-107 . 百度学术
11.	孙永新，蔺鹏臻，杨子江. 考虑黏结-滑移效应的UHPC梁钢筋应力计算方法. 西南交通大学学报. 2024(05): 1058-1067 . 百度学术
12.	邓明科，姚昕，张阳玺，靳梦娜，曹继涛. 基于梁式试验的UHPC-高强钢筋搭接黏结性能. 复合材料学报. 2024(10): 5527-5539 . 百度学术
13.	孙永新，蔺鹏臻，杨子江，冀伟. 考虑黏结-滑移效应的UHPC梁裂缝宽度计算方法. 吉林大学学报(工学版). 2024(09): 2600-2608 . 百度学术
14.	李艳艳，贾会斌，赵川，武凯，刘平，苑宗双. 超低能耗建筑夹芯保温墙板受弯性能试验研究. 建筑科学. 2024(11): 9-18 . 百度学术
15.	刘祖强，任甭优，薛建阳. 高强型钢超高性能混凝土梁受弯性能试验研究及有限元分析. 工程力学. 2023(04): 102-115 . 本站查看
16.	刘晓银，曹锋. 第二类T形截面梁配筋设计的尺寸效应研究. 甘肃科技纵横. 2023(03): 59-62+87 . 百度学术
17.	王凌波，陈杰，杨永清，朱钊，孙宝林，舒灏. 双折线先张预应力高强混凝土Ⅰ型梁抗弯性能足尺模型试验. 中国公路学报. 2023(07): 169-179 . 百度学术
18.	李新星，周泉，李水生. 基于UHPC-钢筋错位连接的预制装配式混凝土梁抗弯性能研究. 混凝土与水泥制品. 2023(09): 47-53 . 百度学术
19.	赵盛杰，张运清，孙涛. 非一致性收缩徐变对小箱梁桥腹板竖向开裂的影响. 山东交通学院学报. 2023(04): 122-126+162 . 百度学术
20.	蔺鹏臻，赵鸿伟，马俊军. 铁路UHPC梁的正截面抗弯承载力计算公式及应用. 铁道工程学报. 2022(05): 33-38+72 . 百度学术
21.	蒋盛钢. 地铁车站装配式轨顶风道力学性能研究. 建筑结构. 2022(S2): 1673-1677 . 百度学术
22.	樊健生，王哲，杨松，陈钒，丁然. 超高性能混凝土板冲切与弯曲性能研究. 工程力学. 2021(04): 30-43 . 本站查看
23.	刘沐宇，赵刚，丁庆军，张强. 轻质超高性能混凝土(LUHPC)梁抗弯性能试验. 武汉理工大学学报(交通科学与工程版). 2021(03): 524-529 . 百度学术
24.	孙宗磊，杨少军，刘琛，高明昌，吕梁. 基于UHPC板和EPS耗能层的落石冲击力研究. 铁道标准设计. 2021(07): 88-92 . 百度学术
25.	韩东，凌俊. 超高性能混凝土在桥梁快速维护中的应用. 人民交通. 2020(03): 69+71 . 百度学术
26.	毕继红，霍琳颖，乔浩玥，赵云. 单向受拉状态下的钢纤维混凝土本构模型. 工程力学. 2020(06): 155-164 . 本站查看
27.	卜一之，刘欣益，张清华. 基于截面应力法的钢-UHPC组合板初裂荷载计算方法研究. 工程力学. 2020(10): 209-217 . 本站查看
28.	刘琛，陈应陶，杨少军，高明昌，王飞华. 兰张高铁十八里堡特大桥56 m UHPC组合简支梁设计研究. 铁道标准设计. 2020(11): 57-61 . 百度学术